3.1. Social-Survey Inference
As expected, the inaccessibility of the population interfered in the reasonably achieved quantitative results. Many residents were not found in their houses, and some had reasons to refuse to answer the survey, such as lack of knowledge about the problem or having an association with the mining company. This was assumed that it could happen, as these were reasons why social assessment in the mining sector has been a challenge [
22]. The social survey was not statistically significant; only 1% of the target population agreed to answer the questionnaire. Therefore, for this work, it was not possible to present a useful metric for the social criteria. Given this scenario, the few obtained results were treated qualitatively to obtain an overview of the problem, considering them as interviews.
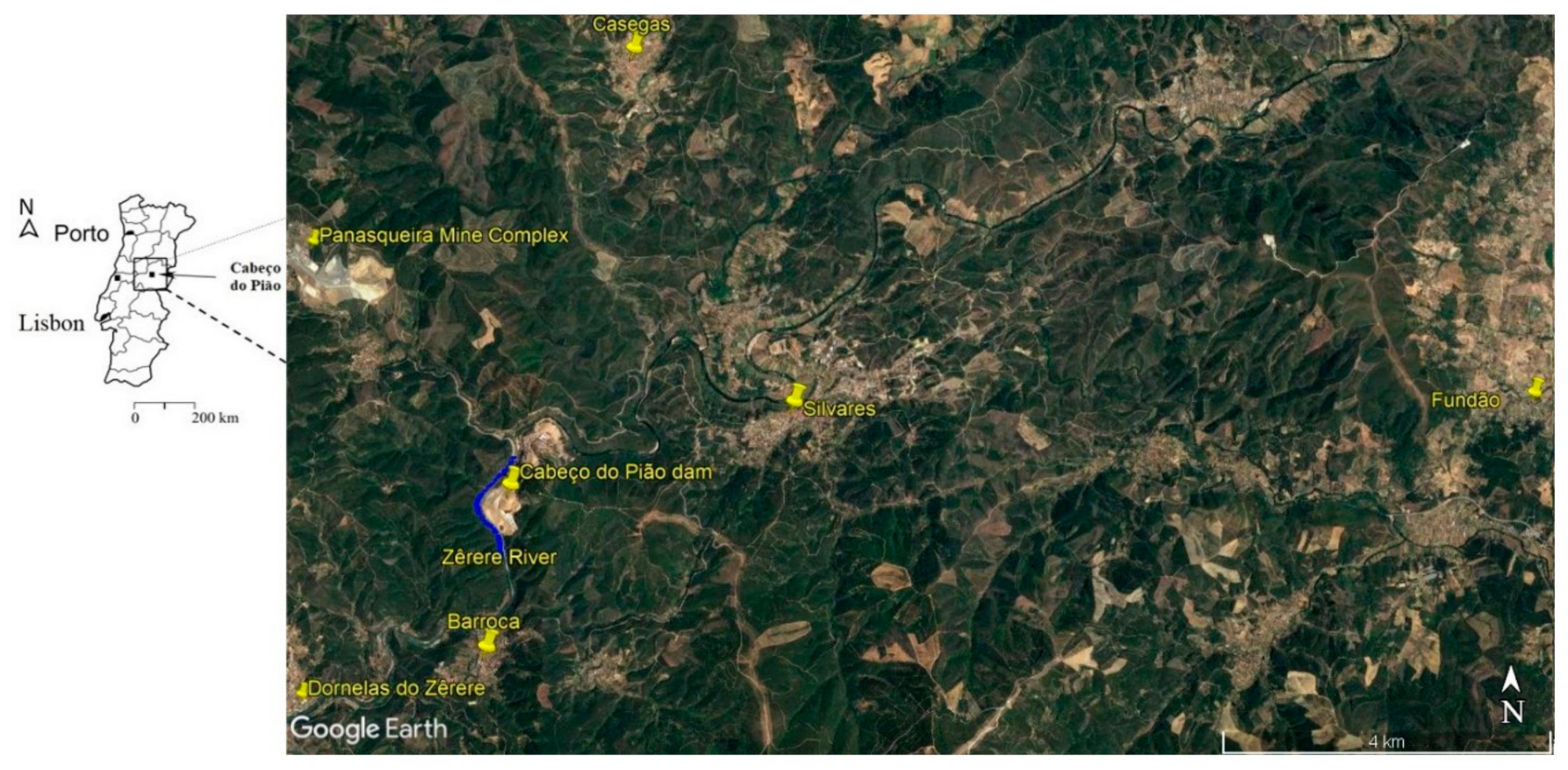
Analysis of the interviews and conversations with the locals made it possible to understand the reality of those who live nearby. According to the interviews, the degraded landscape seemed familiar, and the Cabeço do Pião dam did not seem as being at risk of rupture, or water, soil, and dust contamination to the population of the visited villages. However, since the latest dam collapses occurred in Brazil, social opinion has been changed.
3.2. Physical–Chemical Characterization
XRF analysis results on the content of the detected metals are shown in
Table 2 [
14], as well the descriptive statistics performed on the Microsoft Excel (2016)
Mean contents of the metals of interest in wt% were zinc (0.97%), arsenic (13.55%), and tungsten (0.17%).
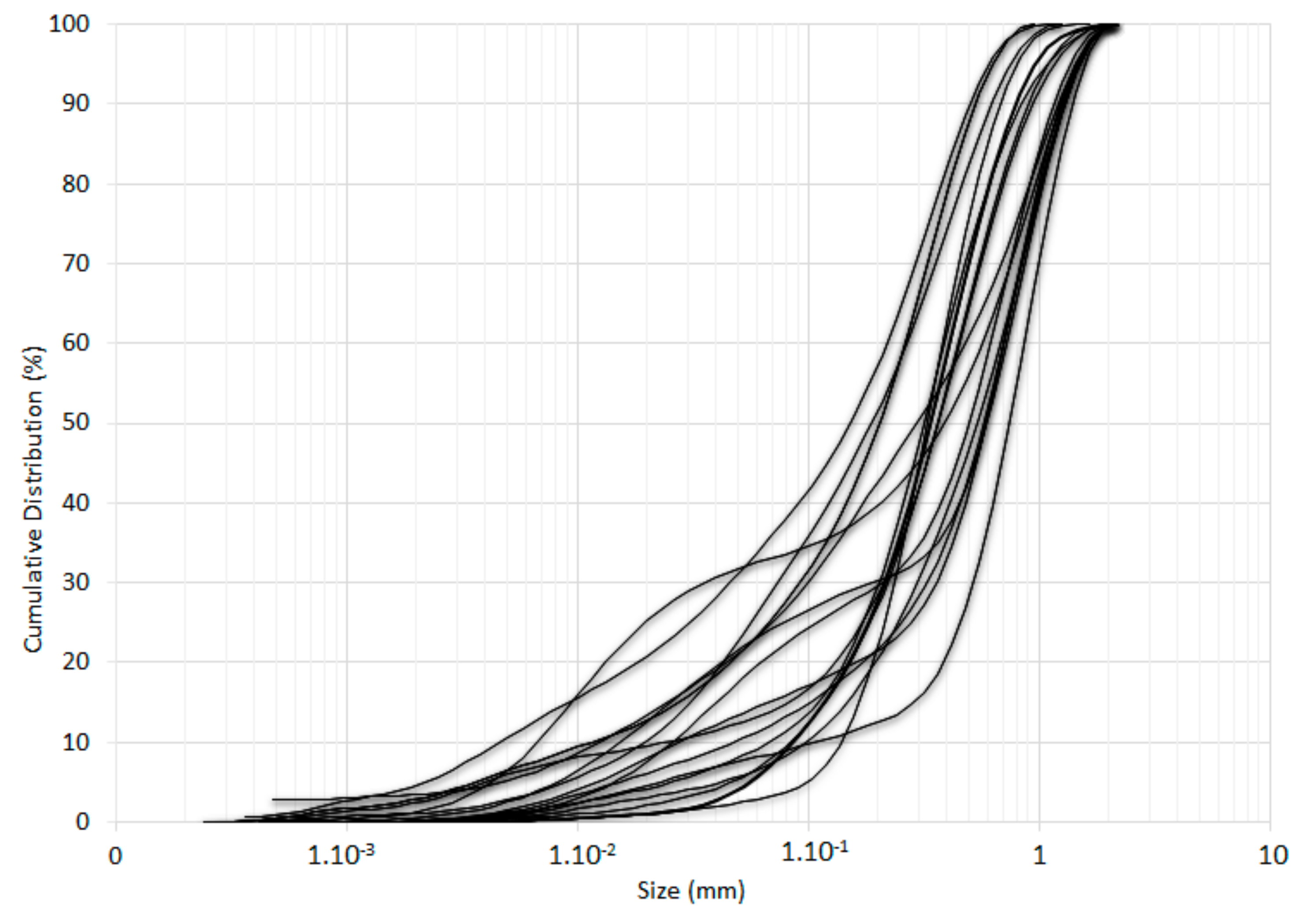
Particle-size distributions of the tailings samples from Cabeço do Pião are shown in
Figure 3.
Analysis from
Figure 3 allowed to conclude that tailings materials had particle size smaller than 1 mm. Granulometric parameter D50 was 0.36 mm on average.
Chemical analysis results of the tailings leachate are shown in
Table 3 [
23].
Analyzing the arsenic concentration in both periods, there was substantial divergence that could be explained by the different locations of the samples, the varied climatic conditions of the two seasons, or the high seasonal variability that is typical of tailings with sulfur content. These results were used in the quantitative environmental-risk analysis [
23] that permitted to conclude that the Cabeço do Pião dam has been affected in all environmental compartments.
3.3. Regression Modeling
Table 4,
Table 5 and
Table 6 present the experiment conditions and responses of zinc extraction, arsenic recovery, and tungsten extraction obtained in the stirred-tank reactor, flotation, and pressure-leaching tests, respectively.
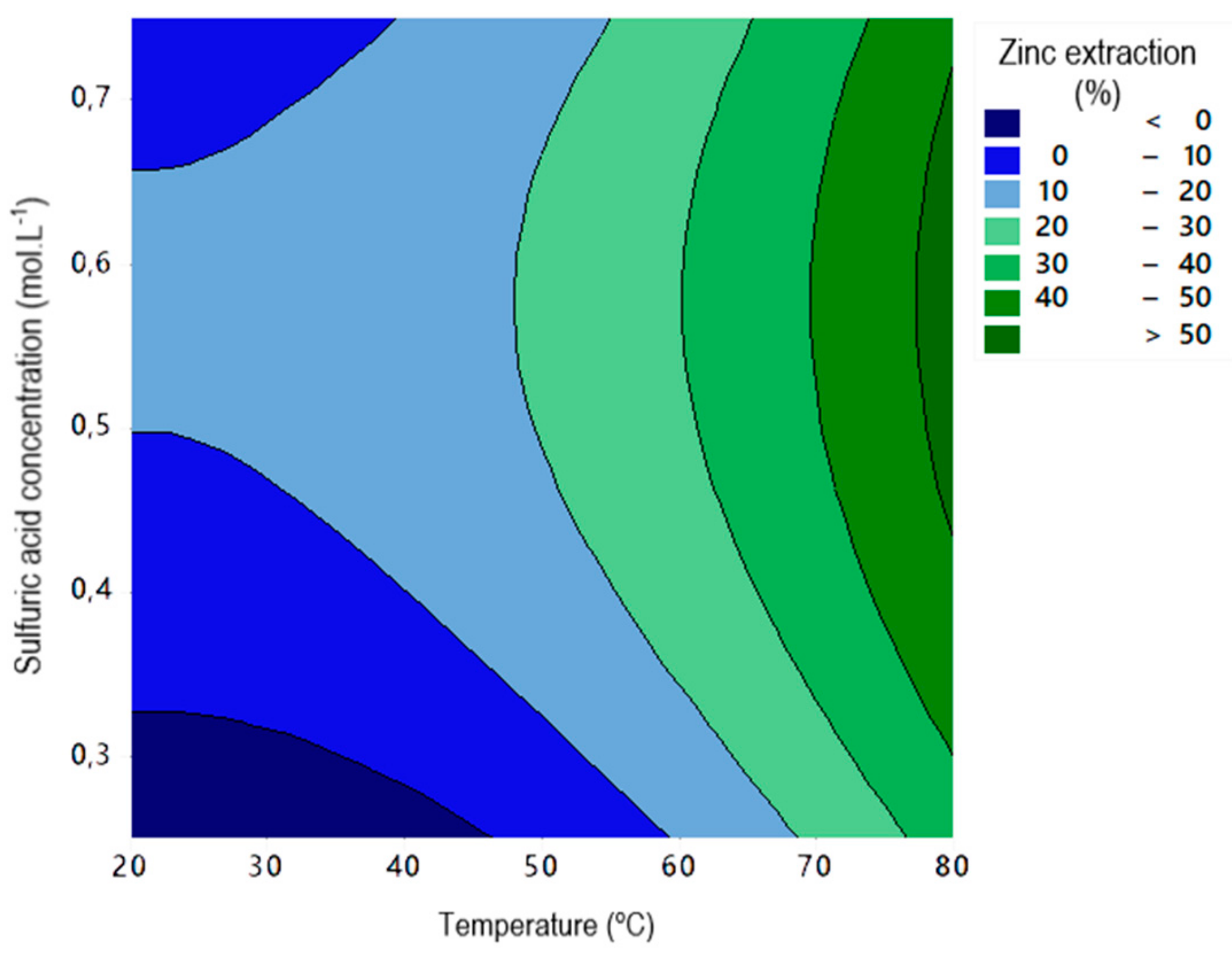
The model’s equation for zinc extraction (
y1) adjusted to experimental data are present below in Equation (2):
considering temperature (
x12) and sulfuric acid concentration (
x13) as independent variables.
For arsenic recovery, the model fitting did not achieve a statistically representative regression model with available data, so it was not possible to present it in this work. For tungsten extraction (
y2), the adjusted model was a second-order regression model as in Equation (3) below:
where pressure (
x22) and residence time (
x23) were the independent variables of y
2.
Analysis of variance (ANOVA) was performed in MINITAB, and the results are presented in
Table 7.
Analyzing the ANOVA table, for the stirred-tank reactor tests, F-value F0 = 37.79 was higher than the F distribution of Snedecor with 0.05% significance. Thus, the model had significance; p-value = 0.002 was decidedly smaller than α = 0.05, which confirmed a strong relationship between variables of temperature and sulfuric acid concentration with the response of zinc extraction. The lack-of-fit test showed a p-value 0.718 higher than the significance level, which confirmed that it did not count as evidence to reject the second-order regression model.
For the pressure-leaching model, a second-order regression model was also adjusted to tungsten extraction. The F-value of this model, F0 = 25.80, was higher than the F distribution of the Snedecor with 0.05% significance; it can be inferred that the model had significance. The p-value = 0.007 was smaller than α = 0.05, which confirmed a strong correlation between the variables of residence time with the response to tungsten extraction. The lack-of-fit test showed a p-value = 0.139 greater than the significance level, which confirmed that the second-order regression model was appropriate to represent the data.
The actual data, or the observed data from the experiment tests, which were used to compare with the predicted model values for both zinc and tungsten extraction models are shown, respectively, in
Figure 4a,b.
Considering
Figure 4a,b, the relation between the observed data and the predicted response on both models was above 95%. Usually, R
2 is used to verify the goodness of a predicted model in experimental design [
18]; however, as the data presented in this work were not set in a complete factorial design, some caution should be taken in the assessment of this parameter. In other words, R
2 values might indicate variability in the predicted model responses. Alternatively, the predicted responses of zinc and tungsten extraction were not significantly different as the observed values.
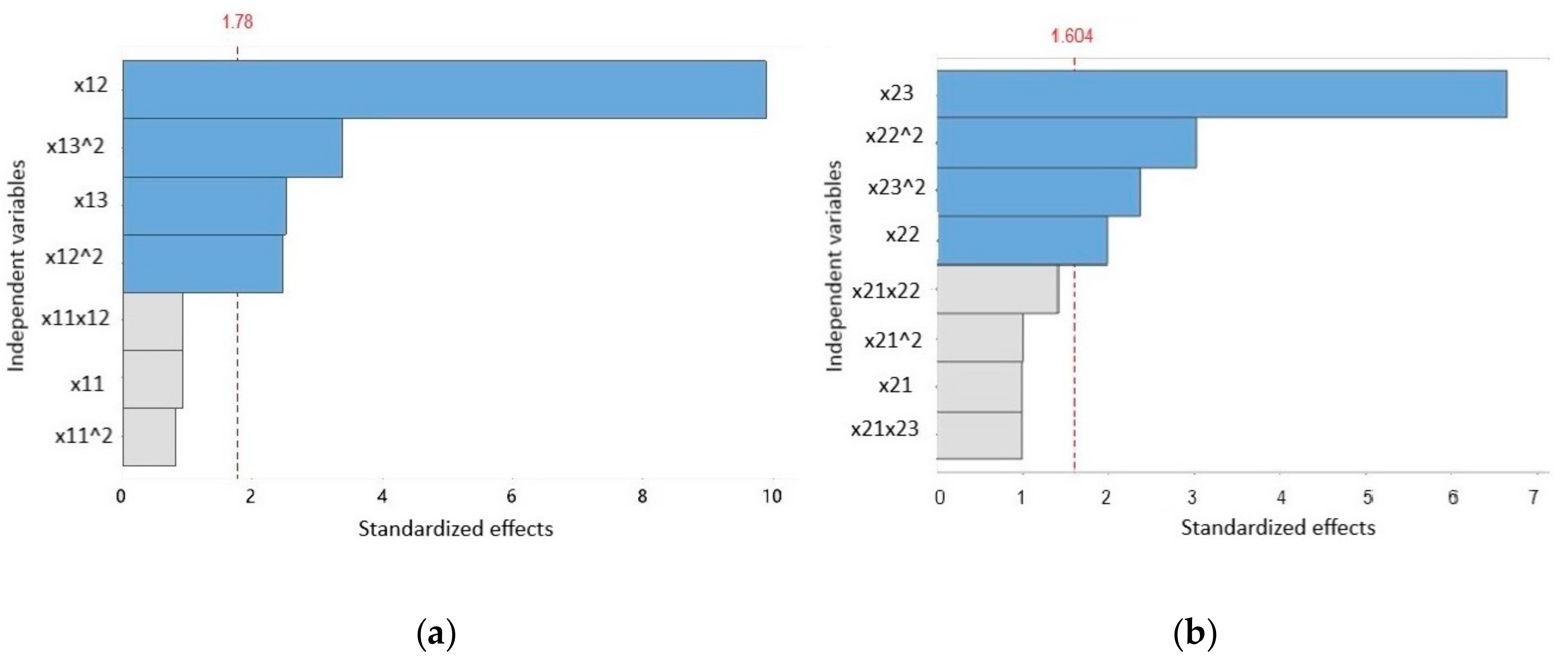
t-Student distribution examined the statistical analysis of the variable models. Then, standardized effects were plotted as shown in
Figure 5a,b for the zinc and the tungsten extraction models, respectively.
The Pareto charts with the absolute values of the standardized effects show all the effects on the response; these standardized effects are t-statistics. However, only standardized effects with values greater than the dashed line were statistically significant. In
Figure 5a, the dashed line marks the 1.78 abscissa, for a 0.15% significance level (0.925 quantiles of t-Student distribution with four degrees of freedom). The statically significant variables and interaction factors, in this case, were x
12, x
122, x
132, and x
13. The greatest variable was temperature (x
12) with t-value = 9.88, followed by the quadratic effect of sulfuric acid concentration (x
132) with t-value = −3.39. The factor of sulfuric acid concentration (x
13) and the quadratic effect of temperature (x
122) had close t-values of ≅ 2.5. According to the t-test, factors x
11 and x
112, and interaction factor x
11x
12 were not statically significant.
In
Figure 5b, the dashed line marks the 1.604 abscissa for a 0.25% significance level (0.875 quantiles of t-Student distribution with four degrees of freedom). The variables and interaction factors that were statically significant in this case were x
22, x
222, x
232, and x
23. The most important variable was residence time (x
23) with t-value = 6.64, followed by the quadratic effect of pressure (x
222) with t-value = 3.03, factor pressure (x
22), and the quadratic effect of residence time (x
232). Considering the t-test, effects x
21 and x
212, and interaction factors x
21x
22 and x
21x
23 were not statically significant, and could also be deleted from the model.
3.5. Conceptual Economic Results
The methodology for cost estimation of a re-mining project is similar but not identical to the one used for a new mine project. In capital and operating cost estimation, some parameters were not considered, and some were added, for example, existing infrastructure (roads, land, building, housing) that is available to be used. Furthermore, mining-development cost was considered as a minimum because the tailings are already exposed.
Academic software MAFMINE [
25] was employed for the assessment of capital and operating costs. In
Table 8, a summary of the capital cost estimation is presented.
The environmental costs of neo-tailings treatment and the tailings-storage facility, as well as the cost of restoration of the damaged area of Cabeço do Pião were not considered here because it lies outside the scope of this study. Operating cost estimation considers the average wage of mining-industry workers in Portugal; estimation results are shown in
Table 9.