Applications and Prospects of Muography in Strategic Deposits

Abstract

With strategic mineral exploration extending to deep and complex geological settings, traditional methods increasingly struggle to dissect metallogenic systems and locate ore bodies precisely. This synthesis of current progress in muon imaging (a technology leveraging cosmic ray muons’ high penetration) aims to address these exploration challenges. Muon imaging operates by exploiting the energy attenuation of cosmic ray muons when penetrating earth media. It records muon transmission trajectories via high-precision detector arrays and constructs detailed subsurface density distribution images through advanced 3D inversion algorithms, enabling non-invasive detection of deep ore bodies. This review is organized into four thematic sections: (1) technical principles of muon imaging; (2) practical applications and advantages in ore exploration; (3) current challenges in deployment; (4) optimization strategies and future prospects. In practical applications, muon imaging has demonstrated unique advantages: it penetrates thick overburden and high-resistance rock masses to delineate blind ore bodies, with simultaneous gains in exploration efficiency and cost reduction. Optimized data acquisition and processing further allow it to capture dynamic changes in rock mass structure over hours to days, supporting proactive mine safety management. However, challenges remain, including complex muon event analysis, long data acquisition cycles, and limited distinguishability for low-density-contrast formations. It discusses solutions via multi-source geophysical data integration, optimized acquisition strategies, detector performance improvements, and intelligent data processing algorithms to enhance practicality and reliability. Future advancements in muon imaging are expected to drive breakthroughs in ultra-deep ore-forming system exploration, positioning it as a key force in innovating strategic mineral resource exploration technologies.

1. Introduction

Strategic minerals, as the core foundation of national development, play irreplaceable roles in economic development, national security, and scientific and technological innovation [1,2,3,4]. Economically, they serve as both the backbone of traditional industries—with iron (Fe), manganese (Mn), and chromium (Cr) underpinning the global steel sector—and drivers of emerging green transitions. Lithium (Li) and cobalt (Co), critical for power batteries, accelerate electrification and reshape global economic competition. In national security, minerals like tungsten (W), molybdenum (Mo), and rare earths are vital for defense. They enable high-performance alloys and precision materials, directly influencing modern weaponry capabilities and military technological advancement [3,5]. For technological innovation, germanium (Ge), gallium (Ga), and beryllium (Be) are foundational: supporting semiconductors, 5G networks, and aerospace engineering, they determine competitiveness in digital and cutting-edge technologies [1,2,5]. Global demand for these minerals has intensified, but exploration faces mounting challenges: most high-quality deposits are already exploited, pushing exploration into deep (>500 m), complex geological settings—such as fractured terrains, thick overburden, or concealed ore bodies [6]. These environments blur surface signals, making it hard to distinguish ore from host rock, and raise costs for drilling and sampling. Addressing these challenges requires precise, non-invasive techniques to map subsurface structures—a role uniquely suited to geophysical exploration.

Geophysical exploration, as a cornerstone of mineral exploration, provides the technical means to transcend surface constraints and detect deep-seated physical property differences. Seismic inversion uses wave reflections to map subsurface structures, while gravity surveys detect density variations, and both are critical for identifying potential ore-hosting zones [7,8,9]. Electromagnetic methods exploit electrical property contrasts to invert subsurface structures, and spectral analysis enables non-destructive compositional detection [7,10]. However, traditional techniques face limitations in deep, complex settings: seismic methods struggle with resolution in highly fractured zones, gravity surveys lack precision for small-scale ore bodies, and electromagnetic signals attenuate rapidly in conductive overburden [7]. Against this backdrop, emerging technologies are gaining attention as potential solutions. Among them, “muon tomography”, which leverages cosmic ray muons’ high penetration, has moved beyond proof-of-concept. Notably, unlike potential field methods in geophysics such as gravimetry and magnetic surveys, muon tomography is inherently directional, meaning that the identification of subsurface density anomalies can be accompanied by their localization [9]. This unique attribute addresses a key shortcoming of conventional methods, offering new possibilities for addressing the limitations of conventional techniques in deep and complex geological environments. While still primarily developed in academic settings, its application in geological exploration is expanding, marking a promising shift in how we tackle strategic mineral exploration challenges.

Cosmic ray muon imaging represents a non-intrusive geophysical detection technique founded upon the penetration properties of natural high-energy muons. Muons, as a species of leptons, exhibit distinct characteristics: a relatively large mass (roughly 207 times that of an electron), remarkable penetrability (enabling them to traverse kilometer-scale rock formations), and extensive natural origins (being the products of cosmic rays interacting with the Earth’s atmosphere) [9,11,12,13]. In the realm of mineral detection, through the statistical analysis of the flux attenuation of muons subsequent to their penetration through the target object, by integrating Monte Carlo simulation with inversion algorithms, this technology is capable of constructing high-resolution 2D to 4D (including the temporal dimension) density profiles. This, in turn, allows for the precise identification of subsurface voids, ore bodies, fault zones, and other structural disparities. When contrasted with traditional geophysical methods (such as gravity and seismic techniques), cosmic ray muon imaging presents several advantages. These include a deep-detection capacity (able to explore dense rock masses located over 1000 m beneath the surface), the absence of artificial radiation sources, environmental friendliness, and the ability to conduct dynamic monitoring. To date, it has been successfully implemented in volcanic magma migration analysis, ore vein localization, and cultural heritage detection [14].

Given that strategic metal deposits, such as those containing W, Sn, Li, Be, Nb, Ta, Co, Ni, Cu, and Au, exhibit significant density differences from standard rocks and strata due to element enrichment, muon imaging technology demonstrates unique advantages in this field, leveraging its high sensitivity to density variations. When muons penetrate the strata, materials of different densities cause varying degrees of attenuation in muon flux. Ore layers rich in strategic metals, characterized by high density, induce more pronounced attenuation changes in muon flux. By capturing these subtle differences and conducting in-depth analysis of muon flux attenuation data with specialized algorithms, muon imaging technology can construct high-precision three-dimensional underground density distribution models, visually presenting the spatial locations and morphologies of strategic metal deposits [15]. This enables geologists to quickly identify potential ore veins. To fully maximize the effectiveness of this technology in strategic metal exploration, it is necessary to further explore the interaction mechanisms between muons and materials of different densities, optimize the flux attenuation model, enhance the sensitivity and resolution of muon detectors, and develop more advanced mathematical inversion algorithms. These efforts will enable more accurate and efficient exploration of strategic metal deposits [16].

Muon tomography holds significant potential for broader application across diverse fields of earth science research. However, the depth of understanding of this technology among earth scientists directly influences the breadth of its application and the direction of innovation. In view of this, this study aims to build a communication bridge between earth science and particle physics. It helps earth scientists clarify the boundaries of the technology and accurately identify needs regarding planning the research path of muon tomography. At the same time, it encourages particle physicists to develop detectors in a targeted way. Together, they can break through technical bottlenecks. It aims to construct a review system of technology popularization—example reference—application guidance for the group of earth scientists who have little experience with muon tomography.

First, in Section 1, the article traces the origin of muon tomography in particle physics, sorts out the historical context of technological development, and explains the evolutionary logic of its cross-disciplinary application from basic physics research to earth science, laying a background foundation for understanding the essence of the technology. Section 2 systematically disassembles the key elements, elaborates on the available muon flux distribution models and their adaptability in detail, deduces the energy loss equation, analyzes the solution methods and applicable conditions to reveal the interaction laws between muons and matter, compares the principles, performances, advantages, and disadvantages of various detectors to assist in technology selection, summarizes the data processing procedures and analysis methods, and refines the key steps. Section 3 positions muon tomography in geoscience practice, contrasting it with traditional techniques (seismic and gravitational) to highlight unique strengths (e.g., non-invasive 3D imaging) and use cases. Section 4 presents typical application cases in the earth science environment, covering scenarios such as strategic mineral deposit exploration and geological structure monitoring, intuitively demonstrating the application scope and practical value of the technology, and helping potential users explore suitable directions. Section 5 analyzes and explores the potential applications of muon imaging technology in mineral exploration. Section 6 addresses adoption barriers (detector limits, data hurdles, and cost gaps) and proposes solutions: detector optimization, integrated geophysical strategies, algorithm advances, and deeper muon-matter research. Finally, the content of this paper is summarized. Through the hierarchical and progressive content structure, this paper provides a complete knowledge chain for earth scientists to understand muon tomography technology, helps the implementation of interdisciplinary cooperation, and unleashes the application potential of the technology in the field of earth science.

2. Principles and Systems of Muon Imaging Technology

Cosmic ray muon imaging is a technique that leverages naturally occurring cosmic ray muons to reconstruct subsurface density structures, with particular suitability for exploring dense ore bodies against lower-density host rocks. This is because muons can penetrate deep subsurfaces—up to several kilometers—with predictable attenuation. Muons are generated by interactions between primary cosmic rays and atmospheric nuclei, reaching sea level with well-characterized properties: a flux of approximately $I\approx 1\mathrm{muon}/({\mathrm{cm}}^2·\min )$, a relativistic energy spectrum, and a regular angular distribution (peaking at vertical incidence, following a $\propto {\cos }^2\theta$ trend). When traversing materials, muons interact through two key mechanisms that underpin imaging:

• Intensity attenuation via ionization: Following the Lambert–Beer law, this creates a measurable link between muon flux reduction and material density.
• Trajectory deflection via Coulomb scattering: Deflection angles depend on the material’s atomic number Z and the muon’s momentum p, encoding structural density variations.

Specialized detection systems—including scintillator detectors, nuclear emulsion detectors, gas detectors, or Cherenkov detectors arranged in multi-layer “telescope” structures—acquire data on muon trajectories, energy loss, and timestamps. After preprocessing (trajectory reconstruction, calibration, and background subtraction), the data are processed using either of the following:

• Transmission tomography: Inverting density information by solving the linear system $\mathbf{A}\mathit{\rho }=\mathbf{L}$;
• Scattering tomography: Deriving density gradients from measured deflection angles.

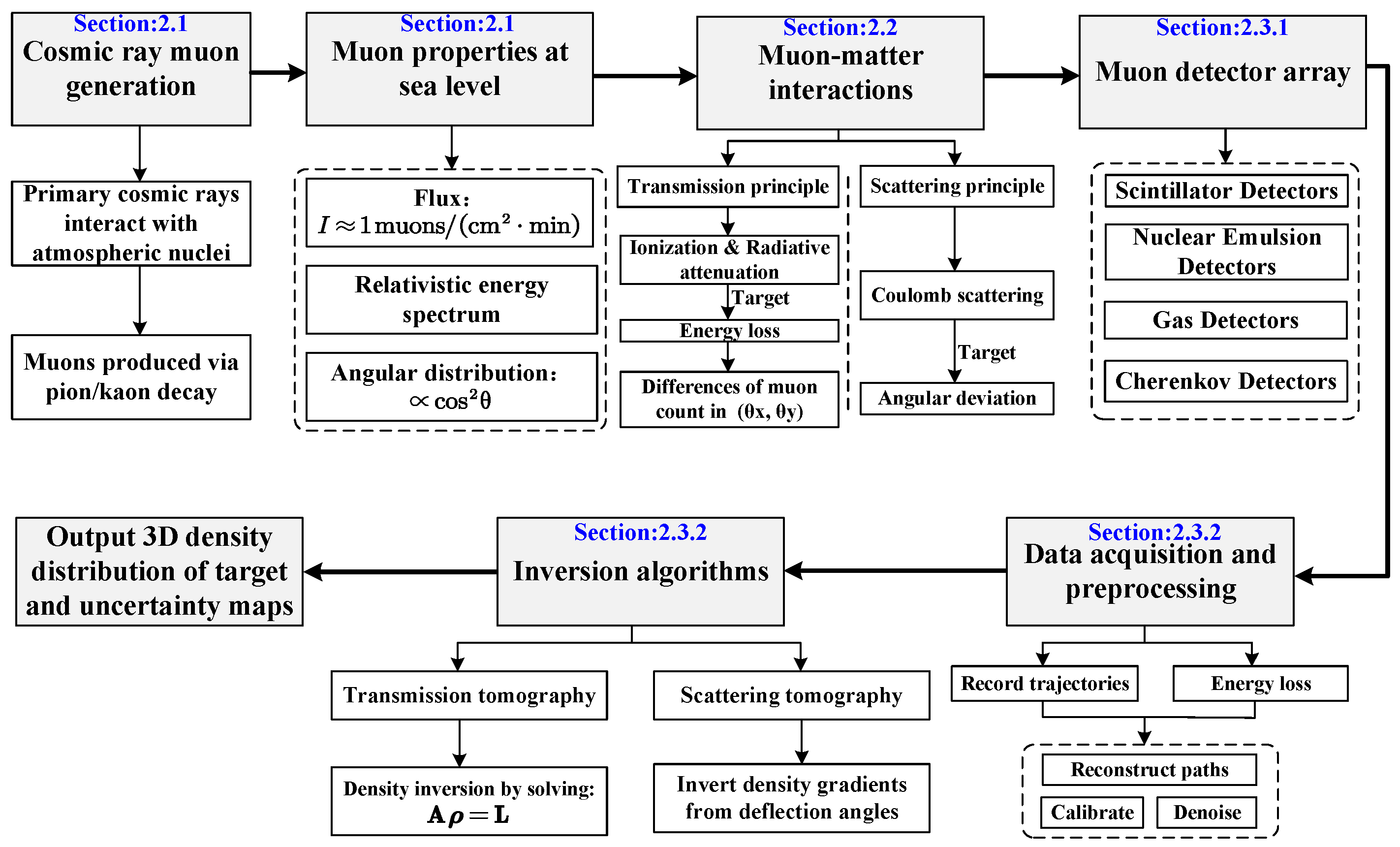
This workflow yields 3D density distributions of targets and associated uncertainty maps, forming a comprehensive framework integrating muon physics, detection technology, and data processing. For a visual overview, Figure 1 presents the framework for the principles of muon imaging technology, where the blue-highlighted sections correspond to specific chapters. Readers seeking detailed explanations of core principles—from muon interactions to inversion algorithms—should refer to the chapters linked in the figure.

2.1. Cosmic Ray Muons

Primary cosmic ray particles interact with atoms and molecules in the upper atmosphere to produce mesons (such as $\pi$ mesons and K mesons). As shown in Figure 2, the key mesons for muon tomography include charged $\pi$ mesons (${\pi }^{-}$,${\pi }^{+}$) and K mesons ($K^{-}$,$K^{+}$). The decay process of $\pi$ mesons is highly specific, with $99.99\%$ of cases producing muons (${\mu }^{-}/{\mu }^{+}$) and neutrinos (anti-neutrinos) through the following reactions:

$$\begin{array}{c}\hfill {\pi }^{+}\to {\mu }^{+}+{\nu }_{\mu }\end{array}$$

(1)

$$\begin{array}{c}\hfill {\pi }^{-}\to {\mu }^{-}+{\overline{\nu }}_{\mu }\end{array}$$

(2)

As weakly interacting particles, although neutrinos are abundantly produced in decays, they have no direct impact on muon imaging. The decay process of K mesons exhibits a cascading characteristic: approximately $67\%$ of $K^{+}/K^{-}$ mesons generate muons through direct decay channels, accompanied by the production of neutral $\pi$ mesons (${\pi }^0$):

$$\begin{array}{c}\hfill K^{+}\to {\pi }^0+{\mu }^{+}+{\nu }_{\mu }\end{array}$$

(3)

$$\begin{array}{c}\hfill K^{-}\to {\pi }^0+{\mu }^{-}+{\overline{\nu }}_{\mu }\end{array}$$

(4)

Approximately $28\%$ of K mesons first decay into ${\pi }^{+}/{\pi }^{-}$ mesons and then indirectly produce muons through the decay channels of $\pi$ mesons, which can be briefly noted as

$$\begin{array}{c}\hfill K^{\pm }\to {\pi }^{\pm }\to {\mu }^{\pm }\end{array}$$

(5)

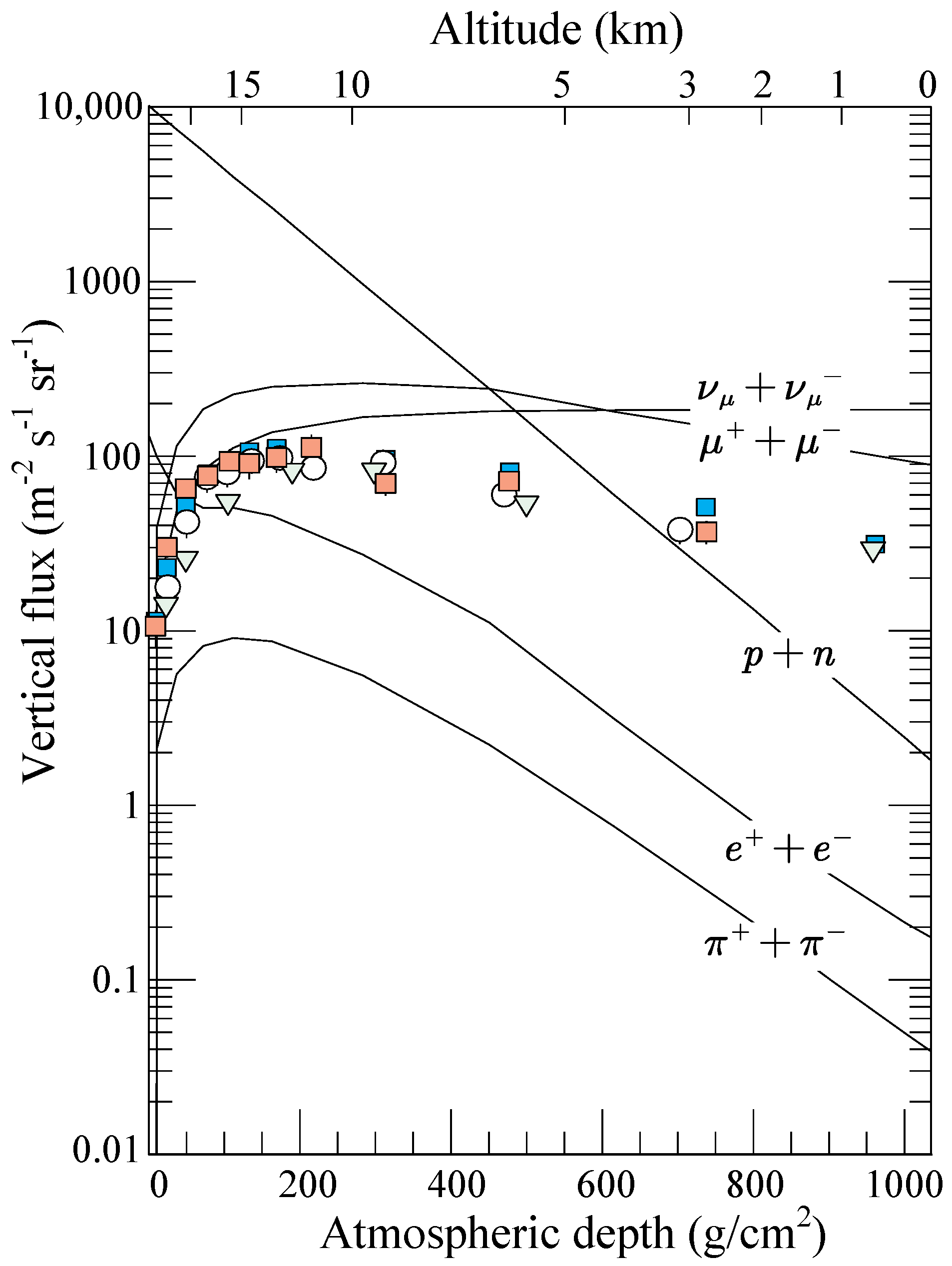
The decay products of the remaining K mesons are mostly irrelevant particles such as electrons, making no substantial contribution to muon tomography. The relationship between the vertical flux of cosmic ray particles and atmospheric depth is shown in Figure 3. It can be seen that muons are the most abundant charged particles at sea level. At sea level, the integral intensity of vertical muons with energies above 1 GeV/c is approximately 70 m⁻² s⁻¹ sr⁻¹, though recent measurements show its normalized value is 10%–15% lower. As is familiar to experimenters, this value measured by horizontal detectors is approximately in the form of $I\approx 1$${\mathrm{cm}}^{-2}{\min }^{-1}$ [17].

After clarifying the generation mechanism of incident muons, a muon flux model can be constructed to describe the characteristics of muon distribution at a specific location. This flux is jointly determined by altitude, longitude, latitude, and incident angle (i.e., the inclination angle relative to the zenith direction). In the application of muon imaging technology, the primary step is to select an appropriate muon differential flux model. This is because the natural muon flux serves as a key observable physical quantity for determining whether attenuation occurs after muons pass through a geological target. Any deviation arising from the analysis of incident muon flux will directly lead to errors in the calculation of the internal density distribution of the target. Commonly used muon flux descriptions include the Tang model (modified Gaisser model) [17,23,24], Reyna–Bugaev model [25,26], Reyna–Hebbeker model [16,27,28], and Sato model [29], among others. A demonstration of commonly used muon flux models is provided in Appendix B.

When muon decay is negligible ($E_{\mu }>100/\cos \theta \mathrm{GeV}$) and Earth’s curvature can be ignored ($\theta <{70}^{\circ }$), at sea level, the muon flux distribution can be approximated as

$$\begin{array}{c}\hfill {\displaystyle \frac{d{N}_{\mu }}{d{E}_{\mu }d\mathrm{\Omega }}}\approx {\displaystyle \frac{0.14E_{\mu }^{2.7}}{{\mathrm{cm}}^2\mathrm{s}\mathrm{sr}\mathrm{GeV}}}\times \left({\displaystyle \frac{1}{1+\frac{1.1E_{\mu }\cos \theta }{115\mathrm{GeV}}}}+{\displaystyle \frac{0.054}{1+\frac{1.1E_{\mu }\cos \theta }{850\mathrm{GeV}}}}\right)\end{array}$$

(6)

where $E_{\mu }$ denotes the muon energy, and $\theta$ is the zenith angle of the muon momentum direction. The two terms in the parentheses represent the contributions from pions and charged kaons, respectively. The coefficients 0.14 and 0.054 correspond to the normalization constants for muons produced by the decay of pions and kaons, respectively, and these parameters are obtained through experimental data fitting [17]. Studies have shown that the flux of cosmic ray muons is influenced by altitude ($\Phi \left(h\right)=\left(e^{h/L}\pm 0.003\right)\Phi \left(h=0\right)$, where $\theta$ denotes the muon flux at an altitude h (in meters), $L=4900\mathrm{m}+750\mathrm{m}{\displaystyle \frac{p}{\mathrm{GeV}}}$, and p is the muon momentum [28]), geomagnetic fields, solar activity, atmospheric temperature, and pressure [16]. Among these, the altitude of the measurement site and atmospheric temperature have a significant impact on muon flux. Therefore, in practical measurements, factors such as regional altitude and seasonal variations are considered to establish corresponding muon flux models.

2.2. Principles of Muon Imaging

The working principle of muon imaging technology is as follows: When muons from natural cosmic rays penetrate a target object, they interact with the matter inside the object. These interactions cause differences in muon energy loss, flux attenuation patterns, and trajectory deflection characteristics, which vary depending on the target’s internal structure and material composition. Muon imaging technology relies on this property to invert the internal structural information of the target by measuring and analyzing parameters such as muon energy, flux, and trajectory. From the perspective of imaging mechanisms, muon imaging technology mainly includes two types: transmission imaging (also known as absorption imaging) and scattering imaging.

2.2.1. Transmission Imaging

Transmission imaging works by statistically analyzing the flux attenuation of muons after they penetrate a target, calculating the energy loss rate using the Bethe–Bloch formula, and then deriving the material density distribution. The energy loss process of muons can be defined by a first-order ordinary differential equation [30]:

$$\begin{array}{c}\hfill -{\displaystyle \frac{dE}{dx}}=\rho \left(x\right)\times [a(x,E)+E\times b(x,E)]\end{array}$$

(7)

Here, E represents the muon energy, x is the position coordinate along the muon’s propagation path, $\rho \left(x\right)$ is the density of the material being traversed, and $a(x,E)$ and $b(x,E)$ correspond to the ionization energy loss term and radiative energy loss term, respectively:

• Ionization process: The incident muon transfers energy to the outer electrons of atoms in the material, causing electron excitation (transition to higher energy levels) or ionization (breaking free from atomic bonds). This process is reflected in the ionization energy loss $a(x,E)$.
• Radiative process: For muons traversing matter, radiative energy loss involves interactions where muons lose energy through photon emission or photon-mediated secondary processes. This includes bremsstrahlung. As charged particles, muons emit photons when accelerated, such as when deflected by atomic nuclei. It also includes subsequent photon-driven processes triggered by these emitted photons. One is electron–positron pair production: high-energy photons from muons convert into electron–positron pairs in a material’s field. Another is photon–nuclear interactions: direct interactions between muon-generated photons and atomic nuclei. Together, these interconnected mechanisms constitute the radiative energy loss term $b(x,E)$.

It is important to note that $\rho$, a, and b are all material-dependent properties, with their specific forms (such as numerical values and functional relationships) varying with the material’s chemical composition (element types and proportions) and physical state (density, temperature, etc.). For example, ionization and radiation loss characteristics differ significantly among elements (e.g., hydrogen, oxygen, and silicon) or compounds (e.g., ${\mathrm{SiO}}_2$, ${\mathrm{CaCO}}_3$), which is why precise matching of material properties is crucial in rock composition modeling. Lechmann et al. (2018) revised the energy loss for geological materials, providing energy loss calculations for several main rock types (e.g., granite, limestone, and basalt) and developing a simple method to account for these compositional differences [31], namely

$$\begin{array}{c}\hfill -{\displaystyle \frac{\mathrm{d}E}{\mathrm{d}x}}={\left\{\rho \left(x\right)\right\}}_{\mathrm{rock}}\times [{\left\{a(x,E)\right\}}_{\mathrm{rock}}+E\times {\left\{b(x,E)\right\}}_{\mathrm{rock}}]\end{array}$$

(8)

Notably, a $1\%$ increase in density difference can lead to a $3\%$ change in muon flux, a property that significantly enhances density contrast. Most cosmic ray muons have energies between 1 GeV and several hundred GeV, and their energy loss is primarily related to the density and thickness of the matter they pass through. Therefore, the attenuation of muon energy and flux can reflect the density and thickness of the matter. Based on this, by collecting muon events after they transmit through the target, calculating the flux loss, and using 3D inversion algorithms, the internal density distribution of the target can be reconstructed. A showcase of the principle of transmission imaging is made in Appendix A.

2.2.2. Scattering Imaging

Scattering imaging utilizes the trajectory deflection caused by the multiple scattering of muons with atomic nuclei, inversely reconstructing the atomic number and density of materials through the width of the angular distribution. When muons traverse matter, they undergo continuous small-angle deflections. After accumulation, the paths of muons exiting the material are distributed within a cone centered on the ideal straight line [17]. The accumulated deflection angle can be approximated by a Gaussian distribution, with its standard deviation given by

$$\begin{array}{c}\hfill \sigma (\Delta \theta )={\displaystyle \frac{13.6\mathrm{MeV}}{\beta pc}}\sqrt{{\displaystyle \frac{l}{X_0}}}\left[1+0.038ln\left({\displaystyle \frac{l}{X_0{\beta }^2}}\right)\right]\end{array}$$

(9)

Here, $\beta =v/c$ (the relativistic velocity factor, where v is the muon velocity and c is the speed of light), p is the muon momentum, l is the track length of the muon in the medium, and $X_0$ is the radiation length of the medium, defined as the average distance a muon travels to lose energy to ${\displaystyle \frac{1}{e}}$ of its original value via radiation. It is approximately positively correlated with the atomic number Z of the medium:

$$\begin{array}{c}\hfill {\displaystyle \frac{1}{X_0}}\propto {\displaystyle \frac{Z(Z+1)}{A}}ln\left({\displaystyle \frac{287}{\sqrt{Z}}}\right)\end{array}$$

(10)

When the medium consists of multiple materials, the equivalent radiation length is

$$\begin{array}{c}\hfill {\displaystyle \frac{W_0}{X_0}}=\sum _i{\displaystyle \frac{W_i}{X_i}}\end{array}$$

(11)

where $W_0$ is the mass of the medium, and $W_i$ and $X_i$ are the mass and radiation length of the i-th material, respectively. The cumulative angular deviation from multiple small-angle scatterings of muons is related to $\sqrt{{\displaystyle \frac{l}{X_0}}}$ (proportional to the number of scattering events per radiation length thickness), with the logarithmic term correcting for higher-order scattering effects. The angular deviation decreases with increasing momentum p and increases with the track length in the medium (the molecular term reflects scattering accumulation).

In summary, multiple scattering causes muon paths to bend: the higher the atomic number Z of the medium through which muons pass, the larger the deflection angle. By measuring the directional change of muons before and after they enter the medium, the internal atomic number distribution of the target can be reconstructed. Therefore, muon scattering imaging technology is suitable for high-precision imaging of small-scale targets. These include mineral deposits within rock formations that span meters to tens of meters. For such targets, the technology can characterize ore body distributions and density contrasts in detail. It does so by leveraging Z-dependent scattering patterns [32]. For instance, the technology can detect subtle Z-dependent scattering signatures to quantify the concentration of high-atomic-number ores (e.g., Fe-Cu sulfides or Pb-Zn minerals) embedded in large ore bodies with volumes up to hundreds of cubic meters. Although muon scattering is not well-suited for large-scale mineral surveys, it can be effectively employed in laboratory settings to investigate relatively small rock samples for elemental identification. In this context, “small” does not necessarily imply physically small specimens, but rather samples that are too large or dense to be analyzed using conventional techniques such as X-Ray radiography. This non-destructive approach is particularly valuable for characterizing complex ore systems where traditional drilling methods may miss localized high-grade deposits, offering a powerful complement to geophysical surveys in targeted mineral exploration.

2.3. Muon Imaging Technology

The muon imaging system consists of three components:

• Detector array: This includes plastic scintillators, gas detectors (such as resistive plate chambers, micro-structured gas detectors), and nuclear emulsions, which must meet requirements of having a large area (several square meters), high angular resolution (sub-milliradian level), and environmental stability.
• Data acquisition system: Electronic devices that convert muon events into digital signals, requiring a unique signal conversion and data readout system for the detector array.
• Data processing and inversion algorithms: Primarily used to process and analyze collected muon detector data, remove errors recorded by the detector array, organize muon incident events, analyze muon incident directions, etc., and then establish a model of the measured target through 3D inversion algorithms.

2.3.1. Detector Technology

Muon detectors are passive devices that only record the flux of cosmic ray muons naturally present at specific positions and directions. Based on the principle of interaction between muons and detectors, they can be categorized into scintillator detectors, nuclear emulsion detectors, gas detectors, and Cherenkov detectors. In terms of their arrangement structure, they are divided into planar detectors and borehole detectors.

Table 1. Comparison of different detector types for muon tomography.

Detector Type	Power Supply Requirement	Real-Time Monitoring Capabilities	Position Resolution	Cost	Volume	Field Applicability
Scintillator Detector	Yes	Yes	Moderate	Low	Standard	Rugged, anti-interference
Nuclear Emulsion Detector	No	No	Ultra-high	High	Portable	Cosmic ray interference, no real-time monitoring
Gas Detector	Yes	Yes	High	Moderate	Standard	Needs gas replacement/maintenance
Cherenkov Detector	Yes	Yes	High	Very High	Large	Difficult to maintain in field environments

1. Color coding in the table: Red = Ultra-high cost/Large volume/Low field applicability, Orange = Moderate cost/Standard volume/Medium field applicability, Green = Low cost/Portable volume/High field applicability. 2. Field applicability evaluates the suitability for on-site use, considering practical operation, environmental adaptability, and maintenance needs.

presents a comprehensive comparison of different detector types, including their power supply requirements, real-time monitoring capabilities, position resolution, cost, volume, and field applicability.

(1) Scintillator detectors

Scintillator detectors consist of a scintillator, a photoelectric conversion unit, and an electronic readout device. Charged particles excite electrons in the scintillating material (such as plastic or crystal), which release photons when de-excited. These photons are then converted into electrical signals by photomultiplier tubes (PMTs) for real-time recording. A single layer cannot record the track of particles passing through, so scintillators need to be stacked vertically and horizontally to form tight multi-layer X-Y planes for 3D track reconstruction. Scintillators are usually solid or liquid materials that can be made into various geometric shapes, such as cuboids or triangular prisms. The number of photons in a scintillator is typically small, so they cannot be directly recorded as a signal. They need to undergo photoelectric conversion and amplification to become measurable electrical signals. This is usually carried out using PMTs or silicon photomultipliers (SiPMs), which convert weak optical signals into electrical signals.

Scintillator detectors are the most widely used in muon imaging, including planar types [15,33,34,35] and borehole types [36,37,38,39], with the latter more suitable for underground mine detection tasks. For example, in planar plastic scintillator detectors, scintillator strips are placed side by side with optical isolation to form a detection surface. As shown in Figure 4, two layers of detector surfaces arranged vertically and horizontally form a 2D sensitive detection plane, and multiple 2D sensitive detection planes constitute a 3D sensitive scanning volume. SiPMs are placed on one or both sides of each scintillator strip, and the electronic readout equipment can monitor muon incident trajectories in real time and record time information. However, the detectors rely on external power supplies, and the equipment is difficult to transport and install due to heavy components, such as scintillator strips, with position resolution limited by component size.

(2) Nuclear emulsion detectors

Nuclear emulsion detectors function in a manner analogous to traditional photographic film. When high-energy muons (${\mu }^{-}/{\mu }^{+}$) penetrate the emulsion film, they engage in ionization interactions with silver bromide ($\mathrm{AgBr}$) crystals. This interaction imparts enough energy to silver ions (${\mathrm{Ag}}^{+}$) within the lattice, enabling them to break free from lattice restrictions. Subsequently, through defect migration, initial latent image centers are formed. Following development with a developer, the silver ions in the latent image are reduced to metallic silver particles, thereby creating optically discernible micro-tracks. By means of micron-level spatial resolution imaging of multi-layer emulsion films and 3D reconstruction of micro-tracks using a stereomicroscope or an automatic scanning system, a base track that traverses the entire layer can be constructed (see Figure 5b for the details). This construction facilitates the tracing of tracks and the energy analysis of incident particles.

This detector uses a passive detection architecture, enabling continuous particle recording without an external power supply. Its modular compact design gives it significant application advantages in extreme environments with limited power or narrow spaces, such as underground laboratories and polar research stations. However, it has inherent performance limitations: the lack of an electronic trigger system makes it impossible to obtain particle arrival time information, making time-resolved measurements difficult. Additionally, the complete data acquisition process involves precise preparation of nuclear emulsion materials, development and fixing in a darkroom, and automatic recognition of micro-tracks using scanning electron microscopes or high-precision optical microscopes, which is complex and time-consuming. Changes in environmental temperature and humidity can alter the physical and chemical properties of the emulsion layer, causing silver particles to aggregate or dissipate, leading to signal degradation. Despite these challenges, this technology has demonstrated unique application value in geosciences, including lithological density tomography of volcanic tops based on muon absorption characteristics [40,41,42] and 3D structural reconstruction of bedrock–glacier interfaces and erosion dynamics prediction through muon scattering analysis [43,44]; the detector is shown in Figure 5a.

Figure 5. (a) Nuclear emulsion detector designed by Nishiyama et al. (they first measured the ice–bedrock interface of alpine glaciers through cosmic muon radiography with nuclear emulsion detectors); (b) the internal structure of the nuclear emulsion detector. Reprinted with permission from [44]. Copyright John Wiley and Sons.

Figure 5. (a) Nuclear emulsion detector designed by Nishiyama et al. (they first measured the ice–bedrock interface of alpine glaciers through cosmic muon radiography with nuclear emulsion detectors); (b) the internal structure of the nuclear emulsion detector. Reprinted with permission from [44]. Copyright John Wiley and Sons.

(3) Gas detectors

Gas detectors achieve detection based on the electron avalanche effect induced by gas molecule ionization, with muons playing a direct role in initiating this process. When cosmic ray muons traverse the gas-filled gap between the anode and cathode (a two-electrode structure with an applied electric field), their high kinetic energy ionizes the working gas molecules (e.g., argon or xenon) along their path. This ionization produces electron–ion pairs: muons transfer energy to gas atoms, ejecting electrons from their orbits to form free electrons, while the atoms themselves become positively charged ions. Under the influence of the electric field, these electrons drift toward the anode, and the ions drift toward the cathode. As electrons accelerate toward the anode, they gain enough energy to ionize additional gas molecules, triggering an electron avalanche that amplifies the initial charge signal. This amplified charge movement induces a measurable current in the detector’s electrodes, with the signal amplitude and spatial distribution directly reflecting the muon’s energy loss and trajectory. Since the number of ion pairs (and, thus, the induced current) is proportional to the muon’s energy deposition in the gas—itself related to the muon’s energy and the density of the traversed medium—this mechanism enables gas detectors to register muon events with high sensitivity. This makes them particularly useful in scenarios requiring precise determination of muon incident positions and energy loss [45,46].

In muon imaging technology, drift chamber detectors are a typical application form of gas detectors [47,48]. As shown in Figure 6a, a single-layer drift chamber can only obtain 2D projection information of particles and cannot determine their movement directions. To address this, a “tracer” system needs to be constructed through spatial stacking of multi-layer structures, following a principle similar to that of scintillator detector arrays. Through the collaborative operation of such multi-layer structures, gas detectors can achieve high-precision 3D reconstruction of muon tracks, having a unique value in imaging applications with strict position resolution requirements [45,49]. However, the normal operation of these detectors relies on a stable external power supply to maintain the detection electric field, as well as a continuous, stable supply of working gas (see Figure 6b). This creates severe challenges for the system’s long-term operational stability and its adaptability to complex field environments, making it a key technical bottleneck that restricts widespread application [46,50,51].

(4) Cherenkov detectors

Cherenkov detectors achieve charged particle detection based on the Cherenkov radiation effect. When charged particles move in a medium faster than the speed of light in that medium, they excite electromagnetic radiation to produce Cherenkov photons, a phenomenon similar to supersonic shock wave effects in air. The photoelectric conversion device inside the detector is responsible for capturing these photons and converting them into measurable electrical signals.

In practical application scenarios, Cherenkov detectors achieve precise inversion of muon kinematic parameters through the precise measurement and analysis of Cherenkov light ring characteristic parameters. The geometric shape and spatial position of the light ring have a definite correspondence with the incident direction of muons, while the radiation intensity and size of the light ring directly reflect muon energy information. With this unique detection mechanism, Cherenkov detectors show extremely high detection sensitivity to relativistic particles and can simultaneously obtain the movement direction and energy information of incident particles in a single detection event. This feature makes them play an irreplaceable role in cutting-edge research fields such as energy spectrum measurement of cosmic ray muons and particle identification in high-energy physics experiments, becoming core detection equipment for related scientific research [52,53,54]. Figure 7 presents a structural schematic of a Cherenkov detector developed by Vesga et al., highlighting its modular design for radiation resistance and optical efficiency.

2.3.2. Muon Imaging Algorithms

Geophysical exploration techniques leverage the relationship between field sources and observation data to invert the distribution of physical properties within surveyed regions. In the realm of earth sciences, forward modeling entails deducing theoretical observation data from known geological parameters. Conversely, inversion employs mathematical and statistical approaches to reconstruct the spatial distribution of subsurface physical properties, including magnetic susceptibility, density, and conductivity, from measured data. In the context of muon imaging, the calculation of sensor detection information, such as muon count rates, based on a predefined target density distribution constitutes forward simulation. On the other hand, the derivation of the target density distribution from muon measurement data is referred to as inversion. Note: Based on the previous descriptions of transmission imaging and scattering imaging, transmission imaging technology is more suitable for mineral exploration. Therefore, the following text will primarily focus on the description of transmission imaging technology.

The foundation of muon imaging inversion lies in understanding muon–matter interactions. When muons pass through matter, the degree of interaction correlates with material density, composition, etc. By measuring changes in muon characteristics, the physical property distribution of the target area can be inferred. However, inversion is (mathematically) an ill-posed inverse problem, requiring the introduction of methods and constraints to stabilize the solution. The density length method is a common technique in muon imaging, originating from the principle of (A1), where L can be calculated from muon flux models, material tables, and measurement results. This has spawned various parameterized forms, such as $l_1{\rho }_1=L$ for a single material or $l_1{\rho }_1+l_2{\rho }_2=L$ for stacked materials (see Figure A1b). However, these equations are often underdetermined and require additional information to solve for parameters—for example, inferring the average density ${\rho }_1$ from a known material thickness $l_1$, or determining $l_1$ and $l_2$ from known densities and total thickness in interface detection. This method is often formulated as a deterministic inverse problem using least squares, solved via matrix equations [32,41].

Three-dimensional inversion algorithms are critical for muon imaging. Their inversion framework consists of governing equations and constraints, optimization mathematical models, and solvers. Governing equations describe the interaction between field sources and targets, establishing a mapping between measured data and target properties. Constraints incorporate prior information to mitigate the ill-posedness (multiple subsurface models can fit the same data) of imaging. Optimization models abstract the goodness of fit (e.g., target properties) into an objective function, while solvers provide iterative strategies. In practice, objective functions often combine residuals between geological model predictions and measured data with regularization (e.g., smoothing constraints, which help narrow solutions to geologically plausible ones, as used in seismic inversion) terms, minimizing them to obtain target density distributions.

To enhance performance, both local optimization algorithms (e.g., simultaneous algebraic reconstruction technique [SART] [55] and least-squares conjugate gradient [LS-CG] [56]) and global optimization algorithms (e.g., Markov chain Monte Carlo [MCMC] [57], maximum a posteriori estimation [58], and simulated annealing [52]) are used. Local algorithms offer high computational efficiency but risk being trapped in local optima, while global algorithms search for global optima but face complexity and parameter sensitivity in high-dimensional problems. Machine learning algorithms have also been applied to inversion and data analysis—for example, Tanaka et al. (2020) improved muon imaging accuracy in volcanic eruption prediction [59], and Cosburn et al. (2022) used decision tree algorithms to invert the Showa Shinzan lava dome, yielding results consistent with traditional Bayesian methods [60].

Similar to other geophysical inversion methods, muon tomography faces “ill-posedness”, and joint inversion strategies have emerged as a key solution. These integrate governing equations from muon imaging and other geophysical methods (e.g., gravity measurements) to expand the equation system without increasing the number of unknowns. Oldenburg et al. (Canada, 2012) first proposed muon–gravity joint inversion to improve result accuracy and resolution [61]. Nishiyama et al. (2014) applied it to imaging the Showa Shinzan lava dome in Japan, reconstructing conduit structures and identifying solidified magma at the top [41]. Lelievre et al. (2019) introduced unstructured (tetrahedral) meshes and density offset corrections to further develop the formulation of the joint inversion and refine applications in the Puy de Dôme volcano, France [62]. Italian research teams have proposed new concepts for optimizing model construction through triangulation techniques and back-projection techniques. Triangulation offers high-dimensional inversion efficiency but may trap in local optima, causing distant anomalies to deform. Back-projection can reconstruct anomalies from single detection points but requires anomalies to lie within the sensor’s reception range and that the distance between the sensor and anomaly is smaller than the ratio of lateral size to angular resolution [63]. Additionally, Liu et al. developed an improved “seed” algorithm by incorporating prior knowledge that identifies the approximate locations of anomalies. This algorithm has been successfully applied to large-area imaging above the roadways of the Zaozigou gold mine in China. It not only accurately reconstructed the gold ore bodies but also clearly identified the limonitized siliceous slate, which has a density similar to that of the surrounding rocks [15].

In the future, muon imaging inversion algorithms are expected to make significant progress in three areas: multidisciplinary integration, adaptation to complex geological conditions, and balancing algorithm efficiency with accuracy. These advancements will enable the algorithms to better serve practical scenarios such as geophysical exploration and geological hazard monitoring.

3. Comparison of Muography with Other Geophysical Methods

To more clearly illustrate how muography differentiates from traditional approaches in strategic mineral exploration, we summarize and further contrast its core performance metrics against key geophysical methods (seismic, gravity, and electromagnetic) using

Table 2. Comparison of key geophysical methods in mineral exploration.

Geophysical and Techniques	Muography	Seismic (Reflection)	Gravity	EM (Electromagnetic)
Estimated Physical Properties	Density ($\rho$)	Mechanical properties (e.g., wave velocities (v), density ($\rho$))	Density ($\rho$)	Electrical conductivity ($\sigma$)
Cost Structure	High initial investment (detectors); low operational cost	High (large equipment teams, data processing)	Moderate (portable instruments, large survey areas)	Moderate to high (depends on equipment scale)
Depth of Investigation	Typically 10–1000 m	Up to 10+ km	Regional (100 s m to 10 s km)	Shallow to 1–2 km
Resolution	∼1–10 m	∼5–50 m (varies with depth)	∼100–500 m	∼ 10–100 m
Acquisition Time	Variable (detector deployment + data integration); e.g., weeks for long-term monitoring	High (large teams + processing); e.g., days–weeks for complex surveys	Moderate (portable gear); e.g., days for regional coverage	Moderate to high; e.g., 1–2 ha/day (EMI)
Field Applicability Notes	Non-invasive; suits rugged/remote areas; blind zone below detectors	Limited by terrain/access; tough in urban/rugged settings	Broadly applicable; little weather/veg impact	Sensitive to conductive overburden (e.g., clay, saline soils)

. This comparison situates muography within the broader mineral exploration toolkit, emphasizing critical trade-offs in depth, resolution, and field applicability. Compared with traditional geophysical methods, muon imaging has distinct characteristics: Seismic (reflection) and electromagnetic (EM) methods can achieve greater maximum detection depths. However, within its effective coverage depth (up to 1000 m), muon imaging provides higher resolution (∼1–10 m vs. seismic’s ∼5–50 m, which varies with depth, the EM method’s ∼10–100 m, and gravity’s coarser ∼100–500 m) [64]. Muography has a longer data acquisition time (ranging from several days to weeks, far longer than the hours scale for seismic surveys). Yet, this trade-off suits it for detailed detection of deep-seated ore bodies within its effective depth range, rather than rapid reconnaissance.

A more fundamental distinction lies in the energy source: muon imaging is a non-contact, passive detection method. It does not rely on artificial excitation sources like seismic waves (for seismic methods) or electromagnetic fields (for EM methods). Instead, it solely captures muons from natural cosmic rays for imaging. Thus, in complex terrains (e.g., mountainous areas or oceans) or sensitive regions (e.g., ecological reserves), it minimizes environmental interference and damage, unlike seismic methods, which are limited by terrain/access (especially tough in urban or rugged settings) and EM methods sensitive to conductive overburden (e.g., clay and saline soils) [65].

Moreover, muon detectors demonstrate flexible deployment adaptability to terrain conditions. For ore-bearing areas in mountainous terrain (where mineralized zones are relatively elevated), detectors can be placed on the surface at lower elevations relative to the ore body. Conversely, when targeting sub-surface ore bodies (e.g., deep-seated veins), deployment requires positioning detectors in underground tunnels or mine shafts situated below the ore body depth. Coupled with long-term data accumulation, this deployment flexibility enables large-scale 3D imaging. Such capabilities make muon imaging uniquely suited for the mineral resource census stage: it rapidly delineates high-potential target areas (even in complex topographies), optimizing subsequent detailed exploration budgets by narrowing focus to viable zones. In summary, for positioning and detecting deep, high-density metal ore bodies, muon imaging, with its unique combination of resolution, passive detection mechanism, and flexible deployment, exhibits irreplaceable advantages compared to seismic, gravity, and EM methods.

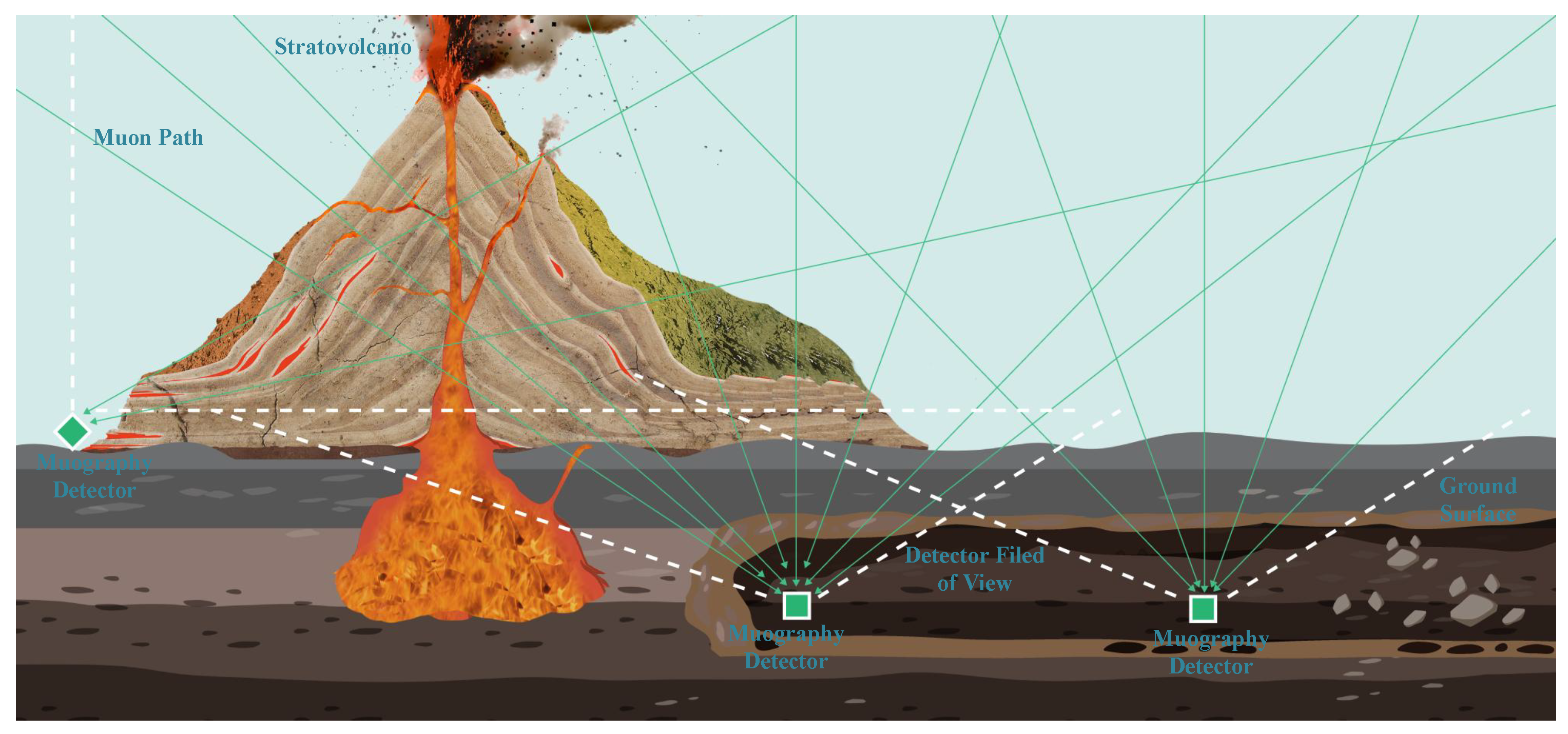
In the internal imaging of large targets, materials such as standard rocks have low atomic numbers, which results in small scattering angles for individual muons. Although cumulative angular changes do occur over a certain penetration length, these cumulative effects are generally extremely slight and have little impact on imaging. Therefore, muon scattering is typically not considered. Similarly, in mineral exploration, transmission imaging technology is more preferable. The practical application of muon imaging technology adheres to specific spatial layout principles: the object to be detected must lie within the observation interval between the detector array and the open airspace (see Figure 8). This technology requires that in underground detection scenarios, the detector system must be installable in underground areas vertically below or horizontally adjacent to the target. In specific implementations, detection devices can be adaptively deployed in various underground spatial structures, including but not limited to geological karst caves, artificial roadways, and engineering boreholes. In environments with favorable topographical features (such as layered mountain structures or open-pit mining areas), observation systems can also be established through ground-based stations [1,66].

4. Applications in Strategic Ore Deposit Exploration

In deep geological exploration, muon imaging technology utilizes the strong penetrating properties of cosmic ray muons (with an effective detection depth of up to 1000 m [32]). By accurately detecting and analyzing changes in muon flux, it realizes the fine inversion of the density distribution inside rock formations. The interaction intensity between muons and substances is proportional to the atomic number (Z) and density, which enables high-density metal deposits such as iron, copper, and rare earths to form high imaging contrast. Thus, they can be effectively distinguished from low-density surrounding rocks (such as silicate rocks), making it particularly suitable for identifying massive or layered enriched ore bodies and providing a new solution for the analysis of complex geological structures.

4.1. Deep Ore Body Localization

Muon imaging technology has been applied in geosciences since the mid-20th century, boasting a rich history of applications and notable achievements. In 1955, E. P. George and colleagues from the University of Sydney, Australia, first applied muon imaging technology in geophysics, estimating the thickness of the overburden above a roadway via muon flux [67]. In 1970, Nobel laureate Luis Walter Alvarez initiated the first exploration of muon imaging in archaeology, attempting to use the technology to locate potential hidden chambers within pyramids [68]. By 1997, E. Caffau’s team from Italy’s National Institute of Nuclear Physics used spark chamber detectors to determine the shape of a cave vault based on muon flux distribution [69]. In 2003, Hiroyuki Tanaka’s team from the University of Tokyo inferred the internal structure of a volcano using the survival rate distribution of muons passing through it [70]. In 2006, M. Menichelli’s team from Italy’s National Institute of Nuclear Physics pioneered the imaging application of borehole-type muon detectors. They used scintillating fiber detectors helically wound around a cylindrical surface, combined with inner cylindrical scintillator strips, to measure muon tracks for transmission imaging of archaeological sites in Italy. In 2011, Hiroyuki Tanaka’s team identified fault zones within a mountain using 2D muon imaging technology, with rainfall data further validating the accuracy of the imaging results [71]. In 2014, Doug Bryman’s team from the University of British Columbia, Canada, achieved the first 3D density imaging of an ore body using muon imaging technology, with imaging results highly consistent with borehole data [72]. In 2017, Ryuichi Nishiyama’s team from the University of Bern, Switzerland, first applied muon imaging technology to glacier imaging, defining the 3D structure of the bedrock–ice interface and inferring rock mass stability based on glacier melting conditions [43]. In the same year, a joint study by Nagoya University (Japan), Dassault Systèmes (France), and Cairo University (Egypt) used nuclear emulsion, plastic scintillators, and gas detectors for muon imaging inside the Great Pyramid of Khufu, successfully discovering hidden chambers of significant archaeological value and elevating the application value of muon imaging technology to new heights [73].

With continuous advancements in detection technology and computing power, muon imaging technology has seen increasingly widespread use in geophysical research. In mineral exploration, it can image the density characteristics of underground ore bodies, accurately identifying and delineating the location, scale, and structure of high-density metal deposits such as iron and copper mines.

4.1.1. Case Study: McArthur River Mine [74]

In 2017, to verify the effectiveness, 3D imaging accuracy, and applicability of muon imaging technology in deep, high-grade uranium ore exploration under complex geological conditions, research institutions from Saskatchewan, Canada, and CRM Geomatics Technology Company in Vancouver jointly conducted a field experiment at the McArthur River uranium mine. As the world’s largest high-grade unconformity-type uranium deposit, the ore body is buried at a depth of 500–640 m, mainly composed of pitchblende with an average density of 4.2 g/${\mathrm{cm}}^3$, which is significantly higher than that of the surrounding rock (2.6 g/${\mathrm{cm}}^3$). Prior intensive drilling has clarified the distribution characteristics of the ore body, providing a reliable geological reference for imaging verification.

The research team developed a compact muon detection system suitable for deep, high-radiation environments. The detector adopts a radiation-resistant scintillation crystal array, combined with a silicon photomultiplier (SiPM) readout module, with an effective detection area of 0.8 ${\mathrm{m}}^2$ and an angular resolution of less than 0.8°. It can withstand a radiation dose of 100 mSv/h and accurately capture the incident direction and track information of muons. The detection system was deployed in the horizontal roadway below the ore body, with a total of six detection points, each approximately 50 m apart. Each point continuously collected data for 3–6 months, accumulating about $5\times {10}^5$ muon data per point. Multi-azimuth observations were used to improve the accuracy of the 3D morphological reconstruction of the ore body.

As shown in Figure 9, in terms of imaging methods, a 3D density inversion algorithm was adopted, combined with a path integration model to process massive muon trajectory data. For data analysis, Monte Carlo simulation and maximum a posteriori probability estimation methods were used to construct the ore body density distribution model through iterative optimization. Meanwhile, a radiation shielding correction module was integrated to eliminate the interference of high radiation in the ore body on the detection data. The inversion results showed that the high-density anomaly area constructed by muon imaging had a consistency of over $90\%$ with the spatial distribution of the known uranium ore body. It successfully identified the extension directions of three main ore veins, and the positioning deviation of the concealed ore veins was less than 15 m. However, due to the limitations of the deep detection environment, the imaging resolution in some areas slightly decreased due to the low muon flux, indicating the importance of long-term data collection for deep ore body detection.

The success of this experiment further verified the unique advantages of muon imaging technology in deep, high-grade uranium ore exploration. It provided a new paradigm for the accurate detection of mineral resources under complex structural conditions and promoted the practical application of this technology in the field of deep resource exploration. The study also found that the accurate interpretation of the target area can be achieved through the cross-validation of data from detectors at multiple depths. In the future, to promote this technology in mineral exploration, it is necessary to develop borehole-type detectors to break through the limitations of existing mine infrastructure.

4.1.2. Case Study: Zaozigou Gold Mine [15]

To validate the feasibility, imaging precision, and engineering adaptability of muon imaging technology for exploring ore bodies with low-density contrasts under complex geological conditions, a collaborative research team from Lanzhou University and Gansu Provincial Bureau of Geology and Mineral Resources Exploration and Development conducted a muon geological imaging experiment at the Zaozigou gold deposit in Gansu Province. As a super-large gold deposit within the West Qinling orogenic belt, Zaozigou is situated at an elevation of approximately 3300 m, with total proven gold reserves reaching 142 t. The mining area hosts narrow-veined gold ore bodies and limonitized siliceous slates, characterized by minimal density differences between ore bodies and surrounding rocks (high-grade ore zones exhibit a density slightly exceeding 2.7 g/${\mathrm{cm}}^3$, while host rocks range from $2.60$ to 2.64 g/${\mathrm{cm}}^3$). Pre-existing drilling data has clarified partial geological structures, which serve as validating geological targets for imaging results.

The research team developed six muon detection systems based on plastic scintillators. Each system comprises four layers of scintillator detector panels and a data acquisition system. Each detector panel consists of 32 triangular prism scintillation strips coupled with silicon photomultipliers (Si-PMs). Two orthogonally arranged layers of detector panels form an X-Y position-sensitive detector capable of reconstructing muon tracks. The system features a sensitive area of $48\times 48{\mathrm{cm}}^2$, an angular resolution of approximately 17 mrad, and a detection efficiency of $97.98\%$. It is equipped with anti-vibration, moisture-resistant, portable, and remote monitoring capabilities, enabling adaptation to the complex mining environment. During the experiment, muon detectors were deployed in an underground tunnel at a depth of 200 m, with six deployment sites established. Each site accumulated muon data over a six-month period.

For the imaging methodology, average density information along penetration paths was derived using statistical analysis of muon survival rates across different directions, combined with path integration. To address the impact of elevation on muon flux, a simplified correction method was proposed: survival rate data at 3300 m were converted to sea-level equivalents by a scaling factor of 1.747. To address the challenge of reconstructing large-scale gold ore bodies above the roadways in the Zaozigou gold mine, a novel 3D reconstruction algorithm termed the “seed algorithm” was developed. This algorithm innovatively incorporates a user-defined “seed” mechanism: initially, these “seeds” are utilized to determine the approximate locations of anomalies, and subsequently, the morphology of the anomalies is gradually constructed and refined through layer-by-layer expansion of the “seeds”. This characteristic enables it to effectively circumvent the inversion distortion that traditional algorithms tend to exhibit when reconstructing distant or occluded anomalies, particularly avoiding stretching distortion along the observation direction, thereby significantly improving the detection accuracy in large-area regions.

As shown in Figure 10, the inversion results demonstrated that muon imaging successfully reconstructed low-density contrast gold ore bodies (density > 2.7 g/cm³), limonitized siliceous slates (density 2.53 g/cm³), and four goafs (including uncompacted backfill zones). These results showed good consistency with drilling data and known geological information. Specifically, reconstructed gold ore bodies were continuously distributed above the tunnel, and potential larger-scale ore bodies were identified. The discovery of goafs provided critical insights for mine safety. However, due to constraints in detector deployment positions, imaging details in certain areas require further optimization.

This experiment marks the first application of muon imaging technology in exploring low-density contrast ore bodies, validating its applicability in complex geological environments. The proposed elevation-correction method and seed algorithm enhance the practicality of the technology, providing a new tool for mineral exploration that considers economic, scientific, and safety aspects and advances the development and application of muon imaging technology.

4.1.3. Case Study: Temperino Mine [11]

In 2018, a research team consisting of institutions such as the University of Florence, the University of Perugia, and the National Institute for Nuclear Physics (INFN) in Italy conducted a study on cavity detection using muon imaging technology at the Temperino mining area in Livorno, Italy. The mining history of this mine dates back to the Etruscan era, with mining activities continuing until 1973, and it has now become a tourist attraction. A large number of historical tunnels and cavities remain inside the mining area, making this research not only of archaeological value but also supportive for safety assessment work, such as ensuring tourist safety.

The project utilized a MIMA muon detector for measurements. The detector is a cubic device with a size of approximately $50\times 50\times 50{\mathrm{cm}}^3$, containing six layers of orthogonally arranged detector panels (each detector panel consists of 21 triangular plastic scintillator strips, with an effective area of $40\times 40{\mathrm{cm}}^2$). It has a position resolution of 1.6 mm and an angular resolution of about 7 mrad, suitable for deployment in narrow spaces with low power consumption. The measurement points were selected in the tourist passage within the mine, with a total of three points, and the detectors were placed horizontally to observe the target area. The target mining area is mainly a skarn deposit containing copper–iron–zinc–lead–silver sulfides, where the skarn is distributed in marble in a nearly vertical form. There are multiple horizontal tunnels and unmapped cavities in the mine. In the experiment, the known “Gran Cava” cavity (approximately 40 m long, 6–7 m wide, and 6–7 m high) was used as a verification object.

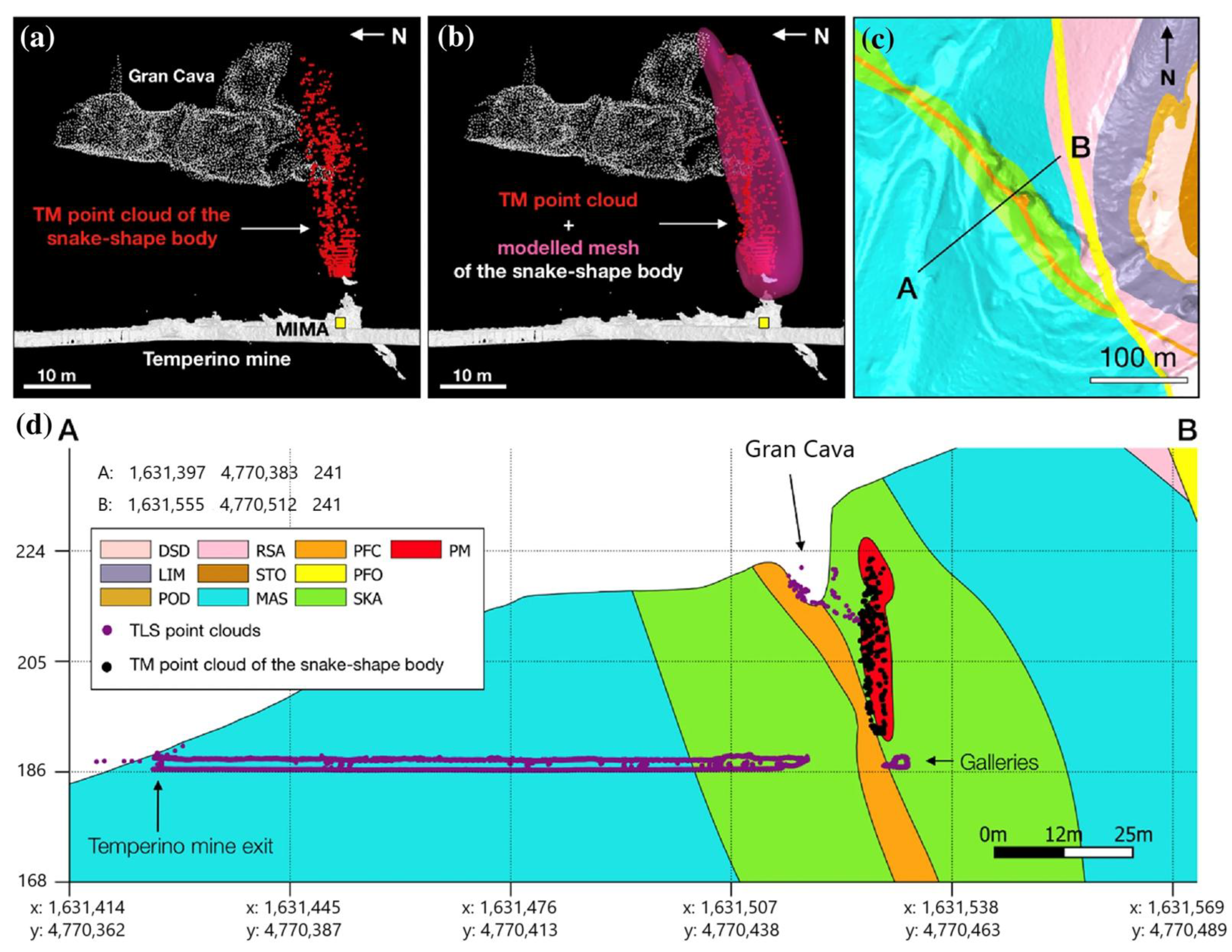
As shown in Figure 11, the research combined muon flux data from the three points and located the cavities through the cone intersection of low-density areas. It successfully identified the Gran Cava and two unknown cavities (A and B). However, due to the close spacing between the points, there was vertical stretching distortion in the results. Compared with the laser scanning results, the 3D morphological difference of the Gran Cava was less than 1 meter, and the thicknesses of the Gran Cava (12–14 m thick), cavity A (8 m thick), and cavity B (6 m thick) were successfully estimated.

This case verified the effectiveness of muon imaging technology in detecting hidden cavities in complex mining environments. The research not only provides a reliable method for discovering unmapped cavities but also offers references for non-invasive detection in the fields of archaeology, geology, and civil engineering. Future plans include conducting more measurements in this mine and adjacent mines to assess safety risks in tourist areas (such as radon infiltration).

4.1.4. Other Cases

Information theory-optimization methods distinguish random errors in muon counts from real geological features, nearly doubling detector sensitivity to discriminate regions with subtle bulk density differences—such as monitoring ∼1% density changes in CO₂ storage reservoirs. This provides technical support for low-contrast scenarios, including density characterization of Li, Be, Co, Ni, and Cu deposits and surrounding rock formations in deep mines [75]. Sub-pixel signal analysis techniques further enhance the spatial resolution of muon imaging, breaking through the physical limitations of traditional detectors and laying the foundation for high-precision imaging of deep rare earth ore bodies [76]. Combined with auxiliary methods like laser scanning and UAV photogrammetry, technical improvements in muon imaging optimize 3D modeling accuracy, advancing the practical application of muon imaging in mineral exploration [77].

These cases show that muon imaging technology is gradually moving from the experimental stage to engineering applications. Its distinct advantages in deep ore body localization, goaf monitoring, and complex geological modeling have the potential to bring new developments to the technical framework of traditional mineral exploration.

4.2. Transformation of Exploration Models

Muon imaging, with its non-invasive advantage, can acquire subsurface density information within a certain depth range (typically several hundred meters). For deep mineral exploration, this provides a new approach to discovering hidden deep-seated ore bodies. Compared with traditional deep exploration methods such as drilling, muon imaging enables large-area scanning of deep regions without damaging subsurface structures. It can preliminarily determine the location of potential ore bodies and provide more precise targets for subsequent operations like drilling, thus reducing exploration costs and risks. However, muon imaging can only detect areas above the horizontal elevation of the detector and faces the issue of non-uniqueness in inversion results. Therefore, the joint inversion of muon imaging data with other types of geophysical data, leveraging the complementarity between datasets to strengthen constraints on subsurface structures while incorporating prior information and regularization techniques, has become key to overcoming these limitations. This approach can effectively reduce non-uniqueness and enhance the reliability of inversion results.

Existing research has preliminarily verified the potential of joint inversion of muon data with other geophysical data. For example, in a synthetic model of the Puy de Dôme volcano in France, the joint inversion of gravity data (which is also sensitive to density) and muon data was able to reconstruct the 3D density structure of volcanic formations more accurately than independent density inversion, significantly improving inversion robustness [32,62]. Seismic data (P-wave and S-wave velocities), although widely used in geological research, are coupled with parameters such as density and elastic constants, making it difficult to accurately extract key information such as formation mechanical properties. The direct density distribution provided by muon imaging, combined with the petrophysical relationship between density and elastic wave velocity, enables the joint inversion of seismic and muon data to overcome the problem of parameter coupling. Kodama et al. further confirmed the advantages of this joint inversion approach in reconstructing density and related parameters through comparisons of synthetic models [78].

The integration of muon imaging with various traditional geophysical techniques can achieve more comprehensive subsurface exploration through the complementarity of multi-physical fields. Different techniques target different properties based on unique physical principles. For example, muon imaging focuses on density distribution; gravity exploration reflects changes in the gravitational field caused by density differences; magnetic methods identify magnetic minerals; electromagnetic exploration detects differences in electrical properties; and remote sensing provides macroscopic regional information. This multi-source data fusion can capture subsurface features from multiple dimensions. For instance, after gravity exploration identifies a region with density anomalies, muon imaging can further refine the density distribution within that region. This helps determine if the region constitutes an ore body, enabling mutual verification and supplementation of data and significantly improving the accuracy of deep mineral exploration.

Mineral exploration increasingly demands innovative methods that balance efficiency, accuracy, and environmental sensitivity. The AGEMERA project has introduced three advanced non-invasive geophysical technologies: muon imaging, ambient noise seismology, and drone-borne electromagnetic (EM) surveying [1,79,80]. Each of these methods makes unique contributions to understanding subsurface features and improving mineral exploration practices [81]. Ambient noise seismology uses naturally generated vibrations to create high-resolution structural models of the subsurface, being particularly effective in shallow to moderate-depth regions [82]. Meanwhile, drone-borne EM surveying enables rapid and extensive assessment of subsurface electrical conductivity, facilitating efficient exploration over large areas [1]. These methods are not standalone solutions but are most effective when applied in conjunction. Their combined advantages enable a comprehensive exploration approach: muon imaging excels at imaging deep, dense structures; ambient noise seismology adds precision to near-surface structural mapping; and EM surveying helps quickly identify conductivity variations across different regions. In this project, three different advanced geophysical methods are employed in a complementary manner, which significantly enhances the accuracy of underground resource assessment. Meanwhile, the environmental impact is minimized, aligning with the sustainable development goals of the European Union [1].

In summary, the joint inversion of muon imaging and geophysical data is a notable innovative direction in deep mineral exploration. Its core advantage is using the density information provided by muons as a link to help mitigate the challenges of parameter coupling and inversion non-uniqueness in traditional techniques. Through the complementary constraints of multi-physical field data, it can enhance the accuracy of ore body localization and exploration reliability to a certain extent. From the characterization of ore body morphology and fracture zones in practical exploration to the synergistic application of multiple technologies, joint inversion has shown clear value. That said, it currently faces technical challenges such as the optimization of prior parameters and the removal of background signals from data. With the continuous improvement of methods, it has the potential to become an important technology that balances exploration efficiency, accuracy, and environmental sensitivity, contributing to the advancement of deep mineral resource exploration.

5. Application Analysis of Muon Imaging Technology in Strategic Mineral Deposits

Muography, a novel imaging method utilizing natural cosmic ray radiation to characterize and monitor changes in the average material density of objects, demonstrates multi-faceted application potential in mineral exploration.

5.1. Identification and Detection of Ore Bodies

Muons in cosmic rays are generated when high-energy cosmic rays interact with the atmosphere. These muons exhibit strong penetrability, capable of traversing solid materials such as rocks. When muons pass through substances with different densities, their flux changes: higher density leads to greater muon flux attenuation. By deploying muon detectors on the surface or underground to measure changes in muon flux, the density distribution of subsurface materials can be inverted, enabling the identification of ore bodies with distinct density characteristics.

Different rock types, such as laterite, saprolite, bauxite, and fresh rock, exhibit density variations that cause differential muon attenuation. This is particularly evident in bauxite exploration: even with a modest bulk density contrast (0.3–0.4 g/${\mathrm{cm}}^3$) relative to surrounding rocks, muography can locate bauxite deposits and characterize their shape, structure, depth, and thickness. A case in point is the Jajce–Poljane area of Bosnia and Herzegovina, where muographic measurements from an underground adit (guided by borehole data) successfully imaged a known bauxite lens overlain by ∼50 $\mathrm{m}$ of limestone. The survey delineated the lens’s uppermost (1072 m) and lowermost (1062 m) extents, confirming that such subtle density differences are detectable via muography [83]. Similarly, in skarn deposits, density differences between various skarn types and their adjacent host rocks render cosmic ray muography applicable for mineral exploration and resource delineation [11].

5.2. Monitoring of Rock Mass Changes

Based on the rock mass density distribution obtained through muon imaging, rock masses can be evaluated and classified, and rock failure and deformation can be monitored. High-quality, intact rock masses typically exhibit relatively uniform and high density, while fractured or heavily weathered rock masses have lower and uneven density. By analyzing muon imaging data, a quantitative assessment of rock mass quality can be achieved, providing a basis for formulating mining plans—such as determining areas suitable for large-scale mining and those requiring special support measures. During mining, rock mass fracturing and deformation cause temporal changes in average material density. Muography can monitor such changes by continuously measuring alterations in muon flux in specific areas, enabling timely detection of internal structural changes and providing early warnings for safe mining. For instance, if a rock mass in a certain area fractures, its density changes, and the resulting muon flux variation is captured by detectors, allowing staff to assess rock mass stability [84].

In addition, water accumulation and flow within mineral deposits pose significant hazards to mining operations, including potential water inrush accidents, rock mass instability due to saturation, and corrosion of mining infrastructure. Muon imaging can detect water-related risks by leveraging the distinct density and atomic number contrast between water ($Z=8$) and rock formations. For example, aqueous zones exhibit lower muon attenuation due to their lower atomic number and density, creating distinguishable flux patterns in muon transmission maps [85]. This capability is critical for avoiding catastrophic water inrushes, particularly in deep mines or regions with complex hydrogeological conditions, where muon imaging provides non-invasive, time-sensitive insights into subsurface water dynamics to enhance mining safety.

5.3. Detection of Geological Structures and Weak Zones

Mines contain various geological structures (e.g., faults and folds), which influence ore body distribution and mining safety. Muography can detect these structures due to density differences between geological structure zones and surrounding rocks. For example, fault zone rocks may exhibit density variations from intact rock masses due to fracturing and filling, leading to distinct muon flux changes as muons pass through, which can be identified by detectors. This helps geologists accurately map geological structures, providing critical information for mineral exploration and mining planning [84,85]. In addition to geological structures, mines may contain isolated weak zones prone to collapse. Muography can scan underground areas to identify these low-density weak zones, enabling proactive measures such as reinforcement or avoidance to ensure worker safety and smooth mining operations [86].

5.4. Application in Tunnel Boring

During tunnel excavation for strategic mineral mining, potential obstacles such as aquifers or boulders may lie ahead. By deploying muon detectors in tunnels to scan the forward rock mass, muon imaging can detect these hazards. For instance, the density difference between the water content in an aquifer and rock causes distinguishable muon flux changes, allowing workers to prepare waterproofing measures in advance. The detection of boulders enables timely adjustment of tunneling plans to avoid equipment damage and construction delays [84,85].

This capability aligns with the characteristics of muography outlined in [87]: as a geophysical remote imaging method leveraging cosmic ray-induced muons, it can identify density variations in subsurface structures ranging from meters to kilometers. Compared to seismic methods, it avoids interference from reflections at geological interfaces, making it well-suited for tunnel hazard detection. Its high sensitivity—capable of detecting density variations as small as 1%–2% at a depth of 100–150 m—further supports the accurate identification of aquifers, boulders, or even post-collapse rock mass changes. Practical applications include installing detectors on tunnel boring machines and using nearby undamaged tunnels or boreholes for monitoring when needed.

5.5. Monitoring of Collapsed Bodies and Location of Residual Ore

In caving-based mining operations, the morphology and internal structure of caved bodies undergo temporal evolution. Muography enables quasi-real-time monitoring of average material density changes in caved bodies, with data acquisition typically requiring hours to days of integration. This monitoring provides insights into compaction degrees and void distributions, guiding subsequent mining strategies. For example, large voids within a caved body may indicate potential for residual ore recovery, though real-time feedback is constrained by muon flux limitations [84,85].

By continuously monitoring caved bodies and comparing muon imaging data with pre-mining geological models, it is possible to infer the locations of residual ore. The density disparities between residual ore and the surrounding caved rocks are manifested as distinguishable features in muon images. This enables precise positioning, which in turn enhances ore recovery rates and minimizes resource waste.

5.6. Potential in Deep Mineral Exploration

Although muon flux decreases rapidly with increasing penetration depth, muography can still acquire subsurface density information within a certain depth range (typically several hundred meters). For deep mineral exploration, this offers a new approach to detect hidden deep-seated ore bodies. Compared with traditional deep exploration methods (e.g., drilling), muography is non-invasive, allowing large-area scanning of deep regions without disturbing subsurface structures. This helps preliminarily identify potential ore body locations, providing precise targets for subsequent drilling and reducing exploration costs and risks.

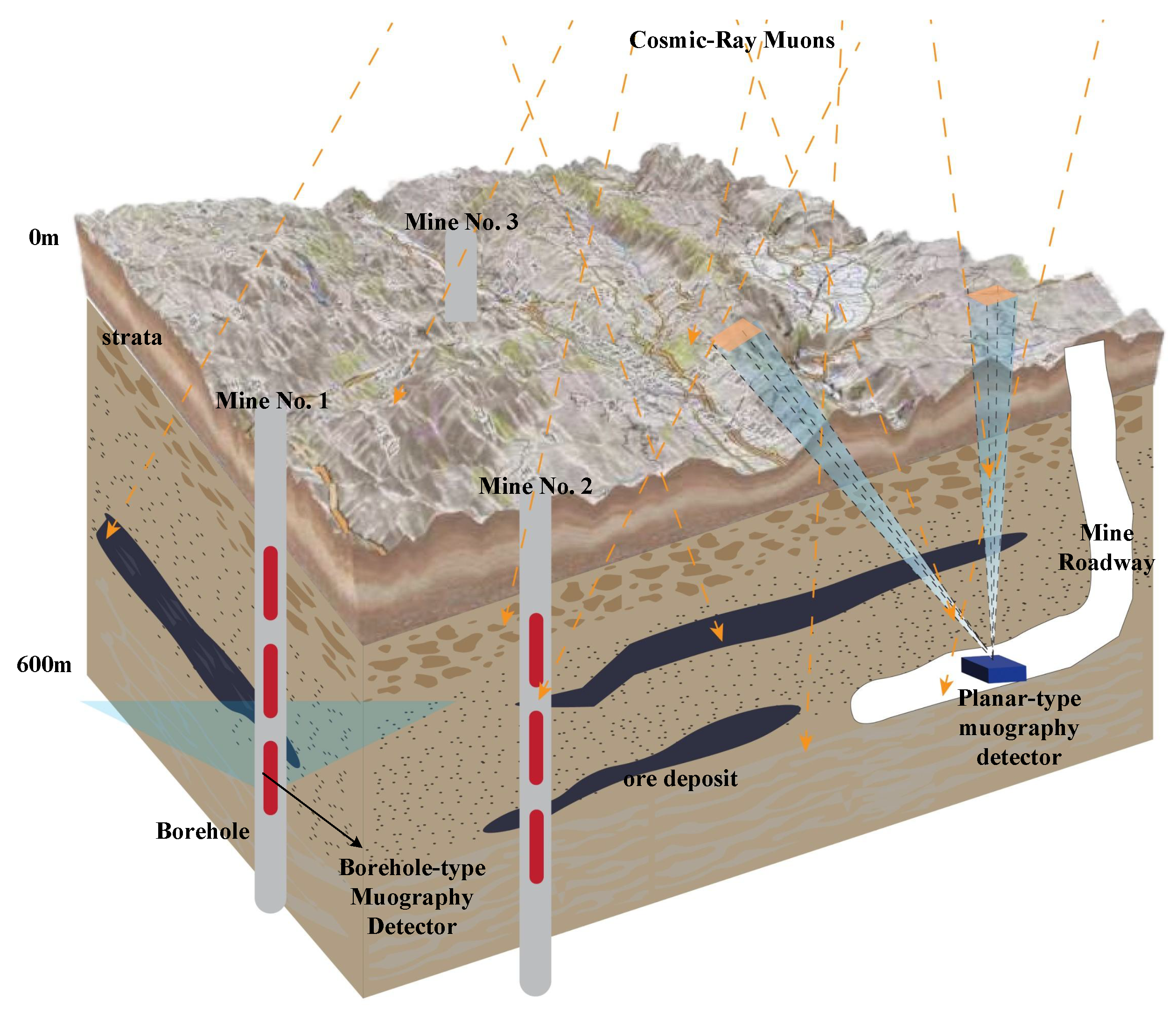
In the exploration of deep-seated underground mineral resources, planar-type muography detectors and borehole-type muography detectors can form a three-dimensional detection system to unleash their synergistic potential. As shown in Figure 12 below, the planar-type muography detectors are deployed in underground roadways. Leveraging their planar-type detection advantages, they scan large-scale areas, capture the attenuation and scattering information of cosmic ray muons when passing through different geological bodies, outline the macroscopic geological structure contours, and delimit large-scale target areas for mineral prospecting. The borehole-type muography detectors go deep into boreholes. Utilizing the vertical channels of the boreholes, they accurately detect the geological details in small-scale and specific-depth deep areas, obtain information such as the local rock layer density and the occurrence state of ore bodies, and make up for the deficiency of planar detectors in fine deep detection [88]. The two types of detectors cooperate: the planar ones provide macroscopic layout guidance, and the borehole-type ones focus on precise characterization of deep areas. From the plane to points, and from macroscopic to microscopic, they synergistically analyze the underground geological structure. This helps improve the detection accuracy of the occurrence position, shape, and scale of deep-seated mineral resources, and facilitates the efficient exploitation of such resources. It also provides more powerful and accurate technical support for mineral exploration, breaking through the detection bottleneck of deep-seated mineral prospecting. Ultimately, this expands the depth and breadth of mineral exploration.

In summary, muography holds broad application prospects in mineral exploration as a non-invasive, large-scale method for acquiring subsurface density information, enhancing exploration efficiency and accuracy, and carrying significant implications for future mining development. However, its current application in mineral exploration remains limited, and the technology is still in a stage of development and improvement, requiring further research and practice to promote its widespread use in this field.

6. Technical Challenges and Solutions

6.1. Technical Challenges

Although muography holds potential in mineral exploration, its widespread application currently faces multiple technical bottlenecks and challenges:

(1) Limited spatial resolution: The resolution of muon imaging is constrained by detector size, muon flux, and reconstruction algorithms, with typical resolutions ranging from meters to tens of meters. This makes it difficult to identify small-scale ore bodies (e.g., thin veins or low-grade mineralized zones). For detailed exploration stages requiring fine-scale characterization of ore body morphology, integration with borehole CT or ultra-high-resolution geophysical methods is necessary [89].

(2) Limitations in real-time imaging performance: Cosmic ray muon flux is low (≈$1\mathrm{muon}/{\mathrm{cm}}^2/\min$ at sea level), necessitating hours to days of data accumulation for high-fidelity imaging. This restricts true real-time applications (e.g., immediate guidance for mineral extraction), but quasi-real-time monitoring (with delayed feedback) remains feasible for gradual structural change detection. For instance, in the case studies of deep mining areas with muon detection depth, as discussed in Section 3, the exploration time for each project was approximately 3 months, which further illustrates the practical time requirements of muon imaging in actual mineral exploration scenarios [11,15,74].

(3) High data processing complexity: Muon trajectory reconstruction, background noise rejection (e.g., other particles in cosmic rays), and 3D inversion require sophisticated algorithms and high-performance computing, imposing strict hardware and software demands. Currently, few commercialized processing platforms exist, with most relying on self-developed solutions by research teams, limiting technology popularization [15].

(4) High costs and deployment difficulties: High-sensitivity muon detectors (e.g., systems based on nuclear emulsions, gas detectors, or scintillator arrays) incur extremely high R&D and manufacturing costs. Additionally, their large size (requiring detection areas of several to hundreds of square meters) and complex mechanical support and power supply needs for field deployment (e.g., mountainous regions and underground mines) hinder large-scale application [36,44,50].

(5) Inadequate detection capability for low-density ore bodies: For low-density non-metallic minerals (e.g., coal, salt deposits, and non-metallic minerals), the weak interaction signals between muons and materials result in low imaging contrast, limiting applicability. Such deposits are more suitable for traditional methods like seismic waves or resistivity surveys [32].

6.1.1. Detector-Related Challenges

(1) Portability and power consumption: Underground muography requires detectors to operate in non-laboratory environments, demanding portability and low power consumption. Current detector systems, however, are bulky and power-intensive, making flexible deployment in diverse terrains and complex environments difficult. For example, in mountainous areas, surveyors must carry heavy equipment over long distances, increasing operational difficulty and costs. In regions without stable power supplies, high-power devices cannot operate continuously, limiting survey duration and scope.

(2) Detector accuracy and resolution: High sensitivity and resolution are critical for accurately identifying mineral distribution, ore body shapes, and structures. Existing detectors, however, may lack precision in measuring muon flux, leading to blurry images or insufficient detail of subsurface structures, affecting accurate resource assessment. For instance, low-resolution detectors may fail to identify thin or low-contrast ore bodies, causing resource omissions or misjudgments.

(3) Detector stability: In complex and variable field environments, such as high-temperature, high-humidity, or strong electromagnetic interference conditions, detector performance is prone to degradation, leading to inaccurate measurement data or equipment failure. For example, in hot and humid tropical rainforest regions, the electronic components of detectors may suffer from moisture-induced performance degradation; in areas with strong electromagnetic interference, such as near high-voltage transmission lines, measurement data may exhibit deviations, thereby affecting the reliability of exploration results.

6.1.2. Data Processing and Analysis Challenges

(1) Data acquisition efficiency and storage: During surveys, muography generates a substantial volume of data, which presents challenges in terms of efficient acquisition and storage. Firstly, the speed of data acquisition needs to be commensurate with survey efficiency to prevent extended operational cycles. Secondly, the vast amount of data necessitates large-capacity storage systems and robust management mechanisms to guarantee data security and traceability. Ineffective data acquisition might result in data gaps, and inadequate storage could lead to data loss or corruption, both of which would have a detrimental impact on subsequent analysis.

(2) Complex data processing and interpretation: The attenuation of muon flux is affected by numerous factors, such as geological structures and ore composition, which give rise to complex data. The extraction of valuable information and the accurate inversion of subsurface mineral distribution and structures necessitate advanced algorithms and specialized knowledge. In complex geological conditions, the current algorithms still face challenges in terms of accuracy and reliability. For instance, the intricate impacts of different ore types on muon flux render it arduous for the existing algorithms to differentiate them precisely, thereby causing misjudgments regarding the properties and distributions of ore bodies.

6.1.3. Cost and Practical Application Challenges

(1) Equipment and operational costs: The high R&D and production costs of muography detectors, coupled with the need for specialized data acquisition and processing equipment in the field, increase overall expenses. Additionally, high operational costs (e.g., equipment maintenance, calibration, and personnel training) limit large-scale adoption by mining exploration enterprises. For instance, high-precision detector systems represent a substantial investment, with ongoing maintenance costs adding to the financial burden, which deters many companies.

(2) Integration with traditional methods: While muography offers unique advantages, it cannot fully replace traditional exploration methods in practice. Effectively integrating it with geological mapping, geophysical surveys, and geochemical exploration to form comprehensive exploration systems remains a challenge. For example, muography may provide a general range for ore body boundaries, but traditional geophysical methods are needed for precise delineation. Currently, the lack of mature integration models and experience hinders its practical adoption.

6.2. Solutions and Future Directions

Muon imaging has shown potential in deep mineral exploration, but enhancing its penetration depth and imaging accuracy requires focus on the following key areas:

6.2.1. Optimizing Detector Performance

(1) Enhancing detector sensitivity: In muon imaging systems, the detector serves as a core component whose sensitivity does not alter the inherent penetration depth of muons (a characteristic intrinsic to the particles themselves) but plays a decisive role in enhancing the imaging accuracy of deep mining areas. By improving detector sensitivity, it is possible to effectively increase the capture efficiency of muon events in the target region, particularly for low-energy muons, thereby providing richer raw data for subsequent image reconstruction.

The core advantage of high-sensitivity detectors lies in their ability to accurately record muon trajectories. Through advanced detection materials and structural designs, such detectors enable efficient acquisition of muon ionization signals. On one hand, novel materials can significantly enhance the signal conversion efficiency of muons after they traverse the target medium. These include scintillator materials with high photon yields, such as rare-earth-doped crystals, and gas detectors with high ionization efficiencies, like high-pressure xenon ionization chambers. This helps minimize the loss of low-energy muon events. On the other hand, optimizing the spatial layout of detector units and readout circuit designs is critical for capturing dense muon shower events—phenomena where high-energy cosmic ray interactions generate a cascade of secondary muons arriving in rapid succession (often within microseconds) and over a localized spatial range.

These events pose unique challenges, including potential pile-up effects (signal overlap) and increased demands on time resolution. By reducing detector dead time (the interval during which a detector cannot register new events) and increasing the fill factor (the ratio of active detection area to total area), the system can better distinguish individual muons within the shower, avoiding data loss from overlapping signals. Additionally, improved time resolution (e.g., sub-nanosecond timing) and optimized spatial coverage (via tightly packed detector arrays) ensure that even densely clustered muon trajectories are accurately recorded, preserving the integrity of shower event data for subsequent inversion analysis.

(2) Increasing detector area: Larger detectors are capable of gathering a greater number of muons, thereby enhancing the signal statistics. A more substantial amount of muon data provides a wealth of information, which is crucial for the precise reconstruction of deep ore body images. In practical applications, the detector area can be expanded through either tiling multiple detector units or developing larger modules. However, this approach necessitates addressing the issues of signal consistency and data synchronization to guarantee the stability and accuracy of the system.

6.2.2. Improving Data Acquisition Strategies

(1) Long-term data acquisition: Extending acquisition time is an effective way to enhance penetration depth and imaging accuracy. Longer acquisition periods allow detectors to collect more muons from deep ore bodies, improving statistical precision. Similar to astronomical observations, where long exposure captures faint signals, extended muon data collection reduces statistical noise and enhances image clarity and accuracy. However, this requires the monitoring and correction of environmental parameters to address data instability caused by changing conditions.

(2) Multi-angle data acquisition: Acquiring data from multiple angles provides comprehensive information for improved imaging accuracy. Muons penetrating ore bodies from different angles carry directional information, and integrated analysis of multi-angle data enables precise 3D reconstruction of ore body structures. For example, rotating detectors or deploying multiple detectors at different positions to scan deep ore bodies from various directions, akin to medical CT scans using X-Rays from multiple angles to construct detailed organ images, can provide comprehensive ore body information.

6.2.3. Integrated Geophysical Exploration

Geophysical techniques aim to understand subsurface geological structures and distributions by observing geophysical fields. Muography can be integrated with other methods (e.g., gravity and electromagnetic surveys), each based on different physical principles and detecting distinct subsurface properties. Combined use allows multi-faceted data acquisition, mutual validation, and improved deep exploration accuracy and reliability.

(1) Integration with seismic methods: Seismic methods yield information regarding deep geological structures through the analysis of the reflection and refraction of seismic waves. When integrated with muography, the structural data obtained from seismic methods can be utilized as prior knowledge to facilitate imaging. For instance, seismic surveys are capable of identifying the general stratum and tectonic location of deep-seated ore bodies. Muography, on the other hand, refines the specific positions and shapes of these ore bodies. The two methods complement each other, thereby enhancing the detection precision.

(2) Integration with electromagnetic methods: Electromagnetic techniques exhibit a high degree of sensitivity to variations in subsurface electrical properties. They are capable of detecting electrical anomalies that are related to ore bodies. In the context of deep exploration, the integration of electromagnetic surveys with muography enables electromagnetic methods to quickly delineate potential ore zones. Subsequently, muography can be employed to create detailed images of these zones, thereby enhancing both efficiency and accuracy. Moreover, the electrical property data obtained from electromagnetic methods can assist in the interpretation of muography results, leading to a more comprehensive understanding of the properties of ore bodies.

(3) Integration with gravity exploration: Gravity surveys are indicative of density variations within the subsurface. A density anomaly detected through gravity measurements can be subjected to further analysis via muography. This enables the determination of detailed density distributions and the identification of potential ore bodies.

6.2.4. Data Processing and Algorithm Optimization

(1) Noise reduction: Noise in muography data can obscure deep ore body signals and degrade imaging accuracy. Advanced noise reduction algorithms are essential for data preprocessing. For example, wavelet transform-based denoising decomposes data into different frequency scales, separating noise from useful signals, which are retained via thresholding. Machine learning-based methods, such as deep autoencoders, can automatically learn noise characteristics from data to remove noise and improve data quality for reliable imaging.

(2) Improved image reconstruction algorithms: Image reconstruction algorithms are critical for converting muon data into ore body images. Traditional algorithms may produce low-resolution or blurry images for complex deep structures, necessitating advanced alternatives. Algebraic reconstruction techniques (ARTs) and their improved versions iteratively optimize reconstruction results to enhance resolution and accuracy. Compressive sensing-based algorithms, leveraging signal sparsity, enable high-quality reconstruction from limited data, vital for low-signal deep exploration.

(3) Model-based fusion algorithms: When integrating muography with other geophysical methods, geological modeling can guide data fusion. For example, in volcanic structure studies, muon flux attenuation data (reflecting density differences) and seismic wave velocity data can be fused within a physical model framework using Bayesian inference. By assigning weights to data based on geological prior knowledge, this approach improves subsurface structure inversion accuracy. For volcanic density inversion, combining muography’s density sensitivity with seismic–velocity–density relationships via Bayesian fusion enhances imaging precision.

(4) Machine learning fusion algorithms: Machine learning excels in data fusion. Artificial neural networks (ANNs) can take muography and other geophysical data (e.g., gravity and magnetic) as input nodes, learning their intrinsic relationships through training to produce accurate exploration results. Using labeled geological structure datasets, ANNs adjust weights to predict subsurface conditions. Support vector machines (SVMs), effective for nonlinear data, classify and fuse geophysical data by finding optimal hyperplanes in feature space.

Recent advances in deep learning further extend these capabilities: convolutional neural networks (CNNs) can directly process raw muon detector images alongside seismic reflection profiles, enabling end-to-end 3D ore body reconstruction. Such integration not only accelerates data processing (from weeks to days in our pilot study) but also captures fine-scale structural details missed by individual methods. These emerging applications underscore how machine learning-driven fusion is pushing the boundaries of muography’s practicality in mineral exploration [90,91].

6.2.5. Deepening Muon-Matter Interaction Research

(1) Precise modeling: Developing more accurate muon–matter interaction models is fundamental. In-depth studies of muon scattering and absorption in different geological media, considering factors like composition, density, and crystal structure, are essential. Combining experimental measurements with theoretical calculations to refine model parameters can accurately describe muon propagation in deep ore bodies and surrounding rocks, enabling precise data correction and inversion during imaging.

(2) Simulation analysis: Computer simulations of muography surveys optimize detection schemes and data processing. By simulating muon paths and detector responses under various geological conditions, researchers can predict outcomes and evaluate parameter impacts (e.g., detector position, angle, and acquisition time) on penetration depth and accuracy. This aids in determining optimal survey designs and understanding muon imaging physics, identifying improvement directions, and supporting field applications.

Through these multi-faceted efforts, muography’s penetration depth and imaging accuracy in deep mineral exploration are expected to improve, enabling broader utility in deep resource exploration.

7. Conclusions

Muon imaging technology, with its unique working principles and specific advantages, has practical application potential in the exploration of strategic ore deposits. In terms of technical principles, it leverages the properties of cosmic ray muons, employing approaches like transmission imaging and scattering imaging. When combined with evolving detector technologies and imaging algorithms, it can provide information about underground ore bodies and geological structures, though the resolution and accuracy of such data depend on factors like muon flux intensity and target depth. In the context of strategic ore deposit exploration, the technology serves a functional role in deep ore body positioning and exploration model optimization. Specifically, it can assist in identifying and detecting certain types of ore bodies, helping to approximate their locations and extents—particularly in scenarios where traditional methods are constrained by depth or terrain. It also offers capabilities for monitoring rock mass changes over time, which may contribute to mining safety assessments, and can aid in detecting specific geological structures or weak zones, supporting engineering planning such as tunnel excavation. Its applications extend to tasks like caved mass monitoring, residual ore prospecting, and deep mineral exploration, though outcomes in these areas are often influenced by site-specific geological complexity. That said, the technology faces notable challenges in practical use. Limitations related to detector sensitivity, data processing efficiency, adaptability to highly complex geological conditions, and operational costs currently restrict its widespread adoption. Advancing its development and application will require targeted improvements across multiple areas. These include enhancing detector performance to improve signal-to-noise ratios, refining data acquisition protocols for reliability under field conditions, integrating with other geophysical methods to compensate for individual limitations, optimizing data processing algorithms to reduce interpretation ambiguities, and deepening research into muon–matter interactions to better account for geological variability. Looking ahead, as key technical barriers are gradually addressed, muon imaging technology may become more effective in specific scenarios of strategic ore deposit exploration. Its continued development could provide supplementary technical support for sustainable mineral resource utilization, though its role will remain complementary to established geophysical methods in most exploration workflows.