Reactive Transport Model of Steel/Bentonite Interactions in the FEBEX In Situ Test
Abstract
1. Introduction
2. Materials and Methods
2.1. FEBEX In Situ Test Description
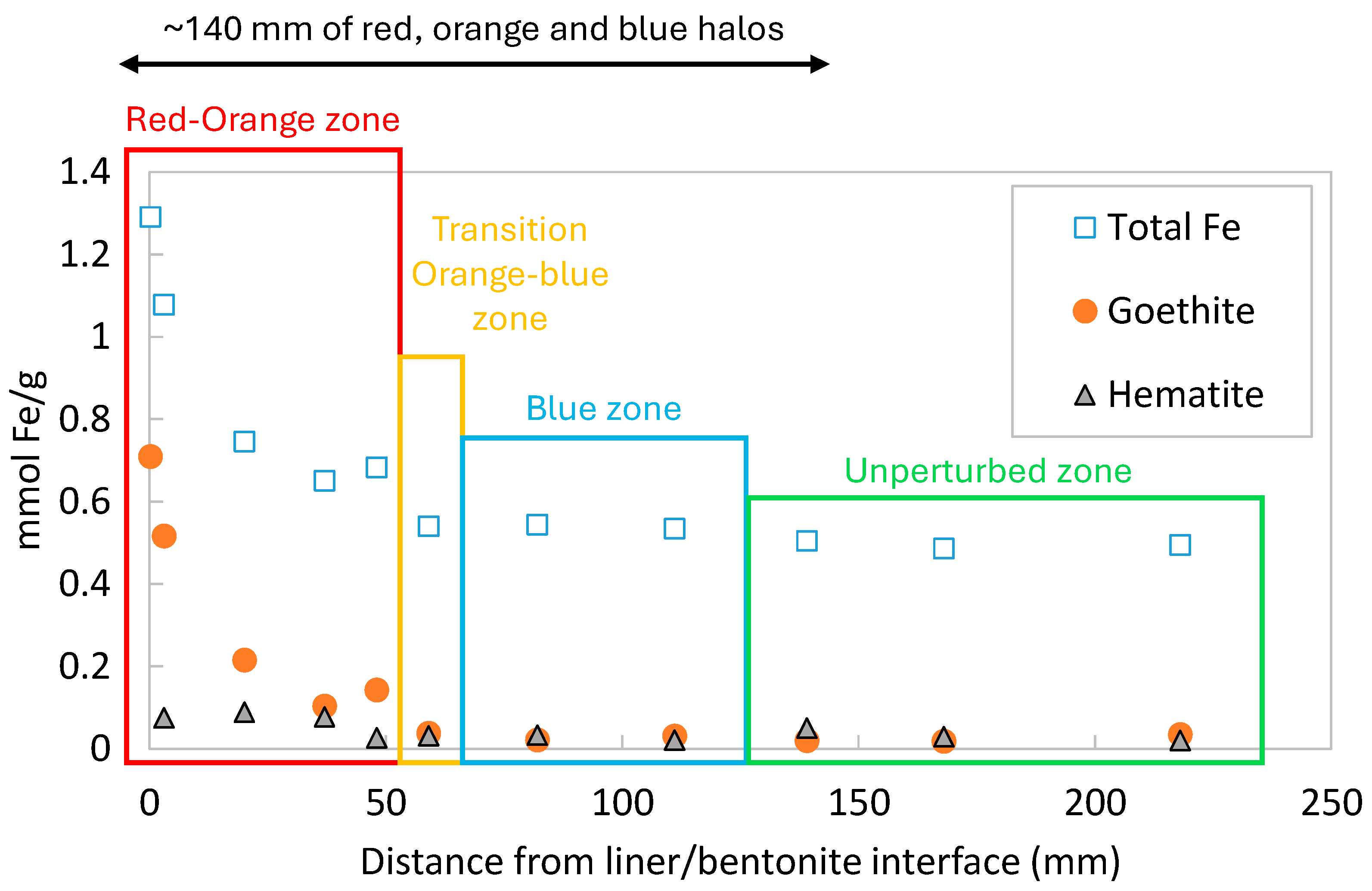
2.2. Post Mortem Analysis
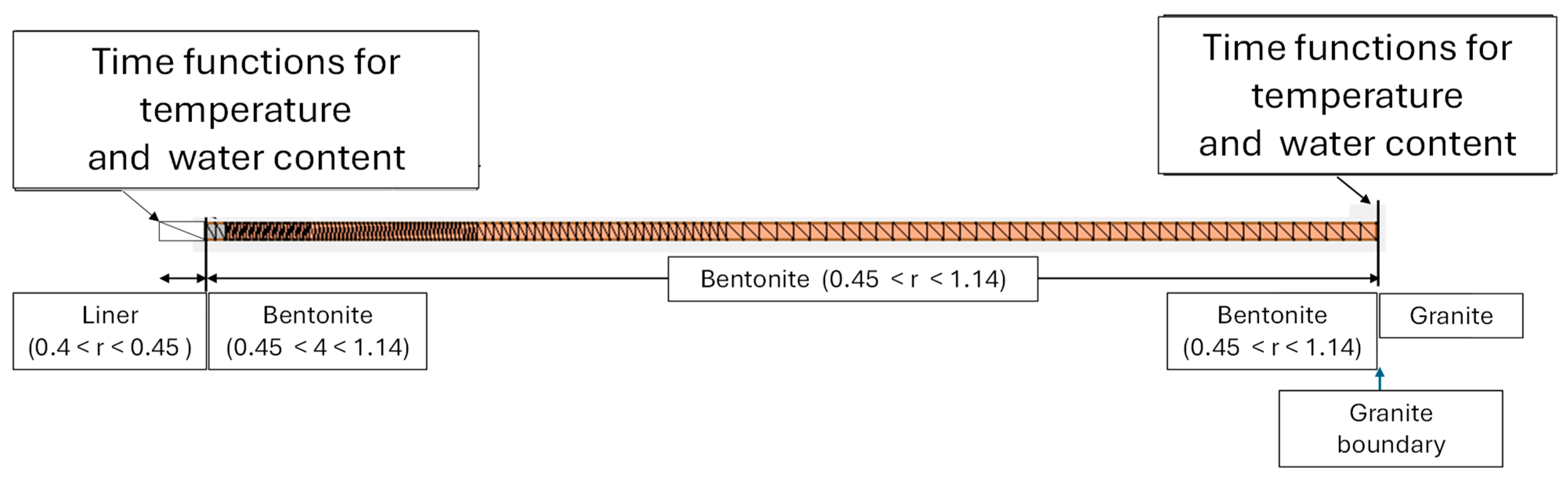
2.3. Conceptual Reactive Transport Model
2.4. Numerical Reactive Transport Model
2.5. Computer Code
3. Model Results
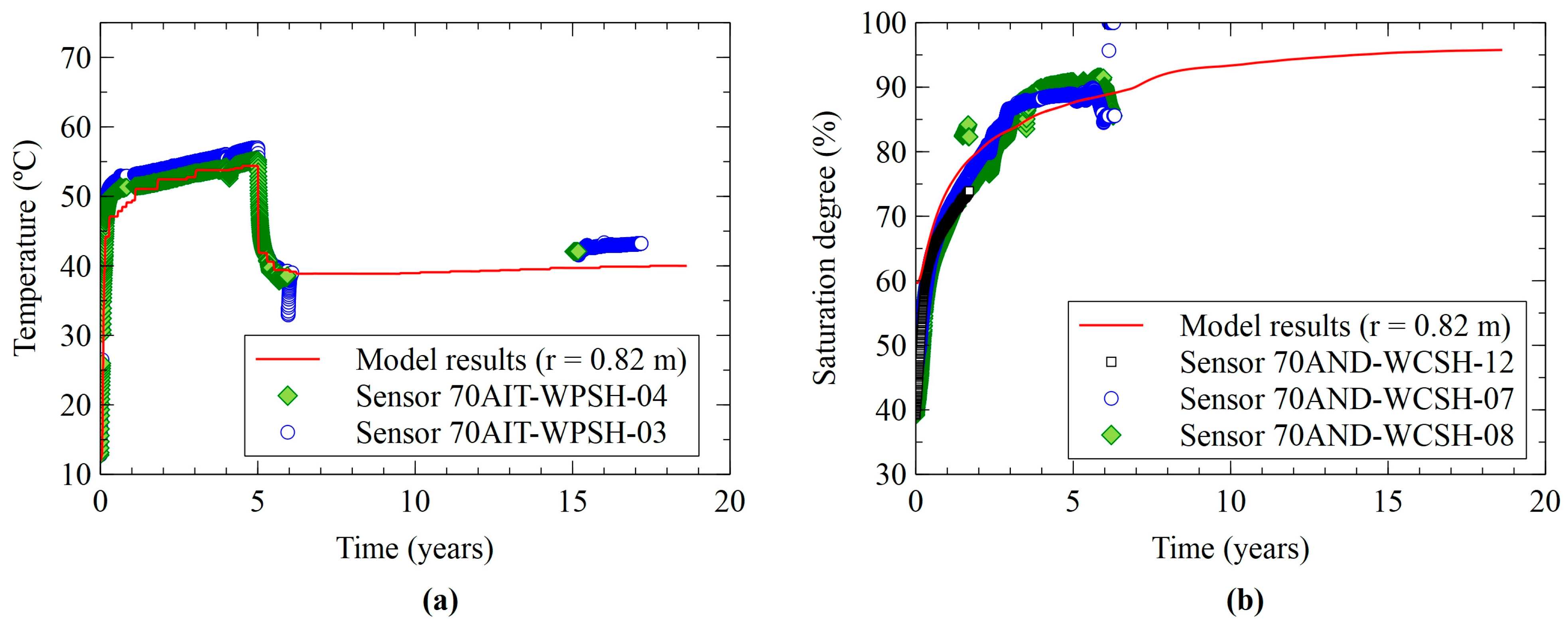
3.1. Thermal and Hydrodynamic Results
3.2. Geochemical Model Results
3.2.1. Dissolved Species Model Results
3.2.2. Mineral Precipitation/Dissolution Model Results
3.2.3. Cation Exchange and Surface Complexation Model Results
3.3. Dissolved, Precipitated, Exchanged, and Sorbed Iron Model Results and Comparison with the Measured Data
3.4. Iron, O2, and H2 Mass Balance
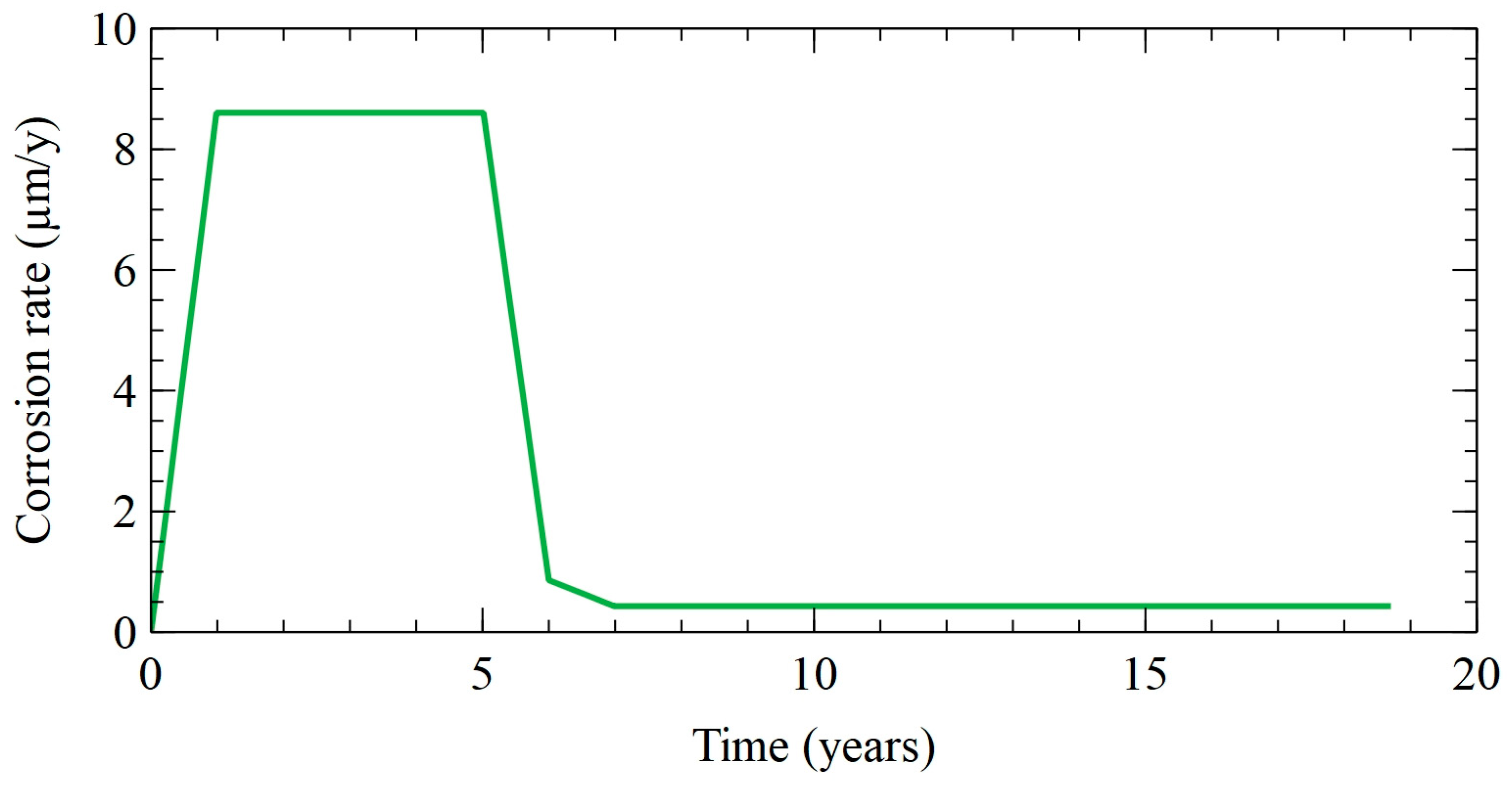
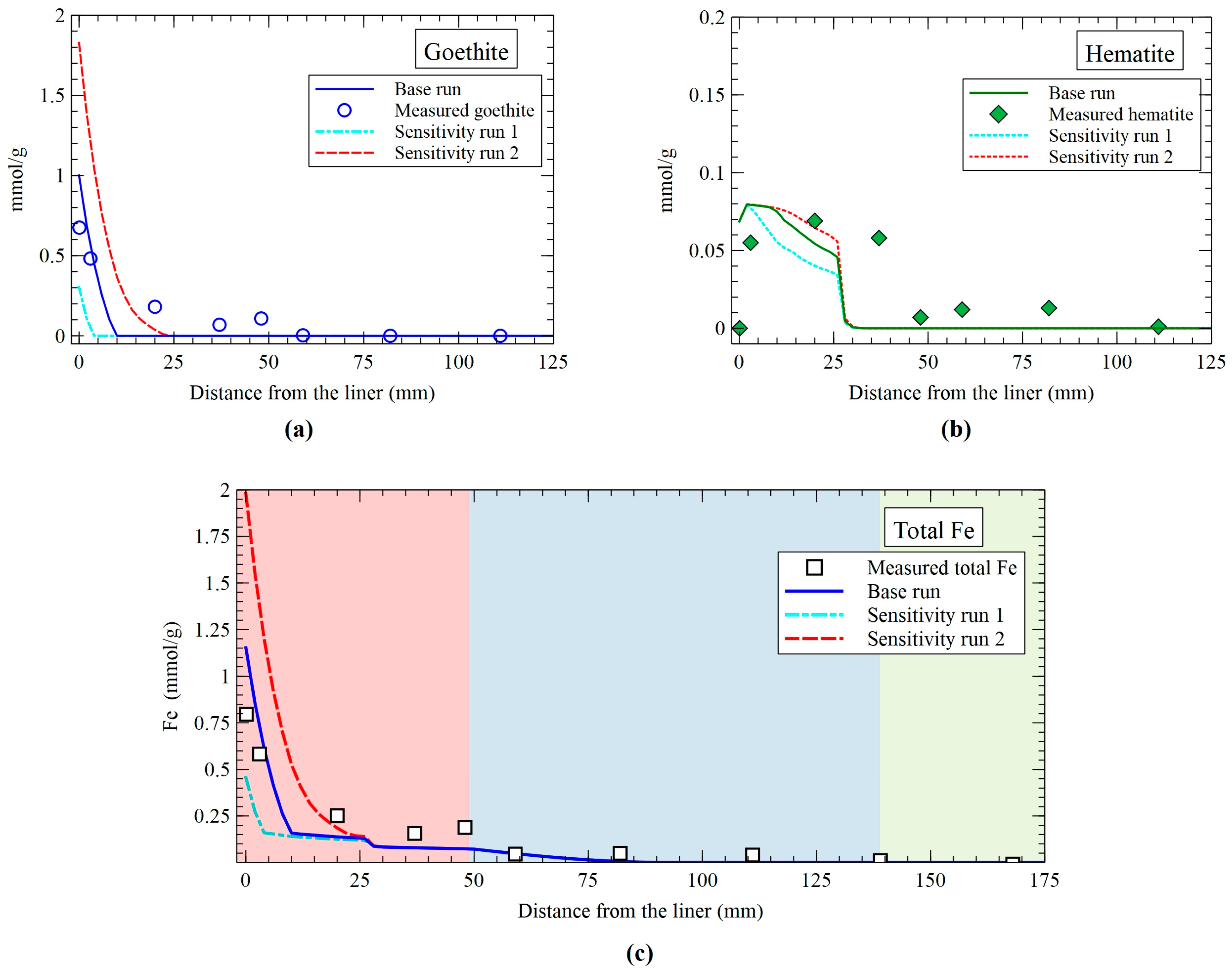
3.5. Sensitivity Analysis
3.6. Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- King, F.; Kolàř, M.; Briggs, S.; Behazin, M.; Keech, P.; Diomidis, N. Review of the Modelling of Corrosion Processes and Lifetime Prediction for HLW/SF Containers—Part 1: Process Models. Corros. Mater. Degrad. 2024, 5, 124–199. [Google Scholar] [CrossRef]
- Lloret, A.; Villar, M.V. Advances on the Knowledge of the Thermo-Hydro-Mechanical Behaviour of Heavily Compacted “FEBEX” Bentonite. Phys. Chem. Earth Parts A/B/C 2007, 32, 701–715. [Google Scholar] [CrossRef]
- Villar, M.V.; Lloret, A. Influence of Dry Density and Water Content on the Swelling of a Compacted Bentonite. Appl. Clay Sci. 2008, 39, 38–49. [Google Scholar] [CrossRef]
- De Windt, L.; Spycher, N.F. Reactive Transport Modeling: A Key Performance Assessment Tool for the Geologic Disposal of Nuclear Waste. Elements 2019, 15, 99–102. [Google Scholar] [CrossRef]
- Claret, F.; Dauzeres, A.; Jacques, D.; Sellin, P.; Cochepin, B.; De Windt, L.; Garibay-Rodriguez, J.; Govaerts, J.; Leupin, O.; Lopez, A.M.; et al. Modelling of the Long-Term Evolution and Performance of Engineered Barrier System. EPJ Nucl. Sci. Technol. 2022, 8, 41. [Google Scholar] [CrossRef]
- Bildstein, O.; Claret, F. Stability of Clay Barriers Under Chemical Perturbations. In Developments in Clay Science; Elsevier: Amsterdam, The Netherlands, 2015; Volume 6, pp. 155–188. ISBN 978-0-08-100027-4. [Google Scholar]
- Marty, N.C.M.; Fritz, B.; Clément, A.; Michau, N. Modelling the Long Term Alteration of the Engineered Bentonite Barrier in an Underground Radioactive Waste Repository. Appl. Clay Sci. 2010, 47, 82–90. [Google Scholar] [CrossRef]
- Savage, D.; Watson, C.; Benbow, S.; Wilson, J. Modelling Iron-Bentonite Interactions. Appl. Clay Sci. 2010, 47, 91–98. [Google Scholar] [CrossRef]
- Savage, D. Prospects for Coupled Modelling; Report STUK-TR 13; STUK: Helsinki, Finland, 2012. [Google Scholar]
- Samper, J.; Naves, A.; Montenegro, L.; Mon, A. Reactive Transport Modelling of the Long-Term Interactions of Corrosion Products and Compacted Bentonite in a HLW Repository in Granite: Uncertainties and Relevance for Performance Assessment. Appl. Geochem. 2016, 67, 42–51. [Google Scholar] [CrossRef]
- Mon, A.; Samper, J.; Montenegro, L.; Naves, A.; Fernández, J. Long-Term Non-Isothermal Reactive Transport Model of Compacted Bentonite, Concrete and Corrosion Products in a HLW Repository in Clay. J. Contam. Hydrol. 2017, 197, 1–16. [Google Scholar] [CrossRef]
- Claret, F.; Marty, N.; Tournassat, C. Modeling the Long-Term Stability of Multi-Barrier Systems for Nuclear Waste Disposal in Geological Clay Formations. In Reactive Transport Modeling; John Wiley & Sons: Hoboken, NJ, USA, 2018; pp. 395–451. ISBN 978-1-119-06003-1. [Google Scholar]
- Bildstein, O.; Claret, F.; Frugier, P. RTM for Waste Repositories. Rev. Mineral. Geochem. 2019, 85, 419–457. [Google Scholar] [CrossRef]
- Mon, A.; Samper, J.; Montenegro, L.; Turrero, M.J.; Torres, E.; Cuevas, J.; Fernández, R.; De Windt, L. Reactive Transport Models of the Geochemical Interactions at the Iron/Bentonite Interface in Laboratory Corrosion Tests. Appl. Clay Sci. 2023, 240, 106981. [Google Scholar] [CrossRef]
- Montenegro, L.; Samper, J.; Mon, A.; De Windt, L.; Samper, A.-C.; García, E. A Non-Isothermal Reactive Transport Model of the Long-Term Geochemical Evolution at the Disposal Cell Scale in a HLW Repository in Granite. Appl. Clay Sci. 2023, 242, 107018. [Google Scholar] [CrossRef]
- Kiczka, M.; Alt-Epping, P.; Hadi, J.; Wersin, P.; Leupin, O.X.; Diomidis, N. Reactive Transport Modelling of Iron Bentonite Interaction in the FEBEX in Situ Experiment. Appl. Geochem. 2024, 170, 106057. [Google Scholar] [CrossRef]
- Wersin, P.; Hadi, J.; Kiczka, M.; Jenni, A.; Grenèche, J.; Diomidis, N.; Leupin, O.X.; Svensson, D.; Sellin, P.; Reddy, B.; et al. Unravelling the Corrosion Processes at Steel/Bentonite Interfaces in in Situ Tests. Mater. Corros. 2023, 74, 1716–1727. [Google Scholar] [CrossRef]
- King, F.; Kolàř, M.; Briggs, S.; Behazin, M.; Keech, P.; Diomidis, N. Review of the Modelling of Corrosion Processes and Lifetime Prediction for HLW/SF Containers—Part 2: Performance Assessment Models. Corros. Mater. Degrad. 2024, 5, 289–339. [Google Scholar] [CrossRef]
- Wittebroodt, C.; Turrero, M.; Torres, E.; Gómez, P.; Garralón, A.; Notario, B.; Sanmiguel, M.; Cuevas, J.; Mota, C.; Ruiz, A.; et al. Final Technical Report on the Steel/Clay Material Interactions Deliverable D2.7: Final Technical Report on the Steel/Clay Material Interactions; HORIZON 2020 Project EURAD. EC Grant Agreement No. 847593; EURAD: Antwerp, Belgium, 2024. [Google Scholar]
- ENRESA Full-Scale Engineered Barriers Experiment for a Deep Geological Repository in Crystalline Host Rock FEBEX Project. EUR 19147 EN, European Commission 2000. Available online: https://cordis.europa.eu/project/id/FIKW-CT-2000-00016/reporting (accessed on 19 July 2025).
- ENRESA. Full-Scale Engineered Barriers Experiment: Updated Final Report; PT 05-02/2006; ENRESA Technical Publication: Madrid, Spain, 2006; p. 589. [Google Scholar]
- Martín, P.L.; Barcala, J.M. Large Scale Buffer Material Test: Mock-up Experiment at CIEMAT. Eng. Geol. 2005, 81, 298–316. [Google Scholar] [CrossRef]
- Wersin, P.; Kober, F. FEBEX-DP—Metal Corrosion and Iron-Bentonite Interaction Studies; Nagra: Wettingen, Switzerland, 2017; Volume NAB 16-16. [Google Scholar]
- Wilson, J. FEBEX-DP: Geochemical Modelling of Iron-Bentonite Interactions. Quintessa’s Contribution on Behalf of RWM; Quintessa Report QRS-1713A-R3 v1.3; Quitessa: Henley-on-Thames, UK, 2017. [Google Scholar]
- Hadi, J.; Wersin, P.; Serneels, V.; Greneche, J.-M. Eighteen Years of Steel–Bentonite Interaction in the FEBEX in Situ Test at the Grimsel Test Site in Switzerland. Clays Clay Miner. 2019, 67, 111–131. [Google Scholar] [CrossRef]
- Samper, J.; Zheng, L.; Montenegro, L.; Fernández, A.M.; Rivas, P. Coupled Thermo-Hydro-Chemical Models of Compacted Bentonite after FEBEX in Situ Test. Appl. Geochem. 2008, 23, 1186–1201. [Google Scholar] [CrossRef]
- Zheng, L.; Samper, J.; Montenegro, L. A Coupled THC Model of the FEBEX in Situ Test with Bentonite Swelling and Chemical and Thermal Osmosis. J. Contam. Hydrol. 2011, 126, 45–60. [Google Scholar] [CrossRef] [PubMed]
- Samper, J.; Mon, A.; Montenegro, L. A Revisited Thermal, Hydrodynamic, Chemical and Mechanical Model of Compacted Bentonite for the Entire Duration of the FEBEX in Situ Test. Appl. Clay Sci. 2018, 160, 58–70. [Google Scholar] [CrossRef]
- Kaufhold, S.; Dohrmann, R.; Ufer, K.; Kober, F. Interactions of Bentonite with Metal and Concrete from the FEBEX Experiment: Mineralogical and Geochemical Investigations of Selected Sampling Sites. Clay Miner. 2018, 53, 745–763. [Google Scholar] [CrossRef]
- Lanyon, G.W.; Gaus, I. Main Outcomes and Review of the FEBEX In Situ Test (GTS) and Mock-Up After 15 Years of Operation; NTB 15-04; Nagra: Wettingen, Switzerland, 2016; 127p. [Google Scholar]
- Fernández, A.; Sánchez-Ledesma, D.; Melón, A.; Robredo, L.; Rey, J.; Labajo, M.; Clavero, M.; Carretero, S.; González, A. Thermo-Hydro-Geochemical Behaviour of a Spanish Bentonite after of the FEBEX In Situ Test at the Grimsel Test Site; Technical Report CIEMAT/DMA/2G216/03/16. Nagra Arbeitsbereicht NAB16-025; NAGRA: Madrid, Spain, 2018; p. 270. [Google Scholar]
- Fernández, A.M. Gas and Water Sampling from the FEBEX In Situ Test; NAGRA Working Report; NAGRA: Wettingen, Switzerland, 2019; p. 211. [Google Scholar]
- Bradbury, M.H.; Baeyens, B. A Mechanistic Description of Ni and Zn Sorption on Na-Montmorillonite Part II: Modelling. J. Contam. Hydrol. 1997, 27, 223–248. [Google Scholar] [CrossRef]
- Giffaut, E.; Grivé, M.; Blanc, P.; Vieillard, P.; Colàs, E.; Gailhanou, H.; Gaboreau, S.; Marty, N.; Madé, B.; Duro, L. Andra Thermodynamic Database for Performance Assessment: ThermoChimie. Appl. Geochem. 2014, 49, 225–236. [Google Scholar] [CrossRef]
- Geochemistry, Groundwater and Pollution C.A.J. Appelo, Dieke Postma. Available online: https://www.taylorfrancis.com/books/mono/10.1201/9781439833544/geochemistry-groundwater-pollution-dieke-postma-appelo (accessed on 19 December 2024).
- Bradbury, M.H.; Baeyens, B. Modelling the Sorption of Mn(II), Co(II), Ni(II), Zn(II), Cd(II), Eu(III), Am(III), Sn(IV), Th(IV), Np(V) and U(VI) on Montmorillonite: Linear Free Energy Relationships and Estimates of Surface Binding Constants for Some Selected Heavy Metals and Actinides. Geochim. Cosmochim. Acta 2005, 69, 875–892. [Google Scholar] [CrossRef]
- Wolery, T.J. EQ3/6, a Software Package for Geochemical Modeling of Aqueous Systems: Package Overview and Installation Guide (Version 7.0); Lawrence Livermore National Lab.: Livermore, CA, USA, 1992; 70p, UCRL-MA--110662-Pt 1. [Google Scholar]
- Fuentes-Cantillana, J.L.; Garcia-Sineriz, J.L. Final Design and Installation of the “In Situ” Test at GRIMSEL; Empresa Nacional de Residuos Radiactivos: Madrid, Spain, 1998; p. 197. [Google Scholar]
- Fernández, A.M.; Cuevas, J.; Rivas, P. Pore Water Chemistry of the Febex Bentonite. MRS Proc. 2000, 663, 573. [Google Scholar] [CrossRef]
- Fernández, A.M.; Baeyens, B.; Bradbury, M.; Rivas, P. Analysis of the Porewater Chemical Composition of a Spanish Compacted Bentonite Used in an Engineered Barrier. Phys. Chem. Earth Parts A/B/C 2004, 29, 105–118. [Google Scholar] [CrossRef]
- Palandri, J.L.; Kharaka, Y.K. A Compilation of Rate Parameters of Water-Mineral Interaction Kinetics for Application to Geochemical Modeling; U.S. Geological Survey: Reston, VA, USA, 2004. [Google Scholar]
- Fernández Águila, J. Reactive Transport Models of Low Permeability Structured Porous and Fractured Media. Ph.D. Thesis, Universidade da Coruña, A Coruña, Spain, 2017. [Google Scholar]
- Idiart, A.; Laviña, M.; Kosakowski, G.; Cochepin, B.; Meeussen, J.C.L.; Samper, J.; Mon, A.; Montoya, V.; Munier, I.; Poonoosamy, J.; et al. Reactive Transport Modelling of a Low-pH Concrete/Clay Interface. Appl. Geochem. 2020, 115, 104562. [Google Scholar] [CrossRef]
- Molinero-Huguet, J.; Samper-Calvete, F.J.; Zhang, G.; Yang, C. Biogeochemical Reactive Transport Model of the Redox Zone Experiment of the Äspö Hard Rock Laboratory in Sweden. Nucl. Technol. 2004, 148, 151–165. [Google Scholar] [CrossRef]
- Zhang, G.; Samper, J.; Montenegro, L. Coupled Thermo-Hydro-Bio-Geochemical Reactive Transport Model of CERBERUS Heating and Radiation Experiment in Boom Clay. Appl. Geochem. 2008, 23, 932–949. [Google Scholar] [CrossRef]
- Martínez, V.; Abós, H.; García-Siñeriz, J.L. FEBEXe: Final Sensor Data Report (FEBEX ’In Situ’Experiment); NAGRA: Wettingen, Switzerland, 2016; p. 244. [Google Scholar]
- Parangusan, H.; Bhadra, J.; Al-Thani, N. A Review of Passivity Breakdown on Metal Surfaces: Influence of Chloride- and Sulfide-Ion Concentrations, Temperature, and pH. Emergent Mater. 2021, 4, 1187–1203. [Google Scholar] [CrossRef]
- Necib, S.; Diomidis, N.; Keech, P.; Nakayama, M. Corrosion of carbon steel in clay environments relevant to radioactive waste geological disposals, Mont Terri rock laboratory (Switzerland). Swiss J. Geosci. 2017, 110, 329–342. [Google Scholar] [CrossRef]
- Wersin, P.; Hadi, J.; Jenni, A.; Svensson, D.; Grenèche, J.-M.; Sellin, P.; Leupin, O.X. Interaction of Corroding Iron with Eight Bentonites in the Alternative Buffer Materials Field Experiment (ABM2). Minerals 2021, 11, 907. [Google Scholar] [CrossRef]


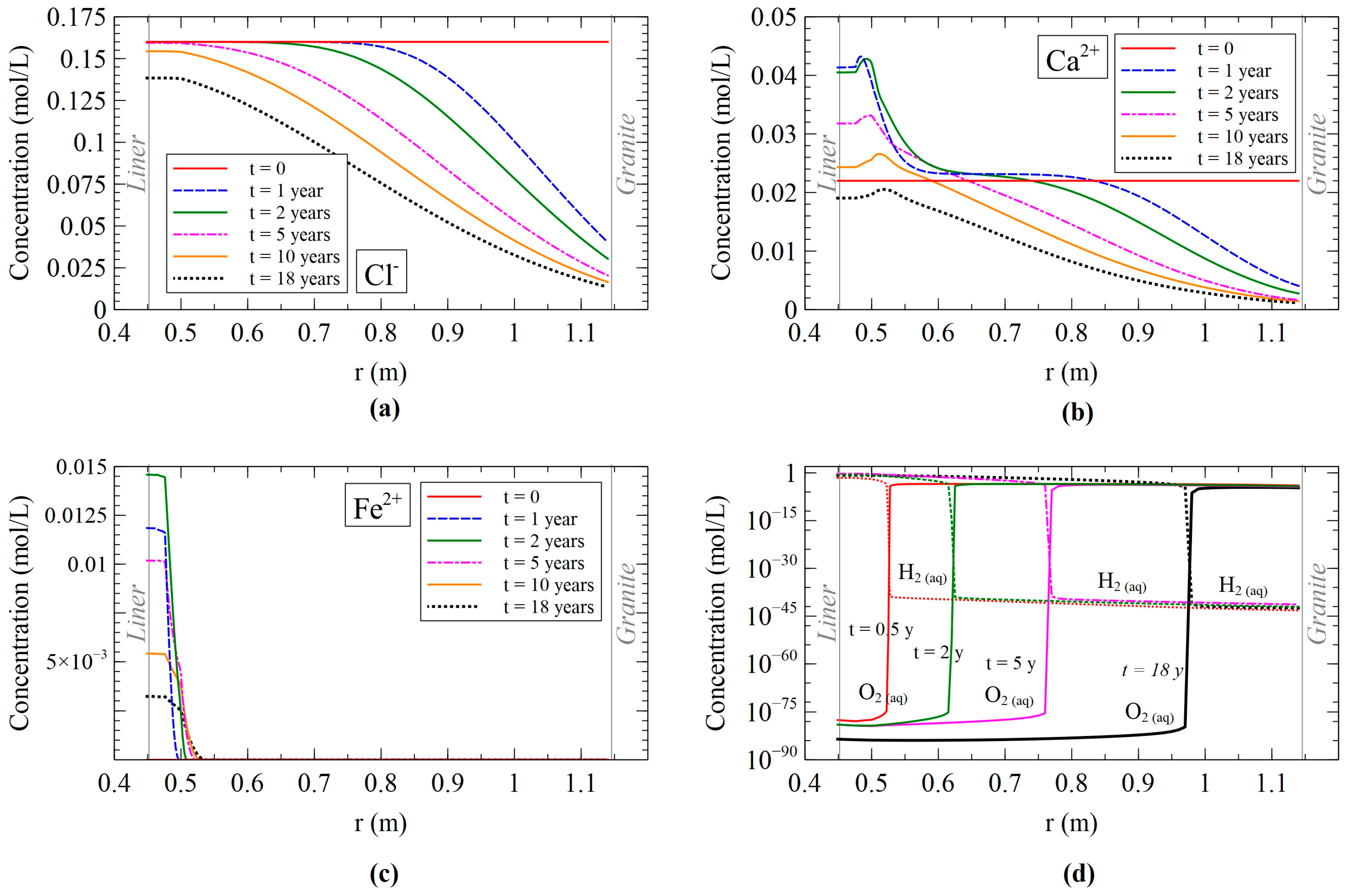
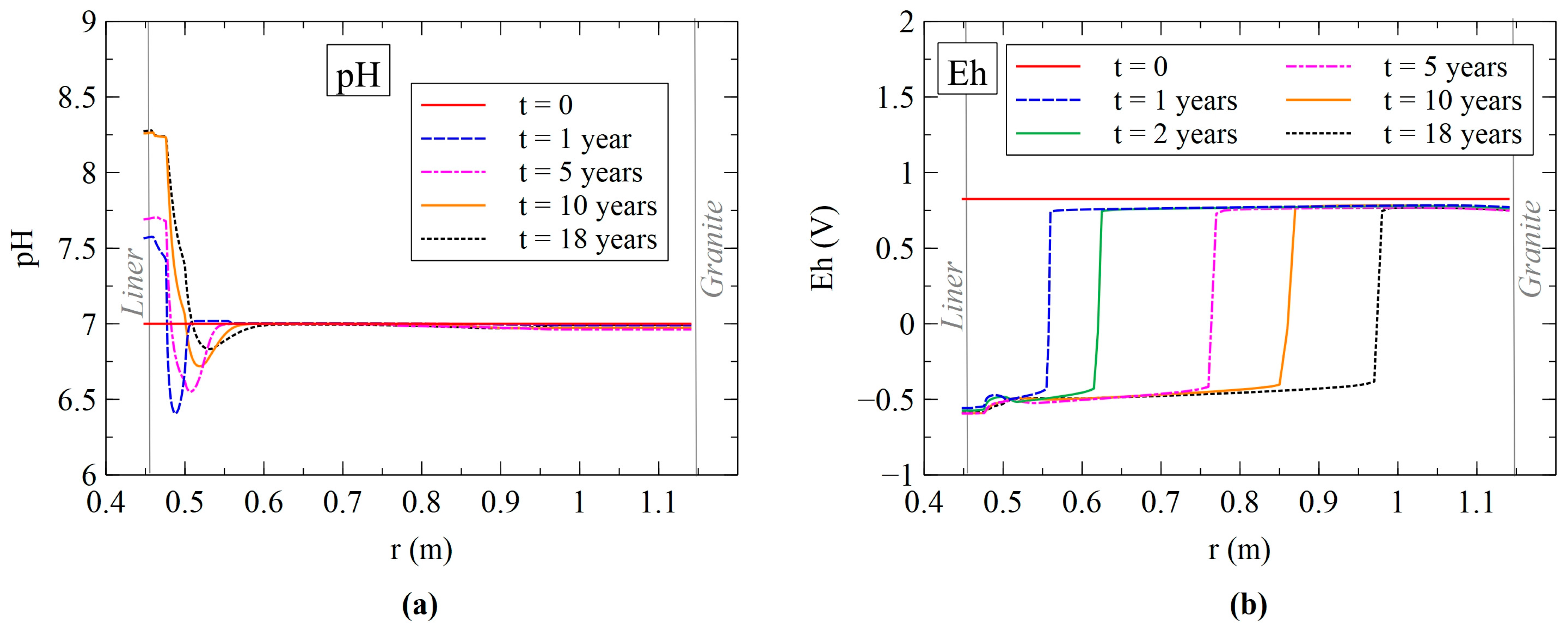
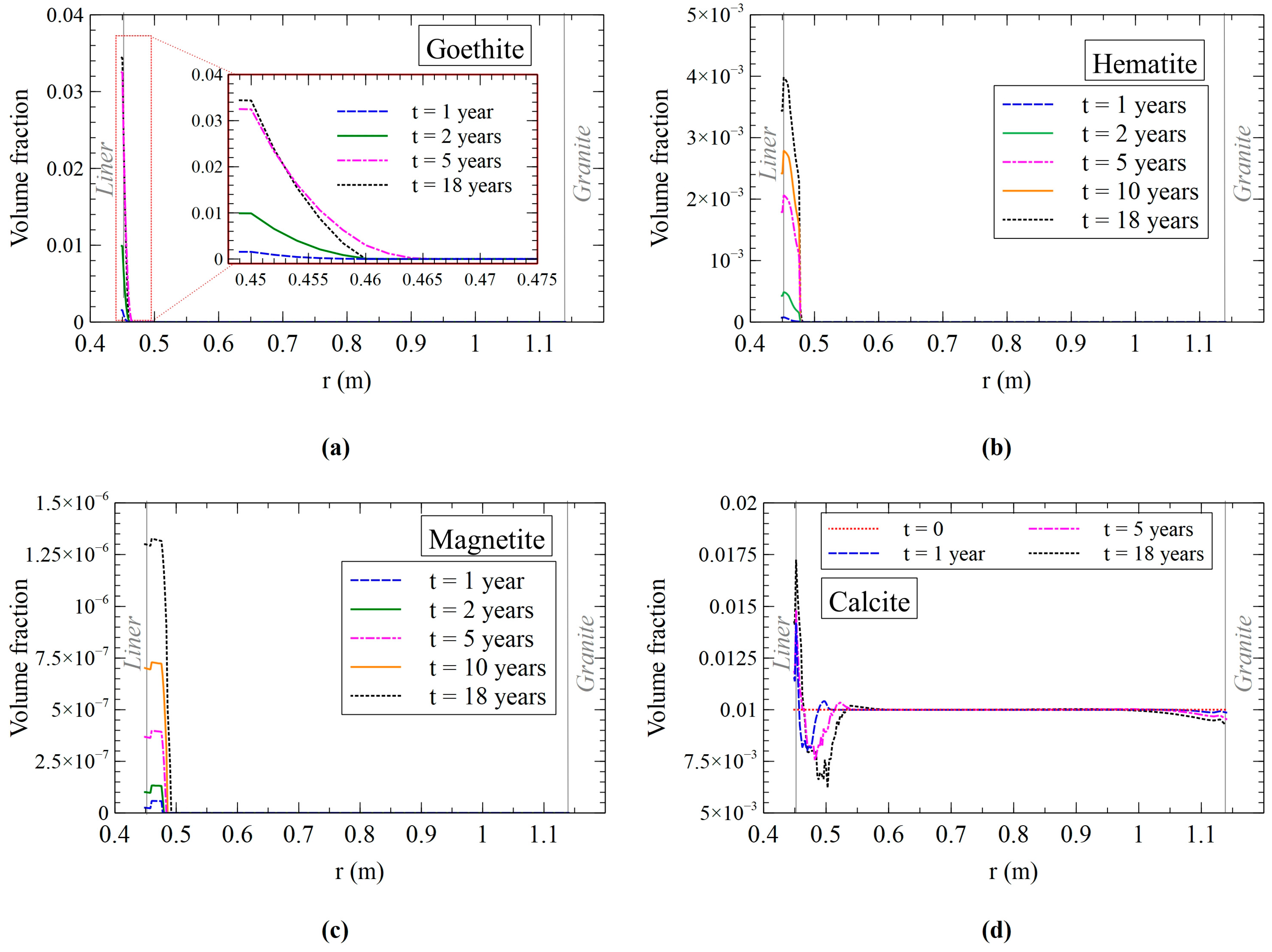
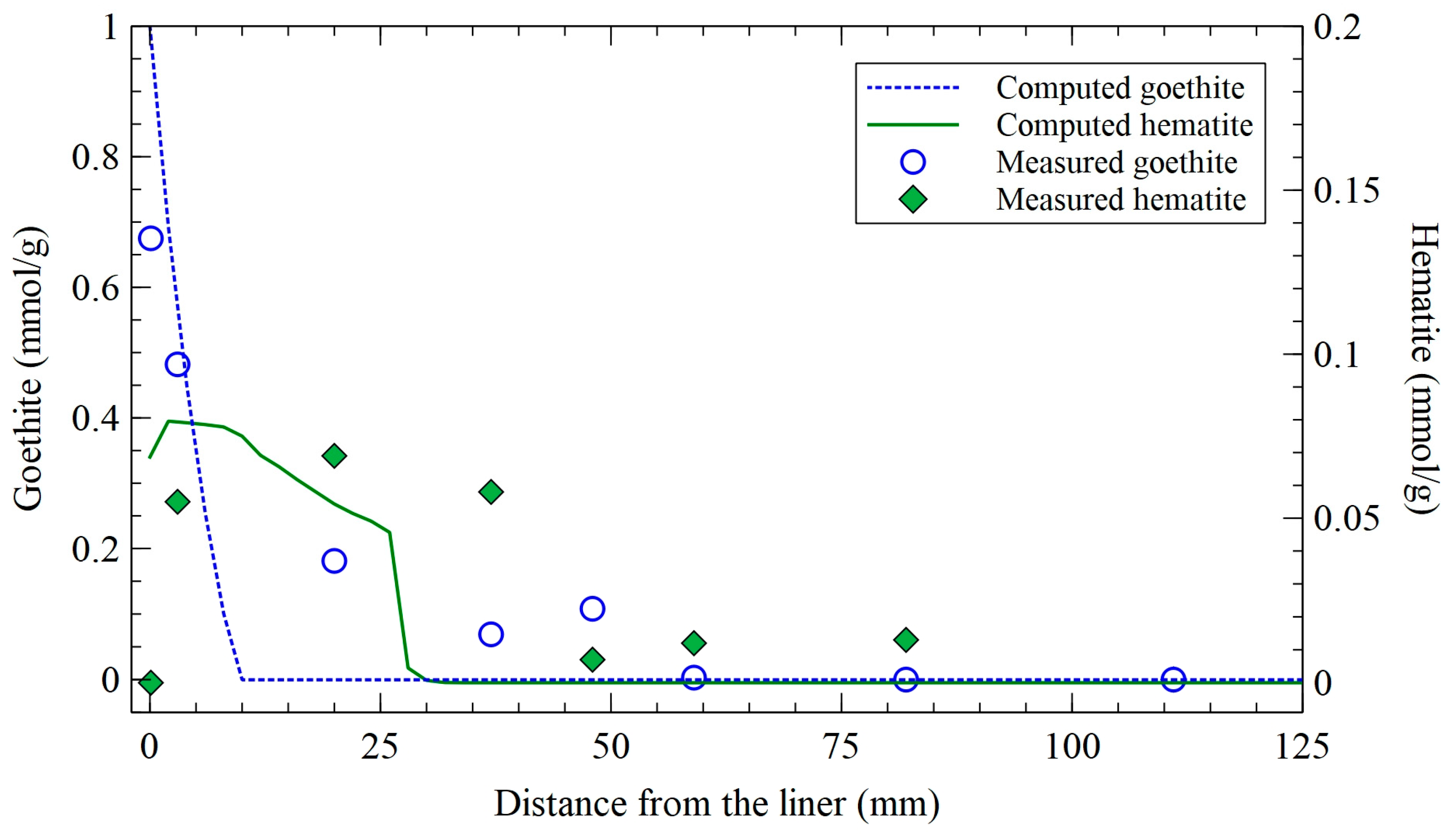


| Aqueous Complexation Reactions | Log K (25 °C) | Aqueous Complexation Reactions | Log K (25 °C) |
| CaCl+ ⇔ Ca2+ + Cl− | 0.290 | NaHCO3(aq) ⇔ Na+ + HCO3− | 0.250 |
| CaCl2(aq) ⇔ Ca2+ + 2Cl− | 0.640 | NaSO4− ⇔ Na+ + SO42− | −0.940 |
| CaCO3(aq) + H+ ⇔ Ca2+ + HCO3− | 7.110 | NaCl(aq) ⇔ Na+ + Cl− | 0.500 |
| CaHCO3+ ⇔ Ca2+ + HCO3− | −1.100 | OH− + H+ ⇔ H2O | 14.000 |
| CaSO4(aq) ⇔ Ca2+ + SO42− | −2.310 | H2(aq) + 0.5O2 ⇔ H2O | 46.070 |
| Ca(H3SiO4)+ + H+ ⇔ Ca2+ + H4SiO4(aq) | 8.830 | Fe3+ + 0.5H2O ⇔ H+ + 0.25O2 + Fe2+ | −8.485 |
| CO2(aq) + H2O ⇔ H+ + HCO3− | −6.350 | FeHCO3+ ⇔ Fe2++ HCO3− | −1.440 |
| CO32− + H+ ⇔ HCO3− | 10.330 | FeCO3 (aq) + H+ ⇔ Fe2+ + HCO3− | 4.640 |
| KSO4− ⇔ K+ + SO42− | −0.880 | FeCl+ ⇔ Fe2++ Cl− | −0.140 |
| KCl(aq) ⇔ K+ + Cl− | 0.500 | FeCl2+ + 0.5H2O ⇔ Fe2+ + H+ + Cl− + 0.25O2 | −9.885 |
| K(OH)(aq) + H+ ⇔ K+ + H2O | 14.460 | FeOH+ + H+ ⇔ Fe2++ H2O | 9.500 |
| MgCl+ ⇔ Mg2+ + Cl− | −0.350 | Fe(OH)3− + 3H+ ⇔ Fe2+ + 3H2O | 31.900 |
| MgCO3(aq) + H+ ⇔ Mg2+ + HCO3− | 7.350 | Fe(OH)2(aq) + 2H+ ⇔ Fe2++ 2H2O | 20.60 |
| MgHCO3+ ⇔ Mg2+ + HCO3− | −1.040 | Fe(OH)2+ ⇔ Fe2++ 0.5H2O + 0.25O2 | −6.295 |
| MgSO4(aq) ⇔ Mg2+ + SO42− | −2.230 | Fe(SO4)2− + 0.5H2O ⇔ Fe2+ + H+ + 0.25O2 + 2SO42− | −13.885 |
| Mg(H3SiO4)+ H+ ⇔ Mg2+ + H4SiO4(aq) | 8.580 | FeSO4(aq) ⇔ Fe2+ + SO42− | −2.200 |
| Na(CO3)− + H+ ⇔ Na+ + HCO3− | 9.060 | FeHSO42+ + 0.5H2O ⇔ Fe2+ + 2H+ + 0.25O2 + SO42− | −12.955 |
| Mineral Dissolution/Precipitation Reactions | Log K (25 °C) | Mineral Dissolution/Precipitation Reactions | Log K (25 °C) |
| Calcite + H+ ⇔ Ca2+ + HCO3− | 1.850 | Magnetite + 6H+ ⇔ 3Fe2+ + 3H2O + 0.5O2(aq) | −6.560 |
| Gypsum ⇔ Ca2+ + SO42− + 2H2O | −4.610 | Hematite + 4H+ ⇔ 2Fe2+ + 2H2O + 0.5O2(aq) | −17.990 |
| Quartz + 2H2O ⇔ H4SiO4(aq) | −3.740 | Goethite + 2H+ ⇔ Fe2+ + 1.5H2O + 0.25O2(aq) | −8.095 |
| Fe(s) + 2H+ + 0.5O2 (aq) ⇔ Fe2+ + H2O | 58.85 | ||
| Cation Exchange Reactions | KNa-cation | Cation Exchange Reactions | KNa-cation |
| Na+ + X-K ⇔ K+ + X-Na | 0.138 | Na+ + 0.5X2-Mg ⇔ 0.5Mg2+ + X-Na | 0.288 |
| Na+ + 0.5X2-Ca ⇔ 0.5Ca2+ + X-Na | 0.294 | Na+ + 0.5X2-Fe ⇔ 0.5Fe2+ + X-Na | 0.5 |
| Surface Complexation Reactions | Log Kint | Surface Complexation Reactions | Log Kint |
| SSOH2+ ⇔ SSOH + H+ | −4.5 | SW2O− + H+⇔ SW2OH | 10.5 |
| SSO− + H+ ⇔ SSOH | 7.9 | SsOFe+ + H+ ⇔ SsOH + Fe2+ | 0.6 |
| SW1OH2+ ⇔ SW1OH + H+ | −4.5 | SsOFeOH + 2H+ ⇔ SsOH + Fe2+ + H2O | 10.0 |
| SW1O− + H+ ⇔ SW1OH | 7.9 | SsOFe(OH)2− + 3H+ ⇔ SsOH + Fe2+ + 2H2O | 20.0 |
| SW2OH2+ ⇔ SW2OH + H+ | −6.0 | SW1OFe+ + H+ ⇔ SW1OH + Fe2+ | 3.3 |
| Parameter | Bentonite |
|---|---|
| Hydraulic conductivity (m/d) | 4.4 × 10−9 |
| Porosity | 0.407 |
| Retention curve relating water saturation degree Sw to suction φ (kPa) | |
| Solid density (kg/m3) | 2700 |
| Specific heat of the solid (cal/g °C) | 0.202 |
| Thermal conductivity of the solid (W/m °C) | 1.15 |
| Effective diffusion coefficient (m2/s) | 4.07 × 10−12 |
| Bentonite | Granite | |
|---|---|---|
| pH | 7.72 | 8.35 |
| O2(aq) (mol/L) | 3.30 × 10−4 | 6.0 × 10−13 |
| Na+ (mol/L) | 1.3 × 10−1 | 3.8 × 10−4 |
| K+ (mol/L) | 1.7 × 10−3 | 7.8 × 10−6 |
| Ca2+ (mol/L) | 2.2 × 10−2 | 1.8 × 10−4 |
| Mg2+ (mol/L) | 2.3 × 10−2 | 1.3 × 10−6 |
| Fe2+ (mol/L) | 8.0 × 10−11 | 1.0 × 10−11 |
| HCO3− (mol/L) | 4.1 × 10−4 | 3.9 × 10−4 |
| SO42− (mol/L) | 3.2 × 10−2 | 7.9 × 10−5 |
| Cl− (mol/L) | 1.6 × 10−1 | 1.3 × 10−5 |
| H4SiO4(aq) (mol/L) | 1.1 × 10−4 | 1.4 × 10−4 |
| t = 0 mol/m | t = 18 Years mol/m | Change mol/m | Change in % of Fe(s) | |
|---|---|---|---|---|
| O2(aq) | 0.006 | 1.47 × 10−4 | −0.0054 | −0.28 |
| H2(aq) | 4.84 × 10−46 | 1.551 | 1.551 | 79.5 |
| Fe(s) | 1.950 | 0.000 | −1.950 | 100 |
| Goethite | 0.033 | 0.888 | 0.855 | 43.83 |
| Hematite | 0.000 | 0.307 | 0.307 | 15.75 |
| Magnetite | 0.000 | 1.08 × 10−4 | 1.08 × 10−4 | 0.01 |
| Sorbed Fe | 1.22 × 10−11 | 0.675 | 0.675 | 34.62 |
| Exchanged Fe | 4.79 × 10−14 | 0.172 | 0.172 | 8.80 |
| Dissolved Fe | 1.35 × 10−9 | 0.007 | 0.007 | 0.36 |
| Total Fe | 1.983 | 2.049 | −0.066 | |
| Error in Fe balance | −0.066 | 3.2% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Samper, J.; Mon, A.; Montenegro, L. Reactive Transport Model of Steel/Bentonite Interactions in the FEBEX In Situ Test. Minerals 2025, 15, 940. https://doi.org/10.3390/min15090940
Samper J, Mon A, Montenegro L. Reactive Transport Model of Steel/Bentonite Interactions in the FEBEX In Situ Test. Minerals. 2025; 15(9):940. https://doi.org/10.3390/min15090940
Chicago/Turabian StyleSamper, Javier, Alba Mon, and Luis Montenegro. 2025. "Reactive Transport Model of Steel/Bentonite Interactions in the FEBEX In Situ Test" Minerals 15, no. 9: 940. https://doi.org/10.3390/min15090940
APA StyleSamper, J., Mon, A., & Montenegro, L. (2025). Reactive Transport Model of Steel/Bentonite Interactions in the FEBEX In Situ Test. Minerals, 15(9), 940. https://doi.org/10.3390/min15090940









