Occurrence State and Controlling Factors of Methane in Deep Marine Shale: A Case Study from Silurian Longmaxi Formation in Sichuan Basin, SW China
Abstract
1. Introduction
2. Geological Setting
3. Models and Methods
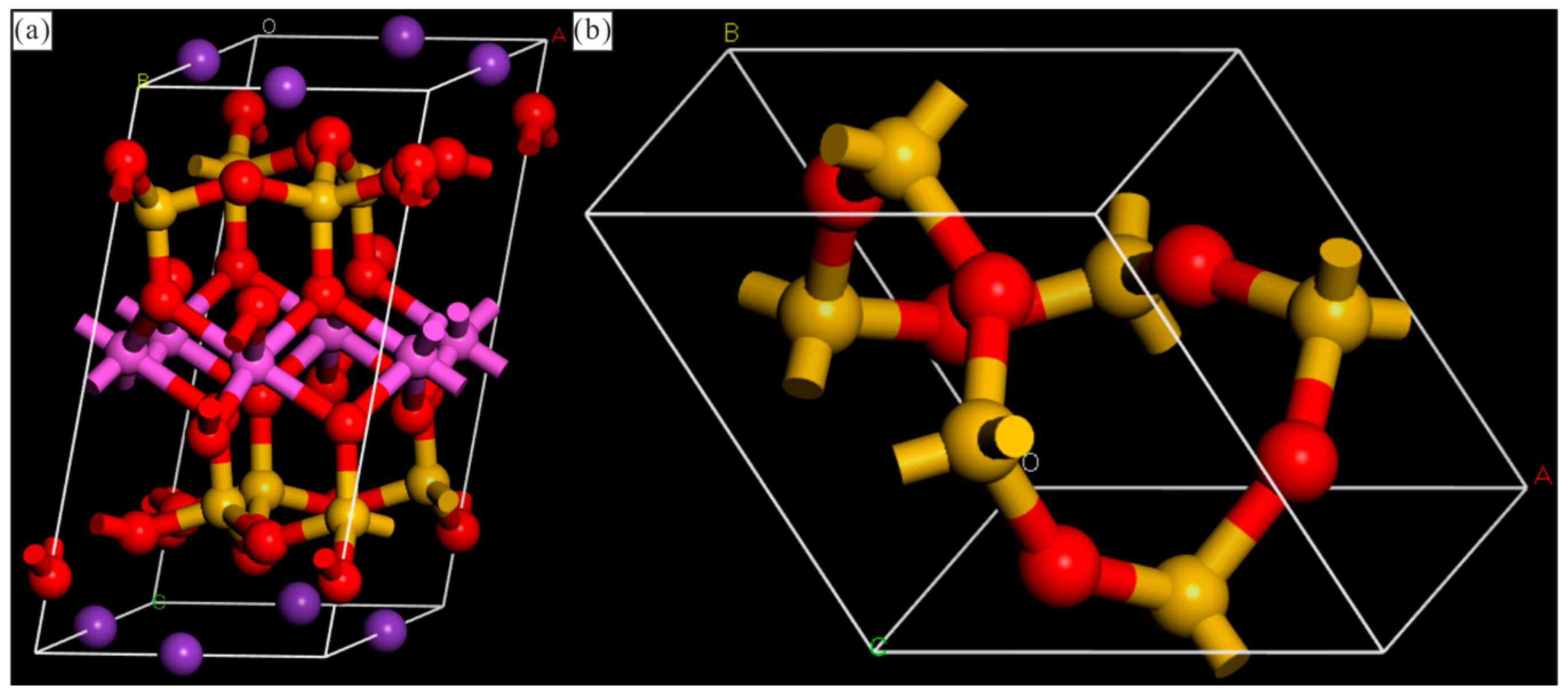
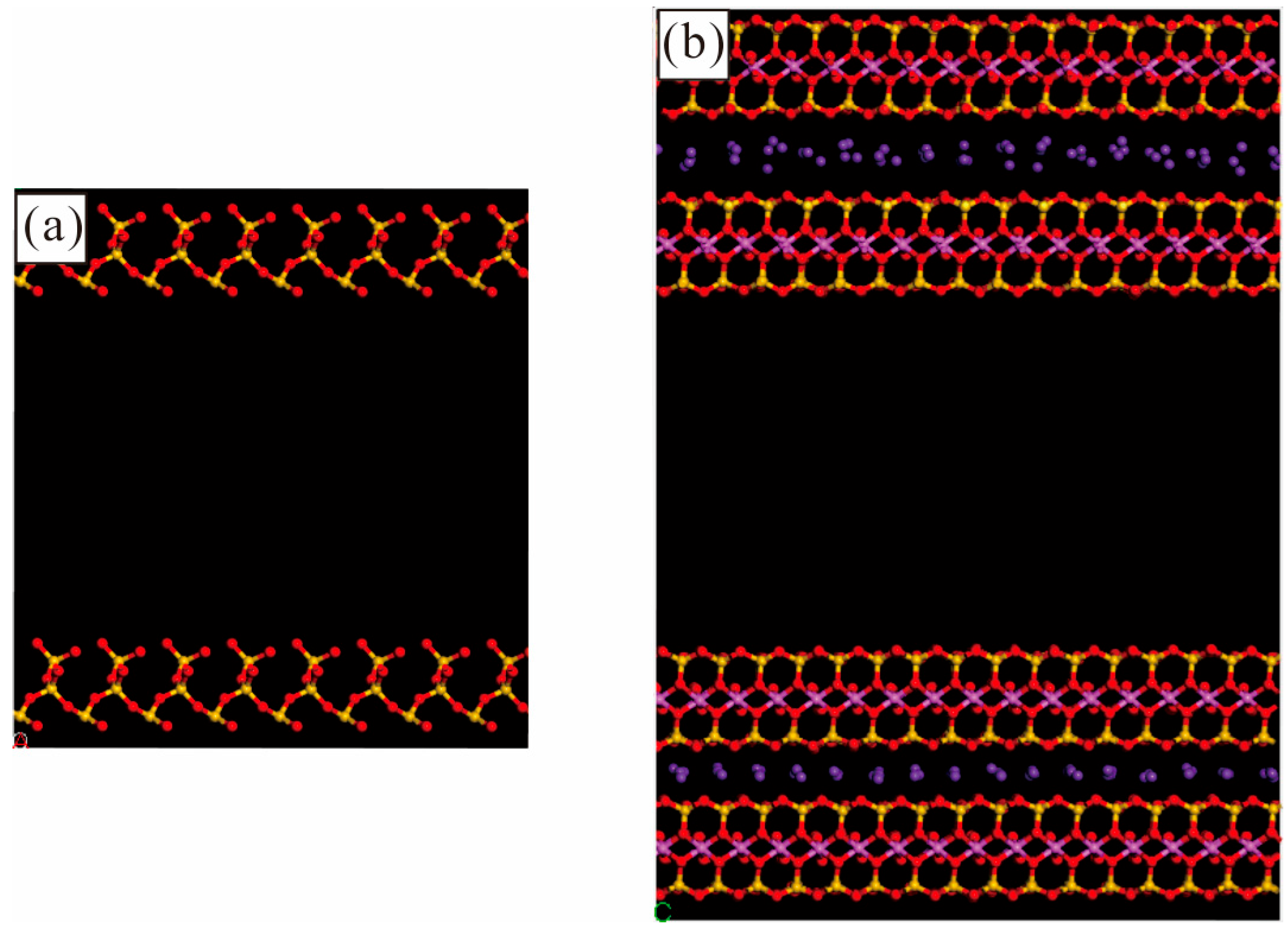
3.1. Shale Composition and Pore Morphology
3.2. Simulation Details
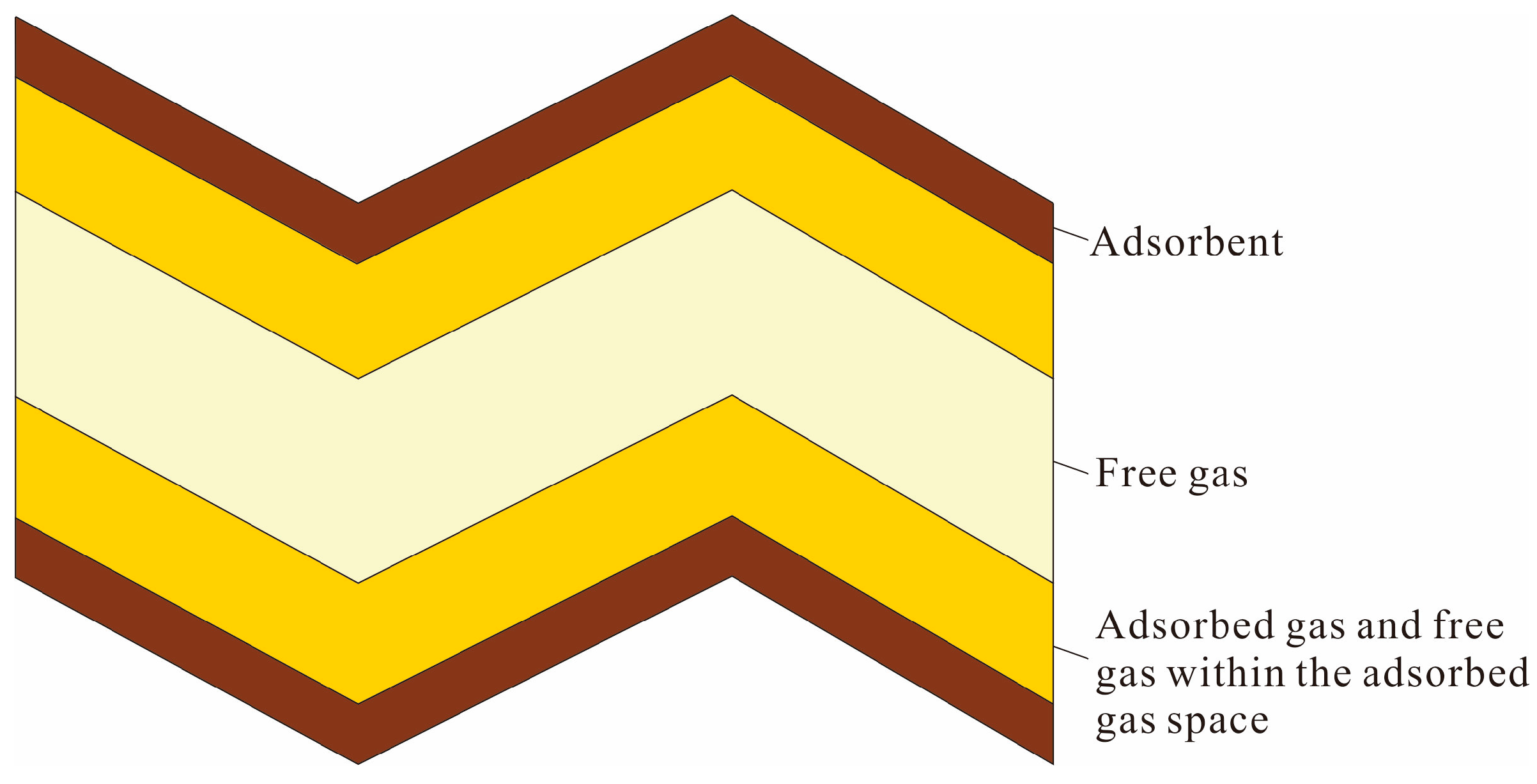
3.3. Excess Adsorption Calculation
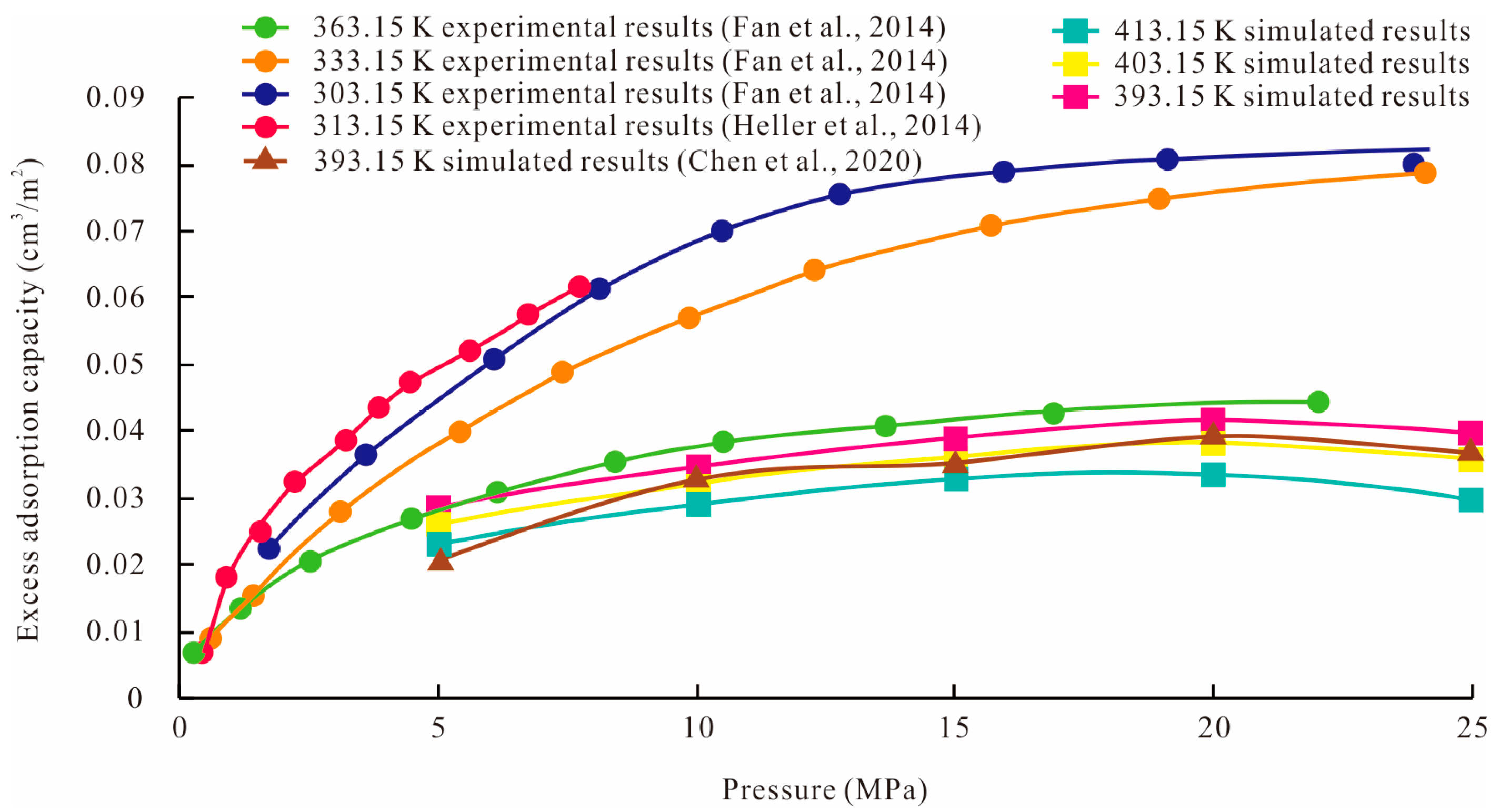
3.4. Validity of Simulation Results
4. Results and Discussion
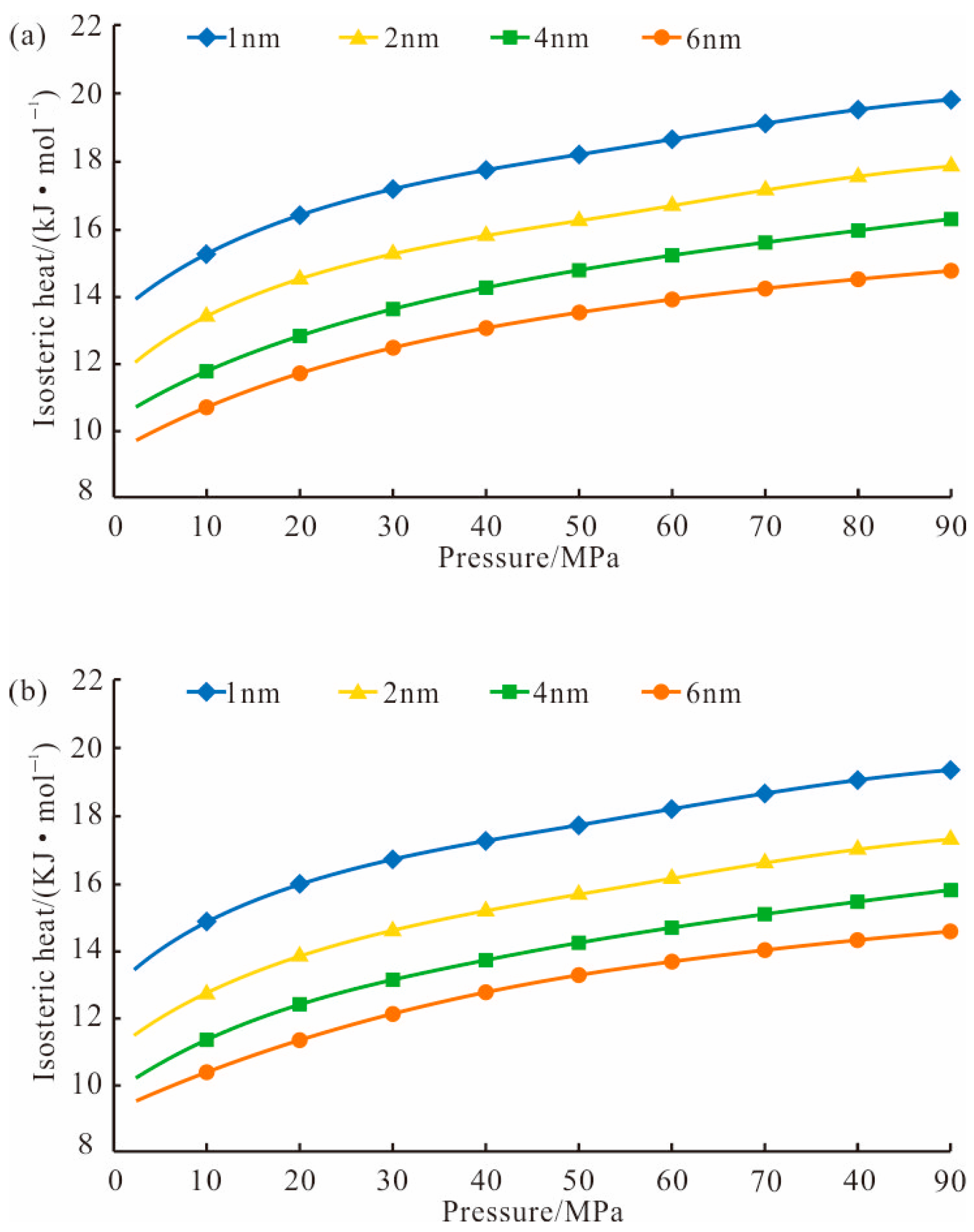
4.1. Methane Isosteric Adsorption Heat
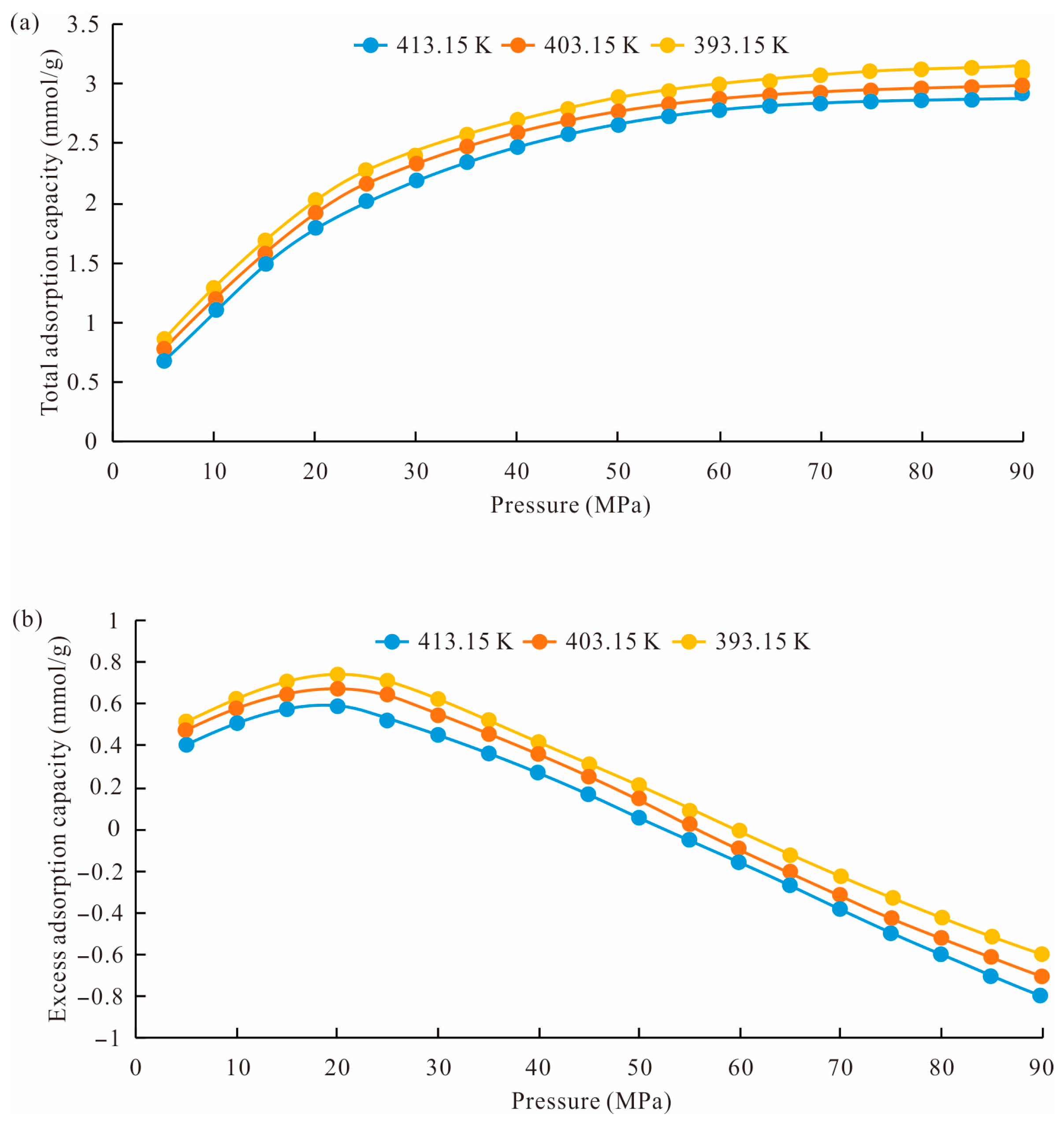
4.2. The Effect of Temperature and Pressure on the Shale Adsorption Capacity
4.3. Effect of Pore Size
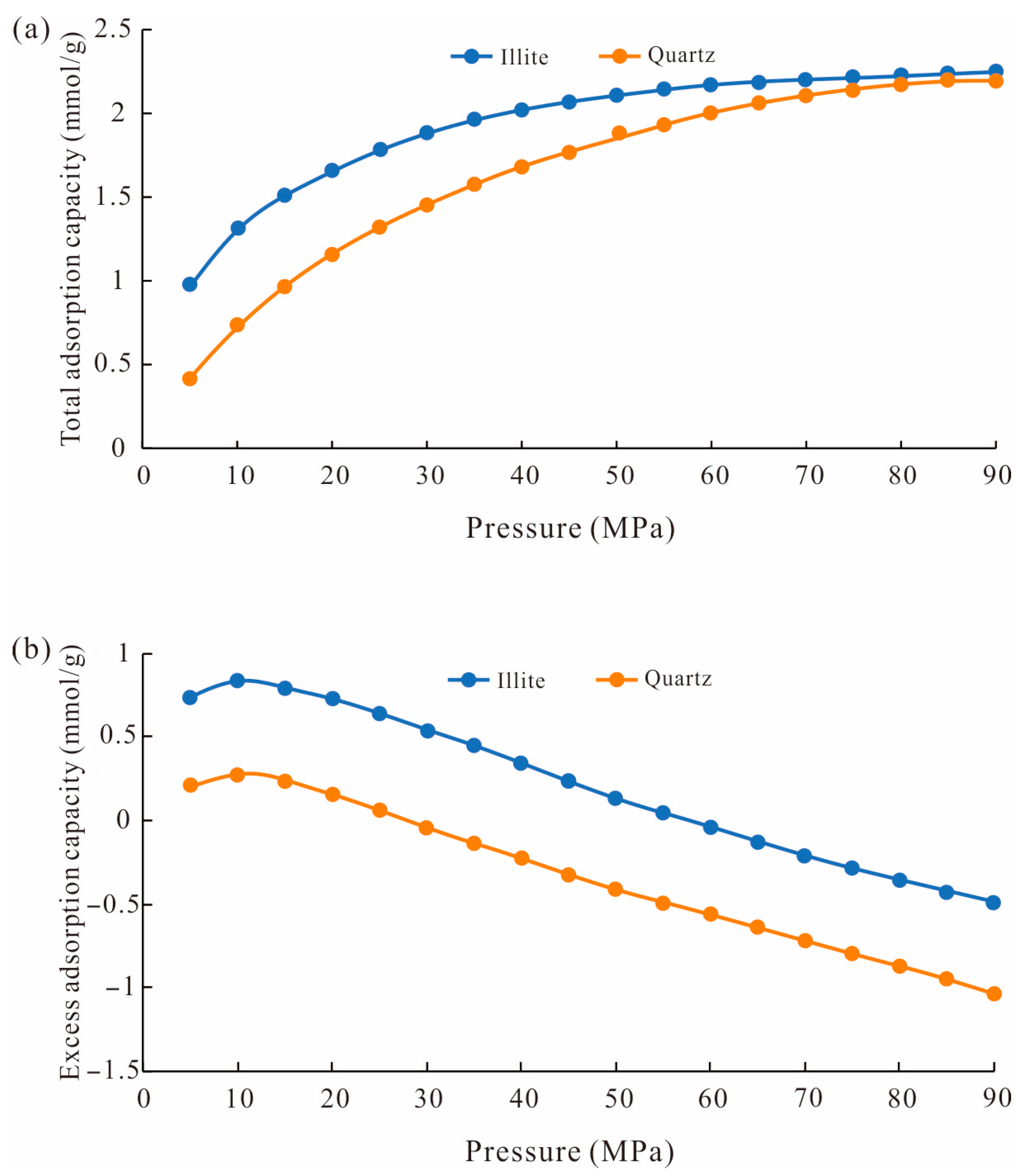
4.4. Effect of Mineral Type
5. Conclusions
- Based on XRD and another method, the pore simulation units of the Longmaxi Formation in the Luzhou area were established, the reliability of each unit was verified, and the methane adsorption simulation of the Longmaxi Formation under in situ conditions was carried out. The isosteric adsorption heat of quartz and illite was less than 42 KJ/mol, which proved that the methane adsorption in the Longmaxi Formation was physical adsorption.
- The methane total adsorption capacity and excess adsorption capacity decreased with the temperature increase. The excess adsorption capacity increased first and then decreased with the increase in pressure. When the pressure reached a high level, the excess adsorption capacity could be negative. And the total methane adsorption capacity was controlled by accommodation space and increased with pore size, while the excess adsorption capacity was affected by the adsorption potential and decreased with the pore size.
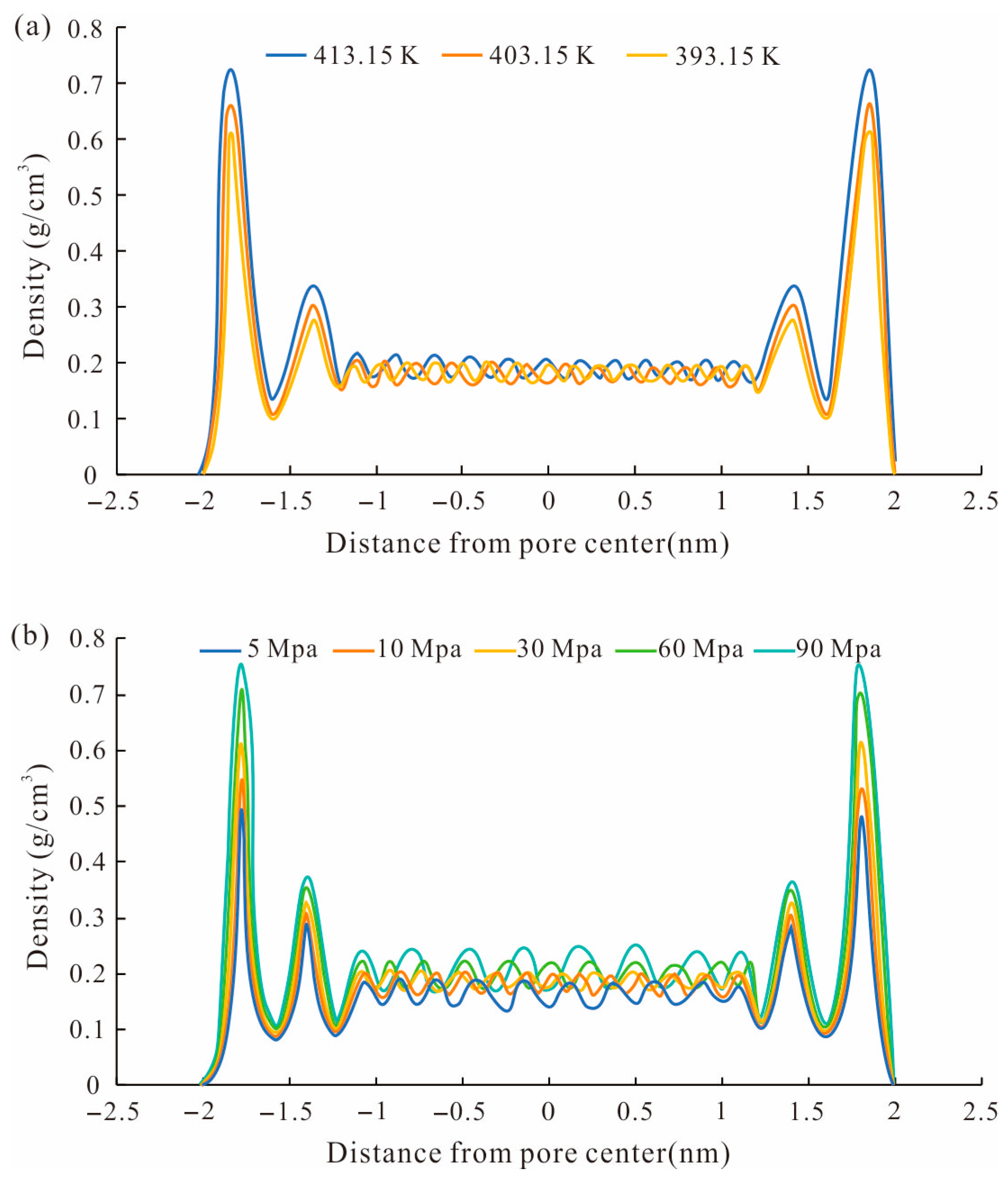
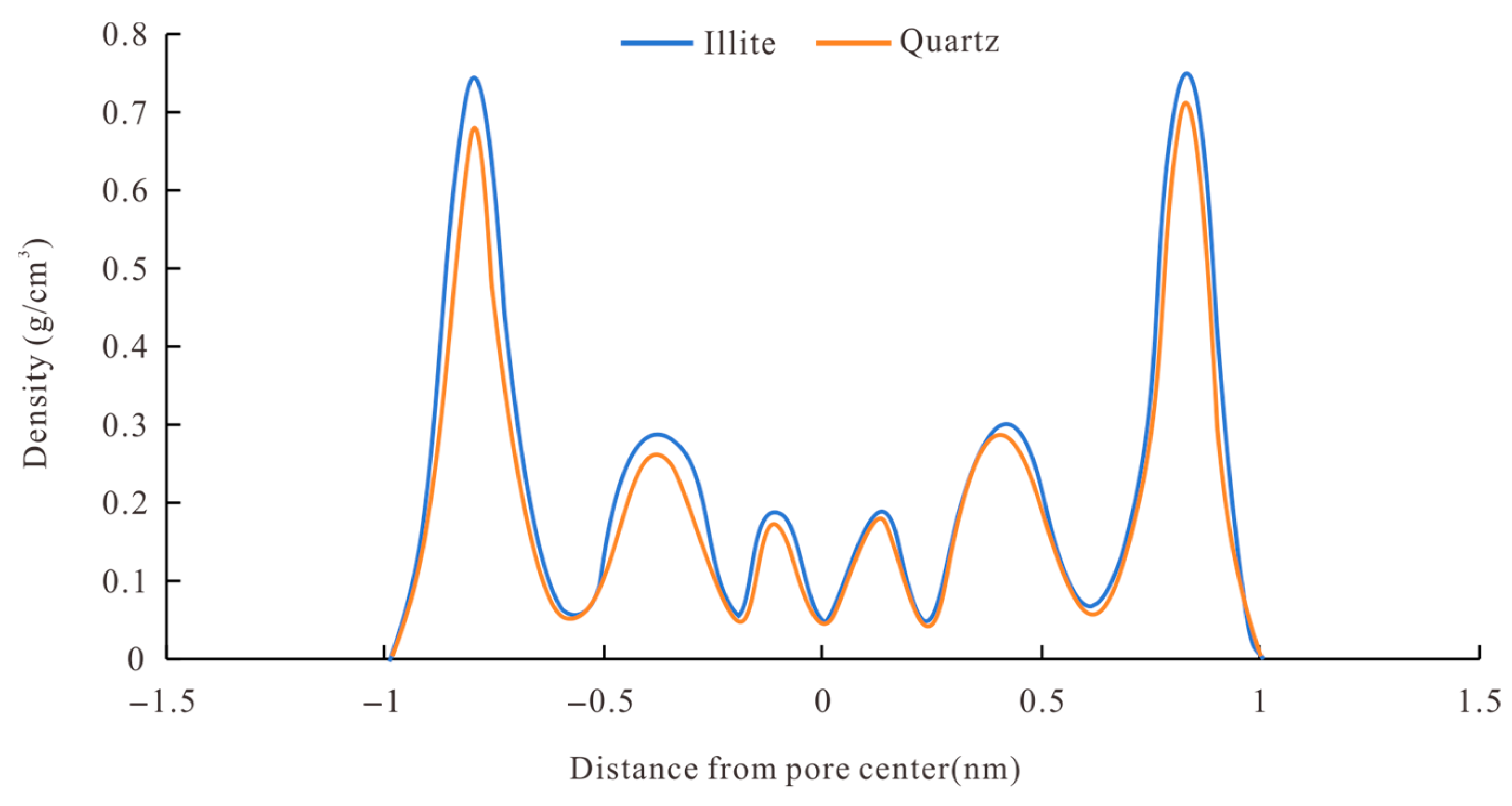
- The adsorbed methane mainly occurred near the pore wall, which was double-layer adsorption, and in thinner pores, there was single-layer adsorption. Methane density distribution in the simulation unit was affected by the mineral types, temperature, and pressure.
- Deep marine shale with high formation pressure and high clay mineral content is conducive to the microscopic accumulation of shale gas in deep marine shale reservoirs
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jia, C.Z. Breakthrough and significance of unconventional oil and gas to classical petroleum geology theory. Pet. Explor. Dev. 2017, 44, 1–10. [Google Scholar] [CrossRef]
- Zou, C.; Yang, Z.; Zhang, G.; Zhu, R.; Tao, S.; Yuan, X.; Hou, L.; Dong, D.; Guo, Q.; Song, Y.; et al. Theory, Technology and Practice of Unconventional Petroleum Geology. J. Earth Sci. 2023, 34, 951–965. [Google Scholar] [CrossRef]
- Nie, H.; Li, P.; Dang, W.; Ding, J.; Sun, C.; Liu, M.; Wang, J.; Du, W.; Zhang, P.; Li, D.; et al. Enrichment characteristics and exploration directions of deep shale gas of OrdovicianSilurian in the Sichuan Basin and its surrounding areas, China. Pet. Explor. Dev. 2022, 49, 744–757. [Google Scholar] [CrossRef]
- Li, J.; Li, H.; Jiang, W.; Cai, M.; He, J.; Wang, Q.; Li, D. Shale pore characteristics and their impact on the gas-bearing properties of the Longmaxi Formation. Sci. Rep. 2024, 14, 16896. [Google Scholar] [CrossRef]
- Ma, X. A golden era for natural gas development in the Sichuan Basin. Nat. Gas Ind. 2017, 4, 163–173. [Google Scholar] [CrossRef]
- Nie, H.; Jin, Z.; Li, P.; Katz, B.J.; Dang, W.; Liu, Q.; Ding, J.; Jiang, S.; Li, D. Deep shale gas in the Ordovician-Silurian Wufeng–Longmaxi formations of the Sichuan Basin, SW China: Insights from reservoir characteristics, preservation conditions and development strategies. J. Asian Earth Sci. 2023, 244, 105521. [Google Scholar] [CrossRef]
- Ma, X.; Xie, J.; Yong, R.; Zhu, Y. Geological characteristics and high production control factors of shale gas reservoirs in Silurian Longmaxi Formation, southern Sichuan Basin, SW China. Pet. Explor. Dev. 2020, 47, 901–915. [Google Scholar] [CrossRef]
- Li, Y.; Hu, Z.; Duan, X.; Wang, X.; Shi, J.; Zhan, H. The general form of transport diffusivity of shale gas in organic-rich nanoslits—A molecular simulation study using Darken approximation. Fuel 2019, 249, 457–471. [Google Scholar] [CrossRef]
- Shiga, M.; Morishita, T.; Aichi, M.; Sorai, M. Effect of Surface Coverage of Water Molecules on Methane Adsorption on Muscovite and Pyrophyllite: Molecular Dynamics Study. Energy Fuels 2021, 35, 19986–19999. [Google Scholar] [CrossRef]
- Sun, C.; Nie, H.; Su, H.; DU, W.; Lu, T.; Chen, Y.; Liu, M.; Li, J. Porosity, permeability and rock mechanics of Lower Silurian Longmaxi Formation deep shale under temperature-pressure coupling in the Sichuan Basin, SW China. Pet. Explor. Dev. 2023, 50, 95–98. [Google Scholar] [CrossRef]
- Sun, C.; Nie, H.; Dang, W.; Chen, Q.; Zhang, G.; Li, W.; Lu, Z. Shale Gas Exploration and Development in China: Current Status, Geological Challenges, and Future Directions. Energy Fuels 2021, 35, 6359–6379. [Google Scholar] [CrossRef]
- Onawole, A.T.; Nasser, M.S.; Hussein, I.A.; Al-Marri, M.J.; Aparicio, S. Theoretical studies of methane adsorption on Silica-Kaolinite interface for shale reservoir application. Appl. Surf. Sci. 2021, 546, 149164. [Google Scholar] [CrossRef]
- Zhou, W.; Wang, H.; Yang, X.; Liu, X.; Yan, Y. Confinement Effects and CO2/CH4 Competitive Adsorption in Realistic Shale Kerogen Nanopores. Ind. Eng. Chem. Res. 2020, 59, 6696–6706. [Google Scholar] [CrossRef]
- Gasparik, M.; Rexer, T.F.T.; Aplin, A.C.; Billemont, P.; De Weireld, G.; Gensterblum, Y.; Henry, M.; Krooss, B.M.; Liu, S.; Ma, X.; et al. First international inter-laboratory comparison of high-pressure CH4, CO2 and C2H6 sorption isotherms on carbonaceous shales. Int. J. Coal Geol. 2014, 132, 131–146. [Google Scholar] [CrossRef]
- Xiong, J.; Liu, X.; Liang, L.; Zeng, Q. Adsorption of methane in organic-rich shale nanopores: An experimental and molecular simulation study. Fuel 2017, 200, 299–315. [Google Scholar] [CrossRef]
- Wang, T.; Tian, S.; Li, G.; Zhang, L.; Sheng, M.; Ren, W. Molecular simulation of gas adsorption in shale nanopores: A critical review. Renew. Sustain. Energy Rev. 2021, 149, 111391. [Google Scholar] [CrossRef]
- Lu, S.; Shen, B.; Xu, C.; Chen, G.; Liu, L.; Xue, Q.; Fang, Z.; He, X. Study on Adsorption Behavior and Mechanism of Shale Gas by Using GCMC Molecular Simulation. Earth Sci. 2018, 43, 1783–1791. [Google Scholar] [CrossRef]
- Grinev, I.V.; Zubkov, V.V.; Samsonov, V.M. Calculation of isosteric heats of molecular gas and vapor adsorption on graphite using density functional theory. Colloid J. 2016, 78, 37–46. [Google Scholar] [CrossRef]
- Wu, J.; Zhao, S.; Li, B.; Liu, Y.; Huang, S.; He, Y.; Wan, S.; Liu, S.; Long, H.; Wang, G.; et al. Occurrence law of pore water in shale matrix: A case study of the Silurian Longmaxi Formation in southern Sichuan Basin. Nat. Gas Ind. 2023, 43, 44–54. [Google Scholar] [CrossRef]
- Sneha, R.; Eswaean, P.; Prusty, B.K. Review of gas adsorption in shales for enhanced methane recovery and CO2 storage. J. Pet. Sci. Eng. 2019, 175, 634–643. [Google Scholar] [CrossRef]
- Li, Z.; Jiang, Z.; Liang, Z.; Yu, H.; Yang, Y. Pore-structure characterisation of tectonically deformed shales: A case study of Wufeng-Longmaxi Formation in western Hunan Province, southern China. Aust. J. Earth Sci. 2019, 66, 1075–1084. [Google Scholar] [CrossRef]
- Zou, C.; Dong, D.; Wang, Y.; Li, X.; Huang, J.; Wang, S.; Guan, Q.; Zhang, C.; Wang, H.; Liu, H.; et al. Shale gas in China: Characteristics, challenges and prospects (II). Pet. Explor. Dev. 2016, 43, 182–196. [Google Scholar] [CrossRef]
- Zhu, B.; Meng, J.; Song, C.; Pan, R.; Zhu, Z.; Jin, J. Complexity and Heterogeneity Evaluation of Pore Structures in the Deep Marine Shale Reservoirs of the Longmaxi Formation, China. J. Mar. Sci. Eng. 2023, 11, 1613. [Google Scholar] [CrossRef]
- Tang, L.; Song, Y.; Zhao, Z.; Jiang, Z.; Jiang, S.; Chen, X.; Li, Z.; Li, Q. Origin and evolution of overpressure in shale gas reservoirs of the Upper Ordovician Wufeng Formation-Lower Silurian Longmaxi Formation in the Sichuan Basin. Nat. Gas Ind. 2022, 42, 37–53. [Google Scholar] [CrossRef]
- Li, J.; Li, H.; Yang, C.; Wu, Y.; Gao, Z.; Jiang, S. Geological Characteristics and Controlling Factors of Deep Shale Gas Enrichment of the Wufeng-Longmaxi Formation in the Southern Sichuan Basin, China. Lithosphere 2022, 2022, 4737801. [Google Scholar] [CrossRef]
- Wang, Q.; Mu, Y.; Chen, X.; Song, Z.; Ma, Z.; Qiu, Q. Characteristics of methane isothermal adsorption of deep shale from lower Silurian Longmaxi Formation in southeastern Sichuan Basin and its geological significance. Pet. Geol. Exp. 2022, 44, 180–187. [Google Scholar] [CrossRef]
- Gouenis, D.; Lapps, A.; Karakassides, M.A.; Tobbens, D.; Moukarika, A. A neutron diffraction study of alkali cation migration in montmorillonites. Phys. Chem. Miner. 2008, 35, 49–58. [Google Scholar] [CrossRef]
- Chong, L.; Myshakin, E.M. Molecular simulations of competitive adsorption of carbon dioxide-methane mixture on illitic clay surfaces. Fluid Phase Equilibria 2018, 472, 185–195. [Google Scholar] [CrossRef]
- Zhou, L.; Li, M.; Zhou, Y.P. Experimental and Modeling Study of the Adsorption of Supercritical Methane on a High Surface Activated Carbon. Sci. China Ser. B 2000, 30, 49–56. [Google Scholar] [CrossRef]
- Huang, L.; Ning, Z.; Wang, Q.; Qi, R.; Zeng, Y.; Qin, H.; Ye, H.; Zhang, W. Molecular simulation of adsorption behaviors of methane, carbon dioxide and their mixtures on kerogen: Effect of kerogen maturity and moisture content. Fuel 2018, 211, 159–172. [Google Scholar] [CrossRef]
- Huang, L.; Chen, Q.; Wu, J.; Yang, Q.; Zhang, J.; Huang, S.; Zhou, W.; Zou, J. Molecular simulation of methane adsorption characteristics in illite nanopores of deep shale reservoirs. J. Cent. South Univ. Sci. Technol. 2022, 53, 3522–3531. [Google Scholar] [CrossRef]
- Wang, H.; Qu, Z.; Yin, Y.; Bai, J.; Yu, B. Review of Molecular Simulation Method for Gas Adsorption/desorption and Diffusion in Shale Matrix. J. Therm. Sci. 2019, 28, 1–16. [Google Scholar] [CrossRef]
- Peng, D.Y.; Robinson, D.B. A new two-constant equation of state. Industrial and engineering chemistry fundamentals. Ind. Eng. Chem. Fundam. 1976, 15, 3069–3078. [Google Scholar] [CrossRef]
- Chen, G.; Lu, S.; Liu, K.; Han, T.; Xu, C.; Xue, Q.; Shen, B.; Guo, Z. GCMC simulations on the adsorption mechanisms of CH4 and CO2 in K-illite and their implications for shale gas exploration and development. Fuel 2018, 224, 521–528. [Google Scholar] [CrossRef]
- Song, W.; Yao, J.; Zhang, K. Study on gas adsorption and transport behavior in shale organic nanopore. Chin. J. Theor. Appl. Mech. 2021, 53, 2179–2192. [Google Scholar] [CrossRef]
- Fan, E.; Tang, S.; Zhang, C.; Guo, Q.; Sun, C. Methane sorption capacity of organics and clays inhigh-over matured shale-gas systems. Energy Explor. Exploit. 2014, 32, 927–942. [Google Scholar] [CrossRef]
- Heller, R.; Zoback, M. Adsorption of methane and carbon dioxide on gas shale and pure mineral samples. J. Unconv. Oil Gas Resour. 2014, 8, 14–24. [Google Scholar] [CrossRef]
- Chen, G.; Lu, S.; Liu, K.; Xu, C.; Xue, Q.; Tian, S.; Li, J.; Lu, S.; Zhang, Y. Occurrence state and micro mechanisms of shale gas on pore walls. Earth Sci. 2020, 45, 1782–1790. [Google Scholar] [CrossRef]
- Chen, L.; Zuo, L.; Jiang, Z.; Jiang, S.; Liu, K.; Tan, J.; Zhang, L. Mechanisms of shale gas adsorption: Evidence from thermodynamics and kinetics study of methane adsorption on shale. Chem. Eng. J. 2019, 361, 559–570. [Google Scholar] [CrossRef]
- Tian, H.; Li, T.; Zhang, T.; Xiao, X. Characterization of methane adsorption on overmature Lower Silurian-Upper Ordovician shales in Sichuan Basin, southwest China: Experimental results and geological implications. Int. J. Coal Geol. 2016, 156, 36–49. [Google Scholar] [CrossRef]
- Amam, N. Sorption and desorption of gases (CH4, CO2). on hard coal and active carbon at elevated pressures. Fuel 1998, 77, 1243–1246. [Google Scholar] [CrossRef]
- Zhou, X.; Yi, H.; Tang, X.; Deng, H.; Liu, H. Thermodynamics for the adsorption of SO2, NO and CO2 from flue gas on activated carbon fiber. Chem. Eng. J. 2012, 200, 399–404. [Google Scholar] [CrossRef]
- Ge, S.; Tan, W.; Li, H.; Wang, Y.; Niu, P.; Qin, Q. Mineralogical and Lithofacies Controls on Gas Storage Mechanisms in Organic-Rich Marine Shales. Energy Fuels 2025, 39, 3846–3858. [Google Scholar] [CrossRef]
- Yang, X.; Chen, Z.; Liu, X.; Xue, Z.; Yue, F.; Wen, J.; Li, M.; Xue, Y. Correction of gas adsorption capacity in quartz nanoslit and its application in recovering shale gas resources by CO2 injection: A molecular simulation. Energy 2022, 240, 122789. [Google Scholar] [CrossRef]







| Pressure/MPa | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Temperature/K | |||||||||||||||||||
| 393.15 | 25.36 | 51.69 | 77.92 | 103.13 | 126.74 | 148.49 | 168.36 | 186.44 | 202.91 | 217.93 | 231.67 | 244.30 | 255.92 | 266.66 | 276.64 | 285.91 | 294.58 | 302.69 | |
| 403.15 | 24.63 | 50.06 | 75.34 | 99.66 | 122.52 | 143.68 | 163.11 | 180.88 | 197.13 | 212.01 | 225.67 | 238.25 | 249.87 | 260.63 | 270.63 | 279.96 | 288.68 | 296.86 | |
| 413.15 | 23.95 | 48.55 | 72.95 | 96.45 | 118.61 | 139.20 | 158.20 | 175.65 | 191.67 | 206.40 | 219.97 | 232.50 | 244.08 | 254.85 | 264.87 | 274.23 | 283.00 | 291.22 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pu, J.; Luo, T.; Li, Y.; Jiang, H.; Qi, L. Occurrence State and Controlling Factors of Methane in Deep Marine Shale: A Case Study from Silurian Longmaxi Formation in Sichuan Basin, SW China. Minerals 2025, 15, 820. https://doi.org/10.3390/min15080820
Pu J, Luo T, Li Y, Jiang H, Qi L. Occurrence State and Controlling Factors of Methane in Deep Marine Shale: A Case Study from Silurian Longmaxi Formation in Sichuan Basin, SW China. Minerals. 2025; 15(8):820. https://doi.org/10.3390/min15080820
Chicago/Turabian StylePu, Junwei, Tongtong Luo, Yalan Li, Hongwei Jiang, and Lin Qi. 2025. "Occurrence State and Controlling Factors of Methane in Deep Marine Shale: A Case Study from Silurian Longmaxi Formation in Sichuan Basin, SW China" Minerals 15, no. 8: 820. https://doi.org/10.3390/min15080820
APA StylePu, J., Luo, T., Li, Y., Jiang, H., & Qi, L. (2025). Occurrence State and Controlling Factors of Methane in Deep Marine Shale: A Case Study from Silurian Longmaxi Formation in Sichuan Basin, SW China. Minerals, 15(8), 820. https://doi.org/10.3390/min15080820





