Quantitative Analysis of Yield Stress and Its Evolution in Fiber-Reinforced Cemented Paste Backfill

Abstract

Fiber-reinforced cemented paste backfill (FR-CPB) has attracted considerable attention in modern mining applications due to its superior mechanical properties and adaptability. Despite its potential, understanding its rheological behavior remains limited, largely because of the absence of quantitative methods for assessing fiber packing behavior within CPB. This study develops a rheology-based approach to determine the maximum packing fraction of polypropylene fibers in fresh CPB, revealing that shorter fibers (3 mm) achieve a maximum packing fraction of 0.661, significantly higher than longer fibers (12 mm) with 0.534. Building on these findings, a quantitative model for the static yield stress of FR-CPB was developed, showing that under a high fiber content (0.9%) and with longer fibers (12 mm), the yield stress reached 274.34 kPa, a 40% increase compared to shorter fibers. Additionally, the study modeled the time-dependent evolution of yield stress, achieving a prediction accuracy with a correlation coefficient of 0.92. These advancements enable the optimization of FR-CPB composition, which can reduce material usage, enhance pipeline transport efficiency, and improve backfill stability in underground voids. By minimizing the risk of structural failure and optimizing resource allocation, this research provides a theoretical foundation for safer and more cost-effective mining operations.

1. Introduction

Cemented paste backfill (CPB), composed of tailings, cementitious materials, and water, is an environmentally friendly construction material extensively utilized in mine backfill operations [1,2,3,4,5]. This material not only facilitates the resourceful utilization of tailings but also ensures the stability of underground structures by filling voids created during mining [6,7,8]. However, the CPB’s inherent brittleness under complex in situ loading conditions can result in catastrophic failure, posing significant safety risks to underground mines [9]. To address this limitation, fiber-reinforced CPB (FR-CPB) has emerged as a prominent research focus, offering substantial potential to enhance toughness and deformation resistance [10,11].

In recent years, research on FR-CPB has grown significantly. Studies have demonstrated that incorporating fibers such as polypropylene fibers [12,13,14], steel fibers [15,16], or polyacrylonitrile fibers [17,18] into CPB markedly enhances its tensile strength, toughness, and shear resistance. Different fiber types exhibit unique reinforcement characteristics, and researchers have extensively investigated the effects of fiber type, content, and distribution on the mechanical properties of FR-CPB [12,13,19,20]. Findings have revealed that fiber addition effectively suppresses crack propagation and enhances deformation resistance by forming a three-dimensional network structure [21,22,23]. Furthermore, fiber incorporation significantly improves the impact resistance of material, increasing its resilience under sudden stress [24]. In fact, impact resistance can be enhanced by up to 30%–40% depending on the type and quantity of the fiber incorporated [25]. Beyond mechanical properties, the rheological behavior of CPB is a critical factor influencing its engineering applications, as it directly affects pipeline transportation efficiency [26]. However, existing research predominantly focuses on the hardened properties of FR-CPB, with relatively few studies examining its rheological behavior, particularly the packing behavior of fibers in backfill materials and their significant influence on rheological performance. Understanding the mechanisms through which fibers affect the rheological properties of backfill is crucial for optimizing FR-CPB design and enhancing construction efficiency.

The maximum packing fraction (${\varphi }_{fm}$) of fibers is a key factor influencing the rheological properties of fiber-reinforced cement-based materials [27]. Martinie et al. [28] proposed that ${\varphi }_{fm}$ is an important parameter for describing the yield stress of cementitious materials containing steel fibers. This conclusion was also drawn by Guo et al. [29] in their study of cement pastes incorporating flexible fibers. The packing behavior of fibers in these materials is closely linked to their length, diameter, surface morphology and the matrix’s water-to-cement ratio [30]. In CPB, the high water content and low cement dosage result in more complex fiber distribution and packing behavior compared to ordinary cement paste [31]. Consequently, existing studies [27,28,29] on fiber packing in cement paste cannot be directly applied to CPB. For example, the high water content in CPB promotes fiber aggregation, which negatively impacts slurry uniformity and, in turn, its rheological performance [32]. Currently, effective methods for measuring the ${\varphi }_{fm}$ of fibers in CPB are lacking, posing challenges for studying and optimizing the rheological properties of FR-CPB. Therefore, systematic research on ${\varphi }_{fm}$ of fibers in CPB, particularly regarding measurement methods, is essential.

Static yield stress (hereafter referred to as yield stress) is a key rheological parameter for assessing the shear resistance of CPB, significantly influencing its stability and transport performance [33]. Excessive yield stress can hinder material transportation, reducing construction efficiency, while insufficient yield stress may compromise the stability of the backfill within voids. Thus, precise control of yield stress is essential to ensure the transportability and long-term stability of CPB. Furthermore, understanding the evolution of yield stress is critical for predicting the material’s behavior under prolonged loading. In practical applications, CPB must maintain long-term stability within voids, and both the magnitude and evolution of yield stress are directly linked to the backfill’s reliability and safety [34]. However, quantitative studies on the yield stress and its evolution in FR-CPB are limited, constraining efforts to predict and optimize its performance in complex underground environments.

In response to the aforementioned issues, this study prepared polypropylene (PP) fibers of varying lengths and formulated FR-CPB with different fiber contents. Additionally, the packing behavior of PP fibers in CPB, as well as the yield stress and its evolution in FR-CPB, were investigated. This study addresses the aforementioned gaps by introducing a novel rheology-based method to determine ${\varphi }_{fm}$ of PP fibers in CPB. This innovative method is inspired by the dynamic response of particle flocs under shear, allowing the quantitative characterization of fiber packing behavior within fresh CPB. To the best of our knowledge, this is the first systematic attempt to apply such a methodology in the context of FR-CPB, enabling a more precise optimization of fiber content and length for tailored material performance. The findings are expected to provide a robust scientific foundation and technical guidance for the practical application of FR-CPB in engineering projects.

2. Methodology

Unlike rigid fibers, flexible fibers such as PP fibers tend to deform under shear, deviating from their original conformation and orientation [35]. This is similar to the flocs’ structural response when subjected to shear, i.e., deformation, deflocculation, and rearrangement (Figure 1a). The structural changes in flocs are accompanied by changes in the rheological properties of the suspension. Based on this, Tregger et al. [36] obtained ${\varphi }_{fm}$ of cement particles. Therefore, flexible fibers can be regarded as a unique form of flocs, and the rheological response corresponding to the change in fiber morphology can serve to obtain ${\varphi }_{fm}$ of the fibers. This is the core idea of the shear rheology-based approach proposed to measure ${\varphi }_{fm}$ of flexible fibers.

According to the results of Sultangaliyeva et al. [27], the viscosity of fiber-reinforced cement-based materials with respect to the volume fraction of fibers is as follows:

$$\begin{array}{c}{\displaystyle \frac{{\eta }^{\prime }}{{\eta }^{″}}}={\left(1-{\displaystyle \frac{{\varphi }_f}{{\varphi }_{fm}}}\right)}^{-2}\end{array}$$

(1)

where ${\eta }^{\prime }$ and ${\eta }^{″}$ represent the viscosity of the suspension and the suspending medium, respectively, ${\varphi }_f$ is the fiber volume fraction, and ${\varphi }_{fm}$ is the maximum packing fraction of the fibers.

It should be noted that, due to the different conformations and orientations of flexible fibers under various shear conditions, ${\varphi }_{fm}$ in Equation (1) more accurately represents the flexible fibers’ packing fraction in a specific deformation state. Considering the dynamic nature of the packing fraction, ${\varphi }_{fm}$ in Equation (1) can be replaced by the effective maximum packing fraction ${\varphi }_{fmeff}\left(\tau \right)$. As the shearing effect increases, the flexible fibers continuously straighten and rearrange, causing ${\varphi }_{fmeff}\left(\tau \right)$ to increase until it stabilizes (Figure 1b). In addition, to enhance the model’s flexibility, an adjusting parameter $“k”$ is introduced, referencing the results of Tregger et al. [36]. In summary, Equation (1) can be further expressed as

If $\tau >{\tau }^{\prime }$

$$\begin{array}{c}\eta \left(\tau \right)={\left[k\left(1-{\displaystyle \frac{{\varphi }_f}{{\varphi }_{fmeff}\left(\tau \right)}}\right)\right]}^{-2}\end{array}$$

(2)

If $\tau \to \mathrm{\infty }$ $\left(\tau \gg {\tau }^{\prime }\right)$

$$\begin{array}{c}\eta ={\left[k^{\prime }\left(1-{\displaystyle \frac{{\varphi }_f}{{\varphi }_{fm}}}\right)\right]}^{-2}\end{array}$$

(3)

where $\eta \left(\tau \right)$ represents the ratio of the suspension’s viscosity to that of the suspending medium, with this ratio being dependent on the shear stress $\tau$; ${\tau }^{\prime }$ denotes the yield stress of the suspension. When $\tau \gg {\tau }^{\prime }$, $\eta \left(\tau \right)$ becomes independent of the shear effect, corresponding to the adjusting parameter $k^{\prime }$.

According to Equations (2) and (3), ${\varphi }_{fm}$ can be directly obtained through experiments with the following steps. First, conduct stress ramp-up tests on FR-CPB samples with different fiber contents to obtain the viscosity–shear stress curves (Figure 2a). Then, plot $1-{\left[\eta \left(\tau \right)\right]}^{-1/2}$ against the fiber volume fraction under different shear stresses, as shown in Figure 2b. When ${\varphi }_f$ approaches ${\varphi }_{fmeff}\left(\tau \right)$, $\eta \left(\tau \right)$ tends to infinity, and thus $1-{\left[\eta \left(\tau \right)\right]}^{-1/2}$ approaches one. By fitting the data, the ${\varphi }_{fmeff}\left({\tau }_1\right)$ of flexible fibers under a specific shear stress ${\tau }_1$ can be obtained. Repeat the above steps to obtain the ${\varphi }_{fmeff}\left(\tau \right)$—$\tau$ curve; ${\varphi }_{fm}$ is the volume fraction corresponding to when the curve tends to be stable (Figure 2c).

3. Materials and Experimental Methods

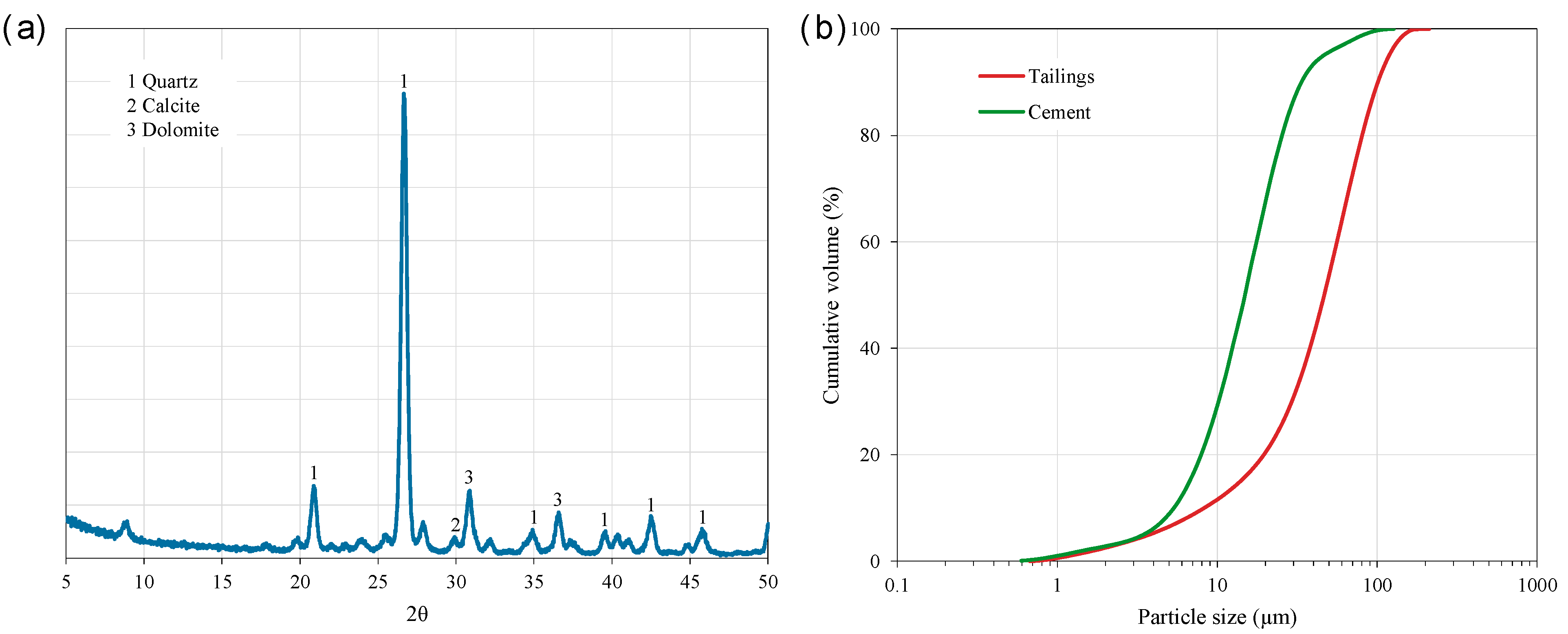
3.1. Raw Materials and Sample Preparation

The materials used to prepare the FR-CPB include tailings, binder, water, and fibers. The tailings used came from a gold mine in northeastern China, with the main components being quartz, calcite, and dolomite (Figure 3a). The content of fines (<20 μm) is 20.66%, classifying it as coarse tailings. The uniformity coefficient and coefficient of curvature of the tailings are 6.81 and 1.81, respectively. The detailed particle size distribution of the tailings is shown in Figure 3b. The specific gravity of the tailings is 2.65. Commercial PO 42.5R ordinary Portland cement (Hailuo brand) was used as the binder in this study to provide the required strength for the material [37]. The particle size distribution of the cement can be seen in Figure 3b. The main chemical components of the cement, determined by X-ray fluorescence (XRF) analysis, are CaO (62.34%), SiO₂ (21.43%), Fe₂O₃ (5.06%), and Al₂O₃ (4.25%), among others [38]. Laboratory tap water was utilized as the mixing water for preparing the backfill samples. Four different lengths of PP fibers (3 mm, 6 mm, 9 mm, and 12 mm) were selected for the experiments in this study. The diameter, density, tensile strength, and Young’s modulus of the fibers are 40 μm, 0.91 g/m³, 398 MPa, and 4.2 GPa, respectively. It should be noted that PP fibers were selected for this study due to their superior mechanical properties (high tensile strength and elasticity modulus), excellent chemical stability in high-alkalinity environments, and cost effectiveness compared to other high-performance fibers [39]. Their lightweight and high toughness enable the formation of a three-dimensional network, enhancing the rheological and mechanical performance of cemented paste backfill [6]. Additionally, their widespread availability and potential applicability to other fiber types make them a practical and insightful choice for this research.

For the mix proportions of the FR-CPB, the solid content and binder dosage were set to 76% and 10%, respectively. As for the fiber content, it varies in different experimental projects. The main scenarios are divided into four categories: determination of ${\varphi }_{fm}$ of PP fibers, yield stress measurement, model validation, and time-dependent yield stress. The specific mix proportions are shown in

Table 1. Summary of the mix compositions of the prepared FR-CPB samples.

Trial Mix	Solid Content (%)	Binder Dosage (%)	Fiber Content		Fiber Length (mm)
			Vol.%	Wt.%
${\varphi }_{fm}$ determination	76	10	0	0	3, 6, 9, 12
			0.08	0.027
			0.1	0.034
Yield stress measurement			0	0
			0.891	0.3
			1.782	0.6
			2.674	0.9
Model validation			0.891	0.3
			1.782	0.6
			2.674	0.9
Time-dependent yield stress			0	0
			0.891	0.3
			1.782	0.6
			2.674	0.9

. The proportions in Table 1 were selected based on a balance between commonly used industrial practices and the specific requirements for evaluating the rheological and mechanical behavior of FR-CPB. After all the raw materials were prepared, the dry materials (cement, tailings, and PP fibers) were mixed for 3 min, and then water was added and mixed for a further 5 min to obtain fresh FR-CPB.

3.2. Experimental Methods

A Brookfield rheometer (RSX-SST), equipped with a four-bladed vane rotor measuring 40 mm in length and 20 mm in diameter, was used in this experiment. Before the main test, pre-shearing was applied at a shear rate of 100 s⁻¹ for 60 s followed by a 30 s resting period. This procedure was intended to eliminate the sample’s shear history and ensure a uniform starting condition for testing [40,41].

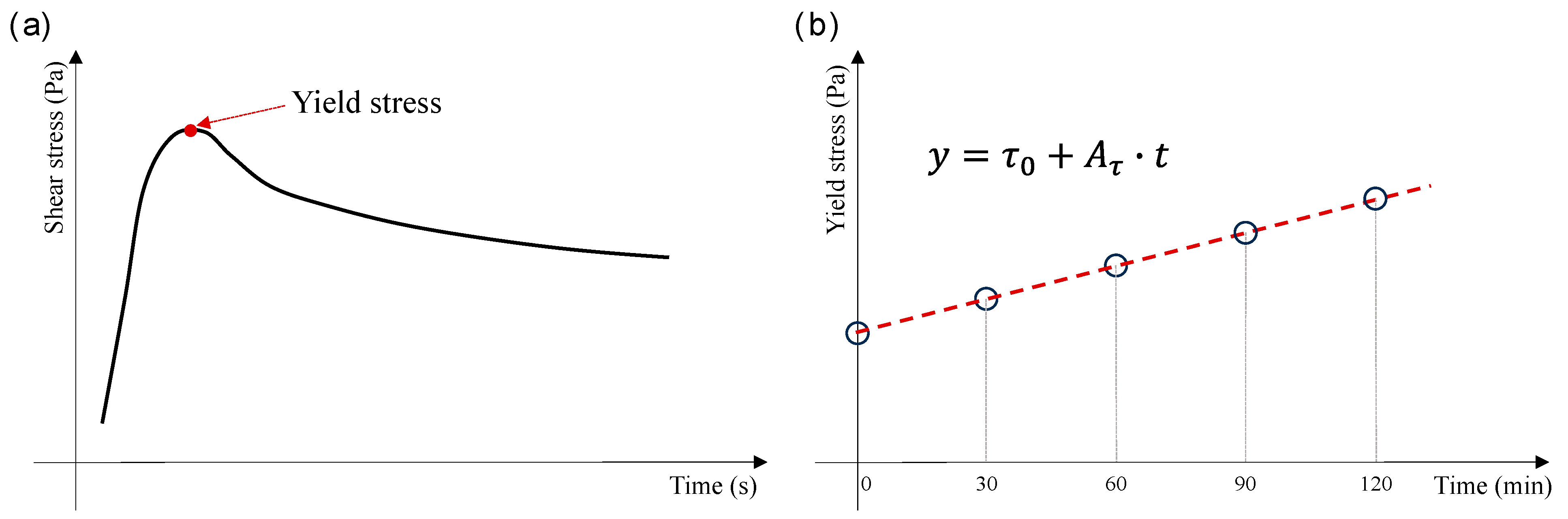
3.2.1. Stress Ramp-Up Test

A stress ramp-up test was performed to generate the flow curves of FR-CPB and to further determine ${\varphi }_{fm}$ of the PP fibers in CPB. During this test, the shear stress increased at a constant rate of 1 Pa/s until reaching 100 Pa. This gradual increase allowed for precise monitoring of the material’s response to varying stress levels, ultimately providing a comprehensive flow curve. The choice of this rheological protocol is, on the one hand, based on [29], and on the other hand, this shear method indeed allows for a comprehensive capture of the configurational changes of the fibers in CPB.

3.2.2. Yield Stress Test

Yield stress tests were conducted to determine the yield stress of FR-CPB. During the experiment, a shear rate of 0.01 s⁻¹ was applied to the samples for 100 s, generating shear stress–time curves. The peak stress on the curve was identified as the yield stress (Figure 4a).

To investigate the evolution of yield stress, tests were performed at intervals of 0, 30, 60, 90, and 120 min. It should be noted that newly prepared samples were used for testing at each time point to prevent structural disturbances or performance variations caused by repeated testing, ensuring the reliability of the results. After all tests were completed, a yield stress–time curve was constructed, and its slope was calculated to represent the yield stress evolution rate ($A_{\tau }$) of the FR-CPB (Figure 4b).

4. Results and Discussion

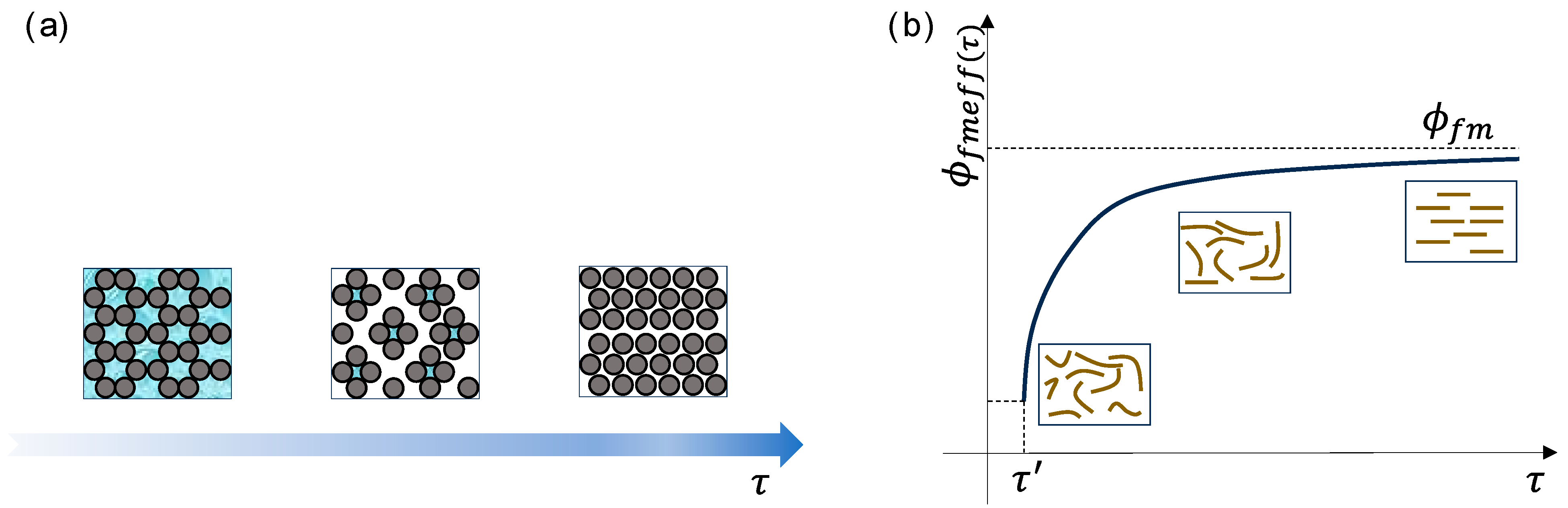
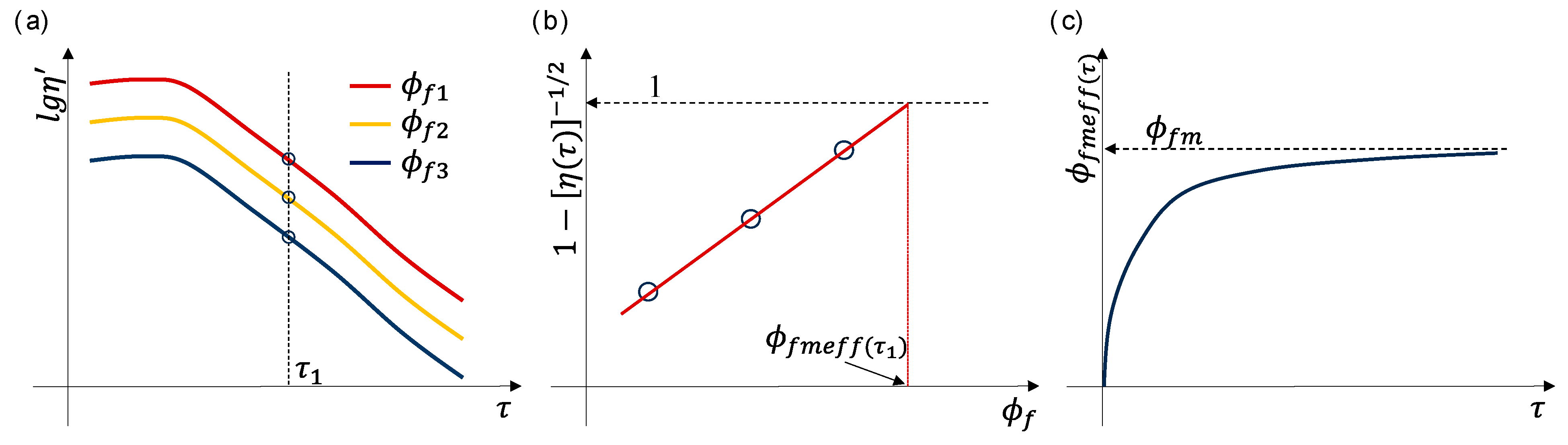
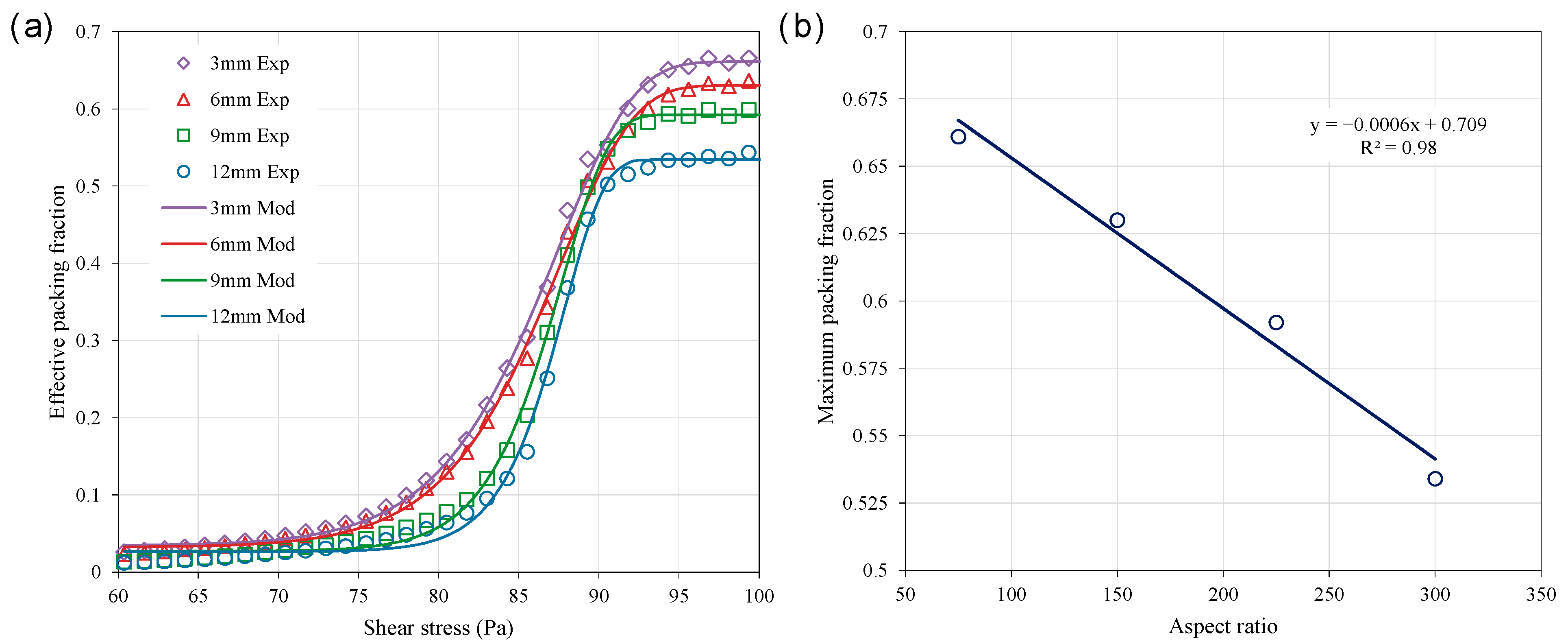
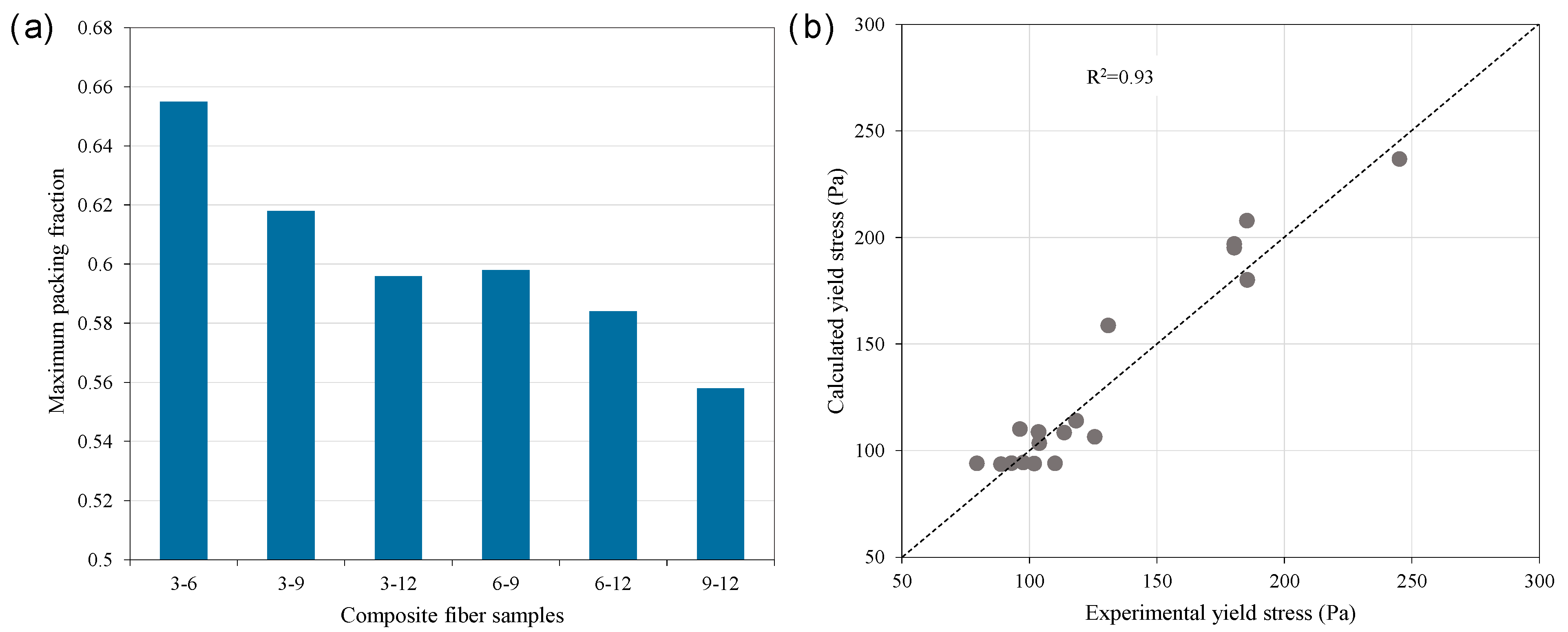
4.1. Maximum Packing Fraction

Figure 5a shows the dynamic nature of the packing fraction of the PP fibers when subjected to shear. Initially, regardless of the fiber length, the curve exhibits a plateau region when the shear stress remains below 75 Pa. This reflects the adaptability of flexible fibers to shear, which results in FR-CPB having a higher yield stress compared to traditional CPB. As the shear stress further increases, the PP fibers gradually straighten and rearrange, resulting in a continuous increase in ${\varphi }_{fmeff}\left(\tau \right)$ until it reaches ${\varphi }_{fm}$, which corresponds to the optimal conformation of the fibers. This dynamic characteristic of the fiber packing fraction under shear also validates the correctness of the method proposed in this study. To quantify this dynamic characteristic and obtain ${\varphi }_{fm}$, the following equation was employed:

$$\begin{array}{c}{\varphi }_{fmeff}\left(\tau \right)={\varphi }_{fmi}+\left({\varphi }_{fm}-{\varphi }_{fmi}\right)\left\{1-exp\left[-{\left({\displaystyle \frac{\tau }{{\tau }_r}}\right)}^{\alpha }\right]\right\}\end{array}$$

(4)

where ${\varphi }_{fmi}$ is the initial packing fraction corresponding to the fiber conformation before the test; ${\tau }_r$ and $\alpha$ are the characteristic stress and characteristic coefficient, respectively.

This equation effectively describes the dynamic characteristics of the fibers (Figure 5a). Through this equation, ${\varphi }_{fm}$ of different fibers can be obtained. The ${\varphi }_{fm}$ values for PP fibers of 3, 6, 9, and 12 mm are 0.661, 0.630, 0.592, and 0.534, respectively. Figure 5b illustrates the relationship between the fiber aspect ratio and ${\varphi }_{fm}$. The figure shows a significant negative linear correlation between the aspect ratio and ${\varphi }_{fm}$, with a correlation coefficient of 0.98. Thus, fibers with smaller aspect ratios exhibit a greater capacity to fill space, leading to higher packing efficiency. This finding is consistent with the observations of Nan et al., who reported that the fiber aspect ratio significantly influences ${\varphi }_{fm}$, with fibers of higher aspect ratios tending to exhibit lower ${\varphi }_{fm}$ [42]. Additionally, Toll also indicated that an increase in the aspect ratio alters the orientation and distribution of fibers, thereby reducing packing efficiency [43].

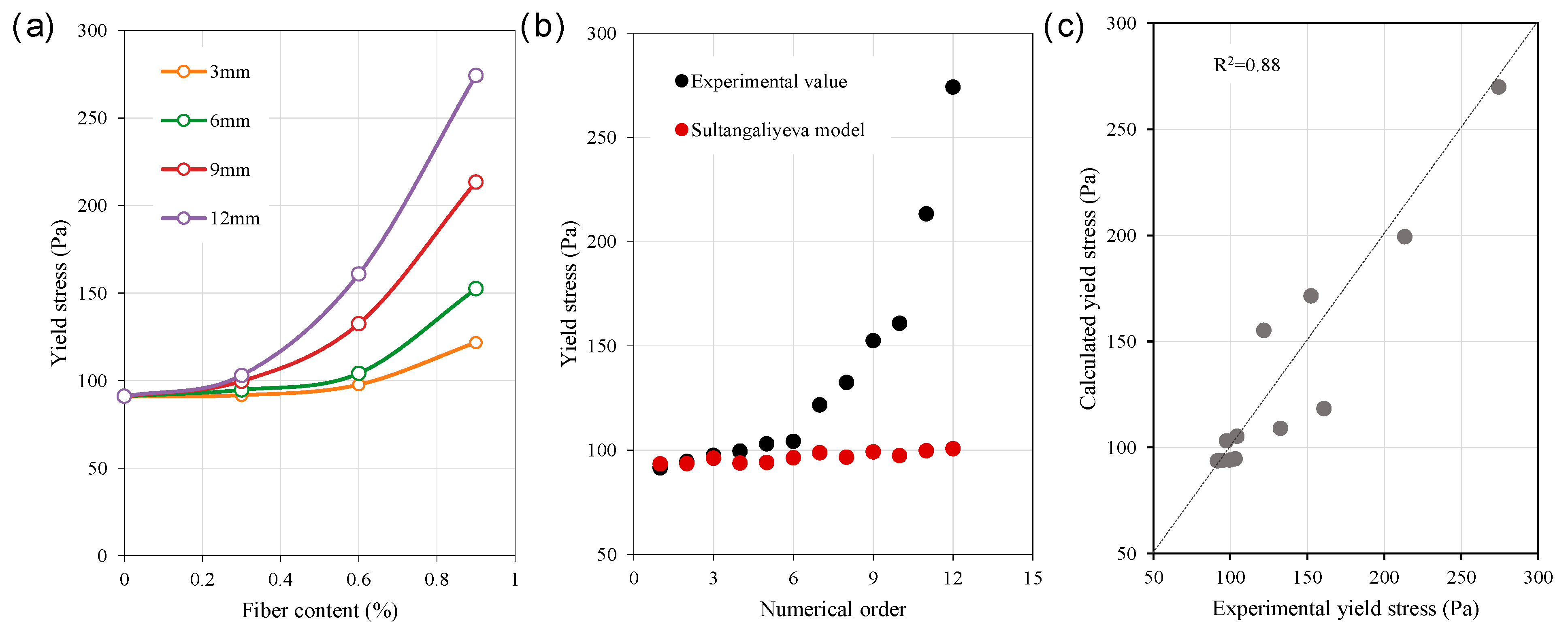
4.2. Yield Stress

Figure 6a presents the yield stress results of the FR-CPB under different lengths (3 mm, 6 mm, 9 mm, and 12 mm) and contents (0%, 0.3%, 0.6%, and 0.9%) of PP fibers. Overall, the yield stress of the FR-CPB increases with the fiber length and content. Similar phenomena were observed by Zhao et al. [6]. For short fibers (3 mm and 6 mm), the increase in yield stress is relatively limited. This may be because short fibers are insufficiently long to interweave and form a stable fiber skeleton structure within the slurry, resulting in weaker constraints on particle flow. Hannant [44] also noted that fibers exhibit significant limitations in forming effective skeleton structures, thus contributing relatively less to enhancing the slurry’s mechanical properties. In contrast, longer fibers (9 mm and 12 mm) effectively interweave to create a more stable skeleton structure in the slurry, substantially improving shear resistance and yielding a notable increase in yield stress. Regarding fiber content, at a low content (0.3%), the increase in yield stress is relatively slow, suggesting limited reinforcement; however, at medium to high contents (0.6% and 0.9%), the yield stress increases significantly. This indicates that a higher fiber content promotes the formation of denser fiber networks, enhancing the overall yield stress of the slurry. Notably, there is a synergistic effect between fiber length and content. Under the combination of high content (0.9%) and long fibers (12 mm), the yield stress reaches a maximum of 274.34 kPa, demonstrating a significant enhancement of the slurry’s shear resistance. This finding also suggests that the packing fraction of fibers plays a crucial role in influencing yield stress, especially at higher fiber contents and longer lengths, where this trend becomes more pronounced.

The Sultangaliyeva model (Equation (5)) [27] is widely employed to predict the yield stress of fiber-reinforced cement paste, with its predictions primarily relying on the packing fraction of fibers. Here, this model was applied for calculations, and the results were compared with experimental measurements, as illustrated in Figure 6b. The comparison reveals noticeable deviations between the model’s predictions and the measured values, particularly under higher fiber content and length, where the discrepancies become more pronounced. These deviations suggest that the Sultangaliyeva model has limitations when applied to CPB, potentially neglecting critical mechanisms influencing yield stress. For instance, fiber–fiber interactions and the reinforcing effects of fibers on the matrix are inadequately accounted for, which likely explains the model’s significant underestimation of yield stress at high fiber contents. Consequently, refining the model is essential to more accurately capture the influence of fibers on the yield stress of CPB, thereby improving its predictive accuracy and applicability.

$$\begin{array}{c}{\tau }_{fc}={\tau }_c\left[{\left(1-{\displaystyle \frac{{\varphi }_f}{{\varphi }_{fm}}}\right)}^{-2}\right]\end{array}$$

(5)

where ${\tau }_{fc}$ and ${\tau }_c$ represent the yield stress of FR-CPB and the CPB matrix, respectively.

Guo et al. [29] demonstrated that fiber–fiber interactions and the reinforcing effects of fibers on the matrix can be expressed as a power function of ${\varphi }_f/{\varphi }_{fm}$. Consequently, Equation (5) can be modified as

$$\begin{array}{c}{\tau }_{fc}={\tau }_c\left[{\left(1-{\displaystyle \frac{{\varphi }_f}{{\varphi }_{fm}}}\right)}^{-2}+a{\left({\displaystyle \frac{{\varphi }_f}{{\varphi }_{fm}}}\right)}^b\right]\end{array}$$

(6)

where a and b are coefficients related to fiber interactions, determined through experimental data.

Using Equation (6) and experimental data, the specific form of the model was obtained through fitting, as shown in Equation (7). As illustrated in Figure 6c, while the data exhibit some dispersion, likely due to the limited sample size, the overall trend closely follows the dashed line (ideal fitting line), with a goodness of fit of 0.88.

$$\begin{array}{c}{\tau }_{fc}={\tau }_c\left[{\left(1-{\displaystyle \frac{{\varphi }_f}{{\varphi }_{fm}}}\right)}^{-2}+9086676.13{\left({\displaystyle \frac{{\varphi }_f}{{\varphi }_{fm}}}\right)}^{5.14}\right]\end{array}$$

(7)

Model Validation

To validate the proposed model, FR-CPB was prepared using various fiber systems, followed by rheological testing and result comparison. In this study, an experimental design was implemented using equi-volume pairwise mixtures of fibers with different lengths to construct composite fiber systems, labeled as 3–6, 3–9, 3–12, 6–9, 6–12, and 9–12, respectively. Here, “3–6” represents a composite system consisting of 3 mm and 6 mm fibers, with other labels following a similar pattern. These composite fibers were used to prepare CPB under fixed experimental conditions: a solid content of 76%, a cement dosage of 10%, and fiber contents of 0.3%, 0.6%, and 0.9%. The yield stress of each system was subsequently measured.

Figure 7a illustrates the ${\varphi }_{fm}$ of composite fiber systems determined using the proposed method. The results reveal that when fibers of different lengths are mixed in equal volumes, the ${\varphi }_{fm}$ of the composite fiber system lies between the ${\varphi }_{fm}$ values of the individual fibers that constitute the system. For example, the ${\varphi }_{fm}$ of the 3–6 combination is 0.655, slightly lower than that of 3 mm fibers (0.661) but higher than that of 6 mm fibers (0.630). A similar trend is observed in other combinations: the ${\varphi }_{fm}$ of the 3–9 system is 0.618, exceeding that of 9 mm single fibers (0.592), while the 3–12 combination achieves a ${\varphi }_{fm}$ of 0.596, surpassing the 0.534 of 12 mm single fibers. In contrast, combinations of longer fibers (e.g., 6–9, 6–12, and 9–12) exhibit a gradual decline in the ${\varphi }_{fm}$, with values of 0.598, 0.584, and 0.558, respectively. These findings suggest that in mixed fiber systems, shorter fibers play a more significant role in improving overall packing performance.

The comparison between the experimental yield stress values and the model predictions for the validation group is illustrated in Figure 7b. Most data align closely with the ideal fitting line, achieving a correlation coefficient of 0.93. These results confirm that the improved model (Equation (7)) effectively captures the yield stress characteristics of FR-CPB, demonstrating high predictive accuracy and broad applicability. However, it should be noted that a noticeable deviation occurs around the 100 Pa range where alignment is reduced. This deviation can be attributed to several factors: (1) the transition zone of fiber interaction, where intermediate fiber content and length combinations result in an underdeveloped fiber network, leading to variability in the packing fraction and fiber distribution; (2) material heterogeneity, as incomplete bridging and inconsistent fiber orientation at intermediate stress levels increase local variations in the rheological behavior; (3) limitations of the model, which assumes uniform fiber dispersion and interaction but may lose predictive accuracy under these conditions; and (4) experimental uncertainty, where slight variations in sample preparation or testing protocols might amplify discrepancies at this range. To address these issues, future studies could incorporate additional data for intermediate stress levels, refine the model to better account for local heterogeneities, and utilize imaging techniques to analyze fiber distribution and orientation within the material.

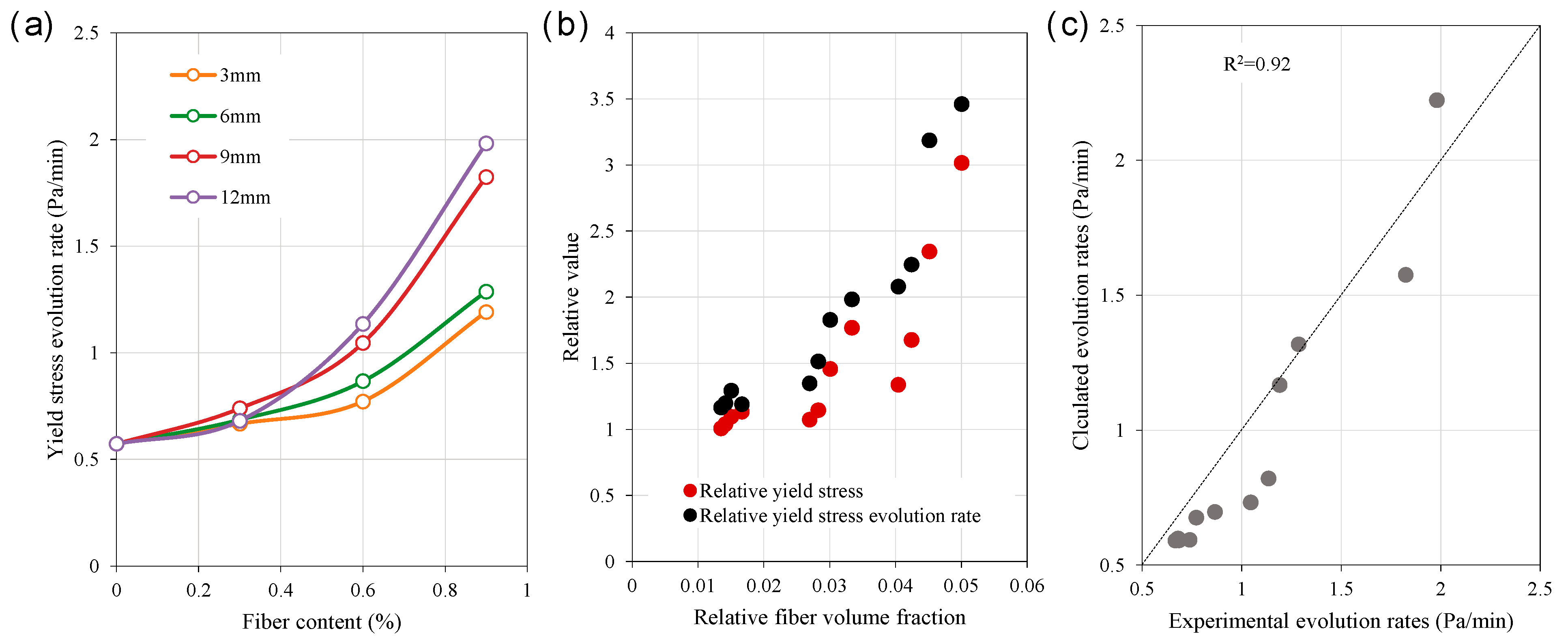
4.3. Time-Dependent Yield Stress

The effects of fiber length and content on the yield stress evolution rate of the FR-CPB (within 2 h) are presented in Figure 8a. The figure shows that the yield stress evolution rate increases with fiber content. This phenomenon can be attributed to the three-dimensional network structure formed by fiber-reinforced cement-based materials. Fibers bridge cement particles to form a continuous network, which enhances the system’s overall stability and reduces cement particle sedimentation [45]. This uniform distribution improves the contact efficiency between cement particles and water, thereby accelerating the hydration reaction [46]. When the fiber content reaches 0.6%, particularly for fibers with a length of 12 mm, the yield stress evolution rate of the samples is significantly higher than that of shorter fibers (3 mm and 6 mm). Additionally, long fibers create a more stable and continuous three-dimensional network within the slurry, promoting the even distribution of cement particles and reducing sedimentation, which in turn enhances the cement hydration efficiency. Conversely, shorter fibers are less effective at bridging, with limited connections between fibers. This reduces contact opportunities among cement particles, leading to incomplete hydration reactions and a less pronounced reinforcement effect. Moreover, long fibers can span larger particle gaps, providing stronger reinforcement, while short fibers fail to achieve this. Thus, the synergistic interaction between fiber length and content determines the variation in the yield stress evolution rate of FR-CPB.

Figure 8b compares the relative yield stress with its evolution rate. Both parameters exhibit a similar upward trend with an increasing relative fiber volume fraction. Notably, the relative yield stress consistently remains lower than the relative yield stress evolution rate, with the gap between them widening as the relative volume fraction increases. This observation suggests that, in addition to fiber–fiber interactions and the reinforcing effects of fibers on the matrix, time-dependent factors significantly influence the yield stress evolution rate. This finding is consistent with previous analyses, indicating that a higher relative fiber volume fraction enhances cement hydration efficiency, thereby accelerating the yield stress evolution rate. Therefore, Equation (7) cannot be directly applied to describe the yield stress evolution rate of FR-CPB without fully considering the effects of cement hydration. Recognizing the critical role of exponential parameters in determining the function’s outcomes, the framework of Equation (7) was retained. By combining experimental data and optimizing the exponential parameters, a yield stress evolution rate model for FR-CPB (Equation (8)) was developed. Figure 8c compares the model predictions with the observed yield stress evolution rate values. Most data align closely with the ideal fitting line, achieving a correlation coefficient of 0.92. This indicates that the model provides an accurate prediction of the yield stress evolution rate for FR-CPB.

$$\begin{array}{c}{R}_{fc}=R_c\left[{\left(1-{\displaystyle \frac{{\varphi }_f}{{\varphi }_{fm}}}\right)}^{-2}+9086676.13{\left({\displaystyle \frac{{\varphi }_f}{{\varphi }_{fm}}}\right)}^5\right]\end{array}$$

(8)

where $R_c$ and $R_{fc}$ represent the yield stress evolution rates of CPB and FR-CPB, respectively.

5. Conclusions

Inspired by the response of particle flocs under shear, this study proposes a method to determine the maximum packing fraction of PP fibers in CPB. Building on this, the maximum packing fraction is used to analyze and model the yield stress and yield stress evolution rate of FR-CPB. The main conclusions are as follows:

• The proposed rheology-based method effectively captures the dynamic characteristics of PP fibers in CPB during the shearing process, enabling the accurate determination of the maximum packing fraction. This approach provides a reliable tool for gaining deeper insights into fiber packing behavior within CPB.
• The maximum packing fraction decreased with increasing fiber length, ranging from 0.661 for 3 mm fibers to 0.534 for 12 mm fibers, highlighting the significant influence of fiber geometry on packing efficiency. Moreover, shorter fibers demonstrate greater advantages in space filling and packing efficiency, while the inclusion of longer fibers dilutes the overall packing performance.
• The improved yield stress model demonstrated high predictive accuracy, with a correlation coefficient of 0.93 between the predicted and experimental values. Additionally, the relative yield stress was always less than the relative yield stress evolution rate due to the influence of cement hydration efficiency. By adjusting the exponential parameters in the yield stress model, the model successfully achieves an accurate description of the yield stress evolution rate.

While the proposed models have demonstrated strong potential for optimizing FR-CPB, future research should explore their applicability to other fiber types, such as steel or natural fibers, to evaluate generalizability. Scaling up the models for large-scale industrial use, particularly in mining operations, is essential to validate their performance under practical field conditions. Additionally, further studies are needed to assess the models’ reliability under varying environmental conditions, such as temperature, humidity, and chemical exposure, as well as their long-term performance considering fiber degradation. Addressing these aspects will refine the models and expand their applicability to optimize FR-CPB systems across diverse and complex conditions.