Experimental Uncertainty Analysis for the Particle Size Distribution for Better Understanding of Batch Grinding Process
Abstract
:1. Introduction
- Will the evaluation parameters that are used to quantify the PSD be sufficient?
- In a milling process, is it possible to detect possible sources of epistemic and stochastic uncertainties through a comprehensive particle size analysis?
- Will the uncertainty be the same for the parameters when they are evaluated in the form of WPES with respect to the CWU or when a PSDM is used?
- Considering the PSCPs that are selected to quantify the milling, how are they influenced by the uncertainty of the PSD?
- Carry out an exhaustive analysis of data gathered from the PSD in order to obtain the most detailed uncertainty analysis.
- Identify potential faults/shortcomings of the traditional way of analysis/reporting on PSD results.
- Propose mathematical expressions that characterise the uncertainty of the PSD.
2. Methodology
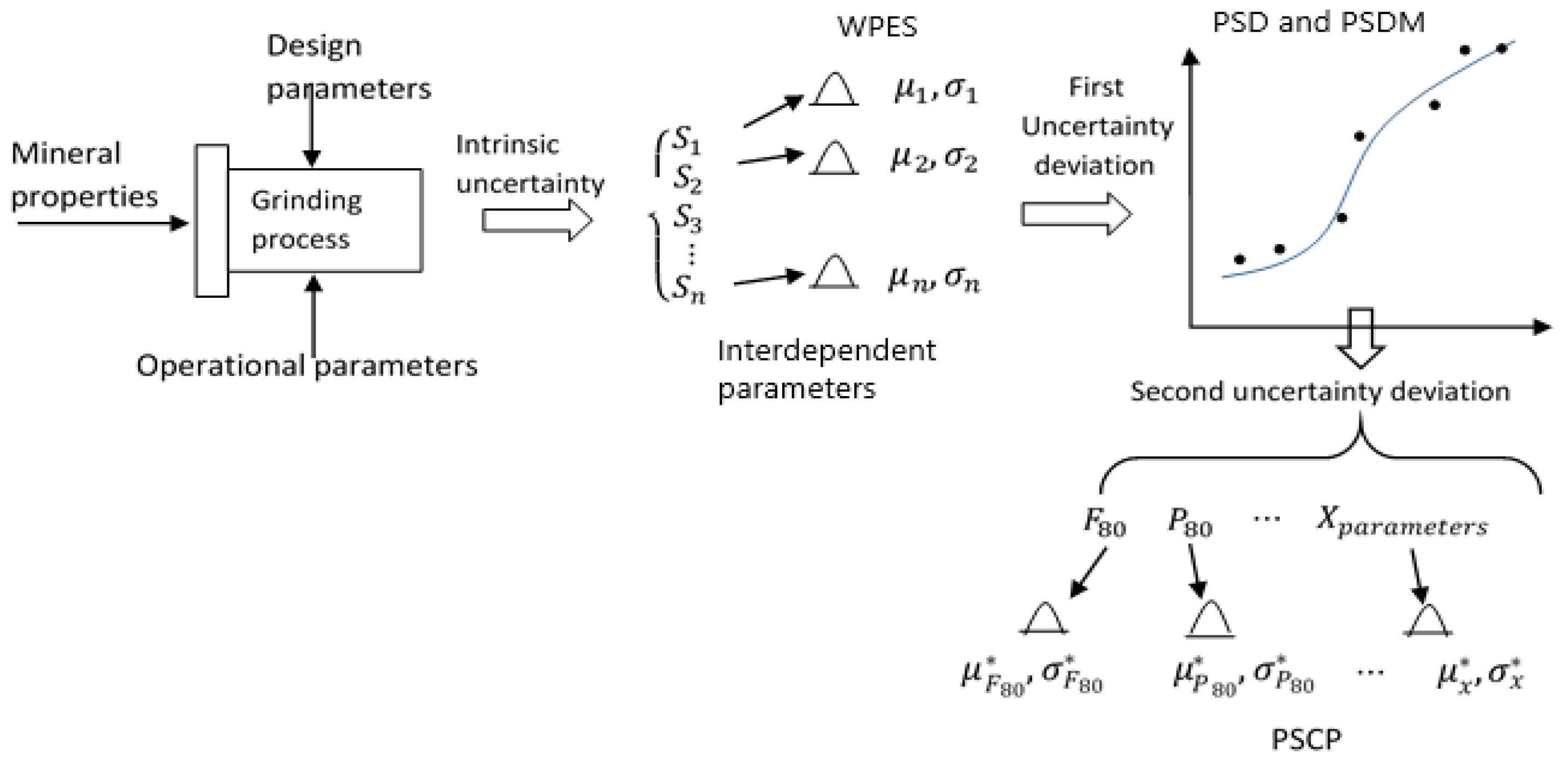
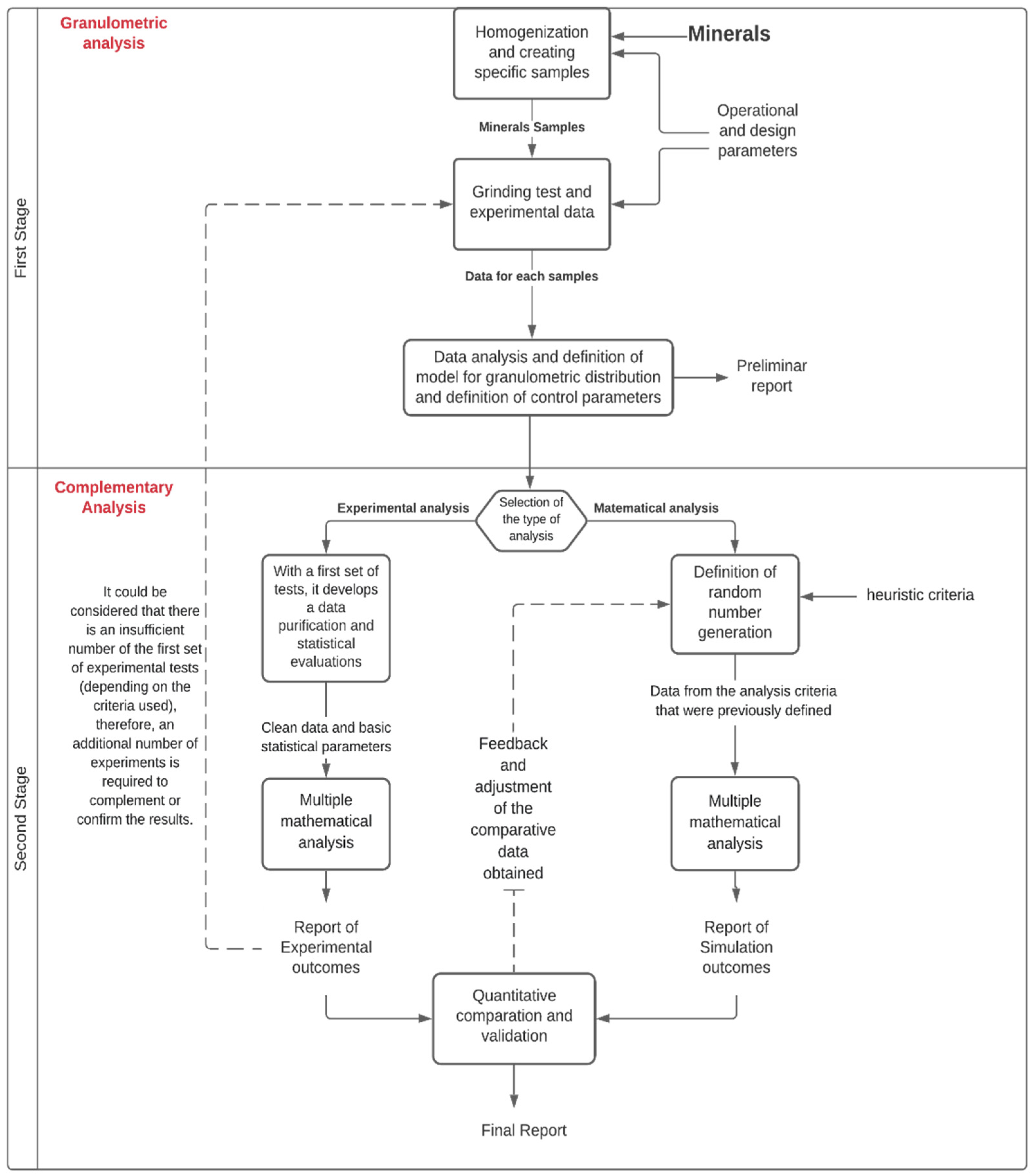
2.1. Proposed Methodology
2.1.1. First Stage—Granulometric Analysis (GA)
2.1.2. Second Stage—Complementary Analysis
3. Results and Discussion
3.1. Phase I: Granulometric Analysis
3.2. Phase II: Complementary Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Size (µm) | PSD (%) | RRM (%) | ε | GGS (%) | ε |
|---|---|---|---|---|---|
| 850–1700 | 100.00 | 100.00 | 0.00 | 100.00 | 0.00 |
| 600–850 | 46.58 | 44.73 | 3.43 | 33.99 | 0.25 |
| 425–600 | 33.50 | 35.06 | 2.44 | 26.27 | 0.88 |
| 300–425 | 25.34 | 27.04 | 2.92 | 20.36 | 0.20 |
| 250–300 | 19.91 | 20.51 | 0.36 | 15.73 | 3.02 |
| 212–250 | 17.47 | 17.67 | 0.04 | 13.75 | 4.19 |
| 150–212 | 15.80 | 15.41 | 0.15 | 12.17 | 0.48 |
| 106–150 | 12.87 | 11.49 | 1.89 | 9.42 | 1.40 |
| 90–106 | 10.61 | 8.51 | 4.38 | 7.29 | 1.34 |
| 74–90 | 8.45 | 7.38 | 1.14 | 6.46 | 0.00 |
| 63–74 | 6.39 | 6.21 | 0.03 | 5.59 | 1.01 |
| 53–63 | 4.58 | 4.62 | 0.00 | 4.37 | 0.37 |
| 43–53 | 3.76 | 3.84 | 0.01 | 3.74 | 13.99 |
| 35–43 | 0.00 | 0.00 | 0.00 | 3.21 | 10.32 |
| 0–35 | 16.79 | 37.44 |
| Size (µm) | PSD (%) | RRM (%) | ε | GGS (%) | ε |
|---|---|---|---|---|---|
| 850–1700 | 100.00 | 97.36 | 6.96 | 100.00 | 0.00 |
| 600–850 | 79.50 | 80.44 | 0.88 | 83.98 | 19.99 |
| 425–600 | 67.39 | 69.21 | 3.32 | 67.04 | 0.12 |
| 300–425 | 56.28 | 57.78 | 2.26 | 54.05 | 4.98 |
| 250–300 | 46.03 | 45.97 | 0.00 | 42.82 | 10.29 |
| 212–250 | 41.78 | 40.49 | 1.66 | 38.06 | 13.85 |
| 150–212 | 37.94 | 35.66 | 5.23 | 34.00 | 15.51 |
| 106–150 | 30.23 | 27.52 | 7.35 | 27.35 | 8.24 |
| 90–106 | 22.94 | 20.75 | 4.81 | 21.85 | 1.18 |
| 74–90 | 20.01 | 18.09 | 3.71 | 19.66 | 0.12 |
| 63–74 | 15.99 | 15.48 | 0.26 | 17.47 | 2.19 |
| 53–63 | 9.60 | 13.31 | 13.80 | 15.61 | 36.15 |
| 43–53 | 8.06 | 11.44 | 11.47 | 13.96 | 34.84 |
| 35–43 | 5.53 | 9.90 | 19.15 | 12.56 | 49.46 |
| 0–35 | 0.0 | 0.00 | 0.00 | 0.00 | 0.00 |
| sum | 80.86 | 196.91 |
| Size (µm) | PSD (%) | RRM (%) | ε | GGS (%) | ε |
|---|---|---|---|---|---|
| 850–1700 | 99.95 | 99.95 | 0.00 | 100.00 | 0.00 |
| 600–850 | 93.07 | 96.06 | 8.95 | 85.21 | 61.79 |
| 425–600 | 87.55 | 89.73 | 4.75 | 74.36 | 174.00 |
| 300–425 | 78.49 | 80.33 | 3.36 | 65.28 | 174.73 |
| 250–300 | 67.30 | 67.72 | 0.18 | 56.70 | 112.21 |
| 212–250 | 61.03 | 60.96 | 0.00 | 52.80 | 67.74 |
| 150–212 | 58.05 | 54.57 | 12.16 | 49.32 | 76.22 |
| 106–150 | 45.99 | 42.98 | 9.04 | 43.24 | 7.53 |
| 90–106 | 35.97 | 32.68 | 10.85 | 37.75 | 3.16 |
| 74–90 | 31.32 | 28.50 | 7.97 | 35.41 | 16.72 |
| 63–74 | 25.50 | 24.35 | 1.31 | 32.98 | 55.90 |
| 53–63 | 15.94 | 20.87 | 24.31 | 30.80 | 220.93 |
| 43–53 | 13.65 | 17.85 | 17.65 | 28.79 | 229.28 |
| 35–43 | 9.59 | 15.35 | 33.15 | 27.00 | 303.11 |
| 0–35 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| sum | 133.70 | 1503.31 |
| Size (µm) | PSD (%) | RRM (%) | ε | GGS (%) | ε |
|---|---|---|---|---|---|
| 850–1700 | 99.97 | 100.00 | 0.00 | 100.00 | 0.00 |
| 600–850 | 97.26 | 99.98 | 7.43 | 100.00 | 7.52 |
| 425–600 | 95.56 | 99.55 | 15.92 | 88.20 | 54.16 |
| 300–425 | 92.20 | 96.78 | 21.05 | 78.21 | 195.57 |
| 250–300 | 85.08 | 87.91 | 8.01 | 68.69 | 268.53 |
| 212–250 | 79.86 | 80.81 | 0.91 | 64.32 | 241.51 |
| 150–212 | 73.90 | 72.86 | 1.09 | 60.40 | 182.36 |
| 106–150 | 57.86 | 56.28 | 2.49 | 53.50 | 19.03 |
| 90–106 | 46.34 | 40.39 | 35.38 | 47.20 | 0.74 |
| 74–90 | 38.29 | 33.94 | 18.88 | 44.50 | 38.53 |
| 63–74 | 28.80 | 27.68 | 1.25 | 41.66 | 165.62 |
| 53–63 | 16.84 | 22.58 | 33.02 | 39.13 | 496.73 |
| 43–53 | 14.46 | 18.34 | 15.03 | 36.76 | 497.14 |
| 35–43 | 9.10 | 14.99 | 34.67 | 34.65 | 652.95 |
| 0–35 | 0 | 0 | 0 | 0 | 0 |
| sum | 195.14 | 2820.41 |
| Size (µm) | Mean (%) | Median (%) | Standard Deviation (%) | Kurtosis | Skewness Coefficient |
|---|---|---|---|---|---|
| 850–1700 | 20.27 | 20.18 | 0.45 | 2.73 | 1.49 |
| 600–850 | 12.30 | 12.22 | 0.34 | 7.17 | 2.58 |
| 425–600 | 11.88 | 12.10 | 0.52 | −0.92 | −0.20 |
| 300–425 | 9.64 | 9.75 | 1.14 | 6.01 | 2.19 |
| 250–300 | 4.21 | 4.21 | 0.04 | 1.63 | 0.04 |
| 212–250 | 3.65 | 3.57 | 0.12 | 0.35 | 1.03 |
| 150–212 | 7.56 | 7.62 | 0.50 | 0.07 | 0.02 |
| 106–150 | 7.55 | 7.54 | 0.32 | 0.08 | 0.59 |
| 90–106 | 3.27 | 3.21 | 0.34 | 1.49 | 0.38 |
| 74–90 | 4.30 | 4.37 | 0.47 | 0.01 | 0.39 |
| 63–74 | 6.25 | 6.25 | 0.18 | 0.88 | 0.49 |
| 53–63 | 1.23 | 1.22 | 0.20 | 0.25 | 0.24 |
| 43–53 | 2.75 | 2.83 | 0.22 | 1.63 | 0.32 |
| 35–43 | 5.06 | 4.99 | 0.36 | 1.12 | 0.34 |
| Size (µm) | Mean (%) | Median (%) | Standard Deviation (%) | Kurtosis | Skewness Coefficient |
|---|---|---|---|---|---|
| 850–1700 | 7.55 | 7.63 | 0.34 | 0.52 | −0.91 |
| 600–850 | 5.49 | 5.51 | 0.04 | −0.69 | 0.25 |
| 425–600 | 8.80 | 8.76 | 0.15 | −0.63 | 0.63 |
| 300–425 | 10.68 | 10.66 | 0.24 | 1.94 | 1.28 |
| 250–300 | 5.62 | 5.59 | 0.26 | 6.18 | 2.29 |
| 212–250 | 4.76 | 5.01 | 0.69 | 6.89 | −2.53 |
| 150–212 | 11.86 | 11.74 | 0.42 | 2.17 | 1.16 |
| 106–150 | 10.23 | 10.09 | 0.31 | 2.78 | 1.70 |
| 90–106 | 4.52 | 4.65 | 0.59 | 5.80 | −2.15 |
| 74–90 | 5.99 | 5.94 | 0.33 | 0.75 | 0.11 |
| 63–74 | 9.28 | 9.18 | 0.58 | 2.21 | 1.32 |
| 53–63 | 2.06 | 2.01 | 0.21 | −1.52 | 0.16 |
| 43–53 | 4.29 | 4.56 | 0.29 | −0.96 | 0.20 |
| 35–43 | 8.81 | 8.68 | 0.43 | −0.07 | 0.99 |
| Size (µm) | Mean (%) | Median (%) | Standard Deviation (%) | Kurtosis | Skewness Coefficient |
|---|---|---|---|---|---|
| 600–850 | 2.00 | 2.09 | 0.34 | 1.56 | 0.97 |
| 425–600 | 1.37 | 1.31 | 0.27 | 0.05 | 0.70 |
| 300–425 | 2.82 | 2.73 | 0.53 | 1.15 | 0.99 |
| 250–300 | 6.37 | 6.29 | 0.67 | 0.53 | 0.59 |
| 212–250 | 5.13 | 5.10 | 0.44 | 3.90 | 1.67 |
| 150–212 | 5.77 | 5.76 | 0.14 | −0.54 | −0.25 |
| 106–150 | 16.76 | 16.84 | 1.12 | −0.33 | 0.03 |
| 90–106 | 11.69 | 11.63 | 0.84 | 3.20 | 0.36 |
| 74–90 | 8.11 | 8.05 | 0.62 | −0.64 | 0.61 |
| 63–74 | 8.66 | 8.20 | 1.16 | 3.95 | 1.89 |
| 53–63 | 10.90 | 11.87 | 1.66 | 1.67 | −1.42 |
| 43–53 | 3.29 | 3.44 | 0.51 | −0.46 | −0.75 |
| 35–43 | 6.01 | 6.05 | 0.52 | −1.04 | −0.04 |
| 0–35 | 11.09 | 11.31 | 1.64 | 1.70 | 0.99 |

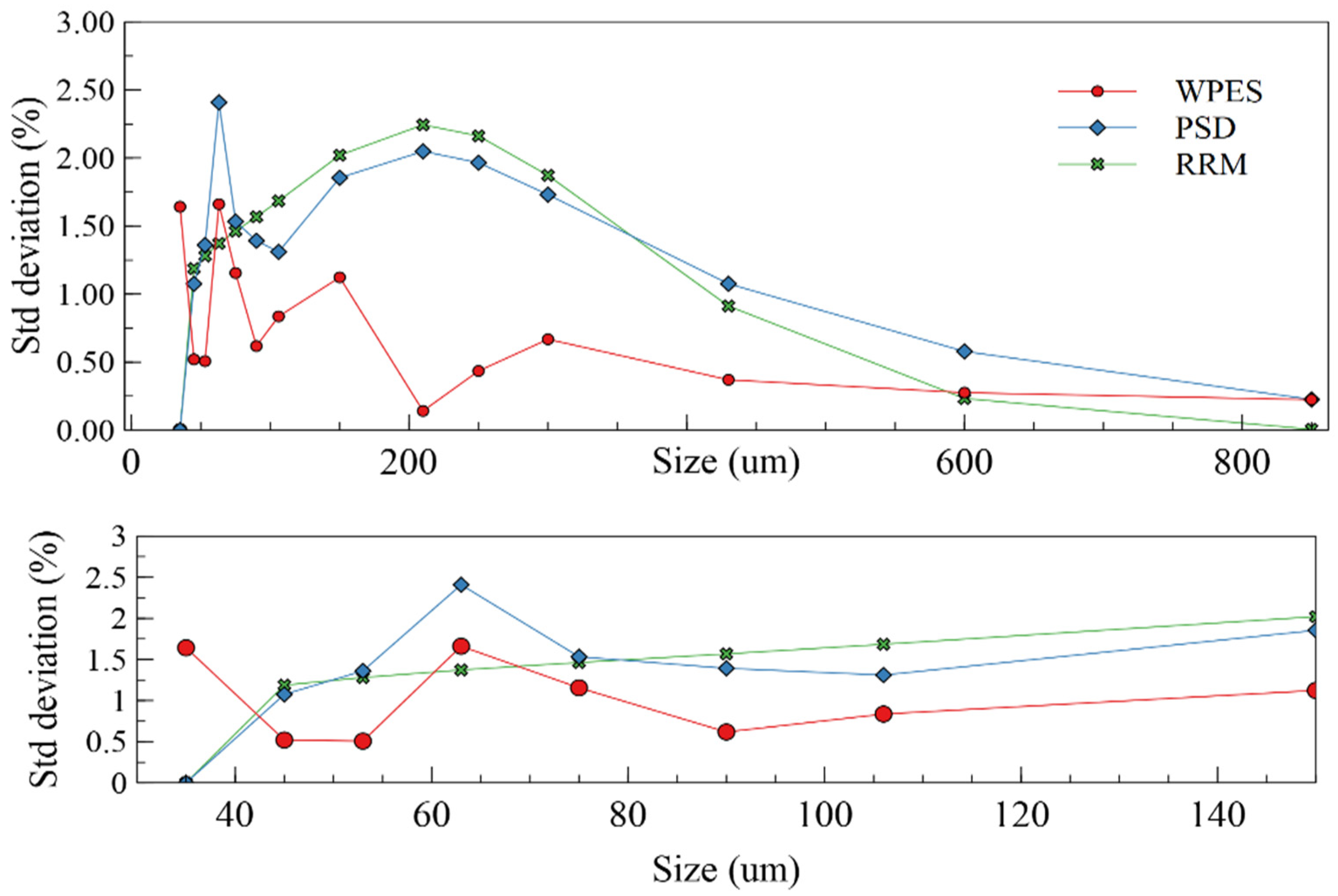
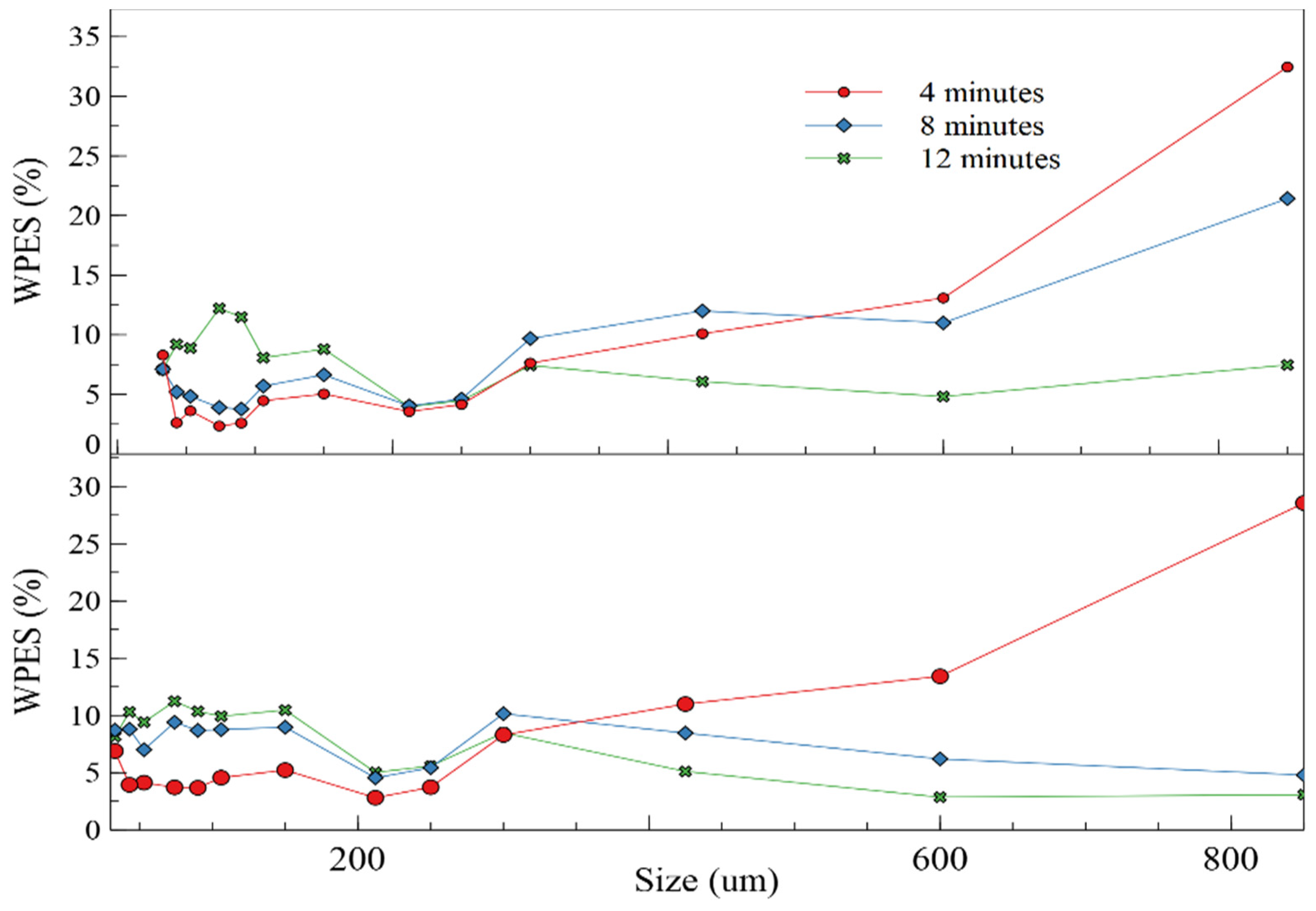
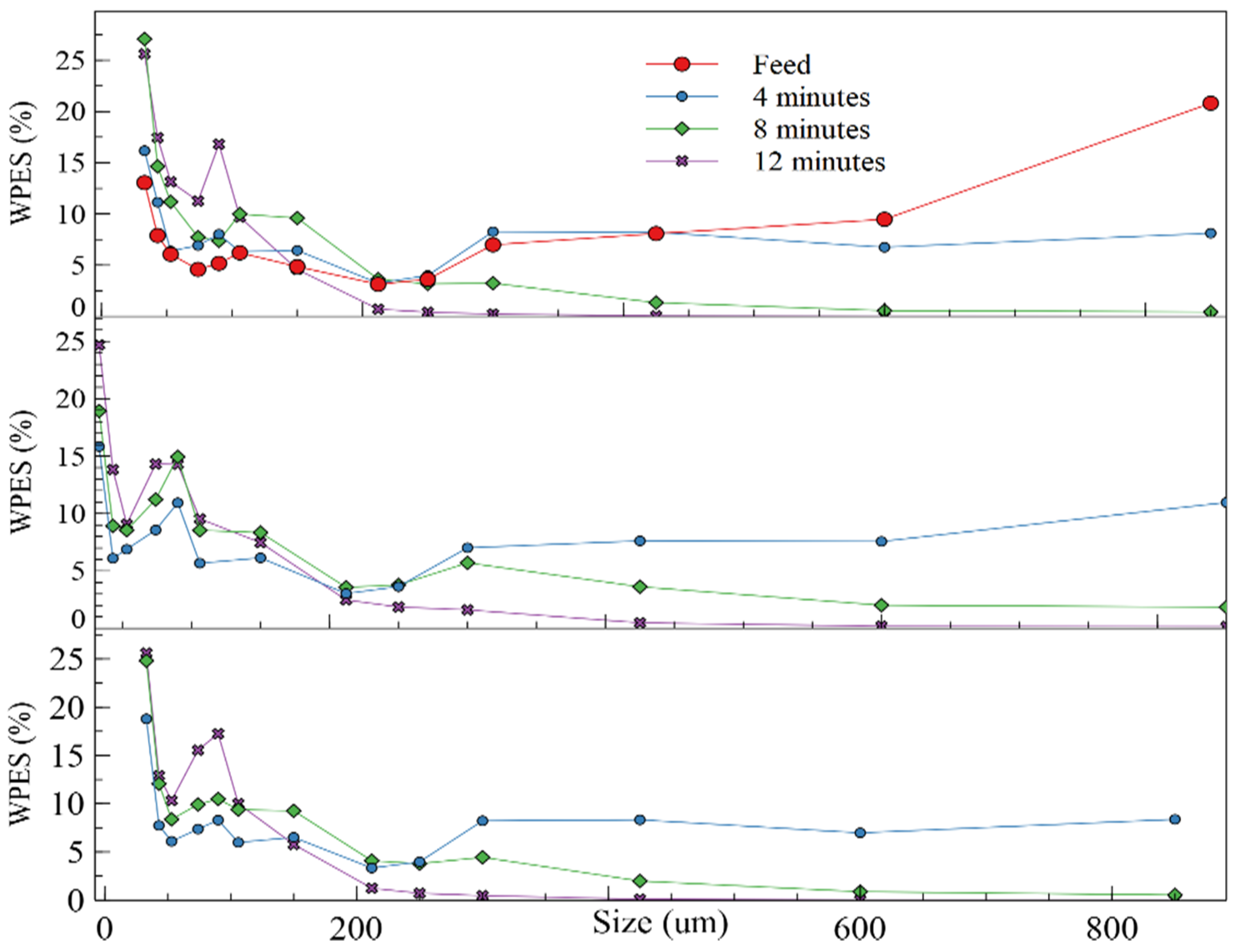
| Size (µm) | W | p-Value | Normal/ Non-Normal | W | p-Value | Normal/ Non-Normal | W | p-Value | Normal/ Non-Normal |
|---|---|---|---|---|---|---|---|---|---|
| 600–850 | 0.91 | 0.31 | Normal | 0.92 | 0.40 | Normal | 0.73 | 0.003 | Non-Normal |
| 425–600 | 0.98 | 0.94 | Normal | 0.94 | 0.58 | Normal | 0.80 | 0.03 | Normal |
| 300–425 | 0.94 | 0.63 | Normal | 0.93 | 0.51 | Normal | 0.89 | 0.24 | Normal |
| 250–300 | 0.73 | 0.003 | Non-Normal | 0.92 | 0.39 | Normal | 0.77 | 0.01 | Non-Normal |
| 212–250 | 0.93 | 0.50 | Normal | 0.91 | 0.30 | Normal | 0.92 | 0.39 | Normal |
| 150–212 | 0.82 | 0.04 | Non-normal | 0.93 | 0.51 | Normal | 0.98 | 0.94 | Normal |
| 106–150 | 0.97 | 0.94 | Normal | 0.91 | 0.28 | Normal | 0.96 | 0.81 | Normal |
| 90–106 | 0.95 | 0.67 | Normal | 0.97 | 0.89 | Normal | 0.97 | 0.91 | Normal |
| 74–90 | 0.96 | 0.80 | Normal | 0.96 | 0.64 | Normal | 0.96 | 0.94 | Normal |
| 63–74 | 0.98 | 0.98 | Normal | 0.97 | 0.87 | Normal | 0.97 | 0.93 | Normal |
| 53–63 | 0.93 | 0.51 | Normal | 0.92 | 0.36 | Normal | 0.97 | 0.87 | Normal |
| 43–53 | 0.97 | 0.89 | Normal | 0.89 | 0.24 | Normal | 0.96 | 0.76 | Normal |
| 35–43 | 0.90 | 0.25 | Normal | 0.93 | 0.45 | Normal | 0.94 | 0.63 | Normal |
| 0–35 | 0.93 | 0.45 | Normal |
| Size (µm) | W | p-Value | Normal/ Non-Normal | W | p-Value | Normal/ Non-Normal | W | p-Value | Normal/ Non-Normal |
|---|---|---|---|---|---|---|---|---|---|
| 600–850 | 0.90 | 0.31 | Normal | 0.92 | 0.40 | Normal | 0.73 | 0.003 | Non-Normal |
| 425–600 | 0.98 | 0.94 | Normal | 0.94 | 0.58 | Normal | 0.80 | 0.03 | Normal |
| 300–425 | 0.94 | 0.63 | Normal | 0.93 | 0.51 | Normal | 0.89 | 0.24 | Normal |
| 250–300 | 0.73 | 0.003 | Non-Normal | 0.92 | 0.39 | Normal | 0.76 | 0.01 | Non-Normal |
| 212–250 | 0.93 | 0.50 | Normal | 0.91 | 0.30 | Normal | 0.92 | 0.39 | Normal |
| 150–212 | 0.82 | 0.04 | Non-normal | 0.93 | 0.51 | Normal | 0.97 | 0.94 | Normal |
| 106–150 | 0.97 | 0.90 | Normal | 0.91 | 0.28 | Normal | 0.96 | 0.81 | Normal |
| 90–106 | 0.95 | 0.66 | Normal | 0.97 | 0.89 | Normal | 0.97 | 0.91 | Normal |
| 74–90 | 0.96 | 0.80 | Normal | 0.95 | 0.64 | Normal | 0.92 | 0.94 | Normal |
| 63–74 | 0.98 | 0.98 | Normal | 0.98 | 0.87 | Normal | 0.97 | 0.93 | Normal |
| 53–63 | 0.93 | 0.51 | Normal | 0.91 | 0.36 | Normal | 0.98 | 0.87 | Normal |
| 43–53 | 0.97 | 0.89 | Normal | 0.89 | 0.24 | Normal | 0.96 | 0.76 | Normal |
| 35–43 | 0.90 | 0.25 | Normal | 0.93 | 0.45 | Normal | 0.94 | 0.63 | Normal |
| 0–35 | 0.93 | 0.45 | Normal |
| Size (µm) | W | p-Value | Normal/ Non-Normal | W | p-Value | Normal/ Non-Normal | W | p-Value | Normal/ Non-Normal |
|---|---|---|---|---|---|---|---|---|---|
| 600–850 | 0.84 | 0.07 | Normal | 0.86 | 0.24 | Normal | 0.89 | 0.22 | Normal |
| 425–600 | 0.93 | 0.46 | Normal | 0.95 | 0.75 | Normal | 0.84 | 0.057 | Normal |
| 300–425 | 0.93 | 0.49 | Normal | 0.91 | 0.35 | Normal | 0.94 | 0.62 | Normal |
| 250–300 | 0.92 | 0.42 | Normal | 0.92 | 0.42 | Normal | 0.99 | 0.98 | Normal |
| 212–250 | 0.83 | 0.05 | Normal | 0.95 | 0.67 | Normal | 0.98 | 0.96 | Normal |
| 150–212 | 0.92 | 0.43 | Normal | 0.95 | 0.68 | Normal | 0.95 | 0.69 | Normal |
| 106–150 | 0.99 | 0.99 | Normal | 0.88 | 0.18 | Normal | 0.94 | 0.57 | Normal |
| 90–106 | 0.76 | 0.01 | Non-Normal | 0.95 | 0.67 | Normal | 0.96 | 0.85 | Normal |
| 74–90 | 0.91 | 0.37 | Normal | 0.96 | 0.79 | Normal | 0.96 | 0.82 | Normal |
| 63–74 | 0.79 | 0.02 | Non-Normal | 0.90 | 0.27 | Normal | 0.95 | 0.70 | Normal |
| 53–63 | 0.80 | 0.02 | Non-Normal | 0.97 | 0.91 | Normal | 0.91 | 0.33 | Normal |
| 43–53 | 0.90 | 0.26 | Normal | 0.96 | 0.77 | Normal | 0.88 | 0.14 | Normal |
| 35–43 | 0.95 | 0.66 | Normal | 0.87 | 0.17 | Normal | 0.85 | 0.07 | Normal |
| 0–35 | 0.87 | 0.17 | Normal |
| Item | Mean | Median | Standard Deviation | Kurtosis | Skewness Coefficient |
|---|---|---|---|---|---|
| (µm) | 864.12 | 859.21 | 16.86 | 2.77 | 1.51 |
| (µm) | 750.02 | 724.85 | 10.37 | 4.05 | 1.82 |
| (µm) | 491.81 | 488.72 | 11.50 | 5.45 | 2.22 |
| (µm) | 147.59 | 149.00 | 2.85 | −0.80 | 0.67 |
| (µm) | 118.21 | 118.25 | 2.66 | −0.33 | 0.25 |
| (µm) | 65.16 | 65.53 | 1.19 | −0.89 | 0.31 |
| Rr | 1.61 | 1.62 | 0.03 | 2.46 | −1.42 |
| Sc | 2.52 | 2.52 | 0.02 | 0.39 | −0.24 |
| Cc | 0.68 | 0.67 | 0.03 | 1.08 | −0.73 |
| Uc | 7.55 | 7.57 | 0.20 | −0.11 | 0.74 |
| Size | Mean | Median | Standard Deviation | Kurtosis | Skewness Coefficient |
|---|---|---|---|---|---|
| (µm) | 463.63 | 464.00 | 5.025 | −0.97 | −0.19 |
| (µm) | 389.53 | 389.34 | 2.03 | 5.51 | 2.23 |
| (µm) | 234.54 | 234.04 | 2.03 | 5.51 | 2.23 |
| (µm) | 88.95 | 89.45 | 1.55 | −0.71 | −0.38 |
| (µm) | 76.15 | 76.17 | 1.44 | −1.45 | 0.11 |
| (µm) | 47.41 | 47.72 | 0.82 | 0.44 | −1.25 |
| Rr | 2.99 | 2.99 | 0.03 | −0.95 | 0.22 |
| Sc | 2.26 | 2.27 | 0.02 | −1.28 | −0.42 |
| Cc | 0.71 | 0.71 | 0.02 | 0.45 | −0.14 |
| Uc | 4.95 | 4.91 | 0.09 | −0.15 | 0.97 |
| Size | Mean | Median | Standard Deviation | Kurtosis | Skewness Coefficient |
|---|---|---|---|---|---|
| (µm) | 234.04 | 230.83 | 14.28 | −0.56 | 0.26 |
| (µm) | 204.75 | 203.68 | 8.26 | −0.39 | 0.47 |
| (µm) | 150.99 | 154.06 | 6.71 | −0.17 | −0.86 |
| (µm) | 73.09 | 72.99 | 2.63 | −0.57 | 0.13 |
| (µm) | 68.19 | 67.89 | 2.57 | 1.17 | −0.88 |
| (µm) | 43.33 | 43.00 | 2.48 | 1.26 | −0.79 |
| Rr | 5.95 | 6.02 | 0.36 | −0.63 | −0.04 |
| Sc | 1.73 | 1.73 | 0.04 | 0.92 | −0.48 |
| Cc | 0.82 | 0.81 | 0.06 | −0.49 | 0.13 |
| Uc | 3.49 | 3.56 | 0.22 | 1.88 | −1.17 |
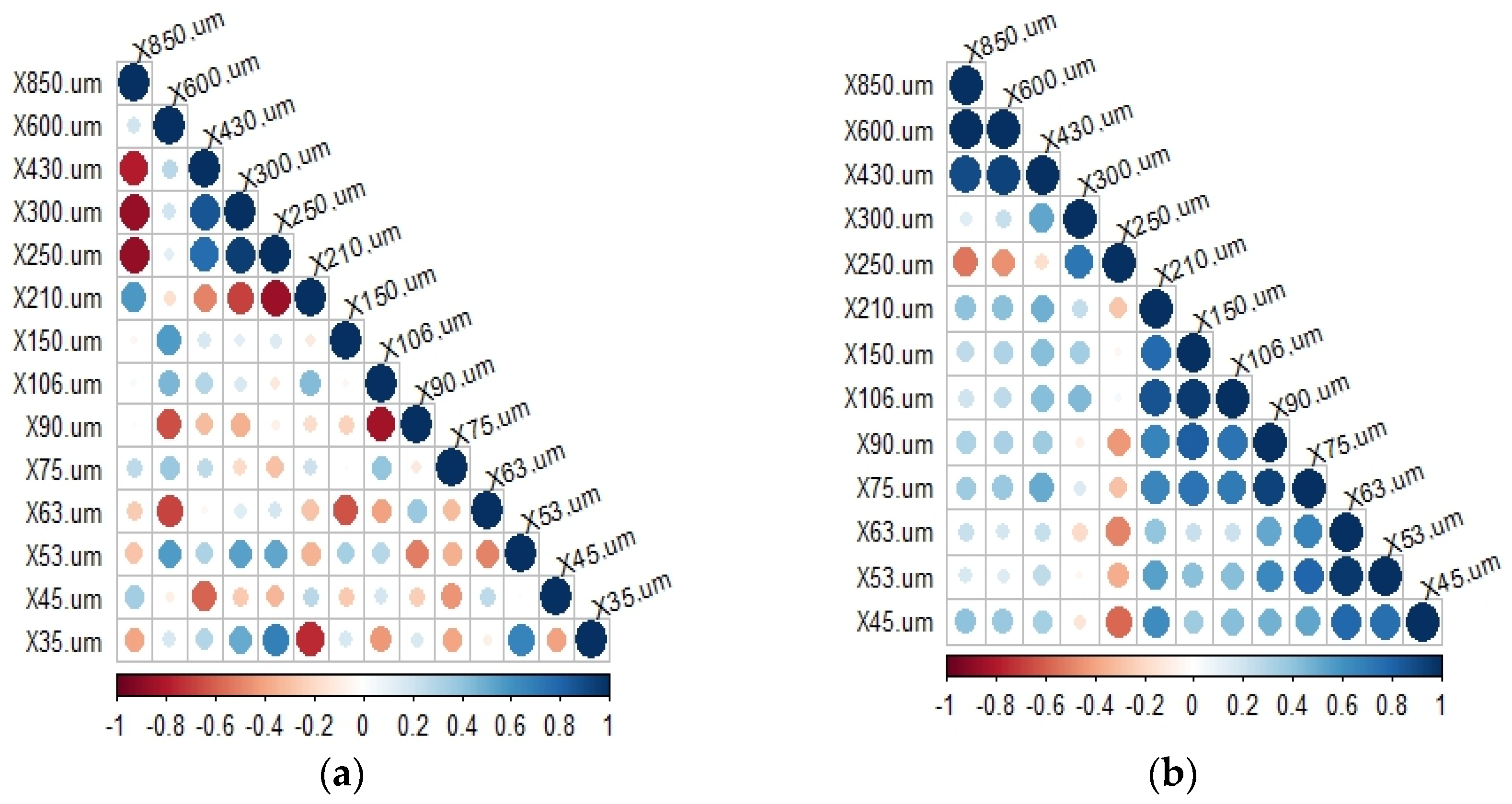
References
- Coleman, H.W.; Steele, W.G. Experimentation, Validation, and Uncertainty Analysis for Engineers, 4th ed.; Wiley: Hoboken, NJ, USA, 2018; ISBN 9781119417989. [Google Scholar]
- Schenck, H.; Richardson, P.D. Theories of engineering experimentation. J. Appl. Mech. ASME 1961, 28, 638. [Google Scholar] [CrossRef]
- ISO—ISO/IEC Guide 98-3:2008—Uncertainty of Measurement—Part 3: Guide to the Expression of Uncertainty in Measurement (GUM: 1995). Available online: https://www.iso.org/standard/50461.html (accessed on 10 January 2021).
- Kline, S.J. The purposes of uncertainty analysis. J. Fluids Eng. Trans. ASME 1985, 107, 153–160. [Google Scholar] [CrossRef]
- Schwer, L.E. Verification and validation in computational solid mechanics and the ASME standards committee. WIT Trans. Built Environ. 2005, 84, 109–117. [Google Scholar]
- Napier-Munn, T.; Wills, B.A. Wills’ Mineral Processing Technology; McGill University: Montréal, QC, Canada, 2005; ISBN 9780750644501. [Google Scholar]
- Semsari, P.P.; Parian, M.; Rosenkranz, J. Breakage process of mineral processing comminution machines—An approach to liberation. Adv. Powder Technol. 2020, 31, 3669–3685. [Google Scholar] [CrossRef]
- Taggart, A.F. Elements of Ore Dressing; John Wiles and Sons: New York, NY, USA, 1951. [Google Scholar]
- Ramkrishna, D.; Singh, M.R. Population Balance Modeling: Current Status and Future Prospects. Annu. Rev. Chem. Biomol. Eng. 2014, 5, 123–146. [Google Scholar] [CrossRef] [Green Version]
- Bilgili, E.; Scarlett, B. Population balance modeling of non-linear effects in milling processes. Powder Technol. 2005, 153, 59–71. [Google Scholar] [CrossRef]
- Cisternas, L.A.; Lucay, F.A.; Botero, Y.L. Trends in modeling, design, and optimization of multiphase systems in minerals processing. Minerals 2020, 10, 22. [Google Scholar] [CrossRef] [Green Version]
- Arancibia-Bravo, M.P.; Lucay, F.A.; López, J.; Cisternas, L.A. Modeling the effect of air flow, impeller speed, frother dosages, and salt concentrations on the bubbles size using response surface methodology. Miner. Eng. 2019, 132, 142–148. [Google Scholar] [CrossRef]
- Gupta, V.K.; Sharma, S. Analysis of ball mill grinding operation using mill power specific kinetic parameters. Adv. Powder Technol. 2014, 25, 625–634. [Google Scholar] [CrossRef]
- Hasan, M.; Palaniandy, S.; Hilden, M.; Powell, M. Simulating product size distribution of an industrial scale VertiMill® using a time-based population balance model. Miner. Eng. 2018, 127, 312–317. [Google Scholar] [CrossRef]
- Herbst, J.A.; Fuerstenau, D.W. Scale-up procedure for continuous grinding mill design using population balance models. Int. J. Miner. Process. 1980, 7, 1–31. [Google Scholar] [CrossRef]
- Powell, M.S.; Morrison, R.D. The future of comminution modelling. Int. J. Miner. Process. 2007, 84, 228–239. [Google Scholar] [CrossRef]
- Sharma, S.; Pantula, P.D.; Miriyala, S.S.; Mitra, K. A novel data-driven sampling strategy for optimizing industrial grinding operation under uncertainty using chance constrained programming. Powder Technol. 2021, 377, 913–923. [Google Scholar] [CrossRef]
- Brownlee, J. Machine Learning Mastery with R; Machine Learning Mastery: Melbourne, Australia, 2018. [Google Scholar]
- Montgomery, D.C.; Runger, G.C.; Wiley, J. Applied Statistics and Probability for Engineers, 3rd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2003; ISBN 0471204544. [Google Scholar]
- Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; Cariboni, J.; Gatelli, D.; Saisana, M.; Tarantola, S. Global Sensitivity Analysis: The Primer; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2008; ISBN 9780470059975. [Google Scholar]
- Siraj-Ud-Doulah, M. A Comparison among Twenty-Seven Normality Tests. Res. Rev. J. Stat. 2019, 8, 41–59. [Google Scholar]
- Das, K.R.; Imon, A.H.M.R. A Brief Review of Tests for Normality. Am. J. Theor. Appl. Stat. 2017, 5, 2–12. [Google Scholar]
- Razali, N.M.; Wah, Y.B. Power comparisons of Shapiro-Wilk, Kolmogorov-Smirnov, Lilliefors and Anderson-Darling tests. J. Stat. Model. Anal. 2011, 2, 21–33. [Google Scholar]
- Das, B.M. Principles of Geotechnical Engineering; Cengage Le.: Stamford, CT, USA, 2010; ISBN 9780495411307. [Google Scholar]
- Wills, B.; Napier-Munn, T. Mineral Processing Technology: An Introduction to the Practical Aspects of Ore Treatment and Mineral Recovery; Elsevier Science & Technology: Burlington, MA, USA, 2006; ISBN 0750644508. [Google Scholar]
- Dallavalle, J.M. Micromeritics: The Technology of Fine Particles; Pitman Publishing Corporation: New York, NY, USA, 1943. [Google Scholar]
- Gagné, F. Descriptive Statistics and Analysis in Biochemical Ecotoxicology. In Biochemical Ecotoxicology: Principles and Methods; Elsevier Inc.: Amsterdam, The Netherlands, 2014; pp. 209–229. [Google Scholar]
- Dallavalle, J.M.; Orr, C.; Blocker, H.G. Fitting Bimodal Particle Size Distribution Curves. Ind. Eng. Chem. 1951, 43, 1377–1380. [Google Scholar] [CrossRef]
- Brittain, H. Particle-size distribution, Part III: Determination by analytical sieving. Pharm. Technol. 2002, 26, 56–64. [Google Scholar]
- Xu, Z.; Gautam, M.; Mehta, S. Cumulative frequency fit for particle size distribution. Appl. Occup. Environ. Hyg. 2002, 17, 538–542. [Google Scholar] [CrossRef] [PubMed]
- King, R.P. Modeling and Simulation of Mineral Processing Systems; Elsevier Inc.: Amsterdam, The Netherlands, 2012; ISBN 0750648848. [Google Scholar]
- Kelly, E.; Spottiswood, D. Introduction to Mineral Processing; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1982; ISBN 978-0471033790. [Google Scholar]
- Kelsall, D.F.; Reid, K.J.; Restarick, C.J. Continuous Grinding in a Smallwet Ball Mill. Part III. A Study of Distribution of Residence Time. Power Technol. 1969, 3, 170–178. [Google Scholar] [CrossRef]
- Roller, P.S. Statistical Analysis of Size Distribution of Particulate Materials, with Special Reference to Bimodal and Frequency Distributions. Correlation of Quartile with Statistical Values. J. Phys. Chem. 1941, 45, 241–281. [Google Scholar] [CrossRef]
- Gaudin, A.M.; Hukki, R.T. Principles of Comminution-Size and Surface Distribution. Trans. SME/AIME 1944, 67, 88–94. [Google Scholar]
- Heywood, H. Measurement of the Fineness of Powdered Materials. Proc. Inst. Mech. Eng. 1938, 140, 257–347. [Google Scholar] [CrossRef]

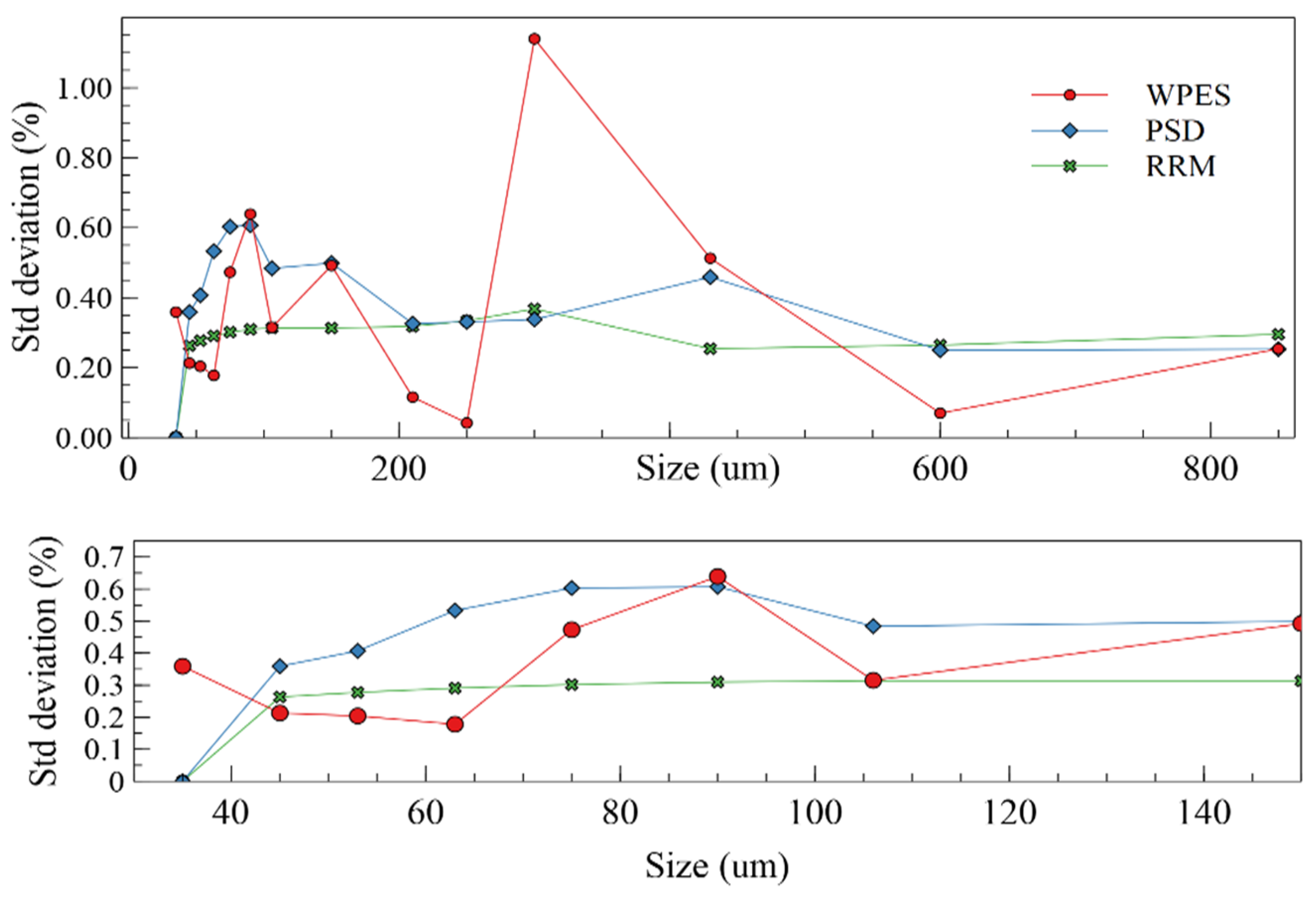
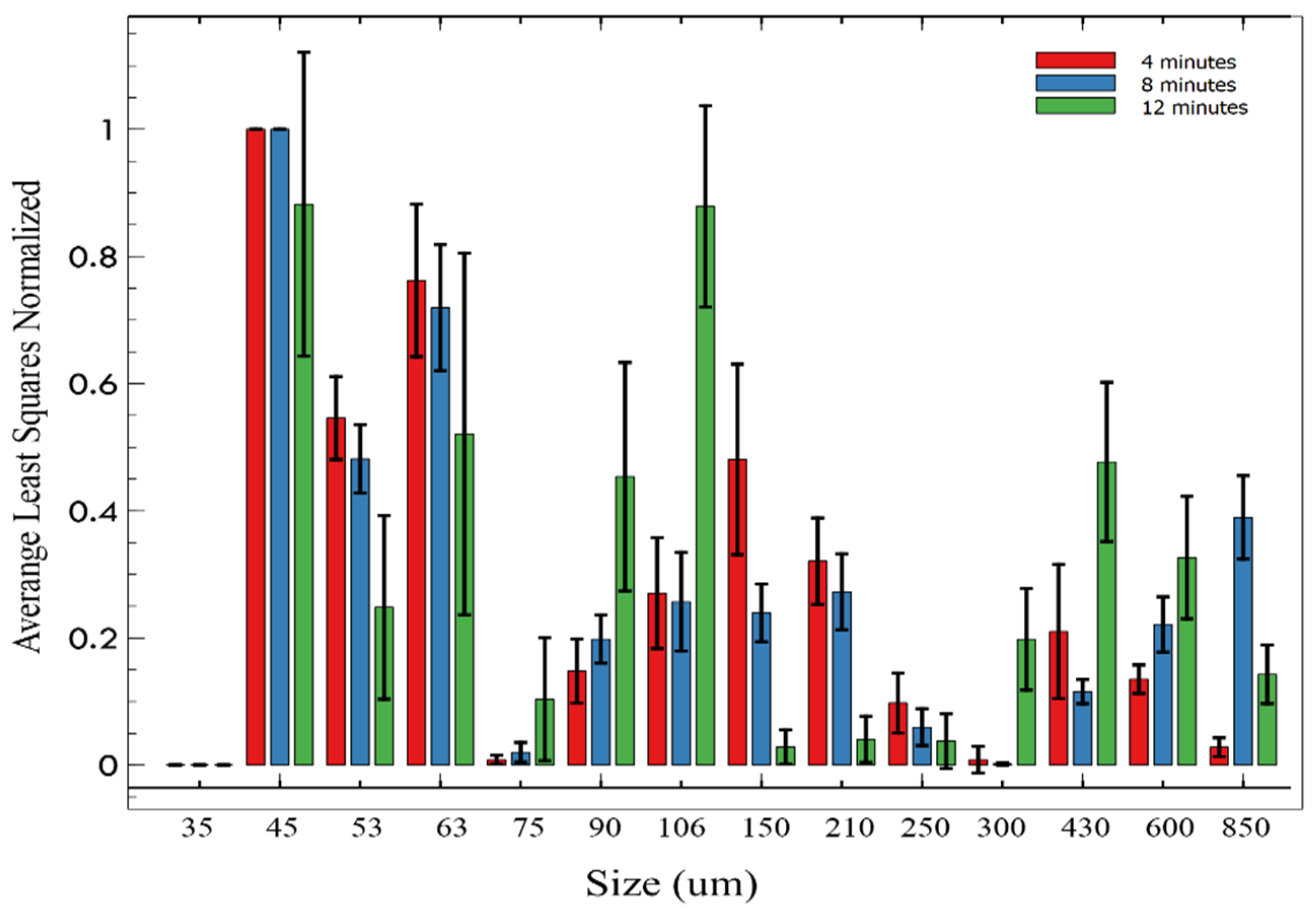
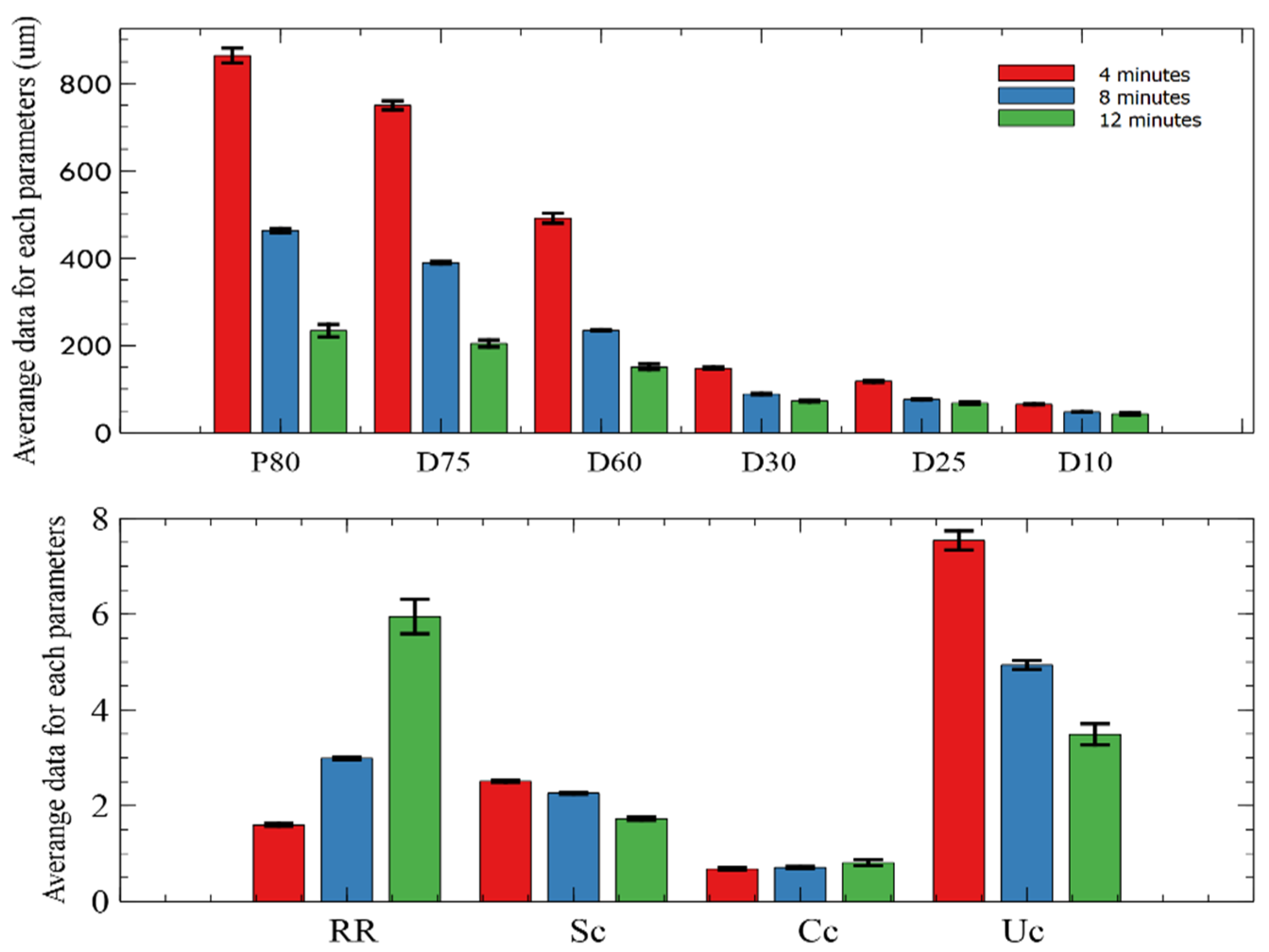
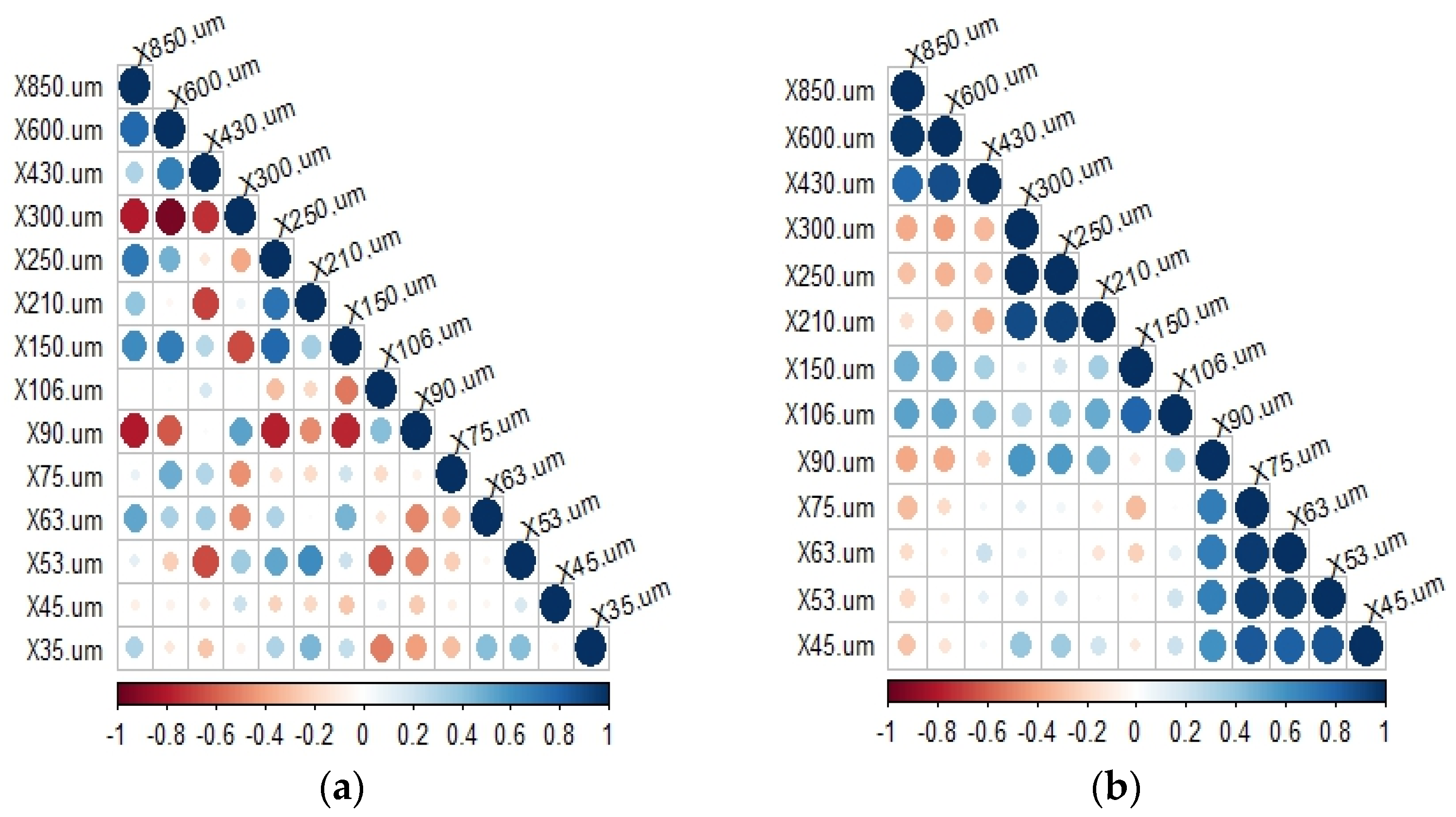
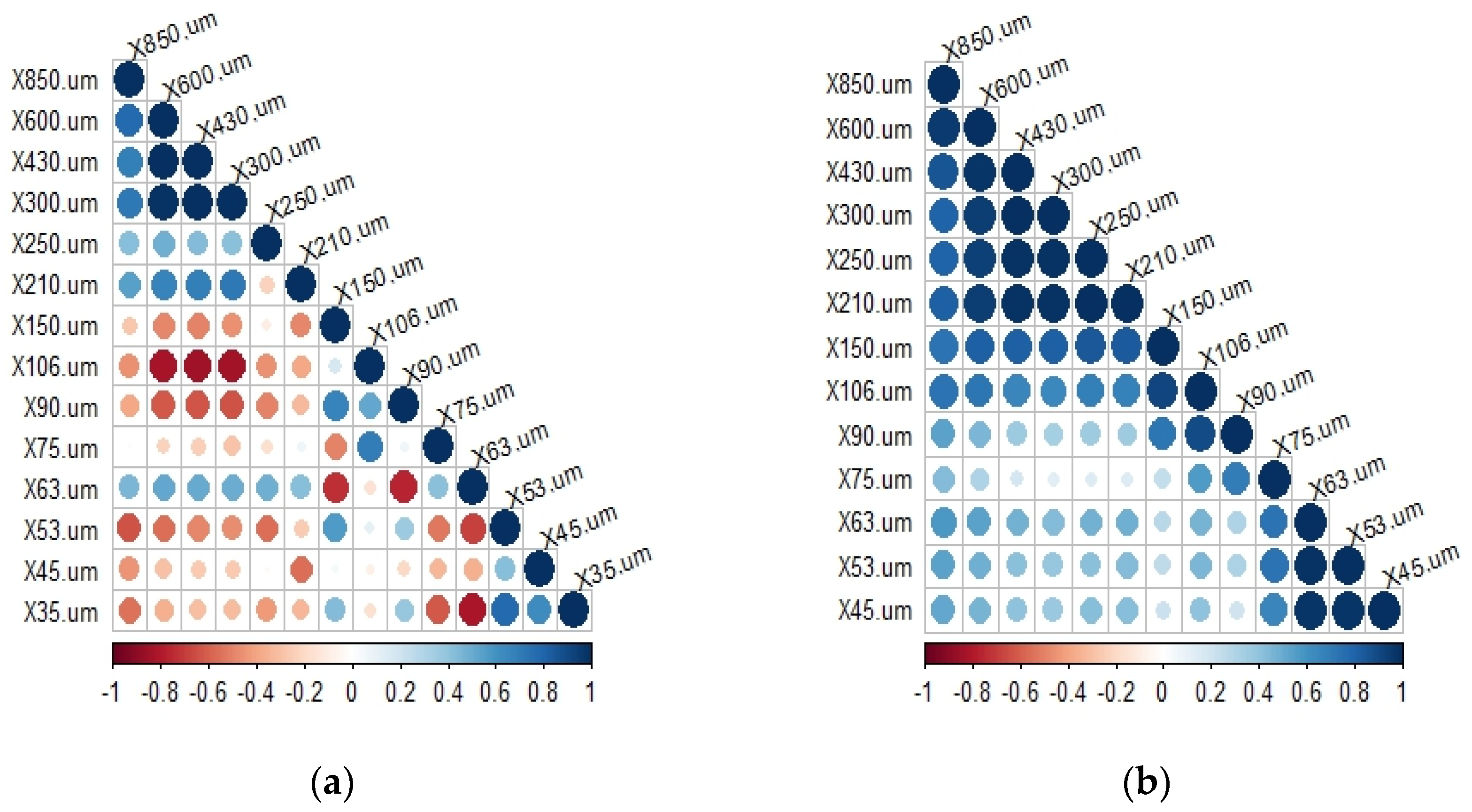
| PSCP | Feed Ore | 4 min | 8 min | 12 min |
|---|---|---|---|---|
| (μm) | 1388.4 | |||
| (μm) | - | 864 | 463 | 234 |
| (μm) | 1309.5 | 753 | 387 | 217 |
| (μm) | 1069.5 | 485 | 236 | 158 |
| (μm) | 523.6 | 149 | 87 | 77 |
| (μm) | 418.1 | 119 | 74 | 72 |
| (μm) | 101.6 | 64 | 46 | 46 |
| RR | - | 1.59 | 3 | 5.5 |
| Sc | 1.85 | 2.52 | 2.28 | 1.74 |
| Cc | 2.52 | 0.71 | 0.69 | 0.81 |
| Uc | 10.52 | 7.57 | 5.14 | 3.39 |
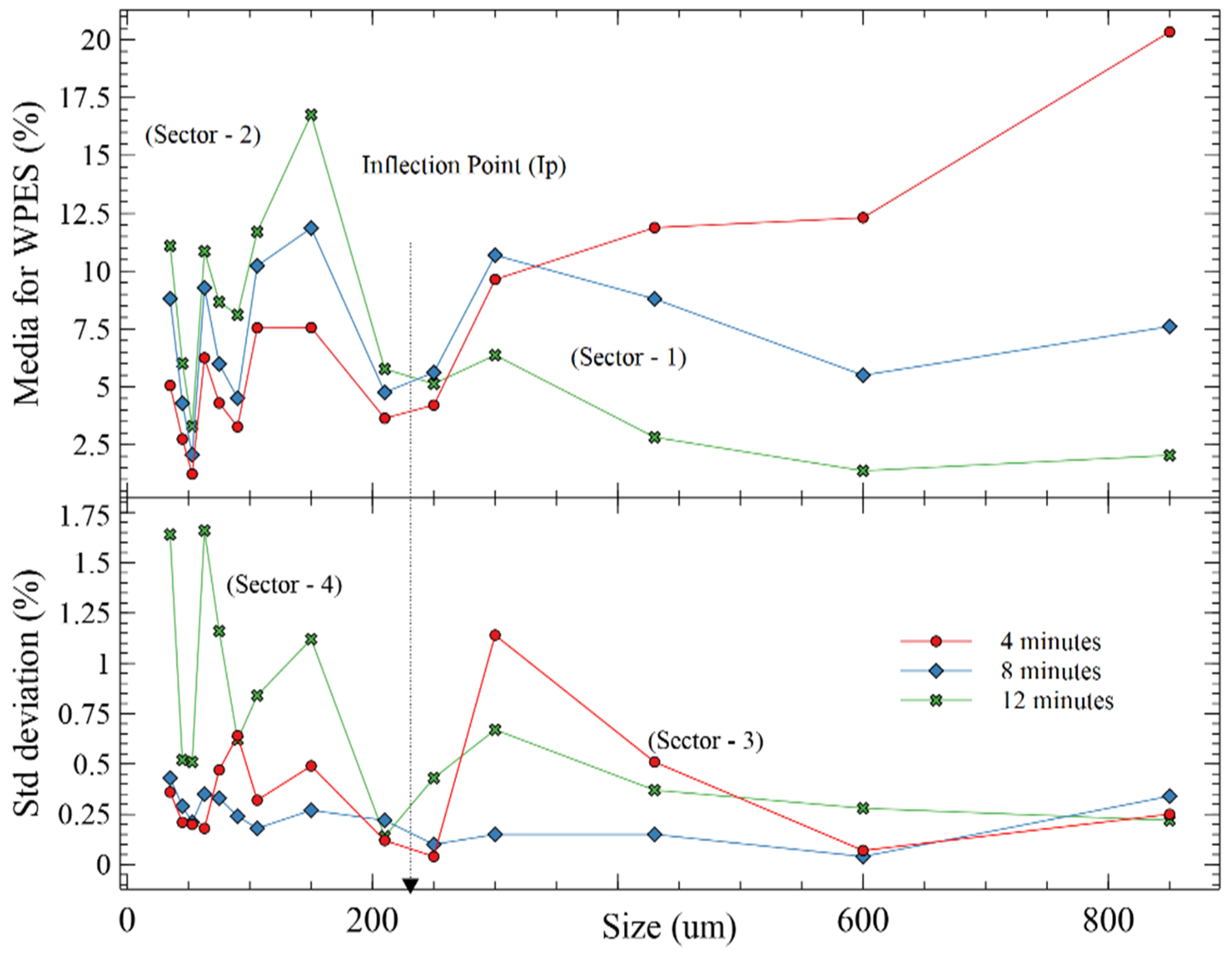
| Size (µm) | 4 min | 8 min | 12 min | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Media (%) | Min. (%) | Max. (%) | Media (%) | Min. (%) | Max. (%) | Media (%) | Min. (%) | Max. (%) | |
| 600–850 | 20.34 | 19.90 | 21.37 | 7.61 | 6.92 | 8.03 | 2.04 | 1.57 | 2.80 |
| 430–600 | 12.31 | 12.12 | 12.92 | 5.50 | 5.44 | 5.57 | 1.37 | 1.03 | 1.87 |
| 300–430 | 11.88 | 11.11 | 12.66 | 8.80 | 8.64 | 9.05 | 2.82 | 2.19 | 3.90 |
| 250–300 | 9.64 | 6.81 | 10.89 | 10.69 | 10.43 | 11.20 | 6.37 | 5.51 | 7.60 |
| 210–250 | 4.21 | 4.15 | 4.26 | 5.62 | 5.38 | 6.26 | 5.13 | 4.68 | 6.15 |
| 150–210 | 3.64 | 3.52 | 3.84 | 4.76 | 2.98 | 5.24 | 5.77 | 5.55 | 5.96 |
| 106–150 | 7.56 | 6.79 | 8.40 | 11.86 | 11.33 | 12.77 | 16.76 | 14.98 | 18.61 |
| 90–106 | 7.55 | 7.13 | 8.12 | 10.23 | 10.01 | 10.93 | 11.70 | 10.16 | 13.41 |
| 75–90 | 3.27 | 2.18 | 4.50 | 4.51 | 3.04 | 5.12 | 8.11 | 7.32 | 9.14 |
| 63–75 | 4.30 | 3.45 | 5.01 | 5.99 | 5.42 | 6.56 | 8.67 | 7.48 | 11.37 |
| 53–63 | 6.25 | 5.94 | 6.46 | 9.28 | 8.70 | 10.54 | 10.86 | 7.28 | 12.17 |
| 45–53 | 1.23 | 0.86 | 1.54 | 2.06 | 1.77 | 2.35 | 3.30 | 2.37 | 3.80 |
| 35–45 | 2.74 | 2.43 | 2.99 | 4.29 | 3.86 | 4.72 | 6.01 | 5.26 | 6.70 |
| 0–35 | 5.06 | 4.54 | 5.60 | 8.81 | 8.35 | 9.59 | 11.09 | 9.10 | 14.55 |
| Sum | 100 | 90.93 | 108.58 | 100 | 92.25 | 107.94 | 100 | 84.48 | 118.03 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Delgado, J.; Lucay, F.A.; Sepúlveda, F.D. Experimental Uncertainty Analysis for the Particle Size Distribution for Better Understanding of Batch Grinding Process. Minerals 2021, 11, 862. https://doi.org/10.3390/min11080862
Delgado J, Lucay FA, Sepúlveda FD. Experimental Uncertainty Analysis for the Particle Size Distribution for Better Understanding of Batch Grinding Process. Minerals. 2021; 11(8):862. https://doi.org/10.3390/min11080862
Chicago/Turabian StyleDelgado, José, Freddy A. Lucay, and Felipe D. Sepúlveda. 2021. "Experimental Uncertainty Analysis for the Particle Size Distribution for Better Understanding of Batch Grinding Process" Minerals 11, no. 8: 862. https://doi.org/10.3390/min11080862
APA StyleDelgado, J., Lucay, F. A., & Sepúlveda, F. D. (2021). Experimental Uncertainty Analysis for the Particle Size Distribution for Better Understanding of Batch Grinding Process. Minerals, 11(8), 862. https://doi.org/10.3390/min11080862







