Seismic Wave Speeds Derived from Nuclear Resonant Inelastic X-ray Scattering for Comparison with Seismological Observations
Abstract
1. Introduction
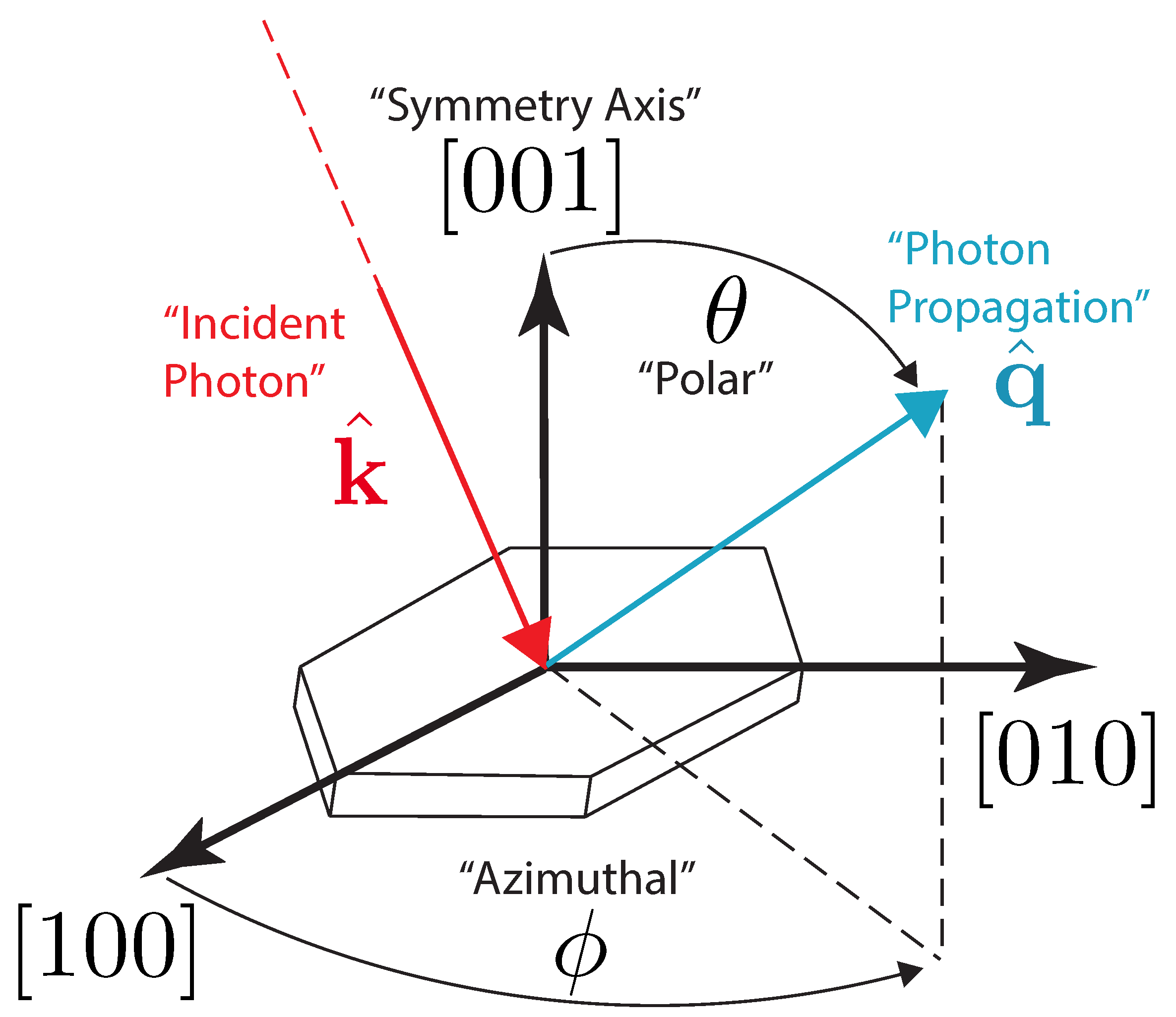
2. Theory
Alternative Expressions for the Debye Speed under Various Simplifying Assumptions
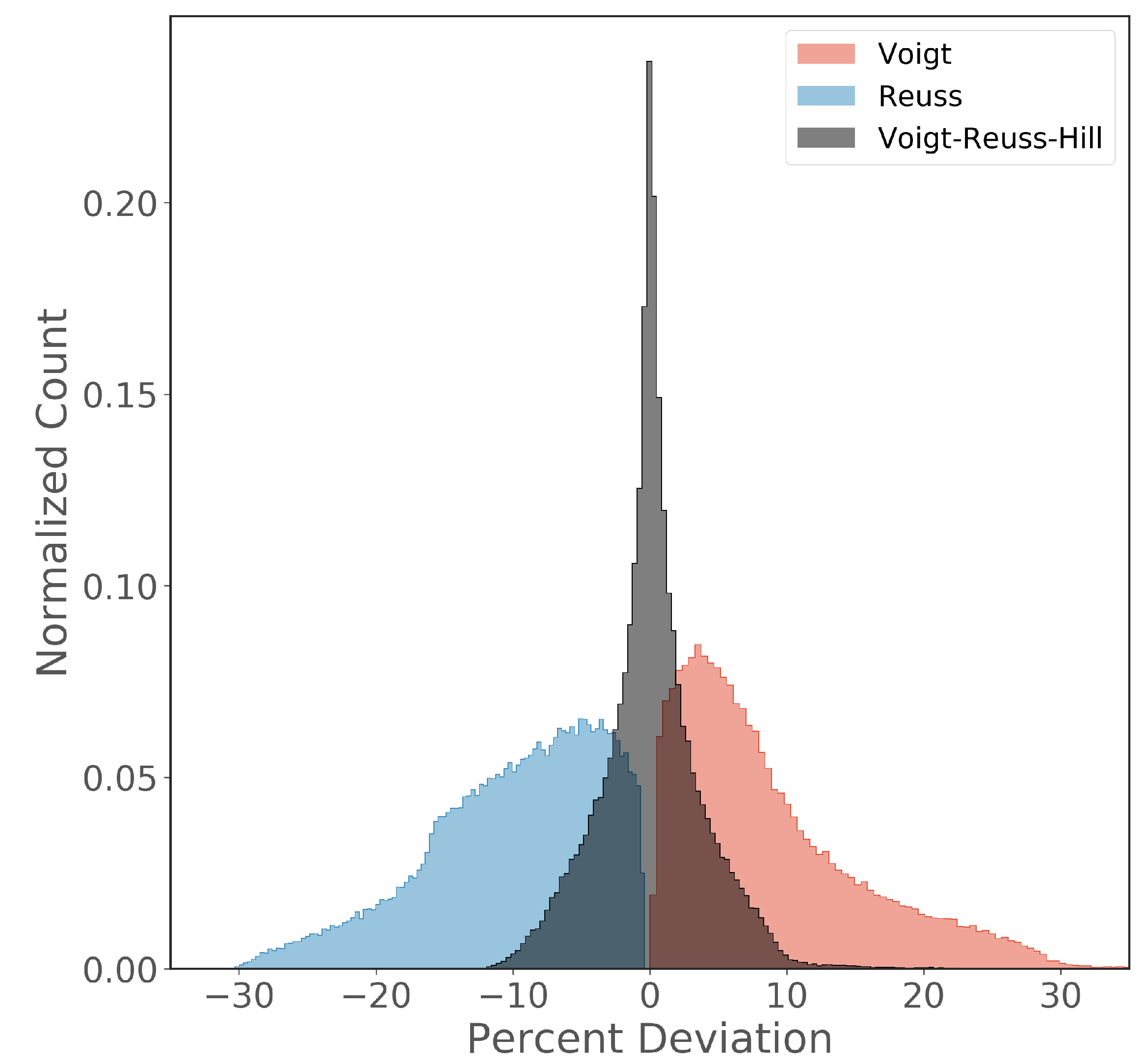
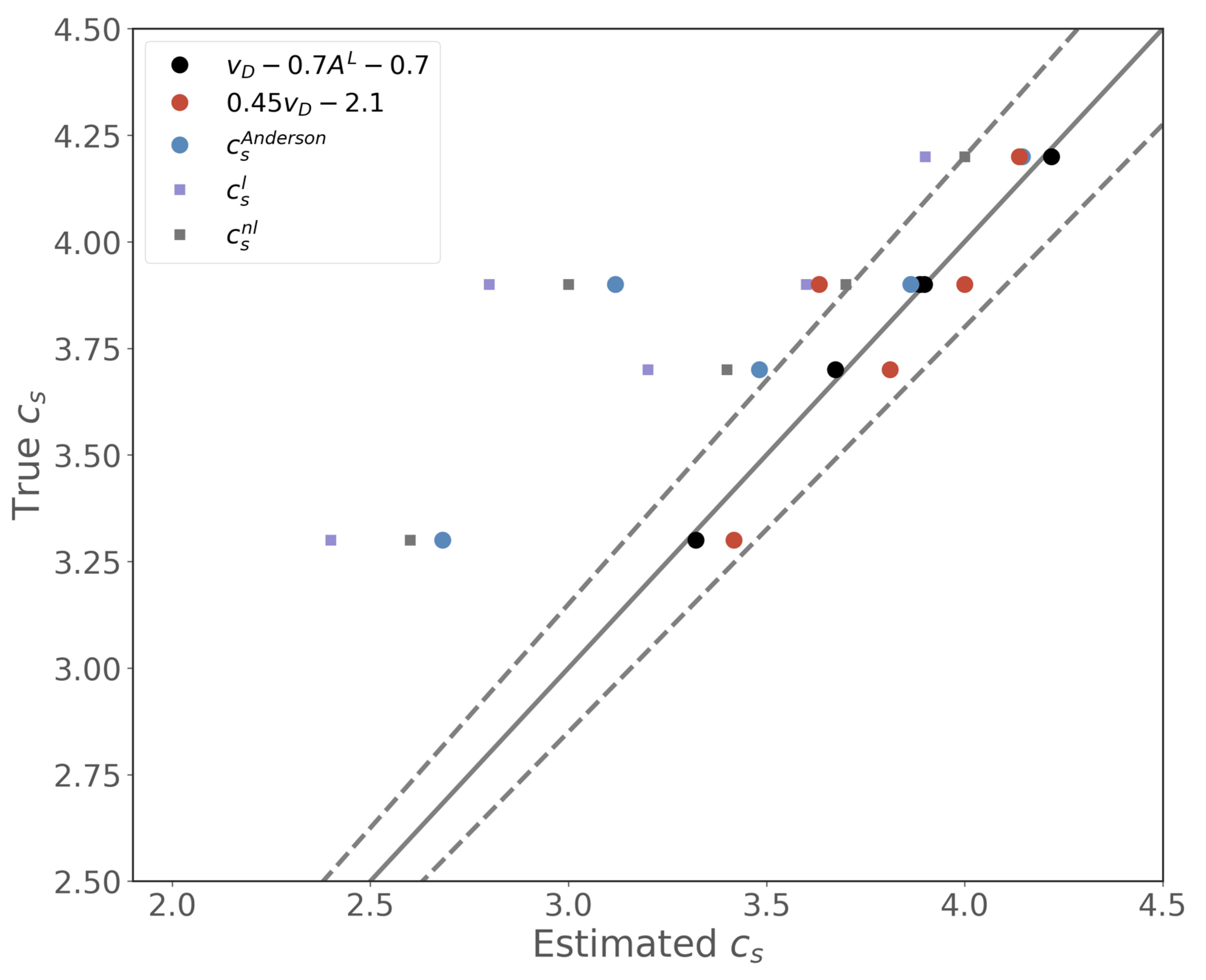
3. Results and Discussion
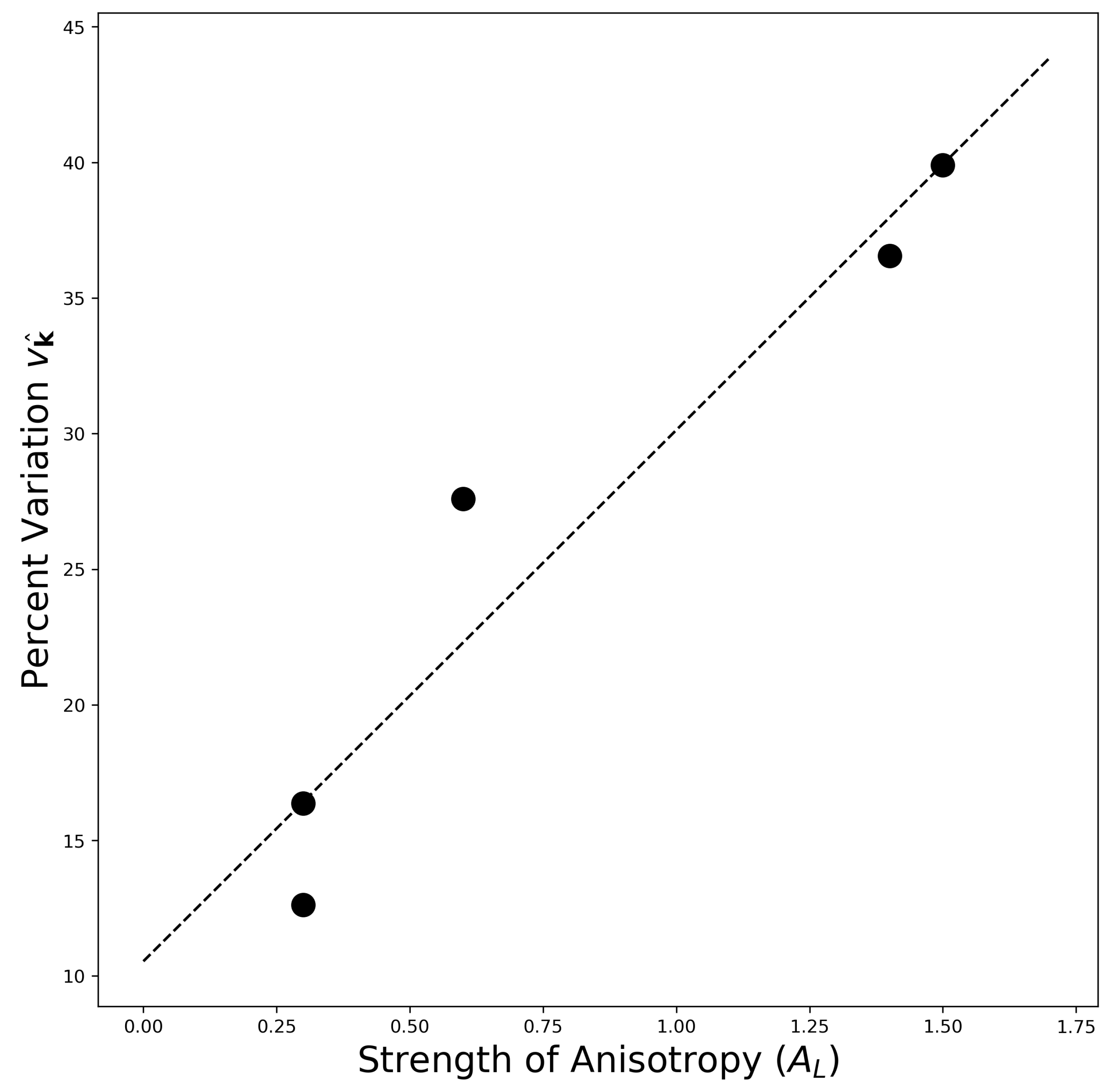
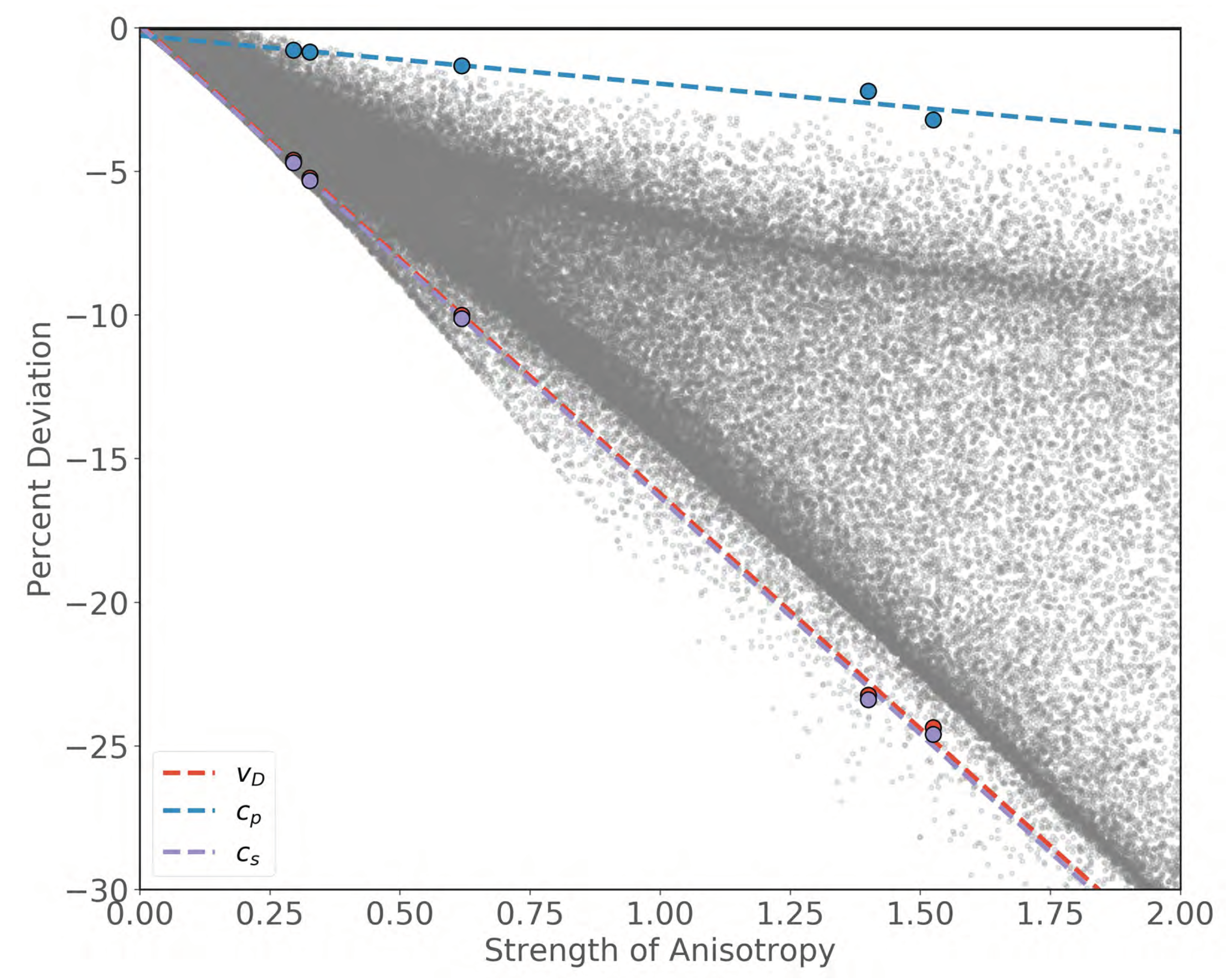
3.1. Variations in the Debye Speed
3.2. Extracting Seismic Wave Speeds
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| NRIXS | Nuclear Resonant Inelastic X-ray Scattering |
Appendix A. Seismic Wave Speeds
Appendix A.1. Hexagonal Symmetry
Appendix A.2. Cubic Symmetry
Appendix B. Experimental Measurements of Cobalt
| Pressure | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 8.8 | 0.09 | 3.44 | 5.7 | 5.7 | 5.8 | - | - | 3.1 | 3.1 | 3.1 | - | - |
| 11 | 9.3 | 0.06 | 3.67 | 6.2 | 6.2 | - | 6.3 | 6.1 | 3.3 | 3.3 | 3.3 | 3.1 | - |
| 40 | 10.3 | 0.03 | 4.18 | 7.3 | 7.3 | - | 7.3 | - | 3.7 | 3.7 | - | 3.9 | - |
Appendix C. Mean Projected Wave Speed for Randomly Oriented Samples
References
- Sturhahn, W. Nuclear resonant spectroscopy. Phys. Condens. Matter 2004, 416, S497–S530. [Google Scholar] [CrossRef]
- Dauphas, N.; Hu, M.Y.; Baker, E.M.; Hu, J.; Tissot, F.L.; Alp, E.E.; Roskosz, M.; Zhao, J.; Bi, W.; Liu, J.; et al. SciPhon: A data analysis software for nuclear resonant inelastic X-ray scattering with applications to Fe, Kr, Sn, Eu and Dy. J. Synchrotron Radiat. 2018, 25, 1581–1599. [Google Scholar] [CrossRef] [PubMed]
- Sturhahn, W.; Jackson, J.M. Geophysical Applications of Nuclear Resonant Spectroscopy; Ohtani, E., Ed.; Advances in High-Pressure Mineralogy; The Geological Society of America: Boulder, CO, USA, 2007; pp. 157–174. [Google Scholar]
- Antonangeli, D.; Ohtani, E. Sound velocity of hcp-Fe at high pressure: Experimental constraints, extrapolations and comparison with seismic models. Prog. Earth Planet. Sci. 2015, 2, 3. [Google Scholar] [CrossRef]
- Singwi, K.S.; Sjölander, A. Resonance absorption of nuclear gamma rays and the dynamics of atomic motions. Phys. Rev. 1960, 120, 1093–1102. [Google Scholar] [CrossRef]
- Sturhahn, W.; Toellner, T.S.; Alp, E.E.; Zhang, X.; Ando, M.; Yoda, Y.; Kikuta, S.; Seto, M.; Kimball, C.W.; Dabrowski, B. Phonon density of states measured by inelastic nuclear resonant scattering. Phys. Rev. Lett. 1995, 74, 3832–3835. [Google Scholar] [CrossRef] [PubMed]
- Chumakov, A.I.; Rüffer, R.; Baron, A.Q.R.; Grünsteudel, H.; Grünsteudel, H.F.; Kohn, V.G. Anisotropic inelastic nuclear absorption. Phys. Rev. B 1997, 56, 10758. [Google Scholar] [CrossRef]
- Kohn, V.G.; Chumakov, A.I.; Rüffer, R. Nuclear resonant inelastic absorption of synchrotron radiation in an anisotropic single crystal. Phys. Rev. B 1998, 58, 8437–8444. [Google Scholar] [CrossRef]
- Anderson, O.L. A simplified method for calculating the Debye temperature from elastic constants. J. Phys. Chem. Solids 1963, 24, 909–917. [Google Scholar] [CrossRef]
- Anderson, O.L. An approximate method of estimating shear velocity from specific heat. J. Geophys. Res. Lett. 1965, 70, 4726–4728. [Google Scholar] [CrossRef]
- Sturhahn, W.; Kohn, V. Theoretical aspects of incoherent nuclear resonant scattering. Hyperfine Interact. 1999, 123, 367–399. [Google Scholar] [CrossRef]
- Hu, M.Y.; Sturhahn, W.; Toellner, T.S.; Mannheim, P.D.; Brown, D.E.; Zhao, J.; Alp, E.E. Measuring velocity of sound with nuclear resonant inelastic X-ray scattering. Phys. Rev. B 2003, 67, 094304. [Google Scholar] [CrossRef]
- Dziewoński, A.M.; Anderson, D.L. Preliminary reference earth model. Phys. Earth Planet. Int. 1981, 25, 297–356. [Google Scholar]
- Delbridge, B.G.; Ishii, M. Reconciling elasticity tensor constraints from mineral physics and seismological observations: Applications to the earth’s inner Core. Geophys. J. Int. 2019. submitted. [Google Scholar]
- Jensen, J.L.W.V. Sur les fonctions convexes et les inegalites entre les valeurmoyennes. Acta Math. 1906, 30, 175–193. [Google Scholar] [CrossRef]
- Roberts, A.W.; Varberg, D.E. Convex Functions; Academic Press: Cambridge, MA, USA, 1973. [Google Scholar]
- Steinle-Neumann, G.; Stixrude, L.; Cohen, R.E.; Gülseren, O. Elasticity of iron at the temperature of the Earth’s inner core. Nature 2001, 413, 57–60. [Google Scholar] [CrossRef]
- Tsuchiya, T.; Kuwayama, Y.; Ishii, M.; Kawai, K. High-P, T elasticity of iron-light element alloys[MR33E-05]. In Proceedings of the 2017 Fall Meeting, AGU, New Orleans, LA, USA, 11–15 December 2017. [Google Scholar]
- Li, Y.; Vočadlo, L.; Brodholt, J.P. The elastic properties of hcp-Fe alloys under the conditions of the Earth’s inner core. Earth Planet. Sci. Lett. 2018, 493, 118–127. [Google Scholar] [CrossRef]
- Martorell, B.; Wood, I.G.; Brodholt, J.; Vočaldo, L. The elastic properties of hcp-Fe1- xSix at Earth’s inner-core conditions. Earth Planet. Sci. Lett. 2016, 451, 89–96. [Google Scholar] [CrossRef]
- Belonoshko, A.B.; Skorodumova, N.V.; Davis, S.; Osiptsov, A.N.; Rosengren, A.; Johansson, B. Origin of the low rigidity of the Earth’s inner core. Science 2007, 316, 1603–1605. [Google Scholar] [CrossRef]
- Kube, C.M. Elastic anisotropy of crystals. AIP Adv. 2016, 6, 095209. [Google Scholar] [CrossRef]
- Ranganathan, S.I.; Ostoja-Starzewski, M. Universal elastic anisotropy index. Phys.Rev. Lett. 2008, 101, 055504. [Google Scholar] [CrossRef]
- Chung, D.H.; Buessem, W.R. The Elastic Anisotropy of Crystals. J. Appl. Phys. 1967, 38, 2010–2012. [Google Scholar] [CrossRef]
- Mao, H.K.; Xu, J.; Struzhkin, V.V.; Shu, J.; Hemley, R.J.; Sturhahn, W.; Hu, M.Y.; Alp, E.E.; Vocadlo, L.; Alfè, D.; et al. Phonon density of states of iron up to 153 gigapascals. Science 2001, 292, 914–916. [Google Scholar] [CrossRef] [PubMed]
- Lin, J.F.; Struzhkin, V.V.; Sturhahn, W.; Huang, E.; Zhao, J.; Hu, M.Y.; Alp, E.E.; Mao, H.K.; Boctor, N.; Hemley, R.J. Sound velocities of iron-nickel and iron-silicon alloys at high pressures. Geophys. Res. Lett. 2003, 30, 11. [Google Scholar] [CrossRef]
- Jackson, J.M.; Hamecher, E.A.; Sturhahn, W. Nuclear resonant X-ray spectroscopy of (Mg, Fe) SiO3 orthoenstatites. Eur. J. Mineral. 2009, 21, 551–560. [Google Scholar] [CrossRef]
- Prescher, C.; Dubrovinsky, L.; Bykova, E.; Kupenko, I.; Glazyrin, K.; Kantor, A.; McCammon, C.; Mookherjee, M.; Nakajima, Y.; Miyajima, N.; et al. High Poisson’s ratio of Earth’s inner core explained by carbon alloying. Nat. Geosci. 2015, 8, 220. [Google Scholar] [CrossRef]
- Wicks, J.K.; Jackson, J.M.; Sturhahn, W.; Zhang, D. Sound velocity and density of magnesiowüstites: Implications for ultra low-velocity zone topography. Geophys. Res. Lett. 2017, 44, 2148–2158. [Google Scholar] [CrossRef]
- Finkelstein, G.J.; Jackson, J.M.; Said, A.; Alatas, A.; Leu, B.M.; Sturhahn, W.; Toellner, T.S. Strongly anisotropic magnesiowüstite in Earth’s lower mantle. J. Geophys. Res. 2018, 123, 4740–4750. [Google Scholar] [CrossRef]
- Anderson, O.L.; Dubrovinsky, L.; Saxena, S.K.; LeBihan, T. Experimental vibrational Grüneisen ratio values for ϵ-iron up to 330 GPa at 300 K. Geophys. Res. Lett. 2001, 28, 399–402. [Google Scholar] [CrossRef]
- Bosak, A.; Krisch, M.; Chumakov, A.; Abrikosov, I.A.; Dubrovinsky, L. Possible artifacts in inferring seismic properties from X-ray data. Phys. Earth Planet. Int. 2016, 260, 14–19. [Google Scholar] [CrossRef]
- Matthies, S.; Humbert, M. On the principle of a geometric mean of even-rank symmetric tensors for textured polycrystals. J. Appl. Crystallogr. 1995, 28, 254–266. [Google Scholar] [CrossRef]
- Fedorov, I. Theory of Elastic Waves in Crystals; Plenum Press: New York, NY, USA, 1968. [Google Scholar]
- Musgrave, M. Crystal Acoustics; Holden-Day Series in Mathematical Physics: San Francisco, CA, USA, 1970; pp. 75–76. [Google Scholar]
- Dahlen, F.; Tromp, J. Theoretical Global Seismology; Princeton University Press: Princeton, NJ, USA, 1998. [Google Scholar]
- Chapman, C. Fundamentals of Seismic Wave Propagation; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Takeuchi, H.; Saito, M. Seismic surface waves. Methods Comput. Phys. 1972, 11, 217–295. [Google Scholar]
- Backus, G.E. Possible forms of seismic anisotropy of the uppermost mantle under oceans. J. Geophys. Res. 1965, 70, 3429–3439. [Google Scholar] [CrossRef]
- Every, A.G. General closed-form expressions for acoustic waves in elastically anisotropic solids. Phys. Rev. B 1980, 22, 1746–1760. [Google Scholar] [CrossRef]
- Tromp, J. Normal-mode splitting due to inner-core anisotropy. Geophys. J. Int. 1995, 121, 963–968. [Google Scholar] [CrossRef]
- Watt, J.P.; Peselnick, L. Clarification of the Hashin-Shtrikman bounds on the effective elastic moduli of polycrystals with hexagonal, trigonal, and tetragonal symmetries. J. Appl. Phys. 1980, 51, 1525–1531. [Google Scholar] [CrossRef]
- Every, A.G. General, closed-form expressions for acoustic waves in cubic crystals. Phys. Rev. Lett. 1979, 42, 1065–1068. [Google Scholar] [CrossRef]
- Antonangeli, D.; Krisch, M.; Fiquet, G.; Farber, D.L.; Aracne, C.M.; Badro, J.; Occelli, F.; Requardt, H. Elasticity of cobalt at high pressure studied by inelastic X-ray scattering. Phys. Rev. Lett. 2004, 93, 215505. [Google Scholar] [CrossRef]
- Antonangeli, D.; Krisch, M.; Fiquet, G.; Badro, J.; Farber, D.L.; Bossak, A.; Merkel, S. Aggregate and single-crystalline elasticity of hcp cobalt at high pressure. Phys. Rev. B 2005, 72, 134303. [Google Scholar] [CrossRef]
- Choy, M.M.; Hellwege, K.H.; Hellwege, A.M. Elastic, Piezoelectric, Pyroelectric, Piezooptic, Electrooptic Constants, and Nonlinear Dielectric Susceptibilities of Crystals: Revised and Expanded Edition of Volumes III/1 and III/2(Vol. 11); Springer: New York, NY, USA, 1979. [Google Scholar]
- Goncharov, A.F.; Crowhurst, J.; Zaug, J.M. Elastic and vibrational properties of cobalt to 120 GPa. Phys. Rev. Lett. 2004, 92, 115502. [Google Scholar] [CrossRef]
| Material | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| hcp Fe | 13.0 | 11.8 | 3.9 | 1.5 | 2150 | 1685 | 990 | 140 | 60 | 2030 |
| hcp Fe-Si | 13.1 | 11.3 | 3.9 | 0.3 | 1674 | 1855 | 1120 | 176 | 137 | 1400 |
| hcp Fe-Si-Ni | 12.5 | 11.8 | 3.3 | 1.4 | 1816 | 1964 | 1224 | 80 | 49 | 1718 |
| hcp Fe-Si-C | 13.1 | 11.6 | 3.7 | 0.6 | 1712 | 2066 | 1263 | 164 | 91 | 1530 |
| hcp Fe-S-C | 13.1 | 11.8 | 4.2 | 0.3 | 1831 | 2091 | 1214 | 183 | 173 | 1485 |
| bcc Fe-Si | 13.6 | 11.5 | 4.2 | 1.7 | 1562 | 1562 | 1448 | 366 | 366 | 1448 |
| Material | |||||||
|---|---|---|---|---|---|---|---|
| hcp Fe | 3.35 | 3.35 | 4.45 | 3.18 | 3.87 | ||
| hcp Fe-Si | 4.23 | 4.22 | 4.47 | 4.16 | 4.32 | ||
| hcp Fe-Si-Ni | 2.89 | 2.96 | 3.78 | 2.77 | 3.32 | ||
| hcp Fe-Si-C | 3.79 | 3.83 | 4.21 | 3.67 | 3.95 | ||
| hcp Fe-S-C | 4.54 | 4.56 | 4.77 | 4.47 | 4.62 | ||
| bcc Fe-Si | 4.04 | 4.04 | 4.79 | 3.33 | 4.13 |
| Material | |||||||
|---|---|---|---|---|---|---|---|
| hcp Fe | 11.8 | 10.7 [–10%] | 11.5 [–3%] | 3.9 | 2.8 [–28%] | 3.0 [–23%] | 3.1 [–20%] |
| hcp Fe-Si | 11.2 | 10.2 [–10%] | 11.2 [–1%] | 3.9 | 3.6 [–8%] | 3.7 [–5%] | 3.9 [–2%] |
| hcp Fe-Si-Ni | 11.8 | 10.8 [–8%] | 11.5 [–2%] | 3.3 | 2.4 [–29%] | 2.6 [–22%] | 2.7 [–20%] |
| hcp Fe-Si-C | 11.6 | 10.6 [–9%] | 11.4 [–1%] | 3.7 | 3.2 [–13%] | 3.4 [–9%] | 3.5 [–6%] |
| hcp Fe-S-C | 11.8 | 10.6 [–10%] | 11.7 [–1%] | 4.2 | 3.9 [–7%] | 4.0 [–5%] | 4.1 [–1%] |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Delbridge, B.; Ishii, M. Seismic Wave Speeds Derived from Nuclear Resonant Inelastic X-ray Scattering for Comparison with Seismological Observations. Minerals 2020, 10, 331. https://doi.org/10.3390/min10040331
Delbridge B, Ishii M. Seismic Wave Speeds Derived from Nuclear Resonant Inelastic X-ray Scattering for Comparison with Seismological Observations. Minerals. 2020; 10(4):331. https://doi.org/10.3390/min10040331
Chicago/Turabian StyleDelbridge, Brent, and Miaki Ishii. 2020. "Seismic Wave Speeds Derived from Nuclear Resonant Inelastic X-ray Scattering for Comparison with Seismological Observations" Minerals 10, no. 4: 331. https://doi.org/10.3390/min10040331
APA StyleDelbridge, B., & Ishii, M. (2020). Seismic Wave Speeds Derived from Nuclear Resonant Inelastic X-ray Scattering for Comparison with Seismological Observations. Minerals, 10(4), 331. https://doi.org/10.3390/min10040331





