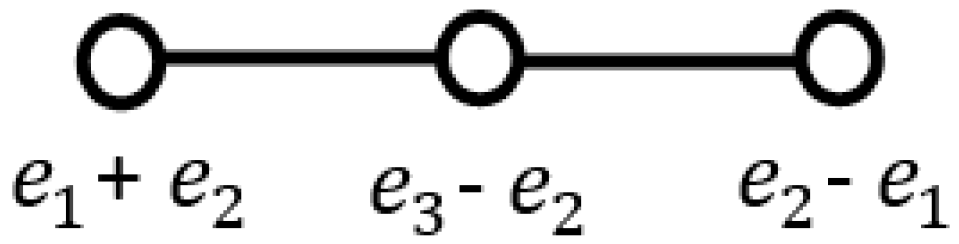Regular and Irregular Chiral Polyhedra from Coxeter Diagrams via Quaternions

Abstract

Vertices and symmetries of regular and irregular chiral polyhedra are represented by quaternions with the use of Coxeter graphs. A new technique is introduced to construct the chiral Archimedean solids, the snub cube and snub dodecahedron together with their dual Catalan solids, pentagonal icositetrahedron and pentagonal hexecontahedron. Starting with the proper subgroups of the Coxeter groups $W\left(A_1\oplus A_1\oplus A_1\right)$,$W\left(A_3\right)$, $W\left(B_3\right)$ and $W\left(H_3\right)$, we derive the orbits representing the respective solids, the regular and irregular forms of a tetrahedron, icosahedron, snub cube, and snub dodecahedron. Since the families of tetrahedra, icosahedra and their dual solids can be transformed to their mirror images by the proper rotational octahedral group, they are not considered as chiral solids. Regular structures are obtained from irregular solids depending on the choice of two parameters. We point out that the regular and irregular solids whose vertices are at the edge mid-points of the irregular icosahedron, irregular snub cube and irregular snub dodecahedron can be constructed.

1. Introduction

In fundamental physics, chirality plays a very important role. A Weyl spinor describing a massless Dirac particle is either in a left-handed state or in a right-handed state. Such states cannot be transformed to each other by the proper Lorentz transformations. Chirality is a well-defined quantum number for massless particles. Coxeter groups and their orbits [1] derived from the Coxeter diagrams describe the molecular structures [2], viral symmetries [3,4], crystallographic and quasi crystallographic materials [5,6,7]. Chirality is a very interesting topic in molecular chemistry. Certain molecular structures are either left-oriented or right-oriented. In three-dimensional Euclidean space, chirality can be defined as follows: if a solid cannot be transformed to its mirror image by proper isometries (proper rotations, translations and their compositions), it is called a chiral object. For this reason, the chiral objects lack the plane and/or central inversion symmetries. In two earlier publications [8,9], we studied the symmetries of the Platonic–Archimedean solids and their dual solids, the Catalan solids, and constructed their vertices. Two Archimedean solids, the snub cube and snub dodecahedron as well as their duals are chiral polyhedral, whose symmetries are the proper rotational subgroups of the octahedral group and the icosahedral group, respectively. Non-regular, non-chiral polyhedra have been discussed earlier [10]. Chiral polytopes in general have been studied in the context of abstract combinatorial form [11,12,13,14]. The chiral Archimedean solids, snub cube, snub dodecahedron and their duals have been constructed by employing several other techniques [15,16], but it seems that the method in what follows has not been studied earlier in this context.

We follow a systematic method for the construction of the chiral polyhedra. Let$G$ be a rank-3 Coxeter graph where$W{\left(G\right)}^{+}$ represents the proper rotation subgroup of the Coxeter group$W\left(G\right).$ For the snub cube and snub dodecahedron, the Coxeter graphs are the $B_3\mathrm{and}{H}_3$, respectively. To describe the general technique, we first begin with simpler Coxeter diagrams A₁ $\oplus$ A₁ $\oplus$ A₁ and $A_3$, although they describe the achiral polyhedra such as the families of regular and irregular tetrahedron and icosahedron, respectively. We explicitly show that achiral polyhedra possess larger proper rotational symmetries transforming them to their mirror images. We organize the paper as follows. In Section 2 we introduce quaternions and construct the Coxeter groups in terms of quaternions [17]. We extend the group W (A₁ $\oplus$ A₁ $\oplus$ A₁) to the octahedral group by the symmetry group$Sym\left(3\right)\mathrm{of}\mathrm{the}\mathrm{Coxeter}\mathrm{diagram}$ A₁ $\oplus$ A₁ $\oplus$ A₁. In Section 3 we obtain the proper rotation subgroup of the Coxeter group W (A₁ $\oplus$ A₁ $\oplus$ A₁) and determine the vertices of an irregular tetrahedron. In Section 4 we discuss a similar problem for the Coxeter-Dynkin diagram $A_3$ leading to an icosahedron and again prove that it can be transformed by the group W(B₃)⁺ to its mirror image, which implies that neither the tetrahedron nor icosahedron are chiral solids. We focus on the irregular icosahedra constructed either by the proper tetrahedral group or its extension pyritohedral group and construct the related dual solids tetartoid and pyritohedron. We also construct the irregular polyhedra taking the mid-points of edges of the irregular icosahedron as vertices. Section 5 deals with the construction of irregular and regular snub cube and their dual solids from the proper rotational octahedral symmetry W(B₃)⁺ using the same technique employed in the preceding sections. The chiral polyhedron taking the mid-points as vertices of the irregular snub cube is also discussed. In Section 6 we repeat a similar technique for the constructions of irregular snub dodecahedra and their dual solids using the proper icosahedral group W(H₃)⁺, which is isomorphic to the group of even permutations of five letters$Alt\left(5\right)$. The chiral polyhedra whose vertices are the mid-points of the edges of the irregular snub dodecahedron are constructed. Irregular polyhedra transform to regular polyhedra when the parameter describing irregularity turns out to be the solution of certain cubic equations. Section 7 involves the discussion of the technique for the construction of irregular chiral polyhedra.

2. Quaternionic Constructions of the Coxeter Groups

Let $q=q_0+q_i{e}_i$, $\left(i=1,2,3\right)$ be a real unit quaternion with its conjugate defined by $\overline{q}=q_0-q_i{e}_i$, and the norm $q\overline{q}=\overline{q}q=1$. The quaternionic imaginary units satisfy the relations:

$$e_i{e}_j=-{\delta }_{ij}+{\epsilon }_{ijk}{e}_k,\left(i,j,k=1,2,3\right)$$

(1)

where ${\delta }_{ij}$ and ${\epsilon }_{ijk}$ are the Kronecker and Levi-Civita symbols, and summation over the repeated indices is understood. The unit quaternions form a group isomorphic to the special unitary group $SU\left(2\right).$Quaternions generate the four-dimensional Euclidean space with the scalar product

$$\left(p,q\right):=\frac{1}{2}\left(\overline{p}q+\overline{q}p\right)=\frac{1}{2}\left(p\overline{q}+q\overline{p}\right)$$

(2)

The Coxeter diagram$A_1\oplus A_1\oplus A_1$ can be represented by its quaternionic roots as shown in Figure 1 where $\sqrt{2}$ is just the norm.

The Cartan matrix and its inverse are given as follows:

$$C=\left[\begin{array}{ccc}2& 0& 0\\ 0& 2& 0\\ 0& 0& 2\end{array}\right],C^{-1}=\frac{1}{2}\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]$$

(3)

The simple roots ${\alpha }_i$ and the weight vectors${\omega }_i$ for a simply laced root system satisfy the scalar product [18,19]

$$({\alpha }_i,{\alpha }_j)=C_{ij},\left({\omega }_i,{\omega }_j\right)={\left(C^{-1}\right)}_{ij},({\alpha }_i,{\omega }_j)={\delta }_{ij},\left(i,j=1,2,3\right).$$

(4)

Note that one can express the roots in terms of the weights or vice versa:

$${\alpha }_i=C_{ij}{\omega }_j,{\omega }_i={\left(C^{-1}\right)}_{ij}{\alpha }_j$$

(5)

If ${\alpha }_i$is an arbitrary quaternionic simple root and $r_i$ is the reflection generator with respect to the plane orthogonal to the simple root${\alpha }_i$, then the reflection of an arbitrary quaternion $\mathsf{\Lambda }$, an element in the weight space${\omega }_1$, ${\omega }_2,{\omega }_3$can be represented as [20]:

$$r_i\mathsf{\Lambda }=-\frac{{\alpha }_i}{\sqrt{2}}\overline{\mathsf{\Lambda }}\frac{{\alpha }_i}{\sqrt{2}}:={\left[\frac{{\alpha }_i}{\sqrt{2}},-\frac{{\alpha }_i}{\sqrt{2}}\right]}^{*}\mathsf{\Lambda }.$$

(6)

It is then straight forward to show that$r_i{\omega }_j={\omega }_j-{\delta }_{ij}{\alpha }_j$. We will use the notations ${\left[p,q\right]}^{*}\mathsf{\Lambda }:=$ p$\overline{\mathsf{\Lambda }}q$ and $\left[p,q\right]\mathsf{\Lambda }:=p\mathsf{\Lambda }q$ for the rotoreflection (rotation and reflection combined) and the proper rotation, respectively, where $p\mathrm{and}q$ are arbitrary unit quaternions. If $\mathsf{\Lambda }$ is pure imaginary quaternion, then${\left[p,q\right]}^{*}\mathsf{\Lambda }:=p\overline{\mathsf{\Lambda }}q=\left[p,-q\right]\mathsf{\Lambda }$.

The Coxeter group $W\left(A_1\oplus A_1\oplus A_1\right)=<r_1,r_2,r_3>$ can be generated by three commutative group elements:

$$r_1={\left[e_1,-e_1\right]}^{*},r_2={\left[e_2,-e_2\right]}^{*},r_3={\left[e_3,-e_3\right]}^{*}.$$

(7)

They generate the elementary abelian group W (A₁ $\oplus$ A₁ $\oplus$ A₁) $\approx$ $C_2\times C_2\times C_2:=2^3$ of order 8. The scaled root system $(\pm e_1,\pm e_2,\pm e_3)$ represents the vertices of an octahedron and has more symmetries than the Coxeter group W (A₁ $\oplus$ A₁ $\oplus$ A₁). The automorphism group of the root system can be obtained by extending the Coxeter group of order 8 by the Dynkin diagram symmetry $Sym\left(3\right)$ of the Coxeter diagram in Figure 1. This is obvious from the diagram where the generators of the symmetric group $Sym\left(3\right)$ of order 6 can be chosen as:

$$s=\left[\frac{1}{2}\left(1+e_1+e_2+e_3\right),\frac{1}{2}\left(1-e_1-e_2-e_3\right)\right],d={[\frac{1}{\sqrt{2}}\left(e_1-e_2\right),-\frac{1}{\sqrt{2}}\left(e_1-e_2\right)]}^{*},$$

$$s^3=d^2=1,dsd=s^{-1}.$$

(8)

It is clear that the generators permute the quaternionic imaginary units as:

$$s:e_1\to e_2\to e_3\to e_1,d:e_1\leftrightarrow e_2,e_3\to e_3,$$

and satisfy the relations $s{r}_i{s}^{-1}=r_{i+1},d{r}_{1}d=r_2$, $d{r}_{3}d=r_3$ where the indices are considered modulo 3.

It is clear that the Coxeter group $<r_1,r_2,r_3>$ is invariant under the permutation group $Sym\left(3\right)$ by conjugation so that the automorphism group of the root system $(\pm e_1,\pm e_2,\pm e_3)$ is an extension of the group $<r_1,r_2,r_3>$ by the group$Sym\left(3\right)$ which is the octahedral group $2^3:Sym\left(3\right)$ of order 48 (here: stands for the semi-direct product). It is clear from this notation that the Coxeter group $2^3$ is an invariant subgroup of the octahedral group. We use a compact notation for the octahedral group in terms of quaternions as the union of subsets:

$$O_h=[T,\pm \overline{T}]{\displaystyle \cup }[T^{\prime },\pm \overline{T^{\prime }}]$$

(9)

where the sets of quaternions $T$ and$T^{\prime }$ are given by:

$$\begin{gathered} T=\{\pm 1,\pm e_1,\pm e_2,\pm e_3,\frac{1}{2}\left(\pm 1\pm e_1\pm e_2\pm e_3\right)\}, \\ {T}^{\prime }=\{\frac{1}{\sqrt{2}}\left(\pm 1\pm e_1\right),\frac{1}{\sqrt{2}}\left(\pm e_2\pm e^3\right),\frac{1}{\sqrt{2}}\left(\pm 1\pm e_2\right),\frac{1}{\sqrt{2}}\left(\pm e_3\pm e_1\right),\frac{1}{\sqrt{2}}\left(\pm 1\pm e_3\right),\frac{1}{\sqrt{2}}\left(\pm e_1\pm e_2\right)\}. \end{gathered}$$

(10)

Here $T$ and $T{\displaystyle \cup }{T}^{\prime }$ represent the binary tetrahedral group and the binary octahedral group, respectively. We have used a short-hand notation for the designation of the groups, e.g., $[T,\pm \overline{T}]$ means the set of all $[t,\pm \overline{t}]\in [T,\pm \overline{T}]$ with $t\in T$. The maximal subgroups of the octahedral group can be written as [21]:

$$\begin{gathered} \mathrm{Chiral}\mathrm{octahedral}\mathrm{group}:O=[T,\overline{T}]{\displaystyle \cup }[T^{\prime },\overline{T^{\prime }}]\approx W{\left(B_3\right)}^{+}, \\ \mathrm{Tetrahedral}\mathrm{group}:T_d=[T,\overline{T}]{\displaystyle \cup }[T^{\prime },-\overline{T^{\prime }}], \\ \mathrm{Pyritohedral}\mathrm{group}:T_h=[T,\pm \overline{T}]. \end{gathered}$$

(11)

The octahedral group, as we will see in what follows, can also be obtained as the $Aut\left(A_3\right)\approx W\left(B_3\right).$

The proper rotation subgroup of the Coxeter group $W\left(A_1\oplus A_1\oplus A_1\right)$ is the Klein four-group $C_2\times C_2$ represented by the elements:

$$I=\left[1,1\right],r_1{r}_2=\left[e_3,-e_3\right],r_2{r}_3=\left[e_1,-e_1\right],r_3{r}_1=\left[e_2,-e_2\right]$$

(12)

We also note in passing that the Klein four-group in (12) is invariant by conjugation under the group generated by$s,\mathrm{with}{s}^3=1$. The Klein four-group together with the group element $s$ generate the tetrahedral rotation group, which is represented by $[T,\overline{T}]$ in our notation.

Next, we use the tetrahedral group $T_d\approx W\left(A_3\right).$Its Coxeter-Dynkin diagram $A_3$ with its quaternionic roots is shown in Figure 2.

The Cartan matrix of the Coxeter diagram $A_3$ and its inverse matrix are given by the respective matrices:

$$C=\left[\begin{array}{ccc}2& -1& 0\\ -1& 2& -1\\ 0& -1& 2\end{array}\right],C^{-1}=\frac{1}{4}\left[\begin{array}{ccc}3& 2& 1\\ 2& 4& 2\\ 1& 2& 3\end{array}\right]$$

(13)

The generators of the Coxeter group $W\left(A_3\right)$ are given by:

$$r_1={[\frac{1}{\sqrt{2}}\left(e_1+e_2\right),-\frac{1}{\sqrt{2}}\left(e_1+e_2\right)]}^{*}$$

$$r_2={[\frac{1}{\sqrt{2}}\left(e_3-e_2\right),-\frac{1}{\sqrt{2}}\left(e_3-e_2\right)]}^{*}$$

(14)

$$r_3={[\frac{1}{\sqrt{2}}\left(e_2-e_1\right),-\frac{1}{\sqrt{2}}\left(e_2-e_1\right)]}^{*}$$

$${\omega }_1=\frac{1}{2}\left(e_1+e_2+e_3\right),{\omega }_2=e_3,{\omega }_3=\frac{1}{2}\left(-e_1+e_2+e_3\right).$$

The generators in (14) generate the Coxeter group [22,23,24] which is isomorphic to the tetrahedral group $T_d$ of order 24. The automorphism group $Aut(A_3)\approx W\left(A_3\right):C_2\approx$ $O_h$where $C_2$ is generated by the Dynkin diagram symmetry $\gamma ={\left[e_1,-e_1\right]}^{*}$, which exchanges the first and the third simple roots and leaves the second root intact in Figure 2.

The Coxeter diagram $B_3$ leading to the octahedral group $W\left(B_3\right)\approx Sym\left(4\right)\times C_2\approx O_h$ is shown in Figure 3.

The Cartan matrix of the Coxeter diagram $B_3$and its inverse matrix are given by:

$$C=\left[\begin{array}{ccc}2& -1& 0\\ -1& 2& -2\\ 0& -1& 2\end{array}\right],C^{-1}=\frac{1}{2}\left[\begin{array}{ccc}2& 2& 2\\ 2& 4& 4\\ 1& 2& 3\end{array}\right]$$

(15)

The generators below generate the octahedral group given in (9) and the weight vectors are given by:

$$\begin{array}{c}{r}_1={[\frac{1}{\sqrt{2}}\left(e_1-e_2\right),-\frac{1}{\sqrt{2}}\left(e_1-e_2\right)]}^{*}\hfill \\ r_2={[\frac{1}{\sqrt{2}}\left(e_2-e_3\right),-\frac{1}{\sqrt{2}}\left(e_2-e_3\right)]}^{*}\hfill \\ r_3={[e_3,-e_3]}^{*}\hfill \end{array}$$

(16)

$${\omega }_1=e_1,{\omega }_2=e_1+e_2,{\omega }_3=\frac{1}{2}\left(e_1+e_2+e_3\right)$$

The group generated by the rotations $r_1{r}_2$ and $r_2{r}_3$ is isomorphic to the rotational octahedral group$<r_1{r}_2,r_2{r}_3>\approx \left\{\left[T,\overline{T}\right]{\displaystyle \cup }\right[T^{\prime },\overline{T^{\prime }}]\text{}}.$

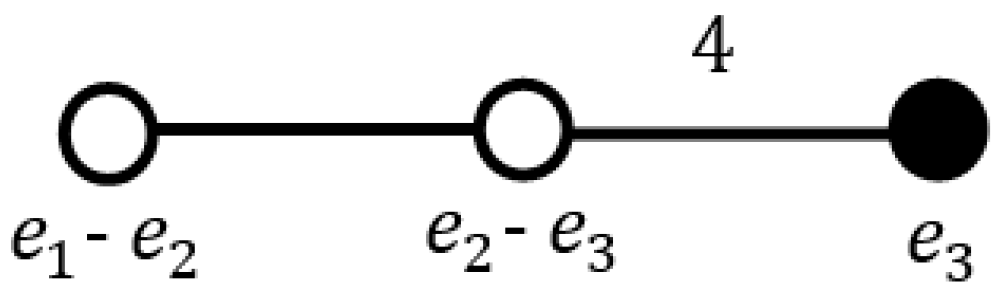
The Coxeter diagram $H_3$ leading to the icosahedral group is shown in Figure 4 with the quaternionic simple roots:

Here $\tau =\frac{1+\sqrt{5}}{2}$ is the golden ratio and $=\frac{1-\sqrt{5}}{2}$. The Cartan matrix of the diagram $H_3,$ its inverse and the weight vectors are given as follows:

$$C=\left[\begin{array}{ccc}2& -\tau & 0\\ -\tau & 2& -1\\ 0& -1& 2\end{array}\right],C^{-1}=\frac{1}{2}\left[\begin{array}{ccc}3{\tau }^2& 2{\tau }^3& {\tau }^3\\ 2{\tau }^3& 4{\tau }^2& 2{\tau }^2\\ {\tau }^3& 2{\tau }^2& \tau +2\end{array}\right]$$

(17)

$${\omega }_1=\frac{\tau }{\sqrt{2}}(\sigma e_1-\tau e_3),{\omega }_2=-\sqrt{2}\tau e_3,{\omega }_3=\frac{\tau }{\sqrt{2}}\left(\sigma e_2-e_3\right)$$

The quaternionic generators of the icosahedral group$I_h\approx Alt\left(5\right)\times C_2\approx W\left(H_3\right)$ are given by:

$$\begin{array}{c}{r}_1={\left[e_1,-e_1\right]}^{*},\hfill \\ r_2={\left[\frac{1}{2}\left(\tau e_1+e_2+\sigma e_3\right),-\frac{1}{2}\left(\tau e_1+e_2+\sigma e_3\right)\right]}^{*},\hfill \\ r_3={\left[e_2,-e_2\right]}^{*},\hfill \end{array}$$

(18)

or shortly, $W\left(H_3\right)=\left[I,\pm \overline{I}\right]$where$I$ is the set of 120 quaternionic elements of the binary icosahedral group generated by the quaternions $e_1$ and $\frac{1}{2}\left(\tau e_1+e_2+\sigma e_3\right)$ [20]. The icosahedral rotation group is represented by the proper rotation subgroup$W{\left(H_3\right)}^{+}=\left[I,\overline{I}\right]\approx Alt\left(5\right)$. All finite subgroups of the groups $O(3)\mathrm{and}O(4)$ in terms of quaternions can be found in the references [17,25].

A general vector in the dual space is represented by the vector$\mathsf{\Lambda }=a_1{\omega }_1+a_2{\omega }_2+a_3{\omega }_3$. We will use the notation $\mathsf{\Lambda }=a_1{\omega }_1+a_2{\omega }_2+a_3{\omega }_3:\left(a_1{a}_2{a}_3\right),$ which are called the Dynkin indices in the Lie algebraic representation theory [26]. We use the notation$W\left(G\right)\mathsf{\Lambda }:={\left(a_1{a}_2{a}_3\right)}_G$ for the orbit of the Coxeter group $W\left(G\right)$ generated from the vector$\mathsf{\Lambda }$ where the letter $G$ represents the Coxeter diagram. A few examples could be useful to illuminate the situation by recalling the identifications [8]:

$$\begin{gathered} {(100)}_{A_3}\left(\mathrm{tetrahedron}\right),{(111)}_{A_3}\left(\mathrm{truncated}\mathrm{octahedron}\right),{(100)}_{B_3}\left(\mathrm{octahedron}\right), \\ {(001)}_{B_3}\left(\mathrm{cube}\right),{(100)}_{H_3}\left(\mathrm{dodecahedron}\right),{(001)}_{H_3}\left(\mathrm{icosahedron}\right),\mathrm{and}{(010)}_{H_3}, \\ \left(\mathrm{icosidodecahedron}\right). \end{gathered}$$

3. The Orbit ${\mathit{C}}_{\mathbf{2}}\times {\mathit{C}}_{\mathbf{2}}\left({\mathit{a}}_{\mathbf{1}}{\mathit{a}}_{\mathbf{2}}{\mathit{a}}_{\mathbf{3}}\right)$ as an Irregular Tetrahedron

The proper rotation subgroup $C_2\times C_2$of the Coxeter group $W\left(A_1\oplus A_1\oplus A_1\right)$transforms a generic vector $\mathsf{\Lambda }$as follows:

$$\begin{gathered} \mathsf{\Lambda }=\frac{1}{2}(a_1{e}_1+a_2{e}_2+a_3{e}_3) \\ {r}_1{r}_2\mathsf{\Lambda }=\frac{1}{2}(-a_1{e}_1-a_2{e}_2+a_3{e}_3), \\ {r}_2{r}_3\mathsf{\Lambda }=\frac{1}{2}(a_1{e}_1-a_2{e}_2-a_3{e}_3), \\ {r}_3{r}_1\mathsf{\Lambda }=\frac{1}{2}(-a_1{e}_1+a_2{e}_2-a_3{e}_3). \end{gathered}$$

(19)

These four vectors define the vertices of an irregular tetrahedron with four identical scalene triangles with edge lengths $\sqrt{{a_1}^2+{a_2}^2}$, $\sqrt{{a_2}^2+{a_3}^2}$, and $\sqrt{{a_3}^2+{a_1}^2}.$An irregular tetrahedron with $a_1=1,a_2=2,a_3=3$ is depicted in Figure 5.

Mid-points of the edges of an irregular tetrahedron are given by the vectors $\pm a_1{e}_1,\pm a_2{e}_2,\pm a_3{e}_3$ forming an irregular octahedron with eight identical scalene triangles of sides $\sqrt{{a_1}^2+{a_2}^2}$, $\sqrt{{a_2}^2+{a_3}^2}$, $\sqrt{{a_3}^2+{a_1}^2}$ and the corresponding interior angles, say, $\alpha ,\beta ,\gamma$. Four triangles with identical face-angles $\alpha$ surround the vertex $a_1{e}_1$. The remaining 4 triangles similarly meet at the opposite vertex $-a_1{e}_1$. This is true for every face-angle around every vertex.

The mirror image of an irregular tetrahedron is obtained by applying any one of the reflection generators on these vectors, which lead to the vectors:

$$\begin{gathered} r_1\mathsf{\Lambda }=\frac{1}{2}(-a_1{e}_1+a_2{e}_2+a_3{e}_3), \\ {r}_2\mathsf{\Lambda }=\frac{1}{2}(a_1{e}_1-a_2{e}_2+a_3{e}_3), \\ {r}_3\mathsf{\Lambda }=\frac{1}{2}(a_1{e}_1+a_2{e}_2-a_3{e}_3), \\ {r}_1{r}_2{r}_3\mathsf{\Lambda }=-\frac{1}{2}(a_1{e}_1+a_2{e}_2+a_3{e}_3). \end{gathered}$$

(20)

The vectors in (20) can also be obtained from those in (19) by quaternion conjugation.

The eight vectors in (19) and (20) form a rectangular prism with edge lengths $a_1,a_2\mathrm{and}{a}_3$ possessing the symmetry $(C_2\times C_2):C_2\approx D_{2h}$ of order 8. Assume now that we apply the one of the Dynkin diagram-symmetry operators $d$ on vector $\mathsf{\Lambda }$ and assume that:

$$\mathsf{\Lambda }=d\mathsf{\Lambda }=\frac{1}{2}\left(a{e}_1+a{e}_2+a_3{e}_3\right).$$

(21)

If we apply the rotation generators as in (19), we obtain an irregular tetrahedron with identical four isosceles triangles. The mirror copy of these vectors can be obtained similar to the procedure in (20) and when all are combined, we obtain a square prism with edge lengths $a\mathrm{and}{a}_3$.

A more symmetric case is obtained by assuming:

$$\mathsf{\Lambda }=s\mathsf{\Lambda }=\frac{1}{2}a\left(e_1+e_2+e_3\right).$$

(22)

In this case, the symmetry is the chiral tetrahedral group, and the vertices in (19) will represent a regular tetrahedron of edge length $\sqrt{2}a$ which is also invariant under the larger tetrahedral symmetry $T_d=[T,\overline{T}]\oplus [T^{\prime },-\overline{T^{\prime }}]$, as expected. A mirror image of the regular tetrahedron is obtained either by reflections as described by (20) or by a rotation of 180° around the $e_1-e_2$ axis, which can be obtained by the group element:

$$\left[\frac{1}{\sqrt{2}}\left(e_1-e_2\right),-\frac{1}{\sqrt{2}}\left(e_1-e_2\right)\right]\in [T^{\prime },\overline{T^{\prime }}].$$

(23)

A tetrahedron is not a chiral solid since it can be converted to its mirror image by a rotation such as the one in (23). A regular tetrahedron with its mirror image constitutes a cube which has the full octahedral symmetry of order 48.

4. The Regular and Irregular Icosahedron Derived from the Orbit $\mathit{W}{\left({\mathit{A}}_{\mathbf{3}}\right)}^{+}\left({\mathit{a}}_{\mathbf{1}}{\mathit{a}}_{\mathbf{2}}{\mathit{a}}_{\mathbf{3}}\right)$

The tetrahedral rotational subgroup $W{\left(A_3\right)}^{+}$of the Coxeter group $W\left(A_3\right)$ is the tetrahedral group of order 12 isomorphic to even permutations of four letters, $Alt\left(4\right),$which can be generated by the generators$a=r_1{r}_2$ and $b=r_2{r}_3$ satisfying the generation relations $a^3=b^3={(ab)}^2=1$. Let $\mathsf{\Lambda }=\left(a_1{a}_2{a}_3\right)$ be a general vector in the weight space of$A_3$. The following sets of vertices form two equilateral triangles.

$$(\mathsf{\Lambda },r_1{r}_2\mathsf{\Lambda },r_2{r}_1\mathsf{\Lambda })\mathrm{and}(\mathsf{\Lambda },r_2{r}_3\mathsf{\Lambda },r_3{r}_2\mathsf{\Lambda })$$

(24)

with respective edge lengths$\sqrt{2\left(a_1^2+a_1{a}_2+a_2^2\right)}$ and $\sqrt{2\left(a_2^2+a_2{a}_3+a_3^2\right)}$. Three more triangles can be obtained by joining the vertex $r_1{r}_3\mathsf{\Lambda }=r_3{r}_1\mathsf{\Lambda }$ to the vertices $\mathsf{\Lambda },r_1{r}_2\mathsf{\Lambda }$ and $r_3{r}_2\mathsf{\Lambda }$ and $r_2{r}_1\mathsf{\Lambda }$ to $r_2{r}_3\mathsf{\Lambda }$. The new edges are of the following lengths.

$$\begin{gathered} \left|r_1{r}_2\mathsf{\Lambda }-r_1{r}_3\mathsf{\Lambda }\right|=\sqrt{2\left(a_2^2+a_2{a}_3+a_3^2\right)}, \\ \left|r_3{r}_2\mathsf{\Lambda }-r_1{r}_3\mathsf{\Lambda }\right|=\sqrt{2\left(a_1^2+a_1{a}_2+a_2^2\right)}, \\ \left|\mathsf{\Lambda }-r_1{r}_3\mathsf{\Lambda }\right|=\left|r_2{r}_1\mathsf{\Lambda }-r_2{r}_3\mathsf{\Lambda }\right|=\sqrt{2\left(a_1^2+a_3^2\right)} \end{gathered}$$

(25)

The vertices joined to vector $\mathsf{\Lambda }$ are illustrated in Figure 6.

Factoring by an overall factor $a_2^2\ne 0$and defining the parameters $x=\frac{a_1}{a_2}$ and $y=\frac{a_3}{a_2}$ we obtain three classes of triangles. After dropping the overall factor $a_2$ we obtain,

$$\begin{gathered} \mathrm{equilateral}\mathrm{triangle}\mathrm{with}\mathrm{edge}\mathrm{length}:A=\sqrt{2\left(1+x+x^2\right)}, \\ \mathrm{equilateral}\mathrm{triangle}\mathrm{with}\mathrm{edge}\mathrm{length}:B=\sqrt{2\left(1+y+y^2\right)}, \\ 3\mathrm{scalene}\mathrm{triangles}\mathrm{with}\mathrm{edge}\mathrm{lengths}:A,B,C=\sqrt{2\left(x^2+y^2\right)} \end{gathered}$$

as shown in Figure 6. The sum of the face-angles at the vertex$\mathsf{\Lambda }$ (at every vertex indeed) is $\frac{2\pi }{3}+\left(\theta +\vartheta +\phi \right)=\frac{5\pi }{3}$where $\theta ,\vartheta ,\mathrm{and}\phi$ are the interior angles of the scalene triangles. The angular deficiency $\delta =2\pi -\frac{5\pi }{3}=\frac{\pi }{3}$ is the same as in the regular icosahedron. Using Descartes’ formula, the number of vertices can also be obtained as in [27].

$$N_0=\frac{4\pi }{\delta }=12.$$

(26)

The vector $\mathsf{\Lambda }$ can be written in terms of quaternions as $\mathsf{\Lambda }=\mathsf{\alpha }{e}_1+\beta e_2+\gamma e_3$ where the new parameters are defined by

$$\mathsf{\alpha }=\frac{x-y}{2},\beta =\frac{x+y}{2},\gamma =\beta +1.$$

(27)

The orbit of the chiral tetrahedral group $W\left(A_3\right)/C_2\approx \left[T,\overline{T}\right]$ generated from the vector $\mathsf{\Lambda }$ can be written as:

$$\begin{gathered} \left[T,\overline{T}\right]\mathsf{\Lambda }=\{\pm \mathsf{\alpha }{e}_1\pm \beta e_2\pm \gamma e_3,\pm \beta e_1\pm \gamma e_2\pm \mathsf{\alpha }{e}_3,\pm \gamma e_1\pm \mathsf{\alpha }{e}_2\pm \beta e_3\} \\ \left(\mathrm{even}\mathrm{number}\mathrm{of}(-)\mathrm{signs}\right). \end{gathered}$$

(28)

The quaternions in (28) with an odd number of $(-)$ signs constitute the mirror image. A rotation element, e.g., the one in (23), transforms the quaternions in (28) to their mirror images. This proves that the set in (28) does not represent a chiral polyhedron. Before we discuss the irregular icosahedral structures, we point out that for $x>0,y=0$ or $y>0,x=0,$ the set of 12 vectors describes a truncated tetrahedron. For $x=y=0,$ it describes an octahedron. More interesting cases arise as we will discuss below.

(1) $A=B=C$,$1+x+x^2=1+y+y^2=x^2+y^2$

Here, all the edges are equal leading to the solution $x=y=x^2-1\Rightarrow x^2-x-1=0,\Rightarrow x=\tau ,\mathrm{or}x=\sigma$. Substituting the first solution for $=\tau \mathrm{which}\mathrm{results}\mathrm{in}$ $\mathsf{\alpha }=0,\beta =\tau ,\gamma ={\tau }^2$, the set of vectors in (28) can be written as:

$$\left[T,\overline{T}\right]\mathsf{\Lambda }=\tau \left\{\pm e_1\pm \tau e_2,\pm e_2\pm \tau e_3,\pm e_3\pm \tau e_1\right\}.$$

(29)

These vertices, which are also invariant under the pyritohedral symmetry, represent a regular icosahedron. Note that the vector$\mathsf{\Lambda }=\tau \left(e_2+\tau e_3\right)$ is invariant under the 5-fold rotation by$s=[\frac{1}{2}(\sigma +e_2+\tau e_3),\frac{1}{2}(\sigma -e_2-\tau e_3)]$ while the other vectors in (29) are transformed to each other. This proves that the pyritohedral group $\left[T,\pm \overline{T}\right]$ can be extended to the icosahedral group $\left[I,\pm \overline{I}\right]$ by the generators so that the set of vertices in (29) is invariant under the icosahedral group of order 120. We emphasize that although (29) has a larger symmetry of the icosahedral group, it is obtained from its chiral tetrahedral subgroup. Its mirror image can be obtained by a rotation of 180° around the vector $e_1-e_2$ implying that icosahedron is not a chiral solid.

There is another trivial solution for $A=B=C$ where $x=-1,y=0$. The number of vertices in (28) reduces to 4 representing a regular tetrahedron.

(2) $A=B\ne C$,$y=\frac{1}{2}\left(-1\pm \sqrt{1+4\left(x^2+x\right)}\right)$

For various values of $x$ and the corresponding $y,$ one obtains an irregular icosahedron with$\left(4+4\right)$equilateral triangles and 12 isosceles triangles. An interesting case would be$x=y=-\tau$ with 12 vertices of$\left\{\pm \tau e_1\pm \sigma e_2,\pm \tau e_2\pm \sigma e_3,\pm \tau e_3\pm \sigma e_1\right\}$ which represent an irregular icosahedron with $\left(4+4\right)$equilateral triangles with edges of length $2$ and 12 isosceles triangles of sides $2,2\tau ,2\tau$ (Robinson triangles). Any irregular icosahedron with $x=y\ne 0$has a pyritohedral symmetry of order 24 as pointed out in (11). Another solution of the quadratic equation$x=-\tau ,y=-\sigma$ leads to an irregular icosahedron of $\left(4+4\right)$equilateral triangles with edge lengths $2$ and 12 isosceles triangles of edge lengths$2,2,\sqrt{6}$.

(3) $A=C\ne B$

This is another case with 12 isosceles triangles but here the 4 sets of equilateral triangles are not equal to the other set of 4 equilateral triangles. We have $x=y^2-1,x\ne \tau \mathrm{or}\sigma \mathrm{and}x\ne 0,y\ne 0.$ For $\mathrm{the}\mathrm{values}y=-\tau ,x=\tau$, the irregular icosahedron consists of 4 equilateral triangles with edge length 2, 4 equilateral triangles with edge length $2\tau$ and 12 Robinson triangles with edge lengths $2,2\tau ,2\tau$ as discussed in (2).

(4) $A\ne C=B$

Here, $y=x^2-1,x\ne \tau \mathrm{or}\sigma$. For $x=-\tau ,y=\tau ,$ the faces of the irregular icosahedron are identical to the one in case (3).

(5) $A\ne C\ne B$

Now we have $x\ne y^2-1$ and $y\ne x^2-1$. Taking $x=1,y=2$ the irregular icosahedron will consist of 4 equilateral triangles with edge of length $\sqrt{6}$, 4 equilateral triangles of edge length $\sqrt{14}$, and 12 scalene triangles with edges $\sqrt{6},\sqrt{10}\mathrm{and}\sqrt{14}.$

4.1. Dual of an Irregular Icosahedron

Now we discuss the construction of a dual of an irregular icosahedron. A dual of an irregular polyhedron can be obtained by determining the vectors orthogonal to its faces. Referring to Figure 6, vectors orthogonal to the equilateral faces #1 and #3 can be taken as$b_1:={\omega }_1\mathrm{and}{b}_3:={\omega }_3$ as they are invariant under the rotations $r_2{r}_3\mathrm{and}{r}_1{r}_2,$respectively. The vectors orthogonal to the faces #2, #4 and #5 can be determined as:

$$\begin{array}{c}{b}_2=n_1{e}_1+n_2{e}_2+n_3{e}_3,\hfill \\ b_4=r_1{r}_2{b}_2=-n_3{e}_1-n_1{e}_2+n_2,\hfill \\ b_5=r_3{r}_2{b}_2=n_3{e}_1+n_1{e}_2+n_2{e}_3,\hfill \end{array}$$

(30)

where $n_1=y-x,n_2=x+y+2xy,n_3=x+y$.

These vectors should be rescaled in order to determine the plane orthogonal to the vector $\mathsf{\Lambda }$. Let us redefine the vectors $d_1:=\lambda {\omega }_1,d_2=b_2,d_3=\varrho b_3,d_4=b_4,d_5=b_5$. The scale factors can be determined as:

$$\begin{gathered} \lambda =\frac{2\left(x+y+2\right)\left(x+y+2xy\right)}{3x+y+2} \\ \varrho =\frac{2\left(x+y+2\right)\left(x+y+2xy\right)}{\left(x+3y+2\right)}. \end{gathered}$$

(31)

The dual solid is an irregular dodecahedron with the sets of vertices:

$$\begin{gathered} \left[T,\overline{T}\right]d_1=\frac{\lambda }{2}\left(\pm e_1\pm e_2\pm e_3\right),\left(\mathrm{even}\mathrm{number}\mathrm{of}(-)\mathrm{signs}\right) \\ \left[T,\overline{T}\right]d_3=\frac{\varrho }{2}\left(\pm e_1\pm e_2\pm e_3\right),\left(\mathrm{odd}\mathrm{number}\mathrm{of}(-)\mathrm{signs}\right) \\ \left[T,\overline{T}\right]d_2=\{\pm n_1{e}_1\pm n_2{e}_2\pm n_3{e}_3,\pm n_2{e}_1\pm n_3{e}_2\pm n_1{e}_3,\pm n_3{e}_1\pm n_1{e}_2\pm n_2{e}_3 \\ \left(\mathrm{even}\mathrm{number}\mathrm{of}(-)\mathrm{signs}\right). \end{gathered}$$

(32)

We will not discuss in detail how an irregular dodecahedron varies with five different cases discussed above. A few examples would be sufficient in the order of increasing symmetry toward regularity. The case (5) above corresponds to the invariance under the chiral tetrahedral group. Substituting $x=1,y=2$ in (32), we obtain an irregular dodecahedron called a tetartoid corresponding to the mineral cobaltite. The vertices $d_1,d_2,d_3,d_4\mathrm{and}{d}_5$ form an irregular pentagon with three different edge lengths. The tetartoid with its dual irregular icosahedron are depicted in Figure 7.

Since under the pyritohedral symmetry $x=y,$ the vertices in (32) take a simpler form where:

$$\lambda =\varrho =\frac{4x{\left(x+1\right)}^2}{\left(2x+1\right)},n_1=0,n_2=2x\left(x+1\right),n_3=2x.,$$

(33)

The edge lengths of the irregular pentagon take the values:

$$\begin{gathered} \left|d_1-d_2\right|=\left|d_2-d_3\right|=\left|d_3-d_4\right|=\left|d_1-d_5\right| \\ =\left|\frac{2x}{\left(2x+1\right)}\right|\sqrt{\left(3x^4+6x^3+7x^2+4x+1\right)} \\ \left|d_4-d_5\right|=4\left|x\right|. \end{gathered}$$

(34)

The irregular dodecahedron with the vertices of (32) with$\lambda \mathrm{and}\varrho$ from (33) is called the pyritohedron. They can also be rearranged and the set can be given in its standard form:

$$\begin{gathered} \left(\pm e_1\pm e_2\pm e_3\right), \\ \left\{\pm \left(1-h^2\right)e_1\pm \left(1+h\right)e_2\right\}, \\ \left\{\pm \left(1-h^2\right)e_2\pm \left(1+h\right)e_3\right\}, \\ \left\{\pm \left(1-h^2\right)e_3\pm \left(1+h\right)e_1\right\}, \end{gathered}$$

(35)

where$h=\frac{x}{x+1}.$

A special case $x=y=5$ discussed in (2) corresponding to $h=\frac{5}{6}$in (35) is plotted in Figure 8.

In the limit of either $x=\tau$ or $x=\sigma ,$ the dodecahedron is regular and the pentagon turns out to be regular with all edges equal either $4\tau$ or $-4\sigma$. After rescaling by $4{\tau }^2$, the set of vertices of the dodecahedron with $x=\tau$ are:

$$\frac{1}{2}\left(\pm e_1\pm e_2\pm e_3\right),\frac{1}{2}\{\pm \tau e_1\pm \sigma e_2,\pm \tau e_2\pm \sigma e_3,\pm \tau e_3\pm \sigma e_1\}.$$

(36)

Each set above is invariant under the pyritohedral group $[T,\pm \overline{T}]$. The 20 vertices of (36) form a dodecahedron with regular faces. As such, they possess a larger icosahedral symmetry $[I,\pm \overline{I}]$.

The first 8 vertices of (36) represent a cube and the second set of 12 vertices, as we recall from previous discussions, represents an irregular icosahedron with $\left(4+4\right)$ equilateral triangles and 12 Robinson triangles. The dual of the irregular icosahedron in second set of 12 vertices in (36) is another irregular dodecahedron whose vertices are the union of a cube and a regular icosahedron albeit with different magnitudes of vectors.

4.2. Regular and Irregular Icosidodecahedron

It is well known that mid-points of the edges of a regular icosahedron or dodecahedron form the Archimedean solid icosidodecahedron with 30 vertices 32 faces (12 pentagons + 20 triangles) and 60 edges which can be obtained from the Coxeter graph of $H_3$ as an orbit ${\left(010\right)}_{H_3}$ [28]. An irregular icosidodecahedron consists of irregular pentagonal faces and scalene triangles in the most general case and will be derived from the chiral tetrahedral group and will be extended by pyritohedral group representing a larger symmetry. One can define five vectors as follows representing the vertices of the irregular pentagon which is orthogonal to the vertex $\mathsf{\Lambda }$:

$$\begin{gathered} c_1=\frac{\mathsf{\Lambda }+r_1{r}_2\mathsf{\Lambda }}{2},c_2=\frac{\mathsf{\Lambda }+r_2{r}_1\mathsf{\Lambda }}{2},c_3=\frac{\mathsf{\eta }\left(\mathsf{\Lambda }+r_2{r}_3\mathsf{\Lambda }\right)}{2},c_4=\frac{\mathsf{\eta }\left(\mathsf{\Lambda }+r_3{r}_2\mathsf{\Lambda }\right)}{2}, \\ {c}_4=\frac{\mathsf{\eta }\left(\mathsf{\Lambda }+r_3{r}_2\mathsf{\Lambda }\right)}{2},c_5=\frac{\mathsf{\kappa }\left(\mathsf{\Lambda }+r_1{r}_3\mathsf{\Lambda }\right)}{2}, \\ \mathsf{\eta }=\frac{x^2+3y^2+2xy+2x+4y+2}{y^2+3x^2+2xy+4x+2y+2}, \\ \mathsf{\kappa }=\frac{x^2+3y^2+2xy+2x+4y+2}{{\left(x+y+2\right)}^2}. \end{gathered}$$

(37)

In terms of $x\mathrm{and}y$ the vertices read:

$$\begin{array}{c}{c}_1=\frac{1}{2}\left[-\left(y+1\right)e_1+y{e}_2+\left(x+y+1\right)e_3\right],\hfill \\ c_2=\frac{1}{2}\left[-y{e}_1+\left(x+y+1\right)e_2+\left(y+1\right)e_3\right],\hfill \\ c_3=\frac{\eta }{2}\left[x{e}_1+\left(x+y+1\right)e_2+\left(x+1\right)e_3\right],\hfill \\ c_4=\frac{\eta }{2}\left[\left(x+1\right)e_1+x{e}_2+\left(x+y+1\right)e_3\right],\hfill \\ c_5=\mathsf{\kappa }\left(\beta +1\right)e_3.\hfill \end{array}$$

(38)

Here, $c_1$ with $c_2$, $c_3$ with $c_4$and $c_5$ define three orbits under the chiral tetrahedral symmetry of sizes 12, 12 and 6, respectively. Imposing the pyritohedral group invariance ($x=y)$ and moreover, letting $x=\tau$ and dividing each vector by a scale factor $2{\tau }^2$, one obtains the usual quaternionic vertices of the icosidodecahedron [28]

$$\begin{gathered} \left\{\frac{1}{2}\left(\pm e_1\pm \sigma e_2\pm \tau e_3\right),\frac{1}{2}\left(\pm \sigma e_1\pm \tau e_2\pm e_3\right),\frac{1}{2}\left(\pm \tau e_1\pm e_2\pm \sigma e_3\right)\right\}, \\ \pm e_1,\pm e_2,\pm e_3 \end{gathered}$$

(39)

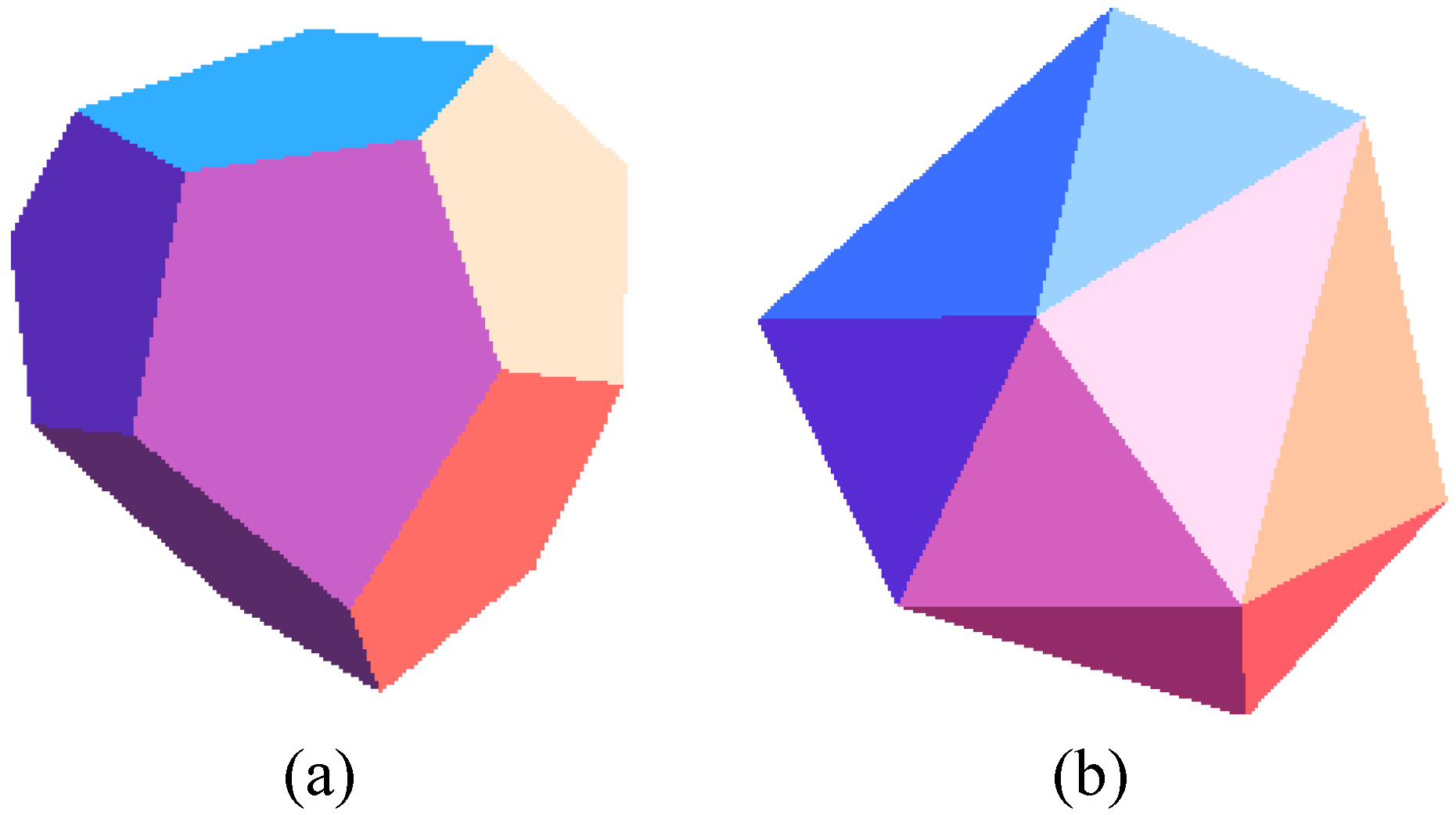
They constitute a subset of the quaternionic binary icosahedral group $I$. An icosidodecahedron consists of regular pentagons and equilateral triangles as shown in Figure 9a. A general irregular icosidodecahedron consists of 12 pentagons of edges $a,b,c$ as shown in Figure 9b. In addition, it has 4 equilateral triangles with edges $a$, 4 equilateral triangles with edges $b$, 12 scalene triangles with edges $a,b,c$ where $a,b,c$ can be expressed in terms of $x\mathrm{and}y$.

5. The Regular and Irregular Snub Cubes Derived from $\mathit{W}{\left({\mathit{B}}_{\mathbf{3}}\right)}^{+}\left({\mathit{a}}_{\mathbf{1}}{\mathit{a}}_{\mathbf{2}}{\mathit{a}}_{\mathbf{3}}\right)$

The snub cube is a chiral Archimedean solid with 24 vertices, 60 edges and 38 faces (8 squares, $6+24$ equilateral triangles). Its vertices and its dual can be determined by employing the same method described in Section 3 and Section 4. The proper rotational subgroup of the Coxeter group $W\left(B_3\right)$ is the rotational octahedral group $Sym\left(4\right)\approx \{\left[T,\overline{T}\right]{\displaystyle \cup }[T^{\prime },\overline{T^{\prime }}]\}$, of order 24, which permutes the diagonals of a cube [21]. The group is generated by two rotation generators $a=r_3{r}_2\mathrm{and}b=r_2{r}_1$ satisfying the generation relations $a^4=b^3={\left(ab\right)}^2=1$. When $\mathsf{\Lambda }$is taken as a general vector, the following sets of vertices form an equilateral triangle and a square, respectively,

$$(\mathsf{\Lambda },r_2{r}_1\mathsf{\Lambda },{\left(r_2{r}_1\right)}^2\mathsf{\Lambda }),(\mathsf{\Lambda },r_3{r}_2\mathsf{\Lambda },{\left(r_3{r}_2\right)}^2\mathsf{\Lambda },r_2{r}_3\mathsf{\Lambda }),$$

(40)

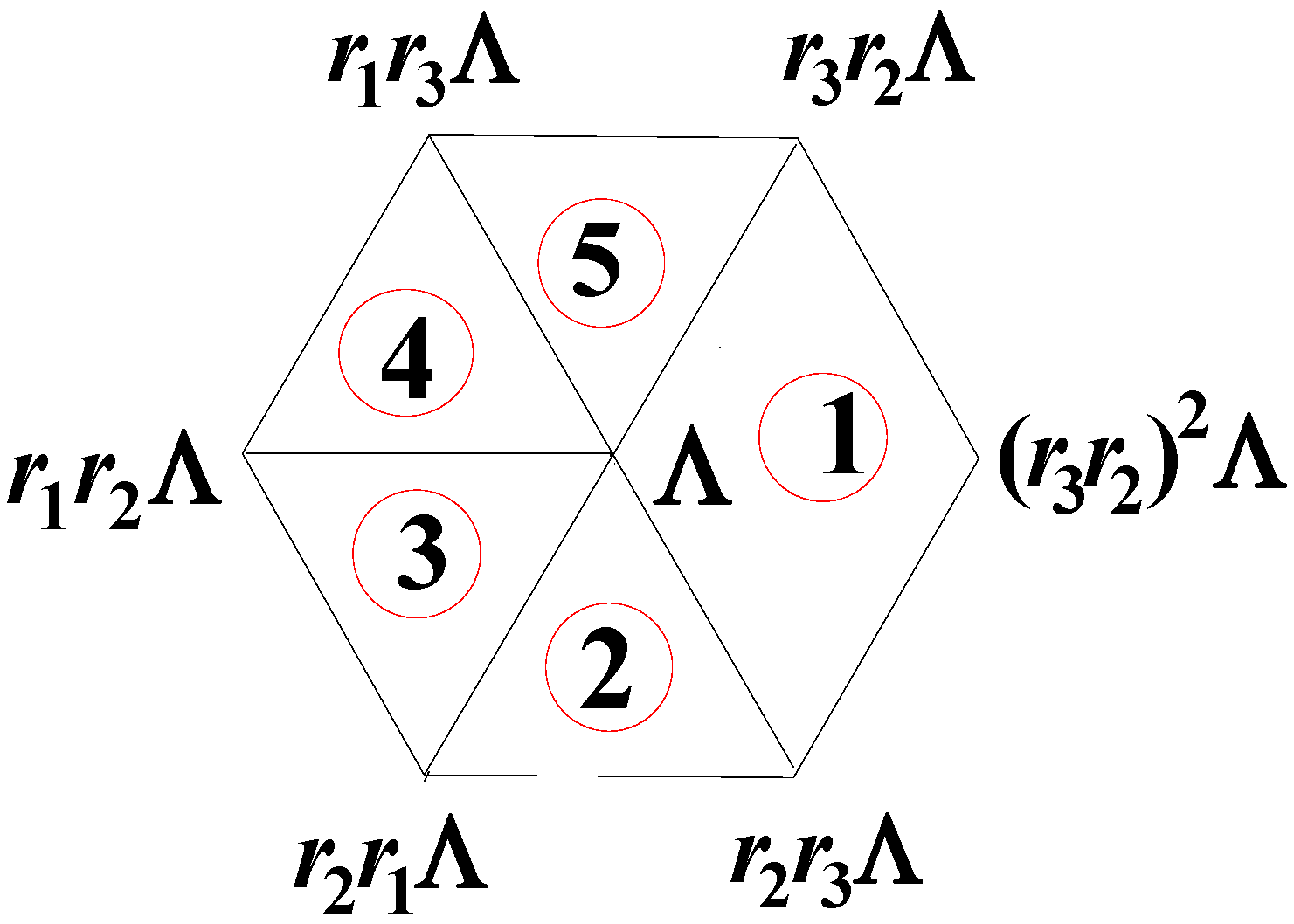
with respective edge lengths$\sqrt{2\left(a_1^2+a_1{a}_2+a_2^2\right)}$ and $\sqrt{2\left(a_2^2+a_2{a}_3+\frac{1}{2}{a}_3^2\right)}$. With the vertex $r_1{r}_3\mathsf{\Lambda }=r_3{r}_1\mathsf{\Lambda },$ we obtain a figure consisting of 7 vertices as shown in Figure 10.

There are 3 different edge lengths among 11 edges which are given as:

$$\begin{gathered} \left|r_1{r}_2\mathsf{\Lambda }-r_1{r}_3\mathsf{\Lambda }\right|=\sqrt{2(a_2^2+a_2{a}_3+\frac{1}{2}{a}_3^2)}, \\ \left|r_3{r}_2\mathsf{\Lambda }-r_1{r}_3\mathsf{\Lambda }\right|=\sqrt{2(a_1^2+a_1{a}_2+a_2^2)}, \\ \left|\mathsf{\Lambda }-r_1{r}_3\mathsf{\Lambda }\right|=\left|r_2{r}_1\mathsf{\Lambda }-r_2{r}_3\mathsf{\Lambda }\right|=\sqrt{2(a_1^2+\frac{1}{2}{a}_3^2)} \end{gathered}$$

(41)

Factoring by $a_2$ $\ne$ 0 redefining $x=\frac{a_1}{a_2}$, $y=\frac{a_3}{a_2}$ and $\alpha =x+\frac{y}{2}+1,\beta =\frac{y}{2}+1,\gamma =\frac{y}{2}$ and dropping $a_2,$one obtains the following classes of faces of the irregular snub cube:

• 6 equilateral triangles with edge length: $A=\sqrt{2\left(1+x+x^2\right)}$,
• 8 squares with edge length:$B=\sqrt{2\left(1+y+y^2\right)},$
• 24 scalene triangles with edge lengths: $A,B,C=\sqrt{2\left(x^2+\frac{1}{2}{y}^2\right)}$.

Since the angular deficiency is $\delta =\frac{\pi }{6}$, the number of vertices of an irregular snub cube is 24.

The vertex $\mathsf{\Lambda }=a_1{\omega }_1+a_2{\omega }_2+a_3{\omega }_3$ can be written in terms of quaternions as$\mathsf{\Lambda }=\mathsf{\alpha }{e}_1+\beta e_2+\mathsf{\gamma }{e}_3$. The orbit generated by the chiral octahedral group reads:

$$\begin{gathered} W{\left(B_3\right)}^{+}\mathsf{\Lambda }=\{\pm \mathsf{\alpha }{e}_1\pm \beta e_2\pm \gamma e_3,\pm \beta e_1\pm \gamma e_2\pm \mathsf{\alpha }{e}_3,\pm \gamma e_1\pm \mathsf{\alpha }{e}_2\pm \beta e_3\}, \\ W{\left(B_3\right)}^{+}\mathsf{\Lambda }\prime =\{\pm \beta e_1\pm \mathsf{\alpha }{e}_2\pm \gamma e_3,\pm \mathsf{\alpha }{e}_1\pm \gamma e_2\pm \beta e_3,\pm \gamma e_1\pm \beta e_2\pm \mathsf{\alpha }{e}_3\}, \end{gathered}$$

(42)

where$\mathsf{\Lambda }\prime =r_1\mathsf{\Lambda }$ is the mirror image of$\mathsf{\Lambda }$. The vertices of (42) represent (1) an octahedron for $a_1=1,a_2=a_3=0$; (2) truncated octahedron for $x=1,y=0$; (3) cube for$a_1=a_2=0,a_3=1$ and (4) cuboctahedron for $a_1=a_3=0,a_2=1$.

The irregular chiral convex solid will have 24 vertices 38 faces (8 square, 6 equilateral triangles and 24 scalene triangles) and 60 edges ($24$of length $A,24\mathrm{of}\mathrm{length}B,12\mathrm{of}\mathrm{length}C$). In what follows we classify them according to their edge lengths of triangles and squares.

(1) The snub cube: $A=B=C,1+x+x^2=1+y+y^2=x^2+\frac{1}{2}{y}^2$

When all edges are equal, one eliminates the variable satisfying $y=x^2-1$and obtains the cubic equation $x^3-x^2-x-1=0$ which can also be written as $x+x^{-3}=2$ The solution is the tribonacci constant $x=\underset{n\to \infty }{\lim }\frac{F_{n+1}}{F_n}\approx 1.8393$ where $F_n$ is the n-th term in the Tribonacci series $0,0,1,1,2,4,7,13,24,44,\dots$.

After dropping an overall factor $\frac{1}{2}(x^2$+1), vertices of the snub cube and its mirror image are given by:

$$\begin{gathered} W{\left(B_3\right)}^{+}\mathsf{\Lambda }=\{\pm x{e}_1\pm e_2\pm x^{-1}{e}_3,\pm e_1\pm x^{-1}{e}_2\pm x{e}_3,\pm x^{-1}{e}_1\pm x{e}_2\pm e_3\} \\ W{\left(B_3\right)}^{+}\mathsf{\Lambda }\prime =\{\pm e_1\pm x{e}_2\pm x^{-1}{e}_3,\pm x{e}_1\pm x^{-1}{e}_2\pm e_3,\pm x^{-1}{e}_1\pm e_2\pm x{e}_3\}. \end{gathered}$$

(43)

For $x=1.8393$, the snub cube is shown in Figure 11.

(2) $A=B\ne C$,$y=-1\pm \sqrt{(1+2\left(x^2+x\right)}$

For $x=1,y=-2\tau ,$ the irregular snub cube consists of 6 equilateral triangles and 8 squares of edges $\sqrt{6}$respectively and 24 isosceles triangles of edges $\sqrt{6},\sqrt{6},\sqrt{2\left(2\tau +3\right)}$as shown in Figure 12.

(3) $A=C\ne B$, $x=\frac{1}{2}{y}^2$ − 1 and x³ − x² − x − 1 ≠ 0

For $y=4\mathrm{and}x=7$ corresponding to $\alpha =10,\beta =3,\gamma =2,$the irregular snub cube consists of squares of edges $\sqrt{13},$equilateral triangles of edges$\sqrt{57}$ and isosceles triangles with edges $\sqrt{57},\sqrt{57}$ and $\sqrt{13}$; all edges scaled by $\sqrt{2}$.

(4) $A\ne B=C,$ y $=x^2-1\mathrm{and}$ x³ − x² − x − 1 ≠ 0

For $x=3,y=8$ the irregular snub cube after rescaling by$\sqrt{2}$ has equilateral triangles of sides $\sqrt{13}$, squares of sides $\sqrt{41}$, and isosceles triangles of edges$\sqrt{41},\sqrt{41},\sqrt{13}$as faces.

(5) $A\ne C\ne B$

The variables should satisfy the inequalities $y\ne x^2-1$ and $y^2\ne 2\left(x+1\right).$

For$x=2$ and $y=4$, the irregular snub cube consists of scaled equilateral triangles of sides $\sqrt{7}$, squares of sides $\sqrt{13}$ and the scalene triangles of sides $\sqrt{7}$, $\sqrt{13}$ and $\sqrt{10}$ as shown in Figure 13.

5.1. Dual of the Irregular Snub Cube

The vectors orthogonal to the faces in Figure 10 can be determined as:

$$\begin{array}{c}{d}_1=\mu e_1,\hfill \\ d_2=\nu \left(n_1{e}_1+n_2{e}_2+n_3{e}_3\right),\hfill \\ d_3=\frac{1}{2}\left(e_1+e_2+e_3\right),\hfill \\ d_4=\nu \left(n_3{e}_1+n_1{e}_2+n_2{e}_3\right),\hfill \\ d_5=\nu \left(n_1{e}_1+n_3{e}_2-n_2{e}_3\right).\hfill \end{array}$$

(44)

Here the parameters are given by:

$$\begin{gathered} n_1=(x+1)y+x,n_2=x,n_3=x\left(y+1\right), \\ \mu =\frac{2x+3y+4}{4x+2y+4},\nu =\frac{1}{2}\frac{2x+3y+4}{\left(xy+x+y\right)\left(2x+y+2\right)+x\left(y+2\right)+yx\left(y+1\right)} \end{gathered}$$

(45)

Vertices of the dual of the irregular snub cube can be written as three sets of orbits under the chiral octahedral group $\{\left[T,\overline{T}\right]\oplus [T^{\prime },\overline{T^{\prime }}]\}$,

$$\begin{gathered} \mu \left(\pm e_1,\pm e_2,\pm e_3\right), \\ \frac{1}{2}\left(\pm e_1\pm e_2\pm e_3\right) \\ \nu \{\left(\pm n_1{e}_1\pm n_2{e}_2\pm n_3{e}_3\right),\left(\pm n_2{e}_1\pm n_3{e}_2\pm n_1{e}_3\right),\left(\pm n_3{e}_1\pm n_1{e}_2\pm n_2{e}_3\right)\}. \end{gathered}$$

(46)

The mirror image can be obtained from (46) by exchanging $e_1\leftrightarrow e_2$.

The dual of the irregular snub cube consists of 24 irregular pentagons with three different edge lengths in general. However, for the special case $y=x^2-1$ and $x^3-x^2-x-1=0$ which corresponds to the regular snub cube, the parameters are given by $\mu =\frac{x}{2}$, $\nu =\frac{x^{-3}}{2}$, $n_1=x\left(2x+1\right),$ $n_2=x$, $n_3=x^3$. The lengths of the edges of the pentagon satisfy the relations

$$\begin{gathered} \left|d_1-d_2\right|=\left|d_1-d_5\right|=\sqrt{\frac{x^2-1}{4x}}, \\ \left|d_2-d_3\right|=\left|d_3-d_4\right|=\left|d_4-d_5\right|=\sqrt{2-x}, \end{gathered}$$

(47)

where $x\approx 1.8393$. The dual of the snub cube is shown in Figure 14.

We shall not discuss all duals of the irregular snub cubes. They can be obtained by substituting $x$ and $y$in (45) and (46) corresponding to each case above. We will illustrate only the case for$x=2$ and $y=4$ where the pentagon has three different edge lengths. This is the dual of the irregular snub cube corresponding to the case of (5). It is depicted in Figure 15 with its pentagonal faces consisting of three different edge lengths satisfying the relations $\left|d_1-d_2\right|=\left|d_1-d_5\right|$, $\left|d_2-d_3\right|=\left|d_3-d_4\right|,\left|d_4-d_5\right|$.

5.2. Chiral Polyhedra with Vertices at the Edge Mid-Points of the Irregular Snub Cube

With a similar discussion to the case of irregular icosidodecahedron in Section 4, we may construct a chiral polyhedron assuming the mid-points of edges of an irregular snub cube as vertices. The vectors whose tips constitute the plane orthogonal to the vector $\mathsf{\Lambda }$ in Figure 10 which are constructed similar to (37) and (38) and are given by:

$$\begin{array}{c}{c}_1=\left[\left(x+y+1\right)e_1+\left(x+y+2\right)e_2+\left(y+1\right)e_3\right],\hfill \\ c_2=\left[\left(x+y+2\right)e_1+\left(y+1\right)e_2+\left(x+y+1\right)e_3\right]\hfill \\ c_3=\mu \prime \left[\left(2x+y+2\right)e_1+e_2+\left(y+1\right)e_3\right],\hfill \\ c_4=\mu \prime \left[\left(2x+y+2\right)e_1+\left(y+1\right)e_2-e_3\right],\hfill \\ c_5=v\prime \left(x+y+2\right)\left(e_1+e_2\right),\hfill \\ \mu \prime =\frac{\left(\alpha +\beta \right)\alpha +\left(\beta +\gamma \right)\beta +\left(\gamma +\alpha \right)\gamma }{2{\alpha }^2+{\beta }^2+{\gamma }^2},v\prime =\frac{\left(\alpha +\beta \right)\alpha +\left(\beta +\gamma \right)\beta +\left(\gamma +\alpha \right)\gamma }{{\left(\alpha +\beta \right)}^2}.\hfill \end{array}$$

(48)

The vertices $c_1$ and $c_2$ are in the same orbit of size 24 under the chiral octahedral group $\{\left[T,\overline{T}\right]{\displaystyle \cup }[T^{\prime },\overline{T^{\prime }}]\}$, and the orbit involving $c_3$ and $c_4$ is of size 24. The orbit of $c_1$ consists of cyclic permutations of the coefficients of the unit quaternions with all possible sign changes. The same argument is valid for the orbit of $c_3$. The orbit of$c_5$ comprises of 12 quaternions obtained as the cyclic permutations of the pair of quaternions with all sign changes. Actually, the orbit of $c_5$ by itself represents the vertices of a cuboctahedron. For all allowed $x$ and $y,$ the chiral polyhedra with 60 vertices can be displayed. However, we will only display the polyhedron corresponding to the special case where the 60 vertices obtained from (48) represent the mid-points of edges of the regular case, namely the snub cube. This is obtained, as we discussed before, substituting $y=x^2-1$and using the real solution of the cubic equation $x^3-x^2-x-1=0$. Then one obtains $\mu \prime =v\prime =1$ and the square lengths of sides of the irregular pentagon obtained from (48) are given by:

$$\left|c_1-c_2\right|=\left|c_2-c_3\right|=\left|c_4-c_5\right|=\left|c_5-c_1\right|=\frac{\left|c_3-c_4\right|}{\sqrt{2}}=\sqrt{2x^3}\approx 3.528$$

(49)

The vector orthogonal to this pentagon is represented by the vector $\mathsf{\Lambda }$ and around this pentagon there are 4 equilateral triangles of sides $\sqrt{2x^3}$and 1 square of sides $2\sqrt{x^3}$. With this pentagonal face, the chiral polyhedron is shown in Figure 16. It has 60 vertices, 62 faces (6 squares, $\left(8+24\right)$ equilateral triangles and 24 irregular pentagons) and 120 edges (96 of sides$3.528\mathrm{and}24\mathrm{of}\mathrm{length}4.989)$.

6. The Regular and Irregular Snub Dodecahedron Derived from $\mathit{W}{\left({\mathit{H}}_{\mathbf{3}}\right)}^{+}\left({\mathit{a}}_{\mathbf{1}}{\mathit{a}}_{\mathbf{2}}{\mathit{a}}_{\mathbf{3}}\right)$

The snub dodecahedron is a chiral Archimedean solid with 60 vertices, 92 faces (20 pentagons $+$80 triangles) and 150 edges. We will discuss how to obtain the snub dodecahedron from an irregular snub dodecahedron. The vertices of an irregular snub dodecahedron, its dual and the chiral polyhedron obtained from the mid-points of edges will be constructed by employing the same technique described in Section 5. The proper rotational subgroup of the icosahedral Coxeter group is also called chiral icosahedral group $W{\left(H_3\right)}^{+}=\left[I,\overline{I}\right]\approx Alt\left(5\right)$ which is a simple group of order 60. They can be generated by the generators$a=r_1{r}_2,b=r_2{r}_3$which satisfy the generation relations$a^5=b^3={\left(ab\right)}^2=1$. Let $\mathsf{\Lambda }=a_1{\omega }_1+a_2{\omega }_2+a_3{\omega }_3$be a general vector where ${\omega }_i,\left(i=1,2,3\right)$can be obtained from (17). The following sets of vertices form a regular pentagon and an equilateral triangle, respectively:

$$(\mathsf{\Lambda },r_1{r}_2\mathsf{\Lambda },{\left(r_1{r}_2\right)}^2\mathsf{\Lambda },{\left(r_1{r}_2\right)}^3\mathsf{\Lambda },{\left(r_1{r}_2\right)}^4\mathsf{\Lambda }),(\mathsf{\Lambda },r_2{r}_3\mathsf{\Lambda },{\left(r_2{r}_3\right)}^2\mathsf{\Lambda })$$

(50)

with respective edge lengths$\sqrt{2\left(a_1^2+\tau a_1{a}_2+a_2^2\right)}$ and$\sqrt{2\left(a_2^2+a_2{a}_3+a_3^2\right)}$. With the addition of the vertex $r_1{r}_3\mathsf{\Lambda }=r_3{r}_1\mathsf{\Lambda }$ as shown in Figure 17, there are three edge lengths including $\sqrt{2\left(a_1^2+a_3^2\right)}$. The discussions of Section 4 and Section 5 will be repeated to obtain the regular and irregular snub dodecahedra. The dual and the chiral polyhedron based on the mid-points of edges follow the same technique.

Numbering of the faces has been done according to the $H_3$diagram of Figure 4. Factoring by $a_2\ne 0$, redefining $x=\frac{a_3}{a_2}$,$y=\frac{a_1}{a_2}$ and dropping $\frac{a_2}{\sqrt{2}}$ one obtains an irregular snub dodecahedron with 12 equilateral triangles with edge length: $A=\sqrt{2\left(1+x+x^2\right)}$, 20 pentagons with edge length:$B=\sqrt{2\left(1+\tau y+y^2\right)}$, 60 scalene triangles with edge lengths: $A,B,C=\sqrt{2\left(x^2+y^2\right)}$. The triangles numbered as $2,4\mathrm{and}5$are identical scalene triangles, but number$1$ is an equilateral triangle. The angular deficiency is $\delta =2\pi -\left(\frac{\pi }{3}+\frac{3\pi }{5}+\left(\theta +\vartheta +\phi \right)\right)=\frac{\pi }{15}$where $\theta ,\vartheta \mathrm{and}\phi$ are the interior angles of the scalene triangles. Descartes’ formula verifies the number of vertices $N_0=60$.

The orbit $\left[I,\overline{I}\right]\mathsf{\Lambda }$ generated from the vector $\mathsf{\Lambda }=-y{e}_1-x{e}_2-\tau \left(\tau y+x+2\right)e_3$ involves 60 vectors representing the vertices of an irregular snub dodecahedron. The mirror image $\left[I,\overline{I}\right]\mathsf{\Lambda }\prime$ can be obtained from the vector $\mathsf{\Lambda }\prime =r_1\mathsf{\Lambda }=y{e}_1-x{e}_2-\tau \left(\tau y+x+2\right)e_3$. A few remarks are in order before we discuss the usual classification. For some special values of the parameters $x$ and $y,$we obtain some of the Archimedean solids. For example,

(i)

$x=1$ and $y=0:\mathrm{Truncated}\mathrm{icosahedron},$

(ii)

$x=0$ and $y=1:$ Truncated dodecahedron,

(iii)

$x=y$ $=0:$ Icosidodecahedron.

Let us follow the sequence of Section 5 to discuss the regular and irregular snub dodecahedra.

(1) The snub dodecahedron:$A=B=C,1+x+x^2=1+\tau y+y^2=x^2+y^2$

Since all edges are equal, it leads to the relations $y=\sigma \left(1-x^2\right)$and $y^2=x+1$resulting in the cubic equation $x^3-x^2-x-\tau =0$. The real solution is approximately$x=1.943$. The snub dodecahedron is shown in Figure 18.

(2) $A=B\ne C$, $y=\frac{1}{2}\left(-\tau \pm \sqrt{({\tau }^2+4\left(x^2+x\right)}\right)$

For $x=-1,y=-\tau ,$ the irregular snub dodecahedron consists of 12 equilateral triangles and 20 pentagons of sides $\sqrt{2}$ and 60 isosceles triangles of sides $\sqrt{2},\sqrt{2},\sqrt{2\left(\tau +2\right)}$

(3) $A=C\ne B$,$y^2=x+1$ and $x^3-x^2-x-\tau \ne 0$

For $y=2\mathrm{and}x=3,$ the corresponding irregular snub dodecahedron consists of pentagons of edge length $\sqrt{2\left(2\tau +5\right)},$equilateral triangles of edge length$\sqrt{26}$ and isosceles triangles with edge lengths $\sqrt{26},\sqrt{26}$ and $\sqrt{2\left(2\tau +5\right)}$

(4) $A\ne B=C,x^2=\tau y+1\mathrm{and}{x}^3-x^2-x-\tau \ne 0$

For $y=1,x=\tau ,$ the irregular snub dodecahedron has pentagons of sides $\sqrt{2\left(\tau +2\right)}$, equilateral triangles of sides$\sqrt{2}\tau$, and isosceles triangle of sides$\sqrt{2\left(\tau +2\right)}$, $\sqrt{2\left(\tau +2\right)}$ and$\sqrt{2}\tau$.

(5) $A\ne C\ne B$

For$x=2$ and $y=3,$the irregular snub dodecahedron consists of equilateral triangles of sides $\sqrt{14}$, pentagons of sides $\sqrt{2\left(3\tau +10\right)}$ and the scalene triangles of sides $\sqrt{14}$, $\sqrt{2\left(3\tau +10\right)}$ and $\sqrt{26}$ as shown in Figure 19.

6.1. Dual of the Irregular Snub Dodecahedron

We obtain 5 vectors as follows to determine the plane orthogonal to the vertex $\mathsf{\Lambda }:$

$$\begin{array}{l}{d}_1=\sqrt{2}{\omega }_1=\tau (\sigma e_1-\tau e_3),\\ d_2=\nu \left[\left(y-\sigma \right)x{e}_1-\sigma y\left(x+1\right)e_2+\left(\tau xy+\tau x+y\right)e_3\right]\\ d_3=\sqrt{2}\mu {\omega }_3=\mu \left(-e_2-\tau e_3\right),\\ d_4=\nu \left[\sigma x{e}_1-\sigma y{e}_2+\left(2xy+\tau x+y\right)e_3\right]\\ d_5=\nu \left[-\sigma x{e}_1+\sigma y{e}_2+\left(2xy+\tau x+y\right)e_3\right],\end{array}$$

$$\mu =\frac{\left(3y+\tau x+2\tau \right)}{\tau y+\left(\sigma +2\right)x+2},\nu =\frac{\left(3y+\tau x+2\tau \right)}{\left(\sigma x-y+2\sigma \right)\left(2xy+\tau x+y\right)}.$$

(51)

The orbits generated from these five vectors represent the vertices of the dual solid of the irregular snub dodecahedron. Faces of the dual consist of irregular pentagons, one of which is represented by the vertices of (51). Note that the orbits $\left[I,\overline{I}\right]d_1$ and $\left[I,\overline{I}\right]d_3$ represent the orbits of sizes 20 and 12, respectively. The other three vertices are in the same orbit; therefore, one single notation $\left[I,\overline{I}\right]d_2$ for this orbit of size 60 suffices. Therefore, the dual consists of 92 vertices, 60 irregular pentagons and 150 edges. The regular case is obtained by substituting $y=\sigma (1-x^2)$ and $x=1.943$ in (51). The dual of the snub dodecahedron, the pentagonal hexecontahedron, is shown Figure 20.

We also illustrate the dual of the irregular snub dodecahedron obtained from 5) by substituting the values $x=2$ and $y=3$ in (51). The 92 vertices with this substitution describe the chiral solid depicted in Figure 21.

6.2. Chiral Polyhedra with Vertices at the Edge Mid-Points of the Irregular Snub Dodecahedron

Similar to the previous discussions, we can construct a chiral polyhedron possessing the mid-points of the edges of the irregular snub cube as vertices. The vectors whose tips constitute the plane orthogonal to the vector $\mathsf{\Lambda }$ in Figure 17 are given by:

$$\begin{gathered} c_1=\frac{1}{2}\left[-\left(2y+\tau \right)e_1+e_2-\tau \left(2\tau y+2x+\tau +2\right)e_3\right], \\ {c}_2=\frac{1}{2}\left[-\left(2y+\tau x+\tau \right)e_1-\left(x+1\right)e_1-\tau \left(2\tau y+2x+\tau +2\right)e_3\right], \\ {c}_3=\frac{\alpha }{2}\left[-\tau \left(\tau y+1\right)e_1-\left(\tau y+2x+1\right)e_2-\tau \left({\tau }^{2}y+2x+\tau +2\right)e_3\right], \\ {c}_4=\frac{\alpha }{2}\left[\tau e_1-\left(2x+1\right)e_2-\tau \left(2\tau y+2x+\tau +2\right)e_3\right], \\ {c}_5=-\beta \tau \left(\tau y+x+2\right)e_3, \end{gathered}$$

$$\begin{gathered} \alpha =\frac{3y^2+2\tau xy+x^2+4\tau y+x\left(\tau +2\right)+\tau +2}{{\tau }^2{y}^2+2\tau xy+x^2\left(\sigma +2\right)+\left(3\tau +1\right)y+4x+\tau +2}, \\ \beta =\frac{3y^2+2\tau xy+x^2+4\tau y+x\left(\tau +2\right)+\tau +2}{{\left(\tau y+x+2\right)}^2} \end{gathered}$$

(52)

In the limit $y=\sigma \left(1-x^2\right)$, $x^3-x^2-x-\tau =0\mathrm{and}\alpha =\beta =1\left(x=1.943\right);$ for a snub dodecahedron, the vertices in (52) are simplified, and the edge lengths of the pentagon satisfy the relations:

$$\left|c_1-c_2\right|=\left|c_2-c_3\right|=\left|c_4-c_5\right|=\left|c_5-c_1\right|=\frac{\left|c_3-c_4\right|}{\tau }=\sqrt{x^2+x+1}$$

(53)

This chiral polyhedron has 150 vertices and 152 faces (12 regular pentagons$+$60 irregular pentagons and $\left(20+60\right)$ equilateral triangles all surrounding 60 irregular pentagons), a typical one of which is represented with the relations of vertices in (53). The chiral polyhedron with 300 edges is illustrated in Figure 22.

7. Concluding Remarks

In this paper we presented a systematic construction of regular and irregular chiral polyhedra, the snub cube, the snub dodecahedron and their duals using proper rotational subgroups of the octahedral group and the icosahedral group. Chiral polyhedra whose vertices are the mid-points of the chiral polyhedra were also constructed. We used the Coxeter diagrams B₃ and H₃ to obtain the quaternionic description of the relevant chiral groups. Employing the same technique for the diagrams A₁ $\oplus$ A₁ $\oplus$ A₁ and A₃ , the irregular tetrahedra and icosahedra have been included although they are not chiral as they can be transformed to their mirror images by the proper rotational subgroup of the octahedral group.

The dual solids of the irregular icosahedron, the tetartoid and the pyritohedron are also constructed representing the chiral symmetries of chiral tetrahedral group and the pyritohedral group, respectively.

This method can be extended to higher dimensional Coxeter groups to determine the irregular-regular chiral polytopes. For example, the snub 24-cell, a chiral polytope in the 4D Euclidean space can be determined using the D₄ Coxeter diagram [29], and its irregular form can be obtained using the same technique used for the irregular icosahedron.