1. Introduction
Crystallography inhabits a borderland fruitfully shared by mathematics, physics, chemistry, and geology, among other disciplines. This borderland is an especially fertile field for geometers, as many crystal forms are polyhedral, their atomic patterns poly-complex, and even basic questions are far from settled [
1]. One such question concerns the most accurate way to model crystalline form and growth. The discovery of X-ray diffraction early in the last century consolidated the then century-old lattice paradigm, which modeled crystal structures as periodic tilings of R
3. This model became the canonical lens through which crystal structure and growth was viewed. It seemed to serve crystallography well: the tiles were metaphorical swatches for atomic patterns, while the regularity of their locations suggested crystal growth intuitively (row upon row, layer upon layer). However, the discovery of aperiodic crystals in 1982 [
2] showed that this model of growth and form cannot be the whole story. The new models proposed to fill this gap are still debated [
3].
The earliest crystal structure models (a perhaps generous description) explained growth in a rudimentary way. In the 17th century, Johannes Kepler in Austria [
4] and Robert Hooke [
5] in England imagined crystals as packings of identical spheres and showed how their polyhedral shapes might arise therefrom. Two centuries later, the French abbé R. J. Häuy [
6] stacked congruent bricks in various ways to show why and how crystals of the same species could have different external forms. Pyrite crystals, for example, grow as cubes, as octahedra, and sometimes as irregular pentagonal dodecahedra or “pyritohedra”.
The centers of the tiles in Häuy’s tilings form point lattices, a fact that led to the focus of geometrical crystallography on lattices. With the discovery of X-ray diffraction in 1912 [
7], it became possible to locate the atomic positions in periodic geometric patterns precisely. The lattice paradigm was, it seemed, thereby confirmed, and with it a simple corollary [
8]: the possible order of rotations for a lattice in dimensions 2 and 3 are 2, 3, 4, and 6. This was known to generations of students as “The Crystallographic Restriction”.
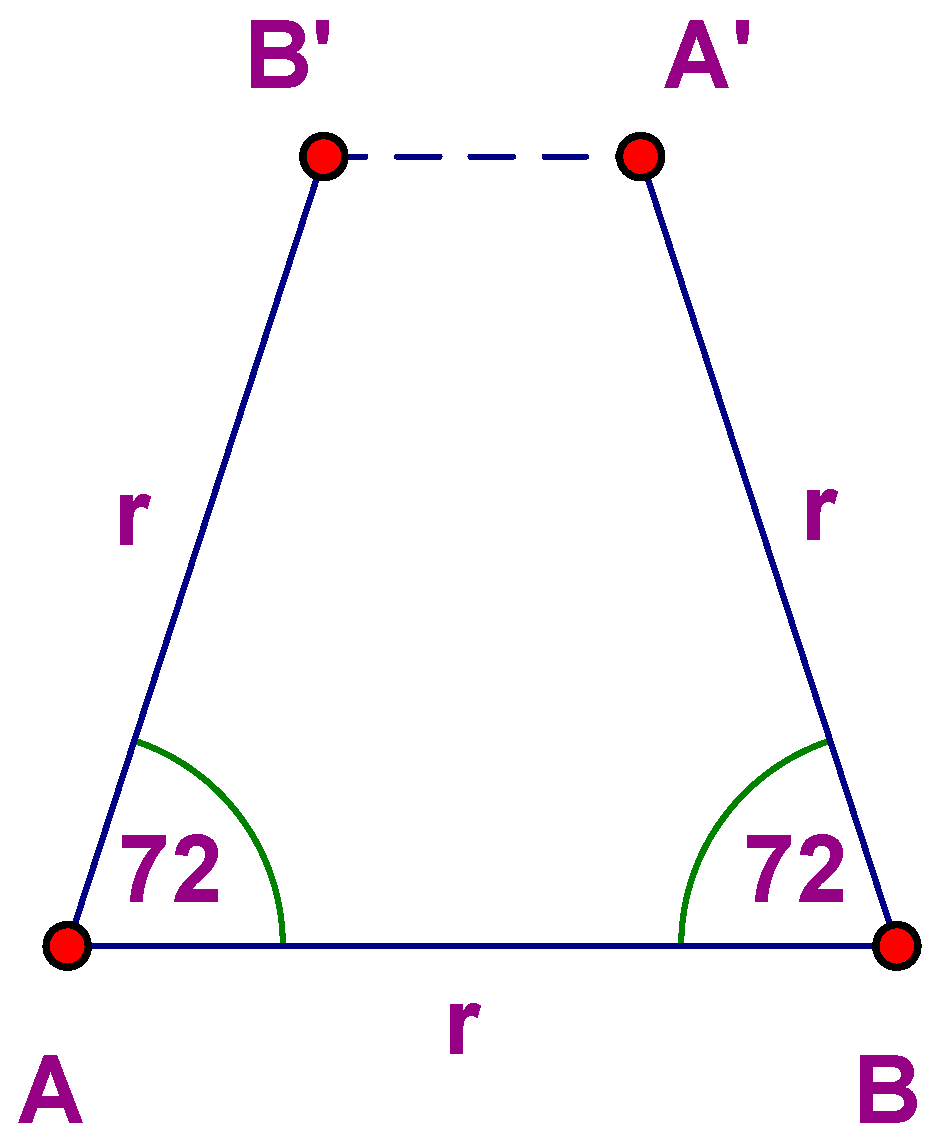
Note the absence of the number 5 (and all integers greater than 6). Why? Let L be a plane lattice and φ
X a 72° rotation about a lattice point X. Choose points A and B such that |AB| = r, where r is the minimum distance between points of L. Thus φ
A(B) is a lattice point B′, and φ
−1B(A) = A′. But then |A′B′| < r, which is impossible (
Figure 1).
A similar argument holds for three-dimensional lattices, since a rotation fixes a plane and an axis orthogonal to it. Thus, icosahedral symmetry is impossible for a three-dimensional point lattice (however, five-fold symmetry is possible for lattices in all dimensions greater than three).
It follows, apparently, that regular dodecahedra and icosahedra are impossible crystal forms. Of course, crystallographers have always understood that the lattice is an abstraction, its points merely placeholders for the motifs—the finite configurations of atoms—that repeat to form the pattern. The Crystallographic Restriction does not forbid
motifs with five-fold symmetry. This was even known to the ancient Egyptians, at least implicitly (
Figure 2).
Indeed, as we shall see, the world of intermetallic crystals is replete with analogous patterns in R3. The complexity of these periodic patterns and their close relation to aperiodic crystals is the central theme of this paper.
Dan Shechtman’s paradigm-shifting discovery of crystals with icosahedral symmetry [
2] showed that the Crystallographic Restriction was merely a theorem about lattices, not a law of nature. A complete understanding of periodic lattices is not sufficient for a complete understanding of crystalline structure.
The skepticism that greeted Shechtman’s discovery moulders in history’s dustbin, nailed shut by his 2011 Nobel prize. Today we define crystals to be materials with atomic long-range order evidenced not by lattice descriptions, but by sharp spots in their diffraction patterns. Crystals whose diffraction patterns exhibit icosahedral symmetry are called icosahedral quasicrystals (iQCs).
The new diffraction-based definition of “crystal”, a major break from the historical lattice paradigm, gives rise to a variety of difficult questions, such as
which non-lattice atomic arrangements have sharp spots in their diffraction patterns, and how aperiodic crystals self-assemble, if they do not grow by rows and layers. The first of these two questions has given rise to a new field of mathematics, “long range aperiodic order” (see [
9,
10]). In this paper, we focus on self-assembly.
At the outset of this paradigm shift, in 1984, many (though, significantly, not all) researchers assumed that aperiodic crystals should and could be described, and their growth modeled, by brick-laying, albeit with bricks of a non-Häuy sort, perhaps three-dimensional Penrose-like tiles assembled in accordance with matching rules. But although three-dimensional tiles can be superimposed on many iQC structures, the subdivision can be artificial, and their very complex matching rules do not model physical crystal growth.
Both the subdivisions and the matching rules can be skirted by recasting the structure in higher dimensions. When—as is the case for all aperiodic crystals known so far—the atomic positions can be indexed by
n > 3 integers, we can consider the n-tuples to be “addresses” in R
n and “lift” the structure to a suitable lattice there [
11]. The popularity of this formalism owes much to the fact that higher-dimensional analogues of tools developed earlier for periodic crystals can be used and the three-dimensional positions of the crystal pattern recovered by projection. But the process is complicated, and tells us nothing about actual crystal growth. Very recently, the atomic positions in an iQC have been determined directly from X-ray diffraction data, without the high-dimensional formalism [
12].
A third model, nested atomic clusters, has also been studied from the outset, although it received less attention until recently. The cluster approach, which builds on the chemists’ concept of coordination polyhedra, holds promise for understanding growth. After a discussion of the features of this model (
Section 2 and
Section 3), we consider one particular example, the Ytterbium-Cadmium iQC whose structure (the first iQC to be “solved”!) was determined in 2007 [
13].
2. Nested Clusters
Thirty years before the discovery of quasicrystals, the British physicist F.C. Frank suggested that icosahedral atomic clusters, with 12 atoms around a central atom, are common in supercooled liquids, where they may be locally favored structures [
14]. That same year, Bergman et al. described icosahedral clusters in certain intermetallic solid crystals [
15]; these clusters, with many more atoms in successive shells, are now eponymously known as Bergman clusters. Ten years later, Mackay proposed the nested clusters that bear his name [
16]. The use of nested clusters as a descriptive tool for complex crystal structures has steadily grown. A searchable database of multi-shelled nanoclusters in complex intermetallics is currently being developed in Russia [
17].
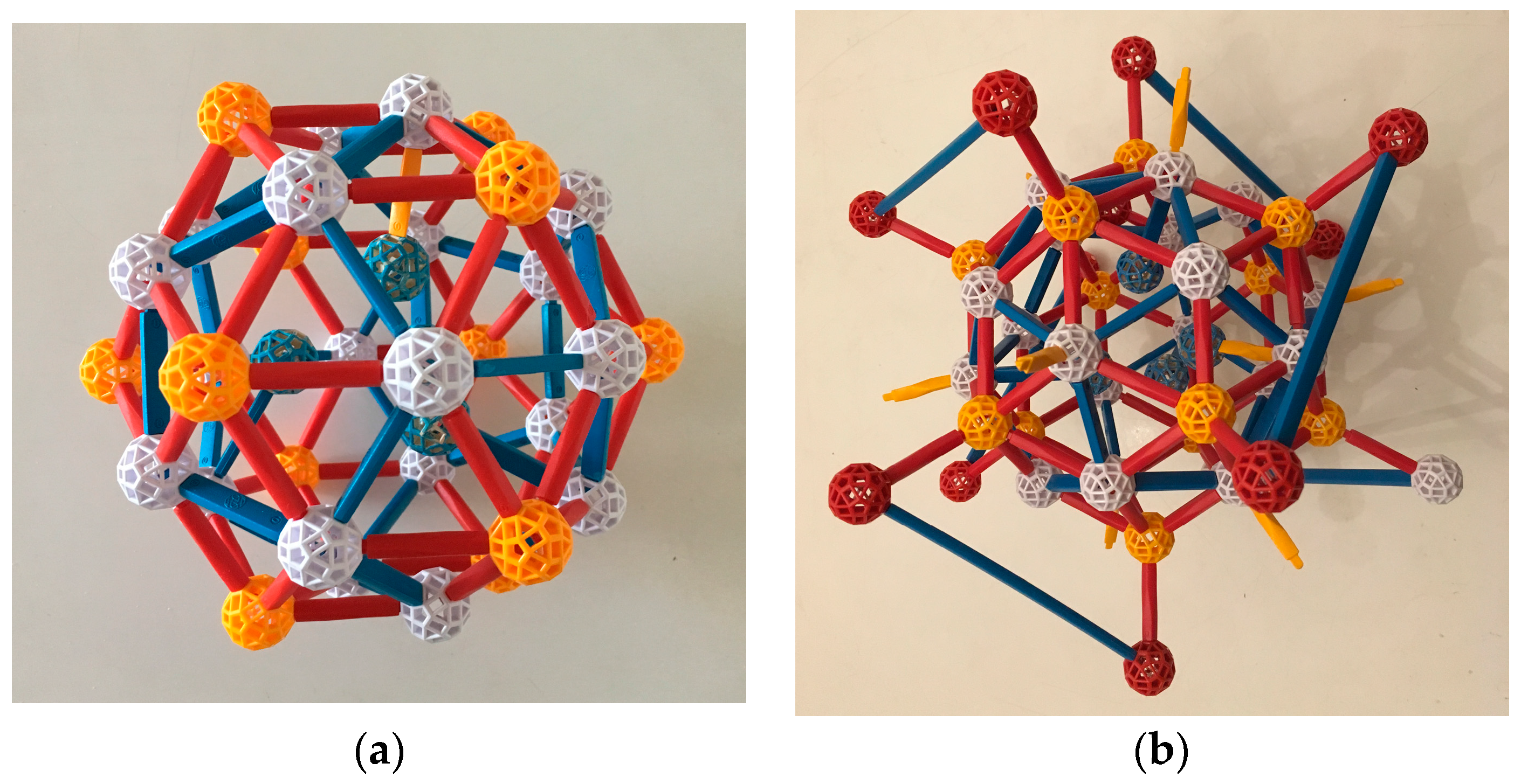
Both the Bergman and Mackay clusters (
Figure 3) can be described in several ways; we follow convention in considering them to be three-shelled. In the Bergman cluster, an icosahedron sits inside a dodecahedron which sits inside a larger icosahedron, for a total of 12 + 20 + 12 = 44 atoms, not counting a (possible) atom at the center. In the Mackay cluster, the second shell is an icosidodecahedron, which has 30 vertices; thus the total number of atoms is 54 (plus, possibly, 1).
To describe the crystal that is the focus of this paper, the Ytterbium-Cadmium (Yb-Cd) iQC, Takakura et al. [
13] use a third type of cluster, named for co-author Ang-Pan Tsai (
Figure 4). The Tsai cluster has five shells: its innermost shell is a regular tetrahedron, which is encased in a dodecahedron. The dodecahedron sits inside an icosahedron, which sits inside an icosidodecahedron and finally, fifth and outermost, a rhombic triacontahedron. The tetrahedron, the only shell without icosahedral symmetry, has several equivalent lower-symmetry positions within the dodecahedron and flips about among them. Yb atoms are centered at vertices of the icosahedron and Cd atoms at all other vertices of these shells, and also at the edge midpoints of the outer one. Thus each Tsai cluster “has” 146 Cd atoms (4 in the tetrahedron, 20 in the dodecahedron, 30 in the icosidodecahedron, 32 in the rhombic triacontahedron, and 60 in its edges) and 12 Yb, a ratio of 12.1666...: 1. Note that these atoms are not identical in size; rather, the ratio of their radii is approximately 1.2:1, the approximate ratio of the “crystal” atomic radii Yb:Cd (
Tables of Physical & Chemical Constants (16th edition 1995). 3.1.2 Properties of the Elements. Kaye & Laby Online. Version 1.0 (2005)
www.kayelaby.npl.co.uk).
3. A Conceptual Breakthrough
In the mid-1980s Christopher Henley, reviewing the literature of periodic but complicated intermetallic crystal structures, noticed that they closely approximated the iQC structures of these same or similar materials, much as rational numbers approximate irrationals. He coined the term “approximant” for these periodic structures to “mean (that) the unit cell is indistinguishable from a fragment commonly occurring in the icosahedral phase”. In the two cases he studied in detail, “each (of these approximant structures) is a bcc packing of clusters which have two concentric atomic shells with full icosahedral symmetry around their center” [
18].
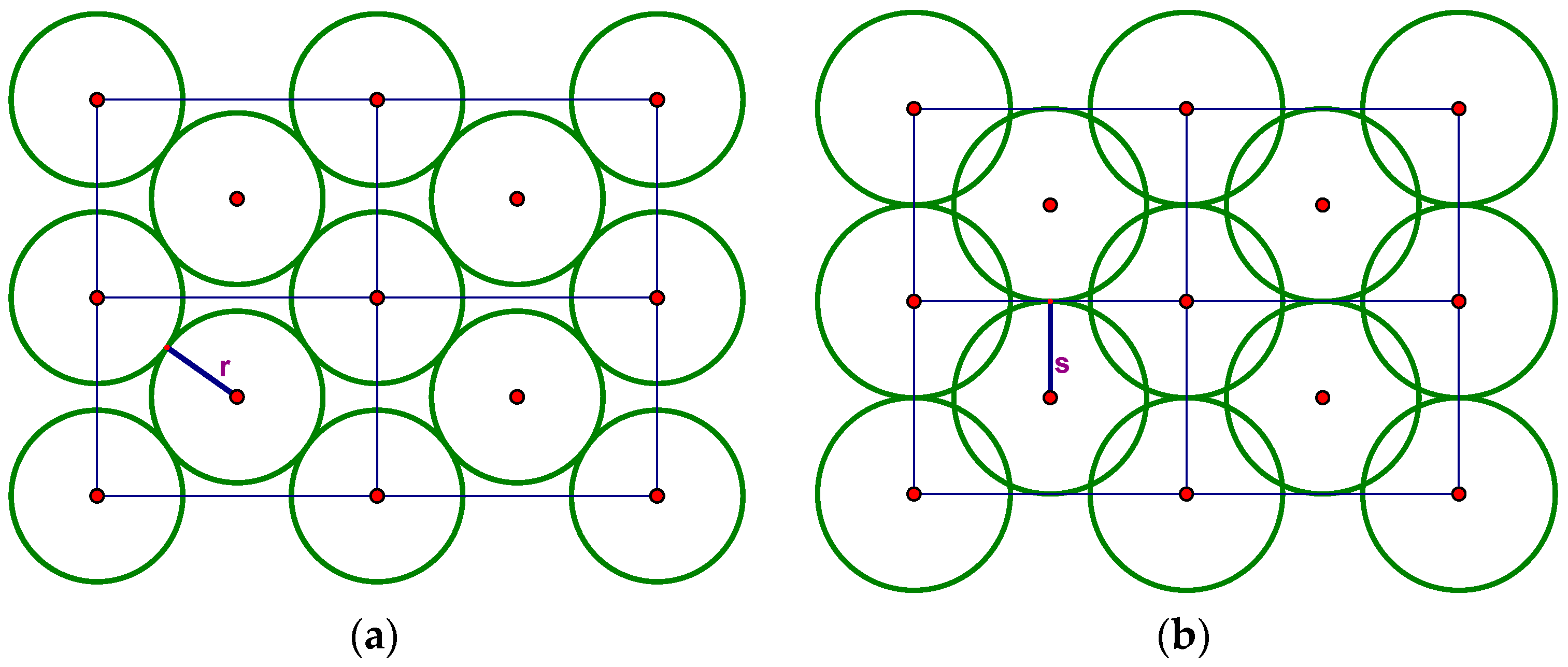
The shorthand “bcc” stands for “body-centered cubic” and refers to the cubic lattice in R
3 whose points are not only the cube vertices but also their centers. To visualize the bcc packing by equal spheres, recall that the Voronoi cell V of the R
3 bcc lattice is a truncated octahedron with six square facets and eight that are regular hexagons. In this lattice, the distance r between the center o of V and the center of a hexagonal facet is one half the minimum interpoint distance, and the distance s from o to the center of a square facet is larger by a factor of approximately 1.15. Thus, spheres of radius r at the bcc lattice points form a packing of R
3 in which the spheres are tangent in the directions of three-fold symmetry but with gaps in the four-fold symmetry directions (
Figure 5a). Alternatively, if we place spheres of radius s at the lattice points, we get an arrangement in which spheres are tangent in the four-fold direction but overlap along the three-fold axes (
Figure 5b).
To envision the structures Henley was describing, replace the spheres in
Figure 5b by Mackay or Bergman clusters, oriented so that four of their ten three-fold axes are the three-fold rotation axes of the cubic lattice and six edges of the icosahedral shell (which in the Bergman cluster are long diagonals of the rhombic facets) are orthogonal to the cubic lattice’s four-fold axes. Depending on the diameter of the clusters and whether they are Bergman or Mackay, this collection could be interpenetrating or not, similarly to the case of
Figure 5a,b.
But this “identification of the basic clusters and linkage rules is only the starting point of a complete structure model”. Henley observed, because “In reality, a metal structure cannot have large voids; additional, so-called “glue” atoms (about 30% of the total) must occupy sites between clusters” [
18].
4. Linkages in the Yb-Cd iQC and Its Approximants
In the structures found by Takakura et al. [
13] for the Yb-Cd iQC and for its approximants, the Tsai clusters overlap, so if two more small clusters (the AR and OR, described below) are included, no additional glue is needed. But as we explain below, in our view of these structures, more glue is there in disguise.
First let us look closely at the geometry of the rhombic triacontahedron (the outer shell of the Tsai cluster). Its rhombic faces are orthogonal to the two-fold axes of its symmetry group, and its three-fold axes pass through opposite 3-valent vertices. Note (
Figure 6) that each 3-valent vertex V is ringed by six vertices, alternately 5- and 3-valent. The vertices of this ring, together with V, are seven of the eight vertices of an obtuse golden rhombohedron, called OR.
Following [
6], we will say that two congruent rhombic triacontahedra sharing a rhombic face (
Figure 7a) are joined by a b-linkage, and are joined by a c-linkage if they share a ring (described above) and thus overlap in an OR (
Figure 7b).
Both OR and acute golden rhombohedron (AR) complexes are found in the iQC structure. In
Figure 8, we show the OR (with Cd at its vertices and mid-edges) and the AR (acute golden rhombohedron, with Cd at its vertices and mid-edges and two Yb on its main diagonal).
The Cd:Yb ratio in the iQC is approximately 5.7:1. Two of its well-studied periodic approximants have ratios of approximately 6:1 and 5.8:1, respectively (the fact that the atomic Cd:Yb ratio in the Yb-Cd iCQ and its approximants (approximately 5.7:1, 5.8:1, and 6:1) is much lower than that of the Tsai cluster is explained by the fact that, in the crystal, the clusters abut and overlap and thus many Cd atoms are shared).
In the 6:1 approximant, the centers of the Tsai clusters are arranged in a bcc lattice (as in
Figure 5). The OR occurs only in c-linkages, and the AR does not occur. The AR occurs in the 5.8:1 crystal, but again the OR only occurs in c-linkages.
A key motif in all three structures consists of three linked Tsai clusters, two joined in a b-linkage and the third c-linked to both. It is described and illustrated below.
5. A Newly Identified Cluster Suitable for Growth
Interlocking clusters, however, do not suggest a growth mechanism. For pre-formed clusters to interlock, they would have to (partially) disassemble and reassemble, and this seems physically unlikely.
We propose instead an alternative description for Tsai-type crystals and their approximants in terms of a smaller unit that could account for growth and perhaps even nucleation, and could also clarify the role of the inner tetrahedron in those processes. Our unit consists of the inner 36 atoms of a Tsai cluster. We call it a TDI cluster (tetrahedron-dodecahedron-icosahedron) and propose that TDIs are the critical element for a new model of the growth of the Tsai-type quasicrystal and its periodic approximants (
Figure 9). In this view, the two outer shells of the Tsai cluster are “glue” that forms spontaneously, depending on the ratio of Yb to Cd atoms in the melt.
Like the Bergman and Mackay clusters, the outer shell of the TDI cluster is a regular icosahedron. One can arrange TDI clusters with their centers in a bcc lattice, again like the Bergman and Mackay clusters, but with space between the clusters. Our suggestion is that, to form the 6:1 alloy, the TDIs join by constructing c-linkages, and the Tsai clusters arise as remaining Cd atoms slip into the voids being created. We suggest a similar underlying mechanism for growth in the case of the 5.8:1 periodic crystal and the iQC.
To see how formation of TDI clusters may lead to growth, we model the TDI with spheres of two sizes located at the atomic positions. We use “Cd” and “Yb” as names for the smaller and larger atoms, respectively.
TDIs formed in the liquid (why they might do so is discussed in the next section) have a Cd:Yb ratio of 24:12, or 2, so the liquid around TDI clusters would be a soup of mainly Cd atoms. Of course, the structure would be dynamic, forming and disassociating.
What glues the TDI’s together? Suppose that two TDIs come close to each other in the melt, so that a Cd (call it V1) in the outer shell of one comes within a natural bond distance to a Cd (call it V2) in the outer shell of the other, forming a temporary bond. We can speculate that the two TDIs might bond such that they have the same orientation, since this is the distance and configuration of TDIs that is in fact seen in all three crystal structures. Note that, in this configuration, the three Yb atoms nearest V1 in its TDI are maximally distant from the three Yb nearest V2 in its TDI. See
Figure 10a; the bond is the yellow strut.
Notice that, in this configuration, there is room for glue, that is, for six Cd atoms in the liquid to slot into the positions in the icosidodecahedral shells that will eventually surround both TDIs, just outside the six TDI dodecahedral edges attached to V1 and V2. Three of them are in place in
Figure 10b as red balls, with the two short bonds to dodecahedral atoms that they would have in Tsai clusters. These are presumed to be low potential energy positions, as they are observed experimentally.
Not only do these added atoms have these two short bonds, but also each of the three additions to the TDI of V1 are in the right spot to complete a third bond with V2. Likewise, each addition to V2 is in the right spot for a bond to V1. These six criss-crossing bonds (not shown in the figures) should help stabilize the two TDI clusters.
The fourth edges of the three red balls added to V2 are shown in
Figure 10c, with red balls at the ends; three edges with balls are also added to V1. These six extra vertices are vertices of the outer shells of both Tsai clusters. Adding edges between them, with balls mid-edge, completes an OR, forming a c-linkage between the two developing Tsai clusters (
Figure 10d). It also creates edges with mid-edge balls that will be in both Tsai clusters.
If now a third TDI forms a similar bond to the first TDI, it might have one of its dodecahedral Cd atoms (call it V2′) bond to a Cd (call it V1′) which is a next-nearest atom in the dodecahedral shell to V1. Then, a full OR can likewise develop between these TDI, and in fact one of the dodecahedral Cd atoms is already in the correct position (
Figure 11a). Additionally, a b-type linkage (shared face) of the growing Tsai clusters of the second and third TDIs is automatically generated (
Figure 11b). The three-unit cluster is shown schematically in
Figure 12.
When the three Tsai clusters are completed, they make the key structure identified in
Section 4, which occurs in the iQC and the two approximants we are discussing. Its core is the two c-linkages and the resulting b-linkage. We conjecture that the assembly of this core via the above mechanism might even be a mechanism of nucleation, if that cluster of three is stable enough. More TDIs can be added in an identical way. When the Cd:Yb ratio is 6:1, it is sufficient to build the entire bcc periodic crystal, with no leftover Yb or Cd atoms.
This cluster of three TDIs and their additional Cd “glue” is fundamental and appears to be a universal way of constructing local ordering. When the Cd:Yb ratio is 5.8:1, the extra Yb (compared to the 6:1 alloy) makes room for itself on the long diagonal of an isolated AR cluster sharing its faces with Tsai clusters (no longer with their centers in a BCC lattice but with a different periodicity). When the ratio is about 5.7:1, the extra Yb contributes to more elaborate collections of ARs with ORs, but still embedded in a network of TDIs joined by c-linkages and b-linkages with “glue” consistent with the outer shells of Tsai clusters; the result is an iQC. For detailed illustrations and a description of how this iQC structure was determined, see Takakura et al. and [
12]. Thus, the focus on c-linkages would yield a reasonable model of growth for both the complex periodic crystals and the icosahedral one. Note that the nature of the b-linkage and especially the c-linkage enforces the same orientation on each TDI and thereby on each Tsai cluster in the completed structure. The long-range order is automatic. Further details of the growth model will be included in our longer, more detailed paper [
19].
6. Why Might TDIs Exist in the Melt?
The TDI is more than a geometric motif around which soup atoms coalesce; it seems to have physical significance in its own right. Such a structure with all positions occupied by one kind of atom closely resembles the densest known packing of 36 identical balls within a spherical container [
20,
21]. This configuration consists of an outer shell of 32 balls lying tangent to the confining sphere, 20 of those located at the vertices of a distorted regular dodecahedron and the other 12 at the vertices of a dual distorted regular icosahedron. The remaining four balls are trapped inside the sphere, their centers at the vertices of an approximately regular tetrahedron.
Of course, unlike a real TDI, all atomic radii (ball sizes) in this packing are identical, and atoms (balls) in the outer shell are equidistant from the center of the cluster. Teich et al. found this densest packing configuration via Monte Carlo simulation: they sampled configurations of hard spheres inside a spherical container in the isobaric ensemble while increasing imposed pressure to a putatively high value, thereby compressing the container [
20]. They found that in the densest packing formed this way, the inner tetrahedron was not completely sterically immobilized by the outer shell, but instead had some “wiggle room” and vibrated slightly even as the cluster reached its densest possible configuration.
This connection may give credence to the idea that the TDI cluster would have a special stability in the melt. Confinement to a sphere may be argued to be a minimal physically reasonable model of the effects of the surrounding liquid on a given set of atoms, since the surrounding liquid will manifest in an isotropic pressure, on average, about that set of atoms.
Alas, as we noted above, the densest known packing of 36 identical balls within a spherical container is not quite a TDI, because 12 atoms of the TDI are bigger than the others. Moreover, attempts to mimic reality more closely by producing dense clusters of spheres of two appropriate radii via the simulation technique described in [
20] did not result in a TDI-like cluster structure in 50 attempts. This indicates that the explanation of the TDI cluster as a purely volume-minimizing one under very high isotropic pressure in the melt is incomplete. The effect of the surrounding melt needs to be considered more carefully, and the atoms modeled more accurately, perhaps including energetic interactions between them rather than sole volume exclusion.
A key additional factor in making the TDI cluster likely to have some fleeting existence in the liquid is that its free energy is reduced by the additional rotational entropy of the inner tetrahedron. It has now been experimentally and computationally verified [
22] that the potential energy barriers to rotation of a tetrahedron inside the dodecahedron-icosahedron combined shells are relatively low, and that the entropy of the extra degrees of freedom when rotation occurs win out at higher temperatures, even when the material remains a solid crystal (Specifically, Euchner et al. found evidence that significant entropy is produced by the rotation of the tetrahedron in the 6:1 periodic approximant to a Tsai-type quasicrystal in the Zinc-Scandium system. They examined closely the structure of single crystals of periodic Zn
6Sc (a structure identical to that of Cd
6Yb), and how it changed with temperature. This periodic approximant has one Tsai cluster per site in a bcc lattice, as described above for the Yb-Cd system. It was known (their refs [
9,
10,
19]) that there is a critical temperature above which the central tetrahedron appears as disordered. Below that temperature, the crystal transforms to a low-temperature phase where the tetrahedra are ordered). At the even higher temperatures of a melt, the entropy contribution will be even greater, and inner tetrahedron rotation may well be sufficient to stabilize a TDI in the melt.