The Roundest Polyhedra with Symmetry Constraints

Abstract

Amongst the convex polyhedra with n faces circumscribed about the unit sphere, which has the minimum surface area? This is the isoperimetric problem in discrete geometry which is addressed in this study. The solution of this problem represents the closest approximation of the sphere, i.e., the roundest polyhedra. A new numerical optimization method developed previously by the authors has been applied to optimize polyhedra to best approximate a sphere if tetrahedral, octahedral, or icosahedral symmetry constraints are applied. In addition to evidence provided for various cases of face numbers, potentially optimal polyhedra are also shown for n up to 132.

1. Introduction

The so-called isoperimetric problem in mathematics is concerned with the determination of the shape of spatial (or planar) objects which have the largest possible volume (or area) enclosed with given surface area (or circumference). The isoperimetric problem for polyhedra can be reflected in a question as follows: What polyhedron maximizes the volume if the surface area and the number of faces n are given? The problem can be quantified by the so-called Steinitz number [1] $S=A^3/V^2$, a dimensionless quantity in terms of the surface area A and volume V of the polyhedron, such that solutions of the isoperimetric problem minimize S. Lindelöf proved that in order to reach the maximum volume, the polyhedron must have an insphere such that all faces are tangent to this sphere at their centroid [2,3]. If the radius of such an inscribed sphere is taken to be unity, one can easily find that $S=27V=9A$. This way, the problem is reformulated so as to find polyhedra with n faces circumscribed about the unit sphere which have the minimum surface area (or volume).

An alternative measure of roundness of solids applied in various fields of science is the so-called isoperimetric quotient ($IQ$) introduced by Pólya [4], which is a normed inverse of the Steinitz number:

$$IQ=36\pi \frac{V^2}{A^3}.$$

(1)

The isoperimetric quotient is a positive dimensionless number that takes unity for the sphere and less for other solids. The closer the $IQ$ is to unity, the more spherical the polyhedron is. Goldberg proposed a lower bound [5] for the Steinitz number, from which a lower bound $A_G\left(n\right)$ for the surface area can be easily obtained if Lindelöf’s necessary condition is satisfied:

$$A_G\left(n\right)=6(n-2)tanE(4{sin}^{2}E-1)$$

(2)

where,

$$E=\frac{n\pi }{6(n-2)}.$$

(3)

Furthermore, on the one hand, as the isoperimetric quotient is inversely proportional to the Steinitz number, for a given n an upper bound $4\pi /A_G$ for the maximum value of $IQ$ can be simply derived as $IQ=36\pi /S=4\pi /A$. On the other hand, any polyhedron constructed with n faces constitutes a lower bound for the maximum value of $IQ$ since it has a surface area larger than or equal to that of the optimal polyhedron. A polyhedron here is referred to as optimal if it has the largest possible $IQ$ among all possible polyhedra of any topology for the given n. Any candidate polyhedron construction is called hereafter conjectural unless rigorous mathematical proof is provided for its optimality.

For this isoperimetric problem where no symmetry constraint is enforced, mathematical proof of optimality exists only in certain cases of a small number of faces. Fejes Tóth [6] proved that Goldberg’s formula provides a lower bound of the minimum value of the Steinitz number for any n, and it is exact for $n=4,6,12$. In this way he proved that the regular tetrahedron, hexahedron, and dodecahedron are the optimal polyhedra in the cases of 4, 6, and 12 faces, respectively. The case of 5 faces is also proven [2,3].

Conjectured solutions with numerically optimized geometry were shown by Goldberg [5] for $n=4$ to $10,12,14$ to $16,20,32,42$, preceding Fejes Tóth’s evidence, and later by Schoen [7,8] for cases up to $n=43$. Mutoh [9] also dealt with polyhedra with minimum volume circumscribed about the unit sphere, and by using a computer-aided search, provided a series of conjectured optimal polyhedra with the number of faces ranging between 4 and 30. In an earlier paper [10] the authors pointed out that in some cases the isoperimetric problem for n faces and the problem of the minimum covering of a sphere by n equal circles have the same proven or conjectured solution (the points of tangency of the faces and the centres of the circles are identical). In some cases, the obtained polyhedra are only topologically identical. Sometimes, the topology of the optimal polyhedron matches that of a suboptimal (nearly optimal) circle covering, and not the optimal one. We developed an iterative numerical method for determining a locally optimal solution of the isoperimetric problem, where the starting point for the topology of the polyhedron is a conjectured optimal circle covering on a sphere. Using this method and starting with the conjectured best coverings with 50 [11] and 72 [12] equal circles, conjectural solutions to the isoperimetric problem for $n=50$ and 72 were obtained [10].

Some of the above-mentioned proven or conjectured solutions have tetrahedral, octahedral or icosahedral symmetry even though such symmetry constraints were not enforced. The solutions for $n=4$, 6, and 12 investigated by Fejes Tóth [6] have tetrahedral, octahedral, and icosahedral symmetry, respectively. The conjectured solution suggested by Goldberg [5] for $n=16$ has tetrahedral symmetry, and for $n=32$ and 42 has icosahedral symmetry. The conjectured solution for $n=72$ provided in [10] has icosahedral symmetry.

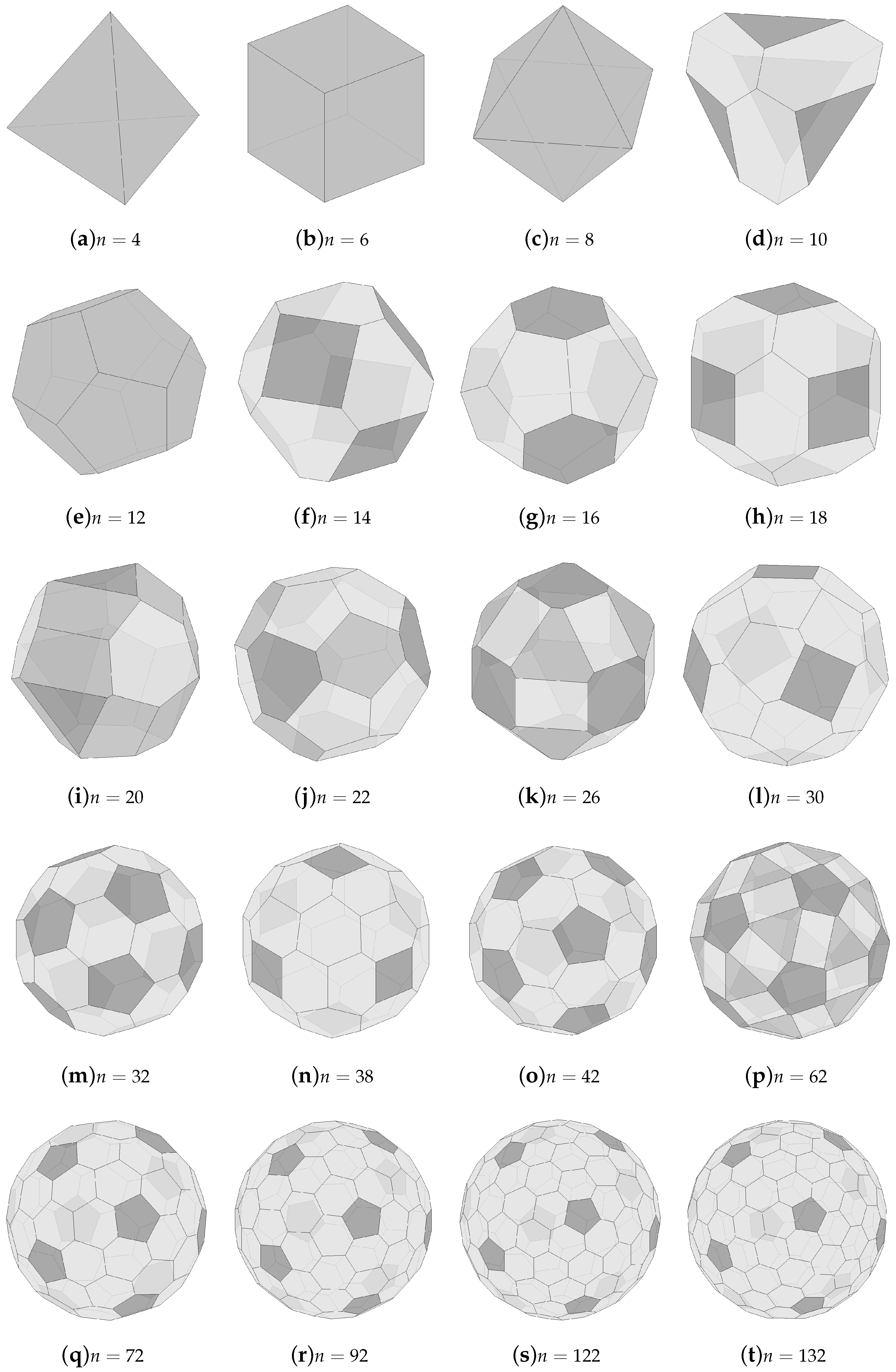
It turns out that in some artistic or practical applications it is not the solutions to the unconstrained isoperimetric problem which play an important role, but rather those with tetrahedral, octahedral or icosahedral symmetry constraints. For instance, a turned ivory piece from Germany, and a wooden die from Korea are exact representations of the conjectured roundest polyhedron with octahedral symmetry constraints for $n=14$ (Figure 1). Similarly, another turned ivory object in Germany and a modern soccer ball show the conjectured roundest polyhedron with icosahedral symmetry constraint for $n=32$ (Figure 2). More details on these artifacts can be found in [13]. Multi-symmetric roundest polyhedra for $n=14,26,32,62$ can be particularly important in practical applications, e.g., soccer ball design [14,15]. The conjectured solution for the case of 14 (32) faces is an isodistant truncation of the octahedron (icosahedron) where the centroids of the faces lie at the vertices and the face centres of a spherical octahedron (icosahedron). A truncation of a Platonic polyhedron is said to be isodistant if the distances from the centre of the Platonic polyhedron to the truncating planes and to the faces of the Platonic polyhedron are equal, that is, if the truncated polyhedron has an insphere. Polyhedra with 26 and 62 faces are obtained by double isodistant truncations of the octahedron and the icosahedron, respectively [14,15].

The artistic and practical interest in finding the roundest object as shown above is an important motivation to study the isoperimetric problem for polyhedra with symmetry constraints. The primary aim of this paper is to prove the solutions for small values of n ($n=8,10,14$) and to present conjectured solutions for $n=18,20,22$. Recalling that some solutions for small even numbers of polygonal faces have been proven by Fejes Tóth [6], our new results complete the sequence of proven and conjectured solutions for even n up to 22. Goldberg [16] has shown how to construct multi-symmetric polyhedra by using a triangular lattice on the tetrahedron, octahedron, and icosahedron (the details will be discussed later in the paper). After his name, these polyhedra now are called Goldberg polyhedra. The secondary aim of this paper is to present octahedrally symmetric Goldberg polyhedra for $n=30$ and 38 as conjectural solutions, and icosahedrally symmetric Goldberg polyhedra for $n=92,122,132$. In this way it is possible to extend the list of icosahedral Goldberg polyhedra up to $n=132$.

2. Multi-Symmetric Point Arrangements on the Sphere

If a plane is tangent to a sphere, then the position of the plane is uniquely determined by the position of the point of tangency. In this way we can investigate the faces of polyhedra having an insphere via investigating the points of tangency on spherical tetrahedra, octahedra, and icosahedra. Identifying and exploring the degrees of freedom of tangent placement on these spherical polyhedra allows the generation of polyhedra with varying face numbers and set symmetries, among which our numerical method can identify the locally optimal (roundest) solution.

Consider the Platonic polyhedra $\{3,q\}$ with triangular faces and q-valent vertices where $q=3,4,5$ (that is the regular tetrahedron, octahedron, icosahedron). Let V, E, and F denote their number of vertices, edges, and faces, respectively. According to the relationships derived in §10.3 of Coxeter’s book [17]:

$$V=\frac{12}{6-q},E=\frac{6q}{6-q},F=\frac{4q}{6-q}.$$

(4)

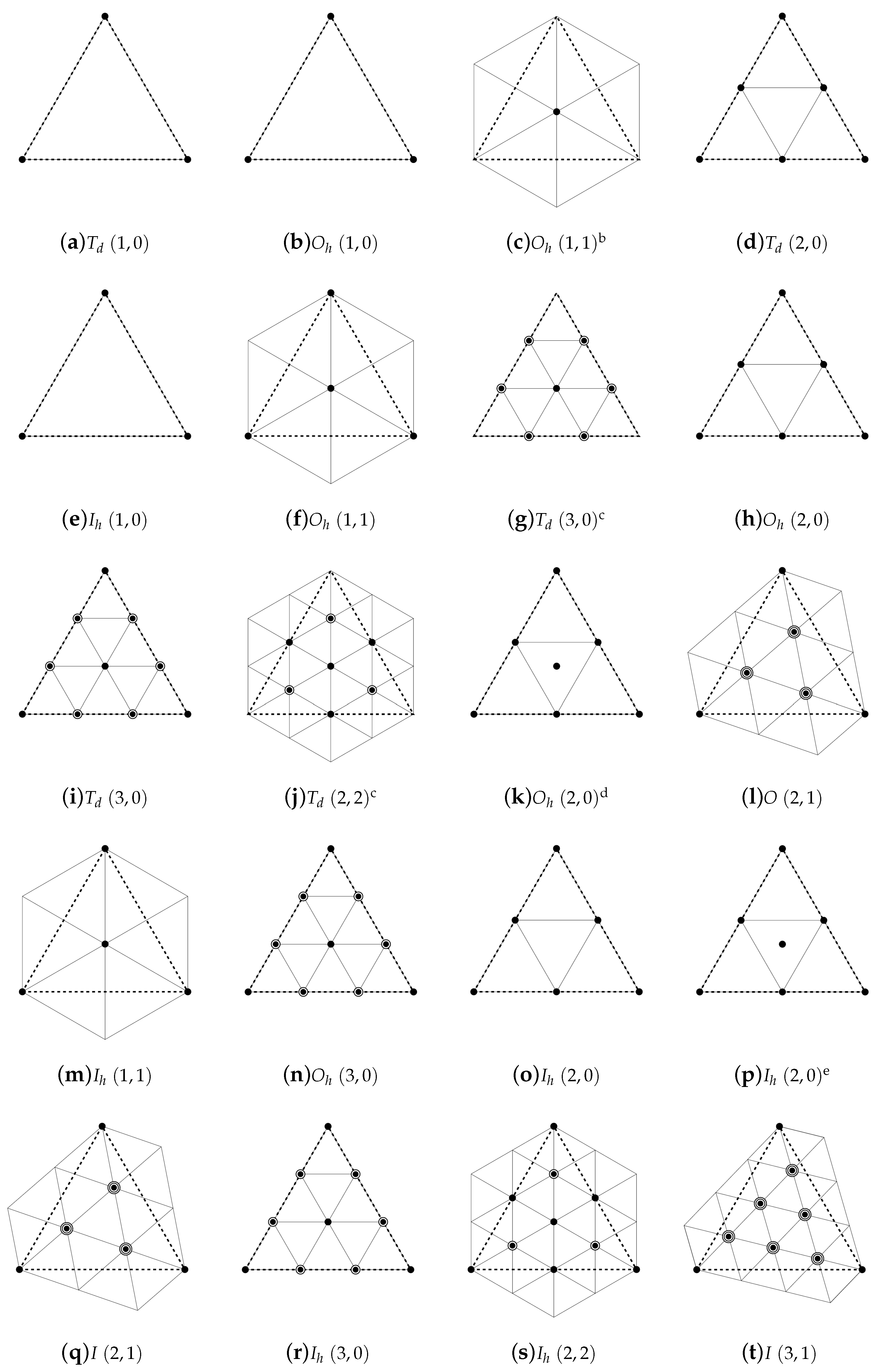
The symmetry of these polyhedra is characterized by the fact that q-fold, 2-fold and 3-fold axes of rotation go through their vertices, edge midpoints and face centres, respectively. If we take one face of the spherical version of these polyhedra, then we can put one point of tangency or none to a vertex, any number of points of tangency on an edge, and a number of points of tangency on a face, divisible by three (points arranged in threefold rotational symmetry) or the remainder after division by three is one (points arranged in threefold rotational symmetry and a point in the face centre). Let v, e, and f denote the number of points of tangency at a vertex, on an edge, and on a face, respectively. Then these non-negative integers can be expressed as follows:

$$v=0\mathrm{or}1,e=0,1,2,3,\dots ,f=3k\mathrm{or}1+3k,k=0,1,2,3,\dots$$

(5)

such that $v+e+f\ne 0$. In this way the number of all points of tangency on the sphere is:

$$n=vV+eE+fF.$$

(6)

Since V, E, and F are even, it is obvious that n is even, too. Additionally, $n\ge 4$.

Proposition 1.

Any even number of points, not less than 4, can be arranged on the sphere in tetrahedral symmetry.

Proof. 

For tetrahedral symmetry, Equation (6) yields $n=4v+6e+4f=2(2v+3e+2f)$. We prove the proposition if we see that $2v+3e+2f$ is an arbitrary natural number $\ge 2$. First select $v=1$, $f=0$, $e=0,1,2,3,\dots$ In this case $2v+3e+2f=2+3k$, $k=0,1,2,3,\dots$ Then select $v=0$, $f=0$, $e=1,2,3,\dots$ In this case $2v+3e+2f=3+3k$, $k=0,1,2,3,\dots$ Finally, select $v=1$, $f=1$, $e=0,1,2,3,\dots$ In this case $2v+3e+2f=4+3k$, $k=0,1,2,3,\dots$ The union of these three sets of numbers contains all natural numbers $\ge 2$, consequently, the set of numbers n contains all even numbers $n\ge 4$. ☐

Remark 1.

From the proposition it follows that for any even number n ≥ 4 there exists a polyhedron with n faces and tetrahedral symmetry. In the proof, for f we used only two values out of the infinitely many. Therefore, for many values of n, there exist not only one but more polyhedra with different topology in tetrahedral symmetry.

In the case of octahedral symmetry, the number of points of tangency takes the form $n=6v+12e+8f$. It can be verified quickly that there exist polyhedra with an even number of faces and octahedral symmetry if $n\ge 6$ except if $n=4+6k$, $k=1,2,3,\dots$

In the case of icosahedral symmetry, the number of points of tangency takes the form $n=12v+30e+20f$. Here, it can be verified quickly that there exist polyhedra with n faces and icosahedral symmetry only for the following values of n: $n=12+30k$, $n=20+30k$, $n=30+30k$, $n=32+30k$, where $k=0,1,2,3,\dots$

The vertices, edge midpoints, and face centres are the points of a face triangle of the tetrahedron, octahedron, and icosahedron, through which rotation axes pass. If a point of tangency is put to such a point, then the position of the point of tangency is fixed. It cannot be slightly moved without destroying the symmetry. We say that the degree of freedom of the point of tangency is zero in this position. If we put one point of tangency on an edge and another one symmetrically to the edge midpoint, then the point and its symmetrical counterpart can be moved along the edge without breaking the symmetry. We say that the degree of freedom of the point of tangency is one. If we put a point of tangency inside the triangle and two others according to threefold symmetry with respect to the face centre, then we can move the point and its symmetrical counterparts simultaneously in the triangle so that the symmetry is maintained. We say that the degree of freedom of the point of tangency is two.

Consider the simplest cases where v, e, and f in Equation (5) take the values 1 or 0. Since here the points of tangency have zero degree of freedom, they uniquely determine the respective polyhedra. Since the number of 3-tuples of a 2-set is $2^3$, we have eight possibilities, but the case $v=e=f=0$, as meaningless, is left out. Thus in each of the tetrahedral, octahedral, icosahedral symmetries, we have seven polyhedra. The face numbers n of these polyhedra (the numbers of points of tangency) are collected in

Table 1. Number of points of tangency n if they lie only on q-fold and/or 2-fold and/or 3-fold rotation axes.

v	e	f	n
			q = 3	q = 4	q = 5
1	0	0	4	6	12
0	1	0	6	12	30
0	0	1	4	8	20
0	1	1	10	20	50
1	0	1	8	14	32
1	1	0	10	18	42
1	1	1	14	26	62

.

Polyhedra determined by the data of Table 1 have also planes of symmetry. Thus, their symmetry groups are the full tetrahedral, octahedral, and icosahedral groups, respectively. Among these 21 polyhedra some are identical. It is trivial to see, for instance, that in the case $n=4$, each of the two polyhedra is the same regular tetrahedron. This kind of coincidence in some other cases will be shown later.

For $n>14$ the tetrahedral arrangements of points of tangency surely will also contain points with one and/or two degrees of freedom. That means that the configuration with the highest $IQ$ can be found only by an optimization process.

For larger values of n, it is expected that trivalent polyhedra with mostly hexagonal faces provide the best results, especially in icosahedral symmetry. Trivalent vertices are found to be visually less “pointed”, consider for example the classic 32-panel soccer ball. Such polyhedra are the Goldberg polyhedra [16] explained below.

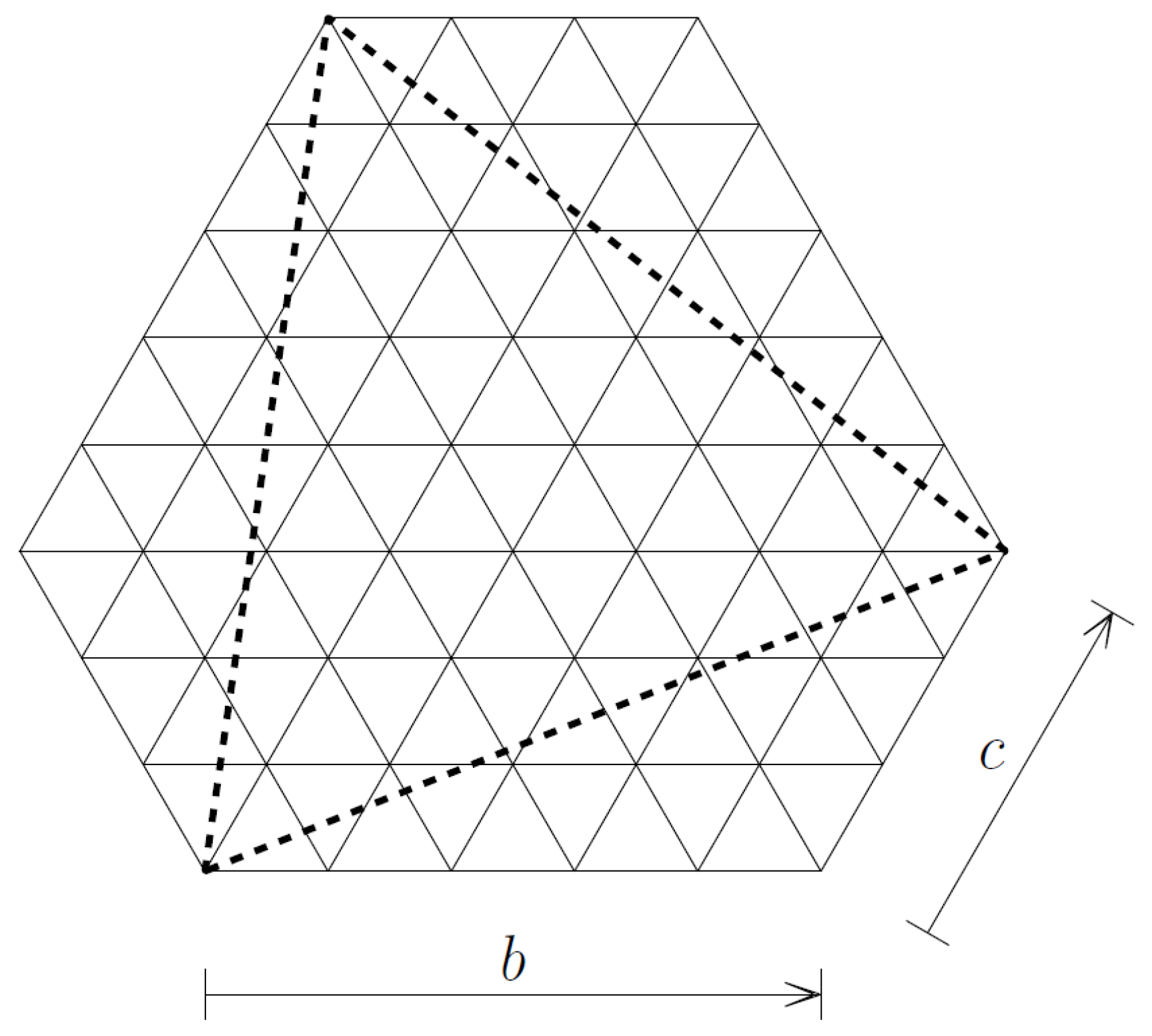
In virus research, Caspar and Klug [18] discovered a regular tessellation on the regular triangle-faced polyhedra $\{3,q\}$, $q=3,4,5$, which consist of small equal equilateral triangles. Coxeter [19] denoted this tessellation by ${\{3,q+\}}_{b,c}$, where $q+$ indicates that q and more than q (i.e., six) small triangles meet at each vertex, some of which are folded, such that they tessellate the surface of the regular polyhedron $\{3,q\}$. The subscripts b and c show that a vertex of the regular polyhedron $\{3,q\}$ can be arrived at from an adjacent one along the edges of the tessellation by b steps on the vertices in one direction, then proceeding by c steps after a change in direction by 60°. Figure 3 shows a part of this tessellation.

The pair of non-negative integers b, c, called Goldberg–Coxeter parameters, generate the tessellation and determine the so-called triangulation number T.

$$T=b^2+bc+c^2.$$

(7)

By “blowing up” the tessellation, we obtain a triangular lattice on the sphere. This lattice determines a polyhedron whose all vertices lie on the sphere and all faces are triangles. Its numbers of vertices $V_T$, edges $E_T$, and faces $F_T$ can be expressed with T, by using the expressions for V, E, and F, respectively in (4), in the form:

$$V_T=T\frac{2q}{6-q}+2,E_T=T\frac{6q}{6-q},F_T=T\frac{4q}{6-q},q=3,4,5.$$

(8)

The reciprocal (dual) of this triangle-faced polyhedron is called Goldberg polyhedron, which is a trivalent polyhedron which has $12/(6-q)$ q-gonal faces, and $(T-1)2q/(6-q)$ hexagonal faces. For $n=V_T$, the Goldberg polyhedra are good candidates for the roundest polyhedra with n faces, especially with octahedral and icosahedral symmetry where,

$$n=4T+2$$

(9)

and,

$$n=10T+2,$$

(10)

respectively.

When the above-mentioned spherical triangular lattice is applied in the case of small values of n, sometimes not all vertices are considered as points of tangency. Sometimes extra points of tangency, which are not vertices of the lattice, are added to the point system. In Figure 4, in a schematic view, we present a part of the triangular lattice—lying on a face of the spherical tetrahedron, octahedron or icosahedron—together with the points of tangency, for the polyhedra shown in Figure 5. The degree of freedom of the points of tangency is also indicated. The subfigures of Figure 4 are in correspondence with those of Figure 5.

3. Method

In a recent paper [10] the authors presented a numerical iterative method for the surface minimization of convex polyhedra circumscribed about the unit sphere with given number of faces and topology (edge graph). The main point of the method is to regard the surface area of a trivalent polyhedron with n faces as the potential energy of a mechanical system to minimize and to create the associated (dual) polyhedron whose faces are considered as triangle elements. Edge forces of the triangle elements are defined as derivatives of the surface area with respect to the lengths, and the resultant of these forces meeting at each vertex can be computed. The set of vertices reaches an equilibrium position (i.e., the surface area is minimized locally) if the resultants at all vertices pass through the centre of the sphere, which implies that the components of the forces lying in the tangent plane (i.e., the plane of the respective face of the parent polyhedron) are in equilibrium at each vertex. We usually start the iteration with the polyhedron determined by the conjectured optimal or suboptimal covering of the sphere by n equal circles. A detailed description and mathematical evaluation of the method is given in [10].

Since we determine the required optimum numerically, despite the care in calculation, we are not able to guarantee that we found the global optimum. What we surely found is a local optimum, and our solution is a conjectured solution.

4. Results

4.1. Small Values of n

4.1.1. $n=8$

Proposition 2.

The roundest polyhedron with 8 faces and with tetrahedral or octahedral symmetry is the regular octahedron.

Proof. 

The proof is simple. According to Table 1 there exist two configurations. The first has tetrahedral symmetry, and the points of tangency are at the vertices and the face centres of the spherical tetrahedron. These points on the sphere are identical to the vertices of a cube. The second has octahedral symmetry, and the points of tangency are at the face centres of the spherical octahedron (Figure 4c). These eight points are identical to the vertices of a cube. Consequently, the two configurations of the points of tangency are congruent, and we have only one polyhedron, which is the reciprocal (dual) of the cube, that is the regular octahedron (Figure 5c). ☐

Its symmetry is $O_h$, and $IQ=0.604599788\dots$

4.1.2. $n=10$

Proposition 3.

The roundest polyhedron with 10 faces and with tetrahedral symmetry is a cube whose four non-adjacent vertices are truncated.

Proof. 

According to Table 1 there exist two configurations, both with tetrahedral symmetry. In the first, say configuration A, the points of tangency are at the vertices and the edge midpoints of the spherical tetrahedron (Figure 4d). In the second, say configuration B, the points of tangency are at the face centres and the edge midpoints of the same spherical tetrahedron. Since the vertices and the face centres of the spherical tetrahedron coincide with the vertices of a spherical cube, and the edge midpoints of the spherical tetrahedron coincide with the face centres of the same spherical cube, configuration A can be taken into coincidence with configuration B by a rotation of 90° about an axis passing through two opposite face midpoints of the spherical cube. Consequently, configurations A and B are congruent, and we have only one polyhedron. The planes tangent to the vertices and edge midpoints of the spherical tetrahedron determine a cube whose four non-adjacent vertices are truncated, or what is the same, a tetrahedron whose edges are chamfered (Figure 5d). ☐

Its symmetry is $T_d$, and $IQ=0.630745372\dots$

4.1.3. $n=14$

Proposition 4.

The roundest polyhedron with 14 faces and with octahedral symmetry is a truncated octahedron (truncated octahedron here does not mean Archimedean-truncated octahedron).

Proof. 

According to Table 1 there exist two configurations. The first has tetrahedral symmetry, and the points of tangency are at the vertices, the edge midpoints and the face centres of the spherical tetrahedron. These points on the sphere are identical to the vertices and the face centres of a spherical cube. The second has octahedral symmetry, and the points of tangency are at the vertices and the face centres of the spherical octahedron (Figure 4f). Because the cube and the regular octahedron are mutually reciprocal to each other, the two configurations of points of tangency on the sphere are congruent, and we have only one polyhedron, that is a truncated octahedron (Figure 5f). ☐

Its symmetry is $O_h$, and $IQ=0.781638893\dots$

4.1.4. $n=18$

According to Table 1 there exists one configuration with octahedral symmetry, where the points of tangency are at the vertices and the edge midpoints of the spherical octahedron (Figure 4h). There are two additional configurations with tetrahedral symmetry, the first for $v=0,e=3,f=0$, the second for $v=0,e=1,f=3$. If only octahedral symmetry is considered then it is obvious, if the tetrahedral symmetry is also considered then it is conjectured that the best configuration is obtained with octahedral symmetry $O_h$, and the roundest polyhedron is the rhombic dodecahedron whose four-valent vertices are truncated, or what is the same, the cube whose edges are chamfered (Figure 5h). For this $IQ=0.823218074\dots$

4.1.5. $n=20$

According to Table 1 there exist two configurations. The first has octahedral symmetry, and the points of tangency are at the edge midpoints and the face centres of the spherical octahedron. The second has icosahedral symmetry, and the points of tangency are at the face centres of the spherical icosahedron. There are two additional configurations with tetrahedral symmetry, the first for $v=1,e=0,f=4$, the second for $v=1,e=2,f=1$ (Figure 4i). The polyhedron with icosahedral symmetry is the regular icosahedron itself, for which $IQ=0.828797719\dots$ The octahedral configuration and the first tetrahedral configuration determine the same polyhedron, if the tetrahedral configuration has planes of symmetry. This common polyhedron is the rhombic dodecahedron whose three-valent vertices are truncated, for which $IQ=0.784085714\dots$ The second tetrahedral configuration, where the points of tangency on the edges can concertedly move with one degree of freedom, is optimized. That resulted in the polyhedron with symmetry $T_d$ in Figure 5i, for which $IQ=0.830222439\dots$ which is the conjectured best for $n=20$.

4.1.6. $n=22$

There are four configurations, all with tetrahedral symmetry: (1) for $v=0,e=3,f=1$; (2) for $v=1,e=1,f=3$; (3) for $v=0,e=1,f=4$, (4) for $v=1,e=3,f=0$. Configuration (4) is not a good candidate since all the points of tangency are concentrated along the edges instead of being more or less uniformly distributed on the sphere. Configuration (1) is not promising either since here apart from rectangular and pentagonal, even nonagonal faces are expected, which is not advantageous. Because of self-duality of the tetrahedron it can be established that configurations (2) and (3) are identical. In this way, only one candidate remained: configuration (3) (Figure 4j). Although the edge graph of the polyhedron related to this configuration is uniquely determined by the data, since $f>1$, the polyhedron itself is not uniquely determined. On a face of the spherical tetrahedron, there is one point of tangency at the face centre, and there are three points of tangency in threefold rotational symmetry with respect to the face centre. In theory, these three points can concertedly move on the face with two degrees of freedom. However, we suppose that the arrangement of the points of tangency has also planes of symmetry, and so we have symmetry $T_d$ instead of T. The three points lie on the three altitudes of the face triangle, where they can concertedly move with one degree of freedom. Consequently, finding the maximum of $IQ$ required optimization in one variable. It resulted in $IQ=0.862408738\dots$ The polyhedron obtained is shown in Figure 5j.

4.2. Octahedral Goldberg Polyhedra

4.2.1. $n=30$

Let the pair of Goldberg–Coxeter parameters be $(2,1)$ for which $T=7$. From Equation (9), $n=30$ is obtained. Here $v=1,e=0,f=3$ (Figure 4l). The three points of tangency can concertedly move with two degrees of freedom on the face triangle of the spherical octahedron, while maintaining threefold symmetry with respect to the face centre. In this way, finding the optimal polyhedron, for which $IQ$ is the maximum, required optimization in two variables. The executed numerical optimization resulted in $IQ=0.896930384\dots$ The obtained polyhedron is presented in Figure 5l. Since the polyhedron has no planes of symmetry, the symmetry of the polyhedron is O.

4.2.2. $n=38$

Let the pair of Goldberg–Coxeter parameters be $(3,0)$ for which $T=9$. The relationship from Equation (9) yields $n=38$. Here $v=1,e=2,f=1$ (Figure 4n). Since $e>1$, the Goldberg polyhedron is not uniquely determined. We have one one-degree-of-freedom point of tangency on one of the edges of the underlying spherical octahedron, and the positions of all the other points on the edges are given by symmetry which is $O_h$, because the arrangement of points of tangency has also planes of symmetry. The value of $IQ$ is a function of the distance between the considered point and the nearest vertex of the octahedron. Finding the polyhedron for which the surface area is the minimum, and so $IQ$ is the maximum, requires optimization in one variable. The obtained maximum is $IQ=0.917445003\dots$ The obtained polyhedron is displayed in Figure 5n.

4.3. Icosahedral Goldberg Polyhedra

4.3.1. $n=92$

Here, the configuration on a face of the underlying spherical polyhedron is the same as that in the case of $n=38$, that is, the pair of Goldberg–Coxeter parameters is $(3,0)$ for which $T=9$, and $v=1,e=2,f=1$ (Figure 4r). However, the underlying polyhedron is not the octahedron but the icosahedron for which the relationship in Equation (10) yields $n=92$. Because of this coincidence, finding the polyhedron for which $IQ$ is a maximum needs optimization in one variable. The obtained maximum $IQ$ is $0.966957236\dots$ The obtained polyhedron having symmetry $I_h$ is shown in Figure 5r.

4.3.2. $n=122$

Let the pair of Goldberg–Coxeter parameters be $(2,2)$ for which $T=12$. From Equation (10), $n=122$ is obtained. Here $v=1,e=1,f=4$ (Figure 4s). On the face of the spherical icosahedron, there is one point of tangency at the face centre, and there are three points of tangency in threefold rotational symmetry with respect to the face centre. In theory, these three points can concertedly move on the face with two degrees of freedom. However, as the configuration of the related spherical covering with 122 equal circles has planes of symmetry [12], we suppose that the arrangement of the points of tangency also has planes of symmetry, and so we have symmetry $I_h$ instead of I. The three points lie on the three altitudes of the face triangle, where they can concertedly move with one degree of freedom. Consequently, finding the maximum of $IQ$ required optimization in one variable. The executed numerical optimization resulted in $IQ=0.975117622\dots$ and in the polyhedron in Figure 5s.

4.3.3. $n=132$

Let the pair of Goldberg–Coxeter parameters be $(3,1)$ for which $T=13$. From Equation (10), $n=132$ is obtained. Here $v=1,e=0,f=6$ (Figure 4t). The six points of tangency form two sets of threes, where the three points in each set can concertedly move with two degrees of freedom on the face triangle of the spherical icosahedron, while maintaining threefold symmetry with respect to the face centre. Since the two sets of points can move independently of each other, the whole arrangement has four degrees of freedom. In this way, finding the optimal polyhedron, for which $IQ$ is the maximum, required optimization in four variables. The numerical optimization process started with a configuration where the centres of the 132 equal circles forming the best known covering of the sphere [20] were considered as the points of tangency of the 132 faces of the polyhedron. The process eventually resulted in $IQ=0.976993221\dots$ The polyhedron shown in Figure 5t. Since the polyhedron has no planes of symmetry, the symmetry of the polyhedron is I.

The roundest multi-symmetric polyhedra proven or conjectured by us together with those previously published by other authors are shown in Figure 5, and the data characterizing these polyhedra are collected in

Table 2. Polyhedra with n faces that maximize the isoperimetric quotient $IQ$ under tetrahedral, octahedral, or icosahedral symmetry constraints. Polyhedra are characterized by n, point group symmetry G, Goldberg–Coxeter parameters $(b,c)$, isoperimetric quotient $IQ$. Upper bound of $IQ$ is given via Goldberg’s formula. Particular properties are discussed in footnotes.

n	G	(b,c)	IQ	Upper Bound	Remarks
4	$T_d$	$(1,0)$	$\mathit{0.302299894}{}^{\mathrm{a}}$	$0.302299894$	Proven, Fejes Tóth [6]
6	$O_h$	$(1,0)$	$\mathit{0.523598775}{}^{\mathrm{a}}$	$0.523598775$	Proven, Fejes Tóth [6]
8	$O_h$	$(1,1){}^{\mathrm{b}}$	$0.604599788$	$0.637349714$	Proven, this work
10	$T_d$	$(2,0)$	$0.630745372$	$0.707318712$	Proven, this work
12	$I_h$	$(1,0)$	$\mathit{0.754697399}{}^{\mathrm{a}}$	$0.754697399$	Proven, Fejes Tóth [6]
14	$O_h$	$(1,1)$	$0.781638893$	$0.788894402$	Huybers [14]; proven, this work
16	$T_d$	$(3,0){}^{\mathrm{c}}$	$0.812189098$	$0.814733609$	Goldberg [5]
18	$O_h$	$(2,0)$	$0.823218074$	$0.834942754$	This work
20	$T_d$	$(3,0)$	$0.830222439$	$0.851179828$	This work
22	$T_d$	$(2,2){}^{\mathrm{c}}$	$0.862408738$	$0.864510388$	This work
26	$O_h$	$(2,0){}^{\mathrm{d}}$	$0.876811431$	$0.885098414$	Huybers [15]
30	O	$(2,1)$	$0.896930384$	$0.900256896$	This work
32	$I_h$	$(1,1)$	$0.905798260$	$0.906429544$	Goldberg [5]
38	$O_h$	$(3,0)$	$0.917445003$	$0.921082160$	This work
42	$I_h$	$(2,0)$	$0.927651905$	$0.928542518$	Goldberg [5]
62	$I_h$	$(2,0){}^{\mathrm{e}}$	$0.945021022$	$0.951478663$	Huybers [15]
72	I	$(2,1)$	$0.957881213$	$0.958189143$	Tarnai et al. [10]
92	$I_h$	$(3,0)$	$0.966957236$	$0.967248411$	This work
122	$I_h$	$(2,2)$	$0.975117622$	$0.975282102$	This work
132	I	$(3,1)$	$0.976993221$	$0.977150391$	This work

${}^{\mathrm{a}}$ Mathematically proven to be the best without enforcing symmetry; ${}^{\mathrm{b}}$ The vertices of the regular octahedron are not points of tangency; ${}^{\mathrm{c}}$ The vertices of the regular tetrahedron are not points of tangency; ${}^{\mathrm{d}}$ The system of the lattice points is supplemented with the face midpoints of the regular octahedron; ^e The system of the lattice points is supplemented with the face midpoints of the regular icosahedron.

.

5. Discussion

A numerical iterative method developed recently by the authors has now been applied to produce conjectured solutions for the isoperimetric problem of polyhedra if tetrahedral, octahedral, or icosahedral symmetry constraints are prescribed. The algorithm ensures that the polyhedra are local optima, and they are either identical or close to global optima if initial face arrangements are chosen appropriately. In some of the cases such initial arrangements for the conjectured solutions proposed by the authors originated from optimal circle coverings on a sphere. The small differences between the actual $IQ$ values and the corresponding upper bounds (e.g., for $n=72,92,122,132$) render the polyhedra likely to be global optima.

Using our numerical investigations, we have found (proven or conjectured) the roundest Goldberg polyhedra with icosahedral symmetry for the Goldberg–Coxeter parameters $(1,0)$, $(1,1)$, $(2,0)$, $(2,1)$, $(2,2)$, $(3,0)$, $(3,1)$; that is for face numbers $n=12,32,42,72,122,92,132$. This list is complete up to $(3,1)$. We also have octahedrally symmetric Goldberg polyhedra for the Goldberg–Coxeter parameters $(1,0)$, $(1,1)$, $(2,0)$, $(2,1)$ and $(3,0)$, that is, for face numbers $n=6,14,18,30$ and 38, as well as tetrahedrally symmetric Goldberg polyhedra for the Goldberg–Coxeter parameters $(1,0)$, $(1,1)$, $(2,0)$ and $(3,0)$, that is for face numbers $n=4,8,10$ and 20. Here the tetrahedral case $(1,1)$ is special because the two trivalent vertices on each of the edges of the underlying tetrahedron coincide forming four-valent vertices, and the hexagons become triangles. In this way, the truncated tetrahedron becomes a regular octahedron. Recently, intense research was conducted into constructing “equilateral” Goldberg polyhedra [21]. This raised the question as to whether these polyhedra could be used to extend the range of the conjectured roundest Goldberg polyhedra. Unfortunately, the answer is in the negative. The “equilateral” Goldberg polyhedra are only “nearly” spherical, and so they have no insphere.

We note that Schoen [22] mentioned that recently Deeter numerically determined the solution for $n=122$ without enforcing any symmetry. The optimal polyhedron he obtained has icosahedral symmetry $I_h$. Unfortunately, the numerical data of this polyhedron are not provided, so we could not decide whether his polyhedron is identical to ours.

Four out of the five Platonic polyhedra are the roundest multi-symmetric polyhedra for $n=4,6,8,12$. A natural question is whether among the semi-regular polyhedra there are some which are the roundest for $n>12$. The semi-regular polyhedra have tetrahedral, octahedral or icosahedral symmetry, look quite spherical, and additionally their $IQ$ values are known [23]. The Archimedean polyhedra are out of question because they have no insphere. However, it is possible to modify them according to isodistant truncation, as happened, for instance, to the truncated octahedron and truncated icosahedron ($n=14$ and 32). The Archimedean duals, that is, the Catalan polyhedra are worth investigating because they do have an insphere. Among the Archimedean duals there are two polyhedra for $n=12$, four polyhedra for $n=24$, one polyhedron for $n=30$, one polyhedron for $n=48$, four polyhedra for $n=60$, and one polyhedron for $n=120$. Polyhedra for $n=12$ are not interesting because the roundest is the regular dodecahedron. Among the four polyhedra for $n=24$, the dual of the snub cube is the best, for which $IQ=0.872628\dots$ However, the points of tangency have two degrees of freedom here, therefore by optimization this $IQ$ value can be increased. In the case of $n=30$, the rhombic triacontahedron has $IQ=0.887200\dots$, which is smaller than that we found for the polyhedron in Figure 5l. In the case of $n=48$, the dual of the great rhombicuboctahedron has $IQ=0.910066\dots$, which is smaller than that for $n=42$ given by Goldberg, therefore it is probably not optimal. Among the four polyhedra for $n=60$, the dual of the snub dodecahedron is the best, for which $IQ=0.945897\dots$ However, because of an argument similar to that in the case of $n=24$, the polyhedron is not optimal. In the case of $n=120$, the dual of the great rhombicosidodecahedron has $IQ=0.957765\dots$, which is much smaller than that we have for $n=92$, therefore, probably it cannot be optimal.

Figure 1 and Figure 2 show some applications for $n=14$ and 32. After having some new results we discovered that the conjectured roundest polyhedron obtained for $n=18$ (Figure 5h) decorates the memorial to Thomas Bodley in the chapel of Merton College, Oxford, which was erected in 1615 [24,25].