1. Introduction
It is well known that historic time series imply the behavior rules of a given phenomenon and can be used to forecast the future of the same event [
1]. Many researchers have developed time series models to predict the future of a complex system, e.g., regression analysis [
2], the autoregressive moving average (ARIMA) model [
3], the autoregressive conditional heteroscedasticity (ARCH) model [
4], the generalized ARCH (GARCH) model [
5], and so on. However, these methods require some premise hypotheses,such as a normality postulate [
6], etc. Meanwhile, models that satisfied the constraints precisely can miss the true optimum design within the confines of practical and realistic approximations. Therefore, Song and Chissom proposed the fuzzy time series forecasting model [
7,
8,
9]. Since then, the FTS model has been applied for forecasting in many nonlinear and complicated forecasting problems, e.g., stock market [
10,
11,
12,
13], electricity load demand [
14,
15], project cost [
16], and the enrollment at Alabama University [
17,
18], etc.
A vast majority of FTS models are first-order and high-order fuzzy AR (autoregressive) models. These models can be considered as an equivalent version of AR (n) based on fuzzy lagged variables of time series. Most of these fuzzy time series models follow the basic steps as Chen proposed [
19]:
- Step 1:
Define the universe U and the number and length of the intervals;
- Step 2:
Fuzzify the historical training time series into fuzzy time series;
- Step 3:
Establish fuzzy logical relationships (FLR) according to the historical fuzzy time series and generate forecasting rules based on fuzzy logical groups (FLG);
- Step 4:
Calculate the forecast values according to the FLG rules and the right-hand side (RHS) of the forecasted point.
In order to improve the accuracy of such kinds of FTS models, researchers have proposed other improved models based on Chen’s model. For example, concerning the determination of suitable intervals, Huarng [
20] proposed averages and distribution methods to determine the optimal interval length. Huarng and Yu [
21] proposed an unequal interval length method based on ratios of data. Since then, many studies [
20,
22,
23,
24,
25,
26,
27] have been carried out for the determination of the optimal interval length using statistical theory. Some authors even employed PSO techniques to determine the length of the intervals [
12]. In fact, in addition to the determination of intervals, the definition of the universe of discourse also has an effect on the accuracy of the forecasting results. In these models, minimum data value, maximum data value, and two suitable positive numbers must be determined to make a proper bound of the universe of discourse.
Concerning the establishment of fuzzy logical relationships, many researchers utilize artificial neural networks to determine fuzzy relations [
28,
29,
30]. The study of Aladag et al. [
28] is considered as a basic high-order method for forecasting based on artificial neural networks. Meanwhile, fuzzy AR models are also widely used in many fuzzy time series forecasting studies [
11,
12,
31,
32,
33,
34,
35]. In order to reflect the recurrence and the weights of different FLR in fuzzy AR models, Yu [
36] used a chronologically-determined weight in the defuzzification process. Cheng et al. [
37] used the frequencies of different right-hand sides (RHS) of FLG rules to determine the weight of each LHS. Furthermore, many studies employed the adaptive fuzzy inference system (ANFIS) method [
38] for time series forecasting. For example, Primoz and Bojan [
39] defined soft constraints based on ANFIS to discrete optimization for obtaining optimal solutions. Egrioglu et al. [
40] proposed a model named the modified adaptive network based fuzzy inference system (MANFIS). Sarica et al. [
41] developed a model based on an autoregressive adaptive network-based fuzzy inference system (AR-ANFIS), etc. Since 2013, considering the impacts of specification errors, fuzzy auto regressive and moving average (ARMA) time series forecasting models were proposed [
42,
43]. The initial first-order ARMA fuzzy time series forecasting model was proposed by Egrioglu et al. [
42] based on the particle swarm optimization method. Kocak [
43] developed a high-order ARMA fuzzy time series model based on artificial neural networks. Kocak [
44] used both fuzzy AR variables and fuzzy MA variables to increase the performance of the forecasting models.
A forecasting model is used to predict the future fluctuation of a time series based on current values. Therefore, we present a novel method to forecast the fluctuation of a stock market based on a high-order AR (n) fuzzy time series model and particle swarm optimization (PSO) arithmetic. Unlike existing models, the proposed model is based on the fluctuation values instead of the exact values of the time series. Firstly, we calculate the fluctuation for each datum by comparing it with the data of its previous day in a historical training time series to generate a new fluctuation trend time series (FTTS). Then, we fuzzify the FTTS into fuzzy-fluctuation time series (FFTS) according to the up, equal, or down range of each fluctuation data value. Since the relationship between historical FFTS and future fluctuation trends is nonlinear, a PSO algorithm is employed to estimate the proportion of each AR and MA parameter in the model. Finally, we use these acquired parameters to forecast future fluctuations. The advantages provided by the proposed method are as follows.
The remaining content of this paper is organized as follows:
Section 2 introduces some preliminaries of fuzzy-fluctuation time series based on Song and Chissom’s fuzzy time series [
7,
8,
9].
Section 4 introduces the process of the PSO machine learning method.
Section 4 describes a novel approach for forecasting based on high-order fuzzy-fluctuation trends and the PSO heuristic learning process. In
Section 5, the proposed model is usedto forecast the stock market using TAIEX datasets from 1997 to 2005, SHSECI from 2007 to 2015, and the year 2015 of the DAX30 index. Conclusions and potential issues for future research are summarized in
Section 6.
2. Preliminaries
Song and Chissom [
7,
8,
9] combined fuzzy set theory with time series and presented the following definitions of fuzzy time series. In this section, we will extend fuzzy time series to fuzzy-fluctuation time series (FFTS) and propose the related concepts.
Definition 1. Let be a fuzzy set in the universe of discourse ; it can be defined by its membership function, , where denotes the grade of membership of , .
The fluctuation trends of a stock market can be expressed by a linguistic set
, e.g., let
g=3,
={down, equal, up}. The element
and its subscript
i is strictly monotonically increasing [
45], so the function can be defined as follows:
. To preserve all of the given information, the discrete
also can be extended to a continuous label
, which satisfies the above characteristics.
Definition 2. Let be a time series of real numbers, where T is the number of the time series. is defined as a fluctuation time series, where . Each element of can be represented by a fuzzy set as defined in Definition 1. Then we call time series to befuzzified into a fuzzy-fluctuation time series (FFTS) .
Definition 3. Let be a FFTS. If is determined by ,
then the fuzzy-fluctuation logical relationship is represented by:
and it is called the nth-order fuzzy-fluctuation logical relationship (FFLR) of the fuzzy-fluctuation time series, where is called the left-hand side(LHS) and is called the right-hand side(RHS) of the FFLR. This model can be considered as an equivalent of the auto-regressive model of AR (n), defined in Equation (2): where represents the portion of for calculating the forecast is , is the calculation error, and is introduced to preserve more information, as described in Definition 1. 3. PSO-Based Machine Learning Method
In this paper, the particle swarm optimization (PSO) is employed to estimate the parameters in Equation (2). The PSO method was introduced as an optimization method for continuous nonlinear functions [
46]. It is a stochastic optimization technique, which is similar to social models, such as birds flocking or fish schooling. During the optimization process, particles are distributed randomly in the design space and their location and velocities are modified according to their personal best and global best solutions. Let
m+1 represent the current time step,
,
,
,
indicate the current position, current velocity, previous position, and previous velocity of particle
i, respectively. The position and velocity of particle
i are manipulated according to the following equations:
where
w is an inertia weight which determines how much the previous velocity is preserved [
47],
c1 and
c2 are the self-confidence coefficient and social confidence coefficient, respectively,
is a random number, and
and
are the personal best position found by particle
i and the global best position found by all particles in the swarm up to time step
m, respectively.
Let the design space be defined by
. If the position of particle
i exceeds the boundary, then
is modified as follows:
4. A Novel Forecasting Model Based on High-Order Fuzzy-Fluctuation Trends
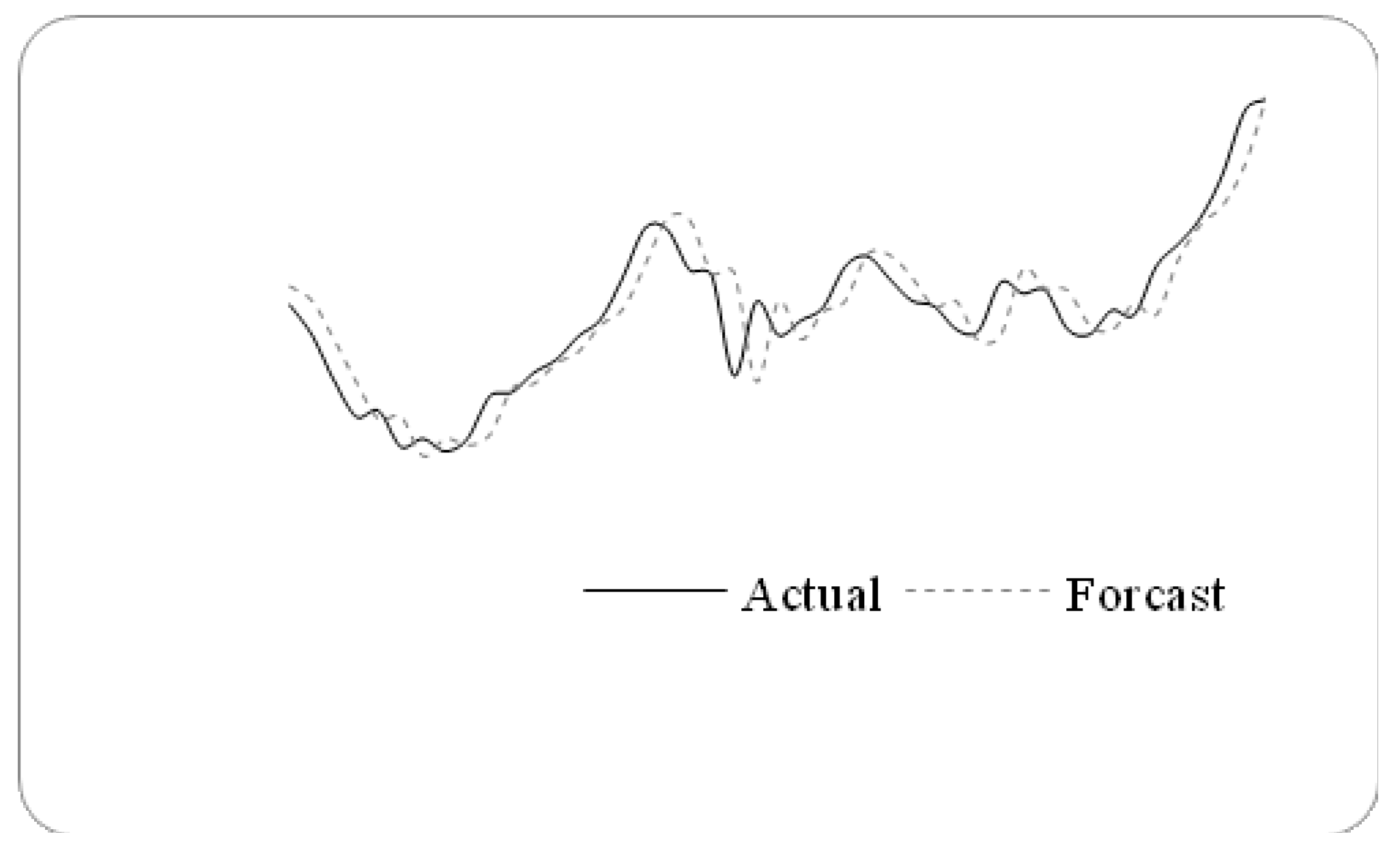
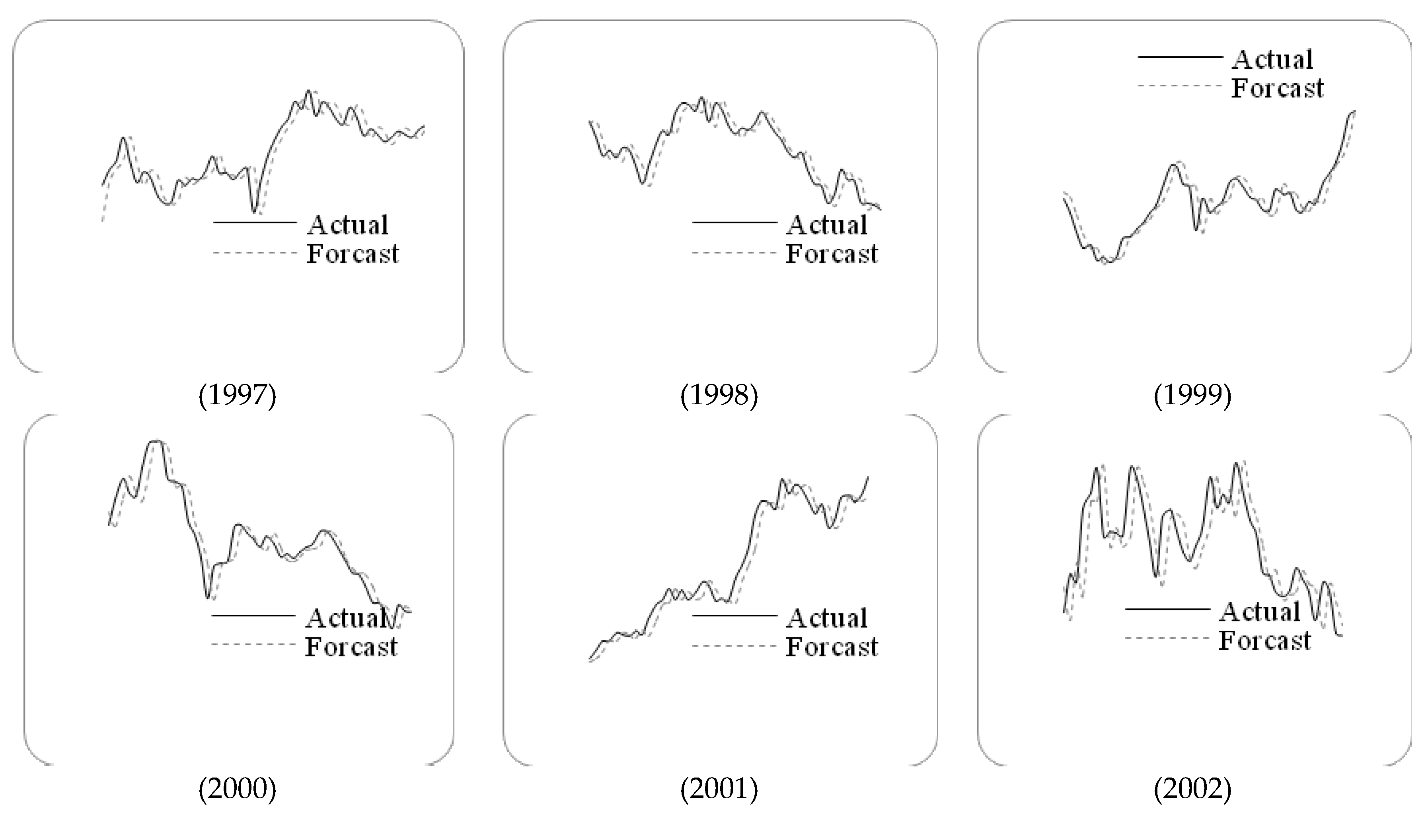
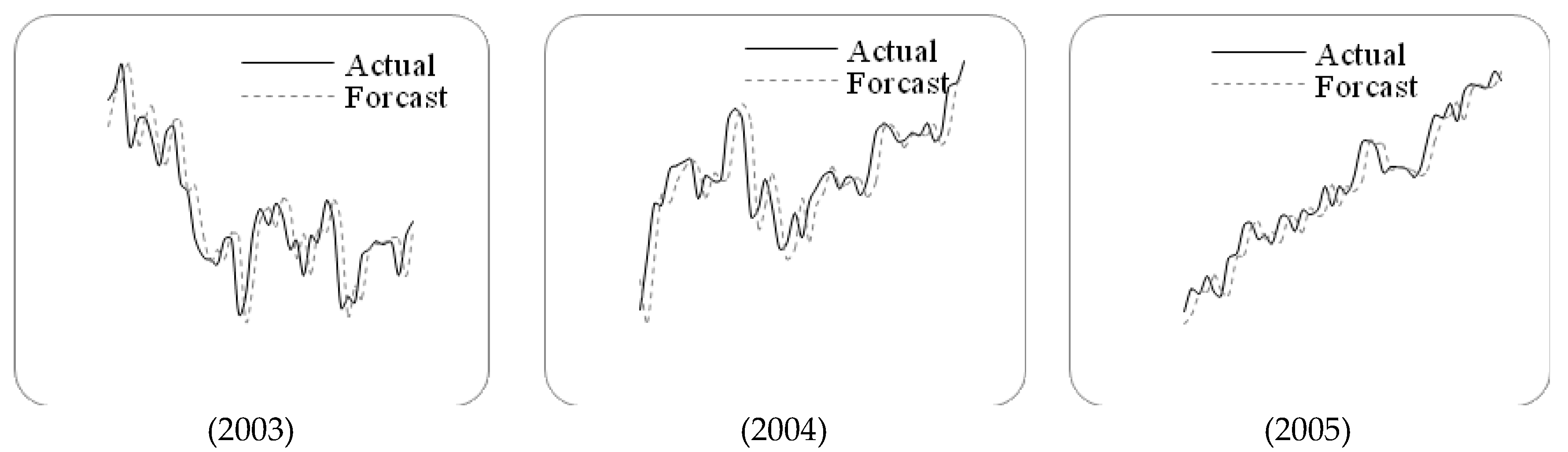
In this paper, we propose a novel forecasting model based on high-order fuzzy-fluctuationtrends and a PSO machine learning algorithm. In order to compare the forecasting results with other researchers’ work [
10,
11,
27,
36,
48,
49,
50,
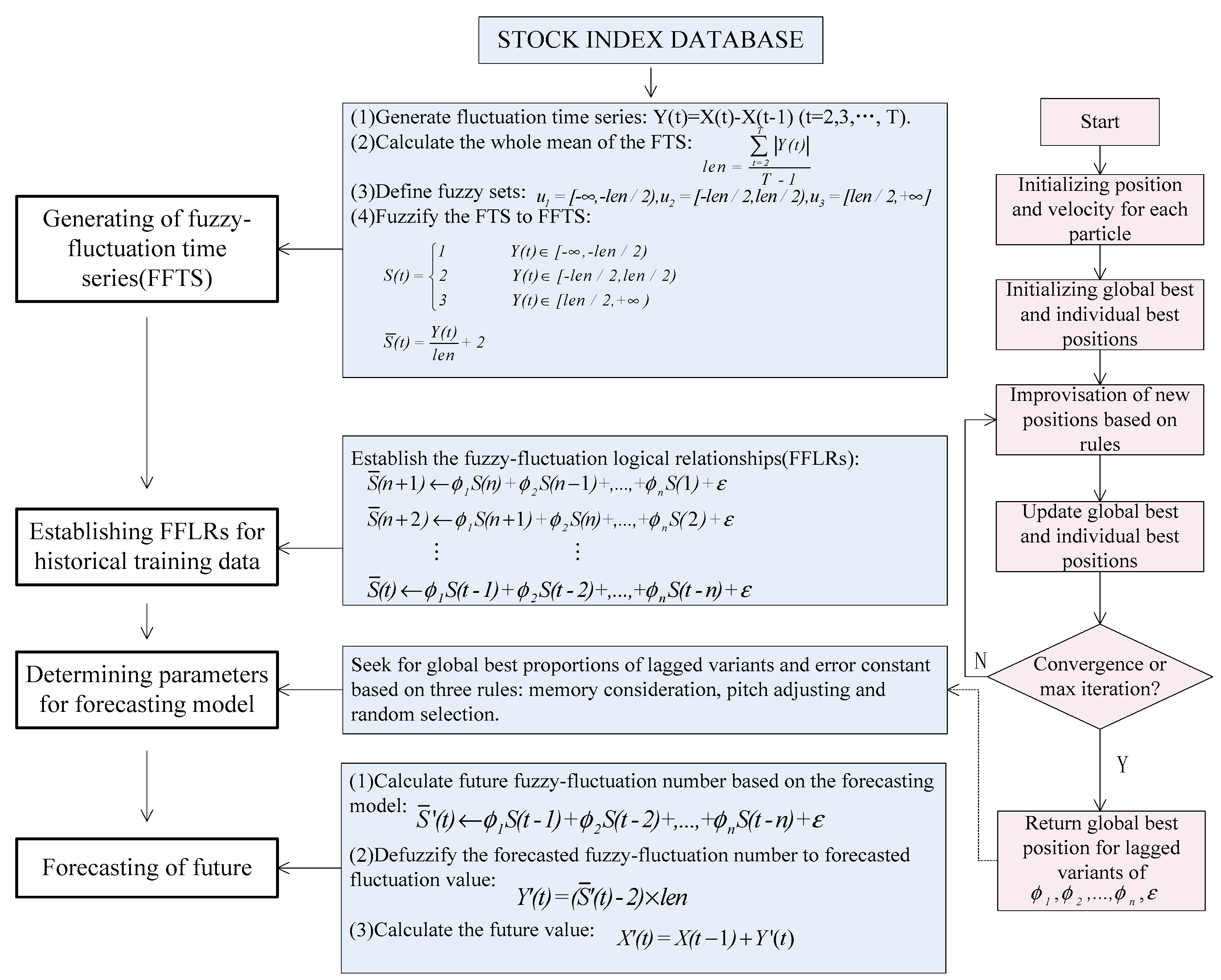
51], the authentic TAIEX (Taiwan Stock Exchange Capitalization Weighted Stock Index) is employed to illustrate the forecasting process. The data from January 1999 to October 1999 are used as training time series and the data from November 1999 to December 1999 are used as testing dataset. The basic steps of the proposed model are shown in
Figure 1.
Step 1: Construct FFTS for historical training data
For each element in the historical training time series, its fluctuation trend is determined by . According to the range and orientation of the fluctuations, can be fuzzified into a linguistic set {down, equal, up}. Let len be the whole mean of all elements in the fluctuation time series , define , , , then can be fuzzified into a fuzzy-fluctuation time series . It is can also be extended to a continuous labeled time series , which preserves the accurate original information of .
Step 2: Establish nth-order FFLRs for the forecasting model
According to Equation (2), each can be represented by its previous n days’ fuzzy-fluctuation number. Therefore, the total of FFLRs for historical training data is pn = T − n − 1.
Step 3: Determine the parameters for the forecasting model based on the PSO machine learning algorithm
In this paper, the PSO method is employed to determine the parameters
and a general error
in Equation (2). The personal best position and global best position are determined by minimizing the root of the mean squared error (RMSE) in the training process:
where
n denotes the number of values forecasted,
forecast(t) and
actual(t)denote the forecasting value and actual valueat time
tin the training process, respectively. For determined
and
, the forecast value at time
t is as follows:
The pseudo-code for the PSO-based machine learning algorithm is shown in
Appendix A.
Step 4: Forecast test time series
For each data in the test time series, its future number can be forecasted according to Equation (7), based on the observed data point X (t − 1), its n-order fuzzy-fluctuation trends, and the parameters generated from the training dataset.