Abstract
Multimodal biometric systems are considered a way to minimize the limitations raised by single traits. This paper proposes new schemes based on score level, feature level and decision level fusion to efficiently fuse face and iris modalities. Log-Gabor transformation is applied as the feature extraction method on face and iris modalities. At each level of fusion, different schemes are proposed to improve the recognition performance and, finally, a combination of schemes at different fusion levels constructs an optimized and robust scheme. In this study, CASIA Iris Distance database is used to examine the robustness of all unimodal and multimodal schemes. In addition, Backtracking Search Algorithm (BSA), a novel population-based iterative evolutionary algorithm, is applied to improve the recognition accuracy of schemes by reducing the number of features and selecting the optimized weights for feature level and score level fusion, respectively. Experimental results on verification rates demonstrate a significant improvement of proposed fusion schemes over unimodal and multimodal fusion methods.
1. Introduction
The recognition of human beings based on physical and/or behavioral characteristics is a trend in places with high security needs. Unimodal biometric systems, which use single-source biometric traits, usually suffer due to several factors such as a lack of uniqueness, non-universality and noisy data [1]. In this respect, multimodality can be employed as a remedy in order to solve the limitations of unimodal systems and improve the system performance by extracting the information from multiple biometric traits.
The present work involves the consideration of face and iris biometric traits due to many similar characteristics of face and iris modalities. Face recognition performance may be affected by variations in terms of illumination, pose and expression [1]; on the other hand, non-cooperative situations lead to degradation of iris recognition performance [2]. In this study, we investigate the effect of information fusion on face- iris modalities at different levels of fusion in order to improve the recognition performance and solve the problems raised by unimodal face and iris traits.
The common biometric systems modules can be categorized as signal acquisition, feature extraction, and matching scores production. Generally, multimodal biometric systems fuse the information at four different fusion levels such as: sensor level; match score level; feature level, and; decision level fusion [1]. Match score level fusion is the most popular among all fusion levels due to the ease in accessing and fusing the scores. It general, three different categories are considered for match score level fusion, namely Transformation-based score fusion, Classifier-based score fusion, and Density-based score fusion. In Transformation-based score fusion, prior to fusion, the normalization of matching scores into a common domain and range is needed because of incompatibility of several biometric traits. In Classifier-based score fusion, the concatenated scores from different classifiers are treated as a feature vector and each matching score is seen as an element of feature vector. Density-based score fusion considers an explicit estimation of genuine and impostor score densities that causes increasing implementation complexity [3]. In feature level fusion, the original feature sets of different modalities are considered to involve richer information about the raw biometric data compared to matching score level fusion.
On the other hand, concatenating the feature sets leads to high dimensionality and redundant data, thus affecting the recognition performance [4]. Feature transformation and feature selection are usually applied as a remedy to reduce the effect of dimensionality and redundancy of feature level fusion [4]. Feature selection attempts to solve the problem by choosing an optimal subset of original feature sets based on a certain objective function. Several feature selection methods such as Particle Swarm Optimization (PSO), Genetic Algorithm (GA), and Sequential Forward Floating Selection (SFFS), have been implemented in different biometric systems for the purpose of optimization [1,5,6,7,8]. On the other hand, feature transformation attempts to represent the feature vector in another vector space by preserving the significant information and, subsequently, the dimension reduction. Principal Component Analysis (PCA), Linear Discriminant Analysis (LDA), Kernel Principal Component Analysis (KPCA), and Independent Component Analysis (ICA) have been applied in different biometric recognition systems as feature transformation methods [9].
In decision level fusion, each biometric matcher individually decides on the best match based on the provided input. In fact, the final decision is achieved by fusing the outputs of multiple matchers [10]. In general, a decision is represented by a logical number , where 1 means “accept” and 0 means “reject”. From the classifiers’ perspective, making any decision is performed by comparing the matching scores with a certain threshold. Majority voting, behavior knowledge space, weighted voting based on the Dempster-Shafer theory of evidence, AND rule and OR rule, etc., can be considered as decision level fusion techniques [11,12,13,14]. Mostly, this level of fusion is less studied in literature due to providing less information content compared to matching scores and features.
This study aims to investigate different fusion schemes at score level, feature level, decision level fusion and at a combination of aforementioned fusion levels using face and iris modalities. The face and iris can be considered as complementary biometric traits in which iris patterns are easily extracted from face images. They both can be acquired using a same camera simultaneously and can be considered as independent biometric traits. Face and iris fusion techniques involve specific feature extractors such as Discrete Wavelet Transform (DWT), Discrete Cosine Transform (DCT) and Gabor filters, the investigation of local and global feature extractors on the face and iris with the concentration on score and feature level fusion or combination of these two modalities, [1,6,15,16,17]. In [8,15,18], authors improve the recognition accuracy of face and iris modalities with different local and global feature extractors at score level and feature level fusion. Well-known techniques such as Weighted Sum Rule, Product Rule, Min Rule and Support Vector Machine (SVM) have been applied for face-iris combination at score level fusion and Particle Swarm Optimization (PSO) is used to explore the effect of feature selection on face and iris multimodal system performance. The authors of [17] proposed an intelligent 2v-support vector machine-based match score fusion algorithm. The proposed method integrates the quality of images in order to improve the recognition performance of face and iris modalities. A face-iris multimodal biometric system based on matching score level fusion using support vector machine (SVM) is applied in [1]. The authors implemented Discrete Cosine Transformation (DCT) to extract facial features and log-Gabor filter for extracting the iris pattern. The article improves the performance of multimodal face and iris biometrics through the selection of optimal features using the Particle Swarm Optimization (PSO) algorithm and the use of SVM for classification. A SVM-based fusion rule is also proposed in [16] to fuse two matching scores of face and iris modalities. Authors of [6] proposed an appropriate pattern representation strategy to extract the information using an over-complete global feature combination and, subsequently, the selection of the most useful features has been performed by Sequential Forward Floating Selection (SFFS). In [19], an identification scheme has been proposed for improving the performance of face and iris multimodal biometric systems. The scheme is based on RBF (radial basis function) neural network fusion rules and applies both transformation-based score and classifier-based score fusion strategies. A new method has been proposed in [20] to fuse face and iris biometric traits with the weighted score level fusion technique to flexibly fuse the matching scores from these two modalities based on their weights availability. A more recent scheme has been proposed by [21], which uses matching score level and feature level fusion combination to improve the face and iris multimodal biometric systems. Optimized Weighted Sum Rule fusion has been applied in their work for score level fusion along with feature selection techniques such as Particle Swarm Optimization (PSO) and the Backtracking Search Algorithm (BSA) at feature level fusion.
The state-of-the-art literature review on face-iris multimodal biometric systems involves score level, feature level and/or a combination of these two levels of fusion. Therefore, this study investigates the effect of decision level fusion on a face-iris multimodal biometric system; in particular, the performance of the system is explored when considering threshold-optimized decision level fusion. We also aim to design a scheme to involve the consideration of matching score level, feature level, along with decision level fusion in order to investigate the effect of combining different fusion levels in designing robust fusion schemes for face and iris multimodal system. In this study, the facial and iris features are extracted using Log Gabor transform [22,23,24]. The Backtracking Search Algorithm (BSA) [25] as a feature selection method is applied to select the optimal set of facial and iris features at feature level fusion. At match score level fusion, the Weighted Sum Rule (WS) [26] is employed to combine the face and iris scores; additionally, BSA is applied to select the set of optimized weights for scores. Finally, at decision level fusion a threshold-optimized decision level fusion [27] is applied for improving the recognition performance of the multimodal system. The state-of-the-art performance of unimodal and multimodal schemes is reported on the CASIA Iris Distance [28] database in the verification context using Receiver Operator Characteristics (ROC) curves, Total Error Rate (TER) and Genuine Acceptance Rate (GAR) at a False Acceptance Rate (FAR) = 0.01%.
The contribution of the present work is to design a robust multimodal face-iris biometric system by combining the advantages of score level, feature level and decision level fusion. Human faces and irises can be considered as significant biometric traits in several surveillance, access control and forensic investigations applications such as airport control boards, criminal investigations, sexual dimorphism, and identity obfuscation applications. In addition, since the face and iris modalities are acquired simultaneously using the same camera, the proposed scheme is motivated to construct a robust multimodal biometric system. Therefore the proposed scheme can be applied practically in individual and multimodal face-iris recognition systems by extracting left and right iris patterns and then fusing them with facial features. The use of BSA as a robust feature and weight selection method in the proposed scheme is of interest for the performance enhancement of the system and overcoming the high computational time. On the other hand, the idea of using threshold-optimized points in the multimodal system is useful in the presence of outliers. Additionally, this work proposes to use the advantages of employing both irises with the face that provides higher verification performance while combining with facial information. In fact, the main difference between this work and prior work done on face and iris fusion is that it applies a hybrid scheme using score, feature and decision levels on the faces and irises of the same subjects, which can be applied practically in any surveillance, access control and forensic investigation applications.
The paper is organized as follows: Section 2 describes unimodal biometric systems, and the detailed implementation of different fusion levels. This section presents the architecture of the proposed scheme and the structure of implemented feature selection algorithm, as well. The detail of experimental results, including the database description and assessment protocols, is presented in Section 3, while Section 4 concludes this study.
2. Materials and Methods
2.1. Unimodal Biometric Systems
Face and iris as complementary biometric traits form the general structure of unimodal system in this study. They are considered as the most attractive areas for biometric schemes [29,30,31,32,33,34,35]. The unimodal face and iris system processing steps include preprocessing, feature extraction and producing matching scores. For face recognition systems, in the preprocessing step, Active Appearance Modeling (AAM toolbox) [36,37] is applied to detect face images based on the center position of the left and right irises. In fact, the precise center position of both irises is obtained by the toolbox to measure the angle of head roll that may happen during acquisition of face images. By using the center positions and the measured angle, both eyes are aligned in the face image. In addition, each image is resized to 60 × 60, and following this step the resized image undergoes histogram equalization (HE) and mean-variance normalization (MVN) [38] to reduce the effect of illumination. The facial features are then extracted using Log-Gabor transform. Generally, on the linear frequency scale, the structure of transfer function of the Log-Gabor transform is presented as [39]:
where is the filter center frequency, ω is the normalized radius from the center and k is the standard deviation of the angular component. In order to achieve the constant shape filter, the ratio should be held constant for varying values of . In this work, the Log-Gabor transform includes four different scales and eight orientations. The values are fixed based on the different trial results. The produced Log-Gabor transformed image is then down-sampled by a fixed ratio on the trials as six. Therefore, the final size of Log-Gabor transformed image is reduced to 40 × 80. Finally, match scores are produced using the Manhattan distance measurement.
On the other hand, common processing steps of an iris recognition system are segmentation, normalization, feature extraction, and feature matching [39,40,41]. In this work, the Hough transform is applied in the segmentation stage of the iris recognition system for localizing the circular iris and pupil region, occluding eyelids and eyelashes, and reflections. The extracted iris region is then normalized into a fixed rectangular block. In feature extraction step, the unique pattern of irises is extracted using Log-Gabor transform with the same strategy as in face recognition. Therefore, the final size of the Log-Gabor transformed iris image is set to 40 × 80. Manhattan distance measurement is employed in feature matching step to produce the match scores.
2.2. Fusion Techniques on Face and Iris Biometrics
Multimodal face-iris biometric system development is one of the most significant steps in the present work. In this section, our aim is to describe the details of different fusion techniques for face and iris modalities. Since the proposed scheme involves the consideration of score level, feature level and decision level fusion, we describe each fusion technique separately at different subsections.
2.2.1. Feature Level Fusion
Feature level fusion concatenates the original feature sets of different modalities and, therefore, this level of fusion involves richer information about the raw biometric data. In this study, Log-Gabor transform is applied to face and iris biometric in order to extract rich and complex information on these two modalities. Indeed, the complementary details of face and iris biometrics, especially when both are acquired simultaneously with a same device, encourage us to fuse them using feature level fusion. On the other hand, the concatenation of face and iris Log-Gabor feature sets leads to high dimension vectors, resulting in the decrease of multimodal biometric system performance. Therefore, designing a scheme to retain the complementary information of the fused features of modalities with the capability to solve the dimensionality and redundancy problems is motivated. Designing a robust scheme needs the consideration of an effective feature selection method to select the optimized set of features by removing the redundant and irrelevant data. Several feature selection methods have been applied in the field of biometrics on fusion of face and iris modalities such as PSO. Recently, Backtracking Search Algorithm (BSA), a novel population-based iterative evolutionary algorithm, has been applied successfully on many numerical optimization benchmark problems [25]. BSA is compared with six widely used optimization methods, including PSO. The result of this comparison shows that BSA is more successful than the others [25]. Figure 1 depicts the block diagram of feature selection and fusion of face and iris modalities. The proposed scheme includes BSA optimization algorithm in order to select the optimized feature sets. The extracted texture features of face using Log-Gabor can be concatenated with extracted Log-Gabor features of the left or right iris as in Figure 1a, and then the best set of features is selected using BSA. In addition, we investigate the effect of considering both irises (left and right) feature sets while they are combined with face features and optimized using the BSA feature selection method, as in Figure 1b on recognition performance of the system. The final size of the face and iris Log-Gabor vector for each image after concatenating the corresponding filtered images is 32000 × 1. Thus, in this paper we project the Log-Gabor vector of face and iris modalities separately onto a linear discriminant space using Linear Discriminant Analysis (LDA) in order to reduce the dimensionality and computational cost prior to feature concatenation, as shown in Figure 1. In LDA, the eigenvectors used for projection is constrained by L-1, where L is number of subjects. We then perform BSA on the concatenated features to further reduce the dimension of each fused sample. Finally, the matching step is performed as depicted in the figure.
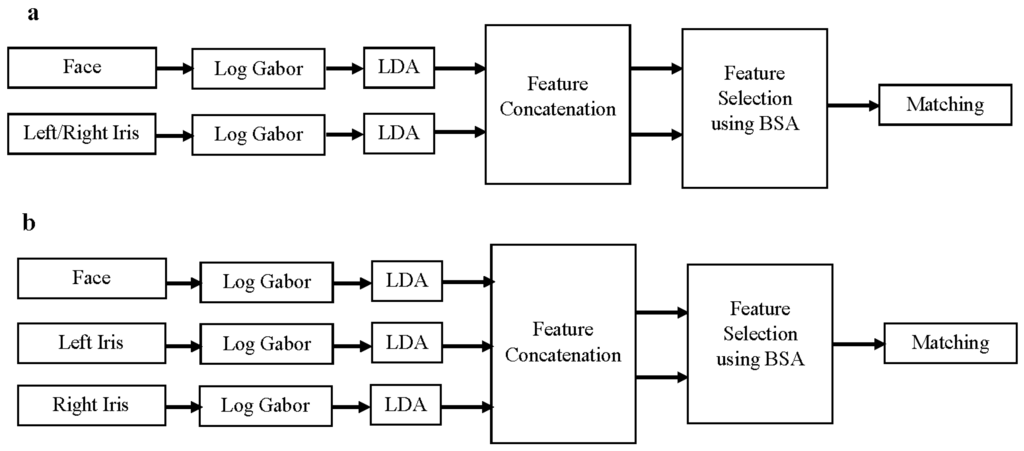
Figure 1.
The block diagram of face-iris feature level fusion. LDA: Linear Discriminant Analysis; BSA: Backtracking Search Algorithm.
2.2.2. Match Score Level Fusion
Matching score level fusion techniques include different rules that combine the produced scores between the pattern vectors of different modalities. Generally, different matchers may produce different scores such as distances or similarity measures with different probability distributions or accuracies [3]. This kind of fusion technique covers several simple or complicated algorithms in order to fuse the scores such as Sum Rule, Weighted Sum Rule, Product Rule, classification using SVM and the estimation of scores density. Recent studies have shown similar and equivalent performance from the aforementioned fusion techniques [3,4,8,15,18]. Match score level fusion for this study involves the combination of left and/or right irises of a certain person with the same individual face scores. Figure 2 depicts the structure of match score level fusion scheme when face scores are fused with only one of the irises, as shown in Figure 2a, and when face scores are fused with both irises, as in Figure 2b.
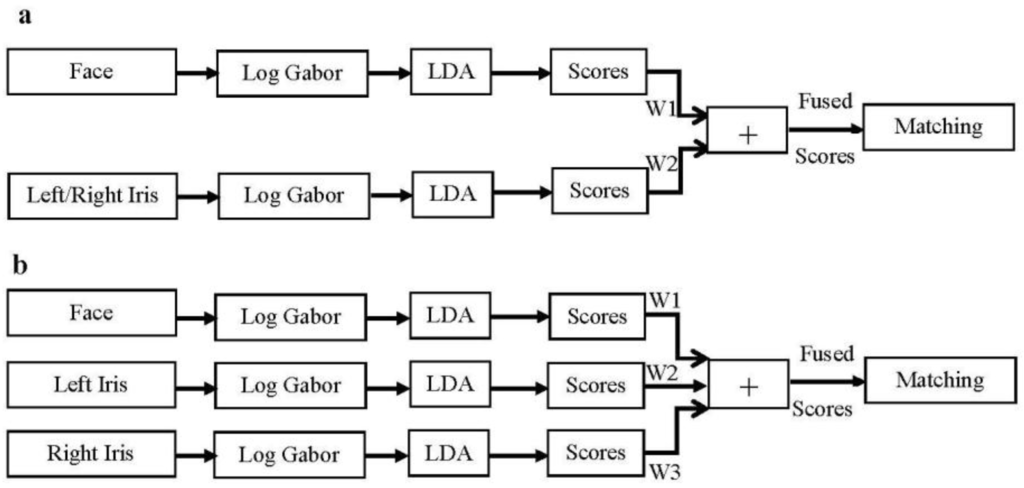
Figure 2.
The block diagram of face-iris score level fusion. W1, W2 and W3: assigned weights for different modalities.
In this study, the Weighted Sum Rule technique is used in order to combine face and iris scores. Finding appropriate weights for different modalities is considered as an important issue to perform efficient fusion and, subsequently, for performance enhancement. In this respect, in [26], a user-specific weight strategy is used to compute the weighted sum of scores from different modalities. In general, the computation of weights is done based on the Equal Error Rate (EER), the distribution of scores, the quality of the individual biometrics or empirical schemes [5]. The Weighted Sum Rule (ws) of different score matchers can be calculated as:
where are the assigned weights for different modalities, and are the computed scores using individual biometric systems. The present work assigns optimized weights to individual biometric systems using BSA feature selection algorithm.
2.2.3. Decision Level Fusion
In decision level fusion, each biometric matcher individually decides on the best match based on the provided input. In fact, the final decision is achieved by fusing the outputs of multiple matchers [10]. In general, a decision is represented by a logical number d ϵ {1,0}, where 1 means “accept” and 0 means “reject”. From the classifiers’ perspective, making any decision is performed by comparing the matching scores with a certain threshold . Generally, this level of fusion is less studied in the literature and is not popular practically due to providing less information content compared to matching scores of different classifiers and the risk of performance degradation compared to score level fusion. Majority voting, weighted majority voting, Bayesian decision fusion, Dempster-Shafer theory of evidence, as well as the AND rule and OR rule can be considered as common decision level fusion techniques.
In this study, we apply the idea of threshold-optimized decision level fusion proposed in [27] to implement an optimized face-iris multimodal decision level fusion scheme. The threshold-optimized decision level fusion combines the decisions by AND and OR rules in an optimal way in which it guaranties to improve the fused classifiers in terms of error rates. The scheme is specifically useful in the presence of outliers when the proposed OR rule is applied [27]. In face and iris recognition systems, outliers can be caused by extraordinary expressions, poses, mis-registration, occlusions, reflections, contrast, luminosity, off angles, rotation, blurring and focus problems. Therefore in this work, we applied the threshold-optimized scheme using OR rule decision level fusion to combine face and iris modalities as depicted in Figure 3. In fact, the optimal operation points of face ROC can be fused with the optimal operation points of only one of the irises, as in Figure 3a, and also with the optimal operation points of both irises, as in Figure 3b.
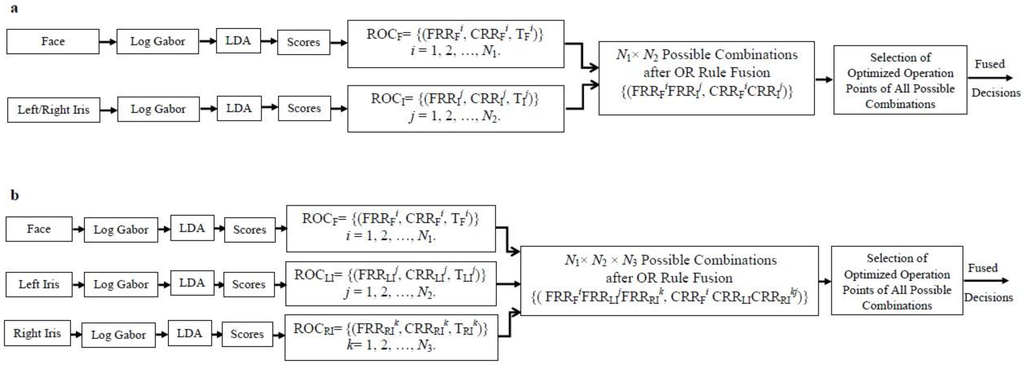
Figure 3.
The block diagram of face-iris decision level fusion. ROC: Receiver Operator Characteristics; FRR: False Accept Rate; CRR: Correct Reject Rate
Generally, each biometric system is described by a ROC (Receiver Operator Characteristics), i.e., the Genuine Accept Rate (GAR = 1 – False Reject Rate (FRR)) as a function of False Accept Rate (FAR), represented by GAR (FAR). The ROC is achieved by varying the threshold that discriminates the genuine and impostor matching scores, thus generating different GAR and FAR. Each point on the ROC, a certain pair (FAR, GAR) is called an operation point, corresponding to a specific threshold T of the matching scores. The threshold-optimized scheme fuses multiple ROCs together simply using the OR rule for performance enhancement. Therefore, the thresholds of matching scores are achieved when the optimal operation points on ROC are calculated.
Given N independent biometric systems, each characterized by its ROC, (FARi, GARi), i = 1, ..., N. In fact, the independency assumption is realistic in practice for fusion of different biometric modalities such as the face and iris. The optimized OR rule decision fusion under the independent assumption when the Correct Reject Rate for the impostors is defined as CRR = 1 − FAR can be described by:
That is the maximal value of the product of the correct rejection rates at a certain optimal combination of FRRi, i = 1, ..., N, which satisfies . In other words, at a fixed FRR the optimal operation points of the component ROCs are achieved by optimizing Equation (3). In fact, the optimization problem defined in Equation (3) is solved in a recursive manner by fusing two arbitrary ROCs in order to generate a new optimal ROC. Then the computed threshold-optimized ROC is fused with the next arbitrary component ROC, and so on. Therefore, each operation point on the final fused ROC corresponds to N-optimized thresholds from N classifiers.
2.2.4. Architecture of the Proposed Scheme
This section describes the general structure of optimal proposed scheme for the fusion of face and iris biometrics. The scheme combines score level, feature level and decision level fusion to investigate the effect of combining different fusion levels in designing robust fusion schemes for a face and iris multimodal system. The block diagram of proposed scheme is depicted in Figure 4. In fact, our aim here is to design an optimal scheme by taking advantage of three aforementioned fusion modes, and eventually obtain a more reliable and robust biometric system. Therefore, the proposed scheme considers the combination of the face and left and right irises due to their complementary information. Our investigation on feature level fusion clarifies that combining facial features with both irises and then selecting an optimal set of features by using an appropriate feature selection method such as BSA leads to the involvement of rich and complex information of biometric data, and thus improves the recognition performance. Therefore, as shown in the block diagram of the proposed scheme in Figure 4, we first extract the optimal subset of face and both iris features at feature level fusion.
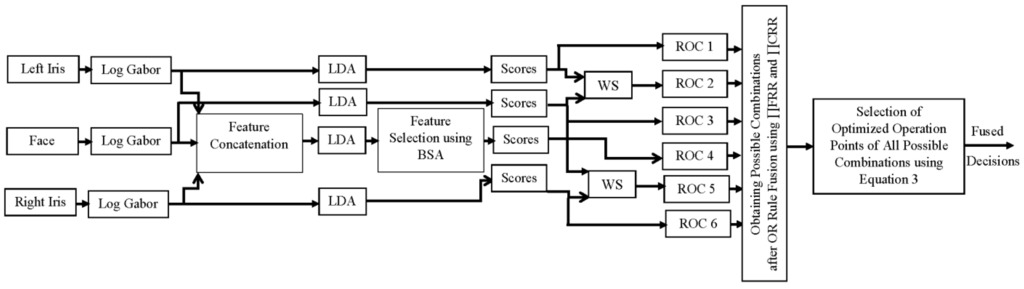
Figure 4.
The block diagram of face-iris Proposed Scheme.
On the other hand, score level fusion contains rich information about the biometric input and is easy to process. In many applications, score-level fusion is able to achieve optimal performance. Therefore, the scheme attempts to fuse the complementary details of both irises with the face as shown in Figure 4. The Weighted Sum Rule fusion technique (WS) is applied to fuse the left and right iris scores separately with the face scores to achieve two optimal set of fused scores.
Decision level fusion schemes are simple and clear from a mathematical perspective. The proposed scheme in this study combines the decisions using the OR rule in an optimal way, and guaranties an improvement in the fused classifiers in terms of error rates. The produced scores from each modality separately, the produced scores after combining and selecting the optimized features at feature level fusion, along with the produced scores at match score level fusion using WS are considered as six different sets of scores to fuse threshold-optimized ROCs. Therefore, in a recursive manner, two arbitrary ROCs are fused to generate a new optimal ROC. Then the computed threshold-optimized ROC is fused with the next arbitrary component ROC, and so on.
2.2.5. BSA Feature Selection Algorithm
BSA has been introduced by Civicioglu [25] to solve numerical optimization problems. BSA tries to reduce the effect of problems faced in Evolutionary Algorithms such as excessive sensitivity to control parameters, premature convergence and slow computation. This algorithm aims to search local and global optimum in an optimization problem. It contains a single parameter, a simple, effective and fast structure that is capable of solving multimodal problems with the ability to adapt itself to different numerical optimization problems. BSA memory uses previous-generation experiences to generate trial populations. The algorithm includes five processes that include initialization, selection-I, mutation, crossover and selection-II. Algorithm 1 shows the general structure of BSA algorithm.
| Algorithm 1 General Structure of Backtracking Search Algorithm [25]. |
| 1. Initialization |
| Repeat |
| 2. Selection-I |
| Generation of Trial Population |
| 3. Mutation |
| 4. Crossover |
| End |
| 5. Selection-II |
| Until stopping conditions are met |
The Initialization step of the BSA algorithm initializes the population P of size n and dimension d randomly. The initial fitness value for each individual in P is calculated according to the fitness function. The direction of search is calculated in the Selection-I step and is called historical population. In fact, historical population is swarm-memory of BSA in which, initially, it is determined randomly and at the beginning of each iteration is updated through advantages of P based on two random numbers and randomly changing the order of individuals in historical population. BSA generates a trial population T using crossover and mutation strategies in order to recombine the crossover and mutation steps. The initial form of T is generated in the Mutation step that derives partial benefit from its experiences from former generations. The final form of T is generated in the Crossover step using a binary matrix (map) of size n × d and a recombination of the crossover and mutation steps. BSA considers a boundary control mechanism to regenerate the individuals beyond the search-space limit. In the Selection-II step, the fitness value for each individual in T is calculated according to the fitness function and, if the fitness values of T are better than fitness values in P, then P is updated by T to form new individuals. Besides exploring local optimum, BSA finds the global optimum by selecting the best individual and fitness value among all individuals in the current iteration. Therefore, the global optimum is updated to be Pbest and the global optimum value is updated to be fitnessPbest.
Indeed, above-mentioned explanations show the relatively simple structure of BSA and, according to its simple principle, it can be used in the implementation of different optimization problems. We use BSA at feature level and score level fusion in this study to select the optimized subset of features and weights. In score level fusion, we consider the idea of using BSA to select the optimized weights for Weighted Sum Rule fusion technique in order to have a better evaluation on the face-iris multimodal system. Basically, assigning appropriate weights in an efficient way to the scores produced using different individuals biometric systems may guarantee the performance improvement of multimodal biometric system.
BSA initialization step initializes population (P) and historical population (oldp) randomly between 0 and 1. The size of P and oldp is considered as the number of weights needed for fusing the scores of different modalities. The initialized weights are then normalized using the constraint , where k is the number of weights and w is the weights. The fitness function is defined as follows for minimization:
where is the set of optimized weights for different modalities and is a set of Equal Error Rates computed from the corresponding modalities scores.
The trial population T is considered as the original equation in [25] based on the following formula:
where F controls the amplitude of search direction matrix and it is set experimentally.
In feature level fusion, the selection of features is based on a binary bit string of length M consisting of “0” and “1”. The value of M indicates the number of features, “0” means the feature is not selected and “1” means the feature is selected. Therefore the dimension of initial population (P) and historical population (oldp) is equal to M, and both are randomly initialized using binary numbers. In this study, we compute the distance between reference and testing samples to find the match scores using the Manhattan distance measurement and then evaluate the lowest distance values. Therefore, the fitness function is defined to maximize GAR at FAR = 0.01%.
The original trial population T of BSA is modified in this study in order to generate binary numbers based on the following formula:
where F controls the amplitude of search direction matrix and it is set experimentally, ˅ and ˄ are logical OR and AND operators.
The stopping condition for both binary and weight selection BSA is set to maximum number of iteration, or obtaining the optimal fitness value or failing to update the last best solution after 300 evaluations. If one of these three conditions is satisfied, the algorithm stops.
3. Results and Discussion
This section presents the detailed description of experimental setup, including database and assessment protocol applied in the current work for evaluating the proposed combined level fusion.
The experiments are carried out on a publicly available database called CASIA-Iris-Distance. The images in this database have been captured by a high-resolution camera, so both dual-eye iris and face patterns are available in the image region with detailed facial features that is appropriate for multimodal biometric information fusion [28]. Some samples of this database images are available in Figure 5.

Figure 5.
Sample of CASIA-Iris-Distance images.
The full database contains the total number of 2567 images of 142 subjects and the images have been acquired at a distance of ~3 m from the camera [28]. The average size of extracted iris in this work is 170 × 150, and the average number of pixels between irises is 760. The availability of different variations on CASIA-Iris-Distance database is summarized in Table 1.

Table 1.
Availability of Different Variations for Face and Irises in CASIA-Iris-Distance Database.
In this work, we extract both irises of each subject from the corresponding face image to fuse the face and iris modalities. In order to validate the performance of unimodal and multimodal schemes in this study, the whole database is divided into two independent sets called Set-I and Set-II. The first set is used as the validation set to fix the parameters of feature level, score level and decision level fusion. BSA parameters (population size, iteration, F and mix-rate) to find optimized features and weights, and also estimation of the optimized thresholds, have been set using the validation set. This set (Set-I) consists of 52 subjects, and each subject possesses 10 samples. In this study, F = 1, mix-rate-rate = 1, population size and iteration are both set to 30 for binary BSA. On the other hand, for the weight selection BSA, F = 1, mix-rate-rate = 1, population size and iteration are set to 20 and 100, respectively. The dimension of search space for the binary BSA is the number of extracted features and for the weight selection BSA, it is number of weights needed for performing weighted sum in the range of [0.00, 1.00] with two-digit precision.
In addition, we consider 90 subjects for Set-II, and each subject possesses 10 samples. This set is divided into two equal partitions presenting five reference and five testing data for all the subjects in the database. The partitioning of these two subsets (reference and testing) is performed 10 times without any overlapping. Accordingly, in each trial 450 reference samples (90 × 5) and 450 testing samples (90 × 5) are considered. Therefore, 450 genuine scores and 40,050 (90 × 89 × 5) imposter matching scores are used to validate the verification performance analysis in this study. The results are averaged over 10 different runs and reported as mean and standard deviations runs in the verification context using ROC curves, Total Error Rate (TER) and Genuine Acceptance Rate (GAR) at False Acceptance Rate (FAR) = 0.01%. Generally, TER is the sum of FAR and FRR, which is equal to twice the value of EER. The implementation of all unimodal and multimodal biometric systems is done using Matlab.
The first set of experiments analyzes the results of the implementation of different unimodal recognition systems such as the left iris, right iris, and face. The experimental results are demonstrated in Table 2 using Log-Gabor.

Table 2.
Verification Performance and Minimum Total Error Rates of Unimodal Systems. TER: Total Error Rate; GAR: Genuine Acceptance Rate; FAR: False Acceptance Rate.
In Table 2, the best verification performance belongs to the face unimodal system at 83.22%. On the other hand, for the iris unimodal system, as shown in the table, the right iris achieves a better verification and TER compared to the left iris. We consider the fusion of face and iris modalities using different levels of fusion in order to observe the effect of fusion on the recognition performance. Thus, as shown in Table 3, we continue the experiments at feature level fusion of face and iris biometrics. Firstly, we perform the feature fusion of face and iris biometrics implemented in Figure 1 without applying BSA, and then BSA as a feature selection strategy is used to investigate the effect of an optimal feature selection algorithm on the verification performance.

Table 3.
Verification Performance and Minimum Total Error Rates of Multimodal Biometric Systems at Feature Level Fusion.
It can be observed from Table 3 that the performance of BSA-based schemes is superior to the schemes without the BSA feature selection. The best performance in terms of TER and GAR is, respectively, 0.86% and 94.91%, and it is achieved using the feature level fusion scheme presented in Figure 1b with BSA. In order to examine the effectiveness of score level fusion on combining face and iris modalities, the experiments are carried out for this level of fusion and the results are reported in Table 4. Comparing Table 3 and Table 4 demonstrates that feature level fusion including optimal set of feature sets achieves a slightly better performance in terms of TER and verification when one of the irises is fused with facial features. However, as Table 4 indicates, match score level fusion outperforms feature level fusion when both irises are combined with the face. The best performance of match score level fusion in terms of TER and GAR is, respectively, 0.81% and 95.00%.

Table 4.
Verification Performance and Minimum Total Error Rates of Multimodal Biometric Systems at Score Level Fusion.
Table 5 shows the set of experiments at decision level fusion using the OR rule threshold-optimized scheme implemented in Figure 3. The best TER and GAR is obtained using Figure 3b when the face and both irises involved are at 0.58% and 96.87%. The optimized scheme achieves 1.87% and 1.96% improvement compared to the best verification performance of score level and feature level fusion schemes. Finally, the last set of experiment in Table 6 evaluates the proposed combined level fusion scheme and compares the corresponding result with achieved GAR and TER of each level of fusion separately.

Table 5.
Verification Performance and Minimum Total Error Rates of Multimodal Biometric Systems at Decision Level Fusion.

Table 6.
Verification Performance and Minimum Total Error Rates of Proposed Multimodal Biometric Systems and Different Levels of Fusions.
As the table demonstrates, the best performance is achieved using the proposed scheme since it involves the consideration of each level of fusion advantage for performing the fusion of face and iris biometrics. Specifically, as it is described in [27], the OR Rule threshold-optimized scheme is useful in the presence of outliers. Thus, involving this significant characteristic of the decision level fusion scheme in our proposed scheme, along with consideration of optimized features and weights at feature level and score level fusion, leads to a robust multimodal biometric system. Comparing the results obtained from different levels of fusion with our combined level fusion shows the superiority of the proposed scheme over all unimodal and multimodal schemes implemented in this study. The proposed scheme performance improvement in terms of GAR and TER is obtained as 98.93% and 0.27%, respectively.
On the other hand, in order to compare our proposed scheme with state-of-the-art face-iris fusion methods, we performed the fusion of face and iris using different fusion techniques on the CASIA-Iris Distance database in Table 7. The experimental results performed in Table 7 show the superiority of the proposed scheme over other face-iris multimodal biometric systems implemented in this study. Recently, the Support Vector Machine (SVM), mainly as a popular method for classification, is used in the area of statistics learning theory. Generally, SVM is targeted based on structural minimization principle and maps the training data into a higher dimensional feature using the kernel trick to construct an optimal hyperplane with large separating margin between two classes of the labeled data. In this work, the radial basis function (RBF) has been applied as the basic kernel function by iterative trials.

Table 7.
Verification Performance and Minimum Total Error Rates of Different Multimodal Biometric Systems and Proposed Scheme. PSO: Particle Swarm Optimization; SVM: Support Vector Machine.
The ROC analysis of the face unimodal system and multimodal biometric systems, including the proposed scheme, is demonstrated in Figure 6. The ROC analysis covers part (b) of the implemented schemes for each level of fusion.
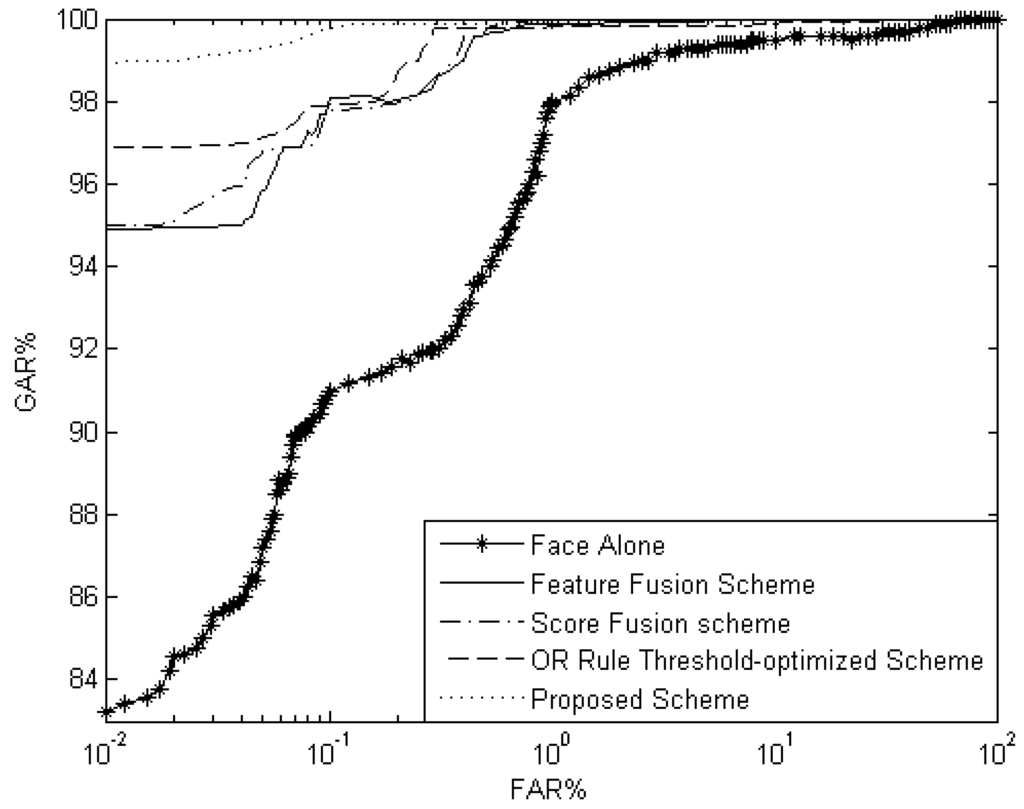
Figure 6.
ROC curves of face unimodal and multimodal systems of different schemes.
On the other hand, Figure 7 compares the ROC analysis of proposed scheme and the OR rule threshold-optimized decision level fusion.
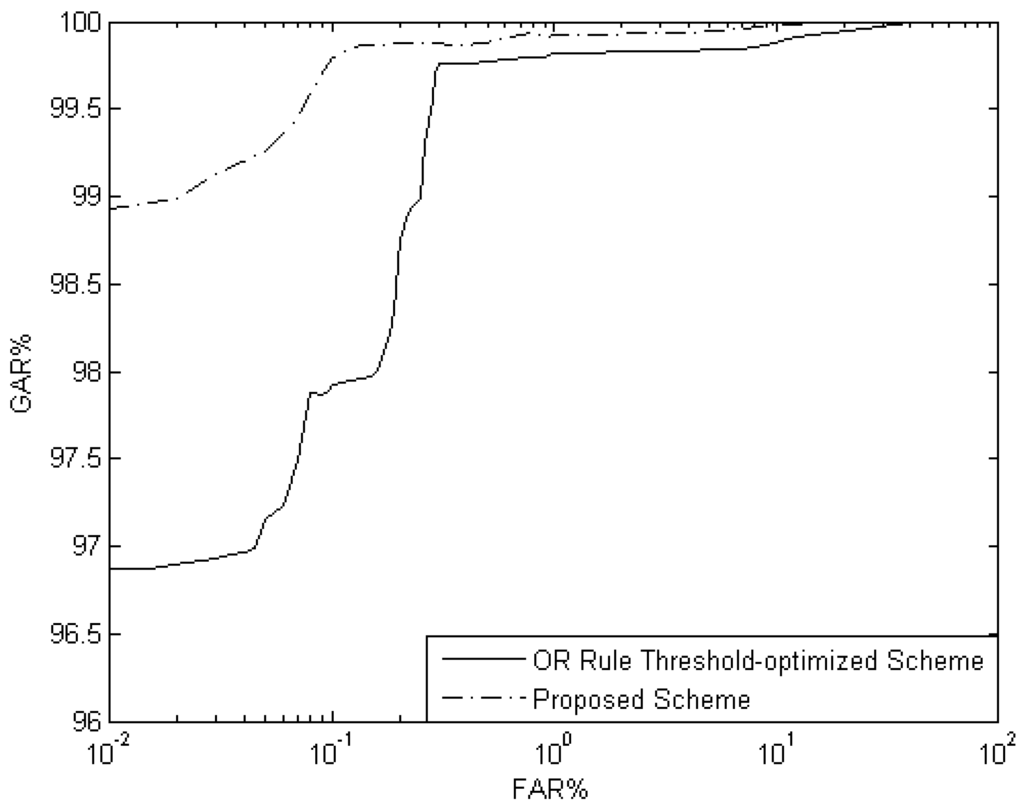
Figure 7.
ROC curves of threshold-optimized and proposed schemes.
As observed from the ROC curves, the proposed scheme outperforms unimodal and all multimodal schemes implemented in this study.
4. Conclusions
In this paper, we have investigated the problem of combining different levels of fusion in a face-iris multimodal biometric system framework. Our aim here was to implement different fusion schemes and then compare them with a scheme, including their complementary advantages, in terms of performance. Therefore, we have designed a robust multimodal face-iris biometric system by combining the advantages of score level, feature level and decision level fusion. The proposed scheme has applied Log-Gabor transform as the feature extraction method on face and iris modalities and, subsequently, the corresponding features and scores have been employed to construct different fusion schemes. We specifically have applied a threshold-optimized scheme at the decision level fusion step of the proposed scheme that is useful in the presence of outliers. In addition, BSA as an effective and recent feature selection method has been used with feature and score level fusion of the proposed scheme to construct a more robust biometric system; this has been done by reducing the number of features and improving the performance, and also optimizing the weights. In fact, based on the experimental results provided in this study, we can attract the attention of new perspectives for face-iris multimodal biometric systems that consider the combination of different levels of fusion, in particular decision level fusion, to efficiently represent a robust system.
Author Contributions
The authors performed the experiments and analyzed the results together. Introduction, unimodal and multimodal biometric systems, feature selection algorithm sections were written by Omid Sharifi; while experimental results, discussion and conclusion sections were written by Maryam Eskandari.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Liau, H.F.; Isa, D. Feature selection for support vector machine-based face-iris multimodal biometric system. Expert Syst. Appl. 2011, 38, 11105–11111. [Google Scholar] [CrossRef]
- Proenca, H.P. Towards Non-Cooperative Biometric Iris Recognition. Ph.D. Thesis, University of Beira Interior Department of Computer Science, Covilhã, Portugal, 2006. [Google Scholar]
- Nandakumar, K.; Chen, Y.; Dass, S.C.; Jain, A.K. Likelihood ratio-based biometric score fusion. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 30, 342–347. [Google Scholar] [CrossRef] [PubMed]
- Ross, A.; Nandakumar, K.; Jain, A.K. Handbook of Multibiometrics; Springer-Verlag: Berlin, Germany, 2006. [Google Scholar]
- Raghavendra, R.; Dorizzi, B.; Rao, A.; Kumar, G.H. Designing efficient fusion schemes for multimodal biometric system using face and palmprint. Pattern Recognit. 2011, 44, 1076–1088. [Google Scholar] [CrossRef]
- Lumini, A.; Nanni, L. Over-complete feature generation and feature selection for biometry. Expert Syst. Appl. 2008, 35, 2049–2055. [Google Scholar] [CrossRef]
- Gökberk, B.; Okan İrfanoğlu, M.; Akarun, L.; Alpaydın, E. Learning the best subset of local features for face recognition. Pattern Recognit. 2007, 40, 1520–1532. [Google Scholar] [CrossRef]
- Eskandari, M.; Toygar, Ö.; Demirel, H. Feature Extractor Selection for Face-Iris Multimodal Recognition. Signal Image Video Process. 2014, 8, 1189–1198. [Google Scholar] [CrossRef]
- Zhang, D.; Jing, X.; Yang, J. Biometric Image Discrimination (BID) Technologies; IGI Global: Hershey, PA, USA, 2006. [Google Scholar]
- Nandakumar, K. Integration of Multiple Cues in Biometric Systems. Master’s Thesis, Michigan State University, East Lansing, MI, USA, 2005. [Google Scholar]
- Lam, L.; Suen, C.Y. Application of Majority Voting to Pattern Recognition: An Analysis of Its Behavior and Performance. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 1997, 27, 553–568. [Google Scholar] [CrossRef]
- Lam, L.; Suen, C.Y. Optimal Combination of Pattern Classifiers. Pattern Recognit. Lett. 1995, 16, 945–954. [Google Scholar] [CrossRef]
- Xu, L.; Krzyzak, A.; Suen, C.Y. Methods for Combining Multiple Classifiers and their Applications to Handwriting Recognition. IEEE Trans. Syst. Man Cybernet. 1992, 22, 418–435. [Google Scholar] [CrossRef]
- Daugman, J. Combining Multiple Biometrics. Available online: http://www.cl.cam.ac.uk/users/jgd1000/combine/combine.html (assessed on 28 October 2016).
- Eskandari, M.; Toygar, Ö. Fusion of face and iris biometrics using local and global feature extraction methods. Signal Image Video Process. 2014, 8, 995–1006. [Google Scholar] [CrossRef]
- Wang, F.; Han, J. Multimodal biometric authentication based on score level fusion using support vector machine. Opto Electron. Rev. 2009, 17, 59–64. [Google Scholar] [CrossRef]
- Vasta, M.; Singh, R.; Noore, A. Integrating image quality in 2v-SVM biometric match score fusion. Int. J. Neural Syst. 2007, 17, 343–351. [Google Scholar]
- Eskandari, M.; Toygar, Ö.; Demirel, H. A new approach for Face-Iris multimodal biometric recognition using score fusion. Int. J. Pattern Recognit. Artif. Intell. 2013, 27. [Google Scholar] [CrossRef]
- Wang, Y.; Tan, T.; Wang, Y.; Zhang, D. Combining face and iris biometric for identity verification. In Proceedinmgs of the 4th International Conference on Audio and Video Based Biometric Person Authentication, Guildford, UK, 9–11 June 2003; pp. 805–813.
- Sim, H.M.; Asmunia, H.; Hassan, R.; Othman, R.M. Multimodal biometrics: Weighted score level fusion based on non-ideal iris and face images. Expert Syst. Appl. 2014, 41, 5390–5404. [Google Scholar] [CrossRef]
- Eskandari, M.; Toygar, Ö. Selection of Optimized features and weights on face-iris fusion using distance images. Comput. Vis. Image Underst. 2015, 137, 63–75. [Google Scholar] [CrossRef]
- Jing, X.Y.; Yao, Y.F.; Yang, J.Y.; Li, M.; Zhang, D. Face and palmprint pixel level fusion and kernel DCV-RBF classifier for small sample biometric recognition. Pattern Recognit. 2007, 40, 3209–3224. [Google Scholar] [CrossRef]
- Yao, Y.; Jing, X.; Wong, H. Face and palmprint feature level fusion for single sample biometric recognition. Neurocomputing 2007, 70, 1582–1586. [Google Scholar] [CrossRef]
- Xiao, Z.; Guo, C.; Yu, M.; Li, Q. Research on log gabor wavelet and its application in image edge detection. In Proceedings of 6th International Conference on Signal Processing (ICSP-2002), Beijing, China, 26–30 August 2002; pp. 592–595.
- Civicioglu, P. Backtracking Search Optimization Algorithm for numerical optimization problems. Appl. Math. Comput. 2013, 219, 8121–8144. [Google Scholar] [CrossRef]
- Jain, A.K.; Ross, A. Learning User-specific Parameters in a Multibiometric System. In Proceedings of International Conference on Image Processing, New York, NY, USA, 22–25 September 2002; pp. 57–60.
- Tao, Q.; Veldhuis, R. Threshold-Optimized decision-level fusion and its application to biometrics. Pattern Recognit. 2009, 42, 823–836. [Google Scholar] [CrossRef]
- Biometrics Ideal Test. Available online: http://biometrics.idealtest.org/dbDetailForUser.do?id=4 (assessed on 30 August 2013).
- Patil, H.; Kothari, A.; Bhurchandi, K. 3-D face recognition: Features, databases, algorithms and challenges. Artif. Intell. Rev. 2015, 44, 393–441. [Google Scholar] [CrossRef]
- Subburaman, V.B.; Marcel, S. Alternative search techniques for face detection using location estimation and binary features. Comput. Vis. Image Underst. 2013, 117, 551–570. [Google Scholar] [CrossRef]
- Gul, G.; Hou, Z.; Chen, C.; Zhao, Y. A dimensionality reduction method based on structured sparse representation for face recognition. Artif. Intell. Rev. 2016. [Google Scholar] [CrossRef]
- Bowyer, K.W.; Hollingsworth, K.; Flynn, P.J. Image understanding for iris biometrics: A survey. Comput. Vis. Image Underst. 2008, 110, 281–307. [Google Scholar] [CrossRef]
- Matey, J.R.; Broussard, R.; Kennell, L. Iris image segmentation and sub-optimal images. Image Vis. Comput. 2010, 28, 215–222. [Google Scholar] [CrossRef]
- Galbally, J.; Ross, A.; Gomez-Barrero, M.; Fierrez, J.; Ortega-Garcia, J. Iris image reconstruction from binary templates: An efficient probabilistic approach based on genetic algorithms. Comput. Vis. Image Underst. 2013, 117, 1512–1525. [Google Scholar] [CrossRef]
- Neves, J.; Narducci, F.; Barra, S.; Proença, H. Biometric recognition in surveillance scenarios: A survey. Artif. Intell. Rev. 2016. [Google Scholar] [CrossRef]
- Huang, C.; Ding, X.; Fang, C. Pose robust face tracking by combining view-based AAMs and temporal filters. Comput. Vis. Image Underst. 2012, 116, 777–792. [Google Scholar] [CrossRef]
- Active Appearance Modeling. Available online: http://cvsp.cs.ntua.gr/software/AAMtools/ (accessed on 20 April 2013).
- Pujol, P.; Macho, D.; Nadeu, C. On real-time mean-and- variance normalization of speech recognition features. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP2006), Toulouse, France, 14–19 May 2006; pp. 773–776.
- Arora, S.; Londhe, N.D.; Acharya, A.K. Human Identification based on Iris Recognition for Distance Images. Int. J. Comput. Appl. 2012, 45, 32–39. [Google Scholar]
- Masek, L.; Kovesi, P. MATLAB Source Code for a Biometric Identification System Based on Iris Patterns. Bachelor’s thesis, the School of Computer Science and Software Engineering, The University of Western Australia, Crawley, Australia, 2003. [Google Scholar]
- Tan, C.W.; Kumar, A. A Unified Framework for Automated Iris Segmentation Using Distantly Acquired Face Images. IEEE Trans. Image Process. 2012, 21, 4068–4079. [Google Scholar] [CrossRef] [PubMed]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).