Morphometric Asymmetry of Frustule Outlines in the Pennate Diatom Luticola poulickovae (Bacillariophyceae)
Abstract
:1. Introduction
2. Materials and Methods
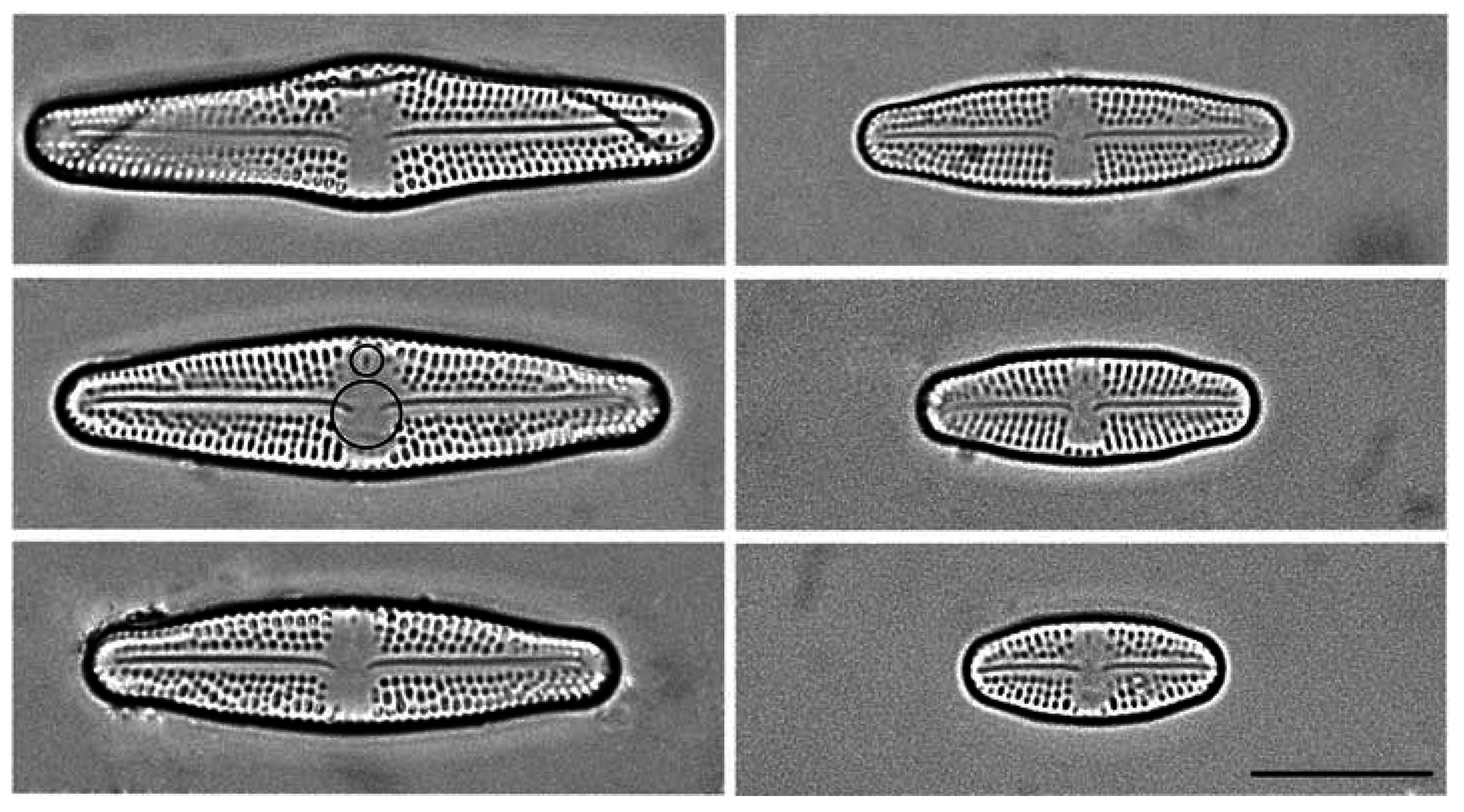
2.1. Culturing and Data Acquisition
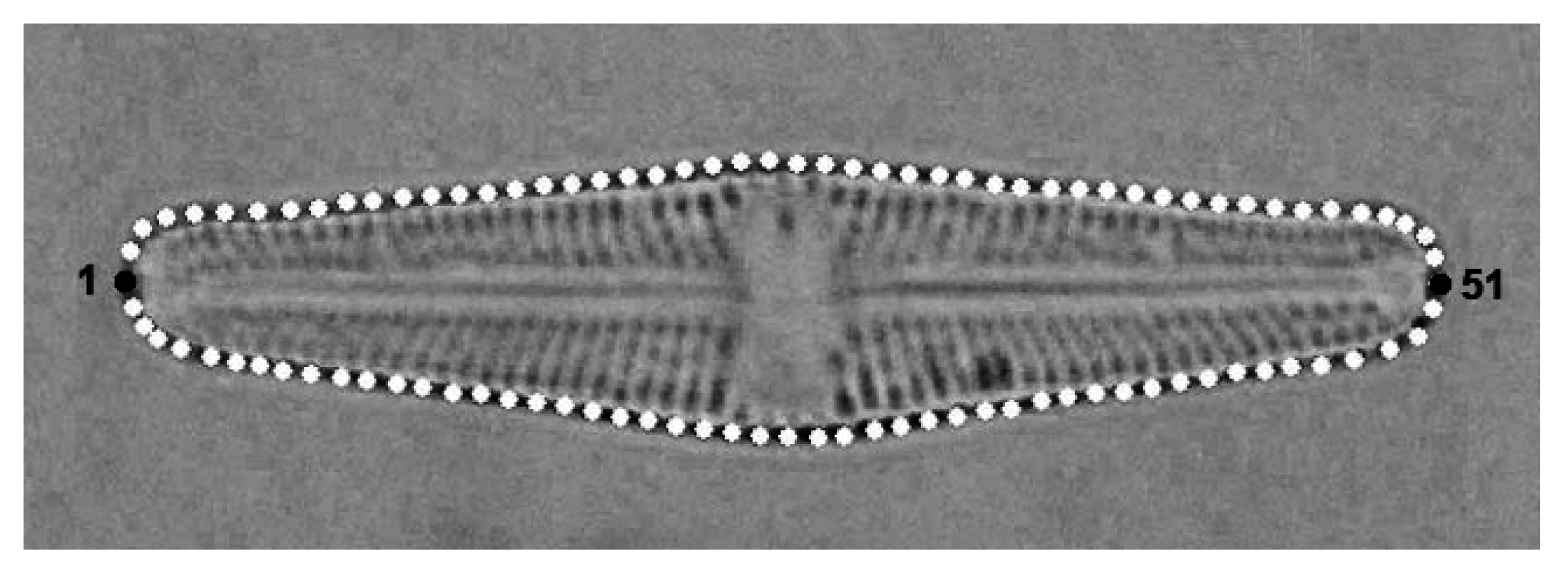
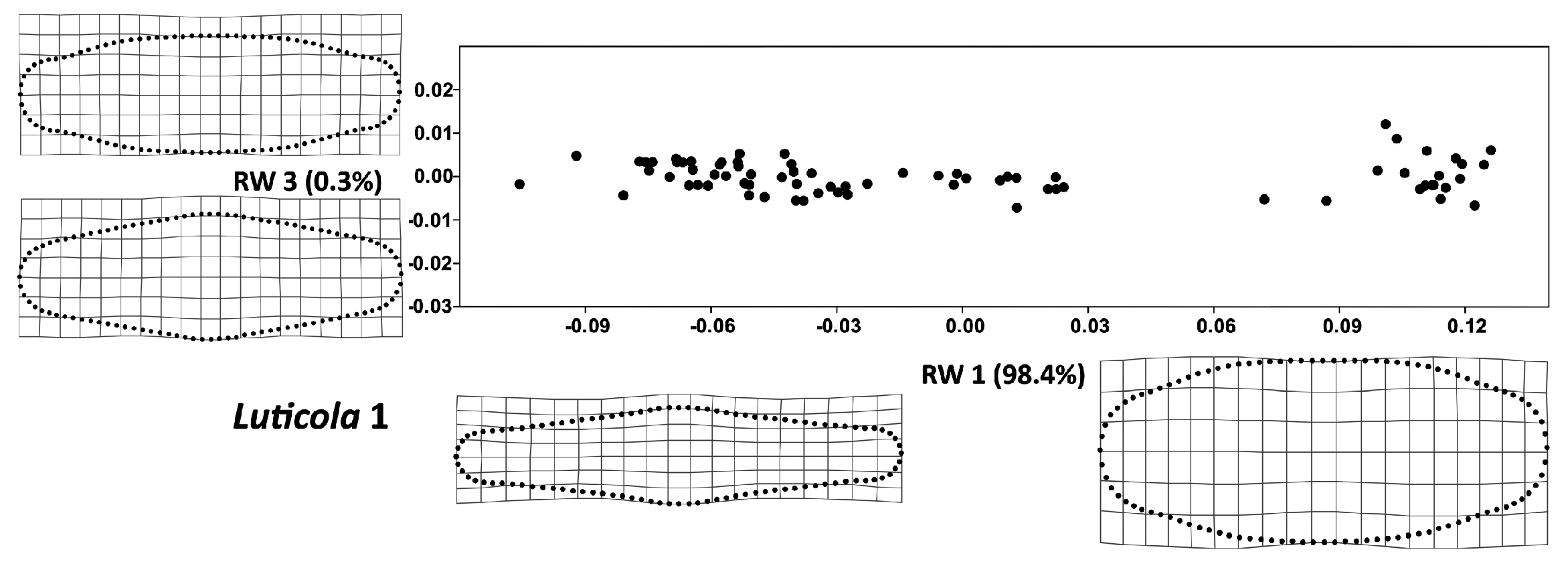
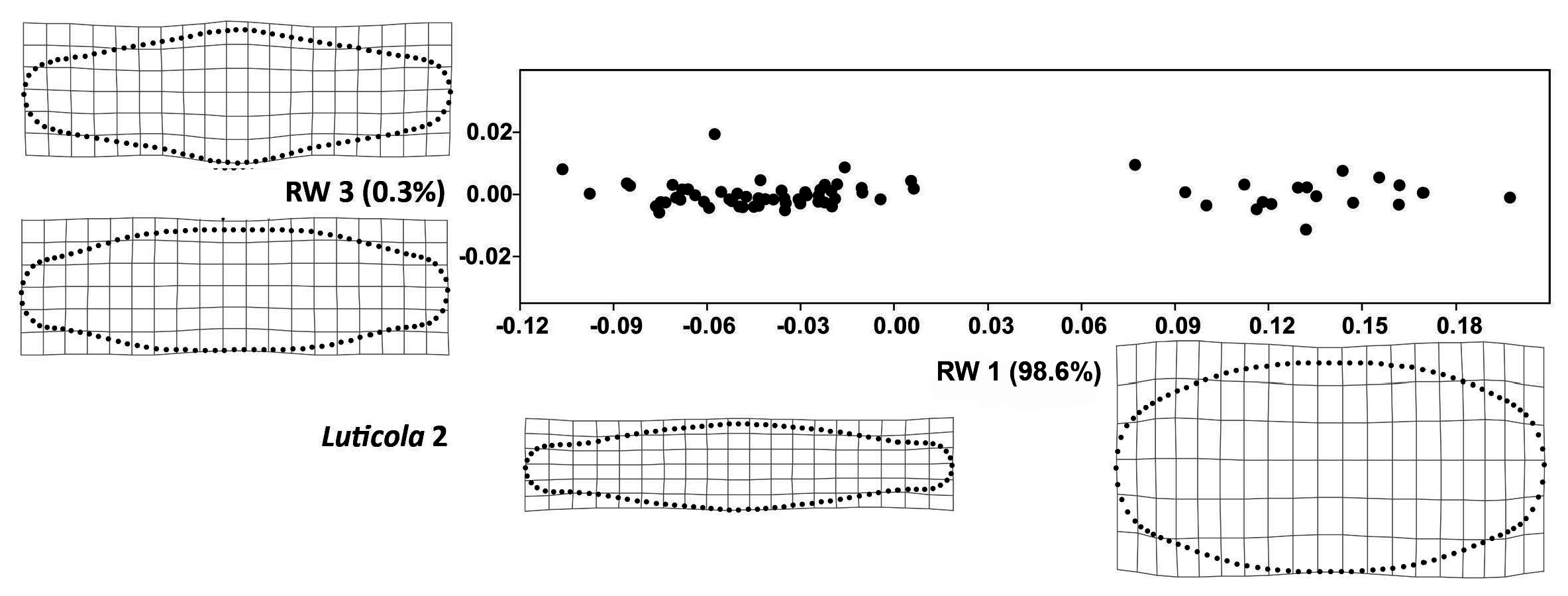
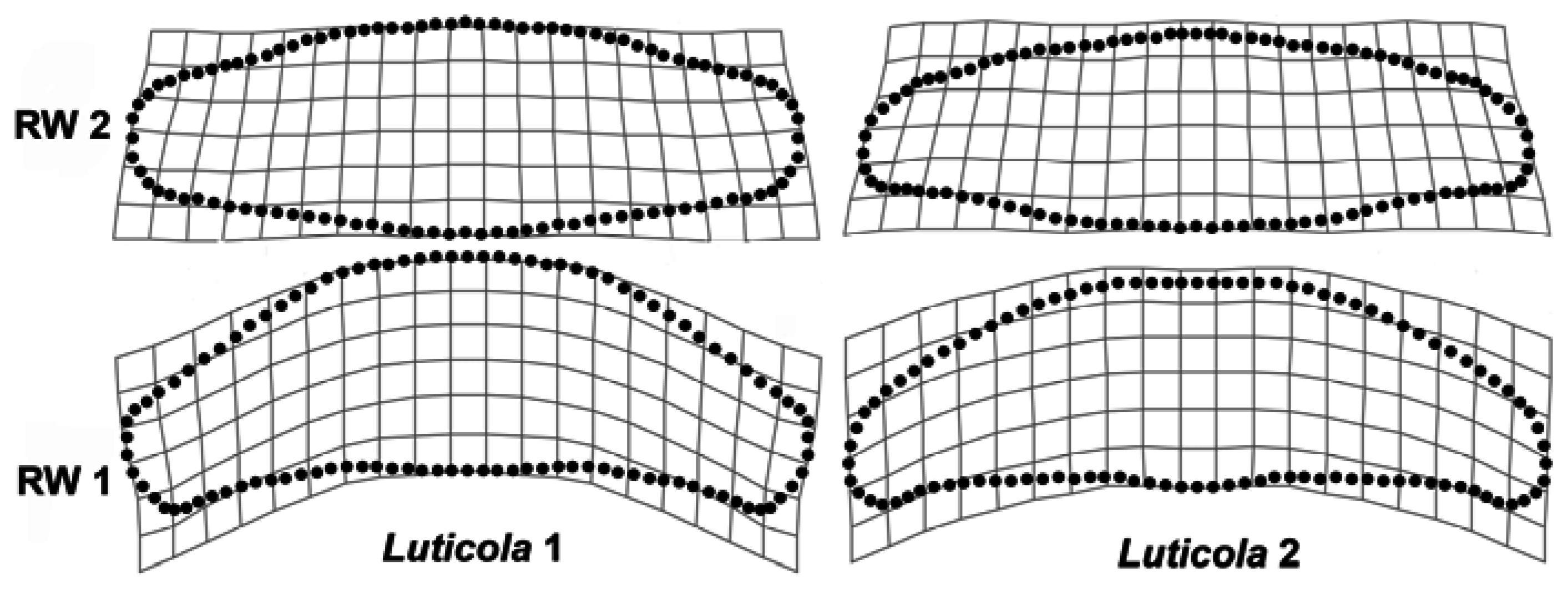
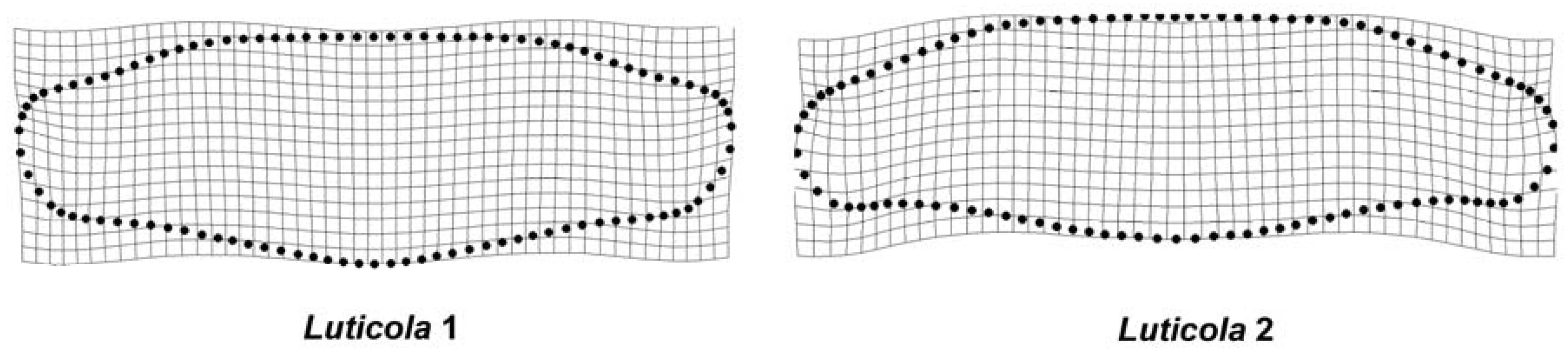
2.2. Geometric Morphometrics
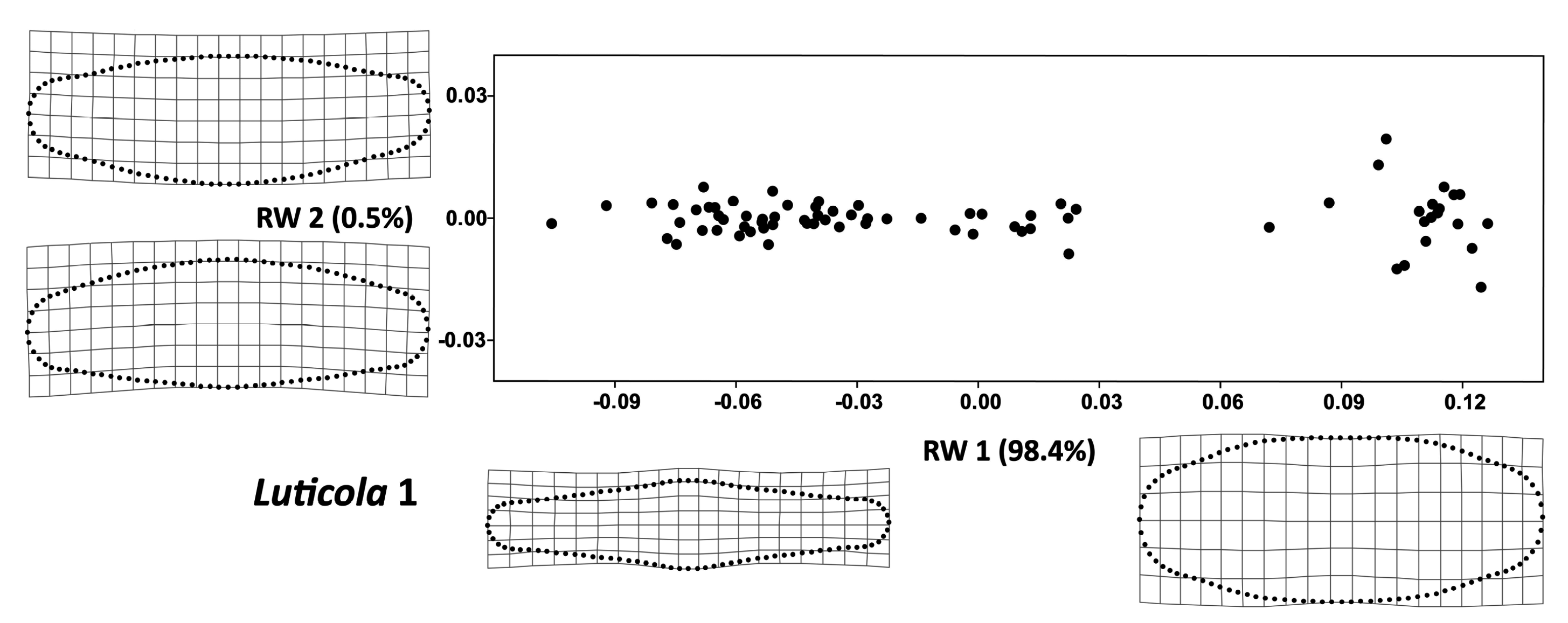
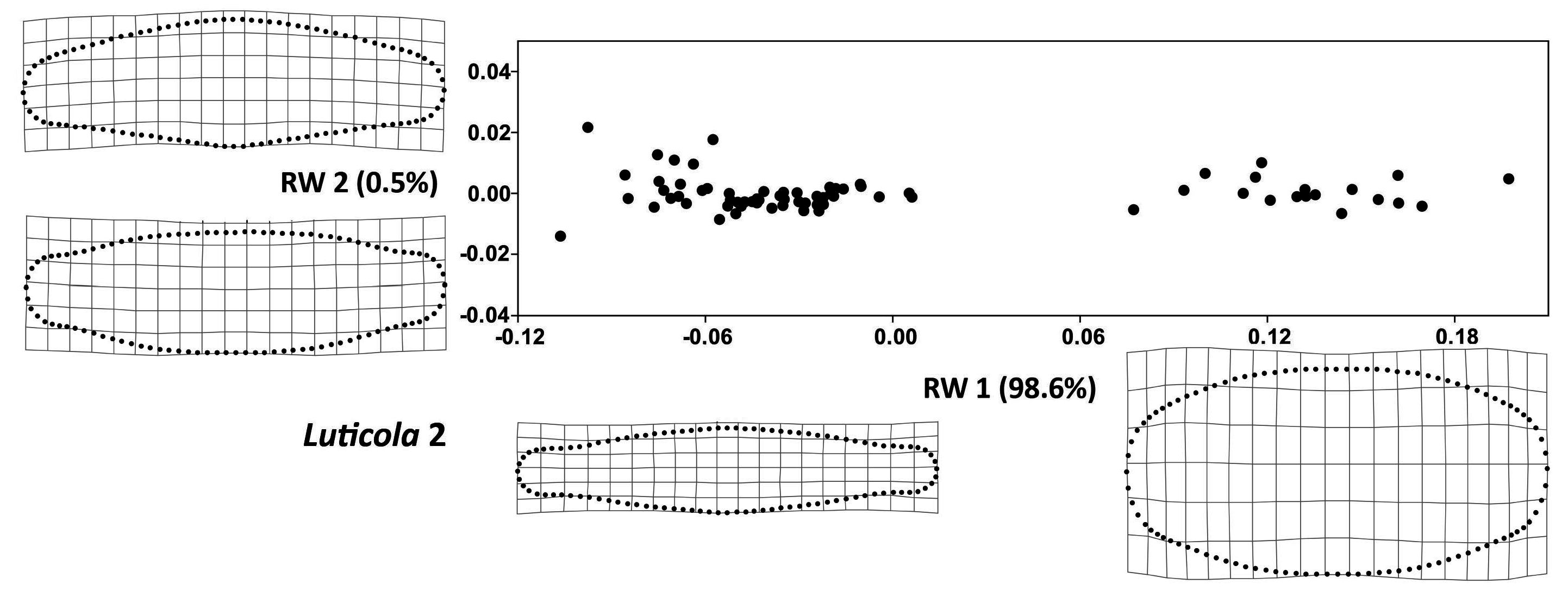
3. Results
4. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Neustupa, J.; Hodac, L. Changes in shape of the coenobial cells of an experimental strain of Pediastrum duplex var. duplex (Chlorophyta) reared at different pHs. Preslia 2005, 77, 439–452. [Google Scholar]
- Lenarczyk, J. Morphological plasticity of the microscopic green alga Pseudopediastrum boryanum (Chlorophyceae) under varying nutrient concentrations. Nova Hedwig. 2016, 102, 373–390. [Google Scholar] [CrossRef]
- Verbruggen, H.; Clerck, O.D.; Coppejans, E. Deviant segments hamper a morphometric approach towards Halimeda taxonomy. Cryptogam. Algol. 2005, 26, 259–274. [Google Scholar]
- Brook, A.J. The Biology of Desmids, 16th ed.; University of California Press: Berkeley, CA, USA, 1981; p. 276. [Google Scholar]
- Savriama, Y.; Neustupa, J.; Klingenberg, C.P. Geometric morphometrics of symmetry and allometry in Micrasterias rotata (Zygnemophyceae, Viridiplantae). Nova Hedwig. Beih. 2010, 136, 43–54. [Google Scholar]
- Neustupa, J. Patterns of symmetric and asymmetric morphological variation in unicellular green microalgae of the genus Micrasterias (Desmidiales, Viridiplantae). Fottea 2013, 13, 53–63. [Google Scholar] [CrossRef]
- Afanasieva, M.S. Radiolarian skeleton: Morphology of spines, internal framework, and primary sphere. Paleontol. J. 2007, 41, 1–14. [Google Scholar] [CrossRef]
- Potapova, M.; Hamilton, P.B. Morphological and ecological variation within the Achnanthidium minutissimum (Bacillariophyceae) species complex. J. Phycol. 2007, 43, 561–575. [Google Scholar] [CrossRef]
- Klingenberg, C.P. Analyzing fluctuating asymmetry with geometric morphometrics: Concepts, methods, and applications. Symmetry 2015, 7, 843–934. [Google Scholar] [CrossRef]
- Klingenberg, C.P.; Barluenga, M.; Meyer, A. Shape analysis of symmetric structures: Quantifying variation among individuals and asymmetry. Evolution 2002, 56, 1909–1920. [Google Scholar] [CrossRef] [PubMed]
- Graham, J.H.; Raz, S.; Hel-Or, H.; Nevo, E. Fluctuating asymmetry: Methods, theory and applications. Symmetry 2010, 2, 466–540. [Google Scholar] [CrossRef]
- Savriama, Y.; Klingenberg, C.P. Beyond bilateral symmetry: Geometric morphometric methods for any type of symmetry. BMC Evol. Biol. 2011, 11, 280. [Google Scholar] [CrossRef] [PubMed]
- Schmid, A.M. Aspects of morphogenesis and function of diatom cell walls with implications for taxonomy. Protoplasma 1994, 181, 43–60. [Google Scholar] [CrossRef]
- Hostetter, H.P.; Hoshaw, R.W. Asexual developmental patterns of the diatom Stauroneis anceps in culture. J. Phycol. 1972, 8, 289–296. [Google Scholar]
- Hostetter, H.P.; Rutherford, K.D. Polymorphism of the diatom Pinnularia brebissonii in culture and a field collection. J. Phycol. 1976, 12, 140–146. [Google Scholar]
- Round, F.E.; Crawford, R.M.; Mann, D.G. The Diatoms: Biology and Morphology of the Genera; Cambridge University Press: Cambridge, UK, 1990; p. 131. [Google Scholar]
- Edgar, S.M.; Theriot, E.C. Phylogeny of Aulacoseira (Bacillariophyta) based on molecules and morphology. J. Phycol. 2004, 40, 772–788. [Google Scholar] [CrossRef]
- Veselá, J.; Neustupa, J.; Pichrtová, M.; Poulíčková, A. Morphometric study of Navicula morphospecies (Bacillariophyta) with respect to diatom life cycle. Fottea 2009, 9, 307–316. [Google Scholar]
- Pappas, J.L.; Kociolek, J.P.; Stoermer, E.F. Quantitative morphometric methods in diatom research. Nova Hedwig. Beih. 2014, 143, 281–306. [Google Scholar]
- Edgar, R.K.; Saleh, A.I.; Edgar, S.M. A morphometric diagnosis using continuous characters of Pinnunavis edkuensis, sp. nov. (Bacillariophyta: Bacillariophyceae), a brackish-marine species from Egypt. Phytotaxa 2015, 212, 1–56. [Google Scholar] [CrossRef]
- Theriot, E.C.; Ashworth, M.; Ruck, E.; Nakov, T.; Jansen, R.K. A preliminary multigene phylogeny of the diatoms (Bacillariophyta): Challenges for future research. Plant Ecol. Evol. 2010, 143, 278–296. [Google Scholar] [CrossRef]
- Spaulding, S.A.; Lubinski, D.J.; Potapova, M. Diatoms of the United States. Available online: http://westerndiatoms.colorado.edu (accessed on 5 December 2016).
- Woodard, K.; Kulichová, J.; Poláčková, T.; Neustupa, J. Morphometric allometry of representatives of three naviculoid genera throughout their life cycle. Diatom Res. 2016, 31, 231–242. [Google Scholar] [CrossRef]
- Falasco, E.; Bona, F.; Badino, G.; Hoffmann, L.; Ector, L. Diatom teratological forms and environmental alterations: A review. Hydrobiologia 2009, 623, 1–35. [Google Scholar] [CrossRef]
- Yang, J.R.; Duthie, H.C. Morphology and ultrastructure of teratological forms of the diatoms Stephanodiscus niagarae and S. parvus (Bacillariophyceae) from Hamilton Harbour (Lake Ontario, Canada). Hydrobiologia 1993, 269, 57–66. [Google Scholar] [CrossRef]
- Peres-Weerts, F. Mise en E´vidence des Effets Toxiques des Me´taux Lourds sur les Diatome´es par L’e´tude des Formes Te´ratoge`nes; Agence de l’Eau Artois Picardie: Douai, France, 2000; p. 24. (In French) [Google Scholar]
- Poulíčková, A. Morphology, cytology and sexual reproduction in the aerophytic cave diatom Luticola dismutica (Bacillariophyceae). Preslia 2008, 80, 87–99. [Google Scholar]
- Andersen, R.A. Algal Culturing Techniques; Elsevier Academic Press: London, UK, 2005; p. 578. [Google Scholar]
- Poulíčková, A.; Mann, D.G. Sexual reproduction in Navicula cryptocephala (Bacillariophyceae). J. Phycol. 2006, 42, 872–886. [Google Scholar] [CrossRef]
- Rohlf, F.J. The TPS series of software. Hystrix Ital. J. Mammal. 2015, 26, 9–12. [Google Scholar]
- Bookstein, F.L. Morphometric Tools for Landmark Data: Geometry and Biology; Cambridge University Press: Cambridge, UK, 1997; p. 436. [Google Scholar]
- Adams, D.C.; Otárola-Castillo, E. Geomorph: An R package for the collection and analysis of geometric morphometric shape data. Methods Ecol. Evol. 2013, 4, 393–399. [Google Scholar] [CrossRef]
- R Development Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2013; Available online: https://www.r-project.org/ (accessed on 9 July 2016).
- Klingenberg, C.P.; McIntyre, G.S. Geometric morphometrics of developmental instability: Analyzing patterns of fluctuating asymmetry with Procrustes methods. Evolution 1998, 52, 1363–1375. [Google Scholar] [CrossRef]
- Collyer, M.L.; Sekora, D.J.; Adams, D.C. A method for analysis of phenotypic change for phenotypes described by high-dimensional data. Heredity 2014, 115, 357–365. [Google Scholar] [CrossRef] [PubMed]
- Slice, D.E. Modern morphometrics. In Modern Morphometrics in Physical Anthropology; Slice, D.E., Ed.; Klewer Press: New York, NY, USA, 2005; pp. 1–45. [Google Scholar]
- Hammer, Ø.; Harper, D.A.T.; Ryan, P.D. PAST: Paleontological statistics software package for education and data analysis. Palaeontol. Electron. 2001, 4, 1–9. [Google Scholar]
- Mann, D.G. A note on valve formation and homology in the Diatom Genus Cymbella. Ann. Bot. 1981, 47, 267–269. [Google Scholar]
- Savriama, Y.; Stige, L.C.; Gerber, S.; Pérez, T.; Alibert, P.; David, B. Impact of sewage pollution on two species of sea urchins in the Mediterranean Sea (Cortiou, France): Radial asymmetry as a bioindicator of stress. Ecol. Indic. 2015, 54, 39–47. [Google Scholar] [CrossRef]
- Zabrodsky, H.; Peleg, S.; Avnir, D. Continuous symmetry measures. J. Am. Chem. Soc. 1992, 114, 7843–7851. [Google Scholar] [CrossRef]
- Graham, J.H.; Whitesell, M.J.; Flemming, M.; Hel-Or, H.; Nevo, E.; Raz, S. Fluctuating asymmetry of plant leaves: Batch processing with LAMINA and continuous symmetry measures. Symmetry 2015, 7, 255–268. [Google Scholar] [CrossRef]
- De Groote, I.; Lockwood, C.A.; Aiello, L.C. Technical note: A new method for measuring long bone curvature using 3D landmarks and semi-landmarks. Am. J. Phys. Anthropol. 2010, 141, 658–664. [Google Scholar] [CrossRef] [PubMed]
- Graham, J.H.; Emlen, J.M.; Freeman, D.C.; Leamy, L.J.; Kieser, J.A. Directional asymmetry and the measurement of developmental instability. Biol. J. Linn. Soc. 1998, 64, 1–16. [Google Scholar] [CrossRef]
- Lezcano, A.H.; Quiroga, M.L.R.; Liberoff, A.L.; van der Molen, S. Marine pollution effects on the southern surf crab Ovalipes trimaculatus (Crustacea: Brachyura: Polybiidae) in Patagonia Argentina. Mar. Pollut. Bull. 2015, 91, 524–529. [Google Scholar] [CrossRef] [PubMed]
- Trono, D.J.V. Fluctuating asymmetry and developmental instability in Protoreaster nodosus (Chocolate Chip Sea Star) as a biomarker for environmental stress. Comput. Ecol. Softw. 2015, 5, 119–129. [Google Scholar]
- Lestrel, P.E. Morphometrics for the Life Sciences; World Scientific: Singapore, 2000; p. 261. [Google Scholar]
- Kociolek, J.P.; Stoermer, E.F. A preliminary investigation of the phylogenetic relationships among the freshwater, apical pore field-bearing cymbelloid and gomphonemoid diatoms (Bacillariophyceae). J. Phycol. 1988, 24, 377–385. [Google Scholar] [CrossRef]
- Pappas, J.L. Theoretical morphospace and its relation to freshwater Gomphonemoid–Cymbelloid diatom (Bacillariophyta) lineages. J. Biol. Syst. 2005, 13, 385–398. [Google Scholar] [CrossRef]
- Pappas, J.L. More on theoretical morphospace and its relation to freshwater gomphonemoid-cymbelloid diatom (Bacillariophyta) lineages. J. Biol. Syst. 2008, 16, 119–137. [Google Scholar] [CrossRef]
- Cox, E.J.; Willis, L.; Bentley, K. Integrated simulation with experimentation is a powerful tool for understanding diatom valve morphogenesis. Biosystems 2012, 109, 450–459. [Google Scholar] [CrossRef] [PubMed]
| Source | df | SS | MS | F | Z | p-Value |
|---|---|---|---|---|---|---|
| Individual | 74 | 0.7385 | 0.009980 | 152.74 | 1.69 | 0.001 |
| Side | 1 | 0.0008 | 0.000749 | 11.47 | 8.39 | 0.001 |
| Individual:Side | 74 | 0.0048 | 0.000065 | 2.76 | 1.17 | 0.020 |
| Measurement error | 150 | 0.0036 | 0.000024 | - | - | - |
| Total | 299 | 0.7477 | - | - | - | - |
| Source | df | SS | MS | F | Z | p-Value |
|---|---|---|---|---|---|---|
| Individual | 71 | 0.9058 | 0.012757 | 184.88 | 1.68 | 0.002 |
| Side | 1 | 0.0013 | 0.001317 | 19.08 | 12.58 | 0.001 |
| Individual:Side | 71 | 0.0049 | 0.000069 | 2.72 | 1.16 | 0.027 |
| Measurement error | 144 | 0.0037 | 0.000025 | - | - | - |
| Total | 287 | 0.9157 | - | - | - | - |
| Luticola 1 | ||||
| Analysis | Pearson’s r | R2 | Parametric p-value | Permutation p-value |
| TA vs. CS | 0.22 | 0.051 | 0.053 | 0.055 |
| FA vs. CS | 0.04 | 0.002 | 0.719 | 0.727 |
| Luticola 2 | ||||
| Analysis | Pearson’s r | R2 | Parametric p-value | Permutation p-value |
| TA vs. CS | −0.01 | 0.0002 | 0.903 | 0.904 |
| FA vs. CS | −0.19 | 0.038 | 0.098 | 0.097 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Woodard, K.; Neustupa, J. Morphometric Asymmetry of Frustule Outlines in the Pennate Diatom Luticola poulickovae (Bacillariophyceae). Symmetry 2016, 8, 150. https://doi.org/10.3390/sym8120150
Woodard K, Neustupa J. Morphometric Asymmetry of Frustule Outlines in the Pennate Diatom Luticola poulickovae (Bacillariophyceae). Symmetry. 2016; 8(12):150. https://doi.org/10.3390/sym8120150
Chicago/Turabian StyleWoodard, Kateřina, and Jiří Neustupa. 2016. "Morphometric Asymmetry of Frustule Outlines in the Pennate Diatom Luticola poulickovae (Bacillariophyceae)" Symmetry 8, no. 12: 150. https://doi.org/10.3390/sym8120150
APA StyleWoodard, K., & Neustupa, J. (2016). Morphometric Asymmetry of Frustule Outlines in the Pennate Diatom Luticola poulickovae (Bacillariophyceae). Symmetry, 8(12), 150. https://doi.org/10.3390/sym8120150







