Fluctuating Asymmetry of Human Populations: A Review
Abstract
:1. Introduction
2. Measuring Fluctuating Asymmetry
3. Human Symmetries and Asymmetries
3.1. Skeletal Asymmetry
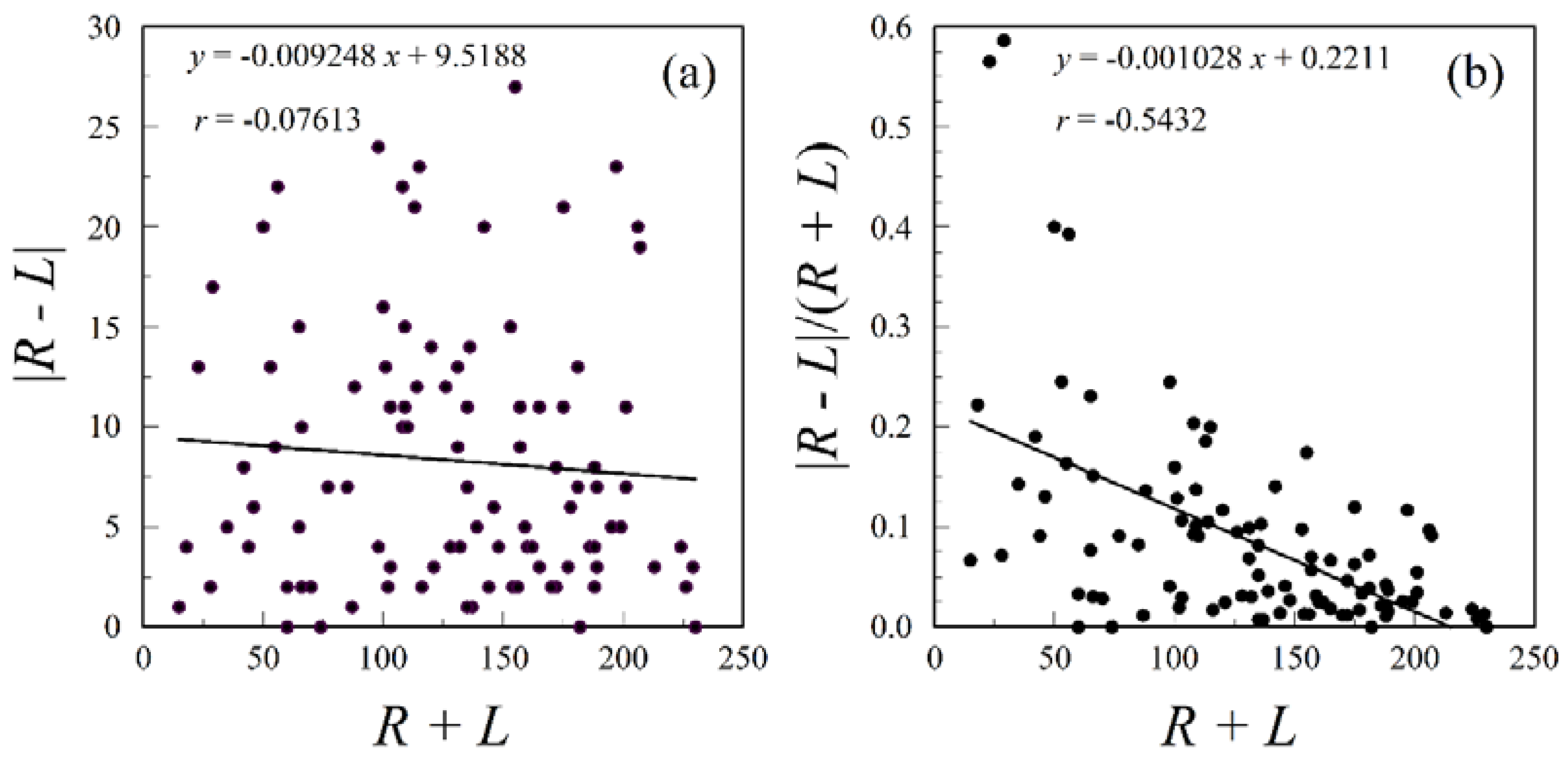
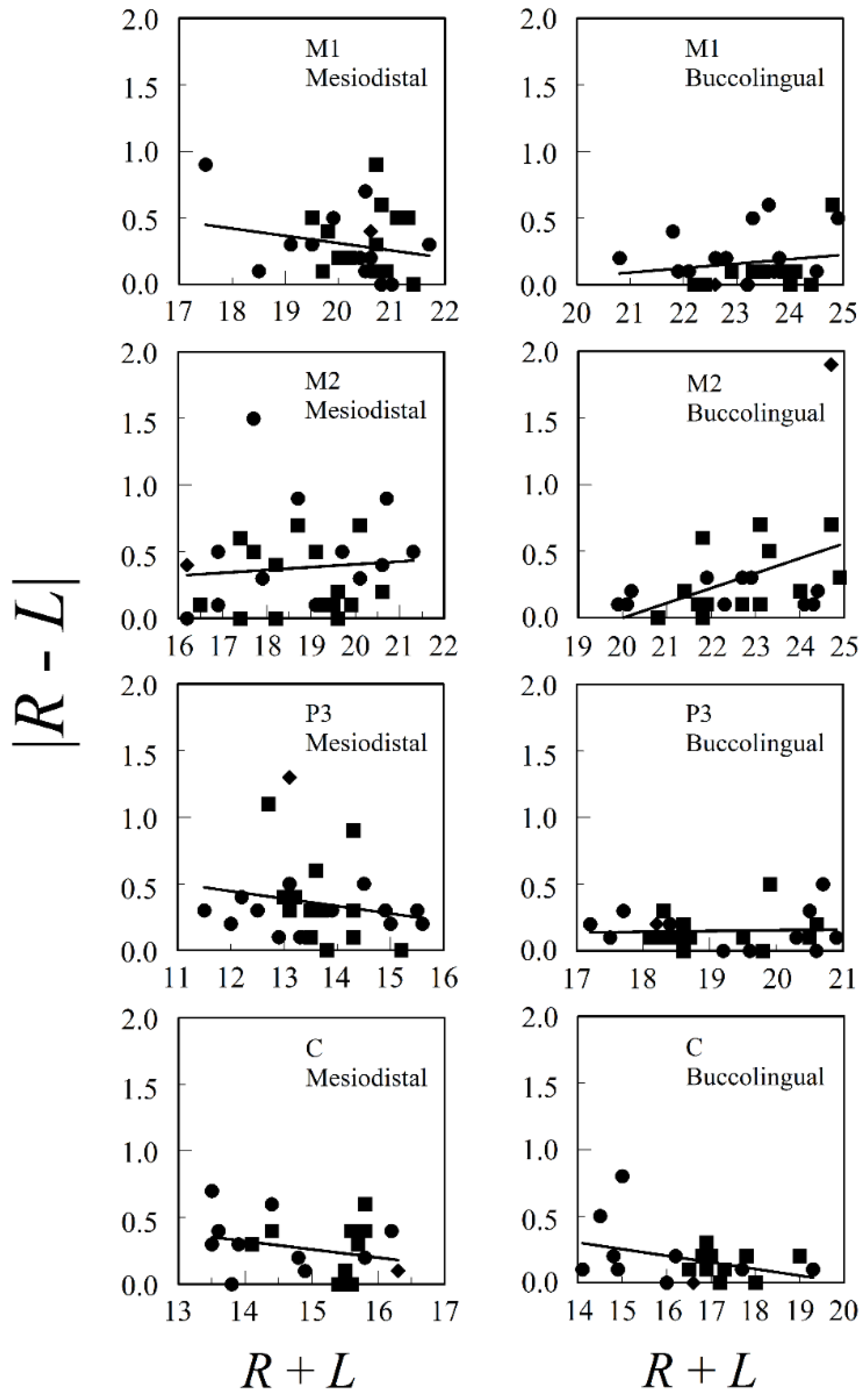
3.2. Dental Asymmetry
3.3. Facial Asymmetry
3.4. Dermatoglyphic Asymmetry
3.5. Brain Laterality
3.6. Asymmetry of Soft Tissues
3.7. Fractal Anatomy and Physiology
3.8. Behavioral Patterns
4. Sex Differences
5. Stressors
5.1. Environmental Stressors
5.1.1. Dietary Inadequacy, Growth, and Socioeconomic Status
5.1.2. Climate
5.1.3. Environmental Toxicology
5.1.4. Drugs
5.1.5. Natural Disasters
5.2. Genetic Stressors
5.2.1. Aneuploidy
5.2.2. Polyploidy
5.2.3. Unbalanced Translocation
5.2.4. Point Mutation
5.2.5. Inbreeding and Heterozygosity
5.2.6. Outbreeding Depression, Heterosis, and Genomic Coadaptation
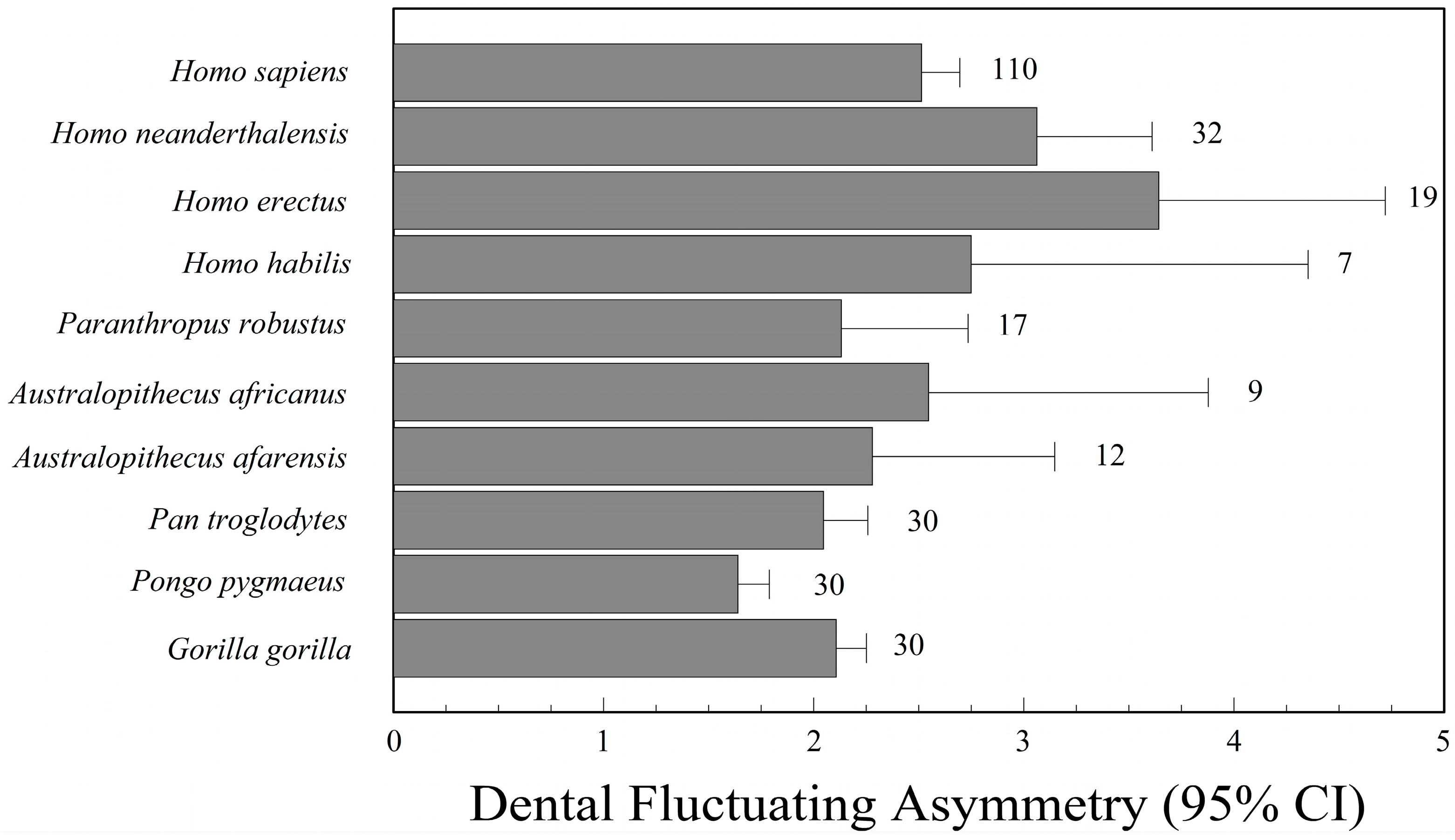
6. Phylogenetic Patterns of Fluctuating Asymmetry in the Hominidae and Other Primates
7. Human Populations
7.1. Fossil Hominids
7.2. Prehistoric and Historic Skeletal Samples
8. Evolutionary Biology
9. Medicine
10. Psychology
11. Discussion
12. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| ANOVA | Analysis of Variance |
| BP | Before Present |
| C | Canine Tooth |
| CFA | Composite Index of Fluctuating Asymmetry |
| CFIT | Culture Fair Intelligence Test |
| E | Expectation |
| M1 | First Molar |
| LB1 | Liang Bua 1 specimen of Homo floresiensis |
| QTL | Quantitative Trait Locus |
| M2 | Second Molar |
| KNM-WT 15000 | Specimen Number of Nariokotome Boy |
| P3 | Third Premolar |
| Var | Variance |
References
- Adams, M.S.; Niswander, J.D. Developmental ‘noise’ and a congenital malformation. Genet. Res. 1967, 10, 313–317. [Google Scholar] [PubMed]
- Bailit, H.L.; Workman, P.L.; Niswander, J.D.; MacLean, C.J. Dental asymmetry as an indicator of genetic and environmental conditions in human populations. Hum. Biol. 1970, 42, 626–638. [Google Scholar] [PubMed]
- Mather, K. Genetical control of stability in development. Heredity 1953, 7, 297–336. [Google Scholar] [CrossRef]
- Van Valen, L. A study of fluctuating asymmetry. Evolution 1962, 16, 125–142. [Google Scholar] [CrossRef]
- Astauroff, B.L. Analyse der erblichen Störungsfälle der bilateralen Symmetrie. Zeitschrift für induktive Abstammungs Vererbungslehre 1930, 55, 183–262. [Google Scholar] [CrossRef]
- Ludwig, W. Das Rechts-Links Problem im Tierreich und heim Menschen; Springer-Verlag: Berlin, Germany, 1932; p. 496. [Google Scholar]
- Waddington, C.H. The Strategy of the Genes. A Discussion of Some Aspects of Theoretical Biology. With an Appendix by H. Kacser; George Allen Unwin: London, UK, 1957; p. ix-262. [Google Scholar]
- Palmer, A.R.; Strobeck, C. Fluctuating asymmetry: Measurement, analysis, patterns. Annu. Rev. Ecol. Syst. 1986, 17, 391–421. [Google Scholar] [CrossRef]
- Zakharov, V.M. Population phenogenetics: Analysis of developmental stability in natural populations. Acta Zool. Fenn. 1992, 191, 7–30. [Google Scholar]
- Van Dongen, S. Fluctuating asymmetry and developmental instability in evolutionary biology: Past, present and future. J. Evol. Biol. 2006, 19, 1727–1743. [Google Scholar] [CrossRef] [PubMed]
- Polak, M. Developmental Instability: Causes and Consequences; Oxford University Press: Oxford, UK, 2003; p. 488. [Google Scholar]
- Graham, J.H.; Raz, S.; Hel-Or, H.; Nevo, E. Fluctuating asymmetry: Methods, theory, and applications. Symmetry 2010, 2, 466–540. [Google Scholar] [CrossRef]
- Parsons, P.A. Fluctuating asymmetry: An epigenetic measure of stress. Biol. Rev. 1990, 65, 131–145. [Google Scholar] [CrossRef] [PubMed]
- Parsons, P.A. Fluctuating asymmetry: A biological monitor of environmental and genomic stress. Heredity 1992, 68, 361–364. [Google Scholar] [CrossRef] [PubMed]
- Graham, J.H.; Emlen, J.M.; Freeman, D.C. Nonlinear dynamics and developmental instability. In Developmental Instability: Causes and Consequences; Polak, M., Ed.; Oxford University Press: New York, NY, USA, 2003; pp. 35–49. [Google Scholar]
- Graham, J.H.; Freeman, D.C.; Emlen, J.M. Developmental stability: A sensitive indicator of populations under stress. In Environmental Toxicology and Risk Assessment; Landis, W.G., Hughes, J.S., Lewis, M.A., Eds.; ASTM International: Philadelphia, PA, USA, 1993; Volume STP1179, pp. 136–158. [Google Scholar]
- Emlen, J.M.; Freeman, D.C.; Graham, J.H. Nonlinear growth dynamics and the origin of fluctuating asymmetry. Genetica 1993, 89, 77–96. [Google Scholar] [CrossRef]
- Klingenberg, C.P.; Nijhout, H.F. Genetics of fluctuating asymmetry: A developmental model of developmental instability. Evolution 1999, 53, 358–375. [Google Scholar] [CrossRef]
- Graham, J.H.; Robb, D.T.; Poe, A.R. Random phenotypic variation of yeast (Saccharomyces cerevisiae) single-gene knockouts fits a double pareto-lognormal distribution. PLoS ONE 2012, 7, e48964. [Google Scholar] [CrossRef] [PubMed]
- Masel, J.; Siegal, M.L. Robustness: Mechanisms and consequences. Trends Genet. 2009, 25, 395–403. [Google Scholar] [CrossRef] [PubMed]
- Siegal, M.L.; Leu, J.-Y. On the nature and evolutionary impact of phenotypic robustness mechanisms. Annu. Rev. Ecol. Evol. Syst. 2014, 45, 496–517. [Google Scholar] [CrossRef] [PubMed]
- Palmer, A.R.; Strobeck, C. Fluctuating asymmetry as a measure of developmental stability: Implications of non-normal distributions and power of statistical tests. Acta Zool. Fenn. 1992, 191, 57–72. [Google Scholar]
- Palmer, A.R.; Strobeck, C. Fluctuating asymmetry analyses revisited. In Developmental Instability: Causes and Consequences; Polak, M., Ed.; Oxford University Press: Oxford, UK, 2003; pp. 279–319. [Google Scholar]
- Mardia, K.V.; Bookstein, F.L.; Moreton, I.J. Statistical assessment of bilateral symmetry of shapes. Biometrika 2000, 87, 285–300. [Google Scholar] [CrossRef]
- Klingenberg, C.P.; Barluenga, M.; Meyer, A. Shape analysis of symmetric structures: Quantifying variation among individuals and asymmetry. Evolution 2002, 56, 1909–1920. [Google Scholar] [CrossRef] [PubMed]
- Klingenberg, C.P. Analyzing fluctuating asymmetry with geometric morphometrics: Concepts, methods, and applications. Symmetry 2015, 7, 843–934. [Google Scholar] [CrossRef]
- Bookstein, F.L. Landmark methods for forms without landmarks: Morphometrics of group differences in outline shape. Med. Image Anal. 1997, 1, 225–243. [Google Scholar] [CrossRef]
- Klingenberg, C.P.; McIntyre, G.S. Geometric morphometrics of developmental instability: Analyzing patterns of fluctuating asymmetry with Procrustes methods. Evolution 1998, 52, 1363–1375. [Google Scholar] [CrossRef]
- Claes, P.; Reijniers, J.; Shriver, M.D.; Snyders, J.; Suetens, P.; Nielandt, J.; De Tré, G.; Vandermeulen, D. An investigation of matching symmetry in the human pinnae with possible implications for 3D ear recognition and sound localization. J. Anat. 2015, 226, 60–72. [Google Scholar] [CrossRef] [PubMed]
- Claes, P.; Walters, M.; Shriver, M.D.; Puts, D.; Gibson, G.; Clement, J.; Baynam, G.; Verbeke, G.; Vandermeulen, D.; Suetens, P. Sexual dimorphism in multiple aspects of 3D facial symmetry and asymmetry defined by spatially dense geometric morphometrics. J. Anat. 2012, 221, 97–114. [Google Scholar] [CrossRef] [PubMed]
- Schlager, S. Soft-tissue Reconstruction of the Human Nose. Ph.D. Thesis, Albert-Ludwigs-Universität, Freiburg, Germany, 2013. [Google Scholar]
- Schlager, S.; Rüdell, A. Analysis of the human osseous nasal shape—Population differences and sexual dimorphism. Am. J. Phys. Anthropol. 2015, 157, 571–581. [Google Scholar] [CrossRef] [PubMed]
- Zabrodsky, H.; Peleg, S.; Avnir, D. Symmetry as a continuous feature. IEEE Trans. Pattern Anal. 1995, 17, 1154–1166. [Google Scholar] [CrossRef]
- Graham, J.H.; Whitesell, M.J.; Fleming, M.I.; Hel-Or, H.; Nevo, E.; Raz, S. Fluctuating asymmetry of plant leaves: Batch processing with LAMINA and Continuous Symmetry Measures. Symmetry 2015, 7, 255–268. [Google Scholar] [CrossRef]
- Zabrodsky, H.; Peleg, S.; Avnir, D. Continuous symmetry measures. J. Am. Chem. Soc. 1992, 114, 7843–7851. [Google Scholar] [CrossRef]
- Palmer, A.R. Fluctuating asymmetry analyses: A primer. In Developmental Instability: Its Origins and Evolutionary Implications; Markow, T.A., Ed.; Kluwer: Dordrecht, The Netherlands, 1994; pp. 335–364. [Google Scholar]
- Holt, S.B. The correlations between ridge-counts on different fingers estimated from a population sample. Ann. Hum. Genet. 1959, 23, 459–460. [Google Scholar] [CrossRef] [PubMed]
- Mellor, C.S. Dermatoglyphic evidence of fluctuating asymmetry in schizophrenia. Br. J. Psychiat. 1992, 160, 467–472. [Google Scholar] [CrossRef]
- Angus, R.A. Quantifying fluctuating asymmetry—Not all methods are equivalent. Growth 1982, 46, 337–342. [Google Scholar]
- Shakibaei, F.; Asadollahi, G.A.; Tabibi, A.P. Dermatoglyphics in patients with schizophrenia. J. Res. Med. Sci. 2011, 16, 1055–1061. [Google Scholar] [PubMed]
- Bookstein, F.L. Morphometric Tools for Landmark Data; Cambridge University Press: Cambridge, UK, 1997; p. 436. [Google Scholar]
- Hopman, S.M.J.; Merks, J.H.M.; Suttie, M.; Hennekam, R.; Hammond, P. 3D morphometry aids facial analysis of individuals with a childhood cancer. Am. J. Med. Genet. A 2016, 9999A, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Graham, J.H.; Shimizu, K.; Emlen, J.M.; Freeman, D.; Merkel, J. Growth models and the expected distribution of fluctuating asymmetry. Biol. J. Linn. Soc. 2003, 80, 57–65. [Google Scholar] [CrossRef]
- Mosimann, J.E.; Campbell, G. Applications in biology: Simple growth models. In Lognormal Distributions: Theory and Applications; Crow, E.L., Shimizu, K., Eds.; Marcel Dekker: New York, NY, USA, 1988; pp. 287–302. [Google Scholar]
- Holt, S.B. Genetics of dermal ridges: Bilateral asymmetry in finger ridge-counts. Ann. Eugenic. 1952, 17, 211–231. [Google Scholar] [CrossRef]
- Livshits, G.; Yakovenko, K.; Kletselman, L.; Karasik, D.; Kobyliansky, E. Fluctuating asymmetry and morphometric variation of hand bones. Am. J. Phys. Anthropol. 1998, 107, 125–136. [Google Scholar] [CrossRef]
- Gutnik, B.; Skurvydas, A.; Zuoza, A.; Zuoziene, I.; Mickevičnienė, D.; Alekrinskis, A.; Nash, D. Evaluation of bilateral asymmetry between upper limb masses in right-handed young adults of both sexes. Percept. Mot. Skills 2015, 120, 804–815. [Google Scholar] [CrossRef] [PubMed]
- Graham, J.H.; Emlen, J.M.; Freeman, D.C.; Leamy, L.J.; Kieser, J.A. Directional asymmetry and the measurement of developmental instability. Biol. J. Linn. Soc. 1998, 64, 1–16. [Google Scholar] [CrossRef]
- Auerbach, B.M.; Ruff, C.B. Limb bone bilateral asymmetry: Variability and commonality among modern humans. J. Hum. Evol. 2006, 50, 203–218. [Google Scholar] [CrossRef] [PubMed]
- Latimer, H.B.; Lowrance, E.W. Bilateral asymmetry in weight and in length of human bones. Anat. Rec. 1965, 152, 217–224. [Google Scholar] [CrossRef] [PubMed]
- Macintosh, A.A.; Pinhasi, R.; Stock, J.T. Divergence in male and female manipulative behaviors with the intensification of metallurgy in Central Europe. PLoS ONE 2014, 9, e112116. [Google Scholar] [CrossRef] [PubMed]
- Hartman, C.; Holton, N.; Miller, S.; Yokley, T.; Marshall, S.; Srinivasan, S.; Southard, T. Nasal septal deviation and facial skeletal asymmetries. Anat. Rec. 2016, 299, 295–306. [Google Scholar] [CrossRef] [PubMed]
- Kanat, A.; Yazar, U.; Ozdemir, B.; Coskun, Z.O.; Erdivanli, O. Frontal sinus asymmetry: Is it an effect of cranial asymmetry? X-ray analysis of 469 normal adult human frontal sinus. J. Neurosci. Rural Pract. 2015, 6, 511–514. [Google Scholar] [CrossRef] [PubMed]
- Johnson, W.; Segal, N.L.; Bouchard, T.J. Fluctuating asymmetry and general intelligence: No genetic or phenotypic association. Intelligence 2008, 36, 279–288. [Google Scholar] [CrossRef]
- Van Dongen, S.; Lens, L.; Molenberghs, G. Mixture analysis of asymmetry: Modelling directional asymmetry, antisymmetry and heterogeneity in fluctuating asymmetry. Ecol. Lett. 1999, 2, 387–396. [Google Scholar]
- Proff, P.; Römer, P. The molecular mechanism behind bone remodelling: A review. Clin. Oral Investig. 2009, 13, 355–362. [Google Scholar] [CrossRef] [PubMed]
- Hallgrímsson, B. Ontogenetic patterning of skeletal fluctuating asymmetry in rhesus macaques and humans: Evolutionary and developmental implications. Int. J. Primatol. 1999, 20, 121–151. [Google Scholar] [CrossRef]
- Palestis, B.G.; Trivers, R. A longitudinal study of changes in fluctuating asymmetry with age in Jamaican youth. Symmetry 2016, 8. [Google Scholar] [CrossRef]
- Guatelli-Steinberg, D. What Teeth Reveal about Human Evolution; Cambridge University Press: Cambridge, UK, 2016; p. 294. [Google Scholar]
- Gawlikowska-Sroka, A.; Dąbrowski, P.; Szczurowski, J.; Staniowski, T. Analysis of interaction between nutritional and developmental instability in mediaeval population in Wrocław. Anthropol. Rev. 2013, 76, 51–62. [Google Scholar] [CrossRef]
- Lawn, B.R.; Lee, J.J.-W.; Chai, H. Teeth: Among nature’s most durable biocomposites. Annu. Rev. Mater. Res. 2010, 40, 55–75. [Google Scholar] [CrossRef]
- Niswander, J.D.; Chung, C.S. The effects of inbreeding on tooth size in Japanese children. Am. J. Hum. Genet. 1965, 17, 390–398. [Google Scholar] [PubMed]
- Garn, S.M.; Lewis, A.B.; Kerewsky, R.S. The meaning of bilateral asymmetry in the permanent dentition. Angle Orthod. 1966, 36, 55–62. [Google Scholar] [PubMed]
- Garn, S.M.; Lewis, A.B.; Kerewsky, R.S. Buccolingual size asymmetry and its developmental meaning. Angle Orthod. 1967, 37, 186–193. [Google Scholar] [PubMed]
- Barrett, C.K.; Guatelli-Steinberg, D.; Sciulli, P.W. Revisiting dental fluctuating asymmetry in neandertals and modern humans. Am. J. Phys. Anthropol. 2012, 149, 193–204. [Google Scholar] [CrossRef] [PubMed]
- Sciulli, P.W. Dental asymmetry in a Late Archaic and late prehistoric skeletal sample of the Ohio Valley Area. Dent. Anthropol. 2002, 16, 33–44. [Google Scholar]
- Pietrusewsky, M.; Douglas, M.T. Database E.4 Individual Records of Measurements of Permanent Dentitions in Adolescents and Adults. Available online: https://core.tdar.org/dataset/376929/database-e4-individual-records-of-measurements-of-permanent-dentitions-in-adolescents-and-adults (accessed on 9 November 2016).
- Varner, T.B. Landmark-Based Approach to Examining Changes in Arch Shape: A Longitudinal Study. Master’s Thesis, University of Iowa, Iowa City, IA, USA, 2015. [Google Scholar]
- Grammer, K.; Thornhill, R. Human (Homo sapiens) facial attractiveness and sexual selection: The role of symmetry and averageness. J. Comp. Psychol. 1994, 108, 233–242. [Google Scholar] [CrossRef] [PubMed]
- Miller, S.F.; Weinberg, S.M.; Nidey, N.L.; Defay, D.K.; Marazita, M.L.; Wehby, G.L.; Moreno Uribe, L.M. Exploratory genotype–phenotype correlations of facial form and asymmetry in unaffected relatives of children with non-syndromic cleft lip and/or palate. J. Anat. 2014, 224, 688–709. [Google Scholar] [CrossRef] [PubMed]
- Cummins, H.; Midlo, C. Palmar and plantar epidermal ridge configurations (dermatoglyphics) in European-Americans. Am. J. Phys. Anthropol. 1926, 9, 471–502. [Google Scholar] [CrossRef]
- Cummins, H.; Midlo, C. Finger Prints, Palms and Soles: An Introduction to Dermatoglyphics; Dover Publications: New York, NY, USA, 1961; p. 319. [Google Scholar]
- Galton, F. Finger Prints; Macmillan and Company: London, UK, 1892; p. 256. [Google Scholar]
- Loesch, D.Z. Quantitative Dermatoglyphics: Classification, Genetics, and Pathology; Oxford University Press: New York, NY, USA, 1983; p. 450. [Google Scholar]
- Babler, W.J. Embryologic development of epidermal ridges and their configurations. Birth Defects Orig. Artic. Ser. 1991, 27, 95–112. [Google Scholar] [PubMed]
- Kücken, M.; Newell, A.C. Fingerprint formation. J. Theor. Biol. 2005, 235, 71–83. [Google Scholar] [CrossRef] [PubMed]
- Arrieta, M.I.; Criado, B.; Martinez, B.; Lobato, M.N.; Gil, A.; Lostao, C.M. Fluctuating dermatoglyphic asymmetry: Genetic and prenatal influences. Ann. Hum. Biol. 1993, 20, 557–563. [Google Scholar] [CrossRef] [PubMed]
- Rose, R.J.; Reed, T.; Bogle, A. Asymmetry of a–b ridge count and behavioral discordance of monozygotic twins. Behav. Genet. 1987, 17, 125–140. [Google Scholar] [CrossRef] [PubMed]
- King, S.; Dancause, K.; Turcotte-Tremblay, A.-M.; Veru, F.; Laplante, D.P. Using natural disasters to study the effects of prenatal maternal stress on child health and development. Birth Defects Res. C 2012, 96, 273–288. [Google Scholar] [CrossRef] [PubMed]
- King, S.; Mancini-Marïe, A.; Brunet, A.; Walker, E.; Meaney, M.J.; Laplante, D.P. Prenatal maternal stress from a natural disaster predicts dermatoglyphic asymmetry in humans. Dev. Psychopathol. 2009, 21, 343–353. [Google Scholar] [CrossRef] [PubMed]
- Penrose, L.S. The distal triradius t on the hands of parents and sibs of mongol imbeciles. Ann. Hum. Genet. 1954, 19, 10–38. [Google Scholar] [CrossRef] [PubMed]
- Jantz, R.L.; Brehme, H. Directional and fluctuating asymmetry in the palmar interdigital ridge-counts. Anthropol. Anz. 1993, 51, 59–67. [Google Scholar] [PubMed]
- Jantz, R.L.; Webb, R.S. Dermatoglyphic asymmetry as a measure of canalization. Ann. Hum. Biol. 1980, 7, 489–493. [Google Scholar] [CrossRef] [PubMed]
- Wijerathne, B.T.B.; Meier, R.J.; Agampodi, T.C.; Agampodi, S.B. Dermatoglyphics in hypertension: A review. J. Physiol. Anthropol. 2015, 34. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.-F.; Lin, C.-L.; Yen, C.-W.; Chang, Y.-H.; Chen, T.-Y.; Su, K.-P.; Nagurka, M.L. Determining the association between dermatoglyphics and schizophrenia by using fingerprint asymmetry measures. Int. J. Pattern Recogn. 2008, 22, 601–616. [Google Scholar] [CrossRef]
- De Bruin, E.I.; Graham, J.H.; Louwerse, A.; Huizink, A.C. Mild dermatoglyphic deviations in adolescents with autism spectrum disorders and average intellectual abilities as compared to typically developing boys. Autism Res. Treat. 2014, 2014, 968134. [Google Scholar] [CrossRef] [PubMed]
- Markow, T.A.; Wandler, K. Fluctuating dermatoglyphic asymmetry and the genetics of liability to schizophrenia. Psychiatry Res. 1986, 19, 323–328. [Google Scholar] [CrossRef]
- Holt, S.B. Genetics of dermal ridges: The relation between total ridge-count and the variability of counts from finger to finger. Ann. Hum. Genet. 1958, 22, 323–339. [Google Scholar] [CrossRef] [PubMed]
- Holt, S.B. Genetics of dermal ridges: Familial correlations for (S/√10), a measurement of the diversity of ridge-counts from finger to finger. Ann. Hum. Genet. 1960, 24, 253–269. [Google Scholar] [CrossRef] [PubMed]
- Micle, S.; Kobyliansky, E. Dermatoglyphic sexual dimorphism in Israelis: Principal components and discriminant analyses applied to quantitative traits. Hum. Biol. 1986, 58, 485–498. [Google Scholar] [PubMed]
- Karmakar, B.; Yakovenko, K.; Kobyliansky, E. Sexual dimorphism: Asymmetry and diversity of 38 dermatoglyphic traits in five endogamous populations of West Bengal, India. Coll. Antropol. 2001, 25, 167–187. [Google Scholar] [PubMed]
- Mathew, L.; Hegde, A.M.; Rai, K. Dermatoglyphic peculiarities in children with oral clefts. J. Indian Soc. Ped. Prev. Dent. 2005, 23, 179–182. [Google Scholar]
- Bonnevie, K. Studies on papillary patterns of human fingers. J. Genet. 1924, 15, 1–111. [Google Scholar] [CrossRef]
- Ponnudurai, R.; Menon, M.S.; Muthu, M. Dermatoglyphic fluctuating asymmetry and symmetry in familial and non familial schizophrenia. Indian J. Psychiatry 1997, 39, 205–211. [Google Scholar] [PubMed]
- Ravindranath, R.; Joseph, A.M.; Bosco, S.I.; Rajangam, S.; Balasubramanyam, V. Fluctuating asymmetry in dermatoglyphics of non-insulin-dependent diabetes mellitus in Bangalore-based population. Indian J. Hum. Genet. 2005, 11, 149–153. [Google Scholar] [CrossRef]
- Saha, S.; Loesch, D.; Chant, D.; Welham, J.; El-Saadi, O.; Fañanás, L.; Mowry, B.; McGrath, J. Directional and fluctuating asymmetry in finger and ab ridge counts in psychosis: A case-control study. BMC Psychiatry 2003, 3, 1–9. [Google Scholar] [CrossRef]
- Russak, O. Dermatoglyphic Asymmetries, Symptoms, and Cognitive Function in Adolescents at Ultrahigh-risk for Psychotic Disorders. Bachelor’s Thesis, University of Colorado, Boulder, CO, USA, 2015. [Google Scholar]
- Russak, O.D.F.; Ives, L.; Mittal, V.A.; Dean, D.J. Fluctuating dermatoglyphic asymmetries in youth at ultrahigh-risk for psychotic disorders. Schizophr. Res. 2016, 170, 301–303. [Google Scholar] [CrossRef] [PubMed]
- Sivkov, S.T.; Akabaliev, V.H.; Akabalieva, K.V. Fluctuating asymmetry in dermatoglyphic traits in schizophrenic patients. Folia Med. 2007, 49, 5–10. [Google Scholar]
- Acree, M.A. Is there a gender difference in fingerprint ridge density? Forensic Sci. Int. 1999, 102, 35–44. [Google Scholar] [CrossRef]
- Cantalupo, C.; Hopkins, W.D. Asymmetric Broca’s area in great apes. Nature 2001, 414, 505. [Google Scholar] [CrossRef] [PubMed]
- Thoma, R.J.; Yeo, R.A.; Gangestad, S.W.; Lewine, J.D.; Davis, J.T. Fluctuating asymmetry and the human brain. Laterality 2002, 7, 45–58. [Google Scholar] [CrossRef] [PubMed]
- Yeo, R.A.; Gangestad, S.W.; Thoma, R.; Shaw, P.; Repa, K. Developmental instability and cerebral lateralization. Neuropsychology 1997, 11, 552–561. [Google Scholar] [CrossRef] [PubMed]
- Schulter, G.; Papousek, I. Believing in paranormal phenomena: Relations to asymmetry of body and brain. Cortex 2008, 44, 1326–1335. [Google Scholar] [CrossRef] [PubMed]
- Manning, J.T.; Scutt, D.; Whitehouse, G.H.; Leinster, S.J. Breast asymmetry and phenotypic quality in women. Evol. Hum. Behav. 1997, 18, 223–236. [Google Scholar] [CrossRef]
- Manning, J.T.; Scutt, D.; Whitehouse, G.H.; Leinster, S.J.; Walton, J.M. Asymmetry and the menstrual cycle in women. Ethol. Sociobiol. 1996, 17, 129–143. [Google Scholar] [CrossRef]
- Domjanic, J.; Fieder, M.; Seidler, H.; Mitteroecker, P. Geometric morphometric footprint analysis of young women. J. Foot Ankle Res. 2013, 6, 27. [Google Scholar] [CrossRef] [PubMed]
- Schlager, S. Sliding semi-landmarks on symmetric structures in three dimensions. Am. J. Phys. Anthropol. 2012, 147, 261. [Google Scholar]
- Alados, C.L.; Escós, J.; Emlen, J.M. Fluctuating asymmetry and fractal dimension of the sagittal suture as indicators of inbreeding depression in dama and dorcas gazelles. Can. J. Zool. 1995, 73, 1967–1974. [Google Scholar] [CrossRef]
- Escos, J.M.; Alados, C.L.; Emlen, J.M. Fractal structures and fractal functions as disease indicators. Oikos 1995, 74, 310–314. [Google Scholar] [CrossRef]
- Graham, J.H.; Emlen, J.M.; Freeman, D.C. Developmental stability and its applications in ecotoxicology. Ecotoxicology 1993, 2, 175–184. [Google Scholar] [CrossRef] [PubMed]
- Kuswandari, S.; Nishino, M. The mesiodistal crown diameters of primary dentition in Indonesian Javanese children. Arch. Oral Biol. 2004, 49, 217–222. [Google Scholar] [CrossRef] [PubMed]
- Albert, A.M.; Greene, D.L. Bilateral asymmetry in skeletal growth and maturation as an indicator of environmental stress. Am. J. Phys. Anthropol. 1999, 110, 341–349. [Google Scholar] [CrossRef]
- Bigoni, L.; Krajíček, V.; Sládek, V.; Velemínský, P.; Velemínská, J. Skull shape asymmetry and the socioeconomic structure of an early medieval central European society. Am. J. Phys. Anthropol. 2013, 150, 349–364. [Google Scholar] [CrossRef] [PubMed]
- Gray, P.B.; Marlowe, F. Fluctuating asymmetry of a foraging population: The Hadza of Tanzania. Ann. Hum. Biol. 2002, 29, 495–501. [Google Scholar] [CrossRef] [PubMed]
- Guatelli-Steinberg, D.; Sciulli, P.W.; Edgar, H.H.J. Dental fluctuating asymmetry in the Gullah: Tests of hypotheses regarding developmental stability in deciduous vs permanent and male vs female teeth. Am. J. Phys. Anthropol. 2006, 129, 427–434. [Google Scholar] [CrossRef] [PubMed]
- Livshits, G.; Smouse, P.E. Multivariate fluctuating asymmetry in Israeli adults. Hum. Biol. 1993, 65, 547–578. [Google Scholar] [PubMed]
- Özener, B. Fluctuating and directional asymmetry in young human males: Effect of heavy working condition and socioeconomic status. Am. J. Phys. Anthropol. 2010, 143, 112–120. [Google Scholar] [CrossRef] [PubMed]
- Simmons, L.W.; Rhodes, G.; Peters, M.; Koehler, N. Are human preferences for facial symmetry focused on signals of developmental instability? Behav. Ecol. 2004, 15, 864–871. [Google Scholar] [CrossRef]
- Trivers, R.; Manning, J.T.; Thornhill, R.; Singh, D.; McGuire, M. Jamaican symmetry project: Long-term study of fluctuating asymmetry in rural Jamaican children. Hum. Biol. 1999, 417–430. [Google Scholar]
- Wilson, J.M.; Manning, J.T. Fluctuating asymmetry and age in children: Evolutionary implications for the control of developmental stability. J. Hum. Evol. 1996, 30, 529–537. [Google Scholar] [CrossRef]
- Noss, J.F.; Scott, G.R.; Potter, R.H.Y.; Dahlberg, A.A. Fluctuating asymmetry in molar dimensions and discrete morphological traits in Pima Indians. Am. J. Phys. Anthropol. 1983, 61, 437–445. [Google Scholar] [CrossRef] [PubMed]
- Özener, B.; Fink, B. Facial symmetry in young girls and boys from a slum and a control area of Ankara, Turkey. Evol. Hum. Behav. 2010, 31, 436–441. [Google Scholar] [CrossRef]
- Ertuğrul, B. Sexually dimorphic human body fat distribution and second-to-fourth digit ratio. Eurasian J. Anthropol. 2013, 3, 54–62. [Google Scholar]
- Ertuğrul, B.; Otağ, İ. Cinsiyete özgü vücut morfolojisi ile elin ikinci ve dördüncü parmak uzunluk oranları arasındaki ilişki. İnsanbilim Dergisi 2012, 1, 94–107. [Google Scholar]
- Fink, B.; Manning, J.T.; Neave, N.; Grammer, K. Second to fourth digit ratio and facial asymmetry. Evol. Hum. Behav. 2004, 25, 125–132. [Google Scholar] [CrossRef]
- Benderlioglu, Z. Fluctuating asymmetry and steroid hormones: A review. Symmetry 2010, 2, 541–553. [Google Scholar] [CrossRef]
- Özener, B. Brief communication: Facial fluctuating asymmetry as a marker of sex differences of the response to phenotypic stresses. Am. J. Phys. Anthropol. 2010, 143, 321–324. [Google Scholar] [CrossRef] [PubMed]
- Davis, E.P.; Sandman, C.A. The timing of prenatal exposure to maternal cortisol and psychosocial stress is associated with human infant cognitive development. Child Dev. 2010, 81, 131–148. [Google Scholar] [CrossRef] [PubMed]
- Bogin, B. Patterns of Human Growth; Cambridge University Press: Cambridge, UK, 1999; Volume 23, p. 472. [Google Scholar]
- Kieser, J.A.; Groeneveld, H.T.; Preston, C.B. Fluctuating odontometric asymmetry in the Lengua Indians of Paraguay. Ann. Hum. Biol. 1986, 13, 489–498. [Google Scholar] [CrossRef] [PubMed]
- Livshits, G.; Davidi, L.; Kobyliansky, E.; Ben-Amitai, D.; Levi, Y.; Merlob, P.; Optiz, J.M.; Reynolds, J.F. Decreased developmental stability as assessed by fluctuating asymmetry of morphometric traits in preterm infants. Am. J. Med. Genet. 1988, 29, 793–805. [Google Scholar] [CrossRef] [PubMed]
- Little, B.B.; Buschang, P.H.; Malina, R.M. Anthropometric asymmetry in chronically undernourished children from Southern Mexico. Ann. Hum. Biol. 2002, 29, 526–537. [Google Scholar] [CrossRef] [PubMed]
- Flinn, M.V.; Leone, D.V.; Quinlan, R.J. Growth and fluctuating asymmetry of stepchildren. Evol. Hum. Behav. 1999, 20, 465–479. [Google Scholar] [CrossRef]
- Wells, J.C.; Hallal, P.C.; Manning, J.T.; Victora, C.G. A trade-off between early growth rate and fluctuating asymmetry in Brazilian boys. Ann. Hum. Biol. 2006, 33, 112–124. [Google Scholar] [CrossRef] [PubMed]
- Özener, B.; Ertuğrul, B. Relationship between shortness of final body height and fluctuating asymmetry in Turkish young males. Ann. Hum. Biol. 2011, 38, 34–38. [Google Scholar] [CrossRef] [PubMed]
- Özener, B. Biomechanical pressures and upper extremity asymmetry: A study on young laborers. Coll. Antropol. 2007, 31, 693–699. [Google Scholar] [PubMed]
- Tomaszewska, A.; Kwiatkowska, B.; Jankauskas, R. Is the area of the orbital opening in humans related to climate? Am. J. Hum. Biol. 2015, 27, 845–850. [Google Scholar] [CrossRef] [PubMed]
- Freeman, D.C.; Graham, J.H.; Emlen, J.M. Developmental stability in plants: Symmetries, stress and epigenesis. Genetica 1993, 89, 97–119. [Google Scholar] [CrossRef]
- Wuytack, T.; Samson, R.; Wuyts, K.; Adriaenssens, S.; Kardel, F.; Verheyen, K. Do Leaf Characteristics of White Willow (Salix alba L.), Northern Red Oak (Quercus rubra L.), and Scots Pine (Pinus sylvestris L.) Respond Differently to Ambient Air Pollution and Other Environmental Stressors? Water Air Soil Pollut. 2013, 224. [Google Scholar] [CrossRef]
- Wuytack, T.; Wuyts, K.; Van Dongen, S.; Baeten, L.; Kardel, F.; Verheyen, K.; Samson, R. The effect of air pollution and other environmental stressors on leaf fluctuating asymmetry and specific leaf area of Salix alba L. Environ. Poll. 2011, 159, 2405–2411. [Google Scholar] [CrossRef] [PubMed]
- Polak, M.; Opoka, R.; Cartwright, I.L. Response of fluctuating asymmetry to arsenic toxicity: Support for the developmental selection hypothesis. Environ. Poll. 2002, 118, 19–28. [Google Scholar] [CrossRef]
- Savriama, Y.; Stige, L.C.; Gerber, S.; Pérez, T.; Alibert, P.; David, B. Impact of sewage pollution on two species of sea urchins in the Mediterranean Sea (Cortiou, France): Radial asymmetry as a bioindicator of stress. Ecol. Indic. 2015, 54, 39–47. [Google Scholar] [CrossRef]
- Allenbach, D.M. Fluctuating asymmetry and exogenous stress in fishes: A review. Rev. Fish Biol. Fish. 2011, 21, 355–376. [Google Scholar] [CrossRef]
- Lajus, D.; Yurtseva, A.; Birch, G.; Booth, D.J. Fluctuating asymmetry as a pollution monitor: The Australian estuarine smooth toadfish Tetractenos glaber (Teleostei: Tetraodontidae). Mar. Pollut. Bull. 2015, 101, 758–767. [Google Scholar] [CrossRef] [PubMed]
- Costa, R.N.; Nomura, F. Measuring the impacts of Roundup Original® on fluctuating asymmetry and mortality in a Neotropical tadpole. Hydrobiologia 2016, 765, 85–96. [Google Scholar] [CrossRef]
- Lazić, M.M.; Kaliontzopoulou, A.; Carretero, M.A.; Crnobrnja-Isailović, J. Lizards from urban areas are more asymmetric: Using fluctuating asymmetry to evaluate environmental disturbance. PLoS ONE 2013, 8, e84190. [Google Scholar] [CrossRef] [PubMed]
- Eeva, T.; Tanhuanpää, S.; Råbergh, C.; Airaksinen, S.; Nikinmaa, M.; Lehikoinen, E. Biomarkers and fluctuating asymmetry as indicators of pollution-induced stress in two hole-nesting passerines. Funct. Ecol. 2000, 14, 235–243. [Google Scholar] [CrossRef]
- Sánchez-Chardi, A.; García-Pando, M.; López-Fuster, M.J. Chronic exposure to environmental stressors induces fluctuating asymmetry in shrews inhabiting protected Mediterranean sites. Chemosphere 2013, 93, 916–923. [Google Scholar] [CrossRef] [PubMed]
- Beasley, D.A.E.; Bonisoli-Alquati, A.; Mousseau, T.A. The use of fluctuating asymmetry as a measure of environmentally induced developmental instability: A meta-analysis. Ecol. Indic. 2013, 30, 218–226. [Google Scholar] [CrossRef]
- Philp, R.B. Ecosystems and Human Health: Toxicology and Environmental Hazards; CRC Press: Boca Raton, FL, USA, 2015; p. 440. [Google Scholar]
- Kieser, J.A. Fluctuating odontometric asymmetry and maternal alcohol consumption. Ann. Hum. Biol. 1992, 19, 513–520. [Google Scholar] [CrossRef] [PubMed]
- Wilber, E.; Newell-Morris, L.; Streissguth, A.P. Dermatoglyphic asymmetry in fetal alcohol syndrome. Neonatology 1993, 64, 1–6. [Google Scholar] [CrossRef]
- Klingenberg, C.P.; Wetherill, L.; Rogers, J.; Moore, E.; Ward, R.; Autti-Rämö, I.; Fagerlund, Å.; Jacobson, S.W.; Robinson, L.K.; Hoyme, H.E. Prenatal alcohol exposure alters the patterns of facial asymmetry. Alcohol 2010, 44, 649–657. [Google Scholar] [CrossRef] [PubMed]
- Kieser, J.A.; Groeneveld, H.T. Effects of prenatal exposure to tobacco smoke on developmental stability in children. J. Craniofac. Genet. Dev. Biol. 1994, 14, 43–47. [Google Scholar] [PubMed]
- Kieser, J.A.; Groeneveld, H.T.; Da Silva, P.C.F. Dental asymmetry, maternal obesity, and smoking. Am. J. Phys. Anthropol. 1997, 102, 133–139. [Google Scholar] [CrossRef]
- Epstein, C.J. The Consequences of Chromosome Imbalance: Principles, Mechanisms, and Models; Cambridge University Press: Cambridge, UK, 2007; Volume 18, p. 510. [Google Scholar]
- Reeves, R.H.; Baxter, L.L.; Richtsmeier, J.T. Too much of a good thing: Mechanisms of gene action in Down syndrome. Trends Genet. 2001, 17, 83–88. [Google Scholar] [CrossRef]
- Shapiro, B.L. Development of human autosomal aneuploid phenotypes (with an emphasis on Down syndrome). Acta Zool. Fenn. 1992, 191, 97–105. [Google Scholar]
- Shapiro, B.L.; Hermann, J.; Opitz, J.M. Down syndrome—A disruption of homeostasis. Am. J. Med. Genet. 1983, 14, 241–269. [Google Scholar] [CrossRef] [PubMed]
- Benda, C.E. Down’s Syndrome: Mongolism and Its Management; Grune & Stratton: New York, NY, USA, 1969; p. 296. [Google Scholar]
- Antonarakis, S.E.; Lyle, R.; Dermitzakis, E.T.; Reymond, A.; Deutsch, S. Chromosome 21 and Down syndrome: From genomics to pathophysiology. Nat. Rev. Genet. 2004, 5, 725–738. [Google Scholar] [CrossRef] [PubMed]
- Korenberg, J.R.; Chen, X.N.; Schipper, R.; Sun, Z.; Gonsky, R.; Gerwehr, S.; Carpenter, N.; Daumer, C.; Dignan, P.; Disteche, C. Down syndrome phenotypes: The consequences of chromosomal imbalance. Proc. Natl. Acad. Sci. USA 1994, 91, 4997–5001. [Google Scholar] [CrossRef] [PubMed]
- Roizen, N.J.; Patterson, D. Down’s syndrome. Lancet 2003, 361, 1281–1289. [Google Scholar] [CrossRef]
- Garn, S.M.; Cohen, M.M.; Geciauskas, M.A. Increased crown-size asymmetry in trisomy G. J. Dent. Res. 1970, 49, 465. [Google Scholar] [CrossRef] [PubMed]
- Barden, H.S. Fluctuating dental asymmetry: A measure of developmental instability in Down syndrome. Am. J. Phys. Anthropol. 1980, 52, 169–173. [Google Scholar] [CrossRef] [PubMed]
- Townsend, G.C. Fluctuating dental asymmetry in Down’s syndrome. Aust. Dent. J. 1983, 28, 39–44. [Google Scholar] [CrossRef] [PubMed]
- Starbuck, J.M.; Cole, T.M.; Reeves, R.H.; Richtsmeier, J.T. Trisomy 21 and facial developmental instability. Am. J. Phys. Anthropol. 2013, 151, 49–57. [Google Scholar] [CrossRef] [PubMed]
- Plato, C.C.; Cereghino, J.J.; Steinberg, F.S. Palmar dermatoglyphics of Down’s syndrome: Revisited. Pediatr. Res. 1973, 7, 111–118. [Google Scholar] [CrossRef] [PubMed]
- Bots, J.; ten Broek, C.M.A.; Belien, J.A.M.; Bugiani, M.; Galis, F.; Van Dongen, S. Higher limb asymmetry in deceased human fetuses and infants with aneuploidy. Sci. Rep. 2014, 4, 3703. [Google Scholar] [CrossRef] [PubMed]
- Hartl, D.L.; Ruvolo, M. Genetics; Jones & Bartlett Publishers: Sudbury, MA, USA, 2011; p. 804. [Google Scholar]
- Debat, V.; Bloyer, S.; Faradji, F.; Gidaszewski, N.; Navarro, N.; Orozco-terWengel, P.; Ribeiro, V.; Schlötterer, C.; Deutsch, J.S.; Peronnet, F. Developmental stability: A major role for Cyclin G in Drosophila melanogaster. PLoS Genet. 2011, 7, e1002314. [Google Scholar] [CrossRef] [PubMed]
- Leamy, L.J.; Workman, M.S.; Routman, E.J.; Cheverud, J.M. An epistatic genetic basis for fluctuating asymmetry of tooth size and shape in mice. Heredity 2005, 94, 316–325. [Google Scholar] [CrossRef] [PubMed]
- Leamy, L.J.; Klingenberg, C.P. The genetics and evolution of fluctuating asymmetry. Annu. Rev. Ecol. Evol. Syst. 2005, 36, 1–21. [Google Scholar] [CrossRef]
- Leamy, L.J.; Routman, E.J.; Cheverud, J.M. Quantitative trait loci for fluctuating asymmetry of discrete skeletal characters in mice. Heredity 1998, 80, 509–518. [Google Scholar] [CrossRef] [PubMed]
- Leamy, L.J.; Routman, E.J.; Cheverud, J.M. An epistatic genetic basis for fluctuating asymmetry of mandible size in mice. Evolution 2002, 56, 642–653. [Google Scholar] [CrossRef] [PubMed]
- Charlesworth, D.; Willis, J.H. The genetics of inbreeding depression. Nat. Rev. Genet. 2009, 10, 783–796. [Google Scholar] [CrossRef] [PubMed]
- Keller, L.F.; Waller, D.M. Inbreeding effects in wild populations. Trends Ecol. Evol. 2002, 17, 230–241. [Google Scholar] [CrossRef]
- Meagher, S.; Penn, D.J.; Potts, W.K. Male–male competition magnifies inbreeding depression in wild house mice. Proc. Natl. Acad. Sci. USA 2000, 97, 3324–3329. [Google Scholar] [CrossRef] [PubMed]
- Miller, P.S. Is inbreeding depression more severe in a stressful environment? Zoo Biol. 1994, 13, 195–208. [Google Scholar] [CrossRef]
- Bihlmeyer, N.A.; Brody, J.A.; Smith, A.V.; Lunetta, K.L.; Nalls, M.; Smith, J.A.; Tanaka, T.; Davies, G.; Yu, L.; Mirza, S.S. Genetic diversity is a predictor of mortality in humans. BMC Genet. 2014, 15, 159. [Google Scholar] [CrossRef] [PubMed]
- Bittles, A.H. Time to get real: Investigating potential beneficial genetic aspects of consanguinity. Public Health Genom. 2011, 14, 169–171. [Google Scholar] [CrossRef] [PubMed]
- Bittles, A.H.; Black, M.L. The impact of consanguinity on neonatal and infant health. Early Hum. Dev. 2010, 86, 737–741. [Google Scholar] [CrossRef] [PubMed]
- Waldmann, P. The effect of inbreeding on fluctuating asymmetry in Scabiosa canescens (Dipsacaceae). Evol. Ecol. 2001, 15, 117–127. [Google Scholar] [CrossRef]
- Beardmore, J.A. Developmental stability in constant and fluctuating temperatures. Heredity 1960, 14, 411–422. [Google Scholar] [CrossRef]
- Carter, A.J.R.; Weier, T.M.; Houle, D. The effect of inbreeding on fluctuating asymmetry of wing veins in two laboratory strains of Drosophila melanogaster. Heredity 2009, 102, 563–572. [Google Scholar] [CrossRef] [PubMed]
- Gomendio, M.; Cassinello, J.; Roldan, E.R.S. A comparative study of ejaculate traits in three endangered ungulates with different levels of inbreeding: Fluctuating asymmetry as an indicator of reproductive and genetic stress. Proc. R. Soc. Lond. B. Biol. Sci. 2000, 267, 875–882. [Google Scholar] [CrossRef] [PubMed]
- Leamy, L. Morphometric studies in inbred and hybrid house mice. V. Directional and fluctuating asymmetry. Am. Nat. 1984, 123, 579–593. [Google Scholar] [CrossRef]
- Van Noordwijk, A.J.; Scharloo, W. Inbreeding in an island population of the great tit. Evolution 1981, 35, 674–688. [Google Scholar] [CrossRef]
- Fowler, K.; Whitlock, M.C. Fluctuating asymmetry does not increase with moderate inbreeding in Drosophila melanogaster. Heredity 1994, 73, 373–376. [Google Scholar] [CrossRef] [PubMed]
- Gilligan, D.M.; Woodworth, L.M.; Montgomery, M.E.; Nurthen, R.K.; Briscoe, D.A.; Frankham, R. Can fluctuating asymmetry be used to detect inbreeding and loss of genetic diversity in endangered populations? Anim. Conserv. 2000, 3, 97–104. [Google Scholar] [CrossRef]
- Hosken, D.J.; Blanckenhorn, W.U.; Ward, P.I. Developmental stability in yellow dung flies (Scathophaga stercoraria): Fluctuating asymmetry, heterozygosity and environmental stress. J. Evol. Biol. 2000, 13, 919–926. [Google Scholar] [CrossRef]
- Keller, L.; Passera, L. Incest avoidance, fluctuating asymmetry, and the consequences of inbreeding in Iridomyrmex humilis, an ant with multiple queen colonies. Behav. Ecol. Sociobiol. 1993, 33, 191–199. [Google Scholar] [CrossRef]
- Kruuk, L.E.B.; Slate, J.; Pemberton, J.M.; Clutton-Brock, T.H. Fluctuating asymmetry in a secondary sexual trait: No associations with individual fitness, environmental stress or inbreeding, and no heritability. J. Evol. Biol. 2003, 16, 101–113. [Google Scholar] [CrossRef] [PubMed]
- Lens, L.; Van Dongen, S.; Galbusera, P.; Schenck, T.; Matthysen, E.; Van de Casteele, T. Developmental instability and inbreeding in natural bird populations exposed to different levels of habitat disturbance. J. Evol. Biol. 2000, 13, 889–896. [Google Scholar] [CrossRef]
- Ben-David, Y.; Hershkovitz, I.; Rubin, D.; Moscona, D.; Ring, B. Inbreeding effects on tooth size, eruption age, and dental directional and fluctuating asymmetry among South Sinai Bedouins. In Structure, Function and Evolution of Teeth; Smith, P., Tchernov, E., Eds.; Freund Publishing House, Ltd.: London, UK, 1992; pp. 361–389. [Google Scholar]
- Livshits, G.; Kobyliansky, E. Fluctuating asymmetry as a possible measure of developmental homeostasis in humans: A review. Hum. Biol. 1991, 63, 441–466. [Google Scholar] [PubMed]
- Markow, T.A.; Martin, J.F. Inbreeding and developmental stability in a small human population. Ann. Hum. Biol. 1993, 20, 389–394. [Google Scholar] [CrossRef] [PubMed]
- Özener, B. Effect of inbreeding depression on growth and fluctuating asymmetry in Turkish young males. Am. J. Hum. Biol. 2010, 22, 557–562. [Google Scholar] [CrossRef] [PubMed]
- Özener, B.; Graham, J.H. Growth and fluctuating asymmetry of human newborns: Influence of inbreeding and parental education. Am. J. Phys. Anthropol. 2014, 153, 45–51. [Google Scholar] [CrossRef] [PubMed]
- Schaefer, K.; Lauc, T.; Mitteroecker, P.; Gunz, P.; Bookstein, F.L. Dental arch asymmetry in an isolated Adriatic community. Am. J. Phys. Anthropol. 2006, 129, 132–142. [Google Scholar] [CrossRef] [PubMed]
- Graham, J.H.; Felley, J.D. Genomic coadaptation and developmental stability within introgressed populations of Enneacanthus gloriosus and E. obesus (Pisces, Centrarchidae). Evolution 1985, 39, 104–114. [Google Scholar]
- Lynch, M. The genetic interpretation of inbreeding depression and outbreeding depression. Evolution 1991, 45, 622–629. [Google Scholar] [CrossRef]
- Brown, A.F. Outbreeding depression as a cost of dispersal in the harpacticoid copepod, Tigriopus californicus. Biol. Bull. 1991, 181, 123–126. [Google Scholar] [CrossRef]
- Edmands, S. Heterosis and outbreeding depression in interpopulation crosses spanning a wide range of divergence. Evolution 1999, 1757–1768. [Google Scholar] [CrossRef]
- Burton, R.S. Hybrid breakdown in developmental time in the copepod Tigriopus californicus. Evolution 1990, 44, 1814–1822. [Google Scholar] [CrossRef]
- Emlen, J.M. Heterosis and outbreeding depression: A multi-locus model and an application to salmon production. Fish. Res. 1991, 12, 187–212. [Google Scholar] [CrossRef]
- Gharrett, A.J.; Smoker, W.W.; Reisenbichler, R.R.; Taylor, S.G. Outbreeding depression in hybrids between odd- and even-broodyear pink salmon. Aquaculture 1999, 173, 117–129. [Google Scholar] [CrossRef]
- Gilk, S.E.; Wang, I.A.; Hoover, C.L.; Smoker, W.W.; Taylor, S.G.; Gray, A.K.; Gharrett, A. Outbreeding depression in hybrids between spatially separated pink salmon, Oncorhynchus gorbuscha, populations: Marine survival, homing ability, and variability in family size. Environ. Biol. Fishes 2004, 69, 287–297. [Google Scholar] [CrossRef]
- Lewis, M.B. Why are mixed-race people perceived as more attractive? Perception 2010, 39, 136–138. [Google Scholar] [CrossRef] [PubMed]
- Little, A.C.; Hockings, K.J.; Apicella, C.L.; Sousa, C. Mixed-ethnicity face shape and attractiveness in humans. Perception 2012, 41, 1486–1496. [Google Scholar] [CrossRef] [PubMed]
- Hallgrimsson, B.; Willmore, K.; Hall, B.K. Canalization, developmental stability, and morphological integration in primate limbs. Yearb. Phys. Anthropol. 2002, 45, 131–158. [Google Scholar] [CrossRef]
- Manning, J.T.; Chamberlain, A.T. Fluctuating asymmetry, sexual selection and canine teeth in primates. Proc. R. Soc. Lond. B. Biol. Sci. 1993, 251, 83–87. [Google Scholar] [CrossRef] [PubMed]
- Manning, J.T.; Chamberlain, A.T. Fluctuating asymmetry in gorilla canines: A sensitive indicator of environmental stress. Proc. R. Soc. Lond. B. Biol. Sci. 1994, 255, 189–193. [Google Scholar] [CrossRef] [PubMed]
- Sarringhaus, L.A.; Stock, J.T.; Marchant, L.F.; McGrew, W.C. Bilateral asymmetry in the limb bones of the chimpanzee (Pan troglodytes). Am. J. Phys. Anthropol. 2005, 128, 840–845. [Google Scholar] [CrossRef] [PubMed]
- Singh, N.; Harvati, K.; Hublin, J.-J.; Klingenberg, C.P. Morphological evolution through integration: A quantitative study of cranial integration in Homo, Pan, Gorilla and Pongo. J. Hum. Evol. 2012, 62, 155–164. [Google Scholar] [CrossRef] [PubMed]
- Willmore, K.E.; Klingenberg, C.P.; Hallgrímsson, B. The relationship between fluctuating asymmetry and environmental variance in rhesus macaque skulls. Evolution 2005, 59, 898–909. [Google Scholar] [CrossRef] [PubMed]
- Kegley, A.D.T.; Kuykendall, K.L. Dental asymmetry in South African australopithecines: A preliminary analysis of odontometric and morphological components. J. Hum. Evol. 2002, 42, A18–A19. [Google Scholar]
- Kegley, A.D.T.; Hemingway, J. Surveying stress and developmental stability in Homo habilis via fluctuating odontometric asymmetry: Assessing generic patterns and australopithecine differentiation. In Voyages in Science: Essays by South African Anatomists in Honour of Phillip V. Tobias’ 80th Birthday; Štrkalj, G., Pather, N., Kramer, B., Eds.; Content Solutions: Pretoria, South Africa, 2005; pp. 35–49. [Google Scholar]
- Frederick, M.J.; Gallup, G.G., Jr. Fluctuating dental asymmetry in great apes, fossil hominins, and modern humans: Implications for changing stressors during human evolution. Acta Psychol. Sin. 2007, 39, 489–494. [Google Scholar]
- Kieser, J.A.; Groeneveld, H.T. The assessment of fluctuating odontometric asymmetry from incomplete hominid fossil data. Anthropol. Anz. 1986, 44, 175–182. [Google Scholar] [PubMed]
- Baab, K.L.; McNulty, K.P. Size, shape, and asymmetry in fossil hominins: The status of the LB1 cranium based on 3D morphometric analyses. J. Hum. Evol. 2009, 57, 608–622. [Google Scholar] [CrossRef] [PubMed]
- Henneberg, M.; Eckhardt, R.B.; Chavanaves, S.; Hsü, K.J. Evolved developmental homeostasis disturbed in LB1 from Flores, Indonesia, denotes Down syndrome and not diagnostic traits of the invalid species Homo floresiensis. Proc. Natl. Acad. Sci. USA 2014, 111, 11967–11972. [Google Scholar] [CrossRef] [PubMed]
- Suarez, B.K. Neandertal dental asymmetry and the probable mutation effect. Am. J. Phys. Anthropol. 1974, 41, 411–416. [Google Scholar] [CrossRef] [PubMed]
- Baab, K.L.; Brown, P.; Falk, D.; Richtsmeier, J.T.; Hildebolt, C.F.; Smith, K.; Jungers, W. A critical evaluation of the Down syndrome diagnosis for LB1, type specimen of Homo floresiensis. PLoS ONE 2016, 11, e0155731. [Google Scholar] [CrossRef] [PubMed]
- Ríos, L.; Rosas, A.; Estalrrich, A.; García-Tabernero, A.; Bastir, M.; Huguet, R.; Pastor, F.; Sanchís-Gimeno, J.A.; de la Rasilla, M. Possible further evidence of low genetic diversity in the El Sidrón (Asturias, Spain) Neandertal group: Congenital clefts of the atlas. PLoS ONE 2015, 10, e0136550. [Google Scholar] [CrossRef] [PubMed]
- Sánchez-Quinto, F.; Lalueza-Fox, C. Almost 20 years of Neanderthal palaeogenetics: Adaptation, admixture, diversity, demography and extinction. Philos. Trans. R. Soc. Lond. B. Biol. Sci. 2015, 370. [Google Scholar] [CrossRef] [PubMed]
- Doyle, W.J.; Johnston, O. On the meaning of increased fluctuating dental asymmetry: A cross populational study. Am. J. Phys. Anthropol. 1977, 46, 127–134. [Google Scholar] [CrossRef] [PubMed]
- Dibennardo, R.; Bailit, H.L. Stress and dental asymmetry in a population of Japanese children. Am. J. Phys. Anthropol. 1978, 48, 89–94. [Google Scholar] [CrossRef] [PubMed]
- Perzigian, A.J. Fluctuating dental asymmetry: Variation among skeletal populations. Am. J. Phys. Anthropol. 1977, 47, 81–88. [Google Scholar] [CrossRef] [PubMed]
- Palmer, A.R.; Strobeck, C. Fluctuating asymmetry and developmental stability: Heritability of observable variation vs. heritability of inferred cause. J. Evol. Biol. 1997, 10, 39–49. [Google Scholar] [CrossRef]
- Steele, J. Handedness in past human populations: Skeletal markers. Laterality 2000, 5, 193–220. [Google Scholar] [PubMed]
- Schiess, R.; Haeusler, M. No skeletal dysplasia in the Nariokotome boy KNM-WT 15000 (Homo erectus)—A reassessment of congenital pathologies of the vertebral column. Am. J. Phys. Anthropol. 2013, 150, 365–374. [Google Scholar] [CrossRef] [PubMed]
- Trinkaus, E.; Churchill, S.E.; Ruff, C.B. Postcranial robusticity in Homo. II: Humeral bilateral asymmetry and bone plasticity. Am. J. Phys. Anthropol. 1994, 93, 1–34. [Google Scholar] [CrossRef] [PubMed]
- Constandse-Westermann, T.S.; Newell, R.R. Limb lateralization and social stratification in western European Mesolithic societies. In People and Culture in Change; Hershkovitz, I., Ed.; British Archeological Reports International Series: Oxford, UK, 1989; pp. 405–433. [Google Scholar]
- Cohen, M.N.; Armelagos, G.J. Paleopathology at the Origins of Agriculture; University Press of Florida: Gainesville, FL, USA, 1984; p. 615. [Google Scholar]
- Hoover, K.C.; Matsumura, H. Temporal variation and interaction between nutritional and developmental instability in prehistoric Japanese populations. Am. J. Phys. Anthropol. 2008, 137, 469–478. [Google Scholar] [CrossRef] [PubMed]
- DeLeon, V.B. Fluctuating asymmetry and stress in a medieval Nubian population. Am. J. Phys. Anthropol. 2007, 132, 520–534. [Google Scholar] [CrossRef] [PubMed]
- Lieberman, D.E.; Devlin, M.J.; Pearson, O.M. Articular area responses to mechanical loading: Effects of exercise, age, and skeletal location. Am. J. Phys. Anthropol. 2001, 116, 266–277. [Google Scholar] [CrossRef] [PubMed]
- Pearson, O.M.; Lieberman, D.E. The aging of Wolff’s “law”: Ontogeny and responses to mechanical loading in cortical bone. Yearb. Phys. Anthropol. 2004, 47, 63–99. [Google Scholar] [CrossRef] [PubMed]
- Frost, H.M. Joint anatomy, design, and arthroses: Insights of the Utah paradigm. Anat. Record 1999, 255, 162–174. [Google Scholar] [CrossRef]
- Hamrick, M.W. A chondral modeling theory revisited. J. Theor. Biol. 1999, 201, 201–208. [Google Scholar] [CrossRef] [PubMed]
- Plochocki, J.H. Bilateral variation in limb articular surface dimensions. Am. J. Hum. Biol. 2004, 16, 328–333. [Google Scholar] [CrossRef] [PubMed]
- Ĉuk, T.; Leben-Seljak, P.; Štefanĉiĉ, M. Lateral asymmetry of human long bones. Var. Evol. 2001, 9, 19–32. [Google Scholar]
- Mays, S.; Steele, J.; Ford, M. Directional asymmetry in the human clavicle. Int. J. Osteoarchaeol. 1999, 9, 18–28. [Google Scholar] [CrossRef]
- Plochocki, J.H. Directional bilateral asymmetry in human sacral morphology. Int. J. Osteoarchaeol. 2002, 12, 349–355. [Google Scholar] [CrossRef]
- Whitlock, M. The heritability of fluctuating asymmetry and the genetic control of developmental stability. Proc. R. Soc. Lond. B. Biol. Sci. 1996, 263, 849–853. [Google Scholar] [CrossRef] [PubMed]
- Whitlock, M. The repeatability of fluctuating asymmetry: A revision and extension. Proc. R. Soc. Lond. B. Biol. Sci. 1998, 265, 1429–1431. [Google Scholar] [CrossRef]
- Tracy, M.; Freeman, D.C.; Duda, J.J.; Miglia, K.J.; Graham, J.H.; Hough, R.A. Developmental instability: An appropriate indicator of plant fitness components. In Developmental Instability: Causes and Consequences; Polak, M., Ed.; Oxford University Press: New York, NY, USA, 2003; pp. 196–212. [Google Scholar]
- Cowart, N.M.; Graham, J.H. Within- and among-individual variation in fluctuating asymmetry of leaves in the fig (Ficus carica L.). Int. J. Plant Sci. 1999, 160, 116–121. [Google Scholar] [CrossRef]
- Leung, B.; Forbes, M.R.; Houle, D. Fluctuating asymmetry as a bioindicator of stress: Comparing efficacy of analyses involving multiple traits. Am. Nat. 2000, 155, 101–115. [Google Scholar] [CrossRef] [PubMed]
- Thornhill, R.; Gangestad, S.W. Facial attractiveness. Trends Cogn. Sci. 1999, 3, 452–460. [Google Scholar] [CrossRef]
- Møller, A.P.; Thornhill, R. Bilateral symmetry and sexual selection: A meta-analysis. Am. Nat. 1998, 151, 174–192. [Google Scholar] [CrossRef] [PubMed]
- Palmer, A.R. Detecting publication bias in meta-analyses: A case study of fluctuating asymmetry and sexual selection. Am. Nat. 1999, 154, 220–233. [Google Scholar] [CrossRef]
- Thornhill, R.; Møller, A.P.; Gangestad, S.W. The biological significance of fluctuating asymmetry and sexual selection: A reply to Palmer. Am. Nat. 1999, 154, 234–241. [Google Scholar] [CrossRef]
- Van Dongen, S. Associations between asymmetry and human attractiveness: Possible direct effects of asymmetry and signatures of publication bias. Ann. Hum. Biol. 2011, 38, 317–323. [Google Scholar] [CrossRef] [PubMed]
- Van Dongen, S.; Gangestad, S.W. Human fluctuating asymmetry in relation to health and quality: A meta-analysis. Evol. Hum. Behav. 2011, 32, 380–398. [Google Scholar] [CrossRef]
- Van Dongen, S. Fluctuating asymmetry and masculinity/femininity in humans: A meta-analysis. Arch. Sex. Behav. 2012, 41, 1453–1460. [Google Scholar] [CrossRef] [PubMed]
- Sim, K. The relationship between sex-typical body shape and quality indicators. J. Soc. Evol. Cult. Psychol. 2013, 7, 97–120. [Google Scholar] [CrossRef]
- Van Dongen, S. Associations among facial masculinity, physical strength, fluctuating asymmetry and attractiveness in young men and women. Ann. Hum. Biol. 2014, 41, 205–213. [Google Scholar] [CrossRef] [PubMed]
- Hughes, S.M.; Harrison, M.A.; Gallup, G.G. The sound of symmetry: Voice as a marker of developmental instability. Evol. Hum. Behav. 2002, 23, 173–180. [Google Scholar] [CrossRef]
- Hughes, S.M.; Pastizzo, M.J.; Gallup, G.G., Jr. The sound of symmetry revisited: Subjective and objective analyses of voice. J. Nonverbal Behav. 2008, 32, 93–108. [Google Scholar] [CrossRef]
- Abend, P.; Pflüger, L.S.; Koppensteiner, M.; Coquerelle, M.; Grammer, K. The sound of female shape: A redundant signal of vocal and facial attractiveness. Evol. Hum. Behav. 2015, 36, 174–181. [Google Scholar] [CrossRef]
- Hill, A.K.; Cárdenas, R.A.; Wheatley, J.R.; Welling, L.L.M.; Burriss, R.P.; Claes, P.; Apicella, C.L.; McDaniel, M.A.; Little, A.C.; Shriver, M.D.; et al. Are there vocal cues to human developmental stability? Relationships between facial fluctuating asymmetry and voice attractiveness. Evol. Hum. Behav. 2016. [Google Scholar] [CrossRef]
- Jones, B.C.; Little, A.C.; Feinberg, D.R.; Penton-Voak, I.S.; Tiddeman, B.P.; Perrett, D.I. The relationship between shape symmetry and perceived skin condition in male facial attractiveness. Evol. Hum. Behav. 2004, 25, 24–30. [Google Scholar] [CrossRef]
- Weinberg, S.M.; Neiswanger, K.; Martin, R.A.; Mooney, M.P.; Kane, A.A.; Wenger, S.L.; Losee, J.; Deleyiannis, F.; Ma, L.; De Salamanca, J.E. The Pittsburgh Oral-Facial Cleft study: Expanding the cleft phenotype. Background and justification. Cleft Palate Cranio-Fac. J. 2006, 43, 7–20. [Google Scholar] [CrossRef] [PubMed]
- Neiswanger, K.; Cooper, M.E.; Weinberg, S.M.; Flodman, P.; Keglovits, A.B.; Liu, Y.; Hu, D.-N.; Melnick, M.; Spence, M.A.; Marazita, M.L. Cleft lip with or without cleft palate and dermatoglyphic asymmetry: Evaluation of a Chinese population. Orthod. Craniofac. Res. 2002, 5, 140–146. [Google Scholar] [CrossRef] [PubMed]
- Flores-Mondragón, G.; Paredes-Espinoza, M.A.; Hernández-Campos, N.A.; Sánchez-Chapul, L.; Paniagua-Pérez, R.; Martínez-Canseco, C.; Renán-León, S.; Araujo-Monsalvo, V.M.; Perea-Paz, J.M.; Flores-Jacinto, A. Facial anthropometry: A tool for quantitative evaluation in patients with peripheral facial paralysis. Int. J. Sci. Eng. Res. 2015, 6, 1657–1660. [Google Scholar]
- Garland, T.; Freeman, P.W. Selective breeding for high endurance running increases hindlimb symmetry. Evolution 2005, 59, 1851–1854. [Google Scholar] [CrossRef] [PubMed]
- Trivers, R.; Palestis, B.G.; Manning, J.T. The symmetry of children’s knees is linked to their adult sprinting speed and their willingness to sprint in a long-term Jamaican study. PLoS ONE 2013, 8, e72244. [Google Scholar] [CrossRef] [PubMed]
- Trivers, R.; Fink, B.; Russell, M.; McCarty, K.; James, B.; Palestis, B.G. Lower body symmetry and running performance in elite Jamaican track and field athletes. PLoS ONE 2014, 9, e113106. [Google Scholar] [CrossRef] [PubMed]
- Oxford, M. The Effect of Muscle Imbalance on Running Performance in Collegiate Level Athletes. Master’s Thesis, University of Windsor, Windsor, ON, Canada, 2013. [Google Scholar]
- Al-Eisa, E.; Egan, D.; Wassersug, R. Fluctuating asymmetry and low back pain. Evol. Hum. Behav. 2004, 25, 31–37. [Google Scholar] [CrossRef]
- Goldberg, C.J.; Fogarty, E.E.; Moore, D.P.; Dowling, F.E. Fluctuating asymmetry and vertebral malformation: A study of palmar dermatoglyphics in congenital spinal deformities. Spine 1997, 22, 775–779. [Google Scholar] [CrossRef] [PubMed]
- Mittal, V.A.; Dean, D.J.; Pelletier, A. Dermatoglyphic asymmetries and fronto-striatal dysfunction in young adults reporting non-clinical psychosis. Acta Psychiatr. Scand. 2012, 126, 290–297. [Google Scholar] [CrossRef] [PubMed]
- Stiles, J.; Jernigan, T.L. The basics of brain development. Neuropsychol. Rev. 2010, 20, 327–348. [Google Scholar] [CrossRef] [PubMed]
- Kavanagh, D.H.; Tansey, K.E.; O’Donovan, M.C.; Owen, M.J. Schizophrenia genetics: Emerging themes for a complex disorder. Mol. Psychiatry 2015, 20, 72–76. [Google Scholar] [CrossRef] [PubMed]
- Reilly, J.L.; Murphy, P.T.; Byrne, M.; Larkin, C.; Gill, M.; O’Callaghan, E.; Lane, A. Dermatoglyphic fluctuating asymmetry and atypical handedness in schizophrenia. Schizophr. Res. 2001, 50, 159–168. [Google Scholar] [CrossRef]
- Cohen, J. Statistical Power Analysis for the Behavior Sciences; Lawrance Eribaum Association: Hillsdale, NJ, USA, 1988; p. 487. [Google Scholar]
- Abrahams, B.S.; Geschwind, D.H. Connecting genes to brain in the autism spectrum disorders. Arch. Neurol. 2010, 67, 395–399. [Google Scholar] [CrossRef] [PubMed]
- Geschwind, D.H. Genetics of autism spectrum disorders. Trends Cognit. Sci. 2011, 15, 409–416. [Google Scholar] [CrossRef] [PubMed]
- Bates, T.C. Fluctuating asymmetry and intelligence. Intelligence 2007, 35, 41–46. [Google Scholar] [CrossRef]
- Furlow, F.B.; Armijo–Prewitt, T.; Gangestad, S.W.; Thornhill, R. Fluctuating asymmetry and psychometric intelligence. Proc. R. Soc. Lond. B. Biol. Sci. 1997, 264, 823–829. [Google Scholar] [CrossRef] [PubMed]
- Prokosch, M.D.; Yeo, R.A.; Miller, G.F. Intelligence tests with higher g-loadings show higher correlations with body symmetry: Evidence for a general fitness factor mediated by developmental stability. Intelligence 2005, 33, 203–213. [Google Scholar] [CrossRef]
- Banks, G.C.; Batchelor, J.H.; McDaniel, M.A. Smarter people are (a bit) more symmetrical: A meta-analysis of the relationship between intelligence and fluctuating asymmetry. Intelligence 2010, 38, 393–401. [Google Scholar] [CrossRef]
- Yeo, R.A.; Gangestad, S.W.; Daniel, W.F. Hand preference and developmental instability. Psychobiology 1993, 21, 161–168. [Google Scholar]
- Somers, M.; Ophoff, R.A.; Aukes, M.F.; Cantor, R.M.; Boks, M.P.; Dauwan, M.; de Visser, K.L.; Kahn, R.S.; Sommer, I.E. Linkage analysis in a Dutch population isolate shows no major gene for left-handedness or atypical language lateralization. J. Neurosci. 2015, 35, 8730–8736. [Google Scholar] [CrossRef] [PubMed]
- Benderlioglu, Z.; Sciulli, P.W.; Nelson, R.J. Fluctuating asymmetry predicts human reactive aggression. Am. J. Hum. Biol. 2004, 16, 458–469. [Google Scholar] [CrossRef] [PubMed]
- Furlow, B.; Gangestad, S.W.; Armijo-Prewitt, T. Developmental stability and human violence. Proc. R. Soc. Lond. B. Biol. Sci. 1998, 265, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Özener, B.; Atamtürk, D.; Duyar, İ. Self-reported aggressiveness is not related to developmental instability. Am. J. Hum. Biol. 2015, 27, 867–870. [Google Scholar] [CrossRef] [PubMed]
- Özener, B.; Pelin, C.; Kürkçüoğlu, A.; Zağyapan, R. Facial symmetry is not a reliable cue of aggressive behavior. Eurasian J. Anthropol. 2012, 3, 32–40. [Google Scholar]
- Manning, J.T.; Wood, D. Fluctuating asymmetry and aggression in boys. Hum. Nat. 1998, 9, 53–65. [Google Scholar] [CrossRef] [PubMed]
- Muñoz-Reyes, J.A.; Gil-Burmann, C.; Fink, B.; Turiegano, E. Facial asymmetry and aggression in Spanish adolescents. Personal. Individ. Differ. 2012, 53, 857–861. [Google Scholar] [CrossRef]
- Holtzman, N.S.; Augustine, A.A.; Senne, A.L. Are pro-social or socially aversive people more physically symmetrical? Symmetry in relation to over 200 personality variables. J. Res. Personal. 2011, 45, 687–691. [Google Scholar] [CrossRef]
- Nuzzo, R. Statistical errors. Nature 2014, 506, 150–152. [Google Scholar] [CrossRef] [PubMed]
- Head, M.L.; Holman, L.; Lanfear, R.; Kahn, A.T.; Jennions, M.D. The extent and consequences of p-hacking in science. PLoS Biol. 2015, 13, e1002106. [Google Scholar] [CrossRef] [PubMed]
- Hurlbert, S.H.; Lombardi, C.M. Final collapse of the Neyman-Pearson decision theoretic framework and rise of the neoFisherian. Ann. Zool. Fenn. 2009, 46, 311–349. [Google Scholar] [CrossRef]
- Lombardi, C.M.; Hurlbert, S.H. Misprescription and misuse of one-tailed tests. Austral Ecol. 2009, 34, 447–468. [Google Scholar] [CrossRef]
- Kozlov, M.V.; Zvereva, E.L. Confirmation bias in studies of fluctuating asymmetry. Ecol. Indic. 2015, 57, 293–297. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Graham, J.H.; Özener, B. Fluctuating Asymmetry of Human Populations: A Review. Symmetry 2016, 8, 154. https://doi.org/10.3390/sym8120154
Graham JH, Özener B. Fluctuating Asymmetry of Human Populations: A Review. Symmetry. 2016; 8(12):154. https://doi.org/10.3390/sym8120154
Chicago/Turabian StyleGraham, John H., and Bariş Özener. 2016. "Fluctuating Asymmetry of Human Populations: A Review" Symmetry 8, no. 12: 154. https://doi.org/10.3390/sym8120154
APA StyleGraham, J. H., & Özener, B. (2016). Fluctuating Asymmetry of Human Populations: A Review. Symmetry, 8(12), 154. https://doi.org/10.3390/sym8120154





