The Standard-Model Extension and Gravitational Tests
Abstract
:1. Introduction
2. Symmetry Violation
2.1. Rotations
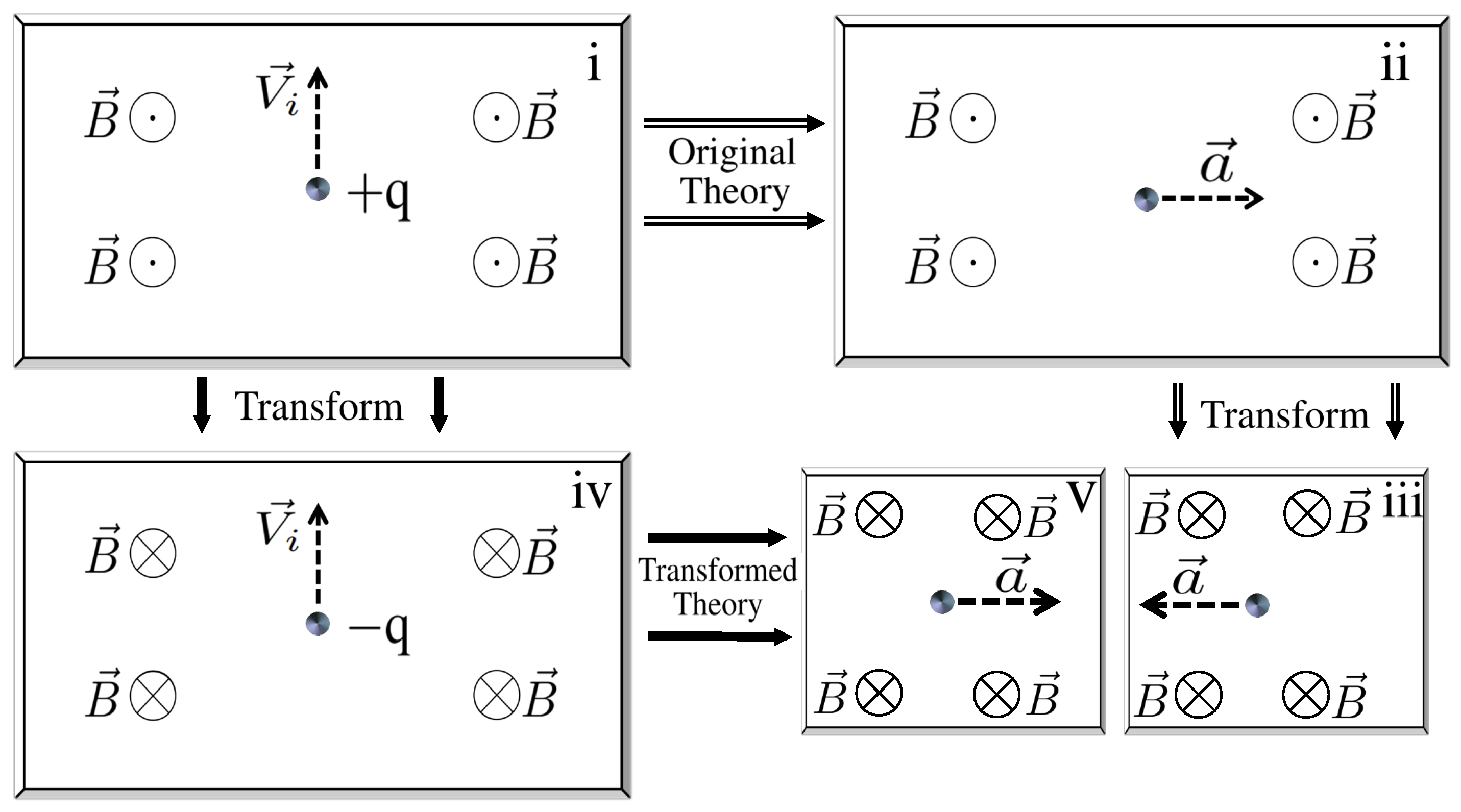
2.2. CPT
3. The SME
3.1. Gravitationally Coupled Matter
3.2. Pure Gravity
4. Gravitational Tests: Existing Results and Proposals
5. Gravitational Čerenkov
6. Conclusions
Conflicts of Interest
References
- Kostelecký, V.A.; Samuel, S. Spontaneous breaking of Lorentz symmetry in string theory. Phys. Rev. D 1989, 39, 683. [Google Scholar] [CrossRef]
- Kostelecký, V.A.; Potting, R. CPT and strings. Nucl. Phys. B 1991, 359, 545. [Google Scholar] [CrossRef]
- Colladay, D.; Kostelecký, V.A. CPT violation and the standard model. Phys. Rev. D 1997, 55, 6760. [Google Scholar] [CrossRef]
- Colladay, D.; Kostelecký, V.A. Lorentz-violating extension of the standard model. Phys. Rev. D 1998, 58, 116002. [Google Scholar] [CrossRef]
- Kostelecký, V.A. Gravity, Lorentz violation, and the standard model. Phys. Rev. D 2004, 69, 105009. [Google Scholar] [CrossRef]
- Kostelecký, V.A.; Mewes, M. Electrodynamics with Lorentz-violating operators of arbitrary dimension. Phys. Rev. D 2009, 80, 015020. [Google Scholar] [CrossRef]
- Kostelecký, V.A.; Mewes, M. Neutrinos with Lorentz-violating operators of arbitrary dimension. Phys. Rev. D 2012, 85, 096005. [Google Scholar] [CrossRef]
- Kostelecký, V.A.; Mewes, M. Fermions with Lorentz-violating operators of arbitrary dimension. Phys. Rev. D 2013, 88, 096006. [Google Scholar] [CrossRef]
- Kostelecký, V.A.; Russell, N. Data tables for Lorentz and CPT violation. Rev. Mod. Phys. 2011, 83, 11. [Google Scholar] [CrossRef]
- Tasson, J.D. What do we know about Lorentz invariance? Rep. Prog. Phys. 2014, 77, 062901. [Google Scholar] [CrossRef] [PubMed]
- Liberati, S. Tests of Lorentz invariance: A 2013 update. Class. Quant. Grav. 2013, 30, 133001. [Google Scholar] [CrossRef]
- Will, C.M. The confrontation between general relativity and experiment. Living Rev. Relativ. 2014, 17, 4. [Google Scholar] [CrossRef]
- Yunes, N.; Pretorius, F. Fundamental theoretical bias in gravitational wave astrophysics and the parametrized post-Einsteinian framework. Phys. Rev. D 2009, 80, 122003. [Google Scholar] [CrossRef]
- Kostelecký, V.A.; Tasson, J.D. Constraints on Lorentz violation from gravitational Čerenkov radiation. Phys. Lett. B 2015, 749, 551. [Google Scholar] [CrossRef]
- Kostelecký, V.A.; Russell, N.; Tasson, J.D. Constraints on torsion from bounds on Lorentz violation. Phys. Rev. Lett. 2008, 100, 111102. [Google Scholar] [CrossRef] [PubMed]
- Tasson, J.D. Lorentz violation, gravitomagnetism, and intrinsic spin. Phys. Rev. D 2012, 86, 124021. [Google Scholar] [CrossRef]
- Bertschinger, T.H.; Flowers, N.A.; Tasson, J.D. Observer and particle transformations. In CPT and Lorentz Symmetry; Kostelecký, V.A., Ed.; World Scientific: Singapore, 2014; Volume VI. [Google Scholar]
- Lehnert, R. CPT symmetry and its violation. Symmetry 2016. submitted. [Google Scholar]
- Díaz, J.S. Testing Lorentz and CPT invariance with neutrinos. Symmetry 2016, 8, 105. [Google Scholar] [CrossRef]
- Itzykson, C.; Zuber, J.-B. Quantum Field Theory; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Tasson, J.D. Antimatter, Lorentz symmetry, and gravity. Hyperfine Interact. in press.
- Bailey, Q.G.; Kostelecký, V.A.; Xu, R. Short-range gravity and Lorentz violation. Phys. Rev. D 2015, 91, 022006. [Google Scholar] [CrossRef]
- Kostelecký, V.A.; Mewes, M. Testing local Lorentz invariance with gravitational waves. Phys. Lett. B 2016, 757, 510. [Google Scholar] [CrossRef]
- Bailey, Q.G. Anisotropic cubic curvature couplings. Phys. Rev. D 2016, 94, 065029. [Google Scholar] [CrossRef]
- Bluhm, R. Explicit versus spontaneous diffeomorphism breaking in gravity. Phys. Rev. D 2015, 91, 065034. [Google Scholar] [CrossRef]
- Bluhm, R. Spacetime symmetry breaking and Einstein-Maxwell theory. Phys. Rev. D 2015, 92, 085015. [Google Scholar] [CrossRef]
- Kostelecký, V.A.; Tasson, J.D. Matter-gravity couplings and Lorentz violation. Phys. Rev. D 2011, 83, 016013. [Google Scholar] [CrossRef]
- Kostelecký, V.A.; Tasson, J.D. Prospects for large relativity violations in matter-gravity couplings. Phys. Rev. Lett. 2009, 102, 010402. [Google Scholar] [CrossRef] [PubMed]
- Bailey, Q.G.; Kostelecký, V.A. Signals for Lorentz violation in post-Newtonian gravity. Phys. Rev. D 2006, 74, 045001. [Google Scholar] [CrossRef]
- Lane, C.D. Spacetime variation of Lorentz-violation coefficients at nonrelativistic scale. Phys. Rev. D 2016, 94, 025016. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. LIGO scientific collaboration and virgo collaboration. Observation of gravitational waves from a binary black hole merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef] [PubMed]
- Yunes, N.; Yagi, K.; Pretorius, F. Theoretical physics implications of the binary black-hole mergers GW150914 and GW151226. Phys. Rev. D 2016, 94, 084002. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. LIGO scientific collaboration and virgo collaboration. GW151226: Observation of gravitational waves from a 22-Solar-Mass binary black hole coalescence. Phys. Rev. Lett. 2016, 116, 241103. [Google Scholar] [CrossRef] [PubMed]
- Kostelecký, V.A.; Melissinos, A.; Mewes, M. Searching for photon-sector Lorentz violation using gravitational-wave detectors. Phys. Lett. B 2016, 761, 1. [Google Scholar] [CrossRef]
- Schreck, M. Looking for Lorentz violation with gravitational waves. 2016; arXiv:1603.07452. [Google Scholar]
- Bonder, Y. Lorentz violation in the gravity sector: The t puzzle. Phys. Rev. D 2015, 91, 125002. [Google Scholar] [CrossRef]
- Flowers, N.A.; Goodge, C.; Tasson, J.D.; Carleton College, Northfield, MN, USA. Unpublished work. 2016.
- Shao, C.-G.; Tan, Y.-J.; Tan, W.-H.; Yang, S.-Q.; Luo, J.; Tobar, M.E.; Bailey, Q.G.; Long, J.C.; Weisman, E.; Xu, R.; et al. Combined search for Lorentz violation in short-range gravity. Phys. Rev. Lett. 2016, 117, 071102. [Google Scholar] [CrossRef] [PubMed]
- Shao, C.-G.; Tan, Y.-J.; Tan, W.-H.; Yang, S.-Q.; Luo, J.; Tobar, M.E. Search for Lorentz invariance violation through tests of the gravitational inverse square law at short-ranges. Phys. Rev. D 2015, 91, 102007. [Google Scholar] [CrossRef]
- Kostelecký, V.A.; Long, J.C. Search for Lorentz violation in short-range gravity. Phys. Rev. D 2015, 91, 092003. [Google Scholar]
- Panjwani, H.; Carbone, L.; Speake, C.C. Laboratory searches for preferred frame effects. In CPT and Lorentz Symmetry; Kostelecký, V.A., Ed.; World Scientific: Singapore, 2011; Volume V. [Google Scholar]
- Bennett, D.; Skavysh, V.; Long, J.C. Search for Lorentz violation in a short-range gravity experiment. In CPT and Lorentz Symmetry; Kostelecký, V.A., Ed.; World Scientific: Singapore, 2011; Volume V. [Google Scholar]
- Battat, J.B.R.; Chandler, J.F.; Stubbs, C.W. Testing for Lorentz violation: Constraints on standard- model-extension parameters via lunar laser ranging. Phys. Rev. Lett. 2007, 99, 241103. [Google Scholar] [CrossRef] [PubMed]
- Bourgoin, A.; Hees, A.; Bouquillon, S.; Le Poncin-Lafitte, C.; Francou, G.; Angonin, M.-C. Testing Lorentz symmetry with lunar laser ranging. 2016; arXiv:1607.00294. [Google Scholar]
- Le Poncin-Lafitte, C.; Hees, A.; Lambert, S. Lorentz symmetry and very long baseline interferometry. 2016; arXiv:1604.01663. [Google Scholar]
- Shao, L. Tests of local Lorentz invariance violation of gravity in the standard model extension with pulsars. Phys. Rev. Lett. 2014, 112, 111103. [Google Scholar] [CrossRef] [PubMed]
- Shao, L. New pulsar limit on local Lorentz invariance violation of gravity in the standard-model extension. Phys. Rev. D 2014, 90, 122009. [Google Scholar] [CrossRef]
- Hees, A.; Bailey, Q.G.; Le Poncin-Lafitte, C.; Bourgoin, A.; Rivoldini, A.; Lamine, B.; Meynadier, F.; Guerlin, C.; Wolf, P. Testing Lorentz symmetry with planetary orbital dynamics. Phys. Rev. D 2015, 92, 064049. [Google Scholar] [CrossRef]
- Bailey, Q.G.; Everett, R.D.; Overduin, J.M. Limits on violations of Lorentz symmetry from gravity probe B. Phys. Rev. D 2013, 88, 102001. [Google Scholar] [CrossRef]
- Hohensee, M.A.; Mueller, H.; Wiringa, R.B. Equivalence principle and bound kinetic energy. Phys. Rev. Lett. 2013, 111, 151102. [Google Scholar] [CrossRef] [PubMed]
- Hohensee, H.M.; Chu, S.; Peters, A.; Mueller, H. Equivalence principle and gravitational redshift. Phys. Rev. Lett. 2011, 106, 151102. [Google Scholar] [CrossRef] [PubMed]
- Chung, K.-Y.; Chiow, S.-W.; Herrmann, S.; Chu, S.; Mueller, H. Atom interferometry tests of local Lorentz invariance in gravity and electrodynamics. Phys. Rev. D 2009, 80, 016002. [Google Scholar] [CrossRef]
- Mueller, H.; Chiow, S.-W.; Herrmann, S.; Chu, S.; Chung, K.-Y. Atom interferometry tests of the isotropy of post-Newtonian gravity. Phys. Rev. Lett. 2008, 100, 031101. [Google Scholar] [CrossRef] [PubMed]
- Dimopoulos, S.; Graham, P.W.; Hogan, J.M.; Kasevich, M.A. Testing general relativity with atom interferometry. Phys. Rev. Lett. 2007, 98, 111102. [Google Scholar] [CrossRef] [PubMed]
- Scaramuzza, N.; Tasson, J.D. Laser gyroscopes, gravity, and the SME. In CPT and Lorentz Symmetry; Kostelecký, V.A., Ed.; World Scientific: Singapore, 2017; Volume VII. [Google Scholar]
- Scaramuzza, N.; Tasson, J.D.; Carleton College, Northfield, MN, USA. Unpublished work. 2016.
- Ortolan, A.; Belfi, J.; Bosi, F.; Di Virgilio, A.; Beverini, N.; Carelli, G.; Maccioni, E.; Santagata, R.; Simonelli, A.; Beghi, A.; et al. The GINGER project and status of the GINGERino prototype at LNGS. J. Phys. Conf. Ser. 2016, 718, 072003. [Google Scholar] [CrossRef]
- Wagner, T.A.; Schlamminger, S.; Gundlach, J.H.; Adelberger, E.G. Torsion-balance tests of the weak equivalence principle. Class. Quantum Grav. 2012, 29, 184002. [Google Scholar] [CrossRef]
- Jennings, R.J.; Tasson, J.D.; Yang, S. Matter-sector Lorentz violation in binary pulsars. Phys. Rev. D 2015, 92, 125028. [Google Scholar] [CrossRef]
- Shao, L.; Stairs, I.H.; Antoniadis, J.; Deller, A.T.; Freire, P.C.C.; Hessels, J.W.T.; Janssen, G.H.; Kramer, M.; Kunz, J.; Lämmerzahl, C.; et al. Testing gravity with pulsars in the SKA era. In Proceedings of the Advancing Astrophysics with the Square Kilometre Array (AASKA14), Giardini Naxos, Italy, 9–13 June 2014.
- Altschul, B.; Bailey, Q.G.; Blanchet, L.; Bongs, K.; Bouyer, P.; Cacciapuoti, L.; Capozziello, S.; Gaaloul, N.; Giulini, D.; Hartwig, J.; et al. Quantum tests of the Einstein Equivalence Principle with the STE-QUEST space mission. Adv. Space Res. 2015, 501, 55. [Google Scholar]
- Bergé, J.; Touboul, P.; Rodrigues, M. Status of MICROSCOPE, a mission to test the Equivalence Principle in space. J. Phys. Conf. Ser. 2015, 610, 12009. [Google Scholar] [CrossRef]
- Nobili1, A.M.; Shao, M.; Pegna, R.; Zavattini, G.; Turyshev, S.G.; Lucchesi, D.M.; De Michele1, A.; Doravari, S.; Comandi, G.L.; Saravanan, T.R.; et al. “Galileo Galilei” (GG): Space test of the weak equivalence principle to 10−17 and laboratory demonstrations. Class. Quantum Grav. 2012, 29, 184011. [Google Scholar] [CrossRef]
- Overduin, J.; Everitt, F.; Worden, P.; Mester, J. STEP and fundamental physics. Class. Quantum Grav. 2012, 29, 184012. [Google Scholar] [CrossRef]
- Kostelecký, V.A.; Vargas, A. Lorentz and CPT tests in hydrogen, antihydrogen, and related systems. Phys. Rev. D 2015, 92, 056002. [Google Scholar] [CrossRef]
- Kellerbauer, A.; Amoretti, M.; Belov, A.S.; Bonomi, G.; Boscolo, I.; Brusa, R.S.; Büchner, M.; Byakov, V.M.; Cabaret, L.; Canali, C.; et al. AEgIS Collaboration. Proposed antimatter gravity measurement with an antihydrogen beam. Nucl. Instrum. Methods Phys. Res. B 2008, 266, 351. [Google Scholar] [CrossRef]
- Amole, C.; Ashkezari, M.D.; Baquero-Ruiz, M.; Bertsche, W.; Butler, E.; Capra, A.; Cesar, C.L.; Charlton, M.; Eriksson, S.; Fajans, J.; et al. Description and first application of a new technique to measure the gravitational mass of antihydrogen. Nat. Commun. 2013, 4, 1785. [Google Scholar] [CrossRef] [PubMed]
- Indelicato, P.; Chardin, G.; Grandemange, P.; Lunney, D.; Manea, V.; Badertscher, A.; Crivelli, P.; Curioni, A.; Marchionni, A.; Rossi, B.; et al. The Gbar project, or how does antimatter fall? Hyperfine Interact. 2014, 228, 141. [Google Scholar] [CrossRef]
- Cronin, A.D.; Phillips, T.J.; Fischler, M.; Hahn, A.; Volk, J.T.; Yeh, G.P.; Greaves, R.G.; Howe, S.D.; Jackson, G.P.; Lewis, R.; et al. Letter of intent: Antimatter antigravity experiment (AGE) at Fermilab. 6 February 2009. [Google Scholar]
- Dittus, H.; Lämmerzahl, C. Tests of the weak equivalence principle for charged particles in space. Adv. Space Res. 2007, 39, 244. [Google Scholar] [CrossRef]
- Kirch, K.; Khaw, K.S. Testing antimatter gravity with muonium. Int. J. Mod. Phys. Conf. Ser. 2014, 30, 1460258. [Google Scholar] [CrossRef]
- Bailey, Q.G.; Tso, R. Light-bending tests of Lorentz invariance. Phys. Rev. D 2011, 84, 085025. [Google Scholar]
- Turyshev, S.G.; Shao, M. Laser astrometric test of relativity: Science, technology, and mission design. Int. J. Mod. Phys. D 2007, 16, 2191. [Google Scholar] [CrossRef]
- Bailey, Q.G. Time-delay and Doppler tests of the Lorentz symmetry of gravity. Phys. Rev. D 2009, 80, 044004. [Google Scholar] [CrossRef]
- Christophe, B.; Andersen, P.H.; Anderson, J.D.; Asmar, S.; Bério, Ph.; Bertolami, O.; Bingham, R.; Bondu, F.; Bouyer, Ph.; Bremer, S.; et al. Odyssey: A Solar System mission. Exp. Astron. 2009, 23, 529. [Google Scholar] [CrossRef]
- Appourchaux, T.; Burston, R.; Chen, Y.; Cruise, M.; Dittus, H.; Foulon, B.; Gill, P.; Gizon, L.; Klein, H.; Klioner, S.; et al. Astrodynamical space test of relativity using optical devices I (ASTROD I)—A class-M fundamental physics mission proposal for cosmic vision 2015–2025. Exper. Astron. 2009, 23, 491. [Google Scholar] [CrossRef]
- Turyshev, S.G.; Lane, B.; Shao, M.; Girerd, A. A search for new physics with the BEACON mission. Int. J. Mod. Phys. D 2009, 18, 1025. [Google Scholar] [CrossRef]
- Moore, G.D.; Nelson, A.E. Lower bound on the propagation speed of gravity from gravitational Cherenkov radiation. JHEP 2001, 0109, 023. [Google Scholar] [CrossRef]
- Catalog of the Highest Energy Cosmic Rays. Available online: http://eas.ysn.ru/catalog (accessed on 1 August 2015).
- Takeda, M.; Hayashida, N.; Honda, K.; Inoue, N.; Kadota, K.; Kakimoto, F.; Kamata, K.; Kawaguchi, S.; Kawasaki, Y.; Kawasumi, N.; et al. Small-scale anisotropy of cosmic rays above 1019 eV observed with the Akeno Giant Air Shower Array. Astrophys. J. 1999, 522, 225. [Google Scholar] [CrossRef]
- Bird, D.J.; Corbato, S.C.; Dai, H.Y.; Elbert, J.W.; Green, K.D.; Huang, M.A.; Kieda, D.B.; Ko, S.; Larsen, C.G.; Loh, E.C.; et al. Detection of a cosmic ray with measured energy well beyond the expected spectral cutoff due to cosmic microwave radiation. Astrophys. J. 1995, 441, 144. [Google Scholar] [CrossRef]
- Cunningham, G.; Edge, D.M.; England, D.; Evans, A.C.; Hollows, J.D.; Hopper, S.J.; Lapikens, L.; Liversedge, B.; Lloyd-Evans, J.; Ogden, J.D.; et al. Catalogue of Highest Energy Cosmic Rays; Wada, M., Ed.; IPCR Itabashi: Tokyo, Japan, 1980; Volume 1. [Google Scholar]
- Abbasi, R.U.; Abu-Zayyad, T.; Allen, M.; Amman, J.F.; Archbold, G.; Belov, K.; Belz, J.W.; Benzvi, S.Y.; Bergman, D.R.; Blake, S.A.; et al. High Resolution Fly’S Eye Collaboration. Search for correlations between HiRes stereo events and active galactic nuclei. Astropart. Phys. 2008, 30, 175. [Google Scholar] [CrossRef]
- Aab, A.; Abreu, P.; Aglietta, M.; Ahn, E.J.; Samarai, I.A.; Albuquerque, I.F.M.; Allekotte, I.; Allen, J.; Allison, P.; Almela, A.; et al. Pierre Auger Collaboration. Searches for anisotropies in the arrival directions of the highest energy cosmic rays detected by the Pierre Auger Observatory. Astrophys. J. 2015, 804, 15. [Google Scholar] [CrossRef]
- Winn, M.M.; Ulrichs, J.; Peak, L.S.; McCusker, C.B.A.; Horton, L. The cosmic-ray energy spectrum above 1017 eV. J. Phys. G 1986, 12, 653. [Google Scholar] [CrossRef]
- Abbasi, R.U.; Abe, M.; Abu-Zayyad, T.; Allen, M.; Anderson, R.; Azuma, R.; Barcikowski, E.; Belz, J.W.; Bergman, D.R.; Blake, S.A.; et al. Indications of intermediate-scale anisotropy of cosmic rays with energy greater than 57 EeV in the northern sky Measured with the surface detector of the Telescope Array experiment. Astrophys. J. 2014, 790, L21. [Google Scholar] [CrossRef]
- Linsley, J. Catalogue of Highest Energy Cosmic Rays; Wada, M., Ed.; IPCR Itabashi: Tokyo, Japan, 1980; Volume 1. [Google Scholar]
- Pravdin, M.I.; Glushkov, A.V.; Ivanov, A.A.; Knurenko, S.P.; Kolosov, V.A.; Makarov, I.T.; Sabourov, A.V.; Sleptsov, I.Y.; Sleptsova, V.R.; Struchkov, G.G. Estimation of the giant shower energy at the Yakutsk EAS array. In Proceedings of the 29th International Cosmic Ray Conference, Pune, India, 3–10 Aug 2005; p. 243.
- Díaz, J.S.; Kostelecký, V.A.; Mewes, M. Testing relativity with high-energy astrophysical neutrinos. Phys. Rev. D 2014, 89, 043005. [Google Scholar] [CrossRef]
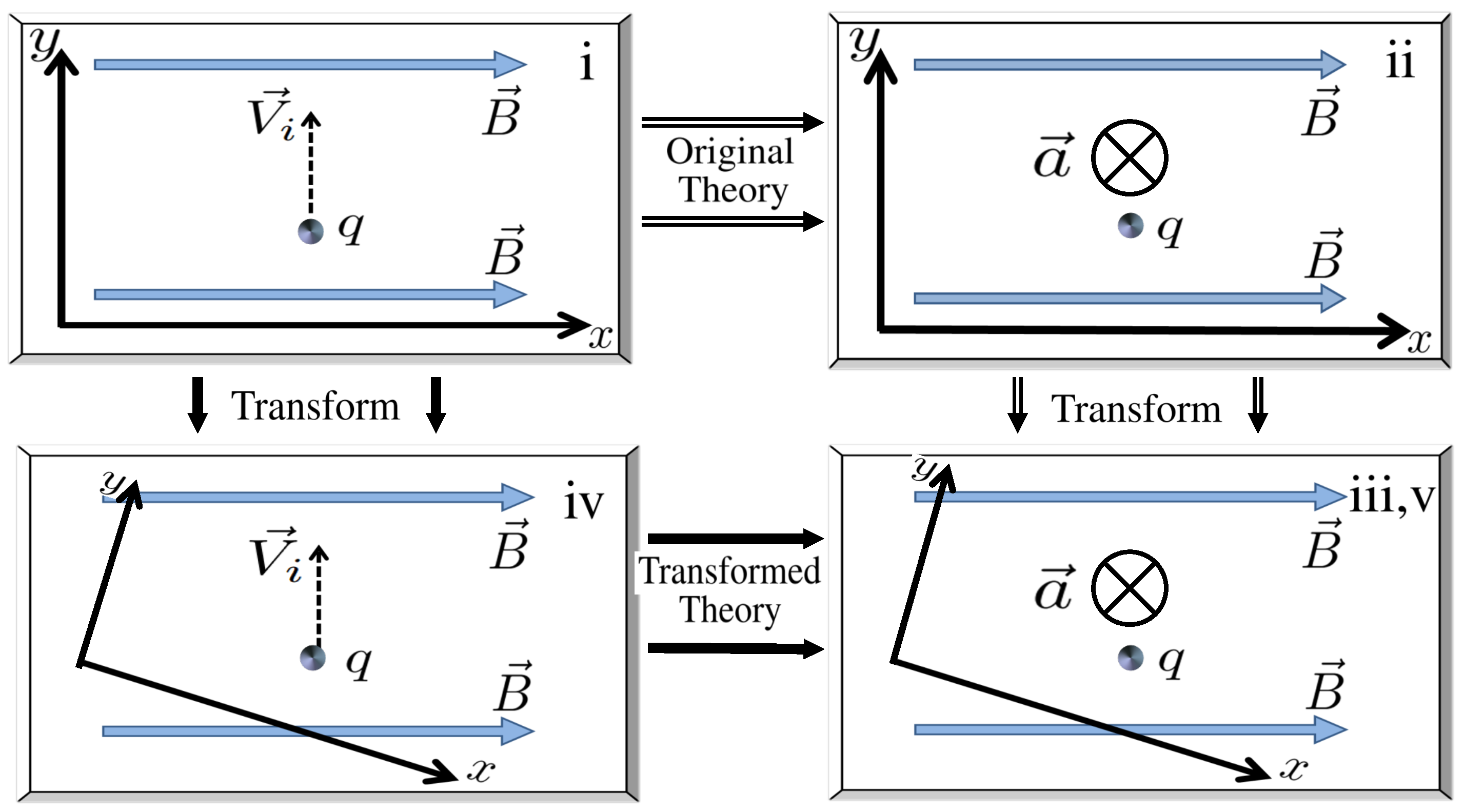
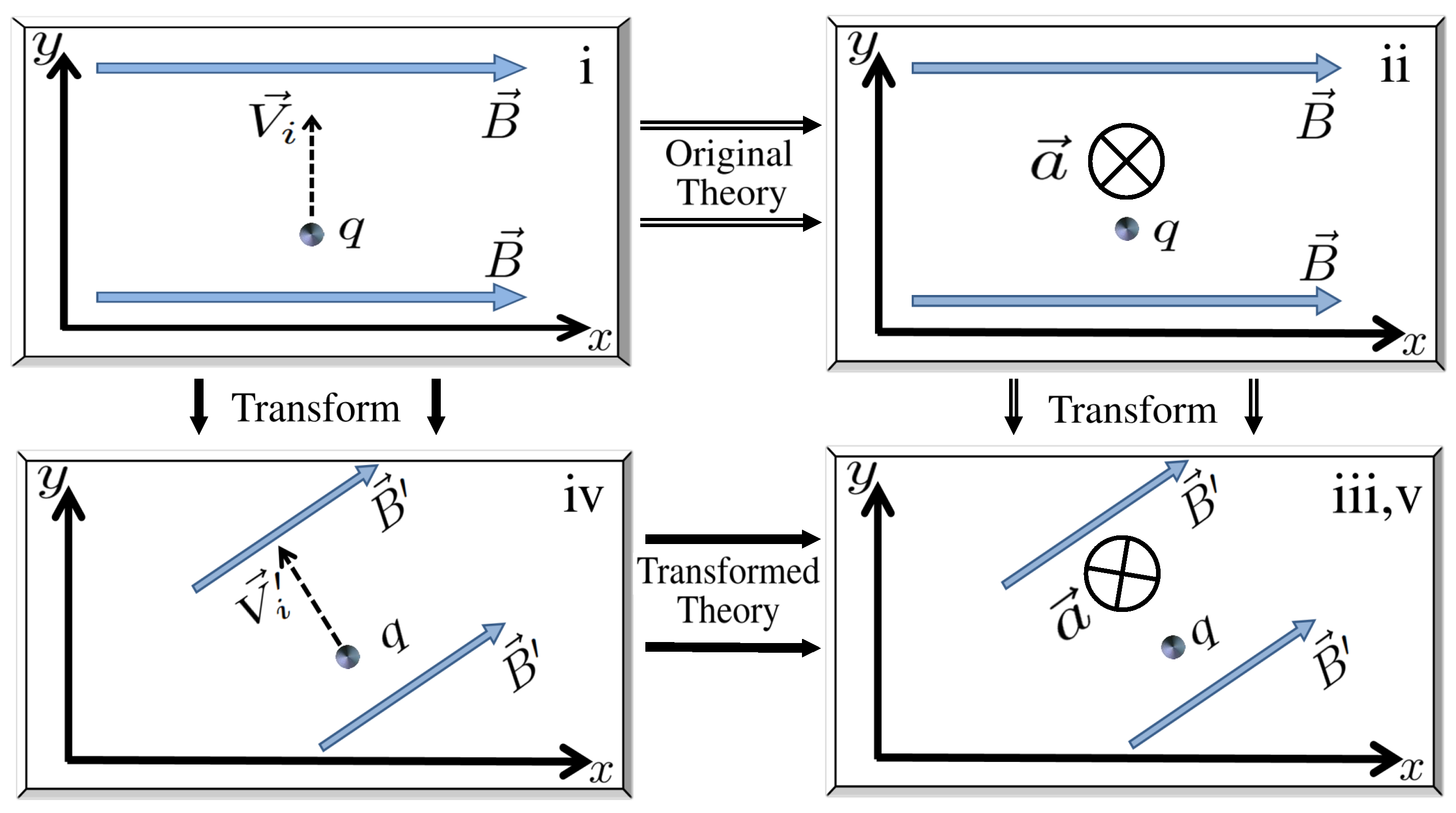
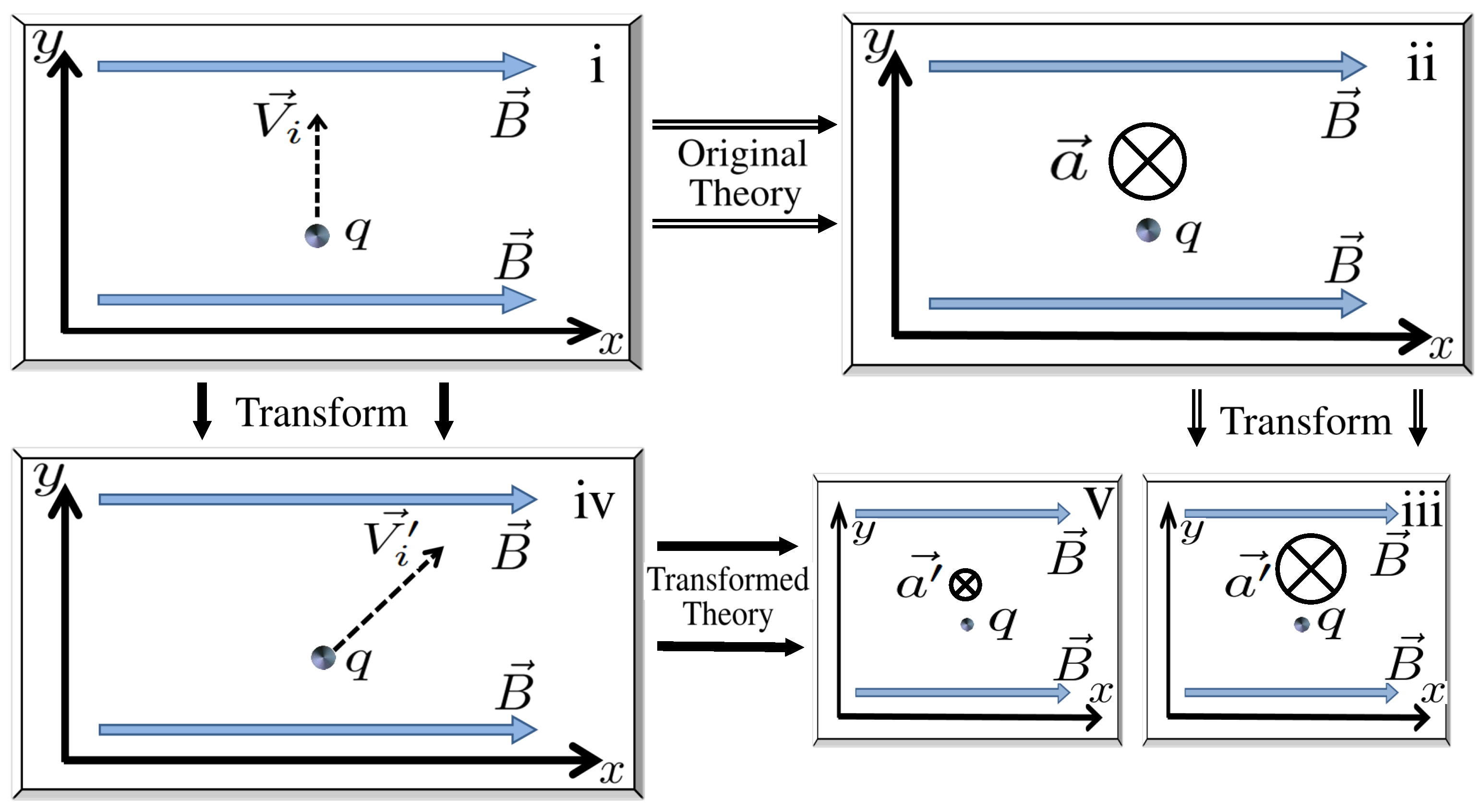
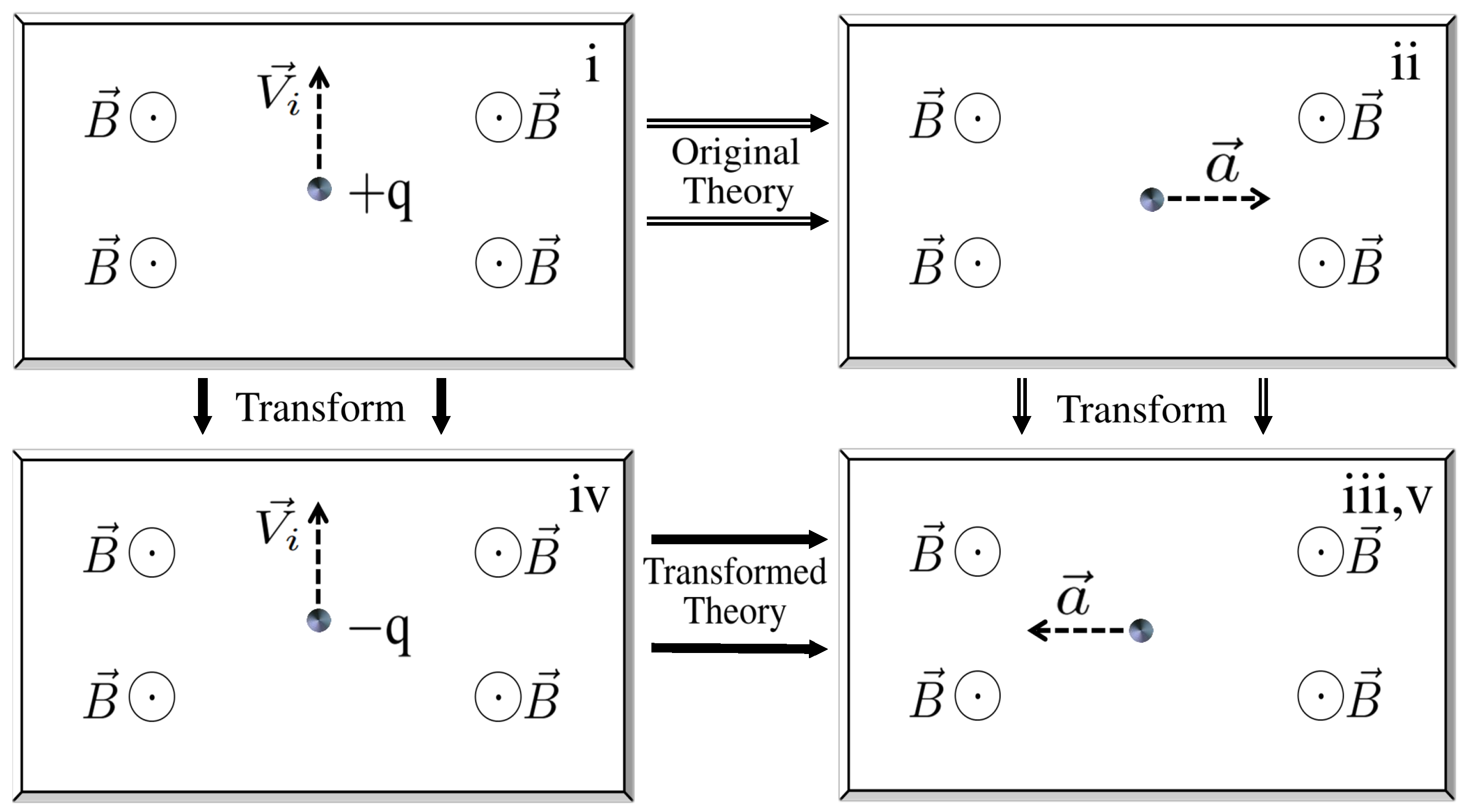
| System | Coefficients | Proposal | Constraints |
|---|---|---|---|
| gravitational Čerenkov radiation | , , , | [14] | [14] [*] |
| superconducting gravimeters | , , | [27,29] | [37] |
| short-range gravity devices | [22,27,29] | [38,39,40,41,42] | |
| gravitational-wave interferometers | , , , | [23] | [23,32] |
| lunar laser ranging | [29] | [43,44] | |
| binary-pulsar observations | [29] | [45,46,47] | |
| planetary ephemerides | , | [48] | [48] |
| gravity probe B | [29] | [49] | |
| bound kinetic energy WEP | , | [27,50] | [50] |
| atom interferometers | , , | [27,29] | [51,52,53] |
| comagnetometry | , | [16] | [16] |
| perihelion precession | , | [27] | [27] |
| equivalence-principle pendulum | [28] | [28] | |
| Solar-spin precession | [29] | [29] |
| System | Coefficients | Proposal | Experiments |
|---|---|---|---|
| atom interferometer | , , | [27] | [54] |
| ring-laser gyroscopes | [55,56] | [57] | |
| torsion pendula | , | [27] | [58] |
| binary pulsars | , , | [24,59] | [60] |
| short-range gravity | [24] | [38,39,42] | |
| gravitational-wave detectors | , , | [23] | [31,33] |
| space-based WEP tests | , | [29,61] | [61,62,63,64] |
| antimatter gravity | , | [27,65] | [66,67,68,69] |
| charged matter WEP | [27] | [70] | |
| muonium free fall | , | [27] | [71] |
| light bending | , , | [72] | [73] |
| time-delay & Doppler tests | [27,74] | [75,76,77] |
| j | Lower Bound | Coeff. | Upper Bound | j | Lower Bound | Coeff. | Upper Bound |
|---|---|---|---|---|---|---|---|
| 0 | 6 | ||||||
| 1 | |||||||
| 2 | |||||||
| 3 | |||||||
| 7 | |||||||
| 4 | |||||||
| 5 | |||||||
| 8 | |||||||
© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tasson, J.D. The Standard-Model Extension and Gravitational Tests. Symmetry 2016, 8, 111. https://doi.org/10.3390/sym8110111
Tasson JD. The Standard-Model Extension and Gravitational Tests. Symmetry. 2016; 8(11):111. https://doi.org/10.3390/sym8110111
Chicago/Turabian StyleTasson, Jay D. 2016. "The Standard-Model Extension and Gravitational Tests" Symmetry 8, no. 11: 111. https://doi.org/10.3390/sym8110111
APA StyleTasson, J. D. (2016). The Standard-Model Extension and Gravitational Tests. Symmetry, 8(11), 111. https://doi.org/10.3390/sym8110111





