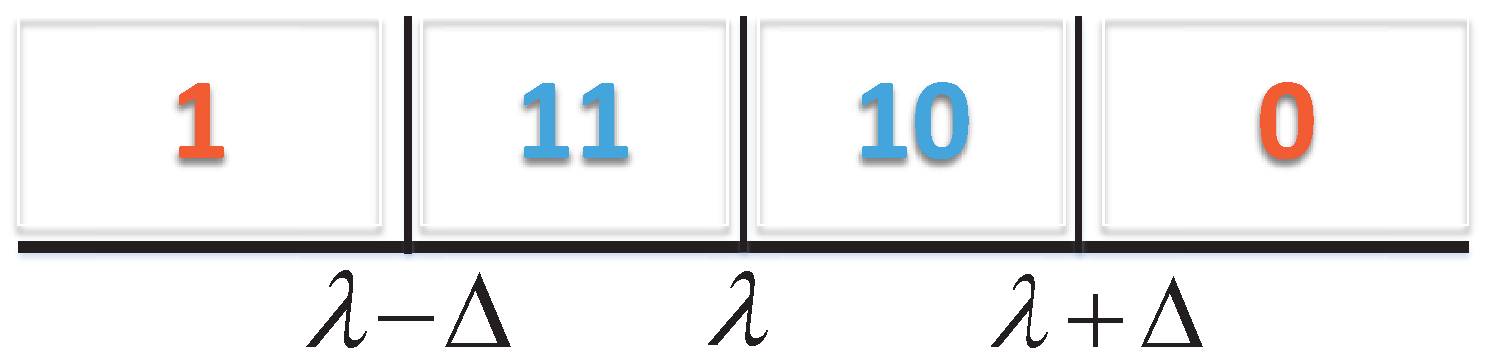1. Introduction
With the rapid development of wireless communication business, demand for wireless spectrum resources has grown exponentially in recent years. Given the limitations of natural frequency spectrums, the current fixed radio spectrum allocation policy makes it impossible to satisfy all of the new requirements. Cognitive radio (CR) [
1], as a kind of spectrum reutilize technology, can improve utilization efficiency by employing dynamic spectrum allocation (DSA) [
2,
3]. Secondary users (SUs) are allowed to use the radio spectrum licensed to the primary users (PUs) when the spectrum is temporarily underutilized. In order to support this spectrum reuse functionality, SUs are required to sense the radio frequency environment and vacate the channel instantly without causing any interference once the PUs are found to be active. Therefore, spectrum sensing is of vital importance in cognitive radio networks (CRNs).
Traditional local detection strategies normally adopt matched filter detection [
4], energy detection [
5] and cyclostationary feature detection [
6]. Both matched filter detection and cyclostationary feature detection require certain prior knowledge about the PU signal as well as large computational costs, which are not suitable to act as a blind detector. Energy detection is shown to be optimal when the cognitive devices do not have prior information about the PU signals, and it possesses low computational costs and is easily implemented. Nevertheless, energy detection is sensitive to noise uncertainty and performs poorly at a low signal-to-noise ratio (SNR). The above traditional detectors are susceptible to noise uncertainty in practical systems, which is a fundamental limitation of current spectrum sensing strategies in detecting the presence of PUs in CRNs. Due to noise uncertainty, the performance of traditional detectors deteriorates rapidly with low SNR.
Fortunately, the entropy-based detectors can effectively overcome the influence of noise uncertainty and improve the robustness of sensing schemes, and hence have obtained extensive research in recent years [
7,
8,
9,
10,
11,
12,
13]. Dr S. Nagaraj combined the entropy-based detection and matched filter in the time domain in [
7,
8], but the matched filter needed prior knowledge about PU features, which required additional overhead as a non-blind detector. Zhang et al. proposed a Shannon entropy-based sensing scheme in the frequency domain based on spectrum amplitude (SASE) in [
9,
10], and the scheme was proved to be robust against noise uncertainty. However, there still exists severe problems such as the maximum entropy distribution in the absence of PUs and detection failure phenomenon. Since an entropy-based detection scheme was proposed, plenty of researchers have conducted comprehensive studies based on Shannon entropy. In [
11], a Shannon entropy-based detection scheme based on spectrum power (SPSE) was depicted, the deficiency of which is that computational complexity increases as well as system overhead. In addition, its performance still can be improved. Waleed et al. proposed a robust entropy-based optimization cooperative sensing scheme in [
12]; however, the method is only applicable in special occasions, say high sea areas; thus, it does not possess the universality for extensive application. A conditional entropy-based detection method improving the detection performance in low SNR was proposed in [
13]. The scheme requires prior information of the system to accurately estimate the unauthorized signal characteristics, which is also a non-blind detection.
In order to enhance sensing performance, more sensing time is needed. However, during the process of sensing, secondary users should stop data transmission to avoid being recognized as primary users. Therefore, more sensing time means lower secondary system capacity, making this approach less attractive. Collaborative spectrum sensing [
14,
15,
16,
17,
18] (CSS), where local secondary users sense and then send sensing information to the fusion center where the final decision is made, has been studied extensively as a promising alternative to improve sensing performance. There are mainly three schemes of CSS: AND-rule-based CSS [
14], OR-rule-based CSS [
15], and VOTING-rule-based CSS [
16]. However, these CSS schemes are quite simple, and their performance is limited. Recently, the CSS schemes based on weight have been proposed [
17,
18] with excellent performance; however, in these schemes, SNR of each SU should be estimated perfectly to get the fusion weight, and it is difficult to realize in practical systems.
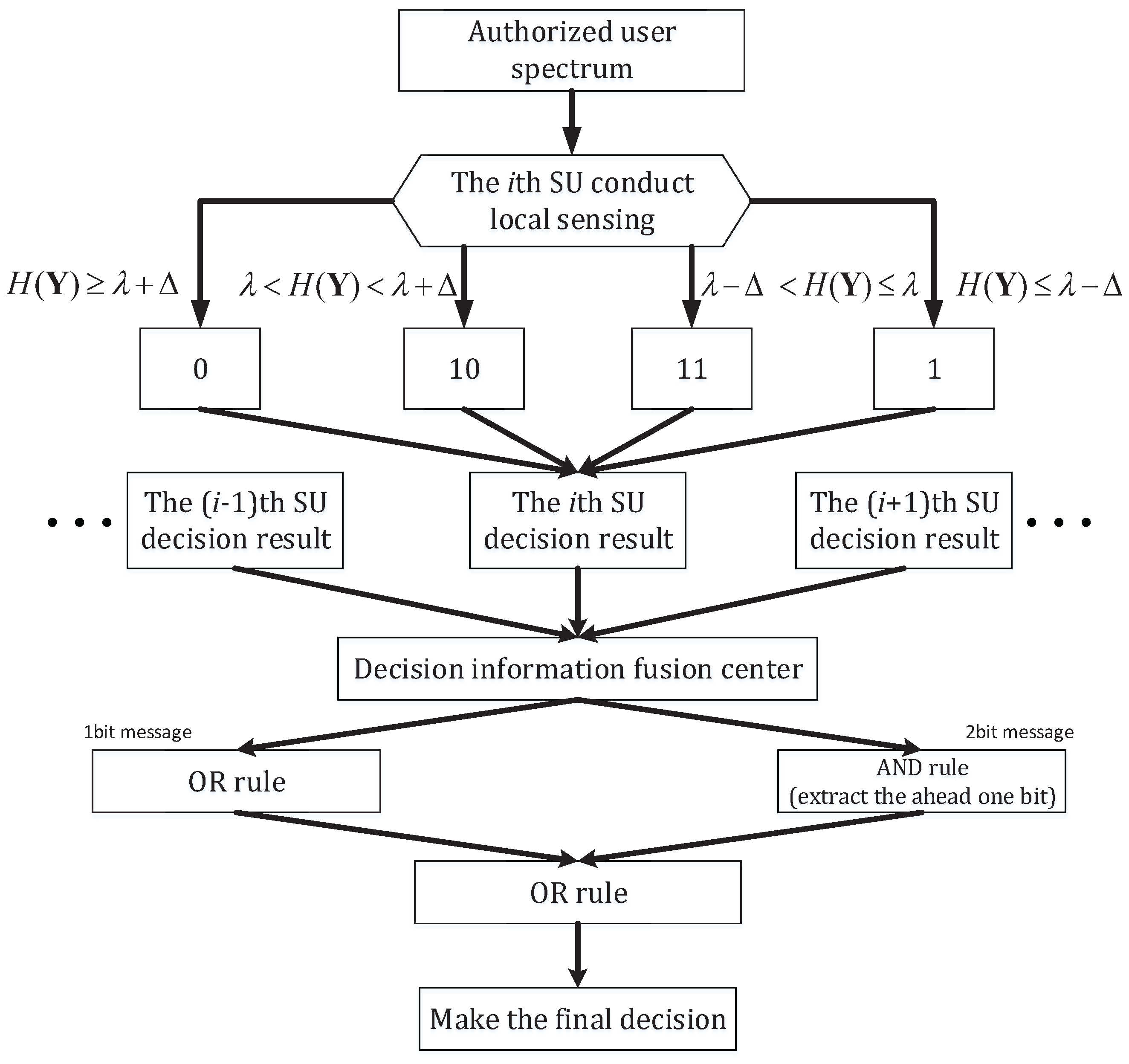
In this paper, a novel collaborative spectrum sensing (CSS) algorithm based on exponential entropy is proposed. Firstly, in order to solve the problem of the maximum entropy distribution in the absence of PUs, and to avoid detection failure phenomenon in Shannon entropy, a non-uniform quantized exponential entropy-based detection (NQEE) scheme is proposed. To further improve the detection reliability, a novel exponential entropy-based collaborative spectrum sensing scheme with the multi-fusion rule, which adopts an NQEE detector in local sensing, is designed. Local exponential entropy estimation are divided into reliable and unreliable information entropy areas according to the decision area classification rule. SUs transmit one bit or two bits to the fusion center (FC) for decision fusion. The detection performance of the novel scheme is much better than classical CSS schemes. In addition, the scheme is proved to be robust against the noise uncertainty.
The rest of the paper is organized as follows.
Section 2 presents the system model for spectrum sensing as well as the defects in previous Shannon entropy-based detectors. In
Section 3, we elaborate on the proposed exponential entropy-based CSS scheme, where the NQEE method is applied in local sensing. In
Section 4, the NQEE-CSS scheme based on a multi-fusion rule is proposed.
Section 5 details performance evaluation and comparisons through plenty of simulations. Finally, conclusions of this paper are drawn in
Section 6.
3. Non-Uniform Quantized Exponential Entropy-Based Spectrum (NQEE) Detector
In order to solve the above problems in SASE, we consider using the characteristic that the spectrum amplitude of the received data sequence obeys Rayleigh distribution to detect whether the received signal only contains noise.
3.1. Definition and Property of NQSE
Definition 1. Given sequential data series, follows the specific distribution , and non-uniform quantized intervals are used to conduct L-level quantization for , and the probability of falling into ith quantized interval is expressed as .
The non-uniform quantized Shannon entropy of is The non-uniform quantized Shannon entropy has the following property:
Property 1. For given sequential data series with specific distribution , non-uniform quantized intervals are confirmed by distribution function , which ensures that fall into each quantized interval with the same probability ; thus, the non-uniform quantized entropy achieves the maximum .
Proof. According to the Maximum Discrete Shannon Entropy theorem [
19]:
where
is the distribution law of discrete random variables, and the equality holds up if and only if
; that is to say, when the discrete random variable follows the uniform probability distribution, the discrete Shannon entropy reaches the maximum value. Hence, for the specific distribution
, the maximum entropy
is guaranteed to be achieved through determining the non-uniform quantized intervals
, as long as the data sequence falls into each quantized interval with equal probability.
It can be seen from the above property that determining the non-uniform quantized space by Rayleigh distribution can ensure the equal probability of quantized interval and the maximum entropy under hypothesis . ☐
3.2. Determination of Non-Uniform Quantized Intervals
Assuming random variable V represents event “X falls into quantized intervals”, , respectively, denotes falling into L quantized intervals. The received signal only contains noise when PU signals does not exist, falls into L quantized intervals with equal probability and discrete random variable V presents uniform probability distribution. Here, the non-uniform quantization entropy of signal spectrum amplitude can achieve the maximum. On the other hand, when the received signal contains primary signals, random variables V no longer obey uniform probability distribution, and the non-uniform quantized spectrum entropy gets smaller. Cognitive users can determine the presence/absence of PUs according to the difference feature of information entropy measure.
Known amplitude sequence of the received signal obeys the Rayleigh distribution, and the probability distribution function (pdf) of Rayleigh distribution is:
In order to obtain the uniform probability distribution, combine Equation (8) with the following formula
Then, the separating points of non-uniform quantized intervals can be obtained by the following expression:
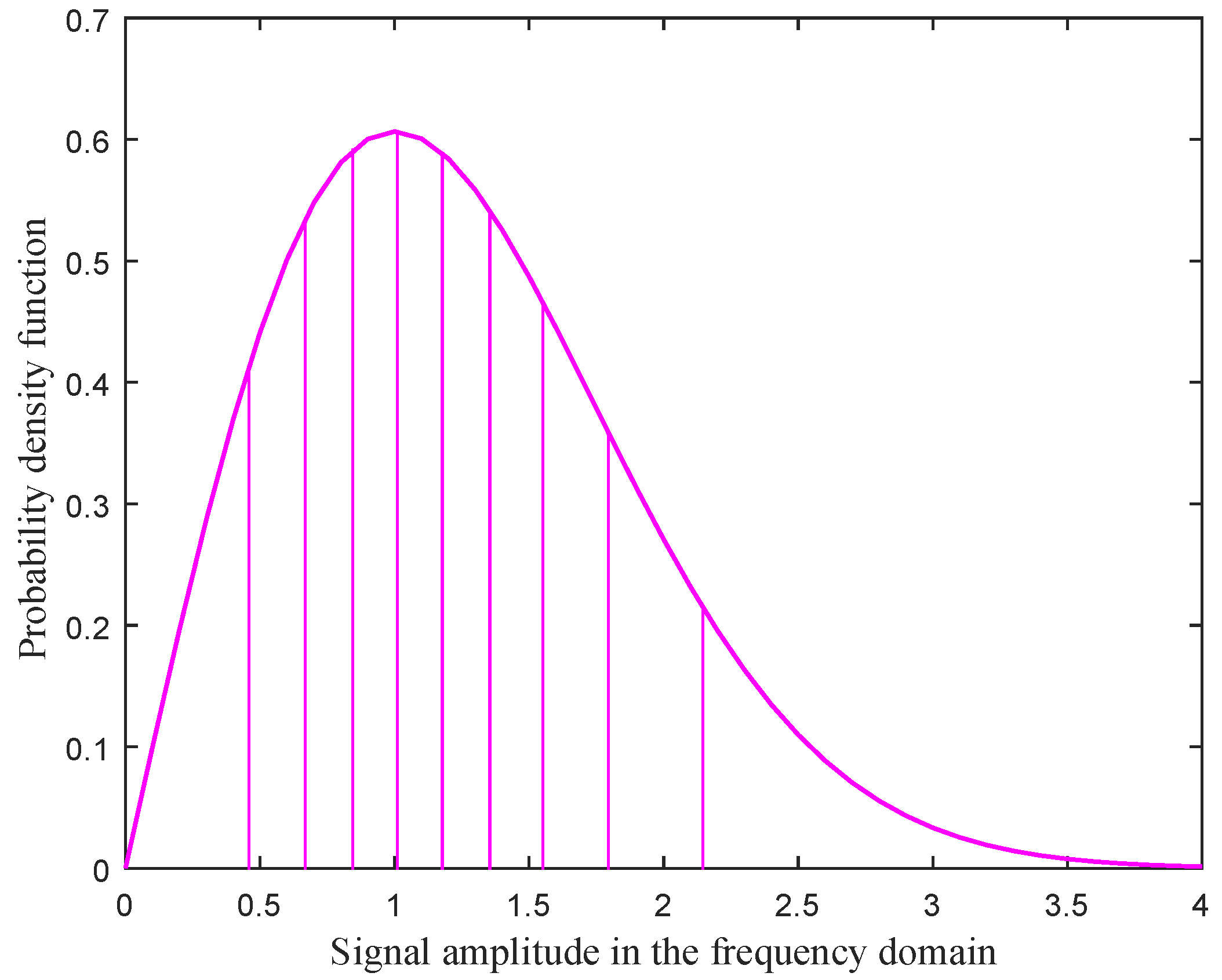
For instance, when the value of
L is 10, subsections of Rayleigh distribution, as shown in
Figure 1, can be acquired through the process of non-uniform quantization. The
x-axis shows the amplitude of the signal in the frequency domain, while the
y-axis represents the probability density function of Rayleigh distribution. The probability of received data falling into certain intervals is the area of that interval. It can be qualitatively seen that sequence
x falls into ten subsections (1–10) with equal probability.
The noise variance is indispensable for dividing quantization intervals; thus, when the estimation of noise variance is inaccurate or noise fluctuates over time, the process of non-uniform quantization interval will be affected. Taking the above issues into account, we perform normalization processing for received information sequence
, making the Rayleigh distribution parameter
as 1, and then the influence of the noise uncertainty can be overcome. The quantization interval boundary can be rewritten as
3.3. Spectrum Sensing Based on NQSE
Based on the above discussions and analyses, we make the following statements about the implementation process of the non-uniform quantized Shannon entropy-based (NQSE) detection algorithm. Firstly, secondary users perform
N-point samples to received signals to obtain the sampling sequence
; then, normalization for received sequences
are conducted to get the normalized sequences
, and the power of received signal sequences become
; afterwards, DFT is used to obtain spectrum sequences
, and the amplitude of spectrum is
; subsequently, calculating the quantization intervals
according to (11), and counting numbers of the sequence
dropping into each interval, denoted by
; thus, the non-uniform quantized Shannon entropy (NQSE) of spectrum sequence is
Finally, compare
with threshold
λ. If test statistic
, the authorised channel is judged as free; otherwise, the channel is occupied.
3.4. Spectrum Sensing Based on NQEE
Hereinbefore, we solve the Problem 1 through the proposal of NQSE. In order to overcome the defect of failure detection problem in SASE, the concept of exponential entropy is introduced into the sensing algorithm. The increment of exponential entropy is zero when probability , and the phenomenon of misconvergence is effectively avoided in the process of estimating entropy. Thus, the problem of failure detection is definitely solved.
The exponential entropy is defined based on the following principles [
20]:
- (1)
Supposing the probability of each state is , then the information content carried by has definition in all points between ;
- (2)
, is limited and greater than or equal to 0;
- (3)
, is limited and greater than or equal to 0;
- (4)
;
- (5)
decreases in exponential form with increasing;
- (6)
Information content and entropy H are consecutive between ;
- (7)
Entropy H reaches the maximum when are all equal, i.e., uniform probability distribution.
The exponential entropy which satisfies all principles above is defined as [
20]:
The specific algorithm procedures of non-uniform quantized exponential entropy-based detection are shown in Algorithm 1, and the only difference between the non-uniform quantized exponential entropy-based detection and NQSE is the calculation method of entropy. Exponential entropy has similar properties to Shannon entropy; for instance, exponential entropy is not affected by noise power. In fact, exponential entropy also has no relationship with noise power. That is to say, the NQEE algorithm also possess robustness to the noise power uncertainty. This property will be attested in the following simulation work. By comparing the exponential entropy calculated in Equation (14) with the threshold, the existence of PU signal can be determined. The decision rule can be expressed as
| Algorithm 1 Non-uniform Quantized Exponential Entropy-based Detection (NQEE) Algorithm |
| Input: , , . |
Output: .
for each sensing event do ←point sampling ← perform normalization to s ← perform Discrete Fourier Transform for quantized intervals for count numbers of each interval end for if then else end if end for
|
The introduction of exponential entropy effectively evades the problem of no definition or zero value of using logarithms to define entropy and also overcoming the deficiency of the Shannon entropy. The problem of failure detection discussed above has been solved skillfully by introducing the exponential entropy into the spectrum detection algorithm.
5. Simulation Results and Analysis
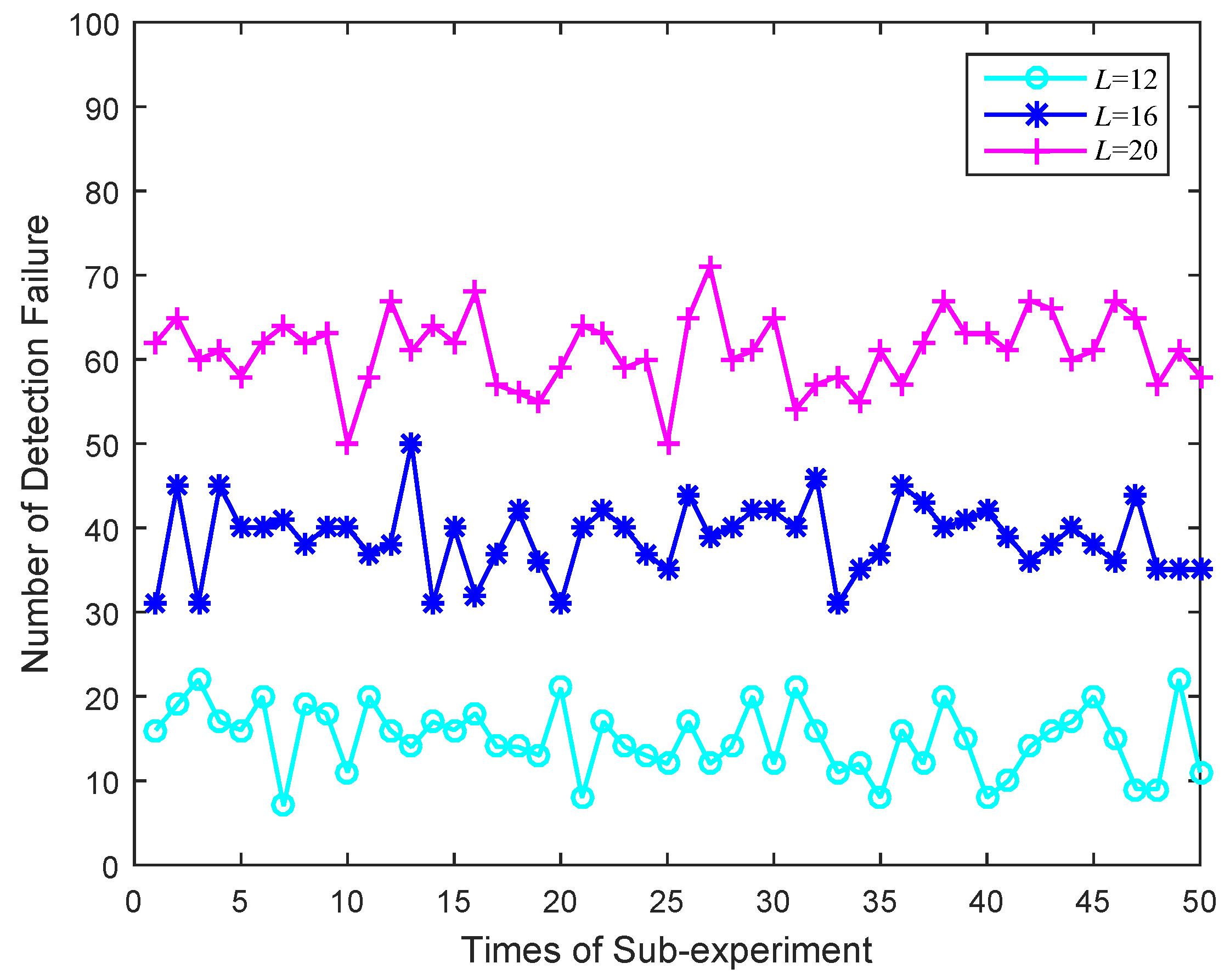
The verification test of detection failure for Shannon entropy is presented in
Figure 5. The experiments are divided into three groups, and each group conducts 50 sub-experiments with detection for 100 times. The received signal is AWGN with length
and the bin number
L in each experiment is
, respectively. The abscissa is set as the experiment times and the ordinate is the times of failure detection. It can be seen that there exist different levels of detection failure phenomenon. The proportion of failure obviously rises with
L increasing, which can be ascribed to fact that the width of the interval decreases when
L increases; therefore, the probability of detection statistics falling into the
th interval becomes higher. When
, the average rate of failure detection reaches above 50%. To a large extent, high ratio of detection failure causes low detection efficiency and waste of system resources.
To evaluate the detection performance of the proposed detection scheme, plenty of simulations are carried out. The signal of the primary user is modulated BPSK signal, baseband symbol rate and carrier frequency . The sampling frequency at the cognitive receiver is set as . The number of non-uniform quantizing interval L of the probability space is 20. The number of Monte Carlo simulation times is 10,000. In all of the entropy-based detectors, the sample size of DFT is equal to 1024 points. The sample size is also equal to 1024 points in energy detection.
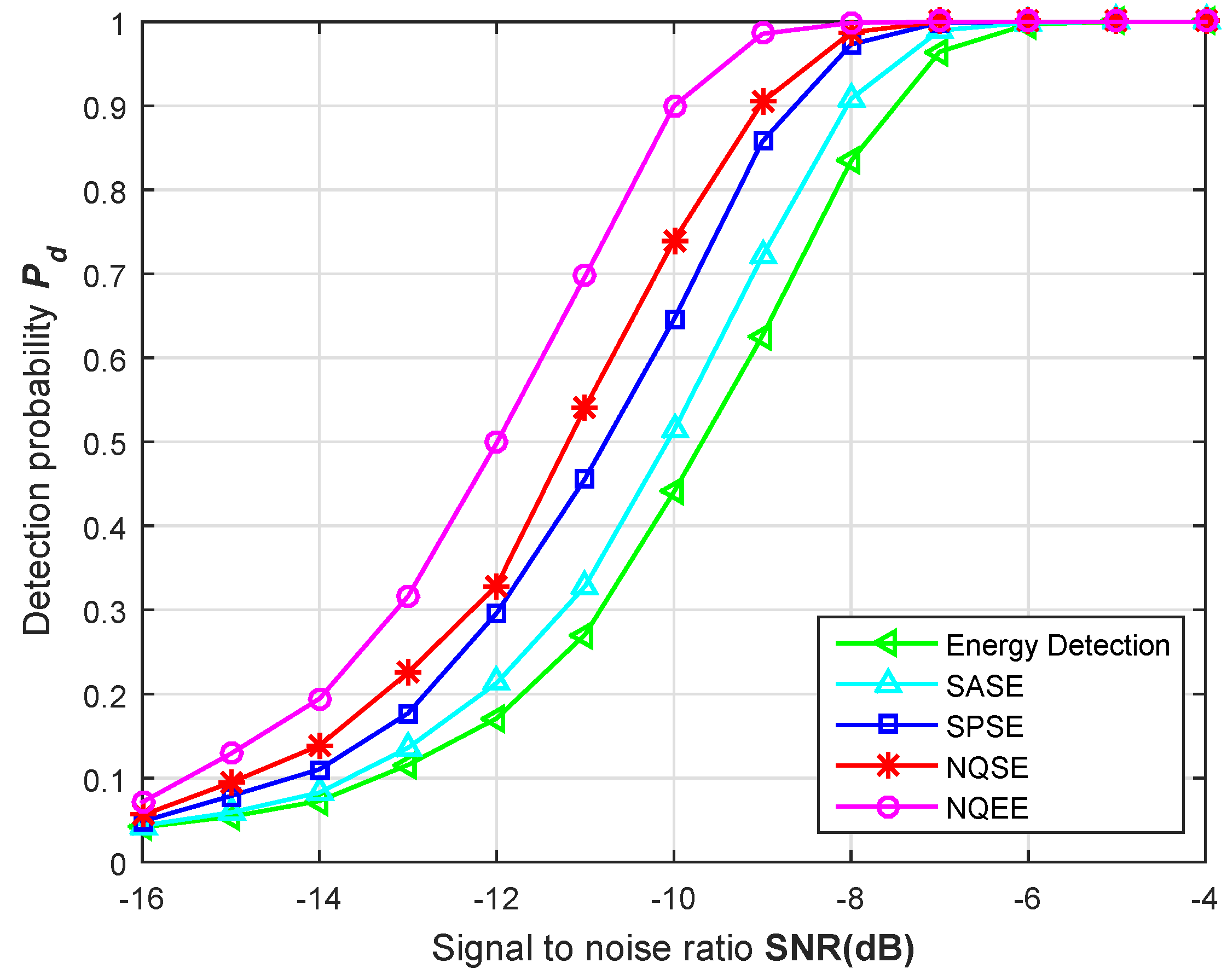
In
Figure 6, we compare the detection probability of proposed non-uniform quantized exponential entropy-based detection with entropy-based scheme based on power spectral, Shannon entropy-based detection and energy detection. False alarm probability
is 0.1, the variation range of SNR is
with step length
. Simulation experiments are under the conditions of the additive white Gaussian noise (AWGN) channel. Overall, the detection performance of the proposed scheme is better than several other solutions. Among which, the NQEE detection conducts non-uniform quantization for probability space according to the characteristics of the spectrum obeying Rayleigh distribution, which ensures that the entropy estimation achieves the maximum, thus its performance is superior to other detection schemes. In addition, the NQEE spectrum detection scheme overcomes the detection failure problem of Shannon entropy on the basis of NQSE, and its detection performance is apparently superior to the NQSE algorithm. In particular, when detection probability
is equal to 0.9, the SNR of the NQEE is about
, realizing a performance improvement effect of about
when compared with SASE of
.
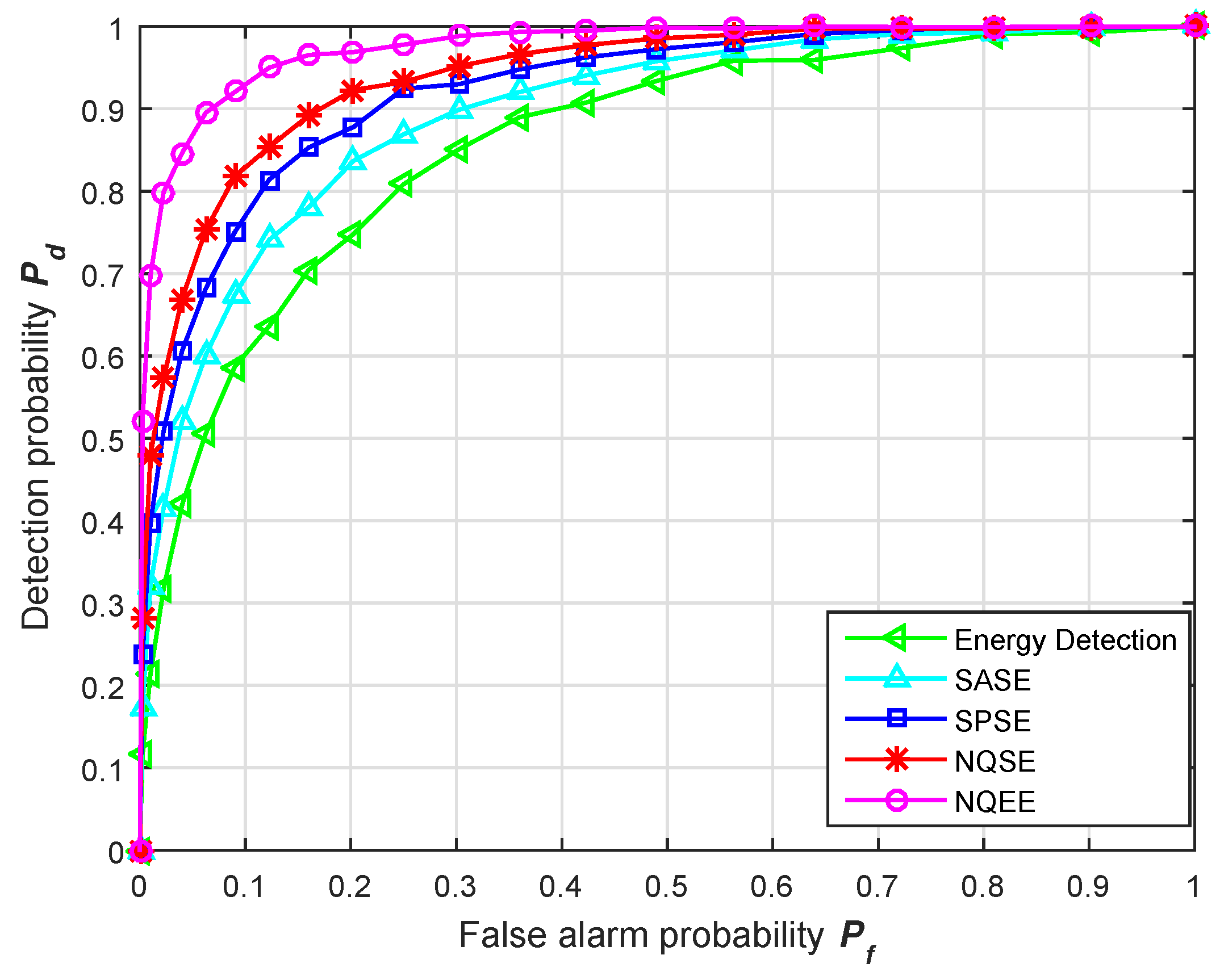
When SNR is equal to
, the simulation about the relationship between detection probability
and false alarm probability
is carried out and the receiver operating characteristics (ROC) curves are shown in
Figure 7. Obviously, the NQEE scheme has the best detection performance. Considering
, detection probability of NQEE and SASE are 0.9357 and 0.6960, respectively; thus, the performance promotion of NQEE is roughly 0.24. When
is greater than 0.3, the detection probability of four kinds of entropy-based schemes are all greater than 0.9, but, in general, we do not care much about the detection performance under high false alarm probability. Due to the standard of the IEEE 802.22 working group, a false-alarm probability less than or equal to 0.1 is the most conducive for full use of valuable spectrum resources. Hence, the detection performance under low false alarm probability should mainly be considered.
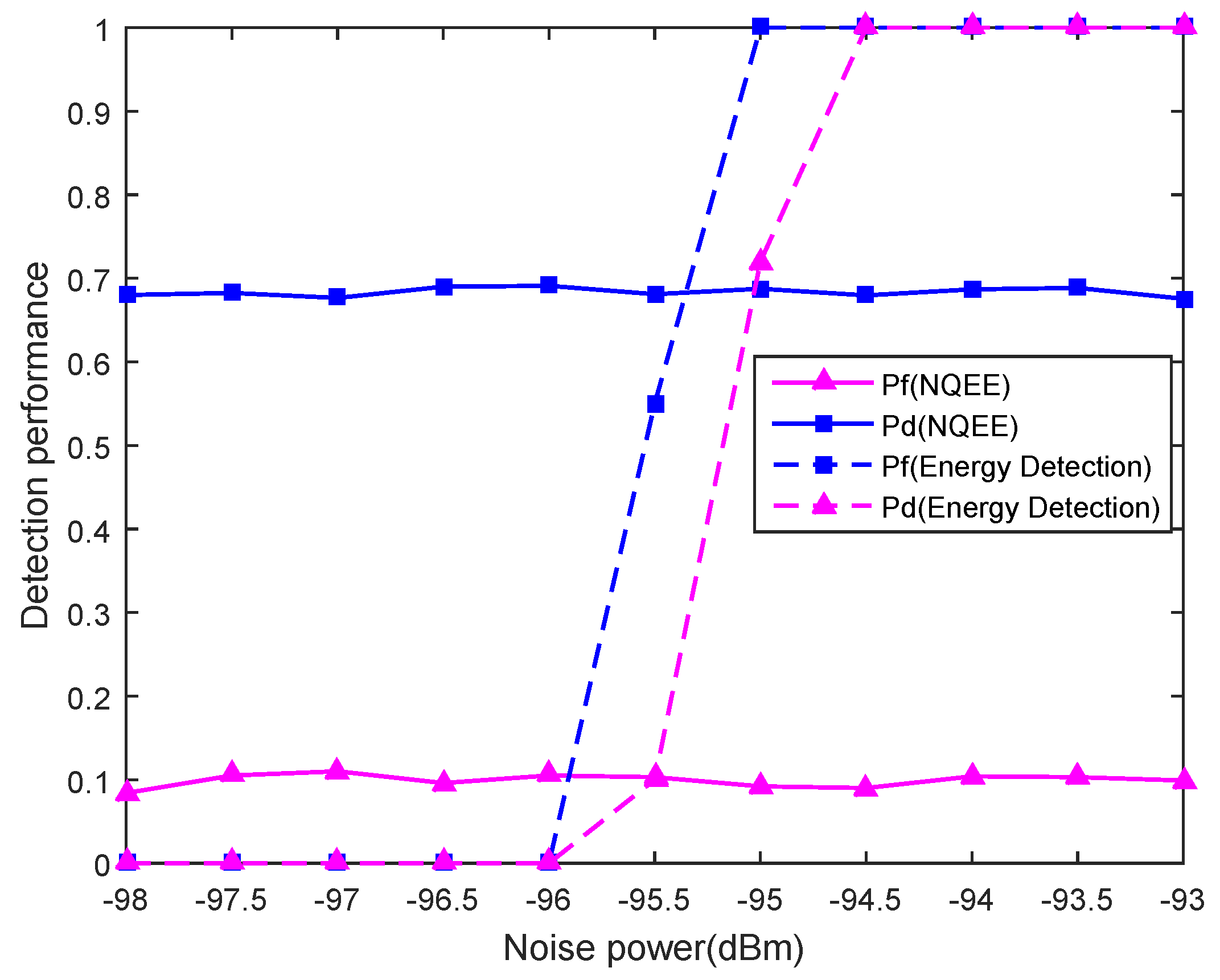
The above simulation and analysis verify that NQEE outperforms similar entropy detection schemes. Besides detection performance, the robustness against noise uncertainty is also presented as a significant measure factor in sensing schemes. While energy detection is very sensitive to the variation of the background noise. Based on this, the simulation concerning the detection performance of NQEE and energy detection under noise uncertainty is conducted in
Figure 8. The change range of background noise power in the experiment is
, and SNR is set as
.
In
Figure 8,
and
of the exponential entropy-based detection remain unchanged with the noise power varying, respectively remaining at 0.6825 and 0.1, which indicates that noise uncertainty cannot affect the performance of the novel entropy-based scheme, and the noise power is
when
of the energy detection and the NQEE detection are both equal to 0.1. The energy detector is extremely sensitive to the noise power uncertainty, and
and
become unsatisfactory with the noise uncertainty larger than only
. Thus, the energy detection with a fixed threshold is hardly applicable to actual networks due to the background noise fluctuating in almost all of the practical communication systems.
Under the condition that primary signals exist in the authorized spectrum, the simulation about the relationship between exponential entropy and SNR is shown in
Figure 9. Sampling numbers are
N1 = 512,
N2 = 1024, interval numbers are
L1 = 12,
L2 = 16, and
L3 = 20, and the changing range of SNR is
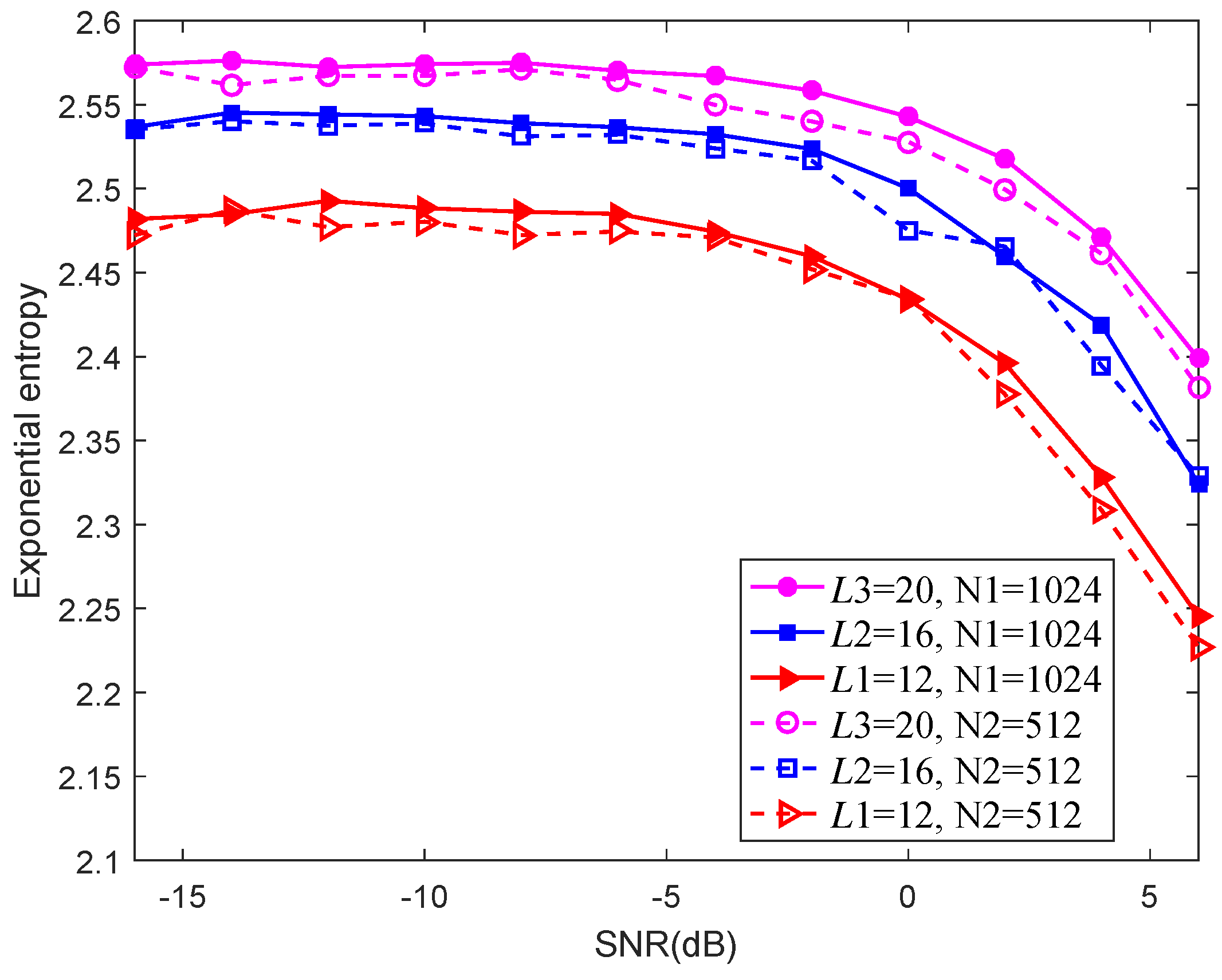
. It can be seen that the exponential entropy estimation gets smaller with the increase of SNR. After confirming the decision threshold, detection probability has obvious improvement as SNR increases. On the other hand, it can be derived through the comparisons of three curves that exponential entropy estimation reduces with the reduction of
L, thus reducing section numbers is also considered as feasible way to improve detection probability under low SNR. In addition, the sampling number also influences the change of entropy estimation. In this experiment, the entropy estimate index decreases with the increase of sampling points, and detection probability increases with the increase of sampling points. In the case of high SNR, the effect that sampling points exert on exponential entropy estimation weakens.
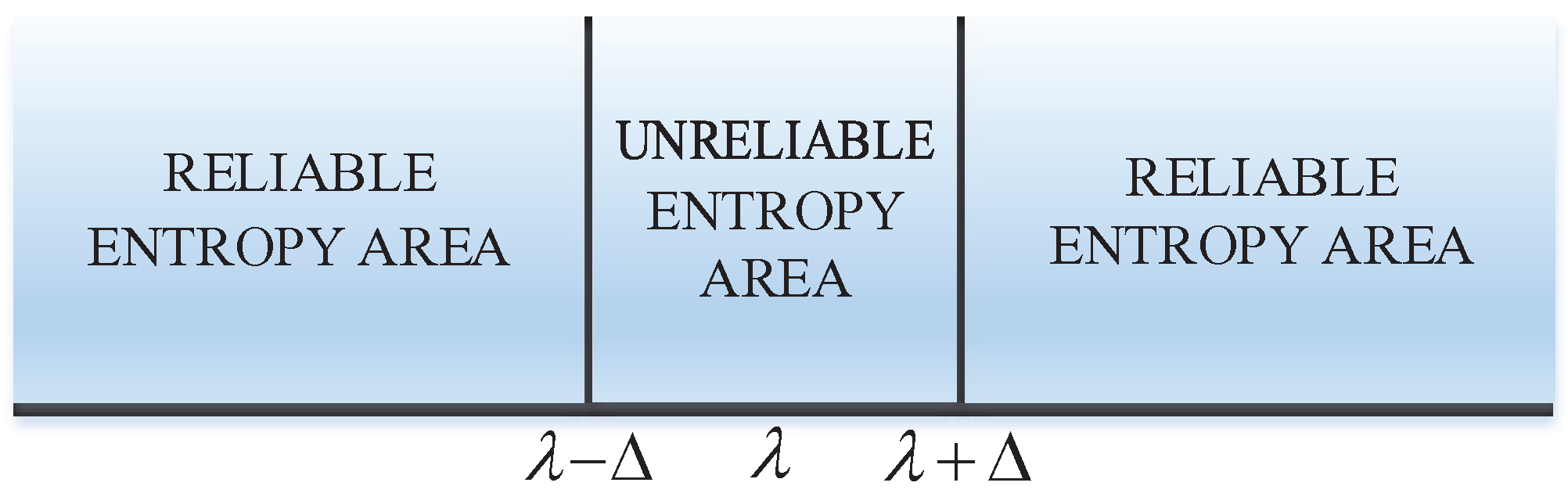
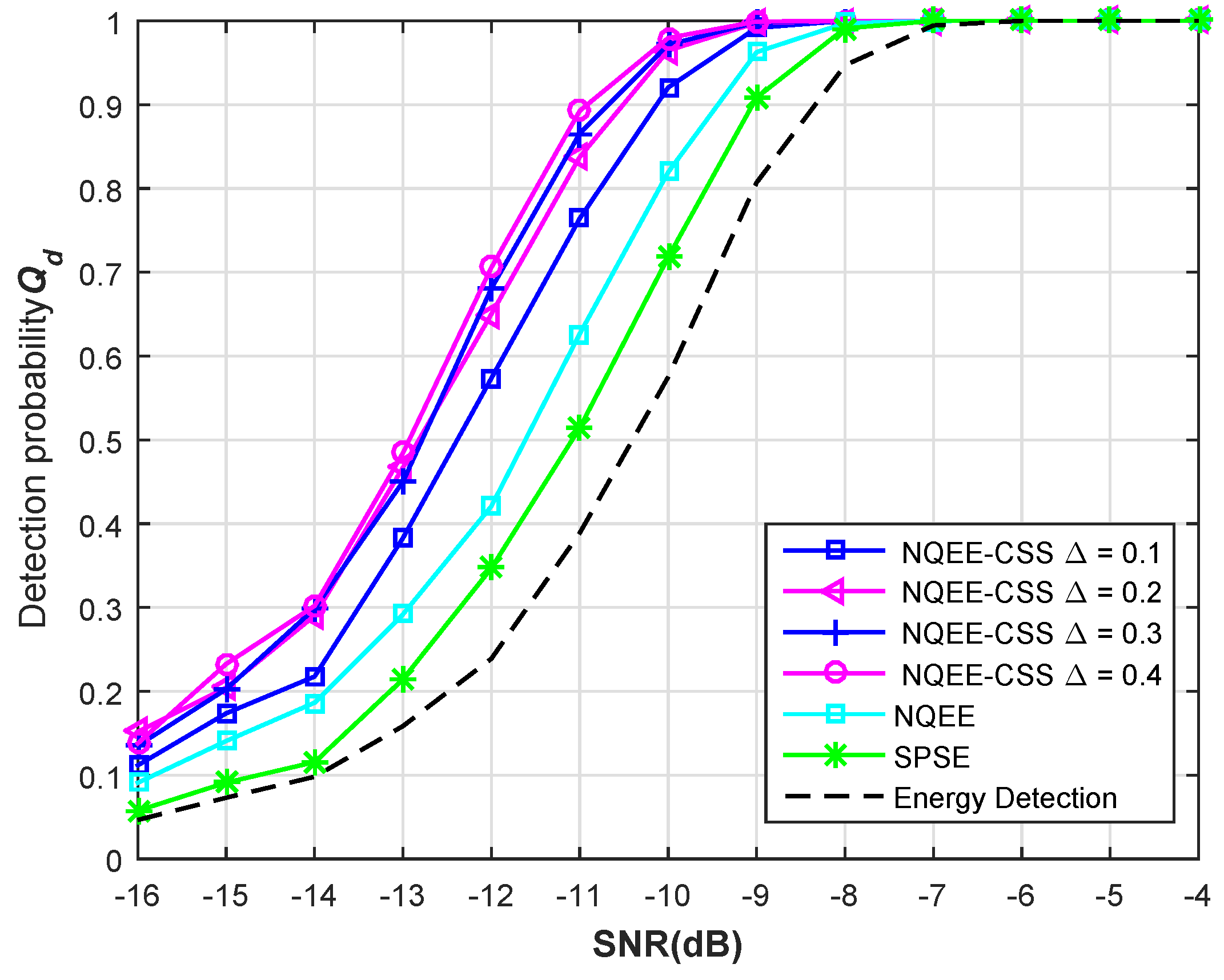
Δ is a significant parameter in an exponential entropy-based CSS scheme, and the setting of its value should be carefully considered. As shown in
Figure 10, we study the relationship between SNR and detection probability
: false alarm probability
and SNR changes from
to
. Parameter Δ is, respectively, set as
. Sample number is 1024, and the number of SUs involved in the CSS
M is equal to five. The simulation of exponential entropy-based detection, power spectral entropy-based detection, and energy detection are also shown as contrast curves in the picture. For the fixed SNR, when Δ increases, the detection probability
also increases. The reason for this phenomenon is that the probability of exponential entropy estimation information falling into
gets larger with the increase of Δ; therefore, the performance of the NQEE-CSS scheme presents an obvious increase. When
, the growth rate of detection performance is very small, almost remaining the same. In addition, as mentioned earlier, the detection performance of exponential entropy-based detection method is superior to the power spectrum entropy detection and the energy detection algorithm.
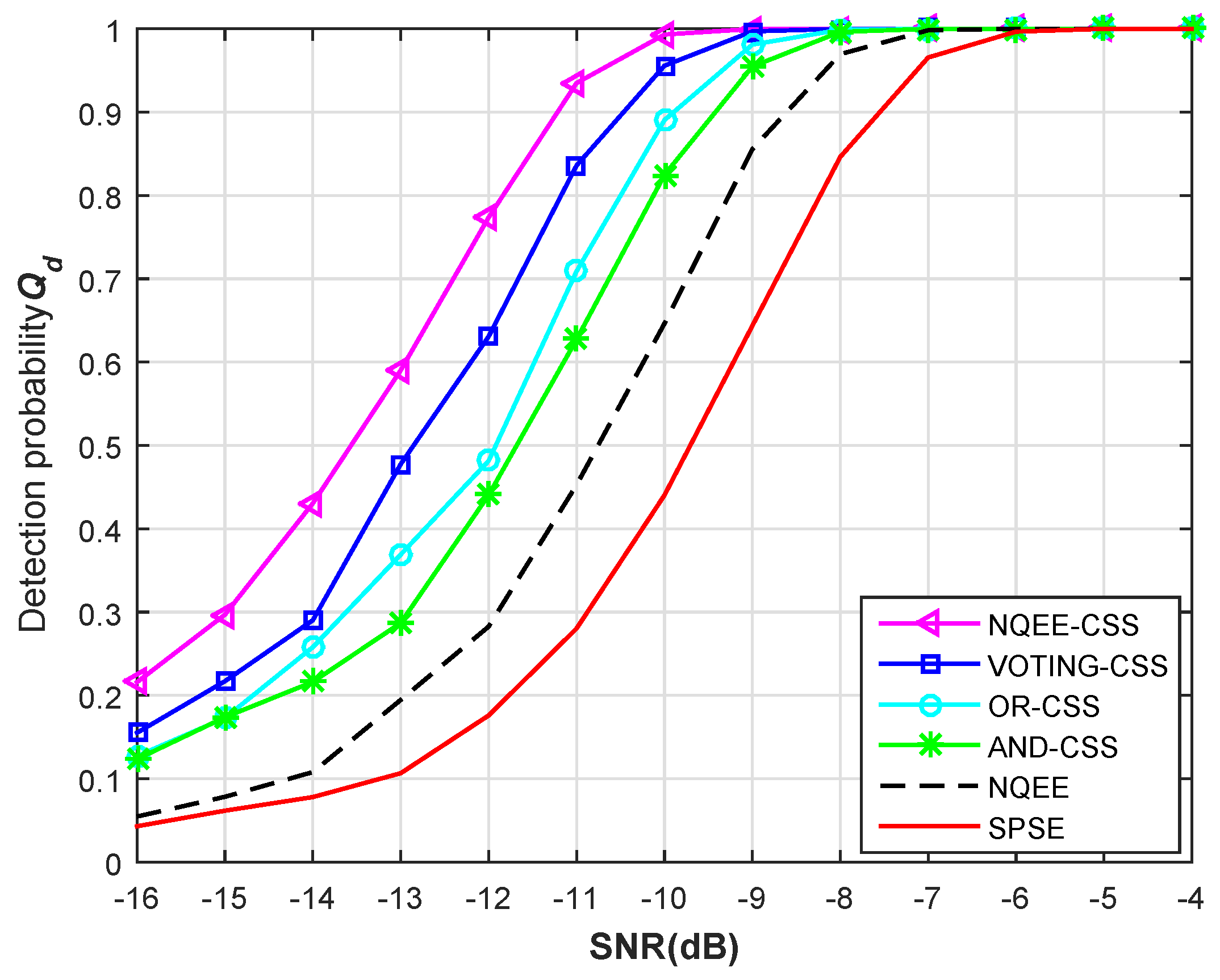
We demonstrate the detection performance of proposed exponential entropy CSS algorithm in
Figure 11 and
Figure 12. In
Figure 11, the SNR range is set as
,
is 0.1,
, parameter Δ is 0.2, and simulation is under the channel of AWGN. The performance of exponential entropy-based detection and power spectral entropy detection with a single secondary user is also analyzed. From the simulation results in
Figure 11, we can see that the
performance of the NQEE-CSS method is much better than the other three traditional cooperative entropy-based detection schemes (AND, OR, and VOTING rules). Especially when SNR is equal to
, the proposed algorithm possesses the 0.162, 0.278 and 0.394 promotion of detection probability, compared with three kinds of traditional collaborative detection methods (based on the exponential entropy), which proves that the proposed CSS algorithm has the superior detection performance with low SNR and is suitable for the actual wireless environment.
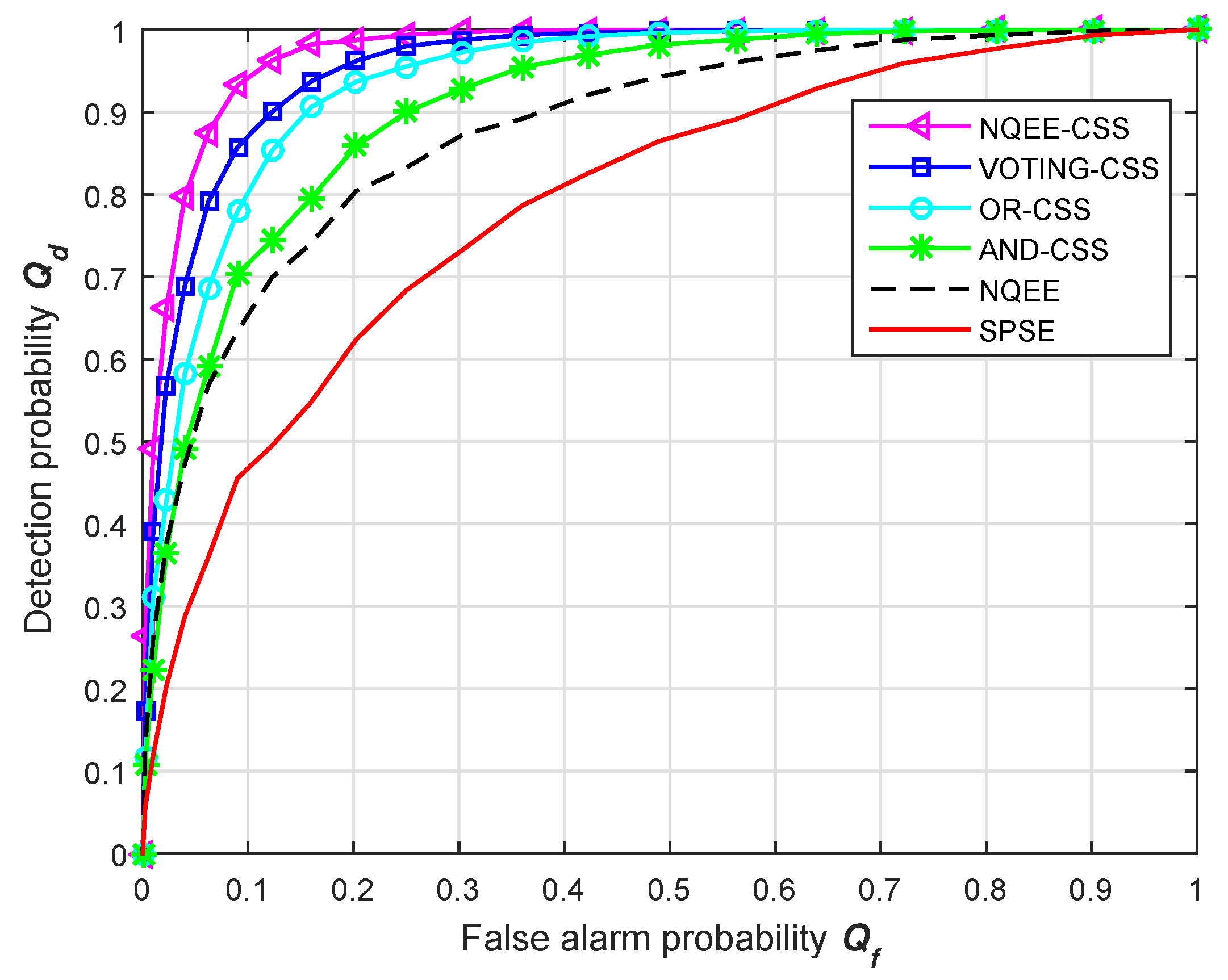
The ROC performances of these entropy-based collaborative detectors are also analyzed and the corresponding ROC curves are depicted in
Figure 12. The parameters of these detectors are the same as those set in
Figure 7. From the simulation results in
Figure 12, we can see that the ROC performance of the cooperative exponential entropy-based detection scheme is obviously much better than that of the other detectors, especially under the condition of low false alarm probability. When
, the detection probability of exponential entropy CSS achieves 0.534 promotion to the VOTING-CSS scheme.