Petrie Duality and the Anstee–Robertson Graph

Abstract

We define the operation of Petrie duality for maps, describing its general properties both geometrically and algebraically. We give a number of examples and applications, including the construction of a pair of regular maps, one orientable of genus 17, the other non-orientable of genus 52, which embed the 40-vertex cage of valency 6 and girth 5 discovered independently by Robertson and Anstee. We prove that this map (discovered by Evans) and its Petrie dual are the only regular embeddings of this graph, together with a similar result for a graph of order 40, valency 6 and girth 3 with the same automorphism group.

1. Introduction

Anyone who has studied the theory of maps on surfaces, or that of polytopes, will be familiar with the classical duality operation D, which transposes the roles of vertices and faces. It leaves the underlying surface of a map invariant, preserving such properties as orientability, genus and boundary components, so it is very useful when studying maps on a given surface. It also preserves the automorphism group of a map, so it is even more useful when studying the most symmetric maps: these are the regular maps, those maps for which the automorphism group acts transitively (and hence regularly) on flags.

This duality operation is less useful when one studies the regular embeddings of a given graph, or family of graphs, since it may (and often does) change the graph embedded by a map. In this situation, there is a more useful but slightly less well-known duality operation, called the Petrie duality P, which has the advantage of preserving the embedded graph. The aim of this note is to define this operation, to describe a little of its history and its general properties, and to show its effectiveness by using it to study some regular graphs which have arisen in a purely graph-theoretic context, namely that of cages.

The cage of valency 6 and girth 5, that is, the smallest graph with these parameters, was described by Robertson in his thesis [1], and was subsequently independently discovered by Anstee [2], Evans [3], and O’Keefe and Wong [4]. This graph, which has 40 vertices, has been further studied by Klin, Muzychuk and Ziv-Av [5], and by Wong [6], the latter giving a proof of its uniqueness. Following [5] we will call this the Anstee–Robertson graph, and denote it by $\mathcal{R}$.

Evans [3] showed that $\mathcal{R}$ can be embedded in an orientable surface as a map $\mathcal{M}$ with pentagonal faces. Our aim here is to show that this map $\mathcal{M}$, which we will call the Evans map, is a regular map of genus 17, a double covering of the regular map ${\{5,6\}}_4$ of genus 9 described by Coxeter and Moser in Section 8.6 and Table 8 of [7]; we will also describe the Petrie dual ${\mathcal{M}}^{\prime }=P\left(\mathcal{M}\right)$ of $\mathcal{M}$, a regular embedding of $\mathcal{R}$ with octagonal faces on a non-orientable surface of genus 52. We will prove in Theorem 2 that these are the only regular maps which embed this graph, together with a similar result (Corollary 3) for another graph ${\mathcal{R}}^{†}$ of order 40 and valency 6 (but girth 3) which has the same automorphism group as $\mathcal{R}$. We will also consider various quotients of $\mathcal{M}$ and ${\mathcal{M}}^{\prime }$, showing that they are isomorphic to various maps which have already appeared in the literature.

2. The Petrie Dual of a Map

One can think of a map as a road-map, with edges representing roads, and vertices representing roundabouts. One can then travel around each face by starting a journey along one edge, and consistently turning first left at each vertex. Even if the surface is non-orientable, one can carry a local orientation along the edges, so that “first left” is always well-defined. Replacing “first left” with “first right” gives the other face incident with the initial edge (in some cases these two faces may coincide).

Suppose that instead we decide to turn alternately first left and first right, following a zigzag path through the map. In a finite map, such a path must eventually close up, giving what is called a Petrie polygon. (Coxeter [8] named these polygons after his lifelong friend, the geometer John Flinders Petrie (1907–1972), who was the son of the great Egyptologist Sir William Flinders Petrie.) As in the case of faces, each edge is in general contained in two Petrie polygons, depending on whether one starts by turning left or right, but again there are examples in which the two polygons coincide.

The Petrie dual $P\left(\mathcal{M}\right)$ of a map $\mathcal{M}$ is the map formed by retaining the vertices and edges of $\mathcal{M}$, but removing its faces, and replacing them with new faces bounded by the Petrie polygons of $\mathcal{M}$. Thus the embedded graph is unchanged, but the surface may be totally different.

For example, if we regard the tetrahedron as a map $\mathcal{T}$ on the sphere, with four triangular faces, then its Petrie polygons have length 4: one is indicated with thick red lines in the map on the left of Figure 1. Then $P\left(\mathcal{T}\right)$ is a map on the real projective plane, with three quadrilateral faces. It is, in fact, the antipodal quotient of the cube, as shown on the right in Figure 1, where antipodal points on the boundary of the disk, shown as a broken line, are identified. Note that in both cases the embedded graph is the complete graph $K_4$, and the automorphism group of the map is isomorphic to $S_4$, acting naturally on the four vertices.

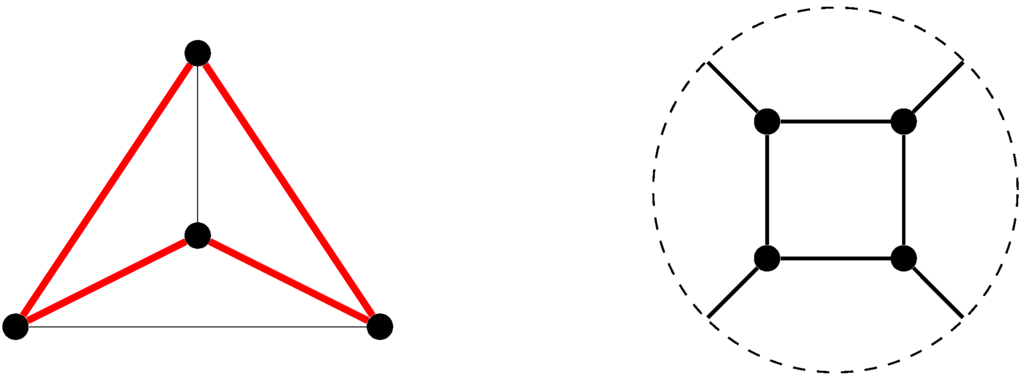
Figure 1. The tetrahedron, with a Petrie polygon, and its Petrie dual.

Figure 1. The tetrahedron, with a Petrie polygon, and its Petrie dual.

If we regard the cube $\mathcal{C}$ as a map on the sphere, then its Petrie polygons, such as that indicated with thick red lines in Figure 2, have length 6. The six quadrilateral faces of $\mathcal{C}$ are replaced in $P\left(\mathcal{C}\right)$ with four hexagonal faces; this map is shown on the right in Figure 2, where opposite sides of the outer hexagon are identified to form a torus, so that there are just two vertices at the corners. Again, the graph ($Q_3$ in this case) and the automorphism group $(S_4\times C_2$) are unchanged.

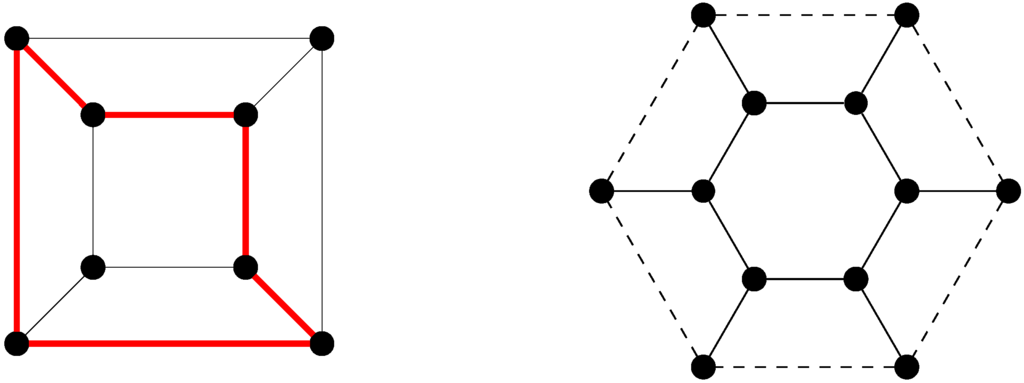
Figure 2. The cube, with a Petrie polygon, and its Petrie dual.

Figure 2. The cube, with a Petrie polygon, and its Petrie dual.

The difference between the Euler characteristics of a map and its Petrie dual can be arbitrarily large. For example, let $\mathcal{M}$ be the regular map on the sphere with two vertices joined by n edges, so that there are n digonal faces. If n is odd there is a single Petrie polygon; since $P\left(\mathcal{M}\right)$ has two vertices, n edges and one face, it has characteristic $3-n$ and genus $(n-1)/2$; in fact, it can be formed by orientably identifying opposite sides of a $2n$-gon (see Figure 3 for the case $n=5$).

Figure 3. A planar map and its Petrie dual.

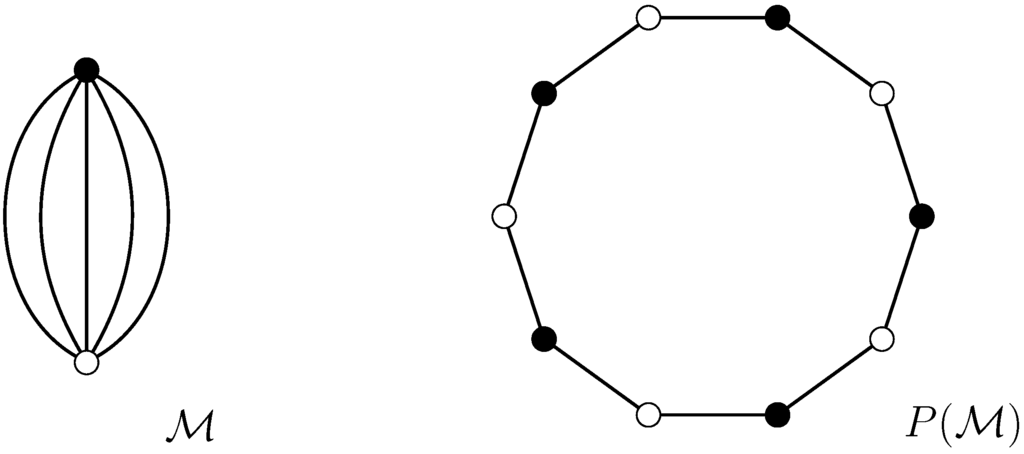
Figure 3. A planar map and its Petrie dual.

This means that Petrie duality can be very useful in creating maps of large genus from those of smaller genus, while preserving the embedded graph and the symmetry properties of the maps. For example, James [9] showed that the complete graph $K_n$ has a regular embedding in a non-orientable surface if and only if $n=3,4$ or 6. There are three obvious examples on the real projective plane, namely the antipodal quotients of the spherical embeddings of a circuit of length 6, the cube (see Figure 1), and the icosahedron. There is, however, a fourth example, the self-dual map N5.3 in Conder’s list of regular maps [10], which is much harder to describe or to visualise since it has genus 5. It is perhaps most easily constructed as the Petrie dual of the last of these three maps, or alternatively as the antipodal quotient of the great dodecahedron (R5.6 in [10], see Section 6.2 in [8]), an orientable map of genus 4 with 12 vertices of valency 5 and 12 pentagonal faces.

3. The Group of Map Operations

Clearly the classical vertex-face duality D and the Petrie duality P are operations of order 2, so they satisfy

$$D^2=P^2=I,$$

(1)

where I denotes the identity operation on maps. One might hope that the dual of the Petrie dual of a map is the same as the Petrie dual of its dual, but in fact the operations D and P do not commute: Wilson [11], building on earlier work of Coxeter in Section 8.6 of [7] and in [12], showed that they satisfy

$$PDP=DPD,\text{or}\text{equivalently}{\left(DP\right)}^3=I,$$

(2)

so they generate a group Ω of operations isomorphic to the symmetric group $S_3$. (See the slightly later paper [13] by Lins for a similar idea.) For example, by applying different operations in this group to the cube we obtain six non-isomorphic maps: there are two each on the sphere and the torus (the maps in Figure 2 and their duals), and a dual pair on a non-orientable surface of genus 4, corresponding to entry N4.2 in [10].

In addition to D and P there is a third involution in Ω, the operation $PDP=DPD$, giving another duality for maps. Wilson called this the “opposite” operation, since it acts by cutting the faces of a map apart along the edges, and then rejoining adjacent faces with the opposite identifications of their common edges. This preserves the set of faces of a map, but transposes vertices and Petrie polygons, so it generally changes both the surface and the embedded graph. Similarly, there are two triality operations on maps, namely the elements $DP$ and $PD$ of order 3 in Ω.

The group Ω thus acts as the symmetric group $S_3$, permuting the three sets consisting of the vertices, faces and Petrie polygons of each map. Only the sets of edges and of flags, together with the automorphism group, remain invariant. This suggests a symmetry between these three features of a map, giving them equal status. This is partially recognised in the notation ${\{p,q\}}_r$ introduced by Coxeter to indicate the extended type of a map: the abbreviated notation $\{p,q\}$ indicates that all faces are p-gons and all vertices have valency q, while the subscript r, indicating that the Petrie polygons all have length r, admits them as at least a junior member of the family.

For each subgroup ${\Omega }_0\le \Omega$, one can find examples of maps $\mathcal{M}$ which are invariant only under the operations in ${\Omega }_0$, so that they lie in an orbit of length $6/|{\Omega }_0|$: this is easy when $|{\Omega }_0|=1$ or 2, and not difficult for ${\Omega }_0=\Omega$, as in the recent papers by Cunningham [14] and by Richter, Širáň and Wang [15] (the simplest example in this case is the embedding of a circuit of length 2 in the sphere), but it is quite hard when ${\Omega }_0$ is the subgroup of order 3 generated by the triality operations, so that $D\left(\mathcal{M}\right)\cong P\left(\mathcal{M}\right)\ncong \mathcal{M}$. Indeed, Wilson originally thought that no such maps could exist. He eventually produced an example in [11], and this was generalised to three infinite families by Poulton and the first author in [16], but none of the constructions is straightforward. According to Conder [17], Wilson’s example, a non-orientable map N72.9 of type ${\{9,9\}}_9$ and genus 72, with automorphism group $PS{L}_2\left(8\right)$, is the smallest such map, while the smallest orientable example has genus 193 and type ${\{16,16\}}_{16}$, with an automorphism group of order 2048.

In the next section we will introduce a group-theoretic description of maps on surfaces, which we will then use to explain this group of operations, together with its analogues in other geometric and combinatorial categories.

4. Maps and Permutations

Let $\mathcal{M}$ be any map. For simplicity, let us assume that the underlying surface is without boundary. (Here, this is no great loss of generality, since maps with non-empty boundary are rarely highly symmetric.) Let Φ be the set of flags $\varphi =(v,e,f)$ of $\mathcal{M}$, where $v,e$ and f are a mutually incident vertex, edge and face. For each $\varphi \in \Phi$ and each $i=0,1,2$, there is one other flag ${\varphi }^{\prime }$ sharing the same j-dimensional components as $\varphi$ for each $j\ne i$. Let us define $r_i$ to be the permutation of Φ transposing all such pairs $\varphi ,{\varphi }^{\prime }$. Figure 4 shows how these three permutations $r_0,r_1$ and $r_2$ act on a typical flag $\varphi$.

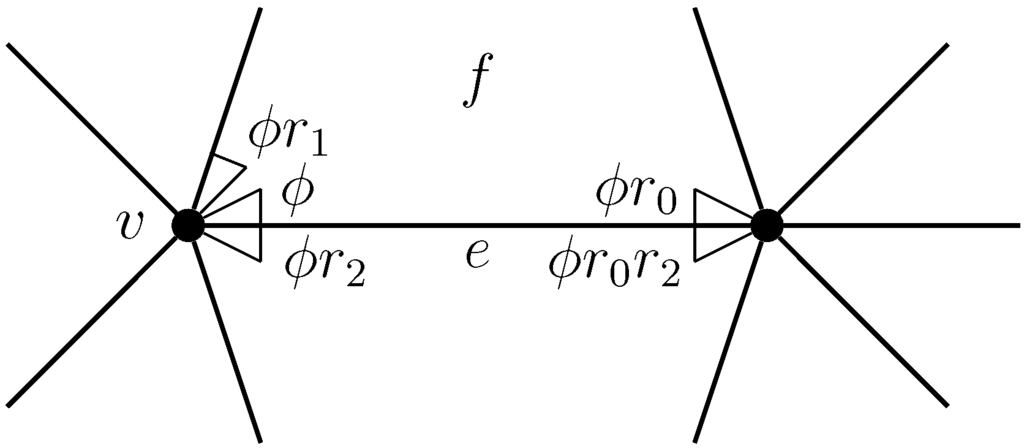
Figure 4. The permutations $r_i$ acting on a flag $\varphi =(v,e,f)$.

Figure 4. The permutations $r_i$ acting on a flag $\varphi =(v,e,f)$.

Let us define the monodromy group of $\mathcal{M}$ to be the subgroup

$$G:=\langle r_0,r_1,r_2\rangle$$

of the symmetric group $\mathrm{Sym}\Phi$ on Φ generated by the permutations $r_0,r_1$ and $r_2$. By their construction, these permutations satisfy

$$r_i^2={\left(r_0{r}_2\right)}^2=1,$$

so let us define Γ to be the abstract group with presentation (in terms of generators and relations)

$$\Gamma =\langle R_0,R_1,R_2\mid R_i^2={\left(R_0{R}_2\right)}^2=1\rangle .$$

(3)

Then there is an epimorphism $\theta :\Gamma \to G$, that is, a permutation representation of Γ on Φ, given by

$$R_i\mapsto r_i(i=0,1,2).$$

Conversely, given any (not necessarily transitive) permutation representation of Γ on a set Φ, one can construct a map $\mathcal{M}$ by taking the vertices, edges and faces to correspond to the orbits on Φ of the subgroups $\langle R_1,R_2\rangle \cong D_{\infty }$, $\langle R_0,R_2\rangle \cong V_4$ and $\langle R_0,R_1\rangle \cong D_{\infty }$, mutually incident when these orbits have non-empty intersection. More specifically, one can construct the barycentric subdivision $B\left(\mathcal{M}\right)$ of $\mathcal{M}$ by taking a set of triangles in bijective correspondence with Φ, each with edges labelled $0,1$ and 2, and joining two triangles along their edges labelled i whenever $r_i$ transposes the corresponding elements of Φ; the embedded graph is the union of all the edges labelled 2 in $B\left(\mathcal{M}\right)$.

The connected components of this map $\mathcal{M}$ correspond to the orbits of G on Φ, so we will assume that $\mathcal{M}$ is connected, or equivalently that Γ acts transitively on Φ. In this case the stabilisers of flags form a conjugacy class of subgroups $M\le \Gamma$, called the map subgroups corresponding to $\mathcal{M}$. These all have index $|\Phi |$ in Γ, so finite maps correspond to subgroups of finite index in Γ. Oriented maps without boundary correspond to map subgroups contained in the even subgroup ${\Gamma }^{+}=\langle R_0{R}_1,R_1{R}_2\rangle$ of index 2 in Γ, consisting of the words of even length in the generators $R_i$.

The automorphism group $A=\mathrm{Aut}\mathcal{M}$ of $\mathcal{M}$ can be regarded as the group of all permutations of the flags commuting with $r_0,r_1$ and $r_2$, or equivalently as the centraliser

$$A=C_{\mathrm{Sym}\Phi }\left(G\right)$$

of G in $\mathrm{Sym}\Phi$. A simple argument then shows that

$$A\cong N_G\left(G_{\varphi }\right)/G_{\varphi }\cong N_{\Gamma }\left(M\right)/M,$$

where N denotes “normaliser”, and $G_{\varphi }$ is the subgroup of G fixing a flag $\varphi$. We say that the map $\mathcal{M}$ is regular if A acts transitively on Φ. Since the centraliser of a transitive group must act semi-regularly (that is, fixed-point freely), another simple argument shows that this is equivalent to G being a regular permutation group, in which case M is a normal subgroup of Γ and

$$A\cong G\cong \Gamma /M.$$

This allows us to identify G and A as abstract groups, though as permutation groups on Φ they are distinct, and can be regarded as the right and left regular representations of the same group.

It is clear from its presentation that Γ decomposes as a free product

$$\langle R_0,R_2\rangle *\langle R_1\rangle \cong V_4*C_2,$$

where $C_2$ and $V_4$ denote a cyclic group of order 2 and a Klein four-group $C_2\times C_2$. This decomposition allows various techniques from combinatorial group theory (see [18,19]) to be applied to maps, as in [20] for example.

The elements $R_0{R}_1$ and $R_1{R}_2$ of Γ induce rotations of flags around their incident faces and vertices, so if a map has type $\{p,q\}$ we have ${\left(r_0{r}_1\right)}^p={\left(r_1{r}_2\right)}^q=1$. When studying maps of a given type $\{p,q\}$ one can therefore add the relations

$${\left(R_0{R}_1\right)}^p={\left(R_1{R}_2\right)}^q=1$$

to the presentation of Γ, giving the extended triangle group

$$\Delta [q,2,p]=\langle R_0,R_1,R_2\mid R_i^2={\left(R_1{R}_2\right)}^q={\left(R_0{R}_2\right)}^2={\left(R_0{R}_1\right)}^p=1\rangle ,$$

which plays the role of Γ for this category of maps. Within this category, the oriented maps without boundary are those whose map subgroups M are contained in the ordinary triangle group

$$\Delta (q,2,p)=\langle X=R_1{R}_2,Y=R_2{R}_0,Z=R_0{R}_1\mid X^p=Y^2=Z^q=XYZ=1\rangle ,$$

the subgroup of index 2 in $\Delta [q,2,p]$ consisting of the words of even length in the generators $R_i$.

5. Operations and Automorphisms

The faces of a map $\mathcal{M}$ correspond to the orbits of the dihedral subgroup $\langle R_0,R_1\rangle$ of Γ on Φ, with the boundary circuit of each face obtained by starting with an incident flag $\varphi$ and alternately applying the permutations $r_0$ and $r_1$. Similarly, the Petrie polygons of $\mathcal{M}$ correspond to the orbits of the dihedral subgroup $\langle R_0{R}_2,R_1\rangle$ of Γ, now obtained by starting with an incident flag $\varphi$ and alternately applying $r_0{r}_2$ and $r_1$. To put this another way, if $\mathcal{M}$ corresponds to a conjugacy class of subgroups M of Γ, then the Petrie dual $P\left(\mathcal{M}\right)$ corresponds to the conjugacy class consisting of their images under the automorphism

$$\pi :R_0\mapsto R_0{R}_2,R_1\mapsto R_1,R_2\mapsto R_2$$

of Γ transposing $R_0$ and $R_0{R}_2$. In a similar way the duality operation D corresponds to the automorphism

$$\delta :R_0\mapsto R_2,R_1\mapsto R_1,R_2\mapsto R_0$$

of Γ, transposing $R_0$ and $R_2$, while the group Ω generated by D and P corresponds to the automorphism group of the Klein four-group $\langle R_0,R_2\rangle$, permuting the three involutions $R_0,R_2$ and $R_0{R}_2$ and inducing a group $\Sigma =\langle \delta ,\pi \rangle$ of automorphisms of Γ isomorphic to $S_3$.

In [20], Thornton and the first author used the free product structure of Γ to show that $\mathrm{Aut}\Gamma$ is the semidirect product of the inner automorphism group $\mathrm{Inn}\Gamma$, isomorphic to Γ, and this group Σ. Since inner automorphisms leave conjugacy classes of map subgroups, and hence their associated maps, invariant, we have an induced action of the outer automorphism group

$$\mathrm{Out}\Gamma =\mathrm{Aut}\Gamma /\mathrm{Inn}\Gamma \cong \Sigma \cong S_3.$$

This gives a group-theoretic interpretation of the six operations on the category of all maps, and also explains why there are no others.

With this machinery available, it is easy to construct regular maps which are invariant under P: take any normal subgroup N of Γ, corresponding to some regular map $\mathcal{N}$, and define $\mathcal{M}$ to be the map corresponding to the normal subgroup $M=N\cap N^{\pi }$. This is the smallest map covering both $\mathcal{N}$ and $P\left(\mathcal{N}\right)$. For example, the icosahedron is a regular map $\mathcal{N}$ of type ${\{3,5\}}_{10}$, so $P\left(\mathcal{N}\right)$ is a regular map of type ${\{10,5\}}_3$ with the same automorphism group $A_5\times C_2$ (it is the dual of the non-orientable map N14.3 of genus 14 in [10]), and a straightforward calculation shows that the resulting self-Petrie-dual map $\mathcal{M}$ is an orientable regular map of type ${\{30,5\}}_{30}$ and genus 961 with automorphism group ${(A_5\times C_2)}^2$.

Similarly, by taking M to be intersection of the images of N under all six automorphisms in Σ we obtain an Ω-invariant orientable regular map of type ${\{30,30\}}_{30}$ and genus 187201 with automorphism group ${(A_5\times C_2)}^3$, the smallest covering $\mathcal{M}$ of the icosahedron $\mathcal{N}$ such that $\mathcal{M}\cong D\left(\mathcal{M}\right)\cong P\left(\mathcal{M}\right)$. There are six distinct images of N, each of the form $A\cap B$ for unique normal subgroups A and B of Γ with quotients $A_5$ and $C_2$; there are three distinct subgroups A and three distinct subgroups B which arise, each set permuted by Σ as $S_3$, but the images of N correspond to an orbit of Σ of length 6 on the nine ordered pairs $(A,B)$, giving six non-isomorphic images of $\mathcal{N}$ under Ω. The three subgroups A and the three subgroups B intersect in normal subgroups with quotients $A_5^3$ and $C_2^3$ respectively, so this calculation, which has been confirmed with the aid of GAP [21], explains why $\mathcal{M}$ has automorphism group ${(A_5\times C_2)}^3$ and not, as one might expect, ${(A_5\times C_2)}^6$. See [14] for generalisations to polyhedra.

As shown by the first author in [22], there are many other categories in which geometric or combinatorial objects can be identified with the permutation representations of a particular group Δ, so that $\mathrm{Out}\Delta$ acts as a group of operations. For maps of a given valency k, for example, the permutations $r_i$ satisfy ${\left(r_1{r}_2\right)}^k=1$, so we can add the relation ${\left(R_1{R}_2\right)}^k=1$ to the presentation for Γ, giving the extended triangle group $\Delta =\Delta [k,2,\infty ]$. In this case, if $k>2$ then $\mathrm{Out}\Delta \cong {\mathbb{Z}}_k^{*}/\{\pm 1\}\times C_2$, with the generator of $C_2$ induced by π, corresponding to the Petrie operation on k-valent maps. The case $k=3$, for cubic maps, is of particular interest, since the corresponding group Δ is the extended modular group $PG{L}_2\left(\mathbb{Z}\right)$, with $\mathrm{Out}\Delta \cong C_2$; the non-identity outer automorphism was discovered by Dyer [23], correcting an error in [24]. Uludaǧ and Ayral [25] give a wide range of applications and manifestations of this outer automorphism, ranging from number theory to dynamical systems.

In contrast with these finite groups of operations, James [26] has shown that for the categories of hypermaps and of oriented hypermaps, where Δ is a free product $C_2*C_2*C_2$ or a free group $F_2$, the groups of operations are infinite, isomorphic to $PG{L}_2\left(\mathbb{Z}\right)$ and $G{L}_2\left(\mathbb{Z}\right)$ respectively. Maps can also be generalised to abstract polytopes of higher rank n, with the role of Δ played by the string Coxeter group

$$\langle R_0,\dots ,R_n\mid R_i^2=1,{\left(R_i{R}_j\right)}^2=1\mathrm{whenever}|i-j|>1\rangle$$

of rank n with Schläfli symbol $\{\infty ,\dots ,\infty \}$. James [27] has shown that for polytopes of each rank $n>3$, the group of operations is isomorphic to the dihedral group $\mathrm{Out}\Delta \cong D_4$ of order 8, generated by involutions D and P corresponding to automorphisms

$$R_i\mapsto R_{n-i}(i=0,\dots ,n)$$

and

$$R_{n-2}\mapsto R_{n-2}{R}_n,R_i\mapsto R_i(i\ne n-2).$$

In the rest of this paper we will focus on the regular maps which embed a particular graph, the Anstee–Robertson graph, together with their regular quotients, showing how Petrie duality can be used to understand them.

6. The Graph $\mathcal{R}$ and Its Group G

It is easy to see that a graph of valency 6 and girth 5 must have at least 37 vertices. In fact the smallest such graph, the $(6,5)$-cage first discovered by Robertson [1], has order 40. There are various constructions of this graph. Here we will use one based on [5] which is particularly useful for studying the automorphism group of the graph.

Let ${\mathbb{F}}^2$ denote the 2-dimensional vector space over the field $\mathbb{F}={\mathbb{F}}_5$ of order 5, and let T be the set of unordered triples $\{v_1,v_2,v_3\}\subset {\mathbb{F}}^2$ which span ${\mathbb{F}}^2$ and satisfy $v_1+v_2+v_3=0$. These conditions imply that each $v_i\ne 0$, so $\left|T\right|=(5^2-1)(5^2-5)/6=80$. The natural action of $G{L}_2\left(5\right)$ on ${\mathbb{F}}^2$ induces a faithful action of this group on T. This action is transitive, since each triple in T is an image of the standard triple

$$\omega =\{e_1=(1,0),e_2=(0,1),e_3=(-1,-1)\}.$$

The stabiliser of ω in $G{L}_2\left(5\right)$ is a subgroup $S\cong S_3$, permuting the three vectors $e_i$.

There is a unique subgroup $K=H{L}_2\left(5\right)$ of index 2 in $G{L}_2\left(5\right)$, consisting of the elements with non-zero square determinant. (Here “H” stands for “half”.) This group K contains the group

$$Z=\{\lambda I\mid \lambda \in {\mathbb{F}}^{*}\}$$

of scalar matrices as a cyclic central subgroup of order 4, with quotient group

$$K/Z\cong PS{L}_2\left(5\right)\cong A_5.$$

The six matrices in S have determinant $\pm 1$, so $S\le K$, and hence K has two orbits on T, each of size $|K:S|=40$. The orbit $V\subset T$ containing ω consists of those triples $\alpha =\{v_1,v_2,v_3\}\in T$ such that $det(v_i,v_j)$ is a square for one (equivalently each) pair $i\ne j$. (Here $(v_i,v_j)$ denotes the $2\times 2$ matrix formed by using the coordinates of $v_i$ and $v_j$ with respect to the standard basis $e_1,e_2$ as its rows.)

Lemma 1. 

The stabiliser $S=K_{\omega }$ of ω in K fixes four elements of V, and has six orbits of length 6 on the remaining elements of V.

Proof. 

The orbits of S on V must have lengths dividing $\left|S\right|=6$. Those of length 1 are the four sets $\left\{\lambda \omega \right\}$ where $\lambda \in {\mathbb{F}}^{*}$; such triples $\lambda \omega$ all lie in V since $det(\lambda e_1,\lambda e_2)={\lambda }^2$. (This shows that the actions of K on its orbits V and $T\backslash V$ are inequivalent, since they have different conjugacy classes of point-stabilisers; these actions differ by an outer automorphism of K, induced by conjugation in $G{L}_2\left(5\right)$.)

A non-trivial orbit of S has length 2 if and only if it contains a triple fixed by the matrix $(e_2,e_3)$ of order 3, i.e. of the form $\{v_1=(a,b),v_2=(b,-a-b),v_3=(-a-b,a)\}$ where $a,b,a-b\ne 0$ (to avoid triples $\lambda \omega$ fixed by S); such a triple is in V if and only if $a^2-ab+b^2$ is a non-zero square. By inspection of $\mathbb{F}$, there are no such orbits.

Similarly, a non-trivial orbit of S has length 3 if and only if it contains a triple $\{v_1=(a,b),v_2=(b,a),v_3=(-a-b,-a-b)\}$ fixed by the matrix $(e_2,e_1)$ of order 2, with $a,b,a-b\ne 0$; such a triple is in V if and only if $a^2-b^2$ is a non-zero square. Again, there are no such orbits.

Any other orbits of S must have length 6, so there are four orbits of length 1, and six of length 6. ☐

The fixed points of S are the triples ${\tau }_i=(i+1)\omega$ for $i=0,\dots ,3$, and the orbits of length 6 are represented by the following triples ${\tau }_i(i=4,\dots ,9)$:

$$\left\{\right(0,1),(1,1),(4,3\left)\right\},\left\{\right(0,1),(1,2),(4,2\left)\right\},\left\{\right(0,2),(2,1),(3,2\left)\right\},$$

$$\left\{\right(0,2),(2,2),(3,1\left)\right\},\left\{\right(0,3),(2,1),(3,1\left)\right\},\left\{\right(0,4),(1,4),(4,2\left)\right\}.$$

These give ten orbitals (K-orbits on $V^2$) $R_i\subset V^2(i=0,\dots ,9)$ for K, with $(\omega ,{\tau }_i)\in R_i$. The corresponding orbital graphs ${\mathcal{R}}_i$, with vertex set V and arc set $R_i$, have valency 1 or 6 as $i\le 3$ or $i\ge 4$. (See [5] for background on orbital graphs.) We will concentrate on the graph $\mathcal{R}:={\mathcal{R}}_5$; this graph is undirected, corresponding to a self-paired orbital $R_5$, since the involution

$$A=\left(\begin{array}{cc}4& 2\\ 0& 1\end{array}\right)\in K$$

transposes ω and its neighbour

$$\tau :={\tau }_5=\{(0,1),(1,2),(4,2)\}.$$

By listing the neighbours of the vertices ω and τ, one can check that these two adjacent vertices have no common neighbours; since K acts transitively on the edges of $\mathcal{R}$ it follows that this graph is triangle-free. Similarly, no neighbour of ω has a common neighbour with τ, other than ω, so there are no cycles of length 4 in $\mathcal{R}$. However, the matrix

$$B=\left(\begin{array}{cc}0& 1\\ 4& 2\end{array}\right)\in K$$

of order 5 sends ω to τ, giving a pentagon, i.e., a cycle $\{\omega B^i\mid i=0,\dots ,4\}$ of length 5 in $\mathcal{R}$. Thus $\mathcal{R}$ has girth 5, so having 40 vertices it must be the unique cage of girth 5 and valency 6 (see [6]). Following [5] we will call $\mathcal{R}$ the Anstee–Robertson graph. It is shown in Figure 5 as a Hamiltonian graph, with a pentagon (appearing here as a pentagram) drawn in thick red lines.

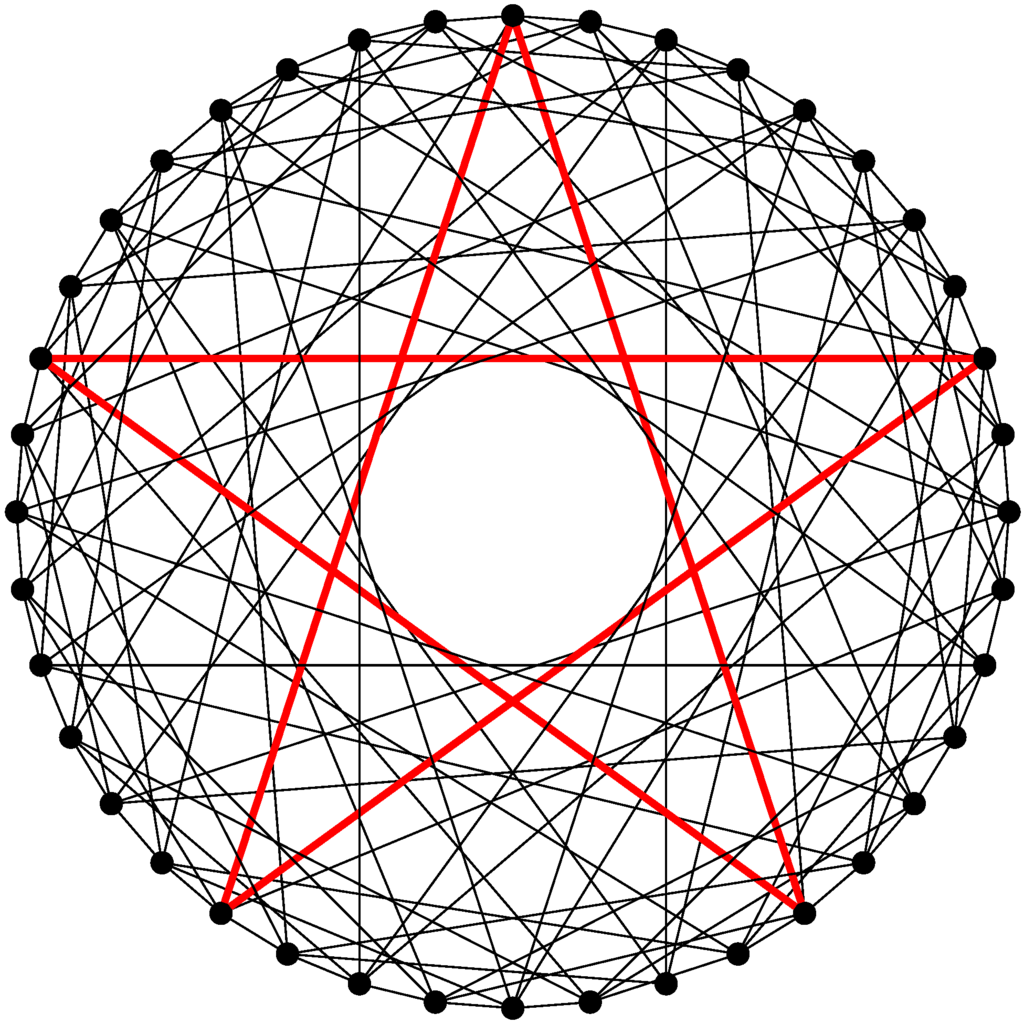
Figure 5. The Anstee-Robertson graph $\mathcal{R}$.

Figure 5. The Anstee-Robertson graph $\mathcal{R}$.

The action of Z partitions the triples in V into ten blocks of size 4, forming a system of imprimitivity for K. Identifying vertices within each block gives a quotient graph $\mathcal{R}/Z$ of order 10 and valency 6, with $K/Z$ acting arc-transitively on it. Now $K/Z\cong PS{L}_2\left(5\right)\cong A_5$, so the action of $K/Z$ on vertices of $\mathcal{R}/Z$ can be identified with the unique transitive action of $A_5$ of degree 10, namely on unordered pairs from $\{1,\dots ,5\}$, showing that $\mathcal{R}/Z$ is isomorphic to the line graph $L\left(K_5\right)$ of $K_5$. The full automorphism group of $L\left(K_5\right)$ is isomorphic to $S_5$, and as shown by Anstee [2] (by treating the adjacency matrix of $\mathcal{R}$ as a $10\times 10$ block matrix) the elements of $S_5$ all lift back to automorphisms of $\mathcal{R}$. This shows that the automorphism group

$$G:=\mathrm{Aut}\mathcal{R}$$

of $\mathcal{R}$ has order $\left|G\right|=480$, and is an extension of a normal subgroup $Z\cong C_4$ by $S_5$, with K, an extension of Z by $A_5$, as a subgroup of index 2. However, Anstee’s assertion that G is a direct product of Z and $S_5$ is incorrect (see [5]): the extension does not split.

(In a slightly different but related context, K is described in [28] as a central product $Z\circ S{L}_2\left(5\right)$ of Z and $S{L}_2\left(5\right)$, amalgamating central subgroups Y of order 2. It arises as the automorphism group of a locally icosahedral graph on V formed by merging the orbitals $R_4$ and $R_9$ of K in Section 9.5 of [5].)

As a permutation group on V, G has rank 7, with suborbits of lengths $1,1,2,6,6,12$ and 12; in particular, the orbitals $R_4$ and $R_7$ are merged in G, as are $R_6$ and $R_8$, whereas $R_5$ and $R_9$ are unmerged.

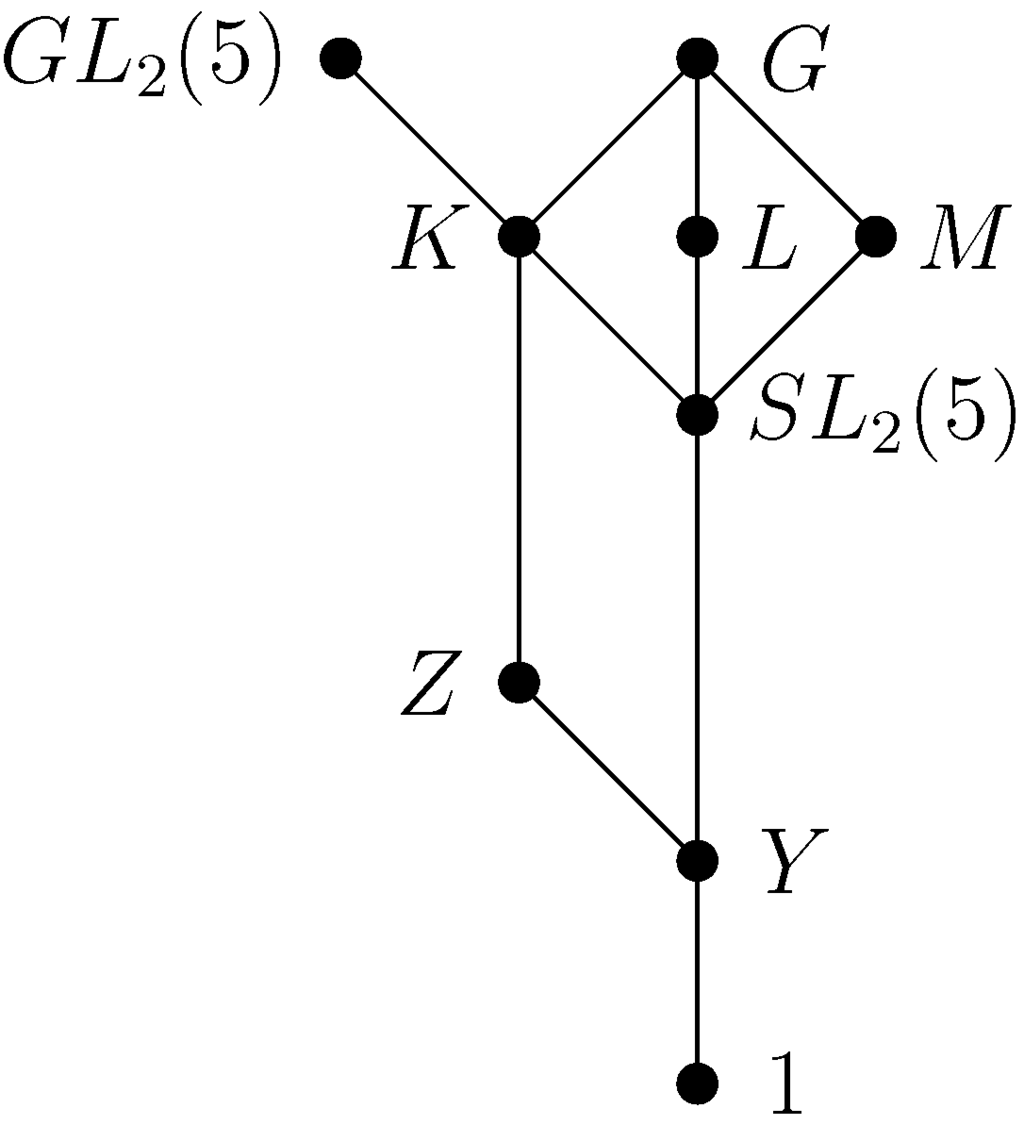
Figure 6. The lattice of normal subgroups of G and $G{L}_2\left(5\right)$.

Figure 6. The lattice of normal subgroups of G and $G{L}_2\left(5\right)$.

Since $G/S{L}_2\left(5\right)\cong V_4$, there are three subgroups $K,L$ and M of index 2 in G containing $S{L}_2\left(5\right)$. The lattice of normal subgroups of G and of $G{L}_2\left(5\right)$ is shown in Figure 6, with $Y:=Z\cap S{L}_2\left(5\right)=\{\pm I\}$: short edges denote index 2 inclusions, long edges denote index 60 inclusions, with quotient group $A_5$.

In order to understand the structure of G, it is important to note that although this group is closely related to $G{L}_2\left(5\right)$, they are not isomorphic. For instance, $G{L}_2\left(5\right)$ has centre $Z\cong C_4$, but this group is inverted in G, so that the centre of G is the subgroup Y of order 2 in Z. Similarly, both $G{L}_2\left(5\right)$ and G are extensions of K by $C_2$, but G is a split extension whereas $G{L}_2\left(5\right)$ is not, since there are no involutions in $G{L}_2\left(5\right)\backslash K$. (There are more details of the structure of G, based on the construction of the regular maps, at the end of the next section.)

The graph $\mathcal{R}$ is a Cayley graph, as shown in Propositions 9.2 and 9.11 of [5], although its quotient $\mathcal{R}/Z\cong L\left(K_5\right)$ is well known not to have this property: the six subgroups of $G/Z\cong S_5$ isomorphic to $AG{L}_1\left(5\right)$ lift back to subgroups of order 80 in G, the normalisers of its six Sylow 5-subgroups; their intersections with L and with M form two conjugacy classes of six subgroups

$$R=\langle x,y\mid x^5=y^8=1,x^y=x^3\rangle \cong C_5⋊C_8$$

acting regularly on the vertices of $\mathcal{R}$. These are non-split double covers of $AG{L}_1\left(5\right)$ with common intersection $Y=R\cap Z=\langle y^4\rangle \cong C_2$.

7. Construction of the Maps

There is a single conjugacy class of elements of order 5 in G, consisting of the 24 non-identity matrices in $S{L}_2\left(5\right)$ with trace 2. A simple matrix argument shows that there are two such matrices sending ω to its neighbour τ: the matrix B given earlier, together with

$$C=\left(\begin{array}{cc}1& 2\\ 0& 1\end{array}\right).$$

This means that the edge $\omega \tau$ of $\mathcal{R}$ is contained in two pentagons, $\left\{\omega B^i\right\}$ and $\left\{\omega C^i\right\}$. By the transitivity of G on arcs, the same applies to each ordered pair of neighbours in $\mathcal{R}$. There are 240 such pairs, so each of the 24 elements of order 5 acts in this way on $480/24=20$ such pairs of neighbours; these lie in $20/5=4$ pentagons, forming an orbit under Z. Each of the twelve mutually inverse pairs of elements of order 5 in G thus yields 4 pentagons, so we obtain $12\times 4=48$ pentagons in $\mathcal{R}$, each invariant under a Sylow 5-subgroup of G. We call these the useful pentagons: one of them is shown using thick red lines in Figure 5. Any other pentagon in $\mathcal{R}$ must have a stabiliser in G of order dividing 2, and hence must lie in an orbit of G of length 240 or 480. (In fact, GAP shows there are 528 pentagons in $\mathcal{R}$, the rest of them forming two G-orbits of length 240.)

The neighbours of ω in the pentagon $\left\{\omega B^i\right\}$ are the vertices

$$\omega B=\tau =\{(0,1),(1,2),(4,2)\}\mathrm{and}\omega B^{-1}=\{(1,0),(2,1),(2,4)\}.$$

These are transposed by the involution

$$D=\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right)\in K,$$

so this pentagon is invariant under a dihedral subgroup of K of order 10, and by the arc-transitivity of K the same applies to every useful pentagon (such a subgroup is clearly visible for the red pentagon in Figure 5). The useful pentagons therefore form two orbits of size $240/10=24$ under K. The dihedral subgroup $\langle B,D\rangle$ must also be the stabiliser in G of the pentagon $\left\{\omega B^i\right\}$, for if this stabiliser were larger then a non-identity element of G would fix this pentagon, whereas the stabiliser in G of ω fixes only one other vertex. It follows that this pentagon lies in an orbit of G of size $480/10=48$, so G acts transitively on the useful pentagons.

Following Evans [3] we now embed $\mathcal{R}$ in a 2-dimensional complex $\mathcal{S}$ by attaching a pentagonal face to each useful pentagon. We need to show that $\mathcal{S}$ is a surface. Since each edge of $\mathcal{R}$ is contained in two useful pentagons, and is therefore incident with two faces, it is sufficient to check that a neighbourhood of each vertex is a disc. By listing the useful pentagons containing a particular vertex v (either by hand as in [3] or by using GAP) one can verify that the faces incident with v form a cycle of length 6 around v, so that a small open neighbourhood of v in $\mathcal{S}$ is homeomorphic to a disc. The transitivity of G on vertices implies that the same is true for every vertex, so $\mathcal{S}$ is a surface (rather than a pseudo-surface, as would be the case if the faces around v formed more than one cycle). This embedding of $\mathcal{R}$ in $\mathcal{S}$ is a map $\mathcal{M}$, which we will call the Evans map. It is a uniform map of type $\{5,6\}$, meaning that the faces are all pentagons and the vertices all have valency 6. This map is illustrated by Evans in Figure 10 of [3].

Any automorphism of $\mathcal{M}$ is also an automorphism of the embedded graph $\mathcal{R}$, so we have $\mathrm{Aut}\mathcal{M}\le \mathrm{Aut}\mathcal{R}=G$. On the other hand, since the faces of $\mathcal{M}$ are bounded by the useful pentagons, which form a set invariant under automorphisms of $\mathcal{R}$, we have $\mathrm{Aut}\mathcal{R}\le \mathrm{Aut}\mathcal{M}$. Thus

$$\mathrm{Aut}\mathcal{M}=\mathrm{Aut}\mathcal{R}=G.$$

Since $\mathcal{M}$ has 120 edges, it has $120\times 4=480$ flags $\varphi =(v,e,f)$, where $v,e$ and f denote an incident vertex, edge and face. In any map, these are permuted semi-regularly by the automorphism group; in this case, since $\left|G\right|=480$, this action is transitive, so $\mathcal{M}$ is a regular map (reflexible in the terminology of [7]).

This implies that G is isomorphic to the monodromy group of $\mathcal{M}$, so it is generated by automorphisms $r_i(i=0,1,2)$ of $\mathcal{M}$, each changing the i-dimensional component of a particular flag $\varphi =(v,e,f)$ while preserving the others. These correspond to the monodromy generators introduced in Section 4 (but now acting as automorphisms by left rather than right multiplication on G), so they satisfy

$$r_i^2={\left(r_0{r}_1\right)}^5={\left(r_0{r}_2\right)}^2={\left(r_1{r}_2\right)}^6=1,$$

where

$$\langle r_1,r_2\rangle =G_v\cong D_6,\langle r_0,r_2\rangle =G_e\cong D_2\cong V_4$$

and

$$\langle r_0,r_1\rangle =G_f\cong D_5.$$

(In fact, one can take $\varphi =(\omega ,\omega \tau ,\left\{\omega B^i\right\})$, $r_0=A$ and $r_1=D$ here, so that $r_0{r}_1=B^{-1}$, with $r_2\in G\backslash K$.) The Euler characteristic of $\mathcal{M}$ is

$$\chi =40-120+48=-32,$$

so $\mathcal{M}$ is either orientable of genus 17 or non-orientable of genus 34. As shown by Evans [3] one can assign consistent orientations to the useful pentagons, so that $\mathcal{M}$ is orientable. (Alternatively, one can use GAP to show that G has a subgroup $G^{+}$ of index 2, the image of ${\Gamma }^{+}$, with each $r_i\in G\backslash G^{+}$, or equivalently that the Cayley graph for G with respect to these generators is bipartite; then $G^{+}$ is the group ${\mathrm{Aut}}^{+}\mathcal{M}$ of orientation-preserving automorphisms of $\mathcal{M}$. In fact, Conder’s list of regular maps [10] shows that there is no non-orientable regular map of genus 34 and type $\{5,6\}$, giving a third proof.)

Inspection of Conder’s list [10] shows that $\mathcal{M}$ must be the map R17.16, the only orientable regular map of genus 17 and type $\{5,6\}$. This map has Petrie length 8, so the Petrie dual ${\mathcal{M}}^{\prime }=P\left(\mathcal{M}\right)$ is a map of type $\{8,6\}$. As explained earlier, this is another regular map, also embedding the Anstee-Robertson graph $\mathcal{R}$, with $\mathrm{Aut}{\mathcal{M}}^{\prime }=G$. It has Euler characteristic

$${\chi }^{\prime }=40-120+30=-50,$$

so inspection of [10] shows that it must be the vertex-face dual of one of the two non-orientable regular maps N52.3 and N52.4 of genus 52 and type $\{6,8\}$. These have Petrie lengths 10 and 5 respectively, and since the Petrie polygons of ${\mathcal{M}}^{\prime }$ correspond to the faces of $\mathcal{M}$, it follows that ${\mathcal{M}}^{\prime }$ is the dual of N52.4 (we will return to N52.3 and its dual later). The entry for N52.4 in [10] includes the comment “mV = 2”, meaning that each pair of adjacent vertices have two edges in common; equivalently, each pair of adjacent faces of ${\mathcal{M}}^{\prime }$, or of adjacent Petrie polygons of $\mathcal{M}$, also share two common edges.

In addition to K, there are two other subgroups of index 2 in G, denoted by L and M in [5], of ranks 9 and 11 on V; any two of these intersect in $G^{\prime }=S{L}_2\left(5\right)$. The stabiliser $G_{\omega }^{+}$ of ω, a cyclic group of order 6, has the following orbits on V: $\left\{\omega \right\}$, an orbit of length 6 consisting of the neighbours of ω, five orbits of length 6 consisting of the vertices at distance 2 from ω, and orbits of length 1 and 2 on the three vertices at distance 3 from ω. Thus $G^{+}$ has rank 9 on Ω, so one can identify this subgroup with L, rather than M.

If H denotes either L or M then $HZ=G$ and $H\cap Z=Y=\{\pm I\}$, the unique subgroup of order 2 in Z, so $H/Y\cong G/Z\cong S_5$. Thus H is a double cover of $S_5$. This cannot be a direct product, for if it were then $G^{\prime }=S{L}_2\left(5\right)$ would have a subgroup of index 2, whereas it is perfect. Thus H must be isomorphic to one of the two nontrivial double covers $2.S_5^{\pm }$ of $S_5$. Now $2.S_5^{-}$ has a unique involution (generating the centre), whereas $2.S_5^{+}$ has non-central involutions. The half-turn $r_0{r}_2$ lies in L and the reflection $r_2$ lies in M: neither can be in K since $r_0,r_1\in K$ and $G=\langle r_0,r_1,r_2\rangle$. It follows that each $H\cong 2.S_5^{+}$. Thus G is a product of $K=H{L}_2\left(5\right)$ and $H(=L\mathrm{or}M)\cong \widehat{S_5}=2.S_5^{+}$ amalgamating a common subgroup $S{L}_2\left(5\right)=\widehat{A_5}=2.A_5$ of index 2 in each.

Our investigations lead to the following uniqueness theorem:

Theorem 2. 

The only regular maps embedding the Anstee-Robertson graph $\mathcal{R}$ are the orientable Evans map $\mathcal{M}$ of type ${\{5,6\}}_8$ and its Petrie dual, the non-orientable map ${\mathcal{M}}^{\prime }$ of type ${\{8,6\}}_5$. In Conder’s lists these are the maps R17.16 and the dual of N52.4.

Proof. 

Since $\mathcal{R}$ has automorphism group G of order twice the number of arcs, any regular map which embeds $\mathcal{R}$ must also have automorphism group G. Now the 6-valent regular maps with automorphism group G correspond to the orbits of $\mathrm{Aut}G$ on generating triples $r_0,r_1,r_2$ of G satisfying

$$r_i^2={\left(r_0{r}_2\right)}^2={\left(r_1{r}_2\right)}^6=1.$$

A search with GAP shows that there are four such orbits: for one pair of orbits the elements $r_0{r}_1$ and $r_0{r}_1{r}_2$ have orders 5 and 8 or vice versa, so these orbits correspond to the maps $\mathcal{M}$ and ${\mathcal{M}}^{\prime }$ of types ${\{5,6\}}_8$ and ${\{8,6\}}_5$. For the other two orbits these elements have orders 10 and 8 or vice versa, giving a Petrie dual pair of maps $\mathcal{N}$ and ${\mathcal{N}}^{\prime }$ of types ${\{10,6\}}_8$ and ${\{8,6\}}_{10}$. However, the graph ${\mathcal{R}}^{†}$ embedded by $\mathcal{N}$ and ${\mathcal{N}}^{\prime }$ is not isomorphic to $\mathcal{R}$, since reconstructing it from the corresponding generators $r_i$ shows that ${\mathcal{R}}^{†}$ has girth 3 rather than 5. □

This graph ${\mathcal{R}}^{†}$ is, in fact, the graph ${\mathcal{R}}_9$ corresponding to the orbital $R_9$ for G defined earlier. (The notation ${\mathcal{R}}^{†}$ commemorates a splendid performance of Verdi’s Macbeth, seen by one of the authors while writing this paper.) By inspection of [10], the maps $\mathcal{N}$ and ${\mathcal{N}}^{\prime }$ are the duals of the orientable map R29.12 and the non-orientable map N52.3. As an immediate corollary to the above proof, we have the following:

Corollary 3. 

The only regular maps embedding the graph ${\mathcal{R}}^{†}$ are the dual of the orientable map R29.12, of type ${\{10,6\}}_8$, and its Petrie dual of type ${\{8,6\}}_{10}$, the dual of the non-orientable map N52.3.

Remark 

The four orbits on generating triples discussed above all have length $\left|\mathrm{Aut}G\right|=960$: the inner automorphism group $\mathrm{Inn}G\cong G/Y$ has order 240, and the outer automorphism group $\mathrm{Out}G=\mathrm{Aut}G/\mathrm{Inn}G$ is a Klein four-group.

8. Quotient Maps

In this section we will describe the quotient maps of $\mathcal{M}$ and ${\mathcal{M}}^{\prime }$ by the groups Y and Z. Since these are normal subgroups of G, the corresponding quotient maps are all regular.

Let Y denote the unique subgroup of order 2 in Z. Then Y is a characteristic subgroup of Z, and Z is normal in G, so Y is a normal (in fact central) subgroup of G. The central involution generating Y is a half-turn around the centres of the Petrie polygons of $\mathcal{M}$, or equivalently around the face-centres of ${\mathcal{M}}^{\prime }$, transposing pairs of edges separating common pairs of Petrie polygons or faces. In fact Y is the kernel of the action of G on the Petrie polygons of $\mathcal{M}$, or equivalently the faces of ${\mathcal{M}}^{\prime }$. The quotient maps $\mathcal{M}/Y$ and ${\mathcal{M}}^{\prime }/Y$ are regular maps with automorphism groups of order 240 isomorphic to

$$G/Y\cong PG{L}_2\left(5\right)\times C_2\cong S_5\times C_2,$$

while $\mathcal{M}/Z$ and ${\mathcal{M}}^{\prime }/Z$ are regular maps with automorphism groups of order 120 isomorphic to

$$G/Z\cong PG{L}_2\left(5\right)\cong S_5.$$

We will now describe these maps, showing that some of them are well-known objects.

Since Y has trivial intersections with the stabilisers in G of the vertices, edges and faces of $\mathcal{M}$, the covering $\mathcal{M}\to \mathcal{M}/Y$ is unbranched, so $\mathcal{M}/Y$ has the same type $\{5,6\}$ as $\mathcal{M}$ and has Euler characteristic $-32/2=-16$. Since Y is contained in the commutator subgroup $G^{\prime }=S{L}_2\left(5\right)$ of G it preserves the orientation of $\mathcal{M}$, so $\mathcal{M}/Y$ is orientable, of genus 9. Inspection of [10] shows that it is R9.16, with Petrie length 4 (the map R9.15, with the same genus and type, is excluded since its Petrie length 10 does not divide that of $\mathcal{M}$). In Table 8 of [7] it is shown that the regular map ${\{5,6\}}_4$, the largest map of type $\{5,6\}$ with Petrie length 4, has an automorphism group of order 240; all other regular maps with this type and Petrie length are quotients of it, so comparing orders gives $\mathcal{M}/Y\cong {\{5,6\}}_4$. (One can construct ${\{5,6\}}_4$ by applying Wilson’s “opposite” operation $PDP=DPD$ (see Section 3) to the median map ${\{5,4\}}_6$ of the great dodecahedron, a map of type $\{5,5\}$ and genus 4.)

Now ${\mathcal{M}}^{\prime }/Y$ must be the Petrie dual ${\{4,6\}}_5$ of $\mathcal{M}/Y={\{5,6\}}_4$, that is, the largest regular map of type $\{4,6\}$ with Petrie length 5. This is non-orientable, of genus 12, isomorphic to N12.1 in [10]. The covering ${\mathcal{M}}^{\prime }\to {\mathcal{M}}^{\prime }/Y$ is branched at the face-centres because $Y\le G_f$ for each face f of ${\mathcal{M}}^{\prime }$.

Since Z contains Y the maps $\mathcal{M}/Z$ and ${\mathcal{M}}^{\prime }/Z$ are quotients of $\mathcal{M}/Y$ and ${\mathcal{M}}^{\prime }/Y$, obtained by factoring out the central subgroups $Z/Y$ in their automorphism groups $G/Y$. The coverings $\mathcal{M}/Y\to \mathcal{M}/Z$ and ${\mathcal{M}}^{\prime }/Y\to {\mathcal{M}}^{\prime }/Z$ are both unbranched, so $\mathcal{M}/Z$ and ${\mathcal{M}}^{\prime }/Z$ have Euler characteristic $-8$ and $-5$. Inspection of [10] shows that $\mathcal{M}/Z$ is the non-orientable map N10.6 of genus 10 and type ${\{5,6\}}_4$ (one of the dodecahedra considered by Brahana and Coble in [29], see Section 8.6 of [7]), while ${\mathcal{M}}^{\prime }/Z$ is its Petrie dual, the non-orientable map N7.1 of genus 7 and type ${\{4,6\}}_5$. These are the two regular embeddings of the line graph $L\left(K_5\right)$ of $K_5$, see Theorem 10 (c) of [30]. In fact, by Corollary 11 of [30], the only regular embeddings of line graphs $L\left(K_n\right)$ of complete graphs $K_n(n\ge 3)$ are these, together with the dihedron $\{3,2\}$ and its Petrie dual (the antipodal quotient of the dihedron $\{6,2\}$) for $n=3$, and the octahedron $\{3,4\}$ and its Petrie dual (a non-orientable map of type ${\{6,4\}}_3$ and genus 4, the dual of N4.2 in [10]) for $n=4$.

9. Maps and Triangle Groups

As explained in Section 4, maps on surfaces can be interpreted in terms of subgroups of triangle groups, so here we will briefly outline how this applies to the maps constructed earlier. As a regular map of type $\{5,6\}$, $\mathcal{M}$ corresponds to a normal subgroup $M\cong {\pi }_1\mathcal{S}$ of the extended triangle group $\Delta =\Delta [6,2,5]$, with

$$\Delta /M\cong \mathrm{Aut}\mathcal{M}\cong G.$$

Since $\mathcal{M}$ is orientable, M is contained in the even subgroup of Δ, the ordinary triangle group ${\Delta }^{+}=\Delta (6,2,5)$. Now the abelianisations ${\Delta }^{\mathrm{ab}}=\Delta /{\Delta }^{\prime }$ and $G^{\mathrm{ab}}=G/G^{\prime }$ of Δ and G are isomorphic (both are Klein four-groups), so M is contained in the commutator subgroup ${\Delta }^{\prime }$ of Δ. This is the ordinary triangle group $\Delta (5,5,3)$, and the normal inclusion of M in $\Delta [5,5,3]$ (a subgroup of index 2 in Δ) corresponds to a regular hypermap $\mathcal{H}$ of type $(5,5,3)$ and genus 17 on $\mathcal{S}$ (a dual of RPH17.7 in [10]). The Walsh bipartite map [31] of $\mathcal{H}$, a map of type $\{6,5\}$ with a 2-colouring of its vertices, is just the dual map $D\left(\mathcal{M}\right)$ of $\mathcal{M}$. This shows that $\mathcal{M}$ is 2-face colourable, giving a partition of the 48 useful pentagons into two sets of 24. The quotient maps $\mathcal{M}/Y$ and $\mathcal{M}/Z$ correspond to normal subgroups of Δ containing M with index 2 and 4 respectively, with quotient groups isomorphic to $G/Y$ and $G/Z$. Since Y and Z have trivial intersections with the stabilisers of vertices, edges and faces in G, these coverings are unbranched, and the quotient maps have the same type $\{5,6\}$ as $\mathcal{M}$. However, the element $r_0{r}_1{r}_2$ of order 8 has order 4 modulo Y and Z, so the Petrie length 8 of $\mathcal{M}$ is reduced to 4 for $\mathcal{M}/Y$ and $\mathcal{M}/Z$.

There is a parallel description of the sequence ${\mathcal{M}}^{\prime }\to {\mathcal{M}}^{\prime }/Y\to {\mathcal{M}}^{\prime }/Z$ of maps and coverings in terms of normal subgroups of the extended triangle group $\Delta [6,2,8]$, with the same quotient groups as above. The only significant differences are that these three maps are non-orientable, so that the corresponding normal subgroups are not contained in $\Delta (6,2,8)$, and that the first covering is branched over the faces, so that the type of the maps changes from $\{8,6\}$ to $\{4,6\}$.