Three Duality Symmetries between Photons and Cosmic String Loops, and Macro and Micro Black Holes

Abstract

We present a review of two thermal duality symmetries between two different kinds of systems: photons and cosmic string loops, and macro black holes and micro black holes, respectively. It also follows a third joint duality symmetry amongst them through thermal equilibrium and stability between macro black holes and photon gas, and micro black holes and string loop gas, respectively. The possible cosmological consequences of these symmetries are discussed.

1. Introduction

Thermal duality relates high-energy and low-energy states of corresponding dual systems in such a way that the thermal properties of a state of one of them at some temperature T are related to the properties of a state of the other system at temperature $1/T$ [1,2,3,4,5,6]. This sets a symmetry between T and $T^{-1}$ states in the physical features of some couples of physical systems, and relates their respective thermodynamic functions.

Macroscopic thermal duality may be a consequence of deeper microscopic duality relations, as for instance, the well-known S duality (between high R and low R systems, being R the compactification radius in superstring theories) and T duality (between strongly coupled and weakly coupled systems), which are so relevant in M theory, because they set a number of relations between the several solutions of superstring theory, thus pointing towards a deep relation between them [7,8]. For instance, in string theory it is known that the T duality between the behaviour of superstrings at long and short length scales, expressed in terms of energy as $E\left(l\right)=E(l_c^2/l)$, which $l_c^2$ a characteristic length, implies a thermal duality symmetry of some of their thermodynamic functions for temperatures T and $T_c^2/T$, with $T_c$ a characteristic temperature [1,2,4].

In this paper, we review some of our results on thermal duality symmetries in two kinds of systems: photon gas/ cosmic string loop gas, and macro black holes/ micro black holes. We bring the basic results and we provide a joint discussion of them. In particular, we point out two symmetries of thermal kind, which are also related to corresponding size dualities, namely a duality between photons and cosmic string loops [9], and a duality between macro and micro black holes [10]. Both dualities may be further related to each other when one considers stable thermodynamic equilibrium between macro black holes and photons, and micro black holes and cosmic string loops in a theoretical finite volume container, which are related through a third joint symmetry [10,11]. For the first time, these results are presented in a joint way and analogies and differences amongst them are analyzed. The relatively long and detailed calculations of the previous references have been skipped, by focusing the attention on the corresponding essential results, and providing a wider perspective on them.

These relations may have a special interest in cosmology, relating early states of the universe, dominated by radiation, to future states, dominated by cosmic string loops. Analogously, the physics on micro black holes is of much interest for the future of the macro black holes, in order to explore whether, through Hawking evaporation, they will have an explosive end in a powerful flash of radiation, or whether they will last for a very long time, evaporating at a very low rate at a late scale [10,11].

2. Duality Symmetry between Cosmic String Loop Thermodynamics and Photon Thermodynamics

In [9], we studied thermal duality between photons and cosmic string loops. Photons are the well-known quanta of electromagnetic radiation, and their thermodynamic properties are well-known: their pressure p is related to their energy density $U/V$ (with U internal energy of a photon gas and V the volume) by ${\displaystyle p=\frac{1}{3}\frac{U}{V}}$, and their energy density is related to their absolute temperature T as ${\displaystyle \frac{U}{V}=a_{SB}{T}^4}$, with $a_{SB}$ a constant related to the Stefan–Boltzmann constant ${\sigma }_{SB}$ by $a_{SB}=4{\sigma }_{SB}/c$.

Cosmic string loops gases are much less known than photon gases. Up to now, cosmic string loops are considered as hypothetical entities, which could be related to topological defects of the space [12,13,14,15,16]. Their thermodynamic properties are much less known, but one of their main features is that ${\displaystyle p=-\frac{1}{3}\frac{U}{V}}$, which is the same relation as that of photons but with opposite sign. In fact, many other aspects are being explored about them: their distribution function, their scaling laws, their rate of formation and destruction, their contribution to gravitational waves cosmic background, and so on [13,14,15,16], but here we will address our attention only to this thermodynamic aspect. As it will be seen, a gas of cosmic string loops is thermodynamically unstable; it may become stable by forming a few long cosmic strings, or some black holes. In any case, we may consider its thermodynamic functions as valid for steady states; namely, as describing the behaviour of a gas of strings which are continuously being formed and disappearing but displaying a constant average temperature, pressure, energy and entropy.

The cosmological interest of the relation $p=-(1/3)(U/V)$ is that, in general relativity, the source of gravitation is ${\displaystyle \frac{U}{V}+3p}$ (which is the trace of the energy-momentum tensor). Thus, cosmic string loops would not contribute to gravitation because for them ${\displaystyle \frac{U}{V}+3p=0}$. In other words, a universe dominated by cosmic string loops would expand at a constant rate, instead of slowing down (if it is dominated by systems for which ${\displaystyle \frac{U}{V}+3p>0}$) or accelerating (if it is dominated by systems for which ${\displaystyle \frac{U}{V}+3p<0}$) [17,18].

After these motivations, we go to the concrete detailed information that we want to explore in this paper. The first thing we need is the energy $E\left(l\right)$ as a function of the characteristic length of these objects. The energy $E\left(l\right)$ of photons of wavelength l is

$$E\left(l\right)=hf=\frac{hc}{l},$$

(1)

with h the Planck constant, and c the speed of the light in vacuo, respectively.

The energy of cosmic string loops of length l is

$$E\left(l\right)=\frac{c^4}{a^{2}G}l,$$

(2)

with G the gravitational constant, and a a dimensionless constant depending on the particular model, and whose value is still unknown but less than ${10}^{10}$, according to current observational restrictions [19,20,21,22,23,24].

Comparison of Equations (1) and (2) shows that $E\left(l\right)\sim l^{-1}$ for photons and $E\left(l\right)\sim l$ for cosmic string loops, which implies that in an expanding universe, the energy of a photon and that of a cosmic string loop will change in a completely different form, the former decreasing and the latter increasing. An alternative way of writing Equations (1) and (2) is

$$E\left(l\right)=E_P^{\prime }\frac{l_P^{\prime }}{l}\text{(photons)},E\left(l\right)=E_P^{\prime }\frac{l}{l_P^{\prime }}\text{(cosmic}\text{strings)},$$

(3)

with $l_P^{\prime }=a{l}_P$, $l_P$ being the Planck lenght ${\displaystyle l_P={(hG/c^3)}^{1/2}}$, and $E_P^{\prime }$ being given by ${\displaystyle E_P^{\prime }=\frac{hc}{l_P^{\prime }}=\frac{E_P}{a}}$, with $E_P$ the Planck energy ${\displaystyle E_P=\frac{hc}{l_P}}$. Expressions (3) show that under the change $l/l_P^{\prime }\to l_P^{\prime }/l$ one goes from Equations (1) to (2) and viceversa. In other terms, $E_{cs}\left(l\right)=E_{ph}({l^{\prime }}_P^2/l)$, or viceversa. Thus, at microscopic level, there is a size-duality symmetry between photons and cosmic string loops.

Here, we are interested in thermal duality symmetry, i.e., in how this symmetry at a microscopic level and for single physical entities is reflected into a macroscopic symmetry in thermal functions for the corresponding collective gases.

In [9], starting from Equations (1) and (2), and two additional hypotheses—namely: (a) that $k_{B}T=$$<E\left(l\right)>$, with the angular brackets $<..>$ standing for equilibrium average (or steady-state average); and (b) that the average separation δ between photons or cosmic string loops is proportional to $<l>$—we obtained the thermodynamic functions for these systems. In fact, we obtained the thermodynamic functions of the general family of hypothetical physical objects for which $E\left(l\right)=E_p^{\prime }{(l/l_P)}^b$, with b a constant exponent $b=-1$ for photons, and $b=1$ for cosmic string loops. The results were then generalized in [5] with $-3\le b\le 3$.

The main results were [5,9]

$$S(U,V)=k_B\frac{3-b}{3\lambda }{\left(\frac{\lambda }{{\tilde{A}}_b}\right)}^{\frac{3}{3-b}}{\left(\frac{U}{V}\right)}^{\frac{3}{3-b}}V,$$

(4)

with λ a constant relating the average length $<l>$ with the average separation δ as $<l>=\lambda \delta$, and ${\tilde{A}}_b$ a constant relating $k_{B}T$ to $<l>$ as $k_{B}T={\tilde{A}}_b{\lambda }^{-b}<l{>}^b$. Since $S(U,V)$ is a full thermodynamic potential, from Equation (4) all the thermodynamic information about the system may be obtained, by taking into account that ${\displaystyle \frac{1}{T}={\left(\frac{\partial S}{\partial U}\right)}_V}$, and ${\displaystyle \frac{p}{T}={\left(\frac{\partial S}{\partial V}\right)}_U}$ [25]. In particular, we get

$$p=-\frac{b}{3}\frac{U}{V},$$

(5)

$$U(T,V)={\lambda }^{-1}{k}_{B}T{\left(\frac{k_{B}T}{{\tilde{A}}_b}\right)}^{-\frac{3}{b}}V,$$

(6)

$$S(T,V)=k_B\frac{3-b}{3\lambda }{\left(\frac{k_{B}T}{{\tilde{A}}_b}\right)}^{-\frac{3}{b}}V,$$

(7)

with $k_B$ the Boltzmann constant, ${\tilde{A}}_{-1}={\lambda }^{-1/3}{a}^{-1/3}hc$, ${\tilde{A}}_1={\left(\lambda \tilde{b}\right)}^{1/3}\mu ,$ with $\mu =c^4/\left(a^{2}G\right)$ the so-called string tension, or string energy per unit length, $\tilde{a}=4{\sigma }_{SB}{\left(hc\right)}^3/\left(c{k}_B^4\right)=69,55\pi$, and $\tilde{b}$ proportional to ${\lambda }^2$, of the order of $\tilde{a}$ [9].

In particular, for $b=-1$ (photons) and for $b=1$ (cosmic string loops), the systems we are considering, we have from Equations (5)–(7)

$$\begin{array}{cc}\hfill \text{(photons}b=-1\text{)}& \text{(cosmic}\text{string}\text{loops}b=1\text{)}\hfill \end{array}$$

$$\begin{array}{cc}\hfill p=\frac{1}{3}\frac{U}{V},& p=-\frac{1}{3}\frac{U}{V},\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill U(T,V)=\tilde{a}{k}_{B}T{\left(\frac{k_{B}T}{hc}\right)}^{3}V,& U(T,V)=\tilde{b}\mu {\left(\frac{\mu }{k_{B}T}\right)}^{2}V,\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill S(T,V)=\frac{4}{3}\tilde{a}{k}_B{\left(\frac{k_{B}T}{hc}\right)}^{3}V,& S(T,V)=\frac{2}{3}\tilde{b}{k}_B{\left(\frac{\mu }{k_{B}T}\right)}^{3}V.\hfill \end{array}$$

(10)

To be more concrete, we may illustrate this duality by focusing our attention on the entropy density. According to Equation (10) we may write, in dimensionless terms,

$$y=\frac{S}{V}\frac{{l^{\prime }}_P^3}{k_B}={\beta }_1{\theta }^3\text{(photons)},$$

(11)

$$y=\frac{S}{V}\frac{{l^{\prime }}_P^3}{k_B}={\beta }_2{\theta }^{-3}\text{(cosmic}\text{string}\text{loops)},$$

(12)

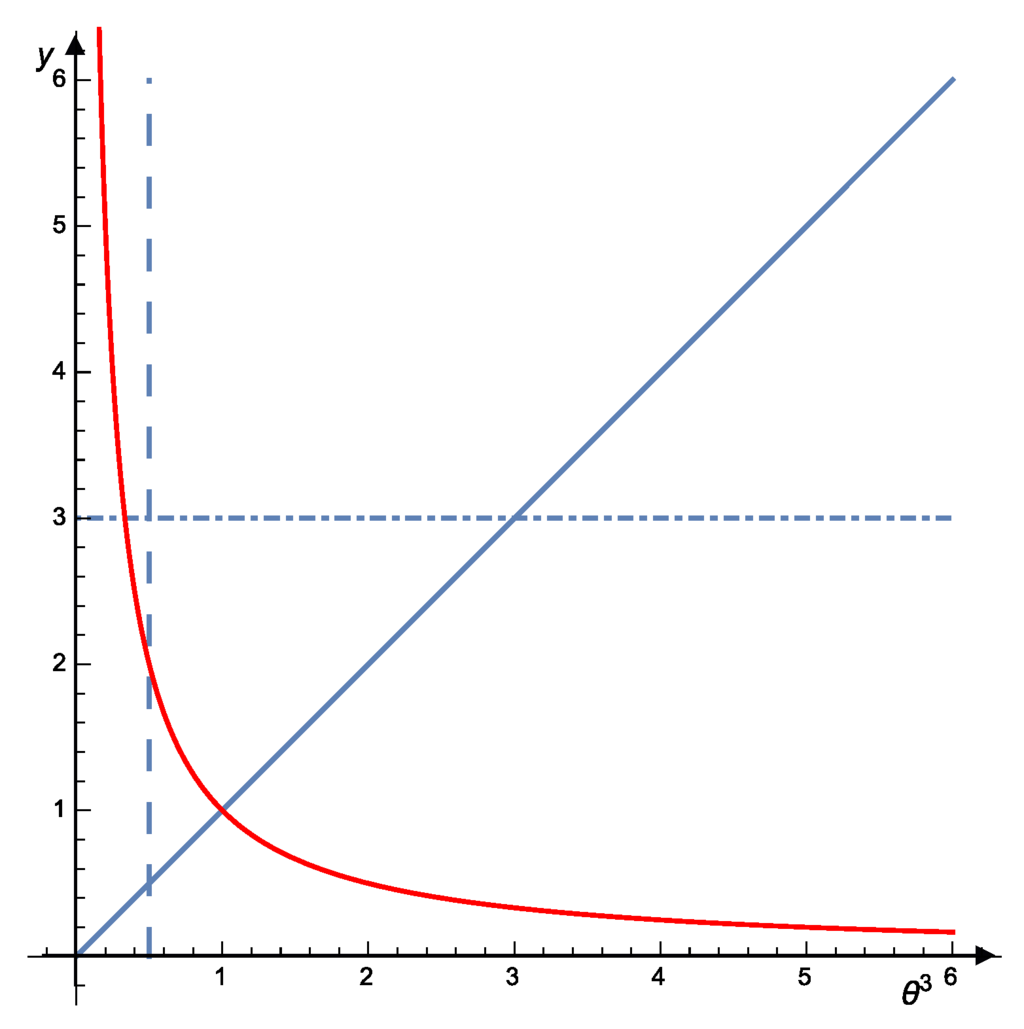
with $\theta =T/T_P$ and ${\beta }_1$ and ${\beta }_2$ dimensionless constants given by ${\beta }_1=(4\tilde{a}/3){\tilde{a}}^3$ and ${\beta }_2=(2\tilde{b}\tilde{a}/3){\left(\mu hc\right)}^3{\tilde{a}}^3$. In Figure 1, we plot y as a function of ${\theta }^3$ for both systems. The plot is analogous to that of Figure 2, but in Figure 2, there is a single curve (a single physical system), whereas here there are two different curves (two different physical systems).

In the horizontal line, we plot the duality between states having the same entropy y but different temperatures θ related by $\theta \simeq {\theta }^{-1}.$ In the vertical line, a complementary dual relation between two dual states having the same θ but different entropies $y\simeq y^{-1}$. The discontinuous lines are analogous to those in Figure 2.

By defining $T^{*}={(\tilde{b}/\tilde{a})}^{1/6}{\left(\mu hc\right)}^3$, we obtain $2S_{cs}\left(T\right)=S_{ph}(T^{*2}/T)$ which shows the duality relation between entropy of cosmic string loops and of photons. Also in terms of $T^{*}$, it is directly seen that, for internal energy, we have ${\displaystyle U_{cs}\left(T\right)={\left(\frac{T^{*}}{T}\right)}^{-2}{U}_{ph}(T^{*2}/T)}$, and for p, ${\displaystyle p_{cs}\left(T\right)=-{\left(\frac{T^{*2}}{T}\right)}^{-2}{p}_{ph}(T^{*2}/T)}$. In [1,2,5,9] there may be found the relations between the different thermodynamic quantities.

Figure 1. Plot of the dimensionless entropy density $y=(S/V)({l^{\prime }}_P^3/k_B)$ in terms of the dimensionless temperature $\theta =T/T_P$ for photons (straight line) and cosmic string loops (hyperbolic line). For the sake of qualitative illustration, in this figure we have taken ${\beta }_1$ and ${\beta }_2$ as unity in Equation (11) and in Equation (12).

Figure 1. Plot of the dimensionless entropy density $y=(S/V)({l^{\prime }}_P^3/k_B)$ in terms of the dimensionless temperature $\theta =T/T_P$ for photons (straight line) and cosmic string loops (hyperbolic line). For the sake of qualitative illustration, in this figure we have taken ${\beta }_1$ and ${\beta }_2$ as unity in Equation (11) and in Equation (12).

From the cosmological point of view, the most relevant features stemming from Equation (8) to Equation (10) are:

1)

cosmic string loops lead to vanishing gravitational effects because $(U/V)+3p=0$, thus implying a cosmic expansion with constant rate, whereas photons slow down the cosmic expansion because $(U/V)+3p=2(U/V)>0$, according to Equation (8);

2)

in an adiabatic reversible expansion, i.e., expansion with $S(V,T)=constant$, and assuming $V\sim R^3$ with R the cosmic scale factor, we have $T^{3}V\sim {\left(TR\right)}^3\sim constant$ for photons, and $T^3/V\sim {(T/R)}^3\sim constant$ for cosmic string loops, according to Equation (10); this also leads to a generalized Wien’s law [26];

3)

in view of the former result and from the behaviour of Equation (9) in $U(T,V)$ we have $U/V\sim R^{-4}$ for photons and $U/V\sim R^{-2}$ for cosmic string loops.

This thermal duality symmetry sets a symmetry between the thermal features of the universe at early period, and those at future times. Indeed, currently, the future of the universe is a topic of much interest. Since observations from 1998, it seems clear that cosmic acceleration is not slowing down. It is usually said that cosmic expansion is accelerating [17,18], and dominated by a dark energy for which $(U/V)+3p<0$, but there are authors which argue that the observational data (and their error bar) are also compatible with an expansion at a constant rate [27].

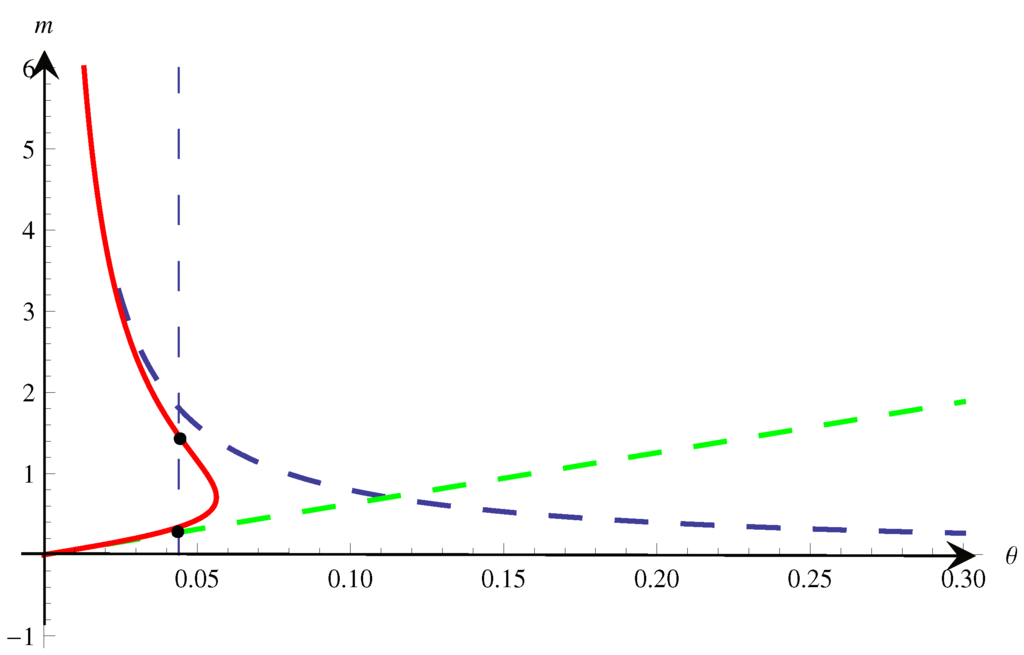
Figure 2. Dimensionless mass m ($M/M_P$) as function of dimensionless temperature θ ($T/T_P$) given by Equation (14) for $b=0$ (Hawking expression) in the upper curve, for $b=\pi /2$ (solid line), and the second term of Equation (16) with $b=\pi /2$ (tilted right line). The vertical line corresponds to a given value of T. The intersecting points of it with the continuous line define the respective thermally dual black holes. Figure from Ref. [11].

Figure 2. Dimensionless mass m ($M/M_P$) as function of dimensionless temperature θ ($T/T_P$) given by Equation (14) for $b=0$ (Hawking expression) in the upper curve, for $b=\pi /2$ (solid line), and the second term of Equation (16) with $b=\pi /2$ (tilted right line). The vertical line corresponds to a given value of T. The intersecting points of it with the continuous line define the respective thermally dual black holes. Figure from Ref. [11].

Here, we do not enter into the debate about the actual physical behaviour of the cosmic expansion, but we comment on it on the light of our mathematical analysis as a simplified model system. Indeed, electromagnetic radiation is assumed to have dominated the early period of the universe, and to have slowed down the expansion because $(U/V)+3p=2(U/V)>0$. According to the former point 3, its energy density would have decreased as ${(1/R)}^4$, with R the cosmic scale factor. In contrast, the energy density of matter would have decreased as ${(1/R)}^3$, and that of cosmic string loops as ${(1/R)}^2$. Thus, the energy density of cosmic string loops, negligible with respect to that of radiation and matter at the early times (small R), would have become dominant after some sufficient time of expansion (increasing R), leading to a constant rate of cosmic expansion, in contrast to a slowing down expansion [27].

Thus, in a hypothetical universe with photons, matter and cosmic string loops, the former ones would have dominated the early times, and the latter ones the future times. In this hypothetical simplified scenario, the duality symmetry examined here would set a symmetry between early cosmic states and late cosmic states.

3. Thermal Duality Symmetry between Macro and Micro Black Holes

The second thermal duality symmetry we consider is between macro black holes and micro black holes. In fact, in [10] we derived it from a variation of the former thermal duality, namely from a duality-invariant Einstein–Planck relation [28], by following a similar lines than those of the crystal model analysis of short-scale behaviour of electromagnetic radiation and black holes [29,30]. However, it is simpler to obtain it in an independent way, by starting from a generalized expression of the entropy of black holes in terms of the area A of their event horizon [31,32,33,34,35]

$$S\left(A\right)=k_B\left[\frac{A}{4l_P^2}+bln\left(\frac{A}{4\pi l_P^2}\right)\right]+k_{B}F,$$

(13)

with b and F positive numerical constants. When b and F are taken to be zero, Equation (13) reduces to the well-known Bekenstein–Hawking expression for the black hole entropy [36,37]. For macro black holes $A\gg l_P^2$, the logarithmic term in Equation (13) is negligible, but for hypothetical micro black holes, it becomes significative. From Equation (13) one may easily obtain the corresponding expression for the thermal equation of state relating energy and temperature. Since the energy of the black hole is $U=M{c}^2$, with M the mass of the black hole, since the radius of the event horizon is $R_S=2GM/c^2$, $R_S$ being the Schwarzschild radius, and since $A=4\pi R_S^2$, it follows from Equation (13) [10]

$$\frac{\partial S}{\partial U}=\frac{1}{T}={\alpha }_{1}M+{\alpha }_2\frac{1}{M}={\alpha }_1^{\prime }U+{\alpha }_2^{\prime }\frac{1}{U},$$

(14)

with the constants ${\alpha }_1$ and ${\alpha }_2$ given by

$${\alpha }_1=\frac{8\pi G^2{k}_B}{c^6{l}_P^2},{\alpha }_2=\frac{2b{k}_B}{c^2},$$

(15)

and ${\alpha }_1^{\prime }={\alpha }_1{c}^{-2}$ and ${\alpha }_2^{\prime }={\alpha }_2{c}^2$.

In Equation (14) it is seen a relation between macro black holes, with $M\simeq T^{-1}$ for high values of M (the usual Bekenstein–Hawking result), and micro black holes with $M\simeq T$ for small values of M, which is the duality symmetric of the former one. This relation between macro and micro black holes is a special case of thermal duality.

We may emphasize both the analogy and the difference with the duality symmetry of Section 2 if we formally consider separately the branches for macro black holes, with ${\displaystyle U_{macro}=\frac{1}{{{\alpha }^{\prime }}_{1}T},}$ and that of micro black holes, with $U_{micro}={\alpha }_2^{\prime }T$. In this case we would have ${\displaystyle U_{micro}\left(T\right)=U_{macro}(T^{*2}/T)}$ with $T^{*2}={\left({\alpha }_1^{\prime }{\alpha }_2^{\prime }\right)}^{-1}$. However, in Equation (14) macro and micro black holes are not considered as different branches, but a self-dual branch.

We consider as dual states those states having the same T, i.e., M and $M^{*}$ would be dual if $T\left(M\right)=T\left(M^{*}\right)$. In Figure 2 we illustrate expression Equation (14) in its dimensionless form

$$\frac{1}{\theta }=4\pi m+\frac{4b}{m}$$

(16)

with b the dimensionless coefficient appearing in Equation (13), with ${\displaystyle m=\frac{M}{M_P}}$ and ${\displaystyle \theta =\frac{T}{T_P}}$, and $M_P$ the Planck mass $M_P=(1/2){(\hslash c/G)}^{1/2}$ and the Planck temperature $k_B{T}_P={(\hslash c^5/G)}^{1/2}$. In Figure 2 we have taken $b=\pi /2$, a value which has not a fundamental special meaning but it is used only for illustration. The discontinuous lines plotted in Figure 2 correspond to the branches $m=(1/4\pi ){\theta }^{-1}$ and $m=4b\theta$, which correspond to the term in M and in $(1/M)$ in Equation (14) respectively. The vertical line intersects the curve of Equation (14) at 2 (or 1, or 0) points. These two points would correspond to respectively dual states.

As seen in Figure 2, there is a maximum value for T beyond which there are no black holes, given by

$$T_{max}^{bh}=\frac{1}{2\sqrt{{\alpha }_1{\alpha }_2}}=\frac{c^4{l}_P}{8G\sqrt{\pi b}}$$

(17)

At such value of T, M takes the value

$$M\left(T_{max}^{bh}\right)=\sqrt{\frac{{\alpha }_2}{{\alpha }_1}}=\sqrt{\frac{b}{4\pi }}\frac{c^2{l}_P}{G}$$

(18)

In this case, the corresponding thermodynamic state is dual to itself.

In the previous section, we have related through the thermal duality symmetry some early states of the universe (dominated by photons) to late states of the universe (dominated by cosmic string loops). The thermal duality symmetry examined in this section also sets a connection between early state of a macro black hole to its late microscopic state. In the standard theory of black holes, $R_S\sim M\sim T^{-1}$, in such a way that evaporation, leading to a decrease of $R_S$, leads to an increase of T and therefore of the rate of evaporation. Eventually, for $R_S\to 0$ this leads to $T\to \infty$, leading to an explosive eventual stage of evaporation in a finite time. In constrast, the duality set here, the behaviour $R_S\to T^{-1}$ for macro black holes tends to $R_S\to T$ for micro black holes. This would imply that the late stages of evaporation would correspond to a low T and therefore to a slow evaporation.

In fact, if one considers the rate of evaporation of black holes as

$$\frac{dU}{dt}=-4\pi R_S^2{\sigma }_{SB}{T}^4,$$

(19)

with ${\sigma }_{SB}$ the Stefan-Boltzmann constant, and since, in the standard theory, $R_S\sim T^{-1}$ at all sizes, this would lead to

$$\frac{c^2}{2G}\frac{d{R}_S}{dt}\sim -R_S^2{T}^4\sim -R_S^{-2}.$$

(20)

Instead, if for micro black holes $R_S$ behaves as T, the shrinking rate of the black hole at the late stages would be

$$\frac{c^2}{2G}\frac{d{R}_S}{dt}\sim -R_S^2{T}^4\sim -R_S^6.$$

(21)

This would imply a very slow rate of evaporation for micro black hole, and would have consequence on the abundance of micro black holes in the universe, which could be very high, in contrast to the extremely small (or null) abundance in the standard theory, because of the fast evaporation rate. Of course, it may be argued whether Stefan-Boltzmann law, setting that the radiation energy emitted per unit time and area is proportional to $T^4$, may be used at small spatial scales but, up to now, we use it only for illustration, because we are lacking of alternative proposals.

From Equation (19) one may make a rough estimation of the order of magnitude of the time required for a primordial Black hole of the mass of the order of a Planck mass ($1.22·{10}^{19}$ GeV) to the characteristic mass of ${10}^2$ Gev of a WIMP (Weakly Interacting Massive Particle), which are a well-known model for dark matter. Taking for the Schwarschild radius $R_S=2GM/c^2$, and taking for T, as a function of M, the relation obtained from Equation (16) for small values of $m=M/M_P$, i.e., $T/T_P=(1/4b)(M/M_P)$, Equation (19) may be rewritten as

$$\frac{dM}{dt}=-\alpha \frac{1}{t_P{M}_P^5}{M}^6$$

(22)

where ${\displaystyle t_P=\frac{\hslash }{c^2{M}_P}}$ and ${\displaystyle M_P={\left(\frac{\hslash c}{G}\right)}^{1/2}}$ and the numerical factor α given by ${\displaystyle \alpha =\frac{{\pi }^3}{960b^4}}$ (which for $b=\pi /2$ becomes ${\displaystyle \alpha =\frac{1}{60\pi }}$). This yields as a solution for the time-depending mass $M\left(t\right)$ along the evaporation process

$${\left(\frac{M_P}{M}\right)}^5=1+5\alpha \frac{t}{t_P}$$

(23)

Since in the situation considered here $M_P/M$ is of the order of ${10}^{17}$, we get for the time t an estimate of ${10}^{85}{t}_P$. Since the Planck time is $5.3·{10}^{-44}$ s, this gives for t an estimate of ${10}^{41}$ s. The estimated age of our universe is some $13.8·{10}^9$ years, which is some $4.35·{10}^{17}$ s. Thus, according to Equations (16) and (19) the characteristic evaporation time for the mentioned reduction of mass (namely, ${10}^{41}$ s) would be orders of magnitude longer than the age of the universe. If, instead of assuming for the initial mass of the primordial black holes the Planck mass $M_P$, one assumes ${10}^{-4}{M}_P$ (in order that the approximation of Equation (16) by the second member of the righ-hand side can be strictly made), the corresponding evaporation time becomes of the order of ${10}^{21}$ s, still much longer than the age of our universe. Thus, there could be many micro black holes as remnants of primordial small black holes. Of course, this is in contrast with classical theory, where micro black holes explosively evaporate, but it does not change the classical theory for big black holes, where the right-hand side of Equation (16) reduces to the first membre, which leads to Hawking’s results.

4. Duality Symmetry of Thermal Equilibrium Photons/Macro Black Holes, Cosmic Loops/Micro Black Holes

There is still a third dual symmetry to be considered here. It relates thermal equilibrium of macro black holes and photon gas in a hypothetical finite box, to thermal equilibrium of micro black holes and cosmic string loop gas, also in a hypothetical finite box. Thus, it relates two couples of systems which have been seen to be connected by the two former duality symmetries.

4.1. Macro Black Holes and Photon Gas

Thermal equilibrium between a macro black hole and a photon gas (assumed as a simple model of Hawking radiation) is a classical topic in black hole thermodynamics [36,37,38]. Indeed, isolated macro black holes are thermodynamically unstable, because their thermal capacity is negative. Indeed,

$$C=\frac{\partial U}{\partial T}=\frac{\partial \left(M{c}^2\right)}{\partial T}=-\frac{c^2}{{\alpha }_1}\frac{1}{T^2},$$

(24)

with ${\alpha }_1$ given in Equation (15). To get a stable equilibrium thermodynamic state, the black hole should radiate Hawking radiation until the stability condition would be fulfilled

$$\frac{1}{T_{bh}^2{C}_{bh}}+\frac{1}{T_{ph}^2{C}_{ph}}\ge 0,$$

(25)

with the constant $C_{ph},$ obtained by differentiating Equation (9) for photons with respect to T i.e., $C_{ph}=4\tilde{a}{k}_B{(k_{B}T/hc)}^{3}V$, is positive and proportional to $T^3$, whereas $C_{bh}$ is negative and proportional to $T^{-2}$. Then, the final equilibrium state, with $T_{bh}=T_{ph}$, would be characterized by a temperature given by the stability condition. This leads to ${\displaystyle k_{B}T<k_B{T}_{max}={\left[\frac{c^5{h}^3{k}_B}{4{\alpha }_1\tilde{a}V}\right]}^{1/5}}$. This yields a minimal mass of the remaining black hole $M_{min}={\left({\alpha }_1{T}_{max}\right)}^{-1}$.

4.2. Micro Black Holes and Loop Gas

The corresponding dual symmetry situation would be that of a gas of cosmic string loops aggregating into a micro black hole. Indeed, in contrast to macro black holes, for which $M\sim T^{-1}$ and $C<0$, dual micro black holes satisfy $M={\alpha }_{2}T$ and therefore $C_{bh}=c^2{\alpha }_2>0$, implying thermal stability. Instead, in contrast to photon gas, for which $U\sim T^{4}V$ and $C>0$, a gas of cosmic string loops is thermodynamically unstable, since $U\sim T^{-2}V$, leading to $C_{cs}=-2\tilde{b}{\mu }^{3}V{k}_B^{-2}{T}^{-3}<0$, as obtained by differentiating Equation (9) for cosmic string loops with respect to T. However, a gas of cosmic string loops could achieve a stable thermal equilibrium by condensing a fraction of it into a micro black holes, provided one would reach the situation in which

$$\frac{1}{T_{bh}^2{C}_{bh}}+\frac{1}{T_{cs}^2{C}_{cs}}\ge 0.$$

(26)

This leads to ${\displaystyle k_{B}T<k_B{T}_{max}={\left[\frac{2{\mu }^3\tilde{b}V{k}_B}{c^2{\alpha }_2}\right]}^{1/3}}$. The duality symmetry thus implies that unstable macro black holes in a finite box should partially evaporate into a (stable) photon gas, until reaching global thermal stability of the joint system, whereas (unstable) gas of cosmic string loops should partially condensate into one or several (stable) micro black holes.

From a formal point of view, the duality would relate the maximum temperature $T_{max}$ for which stability may exist in both systems to the volume of the box which contains them. These relations come from Equations (25) and (26) which may be rewritten as

$$\left|\frac{C_{ph}}{C_{bh}}\right|\le 1,\left|\frac{C_{cs}}{C_{bh}}\right|\le 1.$$

(27)

The heat capacities satisfy the relations

$$\begin{array}{cc}\hfill C_{ph}\sim T^{3}V,& C_{cs}\sim T^{-3}V,\hfill \\ \hfill C_{macro}\sim -T^{-2},& C_{micro}\sim T^0,\hfill \end{array}$$

(28)

which according to Equation (27) lead to $T_{max}^{5}V\sim constant$, and $T_{max}^{-3}V\sim constant$. From here, it follows the exponents of the respective scaling laws

$$T_{max}\sim V^{-1/5},T_{max}\sim V^{1/3},$$

(29)

which appear in the detailed expressions for $T_{max}$ given below Equation (25) and below Equation (26), respectively.

5. Concluding Remarks

We have presented three thermal duality symmetries, which we sketch in Figure 3. The first one has related the thermodynamical functions of a photon gas and those of a gas of cosmic string loops. To summarize into a single equation, in terms of T, we could say that according to Equation (10)

$$\frac{S}{V}\sim T^3\text{(photons)},\frac{S}{V}\sim T^{-3}\text{(cosmic}\text{string}\text{loops)}.$$

(30)

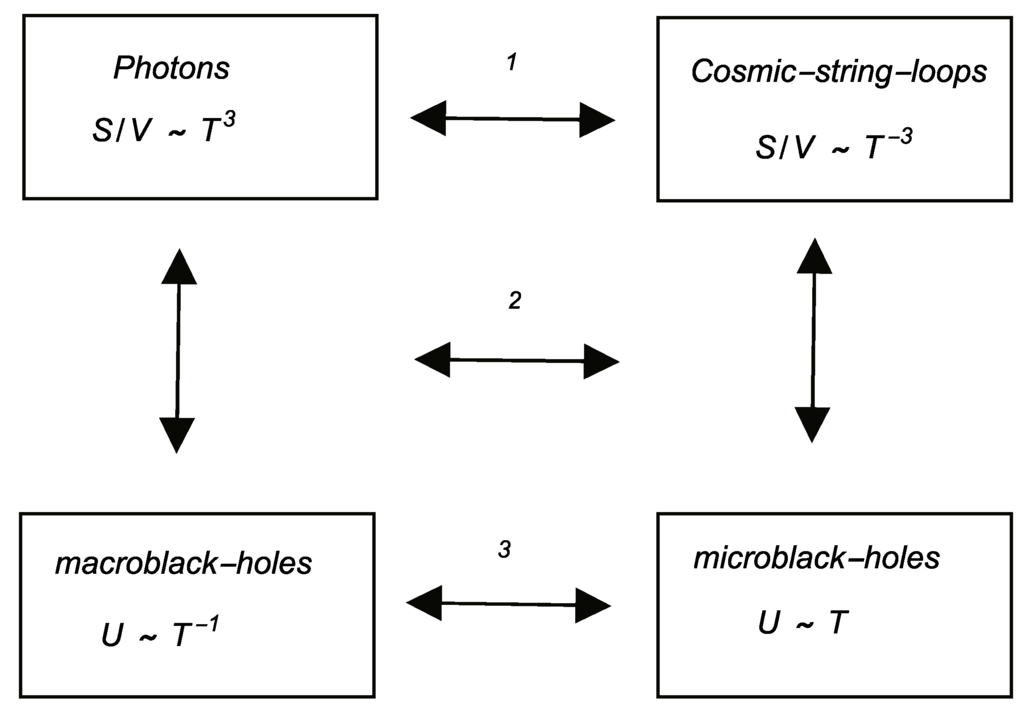
Figure 3. Sketch of the three thermal duality symmetries considered in this paper: (1) duality between photon gas and cosmic string gas; (2) duality between thermal equilibrium (photons/macro black holes) and thermal equilibrium (cosmic string loops/micro black holes); (3) duality between macro black holes and micro black holes.

Figure 3. Sketch of the three thermal duality symmetries considered in this paper: (1) duality between photon gas and cosmic string gas; (2) duality between thermal equilibrium (photons/macro black holes) and thermal equilibrium (cosmic string loops/micro black holes); (3) duality between macro black holes and micro black holes.

The second symmetry has related macro to micro black holes; in terms of temperature and energy we have, according to Equation (14),

$$U\sim T^{-1}\text{(macro}\text{black}\text{holes)},U\sim T\text{(micro}\text{black}\text{holes)}.$$

(31)

The third symmetry has related the thermal equilibrium of an (unstable) macro black hole $(U\sim T^{-1})$ with a (stable) photon gas $(S/V\sim T^3)$, and a (stable) micro black hole $(U\sim T)$ with an (unstable) cosmic string gas ($S/V\sim T^{-3}$). This third symmetry reinforces the two previous symmetries by linking them to each other. Further comments on these symmetries can be carried out. To draw a stronger parallelism, we write symmetry 2 in terms of $k_{B}T$ and $R_S$, the Schwarschild radius of the event horizon of the black holes. Since $M=(2G/c^2)R_S$, expression Equation (14) may be rewritten as

$$T=\frac{T_P^{\prime }}{{\alpha }_1^{\prime \prime }\frac{R_S}{l_P^{\prime }}+{\alpha }_2^{\prime \prime }\frac{l_P^{\prime }}{R_S}},$$

(32)

with ${\alpha }_1^{\prime \prime }$ and ${\alpha }_2^{\prime \prime }$ dimensionless constants related to Equation (15). In contrast with this expression for macro and micro black holes as a single continuum family of physical objects, in the first duality, we have connected two different families of physical objects, namely, photons ($E\left(l\right)=E_p^{\prime }{l}_p^{\prime }/l$) on one side and cosmic string loops ($E\left(l\right)=E_p^{\prime }l/l_p^{\prime }$) on the other side. Analogous with Equation (32), it is tempting to wonder about the possibility of treating these systems as a single family of physical objects, described by

$$E=\frac{E_P^{\prime }}{\frac{l}{l_P^{\prime }}+\frac{l_P^{\prime }}{l}}.$$

(33)

We have proposed this as a “duality-invariant Einstein-Planck” relation [10,28]. In strict terms, this expression would be more than a mere mathematical interpretation. It would suggest that the hypothetical cosmic string loops could be a special limiting form of electromagnetic radiation. This would be possible, if at small scales, the Maxwell equations would incorporate new terms depending on $l_P^{\prime }$, in such a way that the dispersion relation of electromagnetic waves in vacuum would have the form

$$f=\frac{c}{l_P^{\prime }}\frac{E_P^{\prime }}{\frac{l}{l_P^{\prime }}+\frac{l_P^{\prime }}{l}},$$

(34)

with l wavelength. In [28], we studied how this dispersion relation would yield a reduction of the speed of the light for high-energy photons, without need of quantum fluctuations of space-time, a topic much studied nowadays [19,20,21,22,23,24] and in [39] we proposed a generalization of dispersion relation of electromagnetic waves compatible with the duality-invariant form Equation (34). Other authors have proposed a different kind of modification of electromagnetic dispersion relation in the crystal-world model [29,30].

To consider more details on the duality symmetries 2 and 1, one could rewrite Equation (14) for black holes as

$$\theta =\frac{1}{4\pi y+\frac{b}{y}},$$

(35)

with $\theta =T/T_P^{\prime }$ and $y=M/M_P$, with $k_B{T}_P^{\prime }=hc{l}_P^{\prime }$ and $M_P^{\prime }=(1/2){(hc/G)}^{1/2}$. In addition, for the entropy of photons and cosmic string loops, one may try an interpolation between Equations (11) and (12) analogous to that of Equation (35)

$${\theta }^3=\frac{1}{\frac{y}{{\beta }_2}+\frac{{\beta }_1}{y}}.$$

(36)

Comparison between Equations (35) and (36) illustrates the analogies and differences between the thermodynamic relation for macro/micro black holes written in Equation (35), and the hypothetical relation written in Equation (36) in the case that photons would have a dispersion relation like Equation (34) at the Planck scale. Note that, in the first case, θ appears and in the second one ${\theta }^3$.

A last cosmological observation may still be said for a universe composed of photons, matter and cosmic strings. Thermodynamic stability requires

$$\frac{1}{T_{ph}^2{C}_{ph}}+\frac{1}{T_{cs}^2{C}_{cs}}\ge 0,$$

(37)

with C the respective thermal capacities. We assume matter at zero temperature and pressure, not contributing to the thermodynamics, and therefore we do not include it in Equation (37). From Equation (9), it is seen that

$$C_{ph}=4\tilde{a}{k}_B{\left(\frac{k_B{T}_{ph}}{hc}\right)}^{3}V,$$

(38)

$$C_{cs}=-2\tilde{b}{k}_B{\left(\frac{\mu }{k_B{T}_{cs}}\right)}^{3}V.$$

(39)

Thus, we have

$$\frac{{\left(hc\right)}^3}{T_{ph}^{2}4\tilde{a}{\left(k_B{T}_{ph}\right)}^3}-\frac{{\left(k_B{T}_{cs}\right)}^3}{2\tilde{b}{\mu }^3{T}_{cs}^2}\ge 0.$$

(40)

In contrast with what we assumed in Equation (25) and in Equation (26), in Equation (40) we cannot consider that $T_{ph}=T_{cs}$, because in the expansion $T_{ph}$ decreases and $T_{cs}$ increases (because $p_{ph}>0$ and $p_{cs}<0$, which implies that expansion work is lost energy for photons but gained energy for cosmic string loops). Thus, the description of the thermodynamics of the Universe requires to express $T_{ph}$ and $T_{cs}$ in terms of R because $T_{ph}R={\gamma }_1$, $T_{cs}/R={\gamma }_2$, with ${\gamma }_1$ and ${\gamma }_2$ constant depending on the values of the entropy of photons and of cosmic string loops. Then Equation (40) becomes

$$\frac{{\left(hc\right)}^3{R}^5}{4\tilde{a}{k}_B^3{\gamma }_1^5}-\frac{k_B^3{\gamma }_{2}R}{2\tilde{b}{\mu }^3}\ge 0.$$

(41)

Thus, Universe will be stable for ${\displaystyle R^4\ge \frac{4\tilde{a}{\gamma }_1^5{\gamma }_2{k}_B^6}{2\tilde{b}{\left(hc\mu \right)}^3}}$. This suggests a kind of nucleation threshold for the minimum radius of the early universe.

In summary, the four main consequences of this model from a cosmological point of view are the following ones.

1)

Since the evaporation of micro black holes would be much slower than in the classical theory, this could allow for the survival of a number of primordial black holes and could explain why the bright remnants of their explosions are not observed. Thus, if supersymmetric particles of masses around 150 GeV (providing one of the candidates to the WIMPS black matter) are not found in the LHC (Large Hadron Collider) experiments currently at CERN (European Organization for Nuclear Research), micro black holes could provide an alternative candidate. Of course, this is only possible if micro black holes evaporate much more slowly than in the Hawking theory, as it is the case in the present theory. Otherwise, micro black holes of 150 GeV would last only a few Planck times.

2)

Our analysis suggests that the temperature of the universe cannot be identified with the temperature of photons, since the temperature of the different cosmic components (photons, cosmic string loops) will change in different forms along expansion. Indeed, here we have seen that $T_{ph}\sim R^{-1}$ whereas $T_{cs}\sim R$.

3)

Having a duality symmetry between the thermodynamics of photons and of cosmic string loops points a connection between a radiation-dominated universe in the early stages, with R increasing with time as $t^{1/2}$, and a loop-dominated universe at the long-time behaviour, with R increasing with time as t (i.e., without slowing down of the expansion). It does so by just adding a duality symmetry as a hypothetical fundamental ingredient in this model universe.

4)

The duality symmetry would be of interest not only to relate early states with late states of the Universe, but, at every moment of its evolution, it would establish a symmetry between photons and cosmic string loops, in spite of the different behaviour of their temperatures along the cosmic expansion.