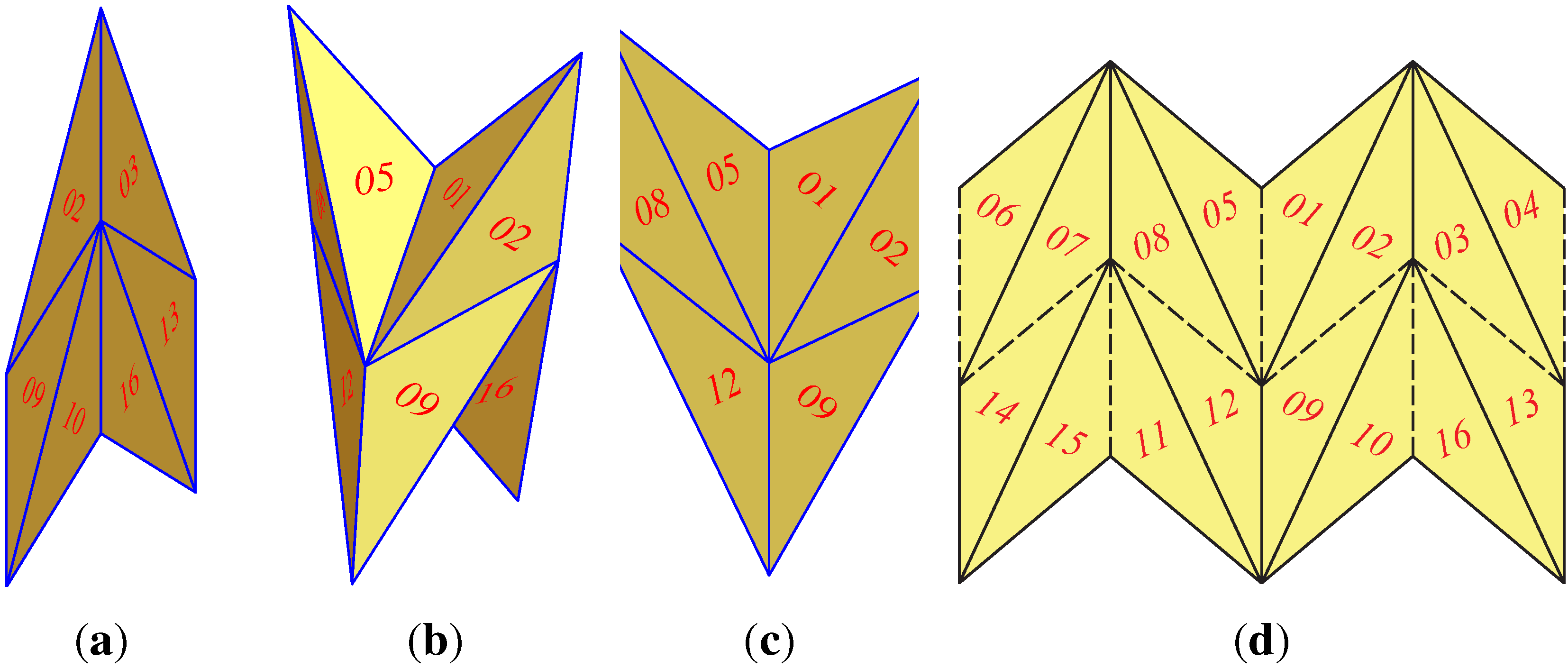
1. Introduction
A polyhedral surface is called (continuously) flexible, when there is a continuous family of mutually incongruent poses, called flexions, sharing the intrinsic metric. Each face is a planar rigid body; only the dihedral angles can vary between faces sharing an edge.
In discrete differential geometry, but also in architecture, there is an interest in polyhedral structures that can change their shape while all faces remain rigid (see, e.g., [
1]). Everybody can simulate this flexibility with real world models made from cardboard. However, one must be careful: the models of theoretically-rigid polyhedral surfaces can show a flexibility, due to imprecision and slight bending of the material. A famous example (see
Figure 1) is described in Schwabe and Wunderlich’s article [
2] and was even exposed at the science exposition “Phänomena” 1984 in Zürich. At that time, it was falsely stated that this polyhedron is flexible. However, it is only snapping between two planar realizations and one spatial pose. The unfolding shows that all faces are congruent isosceles triangles.
Below, we present three examples of flexible polyhedral surfaces that share the property that they have (at least) two flexions where all faces are coplanar. Such poses will be called “flat”.
Firstly, we analyze the geometry behind Miura-ori.
Secondly, we study Kokotsakis’ flexible tessellation of convex quadrangles and a particular case with a second flat pose. These two examples include flexible 3
× 3-complexes of quadrangles, so-called quadrangular Kokotsakis meshes [
3].
Finally, we recall the well-known Bricard octahedra of Type 3. They can be characterized by having no global symmetry, and they admit two flat poses. We will emphasize the role of a particular cubic curve, the strophoid.
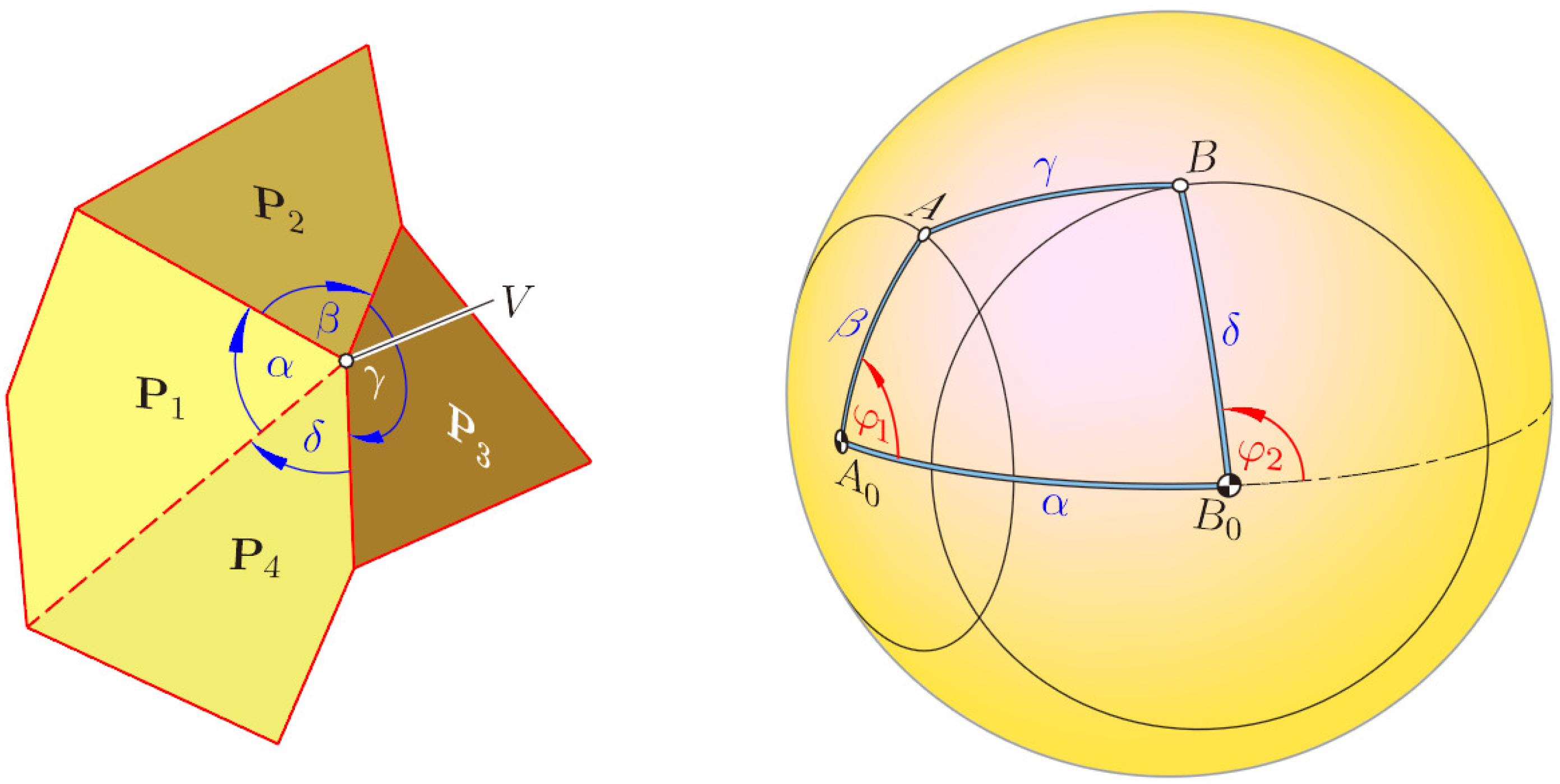
As a preparation, we provide a necessary condition for flexible polyhedral surfaces with two flat flexions. This condition refers to vertices
V where four faces are meeting. Let α, β, γ and δ be the sequence of interior angles at
V. Under the “vertex figure” of
V, we understand the intersection of these four faces with a sphere, which is centered at
V and whose radius is smaller than the shortest edge with endpoint
V. Hence, the vertex figure is a spherical quadrangle with sides of lengths α, β, γ and δ (
Figure 2). It has no effect on the flexions of this spherical quadrangle, when we replace any side of length λ by its complementary arc of length 2
π − λ. Therefore, we can confine ourselves to the case α,…,δ
< π; we call this quadrangle the reduced vertex figure.
Lemma 1. Let a flexible polyhedral surface be given that passes through two flat poses. Then, at each vertex, where four faces are meeting, the reduced vertex figure has either a plane of symmetry, at least after replacing one or two vertices by their antipodes, or the sides coincide in pairs.
Proof. The side lengths of the reduced vertex figure satisfy 0 < α,…,δ
< π (see
Figure 2). The spherical quadrangle admits two aligned poses if two of the following four equations hold:
α+β+γ+δ=2π,
α+β−γ−δ=0,
α−β+γ−δ=0,
α−β−γ+δ=0
It cannot happen that the length of one side, e.g.,
A0B0, equals the sum of the other three, since this spherical quadrangle admits only the aligned position. In any non-aligned pose of the polygon
A0ABB0 with side lengths β, γ and δ, the distance between the initial point and the endpoint would be shorter than α. For a similar reason, a spherical quadrangle with β+γ+δ
−α = 2
π cannot be continuously flexible.
Equations (a) and (b) are equivalent to β =
π − α and δ =
π − γ. When we replace
A and
B by their respective antipodes
and
, we obtain a spherical deltoid
. The same holds in the case where (a) and (d) are satisfied. Replacing one vertex by its antipode means replacing one edge of the pyramid with apex
V by its reflection with respect to
V (note the extensions
and
of
P3 and
P4 in
Figure 6).
Equations (a) and (c) are equivalent to γ = π − α and δ = π − β. Then, the spherical quadrangle
is an isogram, i.e., a spherical quadrangle where opposite sides have the same length. Equations (b) and (c) lead to α = δ and β = γ, i.e., to a spherical deltoid, as well as Equations (c) and (d). Equations (b) and (d) give a spherical isogram.
Spherical kites have either an axis of symmetry or the flexion is trivial, since the sides coincide in pairs. Spherical isograms are either self-intersecting with an axis of symmetry or they have a center of symmetry. When in the latter case two neighboring vertices are replaced by their antipodes, then the axial symmetry of the spherical isogram is transformed into a planar symmetry. □
2. Miura-ori
Miura-ori is a Japanese folding technique named after Prof. Koryo Miura, The University of Tokyo. However, already before K. Miura, this technique was known; according to a personal communication with Gy. Darvas, it was kept as a military secret in Russia in the thirties of the last century. There are many applications of Miura-ori. It is, e.g., used for solar panels, because they can be packed in compact form and deployed into their flat shape by pulling on one corner only [
4]. It serves as a kernel to stiffen sandwich structures. Furthermore, it can be utilized for the design of cupolas [
1].
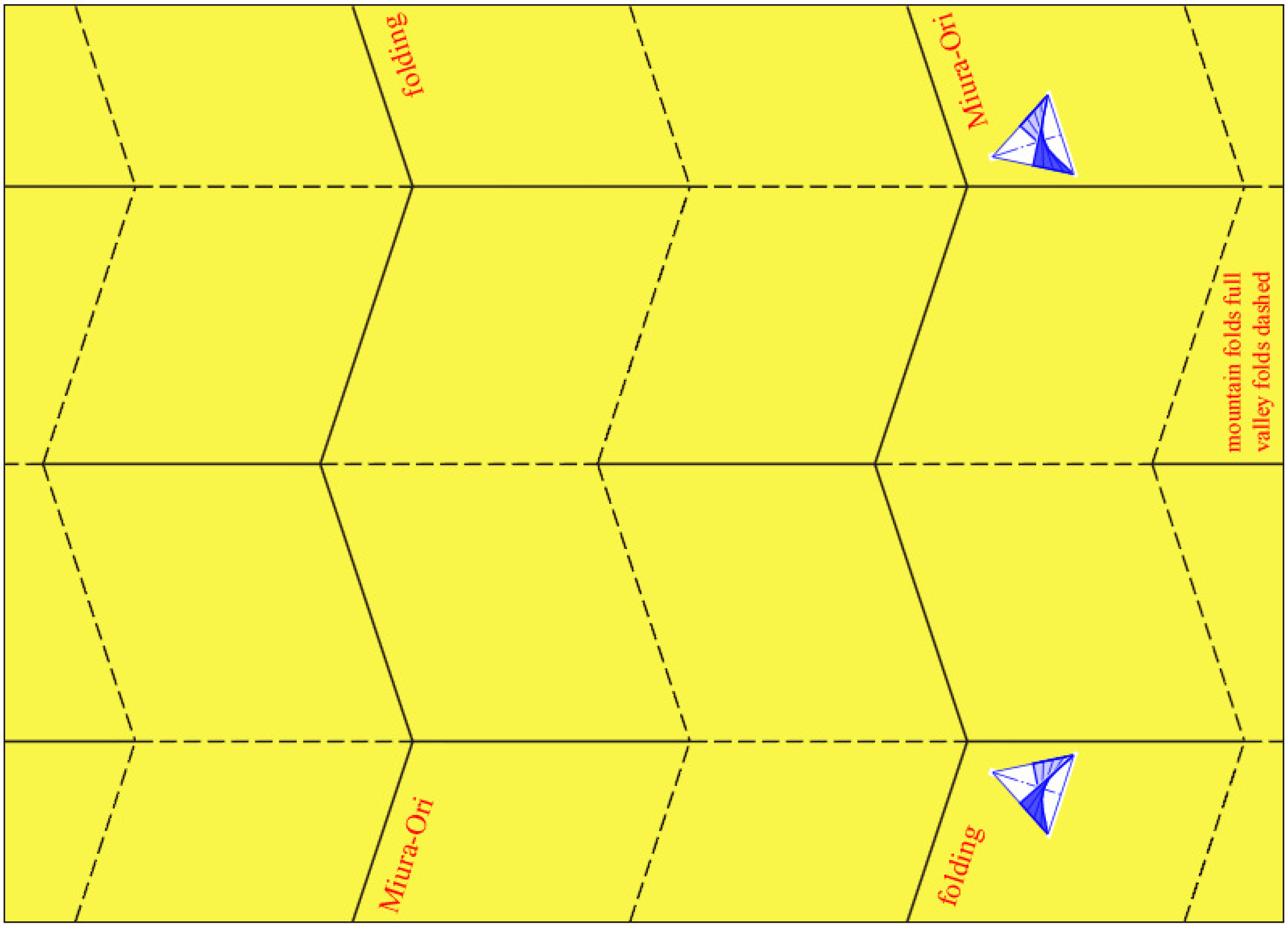
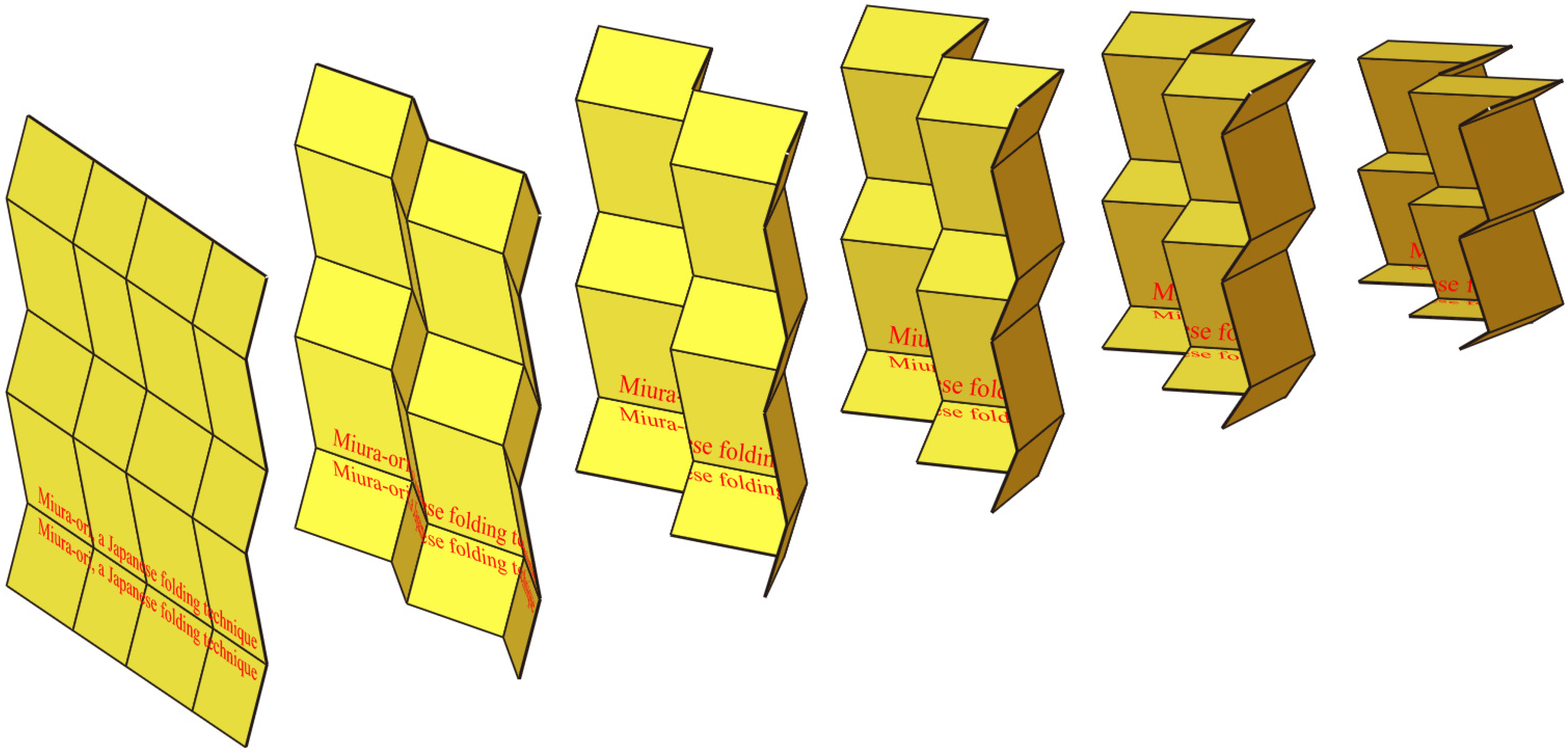
Let us analyze the process of folding a sheet of paper as depicted in
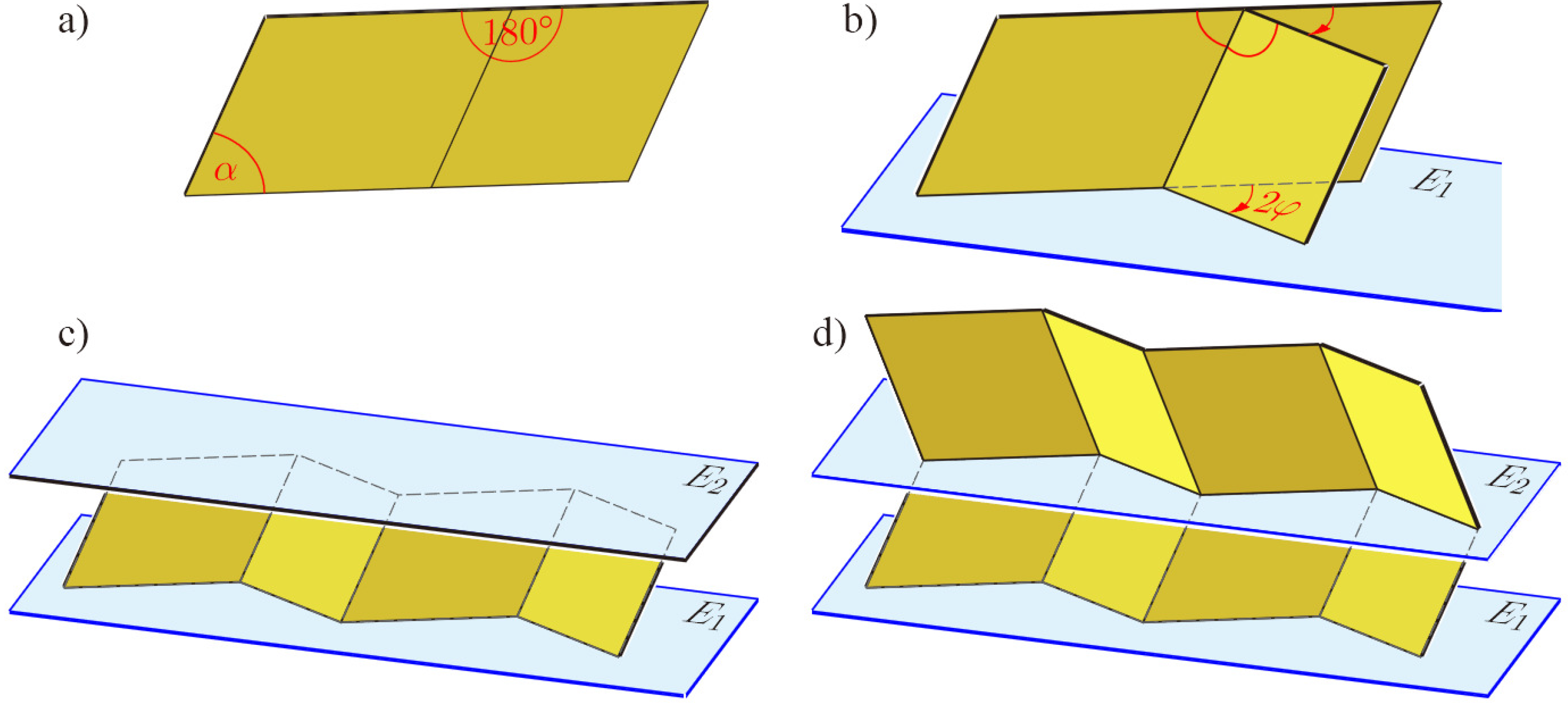
Figure 3 with given valley and mountain folds, thus proving that this quadrangular surface is really continuously flexible. To begin with, we take two coplanar parallelograms with aligned upper and lower sides (
Figure 4a).
Now, we rotate the parallelogram on the right-hand side against the left one about the common edge: the lower sides span a plane
E1, and the upper sides span a plane
E2 parallel to
E1. We continue and extend the two parallelograms to a zig-zag strip by adding parallelograms, which are translatory congruent alternately to the left-hand or right-hand parallelogram of the initial pair. After this, the complete strip has its lower zig-zag boundary still placed in
E1 and the upper one in
E2 (see
Figure 4c). This remains valid when we fix the plane
E1, but vary the bending angle φ.
After iterated reflections in planes
E2 parallel to
E1 (
Figure 4d) or after translations orthogonal to
E1, the complete Miura-ori flexion is obtained as depicted in (
Figure 5). When finally the two initial parallelograms become coplanar due to a bending angle of 180°, Miura-ori reaches a totally folded pose, which is again flat.
The set of edges of Miura-ori can be subdivided into two families of folds. The “horizontal” folds are copies of the zig-zag line in
E1 and placed in horizontal planes. They are aligned in the stretched initial pose as depicted in
Figure 3. The other folds are located in mutually parallel vertical planes, since their edges are obtained by iterated reflections in planes parallel to
E1. We call these folds “vertical”. While the edges of each horizontal fold alternate between valley and mountain fold, all edges of a vertical fold are of the same type, either valley or mountain folds.
Now, we are going to analyze the self-motion of Miura-ori. For the sake of simplicity, we assume that all edges have a unit length (obviously, the side lengths of the zig-zag line in E1 can vary without restricting the flexibility; analogously, the distances between the planes through the horizontal folds need not be the same everywhere).
We fix the planes of one horizontal and one vertical fold, as well as the crossing point
V of these two folds (
Figure 6). Let
P1,…,
P4 be the four parallelograms meeting at
V. We start with the motion of
P1: the two edges of
P1 with the common endpoint
V rotate within the respective fixed planes, such that the included interior angle
α < 90° remains constant (compare with
Figure 4a). The reflection in the horizontal plane
E2 maps
P1 onto the second parallelogram
P2. It has the same interior angle
α at
V and moves like
P1.
Now, we elongate the horizontal edges of the other two parallelograms P3 and P4 (with interior angle 180°−α) beyond the fixed vertical plane by the unit length. This gives two additional parallelograms
and
with the interior angle α at V. Each shares a “vertical” edge with P1 or P2, respectively. Hence, the reflection in the fixed vertical plane must map P1 onto
and P2 onto
.
This reveals a hidden local symmetry of Miura-ori: when at each vertex V two adjacent parallelograms P3, P4 with congruent interior angles at V are replaced by their “horizontal elongations”
and
, respectively, we obtain a pyramid of four congruent parallelograms P1, P2,
,
with apex V. This pyramid flexes, such that it remains symmetrical with respect to the planes of the horizontal fold and the vertical fold passing through V (compare with Lemma 1).
Next, we study the relations between angles: we use a coordinate frame with origin
V, with the
x- and
y-axis in the horizontal plane
E2 and with the [
yz]-plane spanned by the vertical fold passing through
V (see
Figure 6). Let 2φ and 2ψ be the bending angles between consecutive segments of the horizontal and vertical folds, respectively. Thus, the sides of
P1 have the direction vectors:
and we obtain the dot product:
In the stretched position, the parallelogram
P1 is located in the vertical [
yz]-plane; the corresponding (half) bending angles are φ = 0° and ψ = 90°
− α. The other limit is the totally folded position with
P1 in the [
xy]-plane, φ = α and ψ = 90°.
In order to obtain formulas for the dihedral bending angles 2γ and 2δ along edges of the horizontal and vertical folds (see
Figure 6), we need the unit vector perpendicular to the plane of
P1:
Its dot products with the unit vectors along the
x- and
z-axis give:
Theorem 2. During the self-motion of Miura-ori, the horizontal folds remain in mutually-parallel planes. The same holds for vertical folds, and their planes are orthogonal to the planes spanned by the horizontal folds. The dihedral bending angles 2γ
along the edges of the horizontal folds are everywhere the same, as well as the angles 2γ
for the vertical folds. They satisfy Equation (2), while φ
and ψ
are related by Equation (1). The motion depicted in
Figures 4 and
5 is not the only self-motion of Miura-ori. The initial pose admits bifurcations. Trivial flexions arise, e.g., when in the stretched position, we use any aligned horizontal fold as an axis of rotation for a folding. The same can be done, independently of each other, with several aligned horizontal folds. Furthermore, after full 180°-rotations, we obtain an
n-fold covered strip and can treat it like a single strip. Hence, Miura-ori admits more than two flat poses.
Miura-ori is a very particular case of a Voss surface. This is a polyhedral surface with quadrangular faces, such that each 3
× 3 complex is a flexible Kokotsakis mesh [
5] of the isogonal Type 3 (according to the enumeration given in [
6]): at each vertex, opposite interior angles are either equal or complementary (Lemma 1); and there is an additional equation to satisfy ([
7], p. 12). A long lasting open problem, the classification of flexible quadrangular Kokotsakis meshes [
3] has recently been solved by I. Izmestiev [
8]. The classification of flexible Kokotsakis meshes with a central
n-gon and
n ≥ 5 is still open.
There are several generalizations of Miura-ori, among them the impressive approximations of free-form surfaces presented by T. Tachi in [
9]. Some patterns are even examples of rigid origami [
10], designed within the family of Voss surfaces.
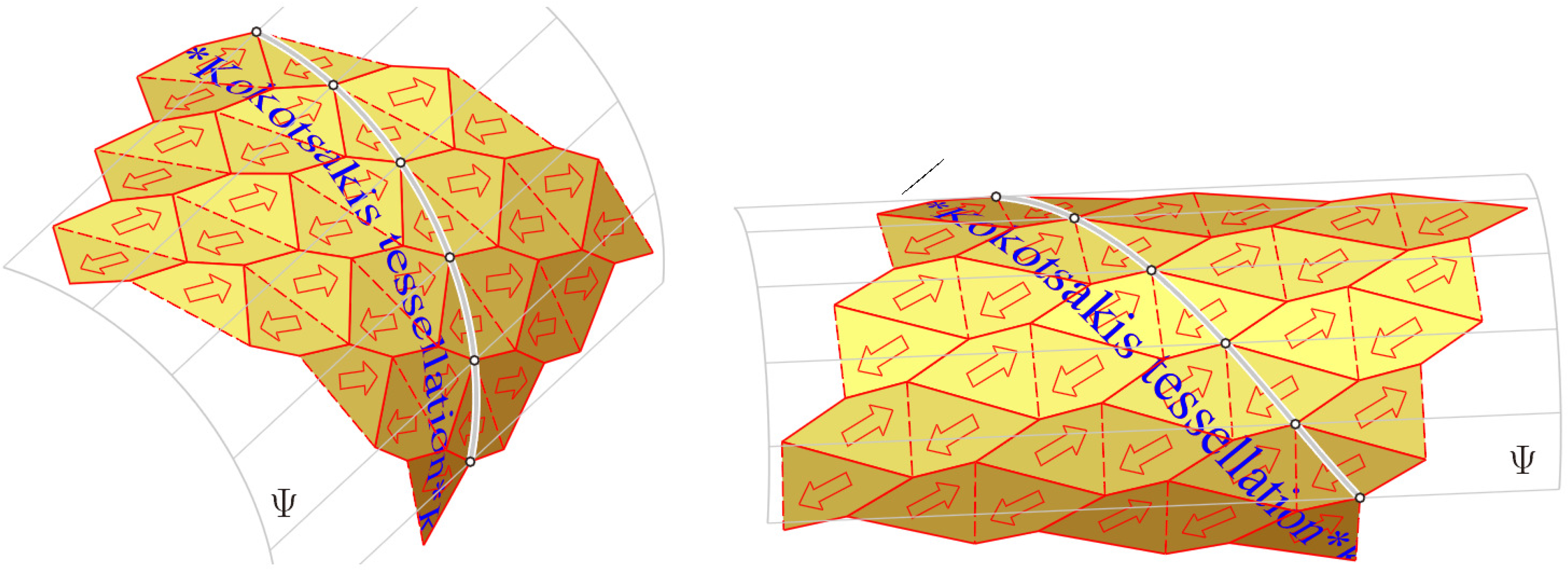
3. Kokotsakis’ Flexible Tessellation
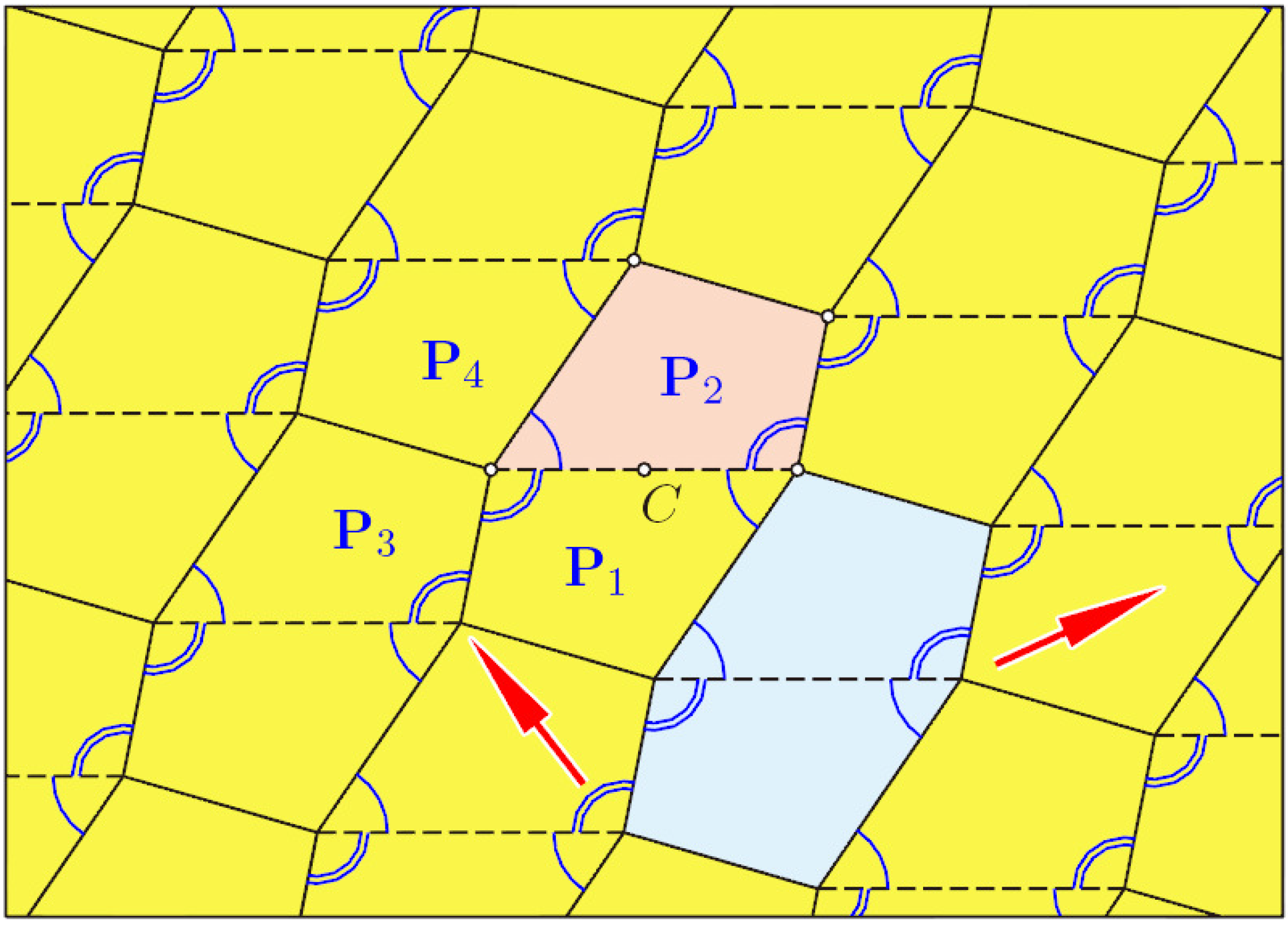
Another remarkable flexible mesh of quadrangles, which also starts from a flat initial pose, dates back to A. Kokotsakis. In [
5] (p. 647), he proved the flexibility of the tessellation displayed in
Figure 7. However, he did not present any geometric property of its spatial poses; this will be done below.
Choose an arbitrary quadrangle
P1. By iterated rotations about the midpoints of the sides, we obtain a well-known regular tessellation of the plane (
Figure 7). We can generate the same tessellation also in another way: when we glue together two adjacent quadrangles, we obtain a central-symmetric hexagon (blue shaded in
Figure 7). Now, the same tessellation arises when this hexagon undergoes iterated translations, as indicated in
Figure 7 by the red arrows.
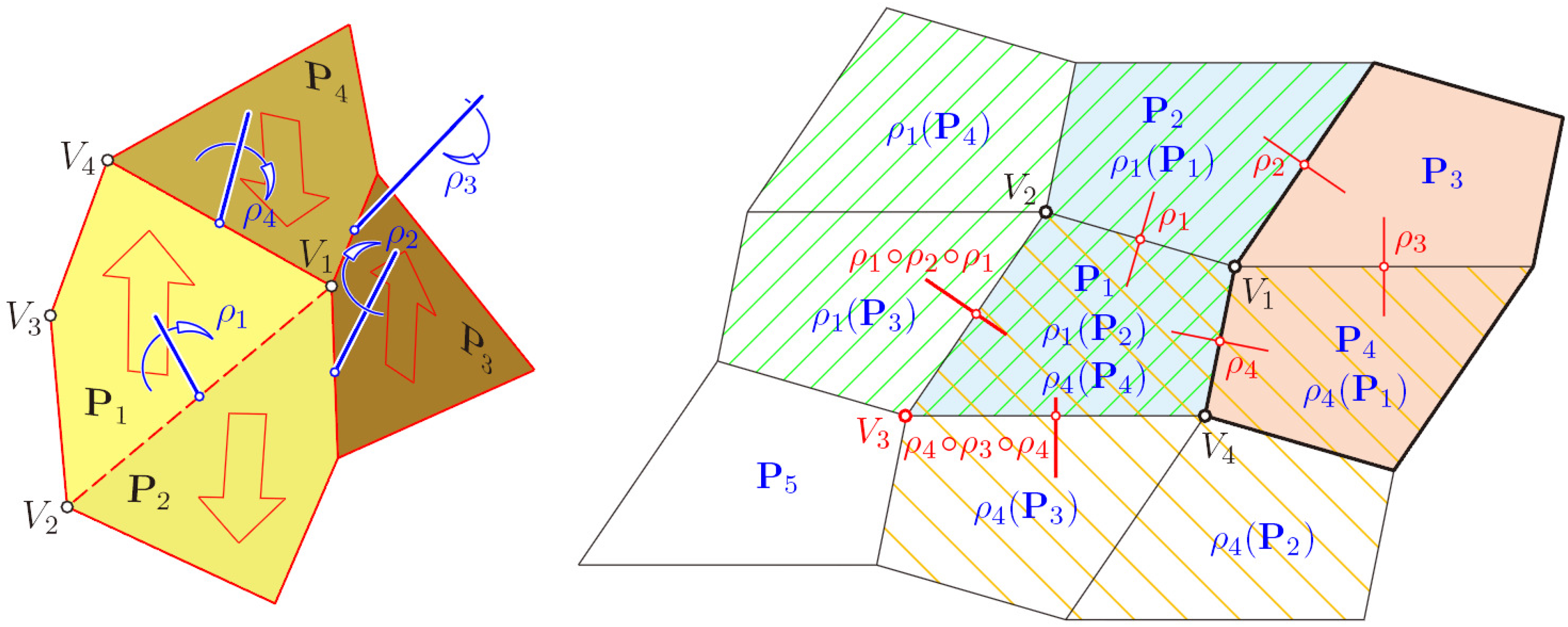
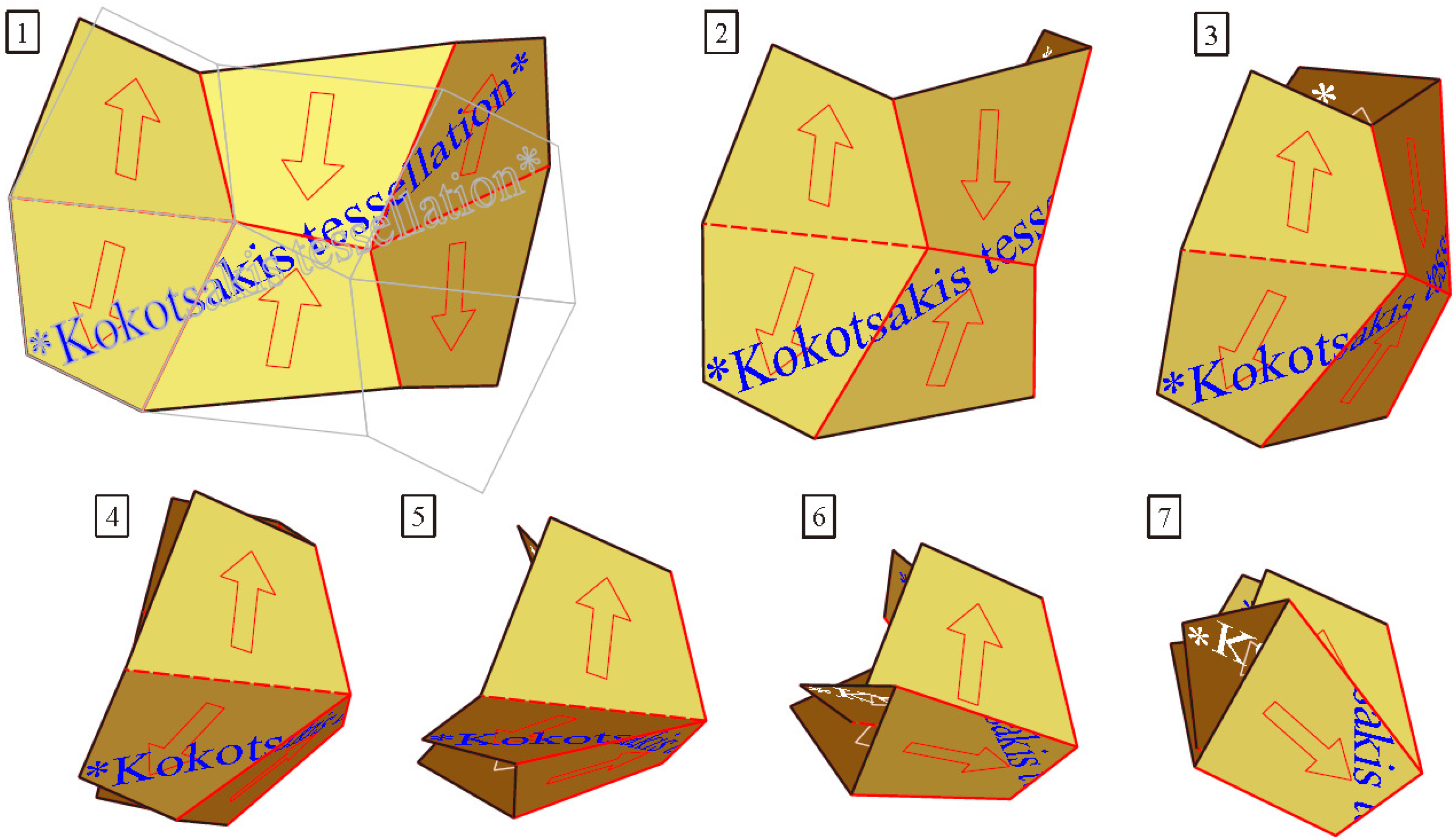
In the following, we prove for convex quadrangles that this polyhedral structure is flexible: let
P1,…,
P4 be four pairwise congruent faces with the common vertex
V1 (shaded area in
Figure 8). They form a four-sided pyramid with apex
V1, and the four interior angles at
V1 are respectively congruent to the four interior angles of a quadrangle. Our pyramid is flexible, provided the fundamental quadrangle is convex; otherwise, one interior angle at
V1 would be greater than the sum of the other three interior angles, so that the only realization is flat.
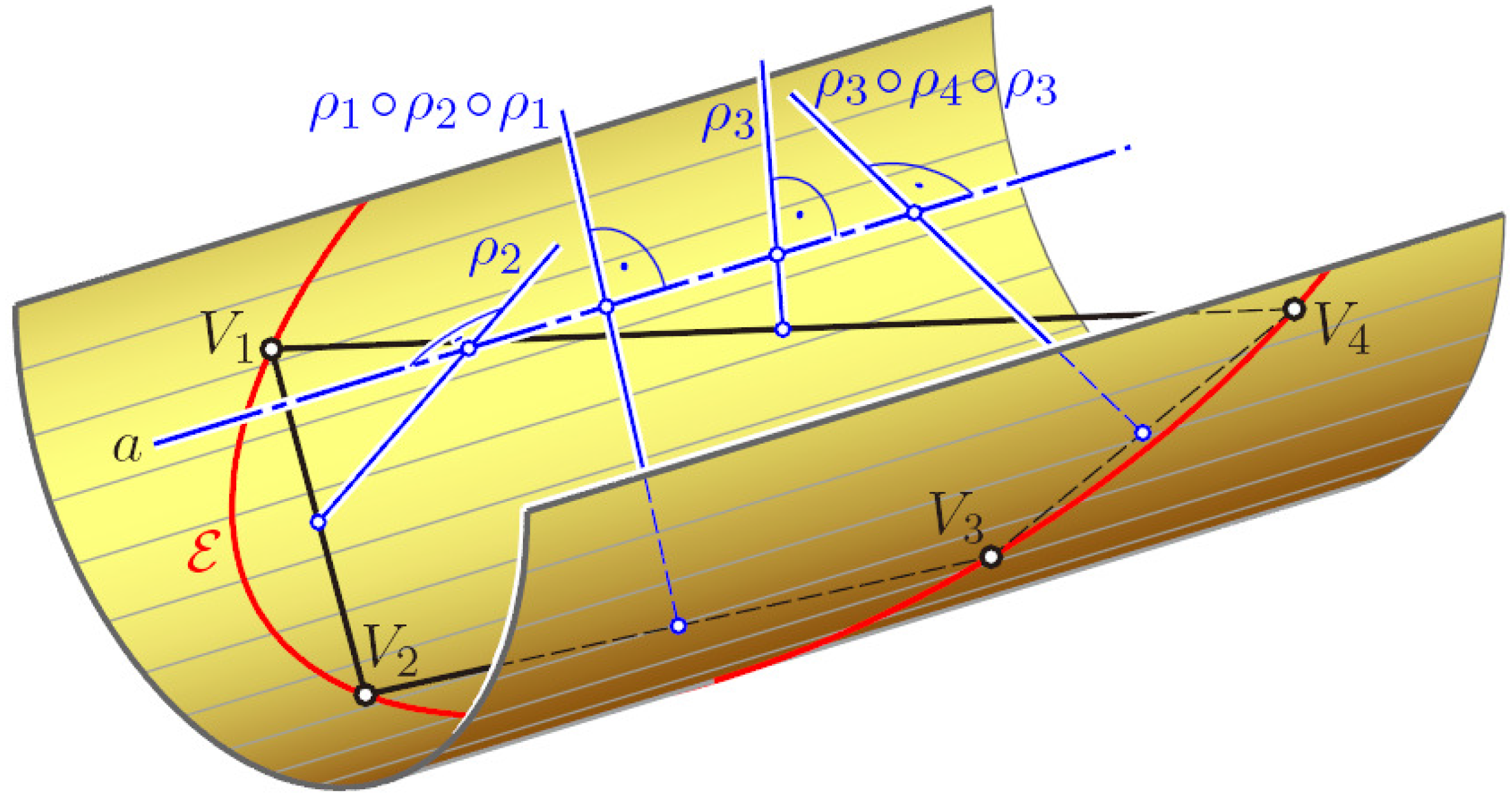
According to the labeling in
Figure 8, left, for any pair of adjacent faces, there is a respective 180°-rotation (“half-turn”)
ρ1,
ρ2,
ρ3 or
ρ4, which exchanges the two faces. Therefore, e.g.,
P2 =
ρ1(
P1). The axis of
ρ1 is perpendicular to the common edge
V1V2 and located in a plane that bisects the dihedral angle between
P1 and
P2.
After applying consecutively all four half-turns to the quadrangle
P1, this is mapped via
P2,
P3 and
P4 onto itself. This implies:
Now, we can extend this flexion of the pyramid step by step to the complete tessellation: the rotation
ρ1 exchanges not only
P1 with
P2, but transforms the pyramid with apex
V1 onto a congruent copy with apex
V2 sharing two faces with its preimage. This is the area hatched in green in
Figure 8, right. Analogously,
ρ4 generates a pyramid with apex
V4 sharing the faces
P1 and
P4 with the initial pyramid. Finally, there are two ways to generate a pyramid with apex
V3. Either we transform
ρ2 by
ρ1 and apply
ρ1 ○
ρ2 ○
ρ1, which exchanges
V2 with
V3, or we proceed with
ρ4 ○
ρ3 ○
ρ4, which exchanges
V4 with
V3. Thus, we obtain two mappings,
ρ1 ○
ρ2 and
ρ4 ○
ρ3, with
V1 ↦
V3, which are equal by virtue of
Equation (3). Hence, each flexion of the initial pyramid with apex
V1 is compatible with a flexion of the 3
× 3 complex of quadrangles. This can be extended to the complete tessellation (in [
6], it is shown that this tessellation is a particular case of the line-symmetric Type 5 of flexible Kokotsakis meshes).
The product of two half-turns is a helical motion about the common perpendicular of the axes of the two half-turns. The angle of rotation and the length of translation is twice the angle and distance, respectively, between the two axes. When the pyramid with apex
V1 is not flat, then the axes of the 180°-rotations
ρ1,…,
ρ4 are pairwise skewed; the common perpendicular of any two of them is unique.
Equation (3) implies that the axes of the four rotations have a common perpendicular
a. Hence, the motions
ρ1 ○
ρ2 and
ρ3 ○
ρ2 =
ρ4 ○
ρ1 are helical motions with a common axis
a. All vertices of the flexion have the same distance to
a; they lie on a cylinder Ψ or revolution (in [
11], T. Tarnai addresses another relation between planar tessellations and cylindrical shapes; he shows how semiregular tessellations can be folded into cylindrical shells).
When the quadrangles
P3 and
P4 are glued together, we obtain a line-symmetric skewed hexagon, one half of our initial pyramid with apex
V1; the half-turn
ρ3 maps this hexagon onto itself (
Figure 8). We can generate the complete flexion by applying iterated helical motions
ρ1 ○
ρ2 and
ρ3 ○
ρ2 on this hexagon.
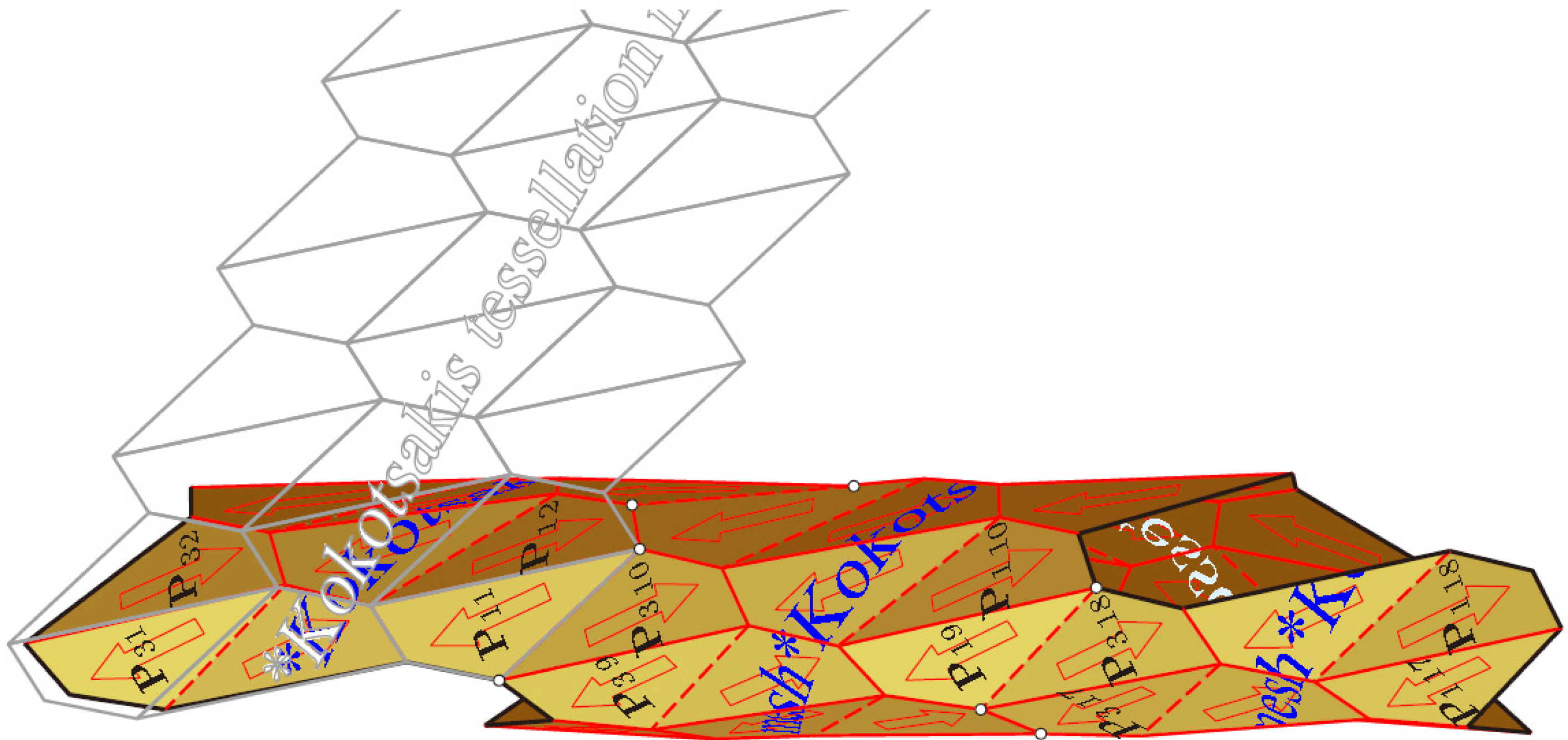
Theorem 3. Any flexion of the Kokotsakis tessellation is obtained from the line-symmetric hexagon consisting of the two planar quadrangles by applying the discrete group of coaxial helical motions generated by ρ1 ○ ρ2 and ρ3 ○ ρ2. In the initial flat pose, these generating motions are the translations applied to a centrally symmetric hexagon, thus generating the regular tessellation in the plane.
The flat initial pose of the pyramid with apex
V1 admits a bifurcation between two continuous motions of the pyramid. Hence, the complete quad mesh admits two self-motions (
Figure 9). When starting with a trapezoid
P1 (compare with
Figure 14 in [
12]), one of these self-motions is trivial: it results from mutually-independent bending along aligned edges of the initial pose.
Once we have clarified that for each non-planar flexion, all vertices lie on a cylinder Ψ of revolution with axis
a, we can give another explanation for the flexibility (see
Figure 10): the plane spanned by the quadrangle
V1…
V4 intersects the circumcylinder Ψ along an ellipse
E. Given a convex quadrangle
V1…
V4, there is a pencil of conics passing through the four vertices. This pencil includes an infinite set of ellipses, which is bounded by parabolas or pairs of parallel lines. Hence, we can specify an ellipse
ε out of this pencil and choose one of the two right cylinders passing through
ε.
Now, we define the half-turns
ρ1 and
ρ4; their axes pass through the midpoints of the sides
V1V2 and
V1V4, respectively, and intersect the cylinder’s axis
a perpendicularly (see
Figure 10). The common normal of the lines
V2V3 and
a is the axis of
ρ1○
ρ2○
ρ1; that between
V3V4 and
a is the axis of
ρ4○
ρ3○
ρ4. Iterations of these half-turns transform our initial face
P1 into all faces of the flexion.
In [
12], cases are studied where a particular flexion of a
m × n-complex closes. This gives rise to an infinitesimally rigid tessellation on a right cylinder by plane quadrangles (see
Figure 11).
Theorem 4. When the basic quadrangle of the flexible Kokotsakis’ tessellation is cyclic, i.e., has a circumcircle, it admits a second flat pose: all quadrangles are packed into a single circumcircle. However, this fails for real-world models, because of self-intersections.
Proof. In the case of a cyclic quadrangle, the pencil of circumscribed conics includes one circle. There is a unique right cylinder passing through this circle, and the corresponding axes of half-turns
ρ1,…,
ρ4 are coplanar. The complete flexion is flat; the circumcircles of all faces coincide (compare with
Figure 12). Similar to Miura-ori, this tessellation mesh can be “packed” into a very small size, such that it finds a place in the circumcircle of one quadrangle, at least “theoretically”,
i.e., without paying attention to self-intersections. However, a real-world model consisting of at least 3
× 3 quadrangles cannot approach such a pose, since the faces have to be placed one upon the other. Then, there is a collision between the “edges” spanning over distant levels and the vertices of quadrangles placed between them. □
In the case of a cyclic quadrangle, opposite angles are complementary. Therefore, this flexible tessellation is an example of a Voss surface, too.
4. Bricards’ Octahedra of Type 3
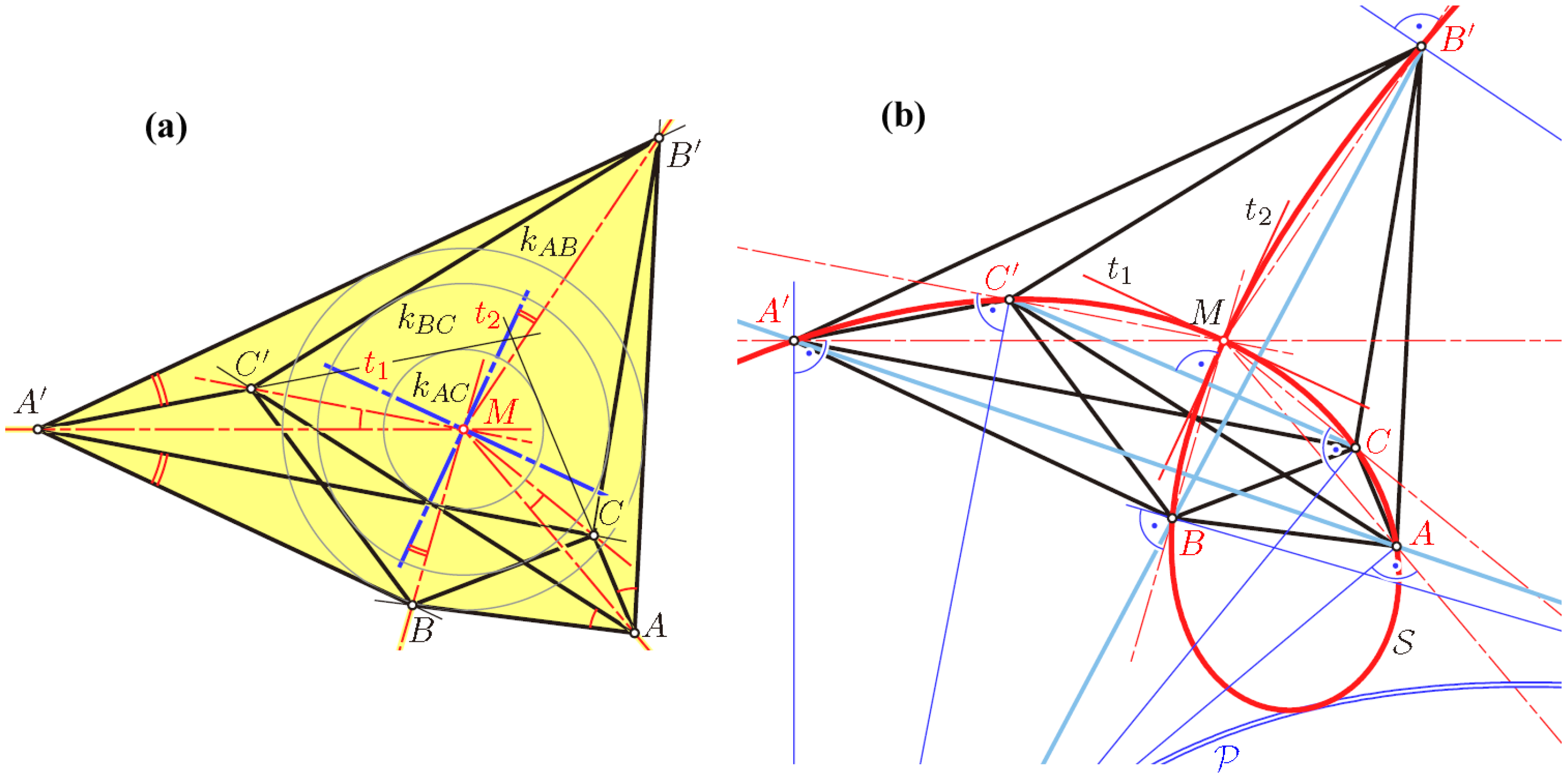
In this final section, an octahedron is understood as a double-pyramid over a quadrangle, which need not be planar. Hence, the octahedron contains three pairs (A, A′), (B, B′) and (C, C′) of opposite vertices. Each of them can be seen as a pair of apices of a double pyramid; the corresponding bases, called “equators”, are the quadrangles BCB′C′, ACA′C′ or ABA′B′, respectively.
According to R. Bricard’s fundamental result [
13], there are three types of flexible octahedra. Those without any symmetry belong to Type 3 and admit two flat poses. They can be defined as shown in
Figure 13a.
Each of the three equators is a quadrangle with sides tangent to a circle with the same center M. Hence, there is a local symmetry at each vertex with respect to an axis, which passes through M (note Lemma 1).
The following theorem relates the given flat pose to a strophoid
S, which is defined as a circular curve of degree three with a node
N and orthogonal tangents at the node. On
S, a symmetric relation can be defined [
14]: two points
P, P′ of
S \ {
N} are called associated if the lines
NP and
NP′ are symmetric with respect to the node tangents
t1 and
t2. Furthermore, the strophoid
S is the locus of points
X with the property that one angle bisector of the lines
XP and
XP′ passes through the node
N. This holds simultaneously for all pairs (
P, P′) of associated points of
S.
As a consequence, at our given flat pose of the octahedron, there must be a strophoid
S with the node
N =
M and associated points (
A, A′), such that
S passes also through
B,
B′,
C and
C′ (
Figure 13b).
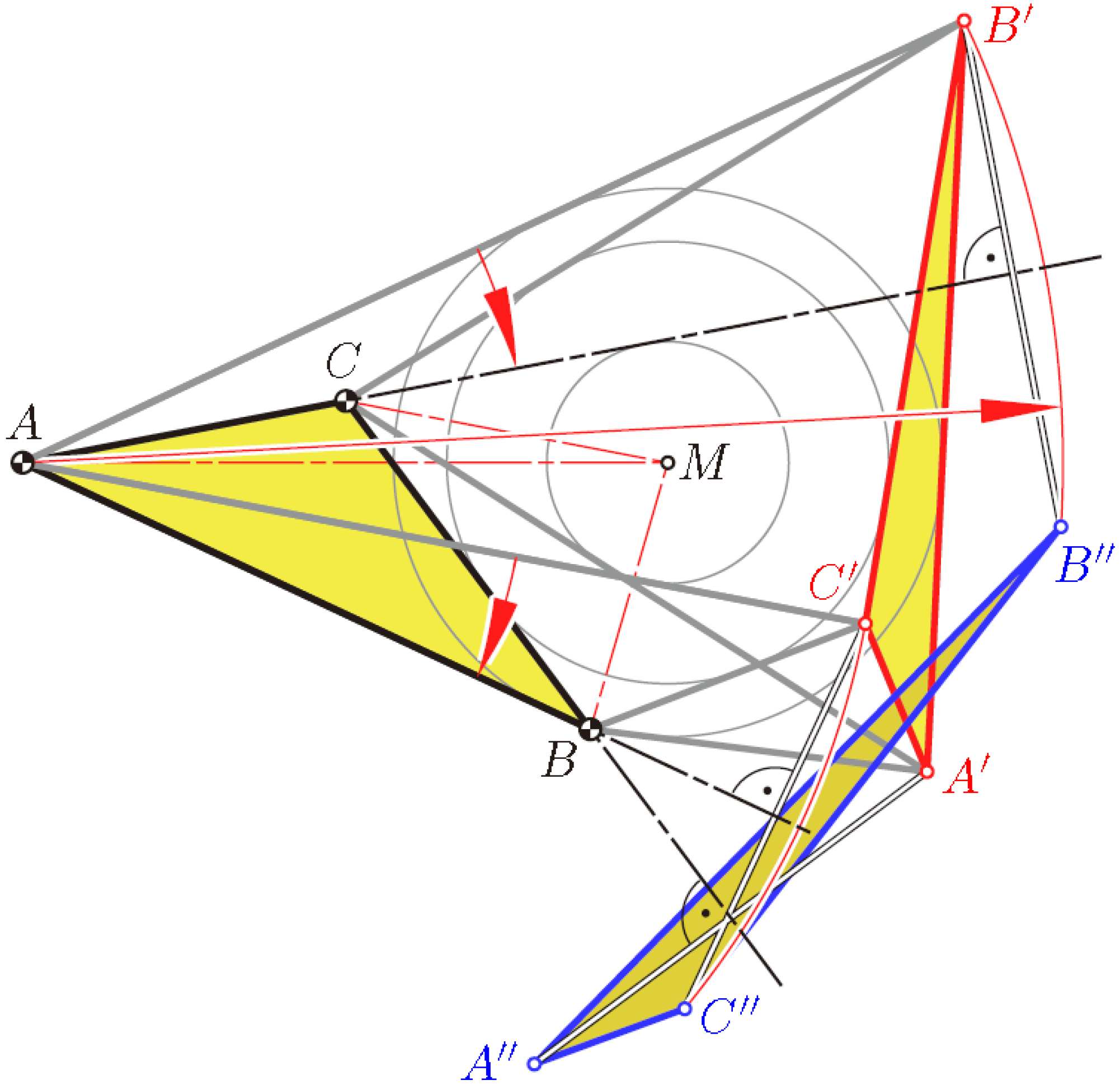
Theorem 5. For any strophoid S, each triple of associated pairs of points (A, A′), (B, B′) and (C, C′) defines a flat pose of a flexible octahedron. This octahedron has a second flat pose.
Proof. In order to obtain the second flat pose, let us keep the face
ABC fixed, while the opposite triangle
A′
B′
C′ is replaced by a congruent copy
A″
B″
C″. Both flat poses must show respectively equal distances
AB′ =
AB″,
AC′ =
AC″,…,
CB′ =
CB″. We show that the reflection in the line
AB maps
C′ onto
C″, the reflection in the line
AC maps
B′ onto
B″ and the reflection in the line
BC maps
A′ onto
A″ (see
Figure 14). Firstly, these reflections preserve the distances to the points of the fixed triangle. Secondly, since both pairs of lines, (
AB, AB′) and (
AC, AC′), are symmetric with respect to
AM, the angles ∢
B′AB″ = 2 ∢
B′
AC and ∢
C′AC″ = 2 ∢
C′AB are equal. Hence, there is a rotation about
A, which sends the side
B′C′ onto
B″
C″ and preserves the length. The same holds for the other sides
A′B′ and
A′C′. □
Furthermore, at spatial poses of the flexible octahedron of Type 3, there is a local symmetry at each vertex
V (Lemma 1): the six planes of symmetry share a common axis
a (see, e.g., [
15],
Figure 3). All equators are placed on one-sheet hyperboloids of revolution with the axis
a. As demonstrated in [
16,
17], even at each spatial pose, there is a particular spatial cubic passing through the six vertices. Of course, this cubic is the spatial analogue of the strophoid
S displayed in
Figure 13b.
All flexible octahedra have self-intersections. Real-world models work only when either they are built as a framework or one pair of opposite faces is removed (see, e.g., [
7],
Figure 5).
There exist also particular flexible octahedra of Type 2,
i.e., with an axis of symmetry, which admit two flat poses. They are a sort of limiting case when point
M in
Figure 13a, tends to infinity (see, e.g., [
15],
Figure 4). G. Nawratil [
18] proved that there is one non-trivial type of a flexible octahedron with some vertices at infinity: it consists of two prisms with a kite as the common basis; the generators of the prisms are orthogonal to the kite’s axis of symmetry. These examples can even be free of self-intersections.
The analogue of Type 3 in the hyperbolic space is also flexible. Of course, more sub-types can be distinguished, since the vertices can be either finite points or on the absolute conic or outside (note [
19]). Recently, A.A. Gaifullin generalized all of this in [
20]: He proved that, in the algebraic sense, Type 3 is the simplest; there exist flexible higher-dimensional analogues, so-called cross-polytopes, in all dimensions, in Euclidean spaces, as well as in spherical and hyperbolic spaces.