Abstract
By insisting on naturalness in both the electroweak and quantum chromodynamics (QCD) sectors of the minimal supersymmetric standard model (MSSM), the portrait for dark matter production is seriously modified from the usual weakly interacting massive particle (WIMP) miracle picture. In supersymmetry (SUSY) models with radiatively-driven naturalness (radiative natural SUSY or radiative natural SUSY (RNS)) which include a Dine–Fischler–Srednicki–Zhitnitsky (DFSZ)-like solution to the strong charge-conjugation-parity (CP) and SUSY µ problems, dark matter is expected to be an admixture of both axions and higgsino-like WIMPs. The WIMP/axion abundance calculation requires simultaneous solution of a set of coupled Boltzmann equations which describe quasi-stable axinos and saxions. In most of parameter space, axions make up the dominant contribution of dark matter although regions of WIMP dominance also occur. We show the allowed range of Peccei-Quinn (PQ) scale fa and compare to the values expected to be probed by the axion dark matter search experiment (ADMX) axion detector in the near future. We also show WIMP detection rates, which are suppressed from usual expectations, because now WIMPs comprise only a fraction of the total dark matter. Nonetheless, ton-scale noble liquid detectors should be able to probe the entirety of RNS parameter space. Indirect WIMP detection rates are less propitious since they are reduced by the square of the depleted WIMP abundance.1. Introduction
The discovery of the Higgs boson [1,2] with mass mh = 125.15 ± 0.24 GeV was a great triumph, but it brings with it a conundrum: how is it that scalar fields can actually occur in nature? The problem lies in the radiative corrections to their masses: they are quadratically divergent in the energy circulating in the loop diagrams. Since quantum mechanics requires one to sum over a complete set of states, those states with the highest energies bring large quantum corrections which must be compensated by adjusting bare mass terms to maintain the measured value of mh. The situation is depicted in Figure 1: here we take the SM Higgs potential as where and Requiring that the quantum corrections not exceed the bare mass (similar to the Gaillard-Lee [3] requirement on which predicted the charm quark mass) implies the Standard Model to only be valid at energy scales TeV. These quadratic divergences—which are endemic to scalar quantum fields—led some physicists to ponder whether fundamental scalar fields could really occur in nature [4].
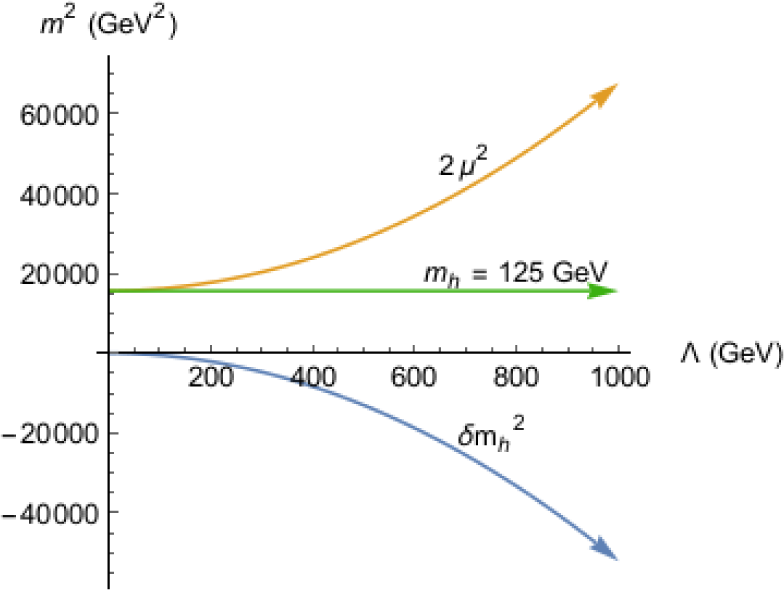
The solution to the above SM naturalness problem was very conservative: expand the fundamental 4-D spacetime symmetry structure which underlies quantum field theory to its most general structure including graded Lie-algebras [5–8]. The expanded symmetry group—called supersymmetry or SUSY for short—provided once and for all the necessary structure so that scalar field quadratic divergences completely canceled. Akin to the doubling of particle spectra which occurred when Dirac included Lorentz symmetry into quantum mechanics, SUSY also requires an approximate doubling: under SUSY, for every boson there is a fermion state and vice versa. Since we see, e.g., no bosonic electrons with the same mass as electron (similar arguments apply to other SM particle states), SUSY must be a broken symmetry. To stabilize the weak scale, it is expected that SUSY breaking is characterized by soft SUSY breaking terms of weak scale magnitude. In fact, in models bases on local supersymmetry (supergravity or SUGRA), the breakdown of SUSY must occur in a “hidden sector” of the model to maintain phenomenological viability [9–13]. Taking the limit of MP → ∞ while keeping the gravitino mass m3/2 fixed, one calculates the soft terms [14–17] as multiples of m3/2 where . Here MP = 2.4 × 1018 GeV is the reduced Planck mass. A hidden sector mass scale mhidden ∼ 1010 GeV gives rise to a weak scale of ∼100 GeV.
From the above arguments, we arrive at the rough expectation that the new matter particles should inhabit the energy scale Q ∼ 100–1000 GeV. Lest one think the above construct is the product of an overly active imagination of theorists, we remark that SUSY is supported by three disparate sets of measurements:
The measured values of the three gauge couplings, when extrapolated to mGUT ≃ 2 × 1016 GeV, very nearly meet at a point [18], as expected in simple unified theories.
The measured value of the top quark, mt = 173.2 GeV, is in just the right range to drive the up-Higgs soft mass to negative values, causing the required breakdown of electroweak symmetry [19–26].
The measured value of the newly discovered higgs boson, mh ≃ 125 GeV, falls squarely within the narrow window mh ∼ 115–135 GeV of SUSY requirements which was expected from the pre-LHC era [27]. In contrast, in the SM the Higgs mass could lie anywhere in the 115–800 GeV mass range.
In addition, SUSY—as embodied by the MSSM—carries with it several dark matter candidates [28] and several baryogenesis mechanisms [29] whereas the SM contains neither.
In spite of these successes, many authors have proclaimed weak-scale SUSY to be in a state of crisis [30–38]. While SUSY solves the big hierarchy problem involving quadratic divergences [39,40], there is a growing Little Hierarchy problem [41–54] typified by the increasing gap between the W, Z and h masses clustered all around ∼100 GeV, and the apparent mass scale of SUSY particles which are seemingly in the multi-TeV range. Presently, LHC8 with 20 fb−1 of data requires TeV in the case of heavy squark masses and TeV in the case of comparable squark masses. Furthermore, the value of mh ∼ 125 GeV requires radiative corrections from top-squarks in the tens of TeV range for small top-squark mixing (although few-TeV top squarks are allowed for large mixing induced by trilinear A terms [55]). The lore is that as the mass scale for the soft terms increases, then one must increasingly fine-tune parameters to maintain mW,Z,h ∼ 100 GeV. Since large fine-tuning usually indicates some pathology in any theoretical construct, a number of authors have questioned whether SUSY as we know it is gradually becoming excluded [30]: if so, then new ideas for physics beyond the Standard model are required.
In the following Section 2, we shall refute this point of view. While we shall conclude that many SUSY models are indeed fine-tuned—including the paradigm minimal supergravity model/constained minimal supersymmetric standard model (mSUGRA/CMSSM)—we will find that models characterized by radiatively-driven naturalness [56,57] (radiatively-driven natural SUSY or RNS) are allowed with modest fine-tunings only at the 10% level. Radiatively-driven naturalness occurs in SUSY models with non-universality of Higgs soft terms (as in the NUHM2 model [58–62]). RNS models are characterized by the presence of light higgsinos with mass µ ∼ 100–200 GeV, the closer to mZ the better. The lightest SUSY particle is a candidate for dark matter and is then a higgsino-like WIMP.
We proceed to examine the consequences of RNS for dark matter. In Section 3, we require that naturalness occurs also in the QCD sector of the MSSM. This brings to bear the QCD axion albeit as one element of a axion supermultiplet containing also a spin-1/2 R-parity odd axino ã and a spin-0 R-parity even saxion field s. The dark matter then consists of a combination of both axions and higgsino-like WIMPs. In Section 4, we present calculations of the expected abundance of axions and WIMPs in RNS SUSY. We display the range in PQ breaking scale fa which is accessible to axion search experiments like ADMX [63–65]. In Section 5, we examine updated prospects for WIMP detection in RNS. While higgsinos may comprise as little as 5%–10% of the total dark matter abundance, they should nonetheless be detectable by ton-scale WIMP direct detection experiments owing to their large couplings to the Higgs boson h. Indirect WIMP detection seems less propitious since the detection rate is proportional to the square of the reduced WIMP abundance. We conclude in Section 6.
2. Measuring Naturalness in SUSY Theories
Any serious discussion of naturalness requires the definition of some measure. However, first, an important point to be made is that any quantity can look fine-tuned if one splits it into dependent pieces. By re-writing an observable as and allowing b to be large, the quantity might look fine-tuned. In this trivial example, however, combining dependent contributions into independent units (b − b = 0) obviously erases the presumed source of fine-tuning. To avoid such pitfalls, a simple fine-tuning rule has been proposed [66]:
When evaluating fine-tuning, it is not permissible to claim fine-tuning of dependent quantities one against another.
2.1. Simple Electroweak Fine-Tuning
The simplest relation between the weak scale and the soft SUSY breaking parameters comes from minimizing the scalar potential of the MSSM to determine the vacuum expectation values (VEVs) [8]. The first minimization condition allows one to trade the bilinear soft term B for the more convenient ratio of VEVs tan β ≡ vu/vd. The second condition is given by
The quantity ΔEW measures this implausibility by comparing the largest contribution on the right-hand-side of Equation (2) to the value of . If they are comparable, then no unnatural fine-tunings are required to generate mZ = 91.2 GeV.
The main requirements for EW naturalness can then be read off from Equation (2). They are the following:
|µ| ∼ 100–200 GeV (the closer to mZ the better) [71–73]. We note here that the lower bound on µ ≳ 100 GeV comes from accommodating LEP2 limits from chargino pair production searches. A low value of ΔEW yields an upper bound on |µ| depending on how much fine-tuning one is willing to tolerate. A value ΔEW < 10 for fine-tuning implies |µ| < 200 GeV.
The value of is driven radiatively to small, and not large, negative values [56,57]. In the mSUGRA/CMSSM model, this occurs in the hyperbolic branch/focus point (HB/FP) region [74–76]. However, the rather large value of mh requires a large trilinear A0 parameter. Such a large trilinear pushes the HB/FP out to typically m0 ∼ 10–30 TeV [77]. At such high m0, then the top squark contributions become large and again one is fine-tuned. Alternatively, in models where the Higgs soft terms are non-universal, such as in the two-extra parameter non-universal Higgs model NUHM2 [58], it is possible to have small µ for any m0 value by simply raising the GUT scale value of (GUT) ∼ (1.3 − 2)m0.
The top squark contributions to the radiative corrections can become large for stops in the multi-TeV region. However, the radiative corrections are minimized for highly mixed (large A0) top squarks [56]. This latter condition also lifts the Higgs mass to mh ∼ 125 GeV.
The measure ΔEW is pre-programmed in the Isajet SUSY spectrum generator called Isasugra [67,78,79].
One advantage of ΔEW is that—within the context of the MSSM—it is (as discussed in Reference [57]) 1. model-independent: if a weak scale spectrum is generated within the pMSSM or via some high scale constrained model, one obtains exactly the same value of naturalness. Other virtues of ΔEW are that it is: 2. the most conservative of the proposed measures, 3. in principle measurable, 4. unambiguous, 5. predictive, 6. falsifiable and 7. simple to calculate.
The principle criticism of ΔEW is that—since it involves only weak scale parameters—it may not display the sensitivity of the weak scale to variations in high scale parameters. Below we discuss two competing measures, ΔHS and ΔBG. Typically, these latter two measures are implemented in violation of the fine-tuning rule. If implemented in accord with the fine-tuning rule, then both essentially reduce to ΔEW. In this case, ΔEW portrays the entirety of electroweak naturalness even including high scale physics.
2.1.1. Large-Log Measure ΔHS
The Higgs mass fine-tuning measure, ΔHS, compares the radiative correction of the soft term, , to the physical Higgs mass :
If we assume the MSSM is valid up to some high energy scale Λ (which may be as high as mGUT or even MP), then the value of can be found by integrating the renormalization group equation (RGE):
Here, we take as usual . By requiring [80–84]
Two problems occur within this approach.
and are not independent: the value of feeds directly into evaluation of via the Xt term: the larger the value of , then the larger is the canceling correction [86]. It also feeds indirectly into by contributing to the evolution of the and terms. Thus, the ΔHS measure as constructed fails the fine-tuning rule [66].
In the SM, the SU(2)L×U(1)Y gauge symmetry can be broken at tree level. However, in the case of SUGRA gauge theories, where SUSY is broken in a hidden sector via the superHiggs mechanism, Thus, for SUGRA models, electroweak symmetry is not even broken until one includes radiative corrections. For SUSY models valid up to some high scale , the large log in Equation (6) is exactly what is required to break EW symmetry in the first place, radiatively driving to negative values [19–26].
A simple fix for ΔHS is to combine the dependent terms into a single quantity. Under such a regrouping [56,57],
2.2. The EENZ/BG Measure
The traditional measure, ΔBG, was proposed by Ellis, Enquist, Nanopoulos and Zwirner [87] and later investigated more thoroughly by Barbieri and Giudice [88]. The proposal is that the variation in with respect to high scale parameter variation be small:
To evaluate ΔBG, we first express m2Z in terms of weak scale SUSY parameters as in Equation (2):
The place where the application of ΔBG can go wrong is in the identification of the fundamental parameter set pi. Usually, the set pi is taken to be the various soft terms of particular effective theories such as the MSSM, mSUGRA, NUHM2, etc. which arise from integrating out the hidden sector of the underlying SUGRA theory. In these effective theories, variation of the soft SUSY breaking parameters allows for a wide range of possibilities for the (unknown) hidden sector and the dynamics of SUSY breaking. However, recall that in SUGRA gage theories with SUSY broken in a hidden sector, all soft parameters are actually computed as multiples of the gravitino mass m3/2. This means that for any given hidden sector, the soft terms are all correlated: if one increases the value of m3/2, then all soft terms increase in magnitude accordingly: i.e., in SUGRA they are not independent. Combining the contributions of the dependent high-scale soft terms to , we arrive at the simple high scale relation
Now, to allow for no large unnatural cancellations in Equation (11), we require (same as ΔEW) and also . This latter condition can be fulfilled if (which now seems highly unlikely in light of LHC8 sparticle search limits and the value of mh) or if m3/2 is large but a is small. Since the µ term hardly evolves between mGUT and mweak, we may equate . Since , then also : i.e., can start off large with magnitude of order m3/2 at mGUT, but can be driven radiatively to small values . This is the case of radiatively-driven naturalness.
3. Naturalness in QCD: The Need for Axions
If we insist on naturalness in the electroweak sector, then it is only fair to insist as well on naturalness in the QCD sector. In the early days of QCD, it was a mystery why the two-light-quark chiral symmetry U(2)L × U(2)R gave rise to three and not four light pions [91]. The mystery was resolved by ’t Hooft’s discovery of the QCD theta vacuum which didn’t respect the U(1)A symmetry [92]. As a consequence of the theta vacuum, one expects the presence of a term
The strong CP problem is elegantly solved by Peccei, Quinn, Weinberg and Wilczek (PQWW) [93–95] via the introduction of PQ symmetry and the concomitant (invisible [96–99]) axion: the offending term can dynamically settle to zero. The axion is a valid dark matter candidate in its own right [100–105].
Introducing the axion in a SUSY context solves the strong CP problem and renders naturalness to QCD. As a bonus, in the context of the SUSY DFSZ axion model [98] where the Higgs superfields carry PQ charge, one gains an elegant solution to the SUSY µ problem. The most parsimonius implementation of the strong CP solution involves introducing a single MSSM singlet superfield S carrying PQ charge QPQ = −1 while the Higgs fields both carry QPQ = +1. The usual µ term is forbidden, but we have a superpotential [106–108]
If PQ symmetry is broken and S receives a VEV , then a weak scale µ term
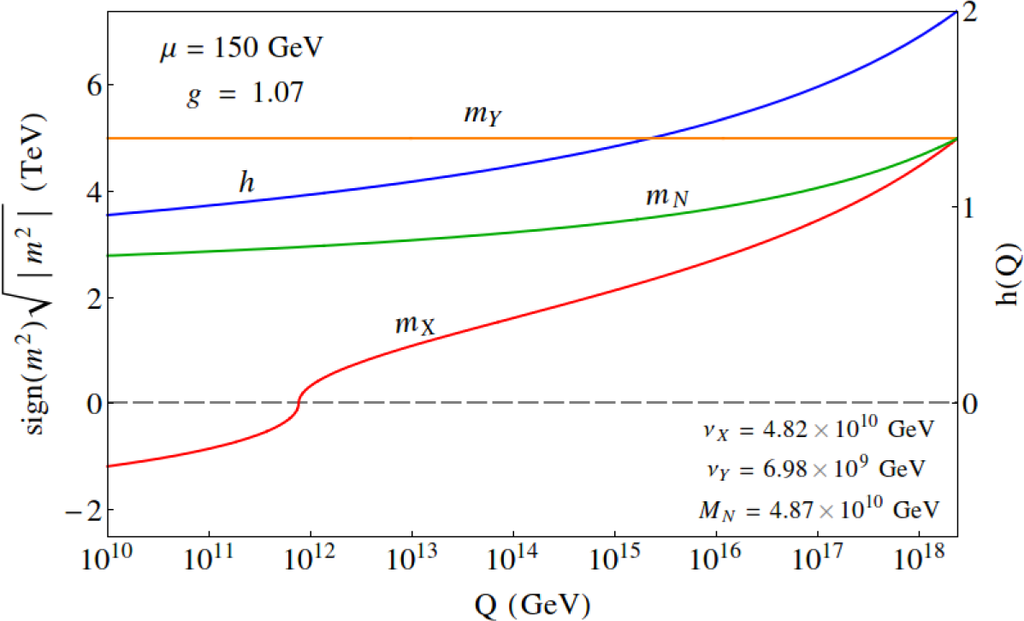
An elegant model which exhibits this behavior was proposed by Murayama, Suzuki and Yanagida (MSY) [109–111]. In the MSY model, PQ symmetry is broken radiatively by driving one of the PQ scalars X to negative mass-squared values in much the same way that electroweak symmetry is broken by radiative corrections driving negative. Starting with multi-TeV scalar masses, the radiatively-broken PQ symmetry induces a SUSY µ term ~100 GeV [112] while at the same time generating intermediate scale Majorana masses for right-hand neutrinos: see Figure 2. Although we get different solutions for the PQ scale by setting m3/2 to different masses at Planck scale, the PQ scalar X is driven to negative mass-squared values without m3/2 dependence at the same Q value. However, the coupling h shifts the position of the Q value where becomes negative; increasing h shifts the point to higher energy scales. In models such as MSY, the Little Hierarchy is no problem at all but is instead just a reflection of the mis-match between PQ and hidden sector mass scales.
4. Relic Abundance of Axions and WIMPs with Implications for Axion Detection
It is straightforward to calculate the thermal abundance of WIMPs in natural SUSY. To a good approximation, it is given by
Naively, one might expect natural SUSY to be ruled out as being incapable of generating a sufficiently large relic density of WIMPs. However, naturalness in both EW and QCD sectors implies the presence of two dark matter particles: the WIMP and the axion. Axions are expected to be produced dominantly via the non-thermal Bosonic Coherent Motion (BCM) [100,115] yielding
However, as mentioned previously, the axion superfield also contains a spin-1/2 axino ã and a spin-0 saxion s. In SUGRA, one expects ms ~ m3/2 while the axino mass is more model-dependent but generally one expects also mã ~ m3/2 [122–125]. The DFSZ axinos can be produced thermally in the early universe at a rate and largely independent of the re-heat temperature TR [126] (in the SUSY KSVZ model, then axino thermal production is proportional to TR). Once axinos are produced, they undergo (late) decays to sparticle plus particle thereby injecting additional WIMPs into the thermal plasma. If enough WIMPs are produced at the axino decay temeprature, they undergo a process of re-annihilation which still yields an enhanced WIMP abundance [127,128], but not as much as one-to-one with the population of thermally produced axinos. Of equal importance to WIMP production from axino decays is the axino decay temperature: if axinos decay before WIMP freeze-out, then the injected WIMPs thermalize and one regains the usual thermal WIMP abundance. If axinos decay after WIMP freeze-out, then they always augment the WIMP abundance.
Saxions can also be produced thermally at rates comparable to axino thermal production. In addition, saxions can be produced via BCM which is especially important at large fa. Since saxions are R-parity even, they can decay to pairs of SM particles, thereby injecting extra entropy into the plasma, or they can decay to pairs of SUSY particles, thus also augmenting the WIMP abundance (depending again on the saxion decay temperature). Depending on a combination of PQ charge assignments and VEVs parametrized by ξs, the saxions may also decay to ãã (if kinematically allowed) thus adding to the WIMP abundance, or they may decay to aa thus injecting additional dark radiation into the thermal plasma. Strong limits on dark radiation—parametrized by the effective number of additional neutrinos present in the universe ΔNeff—have been obtained, with a combination of Planck and other data sets finding Neff = 3.15 ± 0.23 [129] (whereas the SM predicts Neff = 3.046). Thus, too much dark radiation from saxion decay can lead to conflict with measured cosmological parameters. In our numerical study, we consider a conservative constraint ΔNeff < 1 (see Figure 4) at over 3σ with the joint Planck TT+lowP+BAO result [129]. In addition, if saxions or axinos of sufficient initial abundance decay after the onset of BBN, then they can destroy the successful predictions of light element abundances via BBN, and again the model can be excluded.
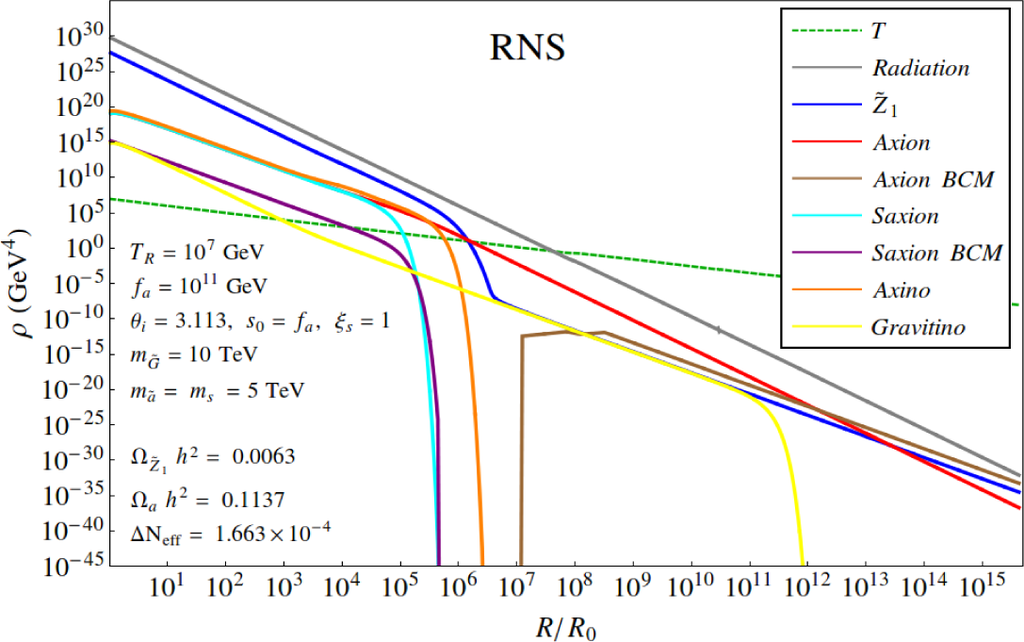
The calculation of the mixed axion-neutralino relic abundance can be calculated via semi-analytic techniques [130,131] or more reliably [132] via the simultaneous solution of eight coupled Boltzmann equations describing the energy densities of 1. radiation, 2. thermally- and decay-produced WIMPs, 3. BCM-produced axion, 4. BCM produced saxions (followed by saxion decay), thermal production and decay of 5. axino, 6. saxions and 7. thermal and decay-induced production of axions and 8. thermal production and decay of gravitinos.
We scan over the following PQ parameters:
The result of these calculations were shown in Reference [132] and in Figure 5 where the energy densities are tracked as a function of scale factor R from the end of inflation with T = TR to the era of entropy conservation.
In Figure 6, we show the calculated relic abundance of both WIMPs (blue and red points) and axions (purple points) as a function of fa for a RNS benchmark SUSY model with m0 = 5000 GeV, m1/2 = 700 GeV, A0 = −8300 GeV, tan β = 10, µ = 110 GeV and mA = 1000 GeV. We first take ξs = 0 so saxion decays to aa and ãã are turned off.
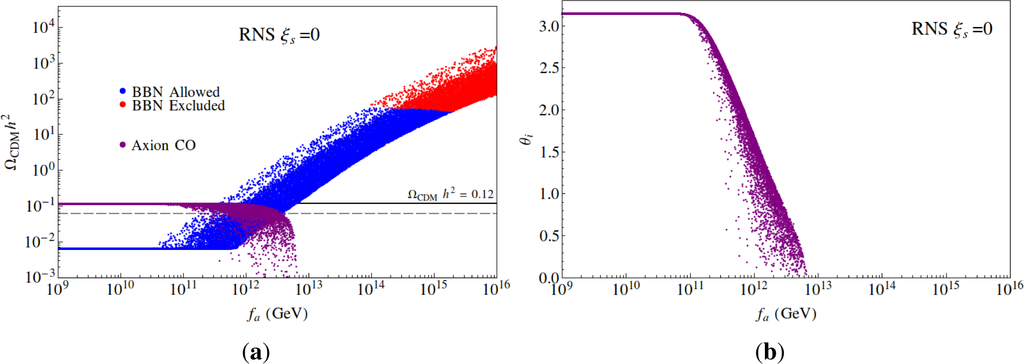
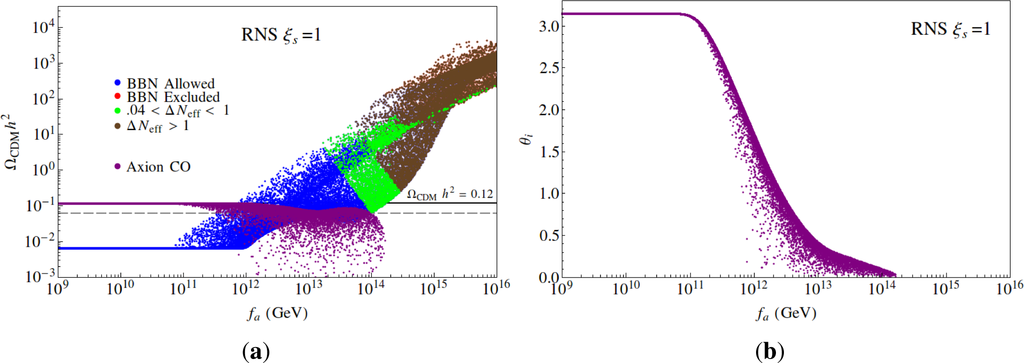
At very low fa, axinos are thermally-produced at a large rate but also decay well before neutralino freeze-out so that the WIMP abundance is still given by its expected thermally-produced value. As fa increases, ultimately axinos begin decaying after freeze-out thus augmenting the WIMP abundance. For fa > 1013 GeV, too many WIMPs are produced and the model parameters are excluded. For very large fa ~ 1015 GeV, all points are doubly excluded by producing too much dark matter and violating limits from BBN [133]. We also show the axion abundance. At very low fa, the CDM is axion-dominated [130] although this requires very high values of θi ~ π (see Figure 6b). which might be considered fine-tuned. For fa ~ 1012 GeV, axions can still dominate the CDM abundance but with θi ~ 1. For these values of fa, the CDM could also easily be WIMP dominated as well.
In Figure 4, we show the neutralino and axion relic abundance for the RNS benchmark with ξs = 1 (saxion decays to axions and axino pairs are turned on). In this case, the additional decay modes allow the saxion to be shorter lived for a given value of ms and fa compared to the ξs = 0 case. As a consequence, there is a greater range of fa where CDM can be axion-dominated. Ultimately, axinos and saxions decay after freeze-out and the WIMP abundance is enhanced at higher fa ~ 1011–1014 GeV. For fa ≳ 1014 GeV, WIMPs are overproduced. Points at very high fa for ξs = 1 can be triply excluded by producing too many WIMPs and by violating both dark radiation and BBN constraints.
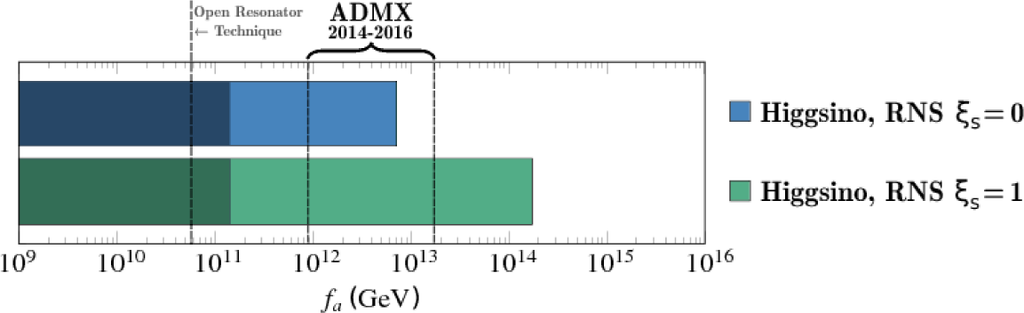
We summarize the results of this section in Figure 7. We display the range of fa where valid solutions for the relic abundance of mixed axion-higgsino CDM can be found for the RNS benchmark model. The upper bar shows the range of fa for ξs = 0 while the lower bar shows the range for ξs = 1. The darker shaded parts of the bars denote θi values > 3 which might be considered less plausible or fine-tuned. We also show by the bracket the range of fa, assuming the bulk of DM is axion, which is expected to be probed by the ADMX experiment within the next several years [134]. This region probes the most natural region where θi ∼ 1. We also show a further region of lower fa which might be explored by a new open resonator technology [135]. About a decade of natural fa ∼ 1014 GeV seems able to elude ADMX searches for the ξs = 1 case.
4.1. Results for Variable µ
We may convert the RNS benchmark point into a model line by allowing for variable µ. In this case, we have variable higgsino mass with the lower bound given by the LEP2 limit while the upper bound is determined by how much fine-tuning one is willing to tolerate with
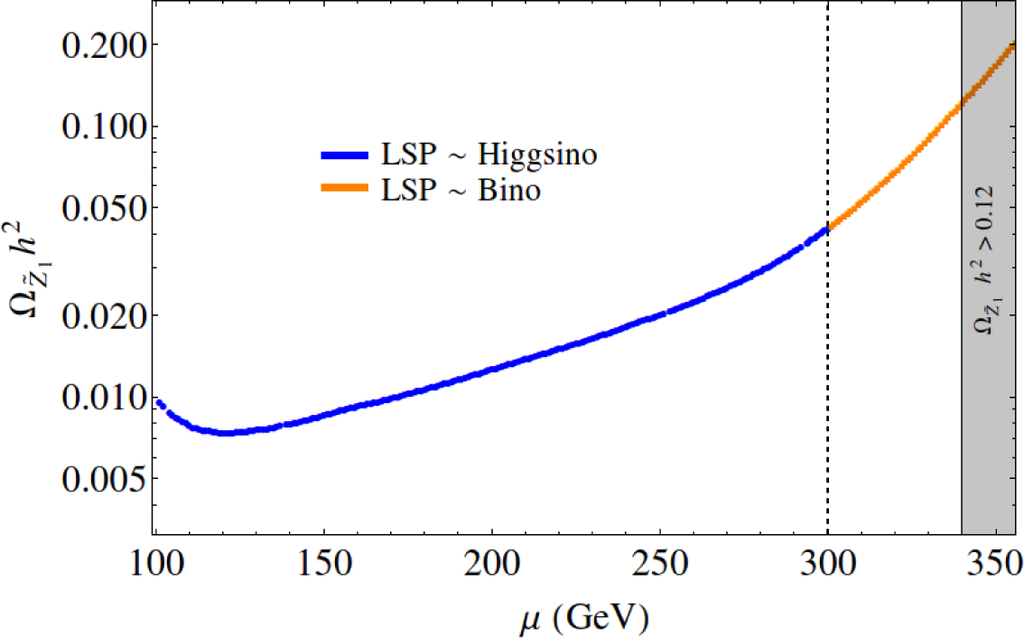
In Figure 8, we show the thermally-produced relic density of neutralinos along the variable µ RNS model line. Here, for low µ but increases as µ increases since the becomes increasingly bino-like. At µ ~ 300 GeV, the becomes more bino-like than higgsino-like, and at µ ∼ 340 GeV, naively too much neutralino dark matter is produced. As we have seen, it is easy to increase the neutralino abundance from its thermal expectation by allowing for axino and saxion production with decay taking place after neutralino freeze-out. It is much harder to reduce the neutralino abundance from its thermal value: the three most common ways include 1. entropy dilution from saxion decay to SM particles only at very high fa ∼ 1015 GeV, 2. allowing for R-parity violation (in which case one must somehow stabilize the proton) or 3. allowing for a lighter LSP than the neutralino (e.g., a light axino or gravitino into which the neutralino may decay).
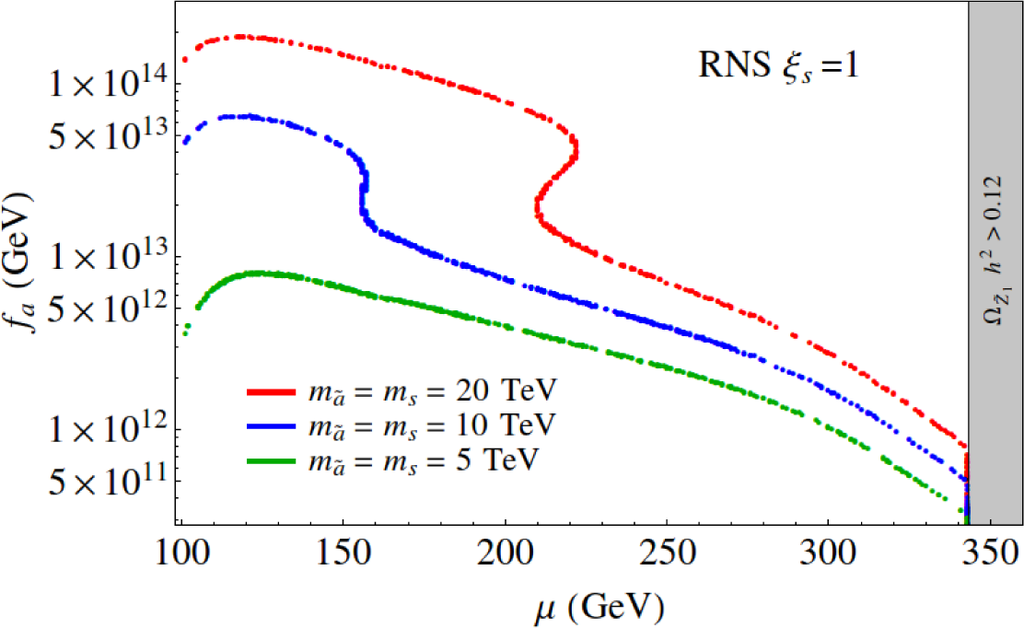
In Figure 9, we plot the contours of allowed regions (allowed below the contours) in the fa vs. µ plane by varying µ along the RNS model line for the ξs = 1 case. We show the boundaries for three different assumptions on the axino/saxion masses: , 10 and 20 TeV. The lower bound is always fa ≳ 109 GeV from supernovae/red giant astrophysical cooling limits [136] (although the lower range requires some tuning on θi ∼ π). For our canonical case where we expect , fa can range up to 1013 GeV beyond which too much neutralino mass density is produced. As µ increases, the upper bound tends to decrease because the neutralino thermal abundance is increasing and there is less “room” for additional neutralino production from axino/saxion decay. As increase, the upper bound on fa increases. This is because as become more massive, their widths increase and their lifetimes decrease: for a given fa value, they are more likely to decay at earlier times and so re-annihilation from decay-produced neutralinos occurs at higher axino/saxion decay temperature (and the re-annihilation yield is inversely proportional to decay temperature [127]). For the ξs = 0 case, we have more constrained upper fa boundaries since saxion decays into axions and axinos are turned off and hence the saxion is longer lived.
5. Direct and Indirect Detection of WIMPs
In this Section, we update our previous projections [137,138] for direct and indirect detection of higgsino-like WIMPs from radiatively-driven natural SUSY. Our current results contain several improvements:
Our previous scan over NUHM2 parameter space was restricted to a range of mA: 0.15–1.5 TeV. However, low ΔEW solutions can be found for much higher mA values [139] and so here we expand the mA range to as far as 20 TeV so that the bounds on our scanned parameter space is dictated by the value of ΔEW rather than an arbitrary parameter cutoff.
We have updated the nucleon mass fraction parameters which enter the quark and gluon matrix elements in IsaReS [140] to values given in Table 1 of Reference [141]. These mainly lessen the contribution from strange quarks from older estimates of the spin-dependent scattering cross section. In our case, the computed values of decrease by typically a factor of two.
We have increased our sampling statistics in NUHM2 parameter space.
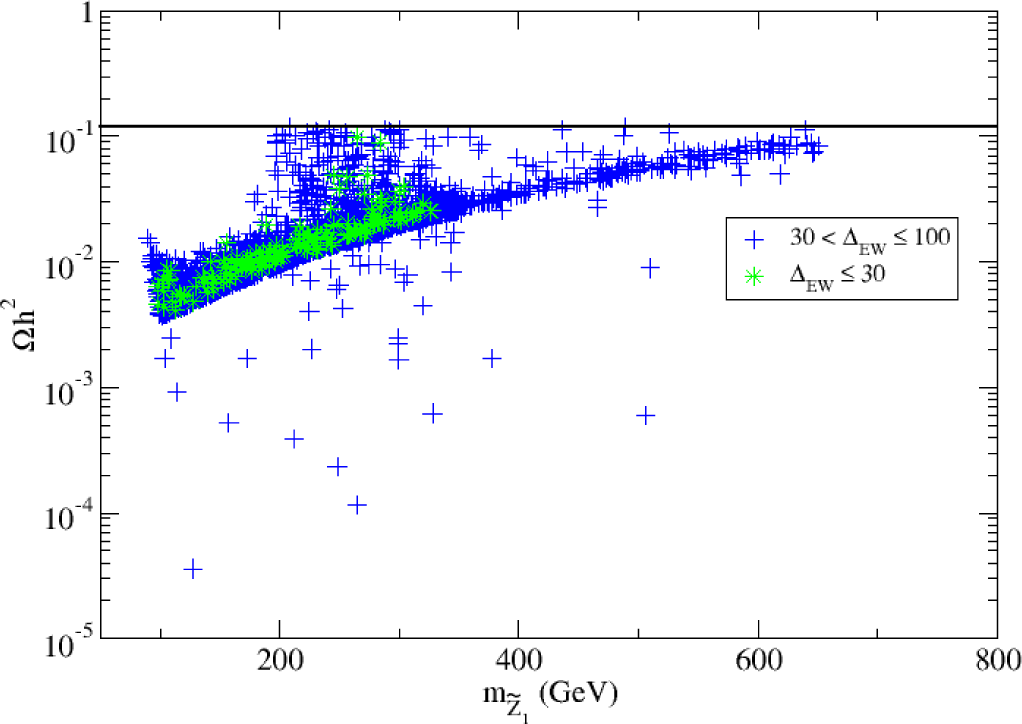
In Figure 10, we show the spin-independent neutralino-proton scattering rate in cm2 as calculated using the updated IsaReS [140]. The result is rescaled by a factor to account for the fact that the local relic abundance might be less than the usually assumed value ρlocal ≃ 0.3 GeV/cm3, as suggested long ago by Bottino et al. [142] (the remainder would be composed of axions). Green stars denote points with ΔEW < 30 while blue crosses denote points with 30 < ΔEW < 100.
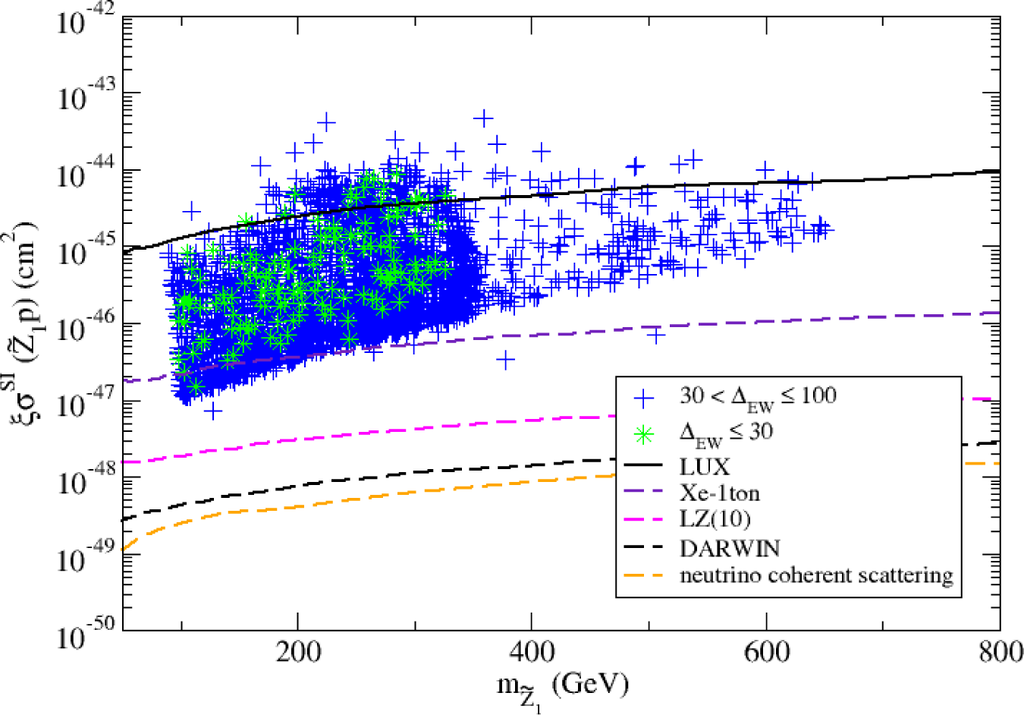
The higgsino-like WIMP in our case scatters from quarks and gluons mainly via h exchange. The coupling involves a product of both higgsino and gaugino components. In the case of RNS models, the is mainly higgsino-like, but since m1/2 is bounded from above by naturalness, the contains enough gaugino component that the coupling is never small: in the notation of Reference [8]
From Figure 10, we see that the current reach from the LUX experiment (solid contour) has begun sampling the upper limits of predicted values. The projected reach of Xe-1-ton, a ton scale liquid Xenon detector, is also shown. It is seen to cover nearly all the predicted parameter space points. We also show the projected reach of LZ(10), an upgrade to LUX. The projected LZ reach is seen to cover the entire set of points generated. Thus, the projected ton scale noble liquid detectors (or other comparable WIMP detectors) can make a complete exploration of the RNS parameter space. Since deployment of these ton-scale detectors is ongoing, it seems that direct WIMP search experiments may either verify or exclude RNS models in the near future. These searches should either verify or rule out a very essential aspect of natural SUSY models.
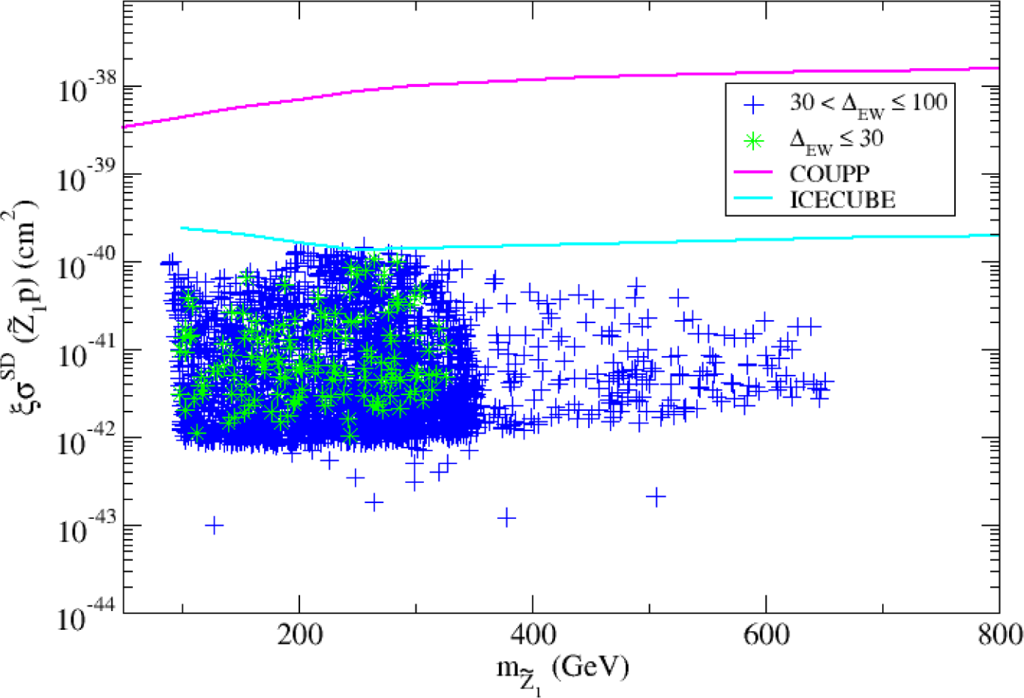
In Figure 11, we show the rescaled spin-dependent neutralino-proton scattering cross section . Here we show recent limits from the COUPP [143] detector. Current limits are still about an order of magnitude away from reaching the predicted rates from RNS models. We also show limits from the IceCube experiment. IceCube searches for high energy neutrinos which could be produced from WIMP annihilations in the solar core. The IceCube expected rates depend on the Sun’s ability to capture WIMPs which in turn depends on a product of spin-dependent neutralino-proton scattering cross section times the local WIMP abundance. (In a previous work [137], it was mistakenly suggested that the IceCube detection rate was independent of local abundance due to equilibration between solar capture rate and WIMP annihilation rate.) The IceCube limits have barely entered the RNS parameter space and excluded just the largest values of .
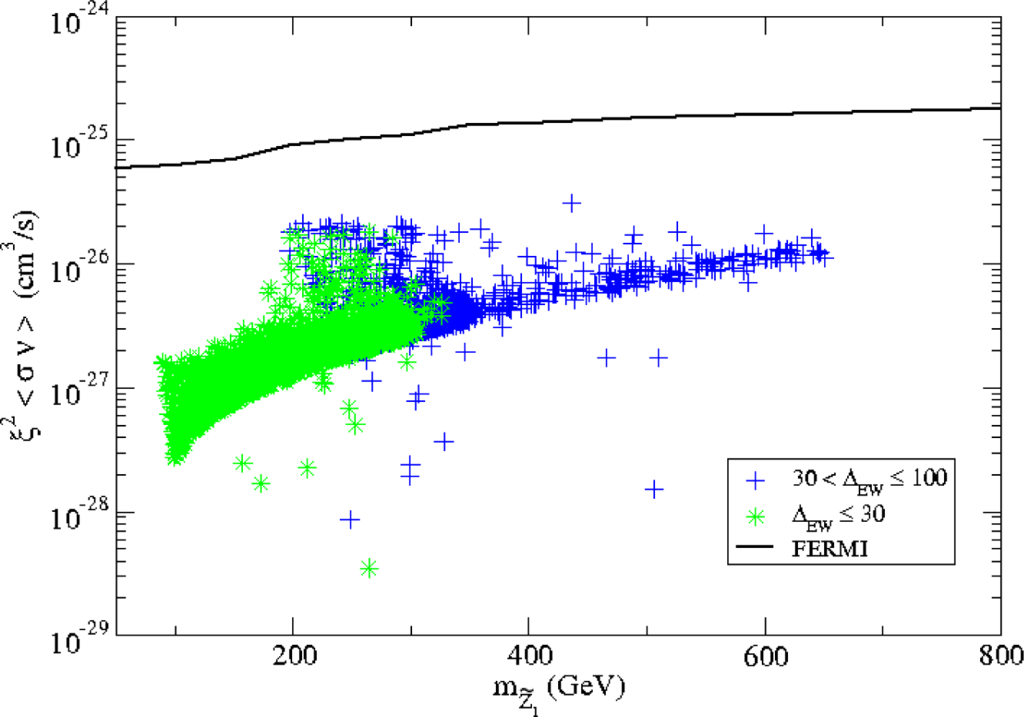
In Figure 12, we show the rescaled thermally-averaged neutralino annihilation cross section times relative velocity in the limit as v → 0: ξ2⟨σv⟩|v→0. This quantity enters into the rate expected from WIMP halo annihilations into γ, e+, or . The rescaling appears as ξ2 since limits depend on the square of the local WIMP abundance [144]. Anomalies in the positron and γ spectra have been reported, although the former may be attributed to pulsars [145,146], while the latter 130 GeV gamma line may be instrumental. On the plot, we show the limit derived from the Fermi LAT gamma ray observatory [147,148] for WIMP annihilations into WW. These limits have not yet reached the RNS parameter space due in part to suppression from the squared rescaling factor.
6. Conclusions
We have found in this paper, and in previous works, that if one insists on naturalness—in both the electroweak and the QCD sectors—then the simple picture of SUSY WIMP dark matter changes radically. Naturalness in the electroweak sector implies a low value of the superpotential µ parameter: the closer to mZ the better. In models with gaugino mass unification, as favored in simple GUTs, this implies the LSP is a higgsino-like neutralino with a predicted thermal abundance a factor of 10–15 below the measured dark matter density. This seeming disaster is in fact an attribute if one also insists on naturalness in the QCD sector, i.e., solving the strong CP problem. In this case, the most compelling solution invokes a PQ symmetry with its concommitant axion. In this situation, the axion makes up the remaining abundance, and in fact over most of parameter space the axion is the dominant CDM component while WIMPs are subdominant.
Invoking the axion in a SUSY context brings along both the axino and the saxion. The dark matter abundance calculation becomes more intertwined since axions can be produced via BCM, via thermal production and via saxion decay. WIMPs can be produced thermally but also via axino, saxion and gravitino decays. If WIMPs are produced via decays at sufficient rates, then WIMP re-annihilation occurs. Additional entropy can be produced at late times by the decays of heavy unstable states, thus diluting all relics which are present. The ensuing abundance calculation is more complicated than the simple WIMP miracle picture, but in many ways it is more elegant and compelling. Our abundance calculations here have used the SUSY DFSZ axion model which provides an elegant solution to the SUSY µ problem. We have outlined the range of fa values which are allowed in RNS, and shown the regions which ADMX and other experiments hope to probe in the near future.
With regard to WIMP detection, higgsino-like LSPs which contain significant gaugino components (as is required in natural SUSY) generally have large rates for both direct and indirect detection, at least compared to binos. However, the propitious detection rates are off-set by the fact that now the WIMPs might comprise only a small fraction of the local abundance instead of the entirety of CDM. To compensate, one must temper detection rates by the factor. For instance, direct detection via SI or SD scattering are both reduced by a factor ξ. Nonetheless, ton-scale noble liquid WIMP detectors are projected to probe the entirety of RNS parameter space: if a WIMP signal is not ultimately seen, then the RNS picture will have to be seriously modified or abandoned. Detection rates for indirect WIMP searches via halo WIMP annihilation into gammas or antimatter are suppressed by a factor of ξ2. This suppression will make detection of WIMPs in these channels more difficult, except in the cases where WIMPs still comprise the bulk of dark matter.
Acknowledgments
We thank Xerxes Tata, Azar Mustafayev, Andre Lessa, Maren Padeffke-Kirkland, Dan Mickelson, Eung Jin Chun and Peisi Huang for collaborations and discussions leading to the results presented here. The computing for this project was performed at the OU Supercomputing Center for Education & Research (OSCER) at the University of Oklahoma (OU). We thank David Cline for soliciting this manuscript and for financial assistance. This work is supported in part by the US Department of Energy Office of High Energy Physics.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Aad, G.; Abajyan, T.; Abbott, B.; Abdallah, J.; Abdel Khalek, S.; Abdelalim, A.A.; Abdinov, O.; Aben, R.; Abi, B.; Abolins, M.; et al. Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC. Phys. Lett. B. 2012, 716, 1–29. [Google Scholar]
- Chatrchyan, S.; Khachatryan, V.; Sirunyan, A.; Tumasyan, A.; Adam, W.; Aguilo, E.; Bergauer, T.; Dragicevic, M.; Ero, J.; Fabjan, C.; et al. Observation of a new boson at a mass of 125 GeV with the CMS experiment at the LHC. Phys. Lett. B 2012, 716, 30–61. [Google Scholar]
- Gaillard, M.K.; Lee, B.W. Rare Decay Modes of the K-Mesons in Gauge Theories. Phys. Rev. D 1974, 10. [Google Scholar] [CrossRef]
- Susskind, L. Dynamics of Spontaneous Symmetry Breaking in the Weinberg-Salam Theory. Phys. Rev. D 1979, 20. [Google Scholar] [CrossRef]
- Nilles, H.P. Supersymmetry, Supergravity and Particle Physics. Phys. Rept. 1984, 110, 1–162. [Google Scholar]
- Martin, S.P. A. Supersymmetry primer. Adv. Ser. Direct. High Energy Phys. 2010, 21, 1–153. [Google Scholar]
- Chung, D.J.H.; Everett, L.L.; Kane, G.L.; King, S.F.; Lykken, J.D.; Wang, L.T. The Soft supersymmetry breaking Lagrangian: Theory and applications. Phys. Rept. 2005, 407, 1–203. [Google Scholar]
- Baer, H.; Tata, X. Weak scale supersymmetry: From superfields to scattering events; Cambridge University Press: Cambridge, UK, 2006; p. 537. [Google Scholar]
- Nilles, H.P. Dynamically Broken Supergravity and the Hierarchy Problem. Phys. Lett. B 1982, 115, 193–196. [Google Scholar]
- Chamseddine, A.; Arnowitt, R.; Nath, P. Locally Supersymmetric Grand Unification. Phys. Rev. Lett. 1982, 49. [Google Scholar] [CrossRef]
- Barbieri, R.; Ferrara, S.; Savoy, C. Gauge Models with Spontaneously Broken Local Supersymmetry. Phys. Lett. 1982, B119, 343–347. [Google Scholar]
- Ohta, N. Grand Unified Theories Based On Local Supersymmetry. Prog. Theor. Phys 1983, 70, 542–549. [Google Scholar]
- Hall, L.; Lykken, J.; Weinberg, S. Supergravity as the Messenger of Supersymmetry Breaking. Phys. Rev. D 1983, 27. [Google Scholar] [CrossRef]
- Soni, S.K.; Weldon, H.A. Analysis of the Supersymmetry Breaking Induced by N = 1 Supergravity Theories. Phys. Lett. B 1983, 126, 215–219. [Google Scholar]
- Kaplunovsky, V.S.; Louis, J. Model independent analysis of soft terms in effective supergravity and in string theory. Phys. Lett. B 1993, 306, 269–275. [Google Scholar]
- Brignole, A.; Ibanez, L.E.; Munoz, C. Towards a theory of soft terms for the supersymmetric Standard Model. Nucl. Phys. B 1994, 422, 125–171, [Erratum-ibid, B. 1995, 436, 747]. [Google Scholar]
- Brignole, A.; Ibanez, L.E.; Munoz, C. Soft supersymmetry breaking terms from supergravity and superstring models. 1997, arXiv:hep-ph/9707209. arXiv.org e-Print archive, Available online: http://arxiv.org/abs/hep-ph/9707209 accessed on 27 May 2015.
- Amaldi, U.; de Boer, W.; Furstenau, H. Comparison of grand unified theories with electroweak and strong coupling constants measured at LEP. Phys. Lett. B 1991, 260, 447–455. [Google Scholar]
- Ibañez, L.E.; Ross, G.G. SU(2)L × U(1) Symmetry Breaking as a Radiative Effect of Supersymmetry Breaking in Guts. Phys. Lett. B 1982, 110, 215–220. [Google Scholar]
- Inoue, K.; Kakuto, A.; Komatsu, H.; Takeshita, S. Aspects of Grand Unified Models with Softly Broken Supersymmetry. Prog. Theor. Phys 1982, 68, 927–946. [Google Scholar]
- Nilles, H.P.; Srednicki, M.; Wyler, D. Weak Interaction Breakdown Induced by Supergravity. Phys. Lett. B 1983, 120, 346–348. [Google Scholar]
- Ibañez, L. Locally Supersymmetric SU(5) Grand Unification. Phys. Lett. B 1982, 118, 73–78. [Google Scholar]
- Ellis, J.; Hagelin, J.; Nanopoulos, D.; Tamvakis, M. Weak Symmetry Breaking by Radiative Corrections in Broken Supergravity. Phys. Lett. B 1983, 125, 275–281. [Google Scholar]
- Alvarez-Gaumé, L.; Polchinski, J.; Wise, M. Minimal Low-Energy Supergravity. Nucl. Phys. B 1983, 221, 495–523. [Google Scholar]
- Ovrut, B.A.; Raby, S. The Locally Supersymmetric Geometrical Hierarchy Model. Phys. Lett. B 1983, 130, 277–284. [Google Scholar]
- Ibanez, L.E.; Ross, G.G. Supersymmetric Higgs and radiative electroweak breaking. Comptes Rendus Phys 2007, 8, 1013–1028. [Google Scholar]
- Carena, M.S.; Haber, H.E. Higgs boson theory and phenomenology. Prog. Part. Nucl. Phys 2003, 50, 63–152. [Google Scholar]
- Bertone, G.; Silk, J.; Moore, B.; Diemand, J.; Bullock, J.; Kaplinghat, M.; Strigari, L.; Mellier, Y.; et al. Particle Dark Matter: Observations, Models and Searches; Cambridge University Press: Cambridge, UK, 2010; p. 738. [Google Scholar]
- Dine, M.; Kusenko, A. The Origin of the matter-antimatter asymmetry. Rev. Mod. Phys 2003, 76. [Google Scholar] [CrossRef]
- Shifman, M. Frontiers Beyond the Standard Model: Reflections and Impressionistic Portrait of the conferernce. Mod. Phys. Lett. A 2012, 27. [Google Scholar] [CrossRef]
- Barbieri, R. Electroweak theory after the first Large Hadron Collider phase. Phys. Scr. T 2013, 158. [Google Scholar] [CrossRef]
- Giudice, G.F. Naturalness after LHC 8. 2013, arXiv:1307.7879. arXiv.org e-Print archive. Available online: http://arxiv.org/abs/1307.7879 accessed on 27 May 2015.
- Altarelli, G. The Higgs: So simple yet so unnatural. Phys. Scr 2014. [Google Scholar] [CrossRef]
- Craig, N. The State of Supersymmetry after Run I of the LHC. 2013, arXiv:1309.0528. arXiv.org e-Print archive, Available online: http://arxiv.org/abs/1309.0528 accessed on 27 May 2015.
- Murayama, H. Future Experimental Programs. Phys. Scr 2013, 158. [Google Scholar] [CrossRef]
- Ross, G.G. SUSY: Quo Vadis? Eur. Phys. J. C 2014, 2014, 99–119. [Google Scholar]
- Lykken, J.; Spiropulu, M. Supersymmetry and the Crisis in Physics. Sci. Am 2014, 310, 34–39. [Google Scholar]
- Dine, M. Naturalness Under Stress. 2015, arXiv:1501.01035. arXiv.org e-Print archive. Available online: http://arxiv.org/abs/1501.01035 accessed on 27 May 2015.
- Witten, E. Dynamical Breaking of Supersymmetry. Nucl. Phys. B 1981, 188, 513–554. [Google Scholar]
- Kaul, R.K. Gauge Hierarchy in a Supersymmetric Model. Phys. Lett. B 1982, 109, 19–24. [Google Scholar]
- Barbieri, R.; Strumia, A. About the fine tuning price of LEP. Phys. Lett. B 1998, 433, 63–66. [Google Scholar]
- Birkedal, A.; Chacko, Z.; Gaillard, M.K. Little supersymmetry and the supersymmetric little hierarchy problem. J. High Energy Phys 2004, 0410. [Google Scholar] [CrossRef]
- Dermisek, R.; Gunion, J.F. Escaping the large fine tuning and little hierarchy problems in the next to minimal supersymmetric model and h → aa decays. Phys. Rev. Lett 2005, 95, 041801. [Google Scholar] [CrossRef]
- Choi, K.; Jeong, K.S.; Kobayashi, T.; Okumura, K.I. Little SUSY hierarchy in mixed modulus-anomaly mediation. Phys. Lett. B 2006, 633, 355–361. [Google Scholar]
- Kim, S.-G.; Maekawa, N.; Matsuzaki, A.; Sakurai, K.; Sanda, A.I.; Yoshikawa, T. A. Solution for little hierarchy problem and b → sγ. Phys. Rev. D 2006, 74, 115016. [Google Scholar] [CrossRef]
- Choi, K.; Jeong, K.S.; Kobayashi, T.; Okumura, K.I. TeV Scale Mirage Mediation and Natural Little SUSY Hierarchy. Phys. Rev. D 2007, 75, 095012. [Google Scholar] [CrossRef]
- Dutta, B.; Mimura, Y. Landscape of Little Hierarchy. Phys. Lett. B 2007, 648, 357–364. [Google Scholar]
- Dutta, B.; Mimura, Y.; Nanopoulos, D.V. No-Scale Solution to Little Hierarchy. Phys. Lett. B 2007, 656, 199–206. [Google Scholar]
- Babu, K.S.; Gogoladze, I.; Rehman, M.U.; Shafi, Q. Higgs Boson, Mass Sparticle Spectrum and Little Hierarchy Problem in Extended MSSM. Phys. Rev. D 2008, 78, 055017. [Google Scholar] [CrossRef]
- Bellazzini, B.; Csaki, C.; Delgado, A.; Weiler, A. SUSY without the Little Hierarchy. Phys. Rev. D 2009, 79, 095003. [Google Scholar] [CrossRef]
- Delgado, A.; Kolda, C.; Olson, J.P.; de la Puente, A. Solving the Little Hierarchy Problem with a Singlet and Explicit µ Terms. Phys. Rev. Lett 105, 091802. [CrossRef]
- Gherghetta, T.; von Harling, B.; Setzer, N. A natural little hierarchy for RS from accidental SUSY. J. High Energy Phys 2011, 7, 1–35. [Google Scholar]
- Feldman, D.; Kane, G.; Kuflik, E.; Lu, R. A new (string motivated) approach to the little hierarchy problem. Phys. Lett. B 2011, 704, 56–61. [Google Scholar]
- Younkin, J.E.; Martin, S.P. Non-universal gaugino masses, the supersymmetric little hierarchy problem, and dark matter. Phys. Rev. D 2012, 85, 055028. [Google Scholar] [CrossRef]
- Baer, H.; Barger, V.; Mustafayev, A. Implications of a 125 GeV Higgs scalar for LHC SUSY and neutralino dark matter searches. Phys. Rev. D 2012, 85, 075010. [Google Scholar] [CrossRef]
- Baer, H.; Barger, V.; Huang, P.; Mustafayev, A.; Tata, X. Radiative natural SUSY with a 125 GeV Higgs boson. Phys. Rev. Lett 2012, 109, 161802. [Google Scholar] [CrossRef]
- Baer, H.; Barger, V.; Huang, P.; Mickelson, D.; Mustafayev, A.; Tata, X. Radiative natural supersymmetry: Reconciling electroweak fine-tuning and the Higgs boson mass. Phys. Rev. D 2013, 87, 115028. [Google Scholar] [CrossRef]
- Matalliotakis, D.; Nilles, H.P. Implications of nonuniversality of soft terms in supersymmetric grand unified theories. Nucl. Phys. B 1995, 435, 115–128. [Google Scholar]
- Nath, P.; Arnowitt, R.L. Nonuniversal soft SUSY breaking and dark matter. 1998, arXiv:hep-ph/9801259. arXiv.org e-Print archive. Available online: http://arxiv.org/abs/hep-ph/9801259 accessed on 27 May 2015.
- Ellis, J.; Olive, K.; Santoso, Y. The MSSM parameter space with nonuniversal Higgs masses. Phys. Lett. B 2002, 539, 107–118. [Google Scholar]
- Ellis, J.; Falk, T.; Olive, K.; Santoso, Y. Exploration of the MSSM with nonuniversal Higgs masses. Nucl. Phys. B 2003, 652, 259–347. [Google Scholar]
- Baer, H.; Mustafayev, A.; Profumo, S.; Belyaev, A.; Tata, X. Direct, indirect and collider detection of neutralino dark matter in SUSY models with non-universal Higgs masses. J. High Energy Phys 2005, 2005, 065. [Google Scholar] [CrossRef]
- Duffy, L.; Sikivie, P.; Tanner, D.B.; Asztalos, S.; Hagmann, C.; Kinion, D.; Rosenberg, L.J.; van Bibber, K.; Yu, D.; Bradley, R.F. Results of a search for cold flows of dark matter axions. Phys. Rev. Lett 2005, 95, 091304. [Google Scholar] [CrossRef]
- Duffy, L.D.; Sikivie, P.; Tanner, D.B.; Asztalos, S.J.; Hagmann, C.; Kinion, D.; Rosenberg, L.J.; van Bibber, K.; Yu, D.B.; Bradley, R.F. A high resolution search for dark-matter axions. Phys. Rev. D 2006, 74, 012006. [Google Scholar] [CrossRef]
- Asztalos, S.J.; Rosenberg, L.; van Bibber, K.; Sikivie, P.; Zioutas, K. Searches for astrophysical and cosmological axions. Ann. Rev. Nucl. Part. Sci 2006, 56, 293–326. [Google Scholar]
- Baer, H.; Barger, V.; Mickelson, D.; Padeffke-Kirkland, M. SUSY models under siege: LHC constraints and electroweak fine-tuning. Phys. Rev. D 2014, 89, 115019. [Google Scholar] [CrossRef]
- Baer, H.; Paige, F.; Protopopescu, S.; Tata, X. ISAJET 7.69: A Monte Carlo event generator for pp, anti-p p, and e+e− reactions. 2003, arXiv:hep-ph/0312045. arXiv.org e-Print archive. Available online: http://arxiv.org/abs/hep-ph/0312045 accessed on 27 May 2015.
- Djouadi, A.; Muhlleitner, M.M.; Spira, M. Decays of supersymmetric particles: The Program SUSY-HIT (SUspect-SdecaY-Hdecay-InTerface). 2006, arXiv:hep-ph/0609292. arXiv.org e-Print archive. Available online: http://arxiv.org/abs/hep-ph/0609292 accessed on 27 May 2015.
- Allanach, B.C. SOFTSUSY: a program for calculating supersymmetric spectra. Comput. Phys. Commun 2002, 143, 305–331. [Google Scholar]
- Porod, W. SPheno, a program for calculating supersymmetric spectra, SUSY particle decays and SUSY particle production at e+e− colliders. Comput. Phys. Commun 2003, 153, 275–315. [Google Scholar]
- Chan, K.; Chattopadhyay, U.; Nath, P. Naturalness, weak scale supersymmetry and the prospect for the observation of supersymmetry at the Tevatron and at the CERN LHC. Phys. Rev. D 1998, 58, 096004. [Google Scholar] [CrossRef]
- Barbieri, R.; Pappadopulo, D. S-particles at their naturalness limits. J. High Energy Phys 2009, 2009, 061. [Google Scholar] [CrossRef]
- Baer, H.; Barger, V.; Huang, P. Hidden SUSY at the LHC: the light higgsino-world scenario and the role of a lepton collider. J. High Energy Phys 2011, 2011, 1–25. [Google Scholar]
- Feng, J.L.; Matchev, K.T.; Moroi, T. Focus points and naturalness in supersymmetry. Phys. Rev. D 2000, 61, 075005. [Google Scholar] [CrossRef]
- Feng, J.L.; Matchev, K.T.; Moroi, T. Naturalness reexamined: Implications for supersymmetry searches. 2000, arXiv:hep-ph/0003138. arXiv.org e-Print archive. Available online: http://arxiv.org/abs/hep-ph/0003138 accessed on 27 May 2015.
- Feng, J.L.; Sanford, D. A. Natural 125 GeV Higgs Boson in the MSSM from Focus Point Supersymmetry with A-Terms. Phys. Rev. D 2012, 86, 055015. [Google Scholar] [CrossRef]
- Baer, H.; Barger, V.; Huang, P.; Mickelson, D.; Mustafayev, A.; Tata, X. Post-LHC7 fine-tuning in the minimal supergravity/CMSSM model with a 125 GeV Higgs boson. Phys. Rev. D 2013, 87, 035017. [Google Scholar] [CrossRef]
- Baer, H.; Chen, C.; Munroe, R.; Paige, F.; Tata, X. Multichannel search for minimal supergravity at and e+e− colliders. Phys. Rev. D 1995, 51, 1046–1050. [Google Scholar]
- Baer, H.; Ferrandis, J.; Kraml, S.; Porod, W. On the treatment of threshold effects in SUSY spectrum computations. Phys. Rev. D 2006, 73, 015010. [Google Scholar] [CrossRef]
- Kitano, R.; Nomura, Y. A. Solution to the supersymmetric fine-tuning problem within the MSSM. Phys. Lett. B 2005, 631, 58–67. [Google Scholar]
- Kitano, R.; Nomura, Y. Supersymmetry, naturalness, and signatures at the LHC. Phys. Rev. D 2006, 73, 095004. [Google Scholar] [CrossRef]
- Papucci, M.; Ruderman, J.T.; Weiler, A. Natural SUSY Endures. J. High Energy Phys. B 2012, 2012. [Google Scholar] [CrossRef]
- Brust, C.; Katz, A.; Lawrence, S.; Sundrum, R. SUSY, the Third Generation and the LHC. J. High Energy Phys 2012, 2012. [Google Scholar] [CrossRef]
- Evans, J.A.; Kats, Y.; Shih, D.; Strassler, M.J. Toward Full LHC Coverage of Natural Supersymmetry. J. High Energy Phys 2014, 2014. [Google Scholar] [CrossRef]
- Baer, H.; Barger, V.; Mickelson, D. How conventional measures overestimate electroweak fine-tuning in supersymmetric theory. Phys. Rev. D 2013, 88, 095013. [Google Scholar] [CrossRef]
- Baer, H.; Barger, V.; Savoy, M. Supergravity gauge theories strike back: There is no crisis for SUSY but a new collider may be required for discovery. Phys. Scripta 2015, 90, 068003. [Google Scholar] [CrossRef]
- Ellis, J.R.; Enqvist, K.; Nanopoulos, D.V.; Zwirner, F. Observables in Low-Energy Superstring Models. Mod. Phys. Lett. A 1986, 1, 57–69. [Google Scholar]
- Barbieri, R.; Giudice, G.F. Upper Bounds on Supersymmetric Particle Masses. Nucl. Phys. B 1988, 306, 63–76. [Google Scholar]
- Ibanez, L.E.; Lopez, C.; Munoz, C. The Low-Energy Supersymmetric Spectrum According to N = 1 Supergravity Guts. Nucl. Phys. B 1985, 256, 218–252. [Google Scholar]
- Lleyda, A.; Munoz, C. Nonuniversal soft scalar masses in supersymmetric theories. Phys. Lett. B 1993, 317, 82–91. [Google Scholar]
- Weinberg, S. The U(1) Problem. Phys. Rev. D 1975, 11, 3583. [Google Scholar] [CrossRef]
- ’t Hooft, G. Symmetry Breaking Through Bell-Jackiw Anomalies. Phys. Rev. Lett 1976, 37, 8–11. [Google Scholar]
- Peccei, R.D.; Quinn, H.R. CP Conservation in the Presence of Instantons. Phys. Rev. Lett 1977, 38, 1440. [Google Scholar] [CrossRef]
- Weinberg, S. A. A New Light Boson? Phys. Rev. Lett 1978, 40, 223. [Google Scholar] [CrossRef]
- Wilczek, F. Problem of Strong p and t Invariance in the Presence of Instantons. Phys. Rev. Lett 1978, 40, 279. [Google Scholar] [CrossRef]
- Kim, J.E. Weak Interaction Singlet and Strong CP Invariance. Phys. Rev. Lett 1979, 43, 103. [Google Scholar] [CrossRef]
- Shifman, M.A.; Vainstein, A.; Zakharov, V.I. Can Confinement Ensure Natural CP Invariance of Strong Interactions? Nucl. Phys. B 1980, 166, 493–506. [Google Scholar]
- Dine, M.; Fischler, W.; Srednicki, M. A. Simple Solution to the Strong CP Problem with a Harmless Axion. Phys. Lett. B 1981, 104, 199–202. [Google Scholar]
- Zhitnitskii, A.P. On Possible Suppression of the Axion Hadron Interactions. Sov. J. Phys 1980, 31, 497–504. [Google Scholar]
- Abbott, L.F.; Sikivie, P. A. Cosmological Bound on the Invisible Axion. Phys. Lett. B 1983, 120, 133–136. [Google Scholar]
- Preskill, J.; Wise, M.; Wilczek, F. Cosmology of the Invisible Axion. Phys. Lett. B 1983, 120, 127–132. [Google Scholar]
- Dine, M.; Fischler, W. The Not So Harmless Axion. Phys. Lett 1983, 120, 137–141. [Google Scholar]
- Turner, M. Cosmic and Local Mass Density of Invisible Axions. Phys. Rev. D 1986, 33. [Google Scholar] [CrossRef]
- Bae, K.J.; Huh, J.H.; Kim, J.E. Update of axion CDM energy. 2008, arXiv:0806.0497. arXiv.org e-Print archive. Available online: http://arxiv.org/abs/0806.0497 accessed on 27 May 2015.
- Visinelli, L.; Gondolo, P. Dark Matter Axions Revisited. Phys. Rev. D 2009, 80, 035024. [Google Scholar] [CrossRef]
- Kim, J.E.; Nilles, H.P. The µ-Problem and the Strong CP-Problem. Phys. Lett. B 1984, 138, 150–154. [Google Scholar]
- Chun, E.J. Dark matter in the Kim-Nilles mechanism. Phys. Rev. D 2011, 84, 043509. [Google Scholar] [CrossRef]
- Bae, K.J.; Chun, E.J.; Im, S.H. Cosmology of the DFSZ axino. J. Cosmol. Astropart. Phys. 2012, 1203, 013. [Google Scholar] [CrossRef]
- Murayama, H.; Suzuki, H.; Yanagida, T. Radiative breaking of Peccei-Quinn symmetry at the intermediate mass scale. Phys. Lett. B 1992, 291, 418–425. [Google Scholar]
- Gherghetta, T.; Kane, G.L. Chaotic inflation and a radiatively generated intermediate scale in the supersymmetric standard model. Phys. Lett. B 1995, 354, 300–306. [Google Scholar]
- Choi, K.; Chun, E.J.; Kim, J.E. Cosmological implications of radiatively generated axion scale. Phys. Lett. B 1997, 403, 209–217. [Google Scholar]
- Bae, K.J.; Baer, H.; Serce, H. Natural little hierarchy for SUSY from radiative breaking of the Peccei-Quinn symmetry. Phys. Rev. D 2015, 91, 015003. [Google Scholar] [CrossRef]
- Baer, H.; Balazs, C.; Belyaev, A. Neutralino relic density in minimal supergravity with coannihilations. J. High Energy Phys. 2002, 0203, 042. [Google Scholar] [CrossRef]
- Bisset, M.A. Detection of Higgs bosons of the minimal supersymmetric standard model at hadron supercolliders. Available online: http://scholarspace.manoa.hawaii.edu/bitstream/handle/10125/10084/?sequence=2 accessed on 27 May 2015.
- Baer, H.; Choi, K.Y.; Kim, J.E.; Roszkowski, L. Dark matter production in the early Universe: Beyond the thermal WIMP paradigm. Phys. Rept 2014, 555, 1–60. [Google Scholar]
- Davis, R.L. Cosmic Axions from Cosmic Strings. Phys. Lett. B 1986, 180, 225–230. [Google Scholar]
- Harari, D.; Sikivie, P. On the Evolution of Global Strings in the Early Universe. Phys. Lett. B 1987, 195, 361–365. [Google Scholar]
- Davis, R.L.; Shellard, E.P.S. Do Axions Need Inflation? Nucl. Phys. B 1989, 324, 167–186. [Google Scholar]
- Hagmann, C.; Chang, S.; Sikivie, P. Axion radiation from strings. Phys. Rev. D 2001, 63, 125018:1–125018:12. [Google Scholar]
- Sakharov, A.S.; Khlopov, M.Y. The Nonhomogeneity problem for the primordial axion field. Phys. Atom. Nucl 1994, 57, 514–516. [Google Scholar]
- Khlopov, M.Y.; Sakharov, A.S.; Sokoloff, D.D. The large scale modulation of the density distribution in standard axionic CDM and its cosmological and physical impact. 1998, arXiv:hep-ph/9812286. arXiv.org e-Print archive. Available online: http://arxiv.org/abs/hep-ph/9812286 accessed on 27 May 2015.
- Goto, T.; Yamaguchi, M. Is axino dark matter possible in supergravity? Phys. Lett. B 1992, 276, 103–107. [Google Scholar]
- Chun, E.J.; Kim, J.E.; Nilles, H.P. Axino mass. 1992, arXiv:hep-ph/9205229. arXiv.org e-Print archive. Available online: http://arxiv.org/abs/hep-ph/9205229 accessed on 27 May 2015.
- Chun, E.J.; Lukas, A. Axino mass in supergravity models. Phys. Lett. B 1995, 357, 43–50. [Google Scholar]
- Kim, J.E.; Seo, M.-S. Mixing of axino and goldstino, and axino mass. Nucl. Phys. B 2012, 864, 296–316. [Google Scholar]
- Bae, K.J.; Choi, K.; Im, S.H. Effective Interactions of Axion Supermultiplet and Thermal Production of Axino Dark Matter. J. High Energy Phys 2011, 2011, 1–35. [Google Scholar]
- Choi, K.Y.; Kim, J.E.; Lee, H.M.; Seto, O. Neutralino dark matter from heavy axino decay. Phys. Rev. D 2008, 77. [Google Scholar] [CrossRef]
- Baer, H.; Lessa, A.; Rajagopalan, S.; Sreethawong, W. Mixed axion/neutralino cold dark matter in supersymmetric models. J. Cosmol. Astropart. Phys. 2011, 1106, 031. [Google Scholar] [CrossRef]
- Ade, P.A.R.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartlett1, J.G.; Bartolo, N.; et al. Planck 2015 results. XIII. Cosmological parameters. 2015, arXiv:1502.01589. arXiv.org e-Print archive. Available online: http://arxiv.org/abs/1502.01589 accessed on 27 May 2015.
- Bae, K.J.; Baer, H.; Chun, E.J. Mainly axion cold dark matter from natural supersymmetry. Phys. Rev. D 2014, 89, 031701. [Google Scholar] [CrossRef]
- Bae, K.J.; Baer, H.; Chun, E.J. Mixed axion/neutralino dark matter in the SUSY DFSZ axion model. J. Cosmol. Astropart. Phys. 2013, 1312, 028. [Google Scholar] [CrossRef]
- Bae, K.J.; Baer, H.; Lessa, A.; Serce, H. Coupled Boltzmann computation of mixed axion neutralino dark matter in the SUSY DFSZ axion model. J. Cosmol. Astropart. Phys. 2014, 1410, 82. [Google Scholar] [CrossRef]
- Jedamzik, K. Big bang nucleosynthesis constraints on hadronically and electromagnetically decaying relic neutral particles. Phys. Rev. D 2006, 74. [Google Scholar] [CrossRef]
- Rybka, G. New Results and New Perspectives from ADMX. New Perspectives on Dark Matter Workshop, Fermilab, IL, USA, 29 April–2 May 2014.
- Rybka, G.; Wagner, A.; Brill, A.; Ramos, K.; Percival, R.; Patel, K. Search for dark matter axions with the Orpheus experiment. Phys. Rev. D 2015, 91, 011701. [Google Scholar] [CrossRef]
- Raffelt, G.G. Axions—Motivation, limits and searches. J. Phys. A 2007, 40, 6607. [Google Scholar] [CrossRef]
- Baer, H.; Barger, V.; Mickelson, D. Direct and indirect detection of higgsino-like WIMPs: Concluding the story of electroweak naturalness. Phys. Lett. B 2013, 726, 330–336. [Google Scholar]
- Baer, H.; Barger, V.; Mickelson, D.; Tata, X. Snowmass whitepaper: Exploring natural SUSY via direct and indirect detection of higgsino-like WIMPs. 2013, arXiv:1306.4183. arXiv.org e-Print archive. Available online: http://arxiv.org/abs/1306.4183 accessed on 27 May 2015.
- Bae, K.J.; Baer, H.; Barger, V.; Mickelson, D.; Savoy, M. Implications of naturalness for the heavy Higgs bosons of supersymmetry. Phys. Rev. D 2014, 90, 075010. [Google Scholar] [CrossRef]
- Baer, H.; Balazs, C.; Belyaev, A.; O’Farrill, J. Direct detection of dark matter in supersymmetric models. J. Cosmol. Astropart. Phys 2003. [Google Scholar] [CrossRef]
- Hisano, J.; Ishiwata, K.; Nagata, N. Direct Search of Dark Matter in High-Scale Supersymmetry. Phys. Rev. D 2013, 87, 035020. [Google Scholar] [CrossRef]
- Bottino, A.; Donato, F.; Fornengo, N.; Scopel, S. Probing the supersymmetric parameter space by WIMP direct detection. Phys. Rev. D 2001, 63, 125003. [Google Scholar] [CrossRef]
- Behnke, E.; Behnke, J.; Brice, S.J.; Broemmelsiek, D.; Collar, J.I.; Conner, A.; Cooper, P.S.; Crisler, M.; Dahl, C.E.; Fustin, D.; et al. First Dark Matter Search Results from a 4-kg CF3I Bubble Chamber Operated in a Deep Underground Site. Phys. Rev. D 2012, 86, 052001. [Google Scholar] [CrossRef]
- Bottino, A.; Donato, F.; Fornengo, N.; Salati, P. Antiproton fluxes from light neutralinos. Phys. Rev. D 2005, 72, 083518. [Google Scholar] [CrossRef]
- Barger, V.; Gao, Y.; Keung, W.; Marfatia, D.; Shaughnessy, G. Dark matter and pulsar signals for Fermi LAT, PAMELA, ATIC, HESS and WMAP data. Phys. Lett. B 2009, 678, 283–292. [Google Scholar]
- Profumo, S. Dissecting cosmic-ray electron-positron data with Occam’s Razor: The role of known Pulsars. Central Eur. J. Phys 2011, 10, 1–31. [Google Scholar]
- Ackermann, M.; Ajello, M.; Albert, A.; Atwood, W.A.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; Bechtol, K.; Bellazzini, R.; et al. (Fermi Collaboration), Constraining Dark Matter Models from a Combined Analysis of Milky Way Satellites with the Fermi Large Area Telescope. Phys. Rev. Lett 2011, 107, 241302. [Google Scholar] [CrossRef]
- Geringer-Sameth, A.; Koushiappas, S.M. Exclusion of canonical WIMPs by the joint analysis of Milky Way dwarfs with Fermi. Phys. Rev. Lett 2011, 107, 241303. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).