Abstract
Some of the outstanding questions of particle physics today concern the neutrino sector, in particular whether there are more neutrinos than those already known and whether they are Dirac or Majorana particles. There are different ways to explore these issues. In this article we describe neutrino-mediated decays of charged pseudoscalar mesons such as π±, K± and B±, in scenarios where extra neutrinos are heavy and can be on their mass shell. We discuss semileptonic and leptonic decays of such kinds. We investigate possible ways of using these decays in order to distinguish between the Dirac and Majorana character of neutrinos. Further, we argue that there are significant possibilities of detecting CP violation in such decays when there are at least two almost degenerate Majorana neutrinos involved. This latter type of scenario fits well into the known neutrino minimal standard model (νMSM) which could simultaneously explain the Dark Matter and Baryon Asymmetry of the Universe.1. Introduction
To date it is unclear whether the neutrinos we know are Dirac of Majorana fermions. Unlike Dirac fermions, Majorana fermions cannot be distinguished from their own antiparticles. As a consequence, processes involving Dirac neutrinos conserve charges such as Lepton Number, while processes involving Majorana neutrinos will not conserve them. There exist several processes which may clarify the Majorana or Dirac nature of neutrinos. Among such processes the most prominent are neutrinoless double beta decays (0νββ) in nuclei [1–10]. Other such processes are specific scattering processes [11–21], and rare meson decays [22–40].
A related issue in neutrinos physics is the absolute mass values of the known neutrinos. While the experimental evidence of neutrino oscillations within the known three flavor states [41–46] clearly shows that these particles cannot all be massless, the oscillations are only sensitive to mass differences, not to their absolute values. In contrast, 0νββ decays are sensitive to the absolute mass and may help in their determination, if neutrinos turn out to be Majorana particles. So far the best bounds on the absolute masses of the light neutrinos come from Cosmology mν ≳ 0.23 eV [47].
A pending question is then why light neutrinos are so light, specifically so much lighter than all other Standard Model (SM) fermions. Interesting enough, the existence of such very light neutrinos can be explained via the seesaw mechanism [48–52] where more neutrinos are required and where all of them are, in general, Majorana particles. In the simplest form of this mechanism, the masses of the light neutrinos are , where is an electroweak scale or lower. At the same time, additional neutrinos, usually much heavier (with masses TeV) and sterile under electroweak interactions except through small mixing with the SM flavors, are required. This mixing is suppressed as . Besides the simplest scenario, there are other seesaw scenarios in which the heavy neutrinos may have lower masses, namely near or below 1 TeV [53–59] and even near the 1 GeV scale or below [15,60–65], and at the same time their mixing with the SM flavors may not be so extremely suppressed as in the original scenarios.
In the first part of this work we discuss lepton number violating (LNV) semileptonic decays of charged pseudoscalar mesons such as K± and B±, mediated by a heavy Majorana neutrino on its mass shell, cf. Ref. [26]. The pions, which are the lightest mesons, can have only leptonic decays; we discuss hypothetical leptonic decays that could be mediated by on-shell heavy neutrinos. Such decays could be either lepton number conserving (LNC) or lepton number violating (LNV) when the mediating neutrinos are Majorana particles, cf. Ref. [37], while only LNC decays occur when the neutrino is of Dirac type. We present ways of determining the nature of neutrinos using the differential decay rates of these processes.
Yet another interesting issue in neutrino physics is the possible existence of CP violation in the lepton sector, a phenomenon that could be measured, for example, in neutrino oscillations [66]. Alternatively, as we present in the second part of this work, leptonic CP violation may show in leptonic LNC and LNV decays of charged pions, cf. Ref. [38], or in semileptonic LNV decays of K± and B±, cf. Refs. [39,40]. It turns out that such CP violation becomes appreciable and possibly detectable in these decays if the scenario contains at least two on-shell heavy neutrinos that are almost degenerate. Interestingly, this scenario fits well into the neutrino minimal standard model (νMSM) [60,61,67–72] which contains two almost degenerate Majorana neutrinos of mass ∼ 1 GeV and another lighter neutrino of mass ∼ 101 keV, besides the three light neutrinos of mass ≲1 eV. This model can explain simultaneously the existence of neutrino oscillations, dark matter and baryon asymmetry of the Universe. Furthermore, in more general frameworks of low-scale seesaw, baryon asymmetry (but not dark matter) is explained while keeping even larger values of the heavy-light mixing [73] than in the νMSM, and in such frameworks the case of almost degenerate Majorana neutrinos is preferred [74] since it allows larger mixings. CP violation effects in the neutrino sector in scenarios with nearly degenerate heavy neutrinos have also been investigated earlier [75,76] using a more detailed formalism, although it amounts to the same effect described here which is the interference of amplitudes with two slightly different dispersive and absorptive parts in the neutrino self energy.
In Section 2 we discuss the LNV semileptonic decays of mesons , mediated by an on-shell Majorana neutrino (which henceforth we call N) where M is a heavy pseudoscalar (M = K, D, Ds, B, Bc), M′ is a lighter pseudoscalar, and ℓj (j = 1, 2) are charged leptons, and we present there the corresponding branching ratios. In Section 3 we present the expressions and values of the branching ratios for the LNC and LNV leptonic decays of charged pions mediated by on-shell N sterile neutrino, π± → e±N → e±e±µ∓ν, as well as the differential branching ratio dBr/dEµ for these decays. We discuss the possibilities of detecting such branching ratios and to discern from them the Majorana or Dirac nature of neutrinos. In Section 4 we then extend the analysis of the mentioned leptonic and semileptonic decays to a scenario where we have at least two heavy on-shell sterile neutrinos involved (N1, N2), and we present an analysis of CP-violating asymmetries for such processes. In Appendices A.1 and A.2 we present explicit formulas for our LNV semileptonic decays, and in Appendices A.4 and A.5 explicit formulas needed for the analysis of our LNC and LNV leptonic decays of the charged pion. Appendix A.3 contains formulas needed for evaluation of the decay width of the heavy neutrino N, and in Appendix A.6 we derive an identity relevant for CP violation asymmetry. In Section 5 we discuss and summarize our results.
2. Lepton Number Violating Semileptonic Decays of Scalar Mesons
If there is a Majorana sterile neutrino N with mass MN ~ 1 GeV, its existence could be discerned by detecting semileptonic LNV decays of heavy mesons mediated by on-shell N. Here we will consider such LNV decays , where M and M′ are pseudoscalar mesons (M = K, D, Ds, B, Bc; M′ = π, K, D, Ds) while ℓ1 and ℓ2 are charged leptons (e, µ or τ), cf. Figure 1.
Large part of this Section uses the results of Refs. [26,37], and for certain general formulas, those of Refs. [39,40].
We consider a scenario where we have at least one heavy sterile neutrino N, which has (small) mixing BℓN with the three known neutrino flavors νℓ (ℓ = e, µ, τ)
Here, νk (k = 1, 2, 3) are the three light mass neutrino eingenstates. The considered decays may be appreciable only if N can go on its mass shell (in the s-type channel, Figure 1), creating a very large resonant enhancement of order mN/ΓN, condition which is fulfilled if
Consequently, only tree level resonant amplitudes need to be considered. The mixing matrix B appearing in Equation (1) should be unitary, implying that the PMNS 3 × 3 block is in general not unitary. If one adds extra and heavy neutrinos—as in most seesaw models—the unitarity of B thus provides upper limit constraints on the heavy-to-light mixing elements [34,77–79]. This is in part one of the reasons for the high suppression suffered by all lepton flavour violating processes involving heavy neutrinos.
2.1. Branching Ratio for
The decay width of the considered decays can be written as final particles’ phase space integral of the square of the reduced decay amplitude (summed over helicities of charged leptons)
Factor 1/2! above is the symmetry factor when the two produced leptons are equal; d3 is the integration differential of the final three-particle phase space
The resulting decay width can be written as
The expressions for T±(X)T±(Y)* (X, Y = D, C) are given in Appendix A.1. T±(X) is the relevant part of the amplitude in the X channel and forms part of the total decay amplitude , cf. Appendix A.1. In Equation (5), notice that subscripts ± for the contributions and are unnecessary because |T+(D)|2 = |T−(D)|2 and |T+(C)|2 = |T−(C)|2. P (X) (X = D, C) are the propagator functions of the intermediate neutrino N in the two channels
The overall constant K2 in Equation (7) is
Here, fM and fM′ are the decay constants of M± and M′∓, and and are the corresponding CKM matrix elements. We denote the valence quark content of M+ as ; of M′+ as .
When the intermediate neutrino N has such a mass that it is on mass shell, Equation (2), the squares of the propagators (8) are reduced to Dirac delta functions because ΓN ≪ MN
The notations used in Equations (12) and (13) are
We note that the expression (12), although having the explicit mixing dependence factored out [cf. Equation (11)], contains the dependence on the mixing coefficients BℓN in the denominator due to the N-decay width there ΓN ∝ |BℓN|2 (ℓ = e, µ, τ, see below). This factor 1/ΓN in of Equation (12) represents the N-on-shell effect Equation (10). As a result, the considered width is by many orders of magnitude larger when N is on-shell than it would be if N were off-shell. For more quantitative analyses, it is thus important to have an expression for ΓN as a function of mass MN. Using the results of Ref. [39], we can write this decay width as
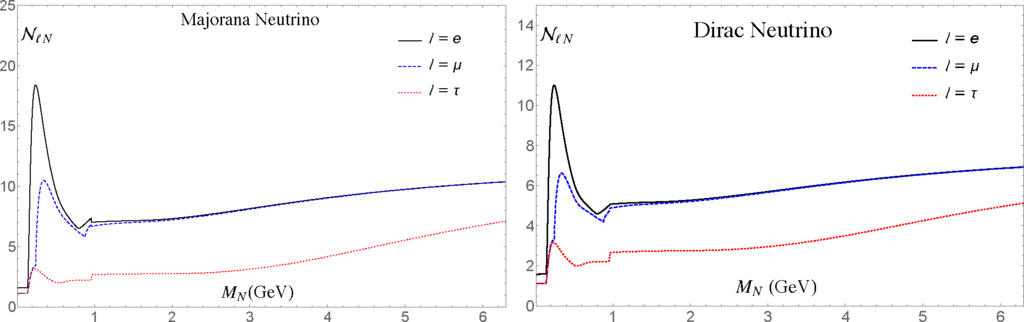
In this expression, are the effective mixing coefficients; these are numbers ∼ 100–101 which depend on the mass MN. In Appendix A.3 we write down the relevant formulas for the evaluation of these coefficients. The results of these evaluations are presented in Figure 2, for the case of Majorana and Dirac neutrino N, in the entire neutrino mass interval 0.1 GeV < MN < 6.3 GeV which will be of interest in this work. For further clarifying remarks we refer to Appendix A.3. Equations (11) and (12) imply that is proportional to . Hence, we can define a canonical branching ratio , being the part of the branching ratio with no explicit or implicit heavy-light mixing factors
Use of the expressions (12) and Equations (16) and (17) then gives for the canonical branching ratio the following expression:
2.2. Effect of the Long Neutrino Lifetime on the Observability of
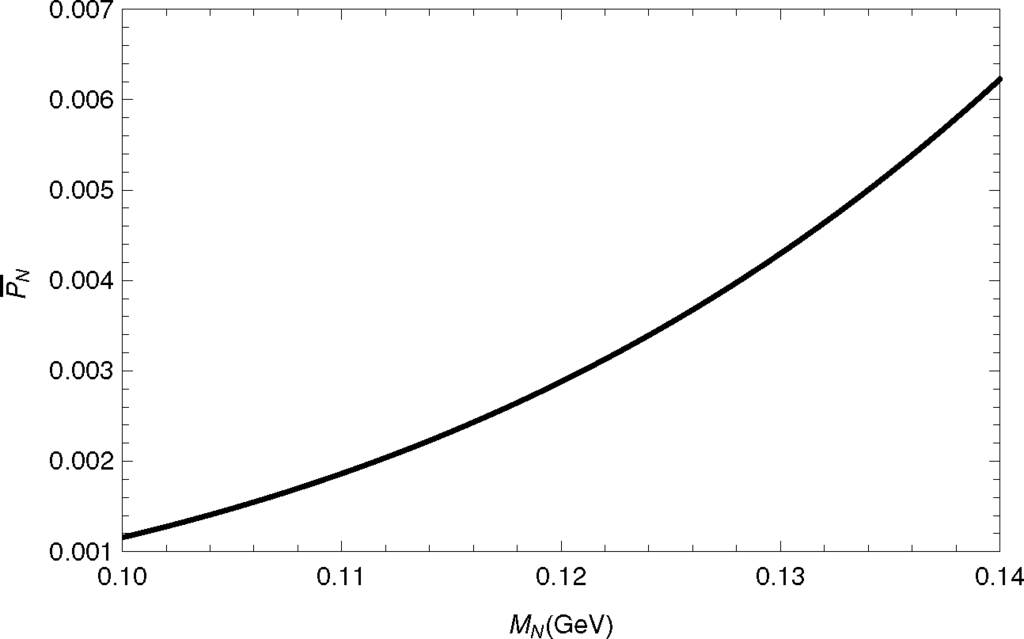
In the mentioned branching ratios, an often important effect of suppression due to the decay (i.e., nonsurvival) probability was not included. Namely, if the detector for the considered decays has a certain length L, the produced (on-shell) massive neutrino N could survive during its flight through the detector, and would decay later outside it. Such decays are thus not detected and should be eliminated from the width and the branching ratio of the considered process , by introducing a suppression factor (nonsurvival probability) PN = 1 − exp[−t/(τNγN)], where t ≈ L/βN is the time of flight of N through the detector (βN is the velocity of N in the lab frame), and is the Lorentz time dilation factor. Hence, the suppression factor, which should multiply the branching ratio, is
In the last relation, we used βN ≈ 1 and τN = 1/ΓN [≡ 1/Γ(N → all)], in the units used here (c = 1 = ħ). This decay-within-the-detector probability PN has been discussed and presented for the processes with intermediate on-shell particle (such as N) in Refs. [16,37–39,80–82]. In this respect, here we follow mostly the notations of Ref. [39]. Usually, the quantity PN is small and is then written as
Here, LN is the decay length, and is the canonical decay length (independent of the mixing parameters Bℓ′N)
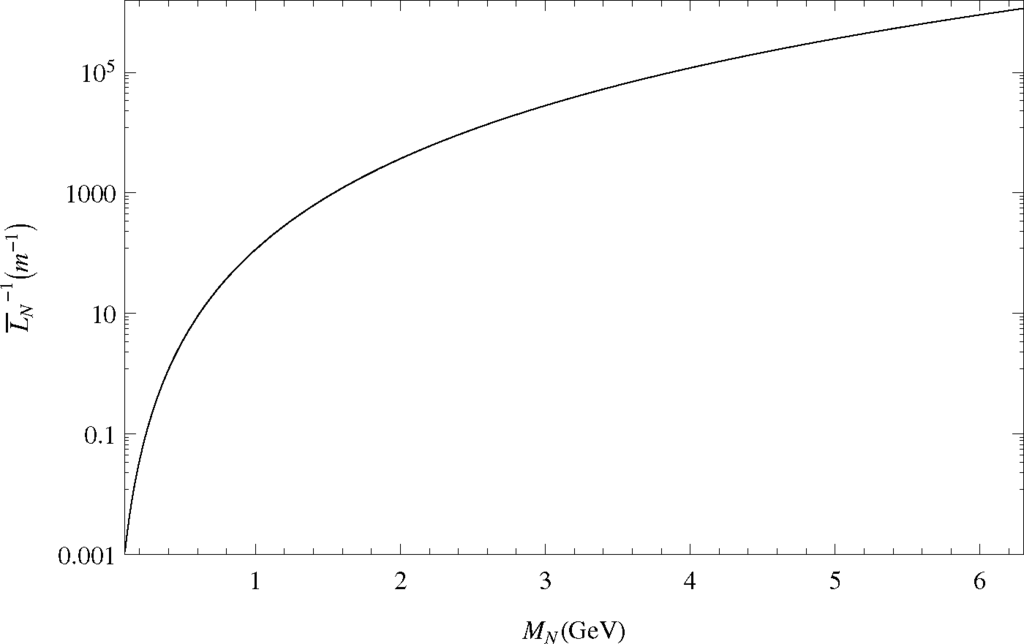
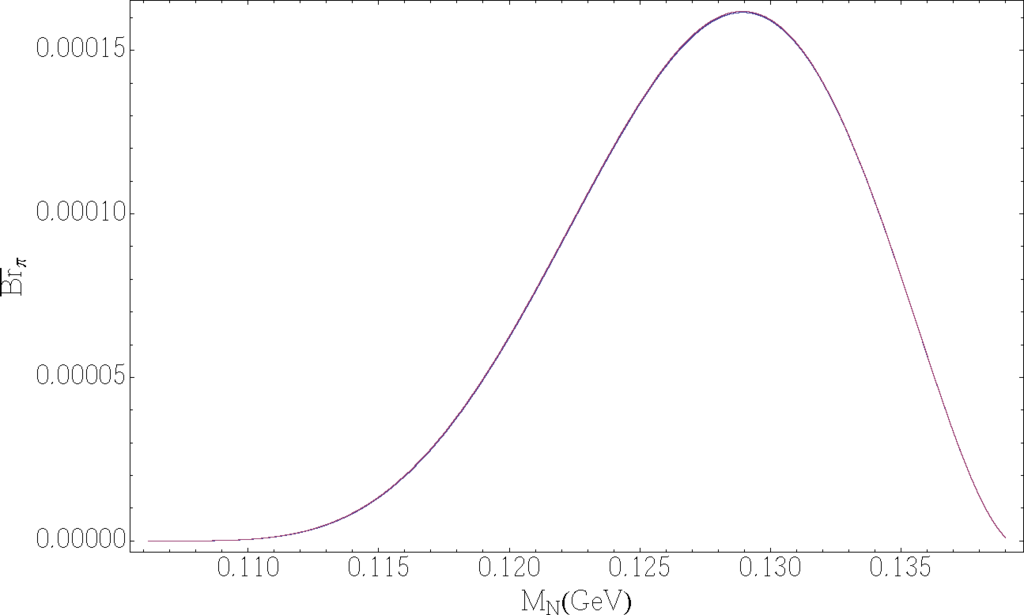
We present the inverse canonical decay length, , for γN = 2, in Figure 3 as a function of MN. We note that increases very fast (as ) when MN increases. Therefore, the supression due to the factor PN may not necessarily be strong (i.e., ) for semileptonic LNV decays of heavier mesons M±, such as B±.
If we use eyeball estimates for the coefficients of the left-hand Figure 2, approximate expressions for the factor of Equation (18) for Majorana neutrinos can be written
In order to estimate better the values of Equations (27) and thus the suppression factor PN Equation (24), we need to know the present upper bounds for the squares |BℓN|2 as a function of . These upper bounds we take from compilation of values of Ref. [29], based in turn on upper bound values obtained in Refs. [83–96]. We present them in Table 1, for specific chosen values of MN in the mass range of interest. We remark that the upper bounds have in some cases strong dependence on the precise values of MN, see Ref. [29] for further details. In order to use only rough estimates for the values of , we present in Table 2 order of magnitude values for upper bounds of |BℓN|2. These rough upper bounds are given for three typical ranges of our interest: MN around 0.25; 1; 3 GeV. They are relevant for the decays of K; (D, Ds); (B, Bc), respectively. The corresponding values of the inverse of the canonical decay length, , are included. As seen in Tables 1 and 2, the upper bounds for |BτN|2 are at present significantly less stringent and are expected to become more stringent in the future. When we combine Equations (24b) with (27) and Table 2, we obtain for the decay-within-the-detector probability the following estimates and upper bounds, relevant for the K decays (MN ≈ 0:25 GeV), D and Ds decays (MN ≈ 1 GeV), and B and Bc decays (MN ≈ 3 GeV), all when L = 1 m and γN = 2:


In order to have the analysis and the formulas simpler, in the rest of this Section we will assume that one mixing parameter, |BℓN|, dominates over the other two mixing parameters:
For example, it may well be that ℓ = µ, i.e., that |BµN| ≫ |BeN|, |BτN|. Then, of the branching ratios the largest will be which, according to Equations (29) and (19) (note that DD* and CC* give the same contribution since ℓ1 = ℓ2 now), is:
Multiplying this expression by the probability PN of the decay in the detector, Equation (26), we obtain the effective branching ratio Breff
We see that in the effective branching ratio, Breff, the complicated dependence on mixing parameters encoded in [cf. Equation (18)] disappeared because factors cancel here. All the mixing effects in Breff are in the simple factor |BℓN|4. Unfortunately, this factor represents a strong suppression, in comparison with Br of Equations (19) where .
In the last identity (31b) we introduced the canonical (i.e., without any mixing dependence) effective branching ratio
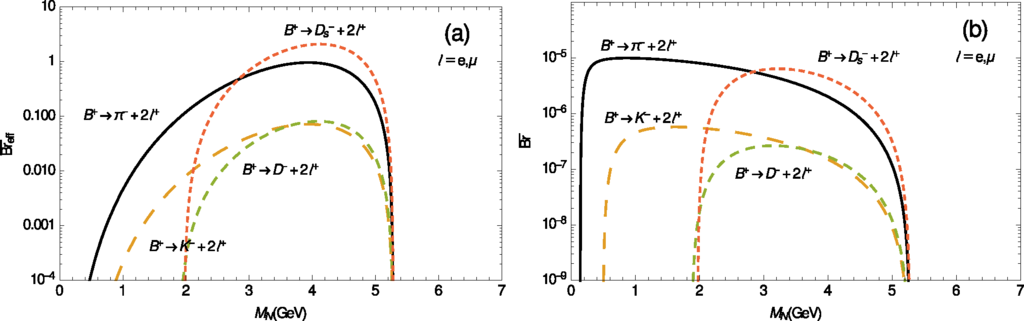
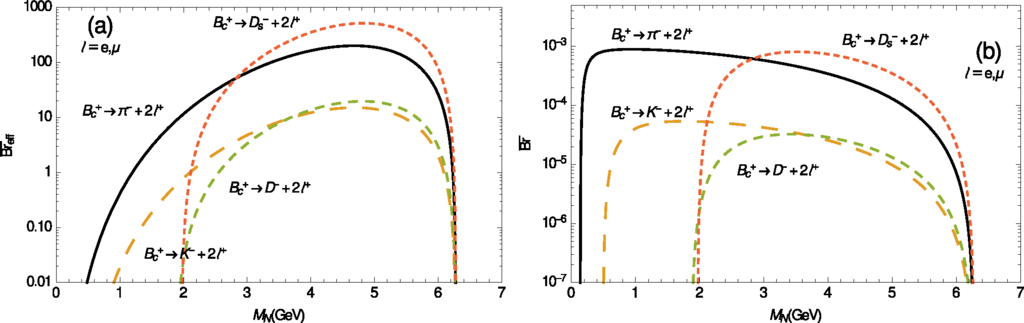
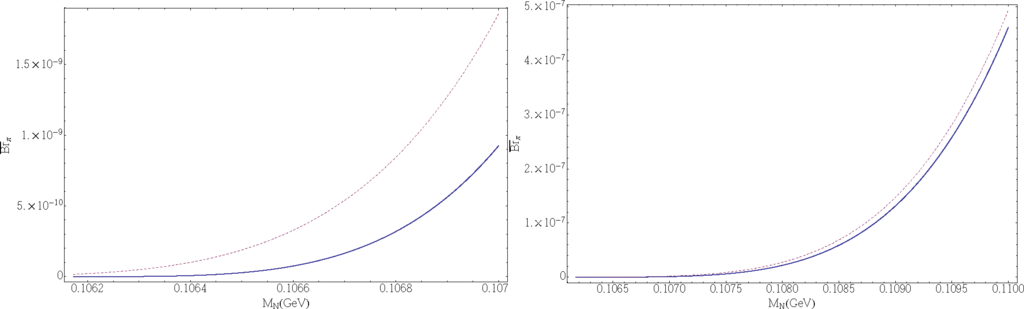
Only when M± = B± or , i.e., when the mass of the on-shell N can be high (MN ≳ 1 GeV), would it be possible to have PN ∼ 1 [Equation (28c)]; and in such a case Equations (31) do not apply, but rather Equations (30), i.e., Breff = Br in this case. Figures 4–7 show the effective canonical branching ratios (32) as a function of the neutrino mass MN, for various considered LNV decays of the type M± → ℓ±ℓ±M′∓: Figure 4 for M = K; Figure 5a, b for M = D, Ds, respectively; Figures 6a and 7a for M = B, Bc, respectively. We took ℓ = e, µ, and L = 1 m and γN = 2. For the case when PN ∼ 1 and hence the estimates Equations (30) apply, Figures 6b and 7b present the branching ratios as a function of MN, for M± = B± and , respectively. For the meson decay constants and CKM matrix elements, needed for the evaluation of K2 factor of Equation (9), and for the masses and lifetimes of the mesons, we used the values of Ref. [97]. The values of the decay constants fB and were taken from Ref. [98]: fB = 0.196 GeV, . We note that the presented formulas for and can be evaluated also for the decays when ℓ1 ≠ ℓ2. Furthermore, when the final leptons are τ leptons (and M± = B± or ), the values of branching ratios turn out to be similar to those in Figures 6 and 7, but the range of MN in this case is shorter: MM′ +Mτ < MN <MM – Mτ. Table 3 displays values of for representative values of MN in the decays M± → ℓ±ℓ±M′∓.
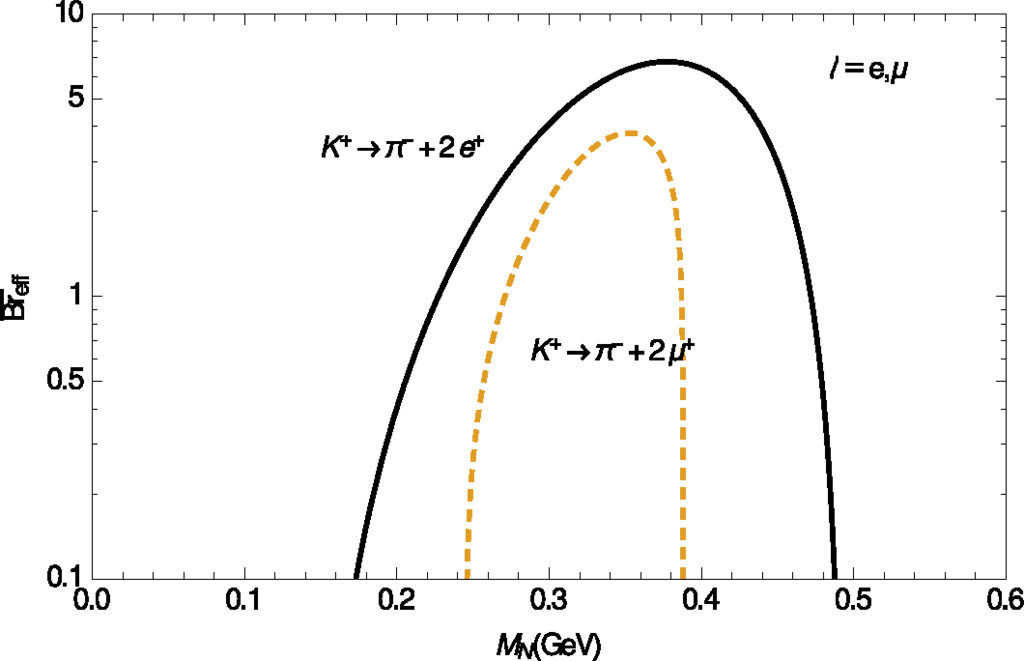
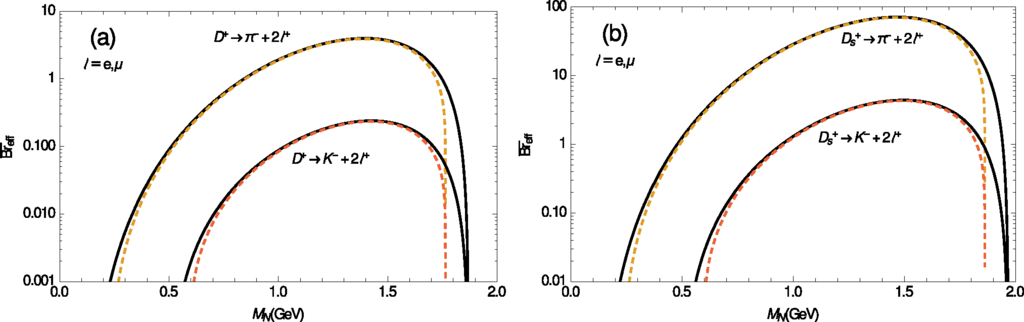

As an illustrative example, let us consider the decays , which is one of the preferred decay modes proposed at CERN-SPS [80,81], and, in addition, let us assume that |BμN|2 is the dominant mixing. In such a case, Equations (31) and Table 3 imply for the experimentally measurable branching fraction Breff
The present rough upper bound on the mixing for MN ≈ 1 GeV is |BµN|2 ≲ 10−7, cf. Table 2. Equation (33) then implies that Br(eff) ≲ 10−12 for such decays. The proposed experiment at CERN-SPS [80,81] could produce D and Ds mesons in numbers by several orders of magnitude higher than 1012, which would open the possibility to explore whether there is a production of sterile Majorana neutrinos N in the mass range MN ∼ 1 GeV.
If the decays are considered (we do not use B± decays as they are CKM-suppressed compared to ), the results of Figure 7a and Equation (31b) imply an effective branching ratio
3. Charged Pion Decays Mediated by On-Shell Massive Neutrinos
In the previous Section we considered semileptonic decays of mesons heavier than the pion. For pion decays, there are purely leptonic modes only, since the pion is the lightest meson. In this Section we present and discuss the branching ratios for the LNC decay π± → e±N → e±e±µ∓νe and the LNV decay . We also consider the differential branching ratios dBr/dEµ, where Eµ is the energy of the produced µ∓. In contrast to the previous Section where the intermediate N neutrino has to be Majorana, here N can be either Majorana or Dirac. In the Dirac case, only the LNC mode is possible, while both LNC and LNV modes occur in the Majorana case. However, the experimental distinction between these two modes cannot be resolved by simply examining the final state, since the produced neutrino (νe or ) is not detectable. The major part of this Section refers to Ref. [37], and for certain details we use here results of Refs. [38,39]. The formalism is somewhat more complicated now because we have four final particles (in the previous Section there were three). Nonetheless, several features turn out to be similar as in the previous Section.
The considered processes are presented in Figures 8 and 9. As in the previous Section, we consider a scenario with at least one heavy sterile neutrino N, which has suppressed heavy-light mixing coefficients BℓN with the first three neutrino flavors νℓ (ℓ = e, µ, τ), cf. Equation (1). The mentioned decay rates may be nonnegligible only if the intermediate neutrino N is on-shell, i.e.,
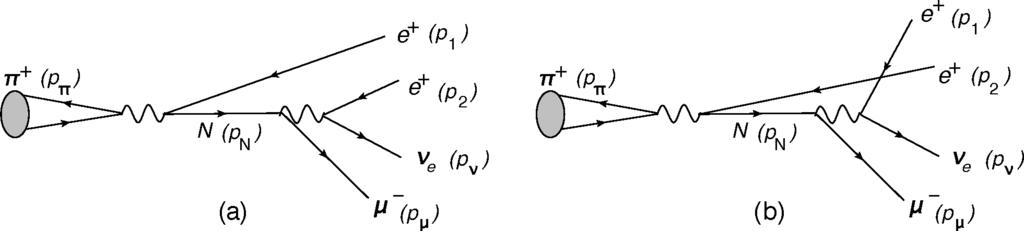
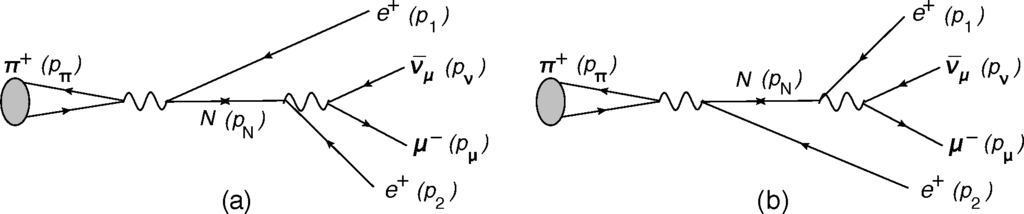
3.1. Branching Ratios for π± → e±e±µ∓ν
The decay widths Γ(X)(π± → e±e±µ∓ν) (X=LNC, LNV) can be written in terms of the corresponding reduced decay amplitudes
Here, 1/2! represents the symmetry factor from two final state electrons, and d4 is the integration element of the phase space of the four final particles
Here, p1 and p2 are the momenta of e; in the direct channel, the e momentum at the first (left-hand) vertex is p1, and in the crossed channel it is p2, cf. Figures 8 and 9. When we use the expressions for the amplitudes of Appendix A.4, for the specific considered case N1 = N (and no N2), the decay width (36) can be written as
The expressions for are given in Appendix A.4, for the direct (YZ* = DD*), crossed (YZ* = CC*) and direct-crossed interference contributions (YZ* = DC*, CD*). We have and , hence the terms and in Equation (38) have no subscripts ±. Further, in Equation (40)P(X) (Y) represent the N propagator functions of the direct and crossed channels (Y = D,C)
It turns out that in the case when the intermediate N neutrino is on-shell, i.e., when its mass is in the interval of Equation (35), the squares of the propagators (41) reduce to simple delta functions due to the inequality ΓN ≪ MN
Here, the normalized decay width turns out to be the same for X = LNC and X = LNV,
It can be checked that the decay rate (44), with N on shell, coincides with the factorized expression
In Appendix A.5 we also provide the differential decay rates dΓ(X)(π± → e±e±µ∓ν)/dEµ with respect to the final muon energy in the rest frame of N neutrino. They turn out to have quite different forms for X = LNC and X = LNV cases (we will return to this later in this Section).
In order to obtain the branching fractions of the considered processes, we need to divide the decay width by the total decay width of the charged pion, Γ(π± → all)
As we can see in Equations (44) and (45), the decay width Γ(π± → e±e±µ∓ν) are inversely proportional to the (very small) decay width Γ(N → all) ≡ ΓN, which in turn is proportional to the mixings , cf. Equations (16)–(18) and Figure 2. As in Section 2.1, this effect represents the N-on-shell effect Equation (43) and it makes the considered width Γ(π± → e±e±μ∓ν) by many orders of magnitude larger than it would be in the case of off-shell N. In the (narrow) mass interval (35) for on-shell N in the considered pion decays, the factor in the width ΓN Equation (16) has the following approximate form (cf. Appendix A.3 and Figure 2):
This expression, within the precision given here, is valid equally for the Majorana and for the Dirac N and agrees with that given in Ref. [38] for the Majorana case. However, the affirmation in Ref. [38] that for Dirac N is smaller by a factor of two is not correct.
In certain analogy with Section 2.1, we can define here the canonical branching ratio as the part of the branching ratio which contains no explicit or implicit heavy-light mixing dependence (and is independent of X = LNC or LNV)
The differential branching ratios dBr(X)/dEµ, where Eµ is the final muon energy in the N-rest frame, are obtained directly from the differential branching ratios , and the latter quantity for X = LNV is given explicitly in Appendix A.5. The canonical differential branching ratios, free of any mixing dependence, can be defined in analogy with the definition of the canonical total branching ratio (53a), and, in contrast to canonical branching ratios (53) they do depend on whether X = LNC or X = LNV
Explicit expressions for these quantities, when X = LNV and X = LNC, are given in Appendix A.5 in Equations (126) and (128), and in the limit Me = 0 in Equation (129).
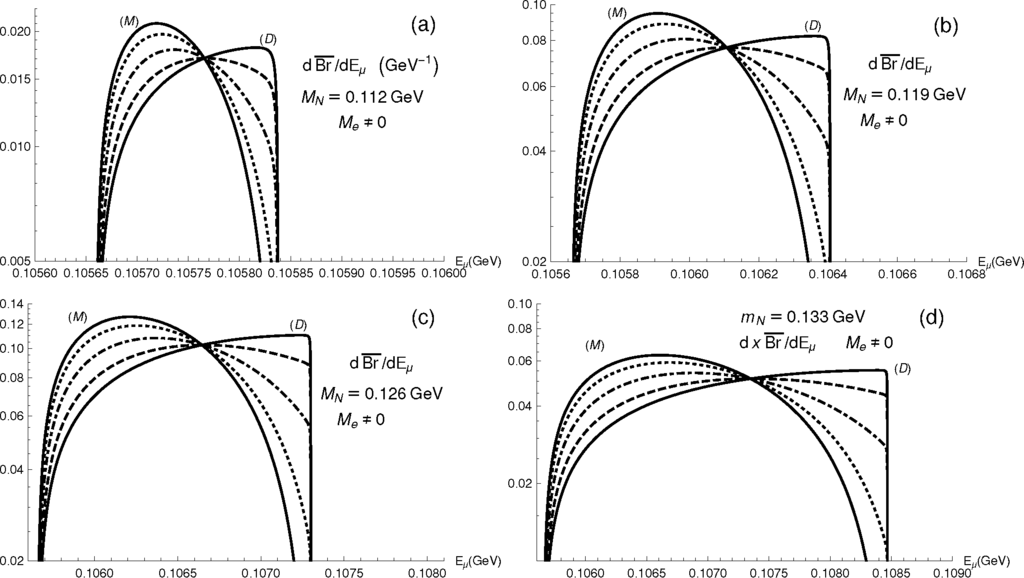
The differential (and full) branching ratios for the process π± → e±e±µ∓ν differ in the cases when the on-shell N is Majorana or Dirac. When N is Dirac, only the X = LNC process contributes. When N is Majorana, both LNC and LNV processes contribute. We can write the differential and full branching ratios in these cases in terms of their canonical counterparts, by defining first the combined canonical differential branching ratios
Integration of the relations (56) over Eµ leads to the full branching ratios
If the differential branching ratios are studied with respect to the muon energy in the pion rest frame, the distinction between the Dirac and Majorana case is more difficult, cf. Ref. [37].
3.2. Effect of the Long Neutrino Lifetime on the Observability of π± → e±e±µ∓ν
The branching ratios presented in this Section so far, Equations (58) in conjunction with Equations (53), should be multiplied by the probability PN for the on-shell neutrino N to decay within the detector (of length L), as explained in Section 2.2, Equations (22)–(26) and Figure 3. As a consequence, the effective (true, measurable) branching ratios are not Br (∼ |BℓN|2) of Equations (58), but Breff = PNBr
In Equations (59a) and (60a) we used the expressions (58) for Br and Equation (26) for PN. In Equations (59b) and (60b) we introduced canonical (i.e., without any mixing dependence) effective branching ratio
As in the case of semileptonic LNV decays of Section 2.2, we notice that also here in the effective branching ratios, Equations (59) and (60), the complicated dependence on the mixing parameters entailed by the factors of ΓN [cf. Equation (18)], cancels out, and there remains only simple dependence on the mixing parameters, in the form or |B |2. Further, in comparison with the branching ratios Br of Equations (58), which are , the effective (true) branching ratios Breff of Equations (59) and (60) are unfortunately significantly more suppressed by the mixing parameters, namely .
The presently known experimental bounds on the mixing parameters in the here relevant narrow mass range (35), are: [99]; [100–102]; [103]; cf. also Refs. [29,74,104,105].
The future pion factories, such as the Project X at Fermilab, will be designed to produce charged pions with lab energies Eπ of a few GeV and luminosities ∼ 1022 cm−2s−1 [106,107], and ∼ 1029 charged pions could be expected per year.
The canonical effective branching ratio (61) can be estimated as
If the larger among the mixing elements is , the LNC processes dominate, and the effective branching ratios (63) have the common upper bounds
If in this case is close to its present upper bound, , we obtain . This implies that up to 109 events π± → e±e±µ∓ν could be detected per year in such a scenario.
On the other hand, if the larger among the mixing elements is , the LNV processes dominate, and the effective branching ratios (63) have the following upper bounds:
In such a case we have, , and up to 107 events could be detected per year.
The present upper bounds on suggest that the first scenario, Equation (64), is more likely.
The measurement of the effective branching ratios alone cannot distinguish between the Dirac and the Majorana character of intermediate neutrino N. However, as argued in Section 3.1 and presented in Figure 12, the measurement of the differential branching ratios for the considered processes is a promising way to discern the character of the neutrinos. However, the differential branching ratios (56) must be multiplied by the nonsurvival probability PN, in order to obtain the effective (true, measurable) differential branching ratios dBreff/dEµ. In analogy with Equations (59) and (60) we obtain, using Equation (56)
4. CP Violation in Charged Meson Decays Mediated by Massive Sterile Neutrinos
CP violation in the lepton sector could be measured by neutrino oscillations [66]. Here we consider the possibilities of measuring CP violation in meson decays mediated by sterile neutrinos N, such as the semileptonic LNV decays of charged heavy pseudoscalar mesons considered in Section 2, or the leptonic (LNV and LNC) decays of charged pions considered in Section 3.
It turns out that CP violation in all such decays is possible in scenarios with at least two massive sterile neutrinos Nj (j = 1, 2). CP violation in the neutrino sector is expected whether neutrinos are Dirac or Majorana particles. However, in the Pontecorvo–Maki–Nakagawa–Sakata (PMNS) mixing matrix [108–110], the number of possible CP-violating phases is larger when the neutrinos are Majorana particles. If is the total number of neutrinos (N is the number of sterile neutrinos), the number of CP-violating phases is n(n − 1)/2 if neutrinos are Majorana, and (n − 1)(n − 2)/2 if neutrinos are Dirac, cf. Ref. [111].
CP violation in the decays was investigated in Ref. [38], and in the decays in Refs. [39,40]. In both cases, it turns out that, even though the rates are extremely small, the CP violation asymmetry in these charged decays may become appreciable, even close to order unity, when the two intermediate neutrinos can go on shell and are almost degenerate in mass . This is to be contrasted with CP violation in charged meson decays due to the standard CKM mechanism in the quarks sector, where the rates are larger but the asymmetries are much smaller, e.g., of order 10−4 in K± → 3π decays [112].
4.1. CP Violation in Semileptonic LNV Decays
As mentioned above, we will consider the scenario with at least two sterile neutrinos, Nj (j = 1, 2), both of which can go on shell in the intermediate state, i.e., with masses satisfying the condition shown in Equation (2). The processes of interest are again those of Figure 1, except that now in both the direct (D) and crossed (C) channels there are two possible neutrinos exchanged: N1 or N2. The relative measure of CP violation for these processes will be the asymmetry:
The corresponding LNV decay widths will be obtained now, in the scenario of two sterile neutrinos , in close analogy with the calculation in Section 2.1 which was performed for the case of one neutrino . The relations (3) and (4) and (9) there hold without change now, but the relations (5)–(8) obtain the following slightly more general form when :
Here, are the mixing coefficients
The expressions for T±(X)T±(Y)∗ (where X, Y = D, C) are the same as in Equation (7) and are given in Appendix A.1, and Pj(X) (X = D, C) are the propagators of the exchanged neutrinos Nj in the direct and crossed channels
We will disregard effects due to non-diagonal neutrino widths in their mass basis. For these details we refer to Ref. [40]. The total decay width of Nj, , is given by Equations (16)–(18), where each Nj has its own mixing parameter Equation (18), i.e., , where the coefficients as a function of are given by the left-hand Figure 2 in Section 2.1.
As we will see below, the CP asymmetry parameter , Equation (68), may acquire a significant nonzero value if simultaneously: (a) the phases of the PMNS heavy-light mixing elements fulfill certain conditions: ; and (b) the mass difference is sufficiently small .
First let us calculate the quantities
For example, in the specific case when , we have . As in Section 2.1, when both Nj are on-shell, it turns out that the interference contributions to the quantities S∓(M) from the direct (D) and crossed (C) channels (DC∗ and CD∗) are suppressed by several orders of magnitude in comparison with the contributions from the direct (DD∗) and crossed (CC*) channels, and we will neglect them (we refer to [39] for details on this point). Then it follows from the expression (69)
In the sum (76), the coefficient δ1 represents the effect of N1-N2 overlap contributions
We expect δ1 ≈ 0 when (where: ); numerical calculations (see later) confirm this expectation and show that δj is practically independent of the channel X = D, C. The normalized decay widths and are those of Equations (12) and (13) of Section 2.1, with the substitutions , [cf. Equation (14b)] and
For evaluation of the CP-violating difference S−(M), Equation (75), the quantity is of central importance. In the integrand of appears as a factor the following combination of the propagators of N1 and N2 [cf. Equation (71)]:
In Equation (79b) we used the narrow width approximation:
This implies that in the case of two almost degenerate sterile neutrinos we have for the factor in Equation (79b) the following identities:
We note that the factor 4 in the denominator on the right-hand side of Equation (83) is nontrivial, because a somewhat different result would have been obtained by a more simple and direct consideration of the expression (79a) in the limit . The result (81) [or equivalently, Equation (83)] has been confirmed also by numerical evaluation of , Refs. [38,39] (see below). The mechanism (79) [with the identity (83)] is of central importance for the CP violation in the processes considered here. The quantity , at fixed ΓN and fixed , achieves its maximum when , i.e., y = 1 [⇔ ΔMN = ΓN (≪ MN)], i.e., when the two sterile neutrinos are almost degenerate. If ΔMN ≁ΓN (i.e., y ≁1), then the quantity η(y)/y = y/(y2 + 1) in Equation (83) is very small and CP violation effects disappear.
The mechanism (79) was used in Ref. [38] in the context of CP violation of leptonic decays of charged pions, and in Refs. [39,40] in the here presented context of CP violation of semileptonic LNV decays of heavy pseudoscalars.
We recall that the expression (79) has the same structure with Dirac delta functions as Equation (10) in Section 2.1; however, the factors in front of these Dirac delta functions are different now. Therefore, integration over the final particles’ phase space can be performed now in the same way as in Section 2.1, i.e., analytically. This leads, in analogy with Equation (12), to the result
From here on in this Section, we will consider the case of near degeneracy of the two on-shell sterile neutrinos (ΔMN ≪ MN, where ), in which case Equations (81) and (82) hold and the quantities Equations (83) and (84) become appreciable and CP violation can thus become significant. Therefore, we have
The normalized decay matrix elements Equation (71), were evaluated in Ref. [39] also numerically, by Monte Carlo integration and using finite small widths in the propagators. The numerical calculations confirmed the presented formulas, among them the expressions (78), (86), and (81)–(83). The form (81) of η(y) was confirmed numerically with a precision better than a few per mille. The numerical evaluations also confirmed that the direct-crossed interference terms (DC* and CD*) are really negligible. We refer to [39] for details.
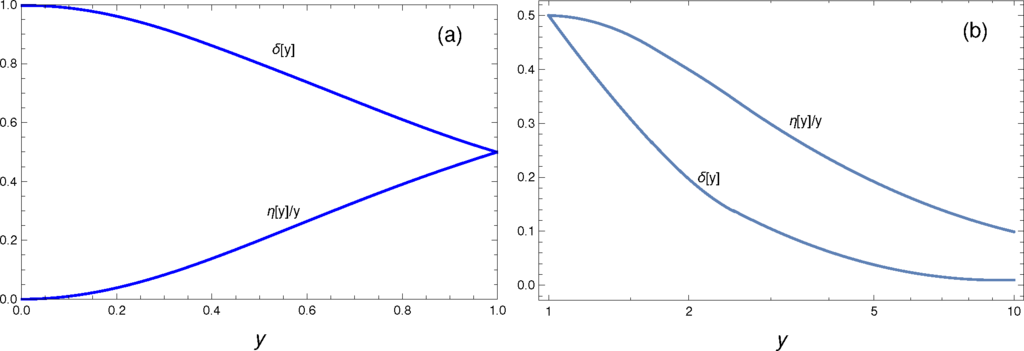
Further, the mentioned numerical evaluations gave us values of the N1-N2 overlap parameter δ1 as defined in Equation (77), i.e., the parameter which appears in the expression (76) and represents the N1-N2 overlap effects. It turned out that the numerical values of the parameters δj (j = 1, 2), as well as of η, are practically independent of: the channel contribution considered (DD* or CC*), of the type of pseudoscalar mesons (M±, M′∓), and of the light leptons (ℓ1, ℓ2 = e, μ) involved in the considered decays. The numerical results show that the parameter δ ≡ (1/2)(δ1 + δ2) is a function of only one variable, namely (the same is true for η)
The numerical values of the parameter δ are given in Table 4 as a function of y. It is not clear whether there exists a simple analytic expression for δ as a function of y. Further, in Figure 14 we present the quantities η/y and δ as a function of y. The values for δ in Table 4 are practically equal to the values of the corresponding δ parameter in the rare leptonic decays of the charged pions π± → e±N → e±e±µ∓ν, cf. next Section 4.1 and Ref. [38].

Branching ratios of experimental significance here can be defined by dividing the expressions S∓(M), Equations (73) and (75) and (76), by the corresponding sum of total decay widths [Γ(M+ → all) + Γ(M− → all)], which is practically equal to 2Γ(M± → all)
If employing the canonical (independent of mixing) branching ratio defined in Equation (20) of Section 2.1, and its CC* analog, , then it turns out that the branching ratios Br±(M) of Equation (88) can be rewritten in terms of , of the heavy-light mixing parameters , and of function η(y)/y = y/(y2 + 1) and the overlap function δ(y) tabulated in Table 4
This leads to an expression for the CP violation parameter defined in Equation (68), which now involves only the heavy-light mixing parameters and [cf. Equation (18)], the function η(y)/y = y/(y2 + 1), where y ≡ ΔMN/ΓN, and the overlap function δ(y) tabulated in Table 4:
In the usually considered case ℓ1 = ℓ2 (≡ℓ), i.e., when the considered decays are M± → ℓ±ℓ±M′∓, the formulas (89) and (90) get simpler, because in such a case , and , and
These formulas become even simpler if the absolute values of the heavy-light mixings of N1 and N2 are equal (but not their phases), i.e., when
In such a case, we have all , and and therefore the expressions (91) reduce to
In these expressions, we assumed, in addition, that the N1-N2 overlap terms are small .
In order to obtain the corresponding effective (true) branching ratios, we have to multiply the above branching ratios Br± by the decay-within-the-detector probability , as in Section 2.2 (L is the length of the detector). Again, the complicated mixing dependence entailed in the parameters gets cancelled in this multiplication. When adopting the simplifying assumption Equation (92), i.e., the validity of Equations (93), we obtain the following effective branching ratio Breff and the CP violation effective branching ratio :
In these formulas, we used the canonical effective branching ratio as defined via Equations (32) and (20) and depicted in Figures 4–7 as a function of . The values of the Lorentz factors in the lab system are taken to be γN = 2 for both N1 and N2, keeping in mind that scales as 1/γN. We recall that . We notice that on the right-hand side of Equation (94a) there is an additional factor two in comparison with Equation (31b) of Section 2.2; this factor two comes from the fact that we now have contributions of two intermediate neutrinos N1 and N2, and we neglected the contributions from the N1-N2 overlap .
As at the end of Section 2.2, let us consider now as an illustrative example the decays . In addition, let us assume that |BµN|2 is the dominant mixing. In such a case, the estimate Equation (33) is still valid, and the CP-violating difference of the effective branching ratios, , is obtained by comparison of Equations (94a) and (94b)
Since for MN ≈ 1 GeV we have at present |BµN|2 ≲ 10−7, cf. Table 2, Equation (95) means that for such decays. As already mentioned at the end of Section 2.2, the proposed CERN-SPS experiment [80,81] could produce D and Ds mesons in numbers by several orders of magnitude higher than 1012, and production of the sterile Majorana neutrinos Nj could be explored. Further, if there exist two almost degenerate sterile neutrinos of mass MN ∼ 1 GeV (this is so in the νMSM model [60,61,67–72]), such that y ≡ ΔMN/ΓN ∼ 1, then we would have η(y)/y ≡ y/(y2+1) ∼ 1. In such a case the estimate (95) would imply that the CP-violating difference of effective branching ratios, , is of the same order as the effective branching ratio Br(eff)(Ds) (if the phase difference ). Therefore, if experiments can discover the mentioned νMSM-type Majorana neutrinos, they will possibly detect also CP violation effects coming from the Majorana neutrinos.
The case of is similar to the case of described above, cf. Equations (33) and (34) at the end of Section 2.2. Therefore, Equation (95) is valid also for CP violation in such decays of . For the relative advantages and disadvantages of and decays, we refer to the comments at the end of Section 2.2.
4.2. CP Violation in Pion Decays
In this Section, we will only briefly outline the calculation of the CP violation asymmetry in the (LNC and LNV) semileptonic decays as described in Section 3. We will assume the presence of at least two nearly degenerate sterile neutrinos Nj (j = 1, 2) that can go on shell in the intermediate state, as in Section 4.1. The present Section is a similar extension of the analysis of the decays of Section 3 to two sterile neutrinos. The results of the present Section are largely based on Ref. [38]. Only few details will be presented here, for further details we refer to Ref. [38].
Similarly to the previous Section 4.1, the quantities relevant for the CP violation will be
As in Section 4.1, the requirement that the quantities sin θ(X) (here: X = LNV, LNC) be nonzero, and the requirement of the near degeneracy of the two neutrinos in conjunction with the expressions Equations (79)–(83) for Im(P1(D)P2(D)∗), are needed in order that the CP violation parameters acquire nonnegligible values. Analysis similar to that of the previous Section 4.1 (but algebraically more complicated) leads then to the results for the quantities defined in Equations (96). More specifically, the results for the Dirac case, and , are the following:
The expression for the canonical quantity , appearing in Equation (98a), is given in Equation (53) in conjunction with the notation (46) in Section 3.1 The results for the Majorana case and are the following:
The function η(y)/y ≡ y/(y2+1). is the same as in Section 4.1 (with: y ≡ ΔMN/ΓN). Even more so numerical evaluations give for the N1-N2 overlap parameter δ(y) the same values as in the semileptonic decays of Section 4.1, cf. Table 4 and Figure 14 there.
If we assume that (for ℓ = e, μ, τ) i.e., Equation (92), then we have , and the expressions for simplify significantly
As in the case of semileptonic LNV decays of the previous Section 4.1, we see that the CP asymmetry parameter can become appreciable and even of order one if the following two conditions are fulfilled simultaneously: (a) at least one of the angles θ(X) (X=LNC,LNV), defined in Equation (97), is appreciable; (b) the quantity y ≡ ΔMN/ΓN is y ∼ 1 (near degeneracy). In such cases, the estimates for the effective (true) branching ratios of Equations (63) and (64) would apply also to the CP-violating difference of effective branching ratios, , where (X) = (Dir.),(Maj.).
5. Conclusions
We have studied lepton number violating (LNV) semileptonic decays of charged pseudoscalar mesons, specifically π±, K±, D±, , B± and , mediated by heavy neutrinos that can go on their mass shell.
We first presented the LNV semileptonic decays of charged Kaons and of the heavier mesons D±, , B± and , in processes of the form , mediated by on-shell massive neutrinos, where M is the decaying meson and M′ a correspondingly lighter meson. We estimated the branching ratios as functions of the neutrino masses and mixing parameters, and found the scenarios where upper limits on the mixing parameters can be obtained. We also studied the effect on the observability of these decays due to the long neutrino lifetime, as the secondary decay vertex is likely to fall outside the detector for the range of neutrino masses that are relevant to these processes.
We then presented our corresponding study of charged pion decays, which in this case are purely leptonic since pions are the lightest mesons. Here we can have modes that conserve lepton number (LNC) as well as modes that violate lepton number (LNV), if the intermediate neutrinos are of Majorana type, while only the former modes occur if the intermediate neutrino is of Dirac type. However, these modes are not distinguished by the final state because the latter involves a standard neutrino, which is not experimentally observable. We find that it could be possible to discern the Majorana or Dirac nature of neutrinos if one is able to observe features in the final state distribution.
We finally explored the possibility of observing CP violation in the lepton sector using these meson decays mediated by massive neutrinos on shell. The CP signal in charged meson decays is the usual asymmetry between the decays of opposite charge mesons. We found that leptonic CP violation may show in semileptonic LNV decays of charged Kaons and charged B mesons, as well as in LNC and LNV decays of charged pions, depending on the mass of the intermediate neutrinos. It turns out that such CP violation becomes appreciable and possibly detectable if there are at least two heavy neutrinos almost degenerate in mass that can go on their mass shell. The neutrino mass splitting that gives maximal CP asymmetries is close to the neutrino decay width. This type scenario fits well into the so called neutrino minimal standard model (νMSM), which contains two almost degenerate Majorana neutrinos of mass near 1 GeV and another lighter neutrino of mass of order 101 keV, a model that can explain simultaneously neutrino oscillations, the dark matter and the baryon asymmetry of the Universe.
Appendix
A.1. Explicit Formulas for Amplitudes of the Nj-mediated Decay
In this Appendix we provide, for completeness, formulas which are used in Sections 2 and 4.1. The formulas were presented in Ref. [39] for the case of exchange of two different neutrinos N1 and N2. Here we present them in a slightly more general form, when the number of exchanged neutrinos is . In Section 2 the simpler case of is taken, because such a case is representative enough for the consideration of the branching ratios there. On the other hand, the case (or: ) is taken in Section 4, with two of the neutrinos (N1, N2) considered on-shell and almost degenerate, because in such a case significant CP violation effects can arise in the Majorana neutrino sector.
The amplitude squared |τ (M±)|2 for the decay of Figure 1 appears in the expression Equation (3) for the decay width , and can be written in the form
Here, i, j = 1, …, are indices of contributions of the exchanges of intermediate neutrinos Ni, Nj, and X = D, C denote contributions of amplitudes of the direct and crossed channels, respectively, cf. Figure 1. Further, are the heavy-light mixing factors for Nj defined in Equation (70); Pj(X) (j = 1, 2; X = D, C) are the propagator functions of Nj neutrino for the D and C channel, Equation (72). K2 is the constant originating from the vertices and is given in Equation (9). These expressions appear in the normalized decay widths in Equation (7) when , and in in Equation (71) when . The quadratic expressions of T±(X)T±(Y )∗ in Equation (101) get simplified after summation over the final helicities of the leptons ℓ1 and ℓ2, and acquire the following form:
Here, is the totally antisymmetric Levi-Civita tensor with the sign convention ∊0123 = +1.
The expression (102), together with the definition (71), imply for the normalized decay widths of Equation (71) various symmetry relations, namely that and are self-adjoint matrices, and that elements of the D-C interference matrices and are simply related
If the two final leptons are of the same flavor (ℓ1 = ℓ2), one can use the property that the integration d3 over the final particles is symmetric under exchange of p1 and p2 (because ), and we have the following additional symmetries:
When , as in Section 2, then we have in the case of ℓ1 = ℓ2
A.2. Explicit Expression for the Function Q
The expression in Equations (12) and (78) is arrived at by using in the integration over the phase space of three final particles [Equations (3) and (4)], for the contribution of the N neutrino, the identity
The first identity can be used for the DD* contribution (where pN = pM − p1) and the second for the CC* contribution (where pN = pM − p2). When one uses the identity (10) in the DD* contribution, and the analogous identity for the CC* contribution, the integration over becomes trivial, and the d2-type of integrations can be performed. Notice that this is equivalent to the factorization approach Γ(M → ℓ1N)Br(N → ℓ2M′), which holds when N is on-shell. The obtained expression for is then the expression Equation (12) when [Equation (78) when ] with the notations (14), where the obtained function Q has the following form:
In the limit of massless charged leptons , this reduces to
A.3. Calculation of the Total Decay Width of Neutrino N
In this Appendix, for completeness, we summarize the formulas needed for evaluation of the total decay width of a massive sterile neutrino N, cf. Equations (16)–(18) and Figure 2.
In Ref. [29] (Appendix C there), the formulas for the leptonic decay and semimesonic decay widths of a sterile neutrino N have been obtained, for the masses MN ≲ 1 GeV. For higher values of the masses MN, the calculation of the semileptonic decay widths becomes difficult because not all the resonances are known. Hence, for such masses the authors of Refs. [30,113] proposed an inclusive approach, based on duality, for the calculation of the total contribution of the semileptonic decay width of N. It consists of representing the various (pseudoscalar and vector) meson channels by quark-antiquark channels. This approach was applied for . Here we summarize the formulas given in Ref. [30] for the decay width channels (cf. also: [29]). In some of these formulas, twice the decay width is given [2Γ(N → …)], signalling the fact that for each possible decay of Majorana neutrino in charged particles, there is an equally possible decay into charge conjugate channel (something not possible if N is Dirac particle).
In Equation (110a) factor 2 was included because for Majorana neutrino N both decays and contribute (ℓ ≠ ℓ).
When , the following semimesonic decays contribute, which involve presudoscalar (P ) and vector (V) mesons:
In the formulas (110)–(112) the notations xY ≡ MY/MN (Y = ℓ, νℓ, P, V, q) are used; and in Equation (112) we denoted: U = u, c; D = d, s, b; q = u, d, c, s, b. The values of quark masses which we used in our evaluations are: Mu = Md = 3.5 MeV; Ms = 105 MeV; Mc = 1.27 GeV; Mb = 4.2 GeV.
We note that in the evaluation of the total decay width ΓN, the expressions (112a) and (112b) should be added when N is Majorana; if N is Dirac, the same summation should be taken, but the expressions (112a) should be multiplied by 1/2. The same approach is valid also in the case of summation of expressions (110) and (111).
In Equations (110b) and (112b) there appear the following SM neutral current couplings:
Further, the neutral current couplings κV of the neutral vector mesons in Equation (111d) are
The following kinematical expressions I1, I2, FP and FV were used:
A.4. Explicit Amplitudes for Nj-Mediated Decays π± → e±e±µ∓ν
In this Appendix we summarize, for completeness, formulas needed in Sections 3 and 4.2. These formulas were derived and presented in Ref. [38], for the case of exchange of two different neutrinos N1 and N2. Here we summarize them in a slightly more general form, for the case of different neutrinos . In Section 3 the simpler case is taken, as it is sufficiently representative for the branching ratios considered there. In Section 4 the case (or: ) is considered, with two (on-shell) neutrinos N1 and N2 almost degenerate, as in such a case significant CP violation effects can occur in the neutrino sector.
The squared amplitude for the Nj-mediated leptonic decays of neutrinos, appearing, for example, in Equation (36) (where X = LNC, LNV), is a combination of contributions from the two channels D (direct) and C (crossed) (cf. Figures 8 and 9), and, in general, of the contributions of neutrinos Nj
The constant is given in Equation (42), and the mixing factors are
In the case of , these coefficients are in Equation (39). are the Nj-propagator functions [when : N-propagator functions of Equation (41)] of the direct and crossed channels (Y = D, C).
Explicit expressions for the direct (DD*), crossed (CC*) and direct-crossed interference (DC* and CD*) terms [ , , , ], appearing in Equations (116), get simplified when summed over the helicities of all the final leptons. In the case of the X = LNV processes (cf. Figure 9) they acquire the following form:
In the case of X = LNC processes (cf. Figure 8), the expressions are
These expressions appear in the definition of the normalized (i.e., without explicit mixing dependence) decay width matrices
When we use the symmetry of the d4 integration under the exchange p1 ↔ p2 (we note: M1 = M2 = Me in our considered case), this leads to the following identities:
In the case of this reduces simply to
A.5. Explicit Expression for and d /dEµ for π± → e±e±µ∓ν with On-Shell N
Equation (45) refers to the expression obtained by performing the integration (36) over the phase space of the four final particles [cf. Equation (37)], of the integrand written explicitly in Appendix 4. In the integration, the on-shellness (43) is assumed, which makes the integration over trivial. At the final stage of integration, the differential decay width over the muon energy Eμ, in the rest frame of the N neutrino, is performed. The expressions for were written in Refs. [37,38], and we write them down here for completeness. In the case of X = LNV it is
The integration of this expression over Eµ can be performed explicitly (in Ref. [37] it was performed only in the limit Me = 0). The result is Equation (45) with notations (46), where the function was obtained in Ref. [38]. We write it down here again, for completeness.
We can obtain the LNV canonical differential decay width, according to Equation (54), from the normalized differential decay width Equation (123). For this, it turns out to be convenient to use the following identity:
The LNC canonical differential decay width turns out to be
It turns out that, upon integration of this expression over Eµ, we obtain the same result as in the X = LNV case, i.e., Equations (53c) with (46) and (124), or equivalently, Equations (45) with (46) and (124). We must add that we found a typographical error in Equation (A.16) of Ref. [37], where must be replaced by , and in Equations (B.1c) and (B3) of Ref. [38], where (Eµ)max should read .
In the limit Me = 0 (which is a good approximation), the canonical differential decay widths (126) and (128) get simplified
The full (integrated) canonical branching ratio in the Me = 0 limit is obtained by taking the xe = 0 limit of Equation (53c)
A.6. Delta Function Approximation for the Imaginary Part of the Propagator Product
In this Appendix we investigate the expression for the imaginary part of the propagator product, Im(P1(D)P2(D)*), Equation (79a) of Section 4.1. For convenience we introduce in this Appendix the following simplified notations x, M2, Δ and ξ:
We note that Δ > 0 by convention; and 0 < ξ < 2. Further, , in accordance with the definition of ΓN Equation (82). Since we always have (the neutrinos Nj are sterile), the relation (80) holds, i.e.,
We can write the right-hand side of Equation (79a) for Im(P1(D)P2(D)*) as
In Equations (134b) and (134d), the identity (132) was used, and we introduced two (dimensionless) parameters ηj (j = 1, 2). We want to obtain these two parameters ηj. They can be obtained by integrating analytically the explicit expressions (134a) and (134c) for over x. For example, integration of gives
Therefore, in the case of near degeneracy (Δ≪M2) we have . If we now use in the integration over dx the expression (134b) instead, take into account in the case of near degeneracy, and compare with (135), we obtain the following expression for the parameter η1 by comparison with (135):
Doing the same procedure with the quantity R2, we obtain for η2 the very same result as for η1
Acknowledgments
This work was supported in part by FONDECYT, Chile Grants No. 1130599 (G.C. and C.S.K.) and No. 1130617 (C.D.), and projects PIIC 2014 and Mecesup FSM1204 (J.Z.S.). The work of C.S.K. was supported by the NRF grant funded by the Korean government of the MEST (No. 2011-0017430) and (No. 2011-0020333).
PACS classifications: 14.60St; 11.30Er; 13.20Cz
Author Contributions
This work is partly based on our previous works [26,37–40]. They represent a common effort of all the authors, and the same applies to the present work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Racah, G. On the symmetry of particle and antiparticle. Nuovo Cim 1937, 14, 322–328. [Google Scholar]
- Furry, W.H. On transition probabilities in double beta-disintegration. Phys. Rev. 1939, 56, 1184–1193. [Google Scholar]
- Primakoff, H.; Rosen, S.P. Double beta decay. Rep. Prog. Phys. 1959, 22, 121–166. [Google Scholar]
- Primakoff, H.; Rosen, S.P. Nuclear double-beta decay and a new limit on lepton nonconservation. Phys. Rev. 1969, 184, 1925–1933. [Google Scholar]
- Primakoff, H.; Rosen, S.P. Baryon number and lepton number conservation laws. Ann. Rev. Nucl. Part. Sci. 1981, 31, 145–192. [Google Scholar]
- Schechter, J.; Valle, J.W.F. Neutrinoless double beta decay in theories. Phys. Rev. D 1982, 25, 2951–2954. [Google Scholar]
- Doi, M.; Kotani, T.; Takasugi, E. Double beta decay and Majorana neutrino. Prog. Theor. Phys. Suppl. 1985, 83, 1–368. [Google Scholar]
- Elliott, S.R.; Engel, J. Double beta decay. J. Phys. G 2004, 30, R183–R215. [Google Scholar]
- Rodin, V.A.; Faessler, A.; Šimković, F.; Vogel, P. Assessment of uncertainties in QRPA 0vββ-decay nuclear matrix elements. In Nucl. Phys. A; 2006; Volume 766, pp. 107–131. [Google Scholar]
- Rodin, V.A.; Faessler, A.; Šimkovic, F.; Vogel, P. Erratum to: “Assessment of uncertainties in QRPA 0νββ-decay nuclear matrix elements” [Nucl. Phys. A 766 (2006) 107]. Nucl. Phys. A 2007, 793, 213–215. [Google Scholar]
- Keung, W.Y.; Senjanović, G. Majorana neutrinos and the production of the right-handed charged gauge boson. Phys. Rev. Lett 1983, 50, 1427–1430. [Google Scholar]
- Tello, V.; Nemevšek, M.; Nesti, F.; Senjanović, G.; Vissani, F. Left-right symmetry: From LHC to neutrinoless double beta decay. Phys. Rev. Lett 2011, 106. [Google Scholar] [CrossRef]
- Nemevšek, M.; Nesti, F.; Senjanović, G.; Tello, V. Neutrinoless double beta decay: Low left-right symmetry scale? Available online: http://arxiv.org/abs/1112.3061 accessed on 27 April 2015.
- Senjanović, G. Neutrino mass: From LHC to grand unification. Riv. Nuovo Cim. 2011, 34, 1–68. [Google Scholar]
- Buchmüller, W.; Greub, C. Heavy Majorana neutrinos in electron-positron and electron-proton collisions. Nucl. Phys. B 1991, 363, 345–368. [Google Scholar]
- Helo, J.; Hirsch, M.; Kovalenko, S. Heavy neutrino searches at the LHC with displaced vertices. Phys. Rev. D 2014, 89. [Google Scholar] [CrossRef]
- Kohda, M.; Sugiyama, M.; Tsumura, K. Lepton number violation at the LHC with leptoquark and diquark. Phys. Lett. B 2013, 718, 1436–1440. [Google Scholar]
- Chen, C.Y.; Bhupal Dev, P.S. Multi-lepton collider signatures of heavy Dirac and Majorana neutrinos. Phys. Rev. D 2012, 85. [Google Scholar] [CrossRef]
- Chen, C.Y.; Bhupal Dev, P.S.; Mohapatra, R.N. Probing heavy-light neutrino mixing in Left-Right Seesaw models at the LHC. Phys. Rev. D 2013, 88. [Google Scholar] [CrossRef]
- Bhupal Dev, P.S.; Pilaftsis, A.; Yang, U.-K. New production mechanism for heavy neutrinos at the LHC. Phys. Rev. Lett 2014, 112, 081801:1–081801:5. [Google Scholar]
- Das, A.; Bhupal Dev, P.S.; Okada, N. Direct bounds on electroweak scale pseudo-Dirac neutrinos from TeV LHC data. Phys. Lett. B 2014, 735, 364–370. [Google Scholar]
- Littenberg, L.S.; Shrock, R.E. Upper bounds on lepton number violating meson decays. Phys. Rev. Lett 1992, 68, 443–446. [Google Scholar]
- Littenberg, L.S.; Shrock, R.E. Implications of improved upper bounds on |ΔL| = 2 processes. Phys. Lett. B 2000, 491, 285–290. [Google Scholar]
- Dib, C; Gribanov, V.; Kovalenko, S.; Schmidt, I. K meson neutrinoless double muon decay as a probe of neutrino masses and mixings. Phys. Lett. B 2000, 493, 82–87. [Google Scholar]
- Ali, A.; Borisov, A.V.; Zamorin, N.B. Majorana neutrinos and same sign dilepton production at LHC and in rare meson decays. Eur. Phys. J. C 2001, 21, 123–132. [Google Scholar]
- Cvetič, G.; Dib, C.; Kang, S.K.; Kim, C.S. Probing Majorana neutrinos in rare K and D, Ds, B, Bc meson decays. Phys. Rev. D 2010, 82. [Google Scholar] [CrossRef]
- Ivanov, M.A.; Kovalenko, S.G. Hadronic structure aspects of decays. Phys. Rev. D 2005, 71. [Google Scholar] [CrossRef]
- De Gouvea, A.; Jenkins, J. A Survey of lepton number violation via effective operators. Phys. Rev. D 2008, 77. [Google Scholar] [CrossRef]
- Atre, A.; Han, T.; Pascoli, S.; Zhang, B. The Search for heavy Majorana neutrinos. JHEP 2009, 0905. [Google Scholar] [CrossRef]
- Helo, J.C.; Kovalenko, S.; Schmidt, I. Sterile neutrinos in lepton number and lepton flavor violating decays. Nucl. Phys. B 2011, 853, 80–104. [Google Scholar]
- Quintero, N.; López Castro, G.; Delepine, D. Lepton number violation in top quark and neutral B meson decays. Phys. Rev. D 2011, 84. [Google Scholar] [CrossRef]
- Quintero, N.; López Castro, G.; Delepine, D. Erratum: Lepton number violation in top quark and neutral B meson decays [Phys. Rev. D 84, 096011 (2011)]. Phys. Rev. D 2012, 86. [Google Scholar] [CrossRef]
- López Castro, G.; Quintero, N. Bounding resonant Majorana neutrinos from four-body B and D decays. Phys. Rev. D 2013, 87. [Google Scholar] [CrossRef]
- Abada, A.; Teixeira, A.M.; Vicente, A.; Weiland, C. Sterile neutrinos in leptonic and semileptonic decays. JHEP 1402, 091. [CrossRef]
- Wang, Y.; Bao, S.S.; Li, Z.H.; Zhu, N.; Si, Z.G. Study Majorana neutrino contribution to B-meson semi-leptonic rare decays. Phys. Lett. B 2014, 736, 428–432. [Google Scholar]
- Boyanovsky, D. Nearly degenerate heavy sterile neutrinos in cascade decay: Mixing and oscillations. Phys. Rev. D 2014, 90. [Google Scholar] [CrossRef]
- Cvetič, G.; Dib, C.; Kim, C.S. Probing Majorana neutrinos in rare decays. JHEP 2012, 1206. [Google Scholar] [CrossRef]
- Cvetič, G.; Kim, C.S.; Zamora-Saá, J. CP violations in meson decay. J. Phys. G 2014, 41. [Google Scholar] [CrossRef]
- Cvetič, G.; Kim, C.S.; Zamora-Saá, J. CP violation in lepton number violating semileptonic decays of K, D, Ds,B, Bc. Phys. Rev. D2014, 89. [Google Scholar] [CrossRef]
- Dib, CO.; Campos, M.; Kim, C.S. CP Violation with Majorana neutrinos in K meson decays. JHEP 2015, 1502. [Google Scholar] [CrossRef]
- Super-Kamiokande Collaboration. Evidence for oscillation of atmospheric neutrinos. Phys. Rev. Lett 1998, 81, 1562–1567.
- SNO Collaboration. Direct evidence for neutrino flavor transformation from neutral current interactions in the Sudbury Neutrino Observatory. Phys. Rev. Lett 2002, 89. [CrossRef]
- Lipari, P. CP violation effects and high-energy neutrinos. Phys. Rev. D 2001, 64. [Google Scholar] [CrossRef]
- Rahman, Z.; Dasgupta, A.; Adhikari, R. Non-standard interaction effect on CP violation in neutrino oscillation with super-beam, Available online: http://arxiv.org/abs/1210.2603 accessed on 28 April 2015.
- Rahman, Z.; Dasgupta, A.; Adhikari, R. Discovery reach of CP violation and non-standard interactions in low energy neutrino factory, Available online: http://arxiv.org/abs/1210.4801 accessed on 28 April 2015.
- KamLAND Collaboration. First results from KamLAND: Evidence for reactor anti-neutrino disappearance. Phys. Rev. Lett. 2003, 90. [CrossRef]
- Planck Collaboration. Planck 2013 results. XVI. Cosmological parameters. Astron. Astrophys. 2014, 571, A16:1–A16:66.
- Minkowski, P. at a rate of one out of 1-billion muon decays? Phys. Lett. B 1977, 67, 421–428. [Google Scholar]
- Gell-Mann, M.; Ramond, P.; Slansky, R. The Family Group in Grand Unified Theories. In Supergravity; van Nieuwenhuizen, P., Freedman, D.Z., Eds.; North-Holland: Amsterdam, The Netherlands, 1979. [Google Scholar]
- Yanagida, T. Horizontal symmetry and masses of neutrinos. Prog. Theor. Phys. 1980, 64, 1103–1105. [Google Scholar]
- Glashow, S.L. Quarks and Leptons; Lévy, M., Basdevant, J.-L., Speiser, D., Weyers, J., Gastmans, R., Jacob, M., Eds.; Cargese, Plenum: New York, NY, USA, 1980. [Google Scholar]
- Mohapatra, R.N.; Senjanović, G. Neutrino mass and spontaneous parity violation. Phys. Rev. Lett 1980, 44, 912–915. [Google Scholar]
- Wyler, D.; Wolfenstein, L. Massless neutrinos in left-right symmetric models. Nucl. Phys. B 1983, 218, 205–214. [Google Scholar]
- Witten, E. Symmetry breaking patterns in superstring models. Nucl. Phys. B 1985, 258, 75–100. [Google Scholar]
- Mohapatra, R.N.; Valle, J.W.F. Neutrino mass and baryon number nonconservation in superstring models. Phys. Rev. D 1986, 34, 1642–1645. [Google Scholar]
- Malinsky, M.; Romao, J.C.; Valle, J.W.F. Novel supersymmetric SO(10) seesaw mechanism. Phys. Rev. Lett 2005, 95, 161801:1–161801:5. [Google Scholar]
- Dev, P.S.B.; Mohapatra, R.N. TeV Scale Inverse Seesaw in SO(10) and Leptonic Non-Unitarity Effects. Phys. Rev. D 2010, 81. [Google Scholar] [CrossRef]
- Dev, P.S.B.; Pilaftsis, A. Minimal Radiative Neutrino Mass Mechanism for Inverse Seesaw Models. Phys. Rev. D 2012, 86. [Google Scholar] [CrossRef]
- Lee, C.H.; Dev, P.S.B.; Mohapatra, R.N. Natural TeV-scale left-right seesaw mechanism for neutrinos and experimental tests. Phys. Rev. D 2013, 88. [Google Scholar] [CrossRef]
- Asaka, T.; Blanchet, S.; Shaposhnikov, M. The νMSM, dark matter and neutrino masses. Phys. Lett. B 2005, 631, 151–156. [Google Scholar]
- Asaka, T.; Shaposhnikov, M. The νMSM, dark matter and baryon asymmetry of the universe. Phys. Lett. B 2005, 620, 17–26. [Google Scholar]
- He, X.G.; Oh, S.; Tandean, S.J.; Wen, C.C. Large mixing of light and heavy neutrinos in seesaw models and the LHC. Phys. Rev. D 2009, 80. [Google Scholar] [CrossRef]
- Del Aguila, F.; Aguilar-Saavedra, J.A.; de Blas, J.; Zralek, M. Looking for signals beyond the neutrino Standard Model. Acta Phys. Polon. B 2007, 38, 3339–3348. [Google Scholar]
- Kersten, J.; Smirnov, A.Y. Right-handed neutrinos at CERN LHC and the mechanism of neutrino mass generation. Phys. Rev. D 2007, 76. [Google Scholar] [CrossRef]
- Ibarra, A.; Molinaro, E.; Petcov, S.T. TeV scale see-saw mechanisms of neutrino mass generation, the Majorana nature of the heavy singlet neutrinos and (ββ)0ν-Decay. JHEP 2010, 1009, 108–129. [Google Scholar]
- Cabibbo, N. Time reversal violation in neutrino oscillation. Phys. Lett. B 1978, 72, 333–335. [Google Scholar]
- Gorbunov, D.; Shaposhnikov, M. How to find neutral leptons of the νMSM? JHEP 2007, 0710. [Google Scholar] [CrossRef]
- Shaposhnikov, M. Is there a new physics between electroweak and Planck scales? Available online: http://arxiv.org/abs/0708.3550 accessed on 28 April 2015.
- Boyarsky, A.; Ruchayskiy, O.; Shaposhnikov, M. The role of sterile neutrinos in cosmology and astrophysics. Ann. Rev. Nucl. Part. Sci. 2009, 59, 191–214. [Google Scholar]
- Shaposhnikov, M. Neutrino physics within and beyond the three flavour oscillation. J. Phys. Conf. Ser. 2013, 408. [Google Scholar] [CrossRef]
- Canetti, L.; Drewes, M.; Shaposhnikov, M. Sterile neutrinos as the origin of dark and baryonic matter. Phys. Rev. Lett 2013, 110. [Google Scholar] [CrossRef]
- Canetti, L.; Drewes, M.; Frossard, T; Shaposhnikov, M. Dark matter, baryogenesis and neutrino oscillations from right handed neutrinos. Phys. Rev. D 2013, 87. [Google Scholar] [CrossRef]
- Canetti, L.; Drewes, M.; Garbrecht, B. Probing leptogenesis with GeV-scale sterile neutrinos at LHCb and Belle II. Phys. Rev. D 2014, 90. [Google Scholar] [CrossRef]
- Drewes, M.; Garbrecht, B. Experimental and cosmological constraints on heavy neutrinos, Available online: http://arxiv.org/abs/1502.00477 accessed on 28 April 2015.
- Pilaftsis, A. CP violation and baryogenesis due to heavy Majorana neutrinos. Phys. Rev. D 1997, 56, 5431–5451. [Google Scholar]
- Bray, S.; Lee, J.S.; Pilaftsis, A. Resonant CP violation due to heavy neutrinos at the LHC. Nucl. Phys. B 2007, 786, 95–118. [Google Scholar]
- Akhmedov, E.; Kartavtsev, A.; Lindner, M.; Michaels, L.; Smirnov, J. Improving Electro-Weak Fits with TeV-scale Sterile Neutrinos. JHEP 2013, 1305. [Google Scholar] [CrossRef]
- Qian, X.; Zhang, C; Diwan, M.; Vogel, P. Unitarity Tests of the Neutrino Mixing Matrix, Available online: http://arxiv.org/abs/1308.5700 accessed on 28 April 2015.
- Basso, L.; Fischer, O.; van der Bij, JJ. Precision tests of unitarity in leptonic mixing. Europhys. Lett. 2014, 105. [Google Scholar] [CrossRef]
- Bonivento, W.; Boyarsky, A.; Dijkstra, H.; Egede, U.; Ferro-Luzzi, M.; Goddard, B.; Golutvin, A.; Gorbunov, D.; Jacobsson, R.; Panman, J.; et al. Proposal to Search for Heavy Neutral Leptons at the SPS, Available online: http://arxiv.org/abs/1310.1762 accessed on 28 April 2015.
- Jacobson, R. Search for heavy neutral neutrinos at the SPS, Presented at High Energy Physics in the LHC Era, UTFSM, Valparaíso, Chile, 16–20 December 2014; Available online: https://indico.cern.ch/event/252857/contribution/215 accessed on 29 April 2015.
- Dib, CO.; Kim, C.S. Remarks on the lifetime of sterile neutrinos and the effect on detection of rare meson decays M+ → M′ − ℓ+ℓ+. Phys. Rev. D2014, 89. [Google Scholar] [CrossRef]
- Beneš, P.; Faessler, A.; Šimković, F.; Kovalenko, S. Sterile neutrinos in neutrinoless double beta decay. Phys. Rev. D 2005, 71. [Google Scholar] [CrossRef]
- Bélanger, G.; Boudjema, F.; London, D.; Nadeau, H. Inverse neutrinoless double beta decay revisited. Phys. Rev. D 1996, 53, 6292–6301. [Google Scholar]
- London, D. Inverse neutrinoless double beta decay (and other ΔL = 2 processes), Available online: http://arxiv.org/abs/hep-ph/9907419 accessed on 28 April 2015.
- Kusenko, A.; Pascoli, S.; Semikoz, D. New bounds on MeV sterile neutrinos based on the accelerator and Super-Kamiokande results. JHEP 2005, 0511. [Google Scholar] [CrossRef]
- WA66 Collaboration. Search for heavy neutrino decays in the BEBC beam dump experiment. Phys. Lett. B 1985, 160, 207–211.
- NA3 Collaboration. Mass and lifetime limits on new longlived particles in 300GeV/c π− interactions. Z. Phys. C 1986, 31, 21–32.
- Bernardi, G.; Carugno, G.; Chauveau, J.; Dicarlo, F.; Dris, M.; Dumarchez, J.; Ferro-Luzzi, M.; Levy, J.-M.; Lukas, D.; Perreau, J.-M.; et al. Further limits on heavy neutrino couplings. Phys. Lett. B 1988, 203, 332–334. [Google Scholar]
- FMMF Collaboration. Search for neutral weakly interacting massive particles in the Fermilab Tevatron wide band neutrino beam. Phys. Rev. D 1995, 52. [CrossRef]
- NuTeV and E815 Collaborations. Search for neutral heavy leptons in a high-energy neutrino beam. Phys. Rev. Lett 1999, 83, 4943–4946.
- L3 Collaboration. Search for isosinglet neutral heavy leptons in Z0 decays. Phys. Lett. B 1992, 295, 371–382.
- CHARM II Collaboration. Search for heavy isosinglet neutrinos. Phys. Lett. B 1995, 343, 453–458, Phys. Lett. B 1995, 351, 387–392.
- DELPHI, Collaboration. Search for neutral heavy leptons produced in Z decays. Z. Phys. C 1997, 74, 57–71. [Google Scholar]
- NOMAD Collaboration. Search for heavy neutrinos mixing with tau neutrinos. Phys. Lett. B 2001, 506, 27–38.
- Orloff, J.; Rozanov, A.N.; Santoni, C. Limits on the mixing of tau neutrino to heavy neutrinos. Phys. Lett. B 2002, 550, 8–15. [Google Scholar]
- Particle Data Group Collaboration. Review of Particle Physics. Chin. Phys. C 2014, 38. [CrossRef]
- Cvetič, G.; Kim, C.S.; Wang, G.L.; Namgung, W. Decay constants of heavy meson of 0-state in relativistic Salpeter method. Phys. Lett. B 2004, 596, 84–89. [Google Scholar]
- PIENU, Collaboration. Search for massive neutrinos in the decay π → eν. Phys. Rev. D 2011, 84. [Google Scholar] [CrossRef]
- Yamazaki, T.; Ishikawa, T.; Akiba, Y.; Iwasaki, M.; Tanaka, K.H.; Ohtake, S.; Tamura, H.; Nakajima, M.; Yamanaka, T.; Arai, I.; et al. Search for Heavy Neutrinos in Kaon Decay. Conf. Proc. C 1984, 840719, 262–262. [Google Scholar]
- Hayano, R.S.; Taniguchi, T.; Yamanaka, T.; Tanimori, T.; Enomoto, R.; Ishibashi, A.; Ishikawa, T.; Sato, S.; Fujii, T.; Yamazaki, T.; et al. Heavy neutrino search using Kμ2 decay. Phys. Rev. Lett 1982, 49. [Google Scholar] [CrossRef]
- Kusenko, A.; Pascoli, S.; Semikoz, D. New bounds on MeV sterile neutrinos based on the accelerator and Super-Kamiokande results. JHEP 2005, 0511. [Google Scholar] [CrossRef]
- Orloff, J.; Rozanov, A.N.; Santoni, C. Limits on the mixing of tau neutrino to heavy neutrinos. Phys. Lett. B 2002, 550, 8–15. [Google Scholar]
- Ruchayskiy, O.; Ivashko, A. Experimental bounds on sterile neutrino mixing angles. JHEP 2012, 1206. [Google Scholar] [CrossRef]
- Deppisch, F.F.; Dev, P.S.B.; Pilaftsis, A. Neutrinos and Collider Physics, Available online: http://arxiv.org/abs/1502.06541 accessed on 28 April 2015.
- Project X and the Science of the Intensity Frontier, Proceedings of the Project X Physics Workshop, Fermilab, USA, 9–10 November 2009; Available online: http://www.fnal.gov/projectx/pdfs/ProjectXwhitepaperJan.v2.pdf accessed on 29 April 2015.
- Geer, S. Private communication; Fermilab: Batavia, IL, USA, 2012. [Google Scholar]
- Pontecorvo, B. Inverse beta processes and nonconservation of lepton charge. Sov. Phys. JETP 1958, 7, 172–173, Zh. Eksp. Teor. Fiz. 1957, 34, 247. [Google Scholar]
- Neutrino experiments and the problem of conservation of leptonic charge. Sov. Phys. JETP 1968, 26, 984–988, Zh. Eksp. Teor. Fiz. 1967, 53, 1717.
- Maki, Z.; Nakagawa, M.; Sakata, S. Remarks on the unified model of elementary particles. Prog. Theor. Phys. 1962, 28, 870–880. [Google Scholar]
- Bilenky, S. Introduction to the Physics of Massive and Mixed Neutrinos; Lecture Notes in Physics 817; Springer Verlag: Berlin, Heidelberg, Germany, 2010. [Google Scholar]
- Gamiz, E.; Prades, J.; Scimemi, I. Charged kaon K → 3π CP violating asymmetries at NLO in CHPT. JHEP 2003, 0310. [Google Scholar] [CrossRef]
- Gribanov, V.; Kovalenko, S.; Schmidt, I. Sterile neutrinos in tau lepton decays. Nucl. Phys. B 2001, 607, 355–368. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).