Fluctuating and Directional Asymmetry of the Blue Mussel (Mytilus edulis): Improving Methods of Morphological Analysis to Explore Species Performance at the Northern Border of Its Range
Abstract
: In this work we examined morphological variation at different levels to study performance and population structuring of the blue mussel Mytilus edulis. Our objectives were: (i) to develop an integrated technique for analyzing morphological variation in blue mussels and, based on this technique; (ii) to perform a morphometric description of mussels from the northern part of their range; and (iii) to verify the hypothesis that populations at the outer range of their distribution have reduced performance due to harsh climatic conditions. Means, directional asymmetry (i.e., systematic differences between left and right structures), fluctuating asymmetry (random deviations from perfect symmetry, a measure of developmental instability), factorial variation (difference between total variance and variance of fluctuating asymmetry, an indirect index of genotypic variation), and measurement error were examined for 14 bilateral characters of muscle scars on mussel shells. Also, we analyzed one non-bilateral character. For the first time directional asymmetry—approaching 13% of the right:left ratio—was described in blue mussels. Measurement error, often ignored in morphometric studies, contributed 26% of total variance. Accurately addressing these methodical challenges is key to further and improved ecological interpretations. Morphological differences were found between (i) samples from estuarine areas in the White and Pechora Seas and (ii) samples from Barents Sea areas with oceanic salinity. Samples from the first group exhibited lower fluctuating asymmetry, indicating higher developmental stability likely due to better feeding conditions and lower factorial variation, which may result from lower genotypic variation. Absence of correlation between fluctuating asymmetry and temperature suggests that low temperatures in the northern border of their range do not degrade the performance of adult blue mussels in this region.1. Introduction
Morphological variation can provide important information on population structuring and performance. In biological systems, morphological variation can be examined at different organizational levels: (i) among populations; (ii) among individuals within a population; and (iii) within an individual. Any single measurement is associated with measurement error (ME), which increases the variance.
Most morphological studies take place at the first level, i.e., comparing populations as represented by an ideal average individual described by the mean values of morphological characters. The mean values are determined by environmental conditions and the population’s gene pool.
The statistical dispersion of individuals around an ideal average characterizes the second level of variation. This includes within-population heterogeneity caused by genetic differences among individuals, macro- and micro-heterogeneity caused by local environmental variation, and ontogenetic variation representing variation among different stages of ontogenesis. Together these second-level components of phenotypic variation make up the heterogeneity of individuals within a population, and can be called factorial components [1–3].
The third level—variation within an individual—expresses differences between an individual’s symmetrical structures, i.e., as fluctuating asymmetry (FA), the random non-directional deviations from perfect symmetry [4]. The third level refers to the stochastic component of total variance [3]. FA has generated interest among population biologists because it reflects one of the components of fitness—developmental stability, i.e., the ability of an organism to consistently produce an “ideal” phenotype in a given environment [5]. Although an association between FA and fitness is not always observed in empirical studies, recent reviews concluded that, overall, FA can be considered a useful tool for assessing a population’s average fitness [6–8].
Developmental stability can be influenced by endogenous and exogenous factors. Factors affecting genetic coadaptation—such as heterozygosity levels, the appearance of new mutant genes, and directional selection—belong to the first group, whereas deviation from optimum environmental conditions belongs to the second group. Organisms experiencing genetic or environmental stress have lower developmental stability and exhibit a greater level of FA. Thus FA is often monitored to detect populations under stress [5,7,9,10].
In addition to FA, there are two other types of asymmetry—directional asymmetry (DA) and antisymmetry [4,9]. Directional asymmetry occurs as a unimodal distribution, where a structure is normally more developed on one side of the body than the other. Antisymmetry appears as a bimodal distribution, where greater structural development occurs on either side of the body with approximately equal frequency. These types of asymmetry are genetic and generally would be expressed in similar degree (within normal variation) for all individuals in a population. Hence, DA and antisymmetry comprise the first level of morphological variation from the ideal average individual that describes the population. This differentiates DA and antisymmetry from FA—a characteristic of within-individual variability. In each measurement, ME can be caused by instrument error, alterations in operator protocol, and changes in specimen position during analysis. ME is of great concern in FA studies: Since levels of FA are typically quite small in comparison with trait size, ME can account for a large fraction of between-side variance. In some cases ME exceeds 50% of FA [11–13]. Therefore, ME must be rigorously accounted for in FA studies because differences in ME across various samples can alter the results of their comparison. Fortunately, it can be evaluated with a series of replicated measurements.
The marine mussel Mytilus edulis dominates many coastal communities in boreal seas, thus determining important ecosystem characteristics. Also common in aquaculture, these widespread, readily available bivalves have always been of interest to scientists [14,15]. In the northwestern Atlantic, blue mussels are distributed all along Europe’s Atlantic coast from France to the southeastern part of the Barents Sea (the Pechora Sea) and the western parts of the Kara Sea, the northeastern limit of the species’ range [16,17]. It was also recently recorded in Svalbard [18].
Arctic areas are characterized by much lower temperatures and a shorter feeding season than more temperate areas like the subarctic White Sea and the western Barents Sea [19,20]. It has been hypothesized that further distribution of this boreal species northeastward is limited by temperature and/or temperature-dependent factors [17,21]. However, contrary to expectations, blue mussels at their northern range limit were found to have growth rates, maximal sizes, longevity, weight indices, and glycogen tissue content similar to conspecifics from the White Sea, the same as from the distributional center [17,22]. No genetic differences between M. edulis from different parts of their range were reported [17,23]. Further investigations focused on other population characteristics may help to explain the performance of the northernmost populations of Mytilus edulis and identify causes limiting their distribution. This is especially important at a time of increasing temperatures, which are more pronounced in the Arctic than in other areas.
In this paper we complete the population and physiological description of blue mussel samples obtained from the southwestern Arctic in the late 1990s (allozyme genetics, physiological performance: [17]; growth performance: [22]). Since that time, temperatures have continuously increased in the Barents Sea [24,25]. Our data therefore can draw a baseline for further monitoring of Arctic mussel populations under changing climate.
The objectives of this study were: (i) to develop a technique for analyzing morphological variation in the blue mussel (Mytilus edulis) and, based on this technique, (ii) to describe the morphology of mussels from the northern part of their range; and (iii) to test the hypothesis that populations at the northern boundary of their range have reduced performance due to harsh climatic conditions.
2. Materials and Methods
2.1. Samples
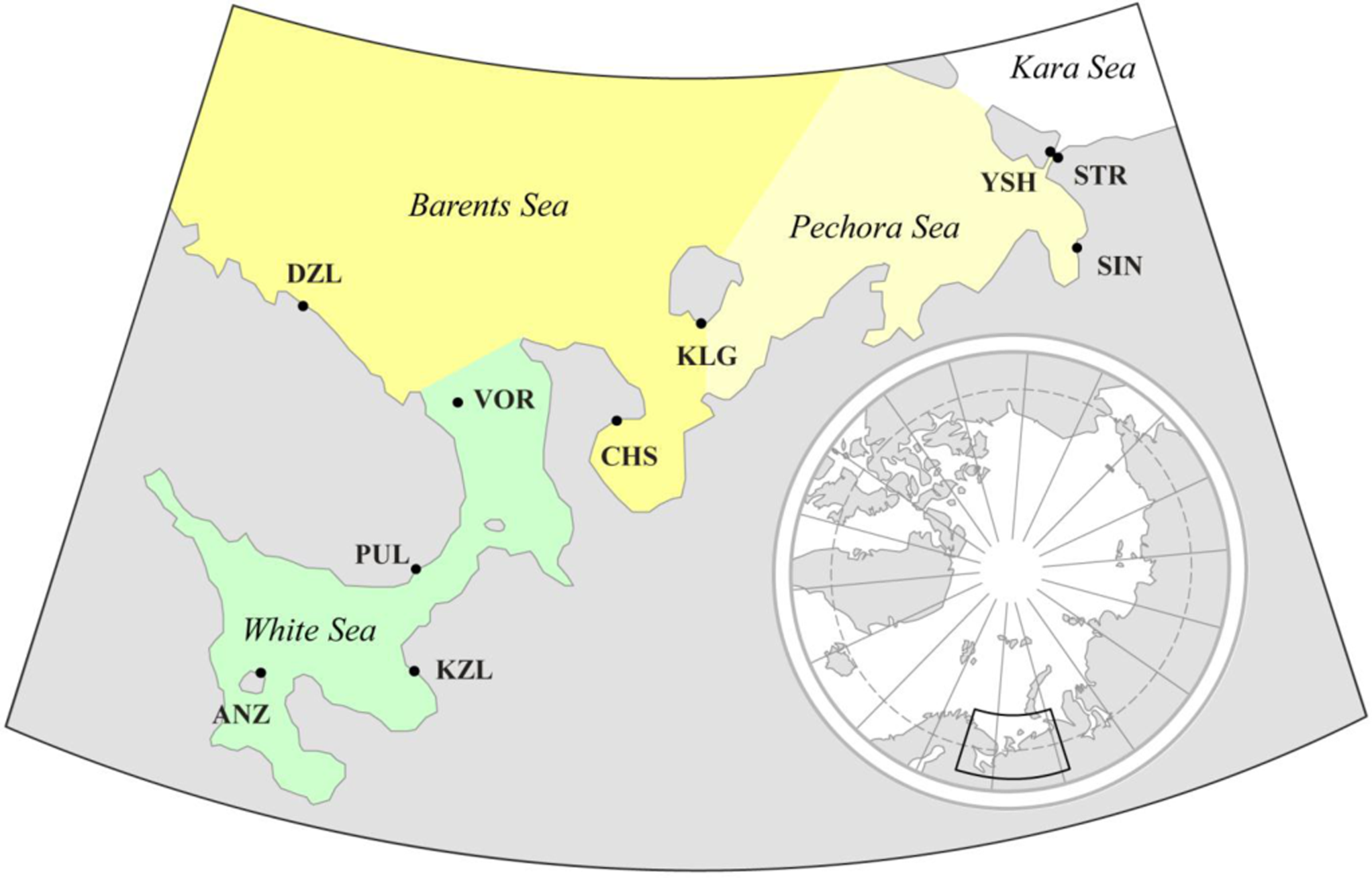
Ten samples of M. edulis were collected in different parts of the White, Barents, and Pechora Seas within a period of two weeks in July–August 1997 during expedition of research vessel “Professor Vladimir Kuznetsov” (Figure 1). Each sample consisted of 40 individuals between 21 and 64 mm in length. A detailed description of samples and environmental conditions is given in Table 1. Each sample was collected from an area with conditions as homogeneous as possible in order to minimize morphological variation caused by environmental heterogeneity. Samples used in this study were obtained from the same locations as those collected by Sukhotin and coauthors [22] (see Table 1 for details), yet we chose different individuals than those examined in 2007. Our study contained fewer samples because not all of them included sufficient numbers of individuals, or covered areas that were sufficiently homogenous. Water temperature and salinity at corresponding depths were measured at the time of sampling (Table 1).
2.2. Morphological Measurements
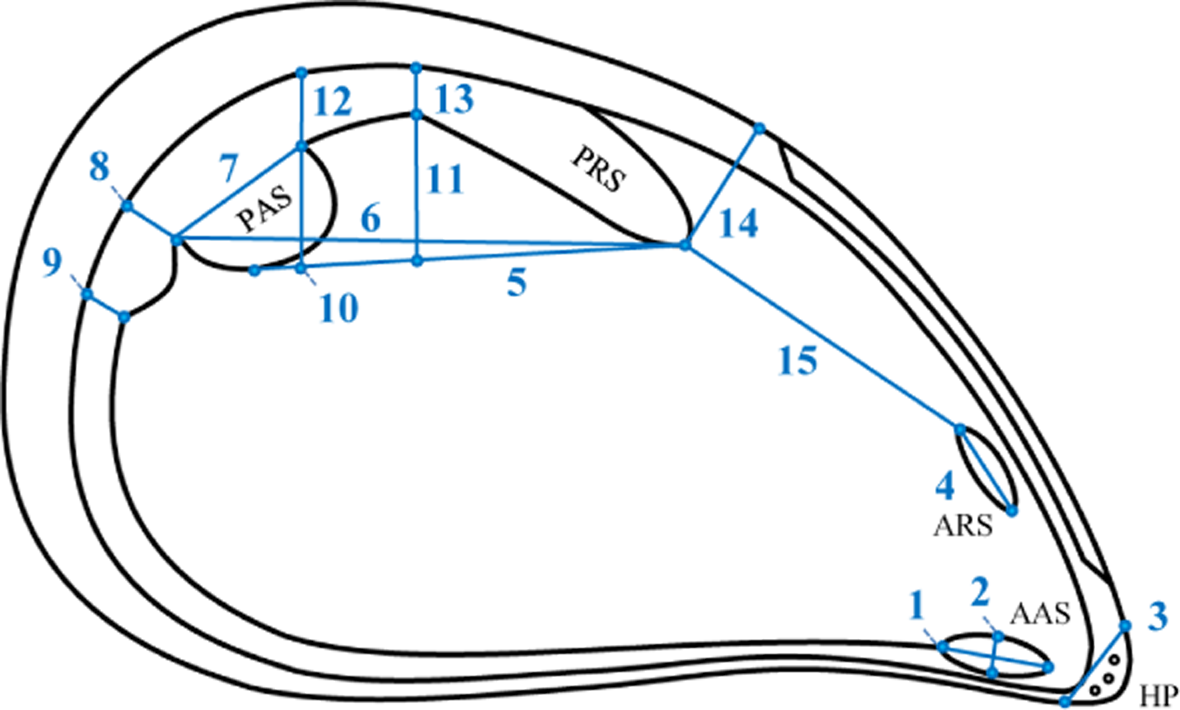
Fifteen characters of muscle scars on the internal shell surface were analyzed (Figure 2). Four of these characters, marked with asterisks on Figure 2, were used in earlier morphological studies of blue mussels [16–20]; the others are used here for the first time. Fourteen characters were measured on both the left and right sides of each shell. Character 3, the length of the hinge plate breakage, was measured on the left side only because it is identical on both sides. Characters were measured using a stereomicroscope MBS-9 fitted with a calibrated eyepiece. To assess measurement error (ME), repeated measurements of 15 shells randomly chosen from each sample were analyzed. All measurements were made by one operator (Marina Katolikova).
2.3. Statistical Analysis
2.3.1. Size and Shape of Muscle Scars
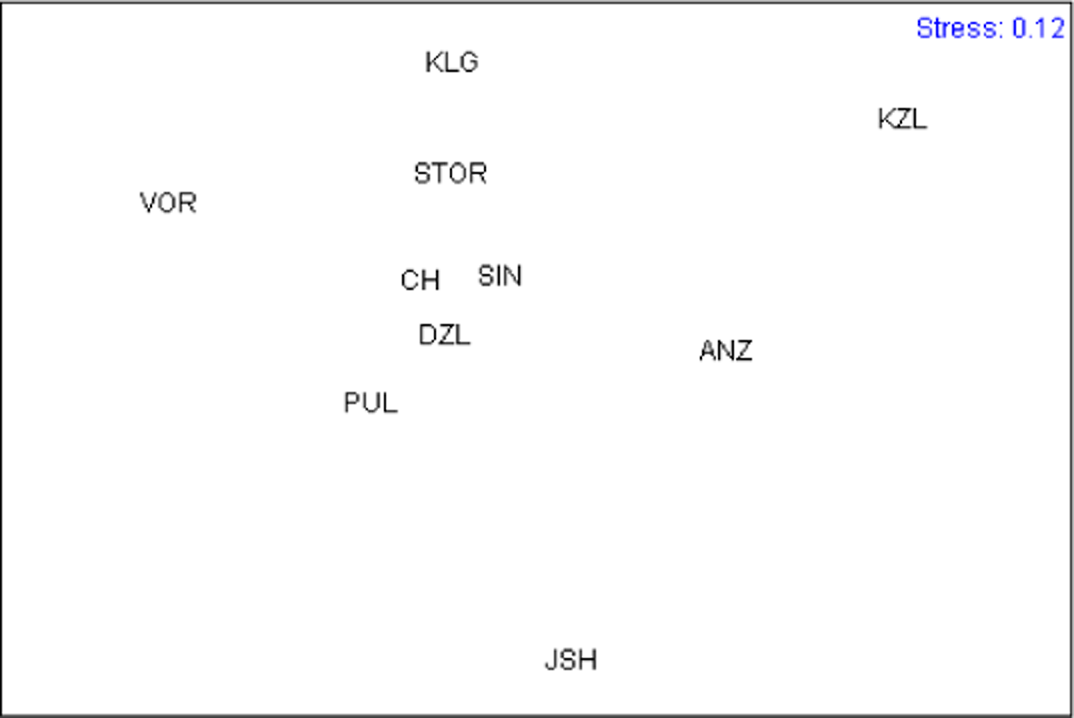
For comparing samples by the size and shape of muscle scars we performed Principal Component Analysis for mean values between the left and right sides. One-way ANOVA tested the significance of the differences between samples in the Principal Component scores. Multidimensional scaling of samples was performed with all Principal Components except PC1, which reflected size, using Euclidean distances as a measure of similarity.
To reveal the characters responsible for the observed patterns of morphological variation, we considered the values of each character predicted for a shell length of 40 mm, based on “log-transformed character–log-transformed shell length” linear regressions calculated for each sample following [2,31].
2.3.2. Directional Asymmetry
A practical way to separate different types of asymmetry is to distinguish directional and non-directional asymmetry (NA), the latter consisting of FA, antisymmetry, and ME [32].
To test for the presence of DA, we analyzed differences between values of characters on the left and right sides of shells using the t-test for paired observations. Individual indices of DA were calculated as differences between log-transformed left and right values of the character, which were averaged to obtain a sample index. To explore differences between samples, individual indices of DA were examined using Principal Component Analysis and ANOVA. Simple ratios allowed us to visual the magnitude of DA.
In order to statistically correct for DA in subsequent analyses of NA, values of a character on the right side were multiplied by the mean of the left/right ratio of that character in the sample [33].
2.3.3. Size Standardization
If character size correlates with the length of individuals and samples differ by the average size of individuals, this correlation should be taken into account. Simple indices, i.e., dividing character values by total length, are unsuitable due to allometric growth. To avoid this problem for DA-corrected data, we calculated size-standardized indices. These indices were obtained from a “log-transformed character–log-transformed shell length” linear regression as residuals divided by predicted values [2,13].
2.3.4. Partitioning the Variance According to Non-Directional Asymmetry and Within-Population Heterogeneity
When DA and allometric effects are eliminated, the residual variance is composed of the NA and within-population heterogeneity of individuals. One-way ANOVA allows for partitioning the total variance (σ2) into a stochastic component (σ2S), representing NA, and a factorial component (σ2F), representing the heterogeneity of individuals, as follows [1,3]:
2.3.5. Analysis of the Non-Directional Asymmetry Component
NA estimated by a stochastic component of phenotypic variance includes antisymmetry, ME, and FA [32]. The presence of antisymmetry was tested using visual observations of R-L distributions and analysis of the kurtosis and skew of distributions [9,34]. ME was calculated as the variance of differences between repeated measurements of each character [2]. FA was calculated as the difference between the stochastic component of variance and ME [3].
2.3.6. Overall Variation of a Sample
The above procedure described the analysis of the variance of a single character. Overall variation of a sample based on multiple characters was estimated as the sum of ranks after ranking the variance of each character across the samples [4]. The significance of the differences among samples of the overall magnitudes of these variances was estimated using Kendall’s coefficient of concordance W [9,34].
2.3.7. Correlation of Morphological Parameters with Environmental Factors and Overall Growth Performance
We studied the correlation of morphological parameters with temperature, salinity, and biotope (depth). To calculate the correlation with biotope we ranked the intertidal zone as 1, the upper subtidal zone with depth of 0.5–5 m as 2, and the subtidal zone deeper than 5 m as 3. We also correlated morphological parameters with published data on the overall growth performance (OGP) of mussels from the same populations. Sukhotin with coauthors ([22], Table II) provided an OGP index for nine of the 10 samples used in our study (the exception is DZL; one sample, SIN, was collected by Sukhotin and coauthors in 1995). The OGP index is proportional to the maximum rate of size increase during the lifetime of an organism. Thus it could be used as an independent measure of fitness. For analyzing correlations we used Pearson’s (for parametric variables) and Spearman’s (for non-parametric variables) correlation coefficients.
In a number of cases involving the statistical analysis of multiple characters and samples, we applied sequential Bonferroni corrections for multiple comparisons [9,35]. This is a controversial procedure and may not always be the best solution because, although it reduces Type I statistical error (i.e., accepting the wrong hypothesis), it can increase Type II error (i.e., rejecting the correct hypothesis) for associations that are not null [36]. While we liberally applied the Bonferroni correction in this study, we paid special attention to the disappearance of significance in the results.
3. Results
3.1. Environmental Variables
A pronounced decrease in temperature was observed in a north-eastward direction, going from the core to the margin of the mussels’ distribution area (correlation of temperature with geographic latitude, r = −0.80, p < 0.01). No significant correlations between environmental factors were found [22,37].
3.2. Size and Shape of Muscle Scars
The values of PC1 were highly correlated with shell length (r = 0.934, df = 8, p < 0.01). Loadings of all the characters on PC1 were positive (Table 2). This explained 60% of the total variation and was interpreted as general size [38]. Other Principal Components were considered to refer to variation in shape [38]. Differences between samples were significant for all 15 Principal Components (one-way ANOVA, df = 9, p < 0.01) with the highest significance for PCs 1, 2, 4, 5, and 6. Characters 7, 8, 9, 11, 13, 14, and 15 (Figure 2) had the highest loadings on Principal Components 2, 4, 5, and 6 (Table 2). Thus we can consider them as having the most discriminative power among samples.
Ordination of the sample means of all Principal Components except PC1 (to exclude the influence of size) is presented in Figure 3. KZL appeared to be the most distinct cluster; the ANZ cluster fell together with YSH; all other samples grouped more or less together, with VOR lying a little apart. Analyzing the predicted values of the characters (Table 3) allowed us to describe specific sample patterns in terms of the shape of muscle scars. This showed that, in relation to other samples, ANZ and KZL are characterized by shorter anterior retractor muscle scars (character 4) and a greater distance between the anterior end of the posterior retractor muscle scar and the dorsal end of the anterior retractor muscle scar (character 15). In KZL, the site where the palial sinus merges with the posterior adductor muscle scar (character 8) is narrower than in other samples. YSH is characterized by a narrower anterior adductor muscle scar (character 2), a shorter posterior adductor muscle scar (character 7), and longer distances between: (i) the anterior end of the posterior retractor muscle scar and the ventral edge of the posterior adductor muscle scar (character 5), (ii) the anterior end of the posterior retractor muscle scar and the posterior end of the posterior adductor muscle scar (character 6), and (iii) the anterior end of the posterior retractor muscle scar and the dorsal shell margin (character 14). VOR is characterized by a wider posterior retractor muscle scar (character 13).
3.3. Directional Asymmetry
A number of the characters showed a tendency towards DA. In 32 of 154 cases, the differences were statistically significant (t-test, df = 39, p < 0.05) and 11 of them remained significant after the Bonferroni correction (Table 4). The ratios between left and right sides ranged from 0.936 to 1.13, but usually differences were smaller—less than 5% (with prevalence on either the left or the right side) in 77% of cases.
When the samples were pooled, differences were statistically significant in 11 of 14 characters (df = 399, p < 0.05), with ratios ranging from 0.965 to 1.061. Application of the Bonferroni correction resulted in a decrease of the number of significant differences, but DA was still significant in 10 of 14 cases. Therefore we conclude that blue mussels are characterized by DA of shell.
A principal component analysis of individual DA indices showed that the proportion of total variance explained by PC1 was 0.13, and characters 5 and 6 had the highest loadings on this component (0.66 and 0.73, respectively). Loadings of other characters were quite low. One-way ANOVA did not show any significant differences between samples in each of 14 characters. Thus, DA was present in blue mussels, and patterns in different samples do not differ.
3.4. Components of Phenotypic Variance
Next we considered the two components of phenotypic variance: the factorial component (σ2F), representing within-population heterogeneity of individuals, and the stochastic component (σ2S), representing NA, which potentially consists of antisymmetry, FA, and ME. We checked deviation from normality with tests for skewness and kurtosis. We found no tendency in individual samples or in a pooled sample to skew distributions (the ratio between left- and right-skewed R-L distributions for all characters in all samples was 73:67). At the same time, we observed a tendency towards leptokurtosis of R-L distributions (ratio of leptokurtic to platykurtic distributions for all the samples was 89:51, p < 0.05, sign test). As antisymmetry would cause platykurtosis but not leptokurtosis of the distributions, we concluded absence of antisymmetry in our material, and therefore NA consisted only of FA and ME.
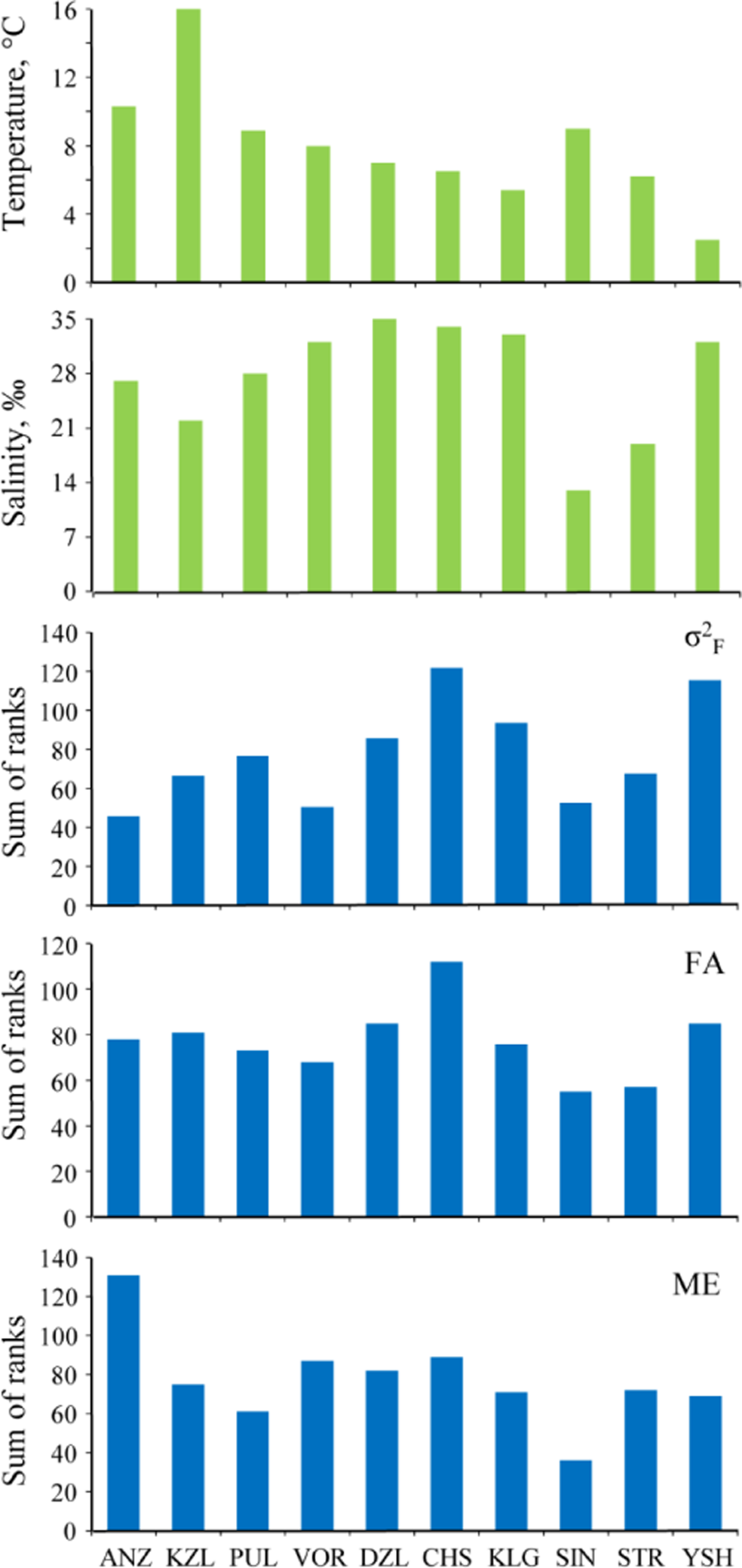
The factorial component varied concordantly across characters: Kendall’s coefficient of concordance W was equal to 0.574 (df = 14, p < 0.01). The highest level of the factorial component in all the samples was observed in characters 13, 8, and 11, while the lowest was observed in characters 6, 5, and 15 (Table 5). Variation of the factorial component across samples was concordant as well (W = 0.389, df = 9, p < 0.01). The highest factorial component was observed in CHS and YSH samples, the lowest in ANZ and VOR (Figure 4). Results of pairwise comparisons of the samples are presented in Table 6. The average contribution of the factorial component to the total phenotypic variance was 55.0% (ranges from 26.1% in ANZ to 67.4% in YSH) (Table 7).
ME across characters showed significant concordance (W = 0.614, df = 14, p < 0.01), revealing that the same characters in different samples had consistently higher ME than the other characters. Characters 8, 9, and 2 exhibited the highest ME, and characters 6, 5, and 7 the lowest (Table 5). Across the samples, the ME of different characters also varied concordantly (W = 0.302, df = 14, p < 0.01), revealing significant differences in the ME level among the samples (see Table 6 for the results of pairwise comparisons). Therefore, ME had to be calculated for each sample separately. The highest ME was observed in the ANZ sample, the lowest in SIN (Figure 4). The average contribution of ME to the total variance was 26.5% (varying from 15.3% in YSH to 64.8% in ANZ) (Table 7). The average contribution of ME to NA was 63.1% (from 43.3% in CHS to 90.9% in STR) (Table 7).
FA varied concordantly across characters: Kendall’s coefficient of concordance W was equal to 0.475 (df = 14, p < 0.01). The highest level of FA occurred in characters 13, 9, and 8, with the lowest in characters 15, 5, and 6 (Table 5). Across samples FA varied concordantly as well (W = 0.389, df = 9, p < 0.01). The highest FA was observed in the CHS, YSH, and DZL samples, the lowest in SIN and STR (Figure 4). The statistical significance of differences between samples is provided in Table 6. The average contribution of FA to the total variance was 18.5% (from 9.15% (ANZ) to 26.4% (KZL)) (Table 7). The average contribution of FA to NA was 36.9% (from 9.12% (STR) to 56.74% (CHS)) (Table 7).
We found positive statistically significant (p < 0.05) correlations between all the components of variance: r for σ2F and FA = 0.852; r for σ2F and ME = 0.759, and r for FA and ME = 0.632 (df = 13).
3.5. Associating Parameters of Morphological Variation with Environmental Factors and Overall Growth Performance Index
Among the principal components obtained from mean character values, PC2 and PC5 showed a significant correlation with temperature (Pearson’s r = 0.64 and r = −0.66, respectively, df = 9, p < 0.05) (Table 8). Character 8, predicted for a shell length of 40 mm, showed a significant correlation with temperature (r = −0.85, df = 9, p < 0.05). Character 13 showed a significant correlation with biotope (depth) (r = 0.72, df = 9, p < 0.05). The factorial component showed a negative correlation with temperature (r = −0.73, df = 9, p < 0.05) and a positive correlation with salinity (r = 0.63, df = 9, p < 0.05). FA correlated positively with salinity (r = 0.70; df = 9, p < 0.05). All other correlations were not significant (Table 8). Analyzing the association of OGP [22] with the morphological parameters obtained in our study showed a negative correlation with FA (Spearman’s correlation coefficient = −0.653, df = 9, p = 0.057).
4. Discussion
4.1. Methodological Aspects of the Morphological Variation Analysis of Blue Mussels
Studies of FA require higher accuracy and precision than analyzing the variation of means, thus if analytical methods meet the criteria for FA studies, they also meet the criteria for analysis of the variation of means. Several methodological problems have kept FA analysis in obscurity. The most widespread are: (i) injudicious choice of characters; (ii) measurement error; (iii) deviation from ideal FA (due to the presence of DA and antisymmetry); and (iv) the association of FA with size [9,10,32,34,39]. The methods we used at least partly address all these problems.
4.2. Characters
Muscle scars on the internal surface of mussel shells are bilaterally symmetrical structures, which thus allow analysis of FA. Morphological variation of muscle scars was previously used in studies of mussels [26–30,40–43]. However, the same morphological structure can be described in different ways by different characters. In our work we paid special attention to the choice of characters, which allowed us to comprehensively describe scar size and shape, and FA at the same time. In the beginning of our work we considered most of the characters used in previous studies of mussel morphology [26,27,29,30]. Since the three earlier studies that considered FA in mussels [30,44,45] used only a few characters, we developed an original set of characters, focusing on their measurement error and discriminative power while comparing samples. We also added new characters to obtain a more complete description of muscle scar shape [46]. These traits (21 in total) were then tested for ME, and characters with the highest degree of ME were excluded from further analyses [47].
Concordant variation of FA levels across different characters and across samples testified that we did catch the biological signal from our measurements of the chosen characters, even though ME error for some of the characters remained high (see details below in the next section). We also managed to describe differences between populations in size and shape of the studied structures. it is noteworthy that characters with high discriminative capacity in our work (length of the posterior adductor muscle scar (character 7), width of the palial sinus where it merges with the posterior adductor muscle scar (character 8), maximal width of the palial sinus (character 9), width of the posterior retractor muscle scar at the place of its confluence with the posterior adductor muscle scar (character 11), width of the posterior retractor muscle scar (in the middle) (character 13), distance between the anterior end of the posterior retractor muscle scar and the dorsal shell margin (character 14), and distance between the anterior end of the posterior retractor muscle scar and the dorsal end of the anterior retractor muscle scar (character 15)) were not earlier reported in the literature as highly discriminative. Most previous studies of mussel morphology, however, focused on describing differences between different species [26,27,29,30,40–43], while we explored differences between populations of the same species. Evidently, different characters may be associated with inter- and intra-specific morphological variation.
4.3. Measurement Error
Morphological characters, muscle scars in particular, were widely analyzed in studies of mussels, but the ME of these characters was rarely discussed. This is because researchers concentrated on comparing the mean population values of characters. In that case ME decreases the significance of an estimate, yet does not systematically change mean character values. Differences among individual researchers may also contribute to differences among means, but we do not discuss this in our study. Detailed analysis of ME is required when studying the magnitude of variance, especially FA [10,34,48]. FA analysis for mussels appears to be quite complicated. Despite eliminating characters with high errors, ME approached moderately high levels in our work. There may be several reasons for this. A major reason is that muscle scars are not often clearly outlined. The visibility of scars differs in different samples depending on the thickness and coloration of the mother-of-pearl layer. The ANZ sample, which exhibits the highest ME level among all the samples, is a good example. ANZ measurements were more difficult to perform and repeatability was very low because scar outlines were faint and the mother-of-pearl layer was thin and semi-transparent, merging in color with the underlying prismatic layer. Fineness of inner shell surface might be influenced by environmental factors. Yet, we found no significant correlation between the ME level in samples and environmental factors such as temperature, salinity, and depth (Table 8).
Another possible reason for high ME might be related to differences between repeated measurements done at different time periods. Operator accuracy may change with increased experience, and can vary among measuring sessions depending on operator condition [10,49,50]. Variance in the ME level due to measurements performed at different times and differences in the clarity of scar outlines may have caused the leptokurtic (R-L) distributions in our study.
The positive correlation between components of phenotypic variance, observed in this study, was found earlier for FA and the factorial component in herring [2]. Correlation between FA and ME also occurred in herring, although this was not reported (for meristic characters it was closed to 0, but for morphometric characters it was high (r = 0.957, df = 19, p < 0.01, analysis based on data from Table 1, [2]). The reasons for that are not clear.
Despite high values, ME does not confound the biological signal completely, which is confirmed by replicated analyses of 150 specimens, and the significant concordance of FA across samples. ME reported here is comparable with ME estimates obtained for other species [13,51,52].
Now morphological studies generally analyze scanned images instead of taking measurements manually. Scanning studies were performed on Mytilus [53,54]. This way of taking measurements allows the use of geometric morphometrics approaches [55]. However, sources and patterns of ME obtained with scanned images and manual measurements can be different. A comparison of the different techniques applied to cranial traits showed that the computerized procedure was more precise and less influenced by the factors that increase ME than manual methods [56]. In using both manual and computerized techniques on blue mussels, we found that scanning usually produced more stable ME estimations (lower inter- and intra-operator variances [47]).
At the same time, using scans of mussel shells does not allow for analysis of some important characters because of the projection of three-dimensional structure in a two-dimensional scan. For instance, anterior adductor and anterior retractor muscles are often not visible in scans because they are covered by the folded shell margin. Manual techniques allow for taking such measurements using rotation. Some structures have a different shape just because of differences in shell incurvature. Another advantage of manual techniques, particularly in blue mussels where the visibility of scars is sometimes poor, is that it permits valve manipulations, giving operators an additional and sometimes better view of the borders of muscle scars, thus reducing measurement error.
At the same time, formal comparison of the measurement errors of different techniques is problematic. For instance, measuring the ME of a scan is usually done by replicating measurements of the same scan. Thus, the inability to account for preparation factors (for instance, altering specimen position, clearing valves) artificially reduces measurement error. In manual procedures, preparation factors cannot be avoided, which allows more objective evaluation of ME. Scanning transparent objects such as plant leaves twice from different sides partially obviates this problem [57,58], but correctly assessing the ME of opaque objects such as mussel valves or bones is more difficult. A partial solution is to obtain independent scans [59], which partially accounts for replicate-scan measurement error.
4.4. Deviations from an Ideal Fluctuating Asymmetry
We did not find antisymmetry in our material, but directional asymmetry (DA) was present, and we corrected for its effect using a technique suggested by [33]. More generic and accurate techniques to correct for directional asymmetry have been developed [60,61], but we consider our approach satisfactory given the low absolute value of directional asymmetry in our study and the absence of differences between samples.
Before our study, DA had not been known for blue mussels [62] although it is quite widespread among other bivalves (oysters, scallops, etc.). In mussels DA can be associated with low motility and, in particular, with the tendency of animals to form spiral aggregations called “druse” [63]. The tendency to form only one type of spiral (either left or right directed) may be associated with DA at individual levels.
Some authors predict a continuum between the three types of asymmetry and claim that DA and antisymmetry may reflect developmental instability as well as FA [64–66]. Indeed, several studies showed a transition from FA to either DA or antisymmetry under the influence of stressful conditions [67,68]. Kark [69] showed an increase in the DA of toe length in populations of chukar partridges Alectoris chukar towards the periphery of their distribution. In our work, however, we found no differences in the degree of DA among samples.
The fact that mussels are characterized by the DA of the shell has consequences for the methodology of morphological studies. If morphological characters are measured on different valves, differences detected between the sides of shells can wrongly be interpreted as differences between populations. Hence, the most trustworthy way of comparing mussel populations is to analyze both valves. It is especially important to account for DA while carrying out FA analysis because DA inflates FA. Without accounting for DA, FA estimates may not reflect developmental instability.
4.5. Differences between Samples in the Shape of Muscle Scars
Accordingly to the results of the analysis (Figure 3), samples from KZL, ANZ, YSH, VOR, and, to a lesser extent, KLG were mostly different from the rest of the samples with respect to the shape of muscle scars. It is always difficult to explain morphological differences between wild populations, because they can depend on a number of factors, but some hypotheses can be considered. The morphological distinctiveness of ANZ and KZL compared to other samples might be explained by their genetic proximity. Reduction of gene flow between populations from the central White Sea and populations outside that area can be caused by hydrological isolation [70]. At the same time, our results do not show greater similarity among samples from the White Sea than among other samples.
VOR and YSH are deep subtidal samples, which may explain their differences from samples collected from intertidal or upper subtidal zones. Biotope, an important factor influencing life history traits of blue mussels in this region [22], may also affect their shape. Morphologically, mussels from deep waters differ from other mussels because their posterior retractor muscle scar is wider in the middle (character 13).
Interestingly, character 8 (width of the palial sinus where it merges with the posterior adductor muscle scar) appears to be associated with temperature. Populations from warmer waters are characterized by a smaller character 8. The correlation between temperature and PC2 is also likely due to character 8, which has the highest loading on this principal component. Also, this character correlates with an overall growth parameter on the samples studied by Sukhotin et al. [22]. However, the functional significance of this association is unclear.
In general, we did not find clear geographical trends in morphological variation in our samples. Thus, we have to invoke local adaptations to explain observed morphological differences. Sukhotin et al. [22] also suggested that local conditions played a leading role in determining growth patterns of mussels in this area.
4.6. The Factorial Component of Total Phenotypic Variance
The factorial component reflects genetic and environmental heterogeneity within a sample [1,3]. Collecting all animals in a sample from similar microenvironments, as we did in our study, reduces the contribution of environmental heterogeneity but certainly does not remove it all. The similar size of individuals minimizes ontogenetic differences.
Samples from areas with low salinity (brackish areas of the White Sea and the Pechora Sea) showed significant decrease in the factorial component. We suggest that specific estuarine conditions, supported by selection, favor some genotypes, thus decreasing overall genetic heterogeneity. In cases where species distribution is limited by extreme environmental conditions, it has been concluded that marginal populations express lower genetic variability than populations from the core of the species range [21,71]. Yet, we found a significant negative correlation between factorial variation with temperature, i.e., samples from the White Sea possessed relatively low factorial variation. This result is unexpected because White Sea populations, like DZL populations from the western part of the Barents Sea, could be affected by the introgression of M. trossulus genes [72]. Nevertheless, our analyses of data from mussels at the northern limit of their distribution do not support the reduced genetic variability of marginal populations hypothesis [71].
4.7. Fluctuating Asymmetry
Shadrin and co-authors [44] found increased FA of valve width and mass in Mediterranean mussels (Mytilus galloprovincialis Lamarck) from the Black Sea in mussels from polluted locations, but tests for ME and DA were not performed. Springer and Heath [45] estimated the FA of five morphological characters in hybrid mussels from two hybrid zones between M. trossulus and M. galloprovincialis to reveal an exogenous selection against hybrids. Gardner [30] studied the phenotypic variability of mussels from the British Isles (M. edulis and M. galloprovincialis) using eight characters of muscle scars measured on the left side of shells. Variance of individual deviations from the population mean was used as an index of developmental instability. However, our results demonstrate that variance reflecting developmental stability (FA) contributes on average only 18.5% of the variance of individual deviations from the population mean (total variance); the rest derive from the factorial component and ME, which were not accounted for by Gardner [30]. Thus, despite numerous developmental stability studies of various species during recent decades, a detailed study of FA in Mytilus had yet to be done.
According to the results of Kendall’s concordance test, blue mussel samples differed significantly in FA level, showing that these differences were not random. Here we explore the reasons for these differences, focusing on salinity, temperature, and tidal zone, which are known to be key environmental variables influencing populations of marine organisms. For statistical analysis we used measurements obtained in time of sampling. Clearly single measurements (especially in estuaries) may be subject to some variation depending on tide, wind, sun radiation, etc. Monthly averages would have been preferable, but systematic data for the entire study area are not available. At the same time, data are available in some areas for the end of hydrological summer [20,73,74] (see also data on monthly mean surface temperature in the White Sea and Pechora Sea in [22], Figure 4). Our measurements corresponded with the data in the literature. Some environmental factors, which potentially may influence developmental instability and shell morphology, such as wave exposure, food supply, competition, pH, etc., were not addressed in this study. Single measurements and non-controlled factors may reduce correlation between environmental variables and biological characteristics such as fluctuating asymmetry, especially when the number of samples is not large. Thus, insignificant correlations do not necessarily mean the absence of associations. In data interpretation we paid attention not only to statistical significance but also to the value of the correlation coefficient.
The observed positive correlation of FA with salinity (S) in the interval 13%–35% (Table 8) shows higher developmental stability for mollusks from brackish waters. Rather than as a direct effect of salinity on developmental stability, this may be explained by the favorable conditions in estuaries per se, in particular, the better food supply due to river outflow. Food supply is one of the most important factors affecting growth rates and the basis for other performance parameters of mollusks [75].
This conclusion is also supported by the negative correlation between FA and the OGP index provided by [22], showing that, at the population level, animals with lower asymmetry (i.e., higher developmental stability) demonstrate better growth performance. Here we see an association between fluctuating asymmetry and fitness. Such an association is intuitively meaningful, but empirical associations between FA and fitness are not always observed (for a review, see [76]). Rather than reflecting principal limitations of fluctuating asymmetry as a measure of fitness, we believe that the absence of an association in many studies is confounded by methodical difficulties, the impossibility of controlling all important factors in the wild, and our a priori expectations. It is quite possible that finding an association between FA and OGP in blue mussels would require considering (after careful selection) a large number of characters, accounting for ME for each individual sample and a detailed analysis of DA.
Correlation of FA with temperature was rather low (r = −0.21) and far from significant. This corroborates conclusions about the high performance of mollusk populations from the Pechora Sea based on weight index, glycogen content, and growth characteristics [17,22]. The conventional point of view that mussels are scarce in the Pechora Sea [16] was recently questioned, since large populations have been observed near Dolgy Island (69°9′ N, 59°11′ E) [77].
Hence, our data, together with other data, do not support the hypothesis that low temperatures cause decreased developmental stability and performance in mussels near the border of their distributional range. The following explanations can be suggested. Marginal populations of mussels could be genetically adapted to harsh temperatures in the eastern Barents Sea, as was suggested for the clam Macoma balthica [21]. However no allozyme differences were recorded between the Pechora Sea samples and samples from other parts of the European range of M. edulis [17,72]. Nor did morphological analyses reveal clear differences between mussel populations in this area.
On the other hand, low temperatures might not influence the growth and developmental stability of adult mussels, but still affect their reproductive capacity, fertilization, or early larval development. In this case marginal populations can be replenished by larvae transported by currents from more temperate regions, whereas adult animals are well adapted to specific environmental conditions in the Arctic Pechora area. Such a strategy for population maintenance was suggested earlier for M. edulis in other regions of northern seas, for example, along the coasts of eastern Murman in the western part of the Barents Sea [78,79]. In the Atlantic salmon (Salmo salar), which is not characterized by dispersion of young stages, we found an increase of fluctuating asymmetry towards the boundary of its range [80]. Thus we suggest that the northeastward distribution of mussels is not limited by harsh temperatures directly, but by other factors, e.g., currents. Furthermore, we assume that rising water temperature in the region will not result in an immediate change in mussel distribution, or their abundance in the Pechora Sea. These conclusions are in accord with results from a recent study of the metabolic cold adaptation and aerobic performance of blue mussels from different latitudes in Greenland and Denmark, which showed that low temperatures per se do not constrain the metabolic activity of adult blue mussels in the Arctic [81].
5. Conclusions
Employing morphological analysis in studying populations of marine mussels faces a number of complex problems dealing with methodology, mussel population structure, and factors influencing performance and distribution. From a methodological point of view, problems are caused by high and heterogeneous sample measurement errors, and by the presence of directional asymmetry. None of these issues have been addressed in previous mussel studies. Thus, we engaged in painstaking methodological analysis and review prior to quantifying phenotypic variance and fluctuating asymmetry. Since the majority of characters used in previous studies showed high measurement error, we identified new and appropriate characters. At the same time, DA was found to represent not only an obstacle to the study of fluctuating asymmetry and means, but also a new morphological marker in blue mussels.
Other variables explored, such as mean values, factorial variation, and fluctuating asymmetry, showed clear heterogeneity among populations near the border of their range. Heterogeneity patterns show no evident cline towards distribution borders (although some associations occurred, for instance the change in shape of the palial sinus with temperature). Absence of correlation between fluctuating asymmetry and temperature suggests that extreme temperatures do not limit the distribution of adult blue mussels at the northeastern border of their range. Limitations are more likely determined by the dispersion and resistance of early ontogenetic stages.
It is probable that local environmental conditions are highly significant for morphological characters in mussels. In general, most morphological variables show differences between (i) samples from more estuarine areas (the White and Pechora Seas) and (ii) samples from the areas of the Barents Sea with oceanic salinity. The first population lives at lower salinity and probably enjoys better feeding conditions. Morphologically, they tend to have lower fluctuating asymmetry, indicating higher developmental stability due to more favorable environmental conditions, and lower factorial variation, which likely results in lower genetic diversity.
Blue mussels exemplify the many and complex methodological challenges for morphological studies. Accurately addressing them is key to improving ecological interpretations. We hope that our results will encourage more rigorous attention to morphological studies of marine mussels, and that our findings pave the way for further studies of the strategies and costs for marine invertebrates living in Arctic seas and on the factors limiting their distribution.
Acknowledgments
This study has been supported by the International Association for the Promotion of Co-operation with Scientists from the New Independent States of the Former Soviet Union (INTAS) grant, project No. 94-391 (to Marina Katolikova, Petr Strelkov, Herman Hummel) and by grants from the Russian Foundation for Basic Research (13-04-00394) (to Dmitry Lajus, Marina Katolikova, Petr Strelkov) and St. Petersburg State University (1.38.253.2014) (to Dmitry Lajus, Marina Katolikova, Petr Strelkov). We thank Alexey Sukhotin for logistic support during the sampling, and Karen Alexander for English language editing.
Author Contributions
Herman Hummel, Petr Strelkov and Dmitry Lajus designed the study. Herman Hummel organized the expedition, Petr Strelkov and Marina Katolikova sampled in the field. Marina Katolikova performed the measurements of specimens. Dmitry Lajus designed statistical analysis, and performed it with assistance of Marina Katolikova. Dmitry Lajus drafted the manuscript, all other authors assisted with writing.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kozhara, A.V. Phenotypic variance of bilateral characters as an indicator of genetic and environmental conditions in bream Abramis brama (L.) (Pisces, Cyprinidae) populations. J. Appl. Ichthyol. 1994, 10, 167–181. [Google Scholar]
- Lajus, D. Variation patterns of bilateral characters: Variation among characters and among populations in the White Sea herring, Clupea pallasi marisalbi (Berg) (Clupeidae, Teleosti). Biol. J. Linn. Soc. 2001, 74, 237–253. [Google Scholar]
- Lajus, D.; Graham, J.; Kozhara, A. Developmental Instability and the Stochastic Component of Total Phenotypic Variance. In Developmental Instability: Causes and Consequences; Oxford University Press: New York, NY, USA, 2003; pp. 343–363. [Google Scholar]
- Van Valen, L. A study of fluctuating asymmetry. Evolution 1962, 16, 125–142. [Google Scholar]
- Zakharov, V.M. Future prospects for population phenogenetics. Sov. Sci. Rev. Sect. F Physiol. Gen. Biol. Rev. 1989, 4, 1–79. [Google Scholar]
- Allenbach, D.M. Fluctuating asymmetry and exogenous stress in fishes: A review. Rev. Fish. Fish. 2011, 21, 355–376. [Google Scholar]
- Graham, J.H.; Raz, S.; Hel-Or, H.; Nevo, E. Fluctuating Asymmetry: Methods, Theory, and Applications. Symmetry 2010, 2, 466–540. [Google Scholar]
- Beasley, D.A.E.; Bonisoli-Alquati, A.; Mousseau, T.A. The use of fluctuating asymmetry as a measure of environmentally induced developmental instability: A meta-analysis. Ecol. Indic. 2013, 30, 218–226. [Google Scholar]
- Palmer, A.R. Fluctuating Asymmetry Analyses: A Primer. In Developmental Instability: Its Origin and Evolutionary Implications; Markow, T.A., Ed.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1994; pp. 335–364. [Google Scholar]
- Palmer, A.R.; Strobeck, C. Fluctuating asymmetry: Measurement, analysis, patterns. Ann. Rev. Ecol. Syst. 1986, 17, 391–421. [Google Scholar]
- Hubert, W.A.; Alexander, C.B. Observer variation in counts of meristic traits affects fluctuating asymmetry. North. Am. J. Fish. Manag. 1995, 15, 156–158. [Google Scholar]
- Merilä, J.; Bjorklund, M. Fluctuating asymmetry and measurement error. Syst. Biol. 1995, 44, 97–101. [Google Scholar]
- Lajus, D.; Alekseev, V. Components of morphological variation in Baikalian endemial cyclopid Acanthocyclops signifer complex from different localities. Hydrobiologia 2000, 417, 25–35. [Google Scholar]
- Suchanek, T.H. Mussels and Their Role in Structuring Rocky Shore Communities. In The Ecology of Rocky Coasts; Moore, P.G., Seed, R., Eds.; Hodder and Stoughton Press: London, UK, 1985; pp. 70–96. [Google Scholar]
- Seed, R.; Suchanek, T.H. Population and Community Ecology of Mytilus. In The Mussel Mytilus; Gosling, E.G., Ed.; Elsevier: Amsterdam, the Netherlands, 1992; pp. 87–169. [Google Scholar]
- Zatsepin, V.I.; Zenkevich, L.A.; Filatova, Z.A. Materials on quantitative study of bottom fauna of tidal zone of Kola Bay. Tr. Gos. Okeanogr. Inst. 1948, 6, 13–54. [Google Scholar]
- Hummel, H.; Collucci, F.; Bogaards, R.H.; Strelkov, P. Genetic and ecophisiological traits in the bivalve Mytilus from Europe, with an emphasis on Arctic populations. Polar Biol. 2001, 24, 44–52. [Google Scholar]
- Berge, J.; Johnsen, G.; Nilsen, F.; Gulliksen, B.; Slagstad, D. Ocean temperature oscillations enable reappearance of blue mussels Mytilus edulis in Svalbard after a 1000 year absence. Mar. Ecol. Prog. Ser. 2005, 303, 167–175. [Google Scholar]
- Treshnikov, A.F. Atlas Arktiki; Glavnoe upravlenie geodezii i kartografii pri Sovete Ministrov SSSR: Moscow, Russia, 1985. [Google Scholar]
- Matishov, G.G. Ekosistemy, Bioresursy i Antropogennoe Zagriaznenie Pecherskogo Moria; Izdatelstvo KNTs RAN: Apatity, Russia, 1996. [Google Scholar]
- Hummel, H.; Bogaards, R.; Bek, T.; Polishchuk, L.; Amiard-Triquet, C.; Bachelet, G.; Desprez, M.; Strelkov, P.; Sukhotin, A.; Naumov, A.; et al. Sensitivity to stress in the bivalve Macoma balthica from the most northern (Arctic) to the most southern (French) populations: Low sensitivity in Arctic populations because of genetic adaptations? Hydrobiologia 1997, 355, 127–138. [Google Scholar]
- Sukhotin, A.A.; Strelkov, P.P.; Maximovich, N.V.; Hummel, H. Growth and longevity of Mytilus edulis (L.) from northeast Europe. Mar. Biol. Res. 2007, 3, 155–167. [Google Scholar]
- Zbawicka, M.; Drywa, A.; Śmietanka, B.; Wenne, R. Identification and validation of novel SNP markers in European populations of marine Mytilus mussels. Mar. Biol. 2012, 159, 1347–1362. [Google Scholar]
- Levitus, S.; Matishov, G.; Seidov, D.; Smolyar, I. Barents Sea multidecadal variability. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Lind, S.; Ingvaldsen, R.B. Variability and impacts of Atlantic water entering the Barents Sea from the north. Deep Sea Res. Part. I Oceanogr. Res. 2012, 62, 70–88. [Google Scholar]
- Seed, R. Morphological variations in Mytilus from the Irish coasts in relation to the occurrence and distribution of M. galloprovincialis Lamark. Cah. Biol. Mar. 1974, 15, 1–25. [Google Scholar]
- Seed, R. Morphological variations in Mytilus from the French coasts in relation to the occurrence and distribution of M. galloprovincialis Lamark. Cah. Biol. Mar. 1972, 13, 357–384. [Google Scholar]
- Kafanov, A.I.; Romeiko, L.V. Morphometric variation of blue mussel Mytilus edulis in the northeastern part of the Sea of Japan. In Fauna i Raspredelenie Molluskov: Severnaya Patsifika. i Poliarny Bassein; Kafanov, A.I., Baranovskaya, N.M., Eds.; DVNTs AN SSSR: Vladivostok, Russia, 1987; pp. 104–114. [Google Scholar]
- McDonald, J.H.; Seed, R.; Koehn, R.K. Allozymes and morphometric characters of three species of Mytilus in the Northern and Southern Hemispheres. Mar. Biol. 1991, 111, 323–333. [Google Scholar]
- Gardner, J.P.A. Developmental stability is not disrupted by extensive hybridization and introgression among populations of the marine bivalve molluscs Mytilus edulis (L.) and Mytilus galloprovinciali s (Lmk.) from south-west England. Biol. J. Linn. Soc. 1995, 54, 71–86. [Google Scholar]
- Lajus, D.; Knust, R.; Brix, O. Fluctuating asymmetry and other parameters of morphological variation of eelpout Zoarces viviparus (Zoarcidae, Teleostei) from different parts of its distributional range. Sarsia N. Atl. Mar. Sci. 2003, 88, 247–260. [Google Scholar]
- Juste, J.; Lopes-Gonzales, C.; Strauss, R.E. Analysis of asymmetries in the African fruit bats Eidolon helvum and Rousettus egyptiacus (Mammalia: Megachiroptera) from the islands of the Gulf of Guinea. I. Variance and size components of bilateral variation. J. Evol. Biol. 2001, 14, 663–671. [Google Scholar]
- Leamy, L. Morphometric studies in inbred and hybrid house mice. V. Directional and fluctuating asymmetry. Am. Nat. 1984, 123, 579–593. [Google Scholar]
- Palmer, A.R.; Strobeck, C. Fluctuating asymmetry analyses revisited. In Developmental Instability: Causes and Consequences; Polak, M., Ed.; Oxford University Press: New York, NY, USA, 2003; pp. 279–319. [Google Scholar]
- Rice, W.R. Analyzing tables of statistical tests. Evolution 1989, 43, 223–225. [Google Scholar]
- Rothman, K.J. No adjustments are needed for multiple comparisons. Epidemiology 1990, 1, 43–46. [Google Scholar]
- Denisenko, S.; Denisenko, N.; Lehtonen, K.; Andersin, A.B.; Laine, A.O. Macrozoobenthos of the Pechora Sea (SE Barents Sea): Community structure and spatial distribution in relation to environmental conditions. Mar. Ecol. Prog. Ser. 2003, 258, 109–123. [Google Scholar]
- Bookstein, F.L.; Chernoff, B.; Elder, R.L.; Humphries, J.M., Jr.; Smith, G.R. Morphometrics in Evolutionary Biology; Special Publications, No. 15; Philadelphia Academy of Natural Sciences: Philadelphia, PA, USA, 1985. [Google Scholar]
- Hoffmann, A.A.; Woods, R.E. Associating Environmental Stress with Developmental Stability: Problems and Patterns. In Developmental Instability: Causes and Consequences; Polak, M., Ed.; Oxford University Press: New York, NY, USA, 2003; pp. 387–401. [Google Scholar]
- Gardner, J.P.A. The Mytilus edulis species complex in southwest England: Effects of hybridization and introgression upon interlocus associations and morphometric variation. Mar. Biol. 1996, 125, 385–399. [Google Scholar]
- Gardner, J.P.A. A historical perspective of the genus Mytilus (Bivalvia: Mollusca) in New Zealand: Multivariate morphometric analyses of fossil, midden and contemporary blue mussels. Biol. J. Linn. Soc. 2004, 82, 329–344. [Google Scholar]
- Innes, D.J.; Bates, J.A. Morphological variation of Mytilus edulis and Mytilus trossulus in eastern Newfoundland. Mar. Biol. 1999, 133, 691–699. [Google Scholar]
- Gardner, J.P.A.; Thompson, R.J. Influence of genotype and geography on shell shape and morphometric trait variation among North Atlantic blue mussel (Mytilus spp.) populations. Biol. J. Linn. Soc. 2009, 96, 875–897. [Google Scholar]
- Shadrin, N.V.; Machkevsky, V.K.; Lezhnev, I.V. Quantified responses of mussels to eutrophication. In Quantified Phenotypic Responses in Morphology and Physiology; Aldrich, J.C., Ed.; Ashford Japaga Publishers: Ashford, Ireland, 1993; pp. 259–270. [Google Scholar]
- Springer, S.A.; Heath, D.D. Environment-specific heterozygote deficiency and developmental instability in hybrid Mytilus. Mar. Biol. Res. 2007, 3, 182–187. [Google Scholar]
- Katolikova, M.V.; Lajus, D.L.; Strelkov, P.P.; Hummel, H. Fluctuating asymmetry of blue mussel Mytilus: Geographical analysis. Vestn. Santk. Peterburgskogo Univ. Ser. 2000, 3, 78–95. [Google Scholar]
- Katolikova, M.; Lajus, D.; Strelkov, P. Saint-Petersburg State University, Saint-Petersburg, Russia. Methods of Morphological Analysis of Mussel Shells: Comparing Digital and Manual Techniques. Unpublished work.
- Simmons, L.W.; Tomkins, J.L.; Kotiaho, J.S.; Hunt, J. Fluctuating paradigm. Proc. R. Soc. B Biol. Sci. 1999, 266, 593–595. [Google Scholar]
- Yezerinac, S.M.; Lougheed, S.C.; Handford, P. Measurement error and morphometric studies: Statistical power and observer experience. Syst. Biol. 1992, 41, 471–482. [Google Scholar]
- Lajus, D.L.; Ciostek, M.; Drszanowska, M.; Sywula, T. Geographic and ontogenetic patterns of chaetotaxy variation in glacial relict Saduria entomon (L.) and intra-individual variations (fluctuating asymmetry). Ann. Zool. Fennici 2003, 40, 411–429. [Google Scholar]
- Brakefield, P.M.; Breuker, C.J. The genetical basis of fluctuating asymmetry for developmentally integrated traits in a butterfly eyespot pattern. Proc. R Soc. B Biol. Sci. 1996, 263, 1557–1563. [Google Scholar]
- Moller, A.P.; Swaddle, J.P. Asymmetry, Developmental Stability, and Evolution; Oxford University Press: Oxford, UK, 1997; pp. 2–4. [Google Scholar]
- Taborsky, D.A.; Chang, X.; Katolikova, M.V. Evaluation of status of cultivated blue mussels Mytilus edulis near the Sonostrov Island (White Sea, Kandalaksha Bay). Almanakh. Sovrem. Nauk I Obraz 2007, 6, 136–142. [Google Scholar]
- Valladares, A.; Manríquez, G.; Suárez-Isla, B.A. Shell shape variation in populations of Mytilus chilensis (Hupe 1854) from southern Chile: A geometric morphometric approach. Mar. Biol. 2010, 157, 2731–2738. [Google Scholar]
- Bookstein, F.L. Morphometric Tools for Landmark Data: Geometry and Biology; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
- Muñoz-Muñoz, F.; Perpiñán, D. Measurement error in morphometric studies: Comparison between manual and computerized methods. Ann. Zool. Fennici 2010, 47, 46–56. [Google Scholar]
- Ambo-Rappe, R.; Lajus, D.L.; Schreider, M.J. Increased heavy metal and nutrient contamination does not increase fluctuating asymmetry in the seagrass Halophila ovalis. Ecol. Indic. 2008, 8, 100–103. [Google Scholar]
- Ambo-Rappe, R.; Lajus, D.L.; Schreider, M.J. Translational fluctuating asymmetry and leaf dimension in seagrass, Zostera capricorni Aschers in a gradient of heavy metals. Environ. Bioindic. 2007, 2, 99–116. [Google Scholar]
- Yurtseva, A.; Lajus, D.; Artamonova, V.; Makhrov, A. Effect of hatchery environment on cranial morphology and developmental stability of Atlantic salmon (Salmo salar L.) from North-West Russia. J. Appl. Ichthyol. 2010, 26, 307–314. [Google Scholar]
- Graham, J.H.; Emlen, J.M.; Freeman, D.C.; Leamy, L.J.; Kieser, J.A. Directional asymmetry and the measurement of developmental instability. Biol. J. Linn. Soc. 1998, 64, 1–16. [Google Scholar]
- Van Dongen, S.; Lens, L.; Molenberghs, G. Mixture analysis of asymmetry: Modelling directional asymmetry, antisymmetry and heterogeneity in fluctuating asymmetry. Ecol. Lett. 1999, 2, 387–396. [Google Scholar]
- Katolikova, M.V.; Lajus, D.L.; Strelkov, P.P. Analysis of morphological variaton of mussels Mytilus edulis from the seas of Northern Europe. Vestn. Santk. Peterburgskogo Univ. Ser. 2005, 3, 92–99. [Google Scholar]
- Lesin, P.A. Druse structure of blue mussels (Mytilus edulis) in the White Sea. Zool. Zhurnal. 2006, 86, 163–166. [Google Scholar]
- Freeman, D.C.; Graham, J.H.; Emlen, J.M. Developmental stability in plants: Symmetries, stress and epigenesis. Genetica 1993, 89, 97–119. [Google Scholar]
- Emlen, J.M.; Freeman, D.C.; Graham, J.H. Nonlinear growth dynamics and the origin of fluctuating asymmetry. Genetica 1993, 89, 77–96. [Google Scholar]
- Graham, J.H.; Emlen, J.M.; Freeman, D.C. Nonlinear Dynamics and Developmental Instability. In Developmental Instability: Causes and Consequences; Polak, M., Ed.; Oxford University Press: New York, NY, USA, 2003; pp. 35–50. [Google Scholar]
- Graham, J.H.; Freeman, D.C.; Emlen, J.M. Developmental stability: A Sensitive Indicator of Populations under Stress. In Environmental Toxicology and Risk Assessment; STP 1179; Landis, W.G., Hughes, J.S., Lewis, M.A., Eds.; American Society for Testing and Materials: Philadelphia, PA, USA, 1993; pp. 136–158. [Google Scholar]
- Lens, L.; Van Dongen, S. Fluctuating and directional asymmetry in natural bird populations exposed to different levels of habitat disturbance, as revealed by mixture analysis. Ecol. Lett. 2000, 3, 516–522. [Google Scholar]
- Kark, S. Shifts in bilateral asymmetry within a distribution range: The case of the chukar partridge. Evolution 2001, 55, 2088–2096. [Google Scholar]
- Derjugin, K.M. Fauna Beloga. i Uslovia ee Suchsestvovania Issledovania; Morei SSSR, 7/8; Gosudarstvennyi Gidrologicheskii Institute: Leningrad, Russia, 1928. [Google Scholar]
- Hoffman, A.A.; Parsons, P.A. Evolutionary Genetics and Environmental Stress; Oxford University Press: New York, NY, USA, 1991. [Google Scholar]
- Väinölä, R.; Strelkov, P. Mytilus trossulus in Northern Europe. Mar. Biol. 2011, 158, 817–833. [Google Scholar]
- Kuznetsov, V.V. Beloe More i Biologicheskie Osobennosti Ego Flory i Fauny; Izdatelstvo Akademii Nauk SSSR: Moscow; Leningrad, Russia, 1960. [Google Scholar]
- Babkov, A.I. Gidrologia Belogo moria Zoologicheskii institut RAN, Belomorskaia Biologicheskaia Stantsia im; O.A. Skarlato: St. Petersburg, Russia, 1998. [Google Scholar]
- Gosling, E. Bivalve Molluscs: Biology, Ecology and Culture; Blackwell Publishing: Malden, MA, USA, 2003. [Google Scholar]
- Lens, L.; Van Dongen, S.; Kark, S.; Matthysen, E. Fluctuating asymmetry as an indicator of fitness: Can we bridge the gap between studies? Biol. Rev. 2002, 77, 27–38. [Google Scholar]
- Sukhotin, A.A.; Krasnov, Y.V.; Galaktionov, K.V. Subtidal populations of the blue mussel Mytilus edulis as key determinants of waterfowl flocks in the southeastern Barents Sea. Polar Biol 2008, 31, 1357–1363. [Google Scholar]
- Agarova, I.Y. Results of Long-Term Observations on Populations of Mytilus edulis L. in one location on Intertidal Bank of Eastern Murman Coast. In Promyslovye Dvustvorchatye Molliuski-midii i ikh Rol’ v Ekosisteme. Akademia Nauk SSSR; Skarlato, O.A., Ed.; Zoologicheskii Institut: Leningrad, Russia, 1979; pp. 8–10. [Google Scholar]
- Strelkov, P.P.; Dobretsov, S.V.; Zubakha, M.A.; Maksimovich, N.V. Reproductive cycle and population dynamics of mussel Mytilus edulis L. in Eastern Murman coast (Barents Sea). Vestn. Santk. Peterburgskogo Univ. Ser. 2001, 3, 46–50. [Google Scholar]
- Yurtseva, A.; Lajus, D.; Makhrov, A.; Artamonova, V. Atlantic salmon (Salmo salar L.) in the border of distribution range: Patterns of osteological variation. J. Appl. Ichthyol. 2014, 30, 721–727. [Google Scholar]
- Thyrring, J.; Rysgaard, S.; Blicher, M.E.; Sejr, M.K. Metabolic cold adaptation and aerobic performance of blue mussels (Mytilus edulis) along a temperature gradient into the High Arctic region. Mar. Biol. 2015, 162, 235–243. [Google Scholar]
| Sampling Region | Sampling Location | Abbreviation | Date of Sampling in 1997 | Coordinates | Tidal Zone | Depth (m) | Temperature (°C) | Salinity (‰) | Length (Mean and Ranges) mm |
|---|---|---|---|---|---|---|---|---|---|
| Barents Sea | Yugorskiy Shar Strait | YSH | 28 July | 69°45′ N, 60°33′ E | subtidal | 18 | 2.5 | 32 | 54.46 (45–64) |
| Barents Sea | Storozhevoy Island | STR | 29 July | 69°41′ N, 60°38′ E | intertidal | <5 | 6.2 | 19 | 43.22 (34–58) |
| Barents Sea | Sin’kin Nos Cape | SIN | 30 July | 68°40′ N, 59°51′ E | intertidal | <5 | 9.0 | 13 | 39.21 (35–42) |
| Barents Sea | Kolguev Island | KLG | 2 August | 68°46′ N, 49°15′ E | tidal | 0 | 5.4 | 33 | 44.55 (21–57) |
| Barents Sea | Chesha Bay | CHS | 3 August | 67°48′ N, 46°28′ E | tidal | 0 | 6.5 | 34 | 30.85 (24–39) |
| Barents Sea | Dal’nie Zelentsy Village | DZL | 20 July | 69°05′ N, 36°03′ E | tidal | 0 | 7.0 | 35 | 26.39 (22–37) |
| White Sea | Voronka Strait | VOR | 5 August | 67°54′ N, 41°23′ E | subtidal | 37 | 8.0 | 32 | 39.31 (34–46) |
| White Sea | Pulonga Village | PUL | 5 August | 66°15′ N, 40°01′ E | intertidal | <0.5 | 8.9 | 28 | 36.88 (30–42) |
| White Sea | Bol’shiye Kozly Village | KZL | 6 August | 65°15′ N, 39°52′ E | intertidal | <0.5 | 16.0 | 22 | 38.57 (32–44) |
| White Sea | Anzersky Island | ANZ | 9 August | 65°09′ N, 36°56′ E | tidal | 0 | 10.3 | 27 | 28.20 (25–35) |
| Character | PC1 | PC2 | PC3 | PC4 | PC5 | PC6 |
|---|---|---|---|---|---|---|
| Ch1 | 0.856 | 0.153 | −0.059 | −0.044 | −0.106 | 0.066 |
| Ch2 | 0.807 | 0.049 | −0.202 | −0.048 | −0.061 | 0.215 |
| Ch3 | 0.838 | 0.130 | 0.247 | 0.080 | −0.024 | 0.032 |
| Ch4 | 0.837 | −0.102 | −0.082 | 0.112 | 0.133 | 0.034 |
| Ch5 | 0.920 | 0.109 | −0.005 | 0.029 | 0.134 | −0.105 |
| Ch6 | 0.959 | 0.068 | 0.004 | 0.055 | 0.081 | −0.089 |
| Ch7 | 0.586 | 0.003 | −0.617 | −0.441 | −0.085 | 0.011 |
| Ch8 | 0.528 | −0.412 | 0.443 | −0.392 | 0.103 | 0.411 |
| Ch9 | 0.572 | −0.066 | 0.435 | −0.528 | −0.088 | −0.400 |
| Ch10 | 0.898 | 0.185 | −0.024 | 0.115 | 0.229 | −0.021 |
| Ch11 | 0.740 | −0.479 | −0.184 | 0.064 | −0.250 | −0.063 |
| Ch12 | 0.841 | 0.192 | −0.189 | −0.085 | 0.305 | −0.036 |
| Ch13 | 0.695 | −0.529 | −0.104 | 0.270 | −0.238 | −0.073 |
| Ch14 | 0.797 | −0.062 | 0.320 | 0.418 | 0.022 | −0.020 |
| Ch15 | 0.520 | 0.648 | 0.169 | 0.005 | −0.451 | 0.124 |
| Proportion of Explained Variance | 0.597 | 0.083 | 0.073 | 0.062 | 0.037 | 0.029 |
| Character | ANZ | KZL | PUL | VOR | DZL | CHS | KLG | SIN | STR | YSH |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 3.69 | 3.94 | 3.63 | 3.83 | 3.28 | 3.30 | 4.06 | 3.72 | 3.89 | 3.76 |
| 2 | 1.46 | 1.42 | 1.51 | 1.54 | 1.40 | 1.56 | 1.60 | 1.43 | 1.39 | 1.13 |
| 3 | 4.98 | 3.98 | 3.92 | 3.91 | 2.83 | 4.29 | 4.89 | 3.77 | 4.31 | 5.53 |
| 4 | 2.40 | 2.36 | 2.82 | 3.14 | 2.67 | 3.32 | 3.09 | 2.80 | 2.96 | 3.30 |
| 5 | 11.65 | 11.91 | 12.43 | 11.94 | 10.42 | 10.42 | 14.13 | 12.53 | 12.44 | 14.33 |
| 6 | 15.62 | 15.90 | 16.63 | 16.87 | 15.59 | 15.15 | 19.03 | 16.48 | 16.55 | 19.35 |
| 7 | 5.91 | 5.83 | 6.04 | 6.72 | 5.87 | 6.73 | 6.88 | 5.46 | 5.83 | 4.07 |
| 8 | 1.07 | 0.79 | 0.99 | 1.20 | 1.08 | 1.37 | 1.31 | 1.05 | 1.30 | 1.26 |
| 9 | 2.01 | 1.42 | 1.27 | 1.25 | 1.43 | 1.59 | 1.77 | 1.58 | 1.65 | 1.75 |
| 10 | 3.01 | 3.34 | 3.71 | 3.44 | 2.65 | 4.16 | 3.77 | 3.39 | 3.11 | 4.30 |
| 11 | 2.30 | 1.77 | 2.29 | 2.97 | 1.86 | 2.44 | 2.56 | 2.05 | 2.56 | 2.28 |
| 12 | 2.71 | 3.20 | 3.44 | 3.36 | 2.76 | 3.75 | 3.73 | 3.03 | 2.88 | 3.65 |
| 13 | 1.29 | 1.17 | 1.94 | 2.71 | 1.58 | 1.83 | 1.56 | 1.83 | 2.00 | 1.94 |
| 14 | 4.32 | 3.45 | 4.84 | 4.44 | 3.45 | 4.29 | 4.27 | 3.73 | 3.93 | 6.41 |
| 15 | 13.83 | 14.27 | 9.17 | 8.32 | 8.36 | 14.20 | 9.35 | 8.18 | 8.08 | 10.80 |
| Character | ANZ | KZL | PUL | VOR | DZL | CHS | KLG | SIN | STR | YSH |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.988 | 0.989 | 1.028 | 0.960 | 1.022 | 1.024 | 0.954 | 0.993 | 0.957 | 0.972 |
| 2 | 1.013 | 0.989 | 1.015 | 0.993 | 1.035 | 1.112 | 0.991 | 1.008 | 1.029 | 0.997 |
| 4 | 1.106 | 1.037 | 1.095 | 1.057 | 1.070 | 1.067 | 1.002 | 1.050 | 1.062 | 1.086 |
| 5 | 0.977 | 0.956 | 0.973 | 0.954 | 0.937 | 0.959 | 0.993 | 0.966 | 0.989 | 0.949 |
| 6 | 1.001 | 0.994 | 0.997 | 0.999 | 0.972 | 0.992 | 1.001 | 0.991 | 0.982 | 0.987 |
| 7 | 1.075 | 1.042 | 1.038 | 1.023 | 1.021 | 1.009 | 1.024 | 1.009 | 1.015 | 1.014 |
| 8 | 1.015 | 1.011 | 0.939 | 1.016 | 1.076 | 0.936 | 1.096 | 1.044 | 1.038 | 1.103 |
| 9 | 1.031 | 1.098 | 1.003 | 0.955 | 0.949 | 1.134 | 1.119 | 1.004 | 1.047 | 0.965 |
| 10 | 0.978 | 1.014 | 0.968 | 0.989 | 0.988 | 0.966 | 0.991 | 0.970 | 0.984 | 1.034 |
| 11 | 1.128 | 0.992 | 1.041 | 1.033 | 1.102 | 1.085 | 1.070 | 1.050 | 1.061 | 1.046 |
| 12 | 1.120 | 1.115 | 1.012 | 1.095 | 1.103 | 1.053 | 1.048 | 1.002 | 1.012 | 1.033 |
| 13 | 1.041 | 0.944 | 0.937 | 1.021 | 0.958 | 1.049 | 1.021 | 1.018 | 0.942 | 0.965 |
| 14 | 1.031 | 0.995 | 1.006 | 1.029 | 1.006 | 1.021 | 1.014 | 1.022 | 1.018 | 0.991 |
| 15 | 1.021 | 1.011 | 1.044 | 1.048 | 1.065 | 1.014 | 1.000 | 0.997 | 1.009 | 1.034 |
| Character | σ2F | σ2S | |
|---|---|---|---|
| FA | ME | ||
| 1 | 0.0126 | 0.0044 | 0.0082 |
| 2 | 0.0200 | 0.0080 | 0.0137 |
| 4 | 0.0157 | 0.0079 | 0.0097 |
| 5 | 0.0059 | 0.0012 | 0.0024 |
| 6 | 0.0041 | 0.0013 | 0.0011 |
| 7 | 0.0109 | 0.0020 | 0.0024 |
| 8 | 0.0410 | 0.0183 | 0.0430 |
| 9 | 0.0215 | 0.0234 | 0.0177 |
| 10 | 0.0165 | 0.0026 | 0.0047 |
| 11 | 0.0230 | 0.0116 | 0.0073 |
| 12 | 0.0191 | 0.0056 | 0.0071 |
| 13 | 0.0391 | 0.0247 | 0.0097 |
| 14 | 0.0106 | 0.0029 | 0.0026 |
| 15 | 0.0065 | 0.0011 | 0.0035 |
| ANZ | KZL | PUL | VOR | DZL | CHS | KLG | SIN | JSH | STR | |
|---|---|---|---|---|---|---|---|---|---|---|
| Factorial Component | ||||||||||
| ANZ | 1 | |||||||||
| KZL | 0.551 | 1 | ||||||||
| PUL | 0.048 | 0.363 | 1 | |||||||
| VOR | 0.925 | 0.245 | 0.096 | 1 | ||||||
| DZL | 0.030 | 0.074 | 0.470 | 0.030 | 1 | |||||
| CHS | 0.011 | 0.002 | 0.022 | 0.002 | 0.074 | 1 | ||||
| KLG | 0.074 | 0.022 | 0.124 | 0.008 | 0.778 | 0.005 | 1 | |||
| SIN | 0.470 | 0.397 | 0.096 | 0.975 | 0.056 | 0.011 | 0.056 | 1 | ||
| JSH | 0.016 | 0.001 | 0.096 | 0.004 | 0.470 | 0.016 | 0.140 | 0.016 | 1 | |
| STR | 0.551 | 0.875 | 0.300 | 0.363 | 0.074 | 0.002 | 0.011 | 0.875 | 0.006 | 1 |
Fluctuating Asymmetry | ||||||||||
| ANZ | 1 | |||||||||
| KZL | 0.363 | 1 | ||||||||
| PUL | 0.683 | 0.594 | 1 | |||||||
| VOR | 0.975 | 0.221 | 0.470 | 1 | ||||||
| DZL | 0.470 | 0.925 | 0.221 | 0.158 | 1 | |||||
| CHS | 0.035 | 0.510 | 0.030 | 0.026 | 0.009 | 1 | ||||
| KLG | 0.778 | 0.594 | 0.551 | 0.433 | 0.925 | 0.048 | 1 | |||
| SIN | 0.826 | 0.030 | 0.048 | 0.177 | 0.109 | 0.005 | 0.221 | 1 | ||
| JSH | 0.331 | 0.875 | 0.433 | 0.300 | 0.925 | 0.124 | 0.925 | 0.064 | 1 | |
| STR | 0.363 | 0.109 | 0.272 | 0.433 | 0.084 | 0.006 | 0.470 | 0.433 | 0.177 | 1 |
Measurement Error | ||||||||||
| ANZ | 1 | |||||||||
| KZL | 0.004 | 1 | ||||||||
| PUL | 0.001 | 0.778 | 1 | |||||||
| VOR | 0.001 | 0.096 | 0.198 | 1 | ||||||
| DZL | 0.002 | 0.300 | 0.041 | 0.778 | 1 | |||||
| CHS | 0.004 | 0.124 | 0.198 | 0.245 | 0.363 | 1 | ||||
| KLG | 0.001 | 0.975 | 0.551 | 0.245 | 0.177 | 0.363 | 1 | |||
| SIN | 0.001 | 0.470 | 0.245 | 0.002 | 0.030 | 0.009 | 0.221 | 1 | ||
| JSH | 0.002 | 0.638 | 0.778 | 0.140 | 0.245 | 0.109 | 0.331 | 0.048 | 1 | |
| STR | 0.002 | 0.730 | 0.826 | 0.048 | 0.510 | 0.170 | 0.875 | 0.013 | 0.638 | 1 |
| Percentage | ANZ | KZL | PUL | VOR | DZL | CHS | KLG | SIN | STR | YSH | Mean |
|---|---|---|---|---|---|---|---|---|---|---|---|
| % σ2F in σ2 | 26.08 | 47.65 | 58.89 | 45.94 | 54.34 | 62.66 | 63.84 | 64.47 | 58.82 | 67.44 | 55.13 |
| % FA in σ2 | 9.15 | 26.40 | 19.82 | 19.42 | 21.65 | 21.74 | 19.43 | 17.12 | 13.11 | 17.28 | 18.51 |
| % ME in σ2 | 64.77 | 25.95 | 21.29 | 34.64 | 24.01 | 15.59 | 16.73 | 18.41 | 28.07 | 15.28 | 26.47 |
| % FA in σ2S | 9.16 | 43.25 | 47.23 | 29.86 | 45.89 | 56.74 | 46.65 | 43.17 | 9.12 | 37.50 | 36.86 |
| % ME in σ2S | 90.84 | 56.75 | 52.77 | 70.14 | 54.11 | 43.26 | 53.35 | 56.83 | 90.88 | 62.50 | 63.14 |
| Parameter | T | S | Biotope |
|---|---|---|---|
| Principal Components (Obtained from Analysis of Mean Values of Characters)
| |||
| PC1 | −0.43 | −0.11 | 0.51* |
| PC2 | 0.64 | −0.29 | −0.38* |
| PC3 | −0.33 | 0.10 | −0.18* |
| PC4 | −0.31 | 0.30 | 0.61* |
| PC5 | −0.66 | 0.18 | −0.32* |
| PC6 | 0.30 | 0.37 | −0.20* |
Predicted Mean Values for Length of 40 mm | |||
| Ch7 | 0.22 | 0.25 | −0.33* |
| Ch8 | −0.85 | 0.39 | 0.01* |
| Ch9 | −0.27 | −0.05 | −0.43* |
| Ch11 | −0.46 | 0.27 | 0.11* |
| Ch13 | −0.46 | 0.13 | 0.72* |
| Ch14 | −0.61 | 0.35 | 0.51* |
| Ch15 | 0.43 | 0.14 | −0.13* |
Components of the Phenotypic Variance (Expressed as a Sum of Ranks) | |||
| FC | −0.73* | 0.63* | 0.03* |
| FA | −0.21* | 0.70* | −0.14* |
| ME | 0.58* | −0.36* | −0.18* |
Contribution of Components into Phenotypic Variance | |||
| % σ2F in σ2 | −0.56 | −0.01 | 0.23* |
| % FA in σ2 | 0.30 | 0.24 | 0.16* |
| % ME in σ2 | 0.37 | −0.07 | −0.29* |
| % FA in σ2S | −0.03 | 0.33 | 0.02* |
| % ME in σ2S | 0.03 | −0.33 | −0.02* |
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lajus, D.; Katolikova, M.; Strelkov, P.; Hummel, H. Fluctuating and Directional Asymmetry of the Blue Mussel (Mytilus edulis): Improving Methods of Morphological Analysis to Explore Species Performance at the Northern Border of Its Range. Symmetry 2015, 7, 488-514. https://doi.org/10.3390/sym7020488
Lajus D, Katolikova M, Strelkov P, Hummel H. Fluctuating and Directional Asymmetry of the Blue Mussel (Mytilus edulis): Improving Methods of Morphological Analysis to Explore Species Performance at the Northern Border of Its Range. Symmetry. 2015; 7(2):488-514. https://doi.org/10.3390/sym7020488
Chicago/Turabian StyleLajus, Dmitry, Marina Katolikova, Petr Strelkov, and Herman Hummel. 2015. "Fluctuating and Directional Asymmetry of the Blue Mussel (Mytilus edulis): Improving Methods of Morphological Analysis to Explore Species Performance at the Northern Border of Its Range" Symmetry 7, no. 2: 488-514. https://doi.org/10.3390/sym7020488
APA StyleLajus, D., Katolikova, M., Strelkov, P., & Hummel, H. (2015). Fluctuating and Directional Asymmetry of the Blue Mussel (Mytilus edulis): Improving Methods of Morphological Analysis to Explore Species Performance at the Northern Border of Its Range. Symmetry, 7(2), 488-514. https://doi.org/10.3390/sym7020488





