Abstract
Nuclear matter is a convenient theoretical laboratory to test many-body theories. When neutron and proton densities are different, the isospin dependence of the nuclear force gives rise to the symmetry energy term in the equation of state. This quantity is a crucial mechanism in the formation of the neutron skin in nuclei, as well as in other systems and phenomena involved in the dynamics of neutrons and protons in neutron-rich systems, such as isospin-asymmetric heavy-ion collisions. In this article, we will review phenomenological facts about the symmetry energy and recent experimental efforts to constrain its density dependence and related quantities. We will then review our microscopic approach to the equation of state of symmetric and asymmetric nuclear matter and present a corresponding set of predictions. Our calculations utilize the Dirac–Brueckner–Hartree–Fock method and realistic meson-theoretic nucleon-nucleon potentials. Chiral perturbation theory is an alternative approach, based on a well-defined scheme, which allows one to develop nuclear forces at each order of the chiral expansion. We will present and discuss predictions based on chiral perturbation theory, where we employ consistent two- and three-body chiral interactions. Throughout the article, one of the focal points is the importance of pursuing ab initio methods towards a deeper understanding of the many-body system.
1. Introduction
Nearly eight decades ago, Bethe and Weizäcker [1,2] proposed the “liquid drop model” for nuclear binding energies, which, in spite of its simplicity, turned out to be remarkably successful. The model is essentially a mass formula that provides the total binding energy per nucleon as the sum of several contributions,
These contributions are the volume, the surface, the Coulomb and the symmetry terms, followed by smaller contributions, such as the pairing term. The (attractive) volume term is the largest and represents the energy per nucleon in an infinite, isospin-saturated system where the Coulomb interaction between protons is not taken into account. Such an idealized system is known as symmetric nuclear matter, and the value of the aV coefficient is therefore the binding energy per nucleon in infinite symmetric matter, approximately 15–16 MeV. Clearly, the (repulsive) Coulomb term favors a nucleus with a large neutron excess. On the other hand, the destabilizing effect of the symmetry term increases with larger values of N − Z = A − 2Z. Fits to empirical nuclear binding energies determine the coefficients of the mass formula, resulting in a value of about 23 MeV for asym. We note that this is not the same as the symmetry energy at the equilibrium density of infinite nuclear matter.
Although this simple model captures the main features of the nuclear binding energies, a deep understanding of nuclear structure and nuclear stability, all the way to the (yet unknown) drip lines, requires a microscopic approach to the interaction between nucleons. This is still a very challenging problem that goes to the very core of nuclear physics. In fact, our present knowledge of the nuclear force in free space is, in itself, the result of decades of struggle [3]. The nature of the nuclear force in the medium is of course a much more complex problem, as it involves aspects of the force that cannot be constrained through free-space nucleon-nucleon (NN) scattering. Predictions of nuclear properties are the ultimate test for many-body theories.
Nuclear matter, as defined above, is an alternative and convenient theoretical laboratory for many-body theories. Being an infinite (and, thus, translationally invariant) system of nucleons subjected only to their mutual strong interactions, it is theoretically simpler than an actual nucleus. A typical outcome of nuclear matter investigations consists of the energy per particle and the pressure as functions of density (and of additional variables, if appropriate) and other quantities, such as free energy and entropy. Such a relation is known as the nuclear matter equation of state (EoS).
Adopting what is known as “local density approximation”, one can relate the EoS to finite systems. This procedure is applied, for instance, in Thomas–Fermi calculations within the liquid drop model, where an appropriate energy functional is written in terms of the EoS [4–6]. Vice versa, empirical information on nuclei can be extrapolated to an infinite system to provide constraints for theoretical models of nuclear matter.
For the case of (cold) isospin-asymmetric nuclear matter, where proton and neutron densities are different, the energy per particle is a function of both the total density and the relative concentrations of protons and neutrons. Naturally, the latter dependence is related to the symmetry term in the Bethe–Weizäcker formula, Equation (1). These aspects will be discussed in more detail in Section 2.
Studies of symmetric nuclear matter date back to the earlier works by Brueckner and others [7–10], where the Brueckner–Hartree–Fock (BHF) theory was first proposed. The Brueckner theory is based on a linked-cluster perturbation series of the ground state energy of a many-body system [7–12]. Such a series was shown to converge when the cluster diagrams are regrouped according to the number of hole lines. The variational approach was also pursued as an alternative method [13,14] and yielded predictions in close agreement with those from Brueckner theory when realistic NN potentials were employed [15].
During the 1980s, the Dirac–Brueckner–Hartree–Fock (DBHF) approach was developed [16–20]. The main break-through came with the observation that the DBHF theory, unlike conventional Brueckner theory, could describe successfully the saturation properties of nuclear matter, that is the saturation energy and density of the equation of state. The DBHF method, reviewed in Section 3, describes the nuclear mean field in terms of strong and competing scalar and vector components that, together, account for the binding of nucleons, as well as the large spin-orbit splitting seen in nuclear states. Mean-field models (relativistic and non-relativistic) [21–28] are a popular, although non-microscopic, alternative to methods that are based on the in-medium reaction matrix, such as BHF and DBHF. In [29], microscopic calculations of neutron matter are conducted within variations of the Monte Carlo method, whereas the authors of [30] report a comparative study with various approaches, including BHF, the self-consistent Green function method and the auxiliary field diffusion Monte Carlo.
More recently, chiral effective theories of the nuclear force, originally proposed by Weinberg [31,32], have become popular as a means to respect the symmetries of quantum chromodynamics (QCD), while retaining the basic degrees of freedom typical of low-energy nuclear physics, pions and nucleons. Chiral effective theories provide a well-defined scheme to determine the appropriate many-body diagrams to be included at each order of the perturbation. Chiral approaches will be revisited in Section 4.
Although predictions of symmetric nuclear matter properties from different models are reasonably convergent, predictions of the symmetry energy can vary dramatically, particularly so for its density dependence. It is the purpose of this article to explore and discuss the present status of our knowledge of the symmetry energy and, more broadly, the EoS of asymmetric matter. One of our main goals is to demonstrate the importance of pursuing a microscopic approach towards a better understanding of the properties of dense many-body systems.
2. The Symmetry Energy
2.1. Empirical Facts
Isospin-asymmetric nuclear matter is characterized by the neutron density, ρn, and the proton density, ρp. It is more convenient to refer to the total density ρ = ρn + ρp and the asymmetry (or neutron excess) parameter
. Clearly, α = 0 corresponds to symmetric matter and α = 1 to neutron matter. In terms of α and the average Fermi momentum, kF, related to the total density in the usual way,
the neutron and proton Fermi momenta can be expressed as:
and
respectively.
Expanding the energy/particle in isospin asymmetric matter with respect to the asymmetry parameter yields:
To a very good degree of approximation, the energy per particle in isospin asymmetric matter can be written as:
which has the same form as the sum of the first and fourth terms on the right-hand side of Equation (1), with α replacing
. A typical value for esym at nuclear matter saturation density (ρ0) is 30 MeV, with theoretical predictions spreading approximately between 26 and 35 MeV.
Equation (6) displays a convenient separation between the symmetric and the asymmetric parts of the EoS, which facilitates the identification of observables that may be sensitive, for instance, mainly to the symmetry energy. Empirical investigations appear to agree reasonably well on parameterizations of the symmetry energy having the form:
The first term is the kinetic contribution. It comes from the difference of the kinetic contributions in neutron and symmetric matter (at the same density), which is:
with
the Fermi energy. Writing the Fermi energy in terms of ρ yields the first term in Equation (7). The exponent γi appearing in the potential energy part is found to be between 0.4 and 1.0. Recent measurements of elliptic flows in 197Au + 197Au reactions at GSI at 400–800 MeV/nucleon favor a potential energy term with γi equal to 0.9 ± 0.4. Giant dipole resonance excitation in fusion reactions [33] is also sensitive to the symmetry energy, since the latter is responsible for isospin equilibration in isospin-asymmetric collisions. Recent efforts to set more stringent constraints on the symmetry energy will be reviewed in the next section.
A measure for the density dependence of the symmetry energy is the parameter defined as:
where we have used Equation (6) with α = 1. Thus, L is sensitive to the gradient of the energy per particle in neutron matter (en.m.), that is, the neutron matter pressure. As to be expected on physical grounds, the neutron skin thickness,
where
and
are the r.m.s. radii of the neutron and proton distributions, is highly sensitive to the same energy gradient. We will come back to this point in Section 2.3.
Predictions of L by phenomenological models show a very large spread. Values ranging from −50 to +100 MeV are found from the numerous parameterizations of Skyrme interactions, all chosen to fit the binding energies and the charge radii of a large number of nuclei [34].
Typically, parameterizations like the one given in Equation (7) are valid at or below saturation density. Efforts to constrain the behavior of the symmetry energy at higher densities are being pursued through observables, such as the π−/π+ ratio, the K+/K0 ratio, neutron/proton differential transverse flow or nucleon elliptic flow [35].
The definition of L in Equation (9) originates from an expansion of the symmetry energy in the powers of the density (relative to saturation density):
where
Consistent with Equation (6), it is also customary to express the incompressibility of asymmetric matter to second order in α,
with K0 the incompressibility of symmetric nuclear matter. Attempts to extract the parameter Kasy from the giant monopole resonances of neutron-rich nuclei have been made, but the extracted value carries very large uncertainties.
Another important quantity, which emerges in conjunction with asymmetric matter, is the symmetry potential. Its definition stems from the observation that the single-particle potentials experienced by the proton and the neutron, Un/p, are different from each other and satisfy the approximate relation:
where, in a neutron-rich environment, the +(−) sign refers to neutrons (protons), and:
Thus, one can expect isospin splitting of the single-particle potential to be effective in separating the collision dynamics of neutrons and protons. In a neutron-rich environment, the symmetry potential tends to expel neutrons and attract protons, thus providing the opportunity of detecting sensitivity to the symmetry energy in observables, such as the yield ratios of ejected neutrons/protons or the rate of isospin diffusion [36].
Furthermore, Usym, being proportional to the gradient between the single-neutron and the single-proton potentials, should be comparable with the Lane potential [37], namely the isovector part of the nuclear optical potential. This suggests that optical potential analyses (in isospin unsaturated nuclei) can be an alternative way to constrain the symmetry energy.
2.2. Experimental Constraints on the Symmetry Energy
In this section, we review some recent measurements and analyses aimed at constraining the symmetry energy. We refer the reader to [36] and the references therein for more details.
Several types of experiments can be exploited for this purpose. They include:
Heavy ion collisions:
The EoS is an important part of the input of transport models describing heavy ion collisions and, thus, can be constrained through measurements of selected observables in ion-ion scattering. Sensitivity to the EoS can be attained by varying the number of protons and neutrons of the colliding nuclei. Emission of particles from neutron-rich or proton-rich systems is sensitive to the symmetry potential, which is repulsive on neutrons and attractive on protons (in a neutron-rich environment), see Equations (14) and (15). Neutron-proton spectral ratios, as well as neutron, hydrogen and fragment flows are sensitive to the density dependence of the symmetry energy and have been used for that purpose. Furthermore, in a collision where the target and projectile have different values of N/Z, the system tends towards a state of constant value of the asymmetry parameter α, a phenomenon known as “isospin diffusion”, the rate of which is controlled by the strength of the symmetry potential. Neutron and proton spectra from central collisions of 124Sn + 124Sn and 112Sn + 112Sn at 50 MeV per nucleon have been measured, as well as transverse collective flows of hydrogen, helium isotopes and other fragments at 35 MeV per nucleon in 70Zn + 70Zn, 64Zn + 64Zn and 64Ni + 64Ni reactions.
Nuclear binding energies:
This method relies on the liquid droplet model we referred to in Section 2. Because the symmetry energy contribution to the total binding energy is small, a reliable determination of both the symmetry energy and its slope can be difficult. All other contributions must be known with very high accuracy. With improved droplet models, which allow one to reproduce binding energies within 0.1%, it was possible to determine the symmetry energy within 1 MeV and its slope within 30 MeV [36].
Neutron skin measurements with hadronic or electroweak probes:
The relation between the thickness of the neutron skin and the slope of the symmetry energy can be understood in terms of the pressure gradient (due to the symmetry potential) that pushes neutrons outwards (and acts in a similar manner in the interior of neutron stars). Experiments aimed at extracting the neutron skin as a measure of the slope of the symmetry energy use either electroweak or hadronic probes. Particularly for the latter, theoretical uncertainties in the models used to analyze the data are hard to quantify. One such experiment is reported in [38], where a skin thickness of 208Pb was extracted through polarized proton elastic scattering data. The proton optical potential was parametrized and constrained via 52Ni measurements and then fit to 204,206,208Pb data by adjusting the neutron densities.
Parity-violating electron scattering experiments are now a realistic option to determine neutron distributions with unprecedented accuracy. The neutron radius of 208Pb is expected to be re-measured at the Jefferson Laboratory in the PREXII experiment planned for the near future. Parity-violating electron scattering at low momentum transfer is especially suitable to probe neutron densities, as the Z0 boson couples primarily to neutrons. A much higher level of accuracy can be achieved with electroweak probes than with hadronic scattering. With the success of this program, reliable empirical information on neutron skins will be able to provide more stringent constraints on the density dependence of the symmetry energy.
Measurements of the neutron skin thickness in 48Ca have also been proposed and are expected to take place in the near future with the CREX experiment [39,40]. Being much lighter than 208Pb, 48Ca is considerably more sensitive to surface and shell effects, which makes it possible to extract useful structure information. Furthermore, ab initio calculations are feasible for calcium isotopes, thus CREX experiments have the potential to test models of three-nucleon forces and density functional theories.
The neutron skin thickness can also be probed through measurements of antiprotonic atoms. More specifically, photons from the decay of antiprotonic states with high orbital angular momentum are observed. The correlation with the neutron radius resides in the fact that the high angular momentum barrier limits the interaction between the antiproton and the neutrons to large distances. Although skin results based on this method have been found to be very model dependent, large systematics of measurements can contribute to improving the general understanding of the neutron skin in relation to the nucleus charge and mass number [36].
Electric dipole strength function:
The interaction of nuclei with an electric dipole field produces nuclear excitations. Some of these states contribute to giant dipole resonances, which are collective vibrations where protons and neutrons move in opposite directions and, thus, enhance the symmetry energy by displacing neutron and proton densities relative to each other. In a neutron-rich nucleus, enhancement of the electric dipole polarizability is expected due to the presence of the skin, because of vibrations of the symmetric (N = Z) core against the neutrons in the skin. The resulting low-energy states are easily excited by electric dipole radiation. In very neutron-rich nuclei, this enhanced low-energy dipole strength can appear in the form of a pygmy dipole resonance. A strong (although model-dependent) correlation was predicted [41] between the skin thickness in 208Pb and the electric dipole strength, providing an alternative way to measure the skin and, thus, extract information on the slope of the symmetry energy.
2.3. The Slope of the Symmetry Energy and the Radii of Neutron Stars
Neutron stars are perhaps the most “isospin-asymmetric” systems found in nature. These very exotic objects have typical masses of 1–2 solar masses and radii of approximately 10 kilometers. Neutron stars contain the most dense form of matter found in the universe and, therefore, are unique laboratories to study the properties of highly compressed (cold) matter. They are held together by gravity and neutron degeneracy pressure. With the assumption that general relativity is the correct theory to describe neutron stars, their structure is completely determined by the EoS used as input for the Tolman–Oppenheimer–Volkoff equations.
Although neutron stars were predicted as early as in the 1930s, hope for their observation remained slim for a long time. In 1967, strange new objects were observed at the University of Cambridge and named pulsars, because they emitted periodic radio signals. To date, about 1700 pulsars have been detected, many in binary systems.
Typically, detection of thermal radiation from the surface of a star is the way to access information about its properties. Furthermore, the possibility of exploring the structure of neutron stars via gravitational waves makes these exotic objects even more interesting.
The densities found in neutron stars range from the density of iron to several times normal nuclear density. Most of the mass consists of highly compressed matter at nuclear and supranuclear densities. The surface region is composed of normal nuclei and non-relativistic electrons, with typical mass densities in the range 104 ≤ ∊ ≤ 106 g·cm−3. As density increases, charge neutrality requires matter to become more neutron rich. In this density range (about 107 < ∊ < 1011 g·cm−3), neutron-rich nuclei appear, mostly light metals, while electrons become relativistic. This is the outer crust. Above densities of approximately 1011 g·cm−3, free neutrons begin to form a continuum of states. The inner crust is a compressed solid with a fluid of neutrons that drip out and populate free states outside the nuclei, which have become neutron-saturated. Densities in the inner crust range between 1011 and 1014 g·cm−3. At densities equal to approximately 1/2 of the saturation density, clusters begin to merge into a continuum. In this phase, matter is a uniform fluid of neutrons, protons and leptons. Above a few times nuclear matter density, the actual composition of stellar matter is not known. Strange baryons can appear when the nucleon chemical potential is of the order of their rest mass. Meson production can also take place. At even higher densities, transitions to other phases are speculated, such as a deconfined, rather than hadronic, phase. The critical density for such a transition cannot be predicted reliably, because it lies in a range where QCD is non-perturbative [42].
The maximum gravitational mass of the star and the corresponding radius are the typical properties used to constrain the EoS. The gravitational mass is inferred mostly from observations of X-ray binaries or binary pulsars. Determination of the mass provides a unique test of both theories of nuclear matter and general relativity. The pulsar in the Hulse–Taylor binary system has a mass of 1.4408 ± 0.0003 M⊙, to date the best mass determination.
One of the heaviest neutron stars (with accurately known mass) has a mass of 1.671 ± 0.008 M⊙ [43]. The observation of a heavier star was confirmed, namely J1614-2230, with a mass of 1.97 ± 0.04 M⊙ [44], one of the highest yet measured with this certainty. Furthermore, a more recent paper has reported the observation of a pulsar with even heavier mass [45], 2.01 ± 0.04 M⊙. Clearly, these observations represent a challenge for the softest EoS.
The minimum mass of a neutron star is also a parameter of interest. For a cold, stable system, the minimum mass is estimated to be 0.09 M⊙ [46]. The smallest reliably estimated neutron star mass is the companion of the binary pulsar, J1756-2251, which has a mass of 1.18 ± 0.02 M⊙ [47].
Measurements of the star radius are considerably less precise than mass measurements [46]. In fact, no direct measurements of the radius exist. Instead, the observed X-ray flux, together with theoretical assumptions [48], can provide information on the radiation or the photospheric radius, R∞, which is related to the actual stellar radius by R∞ = R(1 − 2GM/Rc2)−1/2. Estimates are usually based on thermal emissions of cooling stars, including redshifts, and the properties of sources with bursts or thermonuclear explosions at the surface. A major problem associated with the determination of radii is that the distance from the source is not well known, hence the need for additional assumptions. Much more stringent constraints could be imposed on the EoS if mass and radius could be determined independently of each other.
The problems with obtaining precise measurements of radii pose strong limitations on the possibility to constrain the EoS through astronomical observations. As we argue next, knowledge of the mass-radius relation over a broad range of masses would provide the necessary constraints on the EoS of isospin-asymmetric matter. This is demonstrated in Table 1, which is taken from [49]. The entry “A” represents a quantity that we wish to measure or constrain. The right column displays the correlation coefficient between quantity “A” and the neutron skin thickness in 208Pb (we recall that the correlation coefficient is equal to one for a perfect correlation). The strong correlation between L and the neutron skin thickness was mentioned earlier in the discussion following Equations (9) and (10) and can be seen clearly from the table.

Table 1.
Correlation between “observable” A and the neutron skin thickness in 208Pb. P is the pressure, and Rx is the radius of a neutron star with mass equal to x solar masses.
The correlation between the pressure in stellar matter around saturation density and the skin thickness, also shown in the table, is not surprising. The symmetry potential discussed in Section 2.1 is attractive to protons and repulsive to neutrons, thus pushing neutrons outward to form the skin. A similar mechanism acts within the star. Notice how the correlation with the neutron skin becomes much weaker at higher density. This is understandable, since nuclei do not probe super-high densities. For the same reason, the correlation between the radius of the star and the skin thickness in 208Pb deteriorates for the heaviest stars, which have central densities much higher than those probed by ordinary nuclei. In summary, the larger the predicted skin of a heavy nucleus, the larger the predicted stellar radius of (low-mass) neutron stars. Therefore, constraints from both neutron skins and neutron star radii would be extremely useful for a better understanding of the slope of the symmetry energy.
We close this section by showing in Figure 1 the baryon density and the mass-energy density profile of a neutron star with a mass of 1.4 solar masses (the most probable mass). Our DBHF predictions are compared with those of other microscopic models, which are taken from [50]. There (and in previous work by the same authors), the Brueckner–Hartree–Fock formalism is employed along with microscopic meson-exchange three-body forces. In particular, in [51], the meson-exchange three-body forces are constructed applying the same parameters as those used in the corresponding nucleon-nucleon potentials, which are: Argonne V18 [52] (V18), Bonn B [3] (BOB) and Nijmegen 93 [53] (N93). The popular (but phenomenological) Urbana three-body force [54] (UIX) is also utilized in [51]. At subnuclear densities, all of the EoS considered in the figure are joined with the crustal equations of state from Harrison and Wheeler [55] and Negele and Vautherin [56]. The composition of the crust is crystalline, with light [55] or heavy [56] metals and electron gas.
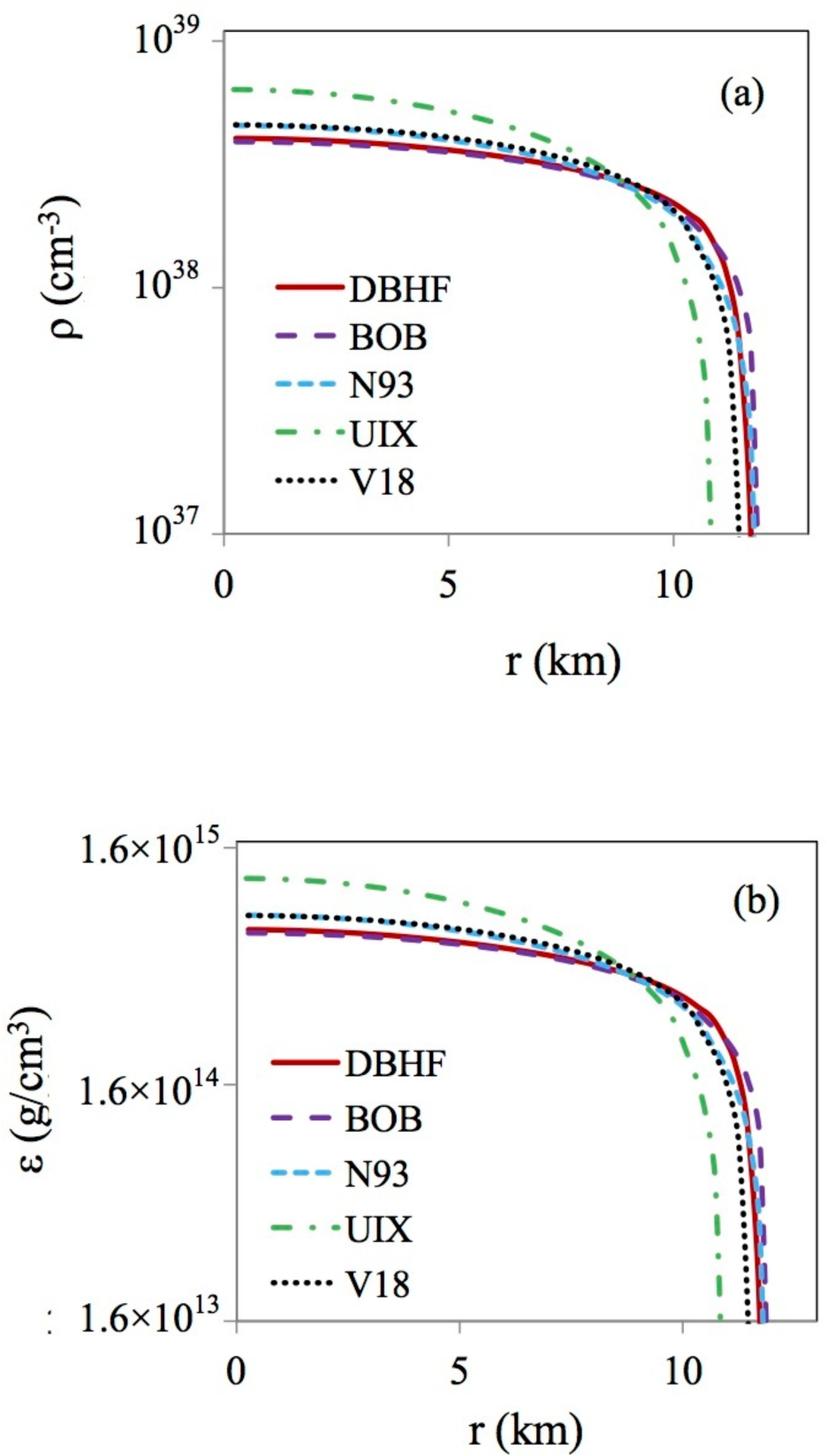
Figure 1.
(a) The baryon density and (b) the mass-energy density profile for a neutron star with a mass of 1.4 solar masses.
The relations shown in Figure 1 are insightful, as they reveal the detailed structure of the star at each radial position. Furthermore, the compactness of the star, whose density profile is reminiscent of the one in a nucleus, a system 55 orders of magnitude lighter, is apparent.
3. Our Microscopic Approach to Isospin-Asymmetric Nuclear Matter
3.1. Brief Review of the Model
Our approach is ab initio in that the starting point of the many-body calculation is a realistic NN interaction, which is then applied in the nuclear medium without any additional free parameters. Thus, the first question to be confronted concerns the choice of how to develop the baseline NN force. As we mentioned in the Introduction, after the development of QCD and the understanding of its symmetries, chiral effective theories [31] were introduced as a way to respect the symmetries of QCD, while keeping the degrees of freedom (nucleons and pions) typical of low-energy nuclear physics. However, chiral perturbation theory has definite limitations as far as the range of allowed momenta is concerned. For the purpose of applications in dense matter, where higher and higher momenta become involved with increasing Fermi momentum, NN potentials based on this approach may be unsuitable.
On the other hand, relativistic meson theory is an appropriate framework to deal with the high momenta encountered in dense matter. In particular, the one-boson-exchange (OBE) model has proven very successful in describing NN elastic data in free space up to high energies and has a good theoretical foundation. The OBE potential is defined as the sum of one-particle-exchange amplitudes of certain bosons with given mass and coupling. In general, six non-strange bosons with masses below 1 GeV/c2 are used. Thus,
with π and η pseudoscalar, σ and δ scalar and ρ and ω vector particles. Naturally, isospin dependence is generated by the isovector mesons, π, ρ and δ, which, therefore, deserve particular attention in a study of isospin-asymmetric systems. We will come back to this point in the next section.
Among the many available OBE potentials, some being part of the “high-precision generation” [52,53,57], we seek a momentum-space potential developed within a relativistic scattering equation, such as the one obtained through the Thompson [58] three-dimensional reduction of the Bethe–Salpeter equation [59]. Furthermore, we require a potential that uses the pseudovector coupling for the interaction of nucleons with pseudoscalar mesons. With these constraints in mind, as well as the requirement of a good description of the NN data, Bonn B [3] is a reasonable choice. As is well known, the NN potential model dependence of nuclear matter predictions is not negligible. The saturation points obtained with different NN potentials move along the famous “Coester band” depending on the strength of the tensor force, with the weakest tensor force yielding the largest attraction. This can be understood in terms of medium effects (particularly Pauli blocking) reducing the (attractive) second-order term in the expansion of the reaction matrix. A large second-order term will undergo a large reduction in the medium. Therefore, noticing that the second-order term is dominated by the tensor component of the force, nuclear potentials with a strong tensor component will yield less attraction in the medium. For the same reason (that is, the role of the tensor force in nuclear matter), the potential model dependence is strongly reduced in pure (or nearly pure) neutron matter, due to the absence of isospin-zero partial waves.
Our nuclear matter calculations are based on the DBHF approach. We provide below a short summary of the DBHF philosophy and the main formal steps in our calculation. A more thorough review can be found in [60,61].
The main strength of the DBHF approach is its inherent ability to account for important three-body forces through its density dependence. In Figure 2, we show a three-body force originating from virtual excitation of a nucleon-antinucleon pair, known as the “Z-diagram”. The main feature of the DBHF method turns out to be closely related to the three-body force depicted in Figure 2, as we will argue next. In the DBHF approach, one describes the positive energy solutions of the Dirac equation in the medium as:
where the nucleon effective mass, m∗, is defined as m∗ = m + US, with US an attractive scalar potential (this will be derived below). It can be shown that both the description of a single nucleon via Equation (17) and the evaluation of the Z-diagram, Figure 2, generate a density-dependent repulsive effect on the energy per particle in symmetric nuclear matter, which provides the saturating mechanism missing from conventional BHF calculations.
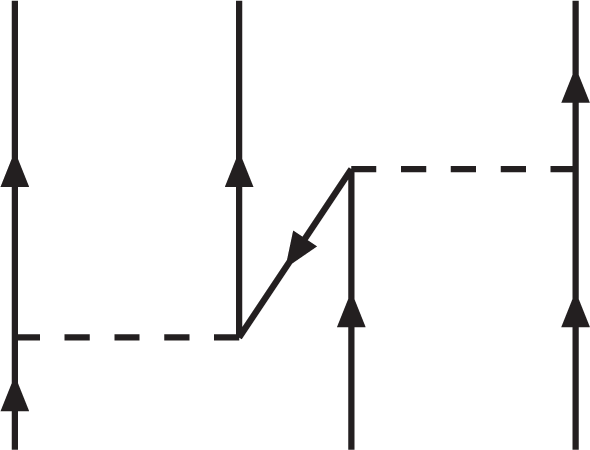
Figure 2.
Three-body force due to virtual pair excitation.
The approximate equivalence of the effective-mass description of Dirac states and the contribution from the Z-diagram has a simple intuitive explanation in the observation that Equation (17), like any other solution of the Dirac equation, can be written as a superposition of positive and negative energy solutions. On the other hand, the “nucleon” in the middle of the Z-diagram, Figure 2, can be viewed as the superposition of positive and negative energy states. In summary, the DBHF method effectively takes into account a particular class of three-body forces, which are crucial for nuclear matter saturation.
In our self-consistent asymmetric nuclear matter calculation, we start from the Thompson [58] relativistic three-dimensional reduction of the Bethe–Salpeter equation [59]. The Thompson equation is applied to nuclear matter in strict analogy to free-space scattering and reads, in the nuclear matter rest frame,
where gij is the in-medium reaction matrix (ij = nn, pp, or np), and the asterisk signifies that medium effects are applied to those quantities. Thus, the NN potential,
, is constructed in terms of effective Dirac states (in-medium spinors) as in Equation (p17). In Equation (18),
,
and
are the initial, final and intermediate relative momenta, and
. The momenta of the two interacting particles in the nuclear matter rest frame have been expressed in terms of their relative momentum and the center-of-mass momentum,
. The energy of the two-particle system is:
and
is the starting energy. The single-particle energy
includes kinetic energy and potential energy contributions. The Pauli operator, Qij, prevents scattering to occupied nn, pp or np states.
With the definitions:
and
one can rewrite Equation (18) as:
which is our working equation and has the convenient feature of being formally identical to its non-relativistic counterpart.
The goal is to determine self-consistently the nuclear matter single-particle potential, which, in the present case, will be different for neutrons and protons. Using a schematic notation to simplify the description, we write, for neutrons,
and for protons,
where each of the four pieces on the right-hand-side of Equations (23) and (24) signifies an integral of the appropriate G-matrix elements (nn, pp or np) obtained from Equation (22). Clearly, the two equations above are coupled through the np component, and so, they must be solved simultaneously. Furthermore, the G-matrix equation and Equations (23) and (24) are coupled through the single-particle energy (which includes the single-particle potential, itself defined in terms of the G-matrix). Therefore, we have a coupled system to be solved self-consistently. That is accomplished through a suitable ansatz and parameterization of the single-nucleon potential [60]. When this procedure has converged, the single-nucleon potentials are available. Finally, the energy per neutron or proton in nuclear matter is calculated from the average values of the kinetic and potential energies as:
The EoS, or energy per nucleon as a function of density, is then written as:
or
Clearly, symmetric nuclear matter is obtained as a by-product of the calculation described above by setting α = 0, whereas α = 1 corresponds to pure neutron matter.
3.2. Microscopic Predictions of the EoS and Related Quantities
In Figure 3, we show EoS predictions for symmetric matter (solid red) and neutron matter (dashed black) as obtained from the Idaho calculation [60,61]. The EoS from DBHF can be characterized as being moderately “soft” at low to medium density and fairly “stiff” at high densities. The predicted saturation density and energy for the symmetric matter EoS in Figure 3 are equal to 0.185 fm−3 and −16.14 MeV, respectively, and the compression modulus is 252 MeV. The increased stiffness featured by the DBHF EoS at the higher densities originates from the strongly density-dependent repulsion characteristic of the Dirac–Brueckner–Hartree–Fock method.
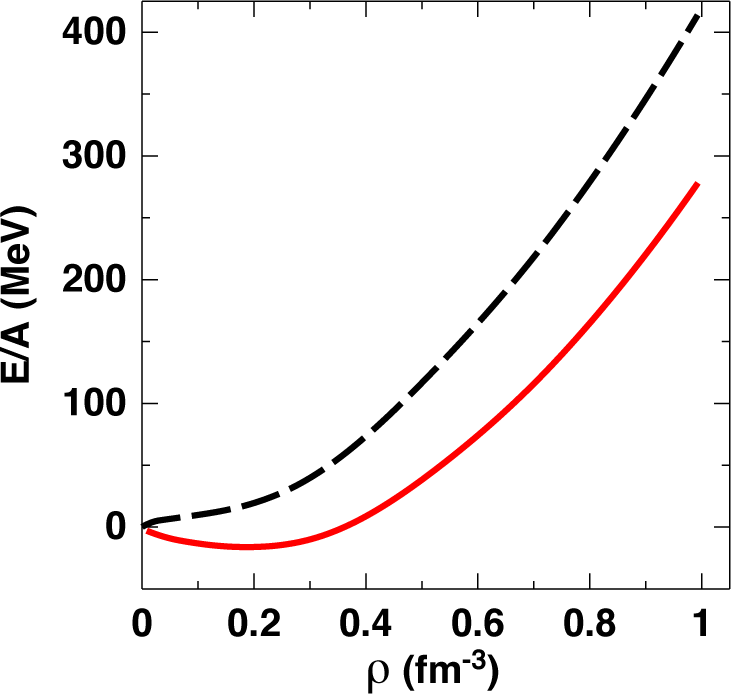
Figure 3.
Our Dirac–Brueckner–Hartree–Fock (DBHF) predictions for the equation of state (EoS) of symmetric matter (solid red) and neutron matter (dashed black).
In Figure 4, we show the pressure in symmetric matter as predicted by the Idaho calculation compared with constraints obtained from flow data [62]. The predictions are seen to fall just on the high side of the constraints and grow rather steep at high density. We display in Figure 6 our DBHF predictions for the pressure in neutron matter (red curve) and β-equilibrated matter (green). The pressure contour is again from [62].
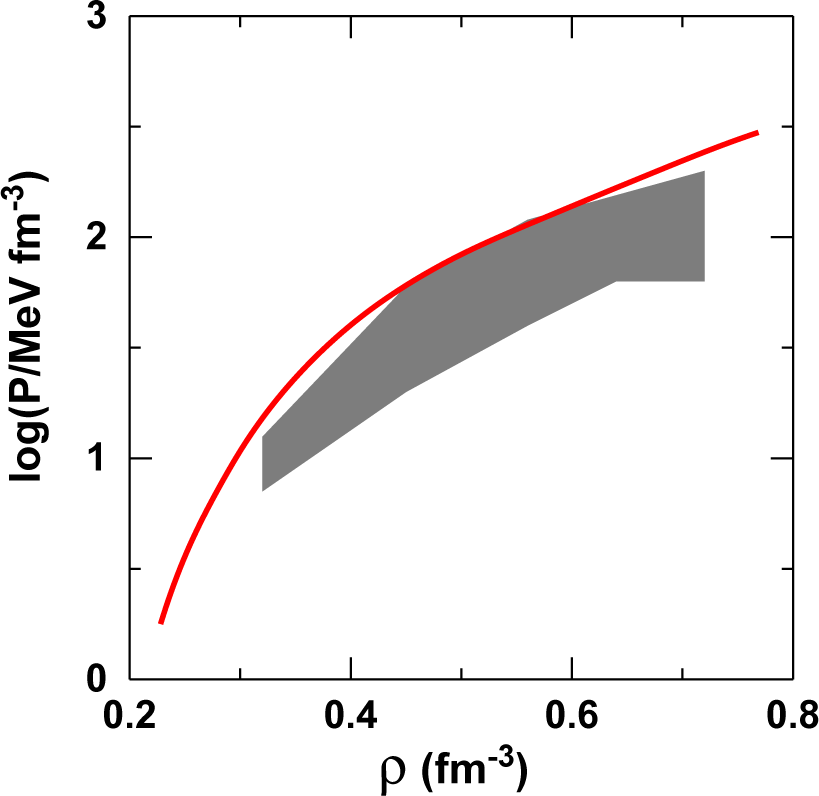
Figure 4.
Pressure in symmetric matter from the Idaho DBHF calculation. The shaded area corresponds to the region of pressure consistent with the flow data analyzed in [62].
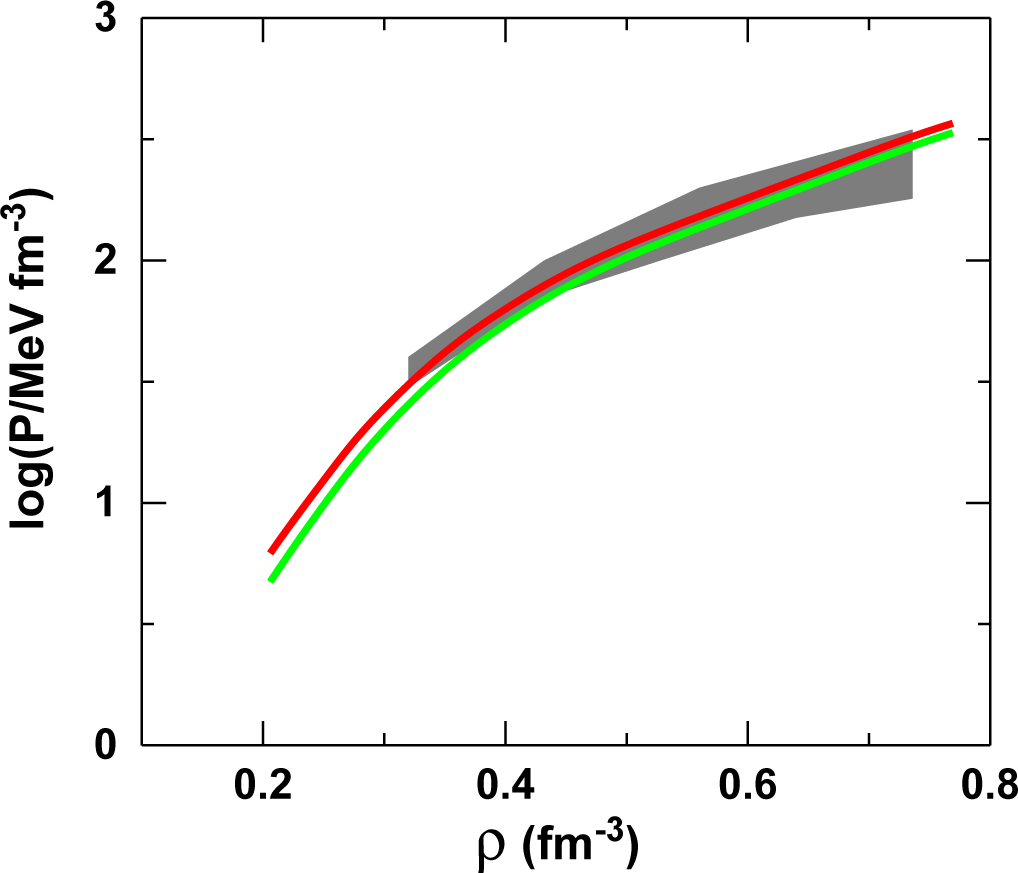
Figure 6.
Pressure in neutron (red curve) and baryon-lepton (green curve) matter from the Idaho DBHF calculation. The shaded area corresponds to the region of pressure consistent with flow data and the inclusion of strong density dependence in the asymmetry terms [62].
In Figure 5, the Idaho DBHF predictions for the symmetry energy are displayed by the solid red curve. The curve is seen to grow at a lesser rate with increasing density, an indication that, at large density, repulsion in the symmetric matter EoS increases more rapidly relative to the neutron matter EoS. This can be understood in terms of increased repulsion in isospin zero partial waves (absent from neutron matter) as a function of density. Our predicted value for the symmetry pressure L (see Equation (9)), is close to 70 MeV.
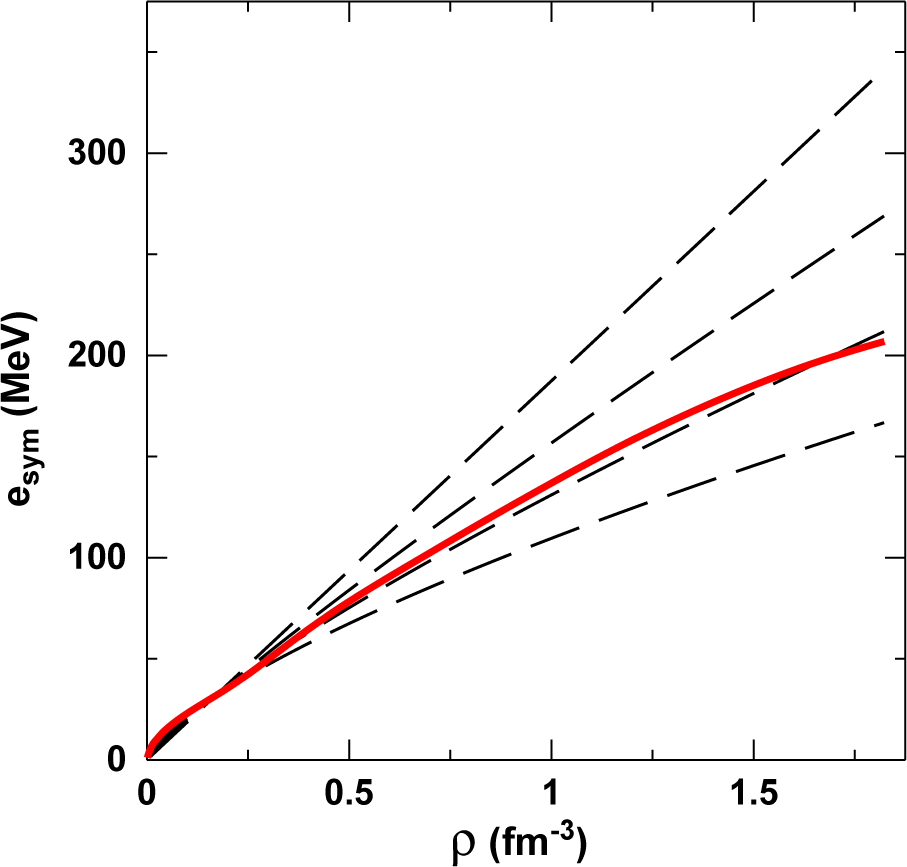
Figure 5.
DBHF prediction for the symmetry energy (solid red) compared with various phenomenological parametrizations (dashed black). See the text for details.
The various black dashed curves in Figure 5 are obtained with the simple parametrization:
with γ increasing from 0.7 to 1.0 in steps of 0.1, and C ≈ 32 MeV. Considering that all of the dashed curves are commonly used parameterizations suggested by heavy-ion data, Figure 5 clearly reflects our limited knowledge of the symmetry energy, particularly, but not exclusively, at the larger densities. As already mentioned in Section 2.2, from the experimental side, intense effort is going on to obtain reliable empirical information for the lesser known aspects of the EoS.
The splitting of the single-nucleon potentials in asymmetric matter as a function of the momentum is displayed in Figure 7 for three different meson-theoretic potentials, Bonn A [3], B [3] and C [3]. We recall that isospin splitting is the crucial mechanism that separates proton and neutron dynamics in a neutron-rich environment. In Figure 8, we demonstrate the approximately linear dependence on the asymmetry parameter of the single-nucleon potentials as anticipated in Equation (14). Again, we include predictions obtained with three different NN potentials. These three models differ mainly in the strength of the tensor force, which is mostly carried by partial waves with isospin equal to zero and, thus, should fade away in the single-neutron potential as the neutron fraction increases. In fact, the figure demonstrates reduced differences among the values of Un predicted with the three potentials at large α.
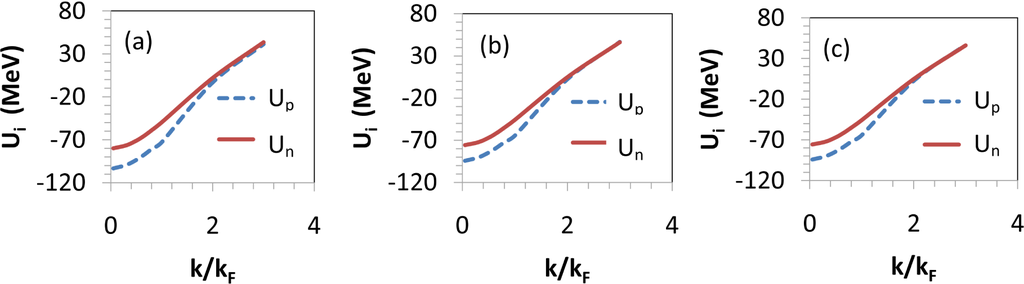
Figure 7.
Momentum dependence of the single-nucleon potential in isospin asymmetric matter, Ui (i = n, p), predicted with Bonn A (a), Bonn B (b) and Bonn C (c). The total density is equal to 0.185 fm−3, and the isospin asymmetry parameter is equal to 0.4. The momentum is given in units of the (average) Fermi momentum, which is equal to 1.4 fm−1.
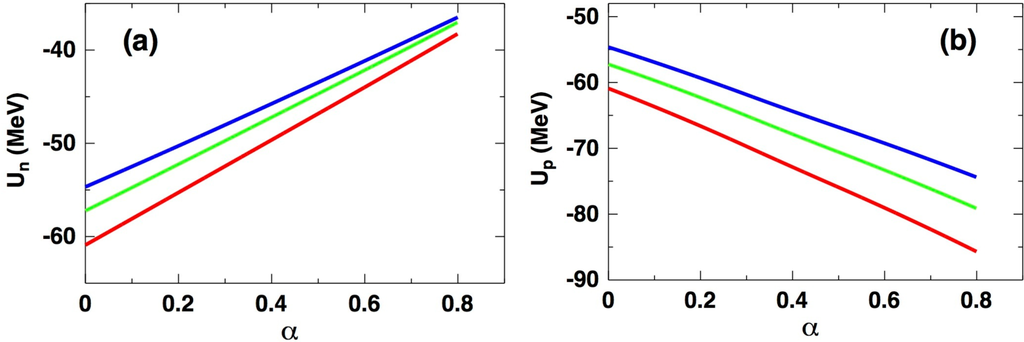
Figure 8.
(a) Neutron and (b) proton single-particle potentials as functions of the asymmetry parameter at fixed average density and momentum equal to the average Fermi momentum, which is equal to 1.4 fm−1.
In Figure 9, we show the density dependence of the symmetry energy with Bonn A, B and C. The potential model dependence comes almost entirely from differences among the predictions of the energy in symmetric matter. With the three sets of predictions, we mean to estimate the uncertainty to be expected when using different parameters for the isovector mesons, while remaining consistent with the free-space NN data.
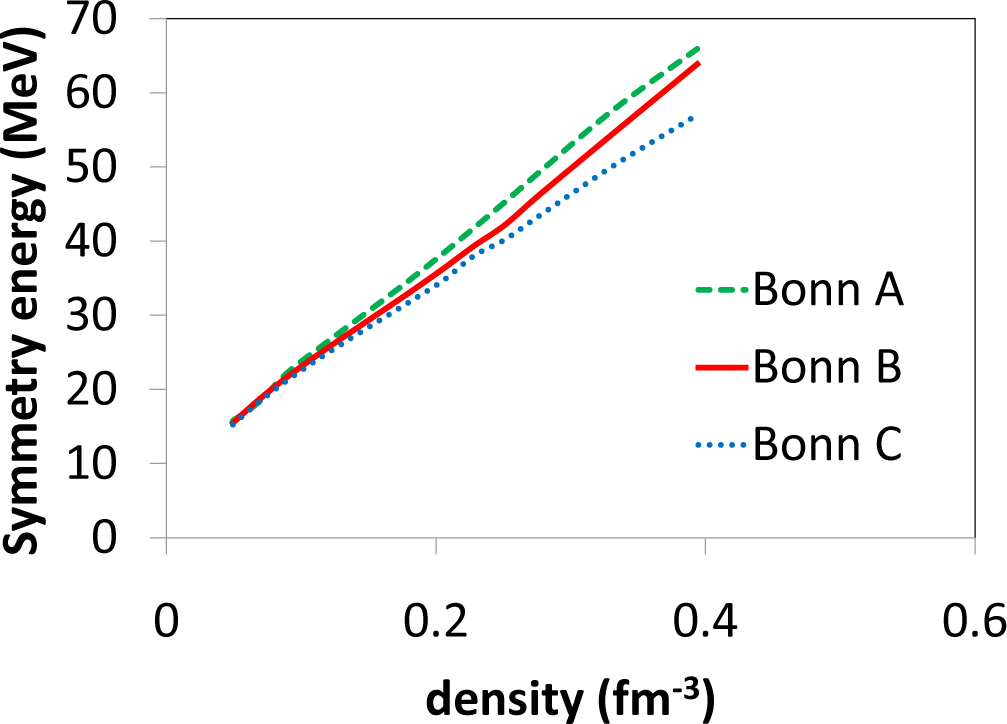
Figure 9.
The symmetry energy as predicted with Bonn A, B and C.
In contrast, we show in Figure 10 predictions of the symmetry energy with the numerous parametrizations of the Skyrme model [34]. Clearly, the constraint from the free-space data reduces dramatically the spread among theoretical predictions.
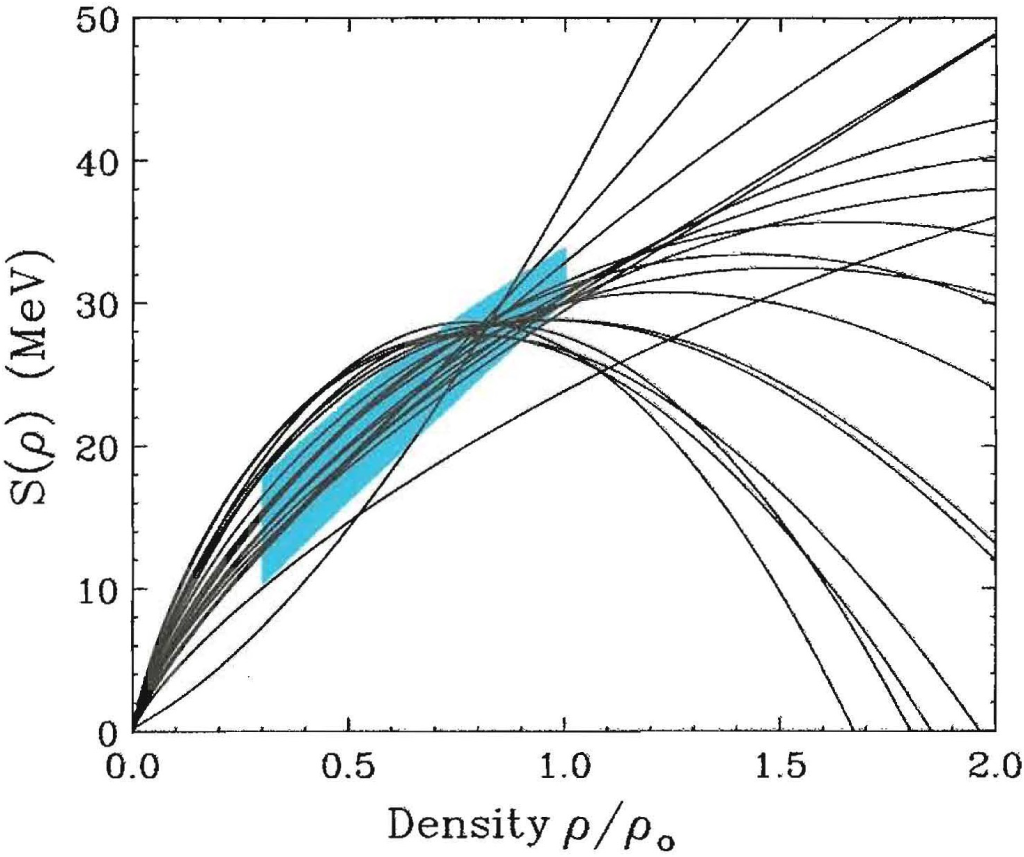
Figure 10.
Predictions of the symmetry energy vs. density for various parameterizations of the Skyrme model.
In [63], we have examined the effect of the isovector mesons on the difference between the potential energies of pure neutron matter and symmetric matter, that is the potential energy contribution to the symmetry energy. Our findings are easily interpreted and understood in terms of the contributions of each meson to the appropriate component of the nuclear force and the isospin dependence naturally generated by isovector mesons.
We find that the pion gives the largest contribution to the potential energy part of the symmetry energy. The contribution of the pion is often overlooked, possibly because this meson is missing from some mean field models, which are popular among users of equations of state. It is our opinion that a microscopic treatment of the pion, together with a proper description of the short-range reduction of the tensor force from the ρ-meson, is essential to reach meaningful conclusions about the isospin dependence of the nuclear force and its behavior in the medium. For accuracy, at this point, we should recall that it is the iterated two-pion exchange that gives a large contribution to “observables”, such as the energy of nuclear matter and the symmetry energy. In mean-field theories, such a contribution is effectively included through the scalar σ meson. Of course, one may debate whether this measure fully captures the features of the two-pion exchange.
With regard to the ρ-meson, it is useful to recall that the interaction Lagrangian, which couples vector mesons with nucleons, contains both a vector coupling and a tensor coupling,
These are related to the electromagnetic properties of the nucleon in the vector dominance model, where the nucleon couples to the photon via a vector meson. In the framework of the vector dominance model [64], a value of 3.7 is obtained for the ratio of the tensor to vector coupling constant, κρ = fρ/gρ, whereas a stronger value of κρ = 6.6 was determined from partial-wave analyses [65]. In other words, a larger value of the ρ tensor coupling as compared to its vector coupling is well supported by evidence. This fact is reflected in meson exchange models where, typically, the ratio κρ is about six. Therefore, a Lagrangian density with only a vector coupling for the ρ may miss the most important part of how this meson couples to the nucleon.
In closing this section, we emphasize again the fundamental differences between our approach and the one of mean field models, particularly pionless QHD theories. Of course, it is fair to recall that QHD theories were not intended to describe free-space NN scattering or the deuteron properties. Nevertheless, our point is that the presence, or absence, of free-space and/or few-body constraints on nuclear forces may impact our conclusions for the many-body problem in a significant way. It is our opinion that a microscopic theory of the nuclear many-body problem should have a basis in the bare NN interaction with all its important ingredients as required from our knowledge and experience with the NN interaction in free space.
4. A Different Approach: Chiral Interactions
Modern ab initio many-body calculations should be based on the following philosophy: the parameters of the two- and many-body forces are constrained by the properties of the two- and few-nucleon systems and not readjusted when such forces are applied in the many-body system. Only in this way can one test the predictive power of the theory.
In the previous section, we have presented and discussed predictions from a relativistic meson-theoretic framework. Other meson-theoretic approaches have been widely used, such as those constructed from non-relativistic NN potentials complemented by three-body forces (3BF) (see, for instance, [50]). Likely inconsistencies between the degrees of freedom present in the two- and the three-body sectors render this approach less than ideal. For instance, large 3BF contributions are known to arise from ∆-isobar intermediate states, whereas one-boson-exchange potentials, which do not contain ∆ degrees of freedom, are typically employed for the NN part. In fact, the ability of DBHF calculations to predict good nuclear matter saturation properties through the inclusion of (only) 3BF arising from the excitation of virtual nucleon-antinucleon pairs appears to support the occurrence of large cancellations between other kinds of 3BF, such as the well-known Fujita–Miyazawa force [66], and the corresponding (medium-modified) two-body diagrams, which are required by consistency arguments.
The philosophy of effective field theories (EFT) is different [31,67]. Ideally, one wishes to base a derivation of the nuclear force on QCD. However, the well-known problem with QCD is that it is non-perturbative in the low-energy regime characteristic for nuclear physics. For many years, this fact was perceived as a great obstacle to a derivation of nuclear forces from QCD, essentially impossible to overcome except with lattice QCD. The effective field theory concept has shown a way out of this dilemma. The main point is to realize that the scenario of low-energy QCD is characterized by pions and nucleons interacting via a force governed by spontaneously broken approximate chiral symmetry. For comprehensive reviews on the development of nuclear forces within EFT, the reader is referred to [68–70]. We will refer to the literature on chiral approaches and nuclear matter later in this section.
Chiral EFT are based on a low-momentum expansion known as chiral perturbation theory (ChPT). The expansion is valid for momenta less than the chiral symmetry breaking scale, Λ, approximately equal to 1 GeV. Therefore, NN potentials based on ChPT are usually multiplied by a regulator function of the form:
with 0.5 GeV being a typical choice for the cutoff Λ.
Chiral perturbation theory, together with power counting, allows for a systematic, order-by-order development of nuclear forces. Two- and many-body forces emerge naturally, and on an equal footing, at each order of the perturbation. Conceptually, this is a very attractive scenario. In practice, though, the number of diagrams to be included at each order quickly grows to unmanageable levels.
The most natural question to ask is therefore: how good is the rate of convergence of the chiral expansion? Within the chiral philosophy, better and better convergence with increasing order should reveal itself as improved cutoff independence. Vice versa, a strong cutoff dependence, at some order, should signal that the chiral expansion has been truncated at too low an order.
Although designed to reproduce similar NN phase shifts, potentials with different regulator functions will yield different predictions in the many-body problem due to their different off-shell behavior. On the other hand, appropriate readjustments, at each order, of the low-energy constants, which appear in the many-body forces, are expected to reduce the dependence on the regulator function. Notice that these are not arbitrary adjustments. Instead, they are determined by refitting the properties of the few-nucleon system.
In this section, we will present and discuss predictions for nuclear matter, neutron matter and the symmetry energy based on chiral two- and three-body interactions, which we incorporate in Brueckner–Hartree–Fock calculations. We will use high-precision NN potentials at next-to-next-to-next-to-leading order (N3LO) [71] along with 3BF at next-to-next-to-leading order (N2LO). High-precision NN potentials at N3LO have been developed for Λ = 450, 500 and 600 MeV [71].
Although order consistency would require both two-body forces (2BF) and 3BF at N3LO, such calculation for nuclear matter is not feasible at this time. Thus, the combination of 2BF at N3LO and 3BF at N2LO is presently state-of-the-art. We note further that four-body forces also appear at this order [72], namely the fourth order in the chiral expansion, but are left out because they are expected to be small [73].
The three-nucleon forces that make their appearance at the third order in the chiral power counting (that is, the leading-order contributions at N2LO) are: the long-range two-pion exchange graph; the medium-range one-pion exchange diagram; and the short-range contact term. The corresponding diagrams are shown in Figure 11.
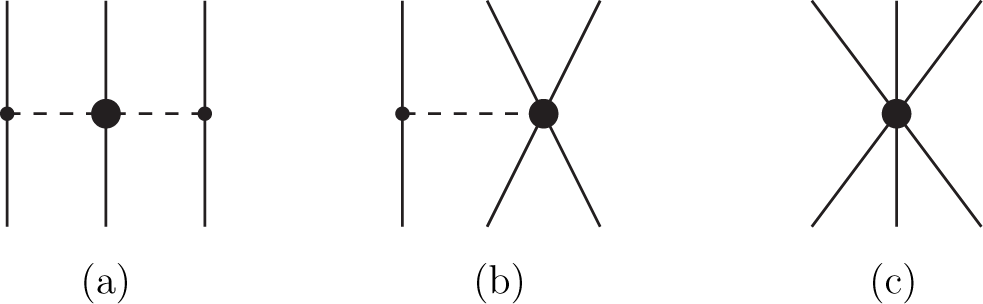
Figure 11.
Leading three-body forces at N2LO: (a) one-pion exchange; (b) two-pion exchange; (c) contact term. See the text for more details.
In [74], density-dependent corrections to the in-medium NN interaction have been derived from the leading-order chiral 3NF. These are effective two-nucleon interactions that reflect the underlying three-nucleon forces and are obtained by integrating one nucleon up to the Fermi momentum. Therefore, they are computationally very convenient, whereas realistic models of three-nucleon forces would be prohibitive. Analytical expressions for these corrections are provided in [74] in terms of the well-known non-relativistic two-body nuclear force operators, which can be conveniently incorporated in the usual NN partial wave formalism and the conventional BHF theory.
A total of six one-loop diagrams contribute at this order. Three are generated by the two-pion exchange graph of the chiral three-nucleon interaction and depend on the low-energy constants c1,3,4, which are fixed in the NN system [71]. Two are generated by the one-pion exchange diagram and depend on the low-energy constant cD. Finally, the short-range component depends on the constant cE. In pure neutron matter, the contributions proportional to the low-energy constants c4, cD and cE vanish [74].
One can see that the potential in Equation (31) does not contain additional parameters besides the low-energy constants c1,3,4, which are already present in the two-pion-exchange 2BF. Concerning the low-energy constants cD and cE appearing in the N2LO 3BF, a very important aspect of our calculations is that they are completely determined from the three-nucleon system. Specifically, they are constrained to reproduce the A = 3 binding energies and the triton Gamow–Teller matrix elements. Their values are given in Table 2 [75,76]. The procedure [75] is based on the consistency of 2BF, 3BF and currents, as required by chiral EFT.

Table 2.
Values of n and low-energy constants used for each type of cutoff in the regulator function as given in Equation (30). The low-energy constants of the dimension-two πN Lagrangian, c1,3,4, are given in units of GeV−1.
In Figure 12, we show predictions for the EoS of symmetric nuclear matter obtained with the procedure described above for the three different values of the cutoff in the regulator function given in Table 2. A similar legend applies to Figure 13 for the EoS of neutron matter and to Figure 14 for the symmetry energy. We note considerable cutoff dependence in symmetric matter. The Λ = 450 MeV curve displays the best saturation properties, with the energy/particle equal to −15.7 MeV at ρ ≈ 0.17 fm−3.
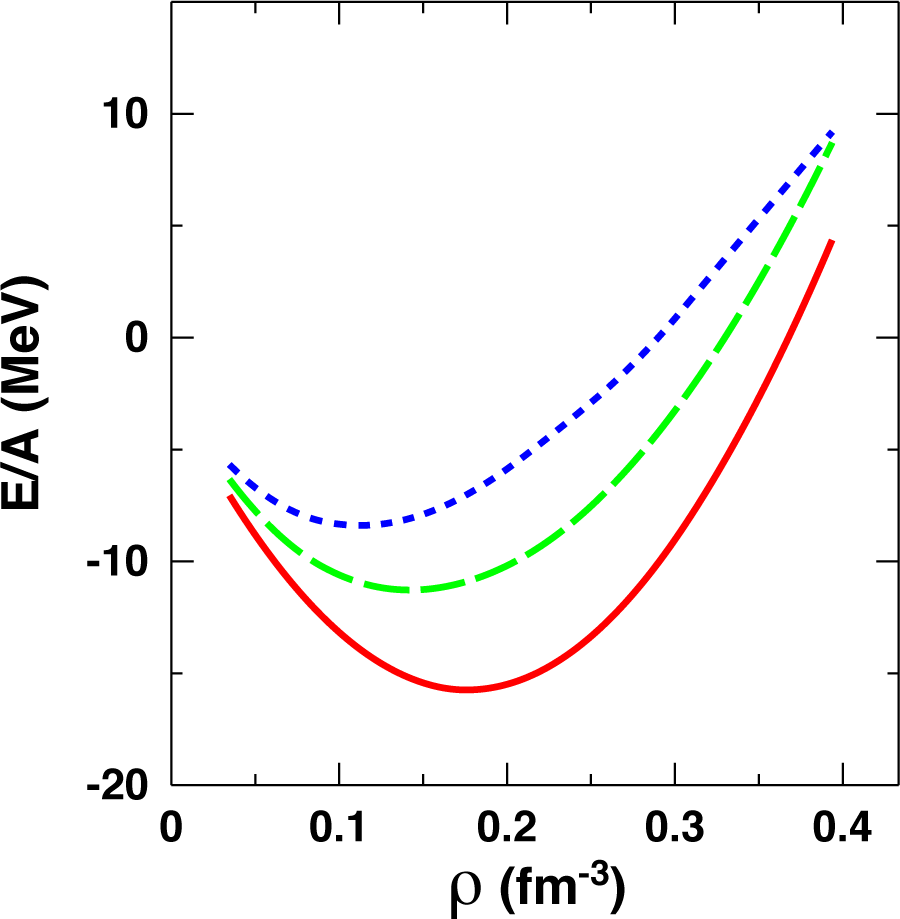
Figure 12.
Energy/particle in symmetric nuclear matter as a function of density obtained with 2BF and 3BF as explained in the text. The solid (red), dashed (green) and dotted (blue) curves correspond to Λ = 450, 500 and 600 MeV, respectively.
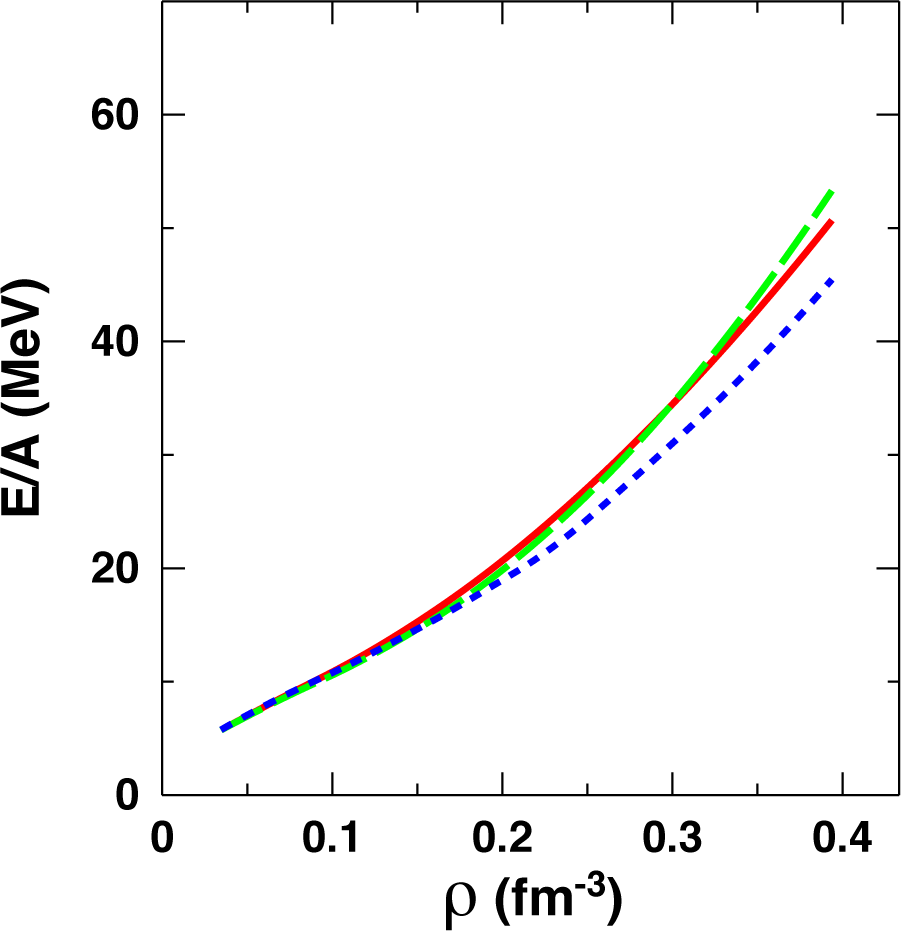
Figure 13.
As in Figure 12, but for neutron matter.
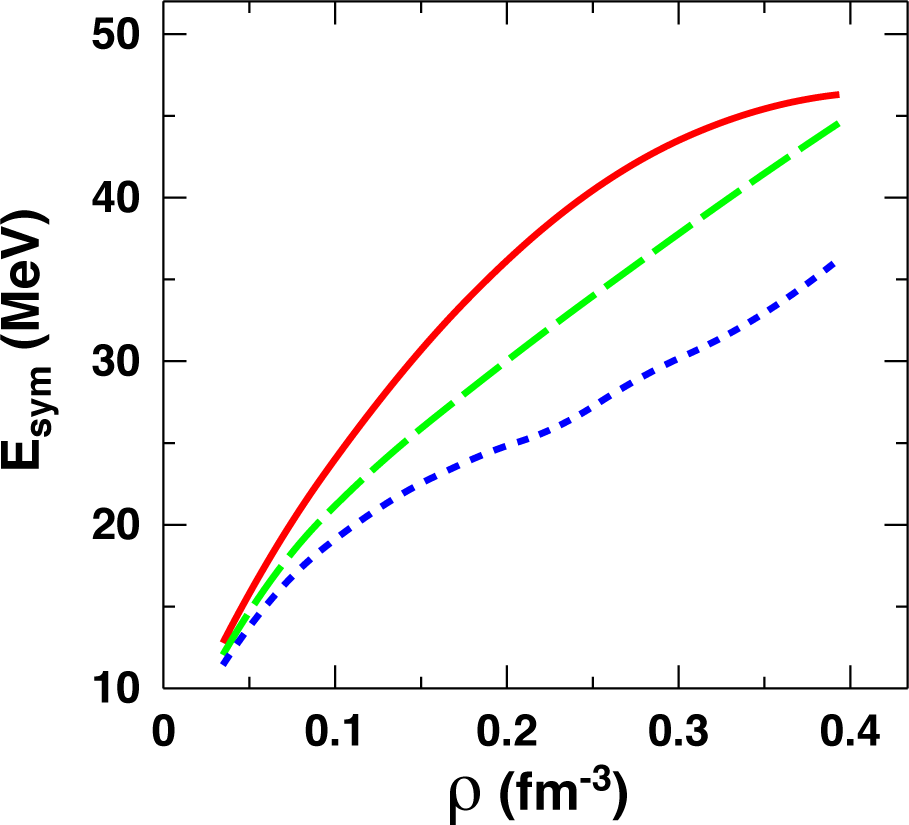
Figure 14.
As in Figure 12, for the symmetry energy.
Cutoff dependence appears strongly reduced in pure neutron matter; see Figure 13. At the two-body level, this points to the tensor force as the most likely source of the cutoff dependence seen in nuclear matter, recalling the chief contribution from the tensor force to the latter, mostly through partial waves with isospin zero. Naturally, cutoff dependence carries on to the symmetry energy, as shown in Figure 14.
In spite of the observed cutoff dependence, we find these predictions encouraging. The ability to obtain realistic nuclear matter predictions with consistent two- and three-body interactions constrained by the properties of the two- and the three-nucleon systems and no additional adjustments of the parameters is an important point and should not be underestimated [76]. Historically, it has been proven to be a non-trivial task, often confronted with the help of phenomenological three-body forces adjusted as needed to improve saturation.
Before concluding this section, we wish to point out some of the extensive literature concerned with chiral dynamics in nuclear matter. In the earlier work by Kaiser and collaborators [77], the nuclear matter equation of state is obtained in the three-loop approximation of chiral perturbation theory as an expansion in powers of the Fermi momentum. In this perturbative, diagrammatic approach, the in-vacuum nucleon propagator is corrected through medium insertions. The impact of the one- and two-pion exchange is explored and the latter is found to be crucial for obtaining realistic binding. These calculations were later extended in [78] to include the two-pion exchange single and double ∆(1232) excitation, with significant impact on the equation of state of neutron matter and the symmetry energy. Energy density functionals have been derived by the same group from chiral two- and three-body forces and extended to include isovector terms in [79]. The authors explore the contribution from the 3BF to the symmetry energy and conclude that the first-order Hartree–Fock approximation works reasonably well for isovector quantities [80]. A comprehensive review of nuclear chiral dynamics by the Munich group can be found in [80].
Other authors have adopted chiral low-momentum interactions to soften the short-range components of the original potentials. A survey of renormalization group methods and their connection to chiral EFT, as well as applications to nuclear matter, can be found in [81,82].
To summarize our observations from this section, at this time, we conclude that, although symmetric nuclear matter predictions show noticeable cutoff dependence at this order, excellent saturation properties can be obtained with ab initio calculations based on fully consistent 2BF and 3BF. A comprehensive and systematic study of the cutoff dependence, order by order, of nuclear and neutron matter energies, as well as the symmetry energy is underway in our group. This will shed light on the accuracy with which these quantities can be predicted in ChPT. How rapidly the expansion converges, as seen through improved cutoff independence with increasing order, is clearly the crucial factor in determining the success of EFT.
5. Summary and Conclusions
Understanding the isospin dependence of nuclear interactions in a hadronic medium is a fundamental issue that goes to the core of nuclear physics. Yet, predictions for such a basic quantity as the symmetry energy still show large model dependence (sometimes, even qualitative disagreement with one another), when it comes to the details of its density dependence and related observables.
In this article, we have reviewed the systematic efforts presently going on to set empirical constraints on the nuclear equation of state, particularly its isospin-asymmetric part.
From the theoretical standpoint, we have emphasized differences between microscopic and phenomenological methods. We reviewed past and on-going theoretical efforts from our group. Our traditional framework relies on relativistic meson theory and the Dirac equation for the motion of a nucleon in nuclear matter. Throughout the article, our emphasis has been on the importance of pursuing microscopic approaches.
While appreciating the convenience of the Dirac–Brueckner approximation, we are aware of, and open to, novel and alternative theories. The philosophy of EFT has become especially popular in the recent past. The possibility of a systematic expansion where, at each order, two- and many-body forces emerge naturally and on an equal footing is unique to this theory. However, regardless of its popularity, every theory has its limitations. In the case of ChPT, the main obstacle, especially from a practical standpoint, would be a poor rate of convergence of the expansion. We have reported predictions from state-of-the-art BHF calculations based on consistent chiral 2BF and 3BF. On the one hand, it is reassuring to see that parameter-free BHF calculations (that is, calculations where the parameters of the theory are completely fixed by the properties of the NN and the few-nucleon systems) are able to predict realistic saturation properties. On the other hand, we observe the dependence of the symmetric nuclear matter EoS on the choice of the cutoff in the regulator function of the chiral NN potentials. A more systematic analysis of order by order convergence will be insightful.
To conclude, we remain firmly anchored to our ab initio philosophy. At the same time, we believe that comparative studies of (microscopic) methods are the key to a better understanding of the nuclear many-body system.
Acknowledgments
This work was supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, under Award Number DE-FG02-03ER41270. The content of Section 4 is part of a collaboration with Luigi Coraggio, Jeremy Holt, Nunzio Itaco, Laura Elisa Marcucci, and Ruprecht Machleidt.
Conflicts of Interest
The author declares no conflict of interest.
References
- Bethe, H.A.; Bacher, R.F. Nuclear Physics A. Stationary states of nuclei. Rev. Mod. Phys 1936, 8. [Google Scholar] [CrossRef]
- Von Weizäcker, C.F. Zur theorie der kernmassen. Z. Phys 1935, 96, 431–458. [Google Scholar]
- Machleidt, R. The meson theory of nuclear forces and nuclear structure. Adv. Nucl. Phys 1989, 19, 189–376. [Google Scholar]
- Oyamatsu, K.; Tanihata, I.; Sugahara, Y.; Sumiyoshi, K.; Toki, H. Can the equation of state of asymmetric nuclear matter be studied using unstable nuclei? Nucl. Phys. A 1998, 634, 3–14. [Google Scholar]
- Furnstahl, R.J. Neutron radii in mean-field models. Nucl. Phys. A 2002, 706, 85–110. [Google Scholar]
- Sammarruca, F.; Liu, P. Neutron skin of 208Pb and density dependence of the symmetry energy. Phys. Rev. C 2009. [Google Scholar]
- Brueckner, K.A.; Levinson, C.A.; Mahmoud, H.M. Two-body forces and nuclear saturation. I. Central forces. Phys. Rev 1954, 95, 217–228. [Google Scholar]
- Bethe, H.A. Nuclear Many-body problem. Phys. Rev 1956, 103, 1353–1366. [Google Scholar]
- Goldstone, J. Derivation of the Brueckner many-body theory. Proc. R. Soc. London Ser. A 1957, 239, 267–279. [Google Scholar]
- Bethe, H.A. Theory of nuclear matter. Annu. Rev. Nucl. Sci 1971, 21, 93–244. [Google Scholar]
- Haftel, M.I.; Tabakin, F. Nuclear saturation and the smoothness of nucleon-nucleon potentials. Nucl. Phys. A 1970, 158, 1–42. [Google Scholar]
- Sprung, D.W.L. Nuclear matter calculations. Adv. Nucl. Phys 1972, 5, 225–343. [Google Scholar]
- Pandharipande, V.R.; Wiringa, R.B. Variations on a theme of nuclear matter. Rev. Mod. Phys 1979, 51, 821–859. [Google Scholar]
- Lagaris, I.E.; Pandharipande, V.R. Variational calculations of realistic models of nuclear matter. Nucl. Phys. A 1981, 359, 349–364. [Google Scholar]
- Day, B.D.; Wiringa, R.B. Brueckner-Bethe and variational calculations of nuclear matter. Phys. Rev. C 1985. [Google Scholar]
- Anastasio, M.R.; Celenza, L.S.; Pong, W.S.; Shakin, C.M. Relativistic nuclear structure physics. Phys. Rep 1983, 100, 327–392. [Google Scholar]
- Horowitz, C.J.; Serot, B.D. Two-nucleon correlations in a relativistic theory of nuclear matter. Phys. Lett. B 1984, 137, 287–293. [Google Scholar]
- Horowitz, C.J.; Serot, B.D. The relativistic two-nucleon problem in nuclear matter. Nucl. Phys. A 1987, 464, 613–699. [Google Scholar]
- Brockmann, R.; Machleidt, R. Nuclear saturation in a relativistic Brueckner–Hartree–Fock approach. Phys. Lett. B 1984, 149, 283–287. [Google Scholar]
- Brockmann, R.; Machleidt, R. Relativistic nuclear structure. I. Nuclear matter. Phys. Rev. C 1990. [Google Scholar]
- Sugahara, Y.; Toki, H. Relativistic mean-field theory for unstable nuclei with non-linear σ and ω terms. Nucl. Phys. A 1994, 579, 557–572. [Google Scholar]
- Lalazissis, G.A.; König, J.; Ring, P. New parametrization for the Lagrangian density of relativistic mean field theory. Phys. Rev. C 1997. [Google Scholar]
- Kubis, S.; Kutschera, M. Nuclear matter in a relativistic mean field theory with isovector scalar meson. Phys. Lett. B 1997, 399, 191–195. [Google Scholar]
- Mueller, H.; Serot, B.D. Relativistic mean-field theory and the high-density nuclear equation of state. Nucl. Phys. A 1996, 606, 508–537. [Google Scholar]
- Stone, J.R.; Miller, J.C.; Koncewicz, R.; Stevenson, P.D. Nuclear matter and neutron star properties calculated with the Skyrme interaction. Phys. Rev. C 2003. [Google Scholar]
- Stone, J.R.; Reinhard, P.-G. The Skyrme interaction in finite nuclei and nuclear matter. Prog. Part. Nucl. Phys 2007, 58, 587–657. [Google Scholar]
- Das, C.B.; Gupta, S.D.; Gale, C.; Li, B.A. Momentum dependence of symmetry potential in asymmetric nuclear matter for transport model calculations. Phys. Rev. C 2003. [Google Scholar]
- Chappert, F.; Girad, M.; Hilaire, S. Toward a new parametrization of the Gogny force: Neutron matter and nuclear binding energies. Phys. Lett. B 2008, 668, 420–424. [Google Scholar]
- Gandolfi, S.; Yu Illarionov, A.; Schmidt, K.E.; Pederiva, F.; Fantoni, S. Quantum Monte Carlo calculation of the equation of state of neutron matter. Phys. Rev. C 2009. [Google Scholar]
- Baldo, M.; Polls, A.; Rios, A.; Schulze, H.-J.; Vidana, I. Comparative study of neutron and nuclear matter with simplified Argonne nucleon-nucleon potentials. Phys. Rev. C 2012, 86. [Google Scholar] [CrossRef]
- Weinberg, S. Phenomenological Lagrangians. Physica A 1979, 96, 327–340. [Google Scholar]
- Weinberg, S. Nuclear forces from chiral lagrangians. Phys. Lett. B 1990, 251, 288–292. [Google Scholar]
- Simenel, C.; Chomaz, P.H.; de France, G. Fusion process studied with a preequilibrium giant dipole resonance. Phys. Rev. C 2007. [Google Scholar]
- Brown, B.A. Neutron Radii in Nuclei and the Neutron equation of State. Phys. Rev. Lett 2000. [Google Scholar]
- Ko, C.M.; Oh, Y.; Xu, J. Medium effects on charged pion ratio in heavy ion collisions. Int. J. Mod. Phys. E 2010, 19, 1763–1772. [Google Scholar]
- Tsang, M.B.; Stone, J.R.; Camera, F.; Danielewicz, P.; Gandolfi, S.; Hebeler, K.; Horowitz, C.J.; Lee, J.; Lynch, W.G.; Kohley, Z.; et al. Constraints on the symmetry energy and neutron skins from experiments and theory. Phys. Rev. C 2012. [Google Scholar]
- Lane, A.M. Isobaric spin dependence of the optical potential and quasi-elastic (p,n) reaction. Nucl. Phys 1962, 35, 676–685. [Google Scholar]
- Zenihiro, J.; Sakaguchi, H.; Murakami, T.; Yosoi, M.; Yasuda, Y.; Terashima, S.; Iwao, Y.; Takeda, H.; Itoh, M.; Yoshida, H.P.; et al. Neutron density distributions of 204,206,208Pb deduced via proton elastic scattering at Ep = 295 MeV. Phys. Rev. C 2010. [Google Scholar]
- 208Pb Radius Experiment PREX. Available online: hallaweb.jlab.org/parity/prex accessed on 20 July 2014.
- C-REX Workshop. Available online: http://www.jlab.org/conferences/crex accessed on 20 July 2014.
- Reinhard, P.-G.; Nazarewicz, W. Information content of a new observable: The case of the nuclear neutron skin. Phys. Rev. C 2010. [Google Scholar]
- Sedrakian, A. The physics of dense hadronic matter and compact stars. Prog. Part. Nucl. Phys 2007, 58, 168–246. [Google Scholar]
- Champion, D.J.; Ransom, S.M.; Lazarus, P.; Camilo, F.; Bassa, C.; Kaspi, V.M.; Nice, D.J.; Freire, P.C.C.; Stairs, I.H.; van Leeuwen, J.; et al. An eccentric Binary Millisecond Pulsar in the Galactic Plane. Science 2008, 320, 1309–1312. [Google Scholar]
- Demorest, P.; Pennucci, T.; Ransom, S.; Roberts, M.; Hessels, J. Shapiro delay measurement of a two solar mass neutron star. Nature 2010, 468, 1081–1083. [Google Scholar]
- Antoniadis, J.; Freire, P.C.C.; Wex, N.; Tauris, T.M.; Lynch, R.S.; van Kerkwijk, M.H.; Kramer, M.; Bassa, C.; Dhillon, V.S.; Driebe, T.; et al. A Massive Pulsar in a Compact Relativistic Binary. Science 2013, 340, 1–9. [Google Scholar]
- Lattimer, J. M.; Prakash, M. Neutron star observations: Prognosis for equation of state constraints. Phys. Rep 2007, 442, 109–165. [Google Scholar]
- Faulkner, A.J.; Kramer, M.; Lyne, A.G.; Manchester, R.N.; McLaughlin, M.A.; Stairs, I.H.; Hobbs, G.; Possenti, A.; Lorimer, D.R.; D’Amico, N.; et al. A new relativistic double neutron star system. Astrophys. J. Lett 2004, 618, L119–L122. [Google Scholar]
- Weber, F. Pulsars as Astrophysical Laboratories for Nuclear and Particle Physic; Institute of Physics Publishing: Bristol, UK; Philadelphia, PA, USA, 1999. [Google Scholar]
- Fattoyev, F.J.; Piekarewicz, J. Neutron skins and neutron stars. Phys. Rev. C 2012. [Google Scholar]
- Li, Z.H.; Lombardo, U.; Schulze, H.-J. Consistent nucleon-nucleon potentials and three-body forces. Phys. Rev. C 2008. [Google Scholar]
- Li, Z.H.; Schulze, H.-J. Neutron star structure with modern nucleonic three-body forces. Phys. Rev. C 2008. [Google Scholar]
- Wiringa, R.B.; Stocks, V.G.J.; Schiavilla, R. Accurate nucleon-nucleon potential with charge-independence breaking. Phys. Rev. C 1995. [Google Scholar]
- Stocks, V.G.J.; Klomp, R.A.M.; Terheggen, C.P.F.; de Swart, J.J. Construction of high-quality NN potential models. Phys. Rev. C 1994. [Google Scholar]
- Pieper, S.C.; Pandharipande, V.R.; Wiringa, R.B.; Carlson, J. Realistic models of pion-exchange three-nucleon interactions. Phys. Rev. C 2001. [Google Scholar]
- Harrison, B.K.; Thorne, K.S.; Wakano, M.; Wheeler, J.A. Gravitation Theory and Gravitational Collapse; University of Chicago Press: Chicago, IL, USA, 1965. [Google Scholar]
- Negele, J.W.; Vautherin, D. Neutron star matter at sub-nuclear densities. Nucl. Phys. A 1973, 207, 298–320. [Google Scholar]
- Machleidt, R. High-precision, charge-dependent Bonn nucleon-nucleon potential. Phys. Rev. C 2001. [Google Scholar]
- Thompson, R.H. Bethe-Salpeter Equation Applied to the Nucleon-Nucleon Interaction. Phys. Rev. D 1970. [Google Scholar]
- Salpeter, E.E.; Bethe, H.A. A Relativistic Equation for Bound-State Problems. Phys. Rev 1951, 84, 1232–1242. [Google Scholar]
- Sammarruca, F. The microscopic approach to nuclear matter and neutron star matter. Int. J. Mod. Phys. E 2010, 19, 1259–1313. [Google Scholar]
- Sammarruca, F. Analysis of the symmetry energy in a microscopic approach. Int. J. Mod. Phys. E 2013, 22, 1–37. [Google Scholar]
- Danielewicz, P.; Lacey, R.; Lynch, W.G. Determination of the equation of state of dense matter. Science 2002, 298, 1592–1596. [Google Scholar]
- Sammarruca, F. Contribution of isovector mesons to the symmetry energy in a microscopic model. Phys. Rev. C 2011. [Google Scholar]
- Sakurai, J.J. Currents and Mesons; University of Chicago Press: Chicago, IL, USA, 1969. [Google Scholar]
- Höhler, G.; Pietarinen, E. The ρ NN vertex in the vector-dominance model. Nucl. Phys 1975, B95, 210–230. [Google Scholar]
- Fujita, J.I.; Miyazawa, H. Pion theory of three-body forces. Prog. Theor. Phys 1957, 17, 360–365. [Google Scholar]
- Weinberg, S. Nonlinear realization of chiral symmetry. Phys. Rev 1968, 166, 1568–1577. [Google Scholar]
- Machleidt, R.; Entem, D.R. Chiral effective field theory and nuclear forces. Phys. Rep 2011, 503, 1–75. [Google Scholar]
- Epelbaum, E. Few-nucleon forces and systems in chiral effective field theory. Prog. Part. Nucl. Phys 2006, 57, 654–741. [Google Scholar]
- Epelbaum, E.; Hammer, H.-W.; Meissner, U.-G. Modern theory of nuclear forces. Rev. Mod. Phys 2009, 81, 1773–1825. [Google Scholar]
- Entem, D.R.; Machleidt, R. Accurate charge-dependent nucleon-nucleon potential at fourth order of chiral perturbation theory. Phys. Rev. C 2003. [Google Scholar]
- Epelbaum, E. Four-nucleon force using the method of unitary transformation. Eur. Phys. J 2007, A34, 197–214. [Google Scholar]
- Rozpedzik, D.; Golak, J.; Skibinski, R.; Witala, H. A. First Estimation of Chiral Four-Nucleon Force Effects in 4He. Acta Phys. Polon 2006, B37, 2889–2904. [Google Scholar]
- Holt, J.W.; Kaiser, N.; Weise, W. Density-dependent effective nucleon-nucleon interaction from chiral three-nucleon forces. Phys. Rev. C 2010. [Google Scholar]
- Marcucci, L.E.; Kievsky, A.; Rosati, S.; Schiavilla, R.; Viviani, M. Chiral effective field theory predictions for muon capture on deuteron and 3He. Phys. Rev. Lett 2012. [Google Scholar]
- Coraggio, L.; Holt, J.W.; Itaco, N.; Machleidt, R.; Marcucci, L.E.; Sammarruca, F. Nuclear matter equation of state with consistent two- and three-body perturbative chiral interactions. Phys. Rev. C 2014. [Google Scholar]
- Kaiser, N.; Fritsch, S.; Weise, W. Chiral dynamics and nuclear matter. Nucl. Phys. A 2002, 697, 255–276. [Google Scholar]
- Fritsch, S.; Kaiser, N.; Weise, W. Chiral approach to nuclear matter: Role of two-pion exchange with virtual delta-isobar excitation. Nucl. Phys. A 2005, 750, 259–293. [Google Scholar]
- Kaiser, N. Isovector part of nuclear energy density functional from chiral two- and three-nucleon forces. Eur. Phys. J 2012, A48, 36–49. [Google Scholar]
- Holt, J.W.; Kaiser, N.; Weise, W. Nuclear chiral dynamics and thermodynamics. Prog. Part. Nucl. Phys 2013, 73, 35–83, and references therein. [Google Scholar]
- Bogner, S.K.; Furnstahl, R.J.; Schwenk, A. From low-momentum interactions to nuclear structure. Prog. Part. Nucl. Phys 2010, 65, 94–147. [Google Scholar]
- Hebeler, K.; Bogner, S.K.; Furnstahl, R.J.; Nogga, A.; Schwenk, A. Improved nuclear matter calculations from chiral low-momentum interactions. Phys. Rev. C 2011. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).