Polar Vector Property of the Stationary State of Condensed Molecular Matter
Abstract
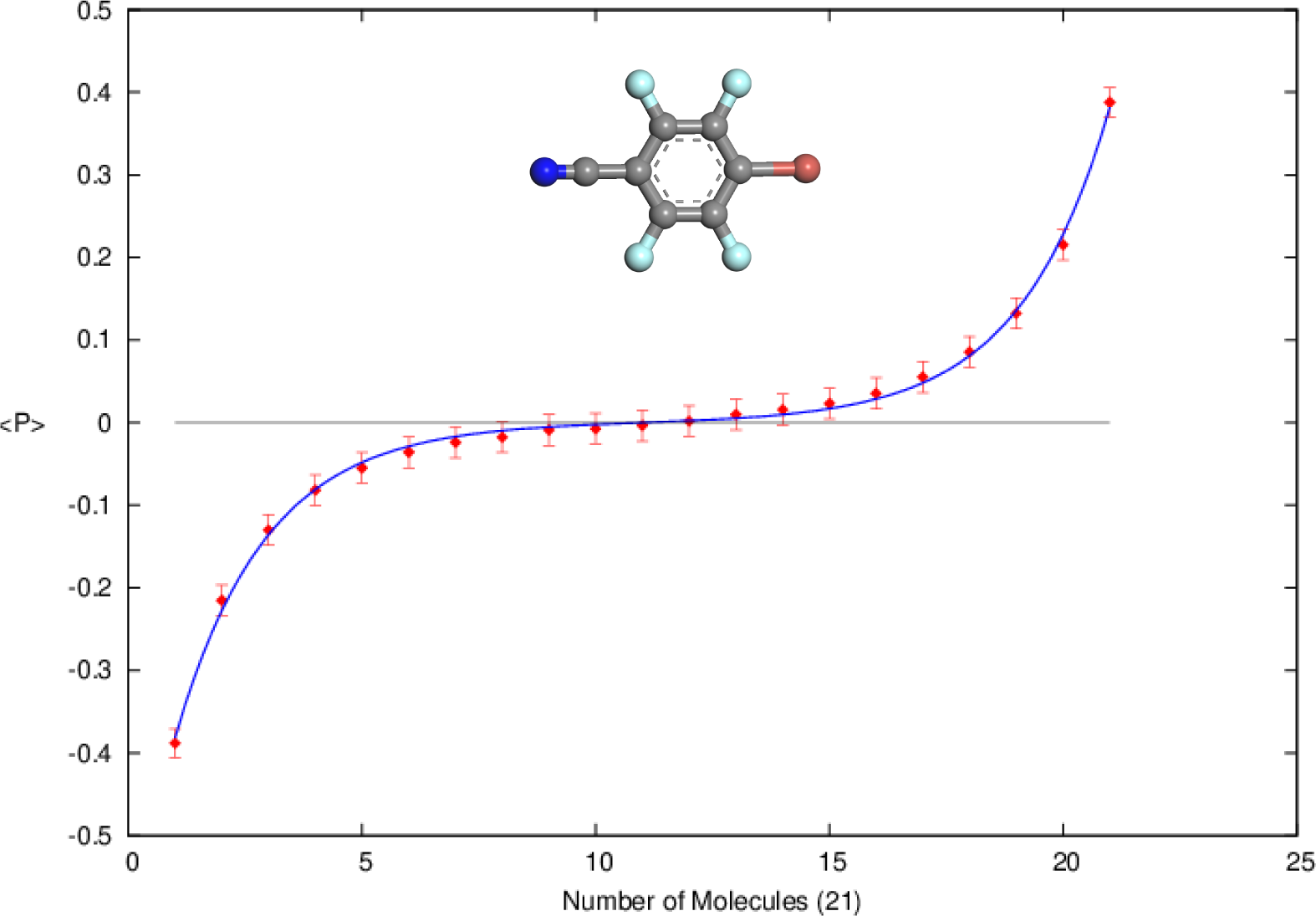
:1. Introduction
2. Symmetry and Conservation
3. Summary and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hulliger, J.; Wüst, T.; Brahimi, K.; Burgener, M.; Aboulfadl, H. A Stochastic principle behind polar properties of condensed molecular matter. New J. Chem. 2013, 37, 2229–2235. [Google Scholar]
- Hulliger, J.; Wüst, T.; Brahimi, K.; Martinez Garcia, J.C. Can mono domain polar molecular crystals exist? Cryst. Growt. Des. 2012, 12, 5211–5218. [Google Scholar]
- Hulliger, J.; Wüst, T.; Rech, M. Symmetry and the polar state of condensed molecular matter. Z. Kristallogr. 2013, 228, 607–610. [Google Scholar]
- Allen, F.H. The Cambridge Structural Database: A quarter of a million crystal structures and rising. Acta Crystallogr. Sect. B. 2002, 58, 380–388. [Google Scholar]
- Curtin, D.Y.; Paul, I. Chemical consequences of the polar axis in organic chemistry. Chem. Rev. 1981, 81, 525–541. [Google Scholar]
- Davey, R.J.; Milisavljevic, B.; Bourne, J.R. Solvent Interactions at Crystal Surfaces: The Kinetic Story of α-Resorcinol. J. Phys. Chem. 1988, 92, 2032–2036. [Google Scholar]
- Chen, B.D.; Garside, J.; Davey, R.J.; Maginn, S.J.; Matsuoka, M. Growth of m-Chloronitrobenzene Crystals in the Presence of Tailor-Made Additives: Assignment of the Polar Axes from Morphological Calculations. J. Phys. Chem. 1994, 98, 3215–3221. [Google Scholar]
- Buguo, W.; Weizhuo, Z.; Cheng, Y.; Erwei, S.; Zhiwen, Y. Analysis of growth habits of polar organic crystal N-4-nitrophenyl-(L)-prolinol (NPP) based on the incorporation of growth units. J. Cryst. Growth. 1996, 160, 375–381. [Google Scholar]
- Ryu, G.; Yoon, C.S. Seeded supercooled melt growth and polar morphology of organic nonlinear optical crystal, meta-nitroaniline (mNA). J. Cryst. Growth. 1998, 191, 190–198. [Google Scholar]
- Hong, H.-K.; Park, J.W.; Lee, K.-S.; Yoon, C.S. Growth of highly nonlinear optical organic crystal, 3-methyl-4-methoxy-4′-nitrostilbene (MMONS). J. Cryst. Growth. 2005, 277, 509–517. [Google Scholar]
- Cuppen, H.M.; Beurskens, S.; Kozuka, S.; Tsukamoto, K.; Smits, J.M.M.; de Gelder, R.; Grimbergen, R.F.P.; Meekes, H. Crystal Structure and Growth Behavior of Aspartame Form I-A. Cryst. Growt. Des. 2005, 5, 917–923. [Google Scholar]
- Srinivasan, K.; Sherwood, J.N. Asymmetric Growth of α-Resorcinol Crystals: Comparison of Growth from the Vapor Phase and from Aqueous Solution. Cryst. Growt. Des. 2005, 5, 1359–1370. [Google Scholar]
- Batagiannis, A.; Wübbenhorst, M.; Hulliger, J. Piezo- and pyroelectric microscopy. Curr. Op. Solid State Mater. Sci. 2010, 14, 107–115. [Google Scholar]
- Behrnd, N.-R.; Couderc, G.; Wübbenhorst, M.; Hulliger, J. Scanning pyroelectric microscopy revealing the spatial polarity distribution in topologically centric crystals of trans-4-chloro-4′-nitrostilbene. Phys. Chem. Chem. Phys. 2006, 8, 4132–4137. [Google Scholar]
- Labat, G.; Behrnd, N.-R.; Couderc, G.; Bonin, M.; Tsuwi, J.; Batagannis, A.; Berger, R.; Bertoni, M.; Prodi-Schwab, A.; Hulliger, J. Polymorphism polar morphology and absolute structure determination of 4-iodo-4′-nitrobiphenyl (INBP). Cryst. Eng. Comm. 2010, 12, 1252–1262. [Google Scholar]
- Feynman, R.P.; Leighton, R.B.; Sands, M. Lectures o. Physics., 17th ed; Addison-Wesley: Reading, MA, USA, 1972; Volume I, III. [Google Scholar]
- Wagnière, G.H. On Chirality and the Universa. Asymmetry.; Wiley: Zürich, Switzerland, 2007. [Google Scholar]
- Blatt, J.M.; Weisskopf, V. Theoretical Nuclea. Physics.; Wiley: New York, NY, USA, 1952; Chapter 7; pp. 23–25. [Google Scholar]
- Spackmann, M.A.; Munshi, P.; Dittrich, B. Dipole moment enhancement in molecular crystals from X-ray diffraction data. Chem. Phys. Chem. 2007, 8, 2051–2063. [Google Scholar]
- Hahn, T. International Tables for Crystallography, Vol. A Space-Group Symmetry, Tab. 10.1 A Space-Group Symmetry, Tab. 10.1.4.2.; Kluwer Acad. Publ.: Dordrecht, NL, 2002; In previous work [2,3] we were using the notation by Shubnikov et al. (∞/∞m), being replaced here by the international symbol. [Google Scholar]
- Authier, A. International Tables for Crystallography Volume D: Physical Properties o. Crystals.; Kluwer Academic Publishers: Dordrecht, the Netherlands, 2003; Chapters 3.2–3.4. [Google Scholar]
- Gervais, C.; Hulliger, J. Impact of Surface Symmetry: On the prediction of Growth-Induced Properties. Cryst. Growt. Des. 2007, 7, 1925–1935. [Google Scholar]
- Cannavacciuolo, L.; Hulliger, J. University of Bern, Bern, Switzerland. . Monte Carlo simulations demonstrating the bi-polar state for a 2D nucleus made of real molecules undergoing long rang. interactions. 2014; Unpublished work. [Google Scholar]
- Greiner, W.; Neise, L.; Stöcker, H. Thermodynamik und Statistisch. Mechanik., 2nd ed; Harri Deutsch: Frankfurt, Germany, 1993; Volume 9. [Google Scholar]
- Paufler, P. Physikalisch. Kristallographie.; Akad. Verlag: Berlin, Germany, 1986; p. 29. [Google Scholar]

© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hulliger, J.; Cannavacciuolo, L.; Rech, M. Polar Vector Property of the Stationary State of Condensed Molecular Matter. Symmetry 2014, 6, 844-850. https://doi.org/10.3390/sym6040844
Hulliger J, Cannavacciuolo L, Rech M. Polar Vector Property of the Stationary State of Condensed Molecular Matter. Symmetry. 2014; 6(4):844-850. https://doi.org/10.3390/sym6040844
Chicago/Turabian StyleHulliger, Jürg, Luigi Cannavacciuolo, and Mathias Rech. 2014. "Polar Vector Property of the Stationary State of Condensed Molecular Matter" Symmetry 6, no. 4: 844-850. https://doi.org/10.3390/sym6040844
APA StyleHulliger, J., Cannavacciuolo, L., & Rech, M. (2014). Polar Vector Property of the Stationary State of Condensed Molecular Matter. Symmetry, 6(4), 844-850. https://doi.org/10.3390/sym6040844



