d-Wave Superconductivity and s-Wave Charge Density Waves: Coexistence between Order Parameters of Different Origin and Symmetry
Abstract
:1. Introduction
2. CDW and Pseudogap Evidence in Cuprates
3. Hamiltonian
4. s-Wave CDW Superconductor
5. d-Wave CDW Superconductor. Formulation
6. d-Wave Superconductor. Phase Diagram Boundaries
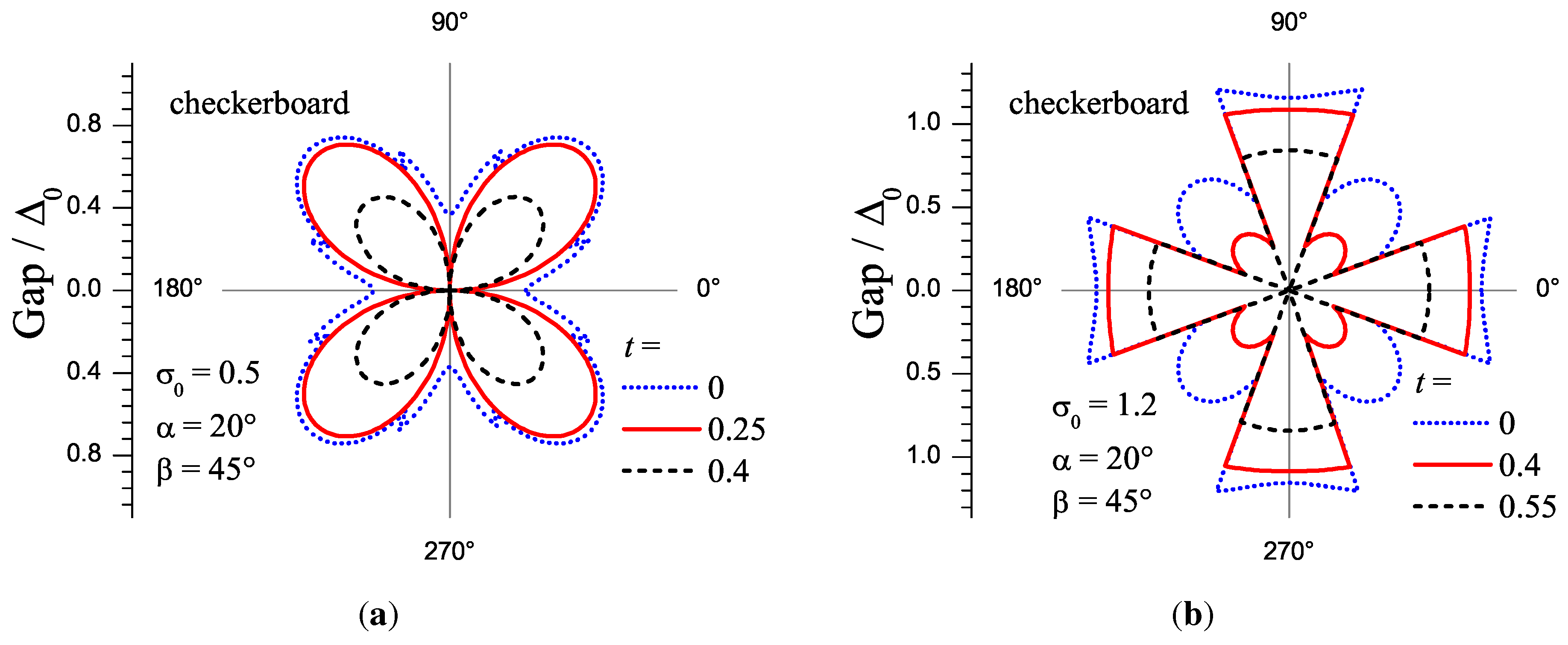
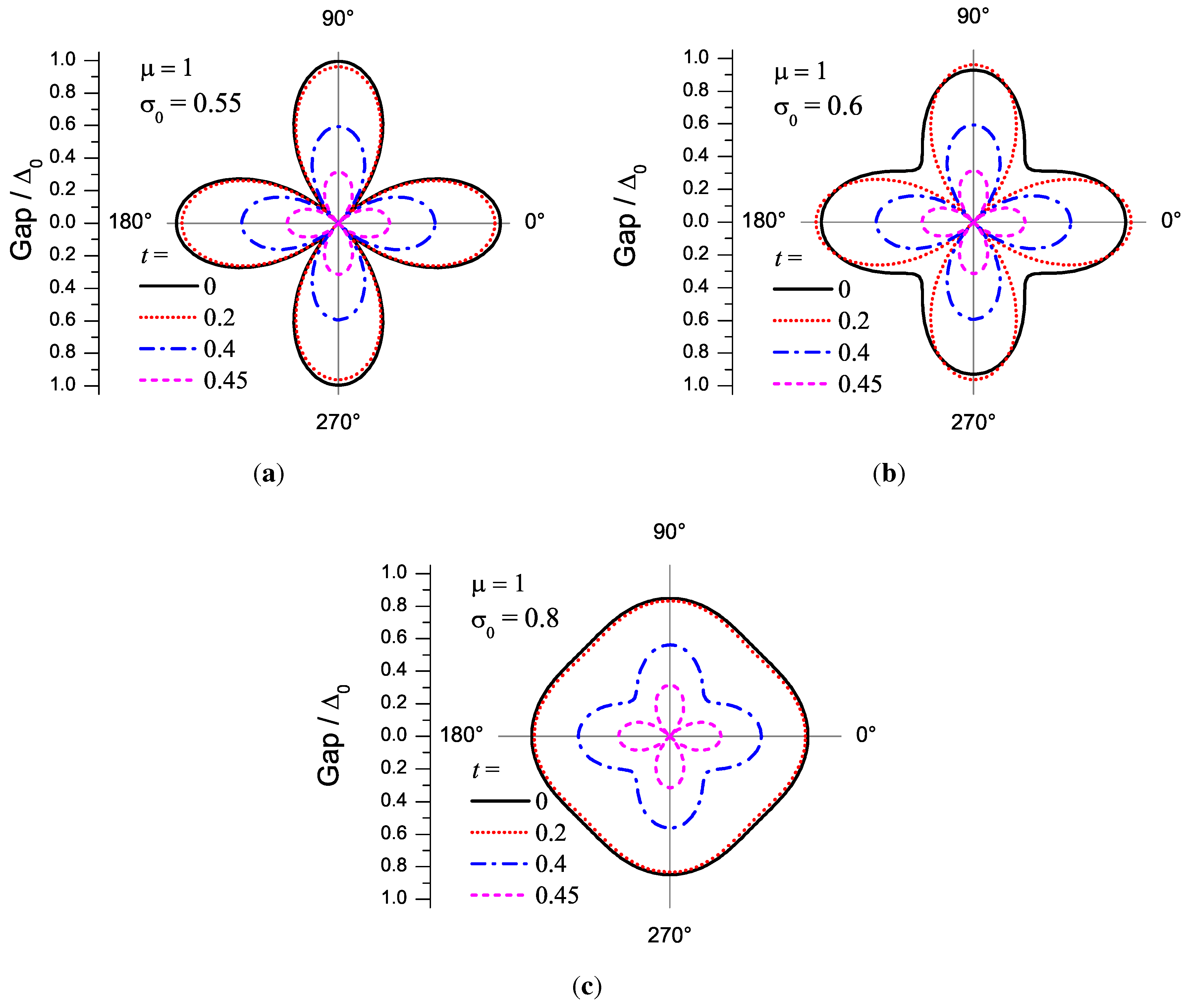
7. Checkerboard CDW Configuration. -Symmetry of the Superconducting linebreak Order Parameter
8. Checkerboard CDW Configuration. Deviations from -Symmetry
9. Complete FS Dielectrization
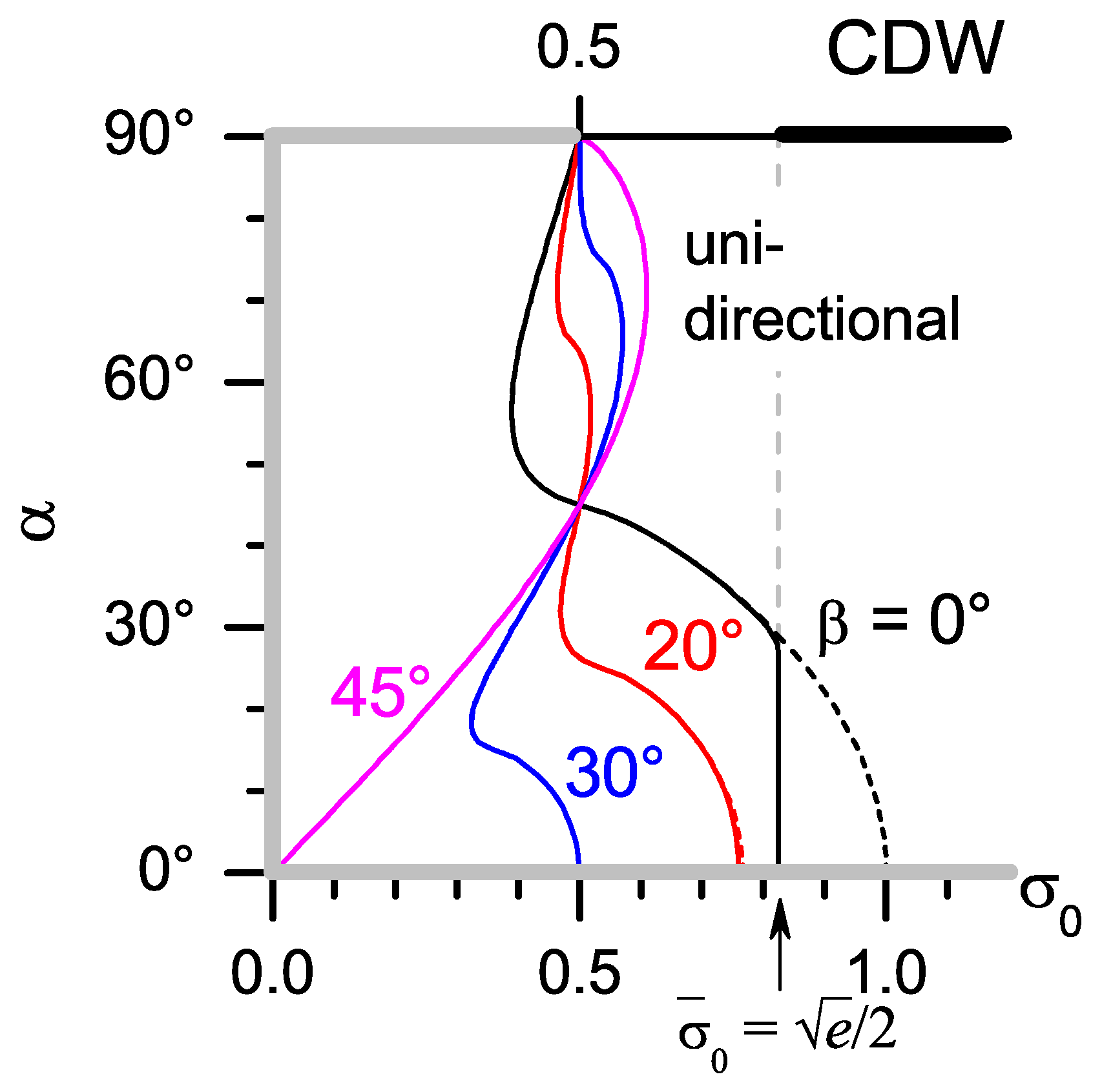
10. Unidirectional CDW Configuration
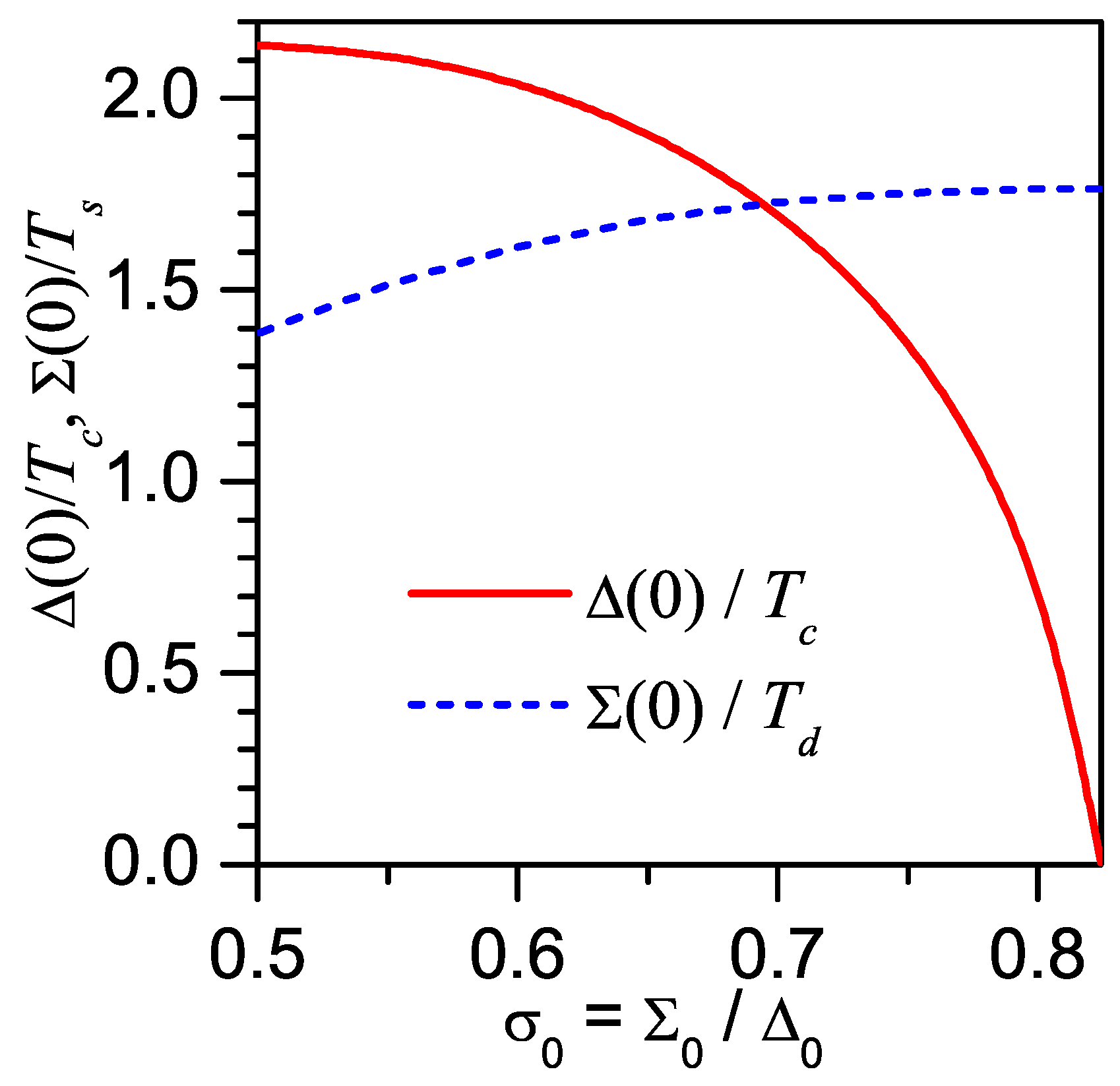
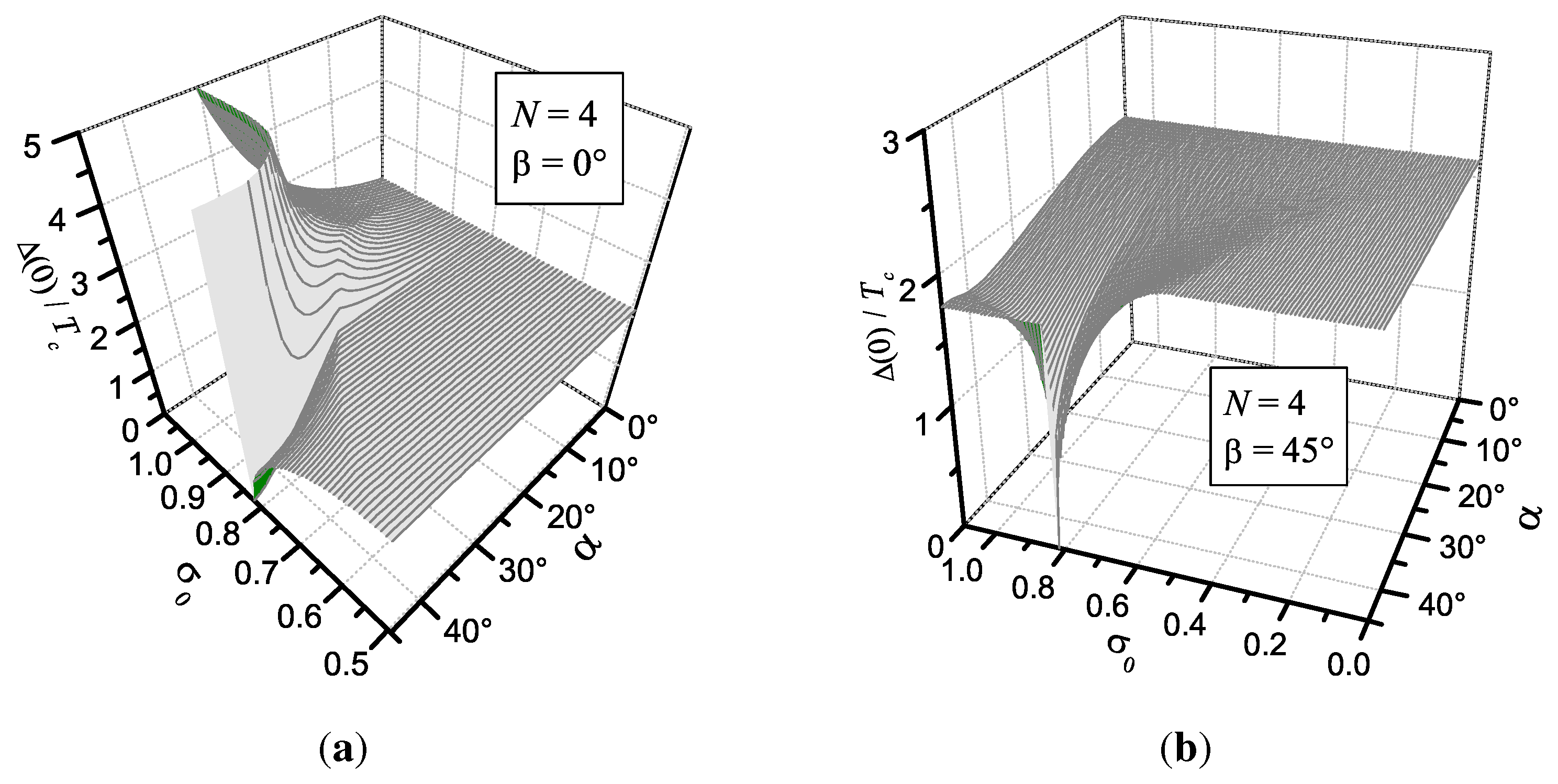
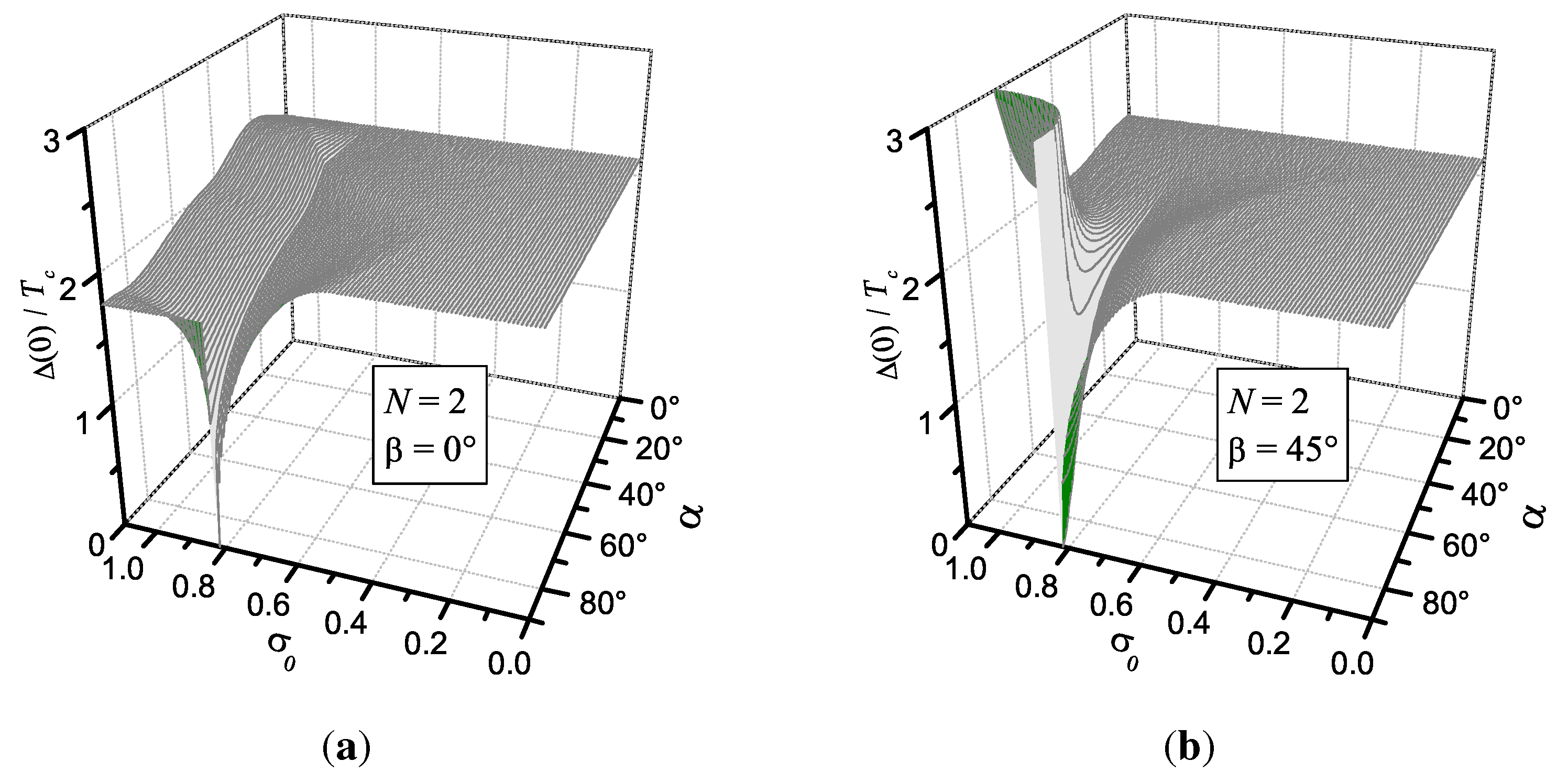
11. Ratio of the Superconducting Gap at Zero Temperature to the Critical Temperature as an Indicator of the CDW Presence
12. Conclusions
Acknowledgements
References
- Bickers, N.E.; Scalapino, D.J. Conserving approximations for strongly fluctuating electron systems. I. Formalism and calculational approach. Ann. Phys. 1989, 193, 206–251. [Google Scholar] [CrossRef]
- Li, Q.; Tsay, Y.N.; Suenaga, M.; Klemm, R.A.; Gu, G.D.; Koshizuka, N. Bi2Sr2CaCu2O8+δ bicrystal c-axis twist josephson junctions: A new phase-sensitive test of order parameter symmetry. Phys. Rev. Lett. 1999, 83, 4160–4163. [Google Scholar] [CrossRef]
- Takano, Y.; Hatano, T.; Fukuyo, A.; Ishii, A.; Ohmori, M.; Arisawa, S.; Togano, K.; Tachiki, M. d-like symmetry of the order parameter and intrinsic Josephson effects in Bi2Sr2CaCu2O8+δ cross-whisker junctions. Phys. Rev. B 2002, 65, 140513. [Google Scholar] [CrossRef]
- Latyshev, Yu.I.; Orlov, A.P.; Nikitina, A.M.; Monceau, P.; Klemm, R.A. c-axis transport in naturally grown Bi2Sr2CaCu2O8+δ cross-whisker junctions. Phys. Rev. B 2004, 70, 094517. [Google Scholar] [CrossRef]
- Klemm, R.A. The phase-sensitive c-axis twist experiments on Bi2Sr2CaCu2O8+δ and their implications. Philos. Mag. 2005, 85, 801–853. [Google Scholar] [CrossRef]
- van Harlingen, D.J. Phase-sensitive tests of the symmetry of the pairing state in the high-temperature superconductors—Evidence for dx2−y2 symmetry. Rev. Mod. Phys. 1995, 67, 515–535. [Google Scholar] [CrossRef]
- Annett, J.F.; Goldenfeld, N.D.; Leggett, A.J. Experimental Constraints on The Pairing State of the Cuprate Superconductors: An Emerging Consensus. In Physical Properties of High Temperature Superconductors V; Ginsberg, D.M., Ed.; World Scientific: River Ridge, NJ, USA, 1996; pp. 375–461. [Google Scholar]
- Tsuei, C.C.; Kirtley, J.R. Pairing symmetry in cuprate superconductors. Rev. Mod. Phys. 2000, 72, 969–1016. [Google Scholar] [CrossRef]
- Mannhart, J.; Chaudhari, P. High-Tc bicrystal grain boundaries. Phys. Today 2001, 54, 48–53. [Google Scholar] [CrossRef]
- Hilgenkamp, H.; Mannhart, J. Grain boundaries in high-Tc superconductors. Rev. Mod. Phys. 2002, 74, 485–549. [Google Scholar] [CrossRef]
- Tsuei, C.C.; Kirtley, J.R. Pairing Symmetry in Cuprate Superconductors: Phase-Sensitive Tests. In The Physics of Superconductors. Vol. 1: Conventional and High-Tc Superconductors; Bennemann, K.H., Ketterson, J.B., Eds.; Springer Verlag: Berlin, Germany, 2003; pp. 647–723. [Google Scholar]
- Tafuri, F.; Kirtley, J.R. Weak links in high critical temperature superconductors. Rep. Prog. Phys. 2005, 68, 2573–2663. [Google Scholar] [CrossRef]
- Latyshev, Yu.I. Evidence for D-Wave Order Parameter Symmetry in Bi-2212 From Experiments on Interlayer Tunneling. In Symmetry and Heterogeneity in High Temperature Superconductors; Bianconi, A., Ed.; Springer Verlag: Dordrecht, The Netherlands, 2006; pp. 181–197. [Google Scholar]
- Kirtley, J.R.; Tafuri, F. Tunneling Measurements of the Cuprate Superconductors. In Handbook of High-Temperature Superconductivity. Theory and Experiment; Schrieffer, J.R., Brooks, J.S., Eds.; Springer Verlag: New York, NY, USA, 2007; pp. 19–86. [Google Scholar]
- Tsuei, C.C.; Kirtley, J.R. Phase-sensitive tests of pairing symmetry in cuprate superconductors. In Superconductivity. Vol. 2: Novel Superconductors; Bennemann, K.H., Ketterson, J.B., Eds.; Springer Verlag: Berlin, Germany, 2008; pp. 869–921. [Google Scholar]
- Prozorov, R. Superfluid density in a superconductor with an extended d-wave gap. Supercond. Sci. Technol. 2008, 21, 082003. [Google Scholar] [CrossRef]
- Zhao, G.-M. Identification of the bulk pairing symmetry in high-temperature superconductors: Evidence for an extended s wave with eight line nodes. Phys. Rev. B 2001, 64, 024503:1–024503:10. [Google Scholar] [CrossRef]
- Brandow, B.H. Arguments and evidence for a node-containing anisotropic s-wave gap form in the cuprate superconductors. Phys. Rev. B 2002, 65, 054503. [Google Scholar] [CrossRef]
- Brandow, B.H. Strongly anisotropic s-wave gaps in exotic superconductors. Philos. Mag. 2003, 83, 2487–2519. [Google Scholar] [CrossRef]
- Zhao, G.M. Unambiguous evidence for extended s-wave pairing symmetry in hole-doped high-temperature superconductors. Philos. Mag. B 2004, 84, 3861–3867. [Google Scholar] [CrossRef]
- Zhao, G.M. The magnetic resonance in high-temperature superconductors: Evidence for an extended s-wave pairing symmetry. Philos. Mag. B 2004, 84, 3869–3882. [Google Scholar] [CrossRef]
- Zhao, G.M. Precise determination of the superconducting gap along the diagonal direction of Bi2Sr2CaCu2O8+y: Evidence for an extended s-wave gap symmetry. Phys. Rev. B 2007, 75, 140510. [Google Scholar] [CrossRef]
- Annett, J.F. Symmetry of the order parameter for high-temperature superconductivity. Adv. Phys. 1990, 39, 83–126. [Google Scholar] [CrossRef]
- Mineev, V.P.; Samokhin, K.V. Intoduction to Unconventional Superconductivity; Gordon and Breach Science Publishers: Amsterdam, The Netherlands, 1999. [Google Scholar]
- Gabovich, A.M.; Voitenko, A.I. Power-law low-temperature asymptotics for spatially nonhomogeneous s-wave superconductors. Fiz. Nizk. Temp. 1999, 25, 677–684. [Google Scholar] [CrossRef]
- Gabovich, A.M.; Voitenko, A.I. Influence of the order parameter nonhomogeneities on low-temperature properties of superconductors. Phys. Rev. B 1999, 60, 7465–7472. [Google Scholar] [CrossRef]
- Gabovich, A.M.; Li, M.S.; Szymczak, H.; Voitenko, A.I. Heat capacity of mesoscopically disordered superconductors: Implications to MgB2. Fiz. Nizk. Temp. 2002, 28, 1126–1137. [Google Scholar] [CrossRef]
- Gabovich, A.M.; Li, M.S.; Pȩkała, M.; Szymczak, H.; Voitenko, A.I. Heat capacity of mesoscopically disordered superconductors with emphasis on MgB2. J. Phys. Condens. Matter 2002, 14, 9621–9629. [Google Scholar] [CrossRef]
- Ekino, T.; Gabovich, A.M.; Li, M.S.; Takasaki, T.; Voitenko, A.I.; Akimitsu, J.; Fujii, H.; Muranaka, T.; Pȩkała, M.; Szymczak, H. Spatially heterogeneous character of superconductivity in MgB2 as revealed by local probe and bulk measurements. Physica C 2005, 426-431, 230–233. [Google Scholar] [CrossRef]
- Phillips, J.C. States in the superconductive energy gap of high-Tc cuprates. Phys. Rev. B 1990, 41, 8968–8973. [Google Scholar] [CrossRef]
- Phillips, J.C. Dopant sites and structure in high Tc layered cuprates. Philos. Mag. B 1999, 79, 1477–1498. [Google Scholar] [CrossRef]
- Phillips, J.C.; Saxena, A.; Bishop, A.R. Pseudogaps, dopants, and strong disorder in cuprate high-temperature superconductors. Rep. Prog. Phys. 2003, 66, 2111–2182. [Google Scholar] [CrossRef]
- Phillips, J.C. Hard-wired dopant networks and the prediction of high transition temperatures in ceramic superconductors. J. Supercond. 2010, 23, 1267–1279. [Google Scholar] [CrossRef]
- Gavrilkin, S.Yu.; Ivanenko, O.M.; Martovitskii, V.P.; Mitsen, K.V.; Tsvetkov, A.Yu. Percolative nature of the transition from 60 to 90 K-phase in YBa2Cu3O6+δ. Physica C 2010, 470, S996–S997. [Google Scholar] [CrossRef]
- Khasanov, R.; Shengelaya, A.; Maisuradze, A.; Di Castro, D.; Savić, I.M.; Weyeneth, S.; Park, M.S.; Jang, D.J.; Lee, S.-I.; Keller, H. Nodeless superconductivity in the infinite-layer electron-doped cuprate superconductor Sr0.9La0.1CuO2. Phys. Rev. B 2008, 77, 184512. [Google Scholar] [CrossRef]
- Valli, A.; Sangiovanni, G.; Capone, M.; Di Castro, C. Possible secondary component of the order parameter observed in London penetration depth measurements. Phys. Rev. B 2010, 82, 132504. [Google Scholar] [CrossRef]
- Buzdin, A.I.; Bulaevskii, L.N.; Kulic, M.L.; Panyukov, S.V. Magnetic superconductors. Usp. Fiz. Nauk 1984, 144, 597–641. [Google Scholar] [CrossRef]
- Machida, K. Coexistence problem of magnetism and superconductivity. Appl. Phys. A 1984, 35, 193–215. [Google Scholar] [CrossRef]
- Buzdin, A.I.; Bulaevskii, L.N. Antiferromagnetic superconductors. Usp. Fiz. Nauk 1986, 149, 45–67. [Google Scholar] [CrossRef]
- Bulaevskii, L.N.; Buzdin, A.I.; Kulić, M.L.; Panjukov, S.V. Coexistence of superconductivity and magnetism. Theoretical predictions and experimental results. Adv. Phys. 1985, 34, 175–261. [Google Scholar] [CrossRef]
- Izyumov, Yu.A.; Katsnelson, M.I.; Skryabin, Yu.N. Itinerant Electron Magnetism; Fiziko-Matematicheskaya Literatura: Moscow, Russia, 1994; p. 368, in Russian. [Google Scholar]
- Santini, P.; Lémanski, R.; Erdös, P. Magnetism of actinide compounds. Adv. Phys. 1999, 48, 537–653. [Google Scholar] [CrossRef]
- Müller, K.-H.; Narozhnyi, V.N. Interaction of superconductivity and magnetism in borocarbide superconductors. Rep. Prog. Phys. 2001, 64, 943–1008. [Google Scholar] [CrossRef]
- Klamut, P.W. Superconductivity and magnetism in the ruthenocuprates. Supercond. Sci. Technol. 2008, 21, 093001. [Google Scholar] [CrossRef]
- Pfleiderer, C. Superconducting phases of f-electron compounds. Rev. Mod. Phys. 2009, 81, 1551–1624. [Google Scholar] [CrossRef]
- Moore, K.T.; van der Laan, G. Nature of the 5f states in actinide metals. Rev. Mod. Phys. 2009, 81, 235–298. [Google Scholar] [CrossRef]
- Johnston, D.C. The puzzle of high temperature superconductivity in layered iron pnictides and chalcogenides. Adv. Phys. 2010, 59, 803–1061. [Google Scholar] [CrossRef]
- Lumsden, M.D.; Christianson, A.D. Magnetism in Fe-based superconductors. J. Phys. Condens. Matter 2010, 22, 203203. [Google Scholar] [CrossRef] [PubMed]
- Fawcett, E.; Alberts, H.L.; Galkin, V.Yu.; Noakes, D.R.; Yakhmi, J.V. Spin-density-wave antiferromagnetism in chromium alloys. Rev. Mod. Phys. 1994, 66, 25–127. [Google Scholar] [CrossRef]
- Gabovich, A.M.; Voitenko, A.I. Superconductors with charge- and spin-density waves: Theory and experiment (Review). Fiz. Nizk. Temp. 2000, 26, 419–452. [Google Scholar] [CrossRef]
- Gabovich, A.M.; Voitenko, A.I.; Annett, J.F.; Ausloos, M. Charge- and spin-density-wave superconductors. Supercond. Sci. Technol. 2001, 14, R1–R27. [Google Scholar] [CrossRef]
- Gabovich, A.M.; Voitenko, A.I.; Ausloos, M. Charge-density waves and spin-density waves in existing superconductors: Competition between Cooper pairing and Peierls or excitonic instabilities. Phys. Rep. 2002, 367, 583–709. [Google Scholar] [CrossRef]
- Jérome, D.; Pasquier, C.R. One Dimensional Organic Superconductors. In Frontiers in Superconducting Materials; Narlikar, A.V., Ed.; Springer Verlag: New York, NY, USA, 2005; pp. 183–230. [Google Scholar]
- Zhang, W.; de Melo, C.A.R.S. Triplet versus singlet superconductivity in quasi-one-dimensional conductors. Adv. Phys. 2007, 56, 545–652. [Google Scholar] [CrossRef]
- Aperis, A.; Varelogiannis, G.; Littlewood, P.B.; Simons, B.D. Coexistence of spin density wave, d-wave singlet and staggered π-triplet superconductivity. J. Phys. Condens. Matter 2008, 20, 434235. [Google Scholar] [CrossRef]
- Vojta, M. Lattice symmetry breaking in cuprate superconductors: Stripes, nematics, and superconductivity. Adv. Phys. 2009, 58, 699–820. [Google Scholar] [CrossRef]
- Gabovich, A.M.; Voitenko, A.I. Superconductivity against dielecrization: Evidence for competition and coexistence. Ukr. Fiz. Zh. 1999, 44, 223–229. [Google Scholar]
- Kusmartsev, F.V.; Saarela, M. Two-component physics of cuprates and superconductor-insulator transitions. Supercond. Sci. Technol. 2008, 22, 014008. [Google Scholar] [CrossRef]
- Kusmartsev, F.V.; Saarela, M. What is the most important for a nanoscale structure formations in HTSC?, spin, phonon or third way in Coulomb interaction and correlations? J. Phys. Conf. Ser. 2008, 108, 012029. [Google Scholar] [CrossRef]
- Gabovich, A.M.; Voitenko, A.I.; Ekino, T.; Li, M.S.; Szymczak, H.; Pȩkała, M. Competition of superconductivity and charge density waves in cuprates: Recent evidence and interpretation. Adv. Condens. Matter Phys. 2010, 2010, 681070. [Google Scholar] [CrossRef]
- Bilbro, G.; McMillan, W.L. Theoretical model of superconductivity and the martensitic transformation in A15 compounds. Phys. Rev. B 1976, 14, 1887–1892. [Google Scholar] [CrossRef]
- Balseiro, C.A.; Falicov, L.M. Superconductivity and charge-density waves. Phys. Rev. B 1979, 20, 4457–4464. [Google Scholar] [CrossRef]
- Gabovich, A.M.; Pashitskii, E.A.; Shpigel, A.S. Paramagnetic limit of superconductors with a dielectric gap on the Fermi surface. Zh. Éksp. Teor. Fiz. 1979, 77, 1157–1166. [Google Scholar]
- Gabovich, A.M.; Moiseev, D.P.; Shpigel, A.S. Thermodynamic properties of superconducting ceramics BaPb1−xBixO3. J. Phys. C 1982, 15, L569–L572. [Google Scholar] [CrossRef]
- Gabovich, A.M.; Moiseev, D.P.; Shpigel, A.S. The nature of superconductivity for solid solutions BaPb1−xBixO3 with a perovskite structure. Role of the electron spectrum dielectrization. Zh. Éksp. Teor. Fiz. 1982, 83, 1383–1388. [Google Scholar]
- Gabovich, A.M.; Shpigel, A.S. Influence of impurity scattering on the critical temperature of superconductors with a partial gap in the electron spectrum. J. Low Temp. Phys. 1983, 51, 581–599. [Google Scholar] [CrossRef]
- Gabovich, A.M.; Moiseev, D.P.; Prokopovich, L.V.; Uvarova, S.K.; Yachmenev, V.E. Experimental proof of bulk superconductivity in perovskite system BaPb1−xBixO3. Zh. Éksp. Teor. Fiz. 1984, 86, 1727–1733. [Google Scholar]
- Gabovich, A.M.; Shpigel, A.S. Thermodynamics of superconductors with charge- and spin-density waves. J. Phys. F 1984, 14, 3031–3039. [Google Scholar] [CrossRef]
- Gabovich, A.M.; Gerber, A.S.; Shpigel, A.S. Thermodynamics of superconductors with charge- and spin-density waves. Δ/Tc ratio and paramagnetic limit. Phys. Status Solidi B 1987, 141, 575–587. [Google Scholar] [CrossRef]
- Gabovich, A.M.; Shpigel, A.S. Upper critical magnetic field of superconductors with a dielectric gap on the Fermi surface sections. Phys. Rev. B 1988, 38, 297–306. [Google Scholar] [CrossRef]
- Gabovich, A.M.; Li, M.S.; Szymczak, H.; Voitenko, A.I. Thermodynamics of superconductors with charge-density waves. J. Phys. Condens. Matter 2003, 15, 2745–2753. [Google Scholar] [CrossRef]
- Gabovich, A.M.; Voitenko, A.I.; Ekino, T. Enhanced paramagnetic limit of the upper critical magnetic field for superconductors with charge-density waves. J. Phys. Condens. Matter 2004, 16, 3681–3690. [Google Scholar] [CrossRef]
- Ekino, T.; Gabovich, A.M.; Voitenko, A.I. Paramagnetic effect of the magnetic field on superconductors with charge-density waves. Fiz. Nizk. Temp. 2005, 31, 55–62. [Google Scholar] [CrossRef]
- Gabovich, A.M. Josephson and quasiparticle tunneling in superconductors with charge density waves. Fiz. Nizk. Temp. 1992, 18, 693–704. [Google Scholar]
- Gabovich, A.M. Josephson and quasiparticle current in partially-dielectrized superconductors with spin density waves. Fiz. Nizk. Temp. 1993, 19, 641–654. [Google Scholar]
- Gabovich, A.M. About tunnel spectroscopy of normal metals with charge or spin density waves. Fiz. Nizk. Temp. 1993, 19, 1098–1105. [Google Scholar]
- Gabovich, A.M.; Voitenko, A.I. Tunneling spectroscopy of normal metals with charge-density or spin-density waves. Phys. Rev. B 1995, 52, 7437–7447. [Google Scholar] [CrossRef]
- Gabovich, A.M.; Voitenko, A.I. Non-stationary Josephson effect for superconductors with charge-density waves: NbSe3. Europhys. Lett. 1997, 38, 371–376. [Google Scholar] [CrossRef]
- Gabovich, A.M.; Voitenko, A.I. Nonstationary Josephson effect for superconductors with charge-density waves. Phys. Rev. B 1997, 55, 1081–1099. [Google Scholar] [CrossRef]
- Gabovich, A.M.; Voitenko, A.I. Josephson tunnelling involving superconductors with charge-density waves. J. Phys. Condens. Matter 1997, 9, 3901–3920. [Google Scholar] [CrossRef]
- Gabovich, A.M.; Voitenko, A.I. Asymmetrical tunneling between similar metallic junctions with charge-density or spin-density waves: The case of broken symmetry. Phys. Rev. B 1997, 56, 7785–7788. [Google Scholar] [CrossRef]
- Gabovich, A.M.; Voitenko, A.I. Nonstationary Josephson effect for superconductors with spin-density waves. Phys. Rev. B 1999, 60, 14897–14906. [Google Scholar] [CrossRef]
- Gabovich, A.M.; Voitenko, A.I. Nonstationary Josephson tunneling involving superconductors with spin-density waves. Physica C 2000, 329, 198–230. [Google Scholar] [CrossRef]
- Gabovich, A.M.; Voitenko, A.I. Charge-density-wave origin of the dip-hump structure in tunnel spectra of the BSCCO superconductor. Phys. Rev. B 2007, 75, 064516. [Google Scholar] [CrossRef]
- Ekino, T.; Gabovich, A.M.; Li, M.S.; Pȩkała, M.; Szymczak, H.; Voitenko, A.I. Analysis of the pseudogap-related structure in tunneling spectra of superconducting Bi2Sr2CaCu2O8+δ revealed by the break-junction technique. Phys. Rev. B 2007, 76, 180503. [Google Scholar] [CrossRef]
- Ekino, T.; Gabovich, A.M.; Li, M.S.; Pȩkała, M.; Szymczak, H.; Voitenko, A.I. Temperature-dependent pseudogap-like features in tunnel spectra of high-Tc cuprates as a manifestation of charge-density waves. J. Phys. Condens. Matter 2008, 20, 425218. [Google Scholar] [CrossRef]
- Morosan, E.; Wagner, K.E.; Zhao, L.L.; Hor, Y.; Williams, A.J.; Tao, J.; Zhu, Y.; Cava, R.J. Multiple electronic transitions and superconductivity in PdxTiSe2. Phys. Rev. B 2010, 81, 094524. [Google Scholar] [CrossRef]
- Monney, C.; Schwier, E.F.; Garnier, M.G.; Mariotti, N.; Didiot, C.; Cercellier, H.; Marcus, J.; Berger, H.; Beck, A.N.T.H.; Aebi, P. Probing the exciton condensate phase in 1T-TiSe2 with photoemission. New J. Phys. 2010, 12, 125019. [Google Scholar] [CrossRef]
- Kudo, K.; Nishikubo, Y.; Nohara, M. Coexistence of superconductivity and charge density wave in SrPt2As2. J. Phys. Soc. Jpn. 2008, 79, 123710. [Google Scholar] [CrossRef]
- van Wezel, J.; Nahai-Williamson, P.; Saxena, S.S. An alternative interpretation of recent ARPES measurements on TiSe2. Europhys. Lett. 2010, 89, 47004. [Google Scholar] [CrossRef]
- Ge, Y.; Liu, A.Y. First-principles investigation of the charge-density-wave instability in 1T-TaSe2. Phys. Rev. B 2010, 82, 155133. [Google Scholar] [CrossRef]
- Li, L.J.; Sun, Y.P.; Zhu, X.D.; Wang, B.S.; Zhu, X.B.; Yang, Z.R.; Song, W.H. Growth and superconductivity of 2H-Ni0.02TaSe2 single crystals. Solid State Commun. 2010, 150, 2248–2252. [Google Scholar] [CrossRef]
- Markiewicz, R.S. A survey of the Van Hove scenario for high-Tc superconductivity with special emphasis on pseudogaps and striped phases. J. Phys. Chem. Solids 1997, 58, 1179–1310. [Google Scholar] [CrossRef]
- Fujita, M.; Goka, H.; Yamada, K.; Tranquada, J.M.; Regnault, L.P. Stripe order, depinning, and fluctuations in La1.875Ba0.125CuO4 and La1.875Ba0.075Sr0.050CuO4. Phys. Rev. B 2004, 70, 104517. [Google Scholar] [CrossRef]
- Meevasana, W.; Ingle, N.J.C.; Lu, D.H.; Shi, J.R.; Baumberger, F.; Shen, K.M.; Lee, W.S.; Cuk, T.; Eisaki, H.; Devereaux, T.P.; Nagaosa, N.; Zaanen, J.; Shen, Z.-X. Doping dependence of the coupling of electrons to bosonic modes in the single-layer high-temperature Bi2Sr2CuO6 superconductor. Phys. Rev. Lett. 2006, 96, 157003. [Google Scholar] [CrossRef] [PubMed]
- Lee, W.S.; Vishik, I.M.; Tanaka, K.; Lu, D.H.; Sasagawa, T.; Nagaosa, N.; Devereaux, T.P.; Hussain, Z.; Shen, Z.-X. Abrupt onset of a second energy gap at the superconducting transition of underdoped Bi2212. Nature 2007, 450, 81–84. [Google Scholar] [CrossRef]
- Wise, W.D.; Boyer, M.C.; Chatterjee, K.; Kondo, T.; Takeuchi, T.; Ikuta, H.; Wang, Y.; Hudson, E.W. Charge-density-wave origin of cuprate checkerboard visualized by scanning tunnelling microscopy. Nat. Phys. 2008, 4, 696–699. [Google Scholar] [CrossRef]
- Nair, S.K.; Zou, X.; Chia, E.E.M.; Zhu, J.-X.; Panagopoulos, C.; Ishida, S.; Uchida, S. Quasiparticle dynamics in overdoped Bi1.4Pb0.7Sr1.9CaCu2O8+δ: Coexistence of superconducting gap and pseudogap below Tc. Phys. Rev. B 2010, 82, 212503. [Google Scholar] [CrossRef]
- Razzoli, E.; Sassa, Y.; Drachuck, G.; Månsson, M.; Keren, A.; Shay, M.; Berntsen, M.H.; Tjernberg, O.; Radovic, M.; Chang, J.; et al. The Fermi surface and band folding in La2−xSrxCuO4, probed by angle-resolved photoemission. New J. Phys. 2010, 12, 125003. [Google Scholar] [CrossRef]
- Vishik, I.M.; Lee, W.S.; He, R.-H.; Hashimoto, M.; Hussain, Z.; Devereaux, T.P.; Shen, Z.-X. ARPES studies of cuprate Fermiology: Superconductivity, pseudogap and quasiparticle dynamics. New J. Phys. 2010, 12, 105008. [Google Scholar] [CrossRef]
- Kondo, T.; Hamaya, Y.; Palczewski, A.D.; Takeuchi, T.; Wen, J.S.; Xu, Z.J.; Gu, G.; Schmalian, J.; Kaminski, A. Disentangling Cooper-pair formation above the transition temperature from the pseudogap state in the cuprates. Nat. Phys. 2011, 7, 21–25. [Google Scholar] [CrossRef]
- Furrer, A. Admixture of an s-Wave Component to the d-Wave Gap Symmetry In High-Temperature Superconductors. In High Tc Superconductors and Related Transition Metal Oxides. Special Contributions in Honor of K. Alex Müller on the Occasion of his 80th Birthday; Bussmann-Holder, A., Keller, H., Eds.; Springer Verlag: Heidelberg, Germany, 2007; pp. 135–141. [Google Scholar]
- Cohen, M.L. Essay: Fifty years of condensed matter physics. Phys. Rev. Lett. 2008, 101, 250001. [Google Scholar] [CrossRef] [PubMed]
- Burgin, M.S.; Kuznetsov, V.I. Scientific problems and questions from a logical point of view. Synthese 1994, 100, 1–28. [Google Scholar] [CrossRef]
- Popper, K.R. Objective Knowledge. An Evolutionary Approach; Clarendon Press: Oxford, UK, 1979. [Google Scholar]
- Krasnov, V.M.; Yurgens, A.; Winkler, D.; Delsing, P.; Claeson, T. Evidence for coexistence of the superconducting gap and the pseudogap in Bi-2212 from intrinsic tunneling spectroscopy. Phys. Rev. Lett. 2000, 84, 5860–5863. [Google Scholar] [CrossRef] [PubMed]
- Oda, M.; Liu, Y.H.; Kurosawa, T.; Takeyama, K.; Momono, N.; Ido, M. On the relations among the pseudogap, electronic charge order and Fermi-arc superconductivity in Bi2Sr2CaCu2O8+δ. J. Phys. Conf. Ser. 2008, 108, 012008. [Google Scholar] [CrossRef]
- Li, Y.; Balédent, V.; Yu, G.; Barišić, N.; Hradil, K.; Mole, R.A.; Sidis, Y.; Steffens, P.; Zhao, X.; Bourges, P.; Greven, M. Hidden magnetic excitation in the pseudogap phase of a high-Tc superconductor. Nature 2010, 468, 283–285. [Google Scholar] [CrossRef]
- Parker, C.V.; Aynajian, P.; da Silva Neto, E.H.; Pushp, A.; Ono, S.; Wen, J.; Xu, Z.; Gu, G.; Yazdani, A. Fluctuating stripes at the onset of the pseudogap in the high-Tc superconductor Bi2Sr2CaCu2O8+x. Nature 2010, 468, 677–680. [Google Scholar] [CrossRef]
- Kudo, K.; Nishizaki, T.; Okamoto, D.; Okumura, N.; Kobayashi, N. STM/STS studies on the energy gap of Pb-substituted Bi2Sr2CuO6+δ in magnetic fields. Physica C 2010, 470, S195–S196. [Google Scholar] [CrossRef]
- van der Marel, D. Beware of the pseudogap. Nat. Phys. 2011, 7, 10–11. [Google Scholar] [CrossRef]
- He, R.-H.; Hashimoto, M.; Karapetyan, H.; Koralek, J.D.; Hinton, J.P.; Testaud, J.P.; Nathan, V.; Yoshida, Y.; Yao, H.; Tanaka, K.; et al. From a single-band metal to a high-temperature superconductor via two thermal phase transitions. Science 2011, 331, 1579–1583. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Fujita, K.; McElroy, K.; Slezak, J.A.; Wang, M.; Aiura, Y.; Bando, H.; Ishikado, M.; Masui, T.; Zhu, J.-X.; Balatsky, A.V.; Eisaki, H.; Uchida, S.; Davis, J.C. Interplay of electron-lattice interactions and superconductivity in Bi2Sr2CaCu2O8+δ. Nature 2006, 442, 546–551. [Google Scholar] [CrossRef]
- Reznik, D.; Pintschovius, L.; Ito, M.; Iikubo, S.; Sato, M.; Goka, H.; Fujita, M.; Yamada, K.; Gu, G.D.; Tranquada, J.M. Electron-phonon coupling reflecting dynamic charge inhomogeneity in copper oxide superconductors. Nature 2006, 440, 1170–1173. [Google Scholar] [CrossRef] [PubMed]
- Boyer, M.C.; Wise, W.D.; Chatterjee, K.; Yi, M.; Kondo, T.; Takeuchi, T.; Ikuta, H.; Hudson, E.W. Imaging the two gaps of the high-temperature superconductor Bi2Sr2CuO6+x. Nat. Phys. 2007, 3, 802–806. [Google Scholar] [CrossRef]
- Yazdani, A. Visualizing pair formation on the atomic scale and the search for the mechanism of superconductivity in high-Tc cuprates. J. Phys. Condens. Matter 2009, 21, 164214. [Google Scholar] [CrossRef]
- Kato, T.; Machida, T.; Kamijo, Y.; Miyashita, R.; Sakata, H. Spatial correlation between the LDOS modulation and electronic inhomogeneity in Bi2Sr2−xLaxCuO6+δ. J. Phys. Conf. Ser. 2009, 150, 052101. [Google Scholar] [CrossRef]
- Parker, C.V.; Pushp, A.; Pasupathy, A.N.; Gomes, K.K.; Wen, J.; Xu, Z.; Ono, S.; Gu, G.; Yazdani, A. Nanoscale proximity effect in the high-temperature superconductor Bi2Sr2CaCu2O8+δ using a scanning tunneling microscope. Phys. Rev. Lett. 2010, 104, 117001. [Google Scholar] [CrossRef]
- Gabovich, A.M.; Voitenko, A.I. Model for the coexistence of d-wave superconducting and charge-density-wave order parameters in high-temperature cuprate superconductors. Phys. Rev. B 2009, 80, 224501. [Google Scholar] [CrossRef]
- Voitenko, A.I.; Gabovich, A.M. Charge-density waves in partially dielectrized superconductors with d-pairing. Fiz. Tverd. Tela 2010, 52, 20–27. [Google Scholar] [CrossRef]
- Voitenko, A.I.; Gabovich, A.M. Charge density waves in d-wave superconductors. Fiz. Nizk. Temp. 2010, 36, 1300–1311. [Google Scholar] [CrossRef]
- Friend, R.H.; Jérome, D. Periodic lattice distortions and charge-density waves in one-dimensional and 2-dimensional metals. J. Phys. C 1979, 12, 1441–1477. [Google Scholar] [CrossRef]
- Friend, R.H.; Yoffe, A.D. Electronic properties of intercalation complexes of the transition metal dichalcogenides. Adv. Phys. 1987, 36, 1–94. [Google Scholar] [CrossRef]
- Vojta, M. Tendencies toward nematic order in YBa2Cu3O6+δ: Uniform distortion vs. incipient charge stripes. Eur. Phys. J. Spec. Top. 2010, 188, 49–59. [Google Scholar] [CrossRef]
- Kordyuk, A.A.; Zabolotnyy, V.B.; Evtushinsky, D.V.; Büchner, B.; Borisenko, S.V. Electrons in cuprates: A consistent ARPES view. J. Electron Spectrosc. Relat. Phenom. 2010, 181, 44–47. [Google Scholar] [CrossRef]
- Kordyuk, A.A.; Zabolotnyy, V.B.; Evtushinsky, D.V.; Inosov, D.S.; Kim, T.K.; Büchner, B.; Borisenko, S.V. An ARPES view on the high-Tc problem: Phonons vs. spin-fluctuations. Eur. Phys. J. Spec. Top. 2010, 188, 153–162. [Google Scholar] [CrossRef]
- Franz, M. Crystalline electron pairs. Science 2004, 305, 1410–1411. [Google Scholar] [CrossRef]
- McElroy, K.; Lee, D.-H.; Hoffman, J.E.; Lang, K.M.; Lee, J.; Hudson, E.W.; Eisaki, H.; Uchida, S.; Davis, J.C. Coincidence of checkerboard charge order and antinodal state decoherence in strongly underdoped superconducting Bi2Sr2CaCu2O8+δ. Phys. Rev. Lett. 2005, 94, 197005. [Google Scholar] [CrossRef]
- Robertson, J.A.; Kivelson, S.A.; Fradkin, E.; Fang, A.C.; Kapitulnik, A. Distinguishing patterns of charge order: Stripes or checkerboards. Phys. Rev. B 2006, 74, 134507. [Google Scholar] [CrossRef]
- Del Maestro, A.; Rosenow, B.; Sachdev, S. From stripe to checkerboard ordering of charge-density waves on the square lattice in the presence of quenched disorder. Phys. Rev. B 2006, 74, 024520. [Google Scholar] [CrossRef]
- Wróbel, P. Checkerboard or stripes: Hard-core bosons on the checkerboard lattice as a model of charge ordering in planar cuprates. Phys. Rev. B 2006, 74, 014507. [Google Scholar] [CrossRef]
- Zhao, H.-W.; Zha, G.-Q.; Zhou, S.-P. Checkerboard-pattern vortex with the long-range Coulomb interaction in underdoped high-temperature superconductors. New J. Phys. 2008, 10, 043047. [Google Scholar] [CrossRef]
- Annett, J.F. Unconventional superconductivity. Contemp. Phys. 1995, 36, 423–437. [Google Scholar] [CrossRef]
- Damascelli, A.; Hussain, Z.; Shen, Z.-X. Angle-resolved photoemission studies of the cuprate superconductors. Rev. Mod. Phys. 2003, 75, 473–541. [Google Scholar] [CrossRef]
- Markiewicz, R.S. STM checkerboards from crossed stripes: A static stripe model. Phys. Rev. B 2005, 71, 220504. [Google Scholar] [CrossRef]
- Lee, P.A. From high temperature superconductivity to quantum spin liquid: Progress in strong correlation physics. Rep. Prog. Phys. 2008, 71, 012501. [Google Scholar] [CrossRef]
- Tranquada, J.M.; Sternlieb, B.J.; Axe, J.D.; Nakamura, Y.; Uchida, S. Evidence for stripe correlations of spins and holes in copper oxide superconductors. Nature 1995, 375, 561–563. [Google Scholar] [CrossRef]
- Zachar, O.; Kivelson, S.A.; Emery, V.J. Landau theory of stripe phases in cuprates and nickelates. Phys. Rev. B 1998, 57, 1422–1426. [Google Scholar] [CrossRef]
- Caprara, S.; Castellani, C.; Di Castro, C.; Grilli, M.; Perali, A. Charge and spin inhomogeneity as a key to the physics of the high-Tc cuprates. Physica B 2000, 280, 196–200. [Google Scholar] [CrossRef]
- Kohsaka, Y.; Taylor, C.; Fujita, K.; Schmidt, A.; Lupien, C.; Hanaguri, T.; Azuma, M.; Takano, M.; Eisaki, H.; Takagi, H.; Uchida, S.; Davis, J.C. An intrinsic bond-centered electronic glass with unidirectional domains in underdoped cuprates. Science 2007, 315, 1380–1385. [Google Scholar] [CrossRef]
- Kivelson, S.A.; Bindloss, I.P.; Fradkin, E.; Oganesyan, V.; Tranquada, J.M.; Kapitulnik, A.; Howald, C. How to detect fluctuating stripes in the high-temperature superconductors. Rev. Mod. Phys. 2003, 75, 1201–1241. [Google Scholar] [CrossRef]
- Daou, R.; Chang, J.; LeBoeuf, D.; Cyr-Choinière, O.; Laliberté, F.; Doiron-Leyraud, N.; Ramshaw, B.J.; Liang, R.; Bonn, D.A.; Hardy, W.N.; Taillefer, L. Broken rotational symmetry in the pseudogap phase of a high-Tc superconductor. Nature 2010, 463, 519–522. [Google Scholar] [CrossRef] [PubMed]
- Fradkin, E.; Kivelson, S.A.; Lawler, M.J.; Eisenstein, J.P.; Mackenzie, A.P. Nematic Fermi fluids in condensed matter physics. Annu. Rev. Condens. Matter Phys. 2010, 1, 153–178. [Google Scholar] [CrossRef]
- Fradkin, E.; Kivelson, S.A. Electron nematic phases proliferate. Science 2010, 327, 155–156. [Google Scholar] [CrossRef] [PubMed]
- Nagaev, E.L. Ferromagnetic domains in a semiconducting antiferromagnet. Zh. Éksp. Teor. Fiz. 1968, 54, 228–238. [Google Scholar]
- Krivoglaz, M.A. Electron states near the phase transition point and in disordered systems. Fiz. Tverd. Tela 1969, 11, 2230–2240. [Google Scholar]
- Krivoglaz, M.A.; Karasevskii, A.I. Condensation in in the system of polarons or fluctuons with the formation of the nonhomogeneous state and peculiarities of conductance. Pis’ma Zh. Éksp. Teor. Fiz. 1974, 19, 454–457. [Google Scholar]
- Emery, V.J.; Kivelson, S.A. Frustrated electronic phase separation and high-temperature superconductors. Physica C 1993, 209, 597–621. [Google Scholar] [CrossRef]
- Emery, V.J.; Kivelson, S.A.; Tranquada, J.M. Stripe phases in high-temperature superconductors. Proc. Natl. Acad. Sci. USA 1999, 96, 8814–8817. [Google Scholar] [CrossRef]
- Carlson, E.W.; Emery, V.J.; Kivelson, S.A.; Orgad, D. Concepts in high temperature superconductivity. In Superconductivity. Vol. 2: Novel Superconductors; Bennemann, K.H., Ketterson, J.B., Eds.; Springer Verlag: Berlin, Germany, 2008; pp. 1225–1348. [Google Scholar]
- Chakravarty, S. Quantum oscillations and key theoretical issues in high temperature superconductors from the perspective of density waves. Rep. Prog. Phys. 2011, 74, 022501. [Google Scholar] [CrossRef]
- Halperin, B.I.; Rice, T.M. The excitonic state at the semiconductor-semimetal transition. Solid State Phys. 1968, 21, 115–192. [Google Scholar]
- Hanaguri, T.; Lupien, C.; Kohsaka, Y.; Lee, D.-H.; Azuma, M.; Takano, M.; Takagi, H.; Davis, J.C. A “checkerboard" electronic crystal state in lightly hole-doped Ca2−xNaxCuO2Cl2. Nature 2004, 430, 1001–1005. [Google Scholar] [CrossRef] [PubMed]
- Shen, K.M.; Ronning, F.; Lu, D.H.; Baumberger, F.; Ingle, N.J.C.; Lee, W.S.; Meevasana, W.; Kohsaka, Y.; Azuma, M.; Takano, M.; Takagi, H.; Shen, Z.-X. Nodal quasiparticles and antinodal charge ordering in Ca2−xNaxCuO2Cl2. Science 2005, 307, 901–904. [Google Scholar] [CrossRef] [PubMed]
- Hoffman, J.E.; Hudson, E.W.; Lang, K.M.; Madhavan, V.; Eisaki, H.; Uchida, S.; Davis, J.C. A four unit cell periodic pattern of quasi-particle states surrounding vortex cores in Bi2Sr2CaCu2O8+δ. Science 2002, 295, 466–469. [Google Scholar] [CrossRef] [PubMed]
- Hoffman, J.E.; McElroy, K.; Lee, D.-H.; Lang, K.M.; Eisaki, H.; Uchida, S.; Davis, J.C. Imaging quasiparticle interference in Bi2Sr2CaCu2O8+δ. Science 2002, 297, 1148–1151. [Google Scholar] [CrossRef] [PubMed]
- Vershinin, M.; Misra, S.; Ono, S.; Ando, Y.A.Y.; Yazdani, A. Local ordering in the pseudogap state of the high-Tc superconductor Bi2Sr2CaCu2O8+δ. Science 2004, 303, 1995–1998. [Google Scholar] [CrossRef] [PubMed]
- Fang, A.; Howald, C.; Kaneko, N.; Greven, M.; Kapitulnik, A. Periodic coherence-peak height modulations in superconducting Bi2Sr2CaCu2O8+δ. Phys. Rev. B 2004, 70, 214514. [Google Scholar] [CrossRef]
- Hashimoto, A.; Momono, N.; Oda, M.; Ido, M. Scanning tunneling microscopy and spectroscopy study of 4a x 4a electronic charge order and the inhomogeneous pairing gap in superconducting Bi2Sr2CaCu2O8+δ. Phys. Rev. B 2006, 74, 064508. [Google Scholar] [CrossRef]
- Ma, J.-H.; Pan, Z.-H.; Niestemski, F.C.; Neupane, M.; Xu, Y.-M.; Richard, P.; Nakayama, K.; Sato, T.; Takahashi, T.; Luo, H.-Q.; Fang, L.; Wen, H.-H.; Wang, Z.; Ding, H.; Madhavan, V. Coexistence of competing orders with two energy gaps in real and momentum space in the high temperature superconductor Bi2Sr2−xLaxCuO6+δ. Phys. Rev. Lett. 2008, 101, 207002. [Google Scholar] [CrossRef]
- Fink, J.; Schierle, E.; Weschke, E.; Geck, J.; Hawthorn, D.; Soltwisch, V.; Wadati, H.; Wu, H.-H.; Dürr, H.A.; Wizent, N.; Büchner, B.; Sawatzky, G.A. Charge ordering in La1.8−xEu0.2SrxCuO4 studied by resonant soft x-ray diffraction. Phys. Rev. B 2009, 79, 100502. [Google Scholar] [CrossRef]
- Fink, J.; Soltwisch, V.; Geck, J.; Schierle, E.; Weschke, E.; Büchner, B. Phase diagram of charge order in La1.8−xEu0.2SrxCuO4 from resonant soft x-ray diffraction. Phys. Rev. B 2011, 83, 092503. [Google Scholar] [CrossRef]
- Li, X.M.; Li, F.H.; Luo, H.Q.; Fang, L.; Wen, H.-H. Transmission electron microscopy study of one-dimensional incommensurate structural modulation in superconducting oxides Bi2+xSr2−xCuO6+δ (0.10 ≤ x ≤ 0.40). Supercond. Sci. Technol. 2009, 22, 065003. [Google Scholar] [CrossRef]
- Sugimoto, A.; Kashiwaya, S.; Eisaki, H.; Yamaguchi, H.; Oka, K.; Kashiwaya, H.; Tsuchiura, H.; Tanaka, Y. Correlation between modulation structure and electronic inhomogeneity on Pb-doped Bi-2212 single crystals. Physica C 2005, 426–431, 390–395. [Google Scholar] [CrossRef]
- Bianconi, A.; Lusignoli, M.; Saini, N.L.; Bordet, P.; Kvick, A.; Radaelli, P.G. Stripe structure of the CuO2 plane in Bi2Sr2CaCu2O8+y by anomalous x-ray diffraction. Phys. Rev. B 1996, 54, 4310–4314. [Google Scholar] [CrossRef]
- Castellan, J.P.; Gaulin, B.D.; Dabkowska, H.A.; Nabialek, A.; Gu, G.; Liu, X.; Islam, Z. Two- and three-dimensional incommensurate modulation in optimally-doped Bi2Sr2CaCu2O8+δ. Phys. Rev. B 2006, 73, 174505. [Google Scholar] [CrossRef]
- LeBoeuf, D.; Doiron-Leyraud, N.; Vignolle, B.; Sutherland, M.; Ramshaw, B.J.; Levallois, J.; Daou, R.; Laliberté, F.; Cyr-Choinière, O.; Chang, J.; Jo, Y.J.; Balicas, L.; Liang, R.; Bonn, D.A.; Hardy, W.N.; Proust, C.; Taillefer, L. Lifshitz critical point in the cuprate superconductor YBa2Cu3Oy from high-field Hall effect measurements. Phys. Rev. B 2011, 83, 054506. [Google Scholar] [CrossRef]
- Vojta, M. Picking the cuprates’ Fermi pockets. Physics 2011, 4. [Google Scholar] [CrossRef]
- Uchida, M.; Ishizaka, K.; Hansmann, P.; Kaneko, Y.; Ishida, Y.; Yang, X.; Kumai, R.; Toschi, A.; Onose, Y.; Arita, R.; et al. Pseudogap of metallic layered nickelate R2−xSrxNiO4 (R = Nd, Eu) crystals measured using angle-resolved photoemission spectroscopy. Phys. Rev. Lett. 2011, 106, 027001. [Google Scholar] [CrossRef]
- Wilson, J.A.; Di Salvo, F.J.; Mahajan, S. Charge-density waves and superlattices in the metallic layered transition metal dichalcogenides. Adv. Phys. 1975, 24, 117–201. [Google Scholar] [CrossRef]
- Borisenko, S.V.; Kordyuk, A.A.; Yaresko, A.; Zabolotnyy, V.B.; Inosov, D.S.; Schuster, R.; Büchner, B.; Weber, R.; Follath, R.; Patthey, L.; Berger, H. Pseudogap and charge density waves in two dimensions. Phys. Rev. Lett. 2008, 100, 196402. [Google Scholar] [CrossRef]
- Inosov, D.S.; Zabolotnyy, V.B.; Evtushinsky, D.V.; Kordyuk, A.A.; Büchner, B.; Follath, R.; Berger, H.; Borisenko, S.V. Fermi surface nesting in several transition metal dichalcogenides. New J. Phys. 2008, 10, 125027. [Google Scholar] [CrossRef]
- Borisenko, S.V.; Kordyuk, A.A.; Zabolotnyy, V.B.; Inosov, D.S.; Evtushinsky, D.; Büchner, B.; Yaresko, A.N.; Varykhalov, A.; Follath, R.; Eberhardt, W.; Patthey, L.; Berger, H. Two energy gaps and Fermi-surface “arcs" in NbSe2. Phys. Rev. Lett. 2009, 102, 166402. [Google Scholar] [CrossRef] [PubMed]
- Inosov, D.S.; Evtushinsky, D.V.; Zabolotnyy, V.B.; Kordyuk, A.A.; Büchner, B.; Follath, R.; Berger, H.; Borisenko, S.V. Temperature-dependent Fermi surface of 2H-TaSe2 driven by competing density wave order fluctuations. Phys. Rev. B 2009, 79, 125112. [Google Scholar] [CrossRef]
- Klemm, R.A. Striking similarities between the pseudogap phenomena in cuprates and in layered organic and dichalcogenide superconductors. Physica C 2000, 341–348, 839–842. [Google Scholar] [CrossRef]
- Lee, P.A.; Rice, T.M.; Anderson, P.W. Fluctuation effects at a Peierls transition. Phys. Rev. Lett. 1973, 31, 462–465. [Google Scholar] [CrossRef]
- Bulaevskii, L.N. Structural (Peierls) transition in quasi-one-dimensional crystals. Usp. Fiz. Nauk 1975, 115, 263–300. [Google Scholar] [CrossRef]
- Brazovskii, S.A.; Matveenko, S.I. Pseudogaps in incommensurate charge density waves and one-dimensional semiconductors. Zh. Éksp. Teor. Fiz. 2003, 123, 625–634. [Google Scholar] [CrossRef]
- Gabovich, A.M.; Medvedev, V.A.; Moiseev, D.P.; Motuz, A.A.; Prikhot’ko, A.F.; Prokopovich, L.V.; Solodukhin, A.V.; Khirunenko, L.I.; Shinkarenko, V.K.; Shpigel, A.S.; Yachmenev, V.E. Superconductivity and temperature anomalies of crystal lattice properties for metaloxide La1.8Ba0.2CuO4-y. Fiz. Nizk. Temp. 1987, 13, 844–847. [Google Scholar]
- Gabovich, A.M. Partial Dielectrization Model for Oxide Superconductivity. In High-Tc Superconductivity, Experiment and Theory; Davydov, A.S., Loktev, V.M., Eds.; Springer Verlag: Berlin, Germany, 1992; pp. 161–169. [Google Scholar]
- Eremin, I.; Eremin, M. CDW as a possible reason for the pseudogap in the normal state of high-Tc cuprates. J. Supercond. 1997, 10, 459–460. [Google Scholar] [CrossRef]
- Ekino, T.; Sezaki, Y.; Fujii, H. Features of the energy gap above Tc in Bi2Sr2CaCu2O8+δ as seen by break-junction tunneling. Phys. Rev. B 1999, 60, 6916–6922. [Google Scholar] [CrossRef]
- Demsar, J.; Hudej, R.; Karpinski, J.; Kabanov, V.V.; Mihailovic, D. Quasiparticle dynamics and gap structure in HgBa2Ca2Cu3O8+δ investigated with femtosecond spectroscopy. Phys. Rev. B 2001, 63, 054519. [Google Scholar] [CrossRef]
- Le Tacon, M.; Sacuto, A.; Georges, A.; Kotliar, G.; Gallais, Y.; Colson, D.; Forget, A. Two energy scales and two distinct quasiparticle dynamics in the superconducting state of underdoped cuprates. Nat. Phys. 2006, 2, 537–543. [Google Scholar] [CrossRef]
- Tanaka, K.; Lee, W.S.; Lu, D.H.; Fujimori, A.; Fujii, T.; Risdiana; Terasaki, I.; Scalapino, D.J.; Devereaux, T.P.; Hussain, Z.; Shen, Z.-X. Distinct Fermi-momentum-dependent energy gaps in deeply underdoped Bi2212. Science 2006, 314, 1910–1913. [Google Scholar] [CrossRef]
- Das, T.; Markiewicz, R.S.; Bansil, A. Competing order scenario of two-gap behavior in hole-doped cuprates. Phys. Rev. B 2008, 77, 134516. [Google Scholar] [CrossRef]
- Lee, W.S.; Vishik, I.M.; Lu, D.H.; Shen, Z.-X. A brief update of angle-resolved photoemission spectroscopy on a correlated electron system. J. Phys. Condens. Matter 2009, 21, 164217. [Google Scholar] [CrossRef] [PubMed]
- Kordyuk, A.A.; Borisenko, S.V.; Zabolotnyy, V.B.; Schuster, R.; Inosov, D.S.; Evtushinsky, D.V.; Plyushchay, A.I.; Follath, R.; Varykhalov, A.; Patthey, L.; Berger, H. Nonmonotonic pseudogap in high-Tc cuprates. Phys. Rev. B 2009, 79, 020504. [Google Scholar] [CrossRef]
- Teague, M.L.; Beyer, A.D.; Grinolds, M.S.; Lee, S.I.; Yeh, N.-C. Observation of vortices and hidden pseudogap from scanning tunneling spectroscopic studies of the electron-doped cuprate superconductor Sr0.9La0.1CuO2. Europhys. Lett. 2009, 85, 17004. [Google Scholar] [CrossRef]
- Seibold, G.; Grilli, M.; Lorenzana, J. Dynamics of electronic inhomogeneities in cuprates. J. Supercond. 2011, 24, 1177–1179. [Google Scholar] [CrossRef]
- Emery, V.J.; Kivelson, S.A. Importance of phase fluctuations in superconductors with small superfluid density. Nature 1995, 374, 434–437. [Google Scholar] [CrossRef]
- Norman, M.; Pines, D.; Kallin, C. The pseudogap: Friend or foe of high Tc? Adv. Phys. 2005, 54, 715–733. [Google Scholar] [CrossRef]
- Chen, Q.; Stajic, J.; Tan, S.; Levin, K. BCS-BEC crossover: From high temperature superconductors to ultracold superfluids. Phys. Rep. 2005, 412, 188. [Google Scholar] [CrossRef]
- Valla, T.; Fedorov, A.V.; Lee, J.; Davis, J.C.; Gu, G.D. The ground state of the pseudogap in cuprate superconductors. Science 2006, 314, 1914–1916. [Google Scholar] [CrossRef] [PubMed]
- Kanigel, A.; Chatterjee, U.; Randeria, M.; Norman, M.R.; Souma, S.; Shi, M.; Li, Z.Z.; Raffy, H.; Campuzano, J.C. Protected nodes and the collapse of Fermi arcs in high-Tc cuprate superconductors. Phys. Rev. Lett. 2007, 99, 157001. [Google Scholar] [CrossRef] [PubMed]
- Kanigel, A.; Chatterjee, U.; Randeria, M.; Norman, M.R.; Koren, G.; Kadowaki, K.; Campuzano, J.C. Evidence for pairing above the transition temperature of cuprate superconductors from the electronic dispersion in the pseudogap phase. Phys. Rev. Lett. 2008, 101, 137002. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.-B.; Rameau, J.D.; Johnson, P.D.; Valla, T.; Tsvelik, A.; Gu, G.D. Emergence of preformed Cooper pairs from the doped Mott insulating state in Bi2Sr2CaCu2O8+δ. Nature 2008, 456, 77–80. [Google Scholar] [CrossRef]
- Shi, M.; Chang, J.; Pailhés, S.; Norman, M.R.; Campuzano, J.C.; Månsson, M.; Claesson, T.; Tjernberg, O.; Bendounan, A.; Patthey, L.; Momono, N.; Oda, M.; Ido, M.; Mudry, C.; Mesot, J. Coherent d-wave superconducting gap in underdoped La2−xSrxCuO4 by angle-resolved photoemission spectroscopy. Phys. Rev. Lett. 2008, 101, 047002. [Google Scholar] [CrossRef]
- Hüfner, S.; Müller, F. Temperature dependence of the gaps of high-temperature superconductors in the Fermi-arc region. Phys. Rev. B 2008, 78, 014521. [Google Scholar] [CrossRef]
- Hüfner, S.; Hossain, M.A.; Damascelli, A.; Sawatzky, G.A. Two gaps make a high-temperature superconductor? Rep. Prog. Phys. 2008, 71, 062501. [Google Scholar] [CrossRef]
- Meng, J.; Zhang, W.; Liu, G.; Zhao, L.; Liu, H.; Jia, X.; Lu, W.; Dong, X.; Wang, G.; Zhang, H.; et al. Monotonic d-wave superconducting gap of the optimally doped Bi2Sr1.6La0.4CuO6 superconductor by laser-based angle-resolved photoemission spectroscopy. Phys. Rev. B 2009, 79, 024514. [Google Scholar] [CrossRef]
- Krasnov, V.M. Interlayer tunneling spectroscopy of Bi2Sr2CaCu2O8+δ: a look from inside on the doping phase diagram of high Tc superconductors. Phys. Rev. B 2002, 65, 140504. [Google Scholar] [CrossRef]
- Chia, E.E.M.; Zhu, J.-X.; Talbayev, D.; Averitt, R.D.; Taylor, A.J.; Oh, K.-H.; Jo, I.-S.; Lee, S.-I. Observation of competing order in a high-Tc superconductor using femtosecond optical pulses. Phys. Rev. Lett. 2007, 99, 147008. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, K.; Lee, W.S.; Hussain, Z.; Shen, Z.X. Direct evidence of two gaps in underdoped Bi2212. J. Phys. Conf. Ser. 2008, 108, 012014. [Google Scholar] [CrossRef]
- Kondo, T.; Khasanov, R.; Takeuchi, T.; Schmalian, J.; Kaminski, A. Competition between the pseudogap and superconductivity in the high-Tc copper oxides. Nature 2009, 457, 296–300. [Google Scholar] [CrossRef] [PubMed]
- Hashimoto, M.; Yoshida, T.; Fujimori, A.; Li, D.H.; Shen, Z.-X.; Kubota, M.; Ono, K.; Ishikado, M.; Fujita, K.; Uchida, S. Effects of out-of-plane disorder on the nodal quasiparticle and superconducting gap in single-layer Bi2Sr1.6L0.4CuO6+δ (L = La,Nd,Gd). Phys. Rev. B 2009, 79, 144517. [Google Scholar] [CrossRef]
- Krasnov, V.M.; Kovalev, A.E.; Yurgens, A.; Winkler, D. Magnetic field dependence of the superconducting gap and the pseudogap in Bi2212 and HgBr2-Bi2212, studied by intrinsic tunneling spectroscopy. Phys. Rev. Lett. 2001, 86, 2657–2660. [Google Scholar] [CrossRef] [PubMed]
- Bondar’, A.V.; Ryabchenko, S.M.; Fedotov, Yu.V.; Motuz, A.A. Temperature dependence anomalies of nuclear relaxation for nuclei 63Cu in YBa2Cu3O7−x. Pis’ma Zh. Éksp. Teor. Fiz. 1989, 50, 133–134. [Google Scholar]
- Krämer, S.; Mehring, M. Low-temperature charge ordering in the superconducting state of YBa2Cu3O7−δ. Phys. Rev. Lett. 1999, 83, 396–399. [Google Scholar] [CrossRef]
- Moncton, D.E.; Axe, J.D.; DiSalvo, F.J. Neutron scattering study of charge-density wave transitions in 2H-TaSe2 and 2H-NbSe2. Phys. Rev. B 1977, 16, 801–819. [Google Scholar] [CrossRef]
- He, R.-H.; Tanaka, K.; Mo, S.-K.; Sasagawa, T.; Fujita, M.; Adachi, T.; Mannella, N.; Yamada, K.; Koike, Y.; Hussain, Z.; Shen, Z.-H. Energy gaps in the failed high-Tc superconductor La1.875Ba0.125CuO4. Nat. Phys. 2009, 5, 119–123. [Google Scholar] [CrossRef]
- Okada, Y.; Kawaguchi, T.; Ohkawa, M.; Ishizaka, K.; Takeuchi, T.; Shin, S.; Ikuta, H. Three energy scales characterizing the competing pseudogap state, the incoherent, and the coherent superconducting state in high-Tc cuprates. Phys. Rev. B 2011, 83, 104502. [Google Scholar] [CrossRef]
- Machida, K. Spin density wave and superconductivity in highly anisotropic materials. J. Phys. Soc. Jpn. 1981, 50, 2195–2202. [Google Scholar] [CrossRef]
- Machida, K.; Matsubara, T. Spin density wave and superconductivity in highly anisotropic materials. II. Detailed study of phase transitions. J. Phys. Soc. Jpn. 1981, 50, 3231–3239. [Google Scholar] [CrossRef]
- Machida, K. Spin density wave and superconductivity in highly anisotropic materials. III. Energy gap structure and non-magnetic impurity effects. J. Phys. Soc. Jpn. 1982, 51, 1420–1427. [Google Scholar] [CrossRef]
- Gabovich, A.M.; Moiseev, D.P. Metalloxide superconductor BaPb1−xBixO3: Unusual properties and new applications. Usp. Fiz. Nauk 1986, 150, 599–623. [Google Scholar] [CrossRef]
- Ishida, Y.; Shimojima, T.; Ishizaka, K.; Kiss, T.; Okawa, M.; Togashi, T.; Watanabe, S.; Wang, X.-Y.; Chen, C.-T.; Kamihara, Y.; Hirano, M.; Hosono, H.; Shin, S. Temperature-dependent pseudogap in the oxypnictides LaFeAsO1−xFx and LaFePO1−xFx seen via angle-integrated photoemission. Phys. Rev. B 2009, 79, 060503. [Google Scholar] [CrossRef]
- Mertelj, T.; Kabanov, V.V.; Gadermaier, C.; Zhigadlo, N.D.; Katrych, S.; Karpinski, J.; Mihailovic, D. Distinct pseudogap and quasiparticle relaxation dynamics in the superconducting state of nearly optimally doped SmFeAsO0.8F0.2 single crystals. Phys. Rev. Lett. 2009, 102, 117002. [Google Scholar] [CrossRef] [PubMed]
- Zabolotnyy, V.B.; Inosov, D.S.; Evtushinsky, D.V.; Koitzsch, A.; Kordyuk, A.A.; Sun, G.L.; Park, J.T.; Haug, D.; Hinkov, V.; Boris, A.V.; et al. (π, π) electronic order in iron arsenide superconductors. Nature 2009, 457, 569–572. [Google Scholar] [CrossRef] [PubMed]
- Littlewood, P.B.; Heine, V. The effect of electron-electron interactions on the Peierls transition in metals with strong nesting of Fermi surfaces. J. Phys. C 1981, 14, 2943–2949. [Google Scholar] [CrossRef]
- Mazin, I.I.; Schmalian, J. Pairing symmetry and pairing state in ferropnictides: Theoretical overview. Physica C 2009, 469, 614–627. [Google Scholar] [CrossRef]
- Rotter, M.; Tegel, M.; Johrendt, D.; Schellenberg, I.; Hermes, W.; Pöttgen, R. Spin-density-wave anomaly at 140 K in the ternary iron arsenide BaFe2As2. Phys. Rev. B 2008, 78, 020503. [Google Scholar] [CrossRef]
- Pickett, W.E. Electronic structure of the high-temperature oxide superconductors. Rev. Mod. Phys. 1989, 61, 433–512. [Google Scholar] [CrossRef]
- Volkov, B.A. Structural and magnetic transformations in narrow-gap semiconductors and semimetals. Trudy Fiz. Inst. Akad. Nauk SSSR 1978, 104, 3–57. [Google Scholar]
- Littlewood, P.B. Collective modes and superconductivity in an extended Hubbard model for copper oxide superconductors. Phys. Rev. B 1990, 42, 10075–10089. [Google Scholar] [CrossRef]
- Grüner, G. Density Waves in Solids; Addison-Wesley Publishing Company: Reading, MA, USA, 1994; p. 259. [Google Scholar]
- van Wezel, J.; Nahai-Williamson, P.; Saxena, S.S. Exciton-phonon interactions and superconductivity bordering charge order in TiSe2. Phys. Rev. B 2011, 83, 024502. [Google Scholar] [CrossRef]
- Morosan, E.; Zandbergen, H.W.; Dennis, B.S.; Bos, J.W.G.; Onose, Y.; Klimczuk, T.; Ramirez, A.P.; Ong, N.P.; Cava, R.J. Superconductivity in CuxTiSe2. Nat. Phys. 2006, 2, 544–550. [Google Scholar] [CrossRef]
- Kusmartseva, A.F.; Sipos, B.; Berger, H.; Forró, L.; Tutiš, E. Pressure induced superconductivity in pristine 1T-TiSe2. Phys. Rev. Lett. 2009, 103, 236401. [Google Scholar] [CrossRef]
- Won, H.; Maki, K. d-wave superconductor as a model of high-Tc superconductors. Phys. Rev. B 1994, 49, 1397–1402. [Google Scholar] [CrossRef]
- Maki, K.; Won, H. Why d-wave superconductivity? J. Phys. I (Paris) 1996, 6, 2317–2326. [Google Scholar] [CrossRef]
- Pickett, W.E.; Krakauer, H.; Cohen, R.E.; Singh, D.J. Fermi surfaces, Fermi liquids, and high-temperature superconductors. Science 1992, 255, 46–54. [Google Scholar] [CrossRef]
- Markiewicz, R.S.; Sahrakorpi, S.; Lindroos, M.; Lin, H.; Bansil, A. One-band tight-binding model parametrization of the high-Tc cuprates including the effect of kz dispersion. Phys. Rev. B 2005, 72, 054519. [Google Scholar] [CrossRef]
- Abrikosov, A.A.; Gor’kov, L.P.; Dzyaloshinskii, I.E. Methods of Quantum Field Theory in Statistical Physics; Prentice Hall: Englewood Cliffs, NJ, USA, 1963. [Google Scholar]
- Mühlschlegel, B. Die thermodynamischen Funktionen des Supraleiters. Z. Phys. 1959, 155, 313–327. [Google Scholar] [CrossRef]
- Loram, J.W.; Mirza, K.A.; Cooper, J.R.; Tallon, J.L. Superconducting and normal state energy gaps in Y0.8Ca0.2Ba2Cu3O7−δ from the elctronic specific heat. Physica C 1997, 282–287, 1405–1406. [Google Scholar] [CrossRef]
- Williams, G.V.M.; Tallon, J.L.; Haines, E.M.; Michalak, R.; Dupree, R. NMR evidence for a d-wave normal-state pseudogap. Phys. Rev. Lett. 1997, 78, 721–724. [Google Scholar] [CrossRef]
- Trunin, M.R.; Nefyodov, Yu.A.; Shevchun, A.F. Superfluid density in the underdoped YBa2Cu3O7−x: Evidence for d-density-wave order of the pseudogap. Phys. Rev. Lett. 2004, 92, 067006. [Google Scholar] [CrossRef] [PubMed]
- Kurosawa, T.; Yoneyama, T.; Takano, Y.; Hagiwara, M.; Inoue, R.; Hagiwara, N.; Kurusu, K.; Takeyama, K.; Momono, N.; Oda, M.; Ido, M. Large pseudogap and nodal superconducting gap in Bi2Sr2−xLaxCuO6+δ and Bi2Sr2CaCu2O8+δ: Scanning tunneling microscopy and spectroscopy. Phys. Rev. B 2010, 81, 094519. [Google Scholar] [CrossRef]
- Dahm, T.; Manske, D.; Tewordt, L. Charge-density-wave and superconductivity d-wave gaps in the Hubbard model for underdoped high-Tc cuprates. Phys. Rev. B 1997, 56, 11419–11422. [Google Scholar] [CrossRef]
- Kim, W.; Zhu, J.-X.; Carbotte, J.P.; Ting, C.S. c-axis response of a high-Tc superconductor with d-density-wave order. Phys. Rev. B 2002, 65, 064502. [Google Scholar] [CrossRef]
- Morr, D.K. A hidden order in the cuprate superconductors: The d-density-wave phase. J. Supercond. 2003, 16, 487–490. [Google Scholar] [CrossRef]
- Andersen, B.M. Two nonmagnetic impurities in the d-wave-superconducting and d-density-wave states of the cuprate superconductors as a probe for the pseudogap. Phys. Rev. B 2003, 68, 094518. [Google Scholar] [CrossRef]
- Oganesyan, V.; Ussishkin, I. Nernst effect, quasiparticles, and d-density waves in cuprates. Phys. Rev. B 2004, 70, 054503. [Google Scholar] [CrossRef]
- Andrenacci, N.; Angilella, G.G.N.; Beck, H.; Pucci, R. Linear response theory around a localized impurity in the pseudogap regime of an anisotropic superconductor: Precursor pairing versus d-density-wave scenario. Phys. Rev. B 2004, 70, 024507. [Google Scholar] [CrossRef]
- Ghosh, A. DDW Order and Its Role in Cuprates. In Progress in Superconductivity Research; Chang, O.A., Ed.; Nova Science: New York, NY, USA, 2008; pp. 123–162. [Google Scholar]
- Zhang, C.; Tewari, S.; Chakravarty, S. Quasiparticle Nernst effect in the cuprate superconductors from the d-density-wave theory of the pseudogap phase. Phys. Rev. B 2010, 81, 104517. [Google Scholar] [CrossRef]
- Ha, K.; Subok, R.; Ilmyong, R.; Cheongsong, K.; Yuling, F. Superconductivity enhanced by d-density wave: A weak-coupling theory. Physica B 2011, 406, 1459–1465. [Google Scholar] [CrossRef]
- Scalapino, D.J. The case for dx2−y2 pairing in the cuprate superconductors. Phys. Rep. 1995, 250, 329–365. [Google Scholar] [CrossRef]
- Leggett, A.J. Quantum Liquids: Bose Condensation and Cooper Pairing in Condensed-Matter Systems; University Press: Oxford, UK, 2006; p. 388. [Google Scholar]
- Pereg-Barnea, T.; Weber, H.; Refael, G.; Franz, M. Quantum oscillations from Fermi arcs. Nat. Phys. 2010, 6, 44–49. [Google Scholar] [CrossRef]
- Hoffman, J.E. To pair or not to pair? Nat. Phys. 2010, 6, 404–405. [Google Scholar] [CrossRef]
- Annett, J.F. Superconductivity, Superfluids and Condensates; University Press: Oxford, UK, 2004; p. 186. [Google Scholar]
- Hackl, A.; Vojta, M.; Sachdev, S. Quasiparticle Nernst effect in stripe-ordered cuprates. Phys. Rev. B 2010, 81, 045102. [Google Scholar] [CrossRef]
- Yang, K.; Sondhi, S.L. Response of a dx2−y2 superconductor to a Zeeman magnetic field. Phys. Rev. B 1998, 57, 8566–8570. [Google Scholar] [CrossRef]
- Jérome, D.; Berthier, C.; Molinié, P.; Rouxel, J. Electronic properties of transition metal dichalcogenides: Connection between structural instabilities and superconductivity. J. Phys. (Paris) Colloq. 1976, 37, C125–C135. [Google Scholar] [CrossRef]
- Bud’ko, S.L.; Canfield, P.C.; Morosan, E.; Cava, R.J.; Schmiedeshoff, G.M. Thermal expansion and effect of pressure on superconductivity in CuxTiSe2. J. Phys. Condens. Matter 2007, 19, 176230. [Google Scholar] [CrossRef]
- Graf, D.; Brooks, J.S.; Almeida, M.; Dias, J.C.; Uji, S.; Terashima, T.; Kimata, M. Evolution of superconductivity from a charge-density-wave ground state in pressurized (Per)2[Au(mnt)2]. Europhys. Lett. 2009, 85, 27009. [Google Scholar] [CrossRef]
- Hamlin, J.J.; Zocco, D.A.; Sayles, T.A.; Maple, M.B.; Chu, J.-H.; Fisher, I.R. Pressure-induced superconducting phase in the charge-density-wave compound terbium tritelluride. Phys. Rev. Lett. 2009, 102, 177002. [Google Scholar] [CrossRef] [PubMed]
- Takeshita, N.; Sasagawa, T.; Sugioka, T.; Tokura, Y.; Takagi, H. Gigantic anisotropic uniaxial pressure effect on superconductivity within the CuO2 plane of La1.64Eu0.2Sr0.16CuO4: Strain control of stripe criticality. J. Phys. Soc. Jpn. 2004, 73, 1123–1126. [Google Scholar] [CrossRef]
- Gabovich, A.M.; Voitenko, A.I. Influence of inelastic quasiparticle scattering on thermodynamic and transport properties of high-Tc oxides. Physica C 1996, 258, 236–252. [Google Scholar] [CrossRef]
- Manske, D. Theory of Unconventional Superconductors. Cooper-Pairing Mediated by Spin Excitations; Springer Verlag: New York, NY, USA, 2004; p. 228. [Google Scholar]
- Abrikosov, A.A. Fundamentals of the Theory of Metals; North-Holland: Amsterdam, The Netherlands, 1988. [Google Scholar]
- de Llano, M.; Annett, J.F. Generalized Cooper pairing in superconductors. Int. J. Mod. Phys. B 2007, 21, 3657–3686. [Google Scholar] [CrossRef]
- Kondepudi, D.; Prigogine, I. Modern Thermodynamics. From Heat Engines to Dissipative Structures; John Wiley and Sons: Chichister, UK, 1999. [Google Scholar]
- Marsiglio, F.; Carbotte, J.P. Electron-Phonon Superconductivity. In Superconductivity. Vol. 1: Conventional and Unconventional Superconductors; Bennemann, K.H., Ketterson, J.B., Eds.; Springer Verlag: Berlin, Germany, 2008; pp. 73–162. [Google Scholar]
- Hasegawa, T.; Ikuta, H.; Kitazawa, K. Tunneling Spectroscopy of Oxide Superconductors. In Physical Properties of High Temperature Superconductors III; Ginsberg, D.M., Ed.; World Scientific: Singapore, 1992; pp. 525–630. [Google Scholar]
- Wei, J.Y.T.; Tsuei, C.C.; van Bentum, P.J.M.; Xiong, Q.; Chu, C.W.; Wu, M.K. Quasiparticle tunneling spectra of the high-Tc mercury cuprates: Implications of the d-wave two-dimensional van Hove scenario. Phys. Rev. B 1998, 57, 3650–3662. [Google Scholar] [CrossRef]
- Gomes, K.K.; Pasupathy, A.N.; Pushp, A.; Ono, S.; Ando, Y.; Yazdani, A. Visualizing pair formation on the atomic scale in the high-Tc superconductor Bi2Sr2CaCu2O8+δ. Nature 2007, 447, 569–572. [Google Scholar] [CrossRef]
- Geilikman, B.T.; Kresin, V.Z.; Masharov, N.F. Transition temperature and energy gap for superconductors with strong coupling. J. Low Temp. Phys. 1975, 18, 241–271. [Google Scholar] [CrossRef]
- Carbotte, J.P.; Jiang, C. Strong-coupling effects in d-wave superconductors. Phys. Rev. B 1993, 48, 4231–4234. [Google Scholar] [CrossRef]
- Miyakawa, N.; Guptasarma, P.; Zasadzinski, J.F.; Hinks, D.G.; Gray, K.E. Strong dependence of the superconducting gap on oxygen doping from tunneling measurements on Bi2Sr2CaCu2O8+δ. Phys. Rev. Lett. 1998, 80, 157–160. [Google Scholar] [CrossRef]
- Kulić, M.L. Interplay of electron-phonon interaction and strong correlations: The possible way to high-temperature superconductivity. Phys. Rep. 2000, 338, 1–264. [Google Scholar] [CrossRef]
- Izyumov, Yu.A.; Kurmaev, E.Z. Strongly electron-correlated materials. Usp. Fiz. Nauk 2008, 178, 25–60. [Google Scholar] [CrossRef]
- Alloul, H.; Bobroff, J.; Gabay, M.; Hirschfeld, P.J. Defects in correlated metals and superconductors. Rev. Mod. Phys. 2009, 81, 45–108. [Google Scholar] [CrossRef]
- Meng, J.-Q.; Brunner, M.; Kim, K.-H.; Lee, H.-G.; Lee, S.-I.; Wen, J.S.; Xu, Z.J.; Gu, G.D.; Gweon, G.-H. Momentum-space electronic structures and charge orders of the high-temperature superconductors Ca2−xNaxCuO2Cl2 and Bi2Sr2CaCu2O8+δ. Phys. Rev. B 2011, 84, 060513. [Google Scholar] [CrossRef]
- Schuster, H.G. Influence of dilute nonmagnetic impurities on the Peierls instability in one-dimensional conductors. Solid State Commun. 1974, 14, 127–129. [Google Scholar] [CrossRef]
- Zittartz, J. Theory of the excitonic insulator in the presence of normal impurities. Phys. Rev. 1967, 164, 575–582. [Google Scholar] [CrossRef]
- Whangbo, M.H.; Canadell, E.; Foury, P.; Pouget, J.P. Hidden Fermi surface nesting and charge density wave instability in low-dimensional metals. Science 1991, 252, 96–98. [Google Scholar] [CrossRef]
- Johannes, M.D.; Mazin, I.I. Fermi surface nesting and the origin of charge density waves in metals. Phys. Rev. B 2008, 77, 165135. [Google Scholar] [CrossRef]
- Raymond, S.; Bouchet, J.; Lander, G.H.; Le Tacon, M.; Garbarino, G.; Hoesch, M.; Rueff, J.-P.; Krisch, M.; Lashley, J.C.; Schulze, R.K.; Albers, R.C. Understanding the complex phase diagram of Uranium: The role of electron-phonon coupling. Phys. Rev. Lett. 2011, 107, 136401. [Google Scholar] [CrossRef]
- Weber, F.; Rosenkranz, S.; Castellan, J.-P.; Osborn, R.; Hott, R.; Heid, R.; Bohnen, K.-P.; Egami, T.; Said, A.H.; Reznik, D. Extended phonon collapse and the origin of the charge-density wave in 2H-NbSe2. Phys. Rev. Lett. 2011, 107, 107403. [Google Scholar] [CrossRef]
- Vedeneev, S.I.; Piot, B.A.; Maude, D.K. Magnetic field dependence of the superconducting energy gap in Bi2Sr2CaCu2O8+δ probed using break-junction tunneling spectroscopy. Phys. Rev. B 2010, 81, 054501. [Google Scholar] [CrossRef]
- Lubashevsky, Y.; Garg, A.; Sassa, Y.; Shi, M.; Kanigel, A. Insensitivity of the superconducting gap to variations in the critical temperature of Zn-substituted Bi2Sr2CaCu2O8+δ superconductors. Phys. Rev. Lett. 2011, 106, 047002. [Google Scholar] [CrossRef] [PubMed]
- Anderson, P.W. The Theory of Superconductivity in the High-Tc Cuprates; Princeton Univeristy Press: Princeton, NJ, USA, 1997; p. 446. [Google Scholar]
- Anderson, P.W.; Lee, P.A.; Randeria, M.; Rice, T.M.; Trivedi, N.; Zhang, F.C. The physics behind high-temperature superconducting cuprates: The “plain vanilla" version of RVB. J. Phys. Condens. Matter 2004, 16, R755–R769. [Google Scholar] [CrossRef]
- Alexandrov, A.S. High-temperature superconductivity: The explanation. Phys. Scr. 2011, 83, 038301. [Google Scholar] [CrossRef]
- Anderson, P.W. BCS: The scientific “love of my life”. Int. J. Mod. Phys. B 2010, 24, 3983–3998. [Google Scholar] [CrossRef]
- Zhao, G.M. The pairing mechanism of high-temperature superconductivity: Experimental constraints. Phys. Scr. 2011, 83, 038302. [Google Scholar] [CrossRef]
- Plakida, N.M. Comment on “The pairing mechanism of high-temperature superconductivity: Experimental constraints". Phys. Scr. 2011, 83, 038303. [Google Scholar] [CrossRef]
- Zhao, G.M. Reply to Comment on “The pairing mechanism of high-temperature superconductivity: Experimental constraints". Phys. Scr. 2011, 83, 038304. [Google Scholar] [CrossRef]
- Anderson, P.W. Personal history of my engagement with cuprate superconductivity, 1986–2010. Int. J. Mod. Phys. B 2011, 25, 1–39. [Google Scholar] [CrossRef]
- Alexandrov, A.S.; Kabanov, V.V. Unconventional high-temperature superconductivity from repulsive interactions: Theoretical constraints. Phys. Rev. Lett. 2011, 106, 136403. [Google Scholar] [CrossRef]
- Basov, D.N.; Chubukov, A.V. Manifesto for a higher Tc. Nat. Phys. 2011, 7, 272–276. [Google Scholar] [CrossRef]
- Norman, M.R. The challenge of unconventional superconductivity. Science 2011, 332, 196–200. [Google Scholar] [CrossRef] [PubMed]
- Ginzburg, V.L. Superconductivity: The day before yesterday, yesterday, today, to-morrow. Usp. Fiz. Nauk 2000, 170, 619–630. [Google Scholar] [CrossRef]
- Schmalian, J. Failed theories of superconductivity. Mod. Phys. Lett. B 2010, 24, 2679–2691. [Google Scholar] [CrossRef]
- Mazin, I. Iron superconductivity weathers another storm. Physics 2011, 4, 26. [Google Scholar] [CrossRef]








© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Ekino, T.; Gabovich, A.M.; Li, M.S.; Pękała, M.; Szymczak, H.; Voitenko, A.I. d-Wave Superconductivity and s-Wave Charge Density Waves: Coexistence between Order Parameters of Different Origin and Symmetry. Symmetry 2011, 3, 699-749. https://doi.org/10.3390/sym3040699
Ekino T, Gabovich AM, Li MS, Pękała M, Szymczak H, Voitenko AI. d-Wave Superconductivity and s-Wave Charge Density Waves: Coexistence between Order Parameters of Different Origin and Symmetry. Symmetry. 2011; 3(4):699-749. https://doi.org/10.3390/sym3040699
Chicago/Turabian StyleEkino, Toshikazu, Alexander M. Gabovich, Mai Suan Li, Marek Pękała, Henryk Szymczak, and Alexander I. Voitenko. 2011. "d-Wave Superconductivity and s-Wave Charge Density Waves: Coexistence between Order Parameters of Different Origin and Symmetry" Symmetry 3, no. 4: 699-749. https://doi.org/10.3390/sym3040699
APA StyleEkino, T., Gabovich, A. M., Li, M. S., Pękała, M., Szymczak, H., & Voitenko, A. I. (2011). d-Wave Superconductivity and s-Wave Charge Density Waves: Coexistence between Order Parameters of Different Origin and Symmetry. Symmetry, 3(4), 699-749. https://doi.org/10.3390/sym3040699



