Symmetry Aspects of the Band Structure and Motion Equations Applied in Calculating the Cyclotron Frequency of Electrons in Metals

Abstract

Cyclotron frequency of a crystal electron is, in general, not an easily accessible parameter. Nevertheless, its calculation can be simplified when the symmetry properties of the band structure and those of the motion equations in the magnetic field are simultaneously taken into account. In effect, a combined symmetry of the electron Hamiltonian and that of the Lorentz equation provide us with a non-linear oscillator problem of high symmetry. In the next step, the kinetic energy of the oscillator can be separated from the whole of electron energy and applied in a new kind of calculation of the cyclotron frequency which is much more simple than before. In consequence, a detailed approach to the electron circulation, also in more complex band structures, becomes a relatively easy task. For different crystal lattices of cubic symmetry taken as examples the cyclotron frequency of the present and a former method are compared numerically giving the same results.

1. Introduction. Outline of the Symmetry Properties Concerning the Crystal Electrons Moving in an External Magnetic Field

In theoretical physics one of the principal aims is to calculate the observed data with a possibly high accuracy. Simultaneously, another aim is that this approach to experiment should be of a not too complicated nature. In the solid state theory these two goals are strictly coupled together by the use of the properties of symmetry.

Conventionally, the symmetry in solids is connected with the crystal geometry given by a regular spatial arrangement of the atoms. This is a well-known simplification entering the potential part of the electron Hamiltonian. However, when an external field is acting on a crystal, much of the original symmetry due to the crystal potential is usually lost. In principle, this situation can lead to difficulties, see e.g., [1]. But if the potential perturbation, for example that of the magnetic field, is chosen in some special direction with respect to the crystal lattice, a loss of symmetry in the geometry of the crystal potential is—to a large extent—compensated by a new kind of symmetry, namely that connected with the dynamics of electrons moving in the magnetic field.

The purpose of the present paper is to demonstrate that this kind of symmetry, which can be next applied in calculating the cyclotron frequency in solids, is due to both the properties of the Lorentz equation governing the electron motion in the presence of the magnetic field and the wave-packet character of electrons contained in the band of states of a solid. The final effect of such a combination is a pair of equations much similar to a pair of the Hamilton equations possessed by a one-dimensional anharmonic oscillator. The variables of the oscillator, which can be associated with the components of the electron wave vector, have—on one hand—the symmetry properties of the dynamical variables of position and momentum of the oscillator. On the other hand, the remainder of the symmetry details are dictated by the crystal Hamiltonian.

In fact, the Hamilton equations coming from the band structure combined with the action of the magnetic field have been derived some time ago by Wannier [2] and Suhl [3]. But these equations were, in our opinion, not sufficiently exploited in describing the motion of the crystal electrons due to the presence of the magnetic field. An attempt to calculate the cyclotron resonance for such electrons has been done in [3], but it was limited to the s-electrons contained in only one, namely simple cubic, crystal lattice. The restriction is perhaps because the formalism applied in [3] to the simple cubic case could not be extended to other lattices. But the experimental interest is focused on crystals rather different than the simple cubic one, moreover the band structure is based on a different kind of the atomic orbits than s, see [4,5]. This provides us with a practical aim of the present paper to give a method directed to bridge a definite computational gap.

Cyclotron frequency $\Omega$ is a fundamental electron parameter entering practically almost any examination of a conducting solid at its Fermi surface in case when an external magnetic field is applied. This frequency is usually easy to assess when the surface is near to a spherical, or ellipsoidal, shape. For, in this very special circumstance, the influence of the crystalline background exerted on the electron states is rather small and the frequency formula is regulated mainly by a suitable choice of the effective electron mass, see e.g., [6]. An extremely simple example is that of free electrons (see below).

In general, when the motion is represented in the space of the wave vector $\overrightarrow{k}$, a conventional attempt is to calculate the planar area S enclosed by a trajectory of an electron having a constant energy in that space, and next differentiate that area with respect to the energy E possessed by the circulating electron. This gives the reciprocal value equal to the cyclotron frequency [6,7]:

$$\Omega =\frac{2\pi eB}{{\hslash }^{2}c}\frac{\partial E(\overrightarrow{k})}{\partial S(\overrightarrow{k})}$$

(1)

For free electrons we have $S=\pi k^2$ and $E=\frac{{\hslash }^2}{2m}{k}^2$, thus the frequency (1) becomes

$$\Omega =\frac{eB}{mc}$$

(2)

which is a well-known result. A characteristic point is that (2) is a constant independent of the electron energy and $\overrightarrow{k}$.

But a circulation of electrons in the crystal lattices does not provide us with so simple results. Consequently, in order to approach that problem in a possibly simple manner, a different formalism than that represented in (1) is applied. This takes into account not only the symmetry of the crystal Hamiltonian but also the properties of symmetry characteristic for the motion equations in the magnetic field.

2. The Formalism

A planar electron motion performed by an electron in a constant magnetic field $\overrightarrow{B}$ is governed by the Lorentz equation. Its essence is that if the action of an external electric field is negligible [8] we have

$$\hslash \frac{d\overrightarrow{k}}{dt}=\frac{e}{c}(\overrightarrow{v}\times \overrightarrow{B})$$

(3)

This equation describes the motion of the electron wave packet labeled by the wave vector $\overrightarrow{k}$ and having in a real space the velocity $\overrightarrow{v}$. It is valid for not too strong B, so the band structure is not essentially perturbed by its degeneracy into Landau levels. In fact, (3) is equivalent to a pair of the Hamilton equations of classical mechanics. This is so because for the field $\overrightarrow{B}$ directed, say, along the axis z, Equation (3) can be presented as an equation pair:

$$\hslash \frac{d{k}_x}{dt}=\frac{e}{c}{v}_y{B}_z$$

(4)

$$\hslash \frac{d{k}_y}{dt}=-\frac{e}{c}{v}_x{B}_z$$

(5)

The components $k_x$, $k_y$ of the wave vector behave in (4), (5) like position and momentum variables, say

$$x=k_x,p_x=k_y$$

(6)

because of the well-known property [7]

$$v_x=\frac{1}{\hslash }\frac{\partial E}{\partial k_x},v_y=\frac{1}{\hslash }\frac{\partial E}{\partial k_y}$$

(7)

where E is the electron energy. It should be noted that the one-electron Hamiltonians for crystals in the magnetic field based on the components of vector $\overrightarrow{k}$ seem to be developed first in [9].

For the sake of simplicity the constant parameters entering (3)–(7) can be abbreviated to

$$B_z=e=c=\hslash =m=1$$

(8)

with the substitutions (6) and (8), Equations (4) and (5) become:

$$\frac{dx}{dt}=\frac{\partial E}{\partial p_x}$$

(9)

$$\frac{d{p}_x}{dt}=-\frac{\partial E}{\partial x}$$

(10)

Equations (9) and (10) simplify essentially the problem, because the energy expressions $E(k_x,k_y)$ for an electron circulating in a $(k_x,k_y)$–-plane (component $k_z$ behaves like a constant parameter) are rather easily accessible quantities. For example, in the tight-binding approach to the s-electrons in cubic crystal lattices, we have the energies [10]

$$E^{\mathrm{sc}}=\beta [3-cos(k_x{a}_{\mathrm{latt}})-cos(k_y{a}_{\mathrm{latt}})-cos(k_z{a}_{\mathrm{latt}})]$$

(11)

for the simple cubic (sc) lattice the nearest neighbors of the central site in $(0,0,0)$ are here in positions $(\pm a_{\mathrm{latt}},0,0)$, $(0,\pm a_{\mathrm{latt}},0)$, $(0,0,\pm a_{\mathrm{latt}})$

$$E^{\mathrm{bcc}}=\beta 1-cos(k_x{a}_{\mathrm{latt}})cos(k_y{a}_{\mathrm{latt}})cos(k_z{a}_{\mathrm{latt}})$$

(12)

for the body-centered cubic (bcc) lattice the nearest neighbors are in positions $(\pm a_{\mathrm{latt}},\pm a_{\mathrm{latt}},\pm a_{\mathrm{latt}})$,

$$2E^{\mathrm{fcc}}=\beta \left[3-cos(k_x{a}_{\mathrm{latt}})cos(k_y{a}_{\mathrm{latt}})-cos(k_y{a}_{\mathrm{latt}})cos(k_z{a}_{\mathrm{latt}})-cos(k_z{a}_{\mathrm{latt}})cos(k_x{a}_{\mathrm{latt}})\right]$$

(13)

for the face centered cubic (fcc) lattice [the nearest neighbors of the central site are in positions $(\pm a_{\mathrm{latt}},\pm a_{\mathrm{latt}},0)$, $(0,\pm a_{\mathrm{latt}},\pm a_{\mathrm{latt}})$, $(\pm a_{\mathrm{latt}},0,\pm a_{\mathrm{latt}})$].

The $\beta$ are multiples of the hopping integrals ${\beta }^{\mathrm{latt}}$ between the nearest atomic neighbors in the crystal lattices, for example in the sc lattice $\beta =2{\beta }^{\mathrm{sc}}$, the $a_{\mathrm{latt}}$ is the edge length of the elementary cube of a crystal cell. The constant terms of 1 and 3 are introduced in order to make (11), (12) and (13) at small $k_x$, $k_y$ and $k_z$ proportional to the free-electron expression:

$$E^{\mathrm{free}}=\frac{\beta }{2}\left(k_x^2+k_y^2+k_z^2\right)a_{\mathrm{latt}}^2=\frac{\beta }{2}\left(x^2+p_x^2+k_z^2\right)a_{\mathrm{latt}}^2$$

(14)

In this case the constant term ${\hslash }^2/2m$ entering the free-electron energy in (1) is replaced by

$$\frac{\beta a_{\mathrm{latt}}^2}{2}$$

(15)

The parameter $\beta$ has dimension of energy. A substitution of (14) into (1) replaces the frequency (2) by

$$\Omega =\frac{eB}{c}\frac{\beta a_{\mathrm{latt}}^2}{{\hslash }^2}$$

(16)

In Section 3, Section 4, Section 5, Section 6, Section 7 and Section 8 we discuss and apply the Hamiltonian expressions of (11)–(13) assuming

$$\beta =a_{\mathrm{latt}}=1$$

(17)

3. Crystal Hamiltonians as the Oscillator Problems

When the motion is limited, for the sake of definiteness, to a plane

$$k_z=\mathrm{const}=0$$

(18)

the energies (11), (12) and (13) become, respectively, equivalent to the following Hamiltonian expressions

$$E^{\mathrm{sc}}(k_z=0)=C^{\mathrm{sc}}=2-cosx-cos{p}_x$$

(19)

$$E^{\mathrm{bcc}}(k_z=0)=C^{\mathrm{bcc}}=1-cosxcos{p}_x$$

(20)

$$2E^{\mathrm{fcc}}(k_z=0)=2C^{\mathrm{fcc}}=3-cosxcos{p}_x-cosx-cos{p}_x$$

(21)

on the condition that the substitutions presented in (6) and (17) are taken into account.

A characteristic point of (19)–(21) is that beyond the symmetry properties dictated by the crystal potential [see (11)–(13)], a supplementary symmetry in the dynamic variables x and $p_x$, namely that due to (9) and (10), occurs in the formalism. In effect of that symmetry, the Hamiltonians (19), (20) and (21) provide us with an anharmonic oscillator problem [11]. The oscillators of this kind are one-dimensional, because x and $p_x$ refer to the motion in a single dimension, say, that extended along the axis x. In consequence, the electron circulation along the edge of a planar cross-section area of the Fermi surface has been replaced by an oscillation between two opposite (symmetrical) points of the axis x:

$$x=-a_0,x=a_0$$

(22)

the axis is lying in a cross-section plane of the Fermi surface labeled by (18).

The distance $a_0$ in (22) is called the amplitude of the oscillator motion. A property of the oscillator is that when $x=k_x=\pm a_0$ we have $p_x=k_y=0$, and vice versa: for $x=k_x=0$ we have $p_x=k_y=\pm a_0$.

In course of its oscillatory motion the electron has a constant energy equal to that possessed by an electron circulating in the $(x,y)$-plane. Consequently, this energy can be considered, for the sake of simplicity, at some special points of the oscillator trajectory, for example those quoted in (22). The values of x, $p_x$ entering that points, when substituted into (19), (20) and (21), give respectively the planar Hamiltonians:

$$C^{\mathrm{sc}}=2-cosx-cos{p}_x=1-cos{a}_0=C^{\mathrm{sc}}(a_0)$$

(23)

$$C^{\mathrm{bcc}}=1-cosxcos{p}_x=1-cos{a}_0=C^{\mathrm{bcc}}(a_0)$$

(24)

$$2C^{\mathrm{fcc}}=3-cosxcos{p}_x-cosx-cos{p}_x=2(1-cos{a}_0)=2C^{\mathrm{fcc}}(a_0)$$

(25)

for each of the considered lattice cases. Our task becomes to calculate the oscillation frequencies for the electron motions represented by the Hamiltonians given in (23), (24) and (25).

4. Symmetry of Oscillators with Respect to the Dynamic Variables x and $p_x$ and Separation of Energy into the Kinetic and Potential Parts

A total electron energy of a one-dimensional oscillator is

$$\frac{1}{2}{\left(\frac{dx}{dt}\right)}^2+V(x)=C^{\mathrm{latt}}(a_0)$$

(26)

where the first term on the left-hand side is a kinetic energy, the second one is a potential energy, and $C^{\mathrm{latt}}(a_0)$ is a total energy of the oscillator which is a parameter constant in time. A differentiation of (26) with respect to time gives

$$\frac{dx}{dt}\frac{d^{2}x}{d{t}^2}+\frac{dV(x)}{dx}\frac{dx}{dt}=0$$

(27)

from which we obtain the well-known relation

$$\frac{d^{2}x}{d{t}^2}=-\frac{dV(x)}{dx}$$

(28)

The left-hand side of (28) can be easily calculated on the basis of the Hamilton equations presented in (9) and (10). These give the acceleration of x:

$$\begin{array}{cc}\hfill \frac{d^{2}x}{d{t}^2}=\frac{d}{dt}\left(\frac{\partial C^{\mathrm{latt}}}{\partial p_x}\right)& =\frac{{\partial }^2{C}^{\mathrm{latt}}}{\partial p_x\partial x}\frac{dx}{dt}+\frac{{\partial }^2{C}^{\mathrm{latt}}}{\partial p_x^2}\frac{d{p}_x}{dt}\hfill \\ & =\frac{{\partial }^2{C}^{\mathrm{latt}}}{\partial p_x\partial x}\frac{\partial C^{\mathrm{latt}}}{\partial p_x}-\frac{{\partial }^2{C}^{\mathrm{latt}}}{\partial p_x^2}\frac{\partial C^{\mathrm{latt}}}{\partial x}=a_x(x,p_x)\hfill \end{array}$$

(29)

Symmetrically, we have the acceleration of $p_x$:

$$\begin{array}{cc}\hfill \frac{d^2{p}_x}{d{t}^2}=\frac{d}{dt}\left(-\frac{\partial C^{\mathrm{latt}}}{\partial x}\right)& =-\frac{{\partial }^2{C}^{\mathrm{latt}}}{\partial x\partial p_x}\frac{d{p}_x}{dt}-\frac{{\partial }^2{C}^{\mathrm{latt}}}{\partial x^2}\frac{dx}{dt}\hfill \\ & =\frac{{\partial }^2{C}^{\mathrm{latt}}}{\partial x\partial p_x}\frac{\partial C^{\mathrm{latt}}}{\partial x}-\frac{{\partial }^2{C}^{\mathrm{latt}}}{\partial x^2}\frac{\partial C^{\mathrm{latt}}}{\partial p_x}=a_{p_x}(x,p_x)\hfill \end{array}$$

(30)

A characteristic point obtained from (30) and (31) is that

$$a_x(x,p_x)=a_{p_x}(p_x,x)$$

(31)

$$a_x(p_x,x)=a_{p_x}(x,p_x)$$

(32)

The Expressions (29)–(30) can be calculated in each lattice case. In the next step, on the basis of the energy Equations (23)–(25), the terms dependent on $p_x$ entering (29) can be replaced by those dependent on x, and the constant terms enter also the energy expressions. In effect, the acceleration term on the left-hand side of (29) becomes a function of x alone and the constant terms. According to (28), its integral over the variable x leads to $V(x)$ with the accuracy to a constant potential term $V_C$.

The term $V_C$ can be obtained from the condition that the points

$$x=\pm a_0$$

(33)

are the turning points of the oscillator. In this case the electron velocity $\frac{dx}{dt}$ as well as the kinetic energy are equal to zero. Therefore,

$$V(\pm a_0)=C^{\mathrm{latt}}(a_0)$$

(34)

This completes the calculation of the potential energy. Examples are presented below separately for each cubic lattice.

But the same reasoning can be applied also to the acceleration expression for the momentum variable $p_x$ in (30). In this case the terms dependent on x are replaced by those dependent on $p_x$ combined with the constant terms entering the energy Equations (23)–(25). This gives the acceleration terms dependent only on $p_x$ and the constant terms. We find that both functional dependencies obtained for (29) and (30) are the same.

In effect, we can write for (29) and (30) respectively

$$\frac{d^{2}x}{d{t}^2}=a_x(x,p_x)=a(x)$$

(35)

and

$$\frac{d^2{p}_x}{d{t}^2}=a_{p_x}(x,p_x)=a(p_x)$$

(36)

This kind of symmetry, represented by the same functional dependence of both accelerations (35) and (36) on x and $p_x$, allows us to derive another equation of motion of a one-dimensional nonlinear oscillator than that given in (26). The new equation concerns the behavior of the momentum variable $p_x$ and has its postulated form similar to (26):

$$\frac{1}{2}{\left(\frac{d{p}_x}{dt}\right)}^2+V(p_x)=C^{\mathrm{latt}}(a_0)$$

(37)

The potential V depends solely on the momentum variable $p_x$ and the constant terms. The amplitude $a_0$ labels now a maximum value of $|p_x|$ which can be admitted by the oscillator. The time differentiation of (37) gives

$$\frac{d^2{p}_x}{d{t}^2}\frac{d{p}_x}{dt}+\frac{dV(p_x)}{d{p}_x}\frac{d{p}_x}{dt}=0$$

(38)

so

$$\frac{d^2{p}_x}{d{t}^2}=-\frac{dV(p_x)}{d{p}_x}=a(p_x)$$

(39)

Examples given below (see Section 5, Section 6 and Section 7) demonstrate that a functional dependence of $V(p_x)$ is the same as $V(x)$. The constant terms entering $V(p_x)$ and $V(x)$ should be the same because $a_0$ is equal to the same amplitude for the oscillations of x and $p_x$.

The kinetic energy of the oscillator in the momentum space is given by the formula:

$$\frac{1}{2}{\left(\frac{d{p}_x}{dt}\right)}^2=\frac{1}{2}{\left(-\frac{\partial C^{\mathrm{latt}}}{\partial x}\right)}^2$$

(40)

Examples of (40) for special lattice cases are given in Section 5.

5. Example 1: The Simple Cubic Lattice

Since

$$\frac{dx}{dt}=\frac{\partial C^{\mathrm{sc}}}{\partial p_x}=sin{p}_x$$

(41)

the acceleration term for electrons oscillating in that lattice is:

$$\frac{d^{2}x}{d{t}^2}=\frac{d}{dt}\left(sin{p}_x\right)=cos{p}_x\frac{d{p}_x}{dt}=-cos{p}_{x}sinx$$

(42)

because of (10) and (19). From Equation (23) we have

$$cos{p}_x=1-cosx+cos{a}_0$$

(43)

so the potential derivative is [see (28)]

$$\frac{dV}{dx}=(1-cosx+cos{a}_0)sinx$$

(44)

This gives

$$V(x)=-cosx(1+cos{a}_0)+\frac{1}{4}cos(2x)+V_C$$

(45)

The constant term $V_C$ is obtained from the condition of vanishing of the kinetic energy at the turning points (33) [see (34)]:

$$V_C=\frac{1}{2}{cos}^2{a}_0+\frac{5}{4}$$

(46)

The validity of calculations can be checked by substituting the kinetic energy derived from the first of the Hamilton Equations (9) and $V(x)$ from (45) and (46) into (26). We obtain

$$\begin{array}{ccc}\hfill C^{\mathrm{sc}}& =& E^{\mathrm{kin}}+V(x)=\frac{1}{2}{sin}^2{p}_x+V(x)=\frac{1}{2}[1-{(1-cosx+cos{a}_0)}^2]+V(x)\hfill \\ & =& \frac{1}{2}(cosx-cos{a}_0)(2-cosx+cos{a}_0)-cosx(1+cos{a}_0)\hfill \\ & & +\frac{1}{4}(2{cos}^{2}x-1)+\frac{1}{2}{cos}^2{a}_0+\frac{5}{4}=1-cos{a}_0\hfill \end{array}$$

(47)

This is a constant result expected on the basis of the energy Equation (23). It shows that relations

$$C^{\mathrm{sc}}-V(x)=\frac{1}{2}{sin}^2{p}_x=\frac{1}{2}{\left(\frac{dx}{dt}\right)}^2=E_{\mathrm{kin}}$$

(48)

hold for any x of the oscillator.

The same energy expression in the momentum space is:

$$C^{\mathrm{sc}}-V(p_x)=\frac{1}{2}{sin}^{2}x=\frac{1}{2}{\left(\frac{d{p}_x}{dt}\right)}^2$$

(48a)

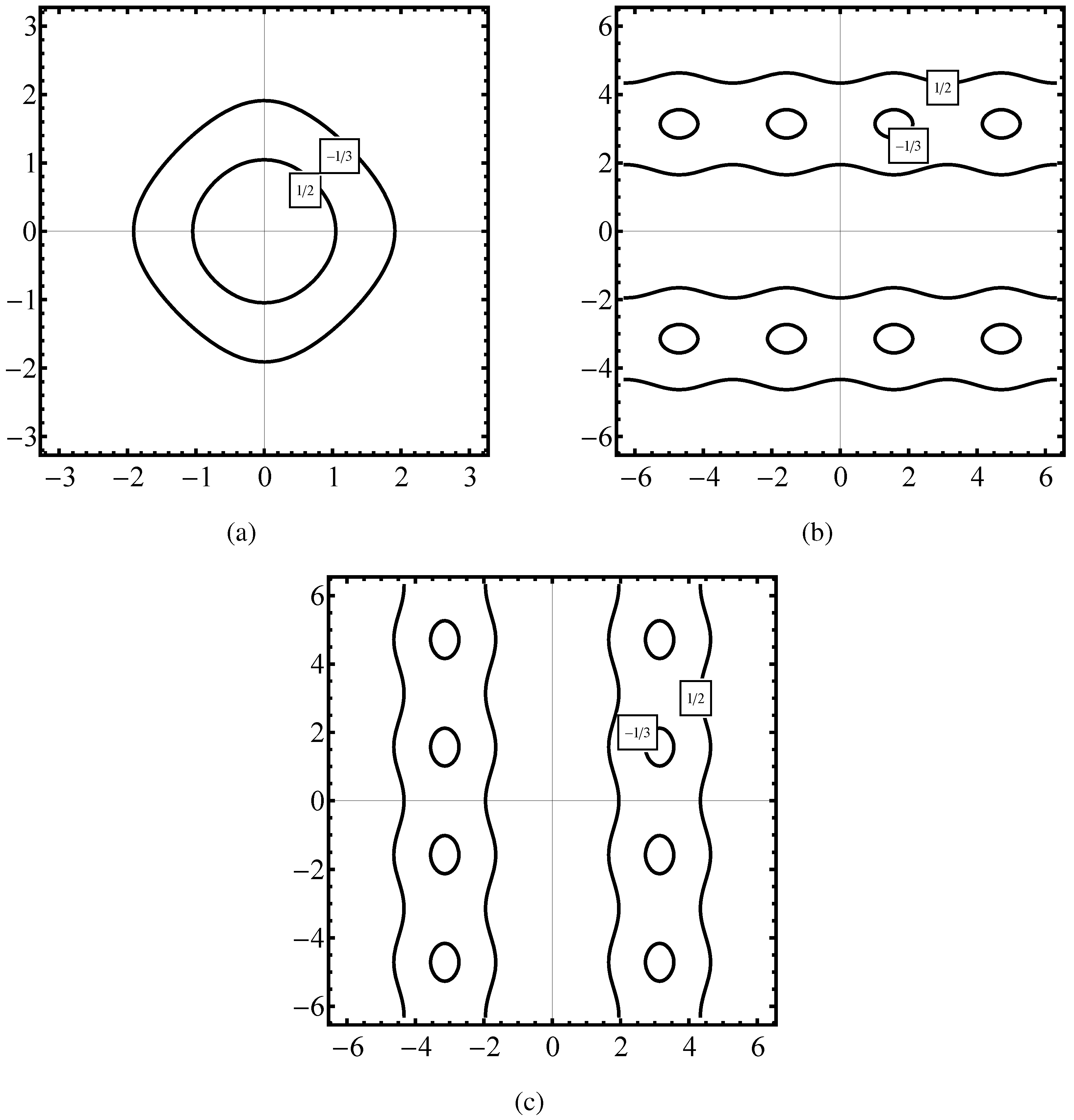
where $V(p_x)$ depends on $p_x$ in the same way as $V(x)$ on x and the constant $V_C$ remains unchanged. In Figure 1 parts (a), (b), (c) we demonstrate the phase space $(x,p_x)$ calculated for three forms of the electron Hamiltonian for the sc lattice. Figure 1(a) is representing a constant energy $C^{\mathrm{sc}}=1-cos{a}_0$ calculated for two values of $cos{a}_0$ in the case of the Hamiltonian (26) which is fully symmetrical in x and $p_x$. Figure 1(b) plots the same energy of $C^{\mathrm{sc}}$ in the case of the Hamiltonian formula given in the first step of (47), Figure 1(c) is a plot of $C^{\mathrm{sc}}$ obtained when the kinetic energy is presented according to (48a).

6. Example 2: The Body-Centered Cubic Lattice

The velocity of the oscillator representing the circulating electron is

$$\frac{dx}{dt}=\frac{\partial C^{\mathrm{bcc}}}{\partial p_x}=cosxsin{p}_x$$

(49)

and

$$\frac{d{p}_x}{dt}=-\frac{\partial C^{\mathrm{bcc}}}{\partial x}=-sinxcos{p}_x$$

(50)

The corresponding acceleration term is:

$$\begin{array}{cc}\hfill \frac{d^{2}x}{d{t}^2}& =-sinx\frac{dx}{dt}sin{p}_x+cosxcos{p}_x\frac{d{p}_x}{dt}\hfill \\ & =-sinxcosx{sin}^2{p}_x+cosxcos{p}_x(-sinxcos{p}_x)\hfill \\ & =-sinxcosx=-\frac{dV}{dx}\hfill \end{array}$$

(51)

In this special (bcc) case (51) is a function of x alone. The potential energy obtained from the integral of the negative acceleration term is:

$$V(x)=-\frac{1}{4}cos(2x)+V_C$$

(52)

The constant $V_C$ can be derived from the energy balance at the turning points at which the oscillator velocity is zero because of $p_x=0$; see (49). This gives the condition:

$$V(\pm a_0)=\frac{1}{4}cos(2a_0)+V_C=1-cos{a}_0$$

(53)

so

$$V_C=1-cos{a}_0+\frac{1}{4}cos(2a_0)$$

(54)

A control of the calculations requires to add the kinetic energy

$$\frac{1}{2}{\left(\frac{dx}{dt}\right)}^2=\frac{1}{2}{cos}^{2}x{sin}^2{p}_x=\frac{1}{2}{cos}^{2}x(1-{cos}^2{p}_x)=\frac{1}{2}({cos}^{2}x-{cos}^2{a}_0)$$

(55)

to the potential one calculated in (52)–(54). In (55) we eliminate the variable $p_x$ with the aid of the relation

$$cosxcos{p}_x=cos{a}_0$$

(56)

obtained from (24). A sum of (55) and (52) supplemented by the result in (54) for $V_C$ gives

$$\begin{array}{cc}\hfill C^{\mathrm{bcc}}=& E_{\mathrm{kin}}+V(x)=\frac{1}{2}({cos}^{2}x-{cos}^2{a}_0)-\frac{1}{4}(2{cos}^{2}x-1)+1-cos{a}_0\hfill \\ & +\frac{1}{4}(2{cos}^2{a}_0-1)=1-cos{a}_0\hfill \end{array}$$

(57)

which is a constant energy term entering Equation (24). In the momentum space a counterpart of (55) is

$$\frac{1}{2}{\left(\frac{d{p}_x}{dt}\right)}^2=\frac{1}{2}{sin}^{2}x{cos}^2{p}_x$$

(55a)

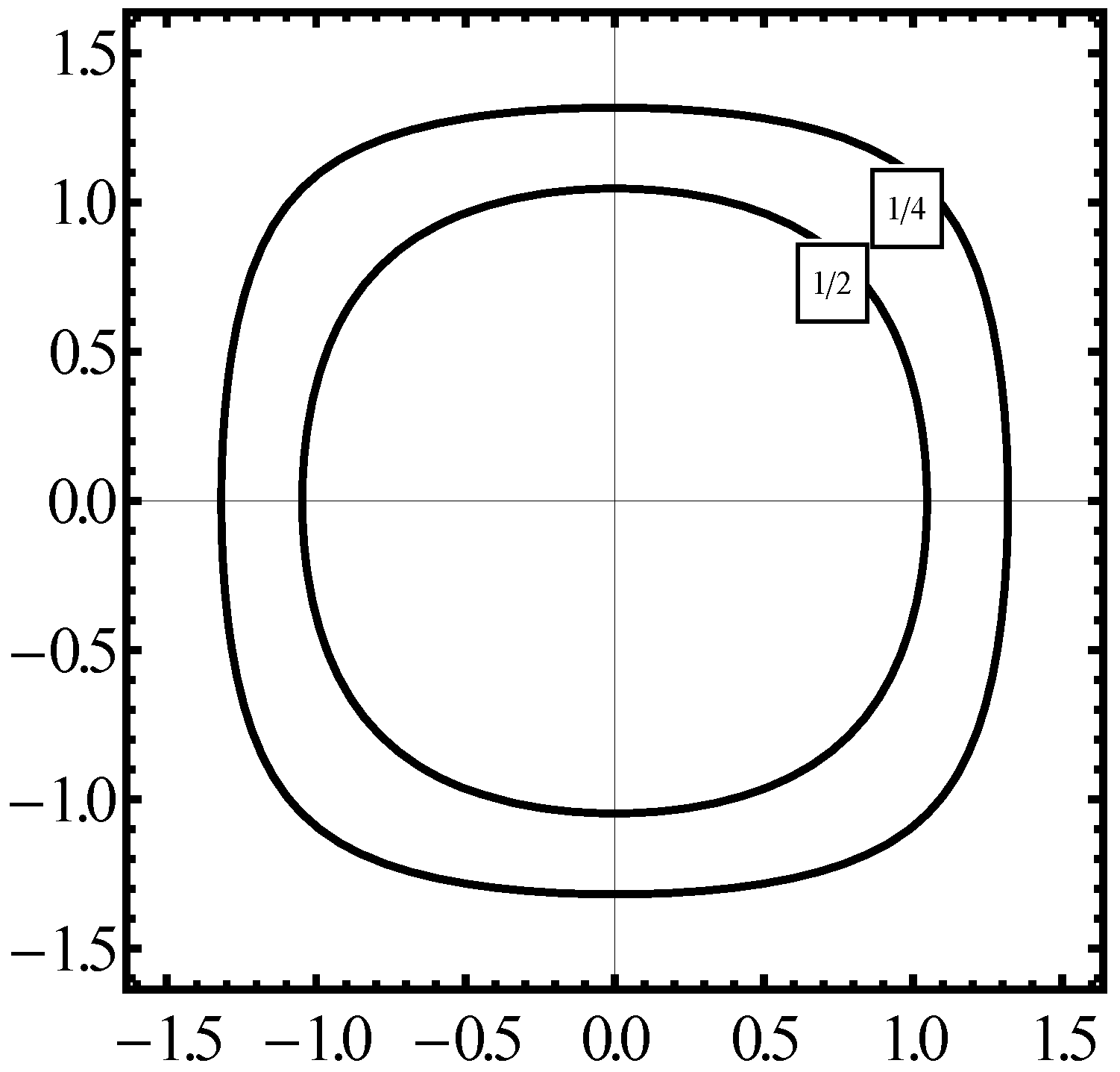
See (55) and a similar change of the variable x into $p_x$ concerns the expression of $V(x)$ in (52). The constant $V_C$ remains unchanged. In Figure 2 we plot the constant energy $C^{\mathrm{bcc}}=1-cos{a}_0$ in the phase space $(x,p_x)$ for the case of a fully symmetrical Hamiltonian formula (24). But an identical plot in $(x,p_x)$ is obtained for $C^{\mathrm{bcc}}$ when $E_{\mathrm{kin}}=E_{\mathrm{kin}}(x,p_x)$ calculated from the first step in (55) and $V(x)$ from the second step in (57) are taken into account. By the property of symmetry the calculation of $C^{\mathrm{bcc}}$ done with the aid of the kinetic energy (55a) and $V(p_x)$ taken instead of $V(x)$ gives a result identical to that of the former two approaches, viz., (24), or (55) and (57).

7. Example 3: The Face-Centered Cubic Lattice

Here

$$\frac{dx}{dt}=\frac{\partial C^{\mathrm{fcc}}}{\partial p_x}=\frac{1}{2}sin{p}_x(1+cosx)$$

(58)

$$\frac{d{p}_x}{dt}=-\frac{\partial C^{\mathrm{fcc}}}{\partial x}=-\frac{1}{2}sinx(1+cos{p}_x)$$

(59)

and

$$\begin{array}{cc}\hfill \frac{d^{2}x}{d{t}^2}& =\frac{1}{2}cos{p}_x\frac{d{p}_x}{dt}(1+cosx)+\frac{1}{2}sin{p}_x(-sinx)\frac{dx}{dt}\hfill \\ & =-cos{p}_x\frac{1}{2}sinx(1+cos{p}_x)(1+cosx)\frac{1}{2}+sin{p}_{x}sinx\frac{1}{2}sin{p}_x(1+cosx)\frac{1}{2}\hfill \\ & =-\frac{1}{4}sinx(1+cosx)(1+cos{p}_x)\hfill \end{array}$$

(60)

A further calculation requires to eliminate the dependence on $p_x$ on the basis of the energy formula in (25). We obtain

$$cos{p}_x=\frac{3-cosx-2(1-cos{a}_0)}{1+cosx}$$

(61)

which can be substituted into (60). This gives:

$$\begin{array}{cc}\hfill \frac{d^{2}x}{d{t}^2}& =-\frac{1}{4}sinx(1+cosx)\left[1+\frac{3-cosx-2(1-cos{a}_0)}{1+cosx}\right]\hfill \\ & =-\frac{1}{2}sinx(1+cos{a}_0)=-\frac{dV}{dx}\hfill \end{array}$$

(62)

The expression in (34) taken with a minus sign should be next integrated over the variable x. The result is

$$V(x)=-\frac{1}{2}cosx(1+cos{a}_0)+V_C$$

(63)

where

$$V_C=1-\frac{1}{2}cos{a}_0+\frac{1}{2}{cos}^2{a}_0.$$

(64)

The constant $V_C$ is obtained from the requirement of the energy conservation at the turning points see (25):

$$V(\pm a_0)=-\frac{1}{2}cos{a}_0(1+cos{a}_0)+V_C=1-cos{a}_0=C^{\mathrm{fcc}}(a_0)$$

(65)

The kinetic energy in the fcc lattice is from (58):

$$E_{\mathrm{kin}}=\frac{1}{2}{\left(\frac{dx}{dt}\right)}^2=\frac{1}{8}{sin}^2{p}_x{(1+cosx)}^2=\frac{1}{2}(cosx-cos{a}_0)(1+cos{a}_0)$$

(66)

This energy added to $V(x)$ gives a constant value equal to $C^{\mathrm{fcc}}(a_0)$ see (25):

$$\begin{array}{cc}\hfill E_{\mathrm{kin}}+V(x)=& \frac{1}{2}(cosx-cos{a}_0)(1+cos{a}_0)-\frac{1}{2}cosx(1+cos{a}_0)\hfill \\ & +1-\frac{1}{2}cos{a}_0+\frac{1}{2}{cos}^2{a}_0=1-cos{a}_0=C^{\mathrm{fcc}}(a_0)\hfill \end{array}$$

(67)

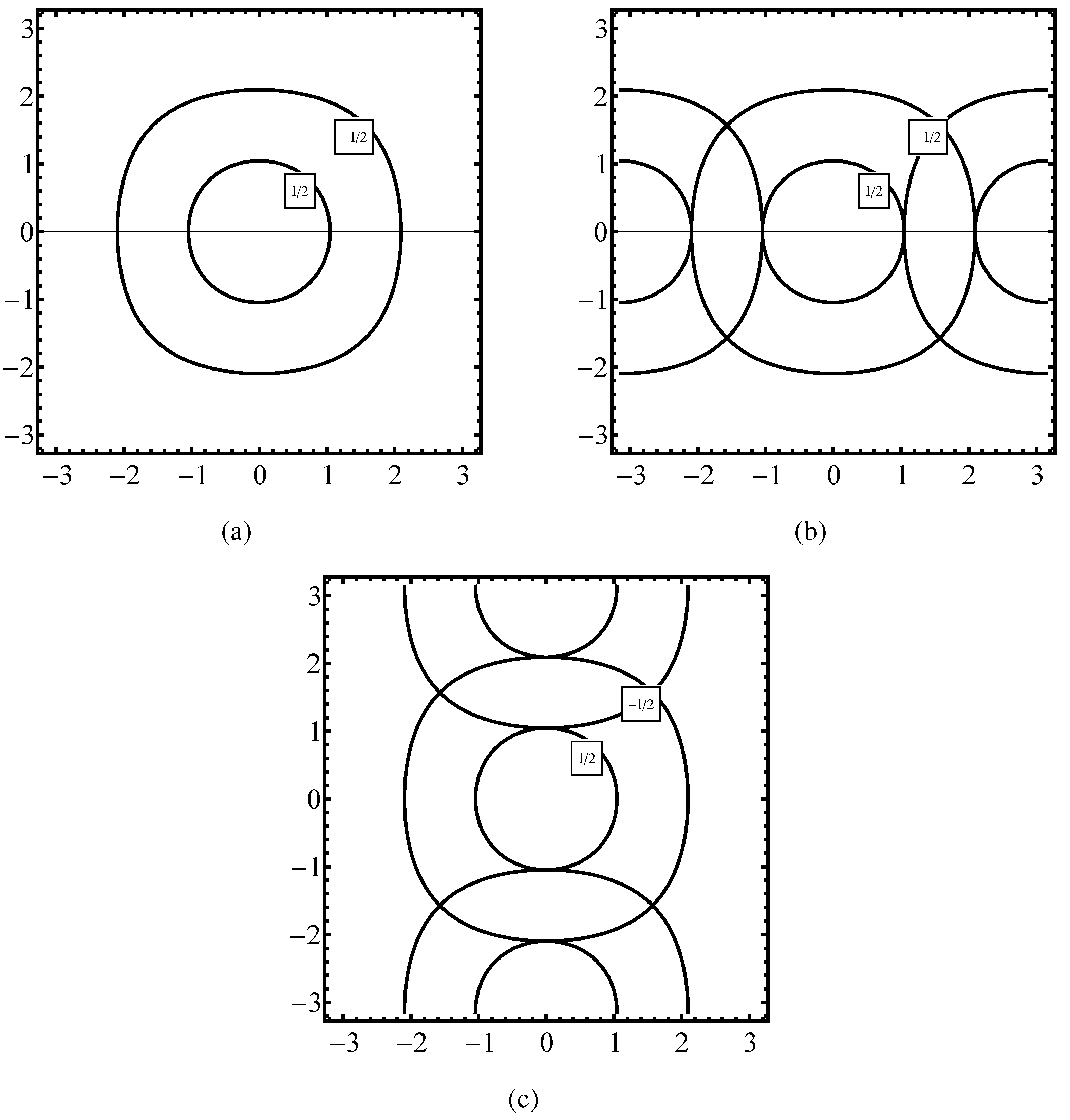
Symmetrical expressions to those in (66) and (67) can be obtained in the momentum space by a replacement–in the first step of (66) and in (67)–of the variable $p_x$ by x, and the variable x by $p_x$. In Figure 3 parts (a), (b), (c) we plot the constant energy $C^{\mathrm{fcc}}=1-cos{a}_0$ in the phase space $(x,p_x)$ calculated: (i) from (25) (see Figure 3(a)), (ii) from $E_{\mathrm{kin}}$ obtained in the first step of (66) and $V(x)$ is taken from (67), (iii) from the formula (37) specified for the case of the fcc lattice. The degeneracy of the plots observed for the bcc case does not exist for the fcc lattice.

8. Equations of Motion as a Basis in Calculating the Cyclotron Frequency

This kind of approach replaces that quoted in Equation (1).

On the first step, the motion of crystal electrons close to a free-electron behavior attained at small $k_x$, $k_y$, $k_x$ is examined; see (14). In this case the energy expressions (23)–(25) of a planar motion ($k_x=x$, $k_y=p_x$) are reduced to the formula

$$C^{\mathrm{free}}=\frac{x^2}{2}+\frac{p_x^2}{2}=\frac{a_0^2}{2}$$

(68)

This is a typical Hamiltonian of the harmonic oscillator. In accordance with the oscillator property at $x=\pm a_0$ is attained $p_x=0$, and vice versa, $p_x=\pm a_0$ is attained at $x=0$.

The electron velocity is

$$\frac{dx}{dt}=\frac{\partial C^{\mathrm{free}}}{\partial p_x}=p_x=\sqrt{a_0^2-x^2}$$

(69)

On the basis of (69) a half of the time period of the oscillator can be readily calculated from the integral

$$\frac{T}{2}=\int dt={\int }_{-a_0}^{a_0}\frac{dx}{\sqrt{a_0^2-x^2}}=arcsin\left(\frac{x}{a_0}\right){|}_{x=-a_0}^{x=a_0}=\frac{\pi }{2}+\frac{\pi }{2}=\pi$$

(70)

In effect

$$T=2\pi$$

(71)

In case the potential $V(x)$ instead of the velocity (69) is considered, we have as a starting point the relation

$$\frac{1}{2}{\left(\frac{dx}{dt}\right)}^2=C^{\mathrm{free}}-V(x)=\frac{a_0^2}{2}-\frac{x^2}{2}$$

(72)

The $V(x)$ in (72) is obtained readily from the acceleration formula

$$\frac{d^{2}x}{d{t}^2}=\frac{d}{dt}\left(\frac{\partial C^{\mathrm{free}}}{\partial p_x}\right)=\frac{d{p}_x}{dt}=-\frac{\partial C^{\mathrm{free}}}{\partial x}=-x=-\frac{dV}{dx}$$

(73)

since the integral of the potential derivative over the variable x gives:

$$V(x)=\frac{x^2}{2}+V_C$$

(74)

At $x=\pm a_0$ we have $dx/dt=0$, so the potential energy should be equal there to a total energy (68). This gives the equation

$$\frac{a_0^2}{2}+V_C=\frac{a_0^2}{2}$$

(75)

so $V_C=0$. In effect, the expression under the integral with respect to x leading to T becomes identical to that applied in (70).

Since the general formula for the circular frequency is

$$\Omega =\frac{2\pi }{T}$$

(76)

we obtain in view of (70)

$$\Omega =\frac{2\pi }{2\pi }=1$$

(77)

This is precisely a result for $\Omega$ obtained in (2), on the condition that the values of parameters (8) are substituted into (2).

The situation for the crystal electrons becomes much similar to that for the free ones. Because the kinetic and potential energies add together to a constant value for any x, it is inessential whether we apply the kinetic, i.e., the velocity-dependent, energy expression, or the potential energy in the calculations. In the velocity case, since

$$\frac{dx}{dt}=\frac{\partial C^{\mathrm{latt}}}{\partial p_x}$$

(78)

the integral formula

$$\frac{T}{2}=\int dt={\int }_{-a_0}^{a_0}{\left(\frac{\partial C^{\mathrm{latt}}}{\partial p_x}\right)}^{-1}dx$$

(79)

can be applied for any lattice. For example, for the sc lattice we have see (41)

$$\frac{\partial C^{\mathrm{sc}}}{\partial p_x}=sin{p}_x={[1-{(1-cosx+cos{a}_0)}^2]}^{1/2}$$

(80)

where the transformation of the dependence on $p_x$ into that on x is obtained on the basis of (43). But the potential $V(x)$ can be also used. In this case, because of the relation

$${\left(\frac{dx}{dt}\right)}^2=2[C^{\mathrm{latt}}-V(x)]$$

(81)

the integral formula becomes:

$$\frac{T}{2}=\int dt=\frac{1}{\sqrt{2}}{\int }_{-a_0}^{a_0}{[C^{\mathrm{latt}}-V(x)]}^{-1/2}dx$$

(82)

An equivalence of the both approaches can be easily demonstrated. For the bcc case we have [see (52)]

$$\begin{array}{cc}\hfill C^{\mathrm{bcc}}-V(x)& =1-cos{a}_0+\frac{1}{4}cos(2x)-1+cos{a}_0-\frac{1}{4}cos(2a_0)\hfill \\ & =\frac{1}{2}({cos}^{2}x-{cos}^2{a}_0)=\frac{1}{2}{\left(\frac{dx}{dt}\right)}^2\hfill \end{array}$$

(83)

where the second and the last step are obtained because of the formulae (54) and (55).

A similar calculation can be done for the fcc lattice, since from (25), (63) and (66) we have:

$$C^{\mathrm{fcc}}-V(x)=\frac{1}{2}(cosx-cos{a}_0)(1+cos{a}_0)=\frac{1}{2}{\left(\frac{dx}{dt}\right)}^2$$

(84)

9. Cyclotron Oscillation Periods and Frequencies

The effect of the crystal potential is represented by the dependence of $\Omega$ on the amplitude $a_0$ absent in (2), (16) and (77). These $\Omega$ are reduced to that obtained in (77) only if $a_0$ is tending to zero, a situation obtained when the crystal electrons approach the behavior of the free-electron particles.

With a substitution

$$sin\frac{x}{2}=sin\frac{a_0}{2}sin\frac{z}{2}$$

(85)

the time period

$$\frac{T}{4}={\int }_0^{a_0}\frac{dx}{{(cosx-cos{a}_0)}^{1/2}{(2+cos{a}_0-cosx)}^{1/2}}$$

(86)

of the electron oscillation in the sc lattice can be represented by the formula

$$\frac{T}{4}={\int }_0^{\pi /2}\frac{dz}{{\left(1-{sin}^2\frac{a_0}{2}{sin}^{2}z\right)}^{1/2}{\left[1-{sin}^2\frac{a_0}{2}(1-{sin}^{2}z)\right]}^{1/2}}$$

(87)

With another substitution

$$k=sin\frac{a_0}{2}$$

(88)

the integral in (87) becomes:

$$\frac{T}{4}={\int }_0^{\pi /2}\frac{dz}{{\left[1-k^2+{\displaystyle \frac{k^4}{4}}{sin}^2(2z)\right]}^{1/2}}=\frac{1}{\sqrt{1-k^2}}{\int }_0^{\pi /2}\frac{dz}{{\left[1+{\displaystyle \frac{k^4}{4(1-k^2)}}{sin}^2(2z)\right]}^{1/2}}$$

Assuming that $2z=w$ the last integral becomes

$$\begin{array}{cc}\hfill \frac{T}{4}& =\frac{1}{\sqrt{1-k^2}}{\int }_0^{\pi /2}\frac{dw}{{\left[1+{\displaystyle \frac{k^4}{4(1-k^2)}}{sin}^{2}w\right]}^{1/2}}\hfill \\ & =\frac{1}{cos\left(\frac{a_0}{2}\right)}{\int }_0^{\pi /2}\frac{dw}{{\left[1+{\displaystyle \frac{1}{4}}{\mathrm{tg}}^2\left({\displaystyle \frac{a_0}{2}}\right){sin}^2\left({\displaystyle \frac{a_0}{2}}\right){sin}^{2}w\right]}^{1/2}}\hfill \end{array}$$

With the aid of the formula (76) this leads to the expression for the cyclotron frequency

$${\omega }^{\mathrm{sc}}=\frac{\pi cos\left({\displaystyle \frac{a_0}{2}}\right)}{2K\left[-{\displaystyle \frac{1}{4}}{sin}^2\left({\displaystyle \frac{a_0}{2}}\right){\mathrm{tg}}^2\left({\displaystyle \frac{a_0}{2}}\right)\right]}$$

(89)

where

$$K(\mu )={\int }_0^{\pi /2}\frac{dz}{{(1-\mu {sin}^{2}z)}^{1/2}}$$

(90)

The expansion of (89) in powers of $a_0$ is presented in

Table 1. Cyclotron frequencies of the tightly-bound s electrons gyrating in cubic crystal lattices see (89), (94) and (98).

sc lattice

${\displaystyle \begin{array}{ccc}\hfill {\omega }^{\mathrm{sc}}& =& 1-\frac{a_0^2}{8}+\frac{5a_0^4}{768}-\frac{17a_0^6}{92160}-\frac{11a_0^8}{16515072}-\frac{5753a_0^{10}}{29727129600}-\frac{46177a_0^{12}}{6278369771520}-\dots \hfill \\ & =& 1.-0.125a_0^2+0.00651042a_0^4-0.000184462a_0^6-6.66058\times {10}^{-7}{a}_0^8\hfill \\ & & -1.93527\times {10}^{-7}{a}_0^{10}-7.35493\times {10}^{-9}{a}_0^{12}-\dots \hfill \end{array}}$

bcc lattice

${\displaystyle \begin{array}{ccc}\hfill {\omega }^{\mathrm{bcc}}& =& 1-\frac{a_0^2}{4}+\frac{a_0^4}{192}-\frac{23a_0^6}{11520}-\frac{2519a_0^8}{5160960}-\frac{140333a_0^{10}}{928972800}-\frac{23798857a_0^{12}}{490497638400}-\dots \hfill \\ & =& 1.-0.25a_0^2+0.00520833a_0^4-0.00199653a_0^6-0.000488087a_0^8\hfill \\ & & -0.000151063a_0^{10}-0.0000485198a_0^{12}-\dots \hfill \end{array}}$

fcc lattice

${\displaystyle \begin{array}{ccc}\hfill {\omega }^{\mathrm{fcc}}& =& 1-\frac{3a_0^2}{16}+\frac{11a_0^4}{1024}-\frac{21a_0^6}{81920}+\frac{1891a_0^8}{440401920}-\frac{1213a_0^{10}}{317089382400}+\frac{75113a_0^{12}}{31890132172800}+\dots \hfill \\ & =& 1.-0.1875a_0^2+0.0107422a_0^4-0.000256348a_0^6+4.29381\times {10}^{-6}{a}_0^8\hfill \\ & & -3.82542\times {10}^{-9}{a}_0^{10}+2.35537\times {10}^{-9}{a}_0^{12}+\dots \hfill \end{array}}$

. This expansion is equal to that calculated earlier with the aid of more conventional, but also more complicated, methods [11].

The bcc problem is equivalent to an elliptic integral similar to that met in the problem of the mathematical pendulum:

$$\frac{T}{4}={\int }_0^{a_0}\frac{dx}{{({cos}^{2}x-{cos}^2{a}_0)}^{1/2}}$$

(91)

A substitution of

$$sinx=sin{a}_{0}sinz$$

(92)

provides us with the formula

$$\begin{array}{cc}\hfill \frac{T}{4}& ={\int }_0^{\pi /2}\frac{sin{a}_{0}coszdz}{{({sin}^2{a}_0-{sin}^2{a}_0{sin}^{2}z)}^{1/2}cosx}\hfill \\ & ={\int }_0^{\pi /2}\frac{dz}{{(1-{sin}^2{a}_0{sin}^{2}z)}^{1/2}}=K({sin}^2{a}_0)\hfill \end{array}$$

(93)

Because of (76) the cyclotron frequency in the bcc lattice becomes

$${\omega }^{\mathrm{bcc}}=\frac{\pi }{2K({sin}^2{a}_0)}$$

(94)

its power expansion in terms of $a_0$ is also presented in Table 1.

The period of the electron oscillation in the fcc lattice is given by the integral:

$$\begin{array}{cc}\hfill \frac{T}{4}& =\frac{1}{{(1+cos{a}_0)}^{1/2}}{\int }_0^{a_0}\frac{dx}{{(cosx-cos{a}_0)}^{1/2}}\hfill \\ & =\frac{1}{\sqrt{2}}\frac{1}{{(1+cos{a}_0)}^{1/2}}{\int }_0^{a_0}\frac{dx}{{[{sin}^2(a_0/2)-{sin}^2(x/2)]}^{1/2}}\hfill \end{array}$$

(95)

A substitution

$$sin\left(\frac{x}{2}\right)=sin\left(\frac{a_0}{2}\right)sinz$$

(96)

provides us with the following expression

$$\begin{array}{cc}\hfill \frac{T}{4}& =\frac{\sqrt{2}}{{(1+cos{a}_0)}^{1/2}}{\int }_0^{\pi /2}\frac{dz}{{[1-{sin}^2(a_0/2){sin}^{2}z]}^{1/2}}\hfill \\ & =\frac{\sqrt{2}}{{(1+cos{a}_0)}^{1/2}}K\left[{sin}^2(a_0/2)\right]\hfill \end{array}$$

(97)

which evidently is also proportional to an elliptic integral. The cyclotron frequency in the fcc lattice is see (76):

$${\omega }^{\mathrm{fcc}}=\frac{\pi {(1+cos{a}_0)}^{1/2}}{2\sqrt{2}K\left[{sin}^2(\frac{a_0}{2})\right]}$$

(98)

A power expansion of it is also given Table 1. The accordance of the expansions in Table 1 with those calculated formally with aid of other methods [11] becomes evident. A physical cyclotron frequency is obtained when ${\omega }^{\mathrm{latt}}$ of Table 1 is multiplied by a factor presented in (16); see the end of Section 1.

An extension of the frequency calculations for the sc and bcc lattices to the case of $k_z\ne 0$ is straightforward. If the energies $E^{\mathrm{sc}}$ in (11) and $C^{\mathrm{sc}}$ in (23) are equal, i.e., they concern the same Fermi surface [see also (17)], we obtain for $k_x=x$, $k_y=p_x$ the relation

$$E^{\mathrm{sc}}=3-cosx-cos{p}_x-cos{k}_z=2-cos{a}_0^{\prime }-cos{k}_z=C^{\mathrm{sc}}=1-cos{a}_0$$

(99)

where $a_0^{\prime }$ is the amplitude of the oscillation on the plane $k_z\ne 0$. Equation (41) holds also in this case, therefore the formula (89) for the cyclotron frequency is valid with $a_0$ replaced by $a_0^{\prime }$. In effect, the $a_0$ entering the expansion for the sc lattice in Table 1 should be replaced by

$$a_0^{\prime }=arccos(1-cos{k}_z+cos{a}_0)$$

(100)

A similar calculation can be done for the bcc lattice. Because of (12), (17) and (24) we have

$$E^{\mathrm{bcc}}=1-cosxcos{p}_{x}cos{k}_z=1-cos{a}_0^{\prime }cos{k}_z=C^{\mathrm{bcc}}=1-cos{a}_0$$

(101)

where

$$cos{a}_0^{\prime }=cosxcos{p}_x$$

(102)

is the formula for the amplitude $a_0^{\prime }$ at $k_z\ne 0$. In this case (49) becomes

$$\frac{dx}{dt}=cosxsin{p}_{x}cos{k}_z={({cos}^{2}x-{cos}^2{a}_0^{\prime })}^{1/2}cos{k}_z$$

(103)

In effect, an infinitesimal oscillation time

$$dt=\frac{dx}{{({cos}^{2}x-{cos}^2{a}_0^{\prime })}^{1/2}}\frac{1}{cos{k}_z}$$

(104)

becomes inversely proportional to $cos{k}_z$. The formula for the oscillation frequency is similar to that in (94), namely

$${\omega }^{\mathrm{bcc}}=cos{k}_z\frac{\pi }{2K({sin}^2{a}_0^{\prime })}$$

(105)

where from (101)

$$a_0^{\prime }=arccos\left(\frac{cos{a}_0}{cos{k}_z}\right)$$

(106)

The calculation of the oscillation frequency at $k_z\ne 0$ for the fcc lattice is based on the energy formulae (13), (17) and (25):

$$\begin{array}{cc}\hfill 2E^{\mathrm{fcc}}& =3-cosxcos{p}_x-cos{p}_{x}cos{k}_z-cos{k}_{z}cosx\hfill \\ & =3-cos{a}_0^{\prime }-cos{k}_z-cos{k}_{z}cos{a}_0^{\prime }=2C^{\mathrm{fcc}}=2-2cos{a}_0\hfill \end{array}$$

(107)

This gives

$$\frac{dx}{dt}=\frac{\partial E^{\mathrm{fcc}}}{\partial p_x}=\frac{1}{2}sin{p}_x(cos{k}_x+cos{k}_z)$$

(108)

from which

$$\begin{array}{cc}\hfill \frac{T}{4}& ={\int }_0^{a_0^{\prime }}\frac{dx}{\frac{1}{2}sin{p}_x(cosx+cos{k}_z)}\hfill \\ & =2{\int }_0^{a_0^{\prime }}\frac{dx}{{\left[1-{\left({\displaystyle \frac{cos{a}_0^{\prime }+cos{k}_z(1+cos{a}_0^{\prime }-cosx)}{cosx+cos{k}_z}}\right)}^2\right]}^{1/2}(cosx+cos{k}_z)}\hfill \end{array}$$

(109)

where

$$cos{a}_0^{\prime }=\frac{1+2cos{a}_0-cos{k}_z}{1+cos{k}_z}$$

(110)

with

$$cosx=1-2{sin}^2\left(\frac{x}{2}\right)$$

(111)

$$cos{a}_0^{\prime }=1-2{sin}^2\left(\frac{a_0^{\prime }}{2}\right)$$

(112)

we obtain

$$\begin{array}{cc}\hfill \frac{T}{8}& =\frac{1}{\sqrt{2}{(1+cos{k}_z)}^{1/2}}\hfill \\ & \times {\int }_0^{a_0^{\prime }}\frac{dx}{{[{sin}^2(\frac{a_0^{\prime }}{2})-{sin}^2(\frac{x}{2})]}^{1/2}{[(1+cos{a}_0)(1+cos{k}_z)-2(1-cos{k}_z){sin}^2(\frac{x}{2})]}^{1/2}}\hfill \end{array}$$

(113)

Another substitution

$$sin\left(\frac{x}{2}\right)=sin\left(\frac{a_0^{\prime }}{2}\right)sinz$$

(114)

gives

$$\begin{array}{cc}\hfill \frac{T}{8}& =\frac{\sqrt{2}}{{(1+cos{k}_z)}^{(}1+cos{a}_0^{\prime }{)}^{1/2}}\hfill \\ & \times {\int }_0^{\pi /2}\frac{dz}{{[1-{sin}^2(\frac{a_0^{\prime }}{2}){sin}^{2}z]}^{1/2}{\left[1-{\displaystyle \frac{2(1-cos{k}_z){sin}^2(\frac{a_0^{\prime }}{2})}{(1+cos{a}_0^{\prime })(1+cos{k}_z)}}{sin}^{2}z\right]}^{1/2}}\hfill \end{array}$$

(115)

By applying the formula [12]

$$\begin{array}{c}\hfill {\int }_0^{\pi /2}\frac{dz}{{(1-m{sin}^{2}z)}^{1/2}{(1-n{sin}^{2}z)}^{1/2}}=\frac{1}{{(1-n)}^{1/2}}{\int }_0^{\pi /2}\frac{dz}{{\left(1-{\displaystyle \frac{n-m}{n-1}}{sin}^{2}z\right)}^{1/2}}\end{array}$$

(116)

a following elliptic integral defines the time period T:

$$\begin{array}{cc}\hfill T& =\frac{8\sqrt{2}}{(1+cos{k}_z){(1+cos{a}_0^{\prime })}^{1/2}cos(\frac{a_0^{\prime }}{2})}\hfill \\ & \times {\int }_0^{\pi /2}\frac{dz}{{\left\{1+{\mathrm{tg}}^2(\frac{a_0^{\prime }}{2})\left[1-{\displaystyle \frac{2(1-cos{k}_z)}{(1+cos{a}_0^{\prime })(1+cos{k}_z)}}\right]{sin}^{2}z\right\}}^{1/2}}\hfill \end{array}$$

(117)

from which the calculation of the cyclotron frequency ${\omega }^{\mathrm{fcc}}$ is straightforward.

Following (76), any time period of the oscillation can be next transformed into the frequency $\Omega$. These $\Omega$ differ from the result of unity for free electrons [see (77)] by the power expansions presented in terms of a dimensionless amplitude parameter $a_0$, or $a_0^{\prime }$ and $k_z$. Physical values of $\Omega$ are obtained by multiplying the dimensionless $\Omega$ by a factor equal to (16); see the end of Section 2.

10. Extensions of the Method to More Complicated Hamiltonians

The Hamiltonians discussed above were symmetrical with respect to an interchange of the variables x and $p_x$. The amplitude $a_0$ can be referred to a crystal state $(k_x,k_y)$ lying in a plane $k_z=0$ by the formula

$$\left|\frac{E^{\mathrm{latt}}(k_x,k_y,k_z=0)-E^{\mathrm{latt}}(0,0,k_z=0)}{{\beta }^{\mathrm{latt}}}\right|=1-cos{a}_0$$

(118)

where $\mathrm{latt}=\mathrm{sc},\mathrm{bcc},\mathrm{fcc}$.

More complicated Hamiltonians can be obtained, for example, when more atomic layers than that of the nearest atomic neighbors are considered. Let the second atomic layer interacting with a central atom be assumed as also important for the band energy in the sc lattice. The atomic distribution in that layer is similar to a layer of the nearest atomic neighbors in the fcc lattice. In this case the oscillation amplitude is referred to the electron energy by the formula

$$\frac{E^{\mathrm{sc}(2\mathrm{layers})}(k_x,k_y,k_z=0)-E^{\mathrm{sc}(2\mathrm{layers})}(0,0,k_z=0)}{{\beta }^{\mathrm{I}}}=(1-cos{a}_0)\left(1+\frac{{\beta }^{\mathrm{II}}}{{\beta }^{\mathrm{I}}}\right)$$

(119)

where ${\beta }^{\mathrm{I}}$ is characteristic for the nearest neighbors in the sc lattice and ${\beta }^{\mathrm{II}}$ for the nearest neighbors in the fcc lattice. Since the interaction between atoms decreases strongly with an increase of the interatomic distance, we may assume that

$$\left|\gamma \right|=\left|\frac{{\beta }^{\mathrm{II}}}{{\beta }^{\mathrm{I}}}\right|<1$$

(120)

The oscillator Hamiltonian for two layers taken together into account becomes

$$\begin{array}{cc}\hfill C^{\mathrm{sc}}+\gamma C^{\mathrm{fcc}}& =2-cosx-cos{p}_x+\frac{1}{2}\gamma (3-cosxcos{p}_x-cosx-cos{p}_x)\hfill \\ & =(1-cos{a}_0)(1+\gamma )\hfill \end{array}$$

(121)

This gives the velocity

$$\frac{dx}{dt}=\frac{\partial (C^{\mathrm{sc}}+\gamma C^{\mathrm{fcc}})}{\partial p_x}=sin{p}_x+\frac{1}{2}\gamma sin{p}_x(cosx+1)$$

(122)

which vanishes at $p_x=0$, and $x=a_0$ is a new amplitude characteristic for this case. The oscillation problem and calculation of the cyclotron frequency become similar to those considered for the Hamiltonians discussed above.

But not only the spherical s-like atomic orbits define the band structure of numerous crystals. In the case of orbits different than s, an asymmetry of the Hamiltonian describing the electron motion in the $(k_x,k_y)$-plane should be usually taken into account. For example, the wave functions based on ${\mathrm{p}}_{\mathrm{x}}$-like atomic orbitals (this symbol should not be confused with the electron momentum) can be considered, see e.g., [10]. In the sc lattice we obtain then different interaction between the nearest atomic neighbors lying in two sites $(\pm a_{\mathrm{latt}},0,0)$ than with the neighbors lying in two sites $(0,\pm a_{\mathrm{latt}},0)$; in the nearest neighbors approximation the interaction with the remaining two sites $(0,0,\pm a_{\mathrm{latt}})$ becomes inessential for the planar motion in the $(x,y)$-plane. In this case the Hamiltonian for three dimensions becomes

$$E^{\mathrm{sc}(p_x\mathrm{orbits})}={\beta }_x[1-cos(k_x{a}_{\mathrm{latt}})+\gamma (2-cos(k_y{a}_{\mathrm{latt}})-cos(k_z{a}_{\mathrm{latt}}))]$$

(123)

Here ${\beta }_x$ refers to the interaction between the nearest atomic neighbors in the x-direction and the ratio

$$\gamma =\frac{{\beta }_{y(x)}}{{\beta }_x}=\frac{{\beta }_{z(x)}}{{\beta }_x}$$

(124)

refers the ${\beta }_x$ interaction to the interaction of the central atom with the neighbors placed in the y and z directions. Assuming the oscillator motion along axis x in the plane $k_z=0$ is considered, the Hamiltonian for that motion which replaces (19) becomes:

$$\begin{array}{cc}\hfill C_{p_x\mathrm{orbits}}^{\mathrm{sc}(x)}& =1-cosx+\gamma (1-cos{p}_x)=1+\gamma -cosx-\gamma cos{p}_x\hfill \\ & =1-cos{a}_{0x}\hfill \end{array}$$

(125)

since $\beta$ in (17) can be replaced by ${\beta }_x$. The last step in (125) is obtained because

$$\frac{dx}{dt}=\frac{\partial C_{p_x\mathrm{orbits}}^{\mathrm{sc}(x)}}{\partial p_x}=\gamma sin{p}_x=0$$

(126)

for $p_x=0$, and in this case $x=a_{0x}$. The kinetic energy of the motion calculated with the aid of (125) and (126) is:

$$\frac{1}{2}{\left(\frac{dx}{dt}\right)}^2=\gamma (cosx-cos{a}_{0x})-\frac{1}{2}{(cosx-cos{a}_{0x})}^2$$

(127)

The potential energy obtained from the acceleration formula

$$\begin{array}{cc}\hfill \frac{d^{2}x}{d{t}^2}& =\frac{d}{dt}\left(\frac{\partial C_{p_x\mathrm{orbits}}^{\mathrm{sc}(x)}}{\partial p_x}\right)=\gamma cos{p}_x\frac{d{p}_x}{dt}=\gamma cos{p}_x\left(-\frac{\partial C_{p_x\mathrm{orbits}}^{\mathrm{sc}(x)}}{\partial x}\right)\hfill \\ & =-\gamma cos{p}_{x}sinx=-\frac{dV}{dx}\hfill \end{array}$$

(128)

becomes

$$V(x)=-cosx(1+\gamma +cos{a}_{0x})+\frac{1}{2}\int sin(2x)dx+V_C$$

(129)

The integration constant $V_C$ can be obtained from the condition that at $x=a_{0x}$ the total energy in (125) is equal to the potential energy. This gives

$$V_C=\gamma cos{a}_{0x}+\frac{1}{4}cos(2a_{0x})-{cos}^2{a}_{0x}$$

(130)

A check of calculations is a sum

$$\frac{1}{2}{\left(\frac{dx}{dt}\right)}^2+V(x)=1-cos{a}_{0x}$$

(131)

which is equal to a constant energy value entering (125). This makes possible to calculate the oscillation period of time by an integration of the electron velocity obtained either from the formula (127), or from the energy balance represented by (129) and (131). The integration should be performed between two turning points, $-a_{0x}$ and $a_{0x}$, of the oscillator.

But an oscillator along the axis y can be equally considered. This changes the amplitude of the oscillation because of the asymmetry of the Hamiltonian in (123). For the sake of convenience this Hamiltonian can be written ($k_x=p_y$, $k_y=y$, $k_z=0$):

$$C_{p_x\mathrm{orbits}}^{\mathrm{sc}(y)}=1-cos{p}_y+\gamma (1-cosy)=\gamma (1-cos{a}_{0y})$$

(132)

We have

$$\frac{dy}{dt}=\frac{\partial C_{p_x\mathrm{orbits}}^{\mathrm{sc}(y)}}{\partial p_y}=\gamma sin{p}_y=0$$

(133)

attained at the amplitude $a_{0y}$ different than $a_{0x}$ because the right-hand side of (132) is different than that in (125). The kinetic energy of the motion is:

$$\frac{1}{2}{\left(\frac{dy}{dt}\right)}^2=\frac{1}{2}{sin}^2{p}_y=\gamma (cosy-cos{a}_0)-\frac{1}{2}{\gamma }^2{(cosy-cos{a}_0)}^2$$

(134)

and the acceleration in direction y:

$$\begin{array}{cc}\hfill \frac{d^{2}y}{d{t}^2}& =\frac{d}{dt}\left(\frac{\partial C_{p_x\mathrm{orbits}}^{\mathrm{sc}(y)}}{\partial p_y}\right)=cos{p}_y\frac{d{p}_y}{dt}=cos{p}_y\left(-\frac{\partial C_{p_x\mathrm{orbits}}^{\mathrm{sc}(y)}}{\partial y}\right)\hfill \\ & =-\gamma cos{p}_{y}siny=-\frac{dV}{dy}\hfill \end{array}$$

(135)

The corresponding potential energy is an integral of (135):

$$V(y)=-\gamma cosy(1+\gamma cos{a}_{0y})+\frac{1}{2}{\gamma }^2\int sin(2y)dy+V_C$$

(136)

with the integration constant

$$V_C=\gamma +\left(\frac{1}{2}{cos}^2{a}_{0y}+\frac{1}{4}\right){\gamma }^2$$

(137)

obtained from the condition that at $y=a_{0y}$ the potential energy (136) should be equal to the total energy in (132). A check of calculations is a sum

$$\frac{1}{2}{\left(\frac{dy}{dt}\right)}^2+V(y)=\gamma (1-cos{a}_{0y})$$

(138)

which gives for any y the result of a constant energy entering (132).

The cyclotron frequency can be calculated equally from the oscillator motions performed in x and y directions. The integral limits in the second case are $(-a_{0y},a_{0y})$.

11. Summary

The paper presents a method of calculating the cyclotron frequency of electrons circulating in cubic crystal lattices upon the action of a constant magnetic field. An approximation of the tightly-bound electrons is mainly assumed for the electron Hamiltonians.

In the first step, an analysis is developed on the symmetry properties of the crystal Hamiltonian as well as the similar properties of the Lorentz equation governing the electron motion in an external magnetic field.

For the field directed along the axis z, the planar motion in the space of the wave vector $\overrightarrow{k}$ has the variable $k_z$ as a constant parameter, and the variables $k_x$ and $k_y$ in the motion plane can be considered as canonical position and momentum variables of an anharmonic one-dimensional oscillator. The second step is based on a separation of the total energy of the oscillator into the kinetic and potential parts, which readily provides us with the analytic integral formulae for the time period of the cyclotron oscillation.

This way is much more simple than a former one [11] in which the oscillation frequencies, or time periods, are obtained either from the action function, or from a direct solution of the differential equation of an oscillator. Moreover, the motion parameters of a crystal electron oscillating upon the action of the magnetic field, for example the electron velocity $\frac{dx}{dt}$, can be easily examined for any electron position within the oscillation limits (22). This velocity can be obtained for any x on the basis of (26):

$$\frac{dx}{dt}=2^{1/2}{[C^{\mathrm{latt}}(a_0)-V(x)]}^{1/2}$$

(139)

on the condition that $V(x)$ is a known function of x. In [11] the same velocity is calculated only with the aid of a rather tedious solution of the equation of motion.

Moreover, the time t at any instant of the motion can be coupled with position x because of the formula:

$$\int dt=\frac{1}{2^{1/2}}\int \frac{dx}{{[C^{\mathrm{latt}}(a_0)-V(x)]}^{1/2}}$$

(140)

This dependence of t on x is absent in [11]. The $V(x)$ entering (139) and (140) is calculated for different lattices in (45), (52), (54) and (63), (64).

A similar examination can be done for the dependence of $p_x$ on x and t, on the condition that we note a coupling between x and $p_x$ due to the energy relations (23)–(25). The same energy formulae can be applied in calculating the speed of the change of $p_x$, namely

$$\frac{d{p}_x}{dt}=-\frac{\partial C^{\mathrm{latt}}}{\partial x}$$

(141)

cf. here (30). The dependence of the electron acceleration $\frac{d^{2}x}{d{t}^2}$ on x is easily obtainable from $V(x)$ on the basis of (28). The dynamical parameters in more complicated band structures than listed in Section 4 (see Section 10) can be examined in a similar way.

The Hamiltonian plots of crystal electrons in the phase space $(x,p_x)$ are also examined. Beyond the original Hamiltonian $H(x,p_x)$, the Hamiltonians $H(x,\frac{dx}{dt})$ and $H(p_x,\frac{d{p}_x}{dt})$ are also considered. This kind of plots in the phase space is obtained when $\frac{dx}{dt}$ and $\frac{d{p}_x}{dt}$ entering H are calculated from the Hamilton equations.

The calculations performed for the s-electrons taken as an example fit the cyclotron frequency data obtained on the basis of more conventional methods; see Table 1. Outlines of an extension of the method to other crystal cases than described by the tight-binding approximation and the s-electron band structure, for example the case of the ${\mathrm{p}}_{\mathrm{x}}$-electron band, are also given.