1. Introduction
This review treats the subject of hexagonal silicon and germanium clusters, paying attention to the two-dimensional aromaticity. The concept of aromaticity is one of the most fascinating problems in chemistry [
1,
2]. Benzene is the archetypical aromatic hexagon of carbon: it is a planar, cyclic, fully conjugated system that possesses delocalized π electrons. The two-dimensional aromaticity of planar monocyclic systems is governed by Hückel’s 4
N + 2 rule, where N is the number of π electrons. The rule is derived from the simple Hückel molecular orbital (HMO) theory, where the σ-framework is completely neglected.
Silicon and germanium belong to Group 14 of the periodic table and thus are expected to be analogous to carbon. The silicon and germanium π-electron systems, however, differ remarkably in structure and stability from a carbon π-electron system [
3,
4,
5,
6,
7,
8], although the electronic structures are analogues and formally the same hybridization occurs. The rings of hexasilabenzene (SiH)
6 and hexagermabenzene (GeH)
6 are puckered as in a chair-like cyclohexane (
Scheme Ia) and are different from planar
D6h-symmetric benzene (
Scheme Ib) [
7,
8]. A common explanation for the difference in geometry between carbon and the heavier Group 14 elements was that the energy separation between valence s and p orbitals is small only in first-row elements, allowing efficient hybridization, and the energy separation in higher rows is much larger. Kutzelnigg revealed, however, that the energy separation between s and p orbitals is rather small in heavy atoms from the experimental data of s-p excitation energy with conservation of spin multiplicity [
9]. Nowadays, the following explanation has been vindicated: the essential difference between the atoms of the first and higher rows is that the cores of the former contain only s-atomic orbitals, whereas the cores of the latter include at least s- and p-atomic orbitals. The s and p valence atomic orbitals of first row atoms are localized in roughly the same region of space, while the p valence atomic orbitals of higher row atoms are much more extended in space. This has the consequence that, for the light main group elements, isovalent hybridization plays a greater role than for the heavy main group elements.
The synthesis of planar silicon and germanium hexagons is extremely challenging and very few are known. Nearly-planar hexagons consisting of Si and Ge were found in solid-state Zintl anions: Si
610− in Ba
4Li
2Si
6 and Ge
610− in Ba
4Li
2Ge
6 [
10]. These species are geometrically similar to benzene, but are Hückel arenes with 10
π electrons. The number of
π electrons is four more than in benzene. The hexagons are coordinated on both sides by barium. Planar hexasilylhexasilacyclohexene anions (Si
12) containing Si
6-ring system of approximate
D6h symmetry was obtained in unusual Zintl phase (Ca
7Mg
7.5±δSi
14) with metallic conductivity [
11], but the Si
6 ring is nonaromatic. The first flat aromatic
D6h-symmetric Si
6 and Ge
6 rings with six
π electrons were computationally designed by us as polyanionic clusters [
12,
13].
In this review, we mainly consider our findings on the flat
D6h-symmetric Si
6 and Ge
6, give the background to reach them, and propose a synthetically accessible molecule. The construction of the rest of the paper will be separated into sections discussing the following topics:
Section 2, the synthetic and theoretical background of unsaturated silicon and germanium compounds;
Section 3, Hückel arenes consisting of silicon and germanium found in Zintl phase of crystal;
Section 4, the stability of polyanionic clusters based on the electron-counting rule (Wade’s rule);
Section 5, the aromaticity of polyanionic Si
6 and Ge
6 rings with
D6h symmetry; and
Section 6, the design of synthetically accessible hexagons with the two-dimensional aromaticity. In each section, special attention is paid to the issue of aromaticity.
Section 7 provides a short summary and conclusion.
2. Synthetic and Theoretical Background of Unsaturated Silicon and Germanium Compounds
This section provides a short history of unsaturated silicon and germanium, highlighting several synthetic milestones, mainly in the case of silicon, and an elegant theory that analytically describes the geometric features. The challenging history in the attempt to obtain unsaturated silicon and germanium compounds as a mimic of the carbon system helps to clarify the difference from the carbon system.
Here, we introduce three significant experiments in the history of unsaturated silicon compounds. The multiple-bond rule took a dogma-status as the golden rule in silicon and germanium chemistry for a long time [
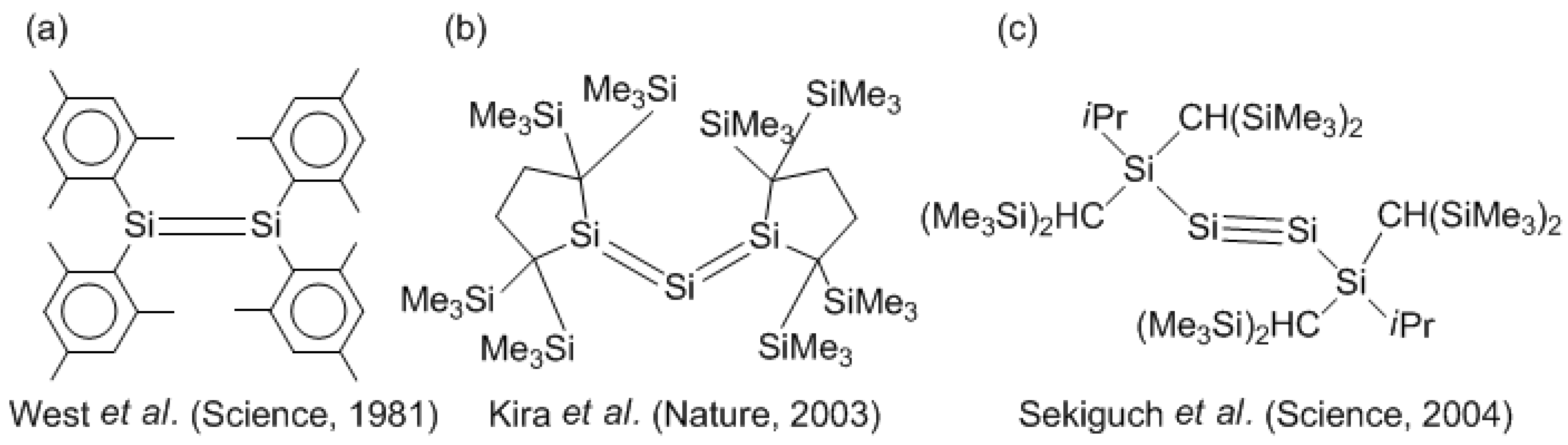
14]. The rule states that heavier Group 14 elements such as silicon and germanium cannot form multiple bonds because of the considerable Pauli repulsion between the electrons of inner shells. In 1981, West, Fink, and Michl broke through the multiple-bond rule with the synthesis of a stable Si–Si double-bond compound, tetramesityldisilene (
Scheme IIa) [
15]; this was the dawn of unsaturated silicon chemistry. The X-ray crystallographic measurement of tetramesityldisilene, performed by Fink, West, and coworkers [
16], revealed an astonishing fact: tetramesityldisilene adopts a
trans-bent geometry at the silicon–silicon double bond in crystal. The fact that the formally
π-conjugating double-bond compound does not have a two-dimensional skeleton stimulated further syntheses of various disilenes and investigations of the structures. Twenty years on from the first synthesis of a stable disilene, the synthesis and X-ray crystal analysis of the silicon-based allene analogue, trisilaallene (
Scheme IIb), were achieved by Kira and coworkers [
17]. The formally
sp-hybridized allene skeleton of the synthesized trisilaallene was not linear, which is different from the linear structure of allene in the carbon system. Soon after the synthesis of trisilaalene, a stable Si–Si triple-bond compound, 1,1,4,4-tetrakis[bis(trimethylsilyl)methyl]-1,4-diisopropyl-2-tetrasilyne (
Scheme IIc), was synthesized by Sekiguchi, Kinjo, and Ichinohe [
18,
19]. The structure of the isolated disilyne was revealed to be
trans-bent. The multiple-bond rule had been conquered, and unsaturated silicon chemistry remarkably progressed due to the synthesis of these three compounds; three milestones in unsaturated silicon chemistry. However, a problem remained, that is, the silicon skeletons of the isolated compounds are bending.
A donor-acceptor bonding model, or the Carter, Goddard, Malrieu, and Trinquier (CGMT) model [
20,
21,
22,
23,
24], explained well the
trans-bending of disilene and disilyne. From the explanation by this model in a valence bond scheme, the unsaturated bond of the
trans-bending disilene and disilyne, weakened by distortion from a classical planar or linear form, is stabilized by the delocalization of the n
σ lone-electron pair of one building block (SiH
2 or SiH) into the empty p
π*–atomic orbital of its partner (
Scheme III). Explaining with the donor-acceptor bonding model in a molecular orbital scheme, the distorted structure is stabilized by σ−π mixing. According to the CGMT model, the singlet-triplet energy separation of the building block,
ΔEST, governs the structural preference, giving planar, linear,
trans-bent, and bridged forms. The classical structure (planar or linear form), as in the carbon system, is obtained when the
ΔEST value is small enough. A planar disilene was theoretically realized by tuning
ΔEST with the electropositive substituent R (e.g., R is equal to Li, BeH, BH
2, and SH
3 in RHSi=SiH
2) [
25]. A classical allenic-type
D2d-symmetric trisilaallene, R
2Si=Si=SiR
2, was theoretically designed by the use of σ-donor π-acceptor substituents (R = BH
2) [
26], where the SiSiSi skeleton is linear, the terminal silicon atoms are planar, and the two terminal BSiB planes are perpendicular to each other. In understanding the less
trans-bent structure of disilyne, RSi≡SiH, it was revealed theoretically that electropositive silyl groups are electronically much more effective [
27,
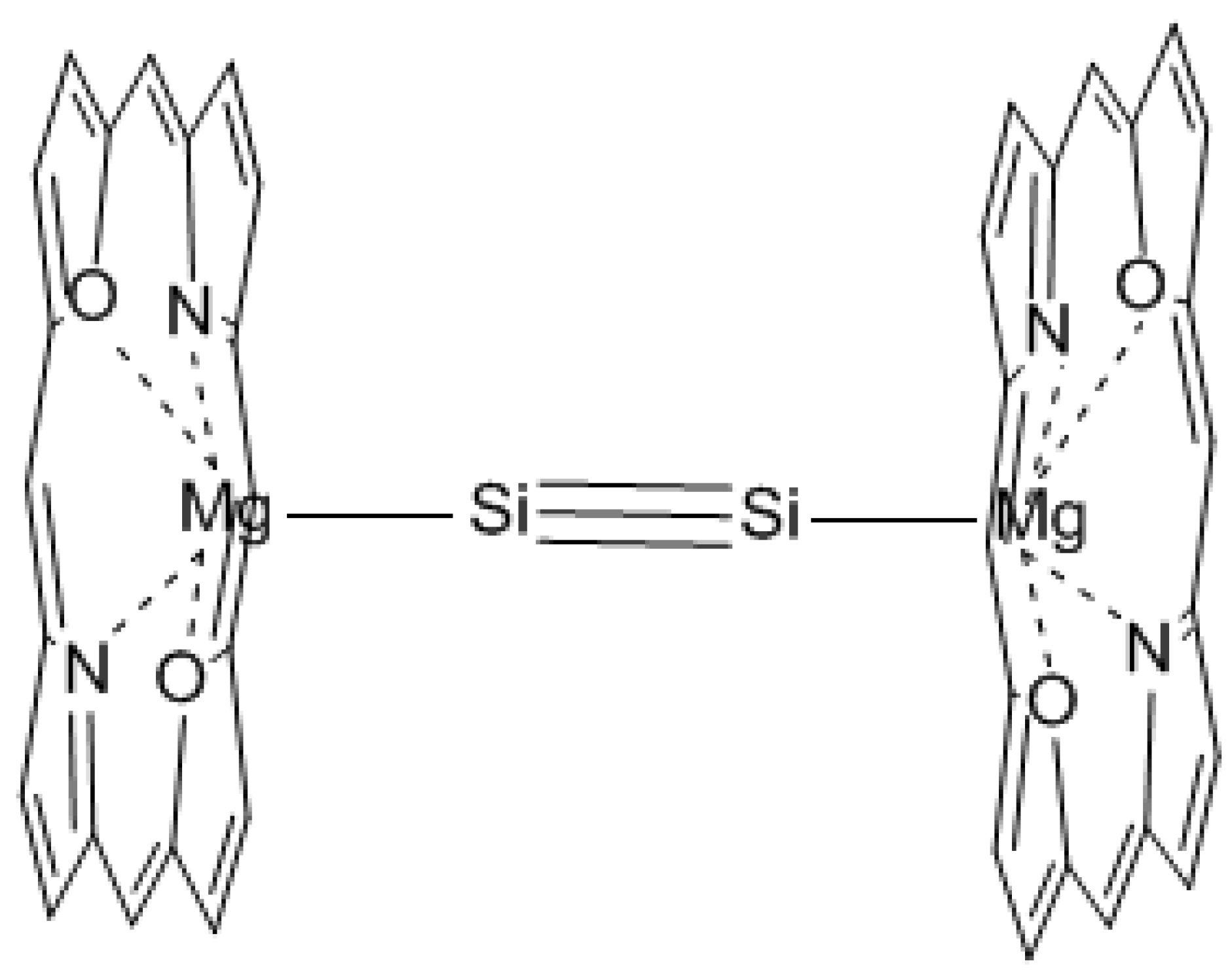
28], however, a complete linear form was not able to be obtained. The classical linear form of disilyne has been, for the first time, designed theoretically by us, where the substituent is an electron-donating magnesium-porphyrin complex which is core-modified to zero oxidation number for magnesium (
Scheme IV) [
29].
The effects of silicon and germanium substitutions on the aromaticity of arenes with 4
N + 2 π electrons have received much attention and the investigation has considerably progressed [
30,
31,
32]. The synthesis of silicon- and germanium-containing hexagons with a cyclic X
nC
6-n backbone (X = Si, Ge) have been reported only with n = 1 and 2 [
33]. Only the hexasilaprismane derivative was synthesized as a hexasila-analogue of (CH)
6 [
34], though five (CH)
6 isomers (benzene, benzvalene, Dewar benzene, prismane, and bicyclopropenyl) have been synthesized. Theoretical investigations supported the synthetic results, that is, hexasilaprismane is the most stable among the (SiH)
6 isomers [
35,
36,
37]. Despite exhibiting less stability compared to hexasilaprismane, hexasilabenzene and its aromaticity have been extensively studied as the analogue of benzene. The theoretically predicted nonplanar and chair-like structure of hexasilabenzene [
7,
8] is due to weaker π-electron donation to the bond than that of benzene. All possible isomerization pathways of hexasilabenzene were theoretically searched by using a newly developed anharmonic-downward-distortion-following (ADD-following) method, which finds all possible transition-states (TS) systematically and automatically [
38]. The search revealed the lowest barrier (only 74 kJ mol
−1) for the six-membered-ring structure. Three lower-lying TS structures identified around hexasilabenzene may be useful for designing a kinetically stable hexasilabenzene derivative that is protected from the isomerization reaction due to the TSs.
Several aromatic pentagons containing Group 14 atoms have been synthesized [
39]. Aromatic behavior such as the equalization of C–C bond lengths, the planar structure of pentagonal rings, and the negative NICS (nucleus-independent chemical shift) values was obtained for the synthesized compounds; the dianions of tetraphenylsilole, tetraphenylgermole, 9-silafluorene, and 9-germafluorene, and also neutral pentagons of diiminosilylenes and diiminogermylenes. These pentagons may be six-π-electron rings due to the donation of an electron from cation or nitrogen.
Homoaromaticity was introduced by Winstein in 1959 to describe compounds that display aromaticity despite one or more saturated linkages interrupting the formal cyclic conjugation, and is nowadays well-established in organic chemistry. Most recently, the 2(N + 1)
2 electron-counting rule for spherical molecules has been employed to design a series of spherically homoaromatic hydrocarbons [
2,
40]. The rule was applied by Chen and coworkers [
41] to a series of spherical sila- and germa-homoaromatic systems with the help of density-functional-theory calculations. The spherical homoaromaticity would be another way to stabilize silicon and germanium clusters.
3. Hückel Arenes Consisting of Silicon and Germanium
Synthetic attempts to obtain planar hexagonal molecules consisting of Si and Ge gave miserable results, but nearly-planar and hexagonal Hückel arenes were found in crystal as Zintl anions. Most of the elements form atomic negative ions, and multiply charged anions are commonly observed in crystal and solution, but no stable anion bearing multiple charges is isolated in the gas phase. Theoretical investigations for the gas-phase anions were limited to monoanion radicals and electron affinities. Recently, we found that multiply charged systems are helpful for a systematic understanding of the stability of silicon π-electron systems [
42].
Three types of anionic hexagons consisting of Si and Ge were found in Zintl crystal [
10,
11]. One contains a planar hexasilylhexasilacyclohexene unit (Si
12) surrounded by Ca and Mg [
11], but the hexagon is not an aromatic ring. The other two are depicted in
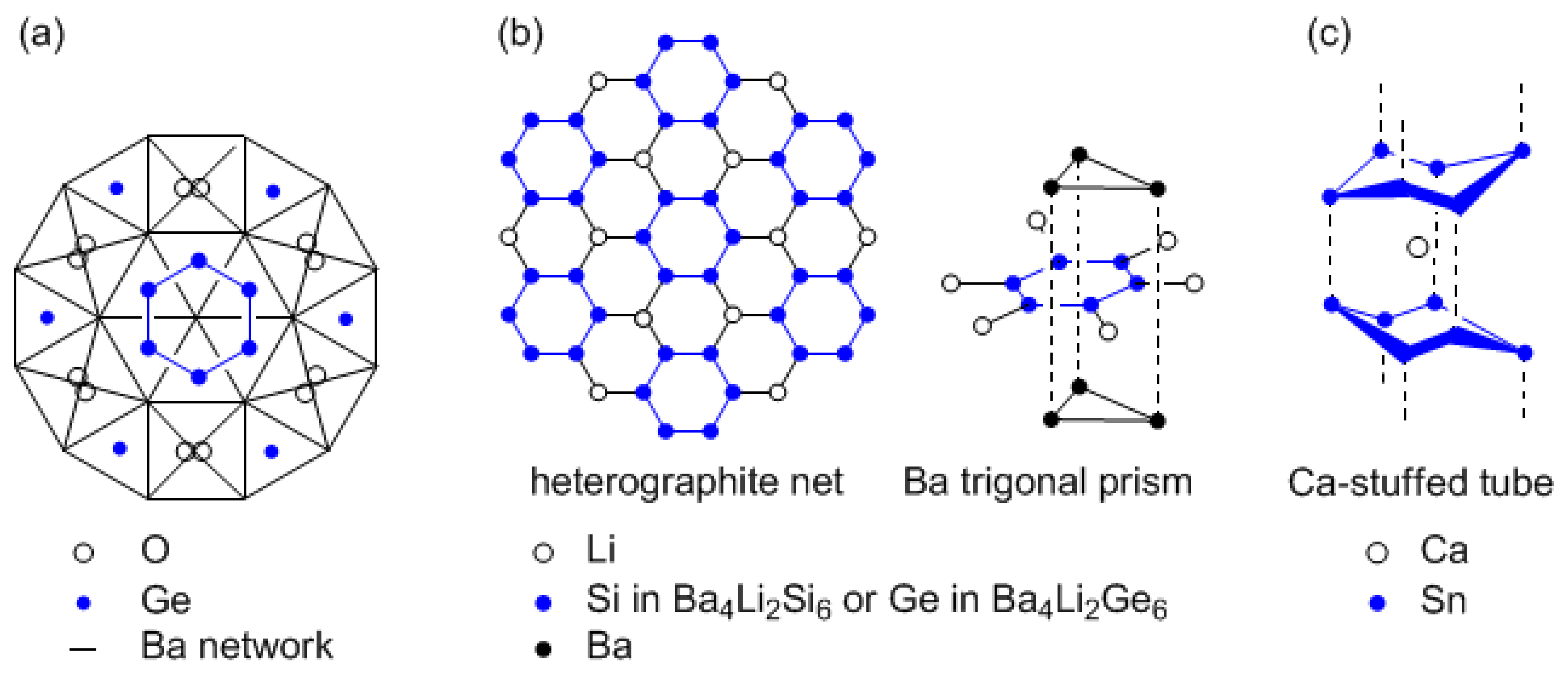
Scheme Va and b. The new, unusual germanium oxide Ba
10Ge
7O
3, containing six-membered germanium rings, was discovered by systematic investigation into the formation of clathrates in the Na/Ba/Ge ternary system (
Scheme Va) [
10]. Here, Ba atoms construct the framework of linked monocapped trigonal prisms and tetragonal bipyramids. The polyhedra are centered either with isolated Ge atoms, with O atoms, or with Ge atoms that belong to six-membered Ge rings. The electron count fulfills the Zintl-Klemm concept with the formal charge distribution according to Ba
2+, O
2−, Ge
4−, Ge
610−. The Ge
610− reveals a cyclic system with 34 electrons. The six-membered silicon and germanium rings in Ba
4Li
2Si
6 and Ba
4Li
2Ge
6 are linked by Li atoms to form a heterographite net and are coordinated on both sides by Ba trigonal prisms (
Scheme Vb), where the hexagons are slightly puckered (boat conformation, torsion angle ±4º). The formal charge distribution is Ba
2+, Li
+, Si
610−, Ge
610−. Bonding within the 34-electron systems in Si
610− and Ge
610− can be elucidated in terms of Hückel formalism. 24 of the 34 electrons construct six σ bonds and six n electron pairs. The remaining 10 electrons contribute to the π system and fill the three bonding and two antibonding molecular orbitals (MOs). The isolated Si
610− and Ge
610− anions can be treated formally as an aromatic system with 10 π electrons. The Si
610− and Ge
610− polyanion with 34 valence electrons, which is analogous to cyclohexene, appears to be particularly stable in the Zintl phase containing very electropositive metals. The existence of planar or nearly-planar silicon and germanium hexagons has been proved for the case of 10-π-electrons systems. The problem of coordination by Ba atoms on both sides, which would interrupt the out-of-plane π conjugation, remains.
A next experimental challenge is to find the planar or nearly-planar silicon and germanium hexagons with six π electrons. The first attempt at producing a six-π−electrons hexagon of Group 14 elements in Zintl crystal was made for tin: Sn
66− rings were synthesized that were separated by alkaline-earth cations in Na
4CaSn
6 [
43]. The resulting compound, synthesized from a stoichiometric mixture of the elements at high temperature, has the “correct” stoichiometry with six tin atoms and six positive charges. However, the Sn
66− rings are puckered into chair-type structure and are interconnected into isolated cylindrical tubes stuffed with Ca
2+ between the rings (
Scheme Vc). The Ca-stuffed tubes of Sn
66− are embedded in a matrix of sodium cations. Zintl crystals opened the way for planar benzene-like hexagons with six π electrons, though Si
66− and Ge
66− have not been synthesized yet. Another problem that remains in the design of planar benzene-like hexagons with six π electrons is to place the cations at noninteracting positions with π orbitals.
4. The Electron-Counting Rule for Aromatic Stabilization
Electron-counting rules frequently play a crucial role in finding the most stable structure of clusters and molecules. A well-known electron-counting rule related to aromaticity is the Hückel 4
N + 2 π-electron rule, where the out-of-plane π electrons of a two-dimensional planar molecule are counted and the orthogonal in-plane σ electrons are completely neglected. Wade’s 2
n + 2 skeletal electron-counting rule was developed in borane chemistry, where n is the number of skeletal atoms and all skeletal electrons of the three-dimensional molecule are counted. The three-dimensional aromatic stabilization of deltahedral borane series following Wade’s rule is connected to that of a planar molecule obeying the Hückel 4
N + 2 π electron rule at the limit of two dimensions. Wade’s rule is a function of two variables: the number of total vertices of the polyhedra and the number of missing vertices with respect to its
closo form. Both of them are exclusively system specific. Jemmis and coworkers reviewed the extension of the electron-counting rule to macropolyhedral boranes [
44]. Hirsch’s 2(
N + 1)
2 electron rule is a recent refinement for the highest symmetrical and most spherically aromatic clusters [
45]. Three-dimensional aromaticity was applied to anionic silicon clusters by Schleyer and King [
46] and was reviewed by King [
47].
Wade’s rule empirically relates the discrete skeletal structure of polyhedral boranes, such as
closo,
nido, and
arachno, to the number of skeletal binding electrons. The skeletal structures of boranes are given the descriptive names of cage-like, nest-like, and cobweb-like, for
closo,
nido, and
arachno types, respectively. In other words, these structures are the closed polyhedron, mono-capped polyhedron, and two-dimensional cluster, respectively. Though exceptions to this rule are also found [
48], it is impossible to understand the several distinct patterns exhibited by polyhedral boranes without this rule. Boron atoms of
closo-borane, having a formula of (BH)
n2−, occupy all vertices of closed three-membered rings of a polyhedron. In
nido-borane, with a formula of (BH)
nH
4, and
arachno-borane, with a formula of (BH)
nH
6, a closed polyhedron with m vertices is assumed by adding one (m = n + 1) and two (m = n + 2) missing vertices, respectively. Boron atoms occupy n vertices among m vertices of the closed polyhedron giving a mono-capped polyhedron in
nido-borane and a two-dimensional cluster in
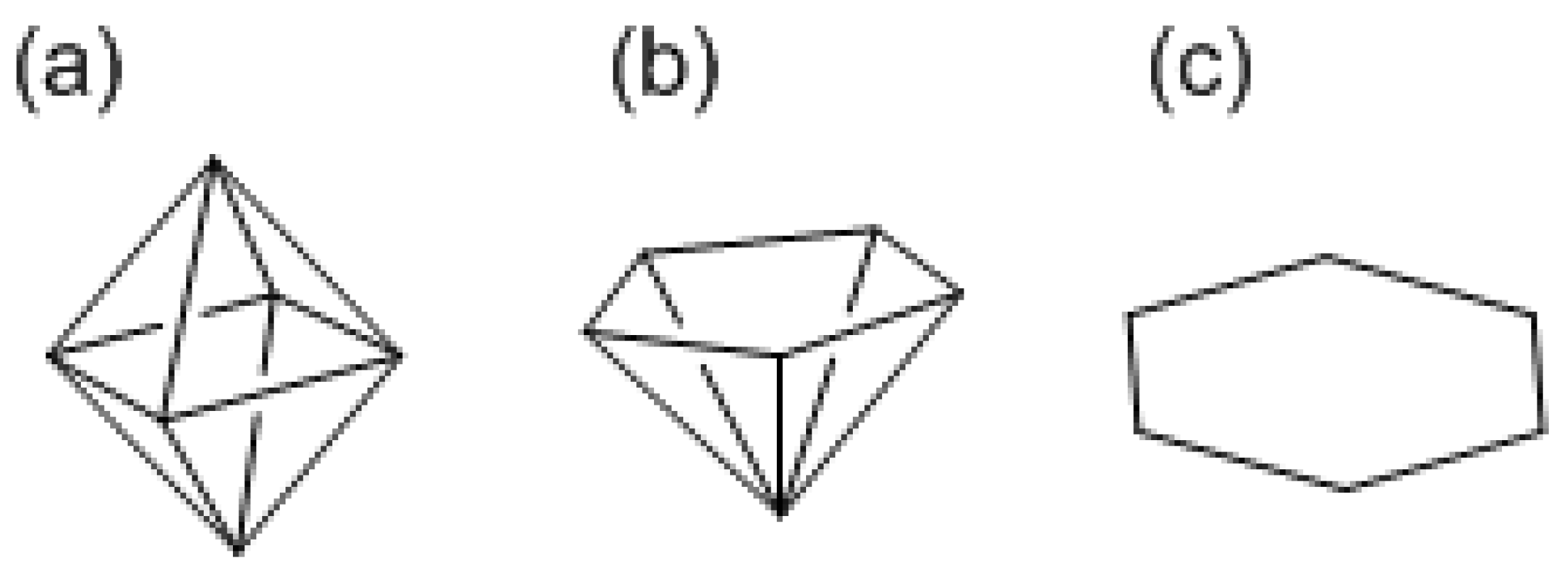
arachno-borane. The number of skeletal binding molecular orbitals is in all cases one more than the number of vertices, m, of the assumed polyhedron, and the number of skeletal binding electrons is 2(m + 1). The skeleton consisting of BH requires two, four, and six extra electrons, respectively. Applying the rule to the clusters with six atoms, the
closo,
nido, and
arachno forms are schematically octahedron, pentagonal pyramid, and hexagon, respectively (
Scheme VI). According to Wade’s rule, there are nine binding orbitals for the hexagon where an eight-vertex polyhedron is assumed for the six-atom
arachno form. The molecular structure of gaseous arachno-B
6H
12 determined by electron-diffraction is nonplanar, consisting of nine B–B bonds and four B–H–B bonds [
49]. Carbon is isoelectronic with BH, and thus C
6H
6 corresponds to (BH)
6H
6, giving an
arachno form as the most stable isomer. The nine orbitals are replaced by six σ and three π in arachno-C
6H
6. The
arachno-form is a contact point between Wade’s rule for three-dimensional aromaticity and Hückel’s 4
N + 2 rule for two-dimensional aromaticity in the carbon system. Silicon is isoelectronic with BH too, and thus Si
6H
6 should give an
arachno form as the most stable structure, like in C
6H
6. The chair-like structure of Si
6H
6 is regarded as a deformed
arachno form.
Before determining the most stable structures of polyanionic Si
6 clusters, we detail all possible structures of (SiH)
6. Among 200 different possible structures for the molecular formula of C
6H
6 [
50], Balaban called the structures described by the formula (CH)
6 as the valence isomers of benzene. Each carbon atom bears a single hydrogen atom in the valence isomer, and the difference between the isomers is the way in which the carbon–carbon single and double bonds connect six CH units. Balaban enumerated the possible valance isomers of (CH)
6 and found there to be a total of six: planar regular hexagon (
1), benzvalene (
2), Dewar benzene (
3), triangular prismane (
4), bicyclopropenyl (
5), and Claus benzene (
Scheme VII). The Claus benzene has carbons at the corners of a regular hexagon, each carbon connected to the nearest (
ortho) neighbors on the perimeter of the hexagon and to the
para carbon diametrically across the hexagon. Octahedron
6 and twisted prismane can have the same connectivity as Claus benzene (in parentheses of
Scheme VII). Octahedron
6 and planar hexagon
1 are regarded as a
closo and an
arachno form, respectively. The chair-like (
7) and twisted-boat (
8) isomers were found in addition to the valence isomers
1–
6 of (CH)
6, for P
6 isoelectronic with (SiH)
6.
7 and
8 are regarded as deformed hexagons. Consequently, the possible valence isomers of (SiH)
6 are a total of eight including the deformed hexagons.
The most stable structures of polyanionic silicon clusters, Si
6n− (
n = 2,4,6), were searched for, starting with the MP2 and B3LYP electronic structure calculations from the eight possible structures of valence isomers enumerated above. We found 12 isomers existing as equilibrium structures for the multiply charged clusters [
51]: six for Si
62−, five for Si
64−, and one for Si
66−. Among them, the most stable structures of Si
62−, Si
64−, and Si
66− are octahedral (
closo), pentagonal pyramidal (
nido), and hexagonal (
arachno), respectively (
Scheme VI). The multiply charged clusters, Si
62−, Si
64−, and Si
66− correspond to the boranes (BH)
62−, (BH)
6H
4, and (BH)
6H
6, respectively, by replacing the respective BH units and hydrogen atoms in borane with the isoelectronic Si and electrons in anionic silicon clusters. Si
66− is isoelectronic with (SiH)
6 as well. Consequently, the relationship between the stable structures of multiply charged silicon clusters and the number of valence electrons matches the prediction of Wade’s rule. In general, as the number of doped electrons increases, the clusters in the gas phase become unstable. However, the octahedral structure of Si
62− is more stable than neutral Si
6 [
51]. The binding energy of electrons in the octahedral geometry is 79 and 196 meV/electron with the MP2 and B3LYP/6-311+G(3df) method, respectively, including zero point energy correction. Two years after our theoretical design of the planar anionic Si
6 rings with
D6h symmetry, Si
6 rings with lithium atoms as an electron donor were computed [
52,
53] and three types of
arachno silicon clusters—depending on the position of lithium atoms—were revealed as an equilibrium structure of (Si
66−)(Li
66+). Unfortunately, the
D2h-symmetric
arachno silicon cluster with short (2.319 Å) and long (2.366Å) Si-–Si bond lengths is the most stable and the
D6h–symmetric one is the second most stable.
Since germanium belongs to the same group as silicon in the periodic table, Ge clusters are expected to show similar structures and properties to the corresponding Si clusters. It is known that neutral (GeH)
6 adopts a nonplanar six-membered ring [
8], as in neutral (SiH)
6, and thus the stable structures of anionic germanium clusters has been investigated. Germanium proved to be a good model post-transition element to avoid the difficulty of high charge in converging to the individual atoms, since the magnitudes of the charges on bare germanium clusters were minimized for the skeletal electron counts of interest for comparison with experimental data [
54]. King and coworkers theoretically investigated the stable structures of Ge
nZ clusters (n = 5–11, Z = – 6 to + 6). Experimentally, a dianion cluster consisting of six germanium atoms with organometallic protective groups was obtained in matrix and the structure of the Ge
6 moiety was revealed to be octahedron [
55]. This means that Ge
62− has the
closo form which agrees with the prediction of Wade’s rule and the result of Si
62−. We have systematically investigated the stable structures of anionic Ge
6 clusters [
13]. A common feature for anionic germanium and silicon clusters is that both anions have preferable structures according to Wade’s rule. The highest occupied molecular orbital (HOMO) of the most stable charged clusters consisted mainly of the lone-electron pair orbitals.
5. Planar and Aromatic Si6 Hexagons
A planar structure is essential for the
π conjugation and
sp2 hybridization, and thus for two-dimensional aromaticity. A planar six-membered silicon ring was not found in neutral molecules for a long time, despite numerous theoretical and experimental attempts. In our theoretical studies of anionic clusters, it was revealed that Si
62− and Si
66− could possibly have a
D6h isomer as benzene [
12]. In this section, the aromaticity of the flat Si
6 ring anions is examined.
To investigate bonding nature and hybridization, we performed natural bond orbital (NBO) analysis [
12]. The analysis of
D6h-symmetric Si
66− showed nine bonding and six lone-electron pair orbitals as well as 30 doubly occupied core orbitals (more than 1.999 occupation) when the occupancy threshold is taken to be 1.60. The nine bonding orbitals are six Si–Si bonds with
sp2.1 hybridization and three Si–Si bonds with
pπ hybridization. Six lone-electron pair orbitals exist at silicon instead of the six C–H bonding orbitals in benzene. From the
D6h symmetry and the hybridization, Si
66− is a system of six
π electrons on a
sp2 silicon backbone like benzene. The Si–Si bond length of
D6h-symmetric Si
66- is 2.378 Å and the length is longer than the Si–Si single bond of neutral silicon compounds (in Si
2H
6, 2.339 Å at the MP2/6-311++G(d,p) level). The unexpectedly long Si–Si bond lengths of
D6h-symmetric Si
66− would be due to the electron repulsion among well accommodated electrons.
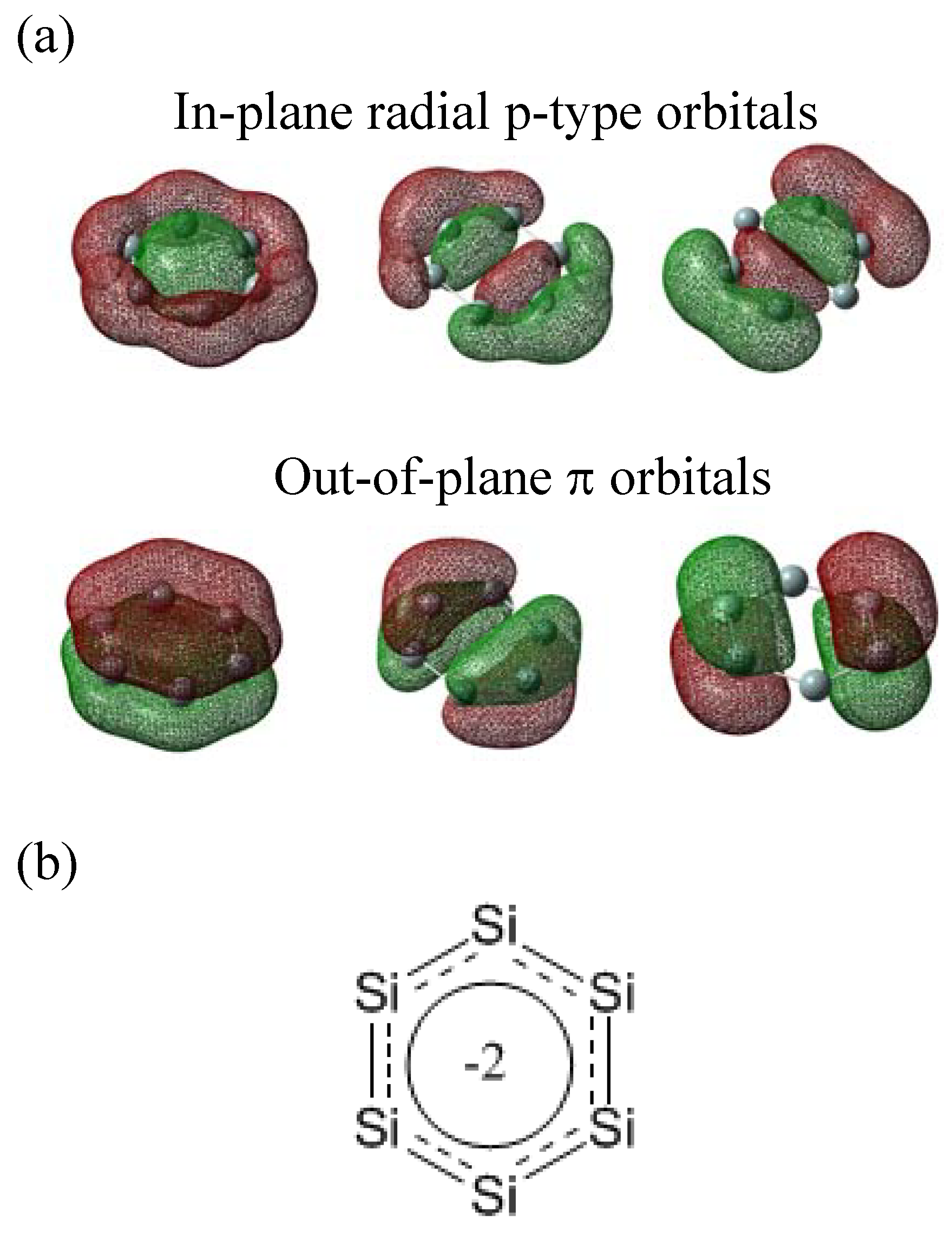
The bonding nature of
D6h-symmetric Si
62− is clearly different from benzene and from
D6h-symmetric Si
66− as well. The NBO analysis showed six p-type orbitals and six
σ orbitals with sp
1.6 and sp
0.8 hybridizations as bonding orbitals. The six p-type orbitals are three Si–Si bonds with
sp14.8 hybridization and three Si–Si bonds with
pπ hybridization. The p-type molecular orbitals of
D6h-symmetric Si
62− are drawn in
Scheme VIIIa. Three of the six are in the molecular plane and the other three are out of the molecular plane. The three in-plane radial-type p orbitals overlap in the center, resulting in σ-bonding and contributing to σ-aromaticity. The Si
62− contains two 6-electron conjugated systems in perpendicular planes (
Scheme VIIIb). Two orthogonal Hückel frameworks within a single molecule are first conceived by Schleyer and coworkers [
56] in 1979, and nowadays are known as double aromaticity. Schleyer and coworkers have later reported the appearance of double aromaticity in
D6h cyclic C
6 cluster [
57] in the carbon system. The Wiberg bond indexes of the neighboring Si-Si bonds on the perimeter of hexagon and diametrical Si-Si bonds are 1.587 and 0.361 at the MP2/6-311++G(3df,3pd) level. The values are larger than those for benzene (1.441 and 0.114) at the same level. Larger Wiberg bond indexes compared with aromatic benzene was also observed in the doubly aromatic
D6h cyclic C
6 cluster. The difference of Si
62− from the doubly aromatic
D6h cyclic C
6 cluster is that the Si
62− cluster is dianion. The occupancy of antibonding orbitals is not negligible (0.3~0.4) but the occupancy of a p-type orbital and the corresponding unoccupied orbital sums up to nearly two (1.99). The delocalization to unoccupied orbital is the same phenomenon as in benzene. It can be concluded that every six p-type electrons are accommodated in the out-of-plane and in-plane radial orbitals, and delocalize. The σ and σ* orbitals accommodate a total of 14 electrons, where the extra two electrons in σ* orbitals leads to dianion. The Si–Si bond length of 2.24 Å is between the Si–Si single and double bonds (2.339 Å for Si
2H
6 and 2.163 Å for Si
2H
4 at the MP2/6-311++G(d,p) level). This feature is the same as in benzene, where the C–C bond length is between the C–C single and double bonds. Unfortunately,
D6h-symmetric Si
62− is much less stable than octahedral Si
62−, by 1.12 eV/Si at the MP2/6-311+G(3df) level. It is interesting that the total number of
π electrons accommodated in the out-of-plane π orbitals is the same as the total number of silicon atoms in both
D6h-symmetric Si
66− and Si
62− and is independent of the number of doped electrons.
From the symmetry and the number of out-of-plane
π electrons revealed by NBO analysis, the Si
62− and Si
66− hexagons are candidates for aromatic six-membered silicon rings. Nucleus independent chemical shift (NICS) is a well-known index of aromaticity [
58,
59,
60]. NICS evaluates the aromaticity/antiaromaticity using absolute magnetic shieldings computed at ring centers with an available quantum mechanics program. To correlate to a familiar convention of NMR chemical shift, the signs of the computed magnetic shielding values are reversed. The proposal of NICS as an aromaticity probe is based on the observation of abnormal chemical shifts of protons located inside the aromatic ring current. Positive NICS values denote antiaromaticity and negative ones aromaticity. To weaken the local contributions of nearby σ bonds, the measuring point of the NMR chemical shift is placed 2 Å away above the ring center in the later refinement. The best performing NICS aromaticity index is NICS(0)
πzz, π molecular orbital contribution to the zz component of the NICS tensor of the molecule in the XY plane [
61]. On the other hand, a more readily available, easy to use, and very good alternative NICS index is NICS(1)
zz, total molecular orbital contribution to the zz component of the NICS tensor computed 1 Å away from the center above rings. The NICS values of
D6h-symmetric Si
66− and
D6h-symmetric Si
62− were calculated to be positive indicating antiaromaticity and negative indicating aromaticity, respectively. Unfortunately,
D6h-symmetric Si
66− is antiaromatic, though the Lewis structure is similar to aromatic benzene. It would be due to the long Si–Si bond length of
D6h-symmetric Si
66− and thus the weak
π interaction. The NICS value of
D6h-symmetric Si
62− has a minimum around 1.5 Å above the ring, which means
π-ring current causes the chemical shift [
60]. It turns out that the
D6h-symmetric Si
62− is doubly aromatic from NBO analysis and it was confirmed from the NICS values that the out-of-plane
π electrons in the doubly aromatic Si
62− actually shows aromaticity. Since the most stable, and thus the most preferable isomer of Si
62− is octahedron, in accord with Wade’s rule, a kinetic stabilization preventing isomerization to octahedron is required to obtain the less stable planar and hexagonal Si
62−.
6. Design of Synthetically Accessible Aromatic Hexagons
We recently reported a singlet dianion, Si
2H
22−, as a doubly bonded species [
12] where lone pair orbitals locate at silicon. Though sodium doped silicon clusters (Si
nNa
m; n = 1~14, m = 1~5) were firstly produced by laser vaporization in 1997, [
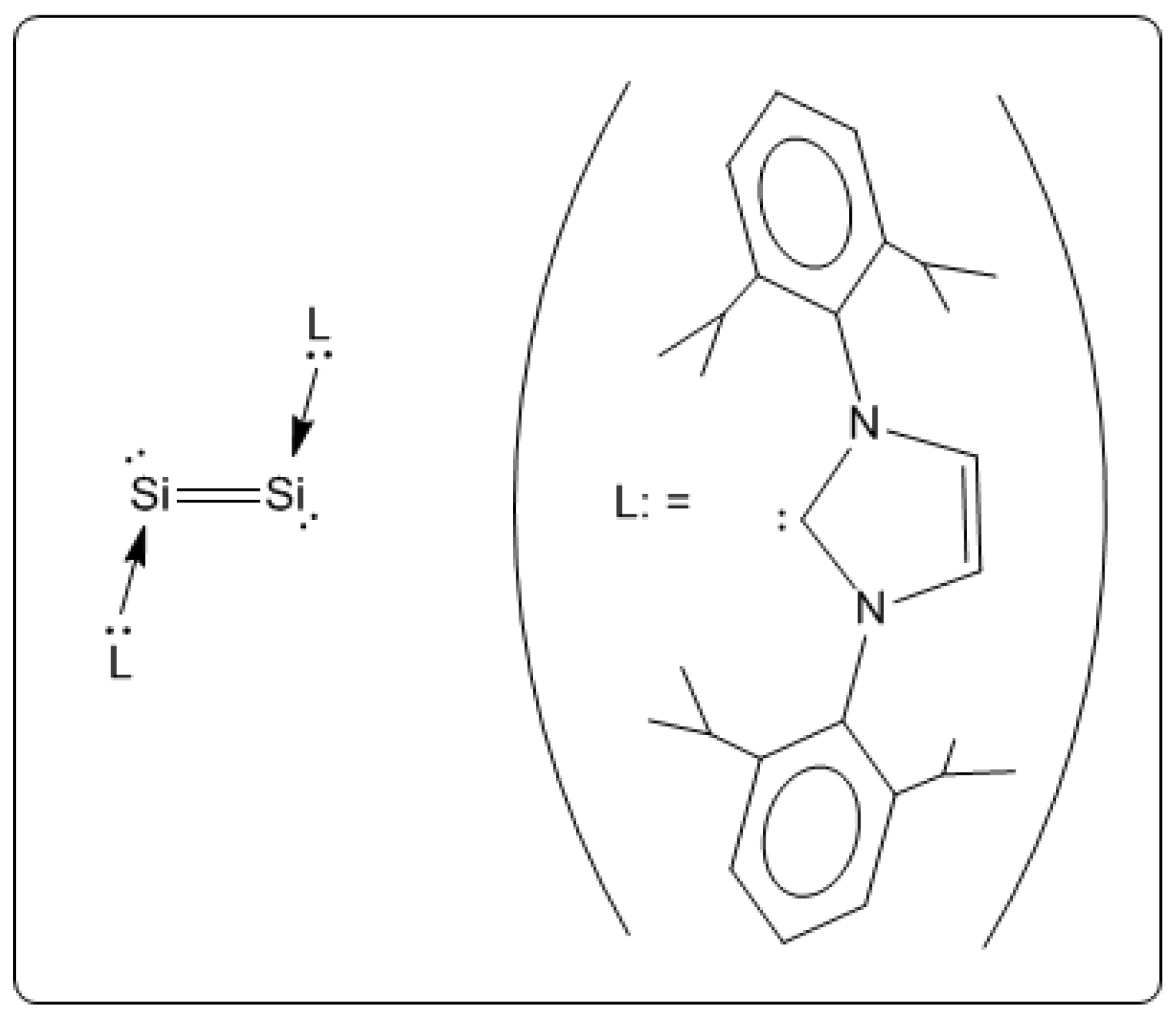
62], the main interest at the time was monoanion (m = 1), and several multiply charged clusters that were observed were nearly neglected. Very recently, after our theoretical design of Si
2H
22−, a carbene-stabilized diatomic silicon molecule L:Si=Si:L (L:= :C{N(2,6-Pr
i2C
6H
3)CH}
2), with Si atoms in the formal oxidation of zero, was synthesized [
63] (
Scheme IX). Dative, or nonoxidative, ligand coordination is common in transition metal complexes, but this bonding motif is rare in compounds of main group elements in the formal oxidation state of zero. The Si–Si bond distance in the carbine-stabilized diatomic silicon molecule is 2.229 Å, which is consistent with a double bond.
Two years after our theoretical finding of planar anionic Si
6 rings with
D6h symmetry [
12], Si
6 rings with a lithium atom as an electron donor were theoretically investigated [
52,
53]. It was confirmed that the resulting planar Si
6Li
6 structure is both stable and aromatic, with lithium atoms found halfway between two adjacent silicons and attracting the formation of three-center bonds (
Scheme Xa). The structure is fully analogous to
D6h-symmetric hexalithiobenzene, C
6Li
6 [
64]. However, from extensive investigation of several isomers of Si
6Li
6 clusters, it was found that the most stable isomer is not the
D6h-symmetric structure, but the
D2h-symmetric structure with four Li atoms in-plane and two Li atoms out-of-plane (
Scheme Xb). The natural population analysis (NPA) charge of the Si
6 ring moiety in
D6h- and
D2h-symmetric isomers totals −5.0 and −5.2 at the B3LYP/6-311++G(3df) level, respectively. It is found that the NPA charge of the
D2h-symmetric structure is a little closer to −6 than that of the
D6h-symmetric structure. Since hexa-anionic Si
66− prefers an
arachno–type structure (hexagon) according to Wade’s rule, the hexagonal structure would be more stable in the arrangement of metal atoms giving the NPA charge closer to −6. The most stable isomer is deformed to lower
D2h symmetry, having long (2.366 Å) and short (2.319Å) Si–Si bond lengths, and has metal atoms over the ring skeleton, unfortunately interrupting π-ring current.
A synthetically accessible molecule containing an ideal
D6h-symmetric Si
6 ring is desired where no metal atom is over the ring skeleton and thus the
π-ring current is not interrupted. We use a planar
D6h-symmetric Si
6Li
6 as the core structure and diethyl ether O(Et)
2 (Et: CH
2CH
3) as the substituents at lithium. LiO(Et)
2 was used previously by us for the synthesis of anionic ethylene [
65]. To prevent the isomerization to
D2h-symmetric Si
6Li
6, diethyl ether is connected by (CH
2)
4 chains (
Figure 1). The equilibrium structure optimized at the B3LYP/6-31G(d) level has Si–Si bond lengths of around 2.31–2.32 Å, which is between the lengths of single and double silicon bonds. The six-membered-ring skeleton is nearly planar with dihedral angles between −3.8° and 5.7°.
7. Conclusions
In this paper, we have summarized and extended our findings presented in [
12,
13,
29,
51]. The goal has been to design the aromatic and planar hexagons of silicon and germanium without the coordination of metal atoms over the ring. After the introduction of geometric features of the unsaturated silicon and germanium compounds, we stated the difficulty in the synthesis of unsaturated silicon and germanium compounds in the second section; a long history of challenges, despite that silicon and germanium belong to Group 14 of the periodic table and are analogous to carbon. We introduced the CGMT model, a current explanation for the nonclassical structure of unsaturated silicon and germanium compounds. In our recent findings by computational studies of the unsaturated silicon and germanium systems with classical structures like
D6h-symmetric benzene and linear acetylene, an anionic system and/or metal substitution were used. In the third section, we introduced anionic hexagons of silicon, germanium, and tin that were found experimentally in the Zintl phase of crystal as Hückel arenes. In the fourth section, we described an electron-counting rule known as Wade’s rule. Wade’s rule predicts the preferable structures of anionic polyhedrons well, and the most stable anionic silicon and germanium clusters are in accord with the prediction of this rule. In the fifth section, we examined the aromaticity of flat Si
6 rings found in anionic system. In the sixth section, we summarized the recent theoretical studies of synthetically accessible aromatic hexagons and proposed a more ideal benzene-like hexagon.
The preferable structure of anionic Si6 and Ge6 clusters obeys the prediction of Wade’s rule, an electron-counting rule. Planar hexagon is regarded as the so-called arachno type in Wade’s rule. So, the Si66− and Ge66− clusters prefer planar hexagons from the number of electrons counted. The electronic feature of silicon and germanium is similar to each other. We investigated the silicon system in more detail. It was revealed that the Lewis structure of Si66− is the same as benzene, but the Si66− ring is antiaromatic due to the weak π-electron interactions and long Si–Si bond length under strong electron repulsions. The most stable structure of Si62− is an octahedron according to Wade’s rule, but Si62− has a planar hexagonal isomer as an equilibrium structure. The hexagon does not take the same Lewis structure as benzene, but is aromatic. The D6h-symmetric Si62− is a doubly aromatic molecule with two 6-electron conjugations in perpendicular planes and has two extra electrons accommodated in the σ* orbital. The two extra electrons have a key role in stabilizing the planar hexagonal structure, because a neutral Si6 cluster gives no planar hexagon as a minimum. By suppressing the isomerization to octahedron with substituents in Si62− system, it would be possible to obtain the doubly aromatic and planar Si6 hexagon.
Finally, we discuss the reason why the classical form was found in anionic system against the explanation of CGMT model. It is well known that the six-membered silicon and germanium rings take a chair-like form due to σ-π mixing as indicated by the CGMT model. However, the anionic hexagons found by us prefer a planar form. We also recently found a classical linear form of silicon-silicon triple bond. Usually the silicon-silicon triple bond takes a bent form due to σ−π mixing and/or donor-acceptor bonding. A common electronic feature among the unsaturated silicon and germanium compounds, providing classical structures as linear triple bond and D6h-symmetric hexagon, is the existence of occupied orbitals above occupied π orbitals; those would prevent the σ-π mixing.