Adaptive Fault-Tolerant Sliding Mode Control Design for Robotic Manipulators with Uncertainties and Actuator Failures
Abstract
1. Introduction
- A novel sliding surface is proposed, which combines both the hyperbolic tangent function-based practical and fast terminal sliding manifolds. This enhances the algorithm’s robustness and the controller’s performance while ensuring global nonsingularity.
- An adaptive strategy is proposed, eliminating the requirement for prior knowledge of upper bounds on uncertainties, thereby enhancing flexibility and applicability.
- This study provides a passive FTC approach with finite-time convergence to address the adverse effects of external disturbances and actuator failures.
2. Problem Statement and Preparation
2.1. Problem Statement
2.2. Preliminaries
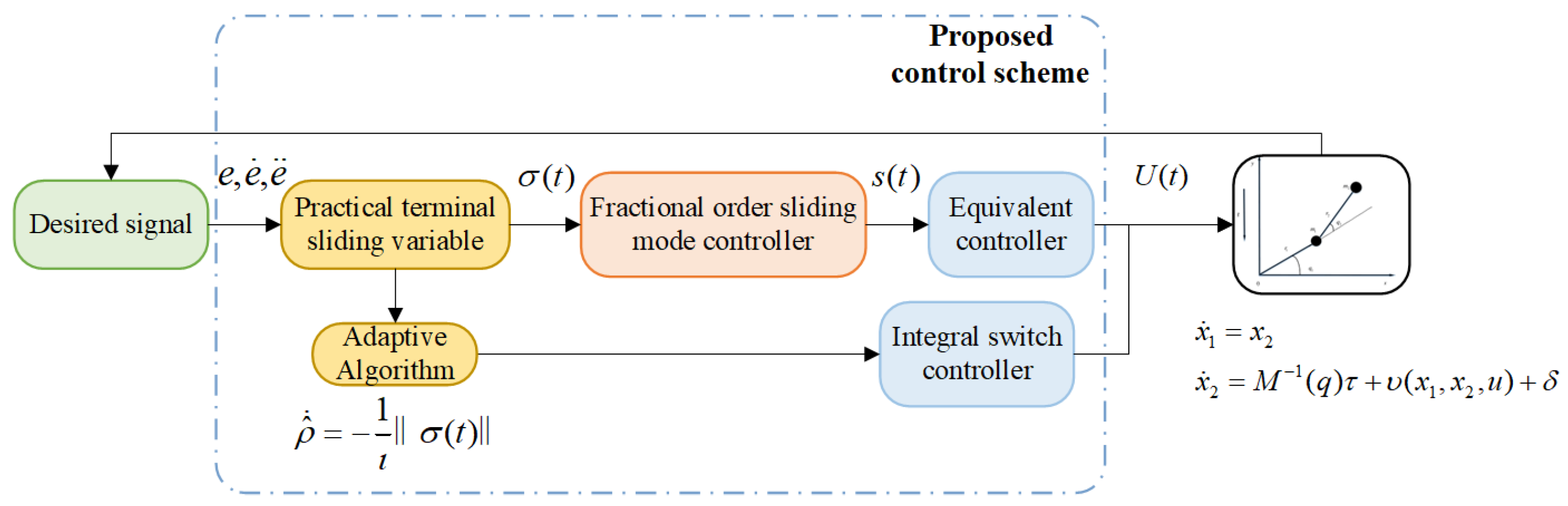
3. Adaptive Full-Order Sliding Mode Controller Design
Stability Analysis
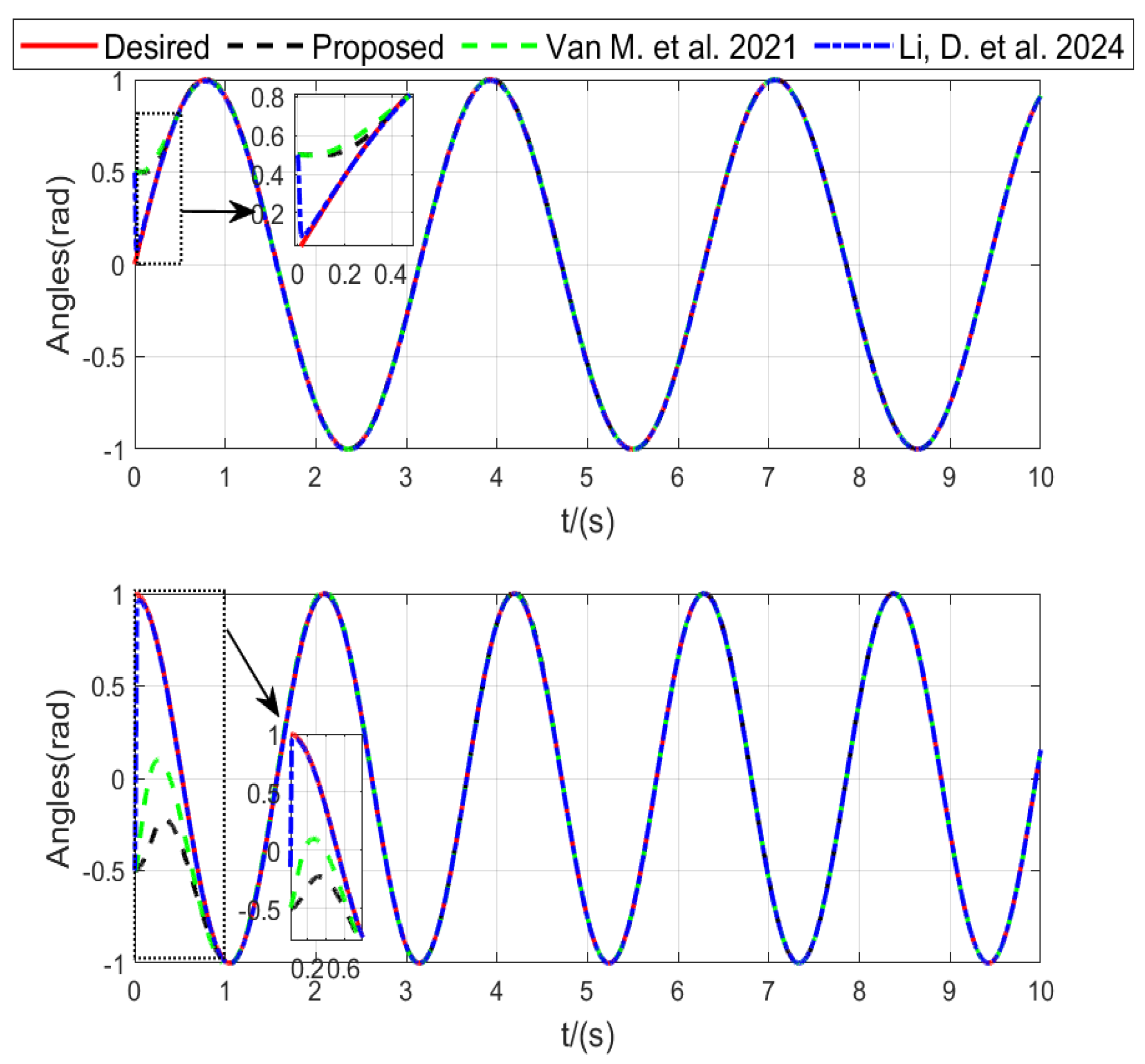
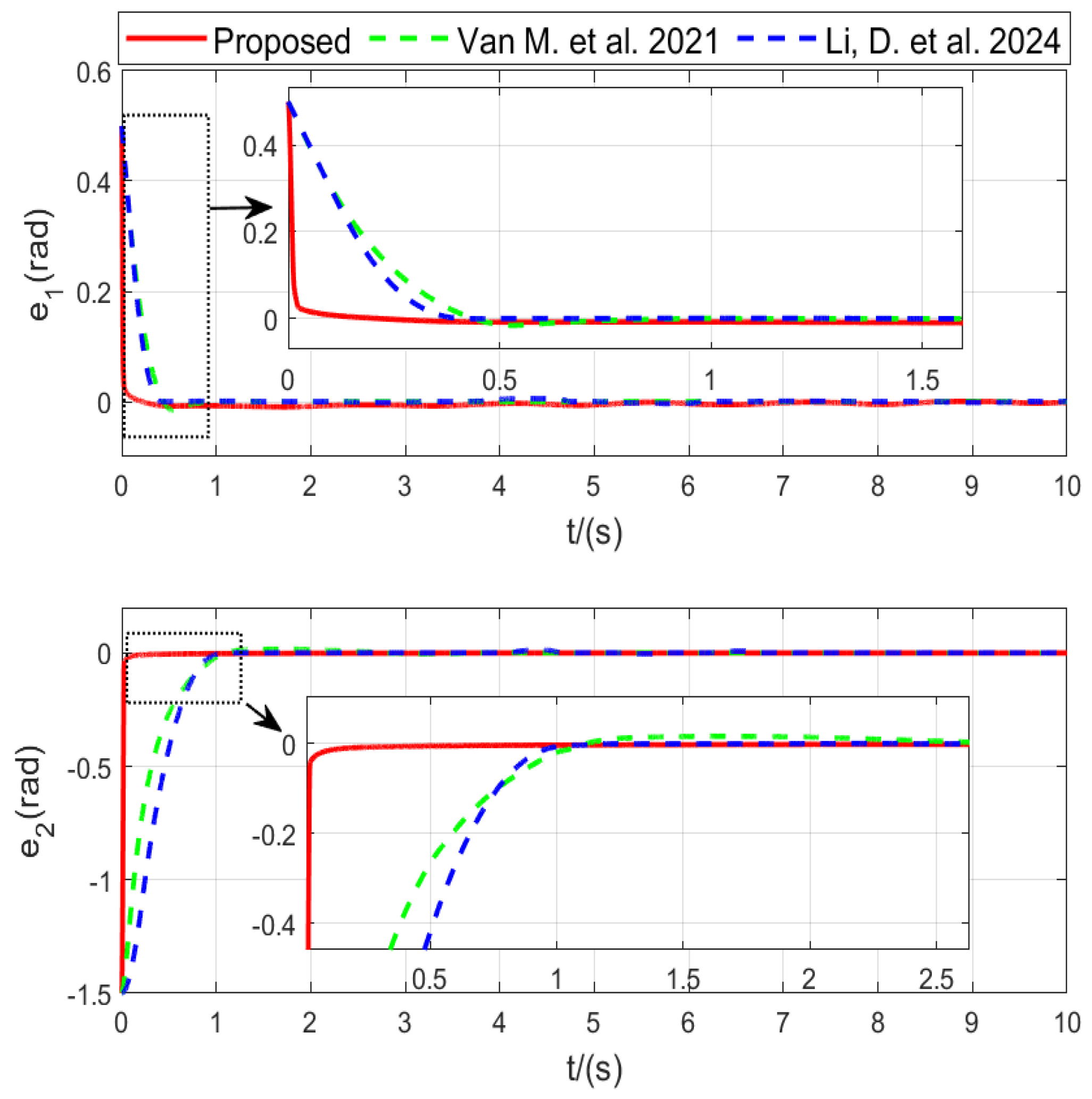
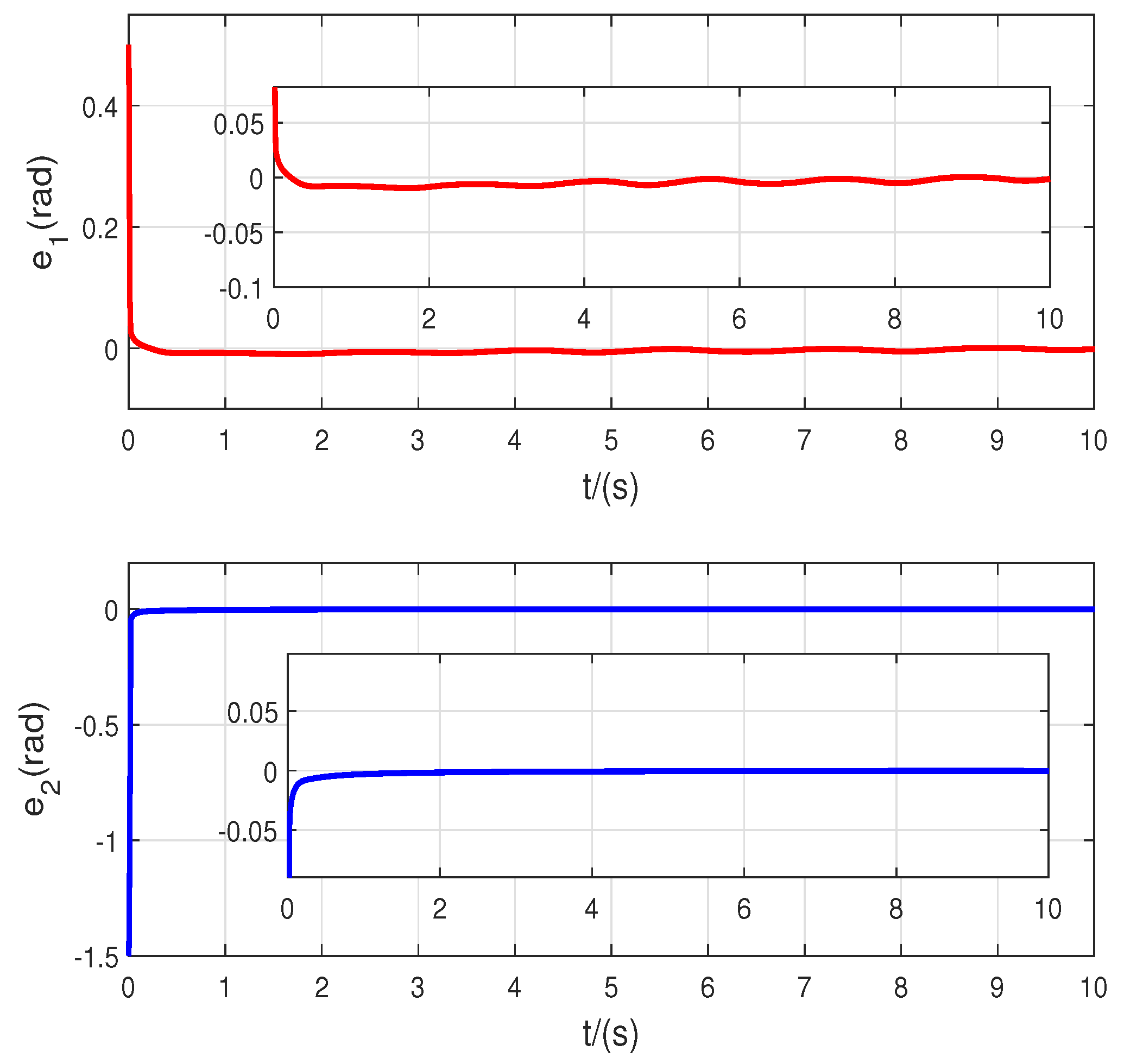
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, J.; Wang, Y.; Wang, T.; Hu, Z.; Yang, X.; Rodriguez-Andina, J.J. Time-delay sliding mode control for trajectory tracking of robot manipulators. IEEE Trans. Ind. Electron. 2024, 71, 13083–13091. [Google Scholar] [CrossRef]
- El Makrini, I.; Rodriguez-Guerrero, C.; Lefeber, D.; Vanderborght, B. The variable boundary layer sliding mode control: A safe and performant control for compliant joint manipulators. IEEE Robot. Autom. Lett. 2016, 2, 187–192. [Google Scholar] [CrossRef]
- Zhang, Y.; Kong, L.; Zhang, S.; Yu, X.; Liu, Y. Improved sliding mode control for a robotic manipulator with input deadzone and deferred constraint. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 7814–7826. [Google Scholar] [CrossRef]
- Saied, H.; Chemori, A.; Bouri, M.; El Rafei, M.; Francis, C. Feedforward super-twisting sliding mode control for robotic manipulators: Application to PKMs. IEEE Trans. Robot. 2023, 39, 3167–3184. [Google Scholar] [CrossRef]
- Li, M.; Zhang, J.; Li, S.; Wu, F. Adaptive finite-time fault-tolerant control for the full-state-constrained robotic manipulator with novel given performance. Eng. Appl. Artif. Intell. 2023, 125, 106650. [Google Scholar] [CrossRef]
- Tian, G.; Tan, J.; Li, B.; Duan, G. Optimal fully actuated system approach-based trajectory tracking control for robot manipulators. IEEE Trans. Cybern. 2024, 54, 7469–7478. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Liu, H.; Tang, D.; Hou, Y.; Wang, Y. Adaptive fixed-time fault-tolerant tracking control and its application for robot manipulators. IEEE Trans. Ind. Electron. 2021, 69, 2956–2966. [Google Scholar] [CrossRef]
- Amin, A.A.; Iqbal, M.S.; Shahbaz, M.H. Development of intelligent fault-tolerant control systems with machine learning, deep learning, and transfer learning algorithms: A review. Expert Syst. Appl. 2024, 238, 121956. [Google Scholar] [CrossRef]
- Jia, F.; Cao, F.; He, X. Active fault-tolerant control against intermittent faults for state-constrained nonlinear systems. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 2389–2401. [Google Scholar] [CrossRef]
- Jia, F.; He, X. Active fault-tolerant control with adaptive estimation error compensation for nonlinear systems: Achieving asymptotic tracking. IEEE Trans. Ind. Inform. 2024, 20, 6612–6621. [Google Scholar] [CrossRef]
- Milecki, A.; Nowak, P. Review of fault-tolerant control systems used in robotic manipulators. Appl. Sci. 2023, 13, 2675. [Google Scholar] [CrossRef]
- Jadidi, S.; Badihi, H.; Zhang, Y. Enhancing Hierarchical Fault-Tolerant Cooperative Control in Wind Farms: The Application of Model Predictive Control and Control Reallocation. In Proceedings of the 2023 12th International Conference on Renewable Energy Research and Applications (ICRERA), Oshawa, ON, Canada, 29 August–1 September 2023; pp. 429–434. [Google Scholar]
- Kang, E.; Qiao, H.; Chen, Z.; Gao, J. Tracking of uncertain robotic manipulators using event-triggered model predictive control with learning terminal cost. IEEE Trans. Autom. Sci. Eng. 2022, 19, 2801–2815. [Google Scholar] [CrossRef]
- El-Hussieny, H.; Hameed, I.A.; Megahed, T.F.; Fares, A. Advancing Robotic Control: Data-Driven Model Predictive Control for a 7-DOF Robotic Manipulator. IEEE Access 2024, 12, 115926–115934. [Google Scholar] [CrossRef]
- Son, J.; Kang, H.; Kang, S.H. A review on robust control of robot manipulators for future manufacturing. Int. J. Precis. Eng. Manuf. 2023, 24, 1083–1102. [Google Scholar] [CrossRef]
- Silaa, M.Y.; Barambones, O.; Bencherif, A.; Rougab, I. An Adaptive Control Strategy with Switching Gain and Forgetting Factor for a Robotic Arm Manipulator. Machines 2025, 13, 424. [Google Scholar] [CrossRef]
- Xu, S.S.D.; Chen, C.C.; Wu, Z.L. Study of nonsingular fast terminal sliding-mode fault-tolerant control. IEEE Trans. Ind. Electron. 2015, 62, 3906–3913. [Google Scholar] [CrossRef]
- Li, W.; Zhang, Z.; Wang, P.; Wan, H. A Faster Fixed-Time Fault Tolerant Sliding Mode Control for Robot Manipulators with Mismatched Disturbances. IEEE Access 2025, 13, 56576–56586. [Google Scholar] [CrossRef]
- Nguyen, V.C.; Vo, A.T.; Kang, H.J. A finite-time fault-tolerant control using non-singular fast terminal sliding mode control and third-order sliding mode observer for robotic manipulators. IEEE Access 2021, 9, 31225–31235. [Google Scholar] [CrossRef]
- Nguyen, V.C.; Tran, X.T.; Kang, H.J. A novel high-speed third-order sliding mode observer for fault-tolerant control problem of robot manipulators. Actuators 2022, 11, 259. [Google Scholar] [CrossRef]
- Montanaro, U.; Martini, S.; Hao, Z.; Gao, Y.; Sorniotti, A. Multi-input enhanced model reference adaptive control strategies and their application to space robotic manipulators. Int. J. Robust Nonlinear Control 2023, 33, 5246–5272. [Google Scholar] [CrossRef]
- Obuz, S.; Tatlicioglu, E.; Zergeroglu, E. Adaptive Cartesian space control of robotic manipulators: A concurrent learning based approach. J. Frankl. Inst. 2024, 361, 106701. [Google Scholar] [CrossRef]
- Jiang, J.; Yu, X. Fault-tolerant control systems: A comparative study between active and passive approaches. Annu. Rev. Control 2012, 36, 60–72. [Google Scholar] [CrossRef]
- Liu, Z.; Zhao, Y.; Zhang, O.; Chen, W.; Wang, J.; Gao, Y.; Liu, J. A novel faster fixed-time adaptive control for robotic systems with input saturation. IEEE Trans. Ind. Electron. 2023, 71, 5215–5223. [Google Scholar] [CrossRef]
- Van, M.; Ceglarek, D. Robust fault tolerant control of robot manipulators with global fixed-time convergence. J. Frankl. Inst. 2021, 358, 699–722. [Google Scholar] [CrossRef]
- Asl, R.M.; Hagh, Y.S.; Palm, R.; Handroos, H. Integral non-singular terminal sliding mode controller for nth-order nonlinear systems. IEEE Access 2019, 7, 102792–102802. [Google Scholar]
- Li, D.; Chen, M.; Peng, K.; Wu, L. Fixed-time fault-tolerant control of manipulator systems based on sliding mode observer. Int. J. Robust Nonlinear Control 2024, 34, 440–455. [Google Scholar] [CrossRef]
- Peng, Z.; Chen, H.; Zheng, J.; Zhang, J.; Xue, M.A.; Long, X.; Zhou, W. Tracking control of underactuated surface vessel based on decoupled cascaded system design with input saturation and time delay. Int. J. Control 2025, 1–9. [Google Scholar] [CrossRef]
- Xu, R.; Chen, H.; Tang, Y.; Long, X. Model-free predictive iterative learning safety-critical consensus control for multi-agent systems with randomly varying trial lengths. Syst. Control Lett. 2025, 196, 105987. [Google Scholar] [CrossRef]
- Long, X.; Chen, H.; Zheng, J.; Zhang, J.; Xue, M.A.; Tang, Y.; Xu, R.; Zhao, Y. Nonfragile memory-based sampled-data control for Unmanned Surface Vehicles with time-varying coupling delay. Ocean Eng. 2024, 313, 119480. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, O.; Gao, Y.; Zhao, Y.; Sun, Y.; Liu, J. Adaptive neural network-based fixed-time control for trajectory tracking of robotic systems. IEEE Trans. Circuits Syst. II Express Briefs 2022, 70, 241–245. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, J.; Zhang, O.; Zhao, Y.; Chen, W.; Gao, Y. Adaptive disturbance observer-based fixed-time tracking control for uncertain robotic systems. IEEE Trans. Ind. Electron. 2024, 71, 14823–14831. [Google Scholar] [CrossRef]
- Liu, J.; Sun, Y.; Liu, Z.; Gao, Y.; Wu, L.; Leon, J.I.; Franquelo, L.G. Predefined-Time Reliable Control for Robotic Systems With Prescribed Performance. IEEE Trans. Ind. Electron. 2025. [Google Scholar] [CrossRef]
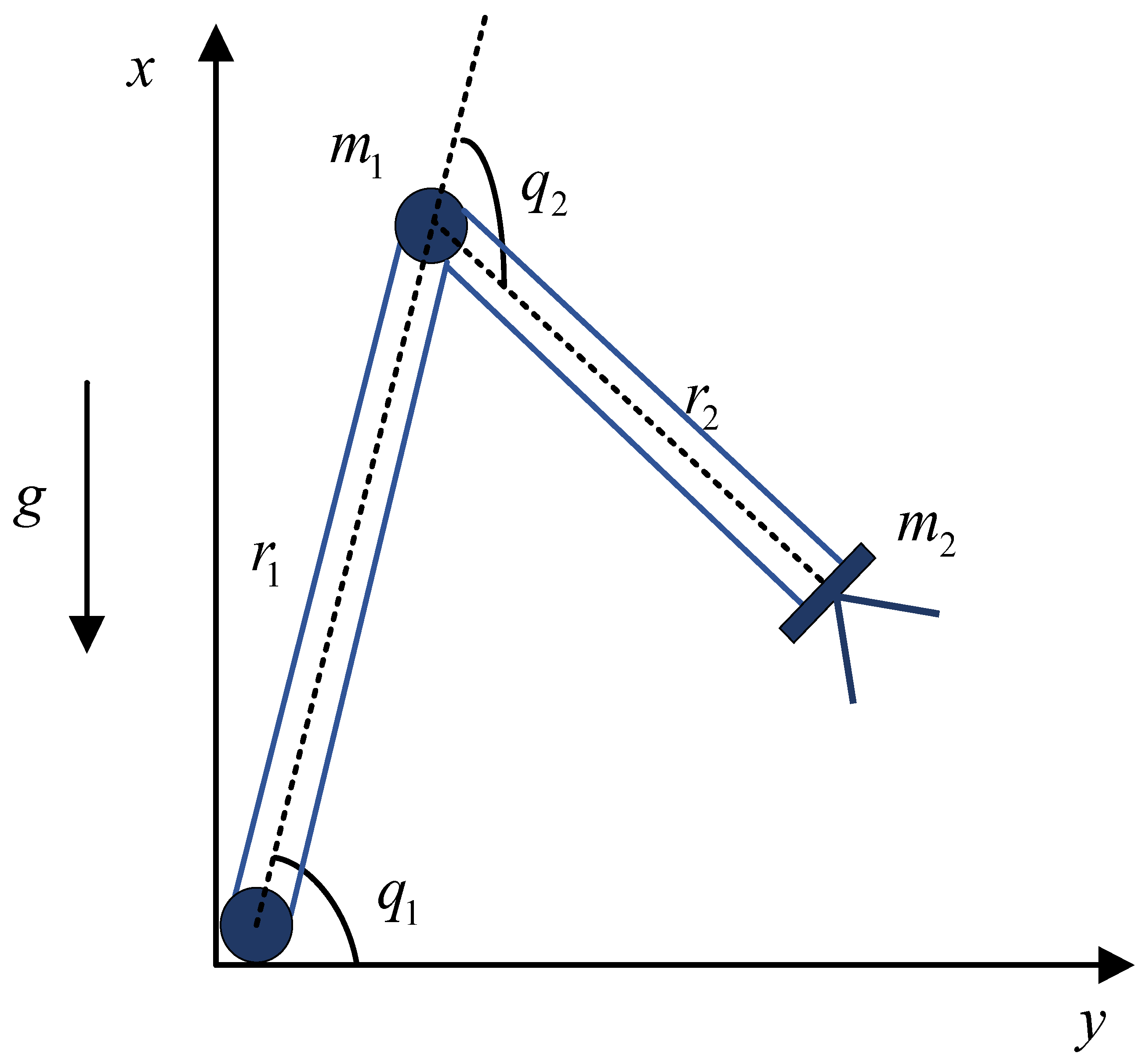


| Parameter | Value | Parameter | Value |
|---|---|---|---|
| 1 m | 1 m | ||
| 10 kg | 1 kg | ||
| 9.8 kg | 0.98 kg | ||
| 0.2 kg | 0.02 kg | ||
| g | 9.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Wang, M. Adaptive Fault-Tolerant Sliding Mode Control Design for Robotic Manipulators with Uncertainties and Actuator Failures. Symmetry 2025, 17, 1547. https://doi.org/10.3390/sym17091547
Wang Y, Wang M. Adaptive Fault-Tolerant Sliding Mode Control Design for Robotic Manipulators with Uncertainties and Actuator Failures. Symmetry. 2025; 17(9):1547. https://doi.org/10.3390/sym17091547
Chicago/Turabian StyleWang, Yujuan, and Mingyu Wang. 2025. "Adaptive Fault-Tolerant Sliding Mode Control Design for Robotic Manipulators with Uncertainties and Actuator Failures" Symmetry 17, no. 9: 1547. https://doi.org/10.3390/sym17091547
APA StyleWang, Y., & Wang, M. (2025). Adaptive Fault-Tolerant Sliding Mode Control Design for Robotic Manipulators with Uncertainties and Actuator Failures. Symmetry, 17(9), 1547. https://doi.org/10.3390/sym17091547