Abstract
In the current digital era, as global industries transform due to technological advancements, tracking trends in emerging services has assumed increased significance. This study proposes an innovative model that integrates circular picture fuzzy sets (CPFSs) with the Weighted Aggregated Sum Product Assessment (WASPAS) method to evaluate and rank various AI-driven trends within the service industry. The CPFS approach offers enhanced responses to uncertainty, symmetric information, indecision, and varying expert opinions, while the WASPAS method ensures a dependable system for ranking prominent trends. To facilitate the evaluation process, experts and relevant studies were consulted to establish criteria that address technological developments, organizational dynamics, and market fluctuations. A hybrid fuzzy Multi-Criteria Decision-Making (MCDM) framework enabled the analysis of several potential innovations related to AI and their prioritization in the context of digitalized sectors, including healthcare, finance, online shopping, retail, and logistics. This framework is a well-structured and flexible tool for professionals and policymakers seeking to navigate the challenges of identifying new trends within unpredictable digital environments. The findings indicate that the circular picture fuzzy WASPAS approach significantly enhances trend prioritization and fosters strategic thinking in digital innovation. Furthermore, the research provides valuable insights into the complexities of fuzzy decision-making and the promotion of AI-based innovation management.
1. Introduction
Artificial intelligence (AI) has started to influence the methods digitalized companies use to offer services. AI is being employed in multiple fields to enhance business decisions, automate various operations, and support firms in serving their customers [1]. Since digital transformation and AI are combined, organizations should respond swiftly as the world in these areas continues to evolve. AI is now being used by many different sectors, such as manufacturing, healthcare, and the public sector, at a rapid pace [2]. Previously, the service industry relied primarily on minor updates, whereas today, better data processing, machine learning, and efficient job solutions are increasingly dominant. AI has become pioneering in this regard, as it assists in the innovation of business services by enhancing its sense, prediction, and response to critical customer needs promptly and accurately. Due to AI, intelligent customer support systems, developed through thoughtful processes and innovative public services, can adjust their structure to deliver more positive results. In parallel, image-driven prediction systems have emerged as powerful tools for automated feature extraction in complex environments, such as pavement core sample analysis, leveraging deep learning and interactive image processing frameworks [3]. These methods can explain how the specific AI-driven computational models process complex, high-dimensional, and uncertain data, based on our goal to categorize and prioritize trends in service innovations within active digital industries. Studies show that the application of AI has a significant impact on how future customers are served and how businesses operate [4]. Digitalization is a driver of innovation for industrial enterprises. Besides decision-making structures, signal processing methods have also gained large-scale applicability as an approach to uncertain and noisy dynamic environments. For example, the dynamic detection mechanism model for acoustic emission in high-speed train axle box bearings illustrates how advanced signal analysis can enhance real-time fault detection and anomaly recognition [5]. The similarities between these approaches lie in their aim to improve reliability in the face of uncertainty, as seen in the case of fuzzy approaches. Applying conventional means to track AI trends cannot effectively address the uncertainty and doubt surrounding some strategies. Sometimes, the problem worsens as experts provide opinions that must be merged with the group’s thoughts. Thus, the CPF technique is helpful because it facilitates modeling uncertain situations, allowing professionals to assign levels of belonging, non-belonging, and uncertainty. When forming decisions using CPF [6], it becomes easier to identify trends and categorize them based on their importance.
1.1. Background
The rapid progress in digital technologies, most notably AI, has led to significant changes in how services are created, delivered to customers, and experienced. Organizations are increasingly utilizing automated customer support, AI-assisted analytics, and intelligent recommendation systems to enhance their workflows, provide customized services, and secure a stronger market position. In digitalized service innovation, it is essential to update technology and carefully plan which AI trends are relevant and how to assess them accurately. However, it is not always simple to make such decisions. Working in an innovation environment can be challenging, as different opinions may clash, essential details are often missing, and individual assessments are not always reliable. At this point, fuzzy set (FS) theory [4] methods help decision-makers make better decisions and handle uncertainty in real-world situations, especially when evaluating expert input. The scholars observed that traditional FS also faced issues, mainly when decision-makers were uncertain or hesitant, as being even slightly unsure or hesitant is very different from being certain. Consequently, intuitionistic fuzzy sets (IFSs) [7] were created. Instead of a simple degree of membership, an IFS offers a degree of non-membership and a hesitation margin, better representing how unsure people might be [8]. This framework has gained the attention of researchers and is utilized in evaluating various decision-making problems, such as site selection [9], safety evaluation in Dublin’s bike sharing system [10], and franchisor selection [11]. This concept was extended into the Pythagorean fuzzy set (PyFS) [12] and then the q-rung fuzzy set (q-ROFS) [13]. However, all these frameworks have some limitations, as they cannot account for the abstinence condition of human opinion. Therefore, by considering this and overcoming the limitation, the concept of picture fuzzy set (PFS) [14] was introduced, which has gained the attention of researchers and is applied in various decision-making scenarios that preserve symmetries [15,16,17]. Moreover, the concept of circular intuitionistic fuzzy set (Cir-IFS) has been defined by Atanassov [18], presenting another approach to decision-making evolution by involving a radius term that depends on t-norms or co-norms and offers a more robust framework for evaluation and application in decision-making [19]. As a result, decision-making became more flexible and practical, mainly because complex problems, such as analyzing innovation trends, can now be effectively managed. This paper extends the concept of PFS and Cir-IFS, defining a circular picture fuzzy set (CPFS) and integrating it with the WASPAS approach. This concept enhances robustness by supporting positive, neutral, and negative thoughts and indicating hesitation, making it ideal for decision-making under dynamic and uncertain conditions, where the criteria, alternatives, or expert evaluations can vary over time.
1.2. Problem Statement
Even though AI is rapidly used in service innovation and digitalized industries, organizations have trouble picking out the most valuable trends. Since digital markets are unpredictable, involve various groups, and have unclear data sources, identifying trends becomes complicated and unreliable. Traditional ways of making decisions are fixed and not well-suited for dealing with the challenges, uncertainties, and contradictory views found in strategic planning for tech companies. As AI developments in various sectors, such as customer care and logistics, move swiftly, organizations must assess their options under uncertain conditions. Conventional models often struggle to incorporate expert opinions, especially if information is missing, unclear, or inconsistent. For this reason, companies are less likely to respond well or on time to new opportunities in the marketplace.
Therefore, to overcome this critical limitation, a strong framework that handles uncertainty and helps prioritize AI-related service improvements is necessary. The study addresses this challenge by suggesting the circular picture fuzzy WASPAS method, which lets you handle expert uncertainty and sort complicated alternatives more accurately and dependably.
1.3. Research Gap
The CPFS approach has been pivotal in FS theory as it is a generalized version of other fuzzy tools. Researchers have introduced several operators and methods based on this concept. In our review and analysis, we believe that existing methods can be expanded. Moreover, we noticed that researchers have encountered specific questions, including the following:
- How should we prioritize the weighted vector to reflect the importance of the criteria?
- How can we establish a new model of the WASPAS technique for aggregation?
- How do we determine a suitable selection from a finite collection of alternatives?
In this context, the proposed work in this manuscript can effectively address various challenges in the fuzzy research domain and bridge the existing gaps. Notably, we found that the WASPAS technique can be enhanced within the CPF information framework, which is credible and adaptable in FS theory. This new approach is crucial for dealing with uncertain data in the identification process, particularly in scenarios requiring an extensive domain for decision-makers Ɗ to articulate their opinions about each element in the universal set, which must fall within closed intervals ranging from 0 to 1. The prior methods outlined in Table 1 fail to provide the necessary information for evaluating alternatives regarding criteria and prioritizing weights based on the importance of criteria within the CPF information framework. Thus, the proposed work effectively addresses this shortcoming.

Table 1.
The literature based on the WASPAS model.
1.4. Motivation
The rapid development and spread of AI make it necessary for decision-makers to develop more effective and advanced systems for informed decision-making. Traditional models, such as VIKOR and TOPSIS, combined with fuzzy extensions like FS, IFS, PyFS, and q-ROFS, are ineffective when forecasting upcoming service innovations that account for uncertainty, hesitation, and personal opinions. This research aims to develop an approach that is reliable, flexible, and accurate, while addressing expert uncertainty without compromising precision. The study has modified the WASPAS technique to work with CPFSs, enabling it to rate and value significant innovation trends that appear in complex circumstances. The aim is to close the gap in methodology between typical MCDM models and what digital transformation and strategic foresight require in AI service industries.
In this study, we expand WASPAS, one of the most used MCDM techniques, to its CPF variant. Zavadskas et al. [21] presented the idea of the weighted sum model (WSM) and weighted product model (WPM), the two parts of the WASPAS approach. The WASPAS technique can readily replace WSM and WPM, as it provides a more robust and efficient solution, resulting in a more thorough assessment than its individual components. Furthermore, this strategy offers a methodical way to make decisions by taking into account both qualitative and quantitative elements, and it allows decision-makers Ɗ to assess and prioritize alternatives based on their preferences and the importance of various attributes.
The traditional decision-making methods, such as classical fuzzy WASPAS, PFS-WASPAS, and Intuitionistic Fuzzy WASPAS, have limitations in that they are incapable of capturing the positive, abstention, and negative membership degrees within a circular fuzzy environment. Moreover, they do not fully consider uncertainty and hesitation in the evaluation process of the alternatives or the criterion weights. The CPFS-WASPAS model proposed helps to fill these gaps, as it can present a more detailed representation of expert opinions and process ambiguous or uncertain information more effectively.
1.5. Objective and Contribution
This study aims to establish a system that accounts for uncertainty and can be used to observe and prioritize AI-related trends in service innovation and digitalized industries. It utilizes the CPFS and WASPAS approaches to enhance how decision-makers address complex and ambiguous situations in innovation. So, the key contributions of this paper are as follows:
- It develops a new symmetric decision-making system by integrating the CPFS approach with the WASPAS approach.
- It tests the suggested model to determine which AI-driven trends impact service innovation and digital transformation most.
- It shows the model’s value by running a practical case study with the help of experts and using several evaluation standards.
- It explains fuzzy and positive thinking concepts and applies them to real issues faced in technology planning and innovation.
1.6. Layout
This article is structured as follows: Section 1 provides a summary of this research, whereas Section 2 defines the literature review of the WASPAS approach. In Section 3, we examine CPFSs and some important operational principles within the context of CPF information. Section 4 addresses the expansion of the WASPAS strategy, methodology, and algorithm within the context of CPF information about the MCDM problem. Further, we implement our proposed methods on the numerical case and perform a sensitivity and comparative analysis. Section 5, delineates the article’s conclusion and limitations and the parameters for further research.
2. Literature Review
This section presents an overview of prior studies on the WASPAS approach in decision-making evaluations and service innovation in digitalized industries, identifying gaps and limitations.
2.1. WASPAS Approach
Zavadskas et al. [21] introduced the concept of the WASPAS technique, which consists of two components: the weighted sum model (WSM) and the weighted product model (WPM). The WASPAS technique can easily be substituted for WSM and WPM, as it offers a more substantial and effective solution, yielding a more comprehensive evaluation than its components. Besides WASPAS extensions, new studies focus on contributing to the practical application of circular fuzzy frameworks in real-world MCDM issues. For example, Ashraf and Chohan [33] implemented circular spherical fuzzy set (CSFS) aggregation operators for risk assessments in industrial expansion projects, achieving better robustness under uncertain expert opinions. Similarly, Amin et al. [34] applied complex circular intuitionistic fuzzy (CIF) logic combined with Dombi operators to biometric authentication systems, Guo et al. used the circular framework for improving the air quality index [19], Rukhsar et al. for green supplier selection [35], and Nazeer et al. for evaluating martial arts teaching skills [15], showcasing the adaptability of circular fuzzy environments for critical technology decisions. The studies provide support for integrating CPFS into hybrid frameworks, such as WASPAS, to address uncertainty and reluctance in the implementation of the decision-making process. Due to its effectiveness and robustness, various scholars have utilized this approach, as discussed in Table 1.
2.2. Service Innovation in Digitalized Industries
Service innovation plays a key role in the competitiveness of digitalized companies today. At first, service innovation merely meant improving how services were given, communicated, and managed. However, the rise of digital technologies and AI now includes giving people personal attention, forecasting their options, automating tasks, and making real-time decisions.
With digitalization, companies can now use innovative technologies in their service processes to interact with customers differently, make operations more flexible, and respond more readily to changing markets. Digitalization as a driver of innovation for industrial enterprises points out that industries are changing to digitalized service ecosystems, meaning new and improved services and structures in partnerships and business operations contribute to innovation. AI, big data analytics, Internet of Things, and cloud computing usually drive these changes. AI has taken the lead in helping businesses innovate their services by enhancing their sense, prediction, and response to customer needs quickly and correctly. Thanks to AI, adaptive service platforms in smart manufacturing and intelligent public services can change their structure and deliver better results throughout the service. Past achievements and future directions in AI-enabled product service innovation argue that AI supports the integration of products and services as one solution and leads to greater value creation in different sectors. AI-based innovations in fintech are changing and disrupting entire industries. Thanks to AI, financial services now include features such as personalized banking, robot-advisory services, fraud detection, and credit scoring. A book focuses on how AI significantly reduces expenses, enhances legal compliance, and lets companies provide highly targeted services. All kinds of public services are now digital. This work points out that AI benefits the government by supporting new tools, managing resources, boosting citizens’ experiences, and ensuring informed policy decisions. AI-powered services on this platform aim to deal with social concerns more effectively and be transparent and responsive. AI has taken the lead in helping businesses innovate their services by enhancing their sense, prediction, and response to customer needs quickly and correctly. Thanks to AI, adaptive service platforms in smart manufacturing and intelligent public services can change their structure and deliver better results throughout the service. Figure 1 gives a graphical representation of service innovation in digitalized industries.
Figure 1.
Service innovation in digitalized industries.
Industries rely on AI to identify new trends and fuel their development amid the rapid changes in today’s digital society. Using large amounts of real-time data, AI can identify shifts in consumer behavior and technological updates more quickly than any traditional approach. Because of this, businesses can identify ways to improve their services or make changes before others do. AI automates specific tasks, gains knowledge from data, adapts to changes, and provides insights that help inform smart decisions. Companies use AI to examine customer trends and develop new services regardless of their industry. Essentially, AI enables the detection of emerging trends and guides the transformation of digitalized businesses through innovative solutions.
3. Preliminaries
Definition 1
([18]). Consider a fixed universe; then, a circular intuitionistic fuzzy set (CIFS) on is defined by
where represents the (membership degree) MD, and represents the (non-membership degree) NMD. These degrees satisfy the condition where the hesitancy degree is . The notion represents the radius of the circle of each element. For continuity, is known as a circular intuitionistic fuzzy value (Cir-IFVS).
Definition 2
([14]). A picture fuzzy set (PFS) on a universe is an object in the form of
where [0, 1] is called the degree of membership of in , [0, 1] is called the degree of abstinence, and [0, 1] is called the degree of non-membership of in and all degrees satisfy the following condition:
and now is called the degree of refusal.
Definition 3
([33]). A circular picture fuzzy set (CPFS) on a universe is an object in the form of
where [0, 1] is called the degree of membership of in , [0, 1] is called the degree of abstinence, and [0, 1] is called the degree of non-membership of in [0, 1] is the radius of the circle and satisfies the following condition:
and is called the degree of refusal.
Definition 4
([33]). The score value and the accuracy value ) of the sorting CPF
are defined by
Definition 5
([33]). For two CPFSs, and , the fundamental operational laws are defined as follows:
- i.
- ii.
- iii.
- iv.
Definition 6
([33]). The CPFWAO (circular picture fuzzy weighted averaging operator) for CPFS is of the form
where the weighted vector such that satisfies the constraint and . Then, the aggregated value of a collection of CPFVs using the CPFWAO is also a CPFV and is given as follows:
Definition 7
([33]). The CPFWGO (circular picture fuzzy weighted geometric operator)
for CPFVs is of the form . Then, the aggregated value of a collection of TSFVs using the CPFWGO is also a CPFV and is given as follows:
4. Methodology
4.1. Circular Picture Fuzzy WASPAS Approach
This study applies the WASPAS method to address an MCDM problem characterized by the CPF framework. To tackle these MCDM challenges, an effective decision-making technique is presented. The primary objective of any MCDM problem is to rank the set of alternatives according to the specified criteria. The opinions of each decision-maker are captured and then aggregated by CPFWAO (averaging operator) or CPFWGO (geometric operator) if the data is only of one type. The CPFWAO and CPFWGO play a pivotal role in the aggregation phase of the proposed decision-making process. CPFWAO (arithmetic operator) combines the views of experts by averaging a CPFS across criteria or decision-makers, thereby maintaining balance and minimizing bias in the assessment of experts, while CPFWGO captures the multiplicative interactions among attributes and is necessary in situations where the total effect of criteria influences performance in a nonlinear fashion, i.e., their combined effect. These operators in the CPFS-WASPAS model aggregate raw judgments into a shared CPF decision matrix after normalization and ranking, ensuring that normative concepts such as expert uncertainty and hesitancy are maintained throughout the aggregation process.
Suppose there are alternatives and criteria along with a criterion weight vector such that and in a CPF environment. Further, represents the evaluation of each alternative for the given alternatives. This matrix represents the MCDM problem in the context of CPFNs.
WASPAS is a powerful technique designed to address MCDM problems. It combines the advantages of WSM and WPM, enabling decision-makers to evaluate options across various conflicting criteria. In CPF information, WASPAS is adapted to manage uncertain and imprecise data, enabling the assessment of alternatives with varying degrees of positive, neutral, and negative membership. This proves invaluable when the decision data is unclear or ambiguous. The detailed steps for CPF-WASPAS are outlined as follows:
- i.
- The first step in the CPF-WASPAS methodology is to collect the data from different experts and arrange that data in the form of a decision matrix within the CPF environment. The decision matrix in the context of CPFN is of the form
- ii.
- The second step involves the normalization of if it contains two types of data, i.e., benefit and cost types of criteria. The decision matrix is linearly normalized for benefit type using the expressionwhere .Normalization for the cost type attributes is given bywhere .
- iii.
- In this step, the relative significance of alternatives is observed through the WSM model, and the entire relative significance of alternatives is observed through WPM model, which is calculated by
- iv.
- In the WASPAS technique, the combined effect of the WSM model and the WPM model is integrated for ordering alternatives using a convex formula, which is given as
- v.
- Finally, the score function is used for to rank the alternatives. In case the score function fails, the accuracy function is used.
The algorithm for WASPAS methodology in the CPF context is illustrated in Figure 2.
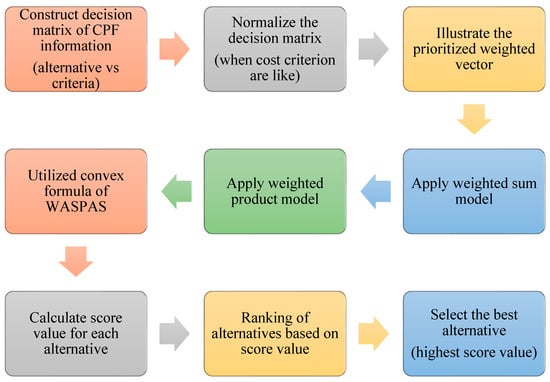
Figure 2.
CPF WASPAS decision algorithm.
4.2. Decision-Making Algorithm
To solve the MCDM problems in the environment of a CPFS by using the proposed WASPAS technique, the following steps should be followed:
- i.
- Form the decision matrix (DM) from the opinion of decision-makers within the CPFS information, which is shown as
- ii.
- The DM should be normalized if CPFS information has two types of attributes, a benefit attribute and a cost attribute, according to the following expression:It is not necessary to assess the data every time if it contains only a benefit attribute in the DM.
- iii.
- Illustrate the prioritized weighted vector for the importance of the attribute. The prioritized weighted vector such that of all attributes satisfies the constraint and
- iv.
- Incorporate the normalized DM represented as CPF information using the CPFWAO or CPFWGO operators in Equation (6) or Equation (8).
- v.
- Calculate the score for each alternative using definition 4, then arrange the alternatives in ascending order. Also, the ranking for each alternative must be determined to identify the best choice.
The flowchart depicting the algorithm using the proposed WASPAS technique in the context of CPF information is shown in Figure 3 for clarity.
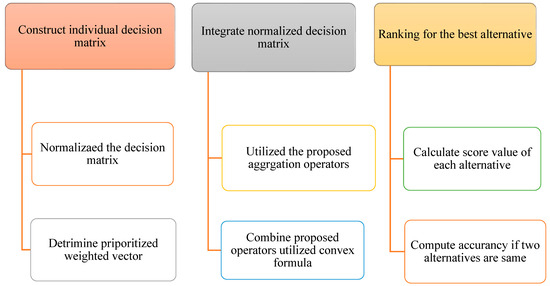
Figure 3.
Evaluation process of the MCDM problem using the proposed model.
4.3. Evaluation of AI-Driven Service Innovation Trends
A group of digital retail service providers is using this case study to identify and select the most significant AI-led service changes that should be integrated into their future digital transformation plans from 2026 to 2030. The group is composed of five firms that work in online stores, interaction programs, and transportation. Their common mission is to implement technologies that benefit working processes, effectively build customer experience, and drive long-term growth in a highly competitive market. Since the future of emerging technologies is uncertain, a panel of twelve experts conducted an evaluation; the panel comprised four researchers in the field of AI, three innovation management consultants, and five top executives directly involved in digital transformation efforts.
The professionals were engaged in systematic decision-making based on the CPF-WASPAS method that facilitated managing hesitation, asymmetric information, and uncertainty during judgments. The criterion weighting was assigned based on the opinion of each expert, on a scale of 0 to 1. Since emerging technology is hard to predict, choices are made with the advice of AI researchers, innovation experts, and executives leading digital transformation. To address the imprecision and varying opinions, the consortium relies on CPF WASPAS, which helps represent hesitation and uncertainty regarding the different options.
4.3.1. Case Study
This case study illustrates the application of the CPF WASPAS method to evaluate and prioritize key AI trends for service innovation. The assessment focuses on four major AI trends (alternatives) across five essential criteria relevant to strategic and innovation analysis.
The evaluation criteria were identified through a mixed-method approach, which included a thorough examination of the current literature on AI-based service innovation in digitalized industries and advice and support from domain-experienced professionals within the consortium companies. Innovation impact, feasibility, scalability, customer value creation, and management of uncertainty are often, in previous studies (e.g., [36,37]), discussed as pivotal in assessing the adoption of technology. All of these five criteria (H1–H5) denote service innovation priorities, both strategic and operational. Each of these alternatives (K1–K4) reflects emerging AI trends that have been or are expected to have an impact on digital service delivery. These were chosen based on their frequent appearance in industry reports, academic research, and the agreement of the panel of experts in early consultations. Table 2 gives details and justifications of the inclusion of all criteria and alternatives.

Table 2.
Criteria and alternatives.
4.3.2. Numerical Evaluation
- i.
- The initial step in the CPF-WASPAS methodology involves gathering data (hypothetically) from various experts and organizing it into a decision matrix within the CPF environment. In the context of CPFNs, this decision matrix is structured as shown in Table 3.
 Table 3. Decision matrix.
Table 3. Decision matrix. - ii.
- The second step involves the normalization of due to the benefit–cost type of criteria. It is essential to normalize data to facilitate similarity in criteria, as some are of a benefit type and others are of a cost type. This is performed to bring normality to the values and not to the relative performance of alternatives and prepare the information to proceed further using the WASPAS approach. The decision matrix is linearly normalized for benefit type in Table 4. The normalization is performed by using Equations (9) and (10) given in Section 3.
 Table 4. Normalization of decision matrix.
Table 4. Normalization of decision matrix.
Here, ; degree of membership (MD), degree of non-membership (NMD), degree of abstinence (AD), and radius (R).
The outcomes of the WASPAS framework are presented in Table 5, which displays the WSM and WPM results of the model by using Equations (11) and (12) of the methodology. These calculations demonstrate the importance of each alternative in meeting all requirements on both additive and multiplicative bases. The outcome of each model is used as the basis to combine the two models, resulting in the integrated WASPAS score.

Table 5.
WSM model and WPM model.
The results in Table 6 present the aggregation of WASPAS scores using a convex combination of the WSM and WPM results. The calculations were performed using Equation (4) given in Definition 4. These scores indicate the general performance of every AI-driven trend in a CPF environment. By combining the two models, the robustness of the decision is enhanced because it factors in both linear and multiplicative solutions.

Table 6.
WASPAS model.
The ranking of AI-driven service innovation alternatives according to the aggregated CPFS-WASPAS scores is provided in Table 7. The most outstanding score is assigned to Alternative (AI-Based Personalization Engines), which means that it outperforms the rest in all the assessment criteria. This reaffirms that it is strategically significant in terms of the digitalization of service innovation, with (Autonomous Process Optimization) coming in a close second, followed by and which Volkswagen intends to prioritize because of its scalability limitations and uncertainty issues.

Table 7.
Ranking of alternatives.
Figure 4 illustrates the ranking results obtained using CPFS-WASPAS. The superiority of K4 is quite evident and should be considered first for adoption in service strategies with AI. A moderate performance has been recorded with and , and the worst overall performance has been recorded with , which accords with the tabular analysis in Table 7.
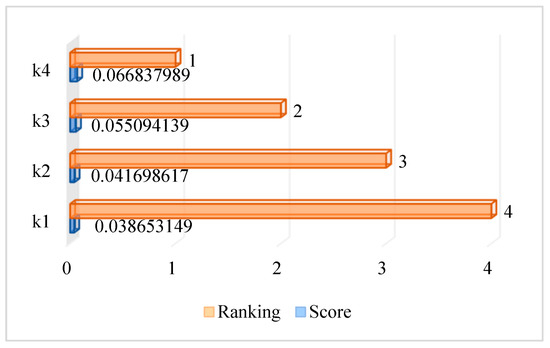
Figure 4.
Pictorial representation of rank.
4.3.3. Result Discussion and Comparison
As shown in Figure 4, the analysis of the CPF WASPAS has shown that AI-driven service innovation alternatives are given different priorities based on the chosen criteria. The study indicates that Alternative K4 received the highest score, suggesting it performed better than the other options across all key criteria. From this, we can deduce that K4 (AI-Based Personalization Engines) is the most significant and suitable trend in service innovation for digital-related industries. Coming in second, Alternative K3 indicates that the company shows strong results in many areas and could potentially excel in pleasing customers and growing quickly. K2 and K1, scoring 0.0417 and 0.0387, came in third and fourth place. This outcome demonstrates the effectiveness of combining the CPFS approach with WASPAS in making decisions when the situation is uncertain and words may be ambiguous. This method enabled experts to express doubt and excuse themselves from direct agreement, thereby making the evaluation more precise than other MCDM methods. This framework allows digital companies to select the most effective and manageable AI solutions for their business and policy-making.
To show the adaptability and reliability of the approach, a comparison analysis has been conducted. The different fuzzy frameworks are compared in Figure 5, pointing out how the CPF-WASPAS method offers greater capabilities.
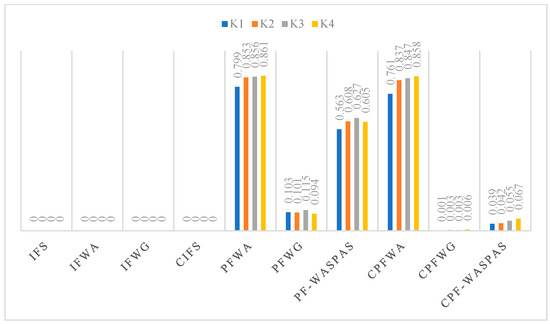
Figure 5.
Comparison analysis.
The numerical comparison shows that all the ranking values obtained with the CPF-WASPAS approach are smaller than those obtained with other evaluated approaches (all criteria, K1, K2, K3, and K4). The values with lower ranks are more stable, more accurate in prioritization, and less sensitive to the changes in input data. Based on this performance, it can be seen that CPF-WASPAS has the most stable and accurate decision-making option among the other fuzzy set techniques considered, and therefore, it can be applied in situations where one is dealing with complex and uncertain environments.
4.3.4. Practical Implications
This study’s findings support vital decisions made by experts and leaders implementing new AI-driven digital entertainment technologies. Many organizations struggle to identify and focus on key AI trends. However, the CPF WASPAS approach offers a reliable and systematic method for evaluating emerging AI trends, especially in contexts where expert insight might be limited or unclear. This framework empowers business and innovation managers to select AI solutions that are both cutting-edge and compatible with their organizations’ structures. It aids in decision-making by mitigating the risks associated with investing in untested or ineffective technologies. Digital transformation teams should leverage this model to align AI adoption with customer needs and ongoing operations. This methodology allows public sector organizations to determine whether AI trends can enhance public service design and improve citizen resource management. With the study’s clear guidelines, AI planning becomes more strategic, leading to quicker adoption and more effective applications across various sectors and industries.
5. Conclusions
This study proposes an integrated decision-making framework that combines the CPFS approach and the WASPAS method to address uncertainty in prioritizing AI-driven trends for service innovation. Its framework will result in the introduction of professional reluctance and asymmetric information, enabling more reliable judgments in dynamic digital conditions. The implementation of the proposed model demonstrated its ability to capture prominent AI trends, with the engines of personalization proving to be the most remarkable. The sensitivity analysis of the results was confirmed. Further studies are needed to investigate a broader range of criterion sets, the practical expertise of the experts, and dynamic modeling to support the shifting trends. Furthermore, to increase the level of applicability across various industries, it may also be beneficial to incorporate forecasting methods and compare the results obtained with those of other sophisticated fuzzy models.
Limitations and Future Direction
Although the CPFS-WASPAS framework provides long-term solutions and allows uncertainty and reluctant expressions of expert opinions to be overcome, it still has some practical limitations. First, the method adds complexity to computation, as it involves calculating many degrees of membership, abstinence, and non-membership, together with the circle radius value, which can become cumbersome in large decision matrices. Second, the CPFS values are based on expert opinion, which can introduce the effects of subjectivity and possible bias in the evaluation process. Third, the model can cause significant processing and memory usage when applied to large datasets, which may raise concerns over its feasibility in real-time decision-making scenarios. Moreover, the approach is effective in identifying trends at a specific time; however, it fails to capture the dynamic development of trends and changes in new technologies. Limitations that could be addressed in future studies include the use of optimized algorithms to reduce computational overhead, automated models such as machine learning, which can assist in parameter estimation, and adaptive models capable of capturing trend evolution in rapidly changing digital environments.
Future research will likely investigate several vital areas, such as applying the CPF WASPAS model in healthcare, education, or logistics, to determine if AI-driven innovation trends vary across industries. Combining forecasting with real-time data analytics or machine learning can enhance the relevance and timeliness of decision-making. Also, comparing this hybrid model to other fuzzy decision-making models, such as the neutrosophic framework [38], cubic framework [39], soft set [40], and t-spherical [41] models, and using a symmetric aggregation operator (AO) such as aczel-alsina [42], Muirhead mean [43], Dombi AO [34], etc., could confirm and potentially improve the accuracy of the results. This approach can be combined with forecasting techniques or scenario analysis to conduct further studies to examine how trends in AI are likely to evolve in the coming years. Although this work is valuable, there is room to further develop it by making it broader, more flexible, and more aligned with advances in AI and digital services.
Author Contributions
Conceptualization, Y.X. and D.Z.; investigation, Y.X. and D.Z.; methodology, Y.X. and D.Z.; resources, Y.X.; validation, Y.X. and D.Z.; writing—original draft, Y.X. and D.Z.; writing—review and editing, Y.X. and D.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The datasets used and/or analyzed during the current study are available from the corresponding author on reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Wang, X.; He, T.; Wang, S.; Zhao, H. The Impact of Artificial Intelligence on Economic Growth From the Perspective of Population External System. Soc. Sci. Comput. Rev. 2025, 43, 129–147. [Google Scholar] [CrossRef]
- Sadeghi, Z.; Alizadehsani, R.; Cifci, M.A.; Kausar, S.; Rehman, R.; Mahanta, P.; Bora, P.K.; Almasri, A.; Alkhawaldeh, R.S.; Hussain, S.; et al. A Review of Explainable Artificial Intelligence in Healthcare. Comput. Electr. Eng. 2024, 118, 109370. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Y.; Chen, Z.; Zhou, B.; Liu, H.; Li, L. Image-Driven Prediction System: Automatic Extraction of Aggregate Gradation of Pavement Core Samples Integrating Deep Learning and Interactive Image Processing Framework. Autom. Constr. 2025, 156, 105114. [Google Scholar] [CrossRef]
- Aldoseri, A.; Al-Khalifa, K.N.; Hamouda, A.M. AI-Powered Innovation in Digital Transformation: Key Pillars and Industry Impact. Sustainability 2024, 16, 1790. [Google Scholar] [CrossRef]
- Han, D.; Qi, H.; Hou, D.; Wang, S.; Kong, J.; Xu, X.; Wang, C. Dynamic Detection Mechanism Model of Acoustic Emission for High? Speed Train Axle Box Bearings with Local Defects. Mech. Syst. Signal Process. 2025, 179, 112943. [Google Scholar] [CrossRef]
- Ullah, K. Picture Fuzzy Maclaurin Symmetric Mean Operators and Their Applications in Solving Multiattribute Decision-Making Problems. Math. Probl. Eng. 2021, 2021, 1098631. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic Fuzzy Sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Imran, R.; Ullah, K.; Ali, Z.; Akram, M. A Multi-Criteria Group Decision-Making Approach for Robot Selection Using Interval-Valued Intuitionistic Fuzzy Information and Aczel-Alsina Bonferroni Means. Spectr. Decis. Mak. Appl. 2024, 1, 1–32. [Google Scholar] [CrossRef]
- Gao, J.; He, Y.; Huang, N.; Meng, Q.; Zhao, S.; Zhang, L. Site Selection of Medium-Deep Geothermal Resource Projects Based on Intuitionistic Fuzzy Environment and MABAC Method. Renew. Energy 2025, 250, 123253. [Google Scholar] [CrossRef]
- Khan, M.R.; Ullah, K.; Raza, A.; Ali, Z.; Senapati, T.; Esztergár-Kiss, D.; Moslem, S. Evaluating Safety in Dublin’s Bike-Sharing System Using the Concept of Intuitionistic Fuzzy Rough Power Aggregation Operators. Measurement 2025, 253, 117553. [Google Scholar] [CrossRef]
- Traneva, V.; Tranev, S. Confidence-Interval Elliptic Intuitionistic Fuzzy Sets to Franchisor Selection. In Recent Advances in Computational Optimization; Fidanova, S., Ed.; Studies in Computational Intelligence; Springer Nature: Cham, Switzerland, 2025; Volume 485, pp. 99–125. ISBN 978-3-031-74757-1. [Google Scholar]
- Yager, R.R. Pythagorean Fuzzy Subsets. In Proceedings of the 2013 joint IFSA World Congress and NAFIPS Annual Meeting (IFSA/NAFIPS), Edmonton, AB, Canada, 24–28 June 2013; pp. 57–61. [Google Scholar]
- Yager, R.R. Generalized Orthopair Fuzzy Sets. IEEE Trans. Fuzzy Syst. 2016, 25, 1222–1230. [Google Scholar] [CrossRef]
- Cường, B.C. Picture Fuzzy Sets. J. Comput. Sci. Cybern. 2014, 30, 409. [Google Scholar] [CrossRef]
- Nazeer, M.S.; Imran, R.; Amin, M.; Rak, E. An Intelligent Algorithm for Evaluating Martial Arts Teaching Skills Based on Complex Picture Fuzzy Dombi Aggregation Operator. J. Innov. Res. Math. Comput. Sci. 2024, 3, 44–70. [Google Scholar] [CrossRef]
- Ashraf, S.; Jana, C.; Sohail, M.; Choudhary, R.; Ahmad, S.; Deveci, M. Multi-Criteria Decision-Making Model Based on Picture Hesitant Fuzzy Soft Set Approach: An Application of Sustainable Solar Energy Management. Inf. Sci. 2025, 686, 121334. [Google Scholar] [CrossRef]
- Mahmoodirad, A.; Pamucar, D.; Niroomand, S.; Simic, V. Data Envelopment Analysis Based Performance Evaluation of Hospitals–Implementation of Novel Picture Fuzzy BCC Model. Expert. Syst. Appl. 2025, 263, 125775. [Google Scholar] [CrossRef]
- Atanassov, K.T. Circular Intuitionistic Fuzzy Sets. J. Intell. Fuzzy Syst. 2020, 39, 5981–5986. [Google Scholar] [CrossRef]
- Guo, F.; Imran, R.; Yin, S.; Ullah, K.; Akram, M.; Pamucar, D.; Elashiry, M. Assessment of Air Purifiers for Improving the Air Quality Index Using Circular Intuitionistic Fuzzy Heronian Means. Complex Intell. Syst. 2025, 11, 1–24. [Google Scholar] [CrossRef]
- Dėjus, T.; Antuchevičienė, J. Assessment of Health and Safety Solutions at a Construction Site. J. Civ. Eng. Manag. 2013, 19, 728–737. [Google Scholar] [CrossRef]
- Chakraborty, S.; Zavadskas, E.K. Applications of WASPAS Method in Manufacturing Decision Making. Informatica 2014, 25, 1–20. [Google Scholar] [CrossRef]
- Ghorabaee, M.K.; Zavadskas, E.K.; Amiri, M.; Esmaeili, A. Multi-Criteria Evaluation of Green Suppliers Using an Extended WASPAS Method with Interval Type-2 Fuzzy Sets. J. Clean. Prod. 2016, 137, 213–229. [Google Scholar] [CrossRef]
- Peng, X.; Dai, J. Hesitant Fuzzy Soft Decision Making Methods Based on WASPAS, MABAC and COPRAS with Combined Weights. J. Intell. Fuzzy Syst. 2017, 33, 1313–1325. [Google Scholar] [CrossRef]
- Stanujkić, D.; Karabašević, D. An Extension of the WASPAS Method for Decision-Making Problems with Intuitionistic Fuzzy Numbers: A Case of Website Evaluation. Oper. Res. Eng. Sci. Theory Appl. 2018, 1, 29–39. [Google Scholar] [CrossRef]
- Kutlu Gundogdu, F.; Kahraman, C. Extension of WASPAS with Spherical Fuzzy Sets. Informatica 2019, 30, 269–292. [Google Scholar] [CrossRef]
- Otay, I.; Kahraman, C.; Öztayşi, B.; Onar, S.Ç. A Novel Single-Valued Spherical Fuzzy AHP-WASPAS Methodology. In Proceedings of the Developments of Artificial Intelligence Technologies in Computation and Robotics, WORLD SCIENTIFIC; Cologne, Germany, 18–21 October 2020, pp. 190–198.
- Simić, V.; Lazarević, D.; Dobrodolac, M. Picture Fuzzy WASPAS Method for Selecting Last-Mile Delivery Mode: A Case Study of Belgrade. Eur. Transp. Res. Rev. 2021, 13, 43. [Google Scholar] [CrossRef]
- Senapati, T.; Chen, G. Picture Fuzzy WASPAS Technique and Its Application in Multi-Criteria Decision-Making. Soft Comput. 2022, 26, 4413–4421. [Google Scholar] [CrossRef]
- Xu, C.; Yuan, X. A Novel Intuitionistic Fuzzy Decision Support System Based on Extended WASPAS Method: A Case Study for the Selection of Basketball Players and Basketball Fields for Maximum Performance. IEEE Access 2025, 13, 81606–81617. [Google Scholar] [CrossRef]
- Lyu, D.; Zhang, X. WASPAS-Based Multi-Expert Decision Algorithm for Physical Education Using Circular Pythagorean Fuzzy Aggregation with Prioritized Weights. Sci. Rep. 2025, 15, 26516. [Google Scholar] [CrossRef]
- Shabani, M.; Khodarahmi, A.; Ghousi, R.; Mohammadi, E.; Ghanbari, H. An Appraisal of Fund of Funds Efficiency Based on Risk-Adjusted Performance Measures: Application of an Augmented WASPAS Methodology. PLoS ONE 2025, 20, e0314918. [Google Scholar] [CrossRef] [PubMed]
- Rasheed, M.W.; Saleh, H.Y.; Salih, A.A.; Karamat, J.; Bilal, M. An Overview of Pink Eye Infection to Evaluate Its Medications: Group Decision-Making Approach with 2-Tuple Linguistic T-Spherical Fuzzy WASPAS Method. Front. Artif. Intell. 2025, 7, 1496689. [Google Scholar] [CrossRef] [PubMed]
- Ashraf, S.; Chohan, M.S. Circular Spherical Fuzzy Aggregation Operators: A Case Study of Risk Assessments on Industry Expansion. Eng. Appl. Artif. Intell. 2025, 145, 110202. [Google Scholar] [CrossRef]
- Amin, M.; Ullah, K.; Akram, M.; Imran, R.; Nazeer, M.S. Advancing AI-Based Biometric Authentication in Multi-Criteria Decision Approach Using Complex Circular Intuitionistic Fuzzy Logic and Dombi Operators. Res. Sq. 2024. preprint. [Google Scholar] [CrossRef]
- Rukhsar, M.; Hussain, A.; Ullah, K.; Moslem, S.; Senapati, T. Intelligent Decision Analysis for Green Supplier Selection with Multiple Attributes Using Circular Intuitionistic Fuzzy Information Aggregation and Frank Triangular Norms. Energy Rep. 2025, 13, 5773–5791. [Google Scholar] [CrossRef]
- Anshari, M.; Hamdan, M.; Ahmad, N.; Ali, E. Public Service Delivery, Artificial Intelligence and the Sustainable Development Goals: Trends, Evidence and Complexities. J. Sci. Technol. Policy Manag. 2025, 16, 163–181. [Google Scholar] [CrossRef]
- Khodayari, M.; Akbari, M.; Foroudi, P. The Sharing Economy: A Systematic Literature Review and Research Agenda. Int. J. Consum. Stud. 2025, 49, e70010. [Google Scholar] [CrossRef]
- Jafar, M.N.; Imran, R.; Hassan, S.; Riffat, A.; Shuaib, R. Medical Diagnosis Using Neutrosophic Soft Matrices and Their Compliments. Int. J. Adv. Res. Comput. Sci. 2020, 11, 1–3. [Google Scholar] [CrossRef]
- Saqlain, M.; Imran, R.; Hassan, S. TOPSIS Technique of MCDM under Cubic Intuitionistic Fuzzy Soft Set Environment. Sci. Inq. Rev. 2023, 7, 33–52. [Google Scholar] [CrossRef]
- Saqlain, M.; Imran, R.; Hassan, S. Cubic Intuitionistic Fuzzy Soft Set and Its Distance Measures. Sci. Inq. Rev. 2022, 6, 59–75. [Google Scholar] [CrossRef]
- Nazeer, M.S.; Ullah, K.; Hussain, A. A Novel Decision-Making Approach Based on Interval-Valued T-Spherical Fuzzy Information with Applications. J. AppliedMath 2024, 2, 79. [Google Scholar] [CrossRef]
- Imran, R.; Ullah, K.; Ali, Z.; Akram, M. An Approach to Multi-Attribute Decision-Making Based on Single-Valued Neutrosophic Hesitant Fuzzy Aczel-Alsina Aggregation Operator. Neutrosophic Syst. Appl. 2024, 22, 43–57. [Google Scholar] [CrossRef]
- Imran, R.; Ullah, K.; Ali, Z.; Akram, M.; Senapati, T. The Theory of Prioritized Muirhead Mean Operators under the Presence of Complex Single-Valued Neutrosophic Values. Decis. Anal. J. 2023, 7, 100214. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).