Coefficient Estimates and Symmetry Analysis for Certain Families of Bi-Univalent Functions Defined by the q-Bernoulli Polynomial
Abstract
1. Introduction
2. Main Results
3. Example and Applications
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Singh, R. On Bazilevič functions. Proc. Am. Math. Soc. 1973, 38, 261–271. [Google Scholar] [CrossRef]
- Babalola, K.O. On λ-pseudo-starlike functions. J. Class. Anal. 2013, 3, 137–147. [Google Scholar]
- Joshi, S.B.; Joshi, S.S.; Pawar, H. On some subclasses of bi-univalent functions associated with pseudo-starlike functions. J. Egypt. Math. Soc. 2016, 24, 522–525. [Google Scholar]
- Prema, S.; Keerthi, B.S. Coefficient bounds for certain subclasses of analytic function. J. Math. Anal. 2013, 4, 22–27. [Google Scholar]
- Wanas, A.K.; Khachi, S.C. Coefficient bounds and Fekete–Szegö inequalities for new families of bi-starlike and bi-convex functions associated with the q-Bernoulli polynomials. Appl. Math. E-Notes 2025, 25, 105–117. [Google Scholar]
- Duren, P.L. Univalent Functions; Springer: New York, NY, USA, 1983. [Google Scholar]
- Srivastava, H.M.; Khan, B.; Khan, N.; Tahir, M.; Ahmad, S.; Khan, N. Upper bound of the third Hankel determinant for a subclass of q-starlike functions associated with the q-exponential function. Bull. Sci. Math. 2021, 167, 102942. [Google Scholar] [CrossRef]
- Richter, W.-D. Deterministic and random generalized complex numbers related to a class of positively homogeneous functionals. Axioms 2023, 12, 60. [Google Scholar] [CrossRef]
- Richter, W.-D. Complex numbers related to semi-antinorms, ellipses or matrix homogeneous functionals. Axioms 2021, 10, 340. [Google Scholar] [CrossRef]
- Ramadhan, A.M.; Al-Ziadi, N.A.J. Initial coefficient estimates for a new subclass of bi-univalent functions based on Horadam polynomials. AIP Conf. Proc. 2023, 2834, 080061. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Motamednezhad, A.; Adegani, E.A. Faber polynomial coefficient estimates for bi-univalent functions defined by using differential subordination and a certain fractional derivative operator. Mathematics 2020, 8, 172. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Mishra, A.K.; Gochhayat, P. Certain subclasses of analytic and bi-univalent functions. Appl. Math. Lett. 2010, 23, 1188–1192. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Raza, N.; AbuJarad, E.S.A.; Srivastava, G.; AbuJarad, M.H. Fekete–Szegö inequality for classes of (p,q)-starlike and (p,q)-convex functions. Rev. Real Acad. Cienc. Exactas Físicas Nat. Ser. A Matemáticas 2019, 113, 3563–3584. [Google Scholar] [CrossRef]
- Adegani, A.; Jafari, E.; Bulboacă, T.; Zaprawa, P. Coefficient bounds for some families of bi-univalent functions with missing coefficients. Axioms 2023, 12, 1071. [Google Scholar] [CrossRef]
- Fekete, M.; Szegö, G. Eine Bemerkung über ungerade schlichte Funktionen. J. Lond. Math. Soc. 1933, 2, 85–89. [Google Scholar] [CrossRef]
- Miller, S.S.; Mocanu, P.T. Differential Subordinations: Theory and Applications; Marcel Dekker: New York, NY, USA, 2000. [Google Scholar]
- Jackson, F.H. On q-definite integrals. Q. J. Pure Appl. Math. 1910, 41, 193–203. [Google Scholar]
- Jackson, F.H. On q-functions and a certain difference operator. Trans. R. Soc. Edinb. 1908, 46, 253–281. [Google Scholar] [CrossRef]
- Exton, H. q-Hypergeometric Functions and Applications; Ellis Horwood: Chichester, UK, 1983. [Google Scholar]
- Gasper, G.; Rahman, M. Basic Hypergeometric Series, 2nd ed.; Cambridge Univ. Press: Cambridge, UK, 2004. [Google Scholar]
- Ghany, H.A. q-Derivative of basic hypergeometric series with respect to parameters. Int. J. Math. Anal. 2009, 3, 1617–1632. [Google Scholar]
- McAnally, M.S. q-exponential and q-gamma functions, II. q-gamma functions. J. Math. Phys. 1995, 36, 574. [Google Scholar] [CrossRef]
- Khan, B.; Srivastava, H.M.; Tahir, M.; Darus, M.; Ahmad, Q.Z.; Khan, N. Applications of a certain q-integral operator to the subclasses of analytic and bi-univalent functions. AIMS Math. 2021, 6, 1024–1039. [Google Scholar] [CrossRef]
- Sakar, F.M.; Hussain, S.; Ahmad, I. Application of Gegenbauer polynomials for bi-univalent functions defined by subordination. Turk. J. Math. 2022, 46, 1089–1098. [Google Scholar] [CrossRef]
- Srivastava, H.M. Operators of basic (or q-) calculus and fractional q-calculus and their applications in geometric function theory of complex analysis. Iran. J. Sci. Technol. Trans. A Sci. 2020, 44, 327–344. [Google Scholar] [CrossRef]
- Al-Salam, W.A. q-Bernoulli numbers and polynomials. Math. Nachr. 1959, 17, 239–260. [Google Scholar] [CrossRef]
- Mahmudov, N.I. Difference equations of q-Appell polynomials. Appl. Math. Comput. 2014, 245, 539–543. [Google Scholar] [CrossRef]
- Al-Asadi, A.M.A.; Al-Ziadi, N.A.J. Exploring new subclasses of bi-univalent functions using Gegenbauer polynomials: Coefficient bounds and Fekete–Szegö problems. AIP Conf. Proc. 2025, 3169, 070013. [Google Scholar]
- Koshy, T. Fibonacci and Lucas Numbers with Applications; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Lupas, A. A Guide of Fibonacci and Lucas Polynomials. Octagon Math. Mag. 1999, 7, 2–12. [Google Scholar]
- Shah, S.A.; Noor, K.I. Study on the q-analogue of a certain family of linear operators. Turk. J. Math. 2019, 43, 2707–2714. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Altinkaya, Ş.; Yalçın, S. Hankel determinant for a subclass of bi-univalent functions defined by using a symmetric q-derivative operator. Filomat 2018, 32, 503–516. [Google Scholar] [CrossRef]
- Swamy, S.R.; Wanas, A.K. A comprehensive family of bi-univalent functions defined by (m,n)-Lucas polynomials. Bol. Soc. Mat. Mex. 2022, 28, 1–10. [Google Scholar] [CrossRef]
- Seoudy, T.M.; Aouf, M.K. Coefficient estimates of new classes of q-starlike and q-convex functions of complex order. J. Math. Inequal. 2016, 10, 135–145. [Google Scholar] [CrossRef]
- Mahmood, S.; Srivastava, H.M.; Khan, N.; Ahmad, Q.Z.; Khan, B.; Ali, I. Upper bound of the third Hankel determinant for a subclass of q-starlike functions. Symmetry 2019, 11, 347. [Google Scholar] [CrossRef]
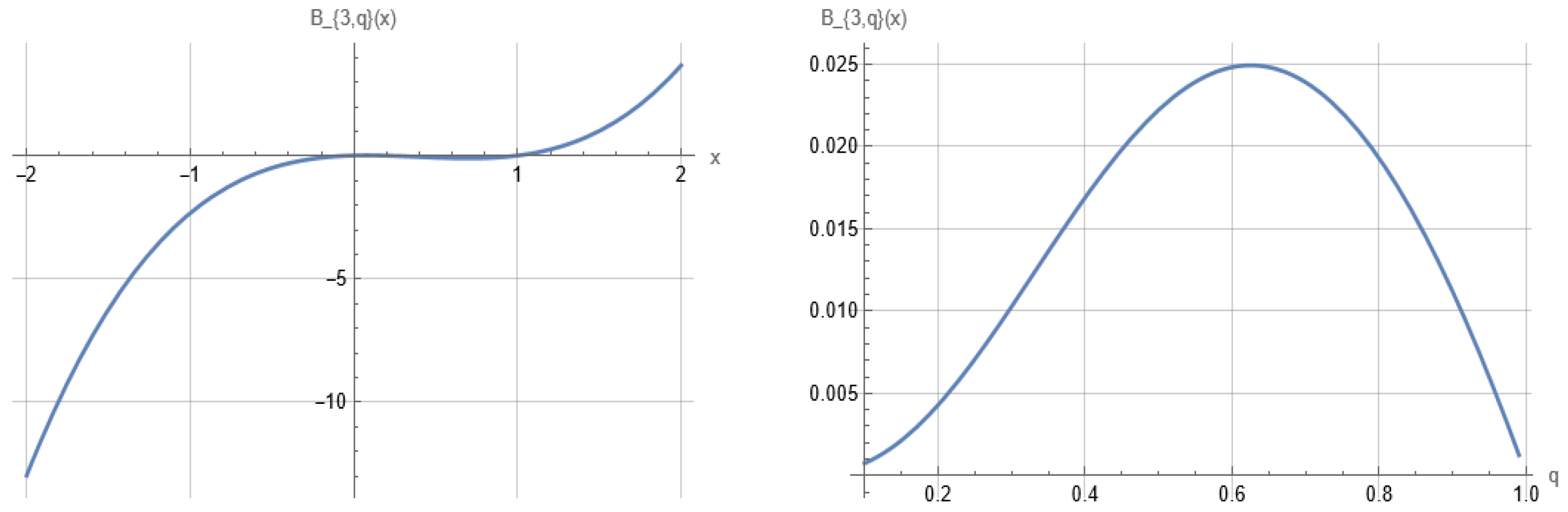
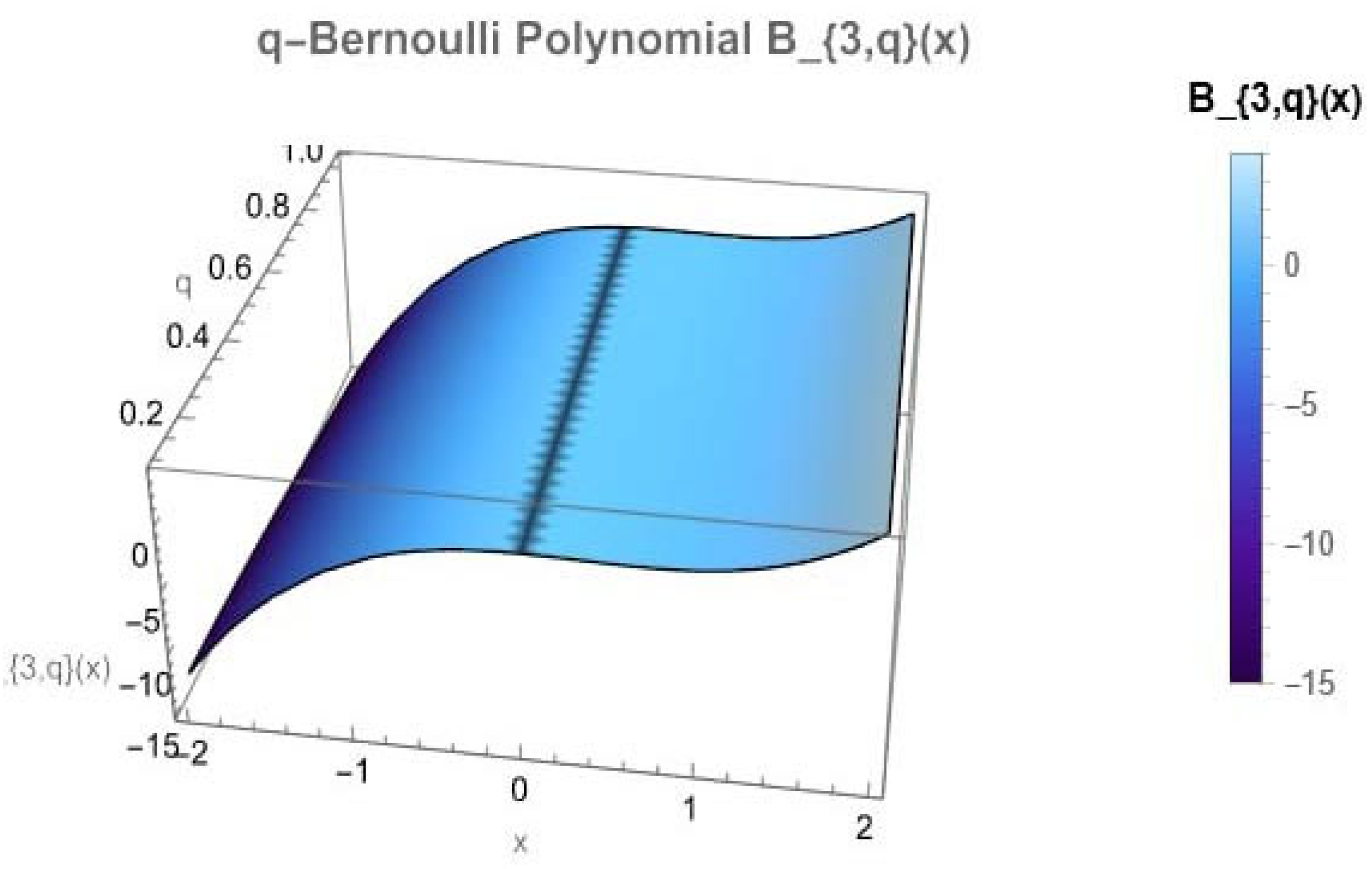
| Functions | Inverse Functions |
|---|---|
| Family | ||
|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wanas, A.K.; Shakir, Q.A.; Catas, A. Coefficient Estimates and Symmetry Analysis for Certain Families of Bi-Univalent Functions Defined by the q-Bernoulli Polynomial. Symmetry 2025, 17, 1532. https://doi.org/10.3390/sym17091532
Wanas AK, Shakir QA, Catas A. Coefficient Estimates and Symmetry Analysis for Certain Families of Bi-Univalent Functions Defined by the q-Bernoulli Polynomial. Symmetry. 2025; 17(9):1532. https://doi.org/10.3390/sym17091532
Chicago/Turabian StyleWanas, Abbas Kareem, Qasim Ali Shakir, and Adriana Catas. 2025. "Coefficient Estimates and Symmetry Analysis for Certain Families of Bi-Univalent Functions Defined by the q-Bernoulli Polynomial" Symmetry 17, no. 9: 1532. https://doi.org/10.3390/sym17091532
APA StyleWanas, A. K., Shakir, Q. A., & Catas, A. (2025). Coefficient Estimates and Symmetry Analysis for Certain Families of Bi-Univalent Functions Defined by the q-Bernoulli Polynomial. Symmetry, 17(9), 1532. https://doi.org/10.3390/sym17091532










