An Analytical Solution for the Uncertain Damped Wave Equation

Abstract

Damped wave equations, as an important class of partial differential equations, have wide applications in fields such as acoustics, signal processing, and fluid mechanics. However, wave propagation is often affected by noise interference, including medium randomness, random external forces and so on. Therefore, an uncertain term needs to be added to the damped wave equation to enhance the model’s fidelity to real-world scenarios. Based on uncertainty theory, this paper introduces the Liu process to the damped wave equation to characterize uncertainties, thereby establishing a new type of equation—the uncertain damped wave equation. In order to solve this equation, the method of separation of variables is employed to derive the analytical solution. The uniqueness of the solution is proved under given initial and boundary conditions. Finally, several examples are provided to illustrate the analytical solutions.

1. Introduction

Partial differential equations can be used to describe many phenomena, such as vibrations of elastic bodies, heat conduction and fluid flow. In particular, the problem of finding analytical solutions to partial differential equations is a crucial research topic, as it is directly related to the accurate description of practical problems in fields such as physics and engineering [1,2]. The wave equation, as a crucial class of partial differential equations, models the propagation of diverse wave types, such as mechanical vibrations, electromagnetic waves, and disturbances in fluids. The study on the wave equation can be traced back as early as the 18th century. In 1747, D’Alembert [3] first derived the one-dimensional wave equation in his investigation of vibrating strings.

However, in reality, the wave propagation inevitably involves energy loss, which makes the wave equation inadequate to model certain phenomena. Consequently, many scholars investigate the wave equation with damping terms. For example, Mickens [4] revised the heat transport equation to derive a damped wave equation and obtained its analytical solution. Su [5] compared the solutions of the phase-lagging heat transport equation and the damped wave equation. Additionally, the damped wave equation has been used to model different types of wave propagation, including pressure wave behaviour in a fluid flowing through porous formations [6], heat conduction in porcine muscle tissue and blood [7], the propagation of pressure waves with viscoelastic effects in fluid flow [8], and electromagnetic wave propagation on transmission lines [9]. However, many phenomena in nature are not entirely deterministic but involve randomness and uncertainty. Thus, some researchers have turned their attention to studying stochastic damped wave equations. In the 1970s, Pardoux [10] investigated nonlinear stochastic damped wave equations. Extensive research on stochastic damped wave equations has been performed by Nguyen [11], Han [12], Cerrai [13] and Cai [14]. The Wiener process is often used to characterize randomness in the stochastic damped wave equation. However, this approach may not be suitable for describing some specific phenomena, such as heat conduction with lagging response. We will explain in detail in Section 4 why it is unreasonable to use the stochastic damped wave equation alone to describe heat conduction with lagging response. This motivates us to explore new tools for characterizing uncertainties in damped wave equations.

In 2007, Liu [15] established uncertainty theory as a mathematical approach for addressing problems involving uncertainty. Moreover, Liu [16] further refined the theory. Liu introduced a special uncertain process named the Liu process, which is characterized by stationary independent increments that follow an uncertain normal distribution. Subsequently, Liu [17] first proposed uncertain differential equation (UDEs) actuated by the Liu process. Chen and Liu [18] obtained analytical solutions for several linear UDEs and established an existence and uniqueness theorem. Then, uncertainty theory was extended to the field of partial differential equations, leading to the proposal of uncertain partial differential equations (UPDEs) [19]. A wealth of relevant research has been performed around UPDEs. Yang and Yao [19] were the first to introduce the uncertain heat equation and derive its analytical solution. Gao and Ralescu [20] put forward the concept of the uncertain wave equation and obtained its analytical solution. Gao [21] further proved the existence and uniqueness theorem of the solution of the uncertain wave equation. Ye and Yang [22] discussed the uncertain heat equation in the three-dimensional space and established its analytical solution. Yang [23] proposed the uncertain age-structured population equation by using the Liu process to model migration noise. Qiu [24] established the uncertain pendulum equation and obtained its solution. He [25] defined higher-order partial derivatives for the first time and verified the solutions of higher-order uncertain partial differential equations. Yang [26] proposed a numerical algorithm for solving uncertain partial differential equations. In uncertainty theory, the Liu process is widely applied to characterize uncertainties in various systems. In this paper, we introduce the Liu process to describe uncertainty in the damped wave equation, thereby providing a new perspective for investigating damped wave equations.

In this paper, an uncertain damped wave equation actuated by the Liu process is proposed. We derive the analytical solution of the uncertain damped wave equation and prove its uniqueness. The rest of the paper is organized as follows. Section 2 presents the uncertain damped wave equation to model heat conduction with an uncertain heat source. In Section 3, we derive the analytical solution of the uncertain damped wave equation and establish the uniqueness of the solution. Section 4 proposes a paradox concerning the stochastic damped wave equation. Finally, the conclusions are provided in Section 5.

2. Uncertain Damped Wave Equation

Based on Fourier’s law and energy conservation law, we develop the uncertain damped wave equation to model heat conduction under an external heat source with uncertain factors.

Fourier’s law governs heat transfer from higher- to lower-temperature regions through solids, liquids, or gases. This heat conduction process is characterized by the flux relation [27]

$$\mathbf{q}(\mathbf{y},\tau )=-K\nabla u(\mathbf{y},\tau ),$$

(1)

where u is the absolute temperature, $\mathbf{y}$ denotes the position vector, $\tau$ denotes the time, and $\mathbf{q}$ and $K>0$ are the heat flux density and the thermal conductivity. However, under high heat flux or low temperature, heat transfer is subject to velocity constraint. Therefore, the heat transfer model should incorporate the lagging response [28,29,30,31]

$$\mathbf{q}(\mathbf{y},\tau +{\lambda }_0)=-K\nabla u(\mathbf{y},\tau ),$$

(2)

where ${\lambda }_0({\lambda }_0>0)$ is the thermal relaxation time. The parameter ${\lambda }_0$ indicates the time lag required for establishing a stable heat conduction state when a temperature gradient is abruptly applied to a volume element. By approximating $\mathbf{q}(\mathbf{y},\tau +{\lambda }_0)$ with its first-order Taylor series, we obtain the Maxwell–Cattaneo law [28,29,31]:

$$\left\{1+{\lambda }_0{\displaystyle \frac{\partial }{\partial \tau }}\right\}\mathbf{q}(\mathbf{y},\tau )=-K\nabla u(\mathbf{y},\tau ).$$

(3)

According to the conservation of energy law, we get

$$\rho c_p{\displaystyle \frac{\partial u(\mathbf{y},\tau )}{\partial \tau }}+\nabla ·\mathbf{q}(\mathbf{y},\tau )=F(y,\tau ,\dot{C_{\tau }}),$$

(4)

where $\rho$ represents the mass density, $c_p$ denotes the specific heat at constant pressure, and $F(y,\tau ,\dot{C_{\tau }})$ is the uncertain heat source. Here, $\dot{C_{\tau }}=\mathrm{d}{C}_{\tau }/\mathrm{d}\tau$ and $C_{\tau }$ is a Liu process [16]. By combining Equations (3) and (4), we have

$${\displaystyle \frac{\partial u(\mathbf{y},\tau )}{\partial \tau }}+{\lambda }_0{\displaystyle \frac{{\partial }^{2}u(\mathbf{y},\tau )}{\partial {\tau }^2}}=\kappa \Delta u(\mathbf{y},\tau )+F(y,\tau ,\dot{C_{\tau }}),$$

(5)

where $\kappa =K/\rho c_p$ represents thermal diffusivity. This UPDE, a special case of the uncertain heat equation, is referred to as the uncertain damped wave equation.

More generally, the one-dimensional uncertain damped wave equation with given initial and boundary conditions

$$\left\{\begin{array}{c}{\displaystyle \frac{{\partial }^{2}u(y,\tau )}{\partial {\tau }^2}}=-\zeta {\displaystyle \frac{\partial u(y,\tau )}{\partial \tau }}+a^2{\displaystyle \frac{{\partial }^{2}u(y,\tau )}{\partial y^2}}+f(y,\tau ,\dot{C_{\tau }}),y\in I,\tau >0,\hfill \\ u(0,\tau )=u(l,\tau )=0,\tau \ge 0,\hfill \\ u(y,0)=\theta \left(y\right),{\displaystyle \frac{\partial u(y,0)}{\partial \tau }}=p\left(y\right),0\le y\le l,\hfill \end{array}\right.$$

(6)

is investigated in this paper, where $\zeta >0$ denotes the damping coefficient, $a>0$ is a constant, $f(y,\tau ,\dot{C_{\tau }})=F(y,\tau ,\dot{C_{\tau }})/{\lambda }_0$, $I=\left\{y\right|0<y<l\}$, $\theta \left(y\right)$ and $p\left(y\right)$ are given functions.

For any given $\omega \in \Omega$, the uncertain damped wave Equation (6) degenerates into a normal damped wave equation

$$\left\{\begin{array}{c}{\displaystyle \frac{{\partial }^{2}u(y,\tau ,\omega )}{\partial {\tau }^2}}=-\zeta {\displaystyle \frac{\partial u(y,\tau ,\omega )}{\partial \tau }}+a^2{\displaystyle \frac{{\partial }^{2}u(y,\tau ,\omega )}{\partial y^2}}+f(y,\tau ,\dot{C_{\tau }}\left(\omega \right)),y\in I,\tau >0,\hfill \\ u(0,\tau ,\omega )=u(l,\tau ,\omega )=0,\tau \ge 0,\hfill \\ u(y,0,\omega )=\theta \left(y\right),{\displaystyle \frac{\partial u(y,0,\omega )}{\partial \tau }}=p\left(y\right),0\le y\le l.\hfill \end{array}\right.$$

(7)

3. Existence and Uniqueness of Solution

Theorem 1. 

If $f(y,\tau ,z)\in C(I\times {\overline{R}}_{+}\times R)$, $\theta \left(y\right)\in C^2\left(R\right)$ and $p\left(y\right)\in C^1\left(R\right)$, then the solution of the uncertain damped wave Equation (6) is

$$u(y,\tau )=\sum _{n=1}^{\infty }{T}_n(\tau ,\dot{C_{\tau }})\sin \left({\displaystyle \frac{n\pi }{l}}y\right),$$

(8)

where

$$T_n(\tau ,\dot{C_{\tau }})=\left\{\begin{array}{c}{a}_1\exp \left({\displaystyle \frac{\sqrt{h}-\zeta }{2}}\tau \right)+a_2\exp \left({\displaystyle \frac{-\sqrt{h}-\zeta }{2}}\tau \right)\hfill \\ +{\displaystyle \frac{1}{\sqrt{h}}}{\int }_0^{\tau }\left(\exp \left({\displaystyle \frac{\sqrt{h}-\zeta }{2}}s\right)-\exp \left({\displaystyle \frac{\sqrt{h}+\zeta }{2}}(-s)\right)\right)f_n(t,\dot{C_t})dt,ifh>0,\hfill \\ \exp \left(-{\displaystyle \frac{\zeta }{2}}\tau \right)(b_0+b\tau )+{\int }_0^{\tau }\exp \left({\displaystyle \frac{-\zeta s}{2}}\right)s{f}_n(t,\dot{C_t})dt,ifh=0,\hfill \\ \exp \left(-{\displaystyle \frac{\zeta }{2}}\tau \right)\left(c_0\cos \left({\displaystyle \frac{\sqrt{-h}}{2}}\tau \right)+c\sin \left({\displaystyle \frac{\sqrt{-h}}{2}}\tau \right)\right)\hfill \\ +{\displaystyle \frac{2}{\sqrt{-h}}}{\int }_0^{\tau }\exp \left(-{\displaystyle \frac{\zeta s}{2}}\right)\sin \left({\displaystyle \frac{\sqrt{-h}}{2}}s\right)f_n(t,\dot{C_t})dt,ifh<0,\hfill \end{array}\right.$$

(9)

in which $f_n(t,\dot{C_t}),{\theta }_n$ and $p_n$ are the Fourier sine series coefficients of the functions $f(y,t,\dot{C_t}),\theta \left(y\right)$ and $p\left(y\right)$, respectively. And $h={\zeta }^2-{\left({\displaystyle \frac{2a\pi n}{l}}\right)}^2$, $s=\tau -t$, $a_1={\displaystyle \frac{\sqrt{h}+\zeta }{2\sqrt{h}}}{\theta }_n+{\displaystyle \frac{p_n}{\sqrt{h}}},a_2={\displaystyle \frac{\sqrt{h}-\zeta }{2\sqrt{h}}}{\theta }_n-{\displaystyle \frac{p_n}{\sqrt{h}}}$, $b_0=c_0={\theta }_n$, $b=p_n+{\displaystyle \frac{\zeta }{2}}{\theta }_n$, $c={\displaystyle \frac{2}{\sqrt{-h}}}{p}_n+{\displaystyle \frac{\zeta }{\sqrt{-h}}}{\theta }_n$.

Proof of Theorem 1. 

Using separation of variables, we assume that the solution of Equation (6) is

$$u(y,\tau )=\sum _{n=1}^{\infty }{T}_n(\tau ,\dot{C_{\tau }})\sin \left({\displaystyle \frac{n\pi }{l}}y\right).$$

(10)

The term $f(y,\tau ,\dot{C_{\tau }})$ is expressed as the Fourier sine series, i.e.,

$$f(y,\tau ,\dot{C_{\tau }})=\sum _{n=1}^{\infty }{f}_n(\tau ,{\dot{C}}_{\tau })\sin \left({\displaystyle \frac{n\pi }{l}}y\right).$$

(11)

Combining Equations (6), (10) and (11), we establish

$$\begin{array}{c}{T}_n^{″}(\tau ,\dot{C_{\tau }})+\zeta T_n^{\prime }(\tau ,\dot{C_{\tau }})+{\left({\displaystyle \frac{an\pi }{l}}\right)}^2{T}_n(\tau ,\dot{C_{\tau }})=f_n(\tau ,{\dot{C}}_{\tau }).\hfill \end{array}$$

(12)

For any given $\omega \in \Omega$, Equation (12) degenerates to a normal ordinary differential equation

$$\begin{array}{c}{T}_n^{″}(\tau ,\dot{C_{\tau }}\left(\omega \right))+\zeta T_n^{\prime }(\tau ,\dot{C_{\tau }}\left(\omega \right))+{\left({\displaystyle \frac{an\pi }{l}}\right)}^2{T}_n(\tau ,\dot{C_{\tau }}\left(\omega \right))=f_n(\tau ,\dot{C_{\tau }}\left(\omega \right)).\hfill \end{array}$$

(13)

Next, we prove $T_n(\tau ,\dot{C_{\tau }}\left(\omega \right))$ satisfies Equation (13) for the following three cases.

(1) If $h={\zeta }^2-{\left({\displaystyle \frac{2a\pi n}{l}}\right)}^2>0$, we obtain the two distinct roots by solving the characteristic Equation (13)

$${\lambda }_1=-{\displaystyle \frac{\zeta }{2}}+{\displaystyle \frac{\sqrt{h}}{2}},{\lambda }_2=-{\displaystyle \frac{\zeta }{2}}-{\displaystyle \frac{\sqrt{h}}{2}}.$$

Based on the variation of parameters, we assume that the solution of Equations (13) takes the form

$$\begin{array}{c}{T}_n(\tau ,\dot{C_{\tau }}\left(\omega \right))={\phi }_1(\tau ,\dot{C_{\tau }}\left(\omega \right))\exp \left({\lambda }_1\tau \right)+{\phi }_2(\tau ,\dot{C_{\tau }}\left(\omega \right))\exp \left({\lambda }_2\tau \right).\hfill \end{array}$$

(14)

Note that

$$\begin{array}{cc}\hfill T_n^{\prime }(\tau ,\dot{C_{\tau }}\left(\omega \right))& ={\lambda }_1{\phi }_1(\tau ,\dot{C_{\tau }}\left(\omega \right))\exp \left({\lambda }_1\tau \right)+{\lambda }_2{\phi }_2(\tau ,\dot{C_{\tau }}\left(\omega \right))\exp \left({\lambda }_2\tau \right)\hfill \\ \hfill & +{\phi }_1^{\prime }(\tau ,\dot{C_{\tau }}\left(\omega \right))\exp \left({\lambda }_1\tau \right)+{\phi }_2^{\prime }(\tau ,\dot{C_{\tau }}\left(\omega \right))\exp \left({\lambda }_2\tau \right).\hfill \end{array}$$

(15)

Letting

$$\begin{array}{c}{\phi }_1^{\prime }(\tau ,\dot{C_{\tau }}\left(\omega \right))\exp \left({\lambda }_1\tau \right)+{\phi }_2^{\prime }(\tau ,\dot{C_{\tau }}\left(\omega \right))\exp \left({\lambda }_2\tau \right)=0,\hfill \end{array}$$

(16)

then we derive

$$\begin{array}{c}{T}_n^{\prime }(\tau ,\dot{C_{\tau }}\left(\omega \right))={\lambda }_1{\phi }_1(\tau ,\dot{C_{\tau }}\left(\omega \right))\exp \left({\lambda }_1\tau \right)+{\lambda }_2{\phi }_2(\tau ,\dot{C_{\tau }}\left(\omega \right))\exp \left({\lambda }_2\tau \right).\hfill \end{array}$$

(17)

From Equations (13), (14) and (17), we obtain

$$\begin{array}{c}{\lambda }_1{\phi }_1^{\prime }(\tau ,\dot{C_{\tau }}\left(\omega \right))\exp \left({\lambda }_1\tau \right)+{\lambda }_2{\phi }_2^{\prime }(\tau ,\dot{C_{\tau }}\left(\omega \right))\exp \left({\lambda }_2\tau \right)=f_n(\tau ,\dot{C_{\tau }}\left(\omega \right)).\hfill \end{array}$$

(18)

By solving Equations (16) and (18), we have

$$\begin{array}{c}{\phi }_1(\tau ,\dot{C_{\tau }}\left(\omega \right))={\displaystyle \frac{1}{\sqrt{h}}}{\int }_0^{\tau }\exp \left({\displaystyle \frac{\zeta -\sqrt{h}}{2}}t\right)f_n(t,\dot{C_t}\left(\omega \right))dt+a_1,\hfill \end{array}$$

(19)

$$\begin{array}{c}{\phi }_2(\tau ,\dot{C_{\tau }}\left(\omega \right))=-{\displaystyle \frac{1}{\sqrt{h}}}{\int }_0^{\tau }\exp \left({\displaystyle \frac{\zeta +\sqrt{h}}{2}}t\right)f_n(t,\dot{C_t}\left(\omega \right))dt+a_2,\hfill \end{array}$$

(20)

where $a_1$ and $a_2$ are constants.

Combining Equations (14), (19) and (20) leads to

$$\begin{array}{cc}\hfill T_n(\tau ,\dot{C_{\tau }}\left(\omega \right))& =a_1\exp \left({\displaystyle \frac{\sqrt{h}-\zeta }{2}}\tau \right)+a_2\exp \left({\displaystyle \frac{-\sqrt{h}-\zeta }{2}}\tau \right)\hfill \\ \hfill & +{\displaystyle \frac{1}{\sqrt{h}}}{\int }_0^{\tau }\left(\exp \left({\displaystyle \frac{\sqrt{h}-\zeta }{2}}s\right)-\exp \left({\displaystyle \frac{\sqrt{h}+\zeta }{2}}(-s)\right)\right)f_n(t,\dot{C_t}\left(\omega \right))dt.\hfill \end{array}$$

(21)

Therefore, the derivative of Equation (21) is

$$\begin{array}{cc}\hfill T_n^{\prime }(\tau ,\dot{C_{\tau }}\left(\omega \right))& ={\displaystyle \frac{\sqrt{h}-\zeta }{2}}{a}_1\exp \left({\displaystyle \frac{\sqrt{h}-\zeta }{2}}\tau \right)-{\displaystyle \frac{\sqrt{h}+\zeta }{2}}{a}_2\exp \left({\displaystyle \frac{-\sqrt{h}-\zeta }{2}}\tau \right)\hfill \\ \hfill & +{\displaystyle \frac{1}{\sqrt{h}}}{\int }_0^{\tau }\left({\displaystyle \frac{\sqrt{h}-\zeta }{2}}\exp \left({\displaystyle \frac{\sqrt{h}-\zeta }{2}}s\right)+{\displaystyle \frac{\sqrt{h}+\zeta }{2}}\exp \left({\displaystyle \frac{\sqrt{h}+\zeta }{2}}(-s)\right)\right)f_n(t,\dot{C_t}\left(\omega \right))dt.\hfill \end{array}$$

(22)

Suppose that $\theta \left(y\right)$ and $p\left(y\right)$ admit the following Fourier series expansions

$$\theta \left(y\right)=\sum _{n=1}^{\infty }{\theta }_n\sin \left({\displaystyle \frac{n\pi }{l}}y\right),p\left(y\right)=\sum _{n=1}^{\infty }{p}_n\sin \left({\displaystyle \frac{n\pi }{l}}y\right).$$

From the initial conditions in Equation (7), we derive

$$\left\{\begin{array}{c}{a}_1+a_2={\theta }_n,\hfill \\ {\displaystyle \frac{\sqrt{h}-\zeta }{2}}{a}_1-{\displaystyle \frac{\sqrt{h}+\zeta }{2}}{a}_2=p_n.\hfill \end{array}\right.$$

(23)

Solving Equation (23), we obtain

$$\begin{array}{c}\hfill a_1={\displaystyle \frac{\sqrt{h}+\zeta }{2\sqrt{h}}}{\theta }_n+{\displaystyle \frac{p_n}{\sqrt{h}}},a_2={\displaystyle \frac{\sqrt{h}-\zeta }{2\sqrt{h}}}{\theta }_n-{\displaystyle \frac{p_n}{\sqrt{h}}}.\end{array}$$

(24)

Therefore, Equation (21) is the solution of Equation (13).

(2) If $h=0$, the characteristic equation of Equation (13) has a repeated root

$$\lambda =-{\displaystyle \frac{\zeta }{2}}.$$

Using variation of parameters, we assume that the solution of Equation (13) is postulated in the form

$$\begin{array}{c}{T}_n(\tau ,\dot{C_{\tau }}\left(\omega \right))=({\phi }_3(\tau ,\dot{C_{\tau }}\left(\omega \right))+\tau {\phi }_4(\tau ,\dot{C_{\tau }}\left(\omega \right)))\exp \left(\lambda \tau \right).\hfill \end{array}$$

(25)

Setting

$$\begin{array}{c}({\phi }_3^{\prime }(\tau ,\dot{C_{\tau }}\left(\omega \right))+\tau {\phi }_4^{\prime }(\tau ,\dot{C_{\tau }}\left(\omega \right)))\exp \left(\lambda \tau \right)=0,\hfill \end{array}$$

(26)

we obtain

$$\begin{array}{c}{T}_n^{\prime }(\tau ,\dot{C_{\tau }}\left(\omega \right))=(\lambda {\phi }_3(\tau ,\dot{C_{\tau }}\left(\omega \right))+\lambda {\phi }_4(\tau ,\dot{C_{\tau }}\left(\omega \right))\tau +{\phi }_4(\tau ,\dot{C_{\tau }}\left(\omega \right)))\exp \left(\lambda \tau \right).\hfill \end{array}$$

(27)

Computing the second derivative of $T_n(\tau ,\dot{C_{\tau }}\left(\omega \right))$ and combining Equations (13), (25) and (27), we have

$$\begin{array}{cc}\hfill & {\phi }_4^{\prime }(\tau ,\dot{C_{\tau }}\left(\omega \right))\exp \left(\lambda \tau \right)+\lambda ({\phi }_3^{\prime }(\tau ,\dot{C_{\tau }}\left(\omega \right))+\tau {\phi }_4^{\prime }(\tau ,\dot{C_{\tau }}\left(\omega \right))\hfill \\ \hfill & +2{\phi }_4(\tau ,\dot{C_{\tau }}\left(\omega \right)))\exp \left(\lambda \tau \right)+\zeta {\phi }_4(\tau ,\dot{C_{\tau }}\left(\omega \right))\exp \left(\lambda \tau \right)=f_n(t,\dot{C_t}\left(\omega \right)).\hfill \end{array}$$

(28)

Solving Equations (26) and (28) gives

$$\begin{array}{c}{\displaystyle {\phi }_3(\tau ,\dot{C_{\tau }}\left(\omega \right))=-{\int }_0^{\tau }\exp \left({\displaystyle \frac{\zeta }{2}}t\right)t{f}_n(t,\dot{C_t}\left(\omega \right))dt+b_0,}\hfill \end{array}$$

(29)

$$\begin{array}{c}{\displaystyle {\phi }_4(\tau ,\dot{C_{\tau }}\left(\omega \right))={\int }_0^{\tau }\exp \left({\displaystyle \frac{\zeta }{2}}t\right)f_n(t,\dot{C_t}\left(\omega \right))dt+b,}\hfill \end{array}$$

(30)

where $b_0$ and b are constants.

Substituting Equations (29) and (30) into (25) gives

$$\begin{array}{c}{\displaystyle T_n(\tau ,\dot{C_{\tau }}\left(\omega \right))=\exp \left(-{\displaystyle \frac{\zeta }{2}}\tau \right)(b_0+b\tau )+{\int }_0^{\tau }\exp \left(-{\displaystyle \frac{\zeta s}{2}}\right)s{f}_n(t,\dot{C_t}\left(\omega \right))dt.}\hfill \end{array}$$

(31)

Note that

$$\begin{array}{cc}\hfill T_n^{\prime }(\tau ,\dot{C_{\tau }}\left(\omega \right))& =\exp \left(-{\displaystyle \frac{\zeta }{2}}\tau \right)\left(\left(1-{\displaystyle \frac{\zeta }{2}}\tau \right)b-{\displaystyle \frac{\zeta }{2}}{b}_0\right)\hfill \\ \hfill & {\displaystyle +{\int }_0^{\tau }\left(\exp \left(-{\displaystyle \frac{\zeta s}{2}}\right)-{\displaystyle \frac{\zeta s}{2}}\exp \left(-{\displaystyle \frac{\zeta s}{2}}\right)\right)f_n(t,\dot{C_t}\left(\omega \right))dt.}\hfill \end{array}$$

(32)

According to the initial conditions, we derive

$$\left\{\begin{array}{c}{b}_0={\theta }_n,\hfill \\ b-{\displaystyle \frac{\zeta }{2}}{b}_0=p_n,\hfill \end{array}\right.$$

which yields

$$\begin{array}{c}\hfill b_0={\theta }_n,b={\displaystyle \frac{\zeta }{2}}{\theta }_n+p_n.\end{array}$$

(33)

Consequently, the solution of Equation (13) is Equation (31).

(3) If $h<0$, the characteristic equation of Equation (13) has two complex roots

$${\lambda }_3=-{\displaystyle \frac{\zeta }{2}}+{\displaystyle \frac{\sqrt{-h}}{2}}i,{\lambda }_4=-{\displaystyle \frac{\zeta }{2}}-{\displaystyle \frac{\sqrt{-h}}{2}}i.$$

Note that these two roots are symmetric with respect to the real axis. By applying variation of parameters, the solution of Equation (13) takes the form

$$\begin{array}{c}{T}_n(\tau ,\dot{C_{\tau }}\left(\omega \right))={\phi }_5(\tau ,\dot{C_{\tau }}\left(\omega \right))\exp \left({\lambda }_3\tau \right)+{\phi }_6(\tau ,\dot{C_{\tau }}\left(\omega \right))\exp \left({\lambda }_4\tau \right).\hfill \end{array}$$

(34)

Similar to the case $h>0$, we have

$$\begin{array}{c}{\phi }_5^{\prime }(\tau ,\dot{C_{\tau }}\left(\omega \right))\exp \left({\lambda }_3\tau \right)+{\phi }_6^{\prime }(\tau ,\dot{C_{\tau }}\left(\omega \right))\exp \left({\lambda }_4\tau \right)=0,\hfill \end{array}$$

(35)

$$\begin{array}{c}{\lambda }_3{\phi }_5^{\prime }(\tau ,\dot{C_{\tau }}\left(\omega \right))\exp \left({\lambda }_3\tau \right)+{\lambda }_4{\phi }_6^{\prime }(\tau ,\dot{C_{\tau }}\left(\omega \right))\exp \left({\lambda }_4\tau \right)=f_n(\tau ,\dot{C_{\tau }}\left(\omega \right)).\hfill \end{array}$$

(36)

From Equations (35) and (36), we derive

$$\begin{array}{c}{\displaystyle {\phi }_5(\tau ,\dot{C_{\tau }}\left(\omega \right))=-{\displaystyle \frac{i}{\sqrt{-h}}}{\int }_0^{\tau }\exp \left(\frac{\zeta -\sqrt{-h}i}{2}t\right)f_n(t,\dot{C_t}\left(\omega \right))dt+d_1,}\hfill \end{array}$$

(37)

$$\begin{array}{c}{\displaystyle {\phi }_6(\tau ,\dot{C_{\tau }}\left(\omega \right))={\displaystyle \frac{i}{\sqrt{-h}}}{\int }_0^{\tau }\exp \left(\frac{\zeta +\sqrt{-h}i}{2}t\right)f_n(t,\dot{C_t}\left(\omega \right))dt+d_2,}\hfill \end{array}$$

(38)

where $d_1$ and $d_2$ are constants.

Substituting Equations (37) and (38) into (34) yields

$$\begin{array}{cc}\hfill T_n(\tau ,\dot{C_{\tau }}\left(\omega \right))& =d_1\exp \left(-{\displaystyle \frac{\zeta \tau }{2}}+{\displaystyle \frac{\tau \sqrt{-h}}{2}}i\right)+d_2\exp \left(-{\displaystyle \frac{\zeta \tau }{2}}-{\displaystyle \frac{\tau \sqrt{-h}}{2}}i\right)\hfill \\ \hfill & +{\displaystyle \frac{2}{\sqrt{-h}}}{\int }_0^{\tau }\exp \left(-{\displaystyle \frac{\zeta s}{2}}\right)\sin \left({\displaystyle \frac{\sqrt{-h}}{2}}s\right)f_n(t,\dot{C_t}\left(\omega \right))dt.\hfill \end{array}$$

(39)

Note that Equation (13) has two complex-valued solutions

$$\exp \left(-{\displaystyle \frac{\zeta \tau }{2}}+{\displaystyle \frac{\tau \sqrt{-h}}{2}}i\right)=\exp \left(-{\displaystyle \frac{\zeta }{2}}\tau \right)\left(\cos \left({\displaystyle \frac{\sqrt{-h}}{2}}\tau \right)+i\sin \left({\displaystyle \frac{\sqrt{-h}}{2}}\tau \right)\right),$$

$$\exp \left(-{\displaystyle \frac{\zeta \tau }{2}}-{\displaystyle \frac{\tau \sqrt{-h}}{2}}i\right)=\exp \left(-{\displaystyle \frac{\zeta }{2}}\tau \right)\left(\cos \left({\displaystyle \frac{\sqrt{-h}}{2}}\tau \right)-i\sin \left({\displaystyle \frac{\sqrt{-h}}{2}}\tau \right)\right).$$

Since the coefficients of Equation (13) are real constants, the real part

$$\exp \left(-{\displaystyle \frac{\zeta }{2}}\tau \right)\cos \left({\displaystyle \frac{\sqrt{-h}}{2}}\tau \right)$$

and the imaginary part

$$\exp \left(-{\displaystyle \frac{\zeta }{2}}\tau \right)\sin \left({\displaystyle \frac{\sqrt{-h}}{2}}\tau \right)$$

are two real-valued solutions to Equation (13). Thus, the solution of Equation (13) is

$$\begin{array}{cc}\hfill T_n(\tau ,\dot{C_{\tau }}\left(\omega \right))& =\exp \left(-{\displaystyle \frac{\zeta }{2}}\tau \right)\left(c_0\cos \left({\displaystyle \frac{\sqrt{-h}}{2}}\tau \right)+c\sin \left({\displaystyle \frac{\sqrt{-h}}{2}}\tau \right)\right)\hfill \\ \hfill & +{\displaystyle \frac{2}{\sqrt{-h}}}{\int }_0^{\tau }\exp \left(-{\displaystyle \frac{\zeta s}{2}}\right)\sin \left({\displaystyle \frac{\sqrt{-h}}{2}}s\right)f_n(t,\dot{C_t}\left(\omega \right))dt.\hfill \end{array}$$

(40)

Then, we have

$$\begin{array}{cc}\hfill T_n^{\prime }(\tau ,\dot{C_{\tau }}\left(\omega \right))& =-{\displaystyle \frac{\zeta }{2}}\exp \left(-{\displaystyle \frac{\zeta }{2}}\tau \right)\left(c_0\cos \left({\displaystyle \frac{\sqrt{-h}}{2}}\tau \right)+c\sin \left({\displaystyle \frac{\sqrt{-h}}{2}}\tau \right)\right)\hfill \\ \hfill & +{\displaystyle \frac{\sqrt{-h}}{2}}\exp \left(-{\displaystyle \frac{\zeta }{2}}\tau \right)\left(c\cos \left({\displaystyle \frac{\sqrt{-h}}{2}}\tau \right)-c_0\sin \left({\displaystyle \frac{\sqrt{-h}}{2}}\tau \right)\right)\hfill \\ \hfill & +{\int }_0^{\tau }\left(\exp \left(-{\displaystyle \frac{\zeta s}{2}}\right)\cos \left({\displaystyle \frac{\sqrt{-h}}{2}}s\right)-{\displaystyle \frac{\zeta }{\sqrt{-h}}}\exp \left(-{\displaystyle \frac{\zeta s}{2}}\right)\sin \left({\displaystyle \frac{\sqrt{-h}}{2}}s\right)\right)f_n(t,\dot{C_t}\left(\omega \right))dt.\hfill \end{array}$$

(41)

Based on the initial conditions, we derive

$$\left\{\begin{array}{c}{c}_0={\theta }_n,\hfill \\ {\displaystyle \frac{\sqrt{-h}}{2}}c-{\displaystyle \frac{\zeta }{2}}{c}_0=p_n,\hfill \end{array}\right.$$

which means

$$\begin{array}{c}\hfill c_0={\theta }_n,c={\displaystyle \frac{\zeta }{\sqrt{-h}}}{\theta }_n+{\displaystyle \frac{2}{\sqrt{-h}}}{p}_n.\end{array}$$

(42)

Therefore, Equation (40) is the solution of Equation (13).

In conclusion, $T_n(\tau ,\dot{C_{\tau }})$ is the solution of Equation (12). □

Theorem 2. 

If $u(y,\tau )$ defined in Equation (8)is a twice continuously differentiable solution of the uncertain damped wave Equation (6), then $u(y,\tau )$ is unique.

Proof of Theorem 2. 

For any $\omega \in \Omega$, assuming that $v_1(y,\tau ,\omega )$ and $v_2(y,\tau ,\omega )$ are two solutions of the Equation (7). Then $g(y,\tau ,\omega )=v_1(y,\tau ,\omega )-v_2(y,\tau ,\omega )$ is the solution of the following problem:

$$\left\{\begin{array}{c}{\displaystyle \frac{{\partial }^{2}g(y,\tau ,\omega )}{\partial {\tau }^2}}-a^2{\displaystyle \frac{{\partial }^{2}g(y,\tau ,\omega )}{\partial y^2}}=-\zeta {\displaystyle \frac{\partial g(y,\tau ,\omega )}{\partial \tau }},0<y<l,\tau >0,\hfill \\ g(0,\tau ,\omega )=g(l,\tau ,\omega )=0,\tau \ge 0,\hfill \\ g(y,0,\omega )=g_{\tau }(y,0,\omega )=0,0\le y\le l.\hfill \end{array}\right.$$

(43)

Let ${\displaystyle E\left(\tau \right)={\displaystyle \frac{1}{2}}{\int }_0^l(g_{\tau }^2(y,\tau ,\omega )+a^2{g}_y^2(y,\tau ,\omega ))dy}$. It follows that

$$\begin{array}{cc}\hfill {\displaystyle \frac{dE\left(\tau \right)}{d\tau }}& ={\int }_0^l(g_{\tau }(y,\tau ,\omega )g_{\tau \tau }(y,\tau ,\omega )+a^2{g}_y(y,\tau ,\omega )g_{y\tau }(y,\tau ,\omega ))dy\hfill \\ \hfill & ={\int }_0^l{g}_{\tau }(y,\tau ,\omega )g_{\tau \tau }(y,\tau ,\omega )dy+{\int }_0^l{a}^2{g}_y(y,\tau ,\omega )d{g}_{\tau }(y,\tau ,\omega )\hfill \\ \hfill & ={\int }_0^l{g}_{\tau }(y,\tau ,\omega )g_{\tau \tau }(y,\tau ,\omega )dy-{\int }_0^l{a}^2{g}_{\tau }(y,\tau ,\omega )g_{yy}(y,\tau ,\omega )dy\hfill \\ \hfill & ={\int }_0^l{g}_{\tau }(y,\tau ,\omega )(g_{\tau \tau }(y,\tau ,\omega )-a^2{g}_{yy}(y,\tau ,\omega ))dy\hfill \\ \hfill & =-\zeta {\int }_0^l{g}_{\tau }^2(y,\tau ,\omega )dy\hfill \\ \hfill & \le 0,\hfill \end{array}$$

which indicates $E\left(\tau \right)$ is monotonically decreasing. Hence, we obtain

$$E\left(\tau \right)\le E\left(0\right).$$

(44)

Since $g(y,0,\omega )=0$, we can deduce $g_y(y,0,\omega )=0$. It follows that

$$E\left(0\right)={\displaystyle \frac{1}{2}}{\int }_0^l{g}_{\tau }^2(y,0,\omega )+a^2{g}_y^2(y,0,\omega )dy=0.$$

(45)

Combining Equations (44) and (45) yields

$$E\left(\tau \right)\le 0.$$

(46)

Additionally, it is evident that

$$E\left(\tau \right)\ge 0.$$

(47)

From Equations (46) and (47), we can derive $E\left(\tau \right)=0$. For any $\tau$, we obtain $g_y(y,\tau ,\omega )\equiv g_{\tau }(y,\tau ,\omega )\equiv 0$. It means that $g(y,\tau ,\omega )$ is a constant function. Because the initial condition $g(0,\tau ,\omega )=0$, we obtain $g(y,\tau ,\omega )\equiv 0$. Therefore, the uncertain damped wave Equation (6) admits a unique solution. □

Next, the following three examples are presented to demonstrate the effectiveness of the analytical solution. In Example 1, the function $f(y,\tau ,\dot{C_{\tau }})$ is linear, while in Examples 2 and 3, it adopts nonlinear forms involving exponential and trigonometric functions.

Example 1. 

Consider an uncertain damped wave equation

$$\left\{\begin{array}{c}{\displaystyle \frac{{\partial }^{2}u(y,\tau )}{\partial {\tau }^2}}=-2{\displaystyle \frac{\partial u(y,\tau )}{\partial \tau }}+{\displaystyle \frac{{\partial }^{2}u(y,\tau )}{\partial y^2}}+\dot{C_{\tau }},0<y<2,\tau >0,\hfill \\ u(0,\tau )=u(2,\tau )=0,\tau \ge 0,\hfill \\ u(y,0)=\sin \left({\displaystyle \frac{\pi }{2}}y\right),{\displaystyle \frac{\partial u(y,0)}{\partial \tau }}={\displaystyle \frac{\pi }{2}}\cos \left({\displaystyle \frac{\pi }{2}}y\right),0\le y\le 2.\hfill \end{array}\right.$$

(48)

Based on Theorem 1, setting $n=1$ yields

$$\begin{array}{cc}\hfill {\theta }_1& ={\int }_0^2{\sin }^2\left({\displaystyle \frac{\pi }{2}}y\right)dy=1,\hfill \end{array}$$

$$\begin{array}{c}\hfill p_1={\displaystyle \frac{\pi }{2}}{\int }_0^2\cos \left({\displaystyle \frac{\pi }{2}}y\right)\sin \left({\displaystyle \frac{\pi }{2}}y\right)dy=0.\end{array}$$

If $n\ge 2$, we obtain

$$\begin{array}{cc}\hfill {\theta }_n& ={\int }_0^2\sin \left({\displaystyle \frac{\pi }{2}}y\right)\sin \left({\displaystyle \frac{n\pi }{2}}y\right)dy={\displaystyle \frac{1}{2}}{\int }_0^2\left(\cos \left({\displaystyle \frac{(1-n)\pi }{2}}y\right)-\cos \left({\displaystyle \frac{(1+n)\pi }{2}}y\right)\right)dy=0,\hfill \end{array}$$

$$\begin{array}{cc}\hfill p_n& ={\displaystyle \frac{\pi }{2}}{\int }_0^2\cos \left({\displaystyle \frac{\pi }{2}}y\right)\sin \left({\displaystyle \frac{n\pi }{2}}y\right)dy\hfill \\ \hfill & ={\displaystyle \frac{\pi }{4}}{\int }_0^2\left(\sin \left({\displaystyle \frac{(n+1)\pi }{2}}y\right)-\sin \left({\displaystyle \frac{(1-n)\pi }{2}}y\right)\right)dy\hfill \\ \hfill & ={\displaystyle \frac{n}{n^2-1}}(1+{(-1)}^n).\hfill \end{array}$$

It can be seen that $h<0$ for any n. Then the coefficients are given by

$$\begin{array}{cc}\hfill T_1(\tau ,\dot{C_{\tau }})& =\exp (-\tau )\left(\cos \left({\displaystyle \frac{\sqrt{{\pi }^2-4}}{2}}\tau \right)+{\displaystyle \frac{2}{\sqrt{{\pi }^2-4}}}\sin \left({\displaystyle \frac{\sqrt{{\pi }^2-4}}{2}}\tau \right)\right)\hfill \\ \hfill & +{\displaystyle \frac{2}{\sqrt{{\pi }^2-4}}}{\int }_0^{\tau }\exp (-s)\sin \left({\displaystyle \frac{\sqrt{{\pi }^2-4}}{2}}s\right){\int }_0^2\dot{C_t}\sin \left({\displaystyle \frac{\pi }{2}}y\right)dydt\hfill \\ \hfill & =\exp (-\tau )\left(\cos \left({\displaystyle \frac{\sqrt{{\pi }^2-4}}{2}}\tau \right)+{\displaystyle \frac{2}{\sqrt{{\pi }^2-4}}}\sin \left({\displaystyle \frac{\sqrt{{\pi }^2-4}}{2}}\tau \right)\right)\hfill \\ \hfill & +{\displaystyle \frac{8}{\pi \sqrt{{\pi }^2-4}}}{\int }_0^{\tau }\exp (-s)\sin \left({\displaystyle \frac{\sqrt{{\pi }^2-4}}{2}}s\right)d{C}_t\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill T_n(\tau ,\dot{C_{\tau }})& ={\displaystyle \frac{2n(1+{(-1)}^n)\exp (-\tau )}{\sqrt{-h}(n^2-1)}}\sin \left({\displaystyle \frac{\sqrt{-h}}{2}}\tau \right)\hfill \\ \hfill & +{\displaystyle \frac{2}{\sqrt{-h}}}{\int }_0^{\tau }\exp (-s)\sin \left({\displaystyle \frac{\sqrt{-h}}{2}}s\right){\int }_0^2\dot{C_t}\sin \left({\displaystyle \frac{n\pi }{2}}y\right)dydt\hfill \\ \hfill & ={\displaystyle \frac{2n(1+{(-1)}^n)\exp (-\tau )}{\sqrt{-h}(n^2-1)}}\sin \left({\displaystyle \frac{\sqrt{-h}}{2}}\tau \right)\hfill \\ \hfill & +{\displaystyle \frac{2}{\sqrt{-h}}}{\int }_0^{\tau }\exp (-s)\sin \left({\displaystyle \frac{\sqrt{-h}}{2}}s\right)\dot{C_t}dt{\int }_0^2\sin \left({\displaystyle \frac{n\pi }{2}}y\right)dy\hfill \\ \hfill & ={\displaystyle \frac{2n(1+{(-1)}^n)\exp (-\tau )}{\sqrt{n^2{\pi }^2-4}(n^2-1)}}\sin \left({\displaystyle \frac{\sqrt{n^2{\pi }^2-4}}{2}}\tau \right)\hfill \\ \hfill & +{\displaystyle \frac{4(1-{(-1)}^n)}{n\pi \sqrt{n^2{\pi }^2-4}}}{\int }_0^{\tau }\exp (-s)\sin \left({\displaystyle \frac{\sqrt{n^2{\pi }^2-4}}{2}}s\right)d{C}_t,\hfill \end{array}$$

where $n\ge 2$.

Therefore, the solution of Equation (48) is

$$\begin{array}{cc}\hfill u(y,\tau )& =\left(\exp (-\tau )\left(\cos \left({\displaystyle \frac{\sqrt{{\pi }^2-4}}{2}}\tau \right)+{\displaystyle \frac{2}{\sqrt{{\pi }^2-4}}}\sin \left({\displaystyle \frac{\sqrt{{\pi }^2-4}}{2}}\tau \right)\right)\right.\hfill \\ \hfill & \left.+{\displaystyle \frac{8}{\pi \sqrt{{\pi }^2-4}}}{\int }_0^{\tau }\exp (-s)\sin \left({\displaystyle \frac{\sqrt{{\pi }^2-4}}{2}}s\right)d{C}_t\right)\sin \left({\displaystyle \frac{\pi }{2}}y\right)\hfill \\ \hfill & +\sum _{n=2}^{\infty }\left({\displaystyle \frac{2n(1+{(-1)}^n)\exp (-\tau )}{\sqrt{n^2{\pi }^2-4}(n^2-1)}}\sin \left({\displaystyle \frac{\sqrt{n^2{\pi }^2-4}}{2}}\tau \right)\right.\hfill \\ \hfill & \left.+{\displaystyle \frac{4(1-{(-1)}^n)}{n\pi \sqrt{n^2{\pi }^2-4}}}{\int }_0^{\tau }\exp (-s)\sin \left({\displaystyle \frac{\sqrt{n^2{\pi }^2-4}}{2}}s\right)d{C}_t\right)\sin \left({\displaystyle \frac{n\pi }{2}}y\right).\hfill \end{array}$$

Example 2. 

Consider an uncertain damped wave equation

$$\left\{\begin{array}{c}{\displaystyle \frac{{\partial }^{2}u(y,\tau )}{\partial {\tau }^2}}=-4{\displaystyle \frac{\partial u(y,\tau )}{\partial \tau }}+{\displaystyle \frac{{\partial }^{2}u(y,\tau )}{\partial y^2}}+\exp (-\tau )\dot{C_{\tau }},0<y<2,\tau >0,\hfill \\ u(0,\tau )=u(2,\tau )=0,\tau \ge 0,\hfill \\ u(y,0)={\displaystyle \frac{\partial u(y,0)}{\partial \tau }}=0,0\le y\le 2.\hfill \end{array}\right.$$

(49)

From Theorem 1, it is evident that ${\theta }_n=p_n=0$. When $n=1$, we obtain $h>0$. Therefore, the coefficient is

$$\begin{array}{cc}\hfill T_1(\tau ,\dot{C_{\tau }})& ={\displaystyle \frac{1}{\sqrt{16-{\pi }^2}}}{\int }_0^{\tau }\left(\exp \left({\displaystyle \frac{\sqrt{16-{\pi }^2}-4}{2}}s\right)-\exp \left(-{\displaystyle \frac{\sqrt{16-{\pi }^2}+4}{2}}s\right)\right){\int }_0^2\exp (-t)\dot{C_t}\sin \left({\displaystyle \frac{\pi }{2}}y\right)dydt\hfill \\ \hfill & ={\displaystyle \frac{1}{\sqrt{16-{\pi }^2}}}{\int }_0^{\tau }\left(\exp \left({\displaystyle \frac{\sqrt{16-{\pi }^2}-4}{2}}s-t\right)-\exp \left(-{\displaystyle \frac{\sqrt{16-{\pi }^2}+4}{2}}s-t\right)\right)\dot{C_t}dt{\int }_0^2\sin \left({\displaystyle \frac{\pi }{2}}y\right)dy\hfill \\ \hfill & ={\displaystyle \frac{4}{\pi \sqrt{16-{\pi }^2}}}{\int }_0^{\tau }\exp \left(-s-\tau \right)\left(\exp \left({\displaystyle \frac{\sqrt{16-{\pi }^2}}{2}}s\right)-\exp \left(-{\displaystyle \frac{\sqrt{16-{\pi }^2}}{2}}s\right)\right)d{C}_t.\hfill \end{array}$$

If $n=2,3,\dots$, we have $h<0$. Hence the coefficients can be written as

$$\begin{array}{cc}\hfill T_n(\tau ,\dot{C_{\tau }})& ={\displaystyle \frac{2}{\sqrt{-h}}}{\int }_0^{\tau }\exp (-2s)\sin \left({\displaystyle \frac{\sqrt{-h}}{2}}s\right){\int }_0^2\exp (-t)\dot{C_t}\sin \left({\displaystyle \frac{n\pi }{2}}y\right)dydt\hfill \\ \hfill & ={\displaystyle \frac{2}{\sqrt{-h}}}{\int }_0^{\tau }\exp (-s-\tau )\sin \left({\displaystyle \frac{\sqrt{-h}}{2}}s\right)\dot{C_t}dt{\int }_0^2\sin \left({\displaystyle \frac{n\pi }{2}}y\right)dy\hfill \\ \hfill & ={\displaystyle \frac{4(1-{(-1)}^n)}{n\pi \sqrt{n^2{\pi }^2-16}}}{\int }_0^{\tau }\exp (-s-\tau )\sin \left({\displaystyle \frac{\sqrt{n^2{\pi }^2-16}}{2}}s\right)d{C}_t.\hfill \end{array}$$

In summary, the solution of Equation (49) is

$$\begin{array}{cc}\hfill u(y,\tau )& =\sin \left({\displaystyle \frac{\pi }{2}}y\right){\displaystyle \frac{4}{\pi \sqrt{16-{\pi }^2}}}{\int }_0^{\tau }\exp (-s-\tau )\left(\exp \left({\displaystyle \frac{\sqrt{16-{\pi }^2}}{2}}s\right)-\exp \left(-{\displaystyle \frac{\sqrt{16-{\pi }^2}}{2}}s\right)\right)d{C}_t\hfill \\ \hfill & +\sum _{n=2}^{\infty }\left({\displaystyle \frac{4(1-{(-1)}^n)}{n\pi \sqrt{n^2{\pi }^2-16}}}{\int }_0^{\tau }\exp (-s-\tau )\sin \left({\displaystyle \frac{\sqrt{n^2{\pi }^2-16}}{2}}s\right)d{C}_t\right)\sin \left({\displaystyle \frac{n\pi }{2}}y\right).\hfill \end{array}$$

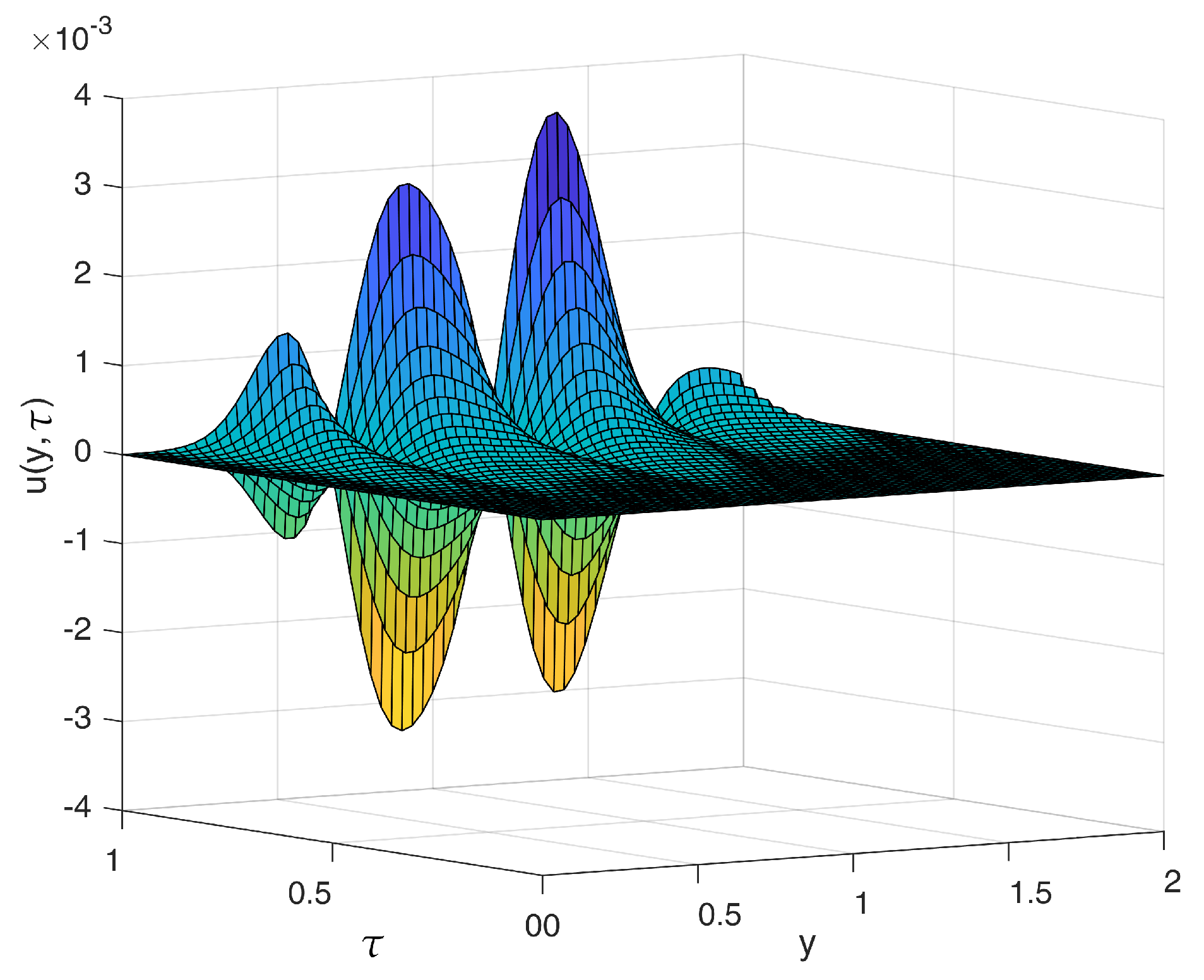
To intuitively present the solution to Example 2, the finite difference method is employed for the numerical solution of the uncertain damped wave Equation (49). An explicit difference scheme is established by approximating ${\partial }^{2}u(y,\tau )/\partial {\tau }^2$, $\partial u(y,\tau )/\partial \tau$, and ${\partial }^{2}u(y,\tau )/\partial y^2$ in the equation using central difference quotients. The uncertain term $\dot{C_{\tau }}$ in the equation is replaced with a randomly generated standard normal uncertain distribution sequence. The simulation process is repeated 1000 times and the average of the 1000 solution samples at each grid point serves as the estimated value of the expectation for the point. Figure 1 illustrates the variation of $u(y,\tau )$ with respect to space y and time $\tau$.

Example 3. 

Consider an uncertain damped wave equation

$$\left\{\begin{array}{c}{\displaystyle \frac{{\partial }^{2}u(y,\tau )}{\partial {\tau }^2}}=-2\pi {\displaystyle \frac{\partial u(y,\tau )}{\partial \tau }}+{\displaystyle \frac{{\partial }^{2}u(y,\tau )}{\partial y^2}}+\cos y\dot{C_{\tau }},0<y<2,\tau >0,\hfill \\ u(0,\tau )=u(2,\tau )=0,\tau \ge 0,\hfill \\ u(y,0)={\displaystyle \frac{\partial u(y,0)}{\partial \tau }}=0,0\le y\le 2.\hfill \end{array}\right.$$

(50)

Following Theorem 1, we conclude that ${\theta }_n=p_n=0$. Letting $n=1$, we have $h>0$. Hence the coefficient is

$$\begin{array}{cc}\hfill T_1(\tau ,\dot{C_{\tau }})& ={\displaystyle \frac{1}{\sqrt{3}\pi }}{\int }_0^{\tau }\left(\exp \left({\displaystyle \frac{\sqrt{3}\pi -2\pi }{2}}s\right)-\exp \left({\displaystyle \frac{\sqrt{3}\pi +2\pi }{2}}(-s)\right)\right){\int }_0^2\dot{C_t}\cos y\sin \left({\displaystyle \frac{\pi }{2}}y\right)dydt\hfill \\ \hfill & ={\displaystyle \frac{1}{\sqrt{3}\pi }}{\int }_0^{\tau }\left(\exp \left({\displaystyle \frac{\sqrt{3}\pi -2\pi }{2}}s\right)-\exp \left({\displaystyle \frac{\sqrt{3}\pi +2\pi }{2}}(-s)\right)\right)\dot{C_t}dt{\int }_0^2\cos y\sin \left({\displaystyle \frac{\pi }{2}}y\right)dy\hfill \\ \hfill & ={\displaystyle \frac{4\pi co{s}^{2}1}{\sqrt{3}\pi ({\pi }^2-4)}}{\int }_0^{\tau }\left(\exp \left({\displaystyle \frac{\sqrt{3}\pi -2\pi }{2}}s\right)-\exp \left({\displaystyle \frac{\sqrt{3}\pi +2\pi }{2}}(-s)\right)\right)d{C}_t.\hfill \end{array}$$

Similarly, if $n=2$ then we obtain $h=0$ and the coefficient $T_2(\tau ,\dot{C_{\tau }})$ is given as

$$\begin{array}{cc}\hfill T_2(\tau ,\dot{C_{\tau }})& ={\int }_0^{\tau }\exp (-\pi s)s{\int }_0^2\dot{C_t}\cos y\sin \left(\pi y\right)dydt\hfill \\ \hfill & ={\int }_0^{\tau }\exp (-\pi s)s\dot{C_t}dt{\int }_0^2\cos y\sin \left(\pi y\right)dy\hfill \\ \hfill & ={\displaystyle \frac{2\pi {\sin }^{2}1}{{\pi }^2-1}}{\int }_0^{\tau }\exp (-\pi s)sd{C}_t.\hfill \end{array}$$

For $n\ge 3$, we have $h<0$ and the coefficients $T_n(\tau ,\dot{C_{\tau }})$ are

$$\begin{array}{cc}\hfill T_n(\tau ,\dot{C_{\tau }})& ={\displaystyle \frac{2}{\sqrt{-h}}}{\int }_0^{\tau }\exp (-\pi s)\sin \left({\displaystyle \frac{\sqrt{-h}}{2}}s\right){\int }_0^2\dot{C_t}\cos y\sin \left({\displaystyle \frac{n\pi }{2}}y\right)dydt\hfill \\ \hfill & ={\displaystyle \frac{2}{\sqrt{-h}}}{\int }_0^{\tau }\exp (-\pi s)\sin \left({\displaystyle \frac{\sqrt{-h}}{2}}s\right)\dot{C_t}dt{\int }_0^2\cos y\sin \left({\displaystyle \frac{n\pi }{2}}y\right)dy\hfill \\ \hfill & ={\displaystyle \frac{4n(1-{(-1)}^n\cos 2)}{\sqrt{n^2-4}(n^2{\pi }^2-4)}}{\int }_0^{\tau }\exp (-\pi s)\sin \left({\displaystyle \frac{\sqrt{n^2-4}}{2}}\pi s\right)d{C}_t.\hfill \end{array}$$

Therefore, the solution of Equation (50) is

$$\begin{array}{cc}\hfill u(y,\tau )& =\sin \left({\displaystyle \frac{\pi }{2}}y\right){\displaystyle \frac{4\pi {\cos }^{2}1}{\sqrt{3}\pi ({\pi }^2-4)}}{\int }_0^{\tau }\left(\exp \left({\displaystyle \frac{\sqrt{3}\pi -2\pi }{2}}s\right)-\exp \left({\displaystyle \frac{\sqrt{3}\pi +2\pi }{2}}(-s)\right)\right)d{C}_t\hfill \\ \hfill & +\sin \left(\pi y\right){\displaystyle \frac{2\pi {\sin }^{2}1}{{\pi }^2-1}}{\int }_0^{\tau }\exp (-\pi s)sd{C}_t\hfill \\ \hfill & +\sum _{n=3}^{\infty }\left({\displaystyle \frac{4n(1-{(-1)}^n\cos 2)}{\sqrt{n^2-4}(n^2{\pi }^2-4)}}{\int }_0^{\tau }\exp (-\pi s)\sin \left({\displaystyle \frac{\sqrt{n^2-4}}{2}}\pi s\right)d{C}_t\right)\sin \left({\displaystyle \frac{n\pi }{2}}y\right).\hfill \end{array}$$

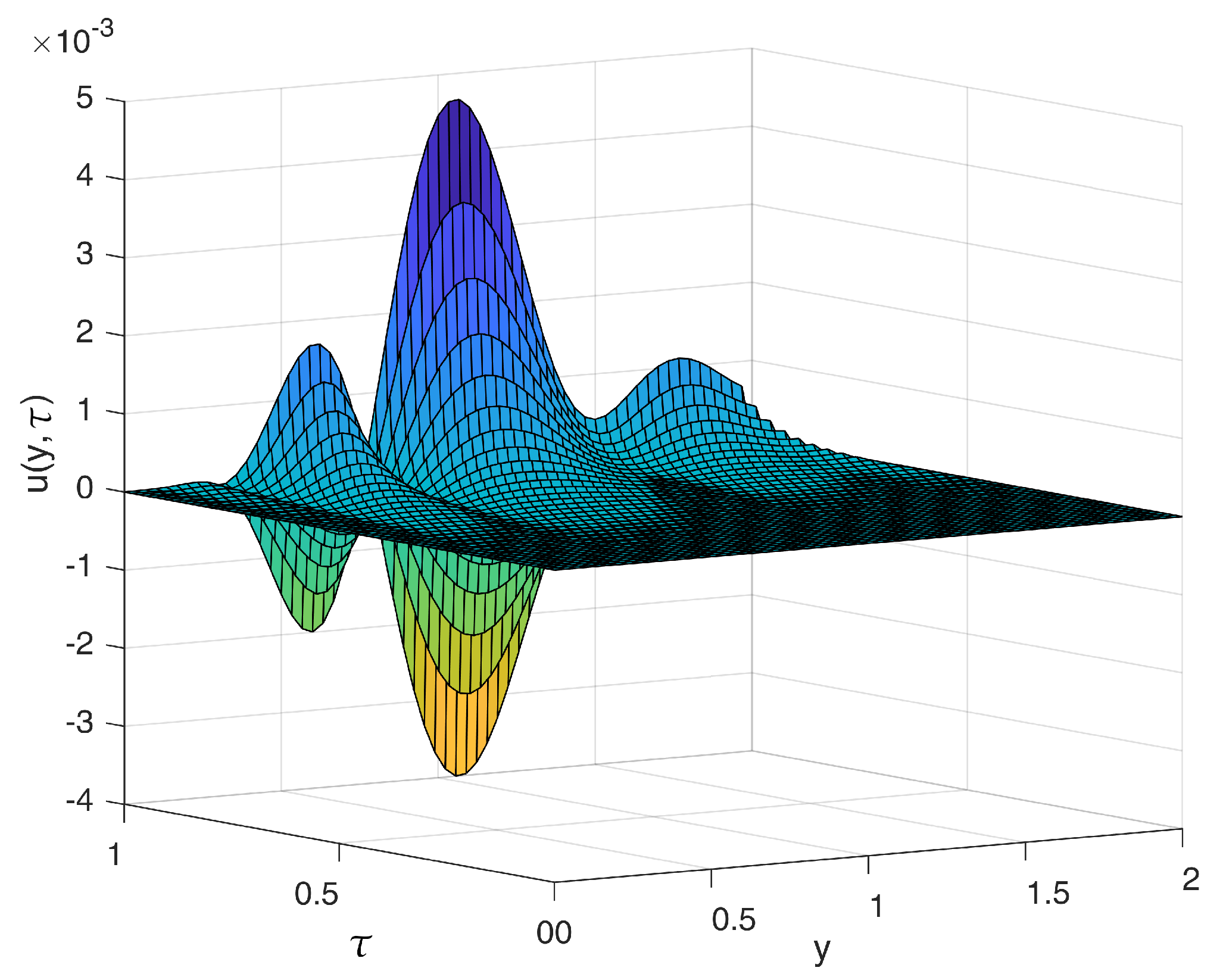
Similarly, we also solve Example 3 by using the numerical method proposed in Example 2. Figure 2 shows the variation of $u(y,\tau )$ with respect to space y and time $\tau$.

4. The Paradox in the Stochastic Damped Wave Equation

This section proposes a stochastic damped wave equation paradox to illustrate the necessity of considering uncertain damped wave equations. We consider a homogeneous, thermally conductive solid rod with constant cross-sectional area and constant thermal diffusivity. Similar to the derivation of Equations (4), if a stochastic process is used to model the external force, we obtain

$$\rho c_p{\displaystyle \frac{\partial u(\mathbf{y},\tau )}{\partial \tau }}+\nabla ·\mathbf{q}(\mathbf{y},\tau )=F(y,\tau ,\dot{W_{\tau }}),$$

(51)

where $F(y,\tau ,\dot{W_{\tau }})$ denotes a stochastic heat source, $W_{\tau }$ is a standard Wiener process and the white noise is defined by $\dot{W_{\tau }}=d{W}_{\tau }/d\tau$. Using the MC law, the following stochastic damped wave equation models the heat conduction in the solid rod [11,12,19]

$${\displaystyle \frac{{\partial }^{2}u(y,\tau )}{\partial {\tau }^2}}=-\zeta {\displaystyle \frac{\partial u(y,\tau )}{\partial \tau }}+a^2{\displaystyle \frac{{\partial }^{2}u(y,\tau )}{\partial y^2}}+f(y,\tau ,\dot{W_{\tau }}),$$

(52)

where $a^2$ is the thermal diffusivity, $u(y,\tau )$ represents the absolute temperature, and $f(y,\tau ,\dot{W_{\tau }})$ is a stochastic heat source. Note that

$$\dot{W_{\tau }}\sim N\left(0,{\displaystyle \frac{1}{d\tau }}\right),$$

which indicates that $\dot{W_{\tau }}$ is a normally distributed random variable with mean 0 and variance $1/d\tau$. To explain the problem simply, we consider the case

$$f(y,\tau ,\dot{W_{\tau }})=g(y,\tau )+\sigma (y,\tau )\dot{W_{\tau }},$$

where $g(y,\tau )$ and $\sigma (y,\tau )$ are real-valued and bounded on their domain. Then we obtain

$${\displaystyle \frac{{\partial }^{2}u(y,\tau )}{\partial {\tau }^2}}=-\zeta {\displaystyle \frac{\partial u(y,\tau )}{\partial \tau }}+a^2{\displaystyle \frac{{\partial }^{2}u(y,\tau )}{\partial y^2}}+g(y,\tau )+\sigma (y,\tau )\dot{W_{\tau }}$$

and

$${\displaystyle \frac{{\partial }^{2}u(y,\tau )}{\partial {\tau }^2}}+\zeta {\displaystyle \frac{\partial u(y,\tau )}{\partial \tau }}-a^2{\displaystyle \frac{{\partial }^{2}u(y,\tau )}{\partial y^2}}\sim N\left(g(y,\tau ),{\displaystyle \frac{{\sigma }^2(y,\tau )}{d\tau }}\right).$$

Therefore, we have

$$\begin{array}{cc}\hfill Pr& \left\{\left|{\displaystyle \frac{{\partial }^{2}u(y,\tau )}{\partial {\tau }^2}}+\zeta {\displaystyle \frac{\partial u(y,\tau )}{\partial \tau }}-a^2{\displaystyle \frac{{\partial }^{2}u(y,\tau )}{\partial y^2}}\right|\ge N\right\}\hfill \\ \hfill & =Pr\left\{\left({\displaystyle \frac{{\partial }^{2}u(y,\tau )}{\partial {\tau }^2}}+\zeta {\displaystyle \frac{\partial u(y,\tau )}{\partial \tau }}-a^2{\displaystyle \frac{{\partial }^{2}u(y,\tau )}{\partial y^2}}\ge N\right)\bigcup \left({\displaystyle \frac{{\partial }^{2}u(y,\tau )}{\partial {\tau }^2}}+\zeta {\displaystyle \frac{\partial u(y,\tau )}{\partial \tau }}-a^2{\displaystyle \frac{{\partial }^{2}u(y,\tau )}{\partial y^2}}\le -N\right)\right\}\hfill \\ \hfill & =Pr\left\{{\displaystyle \frac{{\partial }^{2}u(y,\tau )}{\partial {\tau }^2}}+\zeta {\displaystyle \frac{\partial u(y,\tau )}{\partial \tau }}-a^2{\displaystyle \frac{{\partial }^{2}u(y,\tau )}{\partial y^2}}\ge N\right\}+Pr\left\{{\displaystyle \frac{{\partial }^{2}u(y,\tau )}{\partial {\tau }^2}}+\zeta {\displaystyle \frac{\partial u(y,\tau )}{\partial \tau }}-a^2{\displaystyle \frac{{\partial }^{2}u(y,\tau )}{\partial y^2}}\le -N\right\}\hfill \\ \hfill & =Pr\left\{{\displaystyle \frac{{\displaystyle \frac{{\partial }^{2}u(y,\tau )}{\partial {\tau }^2}}+\zeta {\displaystyle \frac{\partial u(y,\tau )}{\partial \tau }}-a^2{\displaystyle \frac{{\partial }^{2}u(y,\tau )}{\partial y^2}}-g(y,\tau )}{\sigma /\sqrt{d\tau }}}\ge {\displaystyle \frac{N-g(y,\tau )}{\sigma /\sqrt{d\tau }}}\right\}\hfill \\ \hfill & +Pr\left\{{\displaystyle \frac{{\displaystyle \frac{{\partial }^{2}u(y,\tau )}{\partial {\tau }^2}}+\zeta {\displaystyle \frac{\partial u(y,\tau )}{\partial \tau }}-a^2{\displaystyle \frac{{\partial }^{2}u(y,\tau )}{\partial y^2}}-g(y,\tau )}{\sigma /\sqrt{d\tau }}}\le -{\displaystyle \frac{N+g(y,\tau )}{\sigma /\sqrt{d\tau }}}\right\}\hfill \\ \hfill & =1-\Phi \left({\displaystyle \frac{N-g(y,\tau )}{\sigma }}\sqrt{d\tau }\right)+\Phi \left(-{\displaystyle \frac{N+g(y,\tau )}{\sigma }}\sqrt{d\tau }\right)\hfill \\ \hfill & \to 1(d\tau \to 0)\hfill \end{array}$$

where N is a large enough constant and $\Phi$ represents the standard normal distribution function. The result indicates that

$$Pr\left\{\left|{\displaystyle \frac{{\partial }^{2}u(y,\tau )}{\partial {\tau }^2}}+\zeta {\displaystyle \frac{\partial u(y,\tau )}{\partial \tau }}-a^2{\displaystyle \frac{{\partial }^{2}u(y,\tau )}{\partial y^2}}\right|\ge N\right\}=1.$$

This implies that for any y and $\tau$, at least one of ${\partial }^{2}u(y,\tau )/\partial {\tau }^2$, $\partial u(y,\tau )/\partial \tau$, and ${\partial }^{2}u(y,\tau )/\partial y^2$ must be infinite $(\infty )$. However, the three terms ${\partial }^{2}u(y,\tau )/\partial {\tau }^2$ (acceleration of temperature change), $\partial u(y,\tau )/\partial \tau$ (rate of temperature change) and ${\partial }^{2}u(y,\tau )/\partial y^2$ (acceleration of temperature change with respect to y) are bounded for arbitrary y and $\tau$. Thus, it is unreasonable for Equations (52) to follow the heat conduction with stochastic heat source.

In summary, Equation (52) is applicable for modelling heat conduction phenomena where the second time derivative, the first time derivative, or the second spatial derivative of temperature is infinite. However, thermal wave speed is finite in practical cases. Consequently, it is more appropriate to adopt an uncertain damped wave equation to describe such phenomena.

When tackling problems that involve randomness, researchers usually rely on probability theory as their primary mathematical tool. However, due to the inherent variability and complexity of random events, the process of obtaining their distributions consumes large amounts of labour, materials, and technological means. Moreover, as Liu [15] points out, some distributions fail to align sufficiently with real-world true frequencies. This is because the evolution of certain phenomena is non-random, and when emergencies (such as wars, rumours, floods, and earthquakes) occur, people typically lack the historical data needed to address these scenarios. Under such circumstances, the probability theory is no longer applicable. The uncertainty theory is another axiomatic mathematical system specifically developed for handling such uncertain scenarios. Continuous and intensive research is also being conducted on the uncertainty theory.

5. Conclusions

The paper investigates the heat conduction with uncertain heat source using Liu’s uncertainty theory. Actuated by the Liu process, the uncertain damped wave equation, which is a type of UPDE, is proposed. Furthermore, we derive the analytical solution for the uncertain damped wave equation and establish the uniqueness of the solution. In the future, we will study the numerical solutions for the uncertain damped wave equation and explore its applications in financial modelling and physical systems.