Back-Reaction of Super-Hubble Fluctuations, Late Time Tracking, and Recent Observational Results
Abstract
1. Introduction
2. A Model for the Back-Reaction of Super-Hubble Fluctuations
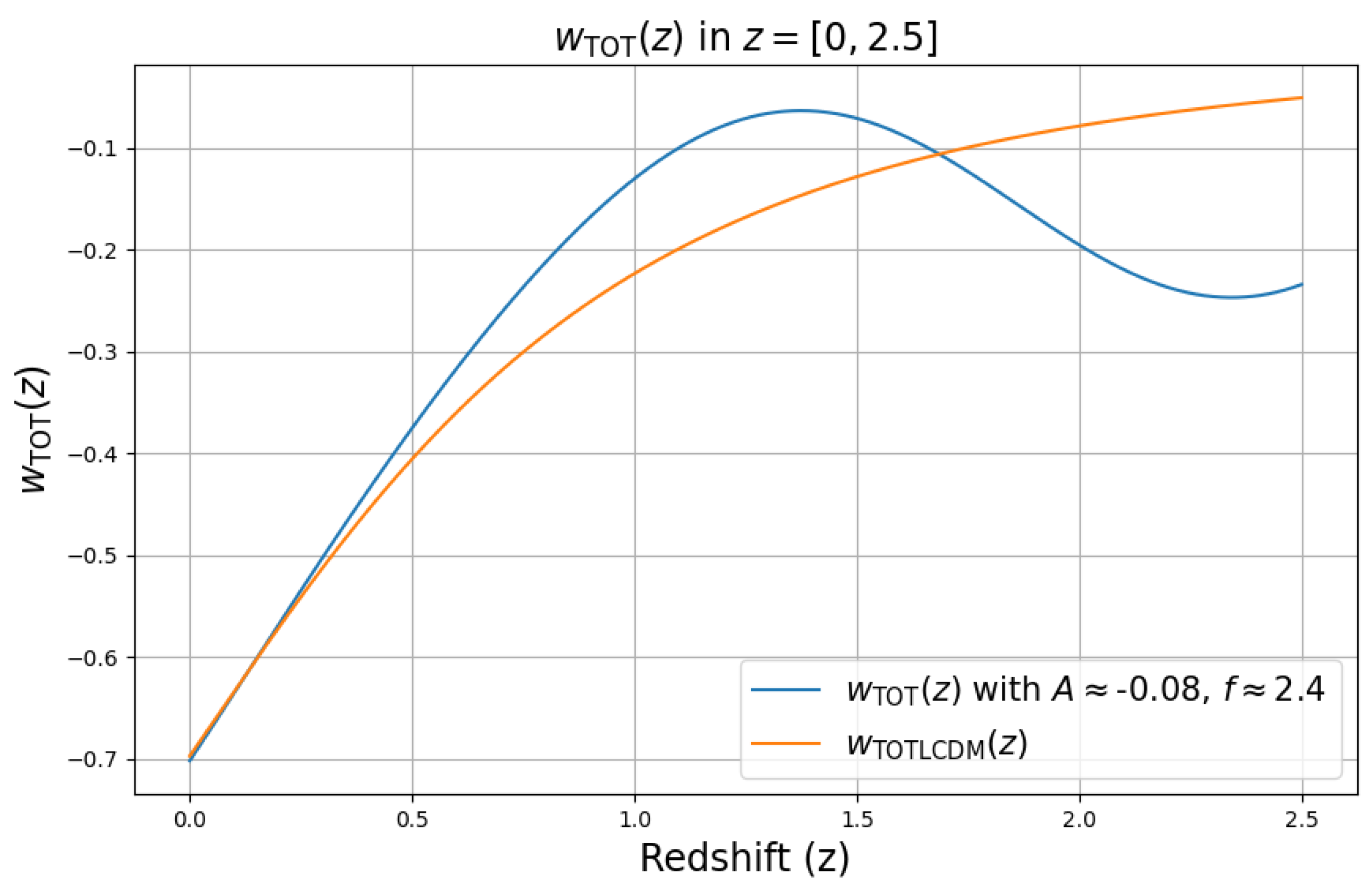
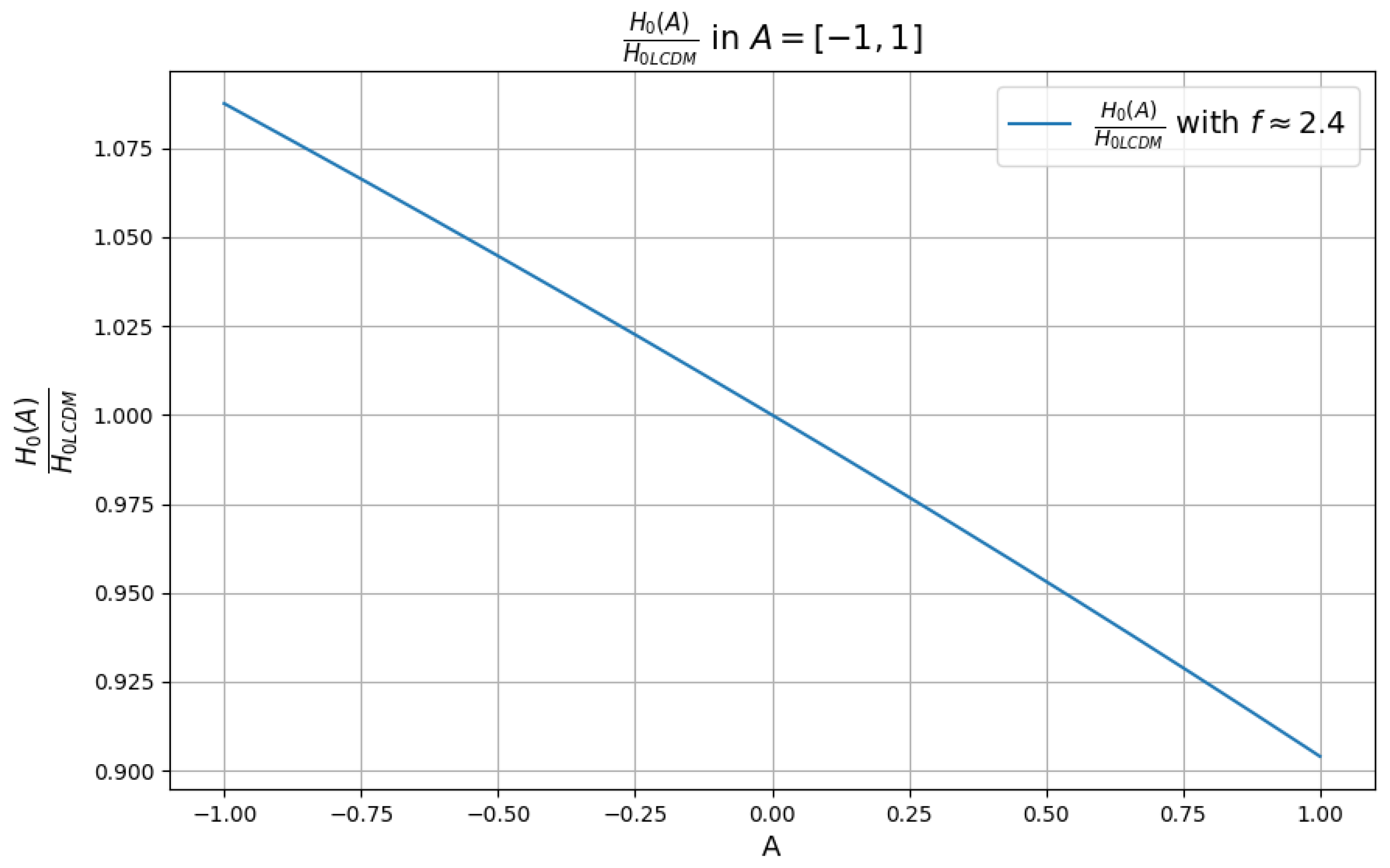
3. Methods and Data Analysis
4. Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Previous DESI DR1 Analysis
| Tracer | Redshift | ||
|---|---|---|---|
| LRG 1 | 0.4–0.6 | ||
| LRG 2 | 0.6–0.8 | ||
| LRG 3 | 0.8–1.1 | ||
| ELG 2 | 1.1–1.6 | ||
| Lyman- | ∼2.33 |

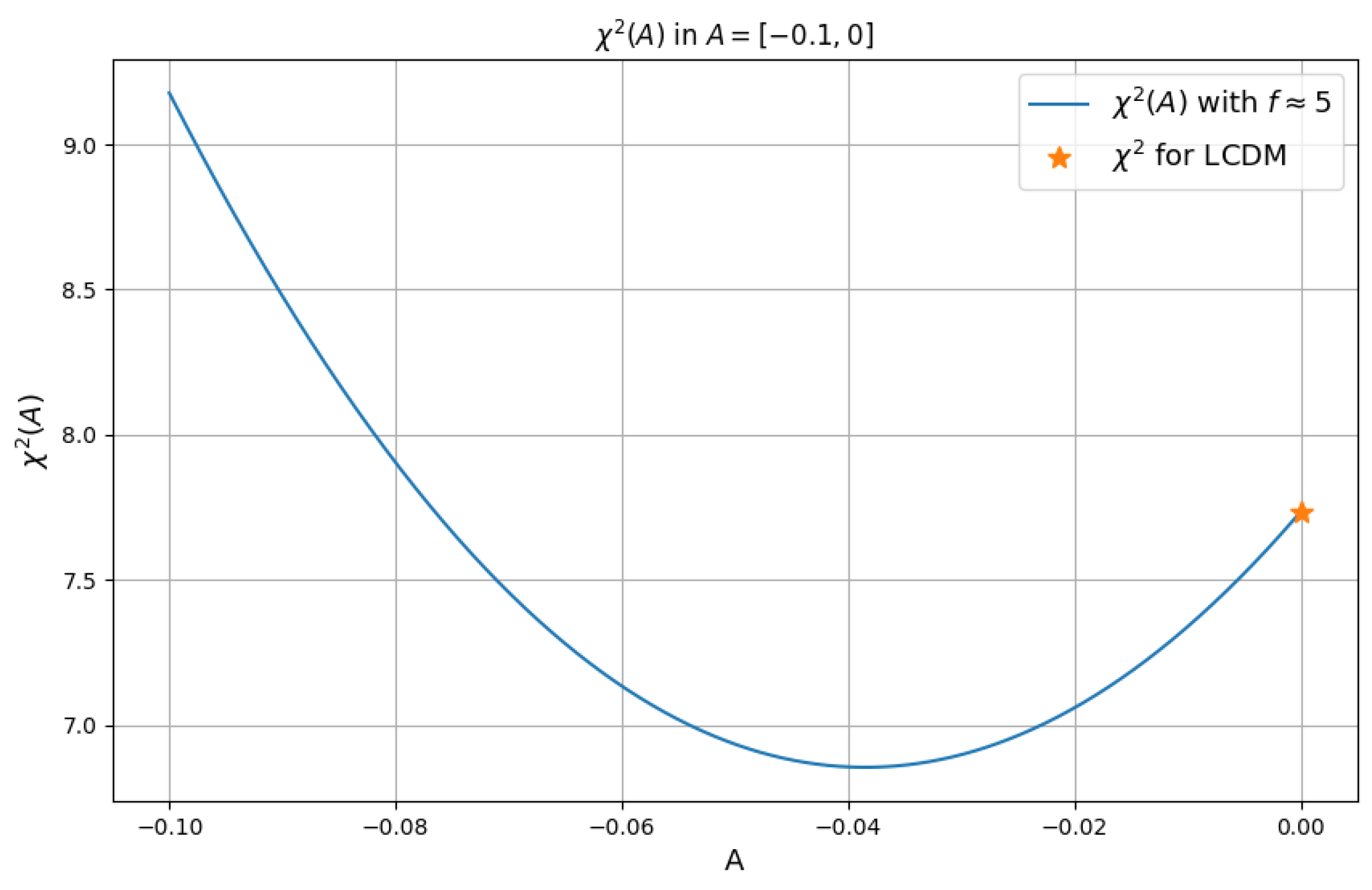
References
- Weinberg, S. The Cosmological Constant Problem. Rev. Mod. Phys. 1989, 61, 1–23. [Google Scholar] [CrossRef]
- Carroll, S.M. The Cosmological constant. Living Rev. Relativ. 2001, 4, 1. [Google Scholar] [CrossRef] [PubMed]
- Weinberg, S. The Cosmological constant problems. In Proceedings of the 4th International Symposium on Sources and Detection of Dark Matter in the Universe (DM 2000), Marina del Rey, CA, USA, 23–25 February 2000; pp. 18–26. [Google Scholar] [CrossRef]
- Li, M.; Li, X.D.; Wang, S.; Wang, Y. Dark Energy. Commun. Theor. Phys. 2011, 56, 525–604. [Google Scholar] [CrossRef]
- Martin, J. Everything You Always Wanted To Know About The Cosmological Constant Problem (But Were Afraid To Ask). Comptes Rendus Phys. 2012, 13, 566–665. [Google Scholar] [CrossRef]
- Velten, H.E.S.; vom Marttens, R.F.; Zimdahl, W. Aspects of the cosmological “coincidence problem”. Eur. Phys. J. C 2014, 74, 3160. [Google Scholar] [CrossRef]
- Di Valentino, E.; Said, J.L.; Riess, A.; Pollo, A.; Poulin, V.; Gómez-Valent, A.; Weltman, A.; Palmese, A.; Huang, C.D.; van de Bruck, C.; et al. The CosmoVerse White Paper: Addressing observational tensions in cosmology with systematics and fundamental physics. Phys. Dark Universe 2025, 49, 101965. [Google Scholar] [CrossRef]
- Lu, Z.; Imtiaz, B.; Zhang, D.; Cai, Y.F. Testing the coupling of dark radiations in light of the Hubble tension. Eur. Phys. J. C 2024, 84, 912. [Google Scholar] [CrossRef]
- Di Valentino, E.; Mena, O.; Pan, S.; Visinelli, L.; Yang, W.; Melchiorri, A.; Mota, D.F.; Riess, A.G.; Silk, J. In the realm of the Hubble tension—A review of solutions. Class. Quantum Gravity 2021, 38, 153001. [Google Scholar] [CrossRef]
- Polyakov, A.M. Infrared instability of the de Sitter space. arXiv 2012, arXiv:1209.4135. [Google Scholar] [CrossRef]
- Polyakov, A.M. De Sitter space and eternity. Nucl. Phys. B 2008, 797, 199–217. [Google Scholar] [CrossRef]
- Mazur, P.; Mottola, E. Spontaneous Breaking of De Sitter Symmetry by Radiative Effects. Nucl. Phys. B 1986, 278, 694–720. [Google Scholar] [CrossRef]
- Mottola, E. THERMODYNAMIC INSTABILITY OF DE SITTER SPACE. Phys. Rev. D 1986, 33, 1616–1621. [Google Scholar] [CrossRef] [PubMed]
- Mottola, E. Particle Creation in de Sitter Space. Phys. Rev. D 1985, 31, 754. [Google Scholar] [CrossRef] [PubMed]
- Tsamis, N.C.; Woodard, R.P. Strong infrared effects in quantum gravity. Ann. Phys. 1995, 238, 1–82. [Google Scholar] [CrossRef]
- Obied, G.; Ooguri, H.; Spodyneiko, L.; Vafa, C. De Sitter Space and the Swampland. arXiv 2018, arXiv:1806.08362. [Google Scholar] [CrossRef]
- Dvali, G.; Gomez, C. Quantum Exclusion of Positive Cosmological Constant? Ann. Phys. 2016, 528, 68–73. [Google Scholar] [CrossRef]
- Danielsson, U.H.; Van Riet, T. What if string theory has no de Sitter vacua? Int. J. Mod. Phys. D 2018, 27, 1830007. [Google Scholar] [CrossRef]
- Dasgupta, K.; Emelin, M.; McDonough, E.; Tatar, R. Quantum Corrections and the de Sitter Swampland Conjecture. J. High Energy Phys. 2019, 01, 145. [Google Scholar] [CrossRef]
- Bedroya, A.; Vafa, C. Trans-Planckian Censorship and the Swampland. J. High Energy Phys. 2020, 09, 123. [Google Scholar] [CrossRef]
- Bedroya, A.; Brandenberger, R.; Loverde, M.; Vafa, C. Trans-Planckian Censorship and Inflationary Cosmology. Phys. Rev. D 2020, 101, 103502. [Google Scholar] [CrossRef]
- Brandenberger, R. Trans-Planckian Censorship Conjecture and Early Universe Cosmology. Lett. High Energy Phys. 2021, 2021, 198. [Google Scholar] [CrossRef]
- Tsamis, N.C.; Woodard, R.P. Relaxing the cosmological constant. Phys. Lett. B 1993, 301, 351–357. [Google Scholar] [CrossRef]
- Tsamis, N.C.; Woodard, R.P. Quantum gravity slows inflation. Nucl. Phys. B 1996, 474, 235–248. [Google Scholar] [CrossRef]
- Abramo, L.R.W.; Brandenberger, R.H.; Mukhanov, V.F. The Energy - momentum tensor for cosmological perturbations. Phys. Rev. D 1997, 56, 3248–3257. [Google Scholar] [CrossRef]
- Finelli, F.; Marozzi, G.; Vacca, G.P.; Venturi, G. Energy momentum tensor of field fluctuations in massive chaotic inflation. Phys. Rev. D 2002, 65, 103521. [Google Scholar] [CrossRef]
- Finelli, F.; Marozzi, G.; Vacca, G.P.; Venturi, G. Energy momentum tensor of cosmological fluctuations during inflation. Phys. Rev. D 2004, 69, 123508. [Google Scholar] [CrossRef]
- Marozzi, G. Back-reaction of Cosmological Fluctuations during Power-Law Inflation. Phys. Rev. D 2007, 76, 043504. [Google Scholar] [CrossRef]
- Brandenberger, R.H. Back reaction of cosmological perturbations. In Proceedings of the 3rd International Conference on Particle Physics and the Early Universe, Trieste, Italy, 27 September–3 October 1999; pp. 198–206. [Google Scholar] [CrossRef]
- Ahmed, M.; Dodelson, S.; Greene, P.B.; Sorkin, R. Everpresent Λ. Phys. Rev. D 2004, 69, 103523. [Google Scholar] [CrossRef]
- Das, S.; Nasiri, A.; Yazdi, Y.K. Aspects of Everpresent Λ. Part I. A fluctuating cosmological constant from spacetime discreteness. J. Cosmol. Astropart. Phys. 2023, 10, 047. [Google Scholar] [CrossRef]
- Das, S.; Nasiri, A.; Yazdi, Y.K. Aspects of Everpresent Λ (II): Cosmological Tests of Current Models. arXiv 2023, arXiv:2307.13743. [Google Scholar] [CrossRef]
- Unruh, W. Cosmological long wavelength perturbations. arXiv 1998, arXiv:9802323. [Google Scholar] [CrossRef]
- Geshnizjani, G.; Brandenberger, R. Back reaction and local cosmological expansion rate. Phys. Rev. D 2002, 66, 123507. [Google Scholar] [CrossRef]
- Abramo, L.R.; Woodard, R.P. No one loop back reaction in chaotic inflation. Phys. Rev. D 2002, 65, 063515. [Google Scholar] [CrossRef]
- Geshnizjani, G.; Brandenberger, R. Back reaction of perturbations in two scalar field inflationary models. J. Cosmol. Astropart. Phys. 2005, 04, 006. [Google Scholar] [CrossRef]
- Marozzi, G.; Vacca, G.P.; Brandenberger, R.H. Cosmological Backreaction for a Test Field Observer in a Chaotic Inflationary Model. J. Cosmol. Astropart. Phys. 2013, 02, 027. [Google Scholar] [CrossRef]
- Finelli, F.; Marozzi, G.; Vacca, G.P.; Venturi, G. Backreaction during inflation: A Physical gauge invariant formulation. Phys. Rev. Lett. 2011, 106, 121304. [Google Scholar] [CrossRef] [PubMed]
- Gasperini, M.; Marozzi, G.; Veneziano, G. Gauge invariant averages for the cosmological backreaction. J. Cosmol. Astropart. Phys. 2009, 03, 011. [Google Scholar] [CrossRef]
- Gasperini, M.; Marozzi, G.; Veneziano, G. A Covariant and gauge invariant formulation of the cosmological ‘backreaction’. J. Cosmol. Astropart. Phys. 2010, 02, 009. [Google Scholar] [CrossRef]
- Marozzi, G. The cosmological backreaction: Gauge (in)dependence, observers and scalars. J. Cosmol. Astropart. Phys. 2011, 01, 012. [Google Scholar] [CrossRef]
- Marozzi, G.; Vacca, G.P. Isotropic Observers and the Inflationary Backreaction Problem. Class. Quantum Gravity 2012, 29, 115007. [Google Scholar] [CrossRef][Green Version]
- Abramo, L.R.; Woodard, R.P. Back reaction is for real. Phys. Rev. D 2002, 65, 063516. [Google Scholar] [CrossRef]
- Losic, B.; Unruh, W.G. Long-wavelength metric backreactions in slow-roll inflation. Phys. Rev. D 2005, 72, 123510. [Google Scholar] [CrossRef]
- Losic, B.; Unruh, W.G. On leading order gravitational backreactions in de Sitter spacetime. Phys. Rev. D 2006, 74, 023511. [Google Scholar] [CrossRef]
- Brandenberger, R.H.; Lam, C.S. Back-reaction of cosmological perturbations in the infinite wavelength approximation. arXiv 2004, arXiv:0407048. [Google Scholar] [CrossRef]
- Afshordi, N.; Brandenberger, R.H. Super Hubble nonlinear perturbations during inflation. Phys. Rev. D 2001, 63, 123505. [Google Scholar] [CrossRef]
- Comeau, V. Perturbative Correction to the Average Expansion Rate of Spacetimes with Perfect Fluids. arXiv 2023, arXiv:2304.14187. [Google Scholar] [CrossRef]
- Comeau, V.; Brandenberger, R. Back-reaction of long-wavelength cosmological fluctuations as measured by a clock field. Eur. Phys. J. C 2024, 84, 272. [Google Scholar] [CrossRef]
- Giani, L.; Von Marttens, R.; Camilleri, R. A novel approach to cosmological non-linearities as an effective fluid. arXiv 2024, arXiv:2410.15295. [Google Scholar] [CrossRef]
- Kolb, E.W.; Marra, V.; Matarrese, S. Cosmological background solutions and cosmological backreactions. Gen. Relativ. Gravit. 2010, 42, 1399–1412. [Google Scholar] [CrossRef][Green Version]
- Kolb, E.W. Backreaction of inhomogeneities can mimic dark energy. Class. Quantum Gravity 2011, 28, 164009. [Google Scholar] [CrossRef]
- Marra, V.; Notari, A. Observational constraints on inhomogeneous cosmological models without dark energy. Class. Quantum Gravity 2011, 28, 164004. [Google Scholar] [CrossRef]
- Brandenberger, R.; Graef, L.L.; Marozzi, G.; Vacca, G.P. Backreaction of super-Hubble cosmological perturbations beyond perturbation theory. Phys. Rev. D 2018, 98, 103523. [Google Scholar] [CrossRef]
- Calderon, R.; Lodha, K.; Shafieloo, A.; Linder, E.; Sohn, W.; de Mattia, A.; Cervantes-Cota, J.; Crittenden, R.; Davis, T.; Ishak, M.; et al. DESI 2024: Reconstructing Dark Energy using Crossing Statistics with DESI DR1 BAO data. arXiv 2024, arXiv:2405.04216. [Google Scholar] [CrossRef]
- Lodha, K.; Shafieloo, A.; Calderon, R.; Linder, E.; Sohn, W.; Cervantes-Cota, J.L.; De Mattia, A.; García-Bellido, J.; Ishak, M.; Matthewson, W.; et al. DESI 2024: Constraints on Physics-Focused Aspects of Dark Energy using DESI DR1 BAO Data. arXiv 2024, arXiv:2405.13588. [Google Scholar] [CrossRef]
- Adame, A.G.; Aguilar, J.; Ahlen, S.; Alam, S.; Alexander, D.M.; Alvarez, M.; Alves, O.; Anand, A.; Andrade, U.; Armengaud, E.; et al. DESI 2024 VI: Cosmological Constraints from the Measurements of Baryon Acoustic Oscillations. arXiv 2024, arXiv:2404.03002. [Google Scholar] [CrossRef]
- Abdul Karim, M.; Aguilar, J.; Ahlen, S.; Alam, S.; Allen, L.; Allende Prieto, C.; Alves, O.; Anand, A.; Andrade, U.; Armengaud, E.; et al. DESI DR2 Results II: Measurements of Baryon Acoustic Oscillations and Cosmological Constraints. arXiv 2025, arXiv:2503.14738. [Google Scholar]
- Lodha, K.; Calderon, R.; Matthewson, W.L.; Shafieloo, A.; Ishak, M.; Pan, J.; Garcia-Quintero, C.; Huterer, D.; Valogiannis, G.; Ureña-López, L.A.; et al. Extended Dark Energy analysis using DESI DR2 BAO measurements. arXiv 2025, arXiv:2503.14743. [Google Scholar]
- Payeur, G.; McDonough, E.; Brandenberger, R. Do Observations Prefer Thawing Quintessence? arXiv 2024, arXiv:2411.13637. [Google Scholar] [CrossRef]
- Gu, G.; Wang, X.; Wang, Y.; Zhao, G.B.; Pogosian, L.; Koyama, K.; Peacock, J.A.; Cai, Z.; Cervantes-Cota, J.L.; Zhao, R.; et al. Dynamical Dark Energy in light of the DESI DR2 Baryonic Acoustic Oscillations Measurements. arXiv 2025, arXiv:2504.06118. [Google Scholar] [CrossRef]
- Brandenberger, R. Why the DESI Results Should Not Be A Surprise. arXiv 2025, arXiv:2503.17659. [Google Scholar] [CrossRef]
- Jiang, J.Q.; Pedrotti, D.; da Costa, S.S.; Vagnozzi, S. Non-parametric late-time expansion history reconstruction and implications for the Hubble tension in light of DESI. arXiv 2024, arXiv:2408.02365. [Google Scholar]
- Escamilla, L.A.; Pan, S.; Di Valentino, E.; Paliathanasis, A.; Vázquez, J.A.; Yang, W. Testing an oscillatory behavior of dark energy. Phys. Rev. D 2025, 111, 023531. [Google Scholar] [CrossRef]
- Akarsu, O.; Colgain, E.O.; Özulker, E.; Thakur, S.; Yin, L. Inevitable manifestation of wiggles in the expansion of the late Universe. Phys. Rev. D 2023, 107, 123526. [Google Scholar] [CrossRef]
- Colgáin, E.O.; Sheikh-Jabbari, M.M. DESI and SNe: Dynamical Dark Energy, Ωm Tension or Systematics? arXiv 2024, arXiv:2412.12905. [Google Scholar] [CrossRef]
- Zhao, G.B.; Raveri, M.; Pogosian, L.; Wang, Y.; Crittenden, R.G.; Handley, W.J.; Percival, W.J.; Beutler, F.; Brinkmann, J.; Chuang, C.H.; et al. Dynamical dark energy in light of the latest observations. Nat. Astron. 2017, 1, 627–632. [Google Scholar] [CrossRef]
- Tamayo, D.; Vazquez, J.A. Fourier-series expansion of the dark-energy equation of state. Mon. Not. R. Astron. Soc. 2019, 487, 729–736. [Google Scholar] [CrossRef]
- Rubano, C.; Scudellaro, P.; Piedipalumbo, E.; Capozziello, S. Oscillating dark energy: A Possible solution to the problem of eternal acceleration. Phys. Rev. D 2003, 68, 123501. [Google Scholar] [CrossRef]
- Linder, E.V. On oscillating dark energy. Astropart. Phys. 2006, 25, 167–171. [Google Scholar] [CrossRef]
- Feng, B.; Li, M.; Piao, Y.S.; Zhang, X. Oscillating quintom and the recurrent universe. Phys. Lett. B 2006, 634, 101–105. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. The Oscillating dark energy: Future singularity and coincidence problem. Phys. Lett. B 2006, 637, 139–148. [Google Scholar] [CrossRef]
- Kurek, A.; Hrycyna, O.; Szydlowski, M. Constraints on oscillating dark energy models. Phys. Lett. B 2008, 659, 14–25. [Google Scholar] [CrossRef]
- Jain, D.; Dev, A.; Alcaniz, J.S. Cosmological bounds on oscillating dark energy models. Phys. Lett. B 2007, 656, 15–18. [Google Scholar] [CrossRef][Green Version]
- Saez-Gomez, D. Oscillating Universe from inhomogeneous EoS and coupled dark energy. Gravit. Cosmol. 2009, 15, 134–140. [Google Scholar] [CrossRef]
- Kurek, A.; Hrycyna, O.; Szydlowski, M. From model dynamics to oscillating dark energy parametrisation. Phys. Lett. B 2010, 690, 337–345. [Google Scholar] [CrossRef]
- Pace, F.; Fedeli, C.; Moscardini, L.; Bartelmann, M. Structure formation in cosmologies with oscillating dark energy. Mon. Not. R. Astron. Soc. 2012, 422, 1186–1202. [Google Scholar] [CrossRef]
- Pan, S.; Saridakis, E.N.; Yang, W. Observational Constraints on Oscillating Dark-Energy Parametrizations. Phys. Rev. D 2018, 98, 063510. [Google Scholar] [CrossRef]
- Panotopoulos, G.; Rincón, A. Growth index and statefinder diagnostic of Oscillating Dark Energy. Phys. Rev. D 2018, 97, 103509. [Google Scholar] [CrossRef]
- Rezaei, M. Observational constraints on the oscillating dark energy cosmologies. Mon. Not. R. Astron. Soc. 2019, 485, 550. [Google Scholar] [CrossRef]
- Yao, T.Y.; Guo, R.Y.; Zhao, X.Y. Constraining neutrino mass in dynamical dark energy cosmologies with the logarithm parametrization and the oscillating parametrization. arXiv 2022, arXiv:2211.05956. [Google Scholar] [CrossRef]
- Rezaei, M. Oscillating Dark Energy in Light of the Latest Observations and Its Impact on the Hubble Tension. Astrophys. J. 2024, 967, 2. [Google Scholar] [CrossRef]
- Tián, S.X. Cosmological consequences of a scalar field with oscillating equation of state: A possible solution to the fine-tuning and coincidence problems. Phys. Rev. D 2020, 101, 063531. [Google Scholar] [CrossRef]
- Adil, S.A.; Akarsu, O.; Di Valentino, E.; Nunes, R.C.; Özülker, E.; Sen, A.A.; Specogna, E. Omnipotent dark energy: A phenomenological answer to the Hubble tension. Phys. Rev. D 2024, 109, 023527. [Google Scholar] [CrossRef]
- Mbonye, M.R. Is cosmic dynamics self-regulating? Int. J. Mod. Phys. D 2023, 32, 2350076. [Google Scholar] [CrossRef]
- Mbonye, M.R. The Big Bang: Origins and initial conditions from Self-Regulating Cosmology (SRC) model. arXiv 2024, arXiv:2404.10799. [Google Scholar] [CrossRef]
- Zhao, G.B.; Xia, J.Q.; Li, M.; Feng, B.; Zhang, X. Perturbations of the quintom models of dark energy and the effects on observations. Phys. Rev. D 2005, 72, 123515. [Google Scholar] [CrossRef]
- Heisenberg, L.; Bartelmann, M.; Brandenberger, R.; Refregier, A. Model independent analysis of supernova data, dark energy, trans-Planckian censorship and the swampland. Phys. Lett. B 2021, 812, 135990. [Google Scholar] [CrossRef]
- Haude, S.; Salehi, S.; Vidal, S.; Maturi, M.; Bartelmann, M. Model-Independent Determination of the Cosmic Growth Factor. arXiv 2019, arXiv:1912.04560. [Google Scholar] [CrossRef]
- Kessler, D.A.; Escamilla, L.A.; Pan, S.; Di Valentino, E. One-parameter dynamical dark energy: Hints for oscillations. arXiv 2025, arXiv:2504.00776. [Google Scholar] [CrossRef]
- Mukhanov, V.F.; Feldman, H.A.; Brandenberger, R.H. Theory of cosmological perturbations. Part 1. Classical perturbations. Part 2. Quantum theory of perturbations. Part 3. Extensions. Phys. Rept. 1992, 215, 203–333. [Google Scholar] [CrossRef]
- Mukhanov, V.F.; Abramo, L.R.W.; Brandenberger, R.H. On the Back reaction problem for gravitational perturbations. Phys. Rev. Lett. 1997, 78, 1624–1627. [Google Scholar] [CrossRef]
- Brandenberger, R.H. Back reaction of cosmological perturbations and the cosmological constant problem. In Proceedings of the 18th IAP Colloquium on the Nature of Dark Energy: Observational and Theoretical Results on the Accelerating Universe, Paris, France, 1–5 July 2002. [Google Scholar]
- Payeur, G.; McDonough, E.; Brandenberger, R. Swampland conjectures constraints on dark energy from a highly curved field space. Phys. Rev. D 2024, 110, 106011. [Google Scholar] [CrossRef]
- Abramo, L.R.W. The Back Reaction of Gravitational Perturbations and Applications in Cosmology. Ph.D. Thesis, Physics Department, Brown University, Providence, RI, USA, 1997. [Google Scholar]
- Weinberg, D.H.; Mortonson, M.J.; Eisenstein, D.J.; Hirata, C.; Riess, A.G.; Rozo, E. Observational Probes of Cosmic Acceleration. Phys. Rept. 2013, 530, 87–255. [Google Scholar] [CrossRef]
- Chen, S.F.; Howlett, C.; White, M.; McDonald, P.; Ross, A.J.; Seo, H.J.; Padmanabhan, N.; Aguilar, J.; Ahlen, S.; Alam, S.; et al. Baryon Acoustic Oscillation Theory and Modelling Systematics for the DESI 2024 results. arXiv 2024, arXiv:2402.14070. [Google Scholar] [CrossRef]
- Adame, A.G.; Aguilar, J.; Ahlen, S.; Alam, S.; Alexander, D.M.; Alvarez, M.; Alves, O.; Anand, A.; Andrade, U.; Armengaud, E.; et al. DESI 2024 III: Baryon Acoustic Oscillations from Galaxies and Quasars. arXiv 2024, arXiv:2404.03000. [Google Scholar] [CrossRef]
- Clifton, T.; Hyatt, N. A radical solution to the Hubble tension problem. J. Cosmol. Astropart. Phys. 2024, 08, 052. [Google Scholar] [CrossRef]
- Ormondroyd, A.N.; Handley, W.J.; Hobson, M.P.; Lasenby, A.N. Comparison of dynamical dark energy with ΛCDM in light of DESI DR2. arXiv 2025, arXiv:2503.17342. [Google Scholar]
- Colgáin, E.O.; Pourojaghi, S.; Sheikh-Jabbari, M.M.; Yin, L. How much has DESI dark energy evolved since DR1? arXiv 2025, arXiv:2504.04417. [Google Scholar] [CrossRef]
- Poulin, V.; Smith, T.L.; Calderón, R.; Simon, T. Impact of ACT DR6 and DESI DR2 for Early Dark Energy and the Hubble tension. arXiv 2025, arXiv:2505.08051. [Google Scholar] [CrossRef]
- Pang, Y.H.; Zhang, X.; Huang, Q.G. The Impact of the Hubble Tension on the Evidence for Dynamical Dark Energy. arXiv 2025, arXiv:2503.21600. [Google Scholar] [CrossRef]
- Adame, A.G.; Aguilar, J.; Ahlen, S.; Alam, S.; Alexander, D.M.; Alvarez, M.; Alves, O.; Anand, A.; Andrade, U.; Armengaud, E.; et al. DESI 2024 IV: Baryon Acoustic Oscillations from the Lyman Alpha Forest. arXiv 2024, arXiv:2404.03001. [Google Scholar] [CrossRef]
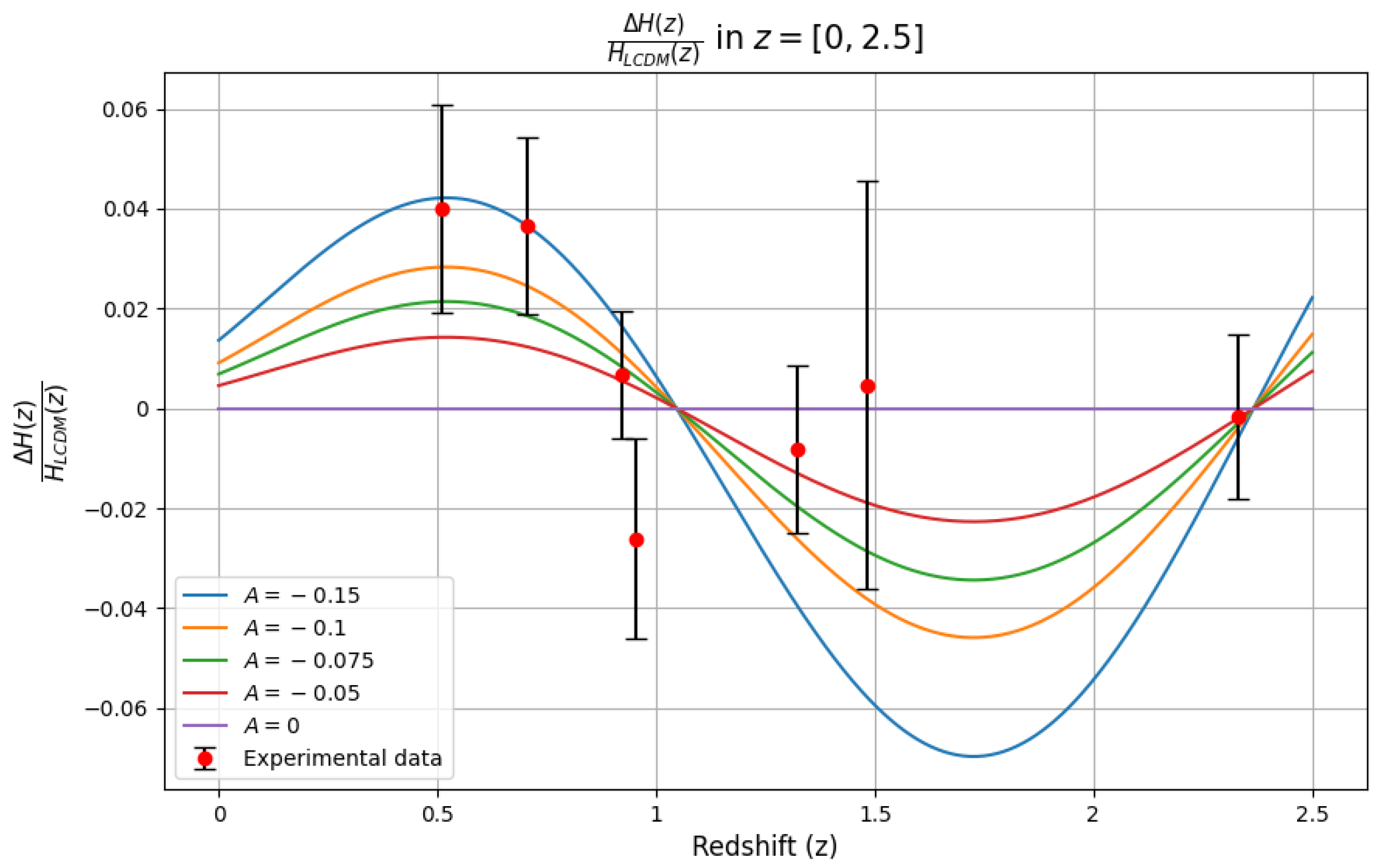
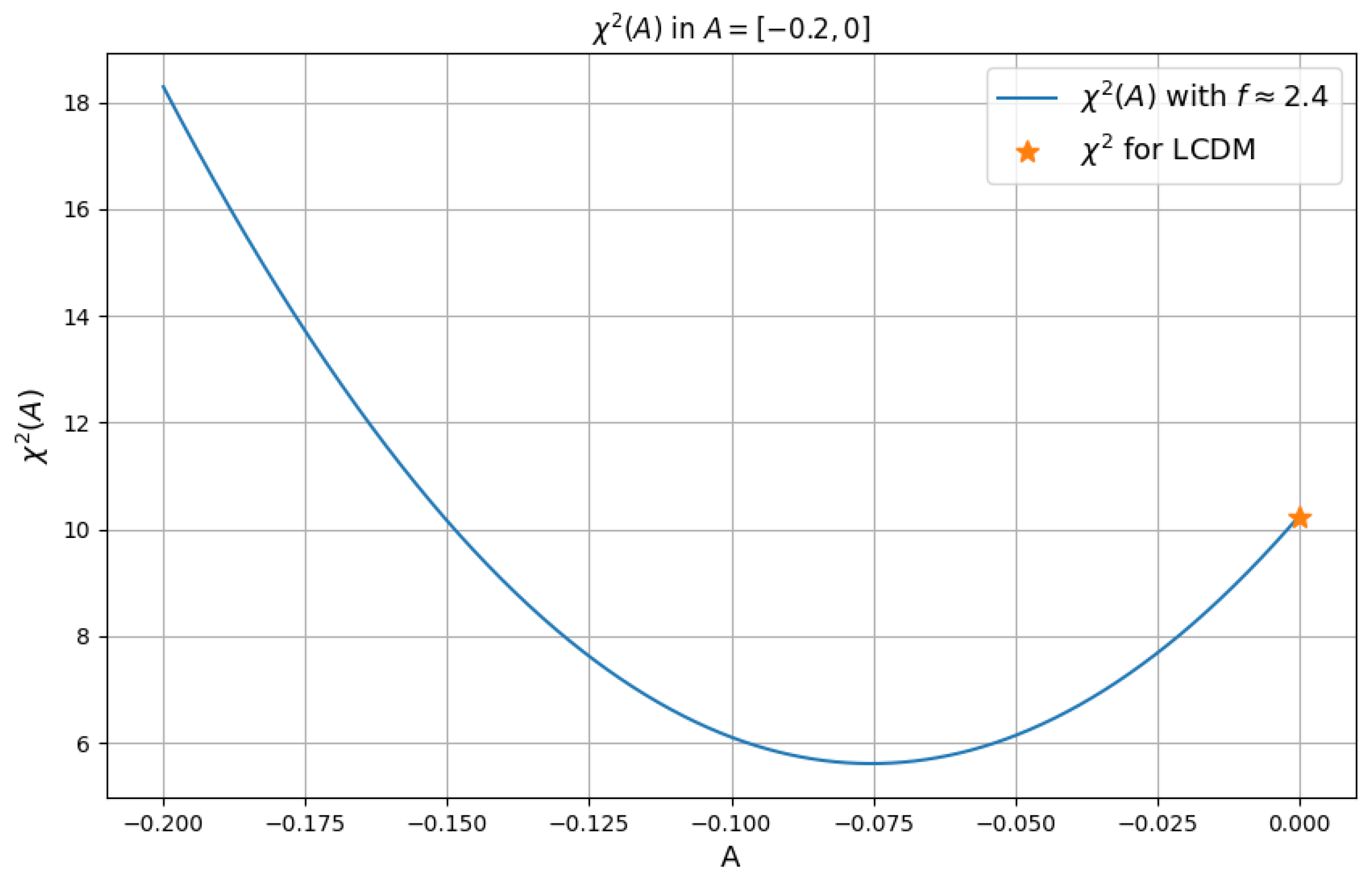
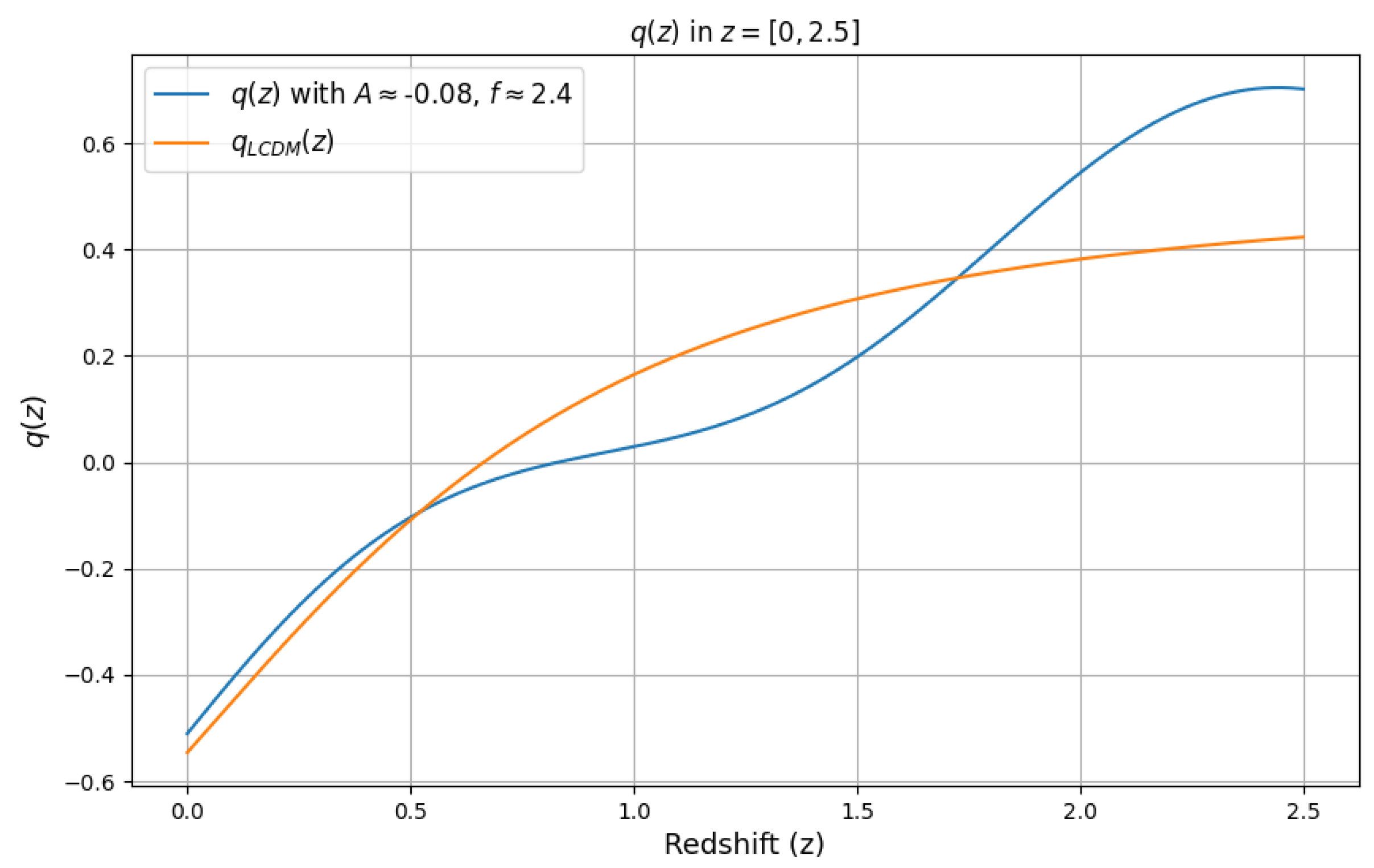
| Tracer | Redshift | ||
|---|---|---|---|
| LRG1 | |||
| LRG2 | |||
| ELG2 | |||
| QSO | |||
| Lya | |||
| LRG3 | |||
| ELG1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alvarez, M.A.; Graef, L.L.; Brandenberger, R. Back-Reaction of Super-Hubble Fluctuations, Late Time Tracking, and Recent Observational Results. Symmetry 2025, 17, 1507. https://doi.org/10.3390/sym17091507
Alvarez MA, Graef LL, Brandenberger R. Back-Reaction of Super-Hubble Fluctuations, Late Time Tracking, and Recent Observational Results. Symmetry. 2025; 17(9):1507. https://doi.org/10.3390/sym17091507
Chicago/Turabian StyleAlvarez, Marco A., Leila L. Graef, and Robert Brandenberger. 2025. "Back-Reaction of Super-Hubble Fluctuations, Late Time Tracking, and Recent Observational Results" Symmetry 17, no. 9: 1507. https://doi.org/10.3390/sym17091507
APA StyleAlvarez, M. A., Graef, L. L., & Brandenberger, R. (2025). Back-Reaction of Super-Hubble Fluctuations, Late Time Tracking, and Recent Observational Results. Symmetry, 17(9), 1507. https://doi.org/10.3390/sym17091507







