Stable and Convergent High-Order Numerical Schemes for Parabolic Integro-Differential Equations with Small Coefficients

Abstract

Singularly perturbed integro-partial differential equations with reaction–diffusion behavior present significant challenges due to boundary layers arising from small perturbation parameters, which complicate the development of accurate and efficient numerical schemes for physical and engineering models. In this study, a uniformly convergent higher-order method is proposed to address these challenges. The approach applies the implicit Euler method for temporal discretization on a uniform mesh and central differences on a Shishkin mesh for spatial approximation, and utilizes the trapezoidal rule for evaluating integral terms; further, extrapolation techniques are incorporated in both time and space to increase accuracy. Numerical analysis demonstrates that the base scheme achieves first-order convergence, while extrapolation enhances convergence rates to second-order in time and fourth-order in space. Theoretical results confirm uniform convergence with respect to the perturbation parameter, and comprehensive numerical experiments validate these analytical claims. Findings indicate that the proposed scheme is reliable, efficient, and particularly effective in attaining fourth-order spatial accuracy when solving singularly perturbed integro-partial differential equations of reaction–diffusion type, thus providing a robust numerical tool for complex applications in science and engineering.

1. Introduction

The following integro-parabolic reaction–diffusion problem involving a small parameter at the highest derivative with initial and Dirichlet boundary conditions is considered:

$$\left\{\begin{array}{cc}{p}_z(\varpi ,z)+{\Gamma }_{\epsilon }p(\eta ,z)=s(\varpi ,z),\hfill & (\varpi ,z)\in A,\hfill \\ p(\varpi ,0)=\zeta \left(\varpi \right),\hfill & \varpi \in \Pi ,\hfill \\ p(0,z)={\zeta }_l\left(z\right),p(1,z)={\zeta }_r\left(z\right),\hfill & \mathrm{on}0\le z\le R,\hfill \end{array}\right.$$

(1)

where

$$\begin{array}{c}\hfill {\displaystyle {\Gamma }_{\epsilon }p(\varpi ,z)=-\epsilon p_{\varpi \varpi }(\varpi ,z)+a\left(z\right)p(\varpi ,z)+\lambda {\int }_0^{1}T(\varpi ,\tau )p(\tau ,z)d\tau .}\end{array}$$

Here, $\Pi =(0,1),A=\Pi \times (0,R]$ and $0<\epsilon \ll 1$. The functions $a\left(z\right),s(\varpi ,z)$ on $\overline{A}=[0,1]\times (0,R]$ and ${\zeta }_l\left(z\right),{\zeta }_r\left(z\right)$, $\zeta \left(\varpi \right)$ possess adequate smoothness and boundedness, and fulfill $a\left(z\right)\ge \beta >0 \mathrm{on} \overline{A}$, and $T(\varpi ,\tau )$ is the kernel function. Because the perturbation parameter $\epsilon$ is present in (1), the same old numerical strategies on a uniform mesh fail to yield accurate results for problem (1) [1]. To address this issue, the use of nonuniform meshes has been proposed, as discussed in [2]. Various numerical methods, including the finite element method (FEM), have been explored; see [3,4,5,6,7,8] for reference. Recently, Lange and Smith [9] established the existence and uniqueness of solutions for singularly perturbed Fredholm integro-ordinary differential equations (SPFIODEs). Sevgin [10] investigated a numerical method for nonlinear first-order singularly perturbed integro-differential equations. Bala et al. [11] addressed partial differential equations with integro-boundary conditions and achieved second-order convergence. Sekar et al. [12] investigated numerical methods for SPFIODEs(reaction-diffusion) and obtained a second-order convergence rate. Since most existing works report a second-order convergence rate, the motivation of this paper is to achieve a higher-order rate of convergence.

The Richardson extrapolation technique (RET) has been employed by several researchers to improve the accuracy and increase the order of convergence for singularly perturbed problems. Sekar Elango et al. [13] studied second-order reaction–diffusion SPFIODEs using a central difference (CD) scheme and the composite trapezoidal rule on nonuniform Shishkin-type meshes. Initially, they achieved second-order convergence and later applied an RET to enhance the convergence to fourth-order. Similarly, Elango et al. [12] handled SPFIODEs (‘reaction–diffusion type’) using central differences and the composite trapezoidal rule on Shishkin-type meshes, achieving a second-order convergence rate, which was subsequently improved to fourth-order via extrapolation.

In the recent contributions by Elango et al. (2025) [12] and Sekar et al. (2025) [13], Richardson extrapolation techniques (RETs) were successfully developed and analyzed for classes of singularly perturbed ordinary differential equations (ODEs). Their results clearly demonstrated that systematic extrapolation can enhance the accuracy and uniform convergence order in the ODE framework. However, those studies were limited to one-dimensional problems where the analytical structure and computational treatment are comparatively simpler. In the present work, we extend the scope of RETs to singularly perturbed partial differential equations (PDEs), thereby addressing a more challenging class of problems. Unlike ODEs, singularly perturbed PDEs involve multiple independent variables and often exhibit anisotropic boundary layers, interaction of reaction–diffusion and convection–diffusion effects, and multiscale solution features that demand nonuniform discretization strategies such as Shishkin meshes. This transition from ODEs to PDEs introduces new analytical challenges, including the need for multidimensional error decomposition, uniform stability analysis for PDE operators, and the treatment of discretization errors that interact across coordinate directions. On the computational side, RET for PDEs requires careful handling of multidimensional meshes and the design of efficient algorithms to manage the increased stiffness and complexity of the problem.

This article focuses on finding a numerical solution to problem (1). The time derivative is discretized using the ‘implicit Euler method’, the spatial derivative using the CD scheme, and the integral term using the trapezoidal rule on a uniform mesh. Initially, this method achieves a 1st-order convergence rate. By applying extrapolation to the ‘implicit Euler method’, the convergence improves to second-order. Further, by applying extrapolation to both the central difference and trapezoidal methods using N mesh points in the spatial direction and $4M$ mesh points in the time direction, a global convergence rate of order four is demonstrated computationally.

The structure of this paper is as follows: the analytical technique applied to the problem is described in Section 2; the construction and evaluation of the numerical technique are discussed in Section 3; the extrapolation method is detailed in Section 4; numerical results, including tables and figures, are presented in Section 5; and concluding remarks are given in Section 6.

In this paper, we use the symbol $\mathbf{K}$ for some arbitrary positive constant, independent of the parameter. For the purpose of analysis, we adopt the normal ‘supremum norm’, denoted by ‘$|.|$’, and defined as ${\displaystyle {\parallel \mathfrak{g}\parallel }_A=\underset{t\in A}{sup}\left|g\left(t\right)\right|.}$

2. Analytic Solution

Lemma 1.

Let $\psi (\varpi ,z)$ be a function such that it is continuous up to the boundary of a domain $\overline{A}$ and twice continuously differentiable within the interior of A. Suppose it satisfies the differential inequality $\left({\displaystyle \frac{\partial }{\partial t}}+{\Gamma }_{\epsilon }\right)\psi (\varpi ,z)\ge 0$ in A and $\psi (\varpi ,z)\ge 0$ on $A.$ Then, $\psi (\varpi ,z)\ge 0$, ∀ $(\varpi ,z)\in \overline{A}$.

Proof. 

Details of the proof are presented in [14]. □

Lemma 2

(Stability). If $a,s\in C^{4,2}\left(\overline{A}\right)$ and ${\displaystyle \frac{{\partial }^n}{\partial {\varpi }^n}}(\varpi ,\tau )\in [0,1]\times [0,1],(n=0,1,2,3,4)$ and $\left|\lambda \right|<{\displaystyle \frac{\alpha }{\underset{0\le \varpi \le 1}{max}\underset{0}{\overset{1}{\int }}\left|T(\varpi ,\tau )\right|d\tau }}$. Then, the solution and its derivative of Equation (1) hold the following bounds:

$$\begin{array}{cc}\hfill \parallel p(\varpi ,z)\parallel & \le \mathbf{K},\hfill \\ \hfill \left|{\displaystyle \frac{\partial p^i(\varpi ,z)}{\partial z^j}}\right|& \le \mathbf{K}\left[1+{ϵ}^{-i/2}\left(e^{-\sqrt{{\displaystyle \frac{\beta }{ϵ}}}\varpi }+e^{-\sqrt{{\displaystyle \frac{\beta }{ϵ}}}(1-\varpi )}\right)\right],\hfill \end{array}$$

where $0\le i+2j\le 4$.

Proof. 

Using the maximum principle for the operator ${\Gamma }_{\epsilon }p=p_z-ϵp_{\varpi \varpi }+a(\varpi ,z)u$,

$$\begin{array}{c}\hfill \parallel p(\varpi ,z)\parallel \le {\alpha }^{-1}\parallel s(\varpi ,z)\parallel +{\alpha }^{-1}\left|\lambda \right|\underset{0\le \varpi \le 1}{max}\left|T(\varpi ,\tau )\right|d\tau \parallel p(\varpi ,z)\parallel ,\end{array}$$

then $\parallel p(\varpi ,z)\parallel \le \mathbf{K}.$ By technique [15], the bounded derivative of $p(\varpi ,z)$ of (1) is derived. □

To establish an $\epsilon$-uniform error estimate, it is essential to derive bounds on the derivatives of the exact solution $p(\varpi ,z)$ of Equation (1). For this purpose, the solution p is decomposed into two parts, a regular component $p_r$ and a singular component $p_s$, such that $p=p_r+p_s.$ For the complete details, one can refer to [16].

3. Approximate Computational Solution

3.1. Partial Discretization with Respect to Time

Over the time interval $[0,R],$ we introduce an equi-spaced grid with time step size $\Delta z,$ defined as ${\Pi }_z^J=\{z_j=j\Delta z,j=0,\dots ,J,z_J=R,\Delta z=R/J\},$ where J denotes the total number of time steps. To approximate the z-variable in Equation (1), we employ the backward Euler scheme, which can be expressed as follows:

$$\left\{\begin{array}{c}(I+\Delta z{\Gamma }_{\epsilon })p^{j+1}=p^j+\Delta z{s}^{j+1},\hfill \\ p^{j+1}\left(0\right)={\zeta }_l\left(z_{j+1}\right),p^{j+1}\left(1\right)={\zeta }_r\left(z_{j+1}\right),\hfill \end{array}\right.$$

(2)

where $s^j=s(\varpi ,z_j),p^j=p(\varpi ,z_j)$ is a semidiscrete numerical estimate of the exact solution $p(\varpi ,z)$ of (1) at given time level $z_j=j\Delta z$.

Definition 3.

The local truncation error associated with the semi-discrete method in the time direction (2) is defined as $e^j=p^j-{\tilde{p}}^j$, where ${\tilde{p}}^j$ satisfies the following equation:

$$\left\{\begin{array}{c}(I+\Delta t{\Gamma }_{\epsilon }){\tilde{p}}^{j+1}={\tilde{p}}^j+s^{j+1}),\hfill \\ {\tilde{p}}^{j+1}\left(0\right)={\zeta }_l\left(z_{j+1}\right),{\tilde{p}}^{j+1}\left(1\right)={\zeta }_r\left(z_{j+1}\right).\hfill \end{array}\right.$$

This error quantifies the influence of each individual $\Delta z$ on the overall error resulting from the time (z) semi-discrete approximation. It is evaluated at a specific time level as follows: $z^j,$ as ${\mathfrak{E}}^j=|p(\varpi ,z^j)-p^i\left(\varpi \right)|$.

Lemma 4.

The exact solution $p(\varpi ,z)$ of (1) remains bounded by a constant $\mathbf{K}$ throughout $\overline{A}$. (i.e., $\mid p(\varpi ,z)\mid \le \mathbf{K},on\overline{A}$).

Proof. 

According to Lemma 1, the solution satisfies $\mid p(\varpi ,z)\mid \le \mathbf{K}z,on \overline{A}$. Since $z\in [0,R]$, it follows that $\mid p(\varpi ,z)\mid \le \mathbf{K},on\overline{A}.$ □

Lemma 5.

If the derivatives of the solution satisfy $\left|{\displaystyle \frac{{\partial }^k}{\partial z^k}}p(\varpi ,z)\right|\le \mathbf{K},for(\varpi ,z)\in \overline{A}=[0,1]\times [0,R],fork=0,1,2$, then the local error of scheme (2) is bounded by $\parallel e^{j+1}{\parallel \le \mathbf{K}(\Delta z)}^2.$

Proof. 

A detailed proof can be found in [17]. □

Theorem 6.

At the jth level, the global error ${\mathfrak{E}}^j$ in the time direction satisfies the bound $\parallel {\mathfrak{E}}^j{\parallel }_{\infty }\le \mathbf{K}\Delta z,$$\forall j\le R/\Delta z$.

Proof. 

The full proof is provided in [5]. □

Theorem 7.

The derivatives of the exact solution $p(\varpi ,z)$ of problem (1) satisfy the following bounds of all positive integers x and y with $0\le x+2y\le 8$:

$$\begin{array}{c}\hfill \left|{\displaystyle \frac{{\partial }^{x+y}p}{\partial {\varpi }^x\partial z^y}}\right|\le \mathbf{K}{\epsilon }^{-x/2},(\varpi ,z)\in A.\end{array}$$

Proof. 

Refer to [18] for the proof of this theorem. □

In this work, problem (1) is discretized with the ‘implicit Euler method’ on an equi-space temporal mesh and the CD scheme on a ‘Shishkin mesh’ for the spatial domain. Details regarding the construction of the ‘Shishkin mesh’ can be found in [1].

3.2. Discretizing the Spatial Variable

Let ‘$\varrho$’ be the parameter governing the mesh transition, defined as ‘$\varrho =min\left\{{\displaystyle \frac{1}{4}},{\rho }_0\sqrt{\epsilon }lnI\right\}$’, where ${\rho }_0\ge 2/\beta$. The spatial domain $\overline{\Pi }=[0,1]$ is divided into three subregions: $\overline{\Pi }=\overline{{\Pi }_l}\cup \overline{{\Pi }_c}\cup \overline{{\Pi }_r}$, where ${\Pi }_l=(0,\varrho ],{\Pi }_c=(\varrho ,1-\varrho ]$ and ${\Pi }_r=(1-\varrho ,1]$. Assume that the number of mesh intervals is $I=2^r$ with $r\ge 3$. We define a piecewise-uniform mesh ${\Pi }_{\varpi }^I=\{{\varpi }_i\in (0,1),i=0,\dots ,I\}$ on $\Pi$, where

$${\varpi }_i=\left\{\begin{array}{cc}i{M}_1,\hfill & \mathrm{for}i=0,\dots ,I/4,\hfill \\ i{M}_2,\hfill & \mathrm{for}i={\displaystyle \frac{I}{4}}+1,\dots ,{\displaystyle \frac{3I}{4}},\hfill \\ i{M}_1,\hfill & \mathrm{for}i={\displaystyle \frac{3I}{4}}+1,\dots ,I,\hfill \end{array}\right.$$

with $M_1={\displaystyle \frac{4\varrho }{I}}$, $M_2={\displaystyle \frac{2(1-2\varrho )}{I}}$. The increments in the spatial variable are expressed as $h_i={\varpi }_i-{\varpi }_{i-1},$ for $i=1,\dots ,I.$

Define the discretized domain $A^I={\Pi }_{\varpi }^I\times {\Pi }_z^J$ on A. We examine the finite difference method applied to the given Equation (1) on domain ${\Pi }_{\varpi }^I$. Let $h_k={\varpi }_k-{\varpi }_{k-1}$ represent the step size between successive mesh points. For a mesh function ${\theta }_k$, the difference operators are defined as follows:

$$\begin{array}{c}\hfill \mathrm{Forward}\mathrm{difference}\mathrm{operator}:B_{\varpi }^{+}{\varphi }_k^j={\displaystyle \frac{{\theta }_{k+1}^j-{\theta }_k^j}{h_{k+1}}}.\\ \hfill \mathrm{Backward}\mathrm{difference}\mathrm{operator}:B_{\varpi }^{-}{\theta }_k^j={\displaystyle \frac{{\theta }_k^j-{\theta }_{k-1}^j}{h_k}}.\\ \hfill \mathrm{Central}\mathrm{difference}\mathrm{operator}:B_{\varpi }^0{\theta }_k^j={\displaystyle \frac{{\theta }_{k+1}^j-{\theta }_{k-1}^j}{h_{k+1}+h_k}}.\end{array}$$

The second-order approximation is as follows:

$$\begin{array}{c}\hfill B_{\varpi }^{+}{B}_{\varpi }^{-}{\varphi }_k^j={\displaystyle \frac{2}{h_k+h_{k+1}}}\left({\displaystyle \frac{{\theta }_{k+1}^j-{\theta }_k^j}{h_{k+1}}}-{\displaystyle \frac{{\theta }_k^j-{\theta }_{k-1}^j}{h_k}}\right).\end{array}$$

Additionally, the time-based backward difference operator is expressed as $B_z^{-}{\theta }_k^j={\displaystyle \frac{{\theta }_k^j-{\theta }_k^{j-1}}{\Delta z}},$ where ${\theta }_k^j=\theta ({\varpi }_k,z_j).$ To numerically solve the problem given by (1), the ‘implicit Euler method’ is employed for discretizing the time derivative, while the CD method is applied to approximate the spatial derivatives. The resulting finite difference scheme can be written as follows:

$$\begin{array}{c}\hfill B_z^{-}{P}_i^{j+1}+\left({\Gamma }_1^I+{\Gamma }_2^I\right)P_i^{j+1}=s_i^j,\mathrm{for}i=1,2,\dots ,I-1,\end{array}$$

(3)

where, ${\Gamma }_1^I{P}_i^j=-\epsilon B_{\varpi }^{+}{B}_{\varpi }^{-}{P}_i^j+a_i{P}_i^j,$ ${\displaystyle {\Gamma }_2^I{P}_i^j=-\lambda \sum _{k=0}^I{\upsilon }_k{T}_{i,k}{P}_k^j,}$ ${\upsilon }_0={\displaystyle \frac{h_0}{2}},{\upsilon }_k={\displaystyle \frac{h_k+h_{k+1}}{2}},$$k=1,2,\dots ,I-1,{\upsilon }_I={\displaystyle \frac{h_I}{2}},$ $s_i^j=s({\varpi }_i,z^j),a_i=a\left({\varpi }_i\right).$

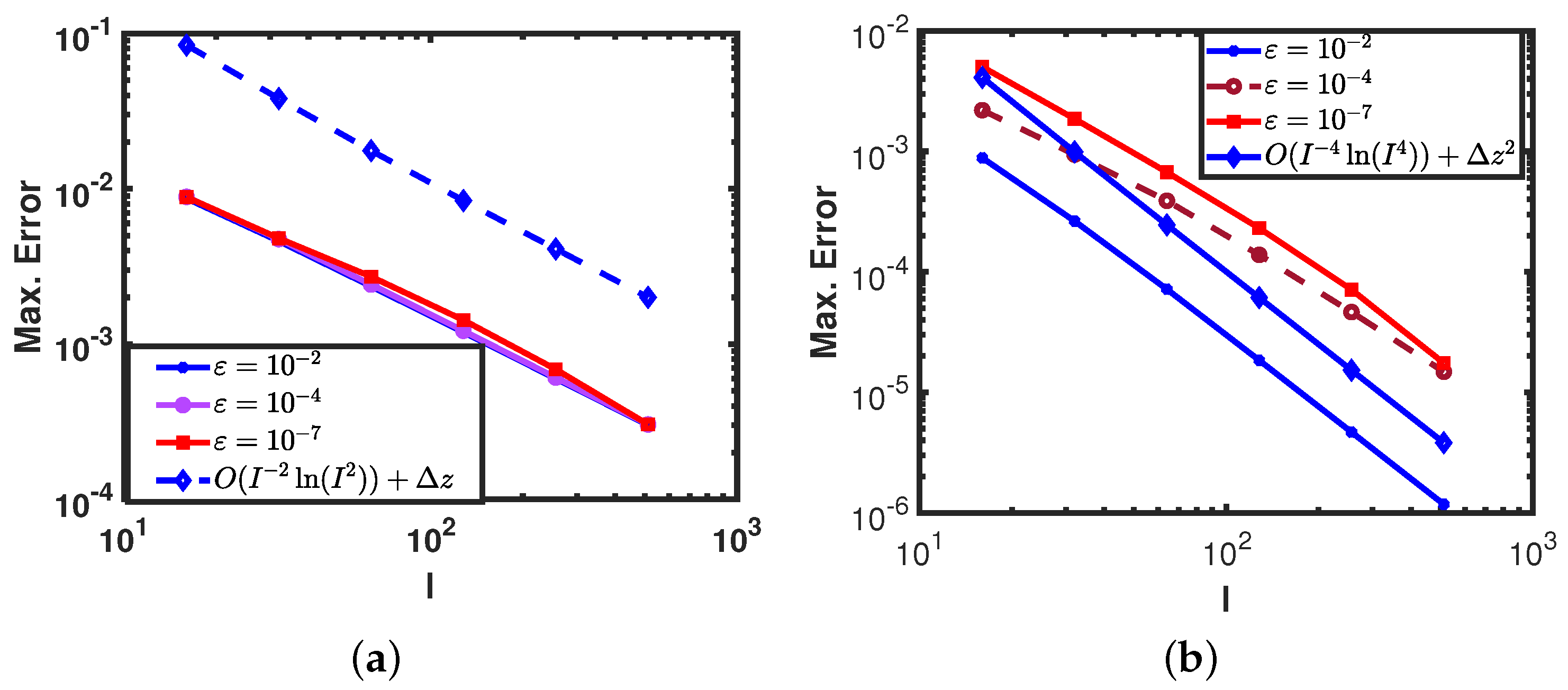
3.3. Estimation of Numerical Error in the Discretization Scheme

Theorem 8.

Let p be the exact solution of Equation (1) and P the numerical solution obtained from finite difference scheme (3), both satisfying the necessary compatibility conditions. Then, the error associated with scheme (3) satisfies the following estimate:

$$\begin{array}{c}\left|(p-P)({\varpi }_i,z_j)\right|\le {(I^{-1}lnI)}^2+\mathbf{K}\Delta z,fori=1,\dots ,I-1\hfill \end{array}$$

where $p({\varpi }_i,z_j)=P_i^j$ for $({\varpi }_i,z_j)\in A^I$.

Proof. 

The numerical solution P is represented as the sum of a regular (smooth) part ($P_r$) and a singular part ($P_s$). Thus, the total error can be written in the following form:

$${\Gamma }^I(P-p)={\Gamma }_1^I(P-p)+{\Gamma }_2^I(P-p).$$

By Miller [1], ${\Gamma }_1^I(P-p)\le \mathbf{K}{(I^{-1}lnI)}^2.$ Now, for operator $L_2$ it holds that

$${\Gamma }_2^I(P-p)={\Gamma }_2^I(P_r-p_r)+{\Gamma }_2^I(P_s-p_s)\le \mathbf{K}{(I^{-1}lnI)}^2.$$

Smooth components:

$$\begin{array}{c}\\ \hfill {\Gamma }_2^I({P_s}_i-{p_s}_i)& =& {\Gamma }_2^I\left(P_s({\varpi }_i,z_j)\right)-{\Gamma }_2^N\left(p_s({\varpi }_i,z_j)\right)\hfill \\ & =& {\displaystyle \lambda \sum _{k=0}^I{\upsilon }_k{T}_{ik}{P_s}_k-\lambda {\int }_0^{1}T(\varpi ,\tau )P_s\left(\tau \right)d\tau }\hfill \\ & =& {\displaystyle \lambda \sum _{k=0}^I{\upsilon }_j{T}_{ik}{p_s}_k-\lambda {\int }_0^{1}T({\varpi }_i,\tau )p_s\left(\tau \right)d\tau }\hfill \\ & \le & {\displaystyle \mathbf{K}\sum _{k=1}^I{\int }_{{\varpi }_{k-1}}^{{\varpi }_k}({\varpi }_k-\eta )(\eta -{\varpi }_{k-1})(1+|p_s^{\prime }\left(\eta \right)|+|p_s^{″}\left(\eta \right)\left|\right)d\eta }\hfill \\ & \le & \mathbf{K}\sqrt{\epsilon }\left(h_i\right)\le \mathbf{K}{I}^{-1}\left(h_i\right)\hfill \\ \hfill {\Gamma }_2^I({P_s}_i-{p_s}_i)& \le & \mathbf{K}{I}^{-2}.\hfill \end{array}$$

By using the stability result, it follows that

$$|P_s({\varpi }_i,z_j)-p_s({\varpi }_i,z_j)|\le \mathbf{K}{I}^{-2}.$$

Singular components:

$$\begin{array}{c}\\ \hfill {\Gamma }_2^I({P_r}_i-{p_r}_i)& =& {\Gamma }_2^I\left(P_r({\varpi }_i,z_j)\right)-{\Gamma }_2^I\left(p_r({\varpi }_i,z_j)\right)\hfill \\ & =& {\displaystyle \lambda \sum _{k=0}^I{\upsilon }_k{T}_{ik}{P_r}_j-\lambda {\int }_0^{1}T({\varpi }_i,\tau )p_r\left(\tau \right)d\tau }\hfill \\ & =& {\displaystyle \lambda \sum _{k=0}^I{\upsilon }_k{T}_{ik}{P_r}_j-\lambda {\int }_0^{1}T({\varpi }_i,\tau )p_r\left(\tau \right)d\tau }\hfill \\ & \le & {\displaystyle \mathbf{K}\sum _{k=1}^I{\int }_{{\varpi }_{k-1}}^{{\varpi }_k}({\varpi }_k-\eta )(\eta -{\varpi }_{k-1})(1+|p_r^{\prime }\left(\eta \right)|+|p_r^{″}\left(\eta \right)\left|\right)d\eta }\hfill \\ & \le & {\displaystyle \mathbf{K}\sum _{k=1}^I{\int }_{{\varpi }_{k-1}}^{{\varpi }_k}({\varpi }_k-\eta )(\eta -{\varpi }_{k-1})\left(\frac{1}{\epsilon }\right)(e^{-\varpi \sqrt{\beta /\epsilon }}+e^{-(1-\varpi )\sqrt{\beta /\epsilon }})d\eta }\hfill \\ & \le & \mathbf{K}{I}^{-1}{\displaystyle \frac{h_i^3}{\epsilon }}\hfill \\ \hfill {\Gamma }_2^I({P_r}_i-{p_r}_i)& \le & \mathbf{K}{I}^{-2}{ln}^{2}I.\hfill \end{array}$$

By the stability result,

$$|P_r({\varpi }_i,z_j)-p_r({\varpi }_i,z_j)|\le \mathbf{K}{I}^{-2}{ln}^{2}I.$$

Therefore,

$$|P({\varpi }_i,z_j)-p({\varpi }_i,z_j)|=|P_s({\varpi }_i,z_j)-p_s({\varpi }_i,z_j)|+|P_r({\varpi }_i,z_j)-p_r({\varpi }_i,z_j)|\le \mathbf{K}{I}^{-2}{ln}^{2}I.$$

(4)

Together, from Equation (4) and Theorem 6, we get the required bound

$$|P({\varpi }_i,z_j)-p({\varpi }_i,z_j)|=|P_s({\varpi }_i,z_j)-p_s({\varpi }_i,z_j)|+|P_r({\varpi }_i,z_j)-p_r({\varpi }_i,z_j)|\le \mathbf{K}{I}^{-2}{ln}^{2}I+\mathbf{K}\Delta z.$$

□

4. Order-Boosting Extrapolation Method

To enhance the accuracy of the numerical solution, we employ the RET. This approach involves solving discrete system (3) on a refined mesh denoted by $A^{2I}={\overline{\Pi }}_{\phi }^{2I}\times {\overline{\Pi }}_z^{4J}$, which consists of $2I$ spatial intervals and $4J$ time intervals. The spatial mesh ${\overline{\Pi }}_{\varpi }^{2I}$ is a ‘piecewise uniform Shishkin mesh’ that retains the same transition points as ${\overline{\Pi }}_{\varpi }^I$ and it is constructed by subdividing each interval of ${\overline{\Pi }}_{\varpi }^I$ into two equal parts. Consequently, the original mesh $A^I=\left\{({\varpi }_i,z_j)\right\}\subset A^{2I}=\left\{({\overline{\varpi }}_i,{\overline{z}}_j)\right\}$ is a subset of the refined mesh ${\overline{\Pi }}_{\varpi }^{2I}=\{{\overline{\varpi }}_i\in (0,1),i=0,\dots ,2I\}$. Hence, the corresponding mesh

$${\overline{\varpi }}_i=\left\{\begin{array}{cc}{\displaystyle \frac{2i\varrho }{I}},\hfill & \mathrm{for}i=0,\dots ,I/2,\hfill \\ {\displaystyle \frac{i(1-2\varrho )}{I}},\hfill & \mathrm{for}i={\displaystyle \frac{I}{2}}+1,\dots ,{\displaystyle \frac{3I}{2}},\hfill \\ {\displaystyle \frac{2i\varrho }{I}},\hfill & \mathrm{for}i={\displaystyle \frac{3I}{2}}+1,\dots ,2I.\hfill \end{array}\right.$$

And ${\overline{z}}_j-{\overline{z}}_{j-1}=\Delta z/4$ for $\overline{z}\in {\overline{\Pi }}_z^{4J}$. Now, from Theorem 8, the error is

$$\begin{array}{cc}(P-p)({\varpi }_i,z_j)\hfill & =\mathbf{K}\left[{(I^{-1}lnI)}^2+\Delta z\right]+o\left({(I^{-1}lnI)}^2+\Delta z\right),\hfill \\ \hfill & =\mathbf{K}\left[{\left(I^{-2}\left({\displaystyle \frac{\varrho }{{\rho }_0\sqrt{\epsilon }}}\right)\right)}^2+\Delta z\right]+o\left({(I^{-1}lnI)}^2+\Delta z\right).\hfill \end{array}$$

(5)

Consider $\overline{P}({\overline{\varpi }}_i,{\overline{z}}_n)$ as the numerical solution of Equation (3) on the discretized domain $A^{2I}$. Then, by invoking the theorem for each $({\overline{\varpi }}_i,{\overline{z}}_n)\in A^{2I}$, it follows that

$$\begin{array}{c}(\overline{P}-p)({\overline{\varpi }}_i,{\overline{z}}_j)=\mathbf{K}\left[{\left({\left(2I\right)}^{-2}\left({\displaystyle \frac{\varrho }{{\rho }_0\sqrt{\epsilon }}}\right)\right)}^2+{\displaystyle \frac{\Delta z}{4}}\right]+o\left({(I^{-1}lnI)}^2+{\displaystyle \frac{\Delta z}{4}}\right).\hfill \end{array}$$

(6)

Excluding the $o\left(I^{-2}\right)$ terms from (5) and (6), we obtain the following approximation:

$$p({\varpi }_i,z_j)-{\displaystyle \frac{1}{3}}\left(4\overline{P}-P\right)({\varpi }_i,z_j)=o\left({(I^{-1}lnI)}^2+\Delta z\right),({\phi }_i,z_j)\in A^I.$$

(7)

Thus, we make use of the following extrapolation expression:

$$P_{expt}({\varpi }_i,z_j)={\displaystyle \frac{1}{3}}\left(4\overline{P}-P\right)({\varpi }_i,z_j).$$

(8)

Theorem 9.

Let p and $P_{expt}$ be the exact and extrapolated solutions of (1) and (8), respectively, using mesh levels $A^I$ and $A^{2I}$. Then, the error can be bounded as follows:

$$\begin{array}{c}|p({\varpi }_i,z_j)-P_{expt}({\varpi }_i,z_j)|\le \mathbf{K}{(I^{-1}lnI)}^4+\mathbf{K}{(\Delta z)}^2,fori=1,\dots ,I-1,\hfill \end{array}$$

Proof. 

The error can be written in the form

$${\Gamma }^I(P_{expt}-p)={\Gamma }_1^I(P_{expt}-p)+{\Gamma }_2^I(P_{expt}-p).$$

We have

$${\Gamma }_1^I(P_{expt}-p)\le \mathbf{K}{(I^{-1}lnI)}^4+\mathbf{K}{(\Delta z)}^2,$$

A detailed proof of the error estimate is provided in [12]. We now turn to the proof of the operator ${\Gamma }_2^I$,

$${\Gamma }_2^I(P_{expt}-p)={\Gamma }_2^I({P_s}_{exp}-p_s)+{\Gamma }_2^I({P_r}_{exp}-p_r)\le \mathbf{K}{(I^{-1}lnI)}^4.$$

We write $\tilde{P}$ on ${\overline{\Pi }}^{2I}$ as the sum of its smooth part $\widetilde{P_r}$ and singular part $\widetilde{P_s}$.

Error in smooth component:

$${\Gamma }_2^I(V_i-v_i)={\Gamma }_2^I\left(P_s(x_i,z_j)\right)-{\Gamma }_2^I\left(p_s(x_i,z_j)\right),\mathrm{for}({\varpi }_i,z_j)\in {\overline{A}}^I,$$

Using the integral remainder form of the Taylor expansion and applying the derivative estimates from Theorem 8, it follows that

$${\Gamma }_2^I({P_s}_i-{p_s}_i)\le \mathbf{K}\left(I^{-2}+I^{-4}\right),$$

$${\Gamma }_2^I({P_s}_i-{p_s}_i)\le \mathbf{K}{I}^{-2}+O\left(I^{-4}\right).$$

From the established stability, it is possible to write

$$\left|({P_s}_i-{p_s}_i)\right|\le \mathbf{K}{I}^{-2}+O\left(I^{-4}\right)\mathrm{for}{\varpi }_i\in {\overline{\Pi }}^I.$$

(9)

Similarly, we can obtain on ${\overline{\Pi }}^{2I}$

$$\left|({\widetilde{P_s}}_i-{p_s}_i)\right|\le \mathbf{K}{\left(2I\right)}^{-2}+O\left(I^{-4}\right)\mathrm{for}{\tilde{\varpi }}_i\in {\overline{\Pi }}^{2I}.$$

(10)

From extrapolation Formula (8), we have

$$\begin{array}{cc}\hfill ({P_s}_{expt}-p_s)\left({\varpi }_i\right)=& \left({\displaystyle \frac{1}{3}}(4\widetilde{P_s}-P_s)\left({\varpi }_i\right)\right)-p_s\left({\varpi }_i\right)\\ \hfill =& {\displaystyle \frac{1}{3}}\left(4(\widetilde{P_s}-p_s)+(P_s-p_s)\right)\left({\varpi }_i\right).\end{array}$$

From (9) and (10), we get

$$\begin{array}{c}\hfill \left|({P_s}_{expt}-p_s)\left({\varpi }_i\right)\right|=\left|{\displaystyle \frac{1}{3}}\left(4(\widetilde{P_s}-p_s)+(P_s-p_s)\right)\left({\varpi }_i\right)\right|\le \mathbf{K}{I}^{-4}.\end{array}$$

Layer components:

$${\Gamma }_2^I({P_r}_i-{p_r}_i)={\Gamma }_2^I\left(P_r\left({\varpi }_i\right)\right)-{\Gamma }_2^I\left(p_r\left({\varpi }_i\right)\right),\mathrm{for}{\varpi }_i\in {\overline{\Pi }}^I,$$

Following the approach in Theorem 8, and utilizing the integral form of Taylor’s theorem combined with the known derivative bounds, we are able to prove that

$${\Gamma }_2^I({P_r}_i-{p_r}_i)\le \mathbf{K}\left(I^{-2}{(lnI)}^2+I^{-4}\right),$$

$${\Gamma }_2^I({P_r}_i-{p_r}_i)\le \mathbf{K}{I}^{-2}{(lnI)}^2+O\left(I^{-4}{(lnI)}^4\right).$$

Employing the stability property, we obtain

$$\left|({P_r}_i-{p_r}_i)\right|\le \mathbf{K}{I}^{-2}{(lnI)}^2+O\left(I^{-4}{(lnI)}^4\right)\mathrm{for}{\varpi }_i\in {\overline{\Pi }}^I.$$

(11)

Similarly, on ${\overline{\Pi }}^{2I}$,

$$\left|({\widetilde{P_r}}_i-{p_r}_i)\right|\le \mathbf{K}{\left(2I\right)}^{-2}{(ln2I)}^2+O\left(I^{-4}{(lnI)}^2\right)\mathrm{for}{\tilde{\varpi }}_i\in {\overline{\Pi }}^{2I}.$$

$$\left|({\widetilde{P_r}}_i-{p_r}_i)\right|\le \mathbf{K}{\left(2I\right)}^{-2}{(lnI)}^2+O\left(I^{-4}{(lnI)}^2\right)\mathrm{for}{\tilde{\varpi }}_i\in {\overline{\Pi }}^{2I}.$$

(12)

From extrapolation Formula (8), we can write

$$\begin{array}{cc}\hfill ({P_r}_{expt}-p_r)({\varpi }_i,z_j)=& \left({\displaystyle \frac{1}{3}}(4\widetilde{P_r}-P_r)({\varpi }_i,z_j)\right)-p_r({\varpi }_i,z_j)\\ \hfill =& {\displaystyle \frac{1}{3}}\left(4(\widetilde{P_r}-P_r)+(P_r-p_r)\right)({\varpi }_i,z_j).\end{array}$$

From (11) and (12), we get

$$\begin{array}{c}\hfill \left|({P_r}_{exp}-p_r)({\varpi }_i,z_j)\right|=\left|{\displaystyle \frac{1}{3}}\left(4(\widetilde{P_r}-p_r)+(P_r-p_r)\right)({\varpi }_i,z_j)\right|\le \mathbf{K}{I}^{-4}{(lnI)}^4.\end{array}$$

Hence, the bound

$$|P_{expt}({\varpi }_i,z_j)-p({\varpi }_i,z_j)|\le \mathbf{K}{I}^{-4}{(lnI)}^4+\mathbf{K}{(\Delta z)}^2.$$

□

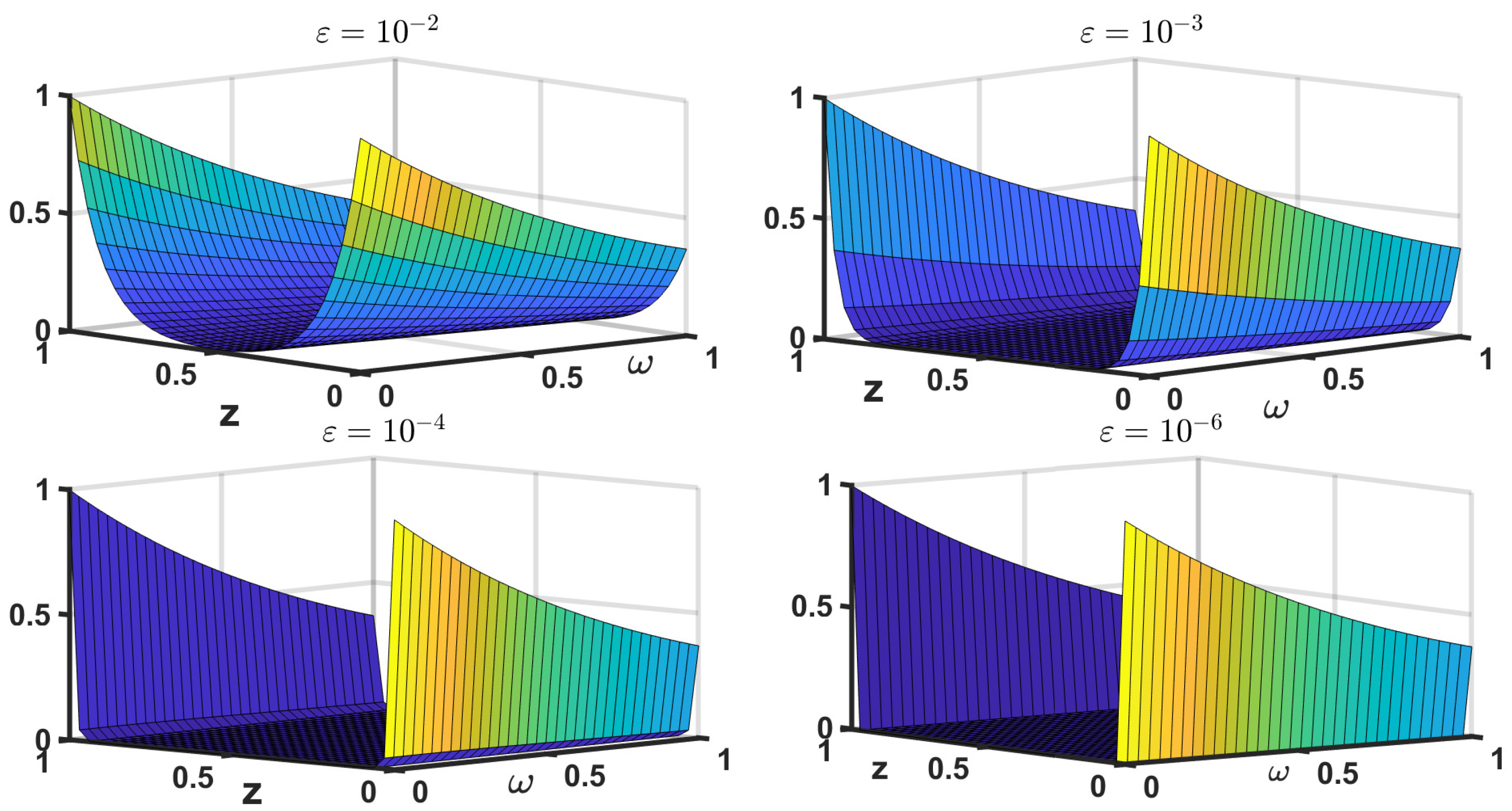
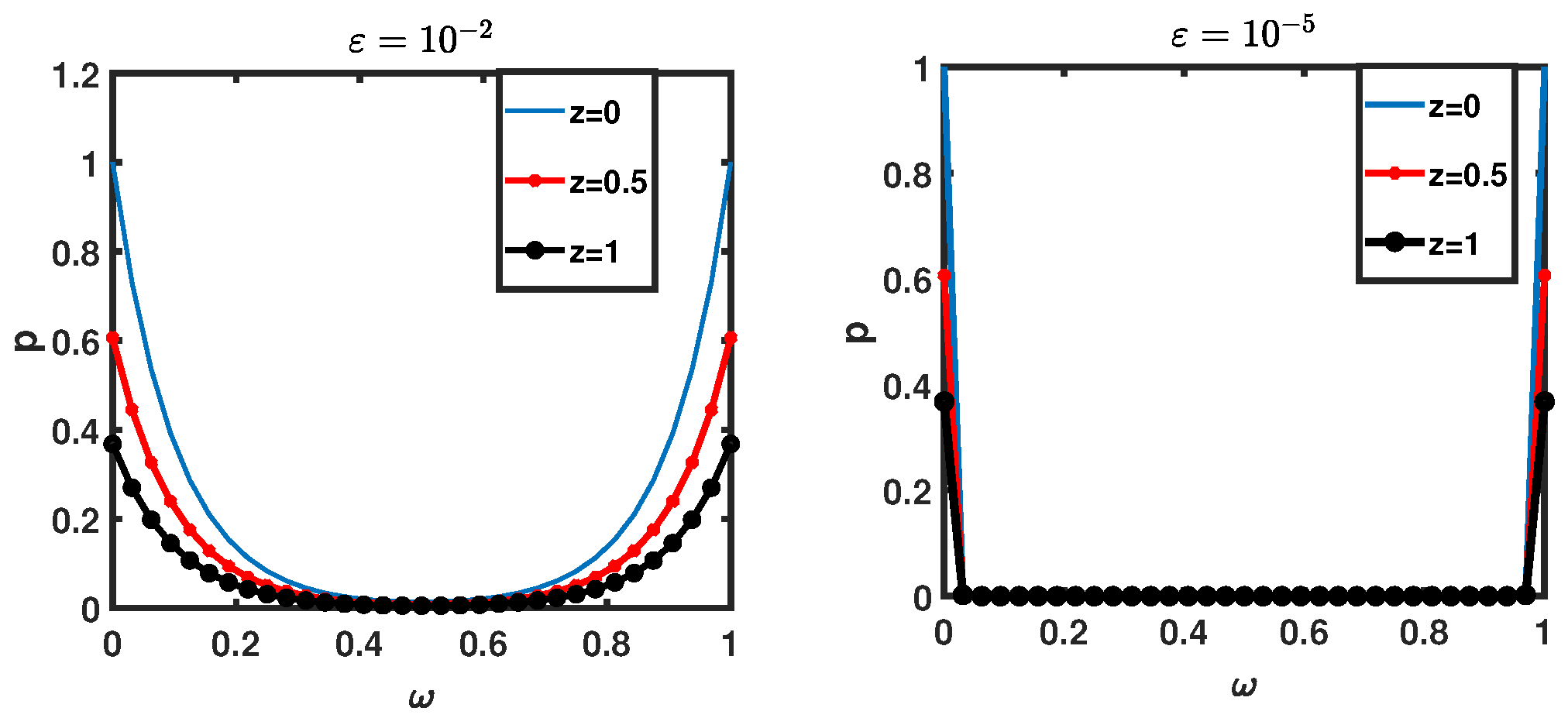
5. Simulation Outcomes and Discussion

This section illustrates the numerical outcomes produced by scheme (3) for a test problem discretized on a piecewise-uniform rectangular mesh. $A^N$. In our simulations, the constant is chosen to be ${\rho }_0=4.1$.

Example 10.

Let us study the following integro-parabolic problem:

$$\begin{array}{c}{\displaystyle p_z-\epsilon p_{\varpi \varpi }+2p(\varpi ,z)+0.5{\int }_0^{1}p(\varpi ,\tau )d\tau =s(\varpi ,z),(\varpi ,z)\in (0,1)\times (0,1],}\hfill \\ p(\varpi ,0)=e^{-\varpi /\sqrt{\epsilon }}+e^{-(1-\varpi )/\sqrt{\epsilon }},(\varpi ,z)\in [0,1],\hfill \\ p(0,z)=e^{-z}+e^{-z-1/\sqrt{\epsilon }},p(1,z)=e^{-z-1/\sqrt{\epsilon }}+e^{-z},z\in [0,1].\hfill \end{array}$$

(13)

The exact solution of Example 10 is $p(\varpi ,z)=e^{-z-\varpi /\sqrt{\epsilon }}+e^{-z-(1-\varpi )/\sqrt{\epsilon }}$. Now, for each $\epsilon$, the maximum pointwise error before and after extrapolation given by ${\displaystyle E_{\epsilon }^{I,\Delta z}=\underset{({\varpi }_i,z_j)\in A^I}{max}|p({\varpi }_i,z_j)-P^{I,\Delta z}({\varpi }_i,z_j)|,}$ and ${\displaystyle E_{\epsilon }^{I,\Delta z}=\underset{({\varpi }_i,z_j)\in A^I}{max}|p({\varpi }_i,z_j)-P_{expt}^{I,\Delta z}({\varpi }_i,z_j)|}$. The corresponding order of convergence is $G_{\epsilon }^{I,\Delta z}={log}_2\left({\displaystyle \frac{E_{\epsilon }^{I,\Delta z}}{E_{\epsilon }^{2I,\Delta z/2}}}\right)$. Here, $p({\varpi }_i,z_j)$ is the exact solution, $P^{I,\Delta z}({\varpi }_i,z_j)$ is the approximate solution before extrapolation, and $P_{expt}^{I,\Delta z}({\varpi }_i,z_j)$ is the numerical solution after extrapolation.

Example 11.

Let us study the following integro-parabolic problem: for $(\varpi ,z)\in (0,1)\times (0,1]$,

$$\begin{array}{c}{\displaystyle p_z-\epsilon p_{\varpi \varpi }+z(1-z)p(\varpi ,z)+0.5{\int }_0^1{e}^z(1+z)\tau (1-\tau )p(\varpi ,\tau )d\tau =s(\varpi ,z),}\hfill \\ p(\varpi ,0)=sin\left(\pi z\right),(\varpi ,z)\in [0,1],\hfill \\ p(0,z)=0,p(1,z)=0,z\in [0,1].\hfill \end{array}$$

(14)

The exact solution of Example 11 is unknown. To find the maximum pointwise error and rate of convergence, we employ the double mesh principle [13].

Figure 1 present the surface plots of the numerical solution for Example 10 and Example 11, while the corresponding contour plots are shown in Figure 2. Additionally, solution profiles at different time levels are displayed in Figure 3. These visualizations clearly illustrate the presence of boundary layers near $x=0$ and $x=1$. The numerical order of convergence before and after extrapolation is illustrated in Figure 4, where the maximum pointwise errors are plotted on a log–log scale. Figure 5 present the surface plots of the numerical solution Example 11.

Table 1. Before applying extrapolation, the proposed method yields the following values for $E_{\epsilon }^{I,\Delta z}$ and $G_{\epsilon }^{I,\Delta z}$.

		Number of Intervals I/(Time Step ($\mathbf{\Delta }\mathit{z}$))
	$\mathit{\epsilon }$	16$\left({\displaystyle \frac{\mathbf{1}}{\mathbf{16}}}\right)$	32$\left({\displaystyle \frac{\mathbf{1}}{\mathbf{32}}}\right)$	64$\left({\displaystyle \frac{\mathbf{1}}{\mathbf{64}}}\right)$	128$\left({\displaystyle \frac{\mathbf{1}}{\mathbf{128}}}\right)$	256$\left({\displaystyle \frac{\mathbf{1}}{\mathbf{256}}}\right)$	512$\left({\displaystyle \frac{\mathbf{1}}{\mathbf{512}}}\right)$
	$1\times {10}^{-2}$	8.6666 $\times {10}^{-3}$	4.6038 $\times {10}^{-3}$	2.3555 $\times {10}^{-3}$	1.1920 $\times {10}^{-3}$	5.9952 $\times {10}^{-4}$	3.0066 $\times {10}^{-4}$
		0.9126	0.9668	0.9827	0.9915	0.9957
	$1\times {10}^{-3}$	8.9084 $\times {10}^{-3}$	4.7452 $\times {10}^{-3}$	2.4187 $\times {10}^{-3}$	1.2186 $\times {10}^{-3}$	6.0891 $\times {10}^{-4}$	3.0372 $\times {10}^{-4}$
		0.9087	0.9722	0.9890	1.0009	1.0035
	$1\times {10}^{-4}$	8.8786 $\times {10}^{-3}$	4.7433 $\times {10}^{-3}$	2.4186 $\times {10}^{-3}$	1.2186 $\times {10}^{-3}$	6.0891 $\times {10}^{-4}$	3.0372 $\times {10}^{-4}$
		0.9044	0.9717	0.9890	1.0009	1.0035
S-mesh	$1\times {10}^{-5}$	8.8601 $\times {10}^{-3}$	4.7413 $\times {10}^{-3}$	2.4184 $\times {10}^{-3}$	1.2186 $\times {10}^{-3}$	6.0891 $\times {10}^{-4}$	3.0372 $\times {10}^{-4}$
		0.9020	0.9712	0.9889	1.0009	1.0035
	$1\times {10}^{-6}$	8.8531 $\times {10}^{-3}$	4.7404 $\times {10}^{-3}$	2.4183 $\times {10}^{-3}$	1.2186 $\times {10}^{-3}$	6.0891 $\times {10}^{-4}$	3.0372 $\times {10}^{-4}$
		0.9012	0.9710	0.9888	1.0009	1.0035
	$1\times {10}^{-7}$	8.8508 $\times {10}^{-3}$	4.8029 $\times {10}^{-3}$	2.7186 $\times {10}^{-3}$	1.4275 $\times {10}^{-3}$	6.8809 $\times {10}^{-4}$	3.0372 $\times {10}^{-4}$
		0.8819	0.8211	0.9293	1.0528	1.1798
	$1\times {10}^{-8}$	8.8500 $\times {10}^{-3}$	4.9226 $\times {10}^{-3}$	2.8466 $\times {10}^{-3}$	1.5618 $\times {10}^{-3}$	8.2144 $\times {10}^{-4}$	4.1043 $\times {10}^{-4}$
		0.8463	0.7902	0.8661	0.9270	1.0010

lists the values $E_{\epsilon }^{I,\Delta z}$ and $G_{\epsilon }^{I,\Delta z}$ before applying the RET for Example 10. The values given in

Table 2. After applying extrapolation, the proposed method yields the following values for $E_{\epsilon }^{I,\Delta z}$ and $G_{\epsilon }^{I,\Delta z}$.

		Number of Intervals I/(Time Step ($\mathbf{\Delta }\mathit{z}$))
	$\mathit{\epsilon }$	16$\left({\displaystyle \frac{\mathbf{1}}{\mathbf{16}}}\right)$	32$\left({\displaystyle \frac{\mathbf{1}}{\mathbf{32}}}\right)$	64$\left({\displaystyle \frac{\mathbf{1}}{\mathbf{64}}}\right)$	128$\left({\displaystyle \frac{\mathbf{1}}{\mathbf{128}}}\right)$	256$\left({\displaystyle \frac{\mathbf{1}}{\mathbf{256}}}\right)$	512$\left({\displaystyle \frac{\mathbf{1}}{\mathbf{512}}}\right)$
	$1\times {10}^{-2}$	8.8286 $\times {10}^{-4}$	2.6361 $\times {10}^{-4}$	7.1711 $\times {10}^{-5}$	1.8444 $\times {10}^{-5}$	4.6737 $\times {10}^{-6}$	1.1757 $\times {10}^{-6}$
		1.7438	1.8782	1.9590	1.9805	1.9910
	$1\times {10}^{-3}$	1.9490 $\times {10}^{-3}$	9.4116 $\times {10}^{-4}$	3.8903 $\times {10}^{-4}$	1.3826 $\times {10}^{-4}$	4.6350 $\times {10}^{-5}$	1.2132 $\times {10}^{-5}$
		1.0502	1.2746	1.4925	1.5768	1.9338
	$1\times {10}^{-4}$	2.1962 $\times {10}^{-3}$	9.4114 $\times {10}^{-4}$	3.8903 $\times {10}^{-4}$	1.3826 $\times {10}^{-4}$	4.6350 $\times {10}^{-5}$	1.4816 $\times {10}^{-5}$
		1.2226	1.2745	1.4925	1.5768	1.6454
S-mesh	$1\times {10}^{-5}$	4.0188 $\times {10}^{-3}$	1.1684 $\times {10}^{-3}$	3.8903 $\times {10}^{-4}$	1.3826 $\times {10}^{-4}$	4.6350 $\times {10}^{-5}$	1.4816 $\times {10}^{-5}$
		1.7822	1.5866	1.4925	1.5768	1.6454
	$1\times {10}^{-6}$	4.7703 $\times {10}^{-3}$	1.6729 $\times {10}^{-3}$	5.3979 $\times {10}^{-4}$	1.4589 $\times {10}^{-4}$	4.6350 $\times {10}^{-5}$	1.4816 $\times {10}^{-5}$
		1.5117	1.6319	1.8875	1.6542	1.6454
	$1\times {10}^{-7}$	5.0251 $\times {10}^{-3}$	1.8608 $\times {10}^{-3}$	6.7161 $\times {10}^{-4}$	2.3043 $\times {10}^{-4}$	7.1139 $\times {10}^{-5}$	1.7476 $\times {10}^{-5}$
		1.4332	1.4702	1.5433	1.6956	2.0253
	$1\times {10}^{-8}$	5.1074 $\times {10}^{-3}$	1.9230 $\times {10}^{-3}$	7.1786 $\times {10}^{-4}$	2.6381 $\times {10}^{-4}$	9.3956 $\times {10}^{-5}$	3.1375 $\times {10}^{-5}$
		1.4092	1.4216	1.4442	1.4895	1.5824

after RET of $E_{\epsilon }^{I,\Delta z}$ and the $G_{\epsilon }^{I,\Delta z}$. In The data indicate that the time derivative term significantly influences the error. Notably, applying extrapolation nearly doubles the convergence rate, achieving second-order accuracy. To further improve accuracy, the time step is refined using $\Delta z=1/2^{2i}$. The results of this refinement are provided in

Table 3. After applying extrapolation and step size reduce, the proposed method yields the following values for $E_{\epsilon }^{I,\Delta z}$ and $G_{\epsilon }^{I,\Delta z}$.

		Number of Intervals I/(Time Step ($\mathbf{\Delta }\mathit{z}$))
	$\mathit{\epsilon }$	16$\left({\displaystyle \frac{\mathbf{1}}{{\mathbf{4}}^{\mathbf{2}}}}\right)$	32$\left({\displaystyle \frac{\mathbf{1}}{{\mathbf{4}}^{\mathbf{3}}}}\right)$	64$\left({\displaystyle \frac{\mathbf{1}}{{\mathbf{4}}^{\mathbf{4}}}}\right)$	128$\left({\displaystyle \frac{\mathbf{1}}{{\mathbf{4}}^{\mathbf{5}}}}\right)$	256$\left({\displaystyle \frac{\mathbf{1}}{{\mathbf{4}}^{\mathbf{6}}}}\right)$	512$\left({\displaystyle \frac{\mathbf{1}}{{\mathbf{4}}^{\mathbf{7}}}}\right)$
S-mesh	$1\times {10}^{-2}$	5.2172 $\times {10}^{-4}$	4.9821 $\times {10}^{-5}$	3.7496 $\times {10}^{-6}$	2.5267 $\times {10}^{-7}$	1.6245 $\times {10}^{-8}$	1.10415 $\times {10}^{-9}$
		3.3884	3.7319	3.8914	3.9591	3.8790
	$1\times {10}^{-3}$	8.5406 $\times {10}^{-4}$	1.0561 $\times {10}^{-4}$	8.7843 $\times {10}^{-6}$	6.0121 $\times {10}^{-7}$	3.8853 $\times {10}^{-8}$	2.6211 $\times {10}^{-9}$
		3.0157	3.5876	3.869	3.9518	3.8898
	$1\times {10}^{-4}$	8.5406 $\times {10}^{-4}$	1.0561 $\times {10}^{-4}$	1.0149 $\times {10}^{-5}$	9.0698 $\times {10}^{-7}$	7.5328 $\times {10}^{-8}$	6.1323 $\times {10}^{-9}$
		3.0157	3.3792	3.4842	3.5898	3.6187
	$1\times {10}^{-5}$	8.8436 $\times {10}^{-4}$	1.1623 $\times {10}^{-4}$	1.3837 $\times {10}^{-5}$	2.2739 $\times {10}^{-6}$	2.5560 $\times {10}^{-7}$	2.7570 $\times {10}^{-8}$
		1.7579	2.9276	3.0704	2.6053	3.2127
	$1\times {10}^{-6}$	9.7356 $\times {10}^{-4}$	1.5259 $\times {10}^{-4}$	1.6265 $\times {10}^{-5}$	1.5376 $\times {10}^{-6}$	1.3717 $\times {10}^{-7}$	1.1724 $\times {10}^{-8}$
		2.6736	3.2298	3.403	3.4867	3.5484
	$1\times {10}^{-7}$	9.7356 $\times {10}^{-4}$	1.5259 $\times {10}^{-4}$	1.6265 $\times {10}^{-5}$	1.5376 $\times {10}^{-6}$	1.3717 $\times {10}^{-7}$	1.1724 $\times {10}^{-8}$
		2.6736	3.2298	3.403	3.4867	3.5484

, which demonstrates a clear trend toward fourth-order convergence. The results in Table 1, Table 2 and Table 3 generally confirm the expected uniform order of convergence. The few cases where the observed rate deviates (for example, when $\epsilon ={10}^{-7}$ in Table 1) can be explained. For such extremely small perturbation parameters, the boundary layer becomes much narrower than the coarse mesh size, so the layer is not fully resolved at lower I. In addition, round-off effects become more noticeable when the solution is very steep. As the mesh is refined, the layer is captured correctly, and the rates quickly align with the theoretical order. These deviations are therefore a numerical artifact rather than a sign of instability of the method. In

Table 4. Time comparison in seconds.

	Before Extrapolation			After Extrapolation
Mesh size ($I=J$)	128	256	512	128	256	512
	1.114	4.493	20.132	7.262	166.171	1234.515

, we compare the execution time of the algorithm (in seconds) before and after extrapolation. It can be observed that the execution time increases after extrapolation, since a larger number of mesh intervals is required. However, this additional cost leads to improved accuracy.

6. Conclusions

This paper presents a numerical approach for solving a parabolic integro-partial differential equation with small parameter of the form (1). The time derivative is discretized using the ‘implicit Euler method’ on a uniform mesh, while the spatial derivative is approximated using a central difference scheme on a ‘Shishkin mesh’, which ensures second-order accuracy in space. To enhance the convergence rate in both spatial and temporal dimensions, the RET is applied. We establish that the proposed method is uniformly convergent and achieves an approximate fourth-order accuracy. The effectiveness of the scheme is validated through numerical experiments on a benchmark problem. The results confirm that the method consistently achieves near-fourth-order convergence. The present study has focused on linear singularly perturbed problems with fixed- coefficient kernels. As part of future work, the proposed approach may be extended to more complex settings, such as nonlinear problems or variable-coefficient kernels. These generalizations are expected to pose additional analytical and computational challenges, but their successful treatment would considerably enhance the scope and applicability of the method to real-world models.