Active Fault Tolerant Trajectory-Tracking Control of Autonomous Distributed-Drive Electric Vehicles Considering Steer-by-Wire Failure
Abstract
1. Introduction
2. Problem Description and Dynamics Model
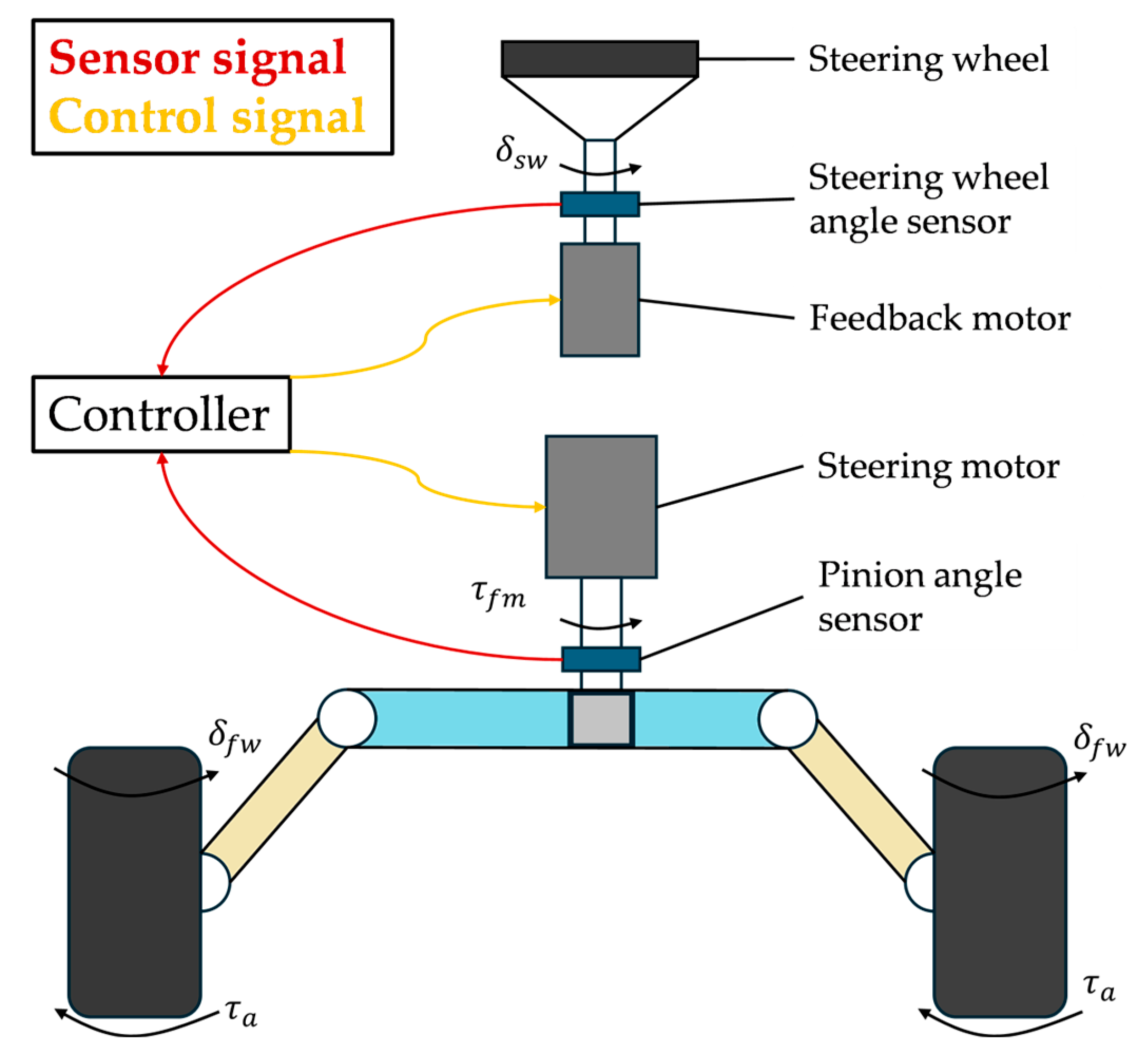
2.1. Analysis of Steer-by-Wire Failure Modes
2.2. Different Steering Dynamics Model
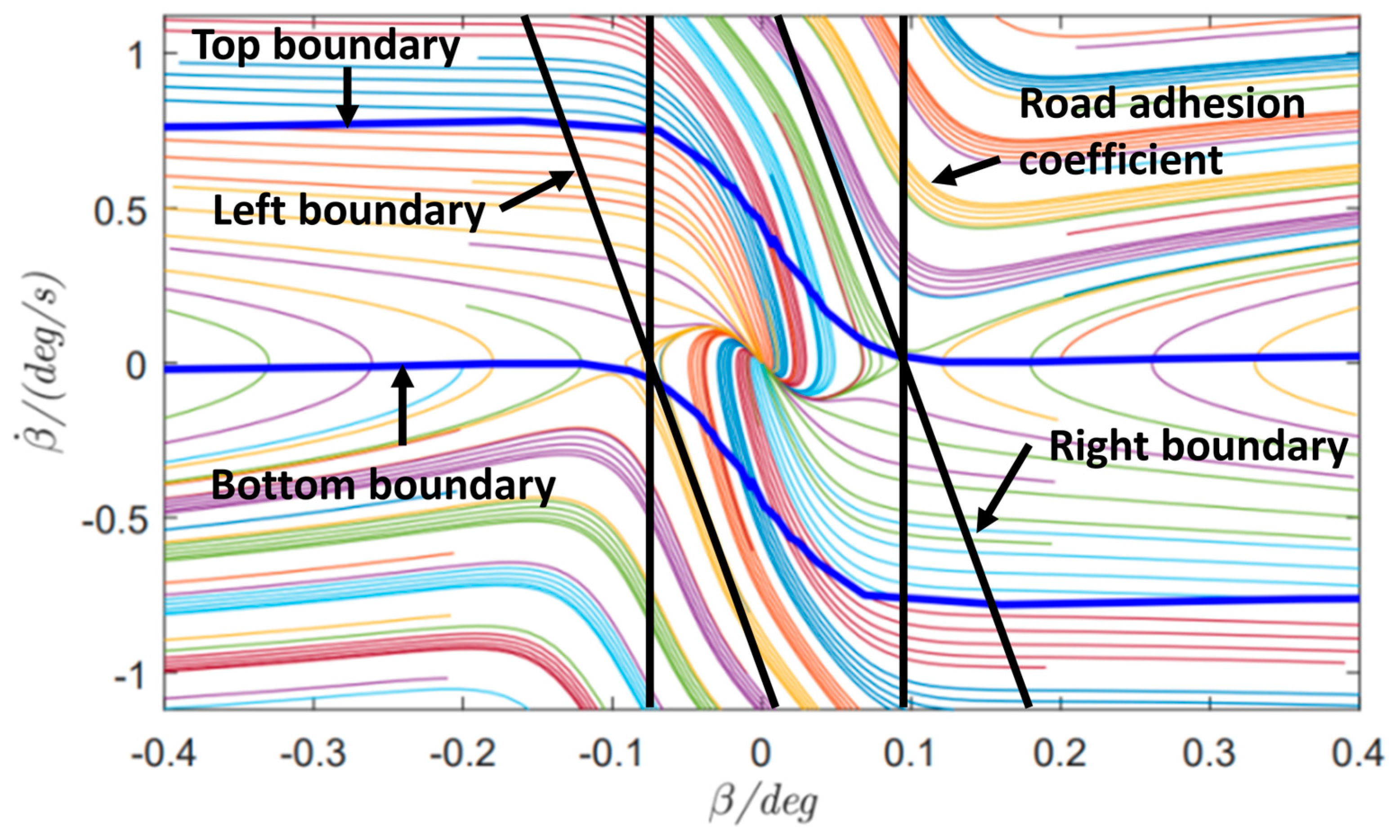
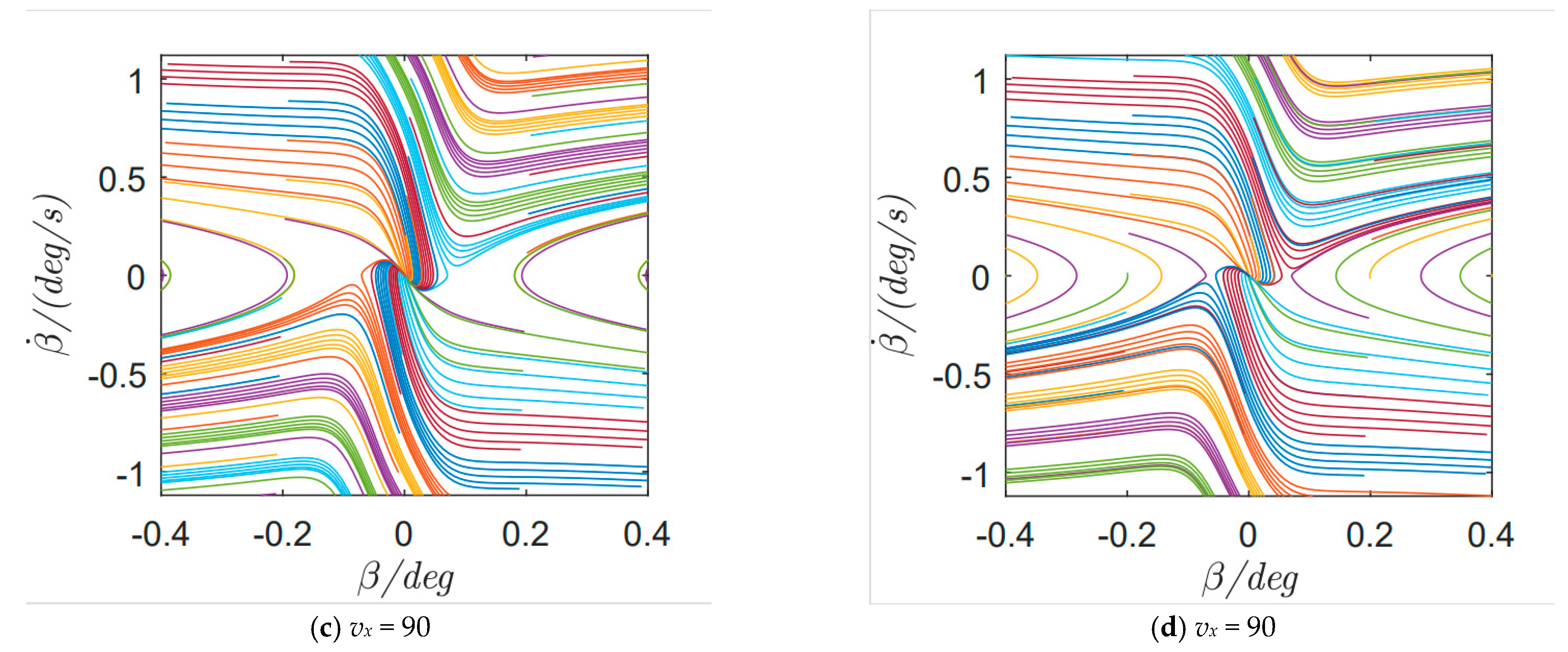
2.3. Analysis of Steering Failure Impact on Vehicle Motion
3. Hierarchical Controller Design
3.1. Cascade Control Overview
3.2. Control Architecture
3.3. Cascade ADRC Yaw Moment Controller
3.4. Stability-Oriented Torque Allocation
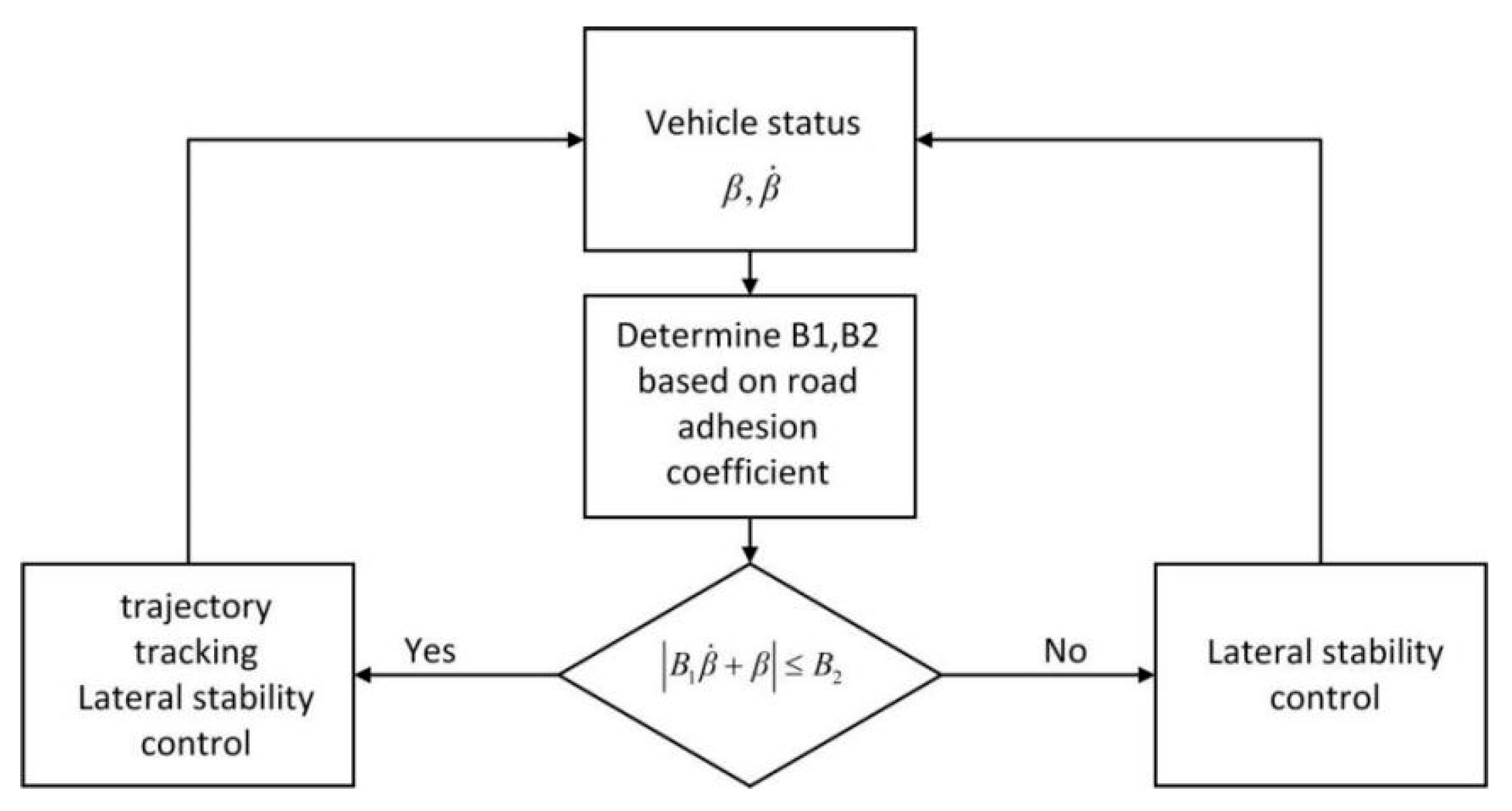
3.5. Stability Criterion
4. Simulation and Results
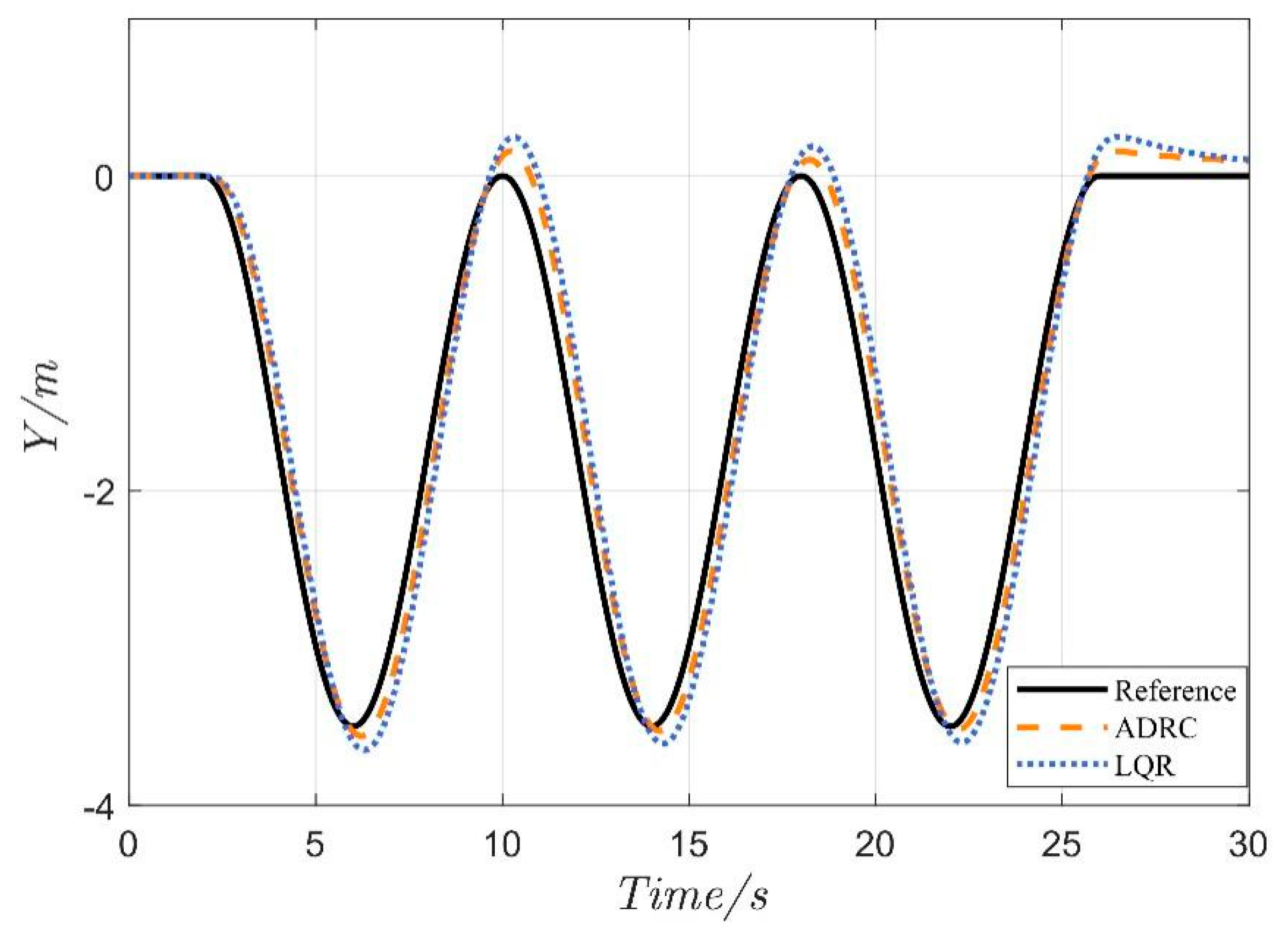
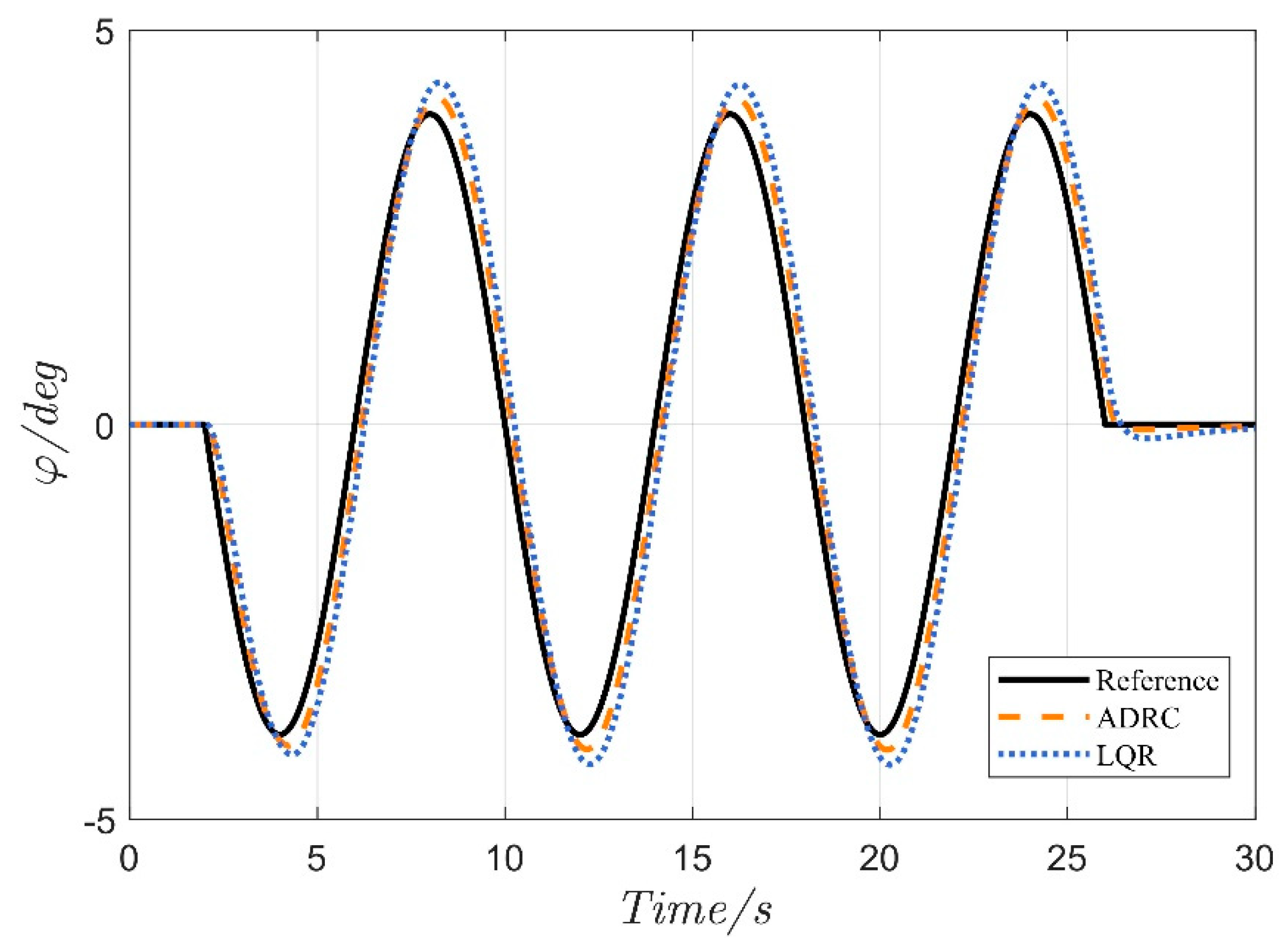
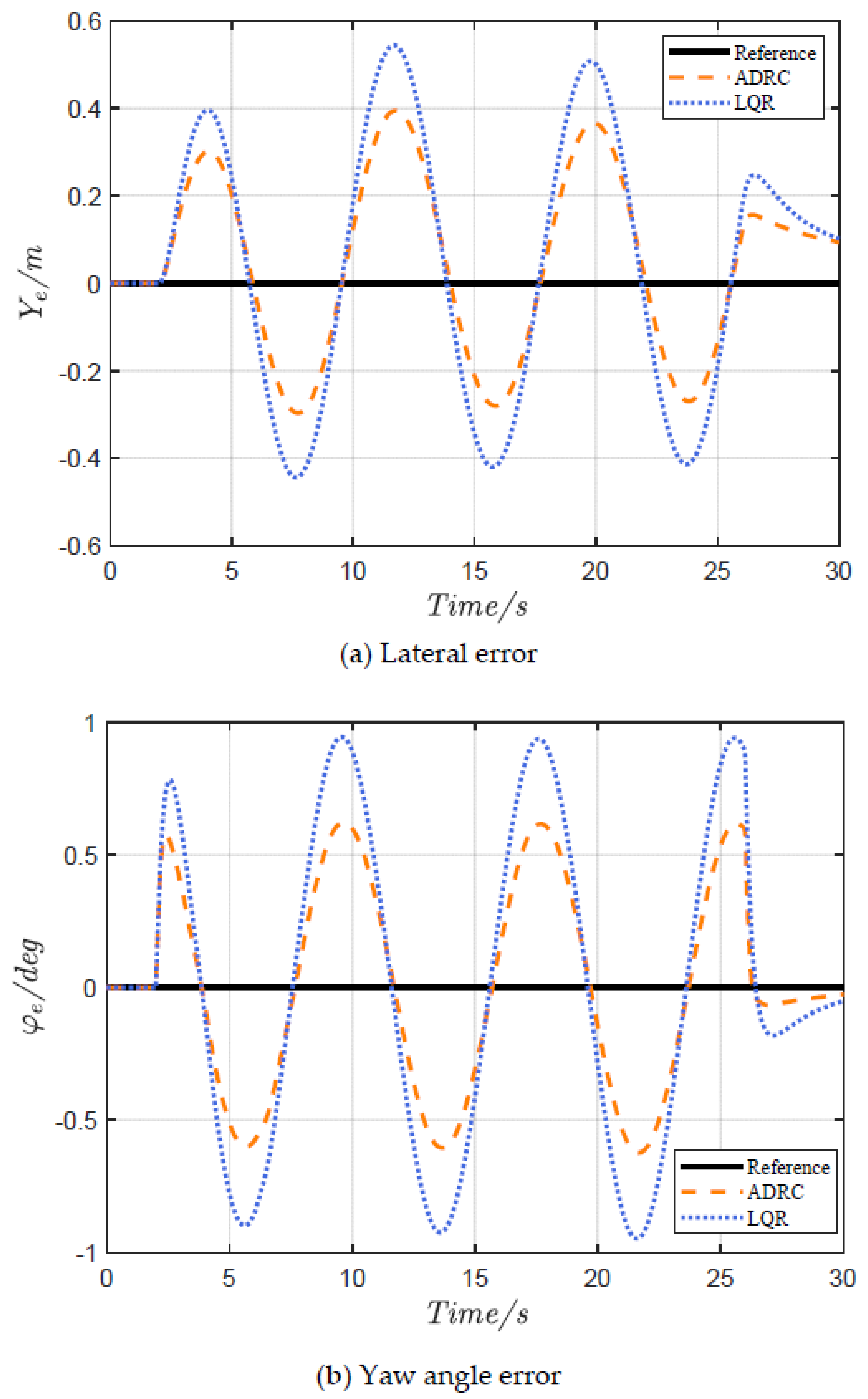
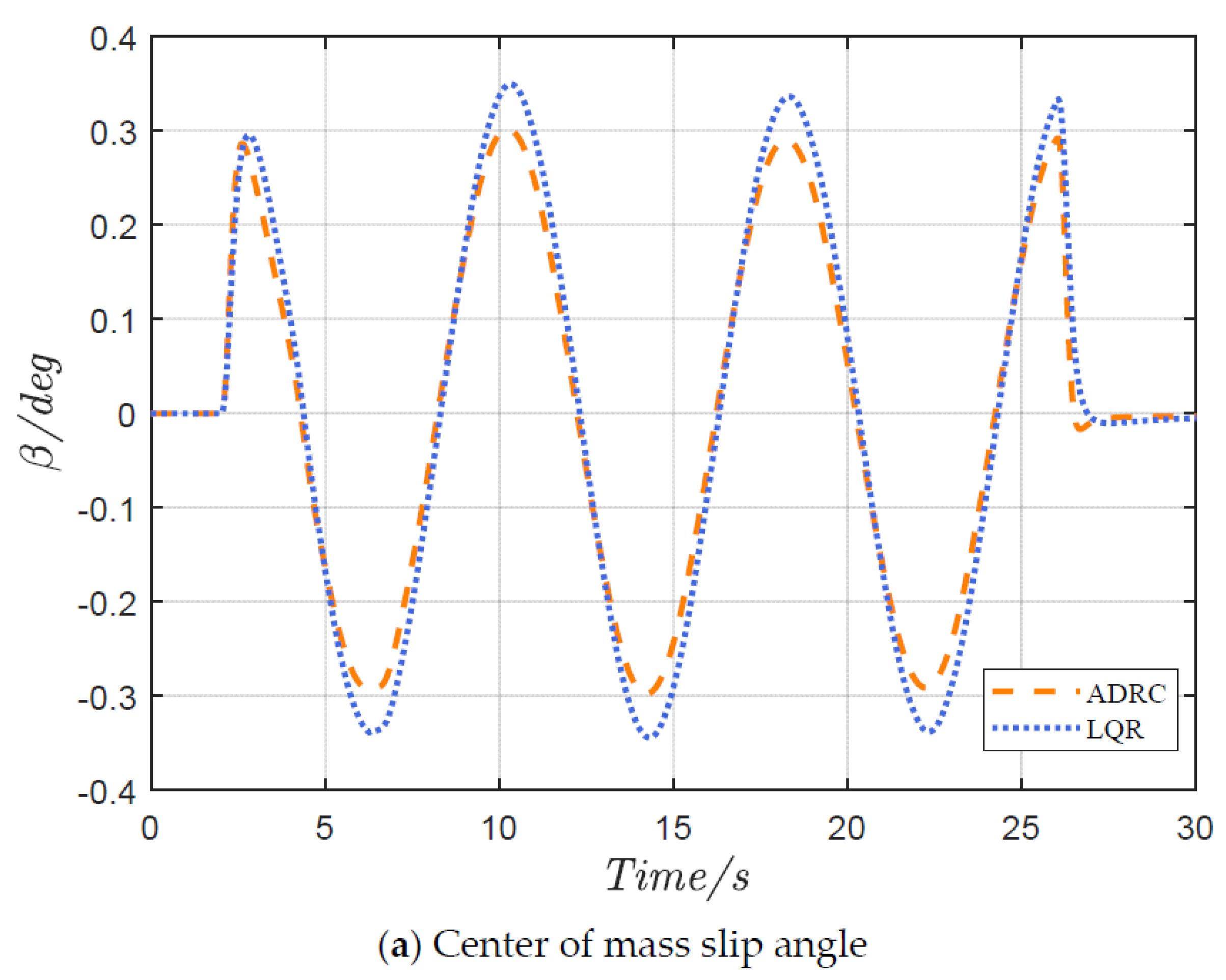
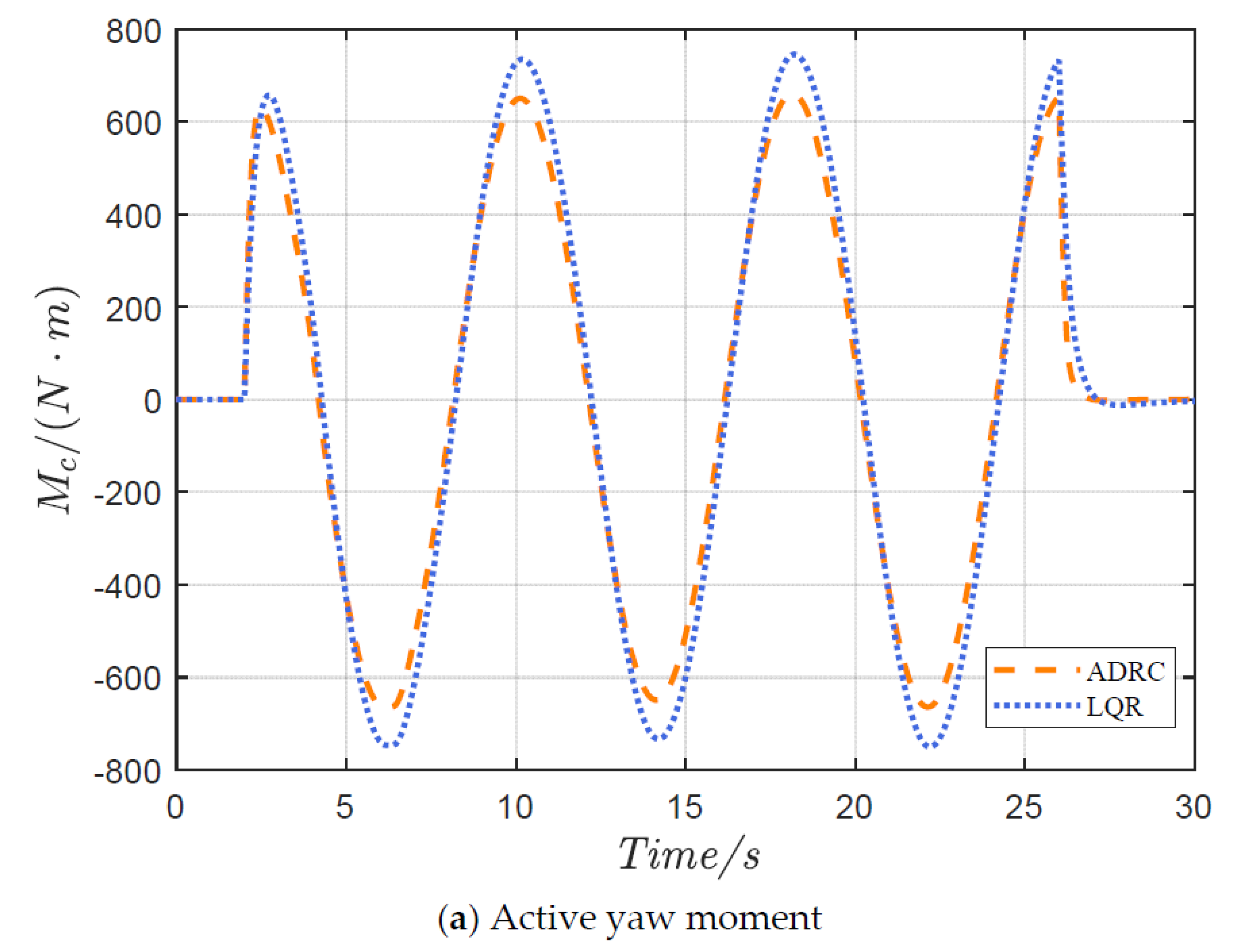
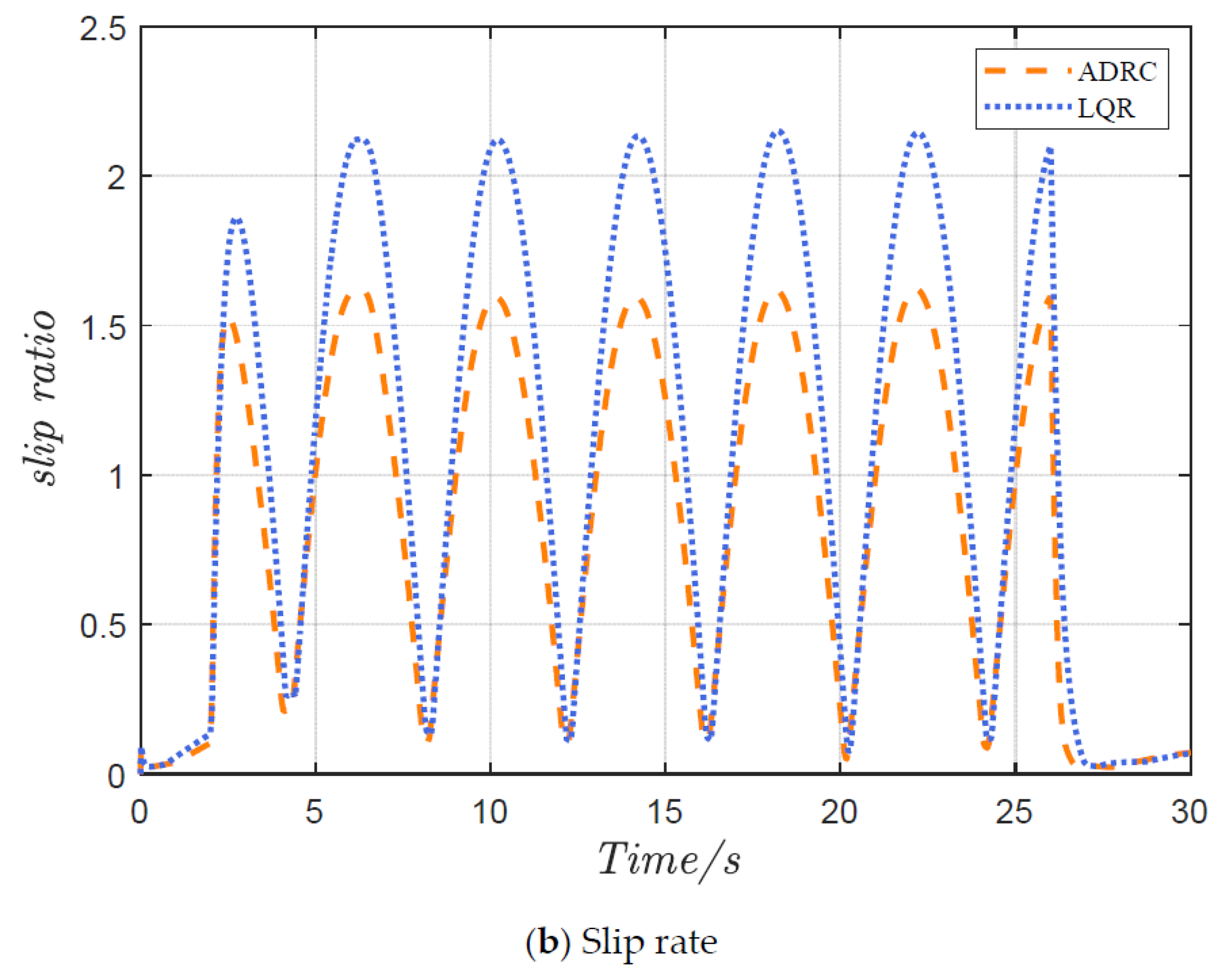
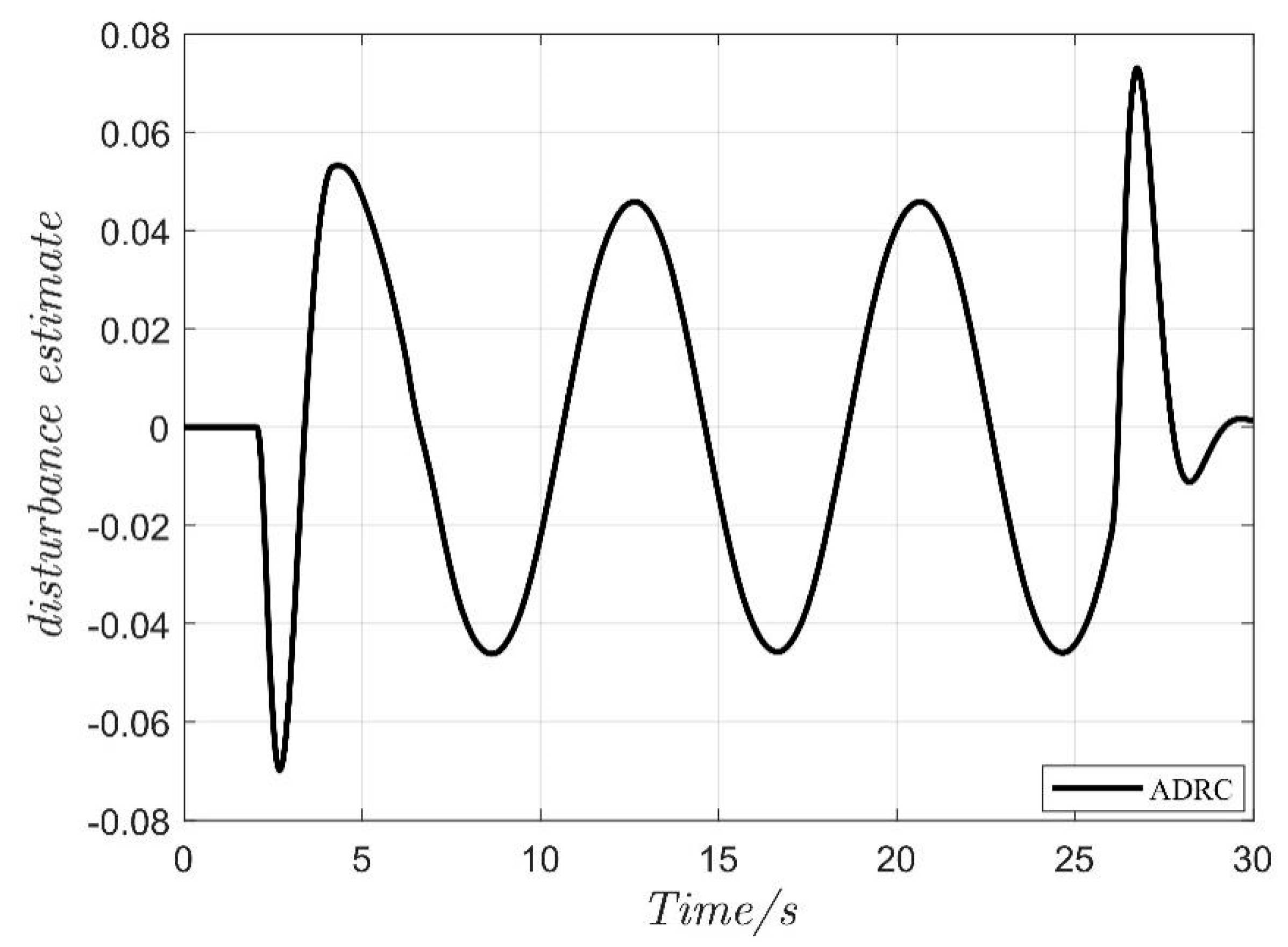
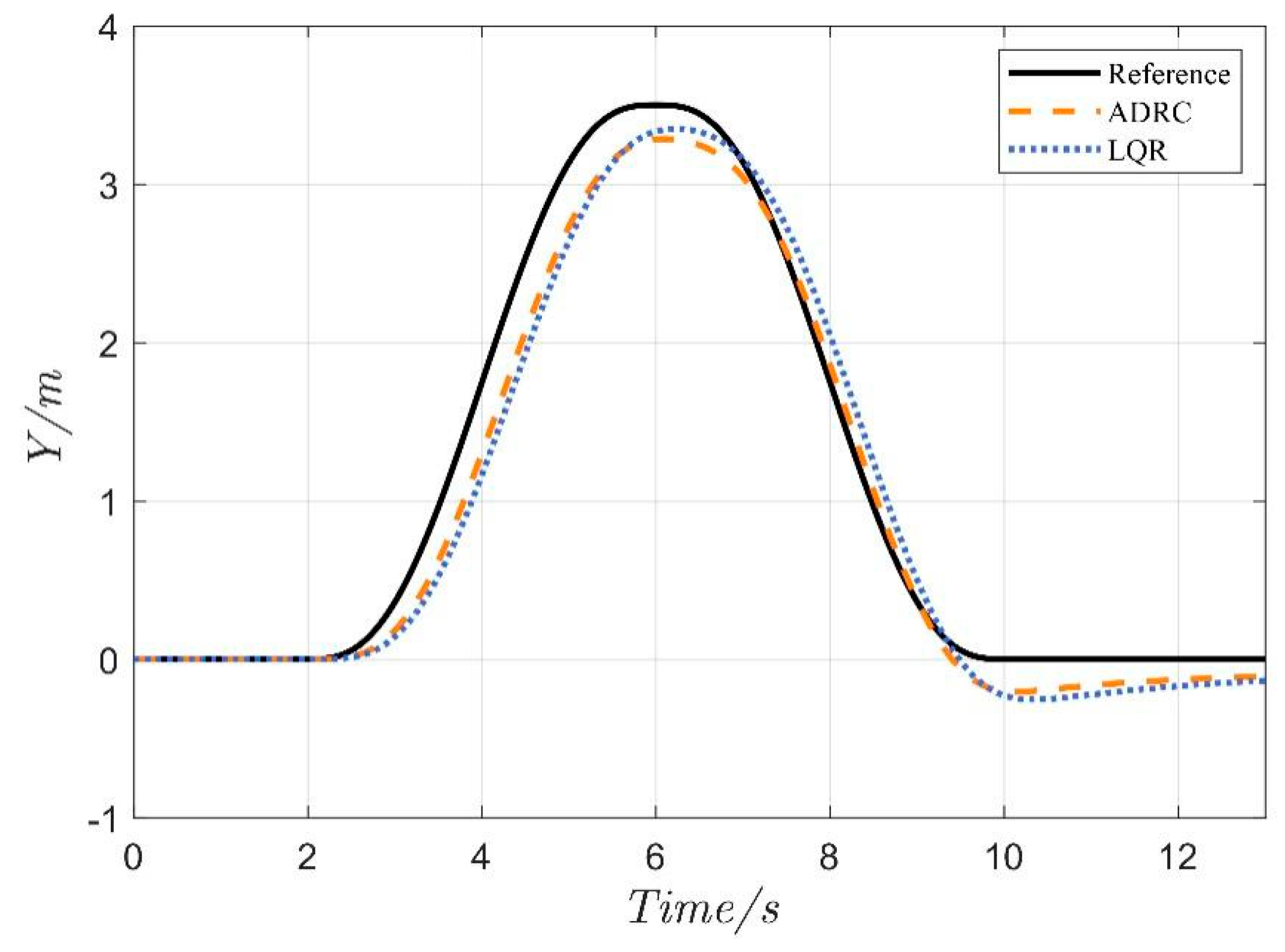
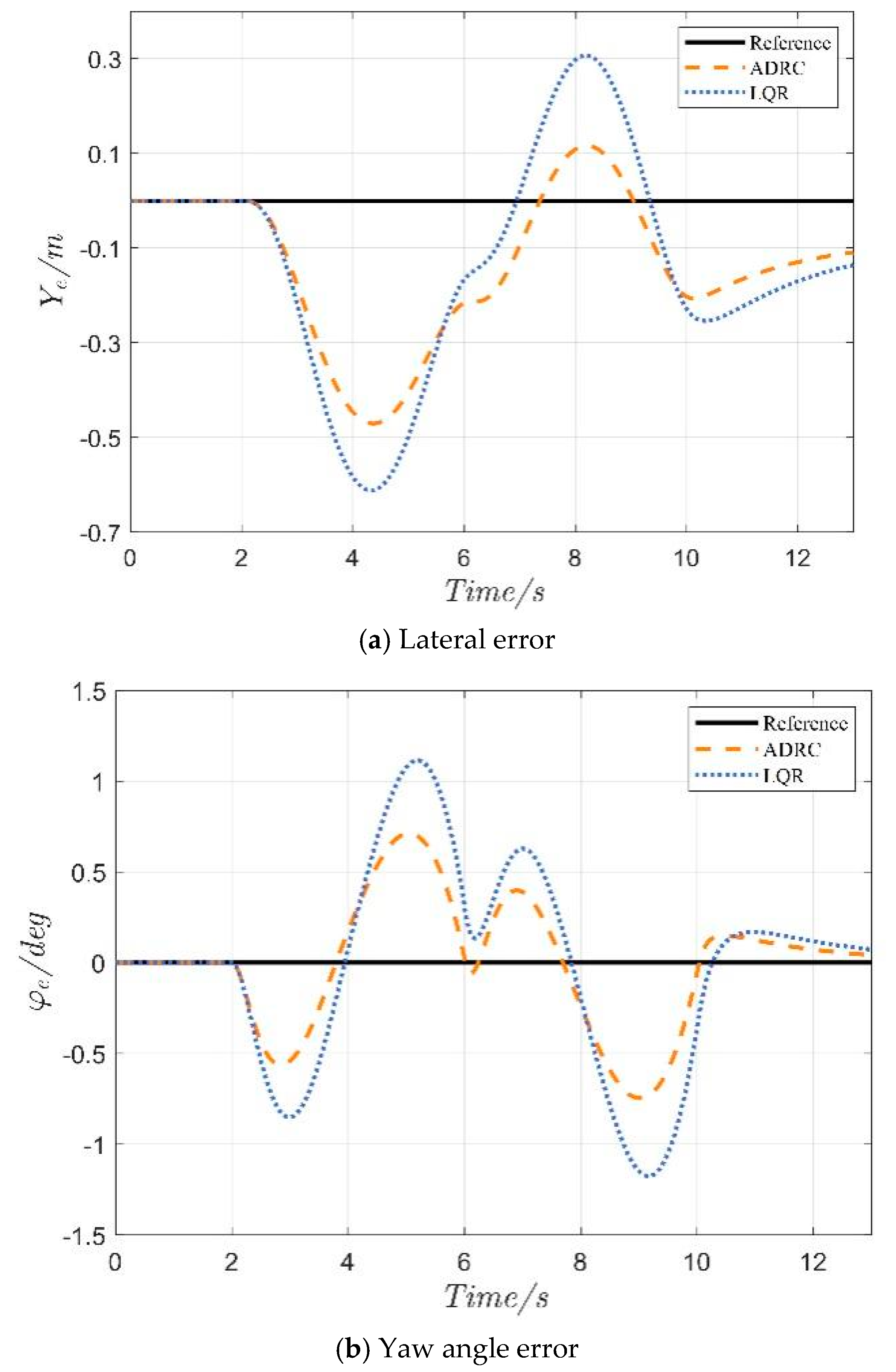
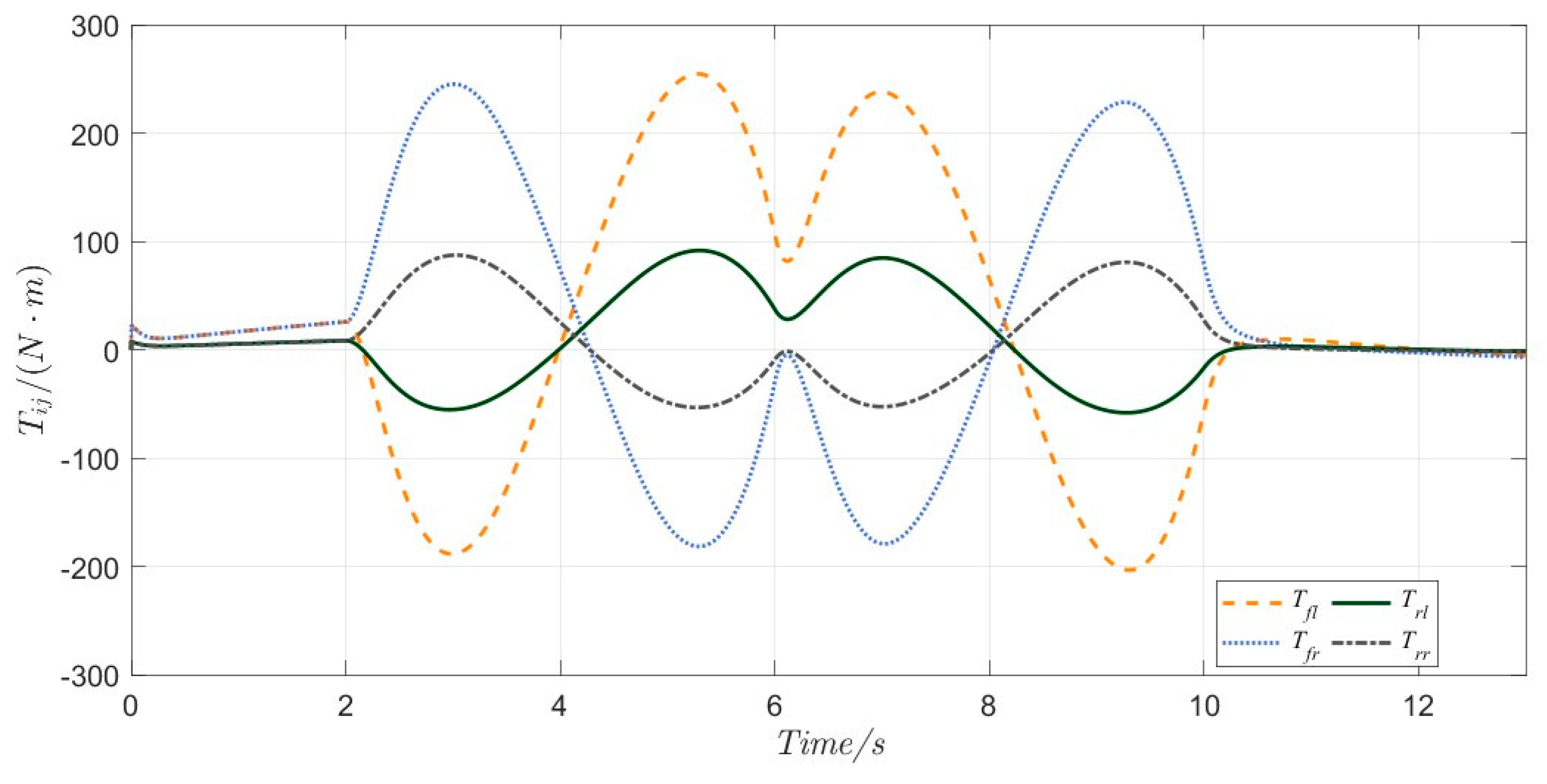
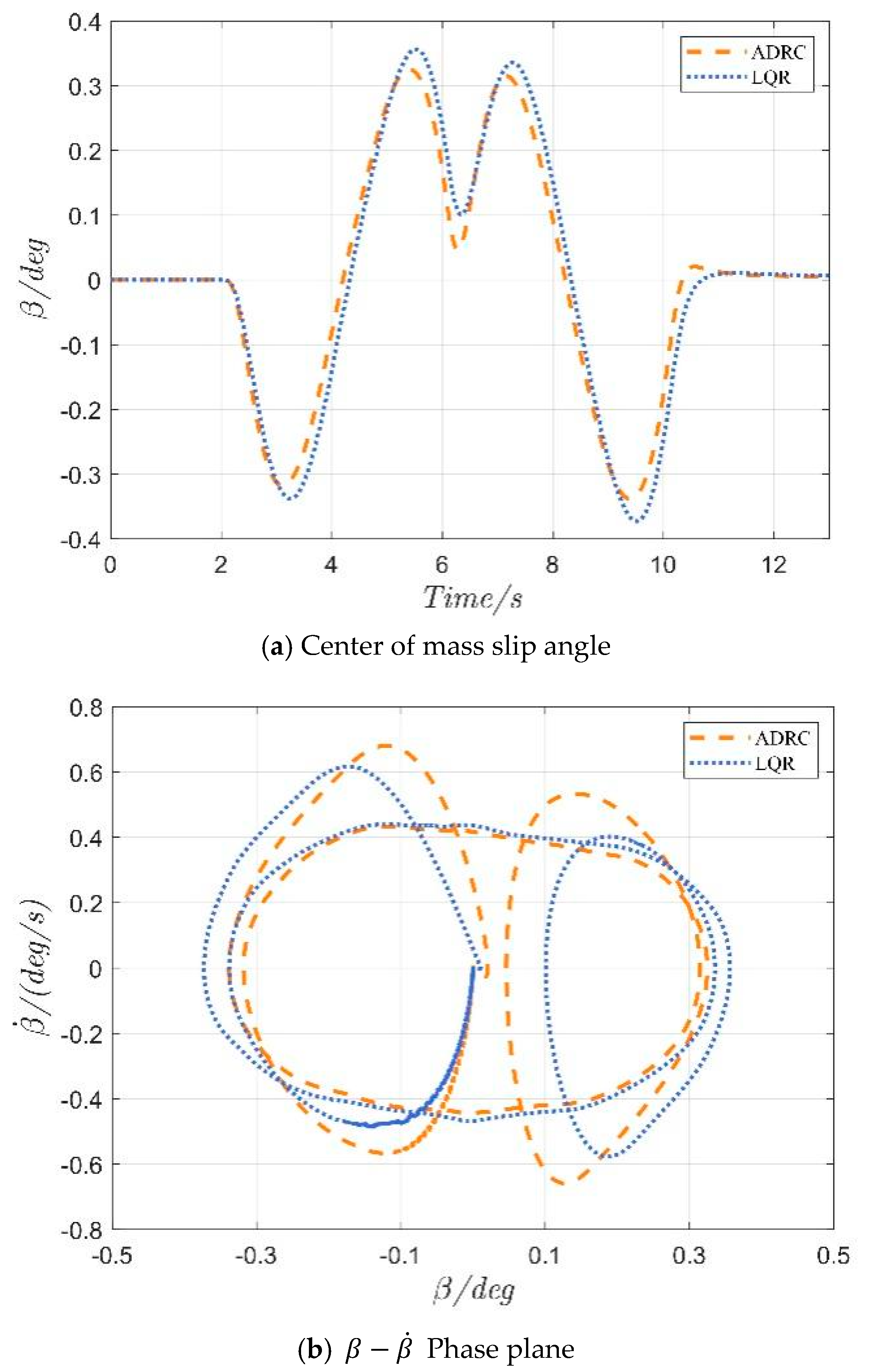
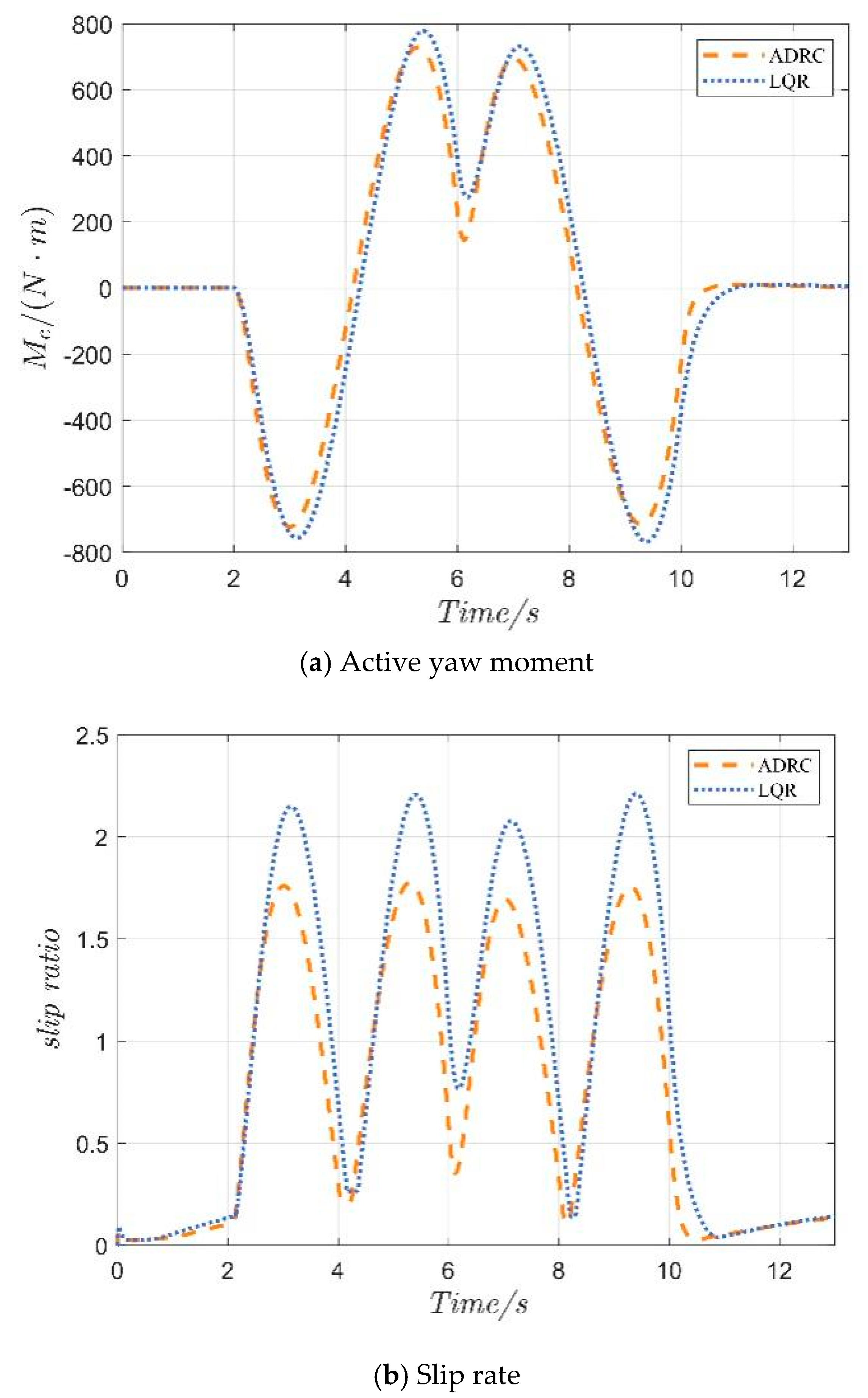
4.1. Serpentine Maneuver
4.2. Double-Lane Change Maneuver
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Deng, H.; Zhao, Y.; Nguyen, A.T.; Huang, C. Fault tolerant predictive control with deep-reinforcement-learning-based torque distribution for four in-wheel motor drive. IEEE/ASME Trans. Mechatron. 2023, 28, 668–680. [Google Scholar] [CrossRef]
- Yassine, A.; Hossain, M.S.; Muhammad, G.; Guizani, M. Double auction mechanisms for dynamic autonomous electric vehicles energy trading. IEEE Trans. Veh. Technol. 2019, 68, 7466–7476. [Google Scholar] [CrossRef]
- Liu, C.; Liu, H.; Han, L.; Wang, W.; Guo, C. Multi-Level Coordinated Yaw Stability Control Based on Sliding Mode Predictive Control for Distributed Drive Electric Vehicles Under Extreme Conditions. IEEE Trans. Veh. Technol. 2023, 72, 280–296. [Google Scholar] [CrossRef]
- Wang, F.; Shen, T.; Zhao, M.; Ren, Y.; Lu, Y.; Feng, B. Lane-Change Trajectory Planning and Control Based on Stability Region for Distributed Drive Electric Vehicle. IEEE Trans. Veh. Technol. 2024, 73, 504–521. [Google Scholar] [CrossRef]
- Barari, A.; Saraygord Afshari, S.; Liang, X. Coordinated control for path-following of an autonomous four in-wheel motor drive electric vehicle. Proc. Inst. Mech. Eng. C J. Mech. Eng. 2022, 236, 6335–6346. [Google Scholar] [CrossRef]
- Gözü, M.; Ozkan, B.; Emirler, M.T. Disturbance observer based active independent front steering control for improving vehicle yaw stability and tire utilization. Int. J. Autom. Technol. 2022, 23, 841–854. [Google Scholar] [CrossRef]
- Fekih, A.; Seelem, S.R. A fault tolerant control design for automatic steering control of ground vehicles. In Proceedings of the 2012 IEEE International Conference on Control Applications, Dubrovnik, Croatia, 3–5 October 2012; pp. 1491–1496. [Google Scholar]
- Huang, C.; Naghdy, F.; Du, H. Delta Operator-Based Fault Estimation and Fault Tolerant Model Predictive Control for Steer-By-Wire Systems. IEEE Trans. Control Syst. Technol. 2018, 26, 1810–1817. [Google Scholar] [CrossRef]
- Huang, C.; Naghdy, F.; Du, H. Observer-Based Fault Tolerant Controller for Uncertain Steer-by-Wire Systems Using the Delta Operator. IEEE/ASME Trans. Mechatron. 2018, 23, 2587–2598. [Google Scholar] [CrossRef]
- Sajjan, A.; Pathak, R.R.; Mathad, S.; Kalligudd, S. Stability Control Using Adaptive Integral SMC Applicable to Variable Speed EV. In Proceedings of the 2024 International Conference on Innovation and Novelty in Engineering and Technology (INNOVA), Vijayapura, India, 20–21 December 2024; pp. 1–6. [Google Scholar]
- Jin, X.; Lv, H.; He, Z.; Li, Z.; Wang, Z.; Ikiela, N.V.O. Design of Active Disturbance Rejection Controller for Trajectory-Following of Autonomous Ground Electric Vehicles. Symmetry 2023, 15, 1786. [Google Scholar] [CrossRef]
- Chen, H.; Tu, Y.; Wang, H.; Shi, K.; He, S. Fault tolerant tracking control based on reinforcement learning with application to a steer-by-wire system. J. Frankl. Inst. 2022, 359, 1152–1171. [Google Scholar] [CrossRef]
- He, S.; Xu, X.; Xie, J.; Wang, F.; Liu, Z.; Zhao, F. Fault detection and fault tolerant control of autonomous steering system for intelligent vehicles combining Bi-LSTM and SPRT. Measurement 2023, 212, 112708. [Google Scholar] [CrossRef]
- Zhao, X.; Zhao, L. Steering angle tracking control of steer-by-wire system with prescribed performance under primary sensor failure. Control Eng. Pract. 2025, 161, 106354. [Google Scholar] [CrossRef]
- Wang, X.; Pan, L.; Tian, Y.; Liu, Y.; Li, L. Adaptive fault tolerant fixed-time sliding mode tracking control for steer-by-wire system with dual-three-phase PMSM. IEEE Trans. Veh. Technol. 2025, 161, 106354. [Google Scholar] [CrossRef]
- Shi, G.; Guo, C.; Wang, S.; Liu, T. Angle tracking and fault tolerant control of steer by-wire system with dual three-phase motor for autonomous vehicle. IEEE Trans. Intell. Transp. Syst. 2024, 25, 5842–5853. [Google Scholar] [CrossRef]
- Jin, X.; Wang, Q.; Yan, Z.; Yang, H.; Yin, G. Integrated robust control of path following and lateral stability for autonomous in-wheel-motor-driven electric vehicles. Proc. Inst. Mech. Eng. D J. Autom. Eng. 2025, 239, 12696–12706. [Google Scholar] [CrossRef]
- Khadraoui, S.; Fareh, R.; Baziyad, M.; Bakr Elbeltagy, M.; Bettayeb, M. A Comprehensive Review and Applications of Active Disturbance Rejection Control for Unmanned Aerial Vehicles. IEEE Access 2024, 12, 185851–185868. [Google Scholar] [CrossRef]
- Lv, H.; Wang, X.; Xie, B.; Shi, B.; Li, Q.; Xu, Y. A Hierarchical Cooperative Control Strategy for In Situ Steering of Distributed Drive Electric Vehicle. IEEE Trans. Transp. Electrif. 2025, 11, 8427–8438. [Google Scholar] [CrossRef]
- Shi, X.; Wang, H.; Chen, L.; Sun, X.; Yang, C.; Cai, Y. Robust Path Tracking Control of Distributed Driving Six-Wheel Steering Commercial Vehicle Based on Coupled Active Disturbance Rejection. IEEE Trans. Veh. Technol. 2023, 72, 13940–13952. [Google Scholar] [CrossRef]
- Tian, Y.; Ma, H.; Ma, L.; Li, S.; Wang, Z.; Wang, X. Path Tracking Control of Commercial Vehicle Emergency Obstacle Avoidance Based on MPC and Active Disturbance Rejection Control. IEEE Trans. Transp. Electrif. 2025, 11, 7162–7170. [Google Scholar] [CrossRef]
- Zou, S.; Zhao, W.; Wang, C.; Liang, W.; Chen, F. Tracking and Synchronization Control Strategy of Vehicle Dual-Motor Steer-by-Wire System via Active Disturbance Rejection Control. IEEE/ASME Trans. Mechatron. 2023, 28, 92–103. [Google Scholar] [CrossRef]
- Cao, Y.; Yang, W.; Wang, S.; He, S.; Liu, Z.; Xie, L. Improved Trajectory Tracking Control for a Continuum Robot Using Error-Driven ADRC With Input Mapping Method. IEEE Trans. Ind. Electron. 2024, 71, 12696–12706. [Google Scholar] [CrossRef]
- Zhang, J.; Cui, C.; Gu, S.; Wang, T.; Zhao, L. Trajectory Tracking Control of Pneumatic Servo System: A Variable Gain ADRC Approach. IEEE Trans. Cybern. 2023, 53, 6977–6986. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, J.; Nie, B.; Liu, Y.; He, X. Adaptive control of PMSM servo system for Steering-by-Wire system with disturbances observation. IEEE Trans. Transport. Electrif. 2022, 8, 2015–2028. [Google Scholar] [CrossRef]
- Han, Z.; Xu, N.; Chen, H.; Huang, Y.; Zhao, B. Energy-efficient control of electric vehicles based on linear quadratic regulator and phase plane analysis. Appl. Energy 2018, 213, 639–657. [Google Scholar] [CrossRef]
- Qin, L.; Hu, J.; Li, H.; Chen, W. Fuzzy logic controllers for specialty vehicles using a combination of phase plane analysis and variable universe approach. IEEE Access 2017, 5, 1579–1588. [Google Scholar] [CrossRef]
- Yu, Z.; Hou, Y.; Leng, B.; Xiong, L.; Li, Y. Disturbance compensation and torque coordinated control of four In-Wheel motor Independent-Drive electric vehicles. IEEE Access 2020, 8, 119758–119767. [Google Scholar] [CrossRef]
- Seiffer, A.; Frey, M.; Gauterin, F. Control allocation approach using differential steering to compensate for steering actuator failure. IEEE Open J. Intell. Transp. Syst. 2024, 5, 756–773. [Google Scholar] [CrossRef]
- Wang, R.; Yu, X.; Sun, Q.; Li, D.; Gui, Y.; Wang, P. The Integrated Reference Region Analysis for Parallel DFIGs’ Interfacing Inductors. IEEE Trans. Power Electron. 2024, 39, 7632–7642. [Google Scholar] [CrossRef]






| Parameter | Numeric | Unit | Parameter | Numeric | Unit |
|---|---|---|---|---|---|
| vx | 72 | Km/h | u | 0.75 | - |
| m | 1270 | Kg | Iz | 1537 | kg·m2 |
| r | 0.325 | m | lf | 1.015 | m |
| Naf | 130,034 | N/rad | Nar | 70,038 | N/rad |
| g | 9.81 | M/s2 | tw | 1.605 | m |
| Jm | 0.002129 | Kg·m2 | Bm | 0.038 | N·s/rad |
| Serpentine Maneuver | Double-Lane Change Maneuver | ||||||
|---|---|---|---|---|---|---|---|
| Parameter | Index | ADRC | LQR | PA1 | ADRC | LQR | PA1 |
| MAE | 0.177 | 0.251 | 29.42% | 0.156 | 0.203 | 22.84% | |
| ye(m) | RMSE | 0.208 | 0.295 | 29.39% | 0.207 | 0.265 | 21.95% |
| MSE | 0.043 | 0.087 | 50.15% | 0.043 | 0.070 | 39.09% | |
| MAE | 0.320 | 0.488 | 34.44% | 0.262 | 0.409 | 36.03% | |
| φe(deg) | RMSE | 0.390 | 0.588 | 33.77% | 0.356 | 0.556 | 35.94% |
| MSE | 0.152 | 0.346 | 56.14% | 0.127 | 0.309 | 58.96% | |
| MAE | 0.150 | 0.173 | 13.06% | 0.129 | 0.142 | 9.24% | |
| β(deg) | RMSE | 0.185 | 0.212 | 12.76% | 0.179 | 0.195 | 8.21% |
| MSE | 0.034 | 0.045 | 23.89% | 0.032 | 0.038 | 15.75% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, X.; Lv, H.; Tao, Y.; Lu, J.; Lv, J.; Opinat Ikiela, N.V. Active Fault Tolerant Trajectory-Tracking Control of Autonomous Distributed-Drive Electric Vehicles Considering Steer-by-Wire Failure. Symmetry 2025, 17, 1471. https://doi.org/10.3390/sym17091471
Jin X, Lv H, Tao Y, Lu J, Lv J, Opinat Ikiela NV. Active Fault Tolerant Trajectory-Tracking Control of Autonomous Distributed-Drive Electric Vehicles Considering Steer-by-Wire Failure. Symmetry. 2025; 17(9):1471. https://doi.org/10.3390/sym17091471
Chicago/Turabian StyleJin, Xianjian, Huaizhen Lv, Yinchen Tao, Jianning Lu, Jianbo Lv, and Nonsly Valerienne Opinat Ikiela. 2025. "Active Fault Tolerant Trajectory-Tracking Control of Autonomous Distributed-Drive Electric Vehicles Considering Steer-by-Wire Failure" Symmetry 17, no. 9: 1471. https://doi.org/10.3390/sym17091471
APA StyleJin, X., Lv, H., Tao, Y., Lu, J., Lv, J., & Opinat Ikiela, N. V. (2025). Active Fault Tolerant Trajectory-Tracking Control of Autonomous Distributed-Drive Electric Vehicles Considering Steer-by-Wire Failure. Symmetry, 17(9), 1471. https://doi.org/10.3390/sym17091471







