Characteristic Model-Based Discrete Adaptive Integral SMC for Robotic Joint Drive on Dual-Core ARM
Abstract
1. Introduction
- Real-Time Second-Order Characteristic Modeling
- 2.
- Hybrid Sliding-Mode Control Architecture
- 3.
- Co-Designed Miniaturized Drive Module
2. Problem Formulation
3. Characteristic Modeling and Controller Design
3.1. Characteristic Modeling
- The system is strictly SISO.
- The power of control input is 1.
- The nonlinear function satisfies when all its arguments are zero.
- is continuously differentiable with respect to all arguments, and its partial derivatives are uniformly bounded.
- The inequality holds for a positive constant , where denotes the sampling interval.
- Both and all arguments of remain bounded—a condition readily satisfiable in practical engineering scenarios.
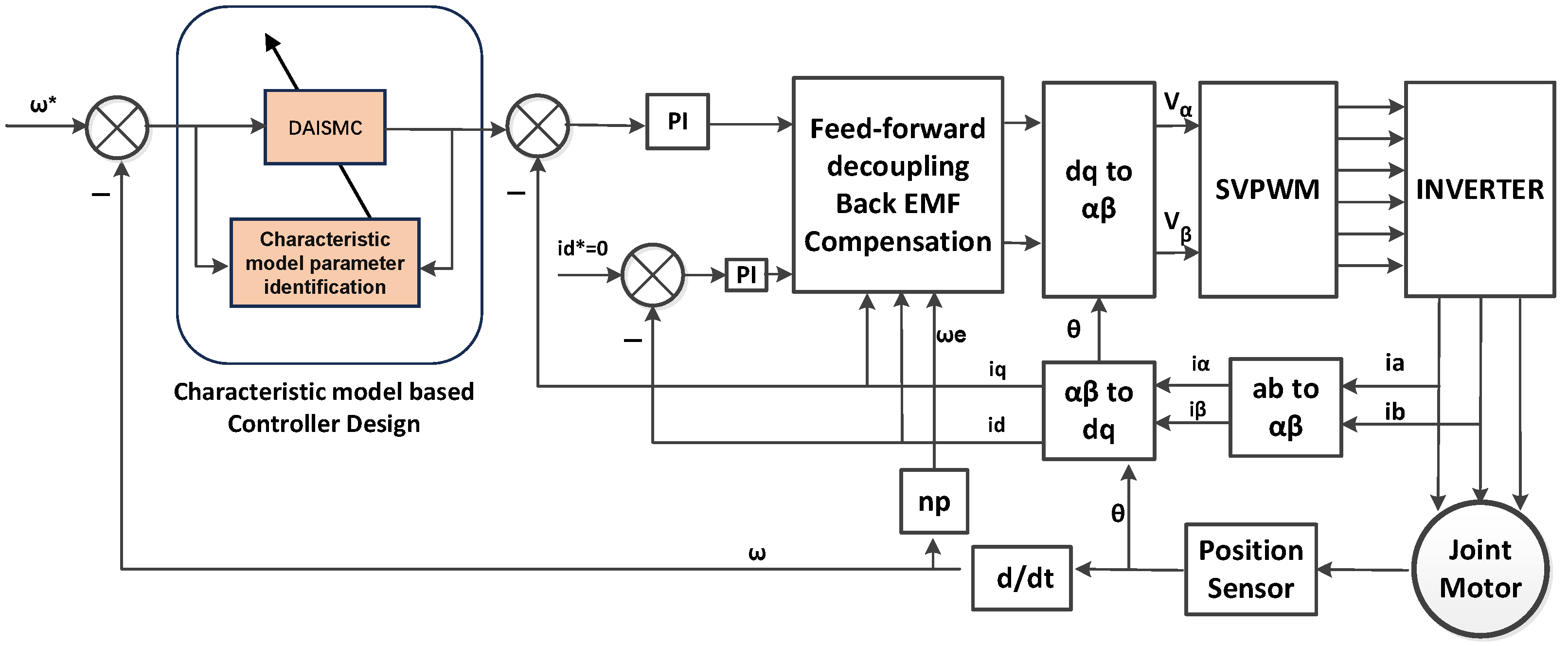
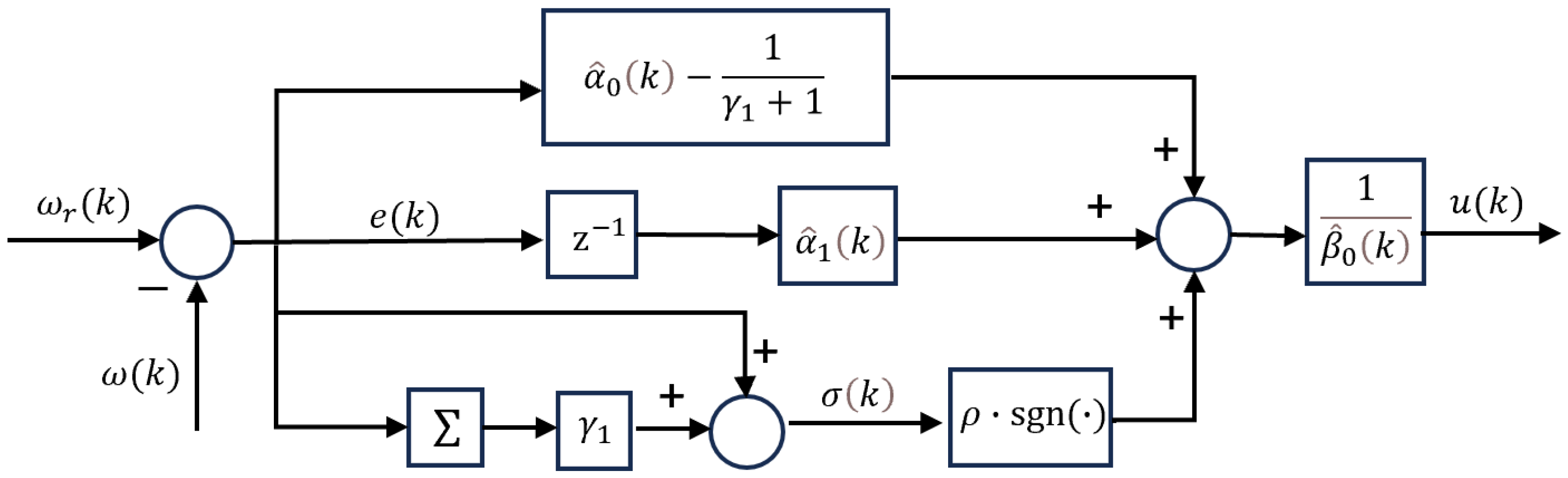
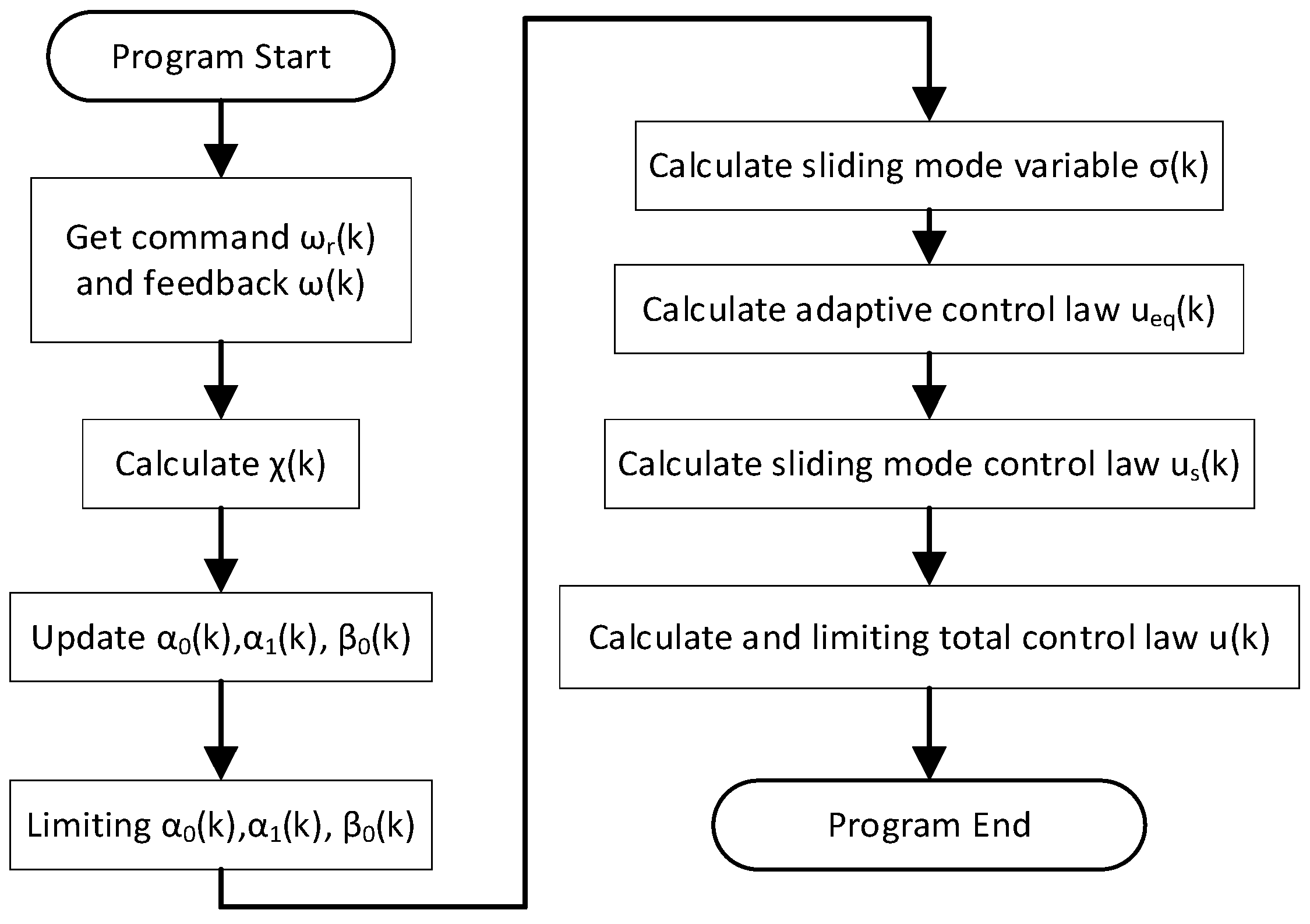
3.2. Controller Design
3.3. Stability Analysis
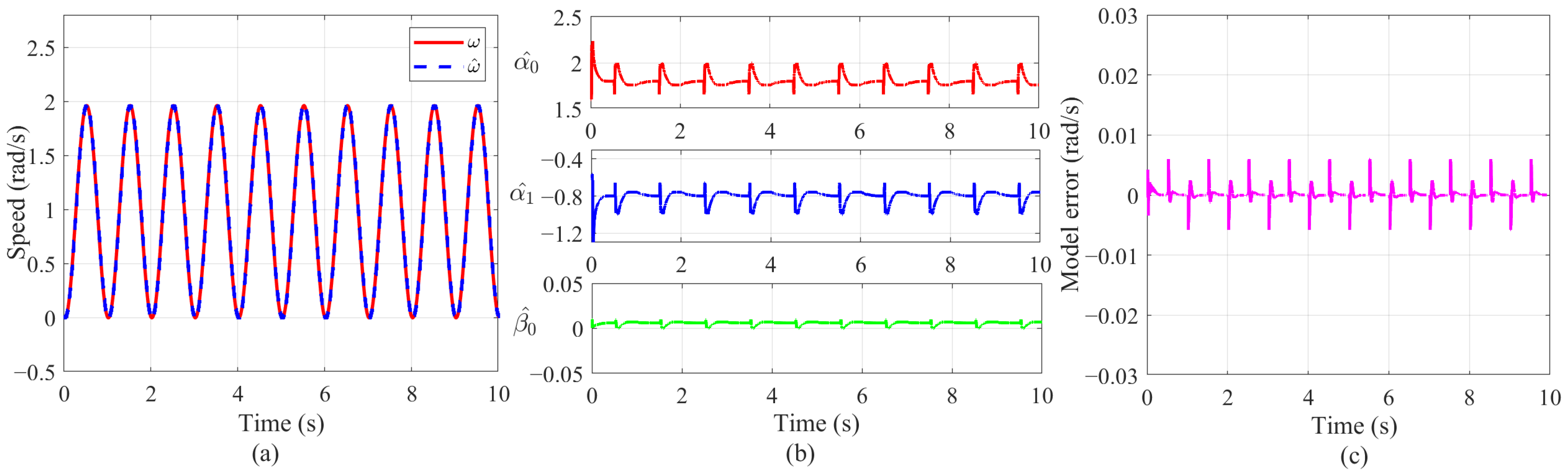
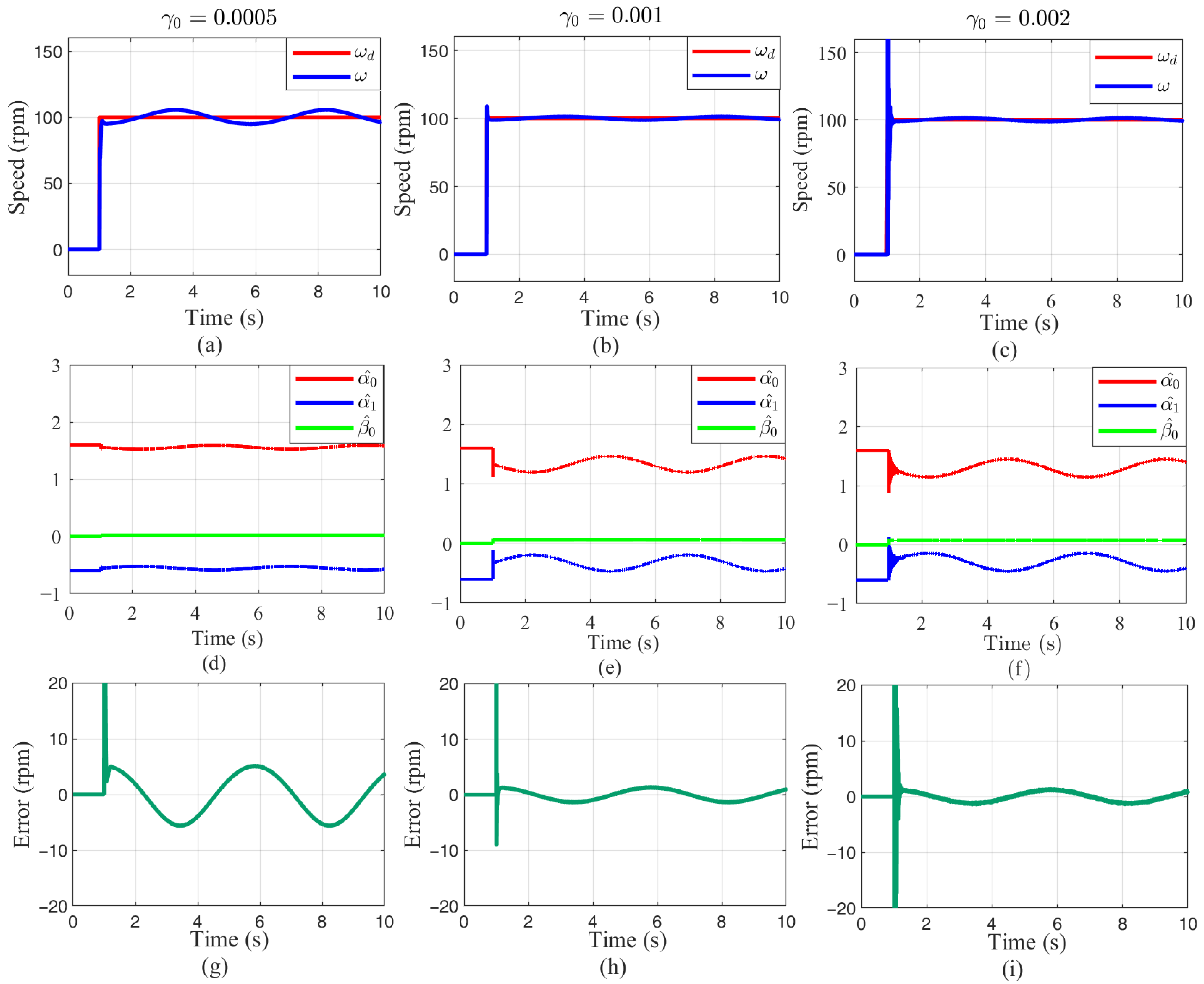
3.4. Numerical Simulation
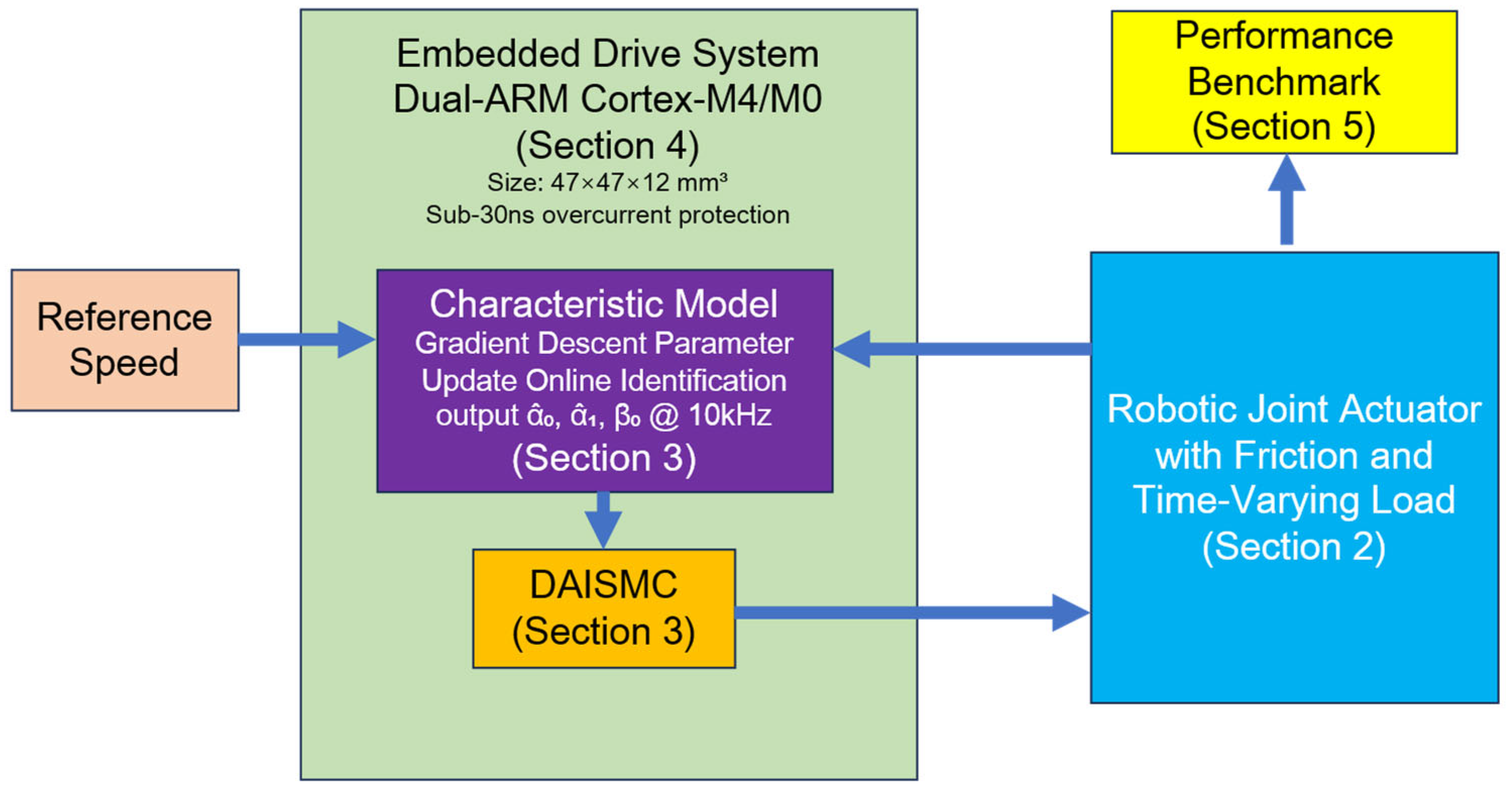
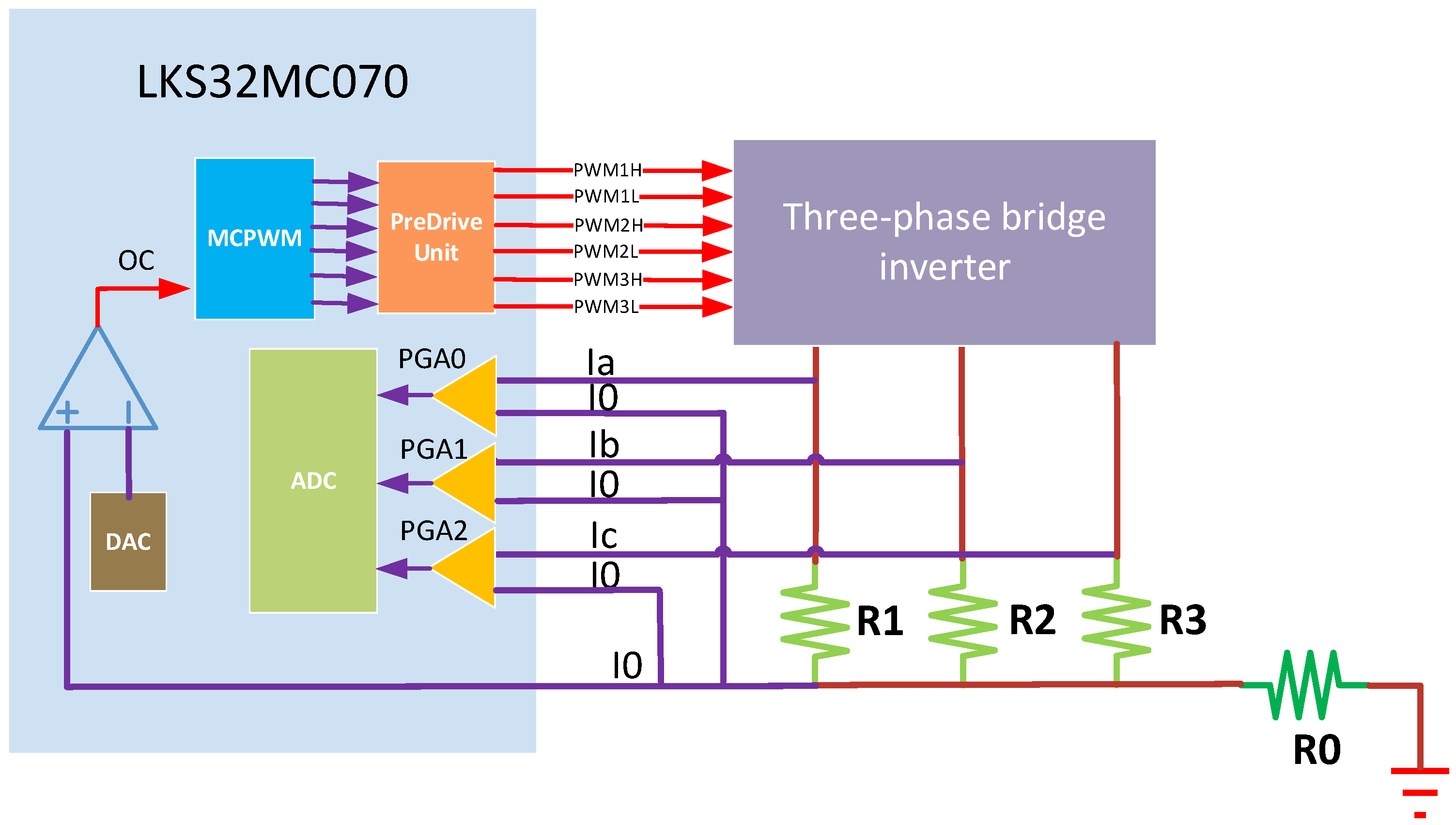
4. Implementation of the Joint Motor Drive System
4.1. Power Supply Design
4.2. Communication and Speed Control Module Design
4.3. FOC and Protection Module Design
4.4. Hardware Implementation
4.5. Software Implementation
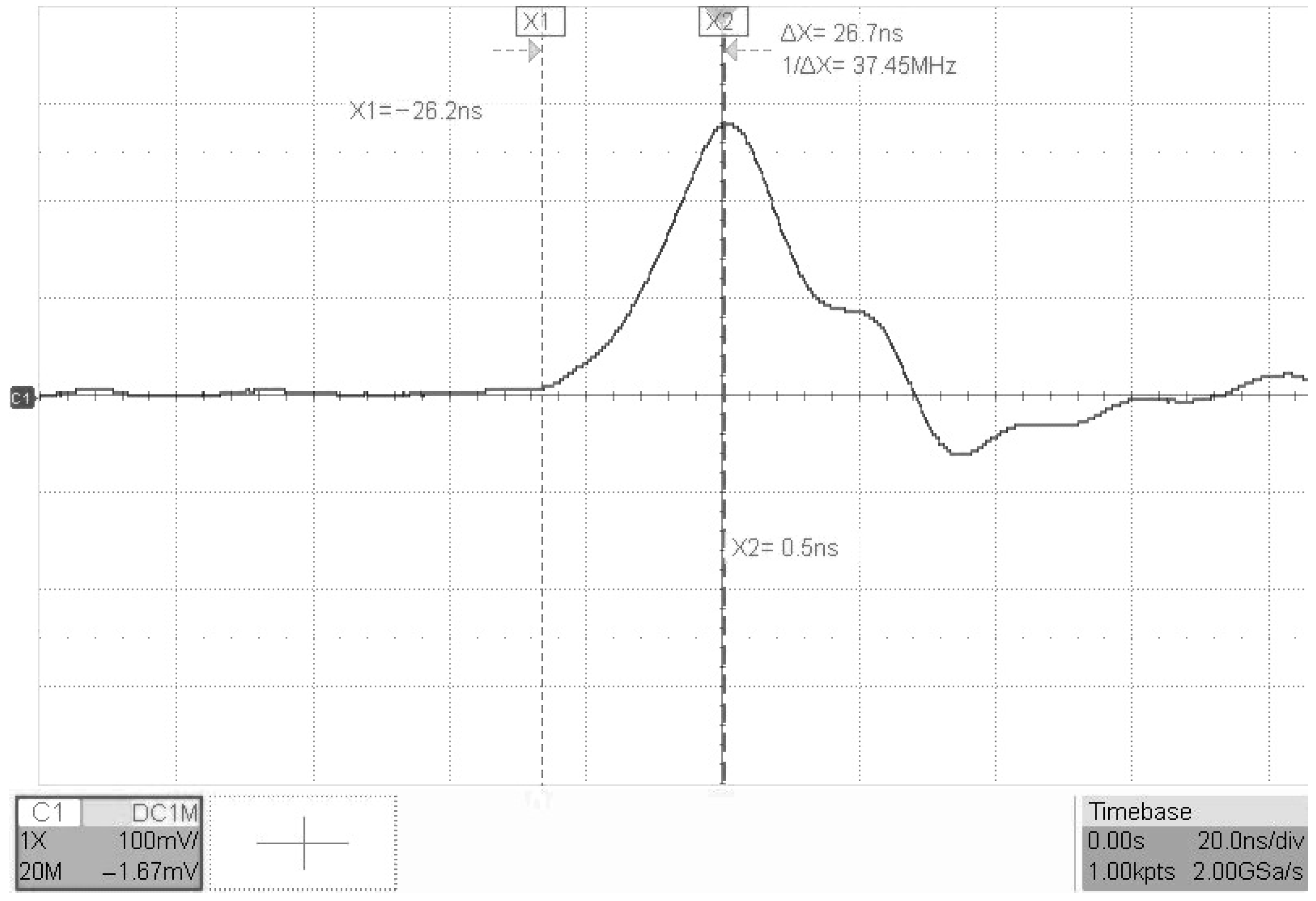
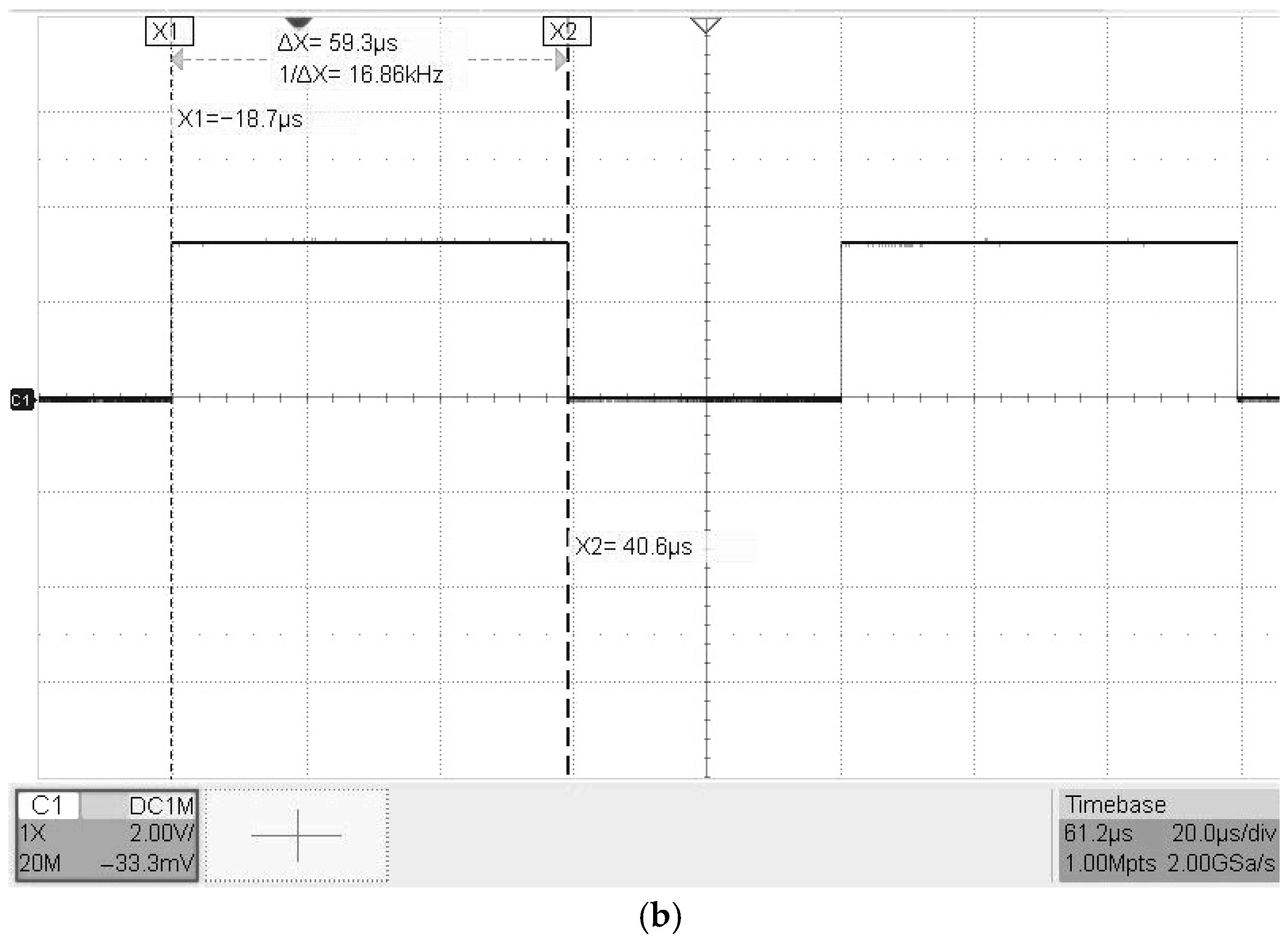
5. Experimental Validation
5.1. Experimental Setup
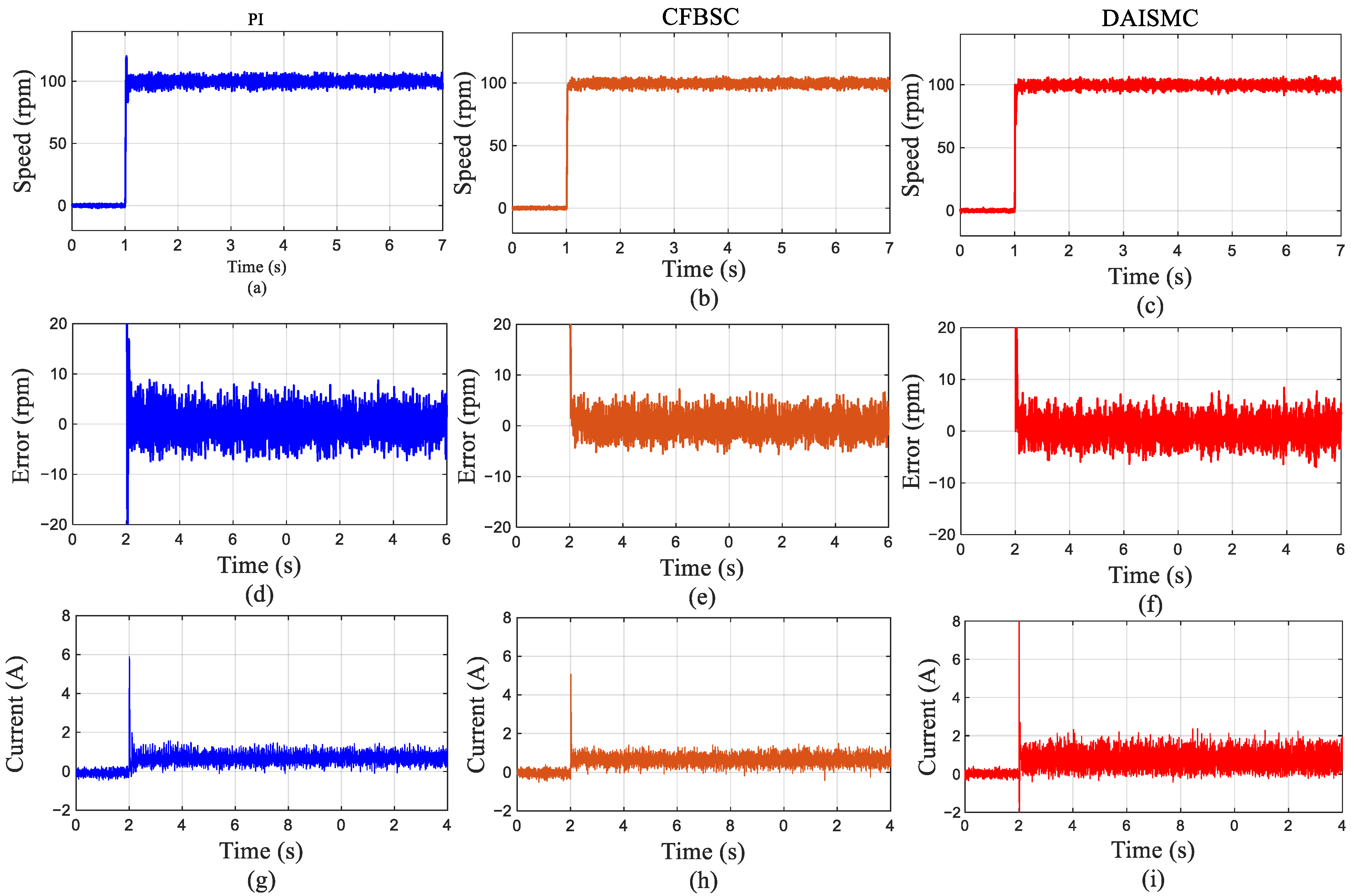
5.2. Control Methods for Comparison
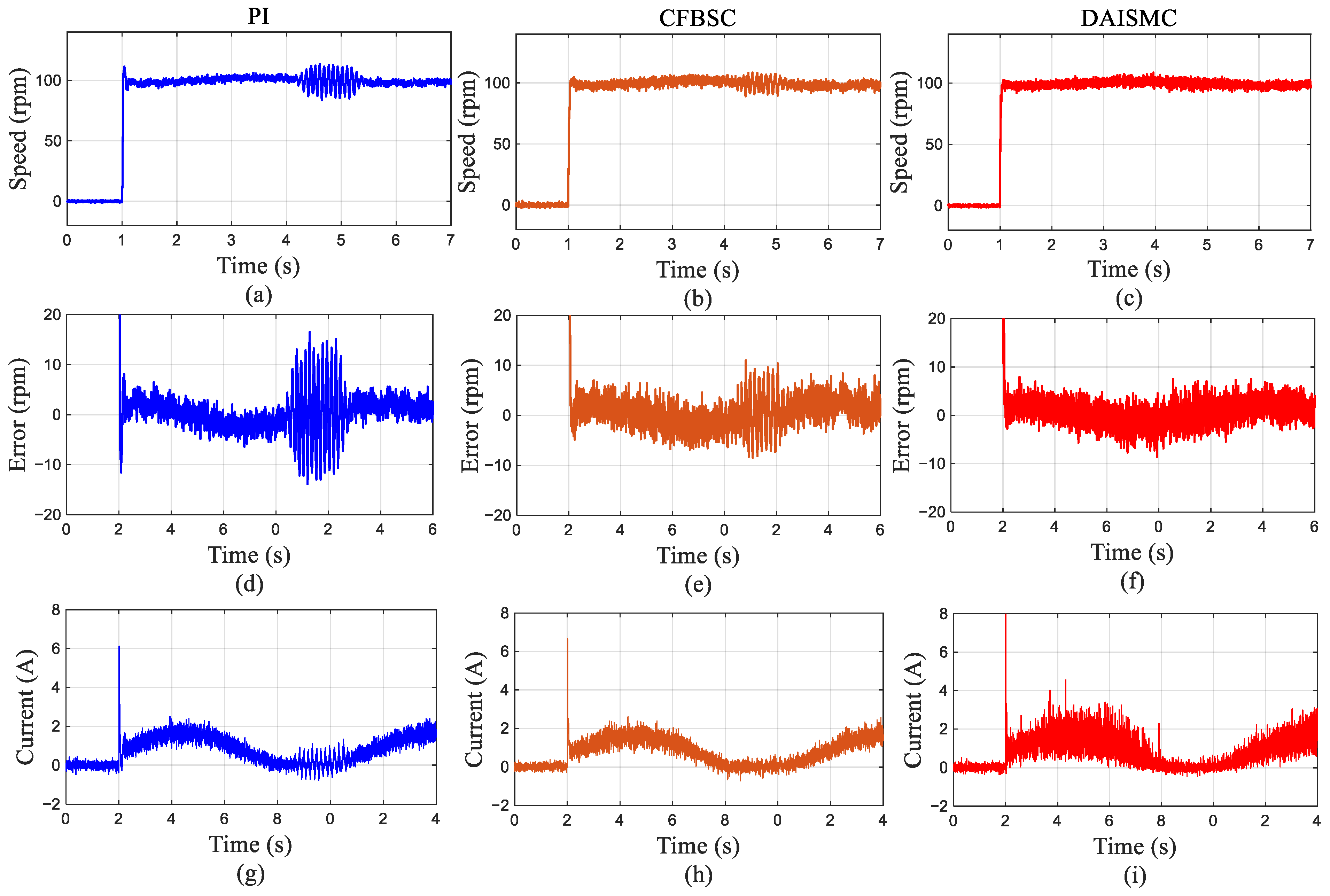
5.3. Experimental Results and Discussion
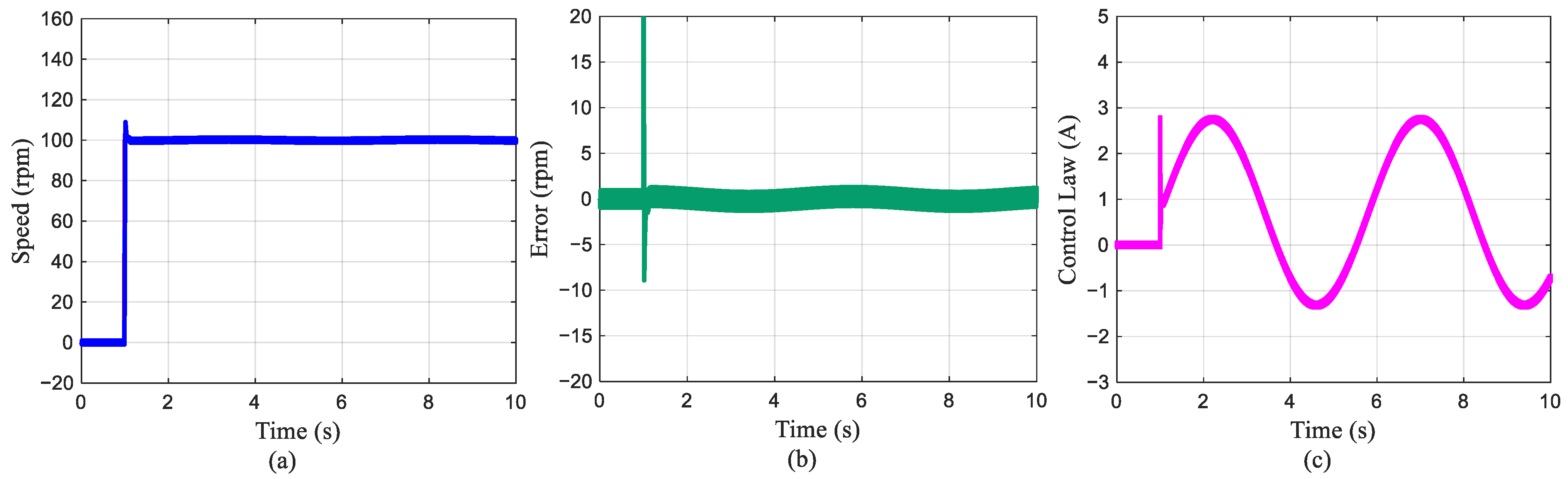
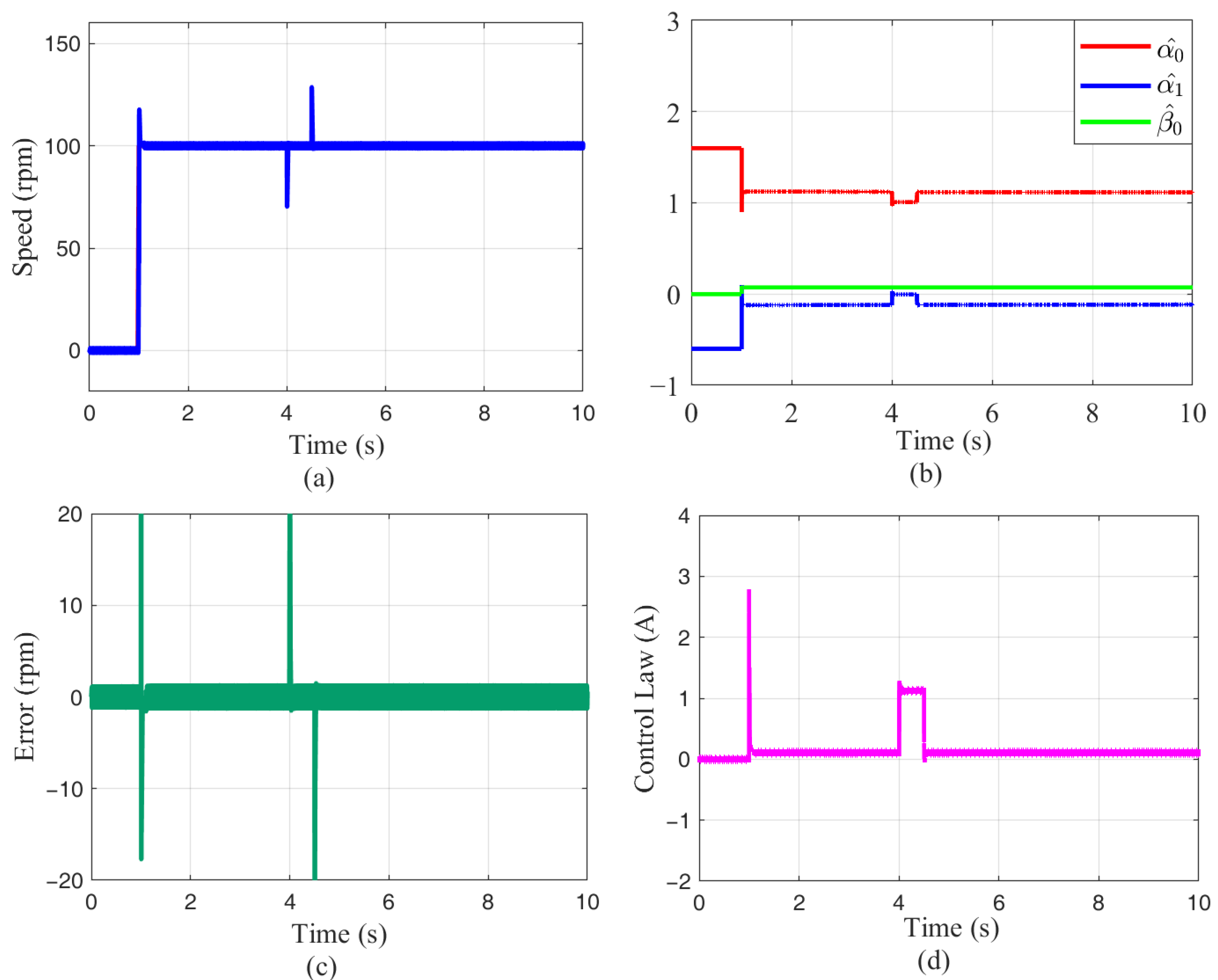
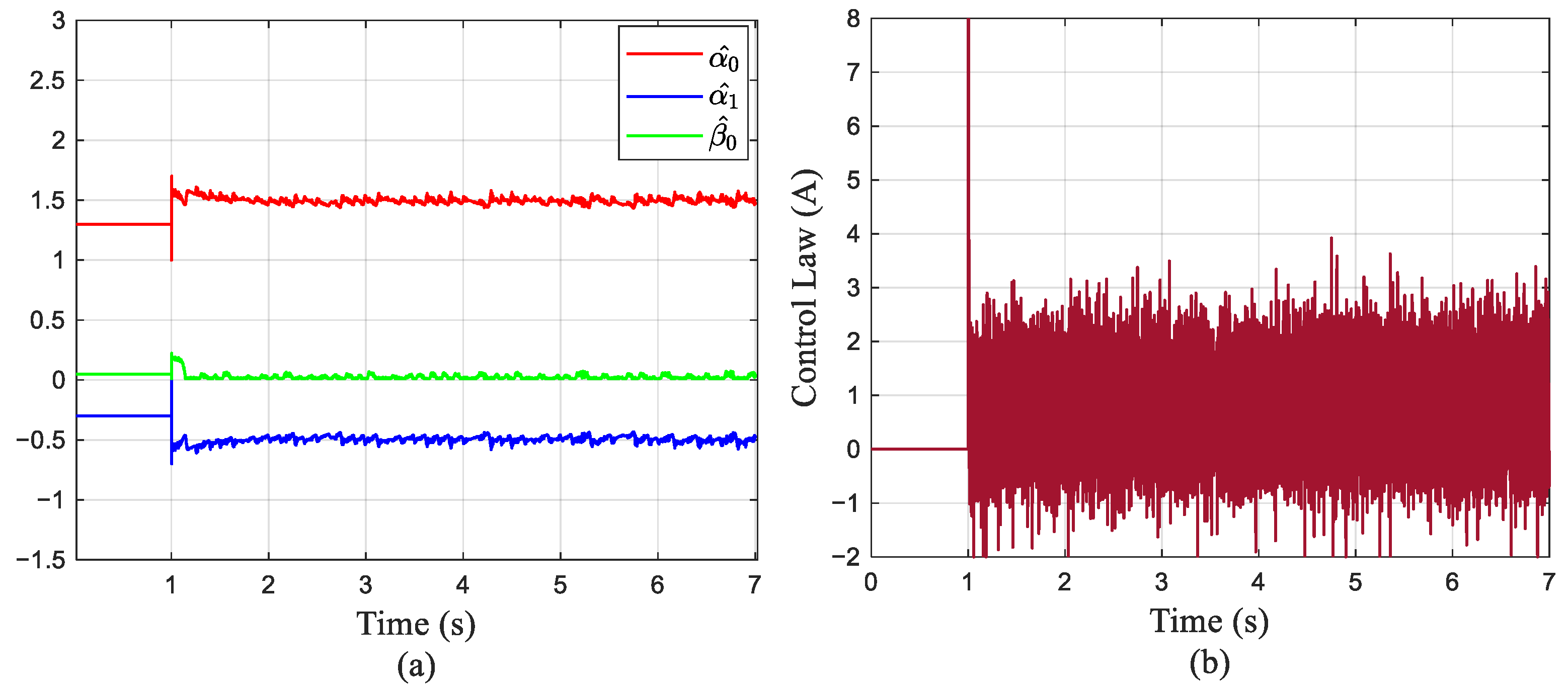
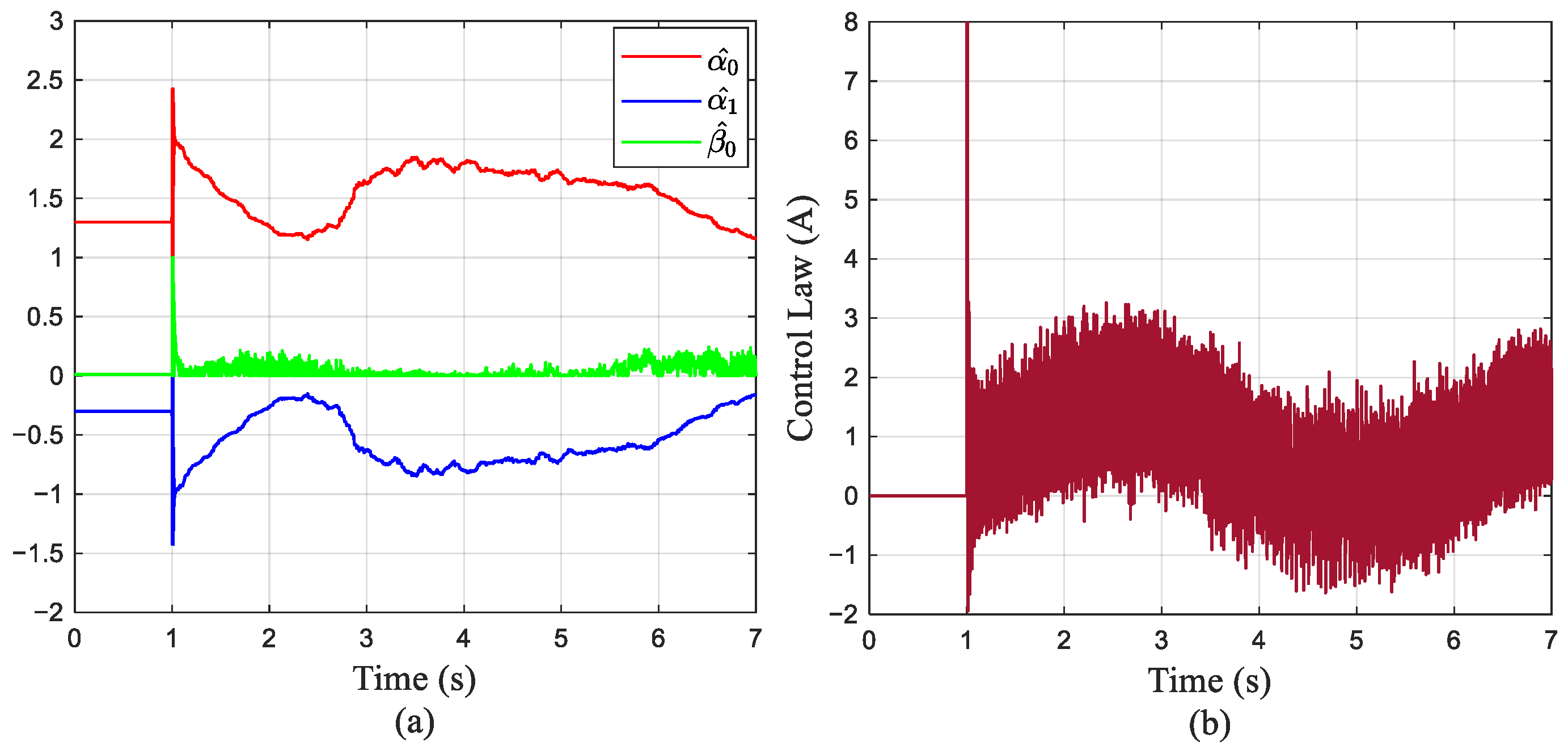
5.3.1. Step Response Analysis Under No-Load Conditions
5.3.2. Step Response Analysis Under Loaded Conditions
6. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, Q.N.; Zhang, F.F.; Mai, Q. Robot adoption and labor demand: A new interpretation from external competition. Technol. Soc. 2023, 74, 102310. [Google Scholar] [CrossRef]
- Xie, D.B.; Chen, L.; Liu, L.C. Actuators and Sensors for Application in Agricultural Robots: A Review. Machines 2022, 10, 913. [Google Scholar] [CrossRef]
- Tsuji, H.; Shii, M.; Yokoyama, S.; Takamido, Y. Reusable robot system for display and disposal tasks at convenience stores based on a SysML model and RT Middleware. Adv. Robot. 2020, 34, 250–264. [Google Scholar] [CrossRef]
- Zong, H.Z.; Ai, J.K.; Fang, L.Z.; Luo, Y.C.; Zhang, J.H.; Xu, B. A novel hydraulic swing actuator with high torque density for legged robots. Smart Mater. Struct. 2025, 34, 015034. [Google Scholar] [CrossRef]
- Veronneau, C.; Denis, J.; Lhommeau, P.; St-Jean, A.; Girard, A.; Plante, J.S.; Bigué, J.P.L. Modular Magnetorheological Actuator with High Torque Density and Transparency for the Collaborative Robot Industry. IEEE Robot. Autom. Lett. 2023, 8, 896–903. [Google Scholar] [CrossRef]
- Li, J.Q.; Cong, D.C.; Yang, Y.; Yang, Z.D. A hydraulic actuator for joint robots with higher torque to weight ratio. Robotica 2023, 41, 756–774. [Google Scholar] [CrossRef]
- Huang, Z.P.; Li, X.J.; Guan, X.K.; Sun, X.Q.; Wang, C.X.; Xu, Y.P.; Yu, B.; Kong, X.D. Biomimetic Lightweight Design of Legged Robot Hydraulic Drive Unit Shell Inspired by Geometric Shape of Fish Bone Rib Structure. J. Bionic Eng. 2024, 21, 1238–1252. [Google Scholar] [CrossRef]
- Gu, C.C.; Liu, S.Y.; Bao, W.J.; Meng, D.Y.; Yang, S.M. End-Effector Trajectory Tracking Control of Stacking Robot Based on LuGre Model. IEEE/ASME Trans. Mechatron. 2025, 1–12. [Google Scholar] [CrossRef]
- Ba, K.X.; Yu, B.; Liu, Y.L.; Jin, Z.G.; Gao, Z.J.; Zhang, J.X.; Kong, X.D. Fuzzy Terminal Sliding Mode Control with Compound Reaching Law and Time Delay Estimation for HDU of Legged Robot. Complexity 2020, 2020, 5240247. [Google Scholar] [CrossRef]
- Kanada, A.; Takahashi, R.; Hayashi, K.; Hosaka, R.; Yukita, W.; Nakashima, Y.; Yokota, T.; Someya, T.; Kamezaki, M.; Kawahara, Y.; et al. Joint-Repositionable Inner-Wireless Planar Snake Robot. IEEE Robot. Autom. Lett. 2025, 10, 4994–5001. [Google Scholar] [CrossRef]
- Jin, H.; Luo, M.L.; Duan, C.Y.; Lu, S.Q.; Li, Y.P. Design and analysis of a single leg robot based on variable stiffness joint. J. Mech. Sci. Technol. 2025, 39, 2139–2150. [Google Scholar] [CrossRef]
- Chen, Z.J.; Liu, J.M.; Gao, F. Real-time gait planning method for six-legged robots to optimize the performances of terrain adaptability and walking speed. Mech. Mach. Theory 2022, 168, 104545. [Google Scholar] [CrossRef]
- Ostyn, F.; Vanderborght, B.; Crevecoeur, G. Improving the Collision Tolerance of High-Speed Industrial Robots via Impact-Aware Path Planning and Series Clutched Actuation. IEEE Trans. Robot. 2024, 40, 4825–4841. [Google Scholar] [CrossRef]
- Ostyn, F.; Vanderborght, B.; Crevecoeur, G. Series Clutched Actuation for Collision-Tolerant High-Speed Robots. J. Mech. Robot. Trans. ASME 2024, 16, 121008. [Google Scholar] [CrossRef]
- Zhen, S.; Li, Y.; Liu, X.; Wang, J.; Chen, F.; Chen, X. A Lyapunov-based robust control for permanent magnet synchronous motor in the modular joint of collaborative robot. Robotica 2023, 41, 1389–1406. [Google Scholar] [CrossRef]
- Li, B.Y.; Xie, X.; Yu, B.; Liao, Y.W.; Fan, D.P. Data-driven friction modeling and compensation for rotary servo actuators. Front. Mech. Eng. 2024, 19, 41. [Google Scholar] [CrossRef]
- Wang, B.F.; Iwasaki, M.; Yu, J.P. Command Filtered Adaptive Backstepping Control for Dual-Motor Servo Systems with Torque Disturbance and Uncertainties. IEEE T. Ind. Electron. 2022, 69, 1773–1781. [Google Scholar] [CrossRef]
- Abbas, S.; Husain, S.; Al-Wais, S.; Humaidi, A.J. Adaptive Integral Sliding Mode Controller (SMC) Design for Vehicle Steer-by-Wire System. SAE Int. J. Veh. Dyn. Stab. NVH 2024, 8, 383–396. [Google Scholar] [CrossRef]
- Humaidi, A.J.; Sadiq, M.E.; Abdulkareem, A.I.; Ibraheem, I.K.; Azar, A.T. Adaptive backstepping sliding mode control design for vibration suppression of earth-quaked building supported by magneto-rheological damper. J. Low Frequation Noise Vib. Act. Control 2022, 41, 768–783. [Google Scholar] [CrossRef]
- Roy, S.; Baldi, S.; Fridman, L.M. On adaptive sliding mode control without a priori bounded uncertainty. Automatica 2020, 111, 108650. [Google Scholar] [CrossRef]
- Sharma, N.K.; Roy, S.; Janardhanan, S. New design methodology for adaptive switching gain based discrete-time sliding mode control. Int. J. Control 2021, 94, 1081–1088. [Google Scholar] [CrossRef]
- Sharma, N.K.; Roy, S.; Janardhanan, S.; Kar, I.N. Adaptive Discrete-Time Higher Order Sliding Mode. IEEE Trans. Circuits Syst. II Exp. Briefs. 2019, 66, 612–616. [Google Scholar] [CrossRef]
- Ubare, P.; Patne, V.; Sonawane, D. Enhancing performance of permanent magnet motor for electric vehicle drives using model predictive control. Proc. Inst. Mech. Eng. D J. Automob. Eng. 2024, 238, 2753–2766. [Google Scholar] [CrossRef]
- Sun, Z.; Xu, Y.; Ma, Z.; Xu, J.; Zhang, T.; Xu, M.; Mei, X. Field programmable gate array-based torque predictive control for permanent magnet servo motors. Micromachines 2022, 13, 1055. [Google Scholar] [CrossRef] [PubMed]
- Novak, Z.; Novak, M. Adaptive PLL-based sensorless control for improved dynamics of high-speed PMSM. IEEE Trans. Power Electron. 2022, 37, 10154–10165. [Google Scholar] [CrossRef]
- Yue, M.Y.; Bai, B. A DSP design and implementation for motor FOC. Acta Electron. Sin. 2020, 48, 2041–2046. [Google Scholar]
- Luo, Y.C.; Zheng, H.H.; Lin, C.H.; Kuo, Y.P. Field-oriented controlled permanent magnet synchronous motor drive with dynamic-parameter speed controller based on generalized regression neural network. Sens. Mater. 2021, 33, 1945–1955. [Google Scholar] [CrossRef]
- Hu, M.; Ahn, H.; Park, J.; You, K. Novel rapid control prototyping for permanent magnet synchronous motor via model-based design and STM32 chip. Int. J. Adv. Manuf. Technol. 2024, 135, 1187–1204. [Google Scholar] [CrossRef]
- Yu, C.H.; Liao, F.; Ji, H.B.; Wu, W.H. Characteristic model-based adaptive control for cryogenic wind tunnels. Trans. Inst. Meas. Control 2021, 43, 1257–1267. [Google Scholar] [CrossRef]
- Wang, X.; Wang, B.F.; Chen, X.K.; Yu, J.P. Characteristic model-based discrete-time adaptive tracking control for multi-motor driving systems with inertia variations. IEEE Trans. Transp. Electrif. 2025, 11, 835–846. [Google Scholar] [CrossRef]
- Wang, J.Y.; Xu, W.; Fang, S.H.; Chen, Y.; Wang, Y.C.; Wang, W. Adaptive control schemes based on characteristic model for servo motor drives. IET Power Electron. 2023, 16, 2238–2248. [Google Scholar] [CrossRef]
- Gao, Y.; Wu, Y.F.; Wang, X.; Chen, Q.W. Characteristic model-based adaptive control with genetic algorithm estimators for four-PMSM synchronization system. Int. J. Control Autom. Syst. 2020, 18, 1605–1616. [Google Scholar] [CrossRef]
- Ziad, H.; Al-Dujaili, A.Q.; Humaidi, A.J. A comparative study of deep learning efficiency in the classification of electrical faults of permanent magnet synchronous motor. Int. Rev. Appl. Sci. Eng. 2025, 16, 292–302. [Google Scholar] [CrossRef]
- Wu, H.X.; Hu, J.; Xie, Y.C. Characteristic Model Based Intelligent Adaptive Control; China Science and Technology Press: Beijing, China, 2009. [Google Scholar]
- Chen, L.; Yan, Y.; Mu, C.; Sun, C. Characteristic model-based discrete-time sliding mode control for spacecraft with variable tilt of flexible structures. IEEE/CAA J. Autom. Sin. 2016, 3, 42–50. [Google Scholar] [CrossRef]
- Chen, Y.; Xie, Q.Q.; Zhou, F.; Liu, X. Research on Dead-zone Compensation of AC Servo System based on voltage feed forward decoupling and FOC. Prz. Elektrotechniczny 2012, 88, 86–89. [Google Scholar]








| Parameters | Value | Parameters | Value |
|---|---|---|---|
| 0.24 Ω | |||
| 14 | |||
| 0.001 | |||
| Motor Parameters | Units | Value |
|---|---|---|
| Rated Voltage | 24 | |
| Rated Torque | 5 | |
| Rated Speed | 120 | |
| Rated Current | 10.5 | |
| Rated Power | 120 | |
| Pole Pairs | - | 14 |
| Torque Coefficient | 0.47 | |
| Line Resistant | Ω | 0.48 |
| Line Inductance | 0.368 | |
| Rotor Mass | 388 | |
| Reduction Ratio | 8:1 |
| Parameter | SAME (rad/s) | SRMSE (rad/s) |
|---|---|---|
| = 10 | 3.11 | 0.82 |
| = 30 | 2.85 | 0.74 |
| = 50 | 2.64 | 0.76 |
| = 70 | 2.63 | 0.81 |
| Controller | Settling Time (s) | Over Shoot (%) | SAME (rad/s) | SRMSE (rad/s) |
|---|---|---|---|---|
| PI | 0.007 | 20.13% | 0.91 | 0.31 |
| CFBSC | 0.005 | 5.64% | 0.68 | 0.22 |
| DAISMC | 0.005 | 4.21% | 0.72 | 0.24 |
| Controller | Settling Time (s) | Over Shoot (%) | SAME (rad/s) | SRMSE (rad/s) |
|---|---|---|---|---|
| PI | 0.007 | 12.39% | 1.73 | 0.42 |
| CFBSC | 0.005 | 4.85% | 1.12 | 0.31 |
| DAISMC | 0.005 | 3.93% | 0.75 | 0.25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, W. Characteristic Model-Based Discrete Adaptive Integral SMC for Robotic Joint Drive on Dual-Core ARM. Symmetry 2025, 17, 1436. https://doi.org/10.3390/sym17091436
Chen W. Characteristic Model-Based Discrete Adaptive Integral SMC for Robotic Joint Drive on Dual-Core ARM. Symmetry. 2025; 17(9):1436. https://doi.org/10.3390/sym17091436
Chicago/Turabian StyleChen, Wei. 2025. "Characteristic Model-Based Discrete Adaptive Integral SMC for Robotic Joint Drive on Dual-Core ARM" Symmetry 17, no. 9: 1436. https://doi.org/10.3390/sym17091436
APA StyleChen, W. (2025). Characteristic Model-Based Discrete Adaptive Integral SMC for Robotic Joint Drive on Dual-Core ARM. Symmetry, 17(9), 1436. https://doi.org/10.3390/sym17091436







