A Multi-Task Strategy Integrating Multi-Scale Fusion for Bearing Temperature Prediction in High-Speed Trains Under Variable Operating Conditions

Abstract

In this paper, the concept of symmetry is utilized to inform the structural design of our multi-sensor fusion framework—that is, the hierarchical feature extraction and spatial–temporal correlation modeling exhibit symmetrical properties across sensor nodes and temporal scales. Monitoring bearing temperature in high-speed train bogies is crucial for assessing system health and ensuring operational safety. Accurate temperature prediction facilitates proactive maintenance. However, existing models struggle to capture multi-scale temporal patterns, long-term dependencies, and spatial correlations among bearings, and they often overlook varying operating conditions. To address these challenges and enhance prediction accuracy in real-world operations, this study proposes MSC-Ada-MTL, a novel framework that integrates multi-scale feature extraction and operating condition recognition through adaptive multi-task learning. The approach employs multi-scale hierarchical temporal networks (MSHNets) to capture temporal features across different scales from multiple bogie sensors. A speed-based recognition strategy classifies operating conditions to enhance model reliability and simplify prediction tasks. By leveraging multi-task learning, the framework simultaneously models temporal dynamics and spatial correlations, creating a comprehensive prediction model. Validation and ablation experiments demonstrate significant improvements in prediction accuracy and robustness across diverse operating scenarios. The proposed method effectively addresses the limitations of existing approaches by synergistically combining temporal multi-scale analysis, operational condition awareness, and spatial–temporal relationship modeling, providing enhanced adaptability for real-world railway maintenance applications.

1. Introduction

High-speed trains are complex integrated systems composed of tens of thousands of components, characterized by intricate structures and diverse operating conditions. These systems operate across a wide range of environments, including extreme heat, freezing temperatures, and severe sandstorms. Onboard equipment must endure harsh conditions, such as significant temperature fluctuations, sand exposure, and high humidity. Additionally, the performance of trains is significantly influenced by external environmental factors and variable operating conditions [1]. Due to the high frequency of operation and the complexity of operating environments, real-time fault diagnosis and comprehensive health assessments are critical to ensuring operational safety [2].

As a core component of the bogie, bearings play a critical role in supporting the rotational components of the mechanical system and are subjected to complex loads and harsh conditions during operation [3]. Over time, internal issues such as friction, fatigue, and wear accumulate, ultimately leading to bearing failure. Such failures not only compromise the operating safety of the train but may also cause cascading effects on other components [4]. Friction and fatigue are closely related to temperature, and wear and failure can be reflected by temperature changes. Therefore, bearing temperature serves as a key indicator of the bearing’s health status, providing foundational data for fault detection and early warning. As internal friction and wear intensify, the bearing temperature gradually rises and approaches its critical threshold, offering a valuable signal of impending failure. Thus, analyzing the trend of bearing temperature variations complements fault diagnosis efforts and provides an essential metric for performance evaluation and health management. Real-time monitoring and analysis of bearing temperature enable early fault detection, significantly enhancing the safety and reliability of high-speed train operations [5].

Current bearing diagnostic methods can be categorized into mechanism modeling approaches and data-driven approaches [6]. Mechanism modeling approaches focus on using physical theories to mathematically model and simulate system behavior to study bearing performance under various operating conditions [7].

For example, Wang et al. [8] introduced a thermal network method to study the temperature field distribution of high-speed train axle box bearings, allowing for the prediction of the temperature of each bearing component under various speeds and fault conditions. Ma et al. [9] developed a coupled model involving both a high-speed train and the axle box bearing, and they used co-simulation to obtain the acceleration vibration response characteristics of the axle box bearing under multi-source fault conditions. Wang et al. [10] developed a thermal analysis model based on vehicle vibration induced by track irregularities that investigated the impacts of key factors on bearing operating temperature under vehicle vibrations. Zheng et al. [2] incorporated the influence of the lubricant proportion involved in lubrication, establishing a detailed temperature transmission system of the axle box system based on analyzing the mechanism of internal friction heat generation in bearings. Wang et al. [11] developed a three-dimensional vehicle–track coupled dynamic model that accurately reflects the dynamic performance of high-speed trains during operation. Wang et al. [12] proposed a mechanical–thermal coupling model for a high-speed train bearing rotor system, considering the impact of thermal inertia (TI), and they compared the differences in vibration response and transient temperature distribution.

In contrast to mechanism modeling approaches, data-driven methods, particularly those based on deep learning (DL), have made significant advances in the field of bearing diagnostics in recent years [2,8,9]. For instance, Yang et al. [13] proposed a hybrid model that includes a physical model reflecting the thermal behavior of axle boxes and a data-driven model, but this model only predicts the temperature of healthy bearings under given operating conditions. Huang et al. [14] proposed a multi-scale convolutional neural network with channel attention (CA-MCNN) model that employs a one-dimensional convolution-based parallel feature fusion mechanism to capture complementary multi-scale information while reducing network complexity. Ren et al. [15] introduced a cross-domain early warning fault diagnosis model called Dynamic Balanced Domain Adversarial Networks (DBDANs), and they designed an adaptive class-level weighting strategy for imbalanced datasets to solve the problem of operating condition class imbalance, although it did not effectively classify operating conditions. Liu et al. [16] proposed a multi-layer long short-term memory isolation forest method for axle box bearing temperature early warning on in-service high-speed trains, but they did not consider the spatial correlation between temperature sensors. Niu et al. [17] presented a deep residual convolutional neural network with enhanced discriminative feature learning and information fusion for multi-task bearing temperature early warning diagnostics. Wang et al. [18] proposed a spatiotemporal attention sequence-to-sequence (Seq2seq) model, introducing spatial and temporal attention mechanisms within the Seq2seq framework to address inter-sensor and intra-sensor correlations, but they did not consider different operating conditions. Gu et al. [19] used the K-means algorithm to classify and identify the operating conditions of high-speed trains and then constructed a bearing temperature prediction model based on a multi-task deep learning framework, but they ignored the spatial correlation between measuring points of different bearings.

In summary, current methods exhibit notable limitations that require further investigation and resolution, particularly in the context of high-speed train bearing temperature prediction. These approaches face significant challenges in practical applications due to the following complex issues. First, the bearing temperature of a high-speed train is influenced by a variety of factors, including train operating conditions (e.g., traction force, speed, and acceleration) and environmental conditions (e.g., ambient temperature). These factors operate on different temporal scales, necessitating the extraction and integration of multi-scale hierarchical time-series features. Second, the variation in bearing temperature is a cumulative process that is not only driven by current influencing factors but also significantly affected by historical conditions, resulting in strong temporal dependencies across different time steps. Finally, multiple bearings with temperature measurement points are typically equipped on the same bogie of a high-speed train, and they exhibit substantial spatial correlations under identical external conditions.

Moreover, many previous architectures lack principled structural design, which limits their ability to efficiently model the inherently structured nature of multi-sensor temperature signals. In response, this study draws inspiration from the concept of symmetry to inform the architectural design of the proposed multi-sensor fusion framework. Specifically, we incorporate symmetrical properties in both hierarchical temporal feature extraction and spatial–temporal correlation modeling. Symmetry in this context refers to the mirrored or consistent structure applied across sensor nodes and time scales, enabling the model to effectively generalize across varying configurations and capture shared patterns of degradation. This symmetry-informed design not only enhances the interpretability and modularity of the model but also aligns with the physical consistency of bearing structures and train configurations.

To address the challenges of multi-scale information fusion and operating condition adaptability in high-speed train bogie bearing temperature prediction, this study proposes MSC-Ada-MTL (Multi-Scale Condition-Adaptive Multi-Task Learning), an innovative framework integrating hierarchical multi-scale temporal networks (MSHNets), dynamic operating condition recognition, and adaptive task-weighting mechanisms. The framework extracts multi-scale temporal features from bearing temperature and performs embedded fusion with operational parameters, aiming to improve the prediction accuracy and the adaptability under varying operating conditions. The key innovations are as follows:

(1)

We design a multi-scale hierarchical time-series network that captures features across different time scales while integrating spatial features using gated recurrent units to effectively reflect complex temporal and spatial correlations and enhance input quality.

(2)

A comprehensive strategy is proposed by combining an operating condition division scheme with a temporal dependence modeling scheme. Data segmentation with gated recurrent units (Seg-GRU) that accounts for speed variations is devised to improve the capture of long-term dependencies while maintaining the simplicity and stability of the prediction model.

(3)

We introduce an adaptive multi-task learning mechanism that adjusts the model’s output based on different operating conditions to increase the accuracy and adaptability of temperature prediction.

2. MSC-Ada-MTL Method

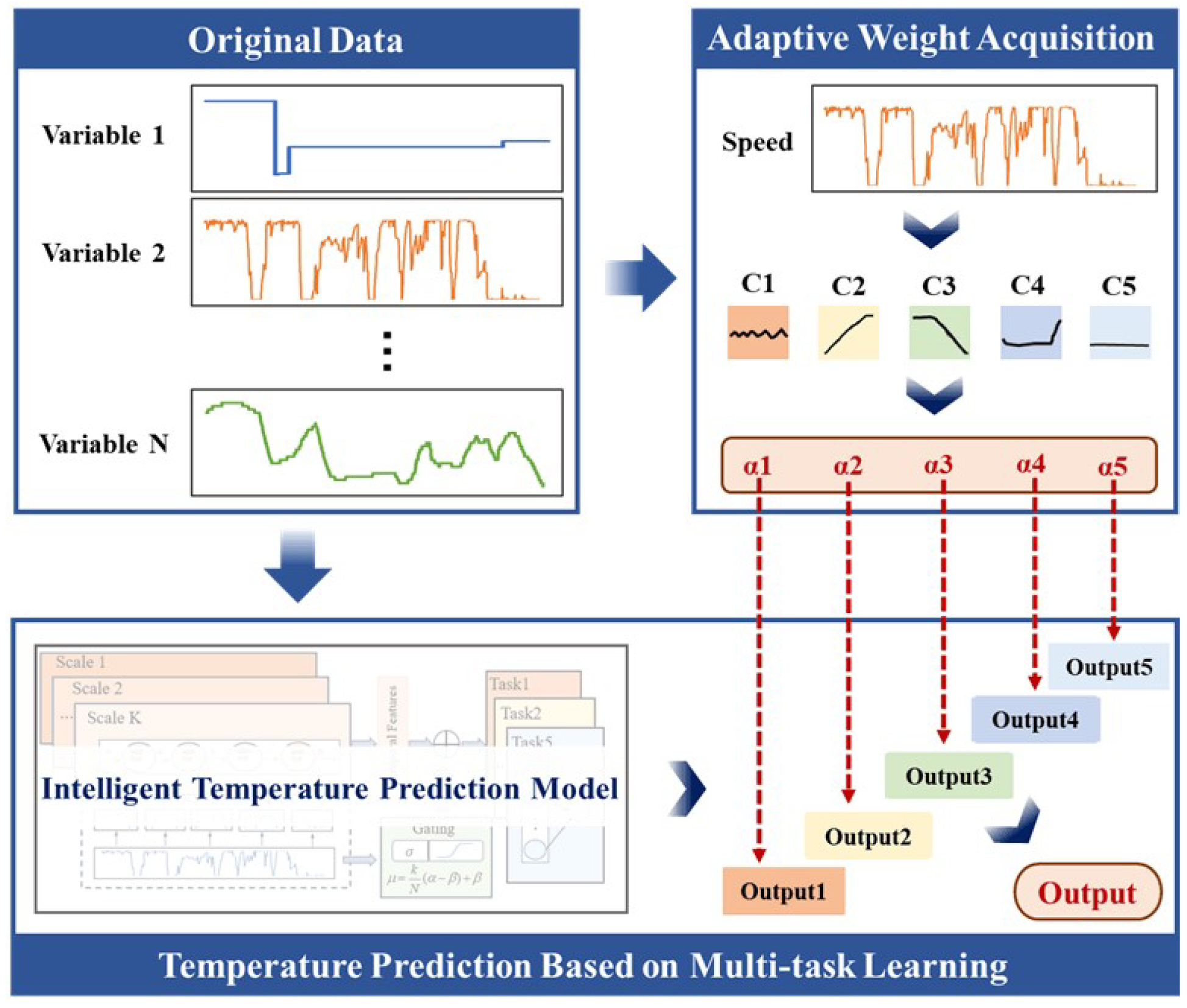
The temperature prediction method for bearings on the bogie, termed MSC-Ada-MTL, comprises three primary modules: the Multi-Scale Temporal Feature Extraction Module, the Operating Condition Recognition Module, and the Adaptive Multi-Task Learning Module. The overall framework is illustrated in Figure 1, and the core steps can be summarized as follows:

(1)

Information Extraction for Multi-Scale Time Series: MSHNets are employed to extract temporal sequence features across multiple scales from variables such as speed and ambient temperature, effectively capturing the dynamic patterns associated with different time scales. Additionally, a Seg-GRU is designed to extract temporal features through a segmented processing strategy, ensuring robust handling of long time-series data.

(2)

Operating Condition Segmentation: A sliding window approach is applied to the locomotive operating data, using continuous speed variations as the segmentation criterion. This strategy enables the automatic identification and extraction of distinct operating states, providing a comprehensive representation of condition variations.

(3)

Adaptive Multi-Task Learning: This module consists of two subunits: the dynamic gating threshold adjustment and the adaptive task head integration. The former integrates temporal and raw features through a dynamic gating mechanism, enhancing the network’s adaptability to varied operating conditions and maintaining prediction performance in complex scenarios. The latter adjusts weights for each task head based on the distribution of operating conditions, ensuring precise condition-specific modeling and improving prediction accuracy.

2.1. Multi-Scale Temporal Feature Extraction

The change in the bearing temperature on a bogie is a typical time-series problem that is affected by variables such as speed and ambient temperature, which change continuously with time. For different variables, the time dependency of time series at different scales is also different. The features on different time scales need to be extracted from each parameter time series to capture short-term local details and long-term trends, which play an important role in ensuring the performance of the prediction model. Therefore, a multi-scale temporal feature extraction strategy that consists of two parts is developed as follows.

2.1.1. Multi-Scale Hierarchical Temporal Networks

MSHNets are designed to preserve latent temporal dependency across various time scales for temperature, speed, and other variables. Following a pyramid-like hierarchical structure, these networks employ multiple pyramid layers to hierarchically transform the original time-series data, representing features from finer to coarser scales. This multi-scale framework offers the opportunity to observe the original time series at different temporal resolutions. Specifically, features at smaller scales retain more granular details, while representations at larger scales capture slower-evolving trends. MSHNets generate multi-scale feature representations through a series of pyramid layers. Each pyramid layer receives the output from the preceding layer as its input and produces a larger-scale feature representation as output. Specifically, given an input multi-scale time series $\mathit{X}\in {\mathrm{R}}^{\mathrm{N}\times \mathrm{T}}$, N denotes the dimensionality of the variables, and T represents the length of the time sequence. MSHNets produce feature representations at k different scales. The feature representation at the kth scale is denoted as $X^k\in {\mathrm{R}}^{\mathrm{N}\times {\displaystyle \frac{\mathrm{T}}{2^{k-1}}}}$. Here, N represents the dimensionality of the variables, and ${\displaystyle \frac{T}{2^{k-1}}}$ is the sequence length at the kth layer.

The pyramid layers in MSHNets utilize convolutional neural networks to capture local patterns along the temporal dimension. Following design principles akin to those in image processing, different pyramid layers employ various sizes of convolutional kernels. Initially, larger kernels are used, and they gradually decrease in size in subsequent layers to control the receptive field size and preserve the characteristics of large-scale time series. For instance, the kernel sizes could be set to 1 × 7, 1 × 5, and 1 × 3, with a convolution stride of 2 at each layer to expand the temporal scale. This can be formally expressed as follows:

$$X_{rec}^k=\mathrm{RELU}\left(Conv1\mathrm{D}(X^{k-1},W_{rec}^k)+b_{rec}^k\right)$$

(1)

Here, $X_{rec}^k$ represents the original features processed through convolutional layers at the kth layer, and $W_{rec}^k$ and $b_{rec}^k$, respectively, represent the convolutional kernel and bias vector at the kth layer. Different pyramid layers are designed to preserve latent temporal dependence at varying time scales. The granularity of temporal dependencies captured between two consecutive pyramid layers is highly dependent on the hyperparameter settings, namely, the size of the convolutional kernels and the stride. Due to the limited flexibility of using a single convolutional neural network, an additional convolutional neural network is introduced. This network employs a convolutional kernel size of 1 × 1 and adds a 1 × 2 pooling layer to operate in parallel with the original convolutional network. This arrangement can be formally expressed as follows:

$$X_{norm}^k=\mathrm{MaxPool}\left(Conv1\mathrm{D}(X^{k-1},W_{norm}^k)+b_{norm}^k\right)$$

(2)

Here, $X_{norm}^k$ is the feature map generated by convolution and pooling operations at the kth layer, and $W_{norm}^k$ and $b_{norm}^k$, respectively, represent the convolutional kernel and bias vector at the kth layer. Subsequently, the outputs of the two convolutional neural networks at each scale are combined through element-wise addition. This process integrates the features captured by both networks, enabling a more comprehensive representation of the temporal dependence at each scale. This operation can be formally expressed as follows:

$$X^k=X_{rec}^k+X_{norm}^k$$

(3)

Following the integration of multi-scale feature representations, the learned features are both flexible and comprehensive, effectively preserving various temporal dependencies. During the process of feature representation learning, to prevent interactions between variables, convolution operations are performed along the temporal dimension while keeping the variable dimension unchanged. Specifically, within each pyramid layer, the convolutional kernels are shared across the variable dimension. This approach ensures that the intrinsic properties of each variable are maintained without cross-interference, optimizing the network’s ability to capture relevant temporal patterns.

2.1.2. Shared Feature Extraction Module

On the foundation of extracting multi-scale features, a shared module from the multi-task learning mechanism is introduced to further capture the temporal dependency characteristics within the data. The term “shared” refers to the use of a common feature extraction module across multiple tasks, which reduces the number of model parameters, improves computational efficiency, and ensures that different tasks can benefit from the same temporal features. By leveraging this shared feature extraction module, the model can more efficiently handle the complex time-series data in multi-task learning (MTL).

To further enhance the model’s ability to process long sequences, a Gated Recurrent Unit (GRU) is employed, offering a simpler network structure with fewer parameters and faster training speed compared to LSTM. However, the traditional GRU still faces challenges such as information loss and vanishing gradients when handling long sequence prediction tasks. To address these limitations, a Segmented GRU (Seg-GRU) strategy is introduced into the model design. This segmentation approach helps improve the transmission of long-term sequence information while mitigating the decay of gradients over extended time spans, thereby enhancing the model’s ability to extract shared temporal features more effectively.

The shared feature extraction layer network is composed of SegGRU_i, where i = 1, 2, …, k, with the specific quantity determined by the dimensionality of the previously extracted multi-scale features. Moreover, the initial hidden state of each SegGRU_i is determined by the multi-scale features as follows:

$${\mathrm{SegGRU}}_i(h_0)=X^i$$

(4)

This module continues to employ multi-scale time series for training; however, it differs in that when the input is fed into SegGRU_i initialized with features of varying scales, X is partitioned into several segments of different scales [xⁱ₁, xⁱ₂, …, xⁱ_j, …, xⁱ_n], where xⁱ_j ∈ R^N×λ and λ represents the segment length, which is determined by the size of the different scales. Each segment is processed separately by a GRU, thereby alleviating the computational burden on a single GRU unit when dealing with excessively long time series. Specifically, the hidden state hⁱ_j−1 extracted by GRUⁱ_j−1 corresponding to segment xⁱ_j−1 serves as the initial value for the hidden state of GRUⁱ_j corresponding to segment xⁱ_j, and the forward propagation operation of the GRU is subsequently performed.

$$h_j^i={\mathrm{GRU}}_j^i(x_j^i,h_{j-1}^i)$$

(5)

Through this approach, the model can more effectively maintain sensitivity to critical information in longer time series while avoiding the issues caused by vanishing gradients. This strategy not only enhances the model’s performance in long-term time-series prediction but also makes the extraction of shared temporal features more stable and efficient.

2.2. Operating Condition Recognition Module

In consideration of multi-scale feature extraction, we further investigated the influence of sensor data from distinct spatial positions on axle temperature variations. However, the dependency relationships between these parameters and bearing temperature exhibit significant discrepancies when locomotives run under different working conditions. As a critical characteristic parameter reflecting locomotive operating status, speed effectively captures the essential features of working conditions. Therefore, we implemented operating condition segmentation based on speed to establish a state recognition model. This methodology substantially mitigates uncertainties introduced by data fluctuations while simultaneously enhancing computational efficiency and prediction accuracy.

Concretely, based on speed data, a sliding window technique is utilized to analyze speed variations and determine the operating state of the locomotive. Specifically, the sliding window step size is set to τ. By examining speed changes across consecutive data points within the window, the operating state can be accurately classified. Through consultations with locomotive engineers and a comprehensive review of the relevant literature, the operating states are categorized into five distinct states: Stationary, High-Speed Operation, Acceleration, Braking, and Constant Speed.

As shown in

Table 1. Operating condition segment division standard.

State	Condition
Stationary $\left(\mathrm{C}1\right)$	$\mathrm{if} v_i<1$
High-Speed Operation $\left(\mathrm{C}2\right)$	$\begin{array}{c}\mathrm{if} \exists k \mathrm{such} \mathrm{that} i\in \left[k, k+\tau -1\right] \mathrm{and} \hfill \\ v_j>110 \mathrm{for} \mathrm{all} j\in \left[k, k+\tau -1\right]\hfill \end{array}$
Acceleration $\left(\mathrm{C}3\right)$	$\begin{array}{c}\mathrm{if} \exists k \mathrm{such} \mathrm{that} i\in \left[k, k+\tau -1\right] \mathrm{and} \hfill \\ \Delta v_j>1 \mathrm{for} \mathrm{all} j\in \left[k, k+\tau -1\right]\hfill \end{array}$
Braking $\left(\mathrm{C}4\right)$	$\begin{array}{c}\mathrm{if} \exists k \mathrm{such} \mathrm{that} i\in \left[k, k+\tau -1\right] \mathrm{and} \hfill \\ \Delta v_j<-1 \mathrm{for} \mathrm{all} j\in \left[k, k+\tau -1\right]\hfill \end{array}$
Constant Speed $\left(\mathrm{C}5\right)$	$\mathrm{otherwise}$

, $C_i, (i=1, 2, \dots , 5)$ corresponds to the five aforementioned states. Specifically, “Stationary” indicates that the speed remains below 10 km/h over τ consecutive data points; “High-Speed Operation” signifies that the speed remains above 110 km/h over τ consecutive data points; “Acceleration” refers to a condition where the speed monotonically increases over τ consecutive data points; “Deceleration” denotes a condition where the speed monotonically decreases over τ consecutive data points. If none of the above conditions are met, the state is classified as “Constant Speed.” Detailed information regarding the condition segmentation is presented in Table 1.

The interval between sampling points for the experimental data is 10 s, and the sliding window size is determined through specific experiments, as detailed in Section 3.1.1.

$v_i$ denotes the speed value at the i-th time step, $\Delta v_j$ represents the speed variation at the j-th time step (where $\Delta v_j=v_j-v_{j-1}$), $k$ indicates the initial time point, and $\tau$ denotes the sliding window length.

2.3. Adaptive Multi-Task Learning Module

In locomotive temperature prediction tasks, where the impact of different operating conditions on temperature varies, MTL offers significant advantages. By treating temperature prediction under different operating conditions as separate tasks, MTL effectively leverages the correlations between these tasks and shares feature representations, thereby enhancing the model’s overall predictive accuracy and generalization capability.

MTL refers to setting multiple training objectives for training samples and jointly training them to improve the model’s generalization performance based on specific correlations among the targets [20]. Compared with single-task learning (STL) in traditional machine learning [21], MTL enhances the prediction and generalization capabilities of the main task by leveraging the interactions between multiple tasks [22].

2.3.1. Gating Threshold Unit

The shared layer trained across all samples tends to focus more on capturing common temporal features, which may result in the loss of specific characteristics unique to individual operating conditions. Simply feeding these shared features into the different task-specific output heads may not achieve the desired performance. Therefore, a gating mechanism, denoted as σ, is introduced to concatenate a portion of the original data X with the extracted temporal features, ${\mathrm{F}}_{\mathrm{SegGRU}}$, and multi-scale temporal representations, ${\mathrm{F}}_{\mathrm{MSHNets}}$. This combined input is used to train each output head, allowing for better learning of the unique characteristics of different operating conditions, ultimately producing the final output Y.

$$H=concatenate\left[\mathsf{\sigma }(X,\mu ),{\mathrm{F}}_{\mathrm{SegGRU}},{\mathrm{F}}_{\mathrm{MSHNets}}\right]$$

(6)

$$Y=L_{\widehat{C}}(H)$$

(7)

The gating structure consists of a nonlinear activation function (Sigmoid) σ, where μ is the threshold of the nonlinear activation function, determining the proportion of original data incorporated, and this is obtained based on the ratio k of the occurrence count of condition $\widehat{C}$ in each sample to the sample sequence length N. Here, α and β represent the upper and lower threshold limits, respectively, and they are determined through experimental procedures.

$$\mu ={\displaystyle \frac{k}{N}}(\alpha -\beta )+\beta$$

(8)

2.3.2. Adaptive Task Head Integration Unit

During the model training phase, the proposed model utilizes the hard sharing mechanism of MTL, where all tasks share the segmented GRU layer for temporal feature extraction. Different tasks then output prediction results through different fully connected layers. Through the operating condition recognition module, the condition category at each time point for the input time series $X\in {\mathrm{R}}^{\mathrm{N}\times \mathrm{T}}$ can be obtained, and the sample can, thus, be augmented to $\widehat{\mathrm{X}}\in {\mathrm{R}}^{\mathrm{N}\times \mathrm{T}+1}$.

$$\widehat{X}=\left[\begin{array}{ccccc}{x}_1^1& x_1^2& \cdots & x_1^T& \mathrm{C}1\\ & & \cdots & & \\ x_{\mathsf{\tau }}^1& x_{\mathsf{\tau }}^2& \cdots & x_{\mathsf{\tau }}^T& \mathrm{C}2\\ x_{\mathsf{\tau }+1}^1& x_{\mathsf{\tau }+1}^2& \cdots & x_{\mathsf{\tau }+1}^T& \mathrm{C}3\\ & & \cdots & & \\ x_{\mathrm{N}}^1& x_{\mathrm{N}}^2& \cdots & x_{\mathrm{N}}^T& \mathrm{Cy}\end{array}\right]$$

(9)

$$\gamma ={\displaystyle \frac{N}{\tau }}$$

(10)

The corresponding output head $y_i$ associated with the most frequently occurring condition in that sample is $\widehat{\mathrm{C}}$ ∈ [C1, C2, C3, C4, C5], aiming to learn the personalized features for each specific condition.

$$\widehat{C}=max\left\{\widehat{X}(C)\right\}$$

(11)

In the model application phase, we designed an adaptive task head integration unit that dynamically adjusts the weights of each output head based on the proportion of each condition within a data segment. This adaptive integration mechanism allows the model to more precisely capture the unique influences of each condition on the bearing temperature, significantly improving the accuracy and adaptability of temperature predictions. By aggregating these weighted task outputs, the accuracy and robustness of the temperature prediction model can be improved under diverse operating conditions.

$${\alpha }_i={\displaystyle \frac{num(C_i)}{N}}$$

(12)

$$y={\alpha }_1{y}_1+{\alpha }_2{y}_2+\dots +{\alpha }_i{y}_i, i=1, 2, 3, 4, 5$$

(13)

${\alpha }_i$ represents the weight of the $i$th task head.

Figure 2 illustrates an intelligent temperature prediction framework based on multi-task learning. The implementation pipeline of the proposed framework can be described as follows: initially, raw time-series data collected from multiple sensors within the same bogie (e.g., speed, temperature) are fed into the model. The operating condition segmentation module automatically identifies five typical operating states of the train (C1–C5) through dynamic analysis and assigns adaptive weights (α1–α5) to each prediction head. Subsequently, the weighted raw features are concatenated and fused with the short-term/long-term dependencies of multivariate time series, critical temporal characteristics captured by the shared feature extraction module, and cross-scale temporal features extracted and integrated by the MSHNets. Ultimately, the multi-task learning architecture employs five prediction heads (Output1–Output5) deployed in parallel to model temperature variation patterns under different operating states while achieving integrated prediction outputs through inter-task feature sharing and collaborative optimization. The proposed methodology significantly enhances the accuracy and model generalization capability of bearing temperature prediction under complex operating conditions by incorporating multi-scale feature fusion and state-adaptive task partitioning mechanisms.

3. Experimental Verification

To validate the performance of the proposed MSC-Ada-MTL method, the real operating data of locomotives are collected. The dataset comprises time-series data collected from a certain type of locomotives between November 2023 and August 2024. Each axle is equipped with six temperature sensors to continuously monitor the operating status of traction motors. Taking the second sensor among the six temperature sensors as an example, it is positioned at the gearbox end of the motor bearing housing and is specifically used to monitor the bearing temperature at that location. In addition to temperature measurements, the dataset also records other key operating parameters, such as speed, acceleration, and traction force. A summary of the primary variables contained in this dataset is provided in

Table 2. The description of the data.

Name	Description
Speed	Train speed (km/h)
Time	Time to collect data
Ambient Temperature	Outside temperature (°C)
Total Weight	Locomotive load capacity (t)
Mileage	Operating mileage (km)
Pressure	Balanced air reservoir pressure (kPa)
Length	Train car length (m)
Traction	Traction of motor (KN)
…	…

and

Table 3. The basic statistics of the data.

Metric	Max	Min	Mean	Std	Var
Locomotive_Speed (km/h)	118.70	0.00	63.86	44.48	1979.07
Brake_Cylinder1_Pressure (k_Pa)	471.00	1.00	86.81	158.50	25,124.82
Equalizing_Reservoir_Pressure (k_Pa)	614.00	1.00	537.20	166.86	27,845.31
Axle3_Position2_Temperature	63.00	18.00	35.92	7.89	62.29
Axle2_Tractive_Braking_Force (k_N)	69.20	0.00	6.38	10.42	108.73
Axle3_Ambient_Temp1	41.00	16.00	25.90	5.08	25.81
Axle3_Ambient_Temp2	40.00	16.00	25.97	5.01	25.12

.

Based on the correlation analysis between Temperature Sensor 2, the other five temperatures, and the main influencing variables (speed, ambient temperature, and traction) under different working states, the results are shown in

Table 4. Correlation analysis.

State	$\mathbf{C}1$	$\mathbf{C}2$	$\mathbf{C}3$	$\mathbf{C}4$	$\mathbf{C}5$
Parameter
Temperature Sensor 1	0.83	0.82	0.92	0.87	0.82
Temperature Sensor 3	0.84	0.79	0.88	0.83	0.74
Temperature Sensor 4	0.75	0.78	0.83	0.83	0.70
Temperature Sensor 5	0.93	0.81	0.91	0.84	0.77
Temperature Sensor 6	0.82	0.85	0.88	0.88	0.81
Speed	0.05	0.28	0.13	0.19	0.30
Ambient Temperature	0.76	0.75	0.79	0.78	0.68
traction	0.19	0.26	0.42	0.37	0.46

. According to the analysis, there are obvious differences in the interdependence between each temperature measuring point and the temperature at position 2 under different operating states. Therefore, the temperature information of different parts is used as the input of the model to fully integrate and make use of these spatial temperature characteristics. In addition, although the correlation between speed and Temperature Sensor 2 under different working conditions is low, in view of the hysteresis effect of temperature change, we still choose speed data as an important input to the model.

3.1. Performance Evaluation

To evaluate comprehensively the performance of the proposed MSC-Ada-MTL model, we conduct a series of experiments to optimize the parameters for condition segmentation. The prediction performance of MSC-Ada-MTL is then compared with that of traditional models, such as Long Short-Term Memory (LSTM), a Recurrent Neural Network (RNN), a Gated Recurrent Unit (GRU), and a Backpropagation Neural Network (BP). Additionally, special attention was given to validating the model’s accuracy across different temperature ranges to ensure its robust and efficient performance under various operating conditions. We use the classic performance metrics Mean Absolute Error (MAE), Root Mean Square Error (RMSE), and Mean Squared Error (MSE) for a comprehensive comparison.

3.1.1. Parameter Optimization

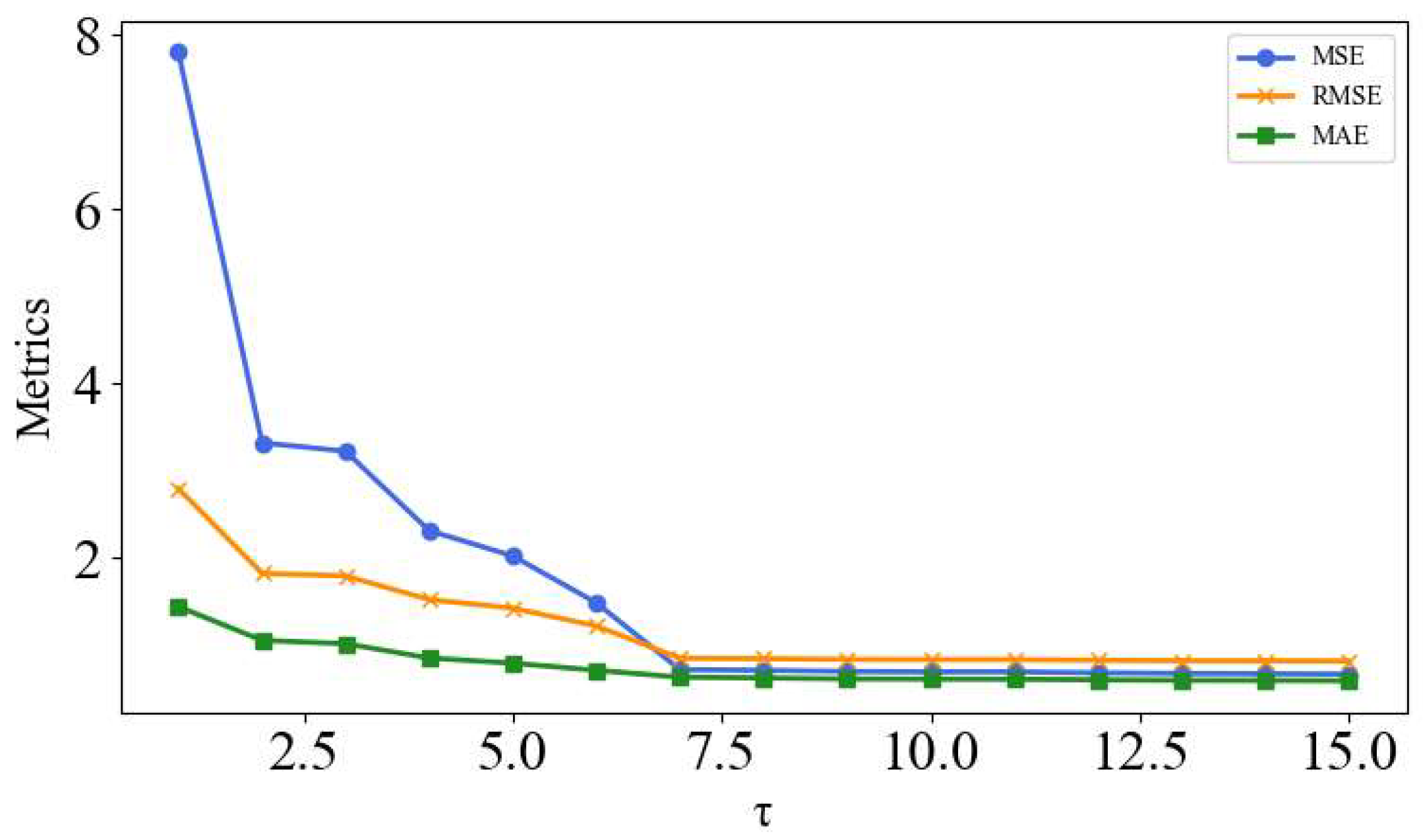
Parameter selection and optimization are critical factors in determining the performance of the MSC-Ada-MTL model. In the operating state recognition module, the sliding window step size τ must be determined based on actual locomotive operational data. Due to the lack of prior references, the initial parameter tuning is conducted by adjusting τ \tau τ. The value range for τ is set from 1 to 15, corresponding to a time range of 10 s to 150 s. This range is carefully designed to account for the data sampling frequency of 10 s while also considering the rapid dynamic changes in locomotive acceleration. This ensures that the time window effectively captures key dynamic features while maintaining reasonable efficiency.

Figure 3 illustrates the variations in three temperature prediction error metrics (Mean Squared Error, MSE; Root Mean Squared Error, RMSE; Mean Absolute Error, MAE) for the MSC-Ada-MTL model across different sliding window step sizes τ (1–15). Data analysis reveals that when τ = 7, the error values reach their lowest levels; as τ continues to increase, the errors stabilize. This indicates that the model achieves optimal prediction accuracy with τ = 7. Although the error values for τ > 7 are very close to those for τ = 7, this results in shorter training times, making it the preferred parameter. This outcome demonstrates that τ = 7 not only delivers high prediction accuracy but also effectively reduces training time, significantly enhancing the model’s practicality.

Furthermore, other hyperparameters (e.g., λ, α, β) are optimized through iterative adjustments to further improve the overall performance of the model. This meticulous parameter optimization strategy ensures the model’s feasibility and efficiency in practical applications while also optimizing the operational efficiency and resource utilization. Detailed settings for the model parameters and hyperparameters are provided in

Table 5. Detailed parameters of the MSC-Ada-MTL structure.

Network Component	Layer Name	Parameter
Inputs	Input Layer	240 × 5
	Conv1	Kernel size = 7, stride = 2
MSHNet	Conv2	Kernel size = 5, stride = 2
	Conv3	Kernel size = 3, stride = 2
Shared feature extractor	GRU layer ∗ ${\displaystyle \frac{N}{\lambda }}$	input: 60 × 10 hidden_size: 12 layer_num: 2
Gating mechanism	Conv 4	Kernel size = 3, BN, RELU
	Linear Layer_1	1 × 200
	Linear Layer_2	1 × 20
Multi-task header	Linear Layer_1 ∗ 5	10 × 1
τ, λ, α, β	/	7, 60, 0.5, 0.1

.

3.1.2. Comparative Experiment

To comprehensively verify the effectiveness of the proposed model, we designed multi-route cross-validation experiments. Vehicle operating data were collected from two independent operational routes (#1 and #2), where our proposed MSC-Ada-MTL model was compared with four prevalent methods, namely, LSTM, RNN, GRU, and BP. The hyperparameter configurations for all compared models are detailed in

Table 6. Detailed parameters of four commonly used methods.

Model	Layers	Parameter
Long Short-Term Memory	2	Hidden_size: 16
Recurrent Neural Network	2	Hidden_size: 16
Gated Recurrent Unit	2	Hidden_size: 16
Backpropagation	2	Hidden_size: 16

.

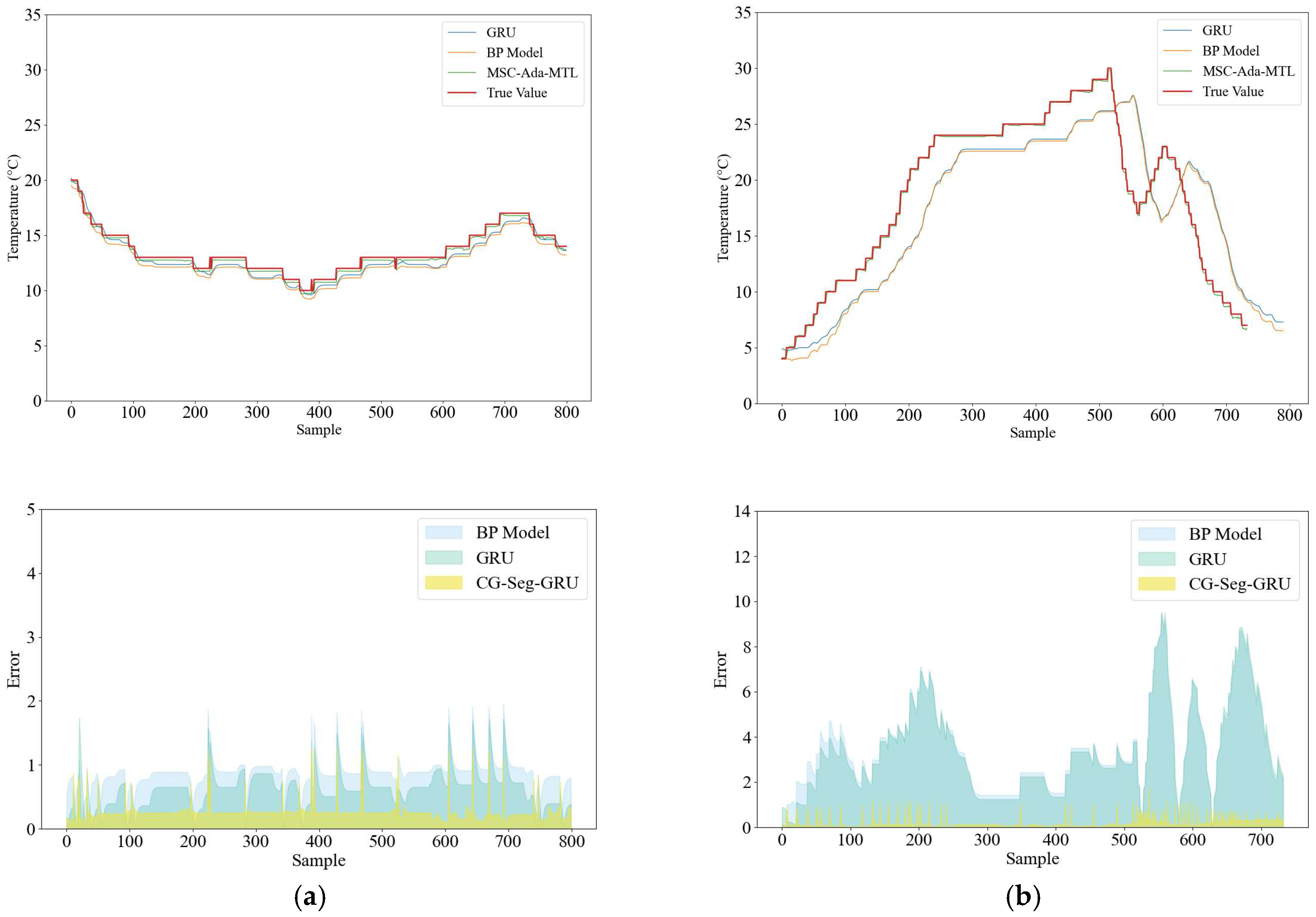
Although the BP model possesses a simple architecture, it demonstrates suboptimal performance in tasks requiring temporal dependency processing. The temporal models (e.g., LSTM, GRU) generally outperform their non-temporal counterparts (e.g., BP) in handling such data due to their enhanced capability to capture sequential dependencies. As demonstrated in Figure 4, the MSC-Ada-MTL model exhibits superior temperature tracking performance compared to baseline methods. Notably, during abrupt thermal fluctuations (e.g., steep surges or plunges), the MSC-Ada-MTL achieves precise alignment with the ground-truth temperature profile, indicating exceptional fitting accuracy. The proposed model demonstrates heightened sensitivity to thermal transients, enabling rapid adaptation to capture sharp variations. In contrast, conventional temporal models (e.g., LSTM, GRU) exhibited discernible response delays under such conditions, revealing their limited adaptability in complex scenarios.

As shown in

Table 7. Comparison of models’ performance using the aforementioned metrics.

Data	Model	MAE	RMSE	MSE
#1	BP	1.078	1.467	2.153
	LSTM	0.825	0.983	0.967
	RNN	0.893	1.0401	1.083
	GRU	0.935	1.093	1.194
	MSC-Ada-MTL	0.607	0.831	0.690
#2	BP	2.139	2.926	8.564
	LSTM	2.082	2.77	7.671
	RNN	2.023	2.76	7.617
	GRU	1.923	2.656	7.063
	MSC-Ada-MTL	0.212	0.388	0.151

, based on the comparison results for various evaluation metrics, it can be concluded that the MSC-Ada-MTL model outperforms all other methods across all metrics (MAE, RMSE, and MSE) for both Vehicle #1 and Vehicle #2, demonstrating the highest prediction accuracy and the lowest error, thereby proving its excellent performance in complex time-series tasks. The GRU/LSTM model follows closely and also performs well, making it a relatively reliable alternative. On the other hand, the traditional BP model performs the worst on these metrics, indicating significant limitations when tackling complex prediction tasks.

3.1.3. Different Temperature Ranges

To comprehensively evaluate the practical value of the proposed model, particularly regarding its long-term operational stability and performance under diverse operating conditions, systematic stability validation experiments were essential. These experiments rigorously assess the model’s ability to maintain predictive fidelity during extended operating, especially when encountering sudden thermal transients or complex temperature disturbances, while verifying its dynamic adaptive mechanisms for sustaining accurate temperature predictions.

Figure 5 further elucidates the model’s dynamic response characteristics under distinct thermal variation patterns. Figure 5a demonstrates the response features under gradual temperature fluctuations, whereas Figure 5b illustrates the evolutionary dynamics in scenarios with intense thermal oscillations. Comparative analysis reveals that the MSC-Ada-MTL architecture maintains exceptional tracking precision for actual temperature trajectories, even during extreme thermal perturbations. The model exhibits remarkable environmental adaptability across critical operational phases, including thermal load ramping and transient thermal shocks, thereby confirming its technical superiority in developing comprehensive predictive maintenance strategies and expanding operational safety boundaries for bearing systems.

3.1.4. Comparative Verification of Multi-Scale Temporal Feature Extraction

In comparison to the MSC-Ada-MTL model, Model A and Model B are single-temporal-scale models with convolutional kernel sizes set to 3 and 5, respectively, while Model C employs three convolutional kernels that are all set to 3, thereby lacking multi-scale convolutional kernel characteristics. As illustrated in Figure 6, MSC-Ada-MTL demonstrates precise predictive performance regardless of whether the bearing temperature fluctuations are abrupt or relatively smooth. The multi-scale hierarchical temporal network effectively captures local patterns and long-term evolutionary trends in time-series data by utilizing convolutional kernels of varying scales. This mechanism is particularly critical for handling complex dynamic temperature variations, enabling the model to simultaneously comprehend both short-term and long-term temporal dependencies. However, when single-scale convolutional kernels are employed, the model can only capture temporal dependencies at a single scale, leading to a significant increase in prediction errors, as shown in

Table 8. Comparison of the models’ performance using the aforementioned metrics.

Model	MAE	RMSE	MSE
Model A	2.21	2.641	6.973
Model B	1.543	2.364	5.587
Model C	1.452	2.32	5.382
MSC-Ada-MTL	0.233	0.306	0.093

, where the RMSE rises from 0.306 to 2.641 and 2.364, respectively. Even when multiple convolutional kernels of the same size are stacked at the same temporal scale, the model still fails to balance fine-grained details at smaller scales and slow-evolving trends at larger scales, resulting in a substantial increase in prediction errors, with the MAE increasing from 0.233 to 1.452, as indicated in Table 8. Therefore, the multi-scale hierarchical temporal network is a core component for enhancing prediction accuracy. Its multi-scale characteristics enable the model to simultaneously capture short-term details and long-term trends in time-series data, achieving high-precision predictions under both rapid temperature changes and relatively stable conditions.

3.2. Ablation Experiment

In order to verify the effectiveness and necessity of our designs, we conduct ablation studies focusing on key components of MSC-Ada-MTL: the operating condition segment division, the gating threshold, and the adaptive task head integration.

3.2.1. Validity Verification of the Operating Condition Recognition Module

To facilitate a more intuitive comparative analysis of prediction accuracy disparities across different operating conditions, we introduce a corresponding predictive accuracy improvement rate evaluation framework, in addition to employing conventional absolute error metrics. Specifically, this framework comprises three key metrics: the Mean Absolute Error Improvement Rate $E_{MAE}$, the Root Mean Square Error Improvement Rate $E_{RMSE}$, and the Mean Absolute Percentage Error Improvement Rate $E_{MSE}$. The mathematical definitions of these improvement rates are provided in Equation (14), and they quantitatively characterize the performance gains of the enhanced model relative to the baseline model across distinct error dimensions. This multidimensional evaluation system enables a rigorous quantification of the proposed model’s advancements in predictive capability from the perspective of complementary error measurement.

$$\left\{\begin{array}{c}{E}_{MAE}=\left(MA{E}_1-MA{E}_2\right)/MA{E}_1\times 100\%\hfill \\ E_{RMSE}=\left(RMS{E}_1-RMS{E}_2\right)/RMS{E}_1\times 100\%\hfill \\ E_{MSE}=\left(MS{E}_1-MS{E}_2\right)/MS{E}_1\times 100\%\hfill \end{array}\right.$$

(14)

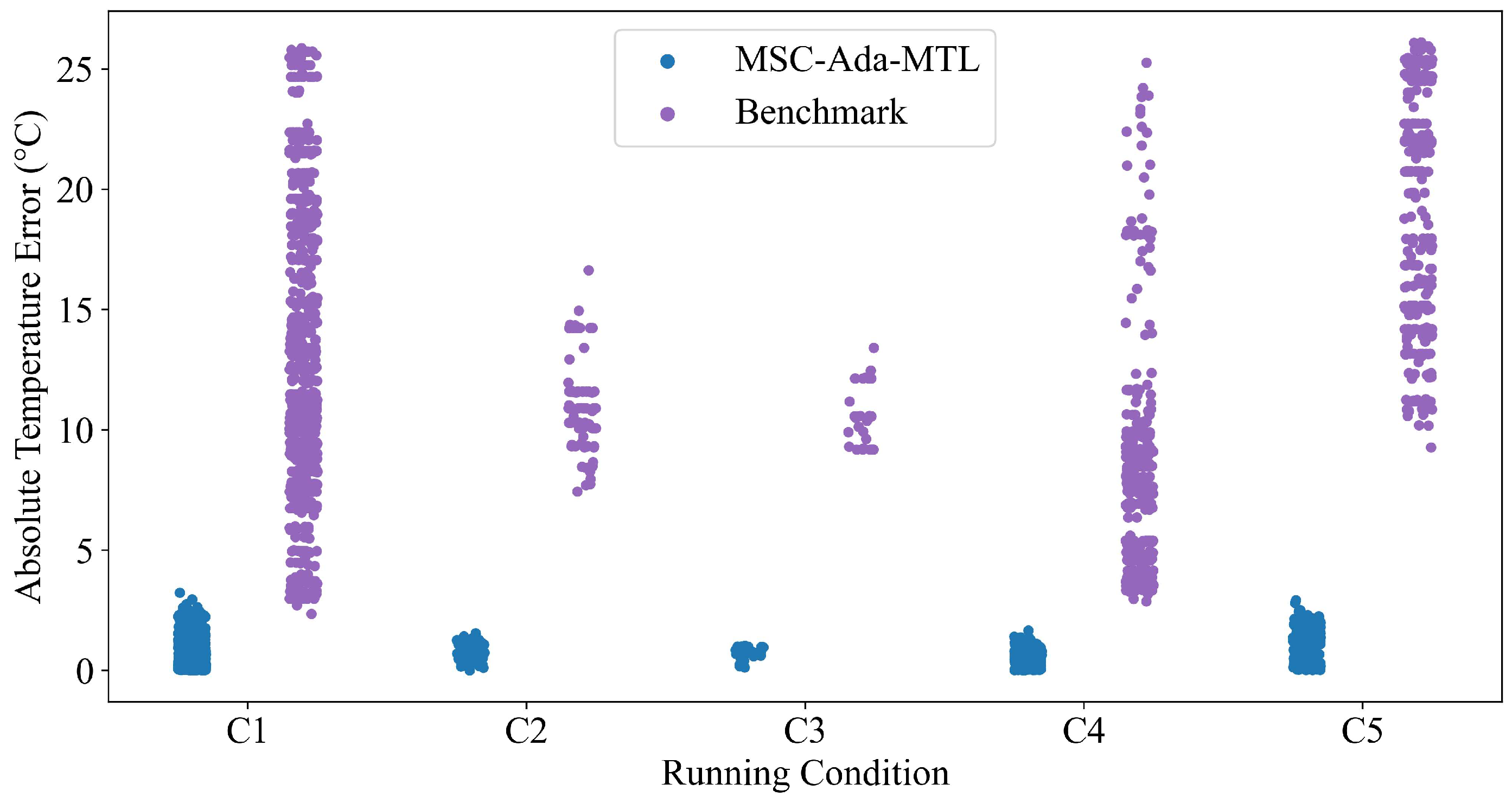
From the analysis of Figure 7 and

Table 9. Comparison of the models’ performance using the aforementioned metrics.

Operating Condition	${\mathit{E}}_{\mathit{M}\mathit{A}\mathit{E}}$	${\mathit{E}}_{\mathit{R}\mathit{M}\mathit{S}\mathit{E}}$	${\mathit{E}}_{\mathit{M}\mathit{S}\mathit{E}}$
C1	75.22	68.19	89.88
C2	72.89	71.61	91.94
C3	77.52	76.90	94.66
C4	62.54	65.25	87.93
C5	44.13	37.24	60.61

, it is evident that the prediction accuracy of the MSC-Ada-MTL model is significantly improved compared to the benchmark model under various operating conditions. Particularly under conditions of acceleration and braking, the errors of the benchmark model significantly increase, while the MSC-Ada-MTL model maintains lower and more stable error levels. This underscores the enhanced robustness of the MSC-Ada-MTL model in handling dynamically changing operating conditions. By integrating a module that differentiates operating conditions, the MSC-Ada-MTL model effectively adapts to different operating states, thus improving the precision of temperature predictions. Moreover, even in stationary conditions, the MSC-Ada-MTL model demonstrates superior performance compared to the benchmark model, further validating its applicability and superiority across various scenarios. Consequently, the design of the MSC-Ada-MTL model significantly enhances the overall performance of temperature prediction tasks, especially under dynamic and extreme conditions. These results highlight the importance of designing specialized models for complex operating conditions.

This suggests that different operating conditions have a considerable impact on the bearing temperature. Without effective differentiation and handling of these conditions, the model struggles to capture these complex dynamic changes, resulting in a sharp increase in prediction error. Therefore, the Operating Condition Segment Division strategy is an important means of improving the model prediction accuracy.

3.2.2. Validity Verification of the Multi-Task Adaptive Weight Module

To validate the efficacy of the proposed the adaptive task head integration unit and gating threshold unit, we conducted a comprehensive ablation study within the MSC-Ada-MTL framework. Specifically, we systematically removed each module to quantitatively assess the individual contributions to the overall model performance.

Benchmark 1: The removal of the adaptive task head integration unit also led to a significant increase in error. As shown in Figure 8, compared to the proposed model, the absence of the task head weight strategy prevents the model from sharing information across different tasks, which, in turn, reduces the model’s generalization ability and prediction accuracy. This emphasizes the critical role of the multi-task learning strategy in enhancing the model’s ability to handle complex data and improving its generalization capability.

Benchmark 2: When the gating threshold unit was removed, the error in Benchmark 2 was significantly higher than that of the proposed model. This indicates that the gating threshold strategy plays a crucial role in filtering and selecting the original input information, effectively supplementing feature information and reducing unnecessary noise or interference and, thereby, enhancing the model’s overall predictive capability. This comparison highlights the important role of the gating threshold strategy in improving the model’s adaptability and robustness to temperature variations in complex dynamic environments.

In conclusion, the experimental results demonstrate that the proposed model achieves better accuracy and stability in bearing temperature prediction under diverse operating conditions and complex environments. The removal of any strategic module results in a significant increase in error metrics, confirming that these modules are indispensable for improving model performance. This also indicates that the comprehensive consideration of different conditions, input information filtering, and multi-task learning during model design is both rational and effective, ensuring the model’s reliability and stability in practical applications.

4. Conclusions

This study presents a novel predictive approach that addresses the challenge of accurately forecasting locomotive bearing temperatures under varying operational conditions. By employing a finely tuned multi-task learning framework, the method enhances both the prediction accuracy and stability. The proposed approach incorporates a multi-scale hierarchical network and a segmented Gated Recurrent Unit (GRU) model, effectively capturing both temporal dependencies across different time scales and spatial relationships among sensor data from multiple locations. This methodology overcomes key technical difficulties, such as the impact of fluctuating locomotive speeds and operating states. The improved model performance offers significant potential for real-time predictive maintenance, contributing to enhanced railway system efficiency and supporting the development of sustainable transportation infrastructure. Future research can focus on integrating additional real-time data and operating parameters to further enhance the model’s accuracy and adaptability, extending its applicability to broader industrial scenarios.