Abstract
Plane geometry problem solving has been a long-term challenge in mathematical reasoning and symbolic artificial intelligence. With the continued advancement of automated methods, the need for large-scale datasets and rigorous evaluation frameworks has become increasingly critical for benchmarking and guiding system development. However, existing resources often lack sufficient scale, systematic difficulty modeling, and quantifiable, process-based evaluation metrics. To address these limitations, we propose FGeo-Eval, a comprehensive evaluation system for plane geometry problem solving, and introduce the FormalGeo30K dataset, an extended dataset derived from FormalGeo7K. The evaluation system includes a problem completion rate metric PCR to assess partial progress, theorem weight computation to quantify knowledge importance, and a difficulty coefficient based on reasoning complexity. By analyzing problem structures and solution dependencies, this system enables fine-grained difficulty stratification and objective performance measurement. Concurrently, FormalGeo30K expands the dataset to 30,540 formally annotated problems, supporting more robust model training and evaluation. Experimental results demonstrate that the proposed metrics effectively evaluate problem difficulty and assess solver capabilities. With the augmented dataset, the average success rate across all difficulty levels for the FGeo-HyperGNet model increases from 77.43% to 85.01%, while the average PCR increases from 88.57% to 91.79%. These contributions provide essential infrastructure for advancing plane geometry reasoning systems, offering standardized benchmarks for model development and guiding optimization of geometry-solving models.
1. Introduction
Solving plane geometry problems has long been recognized as a fundamental challenge in the fields of mathematical reasoning and artificial intelligence [1]. This task involves transforming multimodal geometric information into structured knowledge representations, which is followed by the application of logical reasoning, theorem-based inference, and symbolic computation to derive the intended conclusions. The challenges of this process lie in both the complexity of multimodal problem representation and the intricacies of geometric knowledge structures, which require the use of formal methods to transform textual descriptions, diagrams, and algebraic relations into computable logical representations. Moreover, it requires the accurate prediction of a sequence of applicable theorems and the execution of corresponding deductive reasoning and algebraic computations, which ultimately produce solutions that are interpretable, traceable, and verifiable. Traditional approaches to automated geometry problem solving largely rely on manually defined theorems and inference rules, including search-based strategies [2,3], coordinate-based algebraic methods such as Wu’s method [4], and point elimination techniques based on geometric invariants [5]. Although these methods can solve certain classes of geometry problems, they suffer from notable limitations in problem representation, search efficiency, and scalability to large datasets.
Recent advances in deep learning have motivated a growing body of research that seeks to integrate neural architectures with formal reasoning frameworks, leading to the development of neural-symbolic geometry solvers such as Inter-GPS [6], NGS [7], and AlphaGeometry [8]. These approaches typically employ large-scale training for theorem prediction and proof path selection and have shown promising results. However, most existing work focuses on optimizing model architectures and search strategies, with limited attention to the representation and structural modeling of geometric problems. To address these limitations, we introduce FormalGeo [9], a system grounded in geometric formalization theory, which provides a unified representation framework for structured expression and logical reasoning in geometry problems. FormalGeo encodes geometric conditions and goals using a formal language, supporting the structured modeling and execution of reasoning paths, which enhances the traceability and interpretability of the solution process. In addition, the system captures structural symmetries inherent in geometric reasoning, such as compositional symmetry in figure construction, topological symmetry in theorem dependency graphs, and mirror symmetry between forward and backward inference strategies. These symmetries offer valuable potential to simplify reasoning, expand data, and inform algorithm design.
However, automated geometry problem solving still faces three major challenges. First, current evaluation systems heavily rely on the overall solution accuracy, which lacks quantitative metrics for assessing the completeness and interpretability of the reasoning process. Second, the difficulty stratification of problems often depends on human intuition without an objective framework grounded in theorem complexity and inference depth. Third, existing datasets remain limited in both scale and diversity, which constrains model generalization and limits the comparability and applicability of research findings.
To address these issues, we propose FGeo-Eval, a comprehensive evaluation framework for geometry problems, which was developed on the basis of the FormalGeo system. FGeo-Eval introduces a dual-perspective evaluation scheme. On the one hand, it defines a problem completion rate metric PCR to assess whether the key reasoning paths required to solve a problem have been sufficiently explored, thereby overcoming the limitations of single-metric overall accuracy evaluation. On the other hand, it establishes a problem difficulty stratification system based on the structure of theorem usage and inference depth, enabling an objective assessment of problem complexity that supports data augmentation and model evaluation. Building on this foundation, we further construct the FormalGeo30K dataset. This dataset extends the original FormalGeo7K through a systematic augmentation process that leverages structural symmetries in reasoning paths and patterns in theorem usage. In addition to significantly increasing the number of problems, it enhances the diversity of geometric structures, difficulty levels, and reasoning complexities, providing a more representative benchmark for the training and evaluation of neural-symbolic models.
In summary, the main contributions of this work are as follows:
- We propose a completion-based evaluation metric, Problem Completion Rate PCR, to quantitatively assess the logical completeness and intermediate progress of reasoning paths in geometry problem solving;
- We develop a multi-dimensional difficulty assessment framework based on theorem complexity, reasoning depth, and usage frequency, enabling automatic and interpretable stratification of geometric problems;
- We construct FormalGeo30K, a high-quality and large-scale dataset to support large-scale model training and evaluation;
- We integrate the proposed evaluation mechanisms into symbolic reasoning systems, providing technical foundations for fine-grained analysis, performance diagnosis, and robustness improvement in automated geometry solvers.
2. Related Work
The field of plane geometric problem solving and theorem proving has evolved over decades, transitioning from early search-based synthetic methods and coordinate-based algebraic methods to modern neuro-symbolic systems that integrate deep learning and formal mathematical reasoning. This section systematically reviews these methods and their representative research.
Early efforts in geometric theorem proving relied on logical reasoning and search strategies. In 1959, Gelernter et al. [2] proposed the first geometry theorem prover, which utilized a backward chaining strategy reasoning from the goal backward to generate subgoals until matching the given premises. Subsequently, Zhang Jingzhong et al. [3] proposed a geometric information search system by forward reasoning, which enhanced theorem-proving efficiency through structured data organization and optimized reasoning processes. Nevertheless, traditional search methods (e.g., forward chaining [10] and backward chaining [2]) are still limited by inefficiency, incompleteness, and dependence on manually defined rules, especially in complex geometric constructions and auxiliary line generation.
Among coordinate-based algebraic methods, the most representative is Wu’s method [4], an efficient algebraic approach specifically designed for elementary geometric problems. This method introduces coordinate systems to transform the premises and conclusions of geometric theorems into algebraic equations and inequalities, which are proven through algebraic manipulations. Wu’s method was further extended to geometry over finite fields [11], differential geometry [12], and certain geometric problems involving inequalities [13]. It gradually evolved into a general mathematical mechanization method centered on solving polynomial equations. Notable extensions include polynomial elimination methods incorporating Gröbner bases [14], numerical parallel [15], triangular elimination for polynomial systems [16] and Dimension-reduction algorithms for automated proof of algebraic inequalities [17]. However, proofs generated by such algebraic methods rely on intricate polynomial computations that lack geometric intuitiveness and present significant challenges in rigorously verifying their correctness.
The point elimination method based on geometric invariants [5] establishes connections between given conditions and target conclusions by utilizing geometric invariants and introducing auxiliary points. Through algebraic operations or geometric transformations, it progressively eliminates these auxiliary points, ultimately converting the elimination process into reasoning steps, thereby generating human-readable proofs. This method originated from Zhang’s systematic area method and subsequent introduction of additional geometric invariants such as Pythagorean differences [18], vectors [19], and full angles [20], enhanced its capability to solve a broader range of plane geometry problems. Later, the fundamental principles of this method were further extended to applications in solid geometry [21] and non-Euclidean geometry [22]. Compared to algebraic methods that suffer from intermediate expression explosion during symbolic computations, the point elimination method employs more meaningful representations through geometric invariants, which improves the readability of proofs and reduces computational complexity. However, the difficulty in defining appropriate geometric invariants and establishing robust point elimination principles has constrained its broader application.
With the advancement of machine learning techniques and optimization theory, some studies have begun developing systems capable of automated geometric problem parsing and solving. Representative works in this domain include GEOS [23], GEOS++ [24], GEO-OS [25], and GeoShader [26]. Beyond geometric problem solving, research has also focused on geometric theorem proving [27,28], geometric problem formalization [29,30], and geometric knowledge extraction [31]. However, these methods still rely heavily on manually defined rules, such as using human-annotated symbols as intermediate representations for problem parsing, and their applicability is inherently restricted to specific problem types, which fundamentally limits generalizability.
In recent years, with the advancement of deep learning technologies, the integration of deep learning and symbolic reasoning has become mainstream, leading to the proposal of various data-driven neuro-symbolic automated problem-solving systems based on deep learning and formal mathematics. These methods can be categorized into two types: deductive database (DD) methods [6,8,32] and program sequence generation (PSG) methods [7,33]. DD methods focus on parsing problem texts and diagrams into formal languages and solving problems by applying theorems. This approach requires manually defined theorem libraries and translating symbolic reasoning and algebraic computation processes into computer programs. Essentially, deductive database approaches represent implementations of synthetic methods combined with modern AI techniques, with representative researches including Inter-GPS [6], GeoDRL [34], AlphaGeometry [8], E-GPS [35], FGeo-TP [32], FGeo-DRL [36], and TongGeometry [37]. PSG methods encode the texts and diagrams of geometric problems into unified representations, feed these encodings into decoders to generate program sequences, and then execute these sequences to derive solutions. These methods essentially transform geometric problem solving into sequence generation tasks, with representative approaches including NGS [7], S2G [33], Geoformer [38], DPE [39], SCA-GPS [40], UniMath [41], Dual-GeoSolver [42], GOLD [43], and LANS [44]. Beyond geometric problem-solving tasks, geometric problem parsing [45,46] and automated formalization [47] have also attracted researchers’ attention.
3. FGeo-Eval
In the FormalGeo framework for automated plane geometry problem solving, the system comprises five core modules: the Formal Geometry Problem Solver (FGPS) [48], FGeo-Parser [46], FGeo-TP (Theorem Prover) [32], FGeo-DRL (Deep Reinforcement Learning) [36], and FGeo-HyperGNet (Hypergraph Neural Network) [49]. As the central solving engine, FGPS can automatically solve plane geometry problems in our defined formal language by executing theorem sequences provided by a theorem predictor. FGeo-Parser functions as an upper-level multimodal analysis module, transforming natural language problem descriptions and geometric diagrams into standardized formal language representations. Theorem prediction is addressed through three different approaches: FGeo-TP leverages pretrained language models, FGeo-DRL formulates theorem selection as a reinforcement learning task, and FGeo-HyperGNet incorporates hypergraph-based structural learning. Despite their architectural diversity, all these approaches rely primarily on the overall problem-solving success rate as the core evaluation metric.
However, this single-metric evaluation oversimplifies the assessment of solver performance, failing to capture the logical completeness and intermediate progress within the reasoning process. To address these limitations, we propose FGeo-Eval, a comprehensive evaluation system featuring two key advancements: a problem completion evaluation metric and a difficulty stratification framework. The problem completion evaluation metric quantifies the solver’s progress by reconstructing reasoning dependencies and converting binary success/failure metrics into continuous-valued completion metrics. The difficulty stratification framework establishes a hierarchical difficulty model by quantifying the difficulty of theorems based on application frequency. This system not only provides multidimensional quantitative benchmarks but also drives collaborative optimization across modules through feedback mechanisms derived from process evaluation and difficulty stratification. Ultimately, it establishes a self-improvement cycle of problem parsing, theorem prediction, solution verification, and iterative evaluation, ensuring continuous refinement of the automated problem-solving framework.
3.1. Problem Completion Rate Metric
Current performance evaluations of automated geometric reasoning solvers predominantly rely on two metrics: overall accuracy and step-wise accuracy. However, these metrics quantify problem-solving outcomes through binary success judgments or step counts, which oversimplify the evaluation process and fail to capture critical dynamic process characteristics such as the effectiveness of theorem applications and the progressive achievement of subgoals during reasoning. To address these limitations, we propose the Problem Completion Rate metric PCR based on the solution hypertree of problems. The core mechanism involves reverse traversal of the problem solution hypertree to quantify phased subgoal attainment.
We adopt the solution hypertree structure for PCR design, as it more effectively captures the structural complexity of geometric reasoning than alternative representations such as dependency trees, general graphs, or sequential theorem sequences. Dependency trees, while effective for modeling single-path inference, are inadequate for representing the multi-premise dependencies common in geometric theorems. General graphs provide structural flexibility but lack the hierarchical organization and acyclicity necessary for representing coherent proof paths, thereby complicating backtracking and evaluation. Sequential theorem sequences impose a rigid linear order that fails to capture the inherently branched and concurrent nature of geometric deduction. In contrast, hypertrees naturally support multi-premise reasoning through hyperedges and preserve a topological structure that enables efficient reverse tracing of reasoning paths. These structural advantages make hypertrees particularly suited for modeling proof structures and supporting metrics like PCR that depend on logical dependencies and subgoal tracking.
Accordingly, we represent the geometric problem-solving process as a directed hypergraph consisting of condition hypernodes and theorem hyperedges, as illustrated in Figure 1. The root node corresponds to the initial condition set, the target node represents the geometric proposition to be solved, and intermediate nodes denote the derived conditions generated through theorem applications. When the solver fails to directly deduce the target node, the system initiates reverse dependency path traversal from the target node to identify the first critical theorem hyperedge whose output hypernode remains uncovered by the solver’s conclusions. The input hypernodes of this theorem (its premise conditions) are iteratively validated as new subgoals, and the theorem itself is added to the unpredicted theorem set. This backtracking process continues recursively until subgoals match either the solver’s intermediate conclusions or initial conditions, thereby constructing the maximal unresolved path from the target node to uncovered intermediate properties. Therefore, the incompletion rate of a problem is defined as the proportion of the unpredicted theorem set relative to the required theorem set, which is calculated through the aforementioned process. Consequently, the quantified completion metric is formulated as follows:
where denotes the complete theorem set required for problem resolution, represents the uncovered theorem set that the solver fails to predict, and denotes set cardinality. The complete algorithm is described in Algorithm 1. Our proposed evaluation metric employs a reverse backtracking mechanism to trace dependencies from the final target to achieved subgoals by analyzing the topological dependencies within the solution hypertree. Existing metrics such as success rate, step accuracy, partial credit scoring, and tree edit distance have notable limitations. Success rate reduces evaluation to a binary judgment; step accuracy neglects logical dependencies between inference steps; partial credit scoring relies on manual rubrics, limiting scalability and overlooking cascading errors; and tree edit distance, while capturing structural similarity, lacks robustness to multiple valid solution paths and fails to reveal unresolved subgoals. In contrast, PCR transforms the binary solved/unsolved paradigm into a continuous, phase-based evaluation of subgoal completion, enhancing interpretability and providing targeted optimization insights while ensuring objectivity and reproducibility. This metric offers a fine-grained analytical tool for the performance evaluation of geometric reasoning systems. Furthermore, it facilitates data-driven algorithm iteration (prioritizing the prediction capability for frequently missing steps), thereby advancing automated reasoning models in terms of logical rigor and interpretability.
| Algorithm 1 Problem Completion Rate PCR Calculation |
|
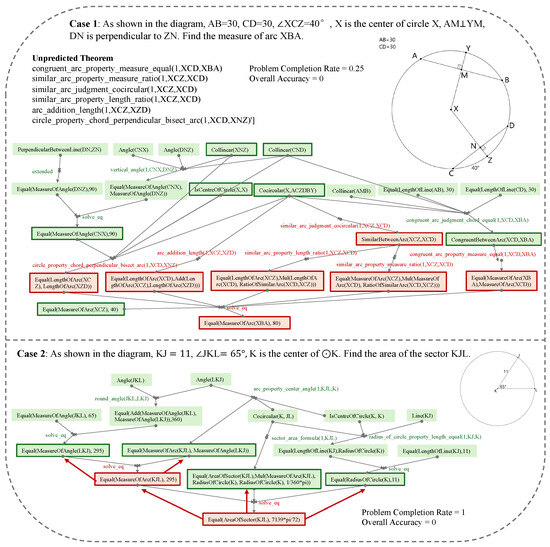
Figure 1.
Two cases for calculating completion rate in solution hypertree.
Although PCR yields continuous values, it is not intended as a prediction target for the model. Instead, it functions as a post-hoc evaluation metric designed to measure the effectiveness of predicted theorem sequences from a classification-based reasoning model when executed by the solver. Our model is trained to generate sequences of theorems required to solve geometry problems rather than to directly regress to a scalar score such as PCR. Nonetheless, PCR is highly compatible with classification outputs: higher PCR scores are strongly associated with higher prediction accuracy and more complete solutions. Moreover, its continuous nature enables finer-grained assessment compared to binary metrics, offering greater interpretability and diagnostic value. This reflects the scoring logic adopted by human experts. For example, in mathematical proof evaluation, partial credit is awarded for correctly establishing intermediate results, which is similar to how PCR evaluates partially completed reasoning chains within the hypertree.
It is also important to emphasize that continuous metrics are commonly employed in classification tasks. Metrics such as accuracy, precision, recall, and F1-score all produce continuous values, even though they are used to evaluate discrete classification outcomes. Therefore, the continuous nature of PCR does not suggest a regression-based task formulation. Predicting PCR values directly would be inappropriate, as the model is not designed to estimate evaluation scores but to identify the set of applicable theorems that can lead to a valid solution. Accordingly, PCR is deliberately designed as an external, task-specific metric for evaluating solution quality in a manner that is both rigorous and consistent with human evaluative practices.
3.2. Problem Difficulty Stratification System
We propose a hierarchical framework for assessing the difficulty of geometric problems by modeling theorem application patterns. The core innovation is the translation of formal reasoning steps into measurable feature representations, which establishes a fine-grained evaluation benchmark for plane geometry problem-solving systems. The framework comprises four key components:
- Modeling Theorem Usage Frequency Distribution: We conduct a comprehensive statistical analysis of theorem sequences across all solution paths in the FormalGeo7K dataset to model the distribution of theorem usage frequency
- Assigning Cognitive Complexity Weights: By applying logarithmic transformation and range normalization, raw frequencies are nonlinearly mapped to the interval [1.0, 2.0] to generate weight coefficients that reflect the cognitive complexity of theorems. High-frequency fundamental theorems are assigned lower weights, whereas low-frequency advanced theorems receive higher weights.
- Defining Problem Difficulty Scores: We define problem difficulty scores as a cumulative function of theorem weights, where the initial application of a theorem contributes its base weight, and repeated applications incur progressive penalties, increasing by 0.1 with each recurrence. This penalty mechanism accounts for the cognitive load accumulation effect in complex reasoning processes. The precise formula for calculating the difficulty score D is as follows:where denotes the weight of theorem i, and represents the number of times theorem i appears, with .
- Establishing a Hierarchical Difficulty Classification: Based on the distribution of difficulty scores across 7000 problems in the FormalGeo7K dataset, as illustrated in Figure 2, we classify problems into the following six progressive difficulty levels: Level 1 (), Level 2 (), Level 3 (), Level 4 (), Level 5 (), Level 6 (). This classification framework provides a graduated scale of problem complexity, progressing from foundational skills at Level 1 to sophisticated logical reasoning at Level 6.
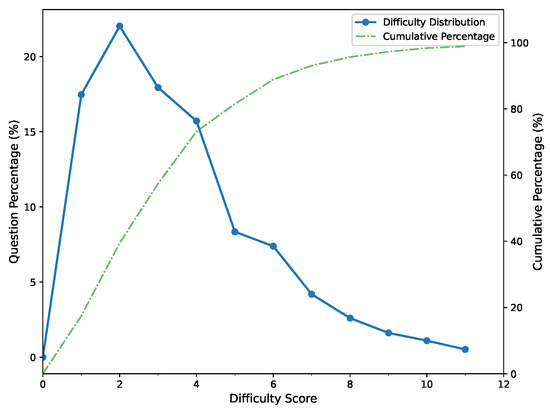 Figure 2. The difficulty coefficient distribution in FormalGeo7K.
Figure 2. The difficulty coefficient distribution in FormalGeo7K.
While the FormalGeo7K dataset covers curricula from grades 6 to 12, our difficulty stratification is derived solely from the statistical distribution of computed difficulty scores without attempting to align with specific school grade levels. Although this stratification is derived from partitioning the computed difficulty score distribution shown in Figure 2, it serves a practical and effective role in establishing a balanced and interpretable classification system. In the absence of a universally recognized theoretical framework for quantifying the difficulty of geometric problems, our empirical strategy enables broad yet representative coverage of varying problem complexities. This approach is consistent with common practices in data-driven educational assessment, where difficulty levels are typically defined according to score distributions rather than strict theoretical boundaries.
By systematically quantifying theorem diversity, application frequency, and combinatorial complexity, our framework provides a structured benchmark for evaluating geometric problem-solving models at a fine-grained level. Analyzing model performance across different difficulty levels allows us to identify key bottlenecks, such as challenges in complex logical reasoning and multi-theorem integration, thereby facilitating the iterative advancement of neuro-symbolic reasoning techniques.
4. FormalGeo7K and FormalGeo30K Datasets
In recent years, significant progress has been made in the field of automated plane geometry problem solving. However, current datasets still exhibit notable limitations, including restricted scale, incomplete annotations, and inconsistencies in formalization standards. For instance, GeoQA [7] and Geometry3K [6] primarily focus on annotating multiple-choice or short-text problems while lacking systematic records of theorem application sequences; PGDP5K [50] specializes in geometric diagram parsing, primarily providing annotations for diagrams and symbols while lacking corresponding textual descriptions or problem statements; PGPS9K [51] demonstrates strong performance in program synthesis tasks but has limited compatibility in its formal annotation framework, constraining its adaptability to multimodal reasoning; UniGeo [38] seeks to unify geometric representations, yet it still requires further refinement in clearly delineating problem conditions from reasoning paths. To address these limitations, we introduce the FormalGeo7K [46] dataset and its extended version, FormalGeo30K, which combine manual annotation, scalable generation, and rigorous validation to establish a structured, comprehensive, and meticulously annotated benchmark for automated geometric reasoning research.
4.1. Description
The FormalGeo7K dataset serves as a foundational benchmark for plane geometry problems, comprising 7000 geometry problems selected from Geometry3K [6] and GeoQA+ [39]. These problems have been re-annotated using the FormalGeo formalization framework to ensure a structured and comprehensive representation. This annotation process standardizes problem statements and diagrams, integrates formalized annotations in the FormalGeo language, and records the theorem sequences used in the solution, thereby establishing a comprehensive problem data framework. Specifically, we adopted a rule-based approach to standardize problem statements in both English and Chinese and utilized the geometric drawing tools provided by GeoGebra to reconstruct problem diagrams. This not only ensures consistency between text and diagram representations but also enhances diagram diversity by embedding relevant textual information directly into the illustrations. For formalized annotations, our FormalGeo system adopts the Conditional Declaration Language (CDL) to represent geometric problem conditions and objectives, which are further categorized into Construction CDL (defining the topological relationships between geometric elements), Image CDL (capturing implicit conditions from diagrams), Text CDL (extracting conditions from problem statements), and Goal CDL (symbolizing the problem-solving objective). This categorization enables a structured and complete representation of problems in formal language. Additionally, each problem file includes a fully annotated theorem sequence that explicitly records the logical reasoning path from the given premises to the target conclusion, thereby enhancing the interpretability of the problem-solving process. To ensure the correctness and necessity of theorem usage, all problems underwent syntactic validation and theorem redundancy pruning through the FGPS framework, resulting in a syntactically rigorous and logically precise dataset.
The annotation of FormalGeo7K was carried out collaboratively by fourteen rigorously trained graduate students, totaling approximately 1500 annotation hours through systematic cross-validation procedures. In summary, the unified formalization framework of FormalGeo7K mitigates annotation fragmentation in existing datasets while establishing a traceable logical foundation for automated plane geometry problem solving. Furthermore, it supports diverse reasoning tasks, including theorem prediction, problem solving, and diagram parsing, serving as a comprehensive benchmark for training and evaluating geometric reasoning models in complex scenarios.
To overcome the scale limitations of current geometric datasets, we propose the FormalGeo30K dataset as an extended version of FormalGeo7K. Building upon the Construction Description Language framework of FormalGeo7K, the FormalGeo30K dataset achieves a significant scale expansion to 30,540 problems through a theorem-driven dynamic generation framework combined with a multi-stage validation mechanism, thereby enhancing the diversity and hierarchical complexity of problem distributions. The expansion process comprises three key phases:
- Goal Generation: Through theorem-guided inference or random search strategies, we dynamically apply geometric theorems to generate two types of extended objectives: (1) Logical goals(proof-oriented), which focus on verifying geometric relationships, where Relation represents qualitative properties such as parallelism and perpendicularity (e.g., Relation(ParallelBetweenLine(AB, CD)) for parallelism), while Equal imposes geometric equivalence constraints (e.g., Equal(LengthOfLine(AB), LengthOfLine(AC)) for length equality). (2) Algebraic goals(calculation-oriented), which target numerical resolution, where Value represents symbolic value solving (e.g., Value(LengthOfLine(AB) for the length of line AB)).
- Path Validation: By tracing back the theorem dependencies in the original solution path, we extract high-order theorem nodes to construct the derived theorem sequence for the extended problem. The logical coherence and acyclicity of the theorem sequence are rigorously validated through a directed acyclic graph (DAG), with redundant branches pruned to ensure solution uniqueness and reasoning consistency.
- Difficulty Stratification: Using the FGeo-Eval system, we calculate a difficulty coefficient for each extended problem. This metric is then applied to filter the extended problems, constrain the number of extensions per original problem, and stratify the overall dataset into distinct difficulty levels.
The FormalGeo30K dataset offers four key advantages that address critical challenges in automated geometric reasoning research. First, enhanced diversity is achieved through the proposed expansion method, which generates two types of problem objectives for calculation and proof that cover a wide range of reasoning scenarios, including geometric relationship verification and geometric attribute value computation. Second, logical rigor is enforced through the DAG verification mechanism, ensuring that every problem has a reproducible and well-structured theorem derivation path. Third, interpretability is prioritized by retaining complete constructive descriptions and explicit theorem dependency graphs, enabling fine-grained analysis of reasoning processes. Finally, balanced difficulty distribution is achieved through adaptive thresholding, ensuring a gradual transition from basic to advanced problem complexities. Through its large-scale goal generation and structured validation framework, FormalGeo30K establishes a benchmark that prioritizes both scalability and quality, offering robust support for research in automated geometric reasoning.
4.2. Statistics
The FormalGeo30K dataset comprises 30,540 plane geometry problems, partitioned into training, validation, and test sets in a ratio of 0.6:0.2:0.2, with difficulty levels corresponding to middle school curricula from grades 6 to 12. The dataset is systematically categorized into two distinct problem types: calculation problems, which emphasize numerical derivation and symbolic computation (e.g., calculating angles, segment lengths, and ratio constraints) and account for 65.9% (20,147 problems); and proof problems, which emphasize logical reasoning and the construction of formal theorem sequences (e.g., geometric relationship inference) and account for 34.1% (10,393 problems). Both problem types are annotated using a unified formalization framework, ensuring broad applicability across different geometric reasoning tasks.
For difficulty stratification, the FormalGeo30K dataset’s difficulty coefficient distribution, derived from the FGeo-Eval evaluation system, is shown in Figure 3. The figure illustrates both the overall difficulty distribution and the difficulty distributions for problems targeting the predicates Relation, Value, and Equal, respectively. Statistical analysis reveals that calculation problems, as indicated by the predicate Value, demonstrate higher average difficulty coefficients, yet they still conform to the overall difficulty distribution of the dataset. Among these, the problems corresponding to MeasureOfAngle and LengthOfLine, which represent calculations of angles and line lengths, account for the largest proportion of computational problems, at 49.4% and 31.4%, respectively. This pattern is similarly reflected in a subset of proof problems denoted by the predicate Equal, with proportions of 44.5% and 33.9%, respectively. In contrast, for problems concerning the properties and relationships of geometric entities represented by the predicate Relation, the inherent complexity of geometric relationships leads to a more diverse distribution of problem types. Notably, the proof problems corresponding to the predicate RightTriangle for right-triangle determination and the predicate PerpendicularBetweenLine for proving parallel relationships account for relatively high proportions, at 16.8% and 16.1%, respectively.
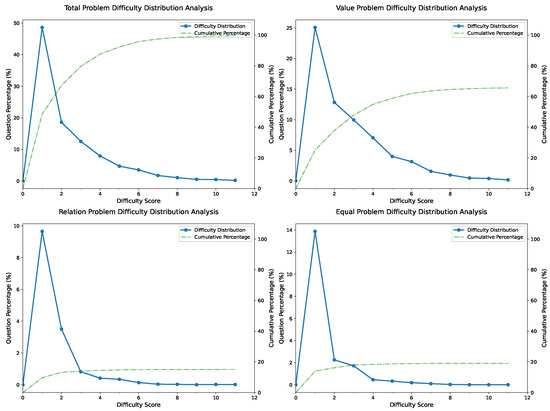
Figure 3.
The difficulty coefficient distribution in different kinds of problems in FormalGeo30K.
Through the detailed statistical analysis and difficulty stratification of the FormalGeo30K dataset, it is evident that the dataset maintains a well-structured and balanced distribution of problem types. As a standardized and scalable benchmark, it provides substantial support for research in the field of automated geometric reasoning and plays a crucial role in advancing formal solution methods for plane geometry problems.
5. Experiment
In this section, we conduct experiments to validate the proposed evaluation system for plane geometry theorem prediction and solving. Specifically, we integrate multiple models with a unified symbolic solver in a consistent experimental setup and systematically explore three key questions: (1) the effectiveness of Completion Rate as the primary evaluation metric, (2) the relationship between the proposed problem difficulty coefficients, intrinsic complexity, and solving efficiency, and (3) the impact of scaling the FormalGeo30K dataset on model generalization.
5.1. Experimental Settings
All experiments were conducted on the FormalGeo7K and FormalGeo30K datasets, both containing formal condition annotations, theorem sequences, and other relevant information, with FormalGeo30K representing a larger-scale extension of FormalGeo7K. Each dataset was split into training, validation, and test sets in a 3:1:1 ratio, and all experiments were conducted in a unified environment equipped with an NVIDIA GeForce RTX 4090 GPU.
To support the multi-dimensional comparative evaluation of the proposed metrics, we assessed three theorem prediction models integrated with the FormalGeo framework’s symbolic solver (FGPS): FGeo-HyperGNet (a neural-symbolic model), BART-base, and T5-small (both serving as generative baselines). FGeo-HyperGNet, the core model in the FormalGeo framework, employs a Transformer architecture without residual connections to encode hypergraphs representing geometric conditions. It utilizes a hypergraph serialization strategy to capture structural relationships, applies a task-specific attention mechanism to assign selection probabilities to candidate theorems, and generates proof paths via beam or greedy beam search. The model was trained using the Adam optimizer with a learning rate of and a batch size of 64 for 50 epochs.
For comparison, we also fine-tuned two Transformer-based pretrained models: BART-base (as used in FGeo-TP) and T5-small (based on the Text-to-Text framework). Both models were optimized with cross-entropy loss and the Adam optimizer, using a learning rate of , trained for 50 epochs, with a maximum sequence length of 30. During decoding, each model produced 40 candidate sequences via beam search, from which the top 20 were retained. All predicted theorem sequences were submitted to the unified FGPS solver for final problem resolution, with a timeout threshold of 600 seconds to ensure consistent experimental conditions.
5.2. Effectiveness of Problem Completion Rate
To validate the effectiveness of the proposed Problem Completion Rate metric PCR, we conducted a systematic evaluation of the three aforementioned models: FGeo-HyperGNet using GB and NB strategies, respectively, BART-base, and T5-small. All of them were paired with the FGPS solver, and we compared PCR with other mainstream performance metrics. Table 1 presents each model’s average solving time, overall PCR, and overall accuracy(success rate). For problems that were not fully solved, it provides a breakdown by failure type (Timeout and Unsolved), reporting the corresponding overall PCR and the number of instances in each category. Figure 4 illustrates the trends of PCR and overall accuracy across different difficulty levels for all models.

Table 1.
Experimental results in FormalGeo7K.
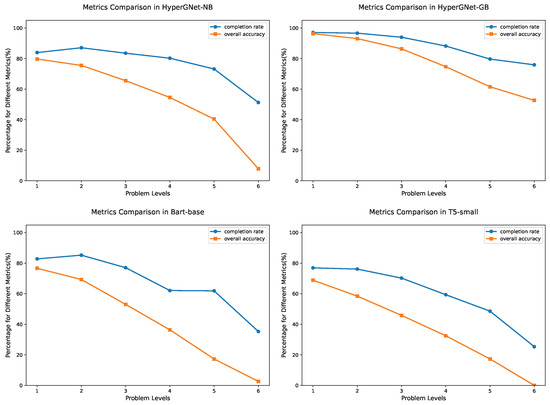
Figure 4.
PCR and overall accuracy at different difficulty levels.
The experimental results demonstrate a high consistency between PCR and overall accuracy in terms of model ranking, confirming PCR’s effectiveness in evaluating overall problem-solving capability. Furthermore, PCR consistently exceeds overall accuracy, indicating its ability to offer finer-grained feedback between partially completed and completely failed solutions. For example, although BART-base achieves an overall accuracy of 61.43%, its PCR reaches 78.08%, suggesting that many unsuccessful cases still contain substantial correct reasoning. HyperGNet-GB leads all models with a PCR of 94.15%, highlighting its strong advantage in reasoning completeness. As shown in Figure 4, both PCR and overall accuracy decline as problem difficulty increases, but the drop in PCR is noticeably smaller—especially for harder problems—demonstrating its ability to capture partial reasoning retained by the models. These findings indicate that PCR not only complements the success rate by addressing its evaluation blind spots but also provides unique value in assessing the completeness of reasoning processes.
Further analysis of Table 1 shows that, compared with the other models, HyperGNet-GB dramatically reduces the number of unsolved instances, approaching zero. However, it exhibits a notably higher count of timeout cases. An examination of these models’ predicted outputs reveals that all theorem prediction models generate parameter-free templates without specific entity bindings. During execution with the FGPS solver, this design forces the system to enumerate a large number of entity combinations for each theorem invocation to identify valid matches. This substantially increases the solving time and may cause theorem instantiations to be overlooked, ultimately resulting in timeouts or failures. This issue is particularly pronounced in HyperGNet-GB due to its higher overall coverage and denser theorem invocation patterns, which exacerbate the efficiency bottleneck caused by the lack of parameterization. To address this problem, we recommend introducing an explicit entity argument prediction mechanism during theorem prediction. By generating theorems with bound entities directly, the model can reduce enumeration overhead, lower timeout risks, and narrow the gap between PCR and overall success rate.
To further quantify the consistency between PCR and the traditional success rate, we conducted a statistical analysis using the prediction results of the HyperGNet-GB model on the FormalGeo7K test set. The results showed a strong positive correlation between the two metrics: the Pearson correlation coefficient was 0.852, the Spearman coefficient was 0.973, and the coefficient of determination from linear regression was . These figures indicate a high degree of alignment in their overall trends, demonstrating that both metrics can effectively reflect the relative problem-solving performance of the model. However, it is worth noting that the two metrics are not entirely consistent. In certain instances, PCR is markedly higher than the success rate, which reveals its capacity to identify cases where the reasoning process was substantially completed even though a final answer was not generated. These are nuances that the traditional success rate does not capture.
Furthermore, PCR can reveal model deficiencies that the traditional success rate fails to detect. In our experiments, we observed that for some unsolved problems, the completion rate reached 1, indicating that the theorem sequence had been fully predicted. However, due to the absence of algebraic operations, the model was unable to produce a final solution, resulting in a success rate of 0. The example shown in Figure 1 case 2 illustrates a scenario where the reasoning steps were present, but the problem was not actually solved. This issue does not stem from the theorem prediction module but rather from limitations within the algebraic reasoning component of the FGPS solver. These findings demonstrate that PCR is sensitive to internal deficiencies in the solving process and can help identify system bottlenecks and guide subsequent optimizations.
In summary, PCR not only maintains a strong correlation with success rate at the macro level but also reveals underlying issues in the problem-solving process at a more granular level. As a result, it serves as an effective and necessary procedural evaluation metric, playing a significant role in advancing automated systems for plane geometry problem solving.
5.3. Reliability of the Difficulty Coefficient
Because the FormalGeo7K dataset used in our study does not include human-annotated difficulty labels, and empirical judgments of problem difficulty are often subjective and inconsistent across annotators or domains, we assess the reliability of the proposed difficulty coefficient by examining its correlation with two commonly accepted proxies for problem complexity: the number of theorem steps required for a solution and the actual solving time. We employed three classical statistical measures: Pearson’s correlation coefficient r to quantify linear relationships, Spearman’s rank correlation coefficient for monotonic associations, and the coefficient of determination from linear regression to assess the proportion of explained variance. Statistical significance is reported using p-values, with indicating highly significant results.
First, we analyzed the number of theorems used in a solution across all 7000 problems in the FormalGeo7K dataset. The results showed a strong positive correlation between the proposed difficulty coefficient and the number of theorem steps, with and (both ), and a regression result of . This indicates that the number of theorem steps accounts for over 82% of the variance in the difficulty coefficient. For example, problems requiring eight theorems received significantly higher difficulty scores than those solvable with only two theorems. This finding aligns with the intuitive notion that more theorem steps correspond to greater problem difficulty in human problem solving.
Next, we evaluated the correlation between actual solving time and the proposed difficulty coefficient. On the FormalGeo7K test set (1400 problems), the solving time of the HyperGNet model (using greedy beam search with a beam size of 5) showed a moderate correlation with the difficulty coefficient. The Pearson coefficient was (), and the Spearman coefficient was (), while the explanatory power of regression remained low ().
These results indicate that the difficulty coefficient partially captures problem-solving efficiency, but it may benefit from further refinement by incorporating deeper indicators such as the topological complexity of the solution hypertree. For further analysis, The relatively weak association may also stem from the asymmetric nature of solving time, which is affected not only by the intrinsic logical complexity of a problem but also by external factors such as theorem prediction accuracy and computational resource allocation. For example, simple problems may require more time due to redundant search paths, whereas complex problems might converge quickly if key theorems are accurately predicted early in the process. Therefore, solving time is more indicative of model efficiency than of the inherent difficulty of the problem.
In summary, the statistical analyses demonstrate that the proposed difficulty coefficient is a highly reliable indicator of geometry problem complexity. Its strong correlation with the number of theorem steps () and substantial explanatory power () highlight its effectiveness in capturing the demands of multi-step reasoning. In contrast, its moderate correlation with solving time reflects the nonlinear interplay between algorithmic efficiency and inherent problem difficulty. Future work may explore the integration of topological features from solution hypergraphs and measures of algebraic computation complexity to construct multimodal regression models and further improve the generalizability of the difficulty coefficient.
5.4. Experiments in FormalGeo30K
We further conducted experiments on the FormalGeo30K dataset. Table 2 presents the results of different models across multiple evaluation dimensions, including overall and level-wise Problem Completion Rate PCR, Success Rate, and inference time. The levels through correspond to the six difficulty tiers defined by our proposed difficulty coefficient.

Table 2.
Experimental results in FormalGeo30K dataset.
Experimental results demonstrate that the substantial expansion of geometric problem data significantly enhances the generalization capabilities of models. For example, HyperGNet, with a greedy beam search strategy(GB), achieves an overall Problem Completion Rate of 97.84% and an Overall Success Rate of 96.38%, clearly outperforming traditional pretrained models. This indicates that a richer combination of theorems and structural patterns not only improves the model’s comprehension of problem structures but also strengthens its robustness and generalization across diverse tasks. Notably, HyperGNet maintains strong performance even on high-difficulty problems (), showing its superiority in complex geometric reasoning tasks.
In addition, compared to its performance on the FormalGeo7K dataset, T5-small exhibits substantial improvement on FormalGeo30K, with its overall success rate surpassing that of the BART-base. This further confirms the critical role of large-scale, diverse data in releasing the full potential of model capabilities.
However, despite the significant improvements in scale and coverage in FormalGeo30K, the distribution of problem difficulty remains imbalanced. A large proportion of the dataset consists of low and medium difficulty problems (), which can artificially inflate aggregate performance metrics. As overall metrics alone are insufficient to accurately reflect a model’s actual problem-solving proficiency, we emphasize performance analysis across difficulty levels. Accordingly, we report the average success rate and average PCR across all difficulty levels, calculated as follows:
where N denotes the number of difficulty levels, and is the success rate or PCR corresponding to the i-th difficulty level. Using this metric, we observe that with the augmented dataset, the FGeo-HyperGNet model’s average success rate improves from 77.43% to 85.01%, while the average PCR increases from 88.57% to 91.79%.
Furthermore, stratified analysis reveals deeper inter-model distinctions. Although BART-base registers lower overall PCR and success rate than HyperGNet, on the highest difficulty problems (), its PCR exceeds that of T5-small by nearly 10% and approaches HyperGNet’s performance. However, its success rate remains similar to that of T5-small and markedly lower than HyperGNet’s. These results suggest that BART-base may possess a structural advantage on certain complex problem types, offering targeted utility in specific sub-tasks despite its overall performance limitations. Consequently, FormalGeo30K facilitates more fine-grained and informative model comparisons.
In conclusion, FormalGeo30K markedly extends both the breadth and depth of model training and evaluation and, through multidimensional metrics, illuminates the capability boundaries of geometric reasoning models. These findings highlight the essential role of large-scale, structurally diverse datasets in advancing geometric problem-solving models.
6. Conclusions
In this paper, we introduce a comprehensive performance evaluation framework, FGeo-Eval, for geometry problem solving, with significant advancements in both solution completeness assessment and difficulty modeling. We propose the Problem Completion Rate metric PCR, which utilizes hypergraph-based structures to effectively capture partial reasoning progress and address the limitations of traditional success rate metrics in identifying incomplete solutions. Our difficulty modeling mechanism, grounded in theorem complexity, systematically estimates and classifies problem difficulty by incorporating reasoning depth and theorem usage frequency. Additionally, we release FormalGeo30K, an extended version of FormalGeo7K, to support large-scale and diverse model training and evaluation. Extensive experiments confirm the validity of the proposed metrics and demonstrate significant performance improvements enabled by large-scale data. In summary, FGeo-Eval provides a robust foundation for model optimization and the development of interpretable, efficient, and scalable AI systems for geometry problem solving.
Nevertheless, the current PCR metric may be influenced by solver-specific behaviors and does not yet account for signals from algebraic reasoning components, which could limit its generalizability. Similarly, the proposed difficulty coefficient primarily reflects theorem usage patterns but does not fully capture aspects such as topological or computational complexity. In future work, we will refine FGeo-Eval by incorporating solver-independent indicators and broader complexity features and further leverage its feedback mechanisms to enhance model components within the FormalGeo framework, pushing automated geometry problem solving toward higher levels of sophistication.
Author Contributions
Conceptualization, Q.H. and T.L.; Methodology, Q.H., X.Z., N.Z., F.Z., and T.L.; Software, Q.H.; Validation, Q.H.; Writing—original draft preparation, Q.H.; Writing—review and editing, Q.H., X.Z., and T.L.; Supervision, T.L.; Funding acquisition, T.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the National Natural Science Foundation of China, grant No. 12071282.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Acknowledgments
Thanks to all researchers involved in academic discussions and the reviewers for their valuable feedback. The authors confirm that the data used in this study were obtained from publicly available online datasets, which have been properly cited. The dataset contains no sensitive or personally identifiable information.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Littman, M.L.; Ajunwa, I.; Berger, G.; Boutilier, C.; Currie, M.; Doshi-Velez, F.; Hadfield, G.; Horowitz, M.C.; Isbell, C.; Kitano, H.; et al. Gathering strength, gathering storms: The one hundred year study on artificial intelligence (AI100) 2021 study panel report. arXiv 2022, arXiv:2210.15767. [Google Scholar]
- Gelernter, H. Realization of a geometry-theorem proving machine. In Computers & Thought; MIT Press: Cambridge, MA, USA, 1995; pp. 134–152. [Google Scholar]
- Zhang, J. The geometry information search system by forward reasoning. Chin. J.-Comput.-Chin. Ed. 1996, 19, 721–727. [Google Scholar]
- Wen-Tsun, W. Basic principles of mechanical theorem proving in elementary geometries. J. Autom. Reason. 1986, 2, 221–252. [Google Scholar] [CrossRef]
- Zhang, J.Z.; Chou, S.C.; Gao, X.S. Automated production of traditional proofs for theorems in Euclidean geometry I. The Hilbert intersection point theorems. Ann. Math. Artif. Intell. 1995, 13, 109–137. [Google Scholar] [CrossRef]
- Lu, P.; Gong, R.; Jiang, S.; Qiu, L.; Huang, S.; Liang, X.; Zhu, S.C. Inter-GPS: Interpretable geometry problem solving with formal language and symbolic reasoning. arXiv 2021, arXiv:2105.04165. [Google Scholar]
- Chen, J.; Tang, J.; Qin, J.; Liang, X.; Liu, L.; Xing, E.P.; Lin, L. GeoQA: A geometric question answering benchmark towards multimodal numerical reasoning. arXiv 2021, arXiv:2105.14517. [Google Scholar]
- Trinh, T.H.; Wu, Y.; Le, Q.V.; He, H.; Luong, T. Solving olympiad geometry without human demonstrations. Nature 2024, 625, 476–482. [Google Scholar] [CrossRef]
- Zhang, X.; Zhu, N.; He, Y.; Zou, J.; Huang, Q.; Jin, X.; Guo, Y.; Mao, C.; Li, Y.; Zhu, Z.; et al. FormalGeo: An Extensible Formalized Framework for Olympiad Geometric Problem Solving. arXiv 2023, arXiv:2310.18021. [Google Scholar]
- Nevins, A.J. Plane geometry theorem proving using forward chaining. Artif. Intell. 1975, 6, 1–23. [Google Scholar] [CrossRef]
- Lin, D.; Liu, Z. Some results on theorem proving in geometry over finite fields. In Proceedings of the 1993 International Symposium on Symbolic and Algebraic Computation, Kiev, Ukraine, 6–8 July 1993; pp. 292–300. [Google Scholar]
- Chou, S.C.; Gao, X.S. Automated reasoning in differential geometry and mechanics using the characteristic set method: Part II. Mechanical theorem proving. J. Autom. Reason. 1993, 10, 173–189. [Google Scholar] [CrossRef]
- Wu, W.T. On a finiteness theorem about problems involving inequalities. J. Syst. Sci. Math. Sci. 1994, 7, 193–200. [Google Scholar]
- Buchberger, B. Applications of Gröbner bases in non-linear computational geometry. In Mathematical Aspects of Scientific Software; Springer: Berlin/Heidelberg, Germany, 1988; pp. 59–87. [Google Scholar]
- Yang, L.; Zhang, J.; Li, C. A prover for parallel numerical verification of a class of constructive geometry theorems. In Proceedings of the International Workshop on Memory Management, St. Malo, France, 17–19 September 1992; Volume 92, pp. 244–250. [Google Scholar]
- Yang, L.; Zhang, J. Searching dependency between algebraic equations: An algorithm applied to automated reasoning. In Technical Report; International Centre for Theoretical Physics: Trieste, Italy, 1990. [Google Scholar]
- Lu, Y. Practical automated reasoning on inequalities: Generic programs for inequality proving and discovering. In Proceedings of the Third Asian Technology Conference in Mathematics, Tsukuba, Japan, 24–28 August 1998; pp. 24–28. [Google Scholar]
- Chou, S.C.; Gao, X.S.; Zhang, J.Z. Automated production of traditional proofs for constructive geometry theorems. In Proceedings of the [1993] Proceedings Eighth Annual IEEE Symposium on Logic in Computer Science, Montreal, QC, Canada, 19–23 June 1993; pp. 48–56. [Google Scholar]
- Chou, S.C.; Gao, X.S.; Zhang, J.Z. Automated geometry theorem proving by vector calculation. In Proceedings of the 1993 International Symposium on Symbolic and Algebraic Computation, Kiev, Ukraine, 6–8 July 1993; pp. 284–291. [Google Scholar]
- Chou, S.C.; Gao, X.S.; Zhang, J.Z. A Collection of 110 Geometry Theorems and Their Machine Produced Proofs Using Full-Angles; Washington State University: Washington, DC, USA, 1994. [Google Scholar]
- Chou, S.C.; Gao, X.S.; Zhang, J.Z. Automated production of traditional proofs in solid geometry. J. Autom. Reason. 1995, 14, 257–291. [Google Scholar] [CrossRef]
- Chou, S.; Gao, X.; Zhang, J. A Collection of 90 Mechanically Solved Geometry Problems from Non-Euclidean Geometries; Washington State University: Washington, DC, USA, 1994. [Google Scholar]
- Seo, M.; Hajishirzi, H.; Farhadi, A.; Etzioni, O.; Malcolm, C. Solving geometry problems: Combining text and diagram interpretation. In Proceedings of the 2015 Conference on Empirical Methods in Natural Language Processing, Lisbon, Portugal, 17–21 September 2015; pp. 1466–1476. [Google Scholar]
- Sachan, M.; Dubey, K.; Xing, E. From textbooks to knowledge: A case study in harvesting axiomatic knowledge from textbooks to solve geometry problems. In Proceedings of the 2017 Conference on Empirical Methods in Natural Language Processing, Copenhagen, Denmark, 9–11 September 2017; pp. 773–784. [Google Scholar]
- Sachan, M.; Xing, E. Learning to solve geometry problems from natural language demonstrations in textbooks. In Proceedings of the 6th Joint Conference on Lexical and Computational Semantics (* SEM 2017), Vancouver, BC, Canada, 3–4 August 2017; pp. 251–261. [Google Scholar]
- Alvin, C.; Gulwani, S.; Majumdar, R.; Mukhopadhyay, S. Synthesis of Solutions for Shaded Area Geometry Problems. In Proceedings of the Thirtieth International Florida Artificial Intelligence Research Society Conference, Marco Island, FL, USA, 22–24 May 2017; pp. 14–19. [Google Scholar]
- Yu, X.; Wang, M.; Gan, W.; He, B.; Ye, N. A framework for solving explicit arithmetic word problems and proving plane geometry theorems. Int. J. Pattern Recognit. Artif. Intell. 2019, 33, 1940005. [Google Scholar] [CrossRef]
- Gan, W.; Yu, X.; Zhang, T.; Wang, M. Automatically proving plane geometry theorems stated by text and diagram. Int. J. Pattern Recognit. Artif. Intell. 2019, 33, 1940003. [Google Scholar] [CrossRef]
- Gan, W.; Yu, X. Automatic understanding and formalization of natural language geometry problems using syntax-semantics models. Int. J. Innov. Comput. Inf. Control 2018, 14, 83–98. [Google Scholar]
- Gan, W.; Yu, X.; Wang, M. Automatic understanding and formalization of plane geometry proving problems in natural language: A supervised approach. Int. J. Artif. Intell. Tools 2019, 28, 1940003. [Google Scholar] [CrossRef]
- Sachan, M.; Dubey, A.; Hovy, E.H.; Mitchell, T.M.; Roth, D.; Xing, E.P. Discourse in multimedia: A case study in extracting geometry knowledge from textbooks. Comput. Linguist. 2020, 45, 627–665. [Google Scholar] [CrossRef]
- He, Y.; Zou, J.; Zhang, X.; Zhu, N.; Leng, T. Fgeo-tp: A language model-enhanced solver for euclidean geometry problems. Symmetry 2024, 16, 421. [Google Scholar] [CrossRef]
- Tsai, S.h.; Liang, C.C.; Wang, H.M.; Su, K.Y. Sequence to general tree: Knowledge-guided geometry word problem solving. arXiv 2021, arXiv:2106.00990. [Google Scholar]
- Peng, S.; Fu, D.; Liang, Y.; Gao, L.; Tang, Z. Geodrl: A self-learning framework for geometry problem solving using reinforcement learning in deductive reasoning. In Proceedings of the Findings of the Association for Computational Linguistics: ACL 2023, Toronto, ON, Canada, 9–14 July 2023; pp. 13468–13480. [Google Scholar]
- Wu, W.; Zhang, L.; Liu, J.; Tang, X.; Wang, Y.; Wang, S.; Wang, Q. E-gps: Explainable geometry problem solving via top-down solver and bottom-up generator. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 18–22 June 2024; pp. 13828–13837. [Google Scholar]
- Zou, J.; Zhang, X.; He, Y.; Zhu, N.; Leng, T. Fgeo-drl: Deductive reasoning for geometric problems through deep reinforcement learning. Symmetry 2024, 16, 437. [Google Scholar] [CrossRef]
- Zhang, C.; Song, J.; Li, S.; Liang, Y.; Ma, Y.; Wang, W.; Zhu, Y.; Zhu, S.C. Proposing and solving olympiad geometry with guided tree search. arXiv 2024, arXiv:2412.10673. [Google Scholar]
- Chen, J.; Li, T.; Qin, J.; Lu, P.; Lin, L.; Chen, C.; Liang, X. Unigeo: Unifying geometry logical reasoning via reformulating mathematical expression. arXiv 2022, arXiv:2212.02746. [Google Scholar]
- Cao, J.; Xiao, J. An augmented benchmark dataset for geometric question answering through dual parallel text encoding. In Proceedings of the 29th International Conference on Computational Linguistics, Busan, Republic of Korea, 12–17 October 2022; pp. 1511–1520. [Google Scholar]
- Ning, M.; Wang, Q.F.; Huang, K.; Huang, X. A symbolic characters aware model for solving geometry problems. In Proceedings of the 31st ACM International Conference on Multimedia, Ottawa, ON, Canada, 29 October–2 November 2023; pp. 7767–7775. [Google Scholar]
- Liang, Z.; Yang, T.; Zhang, J.; Zhang, X. Unimath: A foundational and multimodal mathematical reasoner. In Proceedings of the 2023 Conference on Empirical Methods in Natural Language Processing, Singapore, 6–10 December 2023; pp. 7126–7133. [Google Scholar]
- Xiao, T.; Liu, J.; Huang, Z.; Wu, J.; Sha, J.; Wang, S.; Chen, E. Learning to solve geometry problems via simulating human dual-reasoning process. arXiv 2024, arXiv:2405.06232. [Google Scholar]
- Zhang, J.; Moshfeghi, Y. GOLD: Geometry problem solver with natural language description. arXiv 2024, arXiv:2405.00494. [Google Scholar]
- Li, Z.Z.; Zhang, M.L.; Yin, F.; Liu, C.L. LANS: A layout-aware neural solver for plane geometry problem. arXiv 2023, arXiv:2311.16476. [Google Scholar]
- Zhang, M.L.; Yin, F.; Hao, Y.H.; Liu, C.L. Plane geometry diagram parsing. arXiv 2022, arXiv:2205.09363. [Google Scholar]
- Zhu, N.; Zhang, X.; Huang, Q.; Zhu, F.; Zeng, Z.; Leng, T. FGeo-Parser: Autoformalization and Solution of Plane Geometric Problems. Symmetry 2024, 17, 8. [Google Scholar] [CrossRef]
- Murphy, L.; Yang, K.; Sun, J.; Li, Z.; Anandkumar, A.; Si, X. Autoformalizing euclidean geometry. arXiv 2024, arXiv:2405.17216. [Google Scholar]
- Zhang, X.; Zhu, N.; He, Y.; Zou, J.; Qin, C.; Li, Y.; Leng, T. FGeo-SSS: A Search-Based Symbolic Solver for Human-like Automated Geometric Reasoning. Symmetry 2024, 16, 404. [Google Scholar] [CrossRef]
- Zhang, X.; Zhu, N.; Qin, C.; Li, Y.; Zeng, Z.; Leng, T. FGeo-HyperGNet: Geometric Problem Solving Integrating Formal Symbolic System and Hypergraph Neural Network. arXiv 2024, arXiv:2402.11461. [Google Scholar]
- Hao, Y.; Zhang, M.; Yin, F.; Huang, L.L. PGDP5K: A diagram parsing dataset for plane geometry problems. In Proceedings of the 2022 26th international conference on pattern recognition (ICPR), Montreal, QC, Canada, 21–25 August 2022; pp. 1763–1769. [Google Scholar]
- Zhang, M.L.; Yin, F.; Liu, C.L. A multi-modal neural geometric solver with textual clauses parsed from diagram. arXiv 2023, arXiv:2302.11097. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).