Discrete Memristor-Based Hyperchaotic Map and Its Analog Circuit Implementation
Abstract
1. Introduction
- (1)
- Controllable parameters are integrated into the A-DM map, enabling in-depth investigation of its global and local amplitude control characteristics—with circuit-level validation of the discrete map achieved via analog circuit simulation.
- (2)
- A novel hyperchaotic map—featuring multi-stability, symmetry, high complexity, and an extensive chaotic region—is constructed via parallel coupling operation of the A-DM and sine map.
- (3)
- Circuit simulation with a step power supply provides initial values for SAHM, validating analog circuit realization of coexisting attractors. The NIST test passage of PRNs generated by SAHM confirms its applicability to secure encryption scenarios.
2. Discrete Memristor Chaotic Map
3. Memristor Chaotic Map and Its Dynamic Analysis
3.1. Memristor Chaotic Map
3.2. Dynamic Behavior Analysis of A-DM Map
3.3. Amplitude Control
3.4. The Multistability of A-DM Map
3.5. Analog Circuit Simulation
4. New Map Coupling with A-DM
4.1. Dynamic Analysis of SAHM
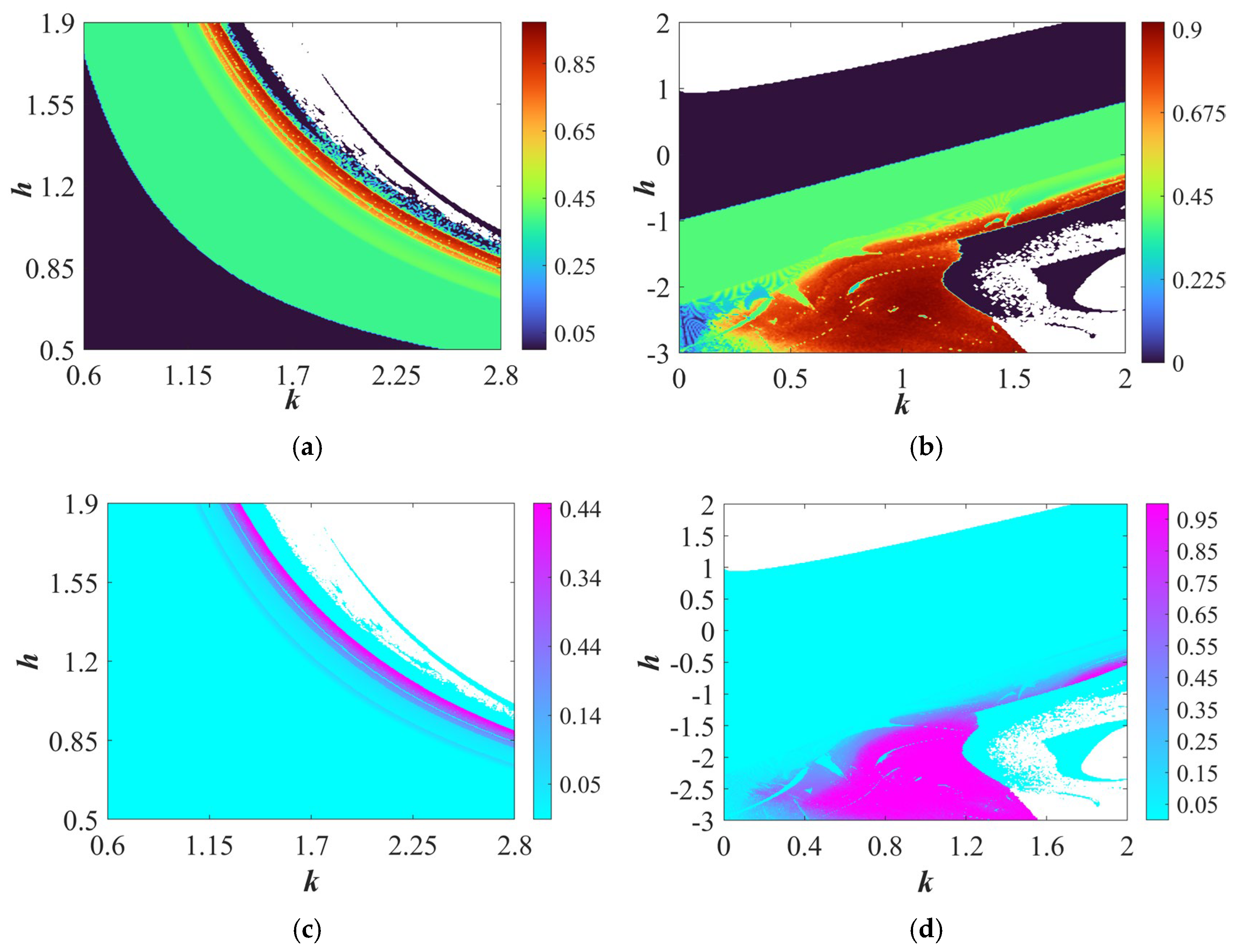
4.2. Dynamic Behavior Analysis of SAHM
4.3. Gottwald-Melbourne 0–1 Test
4.4. Multi-Stability
4.5. Symmetry
4.6. Analog Circuit Simulation of SAHM
5. Complexity and Performance Analysis
5.1. SE and C0 Complexity
5.2. Performance Analysis
6. Application in PRNG
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chua, L. Memristor-The missing circuit element. IEEE Trans. Circuit Theory 1971, 18, 507–519. [Google Scholar] [CrossRef]
- Chua, L.O.; Kang, S.M. Memristive devices and systems. Proc. IEEE 1976, 64, 209–223. [Google Scholar] [CrossRef]
- Lin, T.-C.; Huang, F.-Y.; Du, Z.; Lin, Y.-C. Synchronization of fuzzy modeling chaotic time delay memristor-based Chua’s circuits with application to secure communication. Int. J. Fuzzy Syst. 2015, 17, 206–214. [Google Scholar] [CrossRef]
- Iqbal, M.; Riaz, M.B.; Ur Rehman, M.A.; Martinovic, T.; Martinovic, J. Demonstration of Sensitive analysis and optical soliton patterns in a (4+1) Dimensional Boiti-Leon-Manna Pempinelli Equation: Dynamic insights into bifurcation, chaotic behavior. Chaos Theory Appl. (CHTA) 2025, 7, 1–9. [Google Scholar] [CrossRef]
- Karimov, T.; Mikhailov, A.; Rybin, V.; Sheptunova, V.; Babkin, I.; Butusov, D. Attack-Resistant Chaotic Communication System in Non-ideal Physical Channel. CHF 2025, 2, 28–37. [Google Scholar] [CrossRef]
- Zhou, L.; Wang, C.; Zhou, L. Generating hyperchaotic multi-wing attractor in a 4D memristive circuit. Nonlinear Dyn. 2016, 85, 2653–2663. [Google Scholar] [CrossRef]
- Mannan, Z.I.; Choi, H.; Rajamani, V.; Kim, H.; Chua, L. Chua corsage memristor: Phase portraits, basin of attraction, and coexisting pinched hysteresis loops. Int. J. Bifurc. Chaos 2017, 27, 1730011. [Google Scholar] [CrossRef]
- Xu, Q.; Lin, Y.; Bao, B.; Chen, M. Multiple attractors in a non-ideal active voltage-controlled memristor based Chua’s circuit. Chaos Solitons Fractals 2016, 83, 186–200. [Google Scholar] [CrossRef]
- Min, F.; Xue, L. Routes toward chaos in a memristor-based Shinriki circuit. Chaos Interdiscip. J. Nonlinear Sci. 2023, 33, 023122. [Google Scholar] [CrossRef] [PubMed]
- Qian, K.; Xiao, Y.; Wei, Y.; Liu, D.; Wang, Q.; Feng, W. A Robust Memristor-Enhanced Polynomial Hyper-Chaotic Map and Its Multi-Channel Image Encryption Application. Micromachines 2023, 14, 2090. [Google Scholar] [CrossRef]
- He, S.; Zhan, D.; Wang, H.; Sun, K.; Peng, Y. Discrete memristor and discrete memristive systems. Entropy 2022, 24, 786. [Google Scholar] [CrossRef]
- Bao, H.; Hua, Z.; Li, H.; Chen, M.; Bao, B. Discrete memristor hyperchaotic maps. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 4534–4544. [Google Scholar] [CrossRef]
- Peng, Y.; Sun, K.; He, S. A discrete memristor model and its application in Hénon map. Chaos Solitons Fractals 2020, 137, 109873. [Google Scholar] [CrossRef]
- Peng, Y.; He, S.; Sun, K. A higher dimensional chaotic map with discrete memristor. AEU-Int. J. Electron. Commun. 2021, 129, 153539. [Google Scholar] [CrossRef]
- Ma, M.; Yang, Y.; Qiu, Z.; Peng, Y.; Sun, Y.; Li, Z.; Wang, M. A locally active discrete memristor model and its application in a hyperchaotic map. Nonlinear Dyn. 2022, 107, 2935–2949. [Google Scholar] [CrossRef]
- Laskaridis, L.; Volos, C.; Stouboulos, I.; Antoniades, I.P. A Discrete memristive hyperchaotic map with a modulo function. In Proceedings of the 2023 12th International Conference on Modern Circuits and Systems Technologies (MOCAST), Athens, Greece, 28–30 June 2023; IEEE: New York, NY, USA, 2023; pp. 1–4. [Google Scholar] [CrossRef]
- Fan, Z. Construction, dynamic analysis and DSP implementation of a novel 3D discrete memristive hyperchaotic map. Chaos Solitons Fractals 2023, 177, 114303. [Google Scholar] [CrossRef]
- Feng, W.; Zhang, K.; Zhang, J.; Zhao, X.; Chen, Y.; Cai, B.; Zhu, Z.; Wen, H.; Ye, C. Integrating Fractional-Order Hopfield Neural Network with Differentiated Encryption: Achieving High-Performance Privacy Protection for Medical Images. Fractal Fract. 2025, 9, 426. [Google Scholar] [CrossRef]
- Hong, Q.; Jiang, H.; Xiao, P.; Du, S.; Li, T. A Parallel Computing Scheme Utilizing Memristor Crossbars for Fast Corner Detection and Rotation Invariance in the ORB Algorithm. IEEE Trans. Comput. 2025, 74, 996–1010. [Google Scholar] [CrossRef]
- Xiao, P.; Fang, J.; Wei, Z.; Dong, Y.; Du, S.; Wen, S.; Hong, Q. A Riccati Matrix Equation Solver Design Based Neurodynamics Method and Its Application. IEEE Trans. Autom. Sci. Eng. 2025, 22, 15163–15176. [Google Scholar] [CrossRef]
- Yu, F.; Wu, C.; Xu, S.; Yao, W.; Xu, C.; Cai, S.; Wang, C. Color video encryption transmission in IoT based on memristive hopfield neural network. SIViP 2025, 19, 77. [Google Scholar] [CrossRef]
- Yu, F.; He, S.; Yao, W.; Cai, S.; Xu, Q. Bursting Firings in Memristive Hopfield Neural Network with Image Encryption and Hardware Implementation. IEEE Trans. Comput.-Aided Des. Integr. Circuits. Syst. 2025, 1. [Google Scholar] [CrossRef]
- Li, K.; Bao, H.; Li, H.; Ma, J.; Hua, Z.; Bao, B. Memristive Rulkov neuron model with magnetic induction effects. IEEE Trans. Ind. Inf. 2022, 18, 1726–1736. [Google Scholar] [CrossRef]
- Li, Y.; Li, C.; Lei, T.; Yang, Y.; Chen, G. Offset boosting-entangled complex dynamics in the memristive Rulkov neuron. IEEE Trans. Ind. Electron. 2023, 71, 9569–9579. [Google Scholar] [CrossRef]
- Lai, Q.; Yang, L. Discrete memristor applied to construct neural networks with homogeneous and heterogeneous coexisting attractors. Chaos Solitons Fractals 2023, 174, 113807. [Google Scholar] [CrossRef]
- Bao, H.; Hua, Z.; Wang, N.; Zhu, L.; Chen, M.; Bao, B. Initials-Boosted Coexisting Chaos in a 2-D Sine Map and Its Hardware Implementation. IEEE Trans. Ind. Inf. 2021, 17, 1132–1140. [Google Scholar] [CrossRef]
- Kavehei, O.; Iqbal, A.; Kim, Y.S.; Eshraghian, K.; Al-Sarawi, S.F.; Abbott, D. The fourth element: Characteristics, modelling and electromagnetic theory of the memristor. Proc. R. Soc. A 2010, 466, 2175–2202. [Google Scholar] [CrossRef]
- Peng, Y.; Lan, Z.; Li, W.; Li, Y.; Peng, J. Modeling different discrete memristive sine maps and its parameter identification. Eur. Phys. J. Spec. Top. 2022, 231, 3187–3196. [Google Scholar] [CrossRef]
- Eshraghian, K.; Kavehei, O.; Chappell, J.M.; Iqbal, A.; Al-Sarawi, S.F.; Abbott, D. Memristive device fundamentals and modeling: Applications to circuits and systems simulation. Proc. IEEE 2012, 100, 1991–2007. [Google Scholar] [CrossRef]
- Wang, Q.; Tian, Z.; Wu, X.; Li, K.; Sang, H.; Yu, X. A 5D super-extreme-multistability hyperchaotic map based on parallel-cascaded memristors. Chaos Solitons Fractals 2024, 187, 115452. [Google Scholar] [CrossRef]
- Fu, L.; Wu, X.; He, S.; Wang, H.; Sun, K. A memristive Hénon map based on the state variable difference and its analog circuit implementation. IEEE Trans. Ind. Electron. 2023, 71, 9668–9676. [Google Scholar] [CrossRef]
- Yang, K.; Joshua Yang, J.; Huang, R.; Yang, Y. Nonlinearity in Memristors for Neuromorphic Dynamic Systems. Small Sci. 2022, 2, 2100049. [Google Scholar] [CrossRef]
- Corinto, F.; Ascoli, A.; Gilli, M. Nonlinear Dynamics of Memristor Oscillators. IEEE Trans. Circuits Syst. I 2011, 58, 1323–1336. [Google Scholar] [CrossRef]
- Corinto, F.; Forti, M. Memristor Circuits: Bifurcations without Parameters. IEEE Trans. Circuits Syst. I 2017, 64, 1540–1551. [Google Scholar] [CrossRef]
- Li, K.; Wang, Q.; Hu, C.; Liang, B.; Jian, C.; Zheng, Q.; Tian, Z.; Zhao, J. Dynamical analysis of a novel 2D Lyapunov exponent controllable memristive chaotic map. Chaos Interdiscip. J. Nonlinear Sci. 2024, 34, 083135. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Zhang, H.; Wang, C. Dynamical analysis and applications of a novel 2-D hybrid dual-memristor hyperchaotic map with complexity enhancement. Nonlinear Dyn. 2023, 111, 15487–15513. [Google Scholar] [CrossRef]
- Han, X.; Bi, X.; Sun, B.; Ren, L.; Xiong, L. Dynamical Analysis of Two-Dimensional Memristor Cosine Map. Front. Phys. 2022, 10, 911144. [Google Scholar] [CrossRef]
- Khan, A.; Li, C.; Zhang, X.; Cen, X. A Two-Memristor-based Chaotic System with Symmetric Bifurcation and Multistability. CHF 2025, 2, 1–7. [Google Scholar] [CrossRef]
- Sharma, P.R.; Shrimali, M.D.; Prasad, A.; Kuznetsov, N.V.; Leonov, G.A. Control of multistability in hidden attractors. Eur. Phys. J. Spec. Top. 2015, 224, 1485–1491. [Google Scholar] [CrossRef]
- Emin, B.; Yaz, M. Digital Implementation of Chaotic Systems Using Nvidia Jetson AGX Orin and Custom DAC Converter. CHF 2024, 1, 38–41. [Google Scholar] [CrossRef]
- Alawida, M.; Samsudin, A.; Teh, J.S.; Alshoura, W.H. Digital Cosine Chaotic Map for Cryptographic Applications. IEEE Access 2019, 7, 150609–150622. [Google Scholar] [CrossRef]
- Zhu, H.; Liu, W.; Sun, K.; Wang, H. Sine-modulation Discrete Memristor Chaotic Map and Its Applications. Nonlinear Dyn. 2025, 1–11. [Google Scholar] [CrossRef]
- Chong, Z.; Wang, C.; Zhang, H.; Zhang, S. Sine-Transform-Based Dual-Memristor Hyperchaotic Map and Analog Circuit Implementation. IEEE Trans. Instrum. Meas. 2025, 74, 1–14. [Google Scholar] [CrossRef]
- Hermans, M.; Schrauwen, B.; Bienstman, P.; Dambre, J. Automated Design of Complex Dynamic Systems. PLoS ONE 2014, 9, e86696. [Google Scholar] [CrossRef]
- Falconer, I.; Gottwald, G.A.; Melbourne, I.; Wormnes, K. Application of the 0-1 test for chaos to experimental data. SIAM J. Appl. Dyn. Syst. 2007, 6, 395–402. [Google Scholar] [CrossRef]
- Cetina-Denis, J.J.; Lopéz-Gutiérrez, R.M.; Cruz-Hernández, C.; Arellano-Delgado, A. Design of a chaotic trajectory generator algorithm for mobile robots. Appl. Sci. 2022, 12, 2587. [Google Scholar] [CrossRef]
- Murillo-Escobar, D.; Murillo-Escobar, M.Á.; Cruz-Hernández, C.; Arellano-Delgado, A.; López-Gutiérrez, R.M. Pseudorandom number generator based on novel 2D Hénon-Sine hyperchaotic map with microcontroller implementation. Nonlinear Dyn. 2023, 111, 6773–6789. [Google Scholar] [CrossRef] [PubMed]
- Mashuri, A.; Adenan, N.H.; Abd Karim, N.S.; Siew, W.T.; Zeng, Z. Application of Chaos Theory in Different Fields—A Literature Review. JSML 2024, 12, 92–101. [Google Scholar] [CrossRef]
- Hua, Q.; Shen, B. Simulation of selective catalytic reduction of NO and oxidation of CO and C7H8 over V2O5-TiO2 catalyst. J. Energy Inst. 2025, 119, 101956. [Google Scholar] [CrossRef]
- Pisarchik, A.N.; Hramov, A.E. Multistability in Physical and Living Systems: Characterization and Applications; Springer International Publishing: Cham, Switzerland, 2022. [Google Scholar] [CrossRef]
- Cao, Y.; Li, Z.; He, S. Complex hidden dynamics in a memristive map with delta connection and its application in image encryption. Nonlinear Dyn. 2024, 112, 7597–7613. [Google Scholar] [CrossRef]
- He, S.; Hu, K.; Wang, M.; Wang, H.; Wu, X. Design and dynamics of discrete dual-memristor chaotic maps and its application in speech encryption. Chaos Solitons Fractals 2024, 188, 115517. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Z.; Zhang, L.Y.; Pareschi, F.; Setti, G.; Chen, G. From chaos to pseudorandomness: A case study on the 2-D coupled map lattice. IEEE Trans. Cybern. 2023, 53, 1324–1334. [Google Scholar] [CrossRef] [PubMed]
- Rukhin, A.; Soto, J.; Nechvatal, J.; Smid, M.; Barker, E.; Leigh, S.; Levenson, M.; Vangel, M.; Banks, D.; Heckert, A.; et al. A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications; Department of Commerce, Technology Administration, National Institute of Standards and Technology: Gaithersburg, MD, USA, 2010; Volume 22. [Google Scholar]
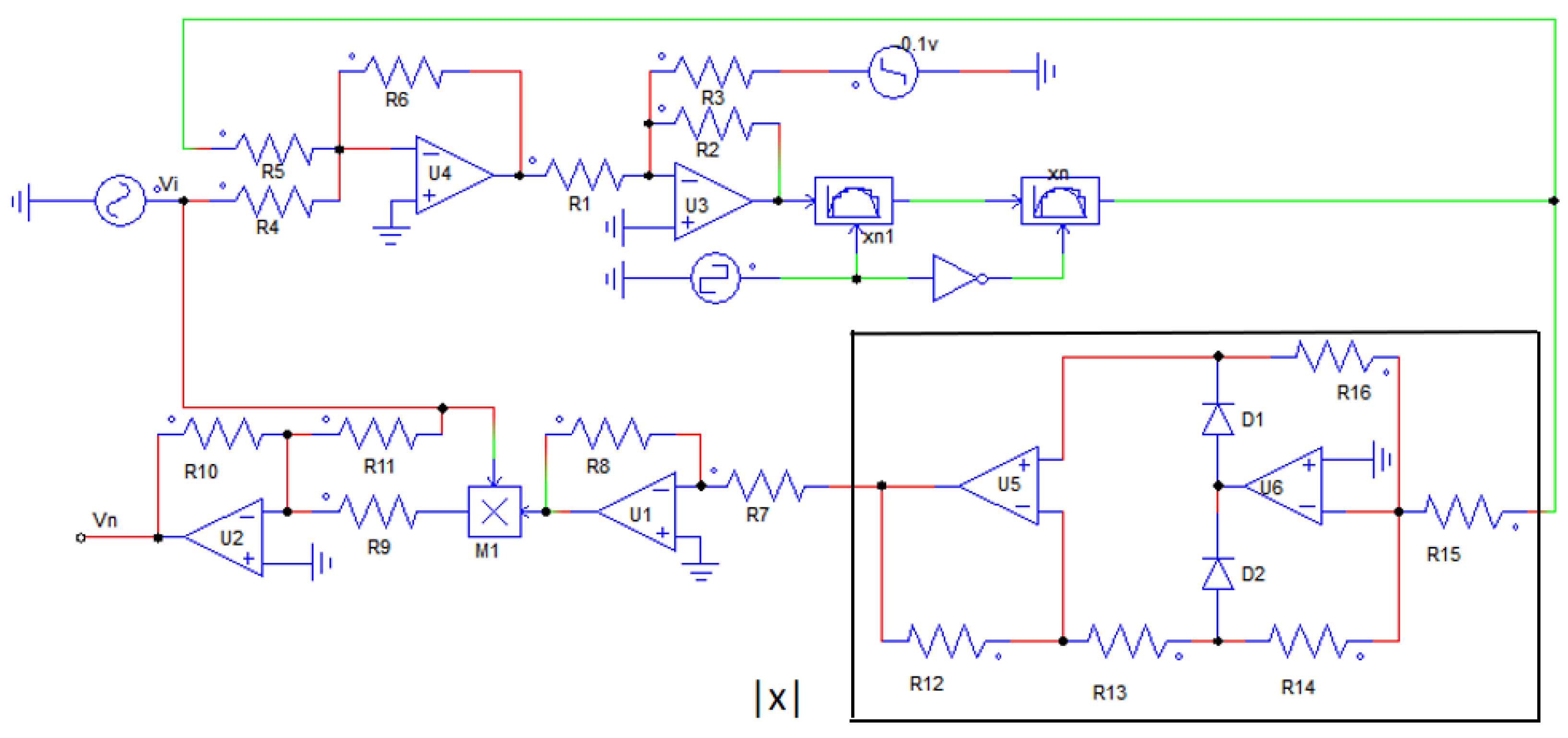
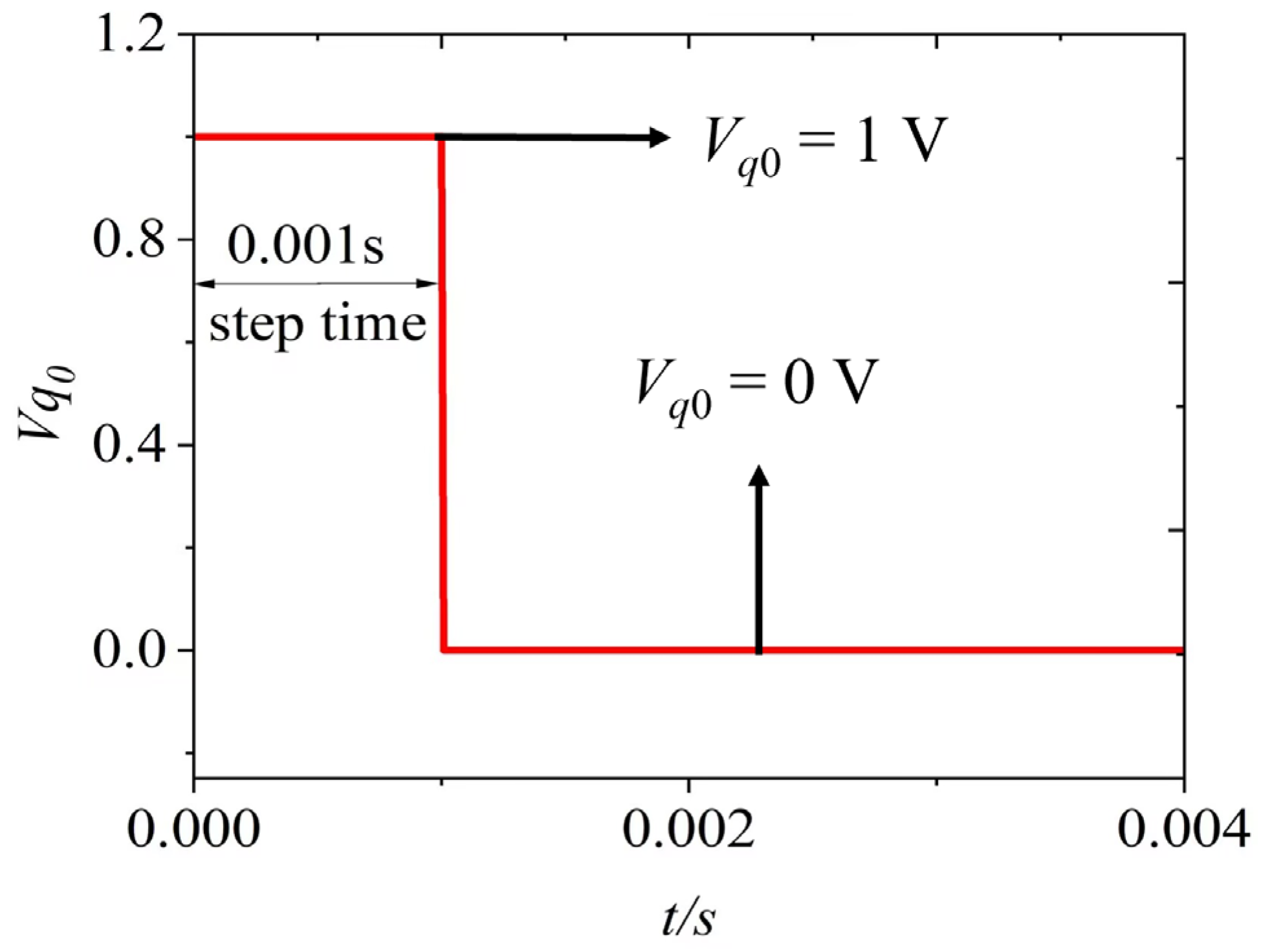
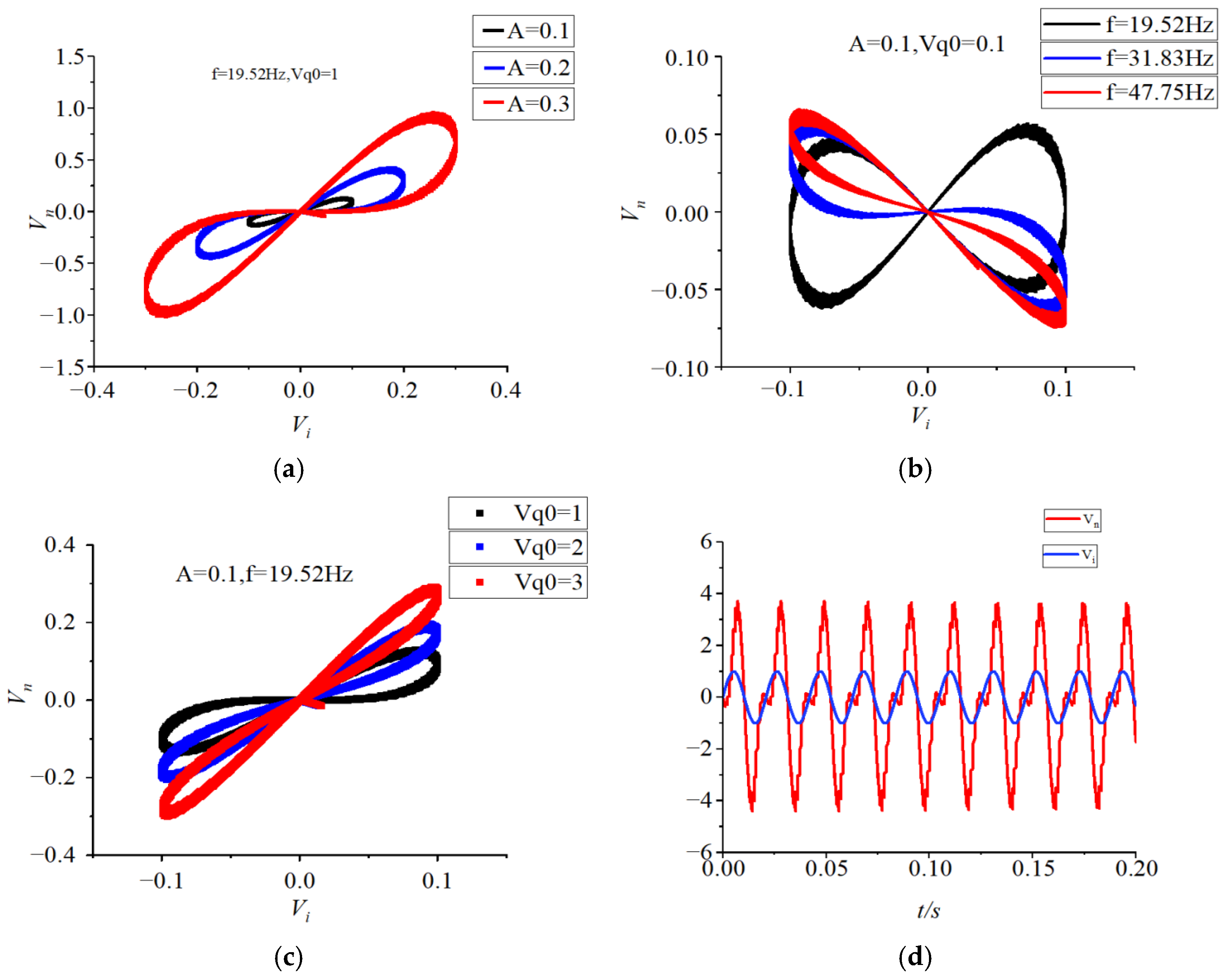
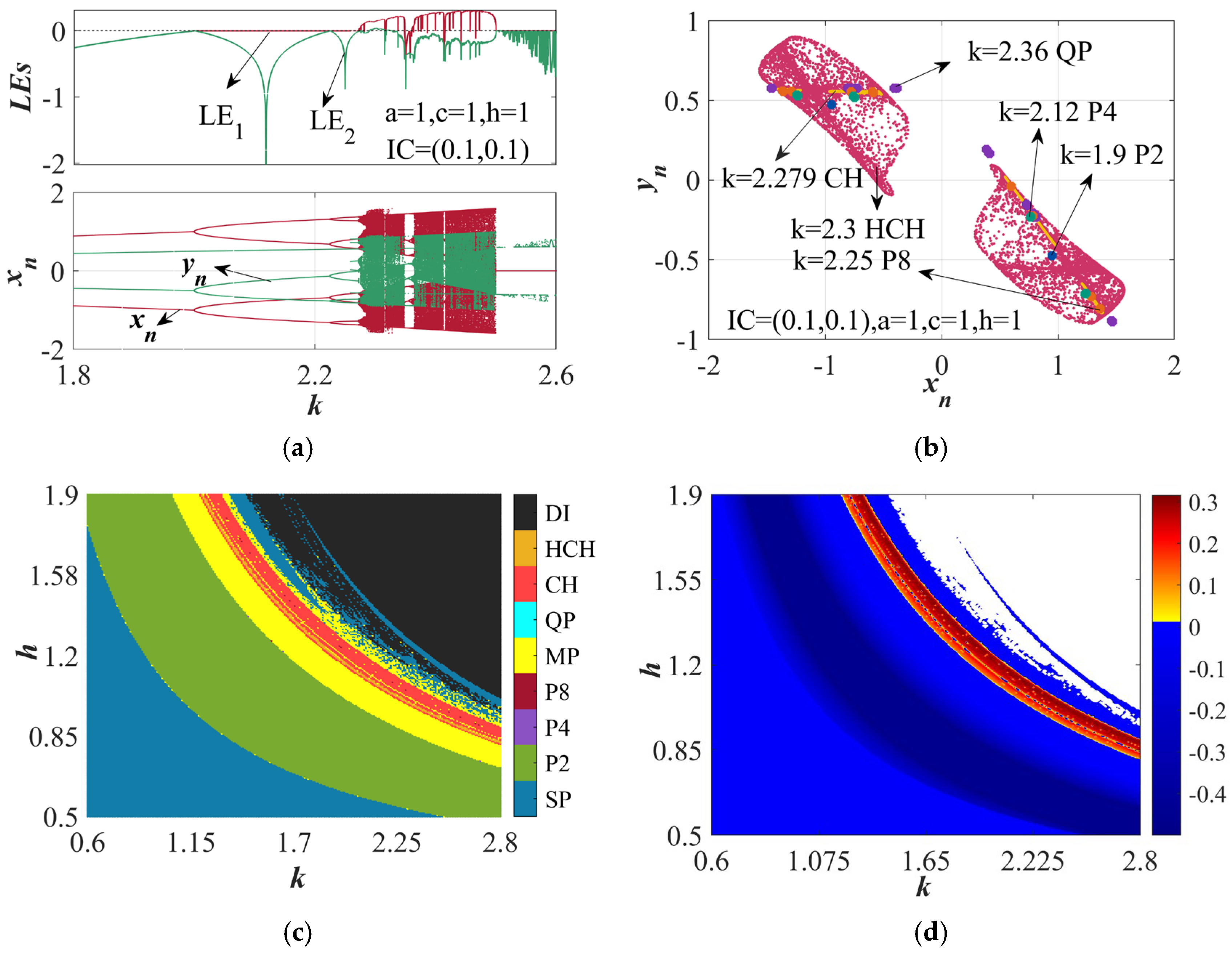
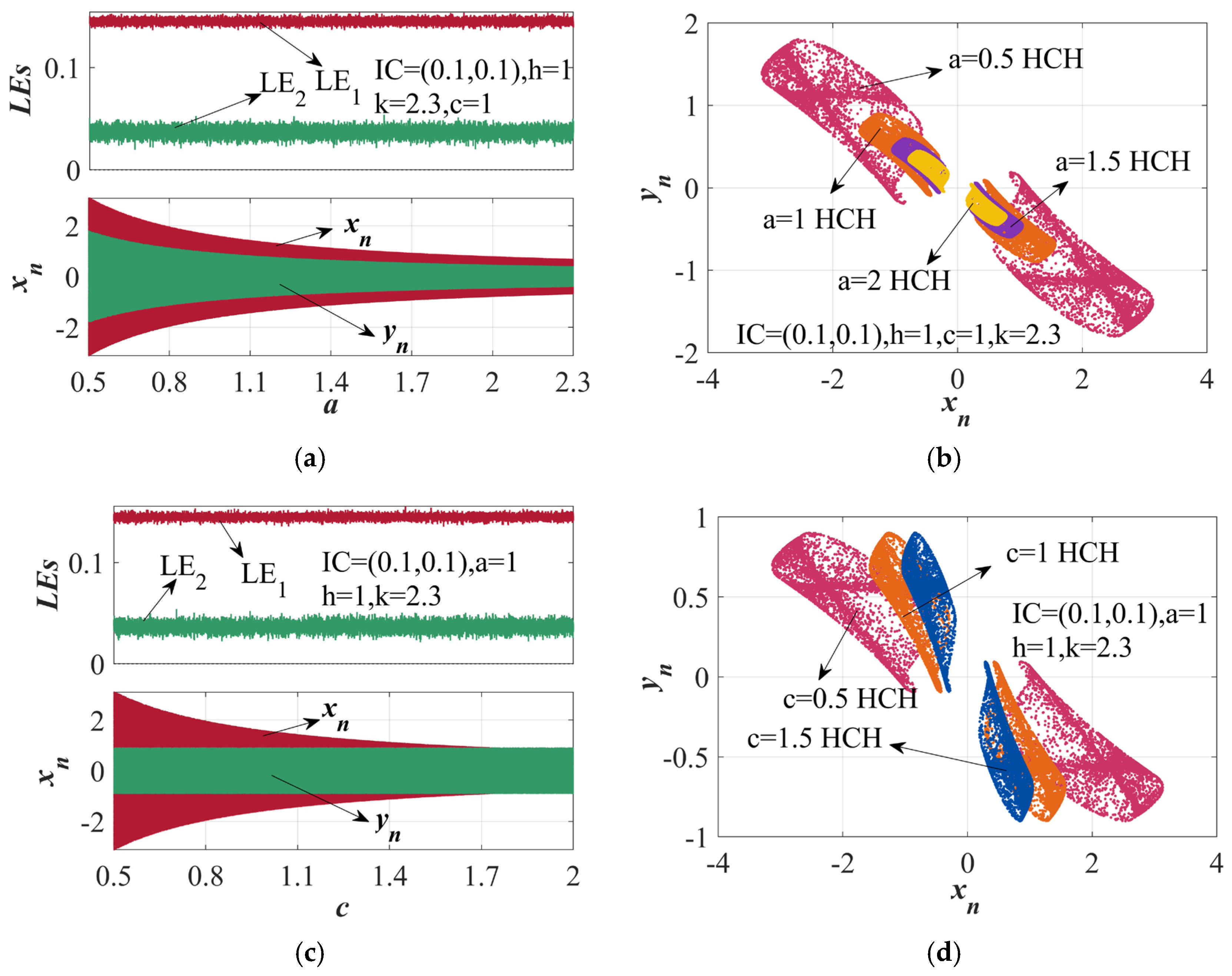

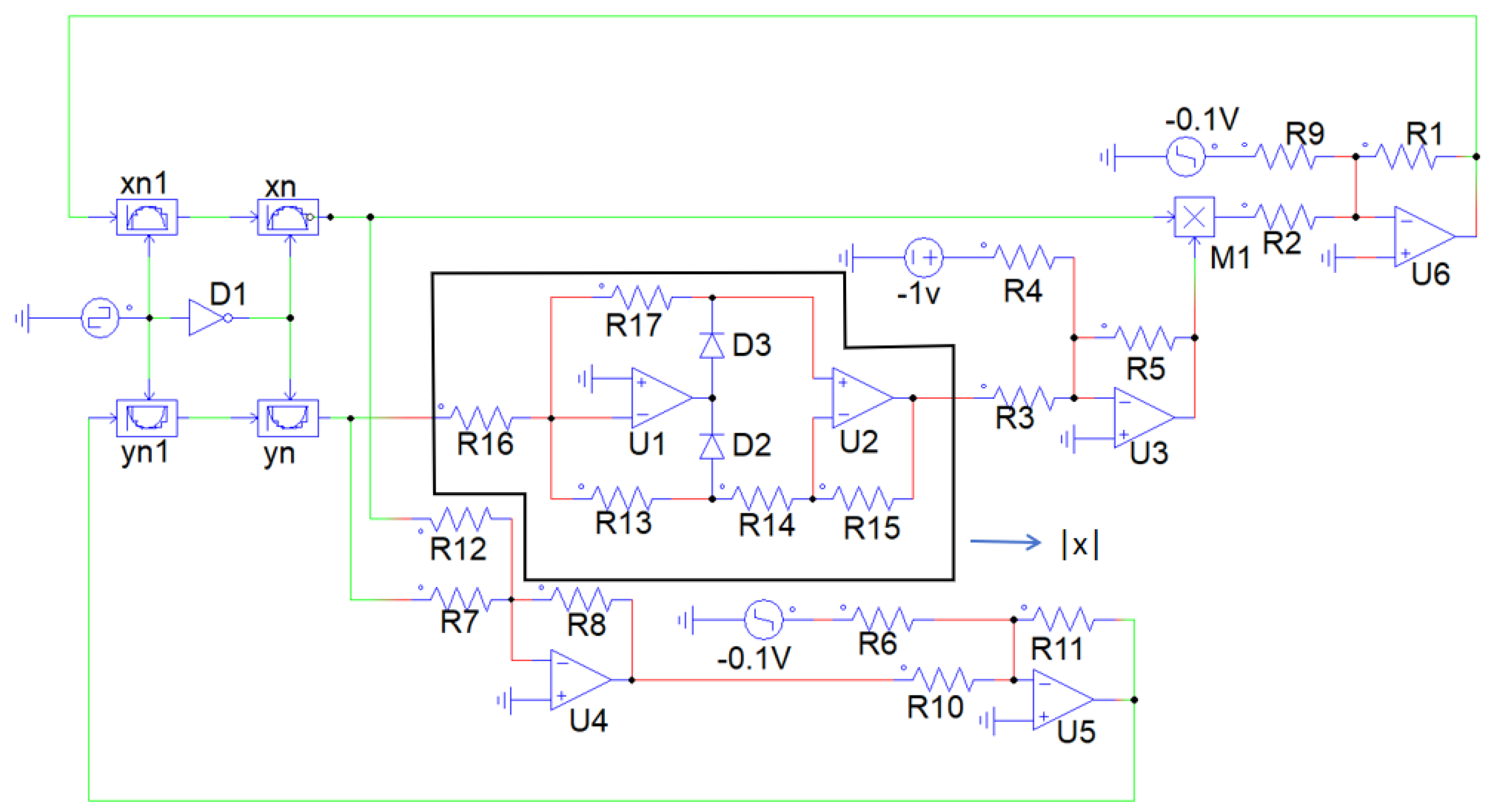

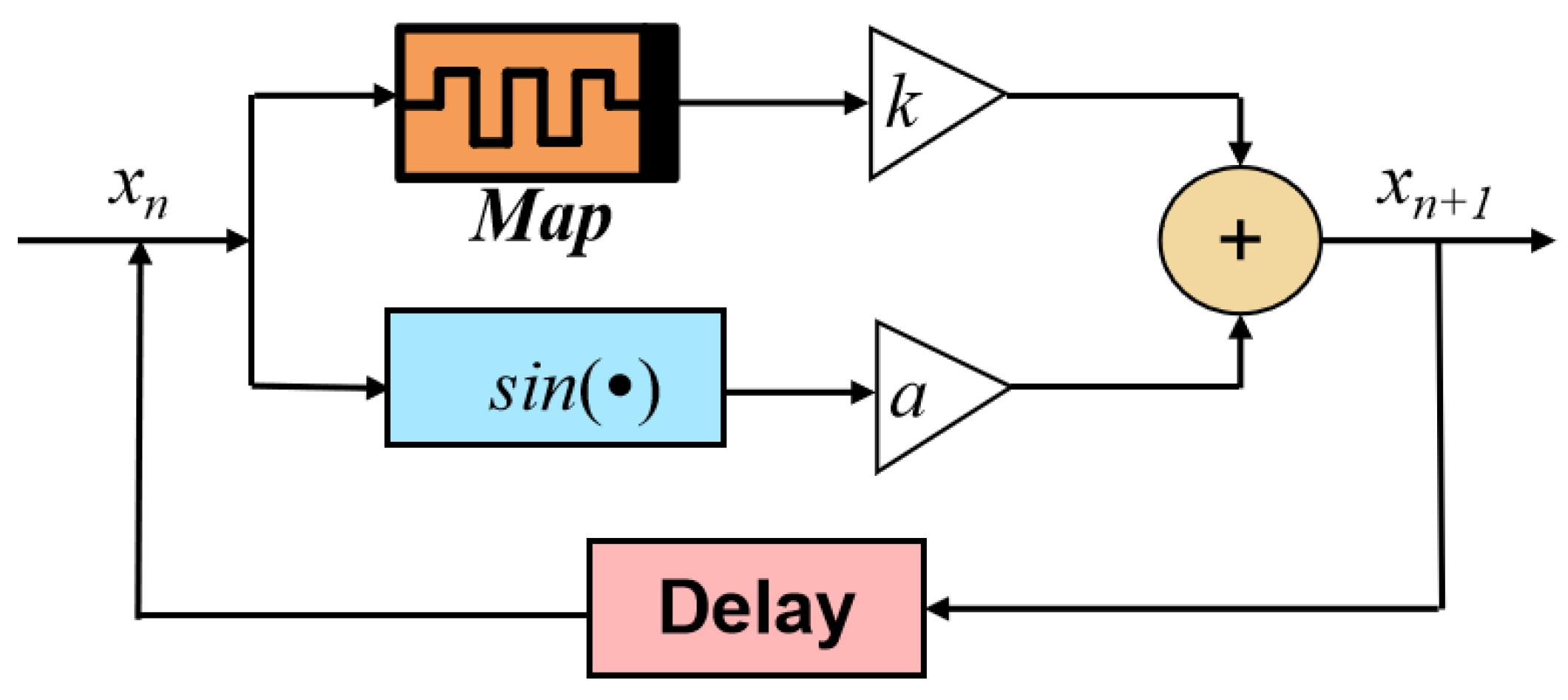
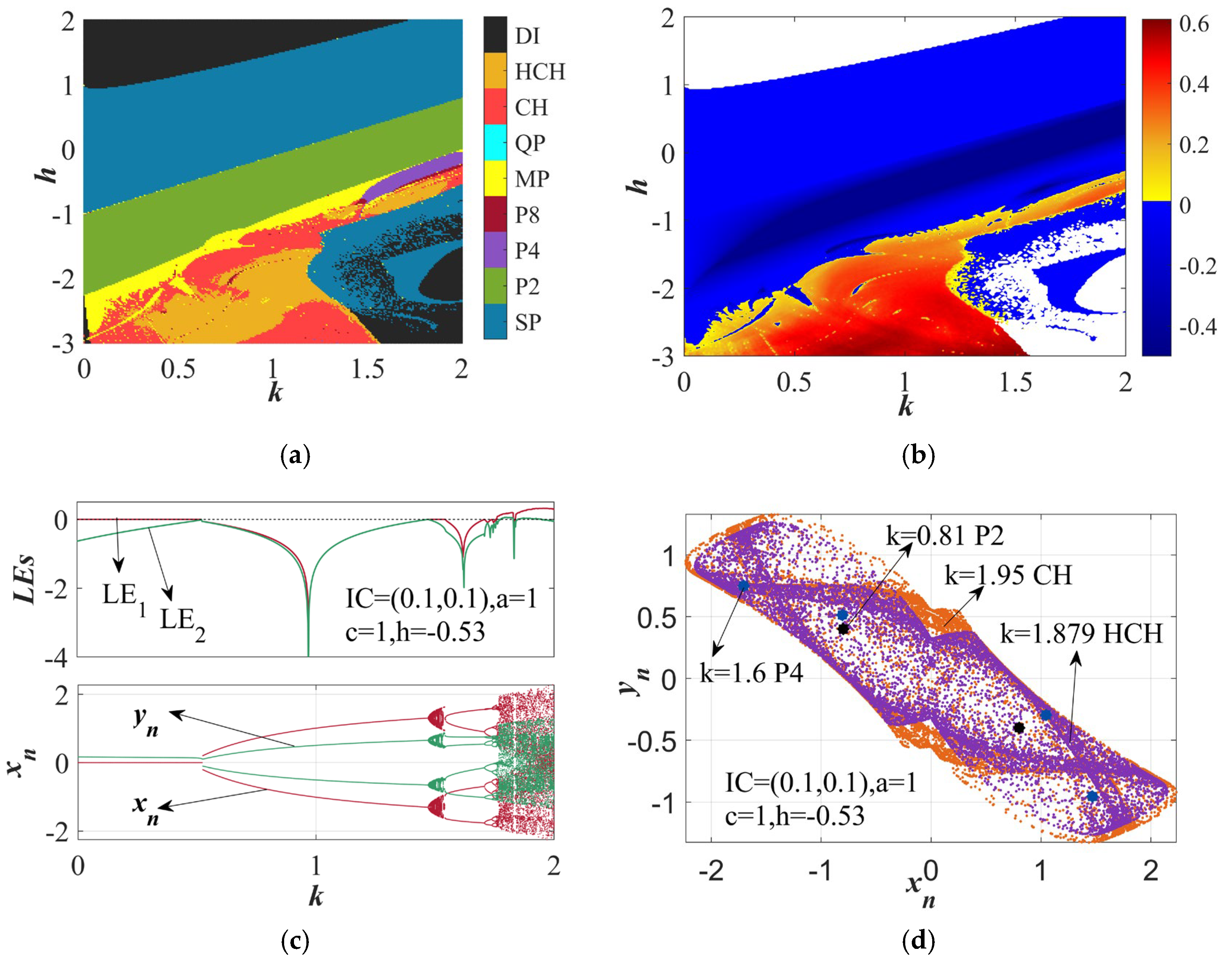
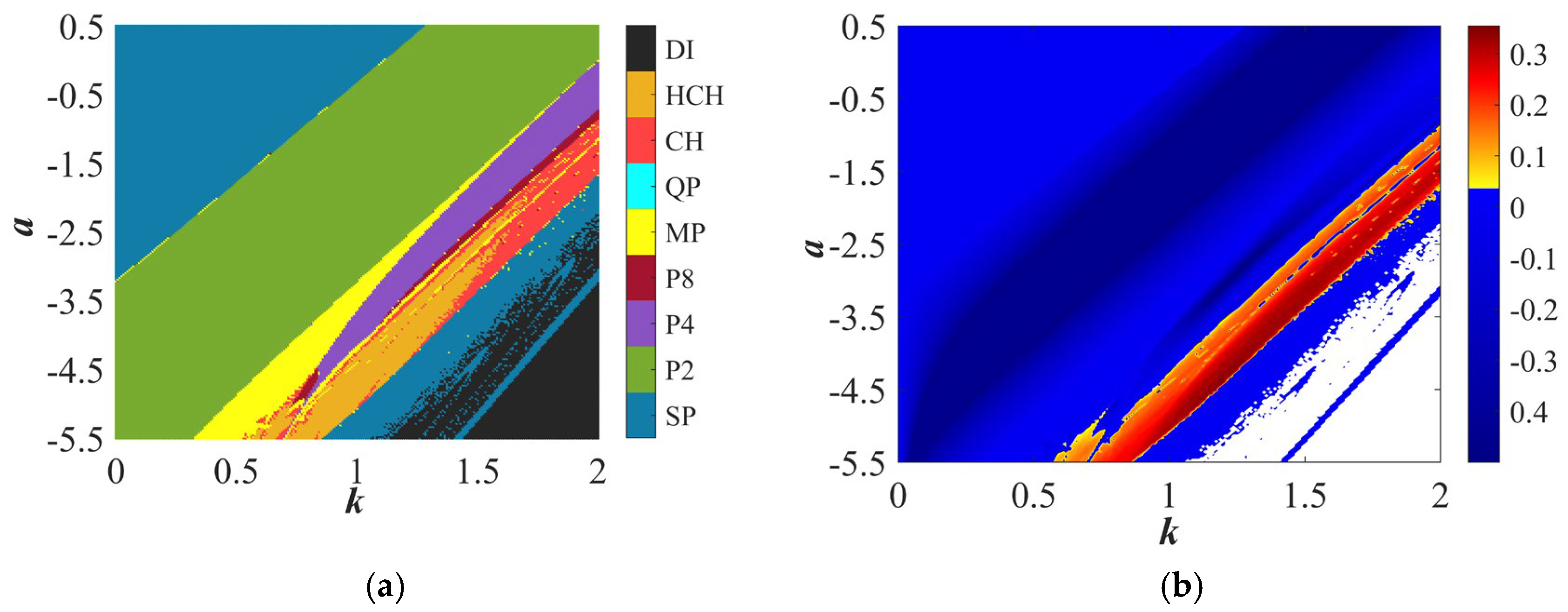
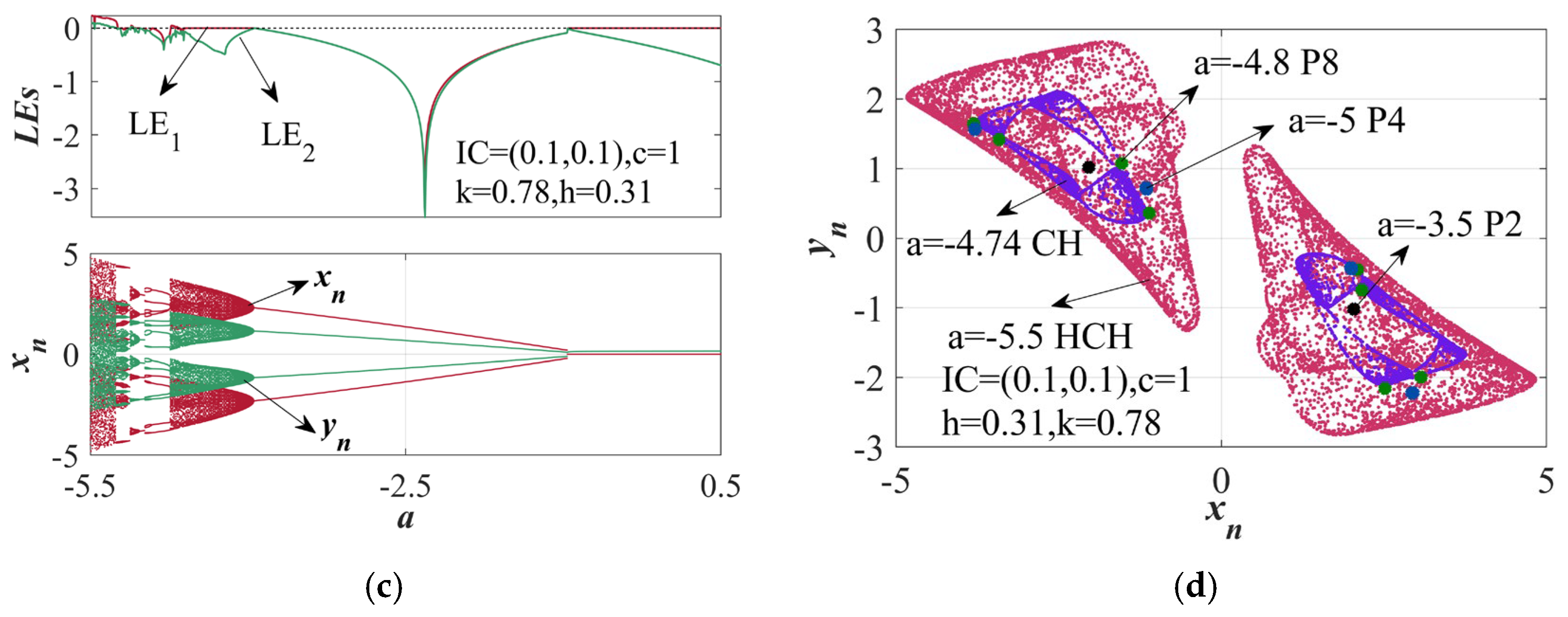
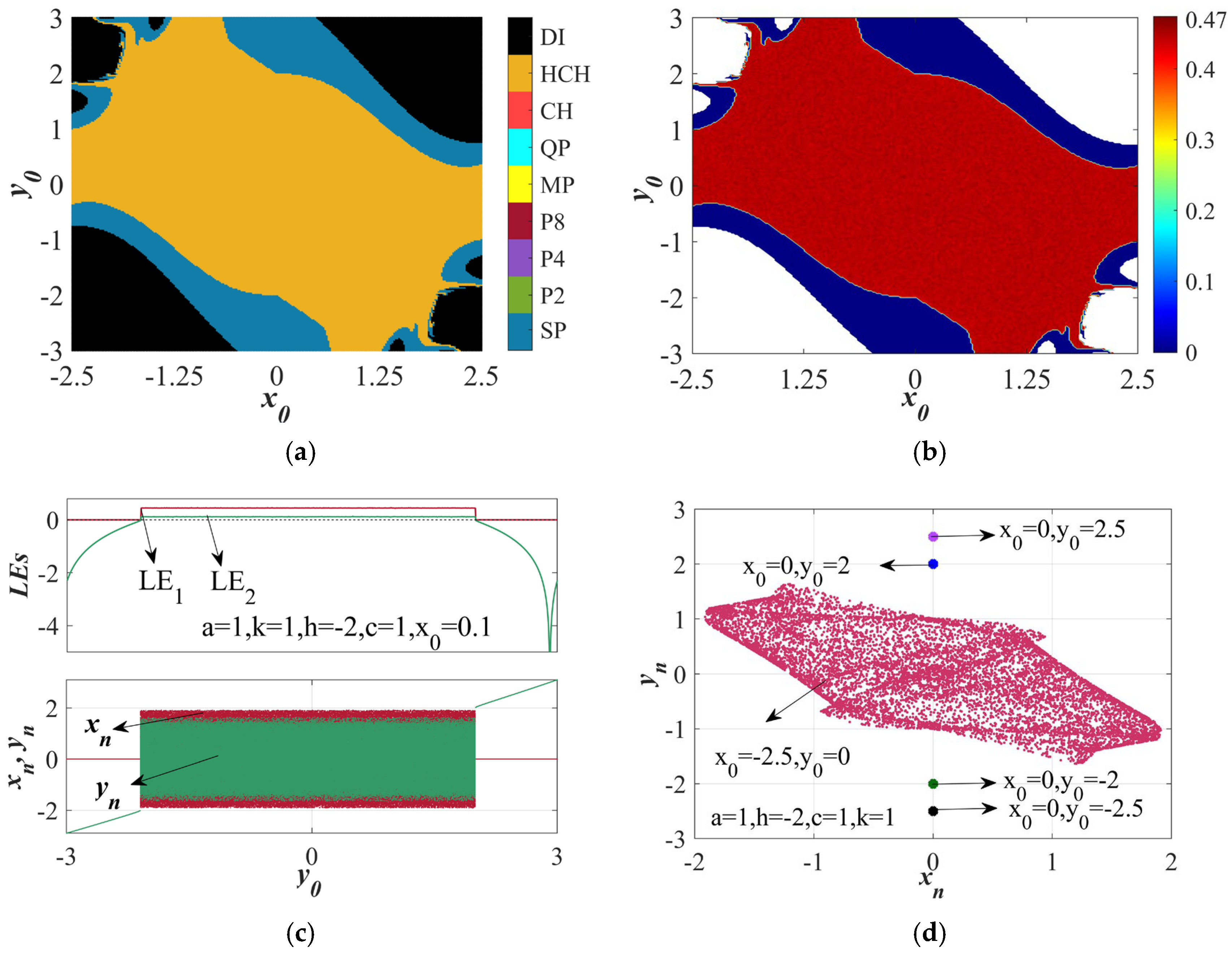

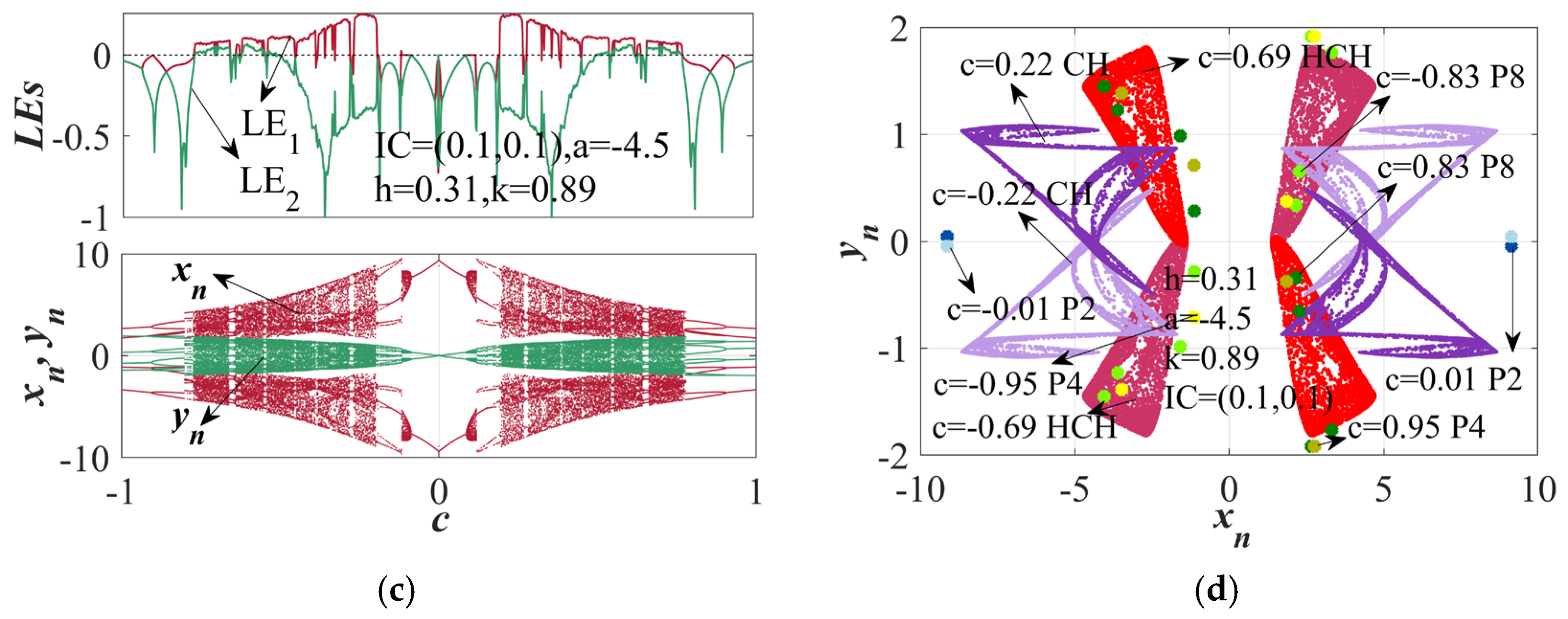
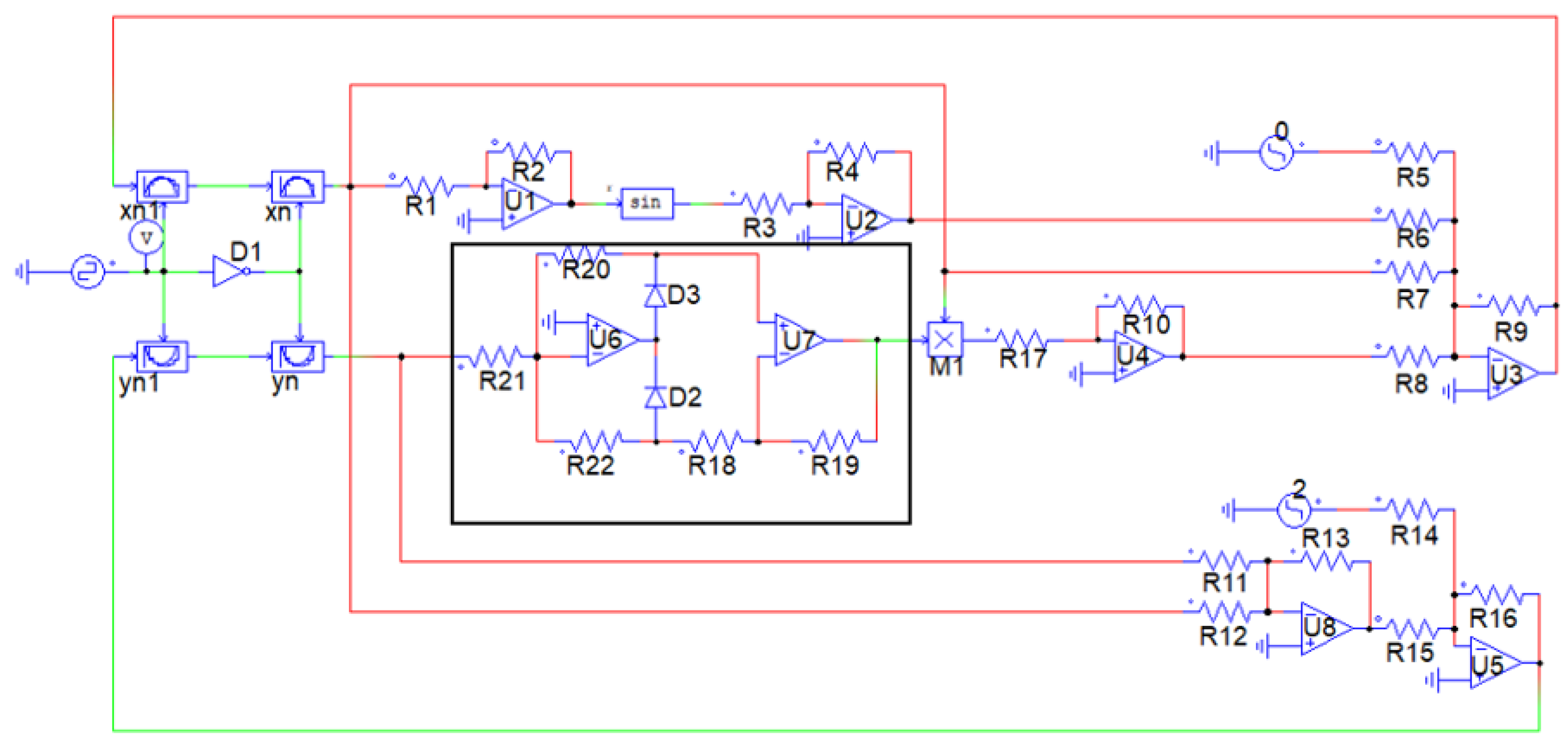

| Parameter Values | Resistor Values |
|---|---|
| a = 0.5, c = 1, k = 2.3, and h = 1 | R2 = R4 = R5 = R6 = R7 = R8 = R9 = R10 = R11 = R12 = R13 = R14 = R15 = R16 = 10 kΩ, R1 = 23 kΩ, R3 = 20 kΩ |
| a = 0.8, c = 1, k = 2.3, and h = 1 | R2 = R4 = R5 = R6 = R7 = R8 = R9 = R10 = R11 = R12 = R13 = R14 = R15 = R16 = 10 kΩ, R3 = 12.5 kΩ |
| a = 1, c = 1, k = 2.3, and h = 1 | R2 = R4 = R5 = R6 = R7 = R8 = R9 = R10 = R11 = R12 = R13 = R14 = R15 = R16 = 10 kΩ, R1 = 23 kΩ, R3 = 10 kΩ |
| a = 1, c = 2, k = 2.3, and h = 1 | R2 = R3 = R4 = R5 = R6 = R8 = R9 = R10 = R11 = R12 = R13 = R14 = R15 = R16 = 10 kΩ, R1 = 23 kΩ, R7 = 5 kΩ |
| a = 1, c = 1, k = 2.3, and h = 1 | R2 = R3 = R4 = R5 = R6 = R8 = R9 = R10 = R11 = R12 = R13 = R14 = R15 = R16 = 10 kΩ, R1 = 23 kΩ, R7 = 10 kΩ |
| a = 1, c = 0.5, k = 2.3, and h = 1 | R2 = R3 = R4 = R5 = R6 = R8 = R9 = R10 = R11 = R12 = R13 = R14 = R15 = R16 = 10 kΩ, R1 = 23 kΩ, R7 = 20 kΩ |
| Parameters and Ics | K(xn) | K(yn) | Status |
|---|---|---|---|
| a = 1, h = −0.53, c = 1, k = 1.6, IC = (0.1, 0.1) | −0.002191 | −0.000236 | P4 |
| a = 1, h = −0.53, c = 1, k = 1.88, IC = (0.1, 0.1) | 0.997722 | 0.998529 | CH |
| a = 1, h = −0.53, c = 1, k = 1.95, IC = (0.1, 0.1) | 0.997651 | 0.998687 | HCH |
| Parameter Values | Resistor Values | Step Voltage |
|---|---|---|
| a = −5.5, h = 0.31, k = 0.78, c = 1 | R1 = R7 = R8 = R10 = R11 = R12 = R13 = R14 = R15 = R16 = R17 = R18 = R19 = R20 = R21 = R22 = 10 kΩ, R2 = 3.1 kΩ, R3 = 20 kΩ, R5 = R6 = R9 = 20 kΩ, R4 = 55 kΩ | [0.1 V, 0.1 V] |
| a = −5, h = 0.31, k = 0.78, c = 1 | R1 = R7 = R8 = R10 = R11 = R12 = R13 = R14 = R15 = R16 = R17 = R18 = R19 = R20 = R21 = R22 = 10 kΩ, R2 = 3.1 kΩ, R3 = 20 kΩ, R5 = R6 = R9 = 20 kΩ, R4 = 50 kΩ | [0.1 V, 0.1 V] |
| a = −4.8, h = 0.31, k = 0.78, c = 1 | R1 = R7 = R8 = R10 = R11 = R12 = R13 = R14 = R15 = R16 = R17 = R18 = R19 = R20 = R21 = R22 = 10 kΩ, R2 = 3.1 kΩ, R3 = 20 kΩ, R5 = R6 = R9 = 20 kΩ, R4 = 48 kΩ | [0.1 V, 0.1 V] |
| a = −3.5, h = 0.31, k = 0.78, c = 1 | R1 = R7 = R8 = R10 = R11 = R12 = R13 = R14 = R15 = R16 = R17 = R18 = R19 = R20 = R21 = R22 = 10 kΩ, R2 = 3.1 kΩ, R3 = 20 kΩ, R5 = R6 = R9 = 20 kΩ, R4 = 35 kΩ | [0.1 V, 0.1 V] |
| a = 1, h = −2, k = 1, c = 1 | R1 = R2 = R3 = R4 = R7 = R8 = R10 = R11 = R12 = R13 = R14 = R15 = R16 = R17 = R18 = R19 = R20 = R21 = R22 = 10 kΩ, R5 = R6 = R9 = 20 kΩ | [−2.5 V, 0 V] |
| a = 1, h = −2, k = 1, c = 1 | R1 = R2 = R3 = R4 = R7 = R8 = R10 = R11 = R12 = R13 = R14 = R15 = R16 = R17 = R18 = R19 = R20 = R21 = R22 = 10 kΩ, R5 = R6 = R9 = 20 kΩ | [0 V, −2.5 V] |
| a = 1, h = −2, k = 1, c = 1 | R1 = R2 = R3 = R4 = R7 = R8 = R10 = R11 = R12 = R13 = R14 = R15 = R16 = R17 = R18 = R19 = R20 = R21 = R22 = 10 kΩ, R5 = R6 = R9 = 20 kΩ | [0 V, −2 V] |
| a = 1, h = −2, k = 1, c = 1 | R1 = R2 = R3 = R4 = R7 = R8 = R10 = R11 = R12 = R13 = R14 = R15 = R16 = R17 = R18 = R19 = R20 = R21 = R22 = 10 kΩ, R5 = R6 = R9 = 20 kΩ | [0 V, 2 V] |
| a = 1, h = −2, k = 1, c = 1 | R1 = R2 = R3 = R4 = R7 = R8 = R10 = R11 = R12 = R13 = R14 = R15 = R16 = R17 = R18 = R19 = R20 = R21 = R22 = 10 kΩ, R5 = R6 = R9 = 20 kΩ | [0 V, 2.5 V] |
| Maps | Parameters | Dem | SE | PE | SampE | IE | C0 |
|---|---|---|---|---|---|---|---|
| SAHM | 1, −2, 1, 1 | 2 | 0.9259 | 2.9315 | 0.6506 | 7.9597 | 0.8218 |
| DMP-SDM [42] | 2,2,1.85 | 2 | 0.9250 | 3.5849 | 0.3912 | 7.6844 | 0.6953 |
| E-SCDM [43] | 1.8, 1.69 | 3 | 0.9162 | 3.6593 | 0.9612 | 7.9845 | 0.1655 |
| TMNM [51] | 1, −3, −0.92 | 4 | 0.8405 | 3.5196 | 0.6210 | 7.7659 | 0.7105 |
| SSM-CM [52] | 1.77,1.77 | 3 | 0.8962 | 3.3258 | 0.4101 | 7.5591 | 0.0366 |
| Testing Items | y0 = 0.1 | y0 = 0.2 | ||
|---|---|---|---|---|
| p-Valuet | Pass Rate | p-Valuet | Pass Rate | |
| Frequency | 0.253551 | 117/120 | 0.012650 | 120/120 |
| Block Frequency | 0.213309 | 120/120 | 0.437274 | 117/120 |
| Runs | 0.484646 | 119/120 | 0.162606 | 120/120 |
| Largest runs | 0.619972 | 118/120 | 0.090906 | 118/120 |
| Rank | 0.035174 | 120/120 | 0.001344 | 120/120 |
| FFT | 0.001490 | 120/120 | 0.275709 | 119/120 |
| None-ovla. Temp. 1 | 0.001399 | 118/120 | 0.006196 | 119120 |
| Ovla. Temp. | 0.213309 | 117/120 | 0.048716 | 118/120 |
| Universal | 0.122325 | 118/120 | 0.931952 | 117/120 |
| Linear complexity | 0.299251 | 119/120 | 0.012650 | 118/120 |
| Serial (1st) | 0.602458 | 120/120 | 0.275709 | 120/120 |
| Serial (2nd) | 0.437274 | 118/120 | 0.437274 | 119/120 |
| Appr. entropy | 0.066882 | 120/120 | 0.090936 | 119/120 |
| Cum. Sums (F) | 0.468595 | 116/120 | 0.875539 | 119/120 |
| Cum. Sums (B) | 0.082177 | 118/120 | 0.213309 | 119/120 |
| Ran. Exc. 2 | 0.020750 | 74/75 | 0.162606 | 75/75 |
| Ran. Exc. Var. 3 | 0.018815 | 74/75 | 0.090963 | 74/75 |
| Success counts | 15/15 | 15/15 | 15/15 | 15/15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sang, H.; Yang, Z.; Liu, X.; Wang, Q.; Yu, X. Discrete Memristor-Based Hyperchaotic Map and Its Analog Circuit Implementation. Symmetry 2025, 17, 1358. https://doi.org/10.3390/sym17081358
Sang H, Yang Z, Liu X, Wang Q, Yu X. Discrete Memristor-Based Hyperchaotic Map and Its Analog Circuit Implementation. Symmetry. 2025; 17(8):1358. https://doi.org/10.3390/sym17081358
Chicago/Turabian StyleSang, Haiwei, Zongyun Yang, Xianzhou Liu, Qiao Wang, and Xiong Yu. 2025. "Discrete Memristor-Based Hyperchaotic Map and Its Analog Circuit Implementation" Symmetry 17, no. 8: 1358. https://doi.org/10.3390/sym17081358
APA StyleSang, H., Yang, Z., Liu, X., Wang, Q., & Yu, X. (2025). Discrete Memristor-Based Hyperchaotic Map and Its Analog Circuit Implementation. Symmetry, 17(8), 1358. https://doi.org/10.3390/sym17081358






