Dynamical Analysis, Feedback Control Circuit Implementation, and Fixed-Time Sliding Mode Synchronization of a Novel 4D Chaotic System
Abstract
1. Introduction
2. Modeling and Dynamical Analysis of a Novel 4D Chaotic System
2.1. Dissipativity
2.2. Equilibria and Stability
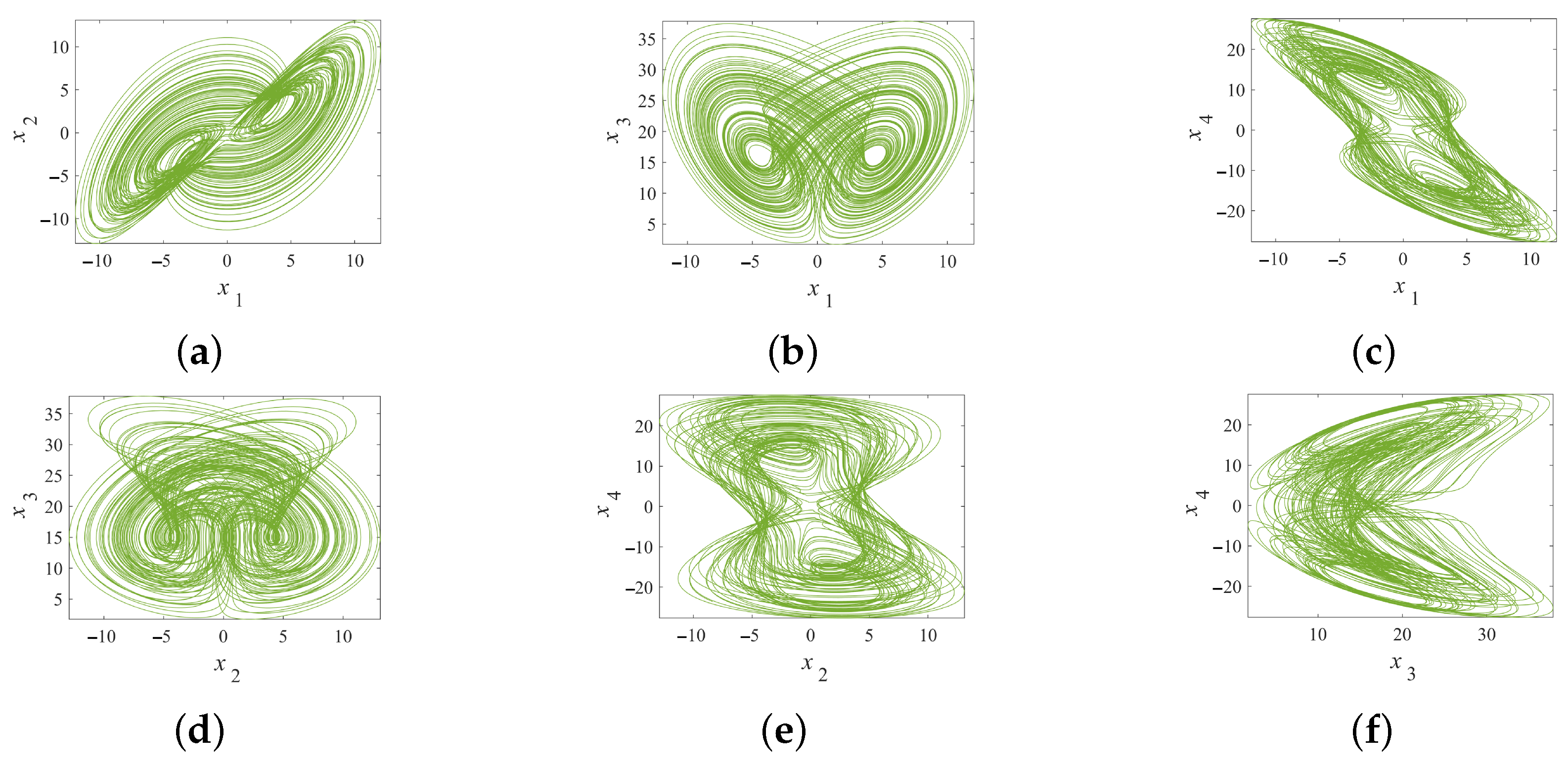
3. Dynamical Analysis of the System
3.1. Dynamical Analysis Under Varying System Parameters
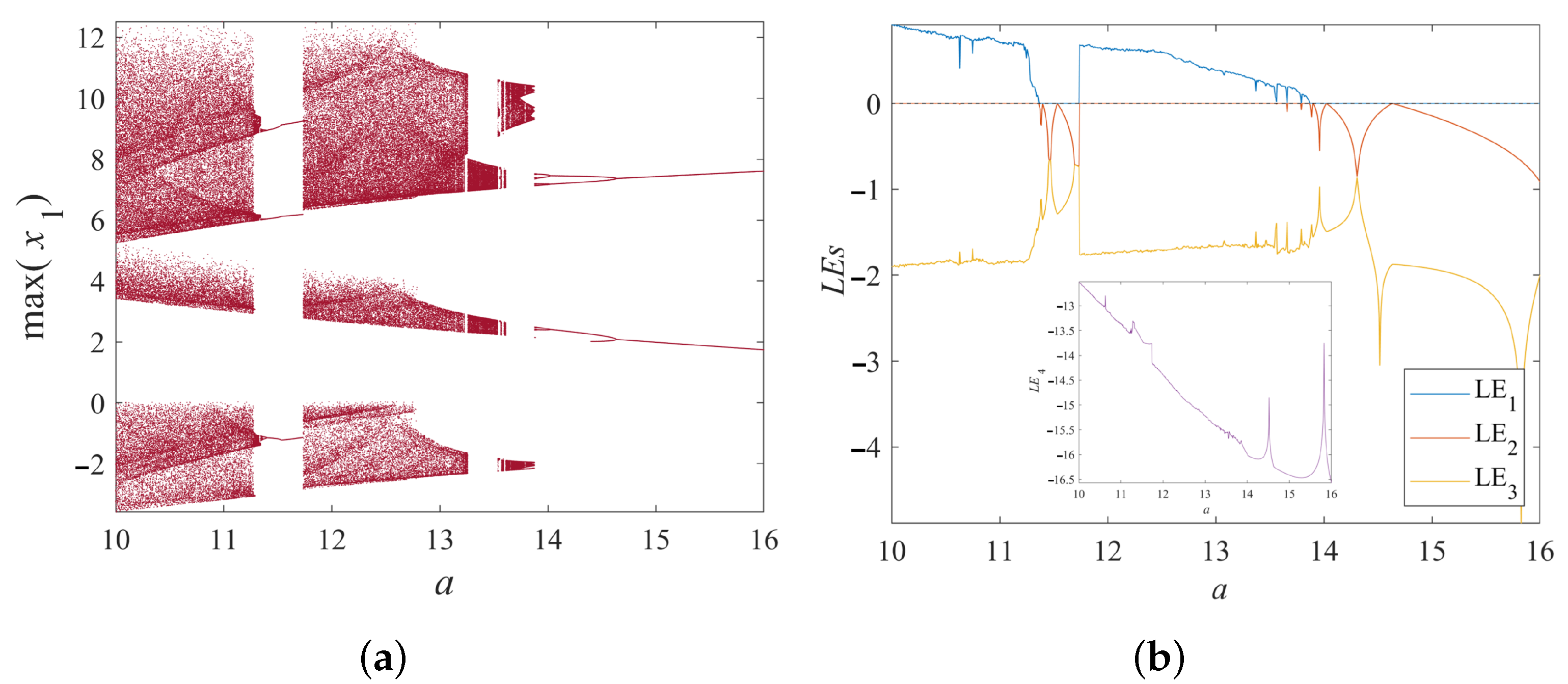
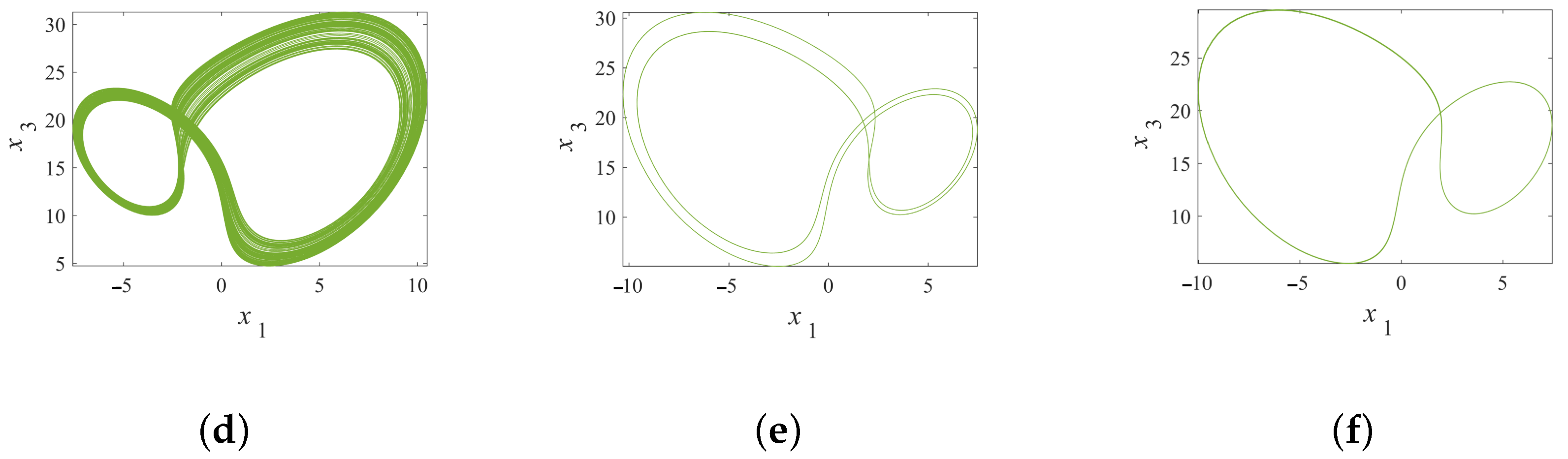
3.1.1. Dynamical Behavior Under Varying Parameter a
3.1.2. Dynamical Behavior Under Varying Parameter b
3.1.3. Dynamical Behavior Under Varying Parameter c
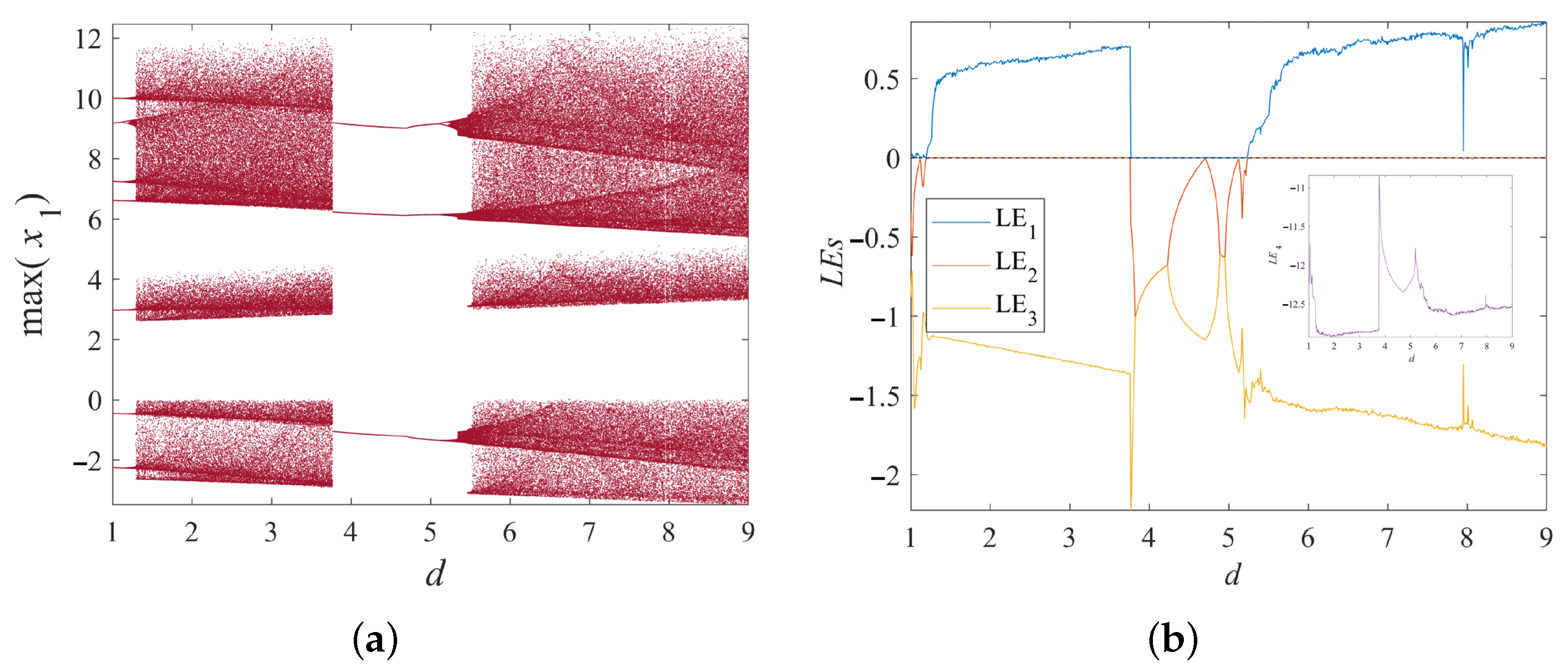
3.1.4. Dynamical Behavior Under Varying Parameter d
3.2. Dynamics Complexity
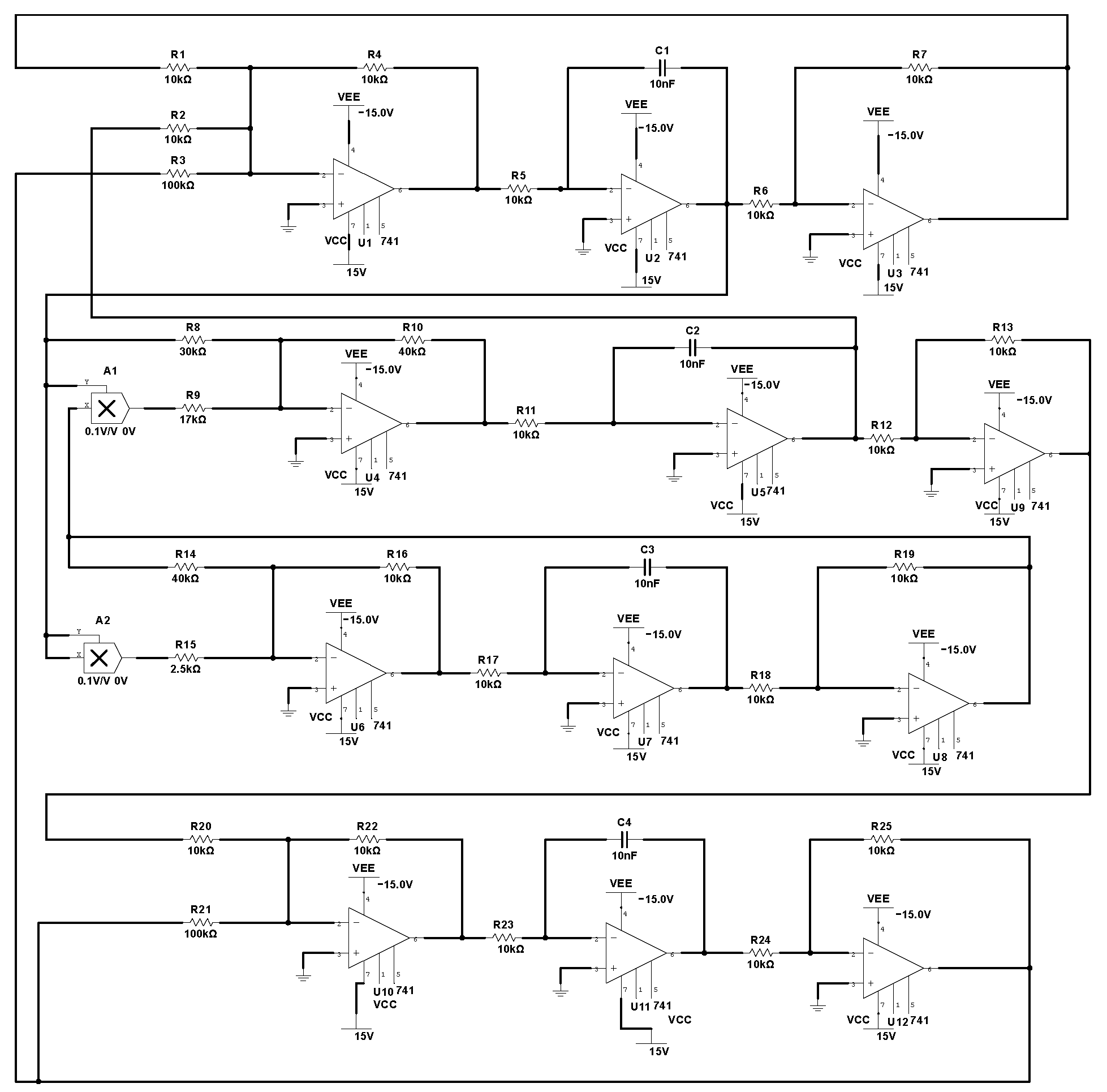
4. System Circuit Implementation
4.1. System Simulation Circuit Implementation
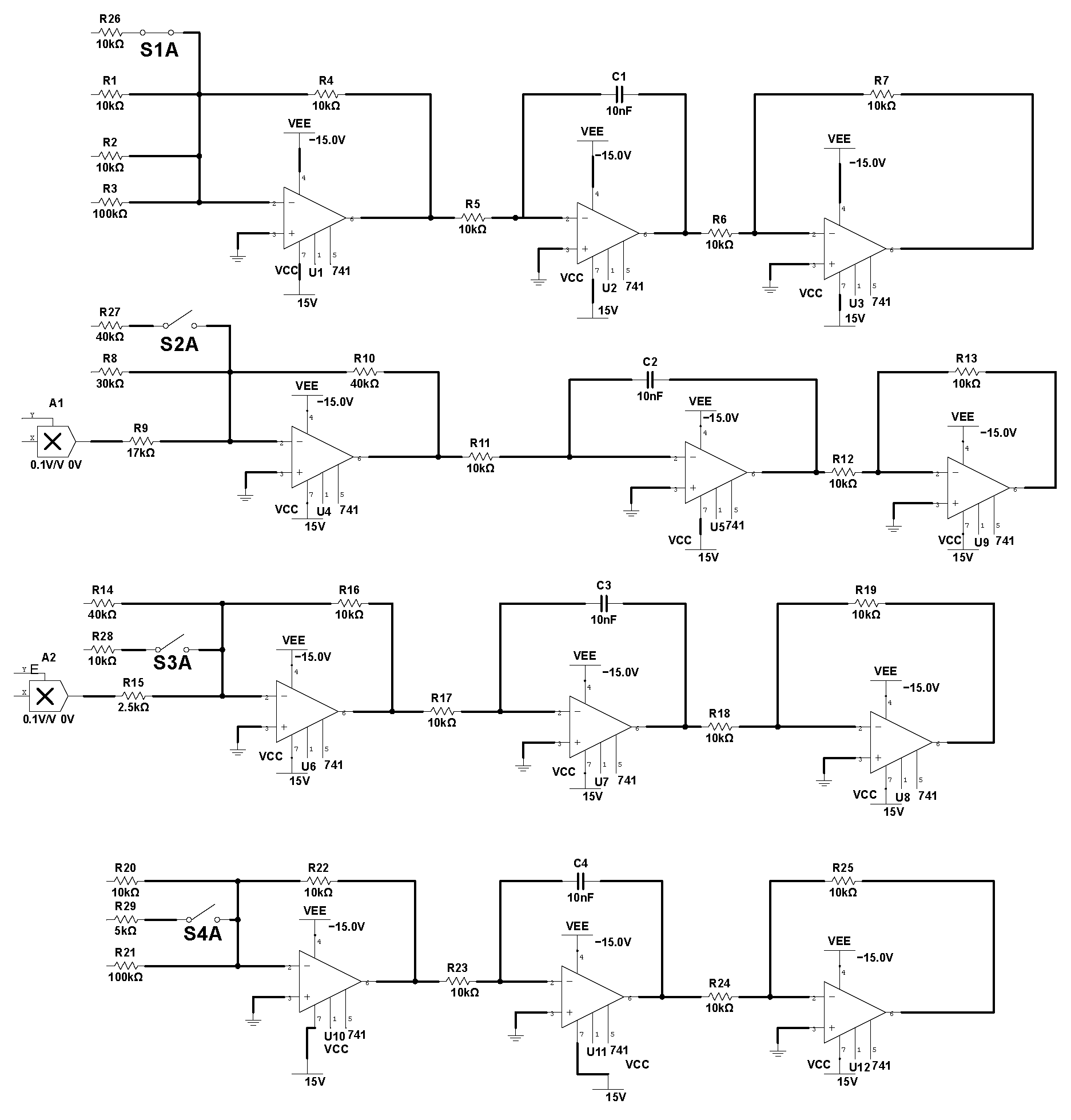
4.2. Feedback Control
5. FTSMS of System (1)
5.1. Establishment of FTSMS Controller
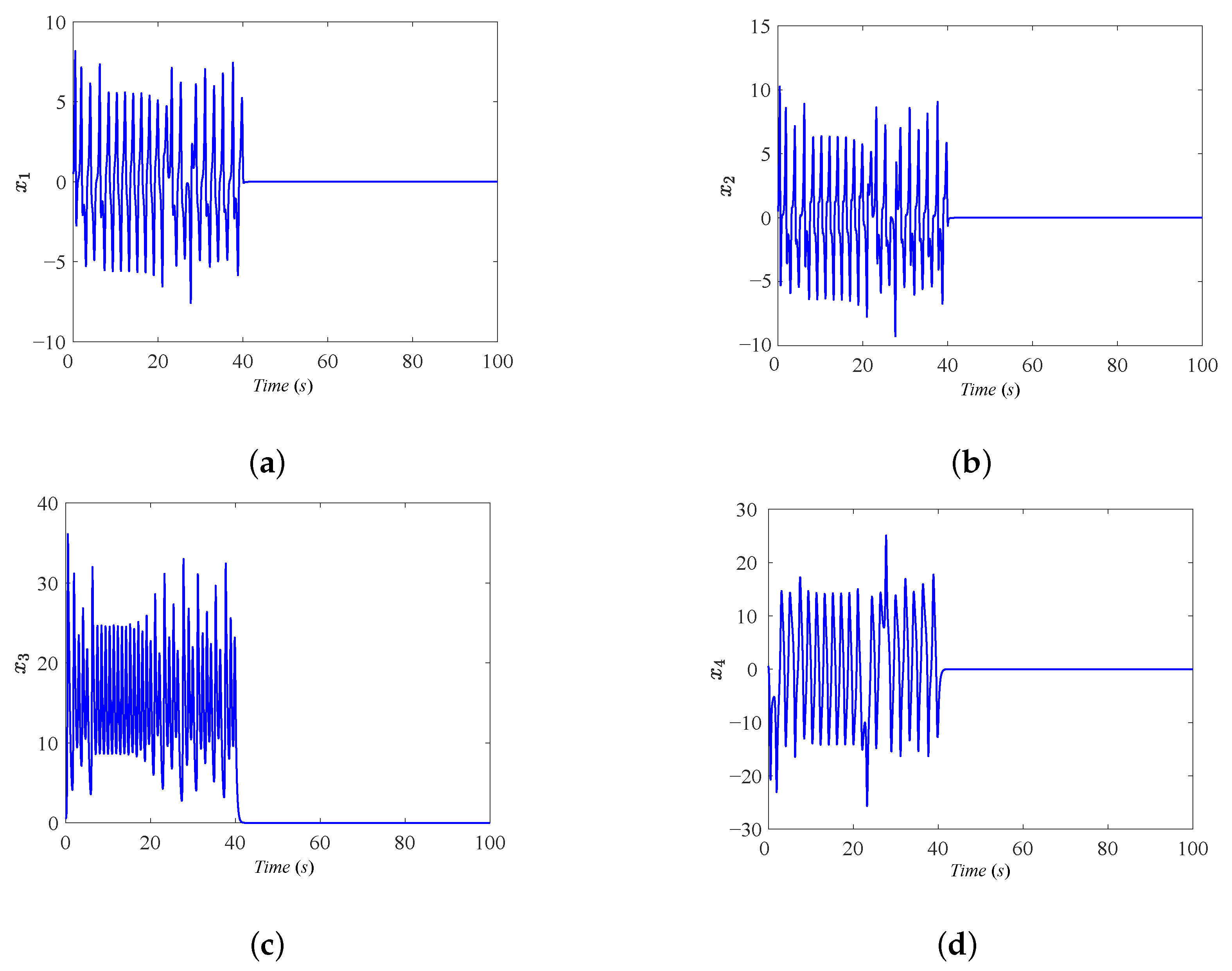
5.2. Numerical Simulation of FTSMS
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shinbrot, T.; Ditto, W.; Grebogi, C.; Ott, E.; Spano, M.; Yorke, J.A. Using the sensitive dependence of chaos (the ‘‘butterfly effect’’) to direct trajectories in an experimental chaotic system. Phys. Rev. Lett. 1992, 68, 2863. [Google Scholar] [CrossRef]
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Zolfaghari, B.; Koshiba, T. Chaotic image encryption: State-of-the-art, ecosystem, and future roadmap. Appl. Syst. Innov. 2022, 5, 57. [Google Scholar] [CrossRef]
- Mahmoud, E.E.; Trikha, P.; Jahanzaib, L.S.; Almaghrabi, O.A. Dynamical analysis and chaos control of the fractional chaotic ecological model. Chaos Solitons Fractals 2020, 141, 110348. [Google Scholar] [CrossRef]
- Wang, Z.; Parastesh, F.; Tian, H.; Jafari, S. Symmetric synchronization behavior of multistable chaotic systems and circuits in attractive and repulsive couplings. Integration 2023, 89, 37–46. [Google Scholar] [CrossRef]
- Boui A Boya, B.F.; Muni, S.S.; Echenausía-Monroy, J.L.; Kengne, J. Chaos, synchronization, and emergent behaviors in memristive hopfield networks: Bi-neuron and regular topology analysis. Eur. Phys. J. Spec. Top. 2024, 1–15. [Google Scholar] [CrossRef]
- Tian, H.; Wang, J.; Ma, J.; Li, X.; Zhang, P.; Li, J. Improved energy-adaptive coupling for synchronization of neurons with nonlinear and memristive membranes. Chaos Solitons Fractals 2025, 199, 116863. [Google Scholar] [CrossRef]
- dos Santos Oliveira, E.; Nackenhorst, U. Sparse polynomial chaos expansion for high-dimensional nonlinear damage mechanics. Probabilistic Eng. Mech. 2024, 75, 103556. [Google Scholar] [CrossRef]
- Zhang, P.; Hu, W.; Wang, Z.; Qiao, Z. Multi-Symplectic Simulation on Soliton-Collision for Nonlinear Perturbed Schrödinger Equation. J. Nonlinear Math. Phys. 2023, 30, 1467–1482. [Google Scholar] [CrossRef]
- Abdechiri, M.; Faez, K.; Amindavar, H.; Bilotta, E. The chaotic dynamics of high-dimensional systems. Nonlinear Dyn. 2017, 87, 2597–2610. [Google Scholar] [CrossRef]
- Liu, T.; Zhao, X.; Sun, P.; Zhou, J. A hybrid proper orthogonal decomposition and next generation reservoir computing approach for high-dimensional chaotic prediction: Application to flow-induced vibration of tube bundles. Chaos Interdiscip. J. Nonlinear Sci. 2024, 34, 033125. [Google Scholar] [CrossRef] [PubMed]
- Es-Sabry, M.; El Akkad, N.; Merras, M.; Satori, K.; El-Shafai, W.; Altameem, T.; Fouda, M.M. Securing images using high dimensional chaotic maps and DNA encoding techniques. IEEE Access 2023, 11, 100856–100878. [Google Scholar] [CrossRef]
- Zeng, Y.; Hu, H.; Shuai, Y. A general method for constructing high-dimensional chaotic maps with topological mixing on the global phase space. Chaos Solitons Fractals 2024, 182, 114818. [Google Scholar] [CrossRef]
- Adel, M.; Khader, M.M.; Algelany, S. High-dimensional chaotic Lorenz system: Numerical treatment using Changhee polynomials of the Appell type. Fractal Fract. 2023, 7, 398. [Google Scholar] [CrossRef]
- Qi, G.; Du, S.; Chen, G.; Chen, Z. On a four-dimensional chaotic system. Chaos Solitons Fractals 2005, 23, 1671–1682. [Google Scholar] [CrossRef]
- Ababneh, M. A new four-dimensional chaotic attractor. Ain Shams Eng. J. 2018, 9, 1849–1854. [Google Scholar] [CrossRef]
- Wang, X.; Feng, Y.; Chen, Y. A new four-dimensional chaotic system and its circuit implementation. Front. Phys. 2022, 10, 906138. [Google Scholar] [CrossRef]
- Halder, A.K.; Paliathanasis, A.; Leach, P.G. Noether’s theorem and symmetry. Symmetry 2018, 10, 744. [Google Scholar] [CrossRef]
- Strocchi, F. Symmetry Breaking; Springer: Berlin/Heidelberg, Germany, 2005; Volume 643. [Google Scholar]
- Kengne, J.; Mogue, R.L.T.; Fozin, T.F.; Telem, A.N.K. Effects of symmetric and asymmetric nonlinearity on the dynamics of a novel chaotic jerk circuit: Coexisting multiple attractors, period doubling reversals, crisis, and offset boosting. Chaos Solitons Fractals 2019, 121, 63–84. [Google Scholar] [CrossRef]
- Qi, G.; Chen, G.; Zhang, Y. On a new asymmetric chaotic system. Chaos Solitons Fractals 2008, 37, 409–423. [Google Scholar] [CrossRef]
- Pham, V.T.; Velichko, A.; Van Huynh, V.; Radogna, A.V.; Grassi, G.; Boulaaras, S.M.; Momani, S. Analysis of memristive maps with asymmetry. Integration 2024, 94, 102110. [Google Scholar] [CrossRef]
- Hubler, A. Adaptive control of chaotic system. Helv. Phys. Acta 1989, 62, 343–346. [Google Scholar]
- Ott, E.; Grebogi, C.; Yorke, J.A. Controlling chaos. Phys. Rev. Lett. 1990, 64, 1196. [Google Scholar] [CrossRef] [PubMed]
- Pecora, L.M.; Carroll, T.L. Synchronization in chaotic systems. Phys. Rev. Lett. 1990, 64, 821. [Google Scholar] [CrossRef]
- Chen, G. Control and anticontrol of chaos. In Proceedings of the 1997 1st International Conference, Control of Oscillations and Chaos Proceedings (Cat. No. 97TH8329), St. Petersburg, Russia, 27–29 August 1997; Volume 2, pp. 181–186. [Google Scholar]
- Wang, J.; Gao, J.; Ma, X. Synchronization control of cross-strict feedback hyperchaotic system based on cross active backstepping design. Phys. Lett. A 2007, 369, 452–457. [Google Scholar] [CrossRef]
- Feng, X.Q.; Shen, K. Controlling hyperchaos and periodic synchronization in DOPO with parameter modulated by an external periodic signal. Chaos Solitons Fractals 2008, 35, 506–511. [Google Scholar] [CrossRef]
- Effati, S.; Saberi-Nadjafi, J.; Nik, H.S. Optimal and adaptive control for a kind of 3D chaotic and 4D hyper-chaotic systems. Appl. Math. Model. 2014, 38, 759–774. [Google Scholar] [CrossRef]
- Li, K.; Li, R.; Cao, L.; Feng, Y.; Onasanya, B.O. Periodically intermittent control of Memristor-based hyper-chaotic bao-like system. Mathematics 2023, 11, 1264. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, Y.; Hou, Y.; Li, H. Fixed-time sliding mode control for uncertain robot manipulators. IEEE Access 2019, 7, 149750–149763. [Google Scholar] [CrossRef]
- Moulay, E.; Léchappé, V.; Bernuau, E.; Defoort, M.; Plestan, F. Fixed-time sliding mode control with mismatched disturbances. Automatica 2022, 136, 110009. [Google Scholar] [CrossRef]
- Rezaie, A. Sliding Mode Control for Chaotic Systems with Unknown Uncertainties. Int. J. Ind. Electron. Control Optim. 2024, 7, 53–60. [Google Scholar]
- Chan, J.C.L.; Lee, T.H.; Tan, C.P. Secure communication through a chaotic system and a sliding-mode observer. IEEE Trans. Syst. Man, Cybern. Syst. 2020, 52, 1869–1881. [Google Scholar] [CrossRef]
- Vaseghi, B.; Pourmina, M.A.; Mobayen, S. Secure communication in wireless sensor networks based on chaos synchronization using adaptive sliding mode control. Nonlinear Dyn. 2017, 89, 1689–1704. [Google Scholar] [CrossRef]
- Abou El Qassime, A.; Nhaila, H.; Bahatti, L.; Zayrit, S. Advanced speech encryption method leveraging a hidden hyperchaotic attractor and its synchronization with robust adaptive sliding mode control. Nonlinear Dyn. 2025, 113, 15553–15578. [Google Scholar] [CrossRef]
- Kuznetsov, Y.A.; Kuznetsov, I.A.; Kuznetsov, Y. Elements of Applied Bifurcation Theory; Springer: Berlin/Heidelberg, Germany, 1998; Volume 112. [Google Scholar]
- Yau, H.T. Design of adaptive sliding mode controller for chaos synchronization with uncertainties. Chaos Solitons Fractals 2004, 22, 341–347. [Google Scholar] [CrossRef]
- Serrano, F.E.; Pham, V.T. Fractional memristive-discrete neural network: Projective terminal sliding mode synchronization. Eur. Phys. J. Spec. Top. 2025, 1–14. [Google Scholar] [CrossRef]









| Iterations | Trend | ||||
|---|---|---|---|---|---|
| 0– | Transition state | ||||
| – | Convergent state | ||||
| – | Stable state |
| a | Attractor Type | Symmetry |
|---|---|---|
| 11.5 | Symmetric Period-2 Attractor | Symmetric |
| 13.1 | Symmetric Double-Scroll Chaos | Symmetric |
| 13.1 → 13.3 | Asymmetric Double-Scroll Chaos | Symmetry Breaking |
| 13.7 | Asymmetric Multi-Period Attractor | Broken State |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, H.; Yi, X.; Zhang, Y.; Wang, Z.; Xi, X.; Liu, J. Dynamical Analysis, Feedback Control Circuit Implementation, and Fixed-Time Sliding Mode Synchronization of a Novel 4D Chaotic System. Symmetry 2025, 17, 1252. https://doi.org/10.3390/sym17081252
Tian H, Yi X, Zhang Y, Wang Z, Xi X, Liu J. Dynamical Analysis, Feedback Control Circuit Implementation, and Fixed-Time Sliding Mode Synchronization of a Novel 4D Chaotic System. Symmetry. 2025; 17(8):1252. https://doi.org/10.3390/sym17081252
Chicago/Turabian StyleTian, Huaigu, Xifeng Yi, Yang Zhang, Zhen Wang, Xiaojian Xi, and Jindong Liu. 2025. "Dynamical Analysis, Feedback Control Circuit Implementation, and Fixed-Time Sliding Mode Synchronization of a Novel 4D Chaotic System" Symmetry 17, no. 8: 1252. https://doi.org/10.3390/sym17081252
APA StyleTian, H., Yi, X., Zhang, Y., Wang, Z., Xi, X., & Liu, J. (2025). Dynamical Analysis, Feedback Control Circuit Implementation, and Fixed-Time Sliding Mode Synchronization of a Novel 4D Chaotic System. Symmetry, 17(8), 1252. https://doi.org/10.3390/sym17081252






