Video Stabilization Algorithm Based on View Boundary Synthesis
Abstract
1. Introduction
- We propose the View Out-boundary Synthesis Algorithm (VOSA) grounded in spatio-temporal coherence and symmetry principles. This algorithm accomplishes the completion of missing pixels via symmetry-preserving optical flow extension and an iterative propagation mechanism.
- We design a lightweight network architecture that can be seamlessly integrated into existing video stabilization pipelines. Through the coordinated operation of the pre-alignment module and the affinity kernel prediction network, this architecture boosts the cropping rate of classic algorithms like MeshFlow [8] by 12.3% without incurring a computational overhead increase of more than 5%.
- We establish a mathematical representation model for symmetry-aware motion propagation across video frames. It is theoretically demonstrated that the optical flow field beyond the boundary can be linearly approximated by local affinity kernels satisfying symmetry constraints.
2. Related Works
3. Methodology
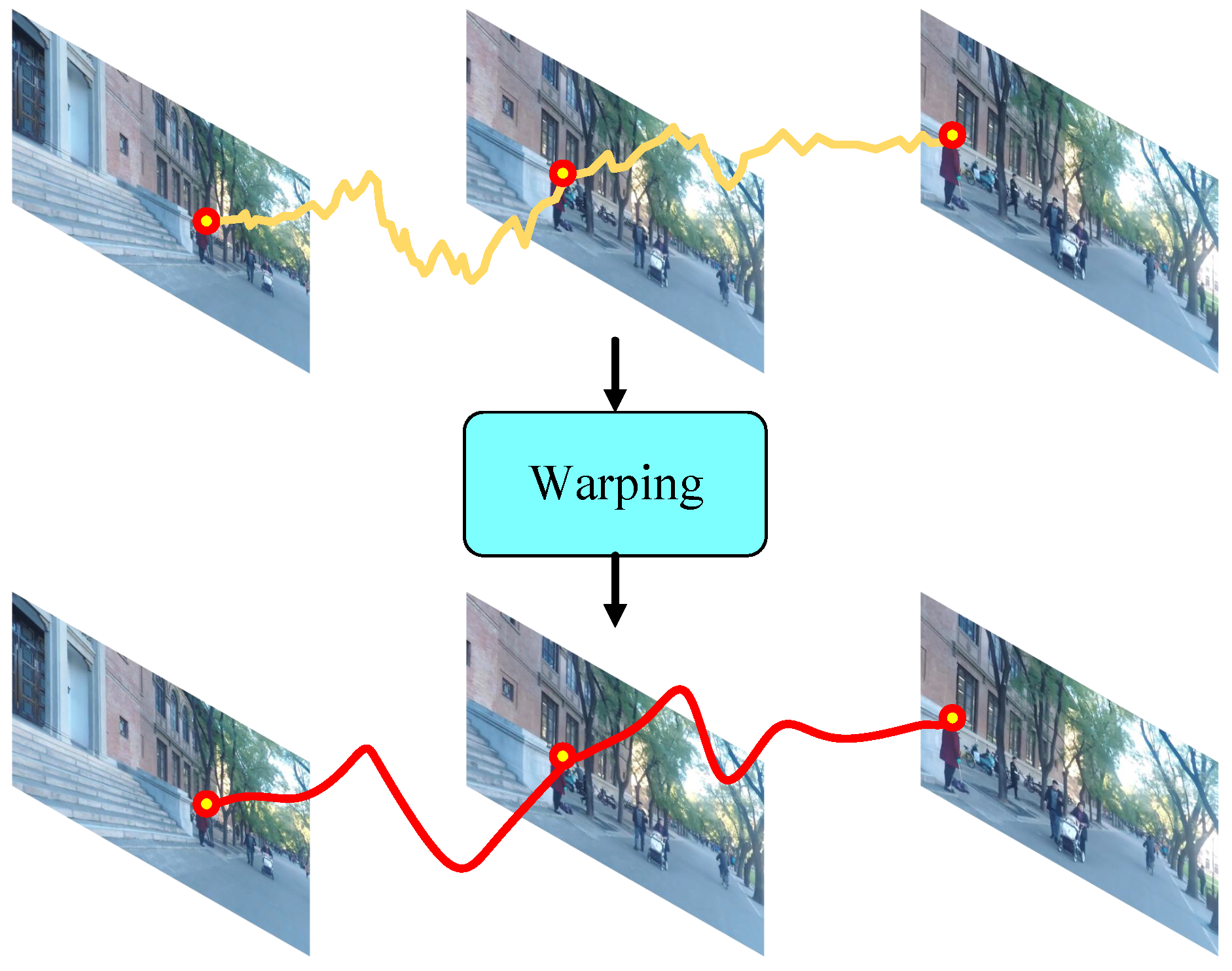
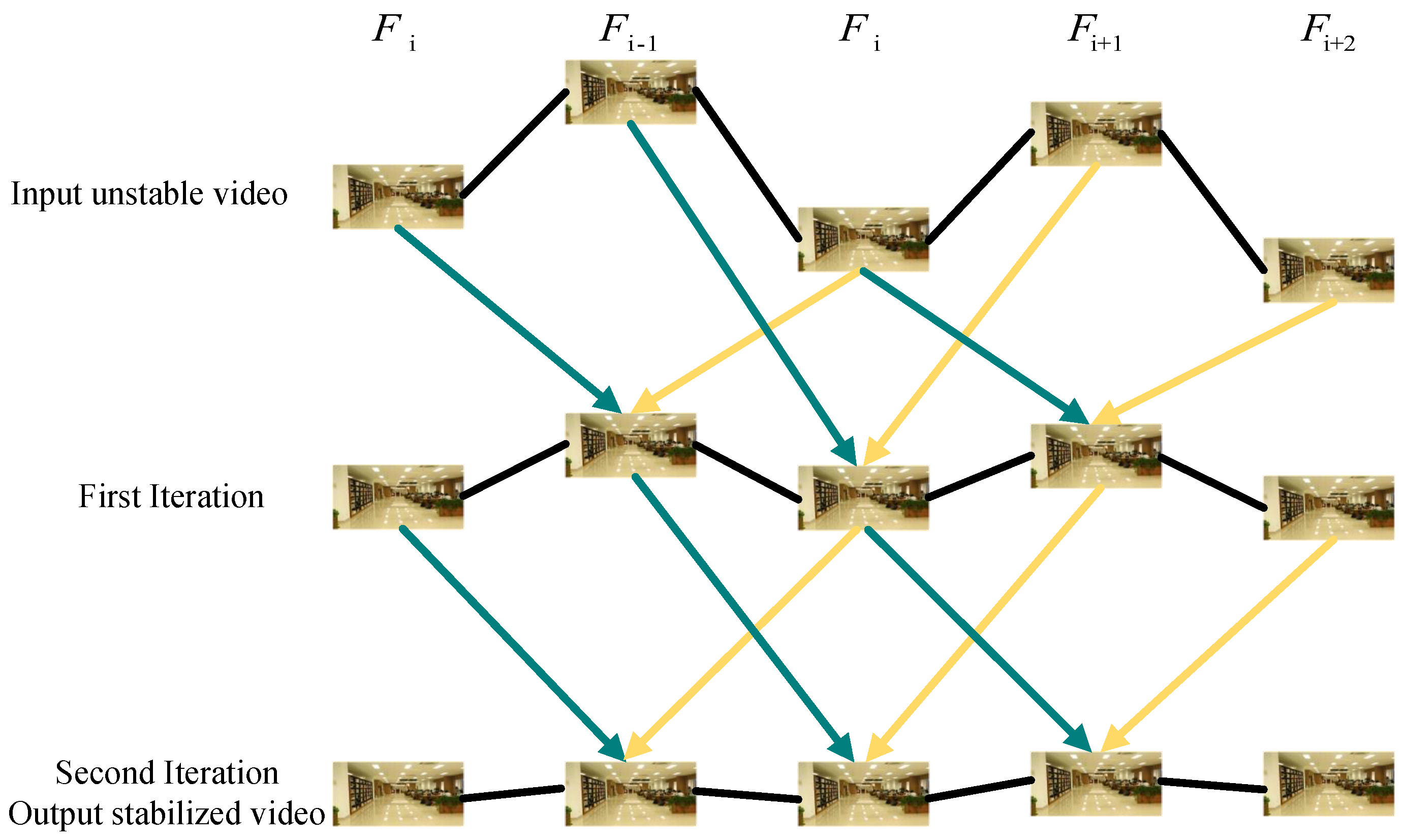
3.1. Overview
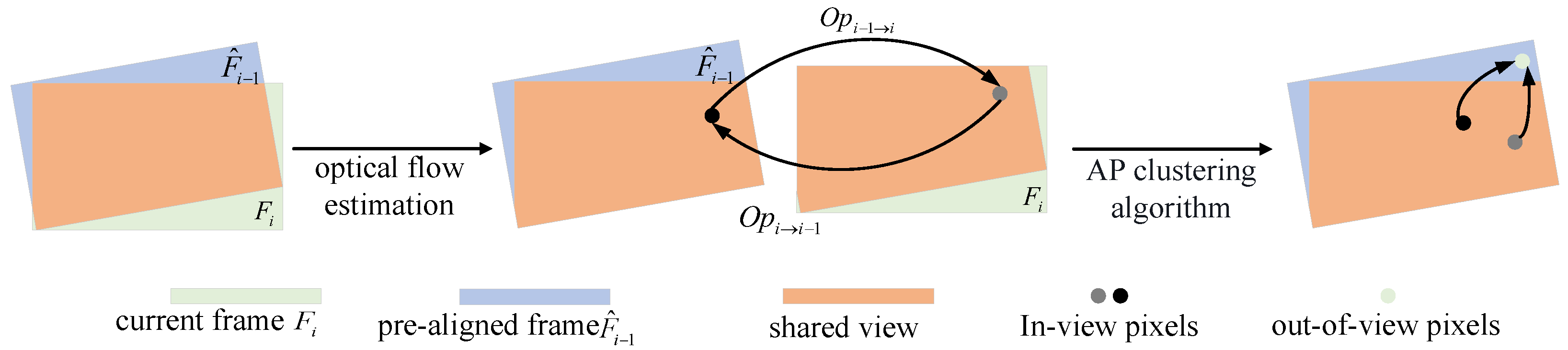
3.2. Frame Boundary Processing
3.3. Network Infrastructure
4. Experiments
4.1. Experimental Setup
4.2. Ablation Experiments
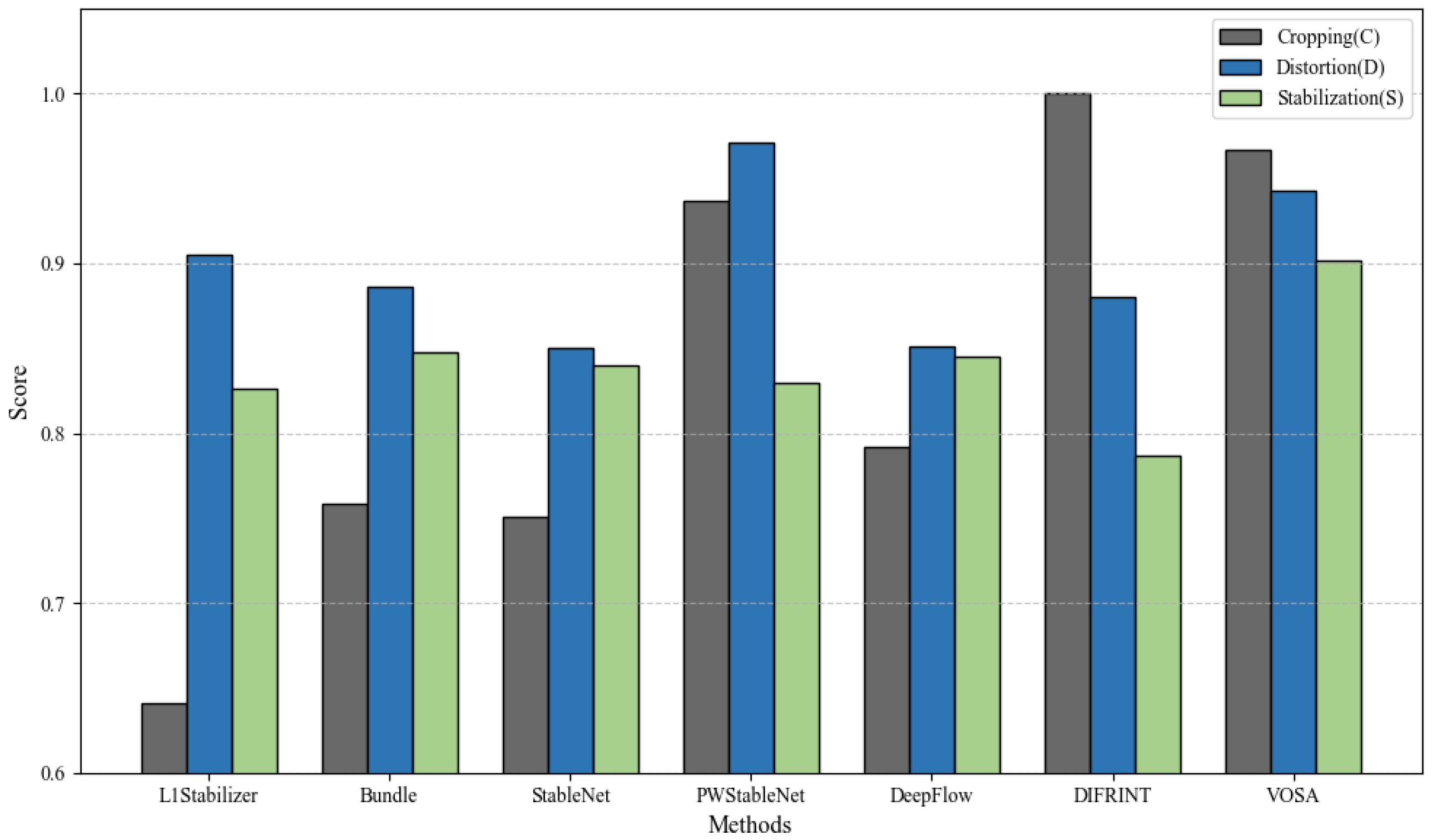
4.3. Comparison Results
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, L.; Xu, Q.K.; Huang, H. A Global Approach to Fast Video Stabilization. IEEE Trans. Circuits Syst. Video Technol. 2017, 27, 225–235. [Google Scholar] [CrossRef]
- Yan, W.; Sun, Y.; Zhou, W.; Liu, Z.; Cong, R. Deep Video Stabilization via Robust Homography Estimation. IEEE Signal Process. Lett. 2023, 30, 1602–1606. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, Z.; Liu, Z.; Tan, P.; Zeng, B. Minimum Latency Deep Online Video Stabilization and Its Extensions. IEEE Trans. Pattern Anal. Mach. Intell. 2025, 47, 1238–1249. [Google Scholar] [CrossRef]
- Ren, Z.; Fang, M.; Chen, C.; Kaneko, S.i. Video stabilization algorithm based on virtual sphere model. J. Electron. Imaging 2021, 30, 021002. [Google Scholar] [CrossRef]
- Zhang, T.; Xia, Z.; Li, M.; Zheng, L. DIN-SLAM: Neural Radiance Field-Based SLAM with Depth Gradient and Sparse Optical Flow for Dynamic Interference Resistance. Electronics 2025, 14, 1632. [Google Scholar] [CrossRef]
- Norbelt, M.; Luo, X.; Sun, J.; Claude, U. UAV Localization in Urban Area Mobility Environment Based on Monocular VSLAM with Deep Learning. Drones 2025, 9, 171. [Google Scholar] [CrossRef]
- Huang, H.Y.; Huang, S.Y. Fast Hole Filling for View Synthesis in Free Viewpoint Video. Electronics 2020, 9, 906. [Google Scholar] [CrossRef]
- Liu, S.; Tan, P.; Yuan, L.; Sun, J.; Zeng, B. MeshFlow: Minimum Latency Online Video Stabilization. In Proceedings of the 2016 European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; Springer: Cham, Switzerland, 2016; pp. 800–815. [Google Scholar]
- Grundmann, M.; Kwatra, V.; Essa, I. Auto-directed video stabilization with robust L1 optimal camera paths. In Proceedings of the CVPR 2011, Colorado Springs, CO, USA, 20–25 June 2011; pp. 225–232. [Google Scholar] [CrossRef]
- Bradley, A.; Klivington, J.; Triscari, J.; van der Merwe, R. Cinematic-L1 Video Stabilization with a Log-Homography Model. arXiv 2020, arXiv:cs.CV/2011.08144. [Google Scholar]
- Liu, S.; Yuan, L.; Tan, P.; Sun, J. SteadyFlow: Spatially Smooth Optical Flow for Video Stabilization. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 4209–4216. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, X.Q.; Kong, X.Y.; Huang, H. Geodesic Video Stabilization in Transformation Space. IEEE Trans. Image Process. 2017, 26, 2219–2229. [Google Scholar] [CrossRef]
- Wu, H.; Xiao, L.; Lian, Z.; Shim, H.J. Locally Low-Rank Regularized Video Stabilization With Motion Diversity Constraints. IEEE Trans. Circuits Syst. Video Technol. 2019, 29, 2873–2887. [Google Scholar] [CrossRef]
- Zhang, F.; Li, X.; Wang, T.; Zhang, G.; Hong, J.; Cheng, Q.; Dong, T. High-Precision Satellite Video Stabilization Method Based on ED-RANSAC Operator. Remote Sens. 2023, 15, 3036. [Google Scholar] [CrossRef]
- Jang, J.; Ban, Y.; Lee, K. Dual-Modality Cross-Interaction-Based Hybrid Full-Frame Video Stabilization. Appl. Sci. 2024, 14, 4290. [Google Scholar] [CrossRef]
- Li, X.; Xu, F.; Liu, F.; Tong, Y.; Lyu, X.; Zhou, J. Semantic Segmentation of Remote Sensing Images by Interactive Representation Refinement and Geometric Prior-Guided Inference. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5400318. [Google Scholar] [CrossRef]
- Li, X.; Xu, F.; Yu, A.; Lyu, X.; Gao, H.; Zhou, J. A Frequency Decoupling Network for Semantic Segmentation of Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2025, 63, 5607921. [Google Scholar] [CrossRef]
- Li, X.; Xu, F.; Zhang, J.; Yu, A.; Lyu, X.; Gao, H.; Zhou, J. Dual-domain decoupled fusion network for semantic segmentation of remote sensing images. Inf. Fusion 2025, 124, 103359. [Google Scholar] [CrossRef]
- Zhao, M.; Ling, Q. PWStableNet: Learning Pixel-Wise Warping Maps for Video Stabilization. IEEE Trans. Image Process. 2020, 29, 3582–3595. [Google Scholar] [CrossRef]
- Yu, J.; Ramamoorthi, R. Learning Video Stabilization Using Optical Flow. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 8156–8164. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, J.; Maybank, S.J.; Tao, D. DUT: Learning Video Stabilization by Simply Watching Unstable Videos. IEEE Trans. Image Process. 2022, 31, 4306–4320. [Google Scholar] [CrossRef]
- Choi, J.; Kweon, I.S. Deep Iterative Frame Interpolation for Full-frame Video Stabilization. ACM Trans. Graph. 2020, 39, 1–9. [Google Scholar] [CrossRef]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision, 2nd ed.; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Wei, X.; Zhang, Y.; Li, Z.; Fu, Y.; Xue, X. DeepSFM: Structure from Motion via Deep Bundle Adjustment. In Proceedings of the Computer Vision—ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part I. Springer: Berlin/Heidelberg, Germany, 2020; pp. 230–247. [Google Scholar] [CrossRef]
- Kim, D.; Woo, S.; Lee, J.Y.; Kweon, I.S. Deep video inpainting. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 5792–5801. [Google Scholar]
- Li, J.; He, F.; Zhang, L.; Du, B.; Tao, D. Progressive Reconstruction of Visual Structure for Image Inpainting. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November October 2019. [Google Scholar]
- Zeng, Y.; Fu, J.; Chao, H. Learning Joint Spatial-Temporal Transformations for Video Inpainting. In Proceedings of the Computer Vision—ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part XVI. Springer: Berlin/Heidelberg, Germany, 2020; pp. 528–543. [Google Scholar] [CrossRef]
- Li, S.; He, F.; Du, B.; Zhang, L.; Xu, Y.; Tao, D. Fast Spatio-Temporal Residual Network for Video Super-Resolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 10514–10523. [Google Scholar]
- Lim, B.; Son, S.; Kim, H.; Nah, S.; Lee, K.M. Enhanced Deep Residual Networks for Single Image Super-Resolution. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Honolulu, HI, USA, 21–26 July 2017; pp. 1132–1140. [Google Scholar] [CrossRef]
- Zhang, Y.; Tian, Y.; Kong, Y.; Zhong, B.; Fu, Y. Residual Dense Network for Image Super-Resolution. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 2472–2481. [Google Scholar] [CrossRef]
- Lowe, D. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Bay, H.; Tuytelaars, T.; Van Gool, L. SURF: Speeded up robust features. In Proceedings of the 9th European Conference on Computer Vision; Graz, Austria, 7–13 May 2006, Volume Part I; Springer: Berlin/Heidelberg, Germany, 2006; pp. 404–417. [Google Scholar] [CrossRef]
- Rublee, E.; Rabaud, V.; Konolige, K.; Bradski, G. ORB: An efficient alternative to SIFT or SURF. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 2564–2571. [Google Scholar] [CrossRef]
- DeTone, D.; Malisiewicz, T.; Rabinovich, A. Deep Image Homography Estimation. arXiv 2016. [Google Scholar] [CrossRef]
- Nguyen, T.; Chen, S.W.; Shivakumar, S.S.; Taylor, C.J.; Kumar, V. Unsupervised Deep Homography: A Fast and Robust Homography Estimation Model. IEEE Robot. Autom. Lett. 2018, 3, 2346–2353. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, C.; Liu, S.; Jia, L.; Ye, N.; Wang, J.; Zhou, J.; Sun, J. Content-Aware Unsupervised Deep Homography Estimation. In Proceedings of the Computer Vision—ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part I. Springer: Berlin/Heidelberg, Germany, 2020; pp. 653–669. [Google Scholar] [CrossRef]
- Ilg, E.; Mayer, N.; Saikia, T.; Keuper, M.; Dosovitskiy, A.; Brox, T. FlowNet 2.0: Evolution of Optical Flow Estimation with Deep Networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 1647–1655. [Google Scholar] [CrossRef]
- Brezinski, C.; Zaglia, M. Extrapolation Methods: Theory and Practice; Studies in Computational Mathematics; Elsevier: North Holland, The Netherlands, 2013. [Google Scholar]
- Shi, Z.; Shi, F.; Lai, W.S.; Liang, C.K.; Liang, Y. Deep Online Fused Video Stabilization. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 3–8 January 2022; pp. 1250–1258. [Google Scholar]
- Liu, S.; Yuan, L.; Tan, P.; Sun, J. Bundled camera paths for video stabilization. ACM Trans. Graph. 2013, 32, 1–10. [Google Scholar] [CrossRef]
- Wang, M.; Yang, G.Y.; Lin, J.K.; Zhang, S.H.; Shamir, A.; Lu, S.P.; Hu, S.M. Deep Online Video Stabilization With Multi-Grid Warping Transformation Learning. IEEE Trans. Image Process. 2019, 28, 2283–2292. [Google Scholar] [CrossRef] [PubMed]






| Category | Hyperparameter | Value |
|---|---|---|
| Optimization | Optimizer | Adam |
| Adam beta parameters | (0.9, 0.99) | |
| Momentum coefficient | 0.9 | |
| Weight decay (initial) | 2 × 10−4 | |
| Boundary Processing | Boundary padding | 80 pixels per side |
| Iteration count for propagation | 10 | |
| SIFT | Contrast threshold | 0.04 |
| Edge threshold | 10 | |
| Octaves | 4 | |
| RANSAC | Distance threshold | 5 pixels |
| Inlier ratio threshold | 0.8 | |
| Network Design | Sobel filter size | 3 × 3 |
| Affinity kernel radius |
| Layer | Kernel | Strides |
|---|---|---|
| Conv1 | 1 | |
| Conv2 | 1 | |
| MaxPool2 | 4 | |
| Conv3 | 1 | |
| MaxPool3 | 4 | |
| Conv4 | 1 | |
| MaxPool4 | 4 | |
| Conv5 | 1 | |
| MaxPool5 | 4 |
| Model | C | D | S |
|---|---|---|---|
| Baseline | 0.910 | 0.949 | 0.900 |
| w/o Pre-Alignment Module | 0.940 | 0.926 | 0.900 |
| w Pre-Alignment Module | 0.967 | 0.943 | 0.902 |
| Loss Parameter | C | D | S |
|---|---|---|---|
| 0.924 | 0.952 | 0.900 | |
| 0.945 | 0.940 | 0.902 | |
| 0.947 | 0.943 | 0.900 | |
| 0.965 | 0.944 | 0.900 | |
| 0.967 | 0.942 | 0.902 | |
| 0.967 | 0.943 | 0.902 |
| Number of Iterations | C | D | S |
|---|---|---|---|
| 0 | 0.910 | 0.949 | 0.900 |
| 5 | 0.947 | 0.951 | 0.900 |
| 10 | 0.967 | 0.943 | 0.902 |
| 15 | 0.967 | 0.931 | 0.902 |
| 20 | 0.970 | 0.915 | 0.902 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shan, W.; Zhao, H.; Li, X.; Huang, Q.; Jiang, C.; Wang, Y.; Chen, Z.; Tong, Y. Video Stabilization Algorithm Based on View Boundary Synthesis. Symmetry 2025, 17, 1351. https://doi.org/10.3390/sym17081351
Shan W, Zhao H, Li X, Huang Q, Jiang C, Wang Y, Chen Z, Tong Y. Video Stabilization Algorithm Based on View Boundary Synthesis. Symmetry. 2025; 17(8):1351. https://doi.org/10.3390/sym17081351
Chicago/Turabian StyleShan, Wenchao, Hejing Zhao, Xin Li, Qian Huang, Chuanxu Jiang, Yiming Wang, Ziqi Chen, and Yao Tong. 2025. "Video Stabilization Algorithm Based on View Boundary Synthesis" Symmetry 17, no. 8: 1351. https://doi.org/10.3390/sym17081351
APA StyleShan, W., Zhao, H., Li, X., Huang, Q., Jiang, C., Wang, Y., Chen, Z., & Tong, Y. (2025). Video Stabilization Algorithm Based on View Boundary Synthesis. Symmetry, 17(8), 1351. https://doi.org/10.3390/sym17081351







