Lorenz and Chua Chaotic Key-Based Dynamic Substitution Box for Efficient Image Encryption
Abstract
1. Introduction
- An optimized reversible S-box using composite field arithmetic is proposed to solve the aforementioned area and power issues.
- The pseudo-random data generated through the hybrid Lorenz–Chua key generation (LCK-SB) method is utilized to produce a key that transforms a static system into a dynamic S-box, making it challenging for hackers to predict the key value. This enhances the non linearity and improves security.
- Security analysis for a side-channel attack (SCA), selected key attack (SKA), and avalanche effect (AE) is conducted for the entire architecture.
- To improve power dissipation, a reversible S-box is proposed, which utilizes an injective logic function with more effectiveness by reducing redundant signals.
2. Different Kinds of Reversible Gates
2.1. Feynman Gate
2.2. Toffoli Gate
2.3. Fredkin Gate
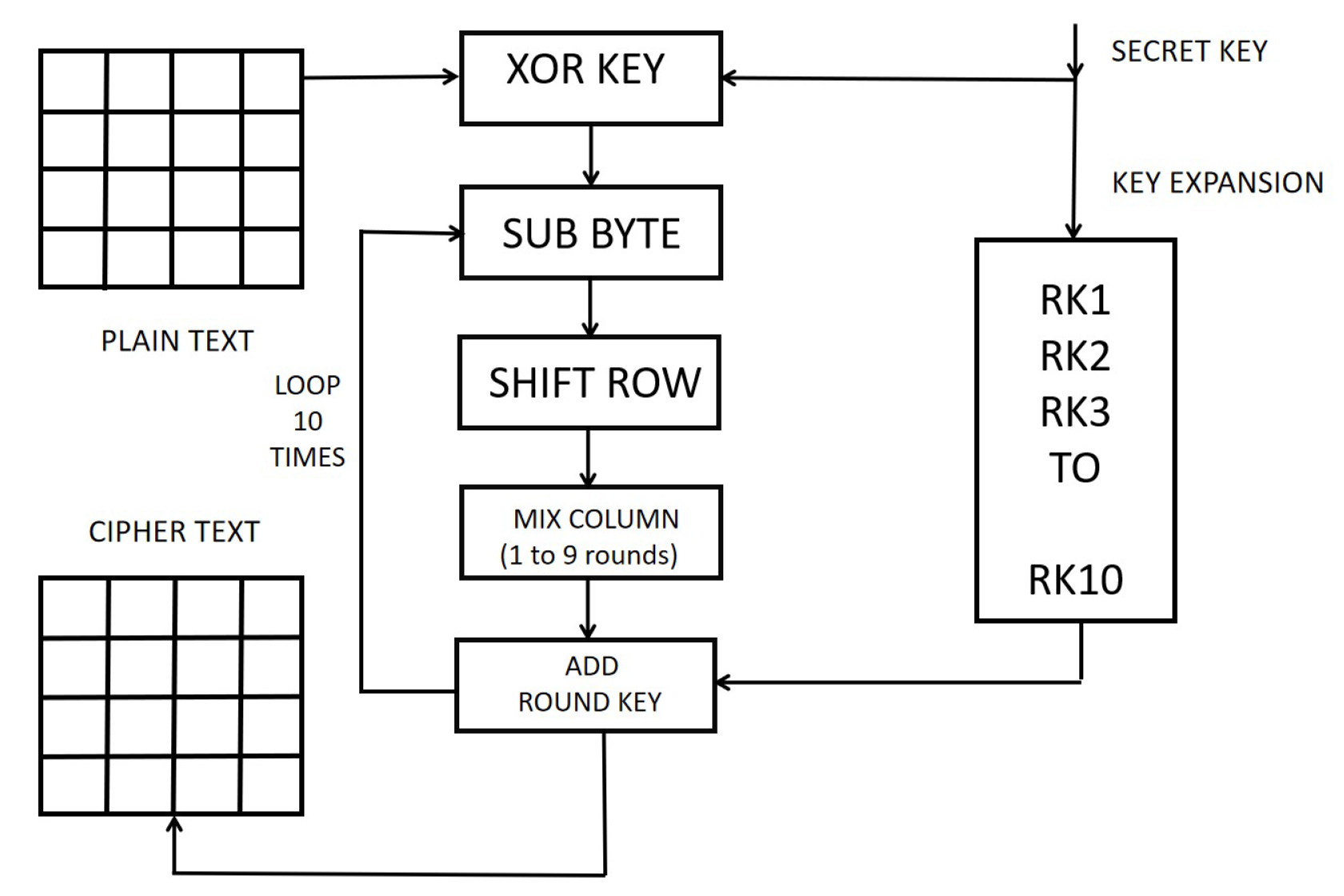
3. AES Algorithm
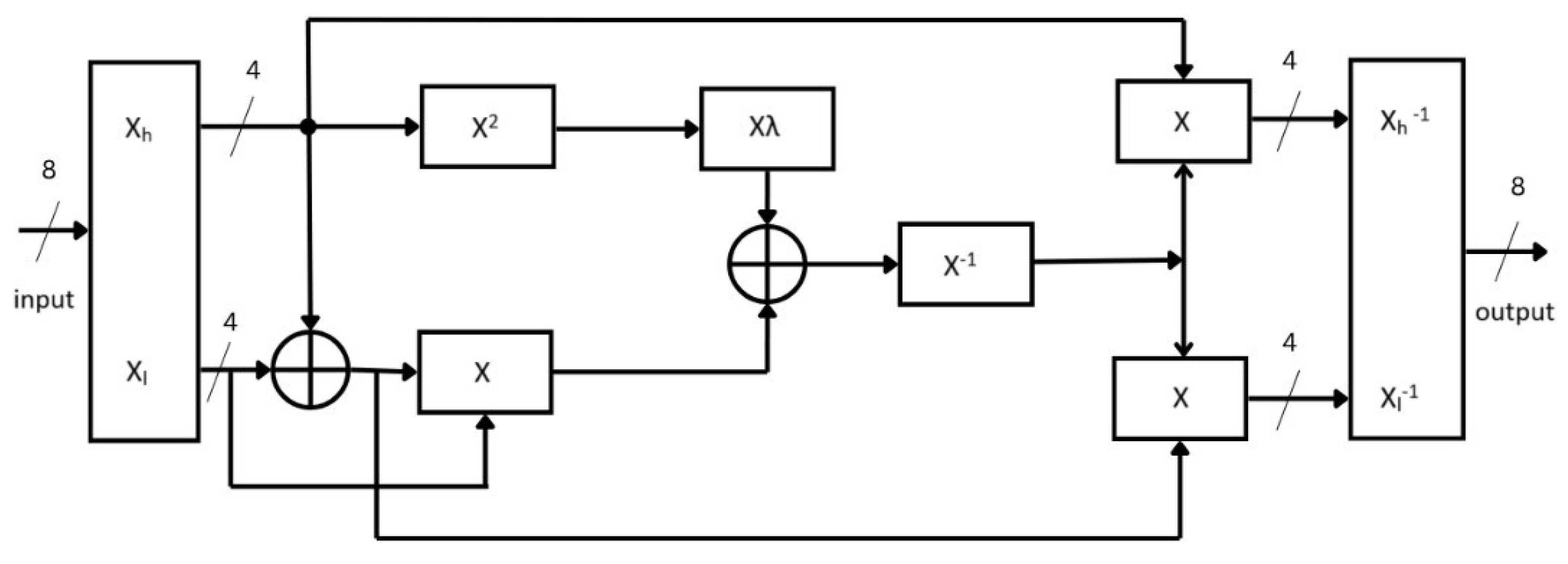
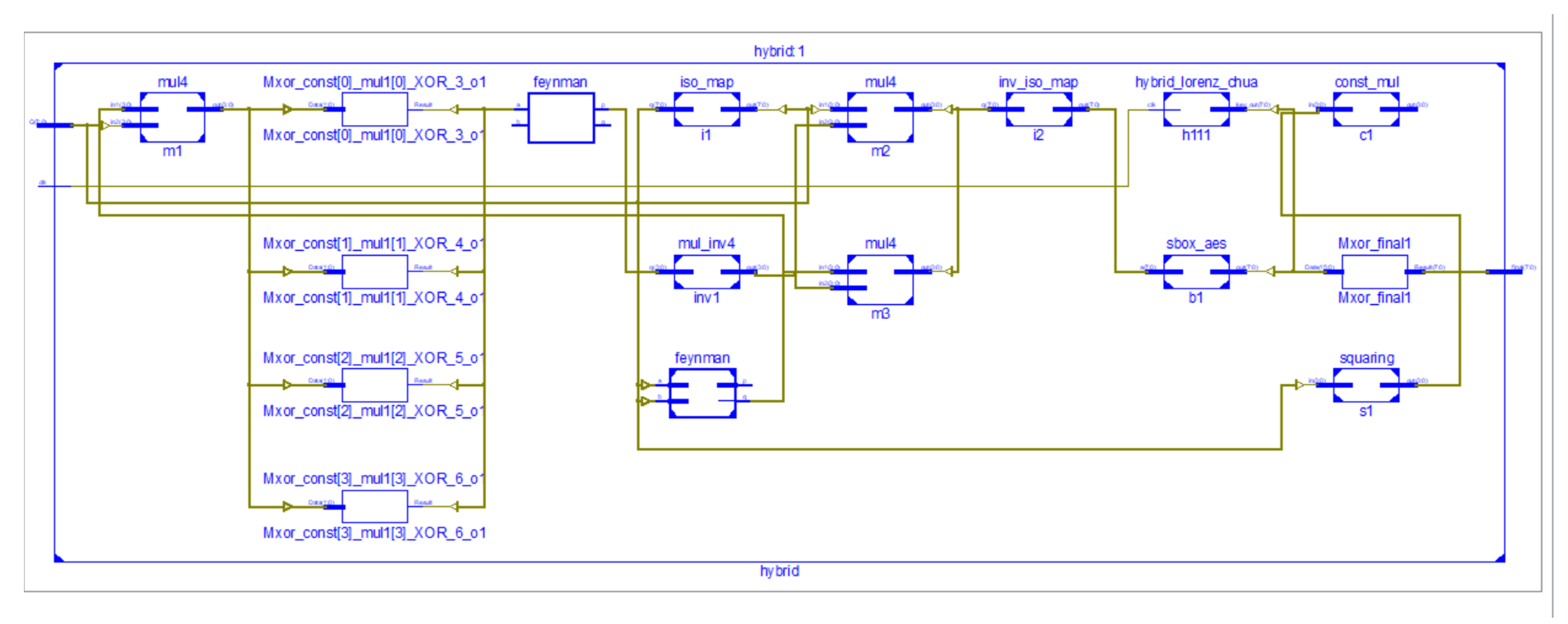
4. Proposed Lorenz–Chua Key Generation-Based S-Box-(LCK-SB) Design
4.1. Substitute Byte Transformation
4.2. Isomorphic Mapping
4.3. Inverse Isomorphic Mapping
4.4. Multiplicative Inverse in Composite Field
- represents 4-bit MSB nibbles in the input.
- represents 4-bit LSB nibbles in the input.
- is a 4-bit squaring circuit.
- X is a 4-bit multiplier.
- is 4-bit multiplier with .
- is 4-bit multiplicative inverse calculator.
4.5. Multiplicative Inverse Operation of GF()
4.6. Affine Transformation
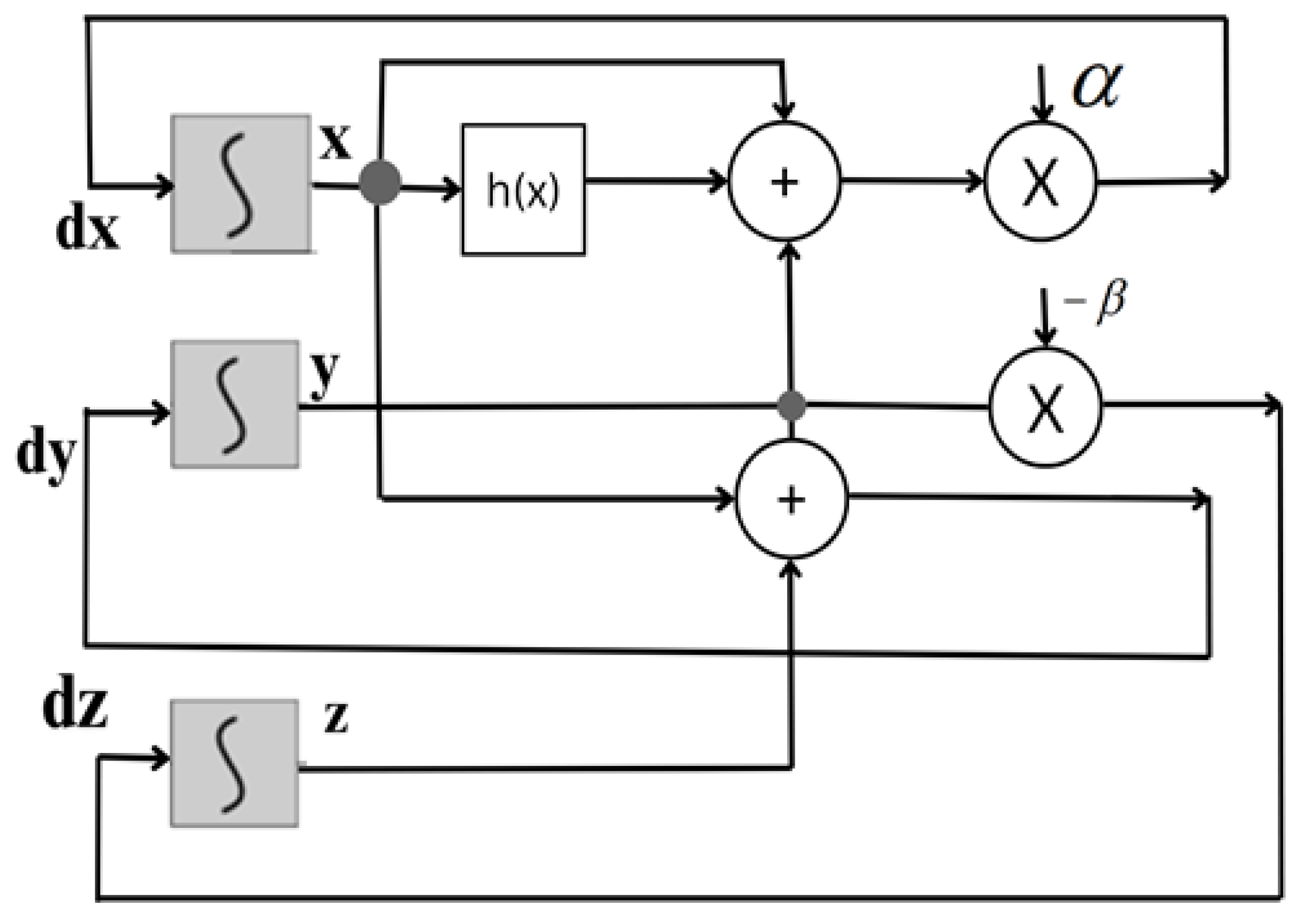
4.7. Lorenz Key Generation
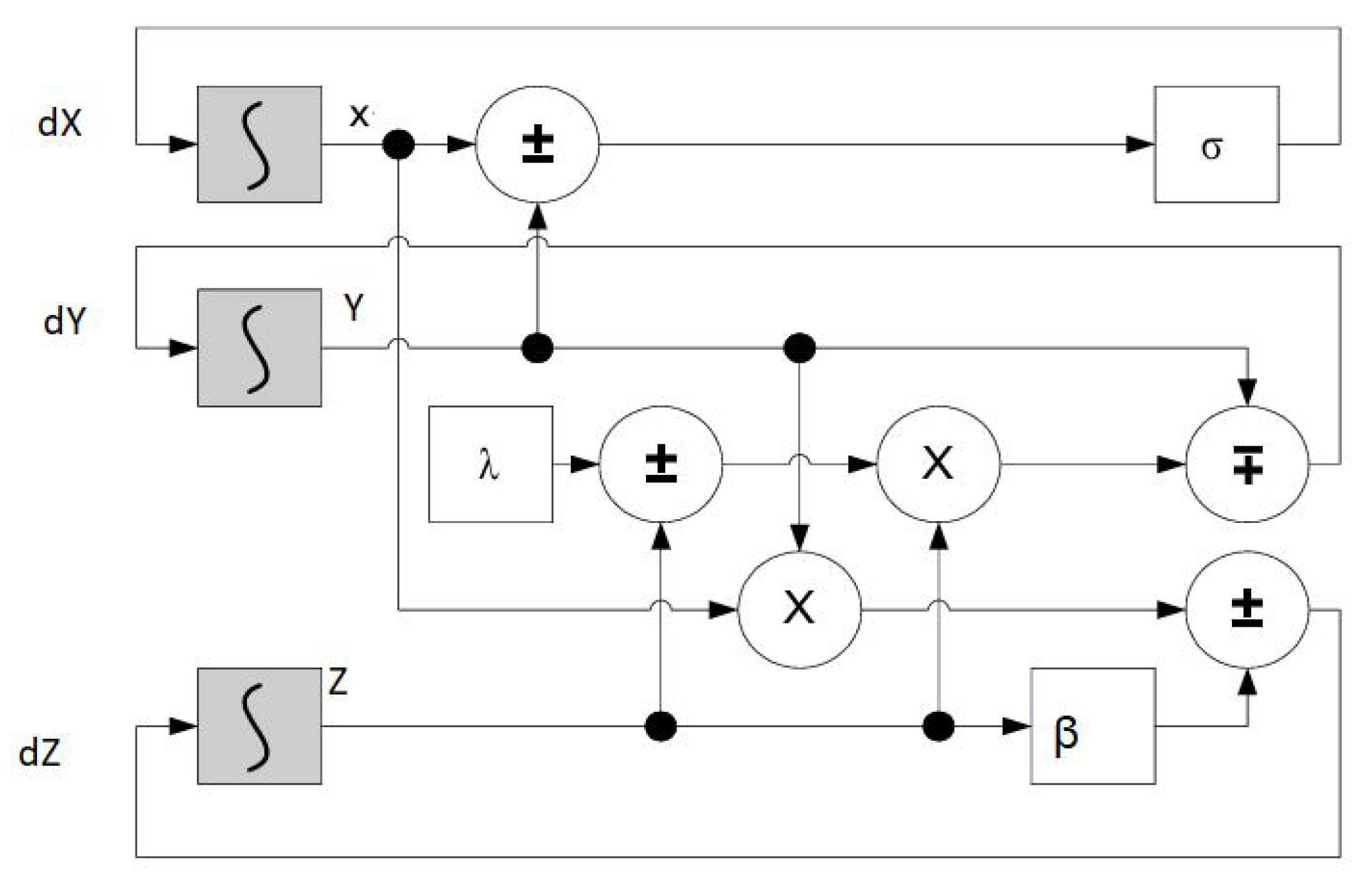
4.8. Chua’s Chaotic System: Differential Equations
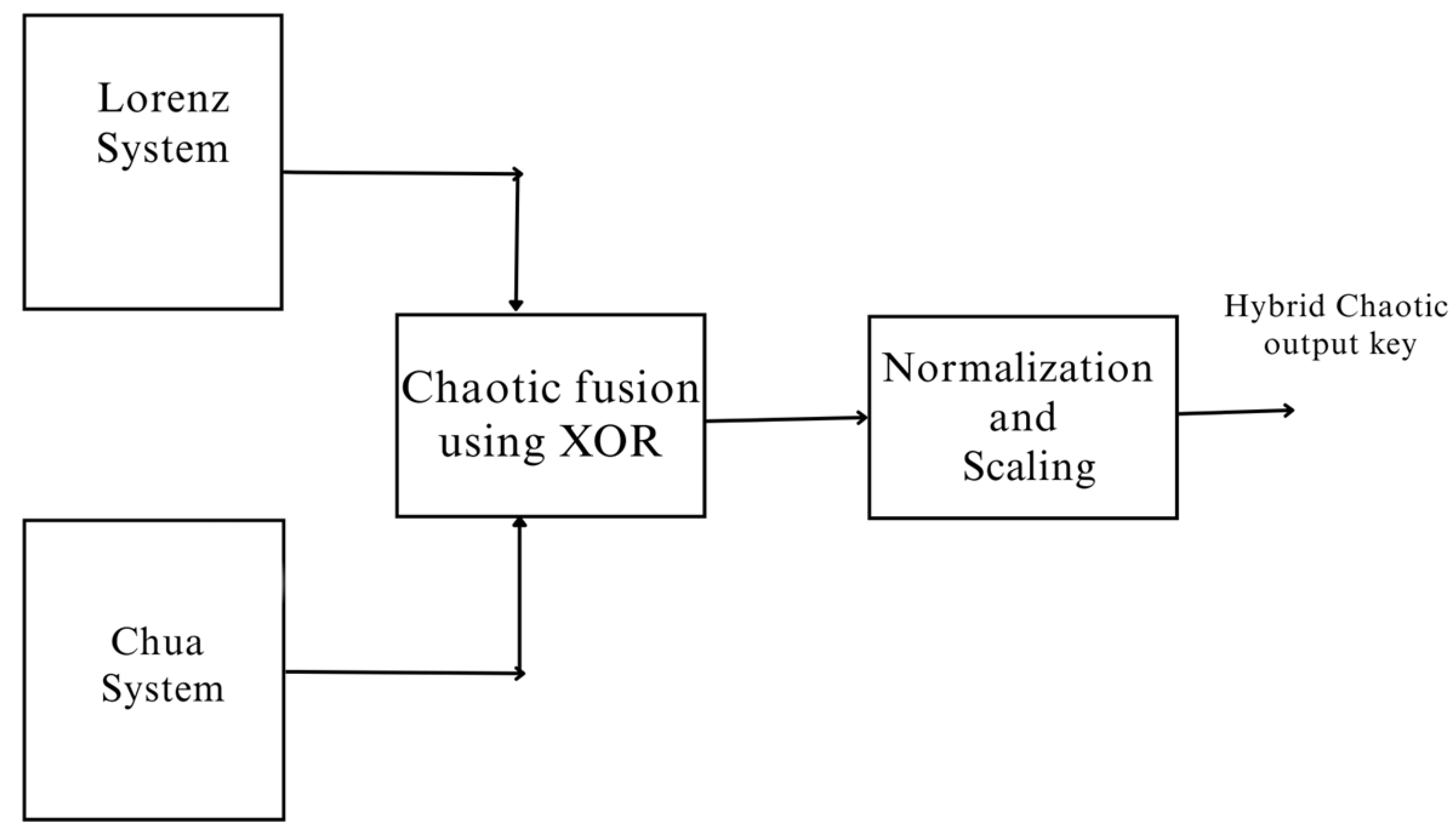
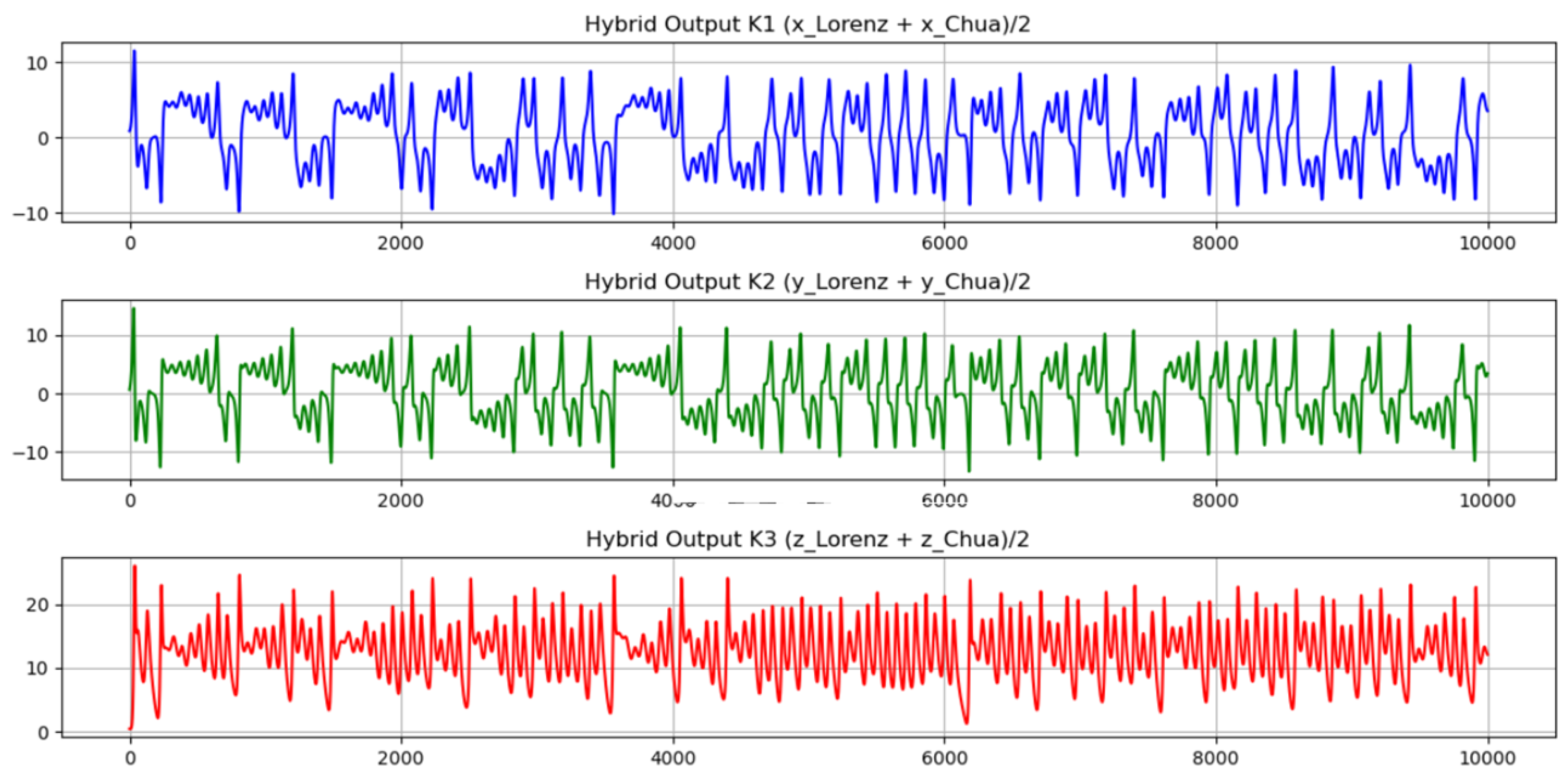
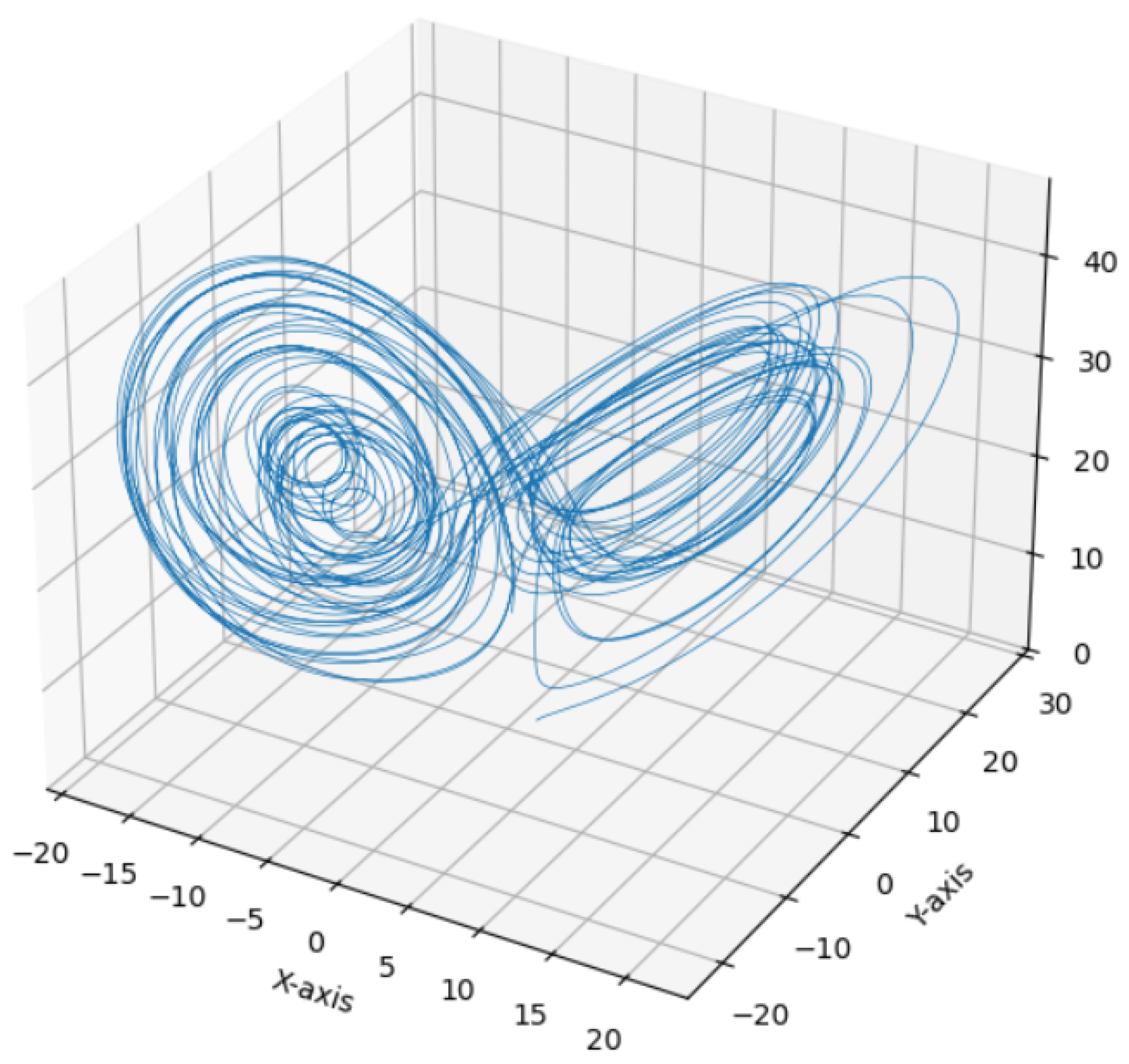
4.9. Hybrid Lorenz–Chua Chaotic Key Generation
| Algorithm 1: Lorenz–Chua chaotic key generator |
|
Mathematical Modeling of the Hybrid Chaotic System
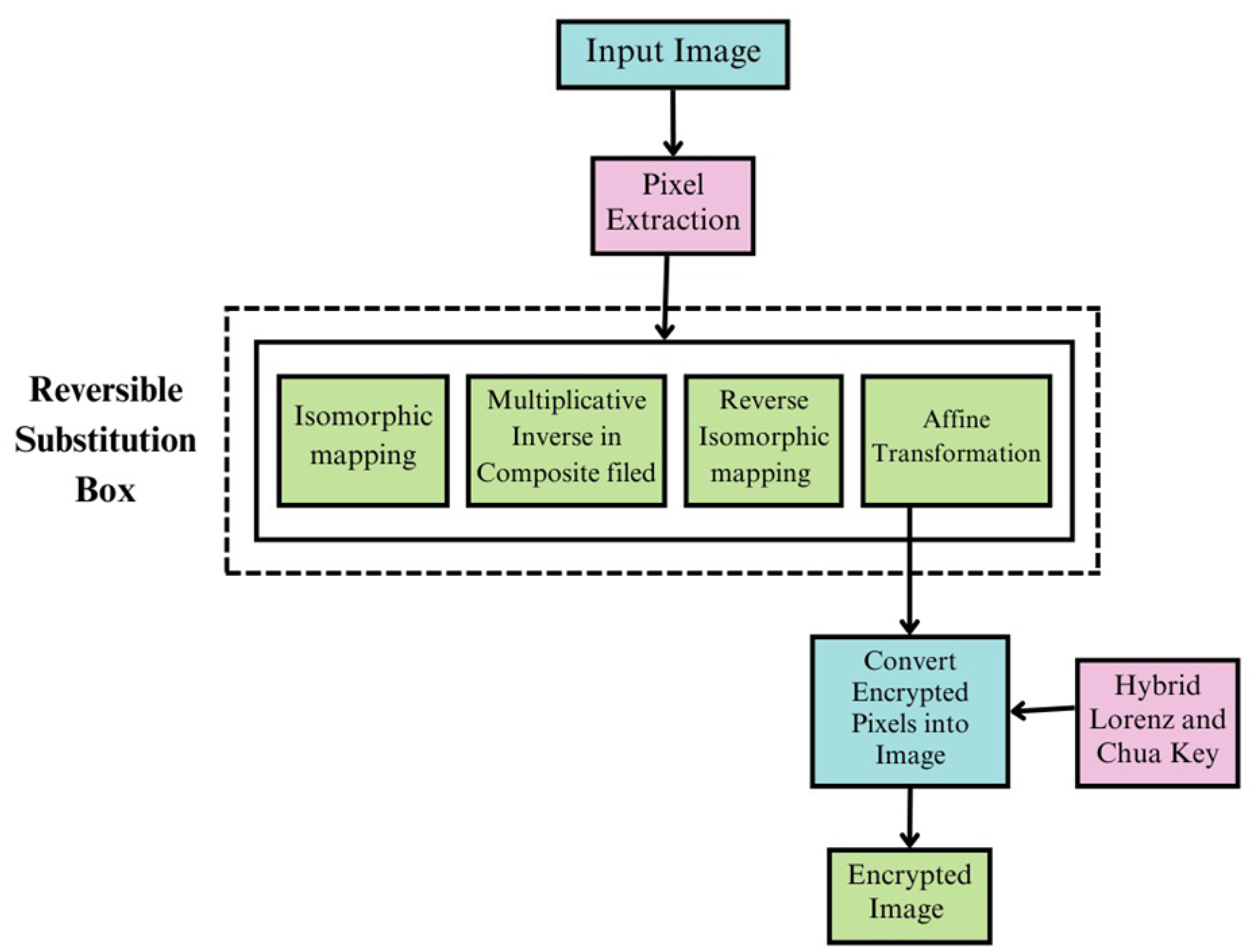
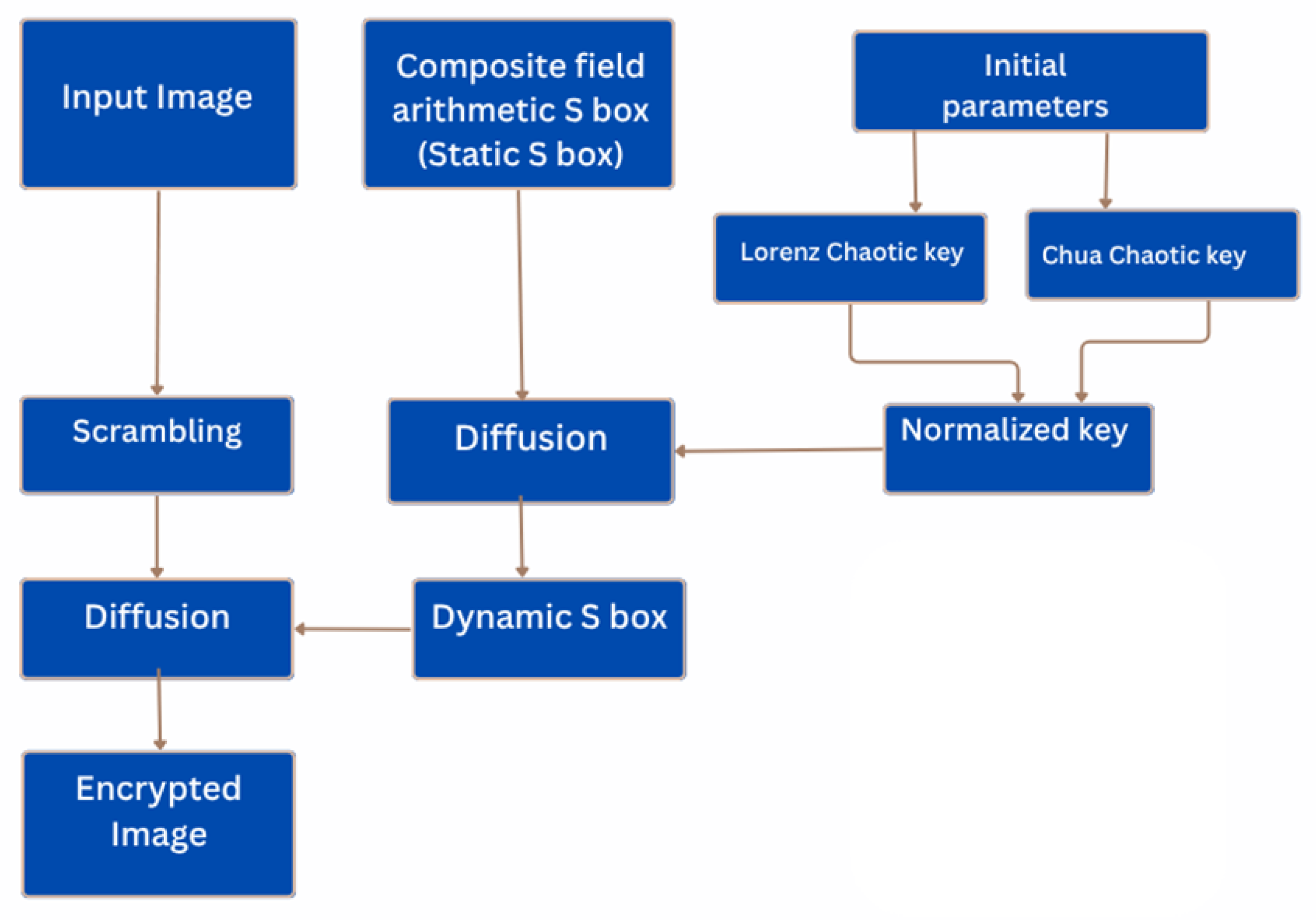
4.10. Image Encryption Using Hybrid Lorenz–Chua Key Generator-Based S-Box
5. Performance Results
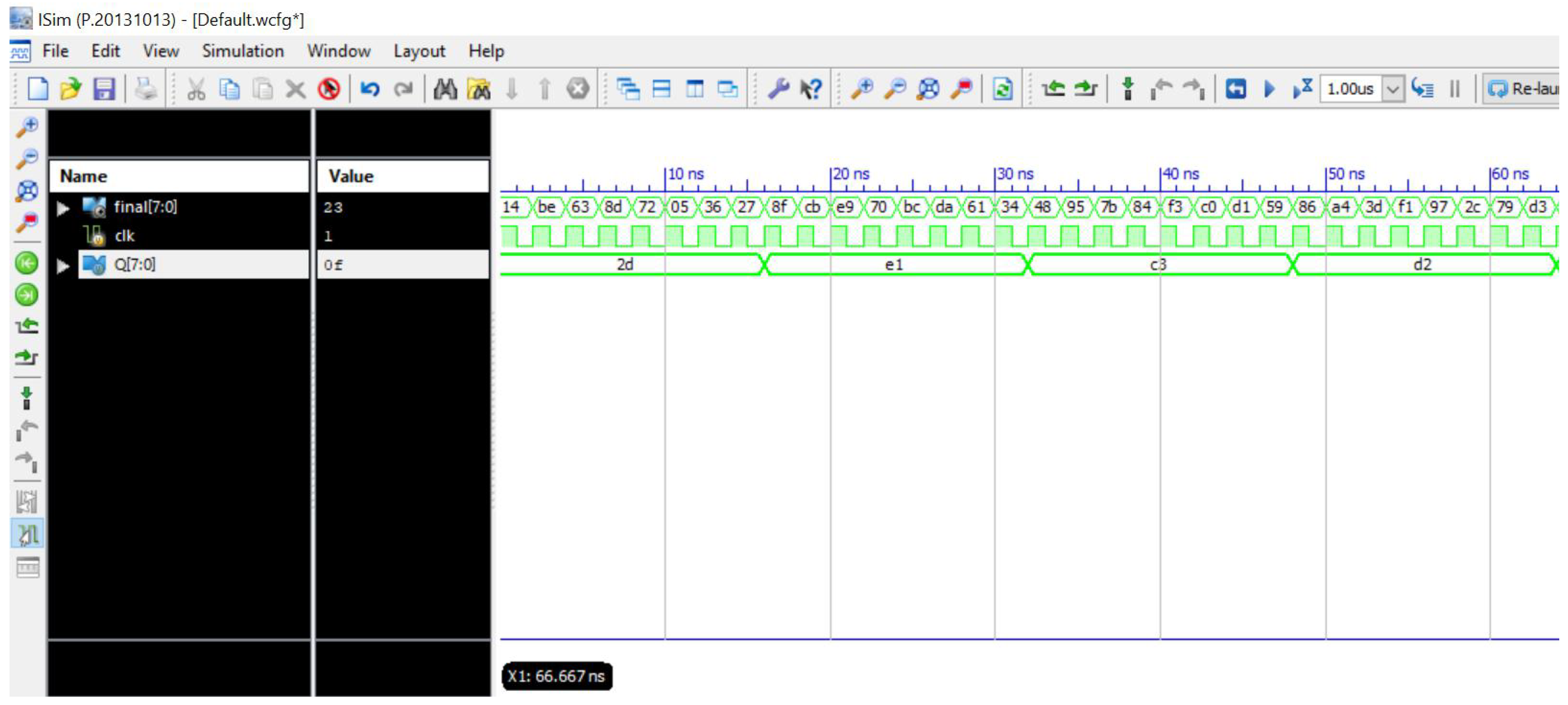
5.1. Simulation and Synthesis Results of Proposed LCK-SB Design
- Hybrid Lorenz–Chua Chaotic Key Generator Block: Initial parameters and clock enable signals were inputs. Functional units were used to implement the Lorenz and Chua chaotic differential equations iteratively (using the Euler method) to generate chaotic key streams with high entropy.
- Normalization and Quantization Units: These were used to normalize the chaotic outputs to a [0, 1) range to avoid overflow. These normalized floating-point values were scaled and converted to fixed-point 8-bit integers suitable for digital logic processing.
- Dynamic S-Box Generation Unit: This received the 8-bit chaotic key values as inputs. Used these values to dynamically generate the substitution values corresponding to each S-box entry (0x00 to 0xFF). Typically, combinational logic based on a Galois field arithmetic static box was converted to a unique dynamic S-box dynamically.
- Control Logic/State Machines: This managed iterative computation steps and synchronization signals, enabled new key generation per clock cycle, and loaded dynamic S-box values into registers for the AES round operations.
- Interface Signals: Clock, reset, and enable signals for synchronization.
- Output buses representing the generated dynamic S-box values and keys fed into the AES encryption pipeline.
5.2. ASIC Performance
5.3. Quantum Cost Analysis
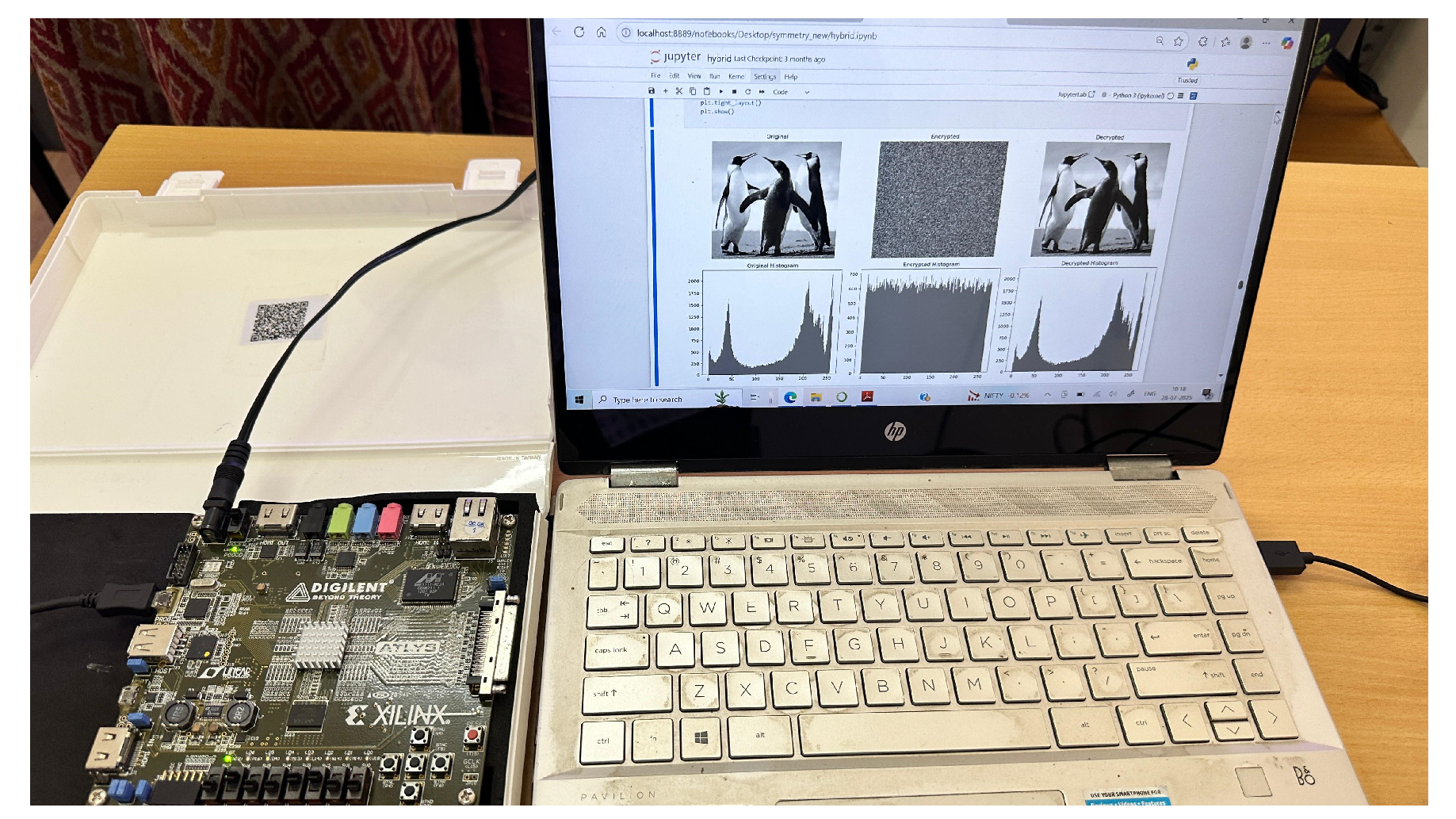
5.4. FPGA Implementation of Image Encryption
5.5. Randomness Analysis of Lorenz–Chua Chaotic Random Key Generator
- If , the sequence passed randomness.
- Otherwise, the sequence was not random.
| Test Name | p-Value | Result |
|---|---|---|
| Frequency (monobit test) | 0.511 | pass |
| Serial test | 0.1037 | pass |
| Runs test | 0.823 | pass |
| Chi square uniformity | 0.972 | pass |
| K-S test | 0.465 | pass |
| Shanon entropy | 7.98 | pass |
6. Security Analysis
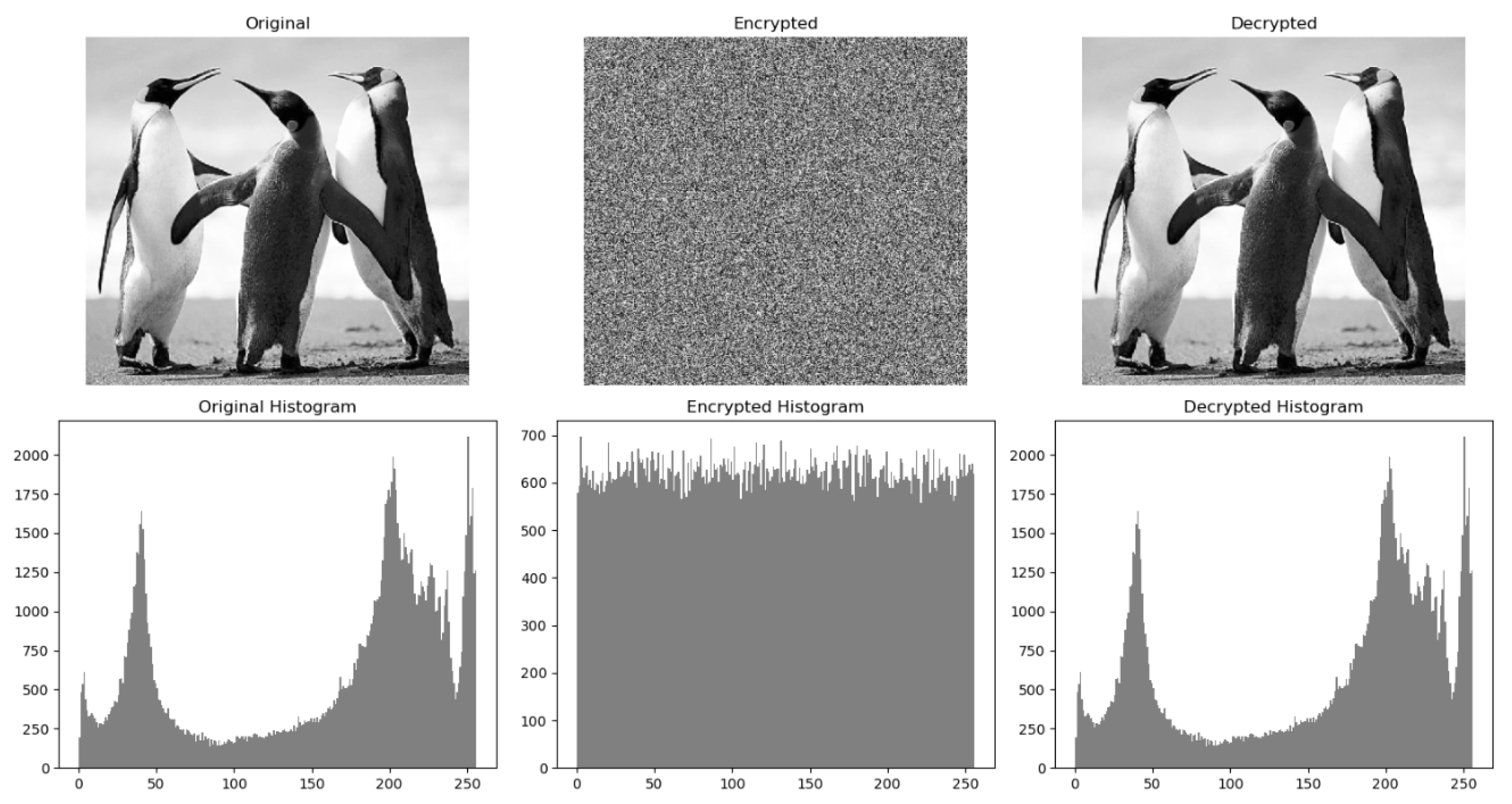
6.1. Histogram Analysis
6.2. AE Security Analysis
6.3. Bit Independence Criterion
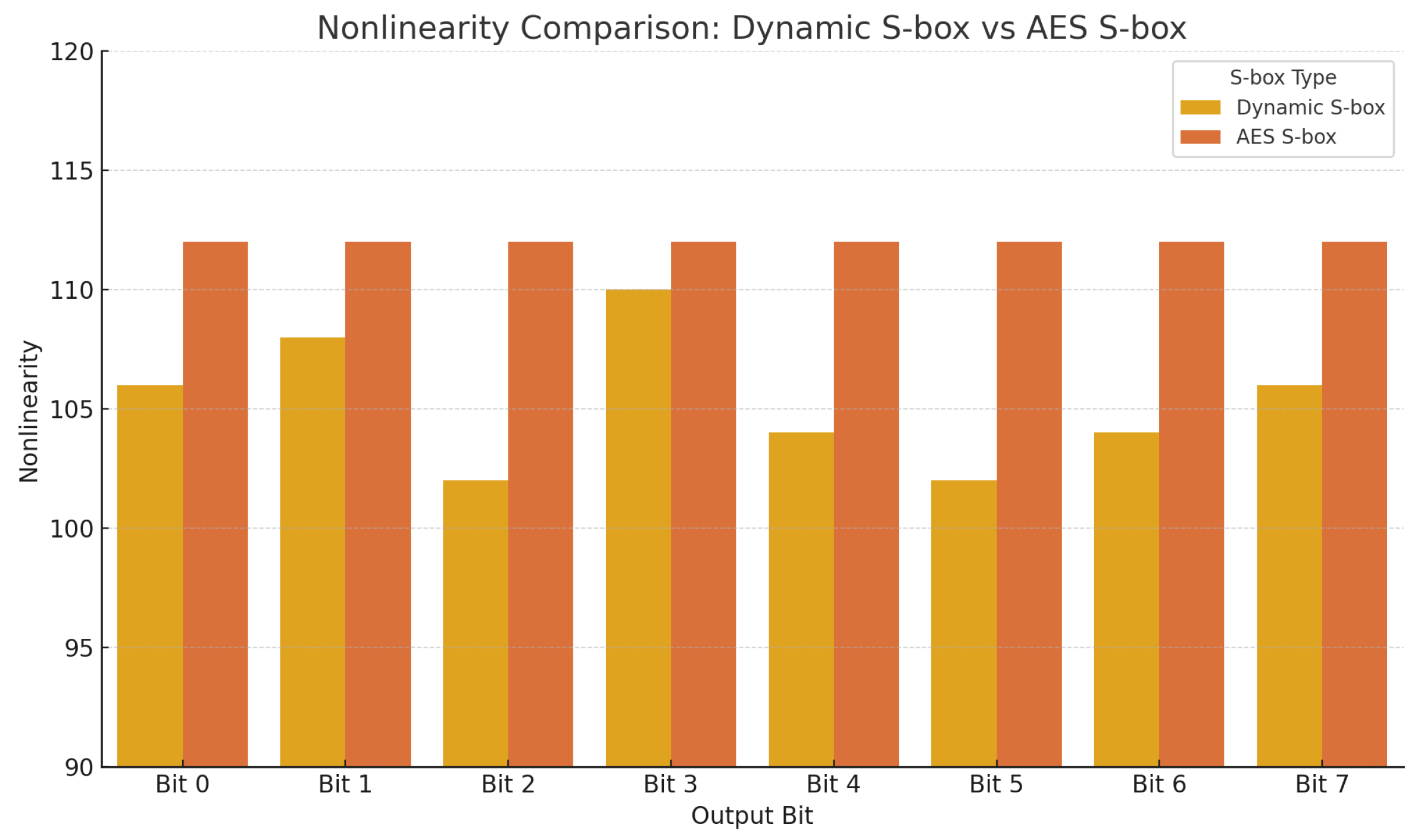
6.4. Non-Linearity
6.5. Selected Key Attack Security Model
6.6. SCA Security Analysis
6.7. Analysis of MSE, PSNR, and SSIM
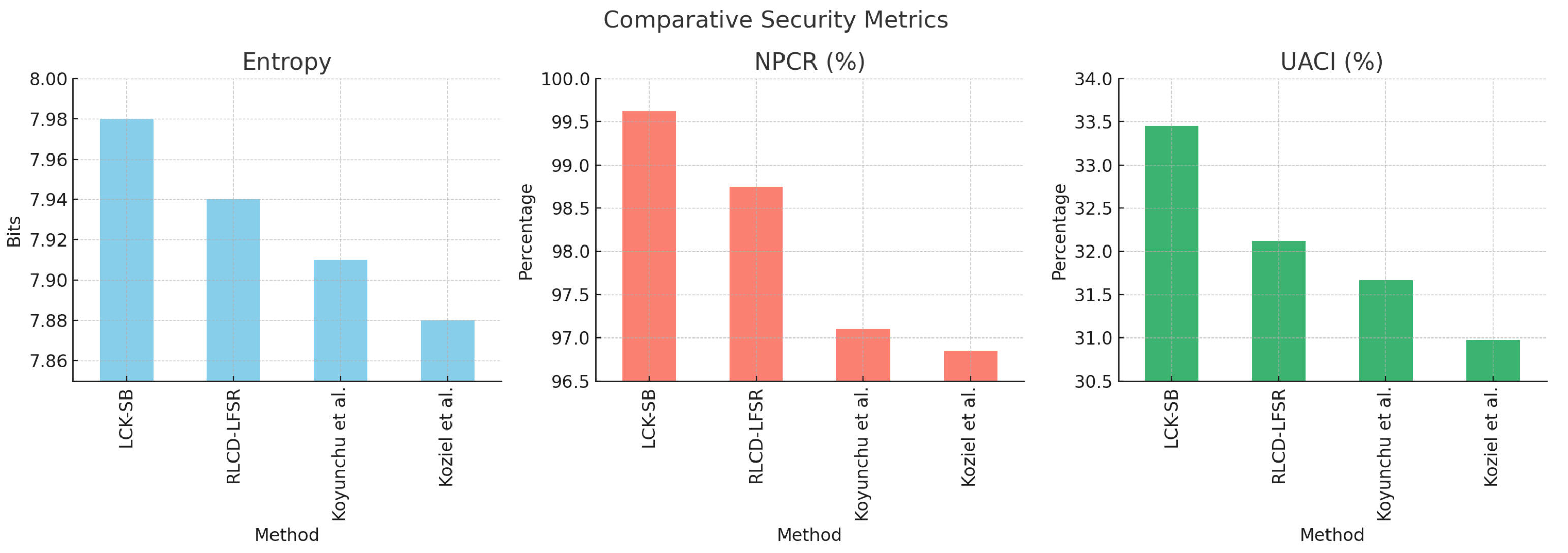
6.8. Comparative Security Metrics
6.9. Encryption Efficiency
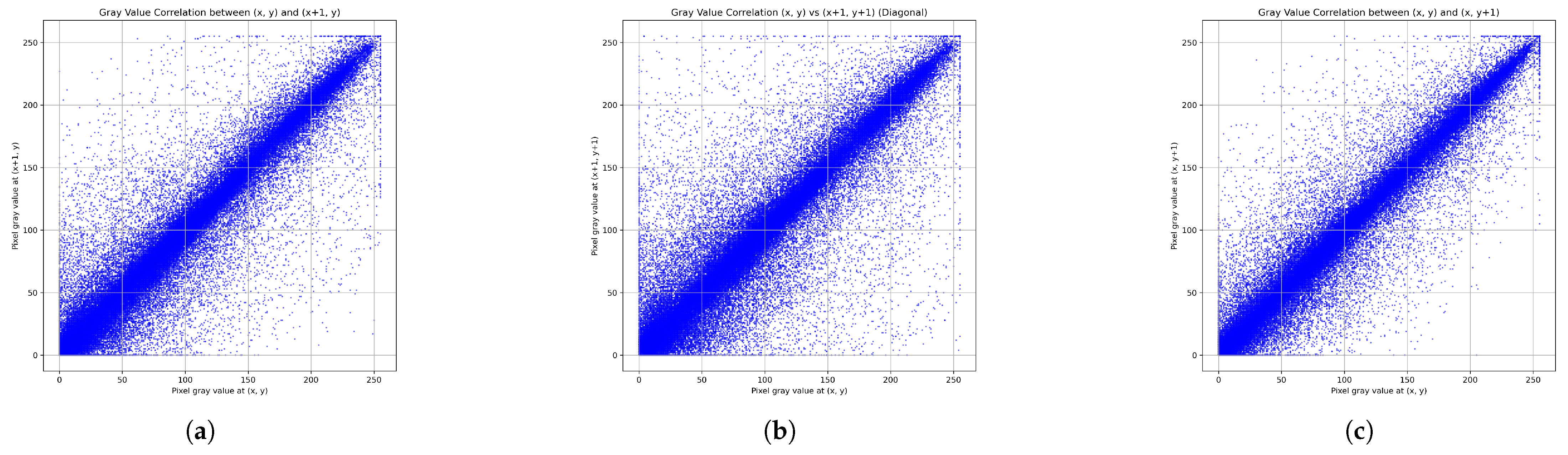
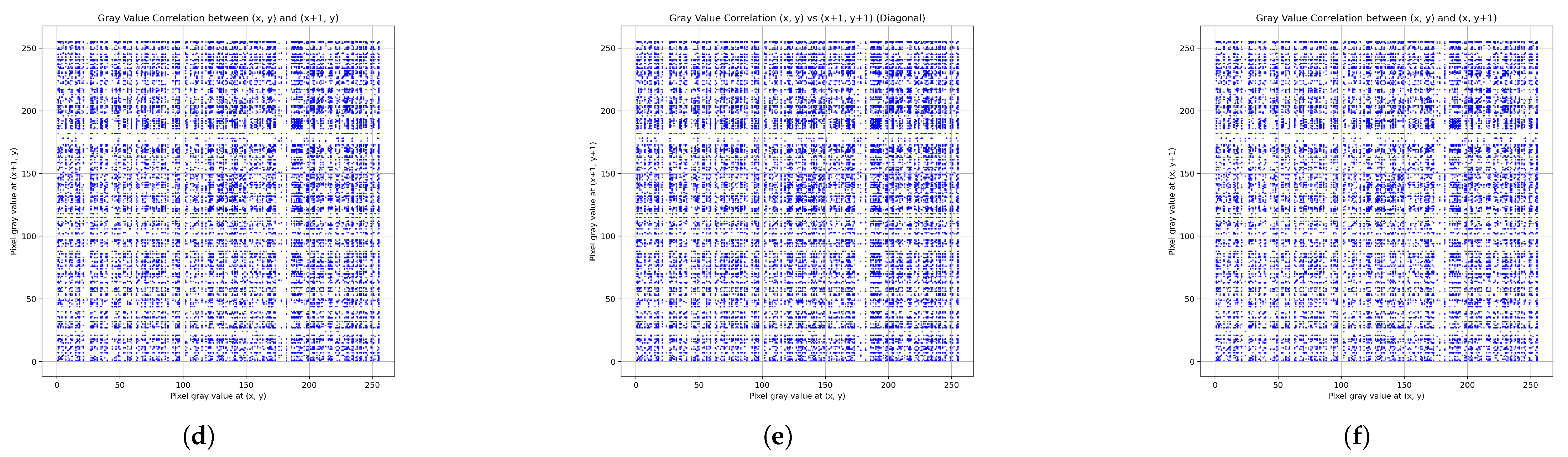
Pixel Correlation
6.10. Comparison with Emerging Chaos-Based Encryption Algorithms
6.11. Hybrid Lorenz–Chua-Based S-Box Generation with Fractional-Order Chaotic Enhancement Algorithm for Robust Key Generation
Algorithm Workflow
- Step 1.
- Initialization:
- Set initial states for Lorenz system:
- Set initial states for Chua system:
- Define
- –
- Fractional order
- –
- Time step
- –
- Total iterations M
- –
- Memory length K (for fractional memory)
- Specify chaotic system parameters:
- –
- Lorenz:
- –
- Chua:
- Step 2.
- Iterative System Simulation (for to M):
- Compute Lorenz derivatives:
- Compute Chua derivatives:where
- Update system states using the Euler method:
- Step 3.
- Fractional-Order Approximation:
- For to M, compute
- These fractional states capture long-term memory effects and enhance system complexity.
- Step 4.
- Combine Chaotic Outputs:
- Fuse and normalize outputs:
- Scale to byte range:
- Step 5.
- S-Box Construction:
- Remove duplicates from H. Pad with unused values to form 256 unique entries.
- For to 255:
- Step 5.1.
- Let
- Step 5.2.
- Apply non-linear transformation:
- Step 5.3.
- Resolve collisions: increment v until unique.
- Step 5.4.
- Assign
- Step 6.
- Return Final S-Box:
- Output as the dynamic, chaos-enhanced substitution box.
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AES | Advanced Encryption Standard |
| LCK-SB | Lorenz and Chua Key-Based Dynamic Substitution Box |
| S-box | Substitution Box |
| LFSR | Linear Feedback Shift Register |
| CFA | Composite Field Arithmetic |
| FPGA | Field-Programmable Gate Array |
| ASIC | Application-Specific Integrated Circuit |
| RL | Reversible Logic |
| PPRM | Positive Polarity Reed-Muller (architecture) |
| DCPAL | Differential Cascade Preresolve Adiabatic Logic |
| SKA | Selected Key Attack |
| SCA | Side-Channel Attack |
| NIST | National Institute of Standards and Technology |
| FFT | Fast Fourier Transform |
| NPCR | Number of Pixels Change Rate |
| UACI | Unified Average Changing Intensity |
| AE | Avalanche Effect |
| BIC-NL | Bit Independence Criterion—Nonlinearity |
| LP | Linear Probability |
| DP | Differential Probability |
| MSE | Mean Squared Error |
| PSNR | Peak Signal-to-Noise Ratio |
| SSIM | Structural Similarity Index Measure |
References
- Alexan, W.; El Beltagy, M.; Aboshousha, A. RGM Image encryption through Cellular Automata,S-Box and the Lorenz system. Symmetry 2023, 42, 535–538. [Google Scholar]
- Sani, R.H.; Behnia, S.; Akshani, A. Creation of S box based on a hierarchy of Julia sets:image encryption approach. Multidimens. Syst. Signal Process. 2022, 33, 39–62. [Google Scholar] [CrossRef]
- Li, T.; Yan, W.; Chi, Z. A new image encryption algorithm based on optimized Lorenz chaotic system. Concurr. Comput. 2022, 34, e5902. [Google Scholar] [CrossRef]
- Ren, H.; Niu, S.; Chen, J.; Li, M.; Yue, Z. A Visually Secure image Encryption Based on the Fractional Lorenz system and Compressive sensing. Fractal Fract. 2022, 6, 302. [Google Scholar] [CrossRef]
- Zou, C.; Zhang, Q.; Wei, X.; Liu, C. Image encryption based on improved Lorenz system. IEEE Access 2020, 8, 75728–75740. [Google Scholar] [CrossRef]
- Bhat, J.; Saqib, M.; Moon, A.H. Fuzzy extractor and Chaos enhanced elliptic curve cryptography for image encryption and authentication. Int. J. Syst. Assur. Eng. Mang. 2022, 13, 697–712. [Google Scholar] [CrossRef]
- Karunamurthi, S.; Natarajan, V.K. Design of area, energy and security optimized reversible architectures for digital image cryptography. Circuits Syst. Signal Process. 2023, 42, 535–538. [Google Scholar]
- Partheeban, P.; Kavitha, V. Dynamic key dependent AES S-box generation with optimized quality analysis. Clust. Comput. 2019, 22, S14731–S14741. [Google Scholar] [CrossRef]
- Rawat, A.; Gupta, I.; Goel, Y.; Sinha, N. Permutation based image encryption algorithm using a block cipher approach. In Proceedings of the 2015 International Conference on Advances in Computing, Communications and Informatics (ICACCI), Kochi, India, 10–13 August 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1877–1882. [Google Scholar]
- Nachtigal, M.; Thapliyal, H. Design of a reversible single precision floating point multiplier based on operand decomposition. In Proceedings of the 10th IEEE International Conference of Nanotechnology Joint Symposium with North Korea, Ilsan, Republic of Korea, 17–20 August 2010; pp. 233–237. [Google Scholar]
- Datta, K.; Shrivastav, V.; Sengupta, I.; Rahaman, H. Reversible logic implementation of AES algorithm. In Proceedings of the 2013 8th International Conference on Design and Technology of Integrated Systems in Nanoscale Era (DTIS), Abu Dhabi, United Arab Emirates, 26–28 March 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 140–144. [Google Scholar]
- Zhang, X.; Parhi, K.K. High-speed VLSI architectures for the AES algorithm. IEEE Trans. Very Large Scale Integr. Syst. 2004, 12, 957–967. [Google Scholar] [CrossRef]
- Manojkumar, T.; Karthigaikumar, P.; Ramachandran, V. An optimized S-box circuit for high speed AES design with enhanced PPRM architecture to secure mammographic images. J. Med. Syst. 2019, 43, 31. [Google Scholar] [CrossRef]
- Prathiba, A.; Madhu, K.; Bhaaskaran, V.K. Differential power analysis (DPA) resistant cryptographic S-box. In VLSI Design: Circuits, Systems and Applications; Select Proceedings of ICNETS2; Springer Singapore: Singapore, 2018; Volume V, pp. 169–178. [Google Scholar]
- Varghese, M.; Daniel, S.K.; Nandakumar, R. VLSI architecture for Montgomery modular multiplication. Int. Res. J. Eng. Technol. 2019, 6, 3575–3580. [Google Scholar]
- Cavuşoğlu, Ü.; Kacar, S.; Pehlivan, I.; Zengin, A. Secure image encryption algorithm design using a novel chaos based S-box. Chaos Solitons Fract. 2017, 95, 92–101. [Google Scholar] [CrossRef]
- Manjula, G.; Mohan, H. Constructing key dependent dynamic S-box for AES block cipher system. In Proceedings of the 2016 2nd International Conference on Applied and Theoretical Computing and Communication Technology (iCATccT), Bengaluru, India, 21–23 July 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 613–617. [Google Scholar]
- Krishnan, M.N.; Ravi, R. Modified AES with random S-box generation to overcome the side channel assaults using cloud. ICTACT J. Soft Comput. 2017, 7, 1373–1380. [Google Scholar]
- Pammu, A.A.; Chong, K.-S.; Ne, K.Z.L.; Gwee, B.-H. High secured low power multiplexer-LUT based AES S-box implementation. In Proceedings of the 2016 International Conference on Information Systems Engineering (ICISE), Los Angeles, CA, USA, 20–22 April 2016; pp. 3–7. [Google Scholar]
- Saravanan, P.; Kalpana, P. Novel reversible design of advanced encryption standard cryptographic algorithm for wireless sensor networks. Wirel. Pers. Commun. 2018, 100, 1427–1458. [Google Scholar] [CrossRef]
- Singha, T.B.; Palathinkal, R.P.; Ahamed, S.R. Implementation of AES using composite field arithmetic for IoT application. In Proceedings of the 2020 Third ISEA Conference on Security and Privacy, Guwahati, India, 27 February–1 March 2020; ISBN 978-1-17281-6708-4. [Google Scholar]
- Agarwal, P.; Singh, A.; Kilicman, A. Development of key dependent dynamic S boxes with dynamic irreducible polynomial and affine constant. In Advances in Mechanical Engineering; Sage: Newcastle, UK, 2018; Volume 10, pp. 1–18. [Google Scholar]
- Jacob, G.; Murugan, A.; Viola, I. Towards the generation of a dynamic key-dependent S-box to enhance security. IACR Cryptol. ePrint Arch. 2015, 92, 1–5. [Google Scholar]
- Rohini, H.; Jyoti, H.; Rajashekar, S. An approach towards design of N-bit AES to enhance security using reversible logic. Commun. Appl. Electron. 2018, 7, 7–13. [Google Scholar] [CrossRef]
- Wang, L.; Cheng, H. Pseudo random number generator based on logistic chaotic system. Entropy 2019, 21, 960. [Google Scholar] [CrossRef]
- Karunamurthi, S.; Natarajan, V.K. A low area FPGA implementation of reversible gate encryption with heterogeneous key generation. Circuits Syst. Signal Process. 2021, 40, 3836–3865. [Google Scholar]
- Zodpe, H.; Sapkal, A. An efficient AES implementation using FPGA with enhanced security features. J. King Saud-Univ.-Eng. Sci. 2018, 32, 115–122. [Google Scholar] [CrossRef]
- Koguncu, I.; Ozcerit, A.T. The design and realization of a new high speed FPGA based chaotic true random number generator. Comput. Elect. Eng. 2017, 58, 203–214. [Google Scholar] [CrossRef]
- Rasappan, S.; Kumaravel, S.K.; Sambas, A.; Moghrabi, I.A.R.; Sulaiman, I.M.; Hassan, B.A. A novel Chua’s based 2–D chaotic system and its performance analysis in cryptography. PLoS ONE 2024, 19, E0306818. [Google Scholar] [CrossRef]
- Ding, S.; Lin, H.; Deng, X.; Yao, W.; Jin, J. A hidden multiwing memristive neural network and its application in remote sensing data security. Expert Syst. Appl. 2025, 277, 127168. [Google Scholar] [CrossRef]
- Lin, H.; Wang, C.; Cui, L.; Sun, Y.; Xu, C.; Yu, F. Brain-like initial-boosted hyperchaos and application in biomedical image encryption. IEEE Trans. Ind. Inform. 2022, 18, 8839–8850. [Google Scholar] [CrossRef]
- Feng, W.; Zhang, J.; Qin, Z. A secure and efficient transmission scheme based on two chaotic maps. Complexity 2021, 2021, 1898998. [Google Scholar] [CrossRef]
- Zhu, H.; Zhang, X.; Yu, H.; Zhao, C.; Zhu, Z. An image encryption algorithm based on compound homogeneous hyper-chaotic system. Nonlinear Dyn. 2017, 89, 61–79. [Google Scholar] [CrossRef]
- Yin, Q.; Wang, C. A new chaotic image encryption scheme using breadth-first search and dynamic diffusion. Int. J. Bifurc. Chaos 2018, 28, 1850047. [Google Scholar] [CrossRef]
- Feng, W.; Zhang, J.; Chen, Y.; Qin, Z.; Zhang, Y.; Ahmad, M.; Wozniak, M. Exploiting robust quadratic polynomial hyperchaotic map and pixel fusion strategy for efficient image encryption. Expert Syst. Appl. 2024, 246, 123190. [Google Scholar] [CrossRef]
- Diaconu, A.-V. Circular inter-intra pixels bit-level permutation and chaos-based image encryption. Inf. Sci. 2016, 355–356, 314–327. [Google Scholar] [CrossRef]
- Ali, T.; Ali, R. A novel color image encryption scheme based on a new dynamic compound chaotic map and S-box. Multimed. Tools Appl. 2022, 81, 20585–20609. [Google Scholar] [CrossRef]
- Jiang, Z.; Ding, Q. Construction of an S-box based on chaotic and bent functions. Symmetry 2021, 13, 671. [Google Scholar] [CrossRef]
- Koziel, B.; Azarderaksh, R.; Kermani, M.M.; Jao, D. Post quantum cryptography on FPGA based on isogenies on elliptic curves. IEEE Trans. Circuits Syst. Regul. Pap. 2017, 64, 86–99. [Google Scholar] [CrossRef]
- Zhou, C.; Li, Z.; Zeng, Y.; Zhang, S. A Novel 3D Fractional-Order Chaotic System with Multifarious Coexisting Attractors. Int. J. Bifurc. Chaos 2019, 29, 1950004. [Google Scholar] [CrossRef]
- Ganie, A.H.; Aljuaydi, F.; Ahmad, Z.; Bonyah, E.; Khan, N.; Alharthi, N.S.; AlBaidani, M.M. A fractal–fractional perspective on chaotic behavior in 4D memristor-nonlinear system. AIP Adv. 2024, 14, 015135. [Google Scholar] [CrossRef]
- Feng, W.; Wang, Q.; Liu, H.; Ren, Y.; Zhang, J.; Zhang, S.; Qian, K.; Wen, H. Exploting Newly Designed Fractional-order 3D Lorenz Chaotic System and 2D Discrete Polynomial Hyper-Chaotic Map for High-Performance Multi-Image Encryption. Fractal Fract. 2023, 7, 887. [Google Scholar] [CrossRef]
- Feng, W.; Yang, J.; Zhao, X.; Qin, Z.; Zhang, J.; Zhu, Z.; Wen, H.; Qian, K. A novel multi-channel image encryption algorithm leveraging pixel reorganization and hyperchaotic maps. Mathematics 2024, 12, 3917. [Google Scholar] [CrossRef]
- Zahid, A.H.; Tawalbeh, L.O.A.I.; Member, S.; Ahmad, M.; Farhan, A.K. Efficient dynamic S-box generation using linear trigonometric transformation for security applications. IEEE Access 2021, 9, 98460–98475. [Google Scholar] [CrossRef]
- Liu, J.; Tong, X.; Zhang, M.; Wang, Z. The design of S-box based on combined chaotic map. In Proceedings of the AEMCSE, Shenzhen, China, 24–26 April 2020. [Google Scholar]
- Farah, T.; Rhouma, R.; Belghith, S. A novel method for designing S-box based on chaotic map and teaching–learning-based optimization. Nonlinear Dyn. 2017, 88, 1059–1074. [Google Scholar] [CrossRef]
- Zhu, H.; Tong, X.; Wang, Z.; Ma, J. A novel method of dynamic S-box design based on combined chaotic map and fitness function. Multimed. Tools Appl. 2020, 79, 12329–12347. [Google Scholar] [CrossRef]
- Lambic, D. A new discrete-space chaotic map based on the multiplication of integer numbers and its application in S-box design. Nonlinear Dyn. 2020, 100, 699–711. [Google Scholar] [CrossRef]
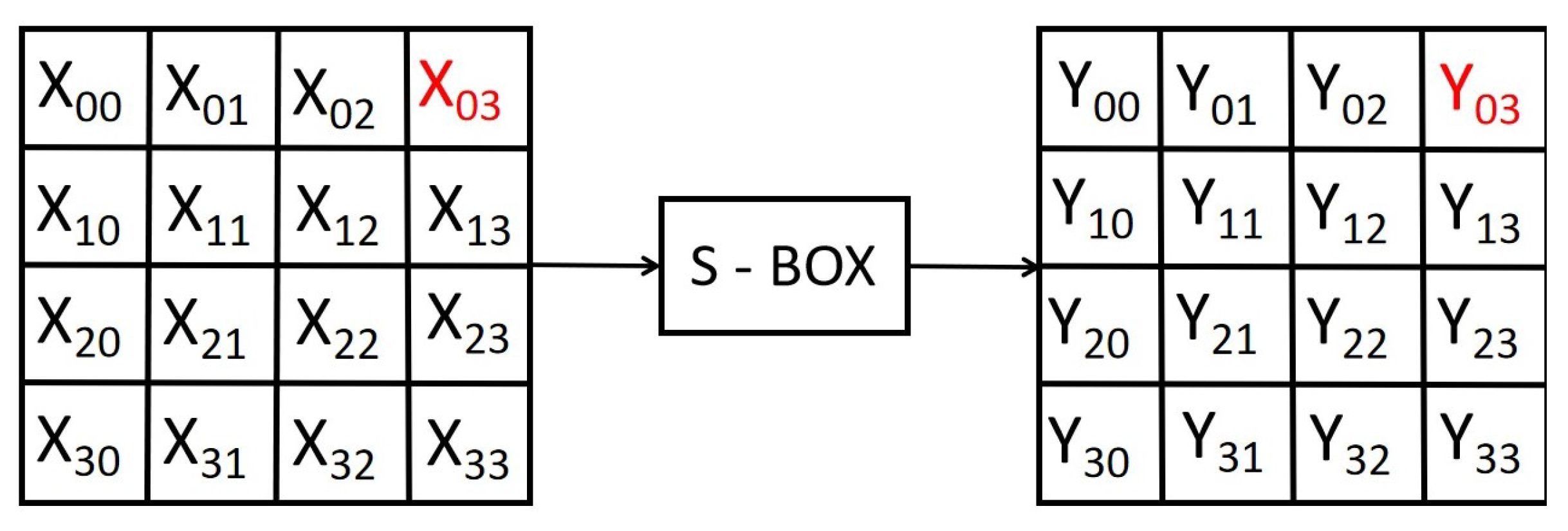







| X[3:0] | Y[3:0] | X[3:0] | Y[3:0] |
|---|---|---|---|
| 0000 | 0000 | 1000 | 1010 |
| 0001 | 0001 | 1001 | 0110 |
| 0010 | 0011 | 1010 | 1000 |
| 0011 | 0010 | 1011 | 0111 |
| 0100 | 1111 | 1100 | 0101 |
| 0101 | 1100 | 1101 | 1110 |
| 0110 | 1001 | 1110 | 1101 |
| 0111 | 1011 | 1111 | 0100 |
| 162 | 59 | 203 | 4 | 169 | 36 | 81 | 113 | 222 | 141 | 184 | 129 | 32 | 74 | 211 | 224 |
| 212 | 131 | 18 | 201 | 115 | 9 | 253 | 21 | 90 | 93 | 130 | 219 | 216 | 134 | 158 | 61 |
| 180 | 84 | 26 | 51 | 37 | 121 | 232 | 144 | 17 | 16 | 240 | 210 | 194 | 112 | 43 | 147 |
| 205 | 230 | 41 | 128 | 75 | 250 | 150 | 178 | 108 | 151 | 30 | 248 | 71 | 69 | 56 | 192 |
| 254 | 8 | 95 | 185 | 13 | 239 | 168 | 223 | 177 | 163 | 11 | 127 | 24 | 241 | 233 | 136 |
| 171 | 135 | 214 | 146 | 15 | 175 | 220 | 189 | 27 | 52 | 25 | 142 | 89 | 234 | 111 | 228 |
| 101 | 132 | 160 | 170 | 78 | 197 | 227 | 164 | 143 | 46 | 231 | 86 | 167 | 73 | 237 | 2 |
| 193 | 31 | 103 | 204 | 96 | 179 | 123 | 124 | 102 | 173 | 80 | 92 | 174 | 66 | 3 | 140 |
| 198 | 72 | 7 | 54 | 154 | 100 | 105 | 246 | 48 | 152 | 215 | 226 | 14 | 126 | 70 | 22 |
| 182 | 242 | 87 | 176 | 209 | 23 | 44 | 236 | 256 | 187 | 35 | 156 | 148 | 88 | 57 | 85 |
| 79 | 68 | 159 | 221 | 137 | 191 | 208 | 251 | 225 | 181 | 145 | 238 | 200 | 206 | 138 | 172 |
| 247 | 98 | 106 | 114 | 19 | 45 | 139 | 38 | 65 | 109 | 125 | 63 | 47 | 183 | 83 | 1 |
| 188 | 235 | 255 | 53 | 77 | 42 | 157 | 20 | 199 | 217 | 29 | 213 | 252 | 58 | 34 | 49 |
| 10 | 28 | 118 | 116 | 190 | 166 | 161 | 82 | 33 | 202 | 55 | 12 | 76 | 117 | 196 | 67 |
| 140 | 3 | 66 | 174 | 92 | 80 | 173 | 102 | 124 | 123 | 179 | 96 | 204 | 103 | 31 | 193 |
| 149 | 91 | 229 | 122 | 155 | 120 | 110 | 133 | 207 | 195 | 244 | 165 | 119 | 97 | 40 | 107 |
| Instance | Static Leakage Power (nW) | Dynamic Switching Power (μW) | Total Power (μW) |
|---|---|---|---|
| S-Box (Lookup Table) | 17.306 | 62.168 | 62.185 |
| Reversible S-Box | 11.596 | 44.553 | 44.565 |
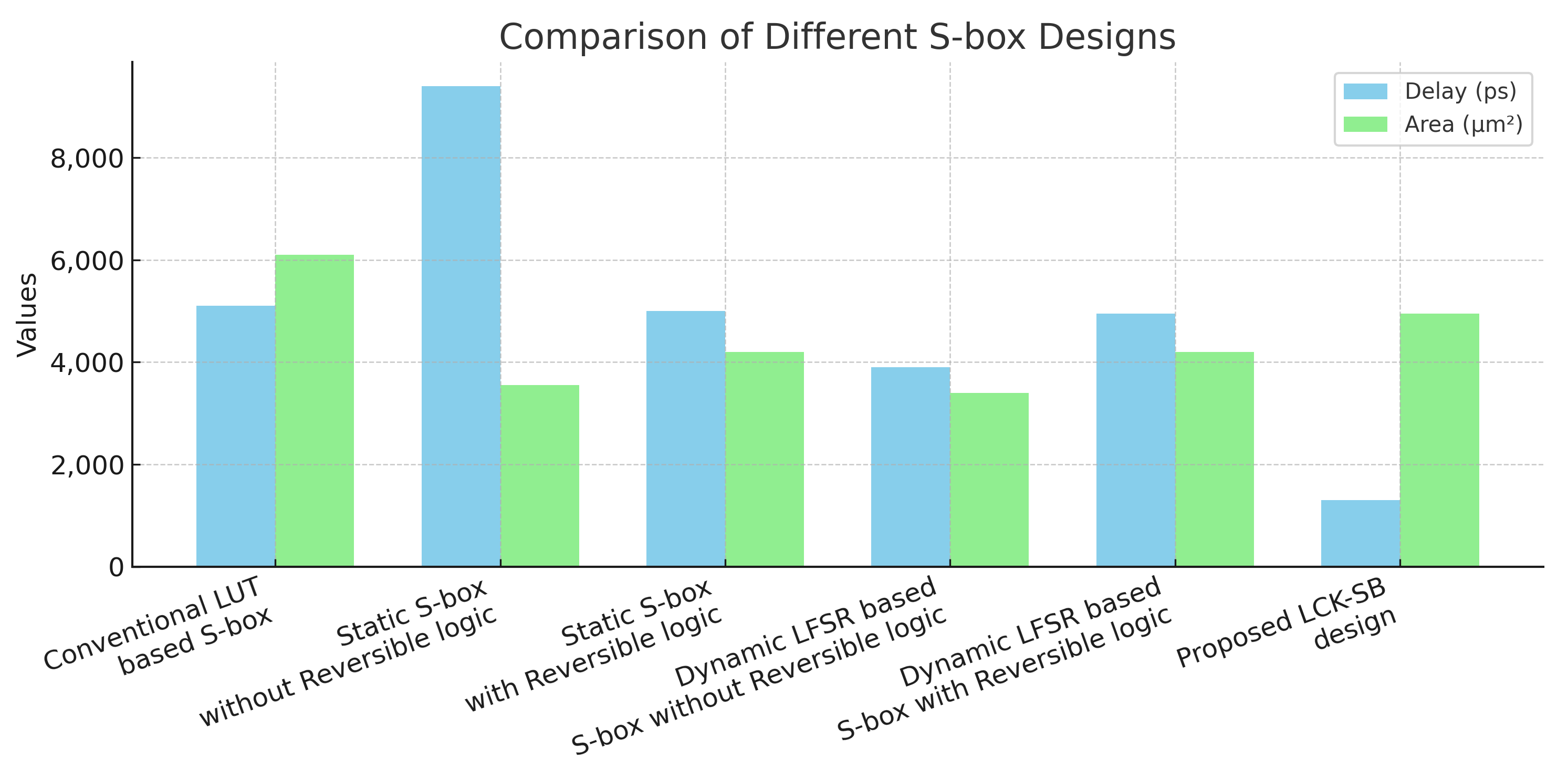
| Different Types of Design | Delay (ps) | Area (μm2) | Power (mW) | APP (μm2 · mW) | ADP (μm2 · ps) |
|---|---|---|---|---|---|
| Dynamic LFSR S-box with RL [7] | 4979 | 4217.875 | 3.89291 | 16,407.51 | 21,000,799.63 |
| Dynamic LFSR S-box without RL [8] | 3937 | 3446.150 | 4.89962 | 16,851.67 | 13,567,492.55 |
| Static S-box with RL [11] | 4979 | 4217.875 | 4.59291 | 19,372.27 | 21,000,774.73 |
| Static S-box without RL [13] | 9526 | 3459.456 | 1.16874 | 4043.20 | 32,954,720.7 |
| Conventional LUT based S-box [14] | 5086 | 6133.882 | 5.415 | 33,214.53 | 31,196,913.68 |
| Proposed LCK-SB | 1263 | 4996.253 | 3.15280 | 15,748.18 | 6,310,263.75 |
| Name of the Block | No. of Garbage Outputs | No. of Reversible Gates |
|---|---|---|
| Isomorphic mapping | 0 | 13 |
| Inverse isomorphic mapping | 0 | 15 |
| Squarer | 0 | 4 |
| Multiplicative inverse | 8 | 23 |
| Multiplier with GF() | 5 | 7 |
| Multiplier with GF() | 4 | 8 |
| Multiplier (x) | 0 | 3 |
| Multiplier (x) | 0 | 1 |
| Affine transformation | 0 | 23 |
| Name of the Block | Quantum Cost of Conventional S-Box Design [13] | Quantum Cost of Proposed Chaotic-Based Design |
|---|---|---|
| Multiplicative inverse in GF() | 146 | 54 |
| Affine transformation | 36 | 25 |
| S-box | 505 | 331 |
| Slice Logic Utilization | Used | Available | Utilization Percentage |
|---|---|---|---|
| Number of slice registers | 208 | 54,576 | 0 |
| Number of slice LUTs | 538 | 27,288 | 1 |
| Number of fully used LUT-FF pairs | 112 | 634 | 17 |
| Number of bonded IOBs | 129 | 190 | 67 |
| Number of BUFGs | 1 | 16 | 6 |
| Number of DSP48A1s | 24 | 58 | 41 |
| FPGA Family | Methods | Number of Slice Registers | Number of Slice LUTs | Number of Flip-Flops |
|---|---|---|---|---|
| Spartan-6 XC6SLX45 CSG324C | AES-PL [18] | 20,818 | 20,147 | 26,417 |
| RLCD-LFSR [1] | 4793 | 8328 | 4703 | |
| RLCD-IWT-HKG [21] | 1423 | 1913 | 69 | |
| LCK-SB | 208 | 538 | 112 |
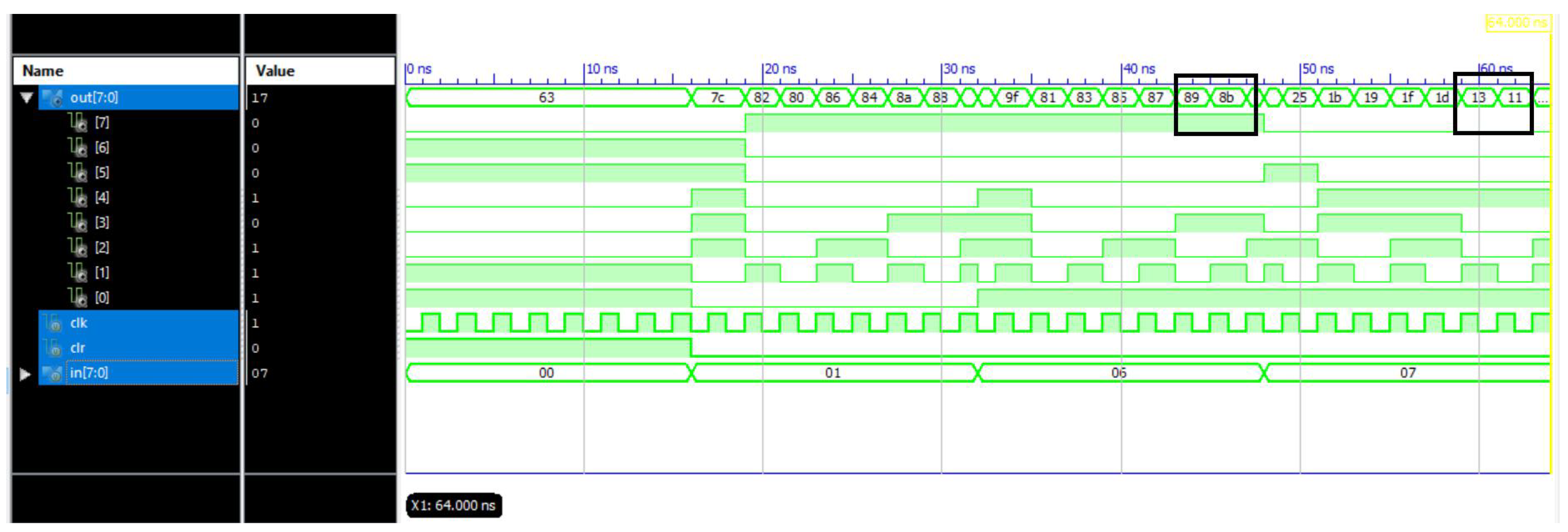
| Plain Text | Cipher Text with Dynamic Key 1 | Cipher Text with Dynamic Key 2 |
|---|---|---|
| (06)h = (0000 0110)2 | (89)h = (1000 1001)2 | (8B)h = (1000 1011)2 |
| (07)h = (0000 0111)2 | (13)h = (0001 0111)2 | (11)h = (0001 0001)2 |
| S-BOX | SAC | BIC-NL | LP | DP |
|---|---|---|---|---|
| Proposed | 0.5080 | 0.004 | 0.132 | 0.039 |
| Ref. [32] | 0.4992 | 0.001 | 0.141 | 0.047 |
| Ref. [33] | 0.4977 | 0.002 | 0.132 | 0.046 |
| Ref. [34] | 0.5060 | 0.006 | 0.125 | 0.039 |
| Ref. [35] | 0.4976 | 0.002 | 0.132 | 0.039 |
| Ref. [36] | 0.4995 | 0.001 | 0.117 | 0.039 |
| Ref. [37] | 0.4995 | 0.001 | 0.128 | 0.039 |
| Ref. [38] | 0.5010 | 0.001 | 0.070 | 0.039 |
| Plain Text | Cipher Text with Dynamic Key 1 | Cipher Text with Dynamic Key 2 |
|---|---|---|
| (06)h = (0000 0110)2 | (89)h = (1000 1001)2 | (8B)h = (1000 1011)2 |
| (07)h = (0000 0111)2 | (13)h = (0001 0111)2 | (11)h = (0001 0001)2 |
| Architecture | MSE | PSNR (dB) | SSIM |
|---|---|---|---|
| RLCD-LFSR [7] | 9.73 | 0.012 | |
| RLCD-IWT-HKG [26] | 7.29 | 0.0098 | |
| Koyunchu et al. [28] | 7.26 | 0.0089 | |
| Koziel et al. [39] | 7.56 | 0.0091 | |
| LCK-SB | 3.525 | 0.009 |
| Method | Entropy (bits) | NPCR (%) | UACI (%) | PSNR (dB) | SSIM |
|---|---|---|---|---|---|
| Proposed (LCK-SB) | 7.98 | 99.62 | 33.45 | 3.52 | 0.009 |
| RLCD-LFSR [7] | 7.94 | 98.75 | 32.12 | 9.73 | 0.012 |
| Koyunchu et al. [28] | 7.91 | 97.10 | 31.67 | 7.26 | 0.0089 |
| Koziel et al. [39] | 7.88 | 96.85 | 30.98 | 7.56 | 0.0091 |
| Scheme | LCK-SB | SIT-SR [32] | CHHCS [33] | Breadth-First Search [34] | Dynamical Chaotic System [36] |
|---|---|---|---|---|---|
| Time (s) | 0.158 | 0.089 | 0.275 | 0.417 | 0.264 |
| Throughput (Mbps) | 8.68 | 5.618 | 1.818 | 1.199 | 1.893 |
| Test | Result of Enhanced S-Box | Ideal Range |
|---|---|---|
| Strict Avalanche Criterion (SAC) | 0.4994 | ≈0.5 |
| Bit Independence Criterion (BIC) | 0.002 | ≈0 |
| Nonlinearity | Avg. 112 | ≤120 |
| Differential Uniformity | Max 4 | 2–4 |
| Number of Pixels Change Rate (NPCR) | 99.621% | ≥99.6% |
| Unified Average Changing Intensity (UACI) | 33.27% | ∼33.4% |
| Linear Approximation Probability (LP) | 0.109 | ≤0.125 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boobalan, S.; Gurunathan Arthanari, S.K. Lorenz and Chua Chaotic Key-Based Dynamic Substitution Box for Efficient Image Encryption. Symmetry 2025, 17, 1296. https://doi.org/10.3390/sym17081296
Boobalan S, Gurunathan Arthanari SK. Lorenz and Chua Chaotic Key-Based Dynamic Substitution Box for Efficient Image Encryption. Symmetry. 2025; 17(8):1296. https://doi.org/10.3390/sym17081296
Chicago/Turabian StyleBoobalan, Sarala, and Sathish Kumar Gurunathan Arthanari. 2025. "Lorenz and Chua Chaotic Key-Based Dynamic Substitution Box for Efficient Image Encryption" Symmetry 17, no. 8: 1296. https://doi.org/10.3390/sym17081296
APA StyleBoobalan, S., & Gurunathan Arthanari, S. K. (2025). Lorenz and Chua Chaotic Key-Based Dynamic Substitution Box for Efficient Image Encryption. Symmetry, 17(8), 1296. https://doi.org/10.3390/sym17081296