Abstract
The modeling of the enthalpy of mixing in binary alloys is essential to thermodynamic assessments and computational alloy design, particularly in data-scarce systems where experimental measurements are limited or incomplete. In this work, we propose a machine learning framework for the prediction of mixing enthalpy in binary alloys under conditions of limited data availability. The method integrates symmetry-augmented embeddings, which enforce physical invariances such as element permutation and compositional mirroring, ensuring consistency across chemically equivalent representations and capturing chemically meaningful similarities between elements, thereby supporting knowledge transfer across alloy systems. To account for data uncertainty and improve trust in predictions, we incorporate Bayesian neural networks, enabling the estimation of predictive confidence, especially in composition ranges lacking experimental data. The model is trained jointly across multiple binary alloy systems, allowing it to share structural insights and improve prediction quality in data-limited concentration intervals. The method achieves a reduction in mean absolute error by more than a factor of eight compared with the classical Miedema model (0.53 kJ·mol−1 vs. 4.27 kJ·mol−1) while maintaining consistent accuracy even when trained on only 25% of the experimental measurements, confirming its robustness thanks to cross-alloy knowledge transfer and symmetry-based data augmentation. We evaluate the method on a benchmark dataset containing both fully and partially characterized binary alloy systems and demonstrate its effectiveness in interpolating and extrapolating enthalpy values while providing reliable uncertainty estimates. The results highlight the value of incorporating domain-specific symmetries and uncertainty-aware learning in data-driven material modeling and suggest that this approach can support predictive thermodynamic assessments even in under-sampled systems.
1. Introduction
Accurate thermodynamic modeling, particularly of the enthalpy of mixing, is fundamental to the design and optimization of advanced metallic materials, describing the energetic interactions between constituent elements across varying compositions. While calorimetric measurement is considered the most accurate method for determining the mixing enthalpy of liquid solutions, it is associated with significant experimental challenges. These include requirements for very-high-purity components and strictly controlled protective atmospheres, making such studies time-consuming, costly, and potentially burdened with measurement uncertainties. Consequently, literature data for mixing enthalpy, even for the same binary systems, often exhibit significant discrepancies or are incomplete.
In the absence of comprehensive experimental data, mixing enthalpy can be determined using theoretical approaches, such as ab initio methods. Simpler semi-empirical models, like the Miedema model—developed nearly fifty years ago and still widely used—are also commonly applied. However, for many systems, these models show only weak correlation with experimental data. Machine learning (ML) techniques have emerged as powerful tools for material property prediction, offering fast and flexible alternatives to traditional thermodynamic assessments. Nevertheless, existing ML approaches to modeling the enthalpy of mixing often face several challenges: they may exhibit poor generalization to sparsely sampled alloy systems or compositions, frequently neglect important symmetry considerations inherent to alloy thermodynamics, and often fail to quantify the uncertainty of their predictions. Ignoring these issues can lead to inconsistent, untrustworthy, or redundant predictions.
In this work, we address these limitations through a novel machine learning framework for the prediction of the enthalpy of mixing in binary alloys, even for systems tested in a limited concentration range. Our approach is built on three key innovations:
- 1.
- Symmetry-augmented embeddings: We develop chemically informed embeddings that explicitly capture physical invariances, such as element permutation and compositional mirroring, ensuring consistent treatment of chemically equivalent alloy representations and improving model robustness.
- 2.
- Constrained global modeling of enthalpy curves: Rather than predicting isolated enthalpy values, our method models the entire concentration-dependent enthalpy of mixing for a given system. This global formulation supports knowledge transfer across multiple alloy systems, boosting generalization and accuracy, especially in data-sparse intervals. A constraint is introduced by learning the full curve, acting as an informed prior guided by known boundary conditions (). This enables a flexible, constrained data-driven framework capable of capturing consistent enthalpy trends and allows for interpretation by polynomial methods, such as the Redlich–Kister polynomial, facilitating their use in calculating phase equilibria via methods like CALPHAD.
- 3.
- Uncertainty quantification via Bayesian neural networks: We integrate Bayesian neural networks to estimate predictive uncertainty, providing calibrated confidence intervals for model outputs. This uncertainty awareness is crucial to trustworthy decision making, particularly in under-sampled composition ranges, and is rarely addressed in existing ML-based mixing enthalpy models.
By combining these contributions, our framework supports the modeling of binary alloy thermodynamics, even in cases where experimental data are sparse or incomplete. More broadly, the approach demonstrates how domain-oriented embedding strategies, cross-system data sharing, and rule-based uncertainty estimation can be integrated into a unified machine learning framework to advance materials science based on available, sometimes incomplete data. While this work focuses on the enthalpy of mixing of binary alloys, the proposed ideas can be extended to other composition-dependent thermodynamic quantities, including for multicomponent systems, using generalized uncertainty-aware and symmetry-consistent prediction models.
The remainder of this paper is organized as follows: Section 2 discusses related work on alloy thermodynamics, machine learning, and symmetry- and uncertainty-aware modeling. Section 3 describes the details of our framework, including its architecture, symmetry embeddings, and Bayesian neural network formulation. Section 4 presents the benchmark datasets and experimental results. Section 5 discusses these results and analyzes performance, and Section 6 provides conclusions and suggests future research directions.
2. Related Work
Machine learning (ML) applications in materials science have seen rapid expansion in recent years, driven by the increasing availability of high-throughput datasets and advancements in algorithmic techniques. In the domain of thermodynamic property prediction, ML models have been developed to approximate key quantities such as phase diagrams, enthalpies of formation, and free energies, with the overarching goal of accelerating or complementing traditional CALPHAD-type assessments [1]. Early studies in this area primarily employed regression models trained on tabulated thermodynamic data. However, these methods typically addressed only pointwise predictions and lacked the capacity to represent entire functional relationships across the composition space of alloys. Furthermore, these approaches often treated each alloy system independently, which limited knowledge transfer between chemically related systems and consequently constrained their predictive performance in sparse-data regimes.
For the specific context of the enthalpy of mixing, a critical thermodynamic property reflecting energetic interactions between constituent elements, the Redlich–Kister polynomial formalism [2], has long been established as the standard representation for binary alloys. This formalism effectively captures excess enthalpy behavior through polynomial expansions that enforce physical boundary conditions and geometric features. Despite its utility, obtaining comprehensive experimental data for thermodynamic properties, even for many binary systems, remains challenging due to high cost, time demands, and experimental difficulties associated with methods like calorimetric measurements, which require high-purity components and strictly controlled atmospheres. Such limitations often lead to incomplete data or discrepancies in the literature.
In the absence of extensive experimental data, the enthalpy of mixing can also be determined using theoretical approaches. These include ab initio methods, such as those utilizing the VASP program [3] and Density Functional Theory (DFT), which have been applied to determine quantities like the enthalpy of mixing for liquid solutions in systems like Au-Mg [4]. Additionally, simpler semi-empirical models are commonly used. One of the most prominent is the Miedema model [5,6,7,8], originally developed in the mid-1970s for binary alloys containing at least one transition metal. This model describes the heat of formation/mixing in terms of a negative term from the difference in chemical potential of electrons and a second term reflecting the discontinuity in electron density at the boundary between dissimilar atomic cells. It has been shown that this formula can be applied to the heat of mixing of liquid alloys, with parameters consistent for both solid and liquid metals. The model parameters evolved over the years, becoming fixed around the end of the 1980s [7]. Boom et al. [9] extended the Miedema model in 2020 to binary systems of magnesium with a wide range of metals, including non-transition metals, by re-estimating a model parameter for Mg and introducing an additional negative contribution for Mg–non-transition metal binaries. The Miedema model has found wide application in contemporary research, including thermodynamic modeling using ML techniques [10,11,12,13] and within the CALPHAD approach for systems lacking experimental data [14], and is a useful tool in the thermodynamic design of high-entropy alloys [15,16]. Despite its widespread use and the fact that no alternative model with higher accuracy has been developed in this field since the mid-1970s, it is important to emphasize that for many systems, the mixing enthalpy predicted by the Miedema model exhibits a weak correlation with experimental data. Recent studies have shown that machine learning models, such as LightGBM, can provide more accurate predictions than the Miedema model [12,13].
Recent data-driven studies have begun to explore machine learning alternatives to the classical Redlich–Kister approach. For example, Deffrennes et al. [12] investigated the application of ML techniques to analyze the enthalpy of mixing in the liquid phase across multiple binary systems, demonstrating that regression models can identify composition-dependent trends and extend existing thermodynamic databases. However, most current data-driven approaches still focus on predicting isolated enthalpy values at specific compositions rather than learning the full enthalpy curve, and rarely incorporate explicit physical or geometric constraints.
Despite the progress brought by machine learning, there are still several significant challenges in existing approaches to modeling the enthalpy of mixing using this method:
- Poor generalization to sparsely sampled alloy systems or compositions: Current models often lack intrinsic mechanisms to effectively transfer knowledge between chemically similar systems, leading to reduced accuracy when data are scarce.
- Neglect of important symmetry considerations: Fundamental physical constraints inherent to alloy thermodynamics, such as the energetic description of an “A–B” alloy being physically equivalent to a “B–A” alloy under the same conditions, or expected symmetries/anti-symmetries across composition space are frequently ignored. This omission can lead to inconsistent, redundant, or even contradictory predictions that violate fundamental physical principles, thereby undermining the trustworthiness of the models, especially when experimental data are sparse or incomplete.
- Lack of uncertainty quantification: Most current data-driven models fail to provide a measure of confidence for their predictions. This is a particularly critical issue in material design applications where models are often used to guide costly experiments or inform high-impact decisions, as highlighted by Gal’s work on uncertainty in deep learning [17]. While Bayesian neural networks (BNNs) and related ensemble approaches have made significant progress in quantifying predictive uncertainty, their systematic application to the thermodynamic modeling of the enthalpy of mixing remains extremely limited. Conventional deep neural networks, by contrast, produce deterministic predictions without any indication of predictive confidence.
In summary, while machine learning has undeniably opened new avenues for alloy thermodynamic modeling, significant gaps persist. Most current approaches do not fully model the entire composition-dependent functional form of the enthalpy of mixing, rarely enforce domain-specific symmetry constraints, and generally ignore predictive uncertainty. This highlights the need for more robust and interpretable models and directly motivates the present work, which aims to address these limitations through a unified framework that combines symmetry-augmented embeddings, constrained global curve learning, and principled Bayesian uncertainty quantification for robust and interpretable prediction of binary alloy enthalpy of mixing.
3. Methods
The proposed framework for uncertainty-aware prediction of the enthalpy of mixing integrates the following fundamental building blocks:
- A symmetry-augmented embedding scheme that encodes element permutation and compositional symmetries;
- A geometrically interpretable representation of the Redlich–Kister polynomial ensuring model numerical stability;
- A Bayesian neural network for regression that provides uncertainty estimates alongside predictions.
Each of these components is described in detail in the subsections below.
3.1. Symmetry-Augmented Embeddings
As a preprocessing step, the chemical identity of binary alloys is encoded using vector representations derived from the mat2vec embedding dataset [18]. For each binary system A-B, the corresponding element embeddings and (each 200-dimensional) are concatenated to form an initial 400-dimensional representation:
To embed physical symmetries such as element permutation and compositional mirroring, the dataset is augmented by including mirrored alloy representations alongside the original , effectively doubling the training samples. This symmetry-based augmentation ensures that the model treats chemically equivalent alloy configurations consistently, embedding permutation and reflection symmetries as inductive biases. Rather than simply duplicating data, this approach encodes fundamental thermodynamic constraints directly into the learning process, improving generalization and reducing the risk of inconsistent predictions. In addition to that, it expands data coverage, which is critical given the limited size of the experimental dataset.
The resulting 400-dimensional embeddings are high-dimensional relative to the dataset size and prone to overfitting. To mitigate this, we compress these representations into a lower-dimensional latent space using an autoencoder. The autoencoder’s architecture, tuned via cross-validation and a grid search for latent dimensionality, consists of an encoder–decoder network with a 32-dimensional “bottleneck” representation. A schematic diagram of this autoencoder architecture is shown in Figure 1.
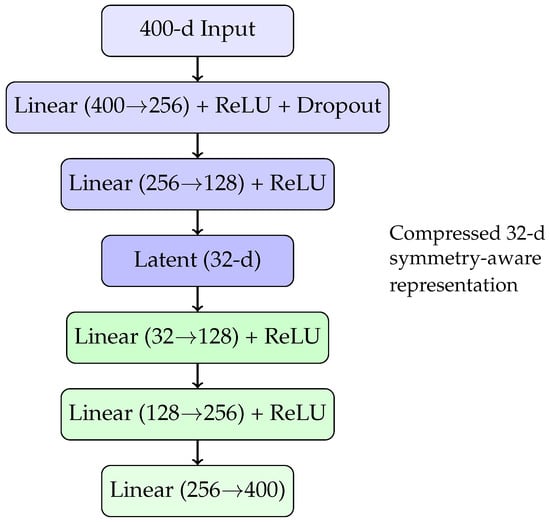
Figure 1.
Autoencoder architecture compressing 400-dimensional raw embeddings into a 32-dimensional symmetry-augmented latent space.
This compressed 32-dimensional latent representation serves as the final alloy embedding for the subsequent regression task, preserving both compositional symmetry and relevant chemical information while helping to prevent overfitting.
3.2. Stable and Interpretable Redlich–Kister Representation
The Redlich–Kister (RK) polynomial is widely used in alloy thermodynamics, particularly within the CALPHAD method, due to its compatibility with the Gibbs–Duhem equation—a fundamental requirement for ensuring thermodynamic consistency in multicomponent systems. Additionally, its formulation satisfies key physical constraints, such as , and, for symmetric systems, mirror symmetry about . The structure naturally enforces vanishing enthalpy at the pure-component limits, providing a physically grounded and robust basis for regression.
Following common practice, we limited the Redlich–Kister polynomial [2] to its first four terms:
where x is the concentration of component B and the coefficients are obtained by fitting the Redlich–Kister polynomial to experimental data.
However, directly regressing these coefficients can be numerically unstable and physically unintuitive, particularly in sparse data settings. To address this, we propose an alternative approach that retains the structure of the RK polynomial but uses a geometrically meaningful and physically interpretable parameterization. Specifically, we describe the polynomial using three quantities:
- 1.
- —the first derivative at ;
- 2.
- —the first derivative at ;
- 3.
- —the enthalpy value at .
This formulation stabilizes curve reconstruction and improves interpretability, as each parameter directly reflects local or global features of the enthalpy curve. To further regularize higher-order variations and avoid unrealistic oscillations, we impose a smoothness constraint by minimizing the integrated squared third derivative:
This encourages a geometrically plausible and physically smooth enthalpy profile across the composition domain.
As a result, the regression problem becomes a multi-output regression task, with the compressed 32-dimensional alloy embedding as input and the triplet as output. The computation of the coefficients from this triplet is straightforward and can be performed analytically. This indirect formulation anchors the model in physically meaningful regimes, with the triplet effectively controlling the skew, symmetry, and peak of the enthalpy curve. Compared with direct regression of the coefficients—which can suffer from high variance due to collinearity—this parameterization leads to more robust fitting and extrapolation.
Remark 1
(Generality of the Approach). Although the RK polynomial is the standard choice for such systems, the proposed method is not inherently limited to this specific functional form. In principle, the same idea can be applied to other empirical or physics-informed function classes—such as splines, neural basis functions, or orthogonal polynomial bases—as long as one can identify a stable and interpretable parameterization (e.g., key derivatives, inflection points, and extrema). The regression task then becomes a parametric optimization problem: given a functional structure and a fitness criterion (e.g., physical accuracy and smoothness), the algorithm finds the optimal parameters. This perspective generalizes beyond Redlich–Kister and emphasizes the value of physics-informed low-dimensional parameter targets over “raw coefficient” regression.
3.3. Bayesian Neural Regression with Uncertainty Quantification
To learn the mapping from the compressed embedding to the selected Redlich–Kister representation, we employ a Bayesian neural network (BNN). In contrast to conventional neural networks that produce only point estimates, BNNs model the weight parameters as probability distributions, thereby providing an estimate of predictive uncertainty alongside the mean prediction. This capability is crucial to thermodynamic modeling, where training data may be sparse or incomplete, and robust uncertainty estimates are needed for high-stakes design decisions. Bayesian modeling thus enables a principled treatment of uncertainty in deep learning by propagating prior information through posterior distributions over the weights, as discussed in Gal’s influential dissertation on Bayesian deep learning [17].
Our BNN architecture uses the Blitz framework [19] with four layers. Each layer uses BayesianLinear modules that approximate their weight posteriors via variational inference, with dropout-based sampling to perform approximate posterior draws during inference. The activation function is ReLU (Rectified Linear Unit), which is standard for introducing nonlinearity while maintaining efficient gradient propagation. The architecture is structured as shown in Figure 2.
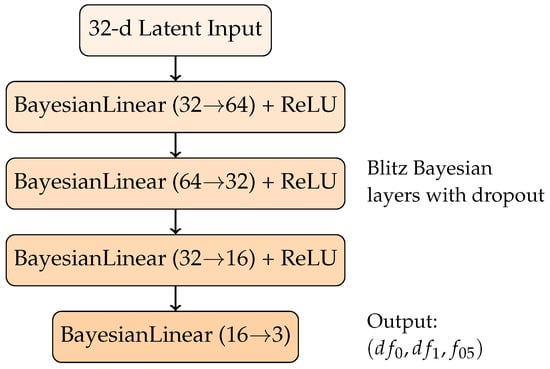
Figure 2.
Bayesian neural network architecture for regression of Redlich–Kister geometric representation with uncertainty quantification.
As described, the model outputs the three target parameters and . Since these targets are not explicitly measured in the enthalpy database [20], the regression is indirectly supervised: the predicted triplet is transformed into the Redlich–Kister curve, and the resulting curve is compared to experimental measurements at the composition points present in the dataset. The loss function employed was the Root Mean Squared Error, i.e., , where is the reconstructed curve (evaluated at the sampled concentrations ) and corresponds to the experimental enthalpy measurements. Using the RMSE rather than the MSE further stabilizes training by normalizing the gradient through its denominator, thereby avoiding excessive sensitivity to outliers during backpropagation.
3.4. Dataset
The dataset used in this work is sourced from the Entall database [21], a curated compilation of experimental thermodynamic data for binary alloys. Specifically, it contains 3951 records of the enthalpy of mixing () across 89 binary alloy systems. Each data point corresponds to the measured enthalpy of mixing at a particular composition for a given A–B binary system.
The majority of the entries in Entall were obtained using high-precision calorimetric techniques. While this ensures physical accuracy, it also means that the dataset reflects the practical constraints of such experiments: data are often sparse, unevenly distributed across compositions, or incomplete for many systems. Moreover, discrepancies in reported values are common due to variations in experimental conditions.
These characteristics make Entall a valuable and realistic benchmark for testing models under data-scarce conditions. Our framework is explicitly designed to address the challenges posed by such sparse, heterogeneous experimental datasets.
3.5. Data Usage and Training Setup
Our task involves learning the continuous mixing enthalpy curves over the entire composition domain for 89 binary alloy systems, using sparse and potentially incomplete measurement data. Many of these systems contain only a few experimental data points due to the difficulty and cost of calorimetric measurements.
The proposed modeling framework is global: the Bayesian neural network (BNN) is trained jointly across all binary systems. Each training point corresponds to an enthalpy measurement at a particular composition in a specific alloy system. The BNN learns to predict the three parameters of the geometric Redlich–Kister representation from the latent 32-dimensional alloy embedding, and these parameters are used to reconstruct the full enthalpy curve. The model is supervised by comparing the predicted curve against available measurements for each alloy system, using the root mean squared error (RMSE) as the loss function.
To evaluate the model’s robustness to reduced data availability, we adopt a restoration-based evaluation strategy, described in Section 4.4. For each binary alloy system, we randomly retain a given fraction (e.g., 90%, 75%, 50%, or 25%) of the available enthalpy measurements and train the model to infer the corresponding Redlich–Kister (RK) curve representation. This setup directly tests the model’s capacity to reconstruct physically consistent mixing enthalpy curves from sparse observations—a central capability in data-scarce thermodynamic modeling.
4. Results
To verify the proposed framework, we conducted a series of numerical experiments and simulations designed to evaluate both the predictive performance and the uncertainty quantification capabilities of our approach. These experiments systematically examine the behavior of the learned embeddings, the regression accuracy compared with traditional models, and the robustness of the predictions under varying data availability. The following subsections present these results in detail.
4.1. Analysis of Embedding Representations
As the foundation of our framework, we leverage the mat2vec embeddings introduced by Tshitoyan et al. [18], which demonstrated that unsupervised word embeddings trained on the materials science literature can capture complex latent knowledge, including relationships encoded by the periodic table and structure–property correlations. This approach highlighted that knowledge accumulated across decades of publications can be distilled in a vectorized, data-driven form without explicit human-coded rules.
We adopt these element-level embeddings as the basis for constructing alloy-level representations. After the concatenation of two element embeddings (for each alloy A–B) and the symmetry-based data augmentation strategy, the resulting 400-dimensional vectors are compressed through an autoencoder into a 32-dimensional latent representation, providing a symmetry-aware, information-dense description of each alloy.
To gain insights into the geometry of the learned latent space, we visualized the high-dimensional mat2vec embeddings using t-distributed Stochastic Neighbor Embedding (t-SNE) [22]. The t-SNE algorithm preserves local neighborhoods, such that elements or alloys with similar chemical and thermodynamic characteristics are mapped closer together in the two-dimensional projection.
In Figure 3, which shows the t-SNE plot of element embeddings, clear chemically consistent groupings emerge. Elements belonging to the same chemical families (e.g., transition metals, alkali metals, and alkaline earth metals) tend to cluster together, reflecting their related bonding and structural tendencies. This organization suggests that the embedding captures relevant similarities based on element roles in the studied alloys and crystal structures.
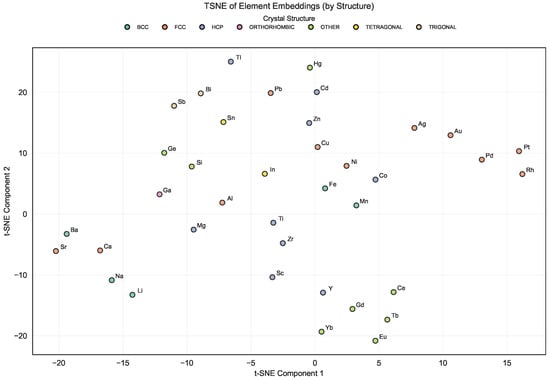
Figure 3.
t-SNE visualization of mat2vec element embeddings for the elements present in the Entall database [20].
Similarly, Figure 4 depicts the two-dimensional t-SNE projection of the alloy embeddings. Here, alloys sharing similar constituent elements are often located close together, suggesting that their latent representations capture not only compositional features but also potential chemical compatibility. For example, alloys involving coinage metals (e.g., Ag, Au, and Cu) tend to form local clusters, reflecting their similar metallic character and phase behavior. In contrast, alloys with highly electropositive elements (e.g., Li- or Na-based ones) occupy more distant regions, highlighting the difference in their bonding character and the diversity of chemical compositions across the studied systems.
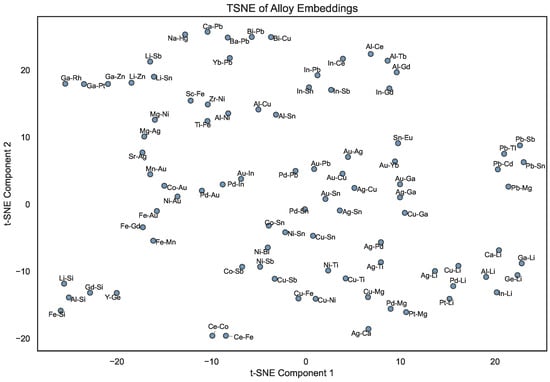
Figure 4.
t-SNE visualization of compressed 32-dimensional alloy embeddings after symmetry-based augmentation (for the alloys present in the Entall database [20]).
4.2. Summary Model Accuracy: Miedema Model vs. BNN-Based Model
To assess and compare the predictive accuracy of the classical Miedema model and the proposed Bayesian neural network (BNN) model, we analyze their performance relative to the enthalpy of mixing, . The BNN framework leverages a data-driven, probabilistic approach aimed at improving prediction quality and capturing uncertainty effectively.
Figure 5 presents side-by-side visualizations of predicted versus experimentally measured values of for both models. Each panel integrates hexbin density plots with scatter points, facilitating an intuitive assessment of both localized prediction errors and overall distributional trends. The red dashed line in each plot corresponds to the ideal case of perfect prediction, where predicted values exactly match experimental observations.
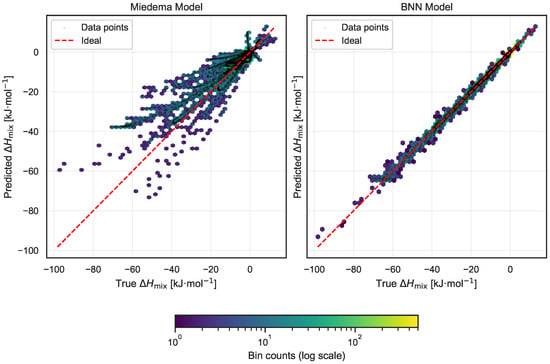
Figure 5.
Comparison of predicted versus experimental enthalpy of mixing () for the Miedema model (left) and the proposed Bayesian neural network (BNN) model (right). Each panel shows a joint hexbin and scatter plot highlighting local and global prediction patterns. The red dashed line indicates the ideal perfect prediction. The BNN predictions are significantly closer to the ideal line, with points tightly clustered and almost no outliers, demonstrating superior accuracy.
The comparison reveals a marked improvement in accuracy with the BNN model. Predictions from the BNN are tightly concentrated along the ideal diagonal, exhibiting minimal scatter and virtually no outliers. This close alignment highlights the model’s ability to capture underlying thermodynamic relationships more effectively. In contrast, the Miedema model displays a broader spread of predictions with a notable presence of outliers, indicating less consistent performance across the dataset.
Quantitatively, this difference is reflected in the mean absolute error (MAE) metrics: the Miedema model yields an MAE of 4.27 kJ·mol−1, whereas the BNN model achieves a substantially lower MAE of 0.53 kJ·mol−1. This eightfold reduction in error underscores the enhanced predictive capability of the Bayesian neural network and supports its potential as a robust tool for mixing enthalpy estimation in alloy systems.
4.3. Detailed Alloy-by-Alloy Analysis
To gain deeper insights into the model’s behavior for individual systems, we present a detailed alloy-by-alloy analysis. Figure 6 shows mixing enthalpy curves, along with the associated predictive uncertainty, for six selected binary alloy systems: Pd–Li, Pt–Li, Pd–Mg, Pt–Mg, Pb–Mg, and Pd–Pb. For each system, the predicted mean mixing enthalpy curve is shown together with uncertainty intervals derived from the Bayesian neural network posterior sampling procedure. The shaded regions correspond to one standard deviation and 95% confidence intervals, highlighting both local uncertainty and global trend consistency.
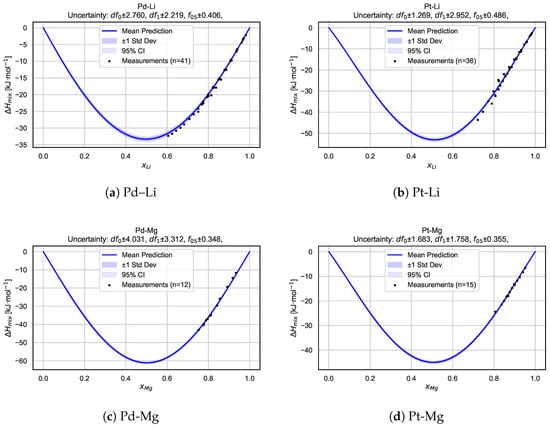
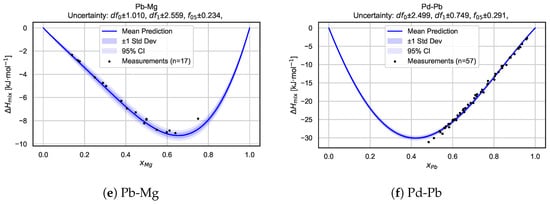
Figure 6.
Predicted mixing enthalpy curves and corresponding uncertainty estimates for six selected binary alloy systems. Each panel shows the mean predicted as a function of composition, with shaded regions indicating standard deviation and 95% confidence intervals based on BNN posterior sampling. Experimental measurements [21] are overlaid as reference points. The consistency between predictions and measurements, along with well-calibrated uncertainty bands, highlights the model’s capacity for the robust and probabilistic modeling of alloy thermodynamics.
Overall, these plots illustrate that the BNN captures key features arising from the mixing of the components while providing realistic uncertainty estimates across the entire composition range. In many cases, the measurement data points are well bracketed by the confidence intervals, demonstrating the model’s ability to generalize beyond sparse experimental data and supporting the reliability of its probabilistic predictions.
4.4. Robustness to Reduced Training Data
We further tested the robustness of the BNN model under reduced data availability. Starting from the complete dataset, we adopted a restoration-based evaluation strategy in which only a randomly selected subset of the measurement data were used to train the model to infer the Redlich–Kister (RK) polynomial coefficients. Specifically, we retained 90%, 75%, 50%, and 25% of the experimental measurements for each binary alloy system for training. The resulting RK curve—derived solely from this reduced subset—was then evaluated against the full set of measurements to quantify how well the model reconstructs the entire mixing enthalpy behavior from sparse data. For each case, joint hexbin plots were produced as in the summary comparisons, along with tabulated MAE and RMSE values.
As shown in Figure 7 and Table 1, the model’s predictive accuracy remains remarkably stable, with MAE between 0.53 and 0.63 kJ·mol−1 and RMSE between 0.89 and 1.16 kJ·mol−1, even when only 25% of the measurement data are retained for training. This strong resilience further validates the robustness of the proposed BNN framework, enabled by global cross-alloy knowledge transfer and symmetry-based data augmentation. The ability to preserve performance under significant data reduction highlights the efficiency of the model’s inter-alloy learning capabilities and its effective utilization of latent domain priors.
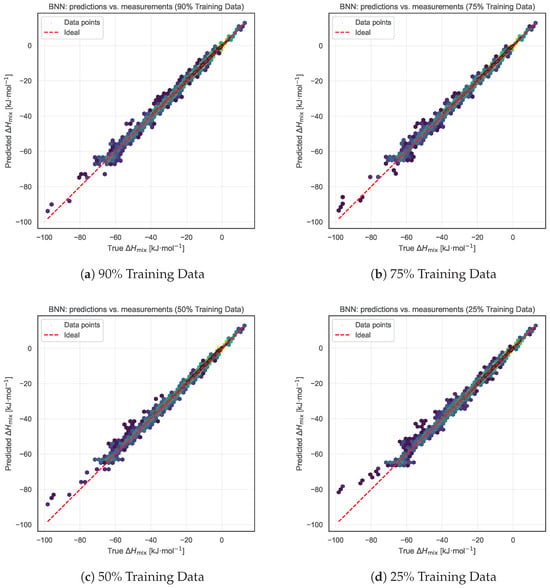
Figure 7.
Impact of reduced training data from the Entall database on model performance. Each panel shows results when progressively smaller fractions of the data are retained for training: (a) 90%, (b) 75%, (c) 50%, and (d) 25%. Despite the reduced data availability, the model maintains nearly constant prediction accuracy (with MAE between 0.53 and 0.63), demonstrating the robustness of the global inter-alloy learning strategy combined with symmetry-based data augmentation.

Table 1.
Mean absolute error (MAE) and root mean square error (RMSE) of the BNN model for various fractions of the measurement data. Frac. indicates the fraction of the measurement dataset used for training. The results demonstrate consistent model performance even with substantial reductions in training data, highlighting its robustness due to global inter-alloy learning and symmetry-based data augmentation.
5. Discussion
The proposed machine learning framework for predicting the enthalpy of mixing in binary alloys effectively addresses critical limitations of existing thermodynamic modeling approaches, especially under data-scarce conditions. A major challenge in materials science is the limited availability of reliable calorimetric measurements, due to their time-consuming, costly, and technically demanding nature. Traditional machine learning models often struggle to generalize to sparsely sampled alloy systems and typically ignore important physical symmetries and uncertainty quantification. Our framework overcomes these challenges through three key innovations.
First, the use of symmetry-augmented embeddings ensures physical consistency. By preprocessing chemical identities with mat2vec embeddings and augmenting the data with mirrored alloy representations (A–B, x, and B–A, ), the model learns and enforces permutation and compositional invariances. This augmentation is not merely data duplication but rather a physics-informed regularization technique that enforces consistent treatment of chemically equivalent systems. It reduces the risk of contradictory or non-physical predictions and improves generalization to unobserved compositions, particularly under data-scarce conditions. The augmentation is critical in limited-data regimes, significantly improving model robustness. To further enhance generalization and prevent overfitting, the raw 400-dimensional embeddings are compressed into a 32-dimensional latent space by using an autoencoder. This low-dimensional representation preserves chemically relevant structural and compositional symmetries while reducing redundancy. The resulting t-SNE visualizations confirm this, showing chemically consistent groupings and validating that the embeddings capture meaningful similarities. The strong empirical performance of the model under reduced training conditions (as described below) provides additional support for the effectiveness of this symmetry-aware embedding and regularization strategy.
Second, the framework’s global modeling of concentration-dependent enthalpy curves represents a substantial advance over single-point enthalpy predictions. Modeling the full enthalpy profile across composition supports knowledge transfer across alloy systems and uses known boundary conditions, , as informed priors. This improves accuracy, especially in data-sparse concentration ranges. A geometrically meaningful Redlich–Kister polynomial representation, defined by first derivatives at the endpoints and the midpoint enthalpy, further stabilizes curve reconstruction and enables physically interpretable targets. A smoothness constraint on the third derivative regularizes higher-order variations, ensuring a consistent and physically realistic enthalpy curve.
Third, integrating Bayesian neural networks (BNNs) provides principled uncertainty quantification, which is essential to trustworthy predictions in under-sampled regions. Unlike traditional deterministic neural networks, BNNs model weights as distributions, offering calibrated confidence intervals alongside mean predictions. This capability is crucial to guiding expensive experiments and making data-driven material design decisions. The BNN architecture, implemented with the Blitz framework, effectively propagates prior knowledge through posterior distributions, yielding robust uncertainty estimates.
Quantitatively, the proposed BNN model achieves a mean absolute error (MAE) of 0.53 kJ·mol−1, an eightfold improvement over the Miedema model’s MAE of 4.27 kJ·mol−1. Its predictions cluster tightly along the ideal diagonal in predicted vs. experimental plots, with minimal scatter and no significant outliers, whereas the Miedema model shows broad scatter and frequent outliers. Alloy-by-alloy analyses confirm the BNN’s ability to accurately capture the shape of enthalpy curves, while the confidence intervals reliably bracket experimental data points, demonstrating realistic uncertainty estimates.
Furthermore, the framework shows remarkable robustness to reduced training data. Even with only 25% of the available measurements, predictive accuracy remains stable (MAE between 0.53–0.63 kJ·mol−1 and RMSE between 0.89–1.16 kJ·mol−1). This resilience underscores the effectiveness of cross-alloy knowledge transfer and symmetry-based data augmentation, making the approach practical for real-world applications where data are often limited.
Overall, this work demonstrates how domain-informed embeddings, cross-system knowledge sharing, and principled uncertainty estimation can be integrated into a unified framework to advance thermodynamic modeling under incomplete data conditions. While this study focuses on binary alloy enthalpies of mixing, the methodology is readily extensible to other composition-dependent thermodynamic quantities and even to multicomponent systems, paving the way for more general, uncertainty-aware, and symmetry-consistent predictive models.
Remark 2.
The BNN model generally produces accurate predictions with well-calibrated confidence intervals, yet a small number of measurement points fall outside the 95% bounds—typically in systems with sparse, noisy, or inconsistent data. In some cases, deviations may also stem from limitations of the Redlich–Kister (RK) representation, which may not fully capture complex thermodynamic behavior such as strong asymmetries. Since the model is trained globally across all binary systems, it benefits from cross-alloy knowledge transfer, yet systems with more atypical interaction profiles may remain challenging. A systematic characterization of such outlier cases based on constituent elements, structural types, or interaction complexity remains an important direction for future research.
6. Conclusions
This work presents a novel machine learning framework for uncertainty-aware prediction of the enthalpy of mixing in binary alloys, explicitly designed to address the challenges of limited experimental data and to improve the trustworthiness of predictions.
The framework’s contributions are centered around three key innovations:
- Symmetry-augmented embeddings, enforcing physical invariances such as element permutation and compositional mirroring, thereby ensuring consistency across chemically equivalent representations and implicitly capturing chemically meaningful relationships between elements that enable inter-system knowledge transfer.
- The constrained global modeling of enthalpy curves, which enables the prediction of the entire concentration-dependent enthalpy profile, supporting knowledge transfer across alloy systems and improving generalization in data-sparse concentration intervals.
- Bayesian neural network-based uncertainty quantification, providing calibrated confidence intervals alongside mean predictions, which is essential to reliable decision making, particularly in under-sampled composition regions.
Evaluation results demonstrate the framework’s strong performance, achieving an eightfold reduction in mean absolute error compared with the classical Miedema model (0.53 kJ·mol−1 vs. 4.27 kJ·mol−1). Moreover, the model maintains consistent accuracy even with only 25% of the available measurement data, highlighting its robustness through effective inter-alloy knowledge transfer and symmetry-based data augmentation.
In summary, this approach advances data-driven material modeling by integrating domain-specific symmetries with principled uncertainty estimation. It offers a robust and interpretable tool for predictive thermodynamic assessment, even in sparse-data scenarios. The principles developed here also provide a foundation for future research, extending these methods to other composition-dependent thermodynamic properties and to multicomponent systems using generalized, uncertainty-aware, and symmetry-consistent predictive models.
Author Contributions
Conceptualization, R.D. and A.D.; methodology, R.D.; software, R.D.; validation, R.D.; formal analysis, R.D., W.G. (Władysław Gąsior), W.G. (Wojciech Gierlotka) and A.D.; investigation, R.D. and A.D.; resources, R.D. and A.D.; data curation, R.D. and A.D.; writing—original draft preparation, R.D., W.G. (Władysław Gąsior), W.G. (Wojciech Gierlotka) and A.D.; writing—review and editing, R.D.; visualization, R.D.; supervision, A.D. All authors have read and agreed to the published version of the manuscript.
Funding
The research presented in this paper was (1) financially supported by the Institute of Metallurgy and Materials Science of the Polish Academy of Sciences as part of the statutory project “Development of databases of physicochemical and thermodynamic properties of materials. Thermodynamic properties of selected liquid alloys”, project No. Z-10/2024-2027, and (2) partially supported by funds from the Polish Ministry of Science and Higher Education allocated to AGH University of Krakow.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Lukas, H.; Fries, S.G.; Sundman, B. Computational Thermodynamics: The Calphad Method; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar] [CrossRef]
- Redlich, O.; Kister, A. Algebraic representation of thermodynamic properties and the classification of solutions. Ind. Eng. Chem. 1948, 40, 345–348. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558. [Google Scholar] [CrossRef] [PubMed]
- Gierlotka, W.; Dębski, A.; Gąsior, W.; Dębski, R.; Pęska, M.; Polański, M. Application of the OpenCalphad software to optimization of the Au-Mg system. Calphad 2025, 89, 102835. [Google Scholar] [CrossRef]
- Boom, R.; De Boer, F.; Miedema, A. On the heat of mixing of liquid alloys—I. J. Less Common Met. 1976, 45, 237–245. [Google Scholar] [CrossRef]
- Boom, R.; De Boer, F.; Miedema, A. On the heat of mixing of liquid alloys—II. J. Less Common Met. 1976, 46, 271–284. [Google Scholar] [CrossRef]
- De Boer, F.R.; Mattens, W.; Boom, R.; Miedema, A.; Niessen, A. Cohesion in Metals: Transition Metal Alloys; North-Holland Publishing Co.: Amsterdam, The Netherlands, 1988. [Google Scholar]
- Zhang, B.; Liao, S.; Shu, X.; Xie, H.; Yuan, X. Theoretical calculation of the mixing enthalpies of 21 IIIB-IVB, IIIB-VB and IVB-VB binary alloy systems. Phys. Met. Metallogr. 2013, 114, 457–468. [Google Scholar] [CrossRef]
- Boom, R.; De Boer, F. Enthalpy of formation of binary solid and liquid Mg alloys–comparison of Miedema-model calculations with data reported in literature. Calphad 2020, 68, 101647. [Google Scholar] [CrossRef]
- Deffrennes, G.; Terayama, K.; Abe, T.; Ogamino, E.; Tamura, R. A framework to predict binary liquidus by combining machine learning and CALPHAD assessments. Mater. Des. 2023, 232, 112111. [Google Scholar] [CrossRef]
- Hart, G.L.; Mueller, T.; Toher, C.; Curtarolo, S. Machine learning for alloys. Nat. Rev. Mater. 2021, 6, 730–755. [Google Scholar] [CrossRef]
- Deffrennes, G.; Hallstedt, B.; Abe, T.; Bizot, Q.; Fischer, E.; Joubert, J.M.; Terayama, K.; Tamura, R. Data-driven study of the enthalpy of mixing in the liquid phase. Calphad 2024, 87, 102745. [Google Scholar] [CrossRef]
- Huang, S.; Wang, G.; Cao, Z. Prediction of Enthalpy of Mixing of Binary Alloys Based on Machine Learning and CALPHAD Assessments. Metals 2025, 15, 480. [Google Scholar] [CrossRef]
- Ait Boukideur, M.; Selhaoui, N.; Alaoui, F.C.; Poletaev, D.; Bouchta, H.; Achgar, K.; Aharoune, A. Thermodynamic assessment of the Ga–Lu system by the combination of ab-initio calculations and the CALPHAD approach. Calphad 2022, 79, 102464. [Google Scholar] [CrossRef]
- Takeuchi, A.; Inoue, A. Mixing enthalpy of liquid phase calculated by miedema’s scheme and approximated with sub-regular solution model for assessing forming ability of amorphous and glassy alloys. Intermetallics 2010, 18, 1779–1789. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, Y. Prediction of high-entropy stabilized solid-solution in multi-component alloys. Mater. Chem. Phys. 2012, 132, 233–238. [Google Scholar] [CrossRef]
- Gal, Y. Uncertainty in Deep Learning. Ph.D. Thesis, University of Cambridge, Cambridge, UK, 2016. Available online: http://106.54.215.74/2019/20190729-liuzy.pdf (accessed on 2 June 2025).
- Tshitoyan, V.; Dagdelen, J.; Weston, L.; Dunn, A.; Rong, Z.; Kononova, O.; Persson, K.A.; Ceder, G.; Jain, A. Unsupervised word embeddings capture latent knowledge from materials science literature. Nature 2019, 571, 95–98. [Google Scholar] [CrossRef] [PubMed]
- Esposito, P. BLiTZ-Bayesian Layers in Torch Zoo (a Bayesian Deep Learing Library for Torch). 2020. Available online: https://github.com/piEsposito/blitz-bayesian-deep-learning/ (accessed on 2 June 2025).
- Dębski, A.; Dębski, R.; Gąsior, W. New features of Entall database: Comparison of experimental and model formation enthalpies. Arch. Metall. Mater. 2014, 59, 1337–1343. [Google Scholar] [CrossRef]
- Dębski, A. Entall-thermodynamic database of alloys. Arch. Metall. Mater. 2013, 58, 1147–1148. [Google Scholar] [CrossRef]
- Van der Maaten, L.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).