An Autoencoder-like Non-Negative Matrix Factorization with Structure Regularization Algorithm for Clustering
Abstract
1. Introduction
2. Related Work
2.1. Non-Negative Matrix Factorization (NMF)
2.2. Graph-Regularized Non-Negative Matrix Factorization (GNMF)
2.3. Principal Component Analysis (PCA)
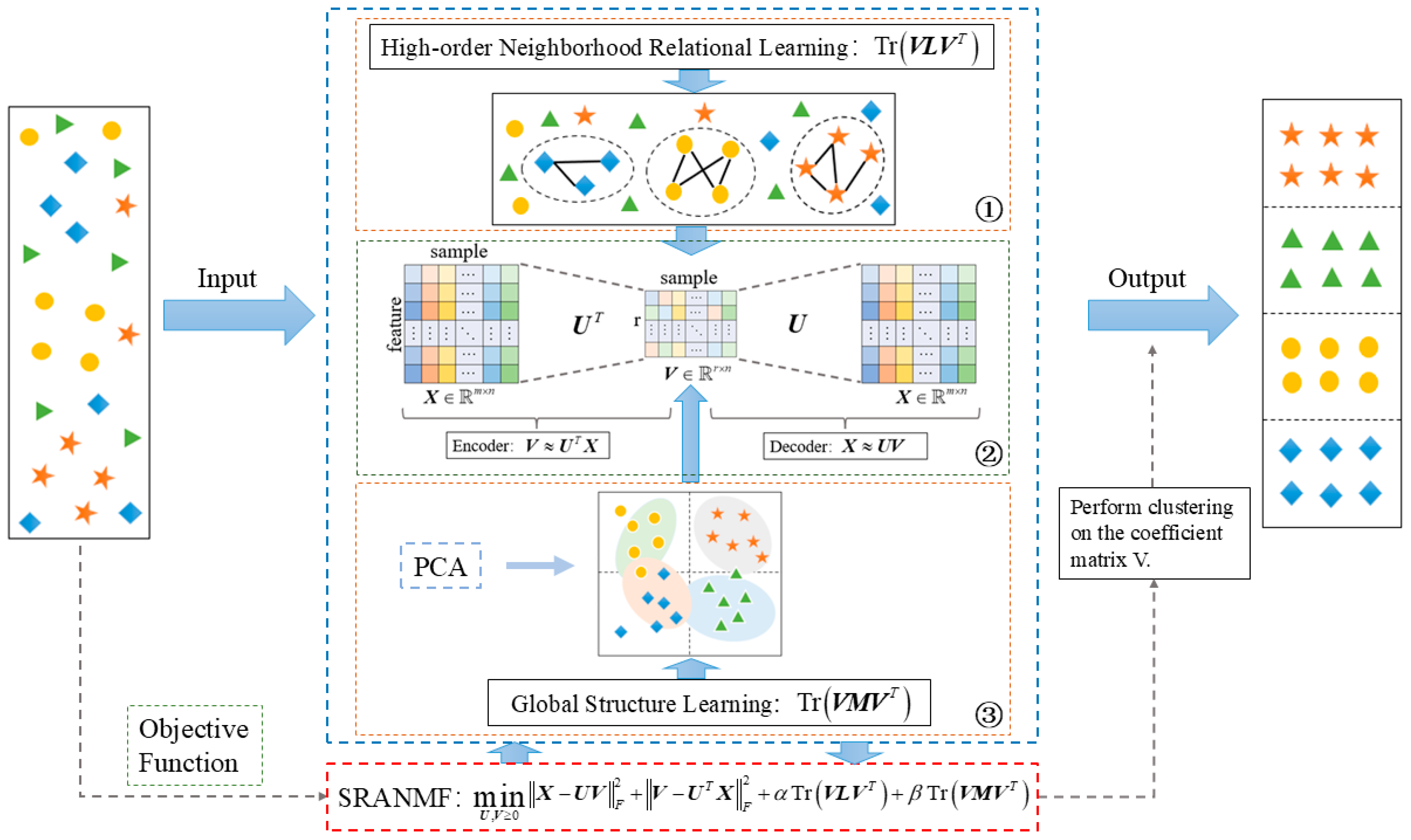
3. Methodology
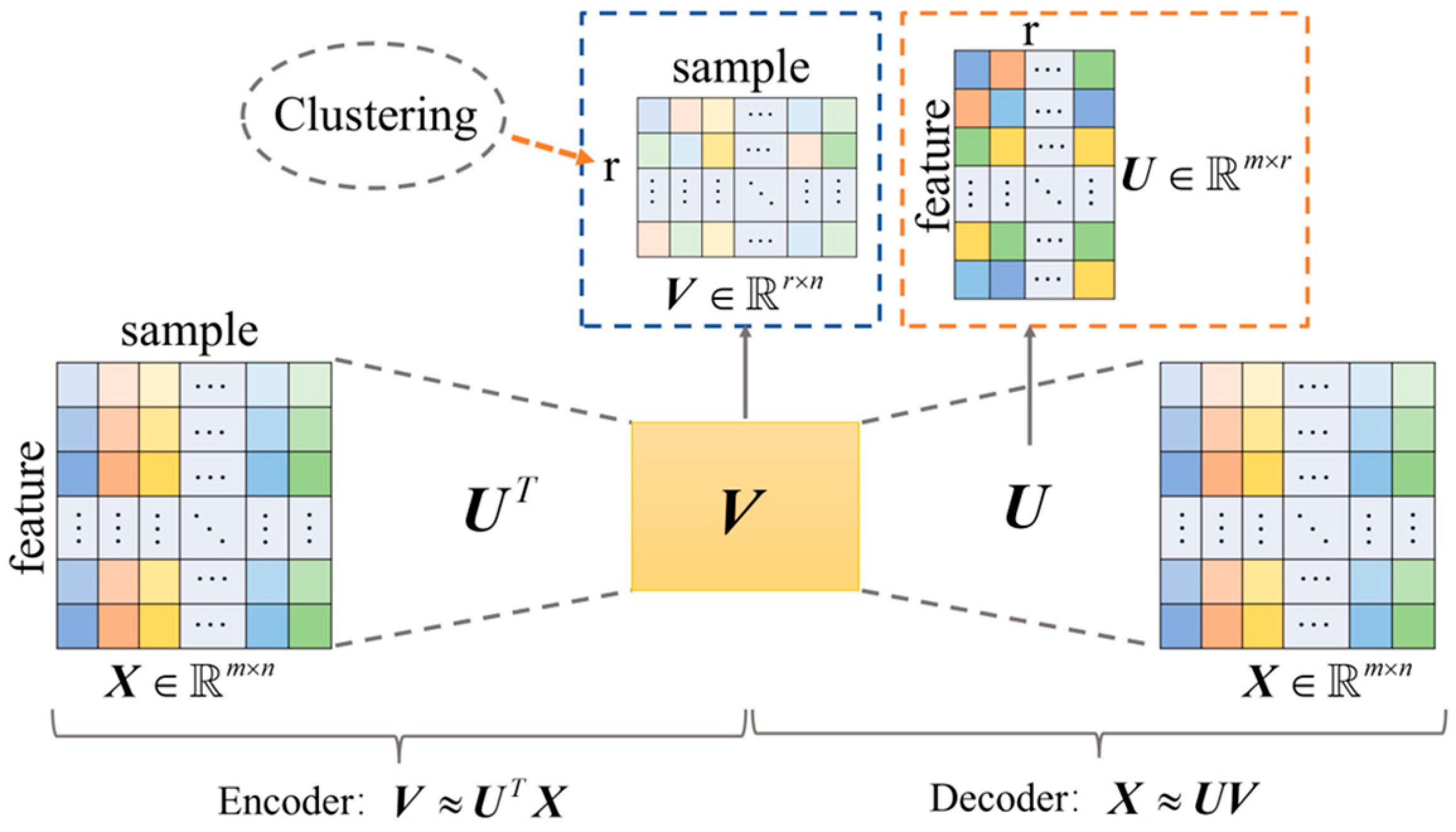
3.1. Autoencoder-like Non-Negative Matrix Factorization
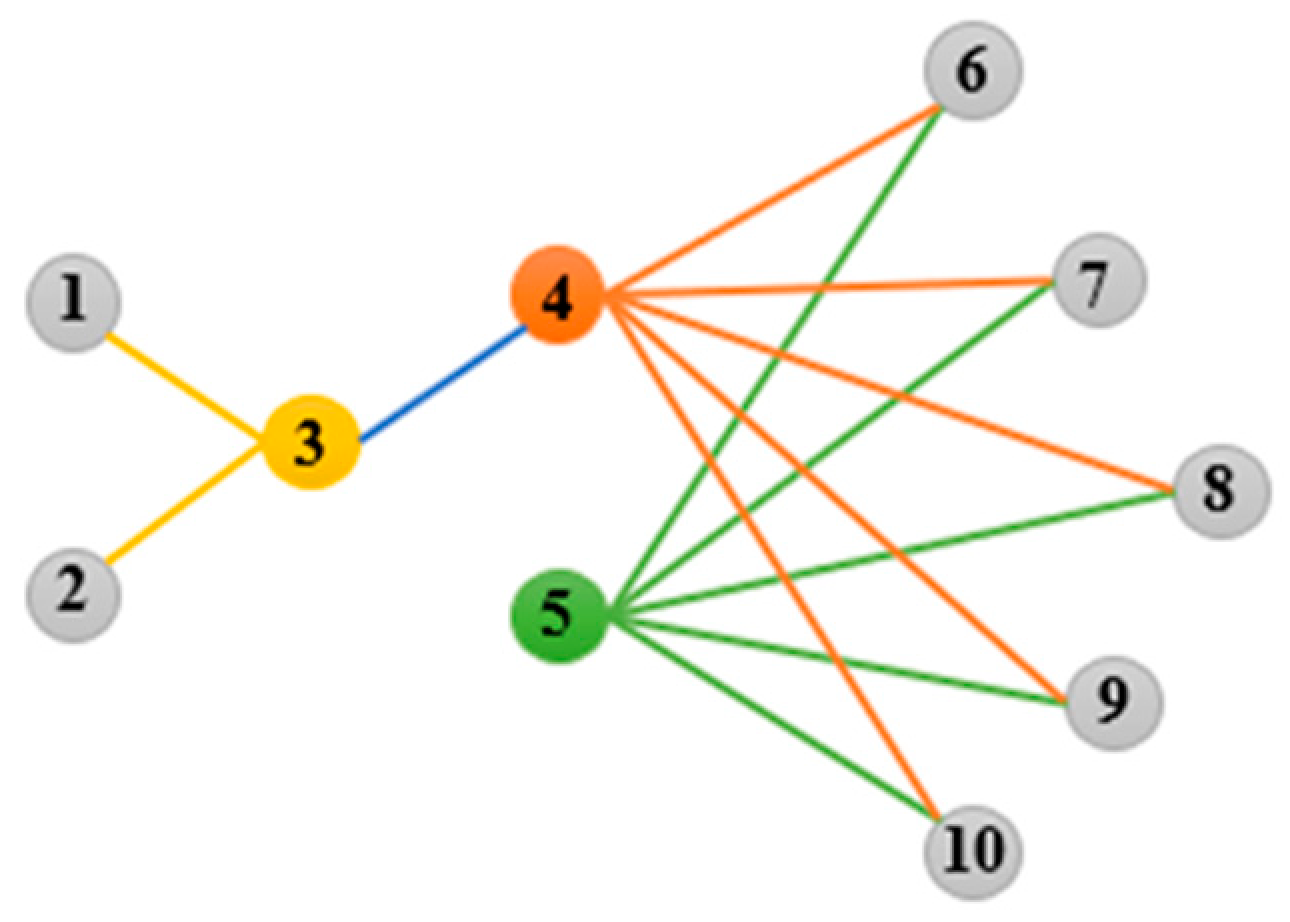
3.2. High-Order Graph Regularization
3.3. Global Structure Learning
3.4. Objective Function
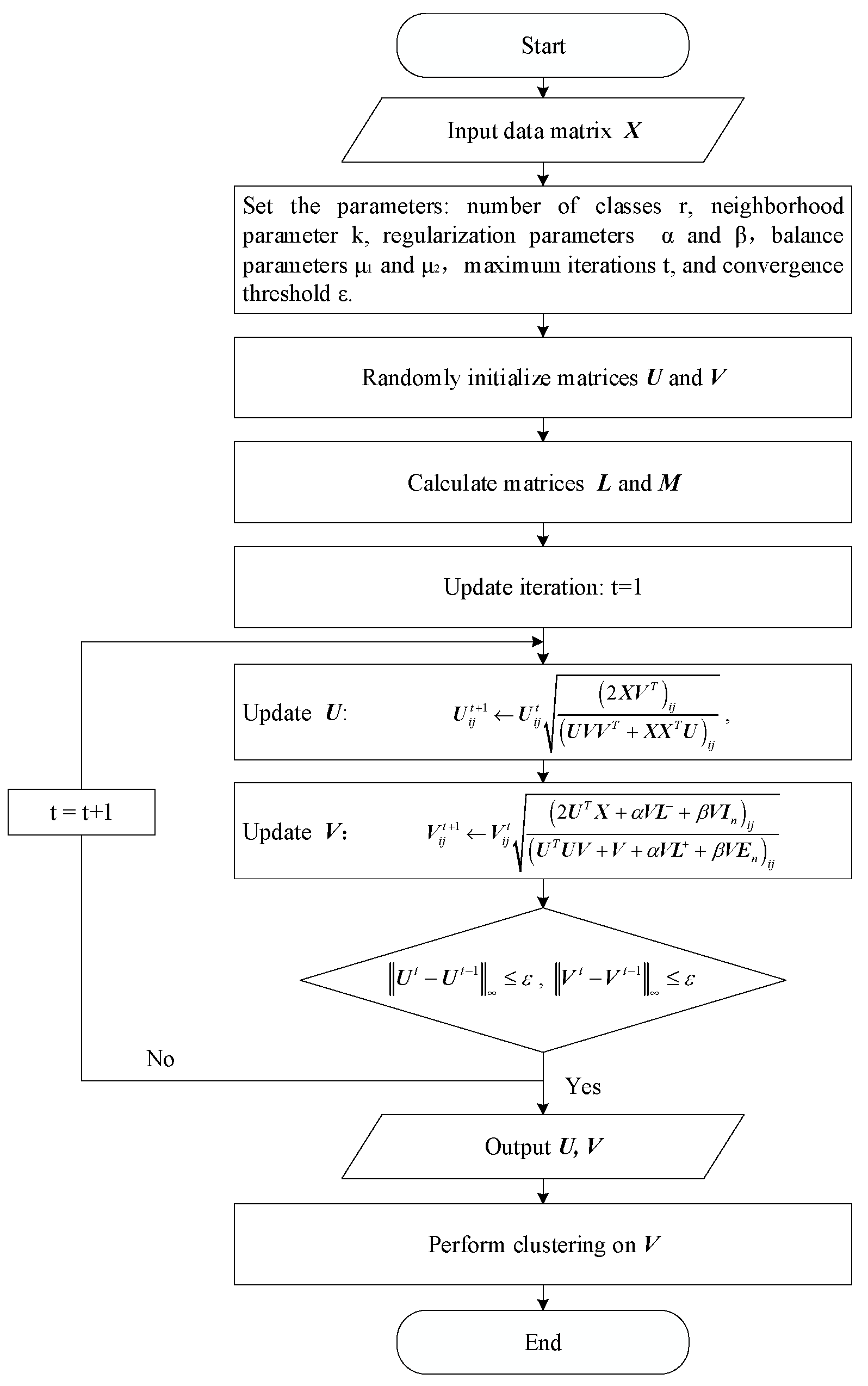
3.5. Optimization Algorithm
3.6. Convergence Analysis
| Algorithm 1. Structure Regularization Autoencoder-Like Non-Negative Matrix Factorization for Clustering (SRANMF) |
| Input: Initial matrix , number of categories , neighborhood parameter , regularization parameters and , balance parameters and , maximum number of iterations , threshold . Output: Basis matrix and coefficient matrix . 1. Initialization: Randomly generate basis matrix and coefficient matrix ; 2. Calculate the optimal Laplacian matrix according to Equations (15)–(18); 3. Calculate matrix according to Equations (20)–(22); 4. Update basis matrix according to Equation (33); 5. Update coefficient matrix according to Equation (34); 6. Termination: When and . 7. Finally, obtain the clustering indicator matrix , and apply k-means to cluster the coefficient matrix . |
3.7. Time Complexity Analysis
4. Experiments and Analysis
4.1. Dataset
4.2. Dataset Clustering Performance Evaluation Metrics
4.2.1. Clustering Accuracy (ACC)
4.2.2. Adjusted Rand Index (ARI)
4.2.3. Normalized Mutual Information (NMI)
4.2.4. Clustering Purity (PUR)
4.3. Comparative Algorithms and Parameter Settings
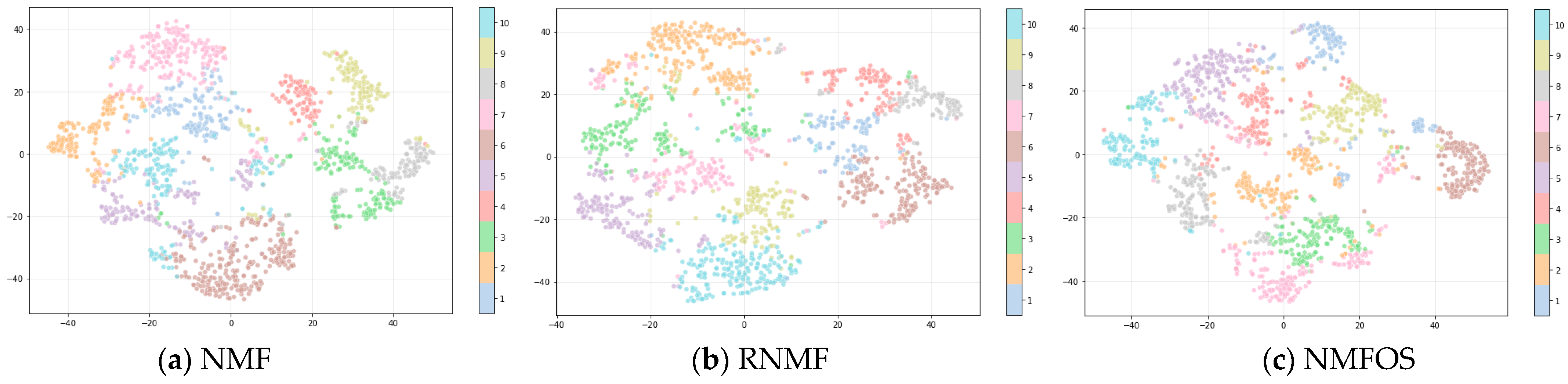
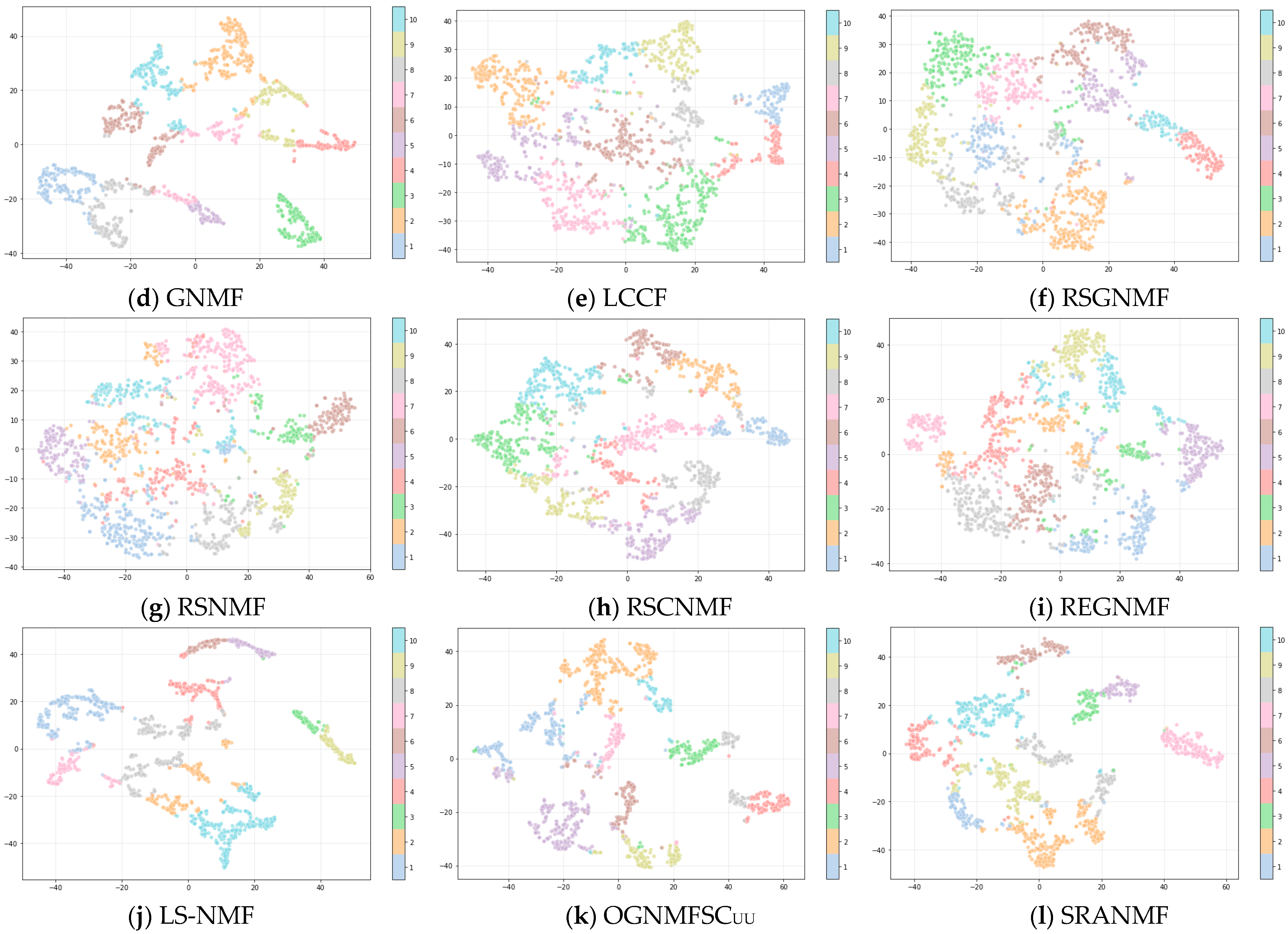
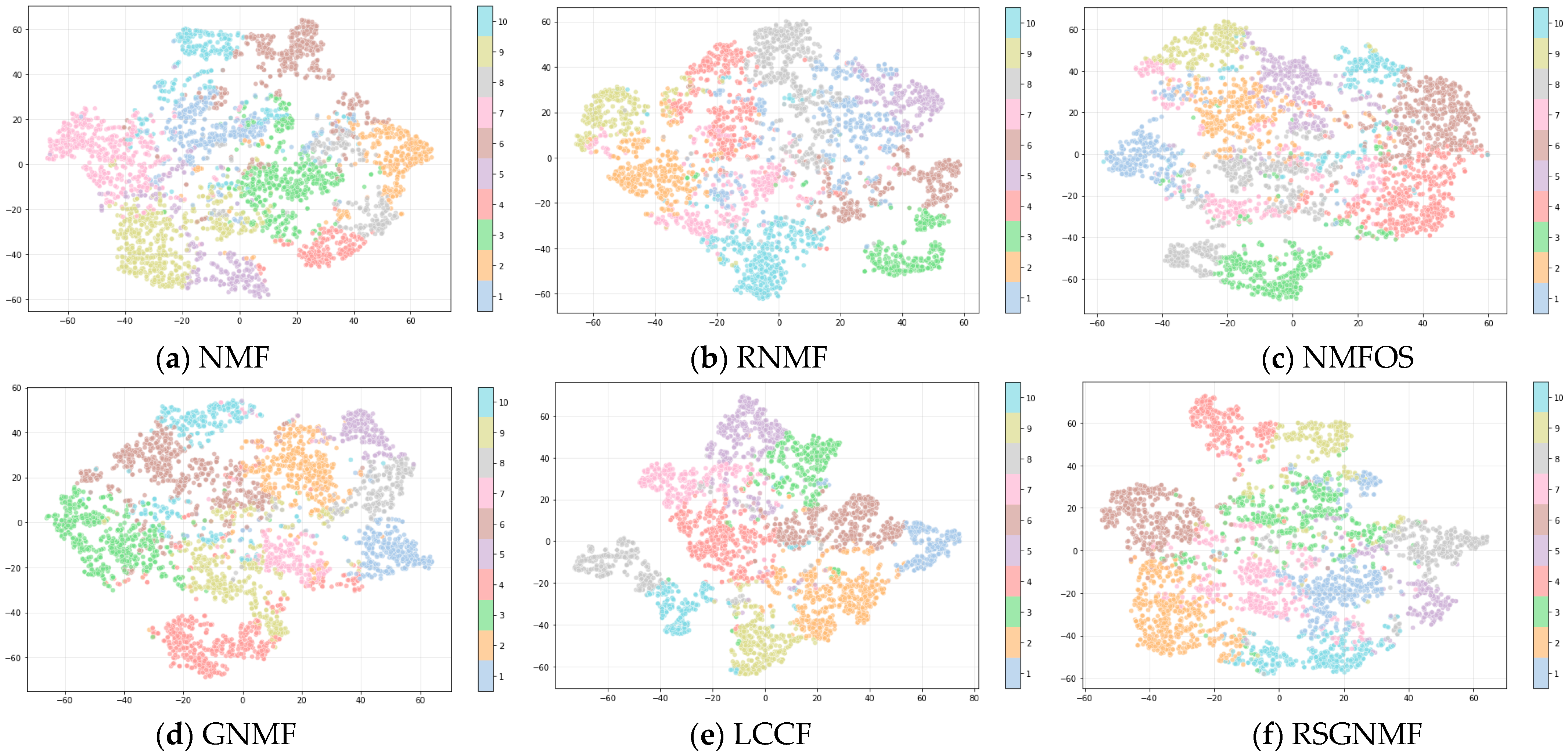
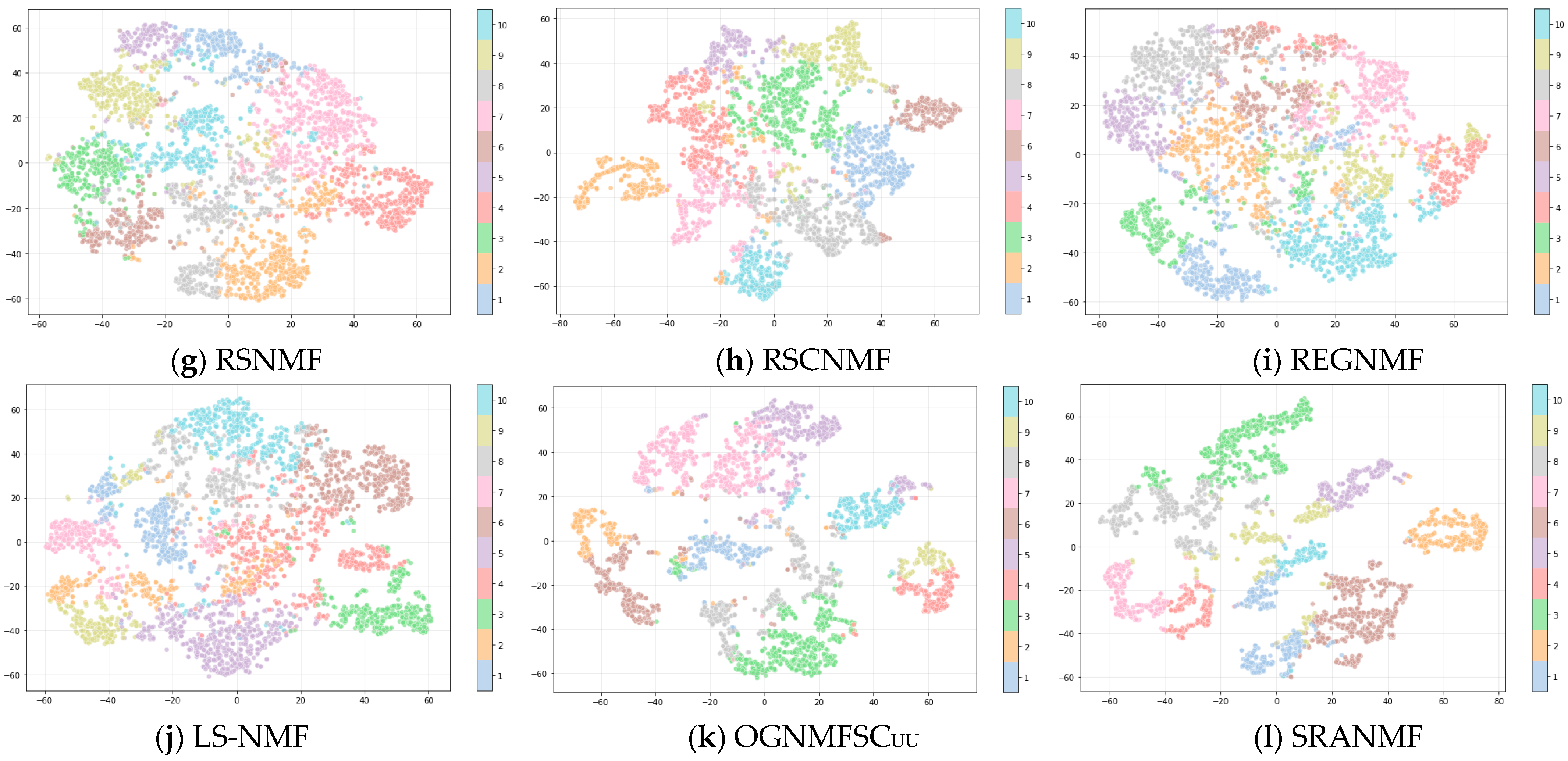
4.4. Results and Analysis
4.5. Ablation Experiments
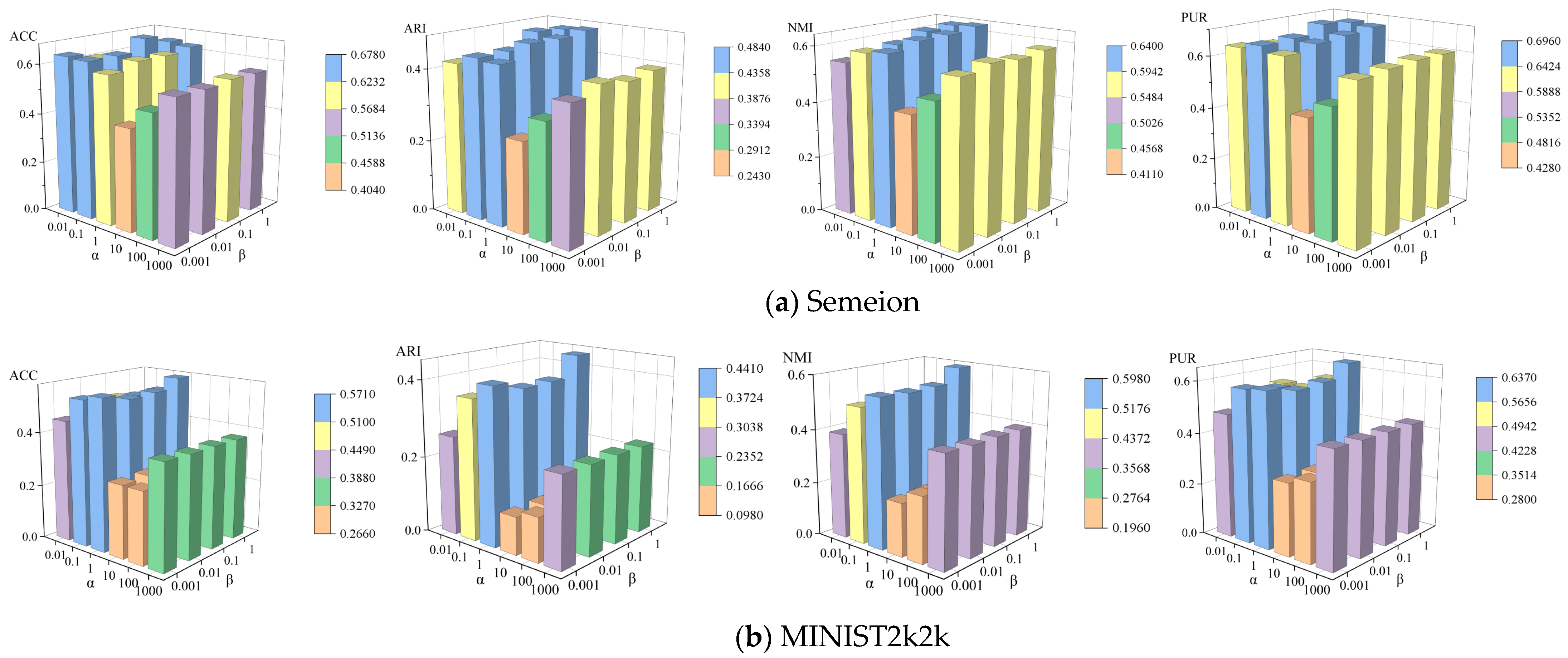
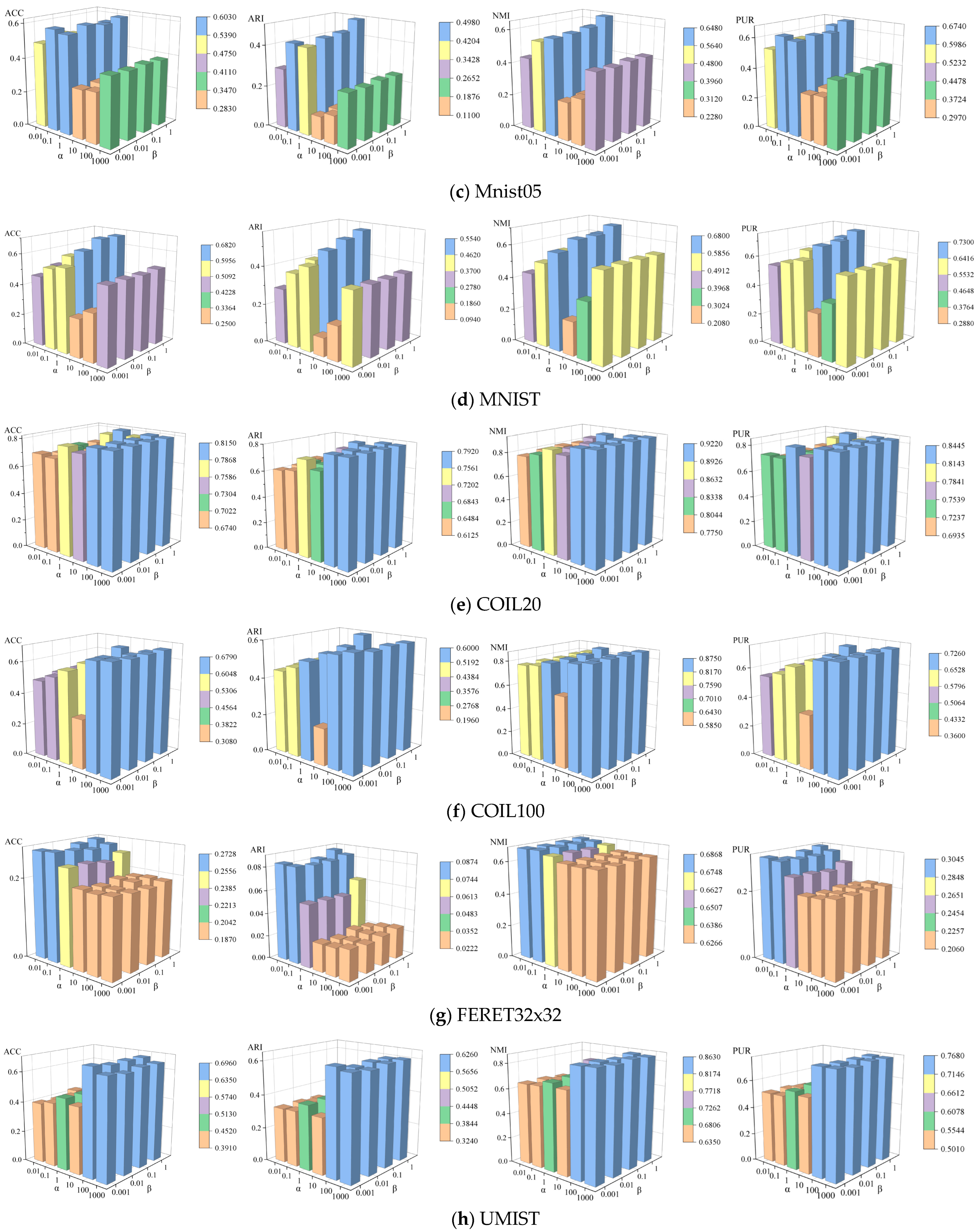
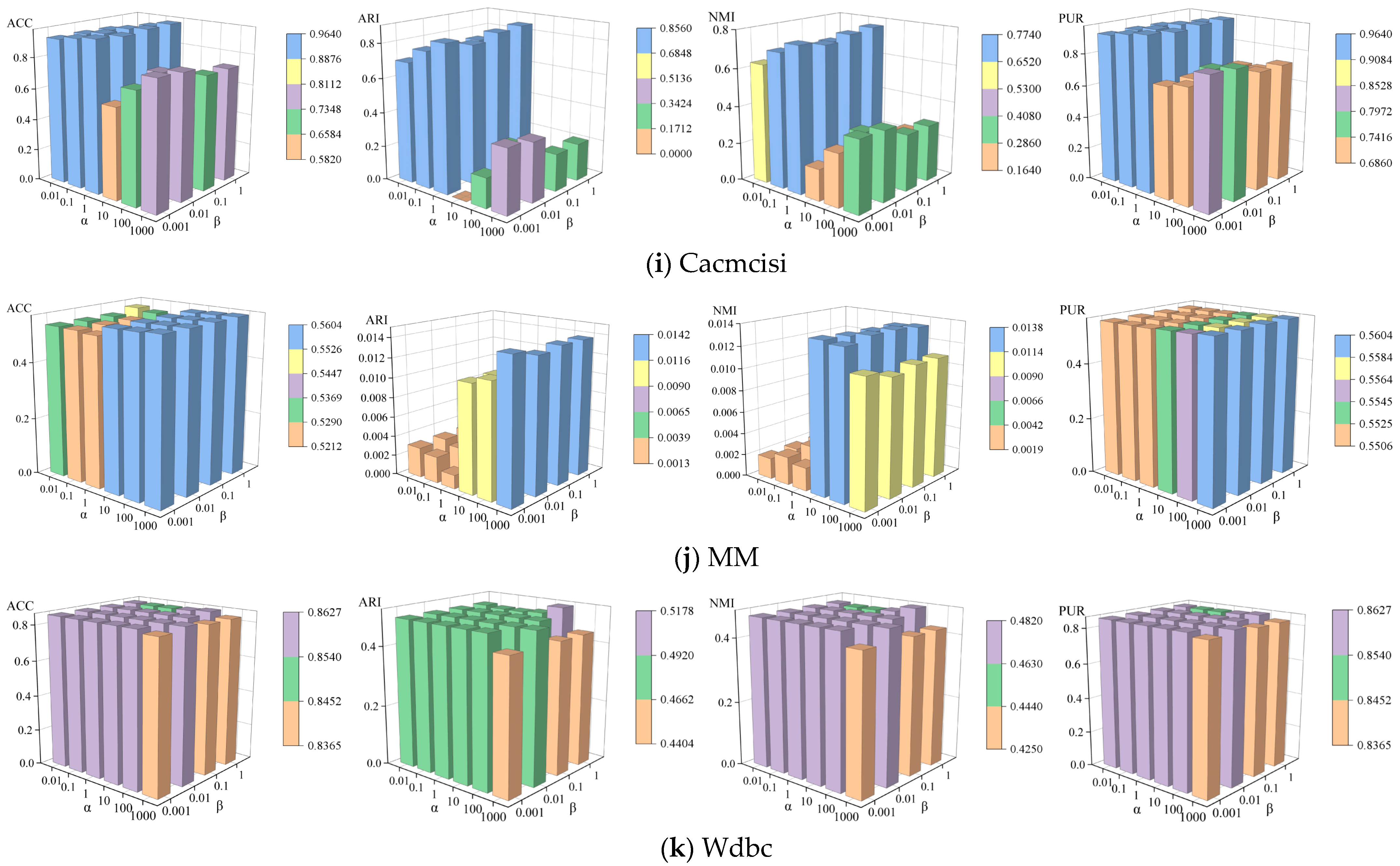
4.6. Parameter Sensitivity Analysis
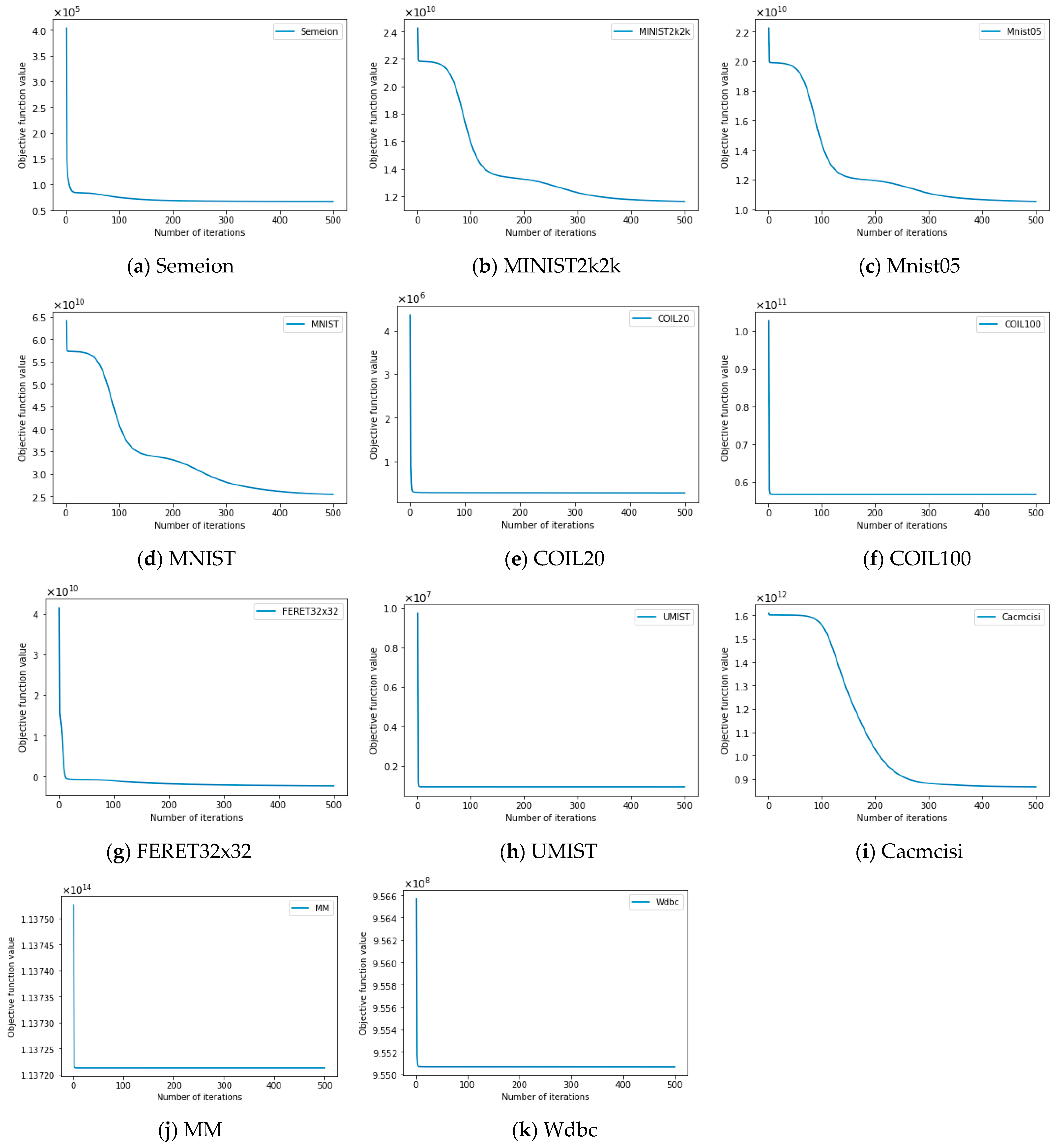
4.7. Empirical Convergence
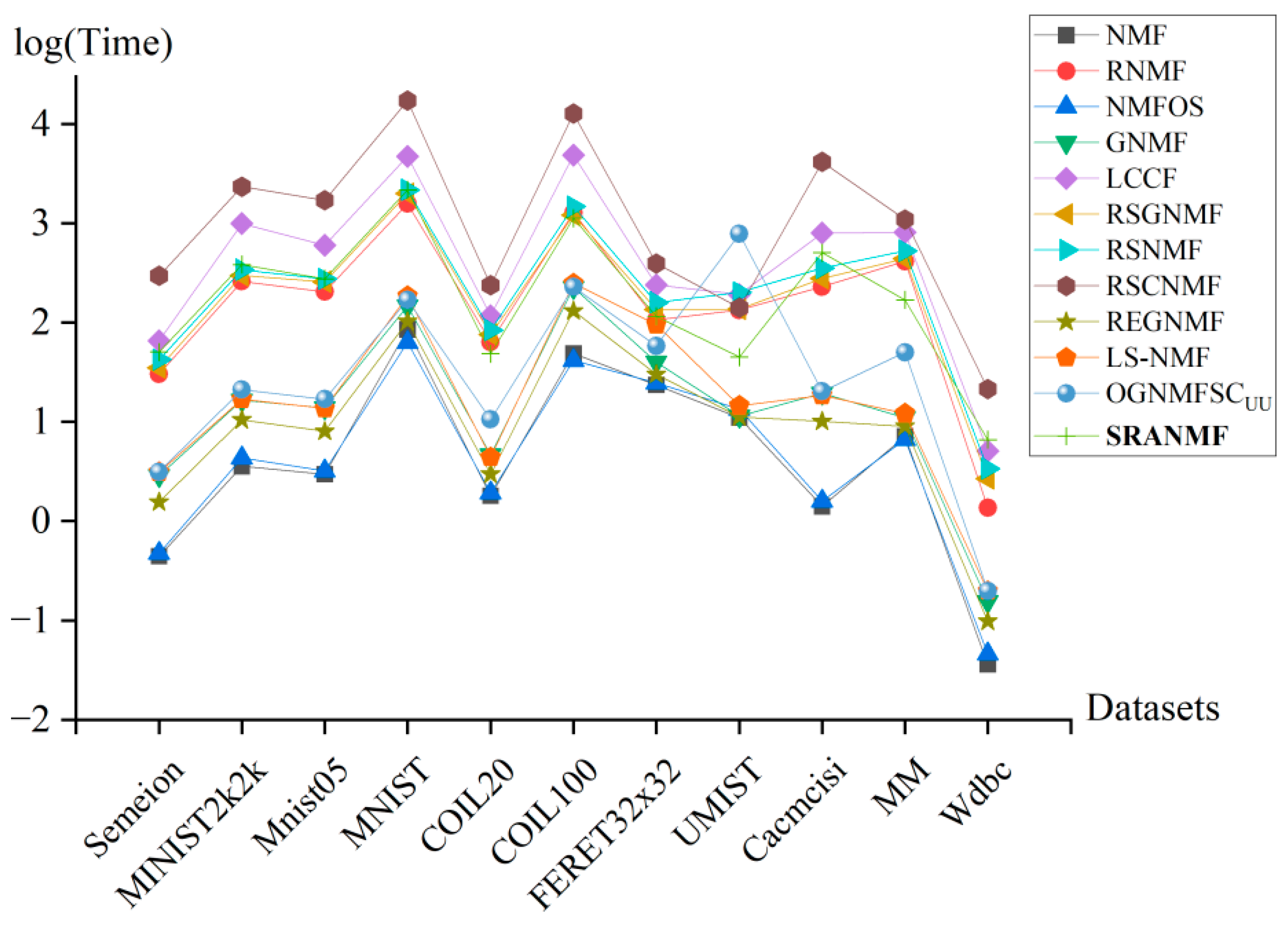
4.8. Runtime Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Huang, S.; Ren, Y.; Xu, Z. Robust multi-view data clustering with multi-view capped-norm K-means. Neurocomputing 2018, 311, 197–208. [Google Scholar] [CrossRef]
- Xing, Z.; Wen, M.; Peng, J.; Feng, J. Discriminative semi-supervised non-negative matrix factorization for data clustering. Eng. Appl. Artif. Intell. 2021, 103, 104289. [Google Scholar] [CrossRef]
- Aghdam, M.H.; Zanjani, M.D. A novel regularized asymmetric non-negative matrix factorization for text clustering. Inf. Process. Manag. 2021, 58, 102694. [Google Scholar] [CrossRef]
- Liu, M.; Yang, Z.; Han, W.; Chen, J.; Sun, W. Semi-supervised multi-view binary learning for large-scale image clustering. Appl. Intell. 2022, 52, 14853–14870. [Google Scholar] [CrossRef]
- He, W.; Zhang, S.; Li, C.G.; Qi, X.; Xiao, R.; Guo, J. Neural normalized cut: A differential and generalizable approach for spectral clustering. Pattern Recogn. 2025, 164, 111545. [Google Scholar] [CrossRef]
- Deng, T.; Ye, D.; Ma, R.; Fujita, H.; Xiong, L. Low-rank local tangent space embedding for subspace clustering. Inf. Sci. 2020, 508, 1–21. [Google Scholar] [CrossRef]
- Zhao, X.; Nie, F.; Wang, R.; Li, X. Robust fuzzy k-means clustering with shrunk patterns learning. IEEE Trans. Autom. Control 2023, 35, 3001–3013. [Google Scholar] [CrossRef]
- Nie, F.; Huang, H.; Cai, X.; Ding, C.H.Q. Efficient and robust feature selection via joint ℓ2,1-norms minimization. Adv. Neural Inf. Process. Syst. 2010, 23, 1813–1821. Available online: https://proceedings.neurips.cc/paper/2010/file/09c6c3783b4a70054da74f2538ed47c6-Paper.pdf (accessed on 25 May 2025).
- Shang, R.; Zhang, Z.; Jiao, L.; Liu, C.; Li, Y. Self-representation based dual-graph regularized feature selection clustering. Neurocomputing 2016, 171, 1242–1253. [Google Scholar] [CrossRef]
- Shang, R.; Wang, W.; Stolkin, R.; Jiao, L. Non-negative spectral learning and sparse regression-based dual-graph regularized feature selection. IEEE Trans. Cybern. 2018, 48, 793–806. [Google Scholar] [CrossRef]
- Yang, X.; Cao, C.; Zhou, K.; Peng, S.; Wang, Z.; Lin, L.; Nie, F. A novel linear discriminant analysis based on alternate ratio sum minimization. Inf. Sci. 2025, 689, 121444. [Google Scholar] [CrossRef]
- Wold, S.; Esbensen, K.; Geladi, P. Principal component analysis. Chemom. Intell. Lab. Syst. 1987, 2, 37–52. [Google Scholar] [CrossRef]
- Hu, Z.; Pan, G.; Wang, Y.; Wu, Z. Sparse principal component analysis via rotation and truncation. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 875–890. [Google Scholar] [CrossRef]
- Yata, K.; Aoshima, M. Effective PCA for high-dimension, low-sample-size data with noise reduction via geometric representations. J. Multivar. Anal. 2011, 105, 193–215. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, Y.; Levine, M.D.; Li, X. Multisensor video fusion based on higher order singular value decomposition. Inf. Fusion 2015, 24, 54–71. [Google Scholar] [CrossRef]
- Lee, D.D.; Seung, H.S. Learning the parts of objects by non-negative matrix factorization. Nature 1999, 401, 788–791. [Google Scholar] [CrossRef] [PubMed]
- Kriebel, A.R.; Welch, J.D. UINMF performs mosaic integration of single-cell multi-omic datasets using nonnegative matrix factorization. Nat. Commun. 2022, 13, 780. [Google Scholar] [CrossRef] [PubMed]
- Lu, H.; Sang, X.; Zhao, Q.; Lu, J. Community detection algorithm based on nonnegative matrix factorization and pairwise constraints. Phys. A Stat. Mech. Appl. 2020, 545, 123491. [Google Scholar] [CrossRef]
- Fan, D.; Zhang, X.; Kang, W.; Zhao, H.; Lv, Y. Video watermarking algorithm based on NSCT, pseudo 3D-DCT and NMF. Sensors 2022, 22, 4752. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Z.; Ke, Z.; Gou, Z.; Guo, H.; Jiang, K.; Zhang, R. The trade-off between topology and content in community detection: An adaptive encoder-decoder-based NMF approach. Expert Syst. Appl. 2022, 209, 118230. [Google Scholar] [CrossRef]
- Kwon, K.; Shin, J.W.; Kim, N.S. NMF-based speech enhancement using bases update. IEEE Signal Process. Lett. 2015, 22, 450–454. [Google Scholar] [CrossRef]
- Ding, C.; Li, T.; Peng, W.; Park, H. Orthogonal nonnegative matrix t-factorizations for clustering. In Proceedings of the 12th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 20–23 August 2006; pp. 126–135. [Google Scholar] [CrossRef]
- Kong, D.; Ding, C.; Huang, H. Robust nonnegative matrix factorization using L21-norm. In Proceedings of the 20th ACM International Conference on Information and Knowledge Management, New York, NY, USA, 24–28 October 2011; pp. 673–682. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, H.; Pei, J. Deep Non-Negative Matrix Factorization Architecture based on Underlying Basis Images Learning. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 1897–1913. [Google Scholar] [CrossRef]
- Hajiveiseh, A.; Seyedi, S.A.; Akhlaghian, T.F. Deep asymmetric nonnegative matrix factorization for graph clustering. Pattern Recogn. 2024, 148, 110179. [Google Scholar] [CrossRef]
- Roweis, S.T.; Saul, L.K. Nonlinear dimensionality reduction by locally linear embedding. Science 2000, 290, 2323–2326. [Google Scholar] [CrossRef]
- Belkin, M.; Niyogi, P. Laplacian eigenmaps and spectral techniques for embedding and clustering. Adv. Neural Inf. Process. Syst. 2001, 14, 585–591. Available online: https://dl.acm.org/doi/10.5555/2980539.2980616 (accessed on 7 July 2025).
- Balasubramanian, M.; Schwartz, E.L. The Isomap algorithm and topological stability. Science 2002, 295, 7. [Google Scholar] [CrossRef] [PubMed]
- Dhanjal, C.; Gaudel, R.; Clémençon, S. Efficient eigen-updating for spectral graph clustering. Neurocomputing 2014, 131, 440–452. [Google Scholar] [CrossRef]
- Cai, D.; He, X.; Han, J.; Huang, T.S. Graph regularized nonnegative matrix factorization for data representation. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 33, 1548–1560. [Google Scholar] [CrossRef]
- Wan, M.; Cai, M.; Yang, G. Robust exponential graph regularization non-negative matrix factorization technology for feature extraction. Mathematics 2023, 11, 1716. [Google Scholar] [CrossRef]
- Chen, Y.; Qu, G.; Zhao, J. Orthogonal graph regularized non-negative matrix factorization under sparse constraints for clustering. Expert Syst. Appl. 2024, 249, 123797. [Google Scholar] [CrossRef]
- Shang, F.; Jiao, L.C.; Wang, F. Graph dual regularization non-negative matrix factorization for co-clustering. Pattern Recogn. 2012, 45, 2237–2250. [Google Scholar] [CrossRef]
- Meng, Y.; Shang, R.; Jiao, L.; Zhang, W.; Yang, S. Dual-graph regularized non-negative matrix factorization with sparse and orthogonal constraints. Eng. Appl. Artif. Intell. 2018, 69, 24–35. [Google Scholar] [CrossRef]
- Huang, S.; Xu, Z.; Kang, Z.; Ren, Y. Regularized nonnegative matrix factorization with adaptive local structure learning. Neurocomputing 2020, 382, 196–209. [Google Scholar] [CrossRef]
- Ma, Z.; Wang, J.; Li, H.; Huang, Y. Adaptive graph regularized non-negative matrix factorization with self-weighted learning for data clustering. Appl. Intell. 2023, 53, 28054–28073. [Google Scholar] [CrossRef]
- Tang, J.; Qu, M.; Wang, M.; Zhang, M.; Yan, J.; Mei, Q. LINE: Large-scale information network embedding. In Proceedings of the 24th International Conference on World Wide Web, Florence, Italy, 18–22 May 2015; pp. 1067–1077. [Google Scholar] [CrossRef]
- Bu, X.; Wang, G.; Hou, X. Motif-based mix-order nonnegative matrix factorization for community detection. Phys. A Stat. Mech. Appl. 2025, 661, 130350. [Google Scholar] [CrossRef]
- Defferrard, M.; Bresson, X.; Vandergheynst, P. Convolutional neural networks on graphs with fast localized spectral filtering. Adv. Neural Inf. Process. Syst. 2016, 29, 3844–3852. [Google Scholar] [CrossRef]
- Huang, Q.; Yin, X.; Chen, S.; Wang, Y.; Chen, B. Robust nonnegative matrix factorization with structure regularization. Neurocomputing 2020, 412, 72–90. [Google Scholar] [CrossRef]
- Zhang, D.; He, J.; Zhao, Y.; Luo, Z.; Du, M. Global plus local: A complete framework for feature extraction and recognition. Pattern Recogn. 2014, 47, 1433–1442. [Google Scholar] [CrossRef]
- de Silva, V.; Tenenbaum, J.B. Global versus local methods in nonlinear dimensionality reduction. Adv. Neural Inf. Process. Syst. 2002, 15, 721–728. Available online: https://dl.acm.org/doi/10.5555/2968618.2968708 (accessed on 7 July 2025).
- Zhou, N.; Xu, Y.; Cheng, H.; Fang, J.; Pedrycz, W. Global and local structure preserving sparse subspace learning: An iterative approach to unsupervised feature selection. Pattern Recogn. 2016, 53, 87–101. [Google Scholar] [CrossRef]
- Chen, J.; Ye, J.; Li, Q. Integrating global and local structures: A least squares framework for dimensionality reduction. In Proceedings of the 2007 IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007; pp. 1–8. [Google Scholar] [CrossRef]
- Liu, X.; Wang, L.; Zhang, J.; Yin, J.; Liu, H. Global and local structure preservation for feature selection. IEEE Trans. Neural Netw. Learn. Syst. 2014, 25, 1083–1095. [Google Scholar] [CrossRef]
- Yang, Q.; Yin, X.; Kou, S.; Wang, Y. Robust structured convex nonnegative matrix factorization for data representation. IEEE Access 2021, 9, 155087–155102. [Google Scholar] [CrossRef]
- Sun, B.J.; Shen, H.; Gao, J.; Ouyang, W.; Cheng, X. A Non-negative symmetric encoder-decoder approach for community detection. In Proceedings of the 2017 ACM Conference on Information and Knowledge Management, New York, NY, USA, 6–10 November 2017; pp. 597–606. Available online: https://dl.acm.org/doi/10.1145/3132847.3132902 (accessed on 7 July 2025).
- Wang, H.; Nie, F.; Huang, H. Globally and locally consistent unsupervised projection. In Proceedings of the Twenty-Eighth AAAI Conference on Artificial Intelligence, Québec City, QC, Canada, 27–31 July 2014; pp. 1328–1333. Available online: https://dl.acm.org/doi/10.5555/2893873.2894079 (accessed on 7 July 2025).
- Vishwanathan, S.V.N.; Schraudolph, N.N.; Kondor, R.; Borgwardt, K.M. Graph kernels. J. Mach. Learn. Res. 2010, 11, 1201–1242. Available online: https://jmlr.csail.mit.edu/papers/volume11/vishwanathan10a/vishwanathan10a.pdf (accessed on 13 May 2025).
- Xu, L.; Niu, X.; Xie, J.; Abel, A.; Luo, B. A local-global mixed kernel with reproducing property. Neurocomputing 2015, 168, 190–199. [Google Scholar] [CrossRef]
- Li, Z.; Wu, X.; Peng, H. Nonnegative matrix factorization on orthogonal subspace. Pattern Recogn. Lett. 2010, 31, 905–911. [Google Scholar] [CrossRef]
- Cai, D.; He, X.; Han, J. Locally consistent concept factorization for document clustering. IEEE Trans. Knowl. Data Eng. 2011, 23, 902–913. [Google Scholar] [CrossRef]
- Yang, S.; Hou, C.; Zhang, C.; Wu, Y.; Weng, S. Robust non-negative matrix factorization via joint sparse and graph regularization. In Proceedings of the 2013 International Joint Conference on Neural Networks (IJCNN), Dallas, TX, USA, 4–9 August 2013; pp. 1–5. [Google Scholar] [CrossRef]
- Peng, C.; Zhang, Y.; Chen, Y.; Kang, Z.; Chen, C.; Cheng, Q. Log-based sparse nonnegative matrix factorization for data representation. Knowl.-Based Syst. 2022, 251, 109127. [Google Scholar] [CrossRef]
- Xu, W.; Gong, Y. Document clustering by concept factorization. In Proceedings of the 27th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval, New York, NY, USA, 25–29 July 2004; pp. 202–209. [Google Scholar] [CrossRef]
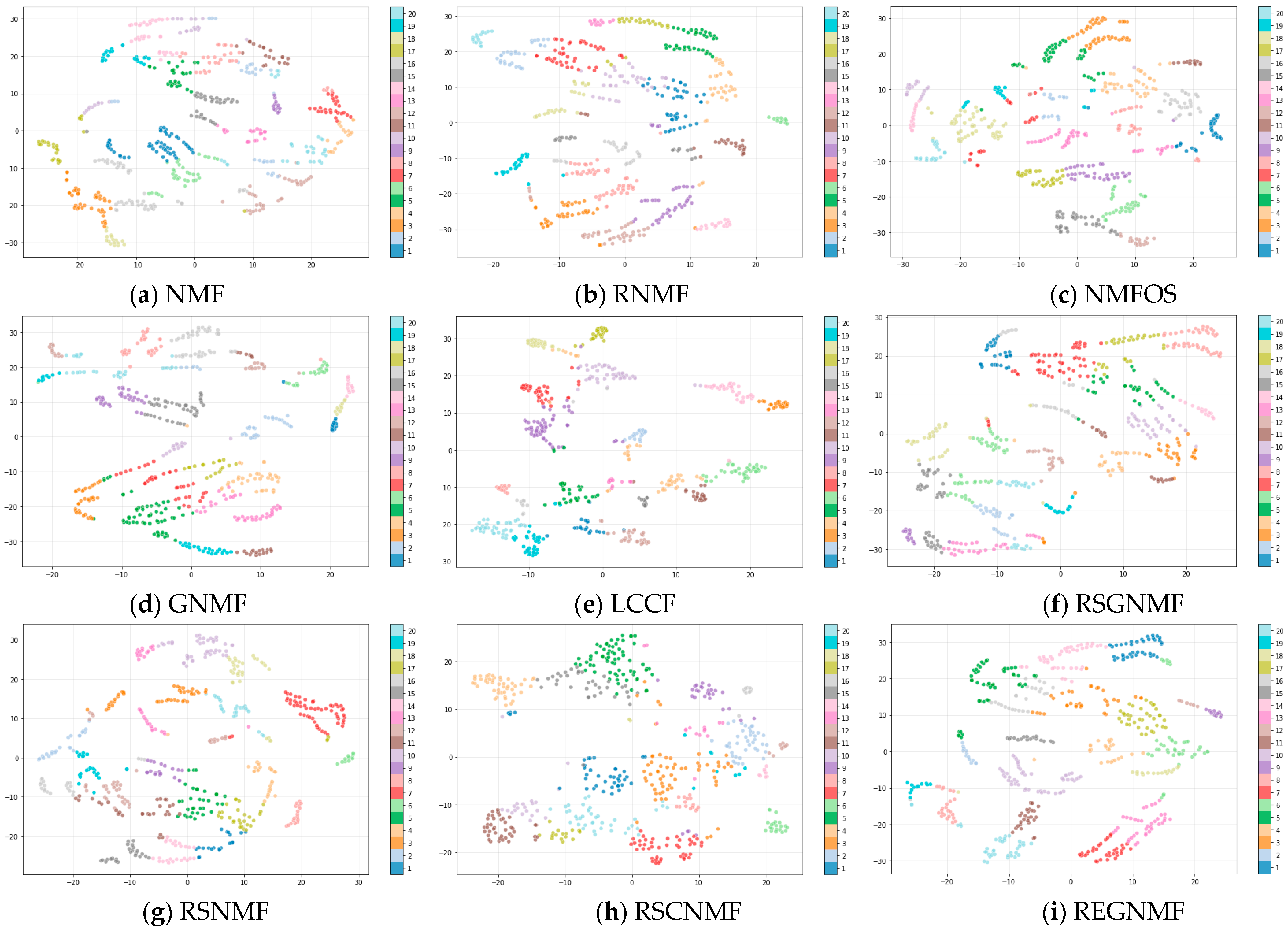
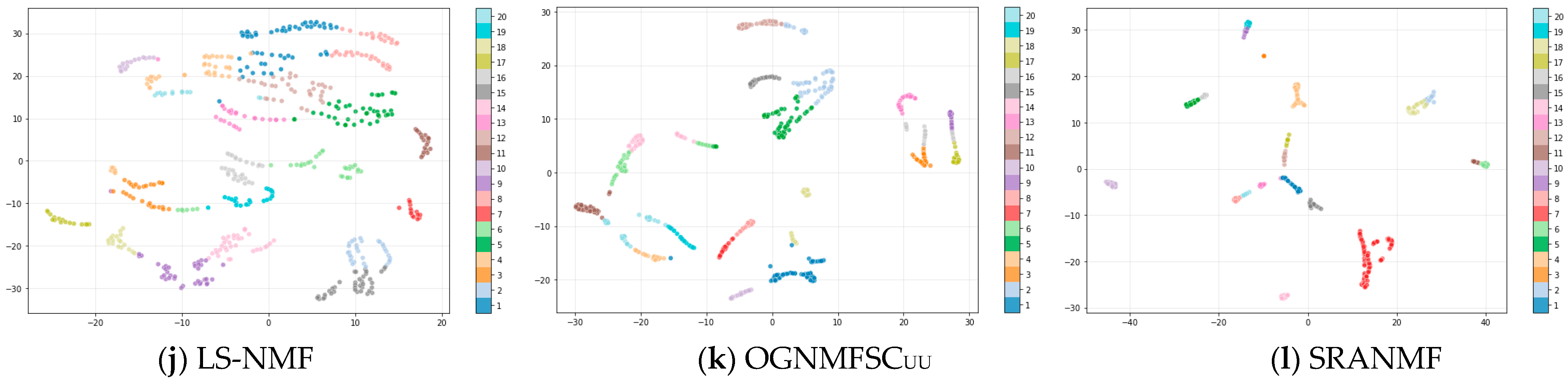
| Algorithm | Objective Function | Time Complexity |
|---|---|---|
| NMF [16] | ||
| RNMF [23] | ||
| NMFOS [51] | ||
| GNMF [30] | ||
| LCCF [52] | ||
| RSGNMF [53] | ||
| RSNMF [40] | ||
| RSCNMF [46] | ||
| REGNMF [31] | ||
| LS-NMF [54] | ||
| OGNMFSCUU [32] | ||
| SRANMF |
| No. | Dataset | Samples () | Features () | Classes () | Data Type | Image Size |
|---|---|---|---|---|---|---|
| 1 | Semeion | 1593 | 256 | 10 | digital images | 16 × 16 |
| 2 | MINIST2k2k | 4000 | 784 | 10 | digital images | 28 × 28 |
| 3 | Mnist05 | 3456 | 784 | 10 | digital images | 28 × 28 |
| 4 | MNIST | 10,000 | 784 | 10 | digital images | 28 × 28 |
| 5 | COIL20 | 1440 | 1024 | 20 | object images | 32 × 32 |
| 6 | COIL100 | 7200 | 1024 | 100 | object images | 32 × 32 |
| 7 | FERET32x32 | 1400 | 1024 | 200 | facial images | 32 × 32 |
| 8 | UMIST | 574 | 10,304 | 20 | facial images | 112 × 92 |
| 9 | Cacmcisi | 4663 | 348 | 2 | document data | —— |
| 10 | MM | 2521 | 2770 | 2 | medical data | —— |
| 11 | Wdbc | 569 | 30 | 2 | medical data | —— |
| No. | Algorithm | Parameter Settings |
|---|---|---|
| 1 2 3 4 5 6 7 8 9 | NMFOS GNMF LCCF RSGNMF RSNMF RSCNMF REGNMF LS-NMF OGNMFSCUU | , , , |
| No. | Dataset | High-Order Graph Regularization Parameter | Global Regularization Parameter |
|---|---|---|---|
| 1 | Semeion | 0.1 | 0.1 |
| 2 | MINIST2k2k | 1 | 1 |
| 3 | Mnist05 | 1 | 1 |
| 4 | MNIST | 1 | 1 |
| 5 | COIL20 | 100 | 1 |
| 6 | COIL100 | 1000 | 1 |
| 7 | FERET32x32 | 0.01 | 1 |
| 8 | UMIST | 100 | 0.001 |
| 9 | Cacmcisi | 1 | 1 |
| 10 | MM | 1000 | 0.001 |
| 11 | Wdbc | 100 | 1 |
| Algorithm | NMF | RNMF | NMFOS | GNMF | LCCF | RSGNMF | RSNMF | RSCNMF | REGNMF | LS-NMF | OGNMFSCUU | SRANMF | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dataset | |||||||||||||
| Semeion | 0.52508 | 0.51689 | 0.53468 | 0.59209 | 0.50816 | 0.53007 | 0.52389 | 0.49981 | 0.52750 | 0.60251 | 0.64338 | 0.67731 | |
| ±0.042 | ±0.046 | ±0.042 | ±0.039 | ±0.026 | ±0.039 | ±0.039 | ±0.046 | ±0.037 | ±0.036 | ±0.029 | ±0.049 | ||
| MINIST2k2k | 0.47441 | 0.47614 | 0.48335 | 0.48682 | 0.49207 | 0.46906 | 0.48636 | 0.49280 | 0.47147 | 0.49959 | 0.53143 | 0.57064 | |
| ±0.029 | ±0.024 | ±0.030 | ±0.032 | ±0.027 | ±0.026 | ±0.031 | ±0.035 | ±0.031 | ±0.029 | ±0.020 | ±0.026 | ||
| Mnist05 | 0.50767 | 0.48163 | 0.50441 | 0.52149 | 0.48981 | 0.49249 | 0.52079 | 0.48921 | 0.48256 | 0.50409 | 0.57815 | 0.60220 | |
| ±0.037 | ±0.025 | ±0.043 | ±0.035 | ±0.029 | ±0.028 | ±0.033 | ±0.034 | ±0.036 | ±0.037 | ±0.018 | ±0.049 | ||
| MNIST | 0.48954 | 0.49022 | 0.49428 | 0.50656 | 0.49208 | 0.47894 | 0.49930 | 0.48975 | 0.48264 | 0.51778 | 0.56602 | 0.67741 | |
| ±0.041 | ±0.037 | ±0.030 | ±0.037 | ±0.032 | ±0.040 | ±0.035 | ±0.032 | ±0.027 | ±0.033 | ±0.027 | ±0.014 | ||
| COIL20 | 0.66406 | 0.65580 | 0.65899 | 0.76844 | 0.57007 | 0.64837 | 0.64073 | 0.52306 | 0.64201 | 0.77361 | 0.73840 | 0.80635 | |
| ±0.029 | ±0.021 | ±0.024 | ±0.013 | ±0.032 | ±0.019 | ±0.029 | ±0.034 | ±0.027 | ±0.014 | ±0.020 | ±0.011 | ||
| COIL100 | 0.47026 | 0.46956 | 0.46760 | 0.48738 | 0.37091 | 0.48122 | 0.46568 | 0.33536 | 0.46773 | 0.48306 | 0.56282 | 0.67259 | |
| ±0.014 | ±0.012 | ±0.017 | ±0.014 | ±0.012 | ±0.012 | ±0.013 | ±0.008 | ±0.010 | ±0.011 | ±0.014 | ±0.006 | ||
| FERET32x32 | 0.22179 | 0.22718 | 0.22893 | 0.24836 | 0.17682 | 0.23218 | 0.21832 | 0.15704 | 0.19607 | 0.24643 | 0.25729 | 0.27275 | |
| ±0.008 | ±0.005 | ±0.009 | ±0.007 | ±0.006 | ±0.007 | ±0.009 | ±0.004 | ±0.008 | ±0.005 | ±0.004 | ±0.005 | ||
| UMIST | 0.41237 | 0.41437 | 0.40976 | 0.45305 | 0.35200 | 0.42003 | 0.40549 | 0.29739 | 0.41211 | 0.46873 | 0.49826 | 0.69582 | |
| ±0.021 | ±0.030 | ±0.020 | ±0.027 | ±0.027 | ±0.032 | ±0.020 | ±0.019 | ±0.021 | ±0.024 | ±0.015 | ±0.029 | ||
| Cacmcisi | 0.92123 | 0.71477 | 0.92084 | 0.92807 | 0.92398 | 0.76114 | 0.90915 | 0.91891 | 0.92283 | 0.92845 | 0.95588 | 0.96333 | |
| ±0.002 | ±0.188 | ±0.002 | ±0.000 | ±0.001 | ±0.186 | ±0.002 | ±0.001 | ±0.000 | ±0.001 | ±0.000 | ±0.000 | ||
| MM | 0.55002 | 0.53550 | 0.54988 | 0.54946 | 0.55655 | 0.54127 | 0.55335 | 0.55242 | 0.54681 | 0.54978 | 0.54127 | 0.56035 | |
| ±0.001 | ±0.001 | ±0.000 | ±0.001 | ±0.002 | ±0.011 | ±0.000 | ±0.001 | ±0.000 | ±0.001 | ±0.000 | ±0.001 | ||
| Wdbc | 0.83691 | 0.82900 | 0.83155 | 0.85018 | 0.79244 | 0.81503 | 0.83910 | 0.82109 | 0.83199 | 0.85185 | 0.85413 | 0.86265 | |
| ±0.017 | ±0.020 | ±0.018 | ±0.010 | ±0.030 | ±0.055 | ±0.014 | ±0.038 | ±0.020 | ±0.005 | ±0.000 | ±0.014 | ||
| Algorithm | NMF | RNMF | NMFOS | GNMF | LCCF | RSGNMF | RSNMF | RSCNMF | REGNMF | LS-NMF | OGNMFSCUU | SRANMF | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dataset | |||||||||||||
| Semeion | 0.31198 | 0.31115 | 0.32481 | 0.44280 | 0.31331 | 0.30996 | 0.31065 | 0.30474 | 0.31534 | 0.45921 | 0.46386 | 0.48390 | |
| ±0.033 | ±0.036 | ±0.031 | ±0.032 | ±0.024 | ±0.026 | ±0.028 | ±0.032 | ±0.028 | ±0.030 | ±0.024 | ±0.032 | ||
| MINIST2k2k | 0.28175 | 0.28836 | 0.28610 | 0.28769 | 0.29241 | 0.28330 | 0.28232 | 0.29412 | 0.28620 | 0.30038 | 0.39003 | 0.44064 | |
| ±0.021 | ±0.017 | ±0.020 | ±0.026 | ±0.021 | ±0.020 | ±0.027 | ±0.026 | ±0.033 | ±0.026 | ±0.017 | ±0.018 | ||
| Mnist05 | 0.32251 | 0.30375 | 0.31815 | 0.33543 | 0.30258 | 0.31378 | 0.33353 | 0.30917 | 0.30604 | 0.32201 | 0.44382 | 0.49691 | |
| ±0.030 | ±0.025 | ±0.034 | ±0.031 | ±0.021 | ±0.021 | ±0.027 | ±0.025 | ±0.029 | ±0.032 | ±0.014 | ±0.033 | ||
| MNIST | 0.31179 | 0.31967 | 0.31243 | 0.32744 | 0.31112 | 0.30683 | 0.31280 | 0.31508 | 0.30051 | 0.33000 | 0.43883 | 0.55214 | |
| ±0.034 | ±0.026 | ±0.024 | ±0.032 | ±0.026 | ±0.028 | ±0.026 | ±0.020 | ±0.021 | ±0.030 | ±0.021 | ±0.017 | ||
| COIL20 | 0.57989 | 0.57112 | 0.57747 | 0.74160 | 0.47552 | 0.56733 | 0.56748 | 0.42036 | 0.54933 | 0.74234 | 0.68559 | 0.79164 | |
| ±0.026 | ±0.022 | ±0.026 | ±0.018 | ±0.044 | ±0.025 | ±0.027 | ±0.046 | ±0.030 | ±0.016 | ±0.025 | ±0.005 | ||
| COIL100 | 0.39584 | 0.39826 | 0.39660 | 0.42371 | 0.27039 | 0.41219 | 0.39125 | 0.25018 | 0.39593 | 0.42067 | 0.51003 | 0.58611 | |
| ±0.016 | ±0.017 | ±0.015 | ±0.010 | ±0.011 | ±0.012 | ±0.017 | ±0.007 | ±0.012 | ±0.011 | ±0.015 | ±0.010 | ||
| FERET32x32 | 0.04401 | 0.04660 | 0.04781 | 0.06384 | 0.02522 | 0.05020 | 0.04254 | 0.02899 | 0.02787 | 0.06205 | 0.08086 | 0.08725 | |
| ±0.004 | ±0.003 | ±0.005 | ±0.005 | ±0.002 | ±0.004 | ±0.005 | ±0.002 | ±0.005 | ±0.003 | ±0.005 | ±0.004 | ||
| UMIST | 0.30261 | 0.30727 | 0.29932 | 0.35447 | 0.23552 | 0.31102 | 0.30157 | 0.15479 | 0.30378 | 0.38209 | 0.42214 | 0.62554 | |
| ±0.027 | ±0.025 | ±0.020 | ±0.024 | ±0.022 | ±0.032 | ±0.016 | ±0.014 | ±0.022 | ±0.024 | ±0.020 | ±0.043 | ||
| Cacmcisi | 0.69786 | 0.29290 | 0.69647 | 0.72263 | 0.70777 | 0.38237 | 0.65468 | 0.68946 | 0.70362 | 0.72400 | 0.82614 | 0.85478 | |
| ±0.007 | ±0.370 | ±0.007 | ±0.002 | ±0.002 | ±0.380 | ±0.006 | ±0.004 | ±0.002 | ±0.003 | ±0.000 | ±0.000 | ||
| MM | 0.00877 | 0.00445 | 0.00872 | 0.00860 | 0.01148 | 0.00616 | 0.00453 | 0.00345 | 0.00752 | 0.00872 | 0.00628 | 0.01417 | |
| ±0.000 | ±0.000 | ±0.000 | ±0.000 | ±0.001 | ±0.004 | ±0.000 | ±0.000 | ±0.000 | ±0.000 | ±0.000 | ±0.000 | ||
| Wdbc | 0.44231 | 0.42038 | 0.42726 | 0.48003 | 0.32577 | 0.39148 | 0.44818 | 0.40243 | 0.42882 | 0.48474 | 0.49142 | 0.51770 | |
| ±0.049 | ±0.055 | ±0.050 | ±0.027 | ±0.078 | ±0.127 | ±0.039 | ±0.099 | ±0.057 | ±0.015 | ±0.000 | ±0.044 | ||
| Algorithm | NMF | RNMF | NMFOS | GNMF | LCCF | RSGNMF | RSNMF | RSCNMF | REGNMF | LS-NMF | OGNMFSCUU | SRANMF | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dataset | |||||||||||||
| Semeion | 0.44162 | 0.44651 | 0.45468 | 0.60790 | 0.45777 | 0.44481 | 0.43992 | 0.45009 | 0.44840 | 0.61489 | 0.62644 | 0.62877 | |
| ±0.025 | ±0.026 | ±0.026 | ±0.020 | ±0.020 | ±0.019 | ±0.021 | ±0.025 | ±0.024 | ±0.019 | ±0.017 | ±0.021 | ||
| MINIST2k2k | 0.40656 | 0.41862 | 0.41075 | 0.41189 | 0.41648 | 0.41567 | 0.40709 | 0.41451 | 0.40768 | 0.42141 | 0.54270 | 0.59725 | |
| ±0.017 | ±0.014 | ±0.013 | ±0.017 | ±0.013 | ±0.017 | ±0.018 | ±0.018 | ±0.022 | ±0.018 | ±0.013 | ±0.009 | ||
| Mnist05 | 0.45080 | 0.43860 | 0.44642 | 0.45790 | 0.43636 | 0.45104 | 0.45181 | 0.43855 | 0.43734 | 0.45000 | 0.59544 | 0.64639 | |
| ±0.019 | ±0.017 | ±0.022 | ±0.021 | ±0.016 | ±0.015 | ±0.019 | ±0.016 | ±0.018 | ±0.022 | ±0.008 | ±0.014 | ||
| MNIST | 0.44170 | 0.44946 | 0.44775 | 0.44919 | 0.44704 | 0.44273 | 0.44561 | 0.43990 | 0.44546 | 0.45253 | 0.61365 | 0.67878 | |
| ±0.024 | ±0.019 | ±0.017 | ±0.020 | ±0.017 | ±0.015 | ±0.019 | ±0.017 | ±0.014 | ±0.018 | ±0.015 | ±0.008 | ||
| COIL20 | 0.76112 | 0.75568 | 0.76032 | 0.88538 | 0.71457 | 0.75895 | 0.75744 | 0.67284 | 0.74549 | 0.88500 | 0.83716 | 0.91358 | |
| ±0.015 | ±0.015 | ±0.016 | ±0.012 | ±0.023 | ±0.015 | ±0.013 | ±0.019 | ±0.018 | ±0.012 | ±0.011 | ±0.004 | ||
| COIL100 | 0.75258 | 0.75202 | 0.75254 | 0.77226 | 0.65453 | 0.76190 | 0.74876 | 0.62179 | 0.75026 | 0.76948 | 0.81406 | 0.87500 | |
| ±0.005 | ±0.005 | ±0.006 | ±0.004 | ±0.005 | ±0.004 | ±0.006 | ±0.004 | ±0.006 | ±0.004 | ±0.004 | ±0.002 | ||
| FERET32x32 | 0.63555 | 0.63873 | 0.63933 | 0.65960 | 0.60544 | 0.64465 | 0.63357 | 0.57718 | 0.59621 | 0.65779 | 0.68067 | 0.68669 | |
| ±0.005 | ±0.004 | ±0.005 | ±0.005 | ±0.003 | ±0.004 | ±0.006 | ±0.005 | ±0.011 | ±0.003 | ±0.003 | ±0.003 | ||
| UMIST | 0.60961 | 0.61241 | 0.60529 | 0.66424 | 0.54408 | 0.61349 | 0.61245 | 0.43449 | 0.61052 | 0.68920 | 0.72371 | 0.85604 | |
| ±0.023 | ±0.018 | ±0.018 | ±0.019 | ±0.019 | ±0.026 | ±0.013 | ±0.014 | ±0.015 | ±0.020 | ±0.015 | ±0.011 | ||
| Cacmcisi | 0.62746 | 0.29794 | 0.62629 | 0.64954 | 0.63582 | 0.36815 | 0.59267 | 0.62345 | 0.63203 | 0.65081 | 0.75056 | 0.77371 | |
| ±0.005 | ±0.298 | ±0.005 | ±0.002 | ±0.002 | ±0.309 | ±0.005 | ±0.003 | ±0.001 | ±0.003 | ±0.000 | ±0.001 | ||
| MM | 0.00407 | 0.00240 | 0.00404 | 0.00402 | 0.00562 | 0.00466 | 0.00178 | 0.00134 | 0.00336 | 0.00408 | 0.00370 | 0.01129 | |
| ±0.000 | ±0.000 | ±0.000 | ±0.000 | ±0.000 | ±0.005 | ±0.000 | ±0.000 | ±0.000 | ±0.000 | ±0.000 | ±0.000 | ||
| Wdbc | 0.43565 | 0.41728 | 0.42400 | 0.45869 | 0.32797 | 0.39097 | 0.44086 | 0.39742 | 0.42454 | 0.46097 | 0.46479 | 0.48198 | |
| ±0.034 | ±0.037 | ±0.034 | ±0.017 | ±0.067 | ±0.112 | ±0.027 | ±0.079 | ±0.038 | ±0.008 | ±0.000 | ±0.026 | ||
| Algorithm | NMF | RNMF | NMFOS | GNMF | LCCF | RSGNMF | RSNMF | RSCNMF | REGNMF | LS-NMF | OGNMFSCUU | SRANMF | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dataset | |||||||||||||
| Semeion | 0.53763 | 0.54105 | 0.55348 | 0.63726 | 0.54630 | 0.54196 | 0.53901 | 0.53205 | 0.54736 | 0.64369 | 0.67891 | 0.69557 | |
| ±0.036 | ±0.039 | ±0.034 | ±0.024 | ±0.029 | ±0.030 | ±0.030 | ±0.036 | ±0.030 | ±0.026 | ±0.018 | ±0.031 | ||
| MINIST2k2k | 0.50405 | 0.51511 | 0.51528 | 0.51387 | 0.52058 | 0.51035 | 0.51220 | 0.51877 | 0.50526 | 0.53059 | 0.60062 | 0.63686 | |
| ±0.023 | ±0.022 | ±0.021 | ±0.028 | ±0.021 | ±0.027 | ±0.027 | ±0.026 | ±0.026 | ±0.024 | ±0.019 | ±0.010 | ||
| Mnist05 | 0.54471 | 0.52665 | 0.53150 | 0.56143 | 0.53069 | 0.53652 | 0.55368 | 0.53330 | 0.52671 | 0.54459 | 0.64442 | 0.67309 | |
| ±0.027 | ±0.024 | ±0.037 | ±0.029 | ±0.024 | ±0.027 | ±0.026 | ±0.026 | ±0.031 | ±0.031 | ±0.011 | ±0.026 | ||
| MNIST | 0.53619 | 0.54132 | 0.54647 | 0.54922 | 0.54581 | 0.52648 | 0.54712 | 0.53659 | 0.53060 | 0.55174 | 0.63465 | 0.72875 | |
| ±0.033 | ±0.037 | ±0.023 | ±0.028 | ±0.020 | ±0.033 | ±0.030 | ±0.025 | ±0.018 | ±0.024 | ±0.018 | ±0.014 | ||
| COIL20 | 0.69135 | 0.68611 | 0.68715 | 0.80715 | 0.61108 | 0.68868 | 0.67403 | 0.56611 | 0.67573 | 0.80892 | 0.76146 | 0.84170 | |
| ±0.024 | ±0.022 | ±0.019 | ±0.017 | ±0.025 | ±0.014 | ±0.023 | ±0.029 | ±0.022 | ±0.018 | ±0.018 | ±0.007 | ||
| COIL100 | 0.52663 | 0.52756 | 0.52577 | 0.54654 | 0.41641 | 0.53986 | 0.52115 | 0.37838 | 0.52601 | 0.54247 | 0.61974 | 0.72546 | |
| ±0.013 | ±0.010 | ±0.014 | ±0.012 | ±0.010 | ±0.009 | ±0.012 | ±0.007 | ±0.009 | ±0.009 | ±0.011 | ±0.005 | ||
| FERET32x32 | 0.26336 | 0.26850 | 0.26939 | 0.28632 | 0.20929 | 0.27068 | 0.25904 | 0.20604 | 0.25200 | 0.28450 | 0.28507 | 0.30418 | |
| ±0.008 | ±0.005 | ±0.008 | ±0.007 | ±0.004 | ±0.006 | ±0.008 | ±0.003 | ±0.006 | ±0.005 | ±0.005 | ±0.004 | ||
| UMIST | 0.47936 | 0.48929 | 0.47840 | 0.52831 | 0.42491 | 0.49242 | 0.47465 | 0.34303 | 0.48310 | 0.54861 | 0.58362 | 0.76768 | |
| ±0.029 | ±0.024 | ±0.019 | ±0.029 | ±0.028 | ±0.033 | ±0.018 | ±0.021 | ±0.021 | ±0.024 | ±0.017 | ±0.013 | ||
| Cacmcisi | 0.92123 | 0.79283 | 0.92084 | 0.92807 | 0.92398 | 0.81982 | 0.90915 | 0.91891 | 0.92283 | 0.92845 | 0.95588 | 0.96333 | |
| ±0.002 | ±0.117 | ±0.002 | ±0.000 | ±0.001 | ±0.121 | ±0.002 | ±0.001 | ±0.000 | ±0.001 | ±0.000 | ±0.000 | ||
| MM | 0.55063 | 0.55058 | 0.55060 | 0.55058 | 0.55655 | 0.55246 | 0.55335 | 0.55242 | 0.55058 | 0.55058 | 0.55058 | 0.56035 | |
| ±0.000 | ±0.000 | ±0.000 | ±0.000 | ±0.002 | ±0.005 | ±0.000 | ±0.001 | ±0.000 | ±0.000 | ±0.000 | ±0.001 | ||
| Wdbc | 0.83691 | 0.82900 | 0.83155 | 0.85018 | 0.79244 | 0.81511 | 0.83910 | 0.82109 | 0.83199 | 0.85185 | 0.85413 | 0.86265 | |
| ±0.017 | ±0.020 | ±0.018 | ±0.010 | ±0.030 | ±0.055 | ±0.014 | ±0.038 | ±0.020 | ±0.005 | ±0.000 | ±0.014 | ||
| No. | High-Order Graph Regularization | Global Structure Regularization | Objective Function After SRANMF Degradation | Algorithm Name |
|---|---|---|---|---|
| 1 | SRANMF-1 | |||
| 2 | SRANMF-2 | |||
| 3 | SRANMF-3 | |||
| 4 | SRANMF-4 | |||
| 5 | SRANMF-5 | |||
| 6 | SRANMF |
| Dataset | ACC | ARI | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SRANMF-1 | SRANMF-2 | SRANMF-3 | SRANMF-4 | SRANMF-5 | SRANMF | SRANMF-1 | SRANMF-2 | SRANMF-3 | SRANMF-4 | SRANMF-5 | SRANMF | |
| Semeion | 0.60835 | 0.60524 | 0.67053 | 0.52687 | 0.62746 | 0.67731 | 0.39076 | 0.39191 | 0.47604 | 0.32052 | 0.41245 | 0.48390 |
| ±0.034 | ±0.038 | ±0.047 | ±0.038 | ±0.036 | ±0.049 | ±0.022 | ±0.030 | ±0.031 | ±0.032 | ±0.029 | ±0.032 | |
| MINIST2k2k | 0.46061 | 0.45415 | 0.54909 | 0.47605 | 0.55394 | 0.57064 | 0.27347 | 0.26693 | 0.40452 | 0.28133 | 0.39323 | 0.44064 |
| ±0.018 | ±0.026 | ±0.024 | ±0.032 | ±0.030 | ±0.026 | ±0.012 | ±0.018 | ±0.019 | ±0.022 | ±0.037 | ±0.018 | |
| Mnist05 | 0.48785 | 0.48521 | 0.58760 | 0.50010 | 0.57575 | 0.60220 | 0.30083 | 0.30044 | 0.43420 | 0.31685 | 0.43050 | 0.49691 |
| ±0.025 | ±0.023 | ±0.041 | ±0.029 | ±0.038 | ±0.049 | ±0.020 | ±0.024 | ±0.032 | ±0.027 | ±0.032 | ±0.033 | |
| MNIST | 0.47094 | 0.46072 | 0.59252 | 0.50958 | 0.56690 | 0.67741 | 0.28926 | 0.26267 | 0.45214 | 0.31191 | 0.42760 | 0.55214 |
| ±0.032 | ±0.028 | ±0.031 | ±0.022 | ±0.040 | ±0.014 | ±0.019 | ±0.023 | ±0.031 | ±0.018 | ±0.026 | ±0.017 | |
| COIL20 | 0.68090 | 0.67622 | 0.80340 | 0.78337 | 0.70521 | 0.80635 | 0.61053 | 0.60588 | 0.78861 | 0.76195 | 0.64857 | 0.79164 |
| ±0.029 | ±0.030 | ±0.007 | ±0.005 | ±0.027 | ±0.011 | ±0.027 | ±0.027 | ±0.005 | ±0.009 | ±0.022 | ±0.005 | |
| COIL100 | 0.50681 | 0.50456 | 0.66908 | 0.50236 | 0.67097 | 0.67259 | 0.45622 | 0.45413 | 0.58282 | 0.44097 | 0.56078 | 0.58611 |
| ±0.016 | ±0.011 | ±0.007 | ±0.013 | ±0.010 | ±0.006 | ±0.013 | ±0.012 | ±0.012 | ±0.015 | ±0.015 | ±0.010 | |
| FERET32x32 | 0.26493 | 0.26975 | 0.26657 | 0.22275 | 0.26307 | 0.27275 | 0.08414 | 0.08852 | 0.08518 | 0.04657 | 0.07363 | 0.08725 |
| ±0.007 | ±0.008 | ±0.004 | ±0.005 | ±0.005 | ±0.005 | ±0.005 | ±0.006 | ±0.003 | ±0.003 | ±0.003 | ±0.004 | |
| UMIST | 0.41159 | 0.41254 | 0.69207 | 0.47831 | 0.53563 | 0.69582 | 0.32193 | 0.32032 | 0.61694 | 0.39414 | 0.47203 | 0.62554 |
| ±0.014 | ±0.017 | ±0.013 | ±0.027 | ±0.035 | ±0.029 | ±0.014 | ±0.015 | ±0.020 | ±0.021 | ±0.039 | ±0.043 | |
| Cacmcisi | 0.91720 | 0.91633 | 0.95436 | 0.92163 | 0.92803 | 0.96333 | 0.68337 | 0.68024 | 0.82652 | 0.69929 | 0.72244 | 0.85478 |
| ±0.001 | ±0.000 | ±0.033 | ±0.001 | ±0.001 | ±0.000 | ±0.002 | ±0.000 | ±0.105 | ±0.005 | ±0.004 | ±0.000 | |
| MM | 0.53167 | 0.55766 | 0.55992 | 0.54994 | 0.50506 | 0.56035 | 0.00338 | 0.00706 | 0.01397 | 0.00885 | -0.00070 | 0.01417 |
| ±0.001 | ±0.001 | ±0.001 | ±0.001 | ±0.001 | ±0.001 | ±0.000 | ±0.001 | ±0.000 | ±0.000 | ±0.000 | ±0.000 | |
| Wdbc | 0.85378 | 0.85343 | 0.86125 | 0.85413 | 0.85413 | 0.86265 | 0.49039 | 0.48935 | 0.51311 | 0.49142 | 0.49142 | 0.51770 |
| ±0.001 | ±0.001 | ±0.010 | ±0.000 | ±0.000 | ±0.014 | ±0.002 | ±0.003 | ±0.031 | ±0.000 | ±0.000 | ±0.044 | |
| Dataset | NMI | PUR | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SRANMF-1 | SRANMF-2 | SRANMF-3 | SRANMF-4 | SRANMF-5 | SRANMF | SRANMF-1 | SRANMF-2 | SRANMF-3 | SRANMF-4 | SRANMF-5 | SRANMF | |
| Semeion | 0.52027 | 0.52478 | 0.62211 | 0.45363 | 0.54607 | 0.62877 | 0.62439 | 0.62370 | 0.68955 | 0.54513 | 0.64256 | 0.69557 |
| ±0.017 | ±0.027 | ±0.020 | ±0.029 | ±0.022 | ±0.021 | ±0.022 | ±0.030 | ±0.030 | ±0.032 | ±0.025 | ±0.031 | |
| MINIST2k2k | 0.39753 | 0.39269 | 0.54917 | 0.40673 | 0.53798 | 0.59725 | 0.50824 | 0.50221 | 0.59606 | 0.50564 | 0.59959 | 0.63686 |
| ±0.012 | ±0.018 | ±0.017 | ±0.017 | ±0.027 | ±0.009 | ±0.016 | ±0.023 | ±0.022 | ±0.028 | ±0.034 | ±0.010 | |
| Mnist05 | 0.43207 | 0.43001 | 0.57920 | 0.44462 | 0.58179 | 0.64639 | 0.53229 | 0.53137 | 0.61391 | 0.54468 | 0.62096 | 0.67309 |
| ±0.016 | ±0.021 | ±0.020 | ±0.017 | ±0.020 | ±0.014 | ±0.024 | ±0.026 | ±0.027 | ±0.025 | ±0.030 | ±0.026 | |
| MNIST | 0.42480 | 0.39918 | 0.61049 | 0.43955 | 0.57901 | 0.67878 | 0.52860 | 0.48230 | 0.64210 | 0.53806 | 0.62098 | 0.72875 |
| ±0.017 | ±0.015 | ±0.025 | ±0.016 | ±0.015 | ±0.008 | ±0.018 | ±0.019 | ±0.032 | ±0.018 | ±0.018 | ±0.014 | |
| COIL20 | 0.78760 | 0.78360 | 0.91201 | 0.89612 | 0.83641 | 0.91358 | 0.70972 | 0.70635 | 0.83858 | 0.82330 | 0.74885 | 0.84170 |
| ±0.012 | ±0.012 | ±0.004 | ±0.008 | ±0.009 | ±0.004 | ±0.023 | ±0.025 | ±0.004 | ±0.008 | ±0.017 | ±0.007 | |
| COIL100 | 0.77205 | 0.77055 | 0.87428 | 0.78920 | 0.86035 | 0.87500 | 0.56021 | 0.55783 | 0.72290 | 0.56563 | 0.72298 | 0.72546 |
| ±0.005 | ±0.003 | ±0.002 | ±0.005 | ±0.003 | ±0.002 | ±0.015 | ±0.008 | ±0.005 | ±0.011 | ±0.007 | ±0.005 | |
| FERET32x32 | 0.68300 | 0.68586 | 0.68403 | 0.63812 | 0.67072 | 0.68669 | 0.29789 | 0.30318 | 0.29404 | 0.26407 | 0.29579 | 0.30418 |
| ±0.003 | ±0.004 | ±0.002 | ±0.004 | ±0.002 | ±0.003 | ±0.006 | ±0.009 | ±0.004 | ±0.003 | ±0.005 | ±0.004 | |
| UMIST | 0.64102 | 0.64040 | 0.85420 | 0.70106 | 0.75839 | 0.85604 | 0.51324 | 0.50793 | 0.76134 | 0.55906 | 0.63676 | 0.76768 |
| ±0.011 | ±0.010 | ±0.009 | ±0.014 | ±0.021 | ±0.011 | ±0.013 | ±0.015 | ±0.007 | ±0.017 | ±0.028 | ±0.013 | |
| Cacmcisi | 0.61484 | 0.61280 | 0.74573 | 0.62828 | 0.65120 | 0.77371 | 0.91720 | 0.91633 | 0.95436 | 0.92163 | 0.92803 | 0.96333 |
| ±0.001 | ±0.000 | ±0.102 | ±0.004 | ±0.004 | ±0.001 | ±0.001 | ±0.000 | ±0.033 | ±0.001 | ±0.001 | ±0.000 | |
| MM | 0.00171 | 0.00331 | 0.01110 | 0.00422 | 0.00009 | 0.01129 | 0.55058 | 0.55766 | 0.55992 | 0.55075 | 0.55058 | 0.56035 |
| ±0.000 | ±0.001 | ±0.000 | ±0.000 | ±0.000 | ±0.000 | ±0.000 | ±0.001 | ±0.001 | ±0.000 | ±0.000 | ±0.001 | |
| Wdbc | 0.46398 | 0.46317 | 0.47904 | 0.46479 | 0.46479 | 0.48198 | 0.85378 | 0.85343 | 0.86125 | 0.85413 | 0.85413 | 0.86265 |
| ±0.002 | ±0.002 | ±0.017 | ±0.000 | ±0.000 | ±0.026 | ±0.001 | ±0.001 | ±0.010 | ±0.000 | ±0.000 | ±0.014 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, H.; Zhong, L. An Autoencoder-like Non-Negative Matrix Factorization with Structure Regularization Algorithm for Clustering. Symmetry 2025, 17, 1283. https://doi.org/10.3390/sym17081283
Gao H, Zhong L. An Autoencoder-like Non-Negative Matrix Factorization with Structure Regularization Algorithm for Clustering. Symmetry. 2025; 17(8):1283. https://doi.org/10.3390/sym17081283
Chicago/Turabian StyleGao, Haiyan, and Ling Zhong. 2025. "An Autoencoder-like Non-Negative Matrix Factorization with Structure Regularization Algorithm for Clustering" Symmetry 17, no. 8: 1283. https://doi.org/10.3390/sym17081283
APA StyleGao, H., & Zhong, L. (2025). An Autoencoder-like Non-Negative Matrix Factorization with Structure Regularization Algorithm for Clustering. Symmetry, 17(8), 1283. https://doi.org/10.3390/sym17081283






