Abstract
Reconfigurable Intelligent Surfaces (RISs) and Non-Orthogonal Multiple Access (NOMA) have emerged as key technologies for next-generation (6G) wireless networks, attracting significant attention from researchers. As an advanced extension of RISs, Simultaneously Transmitting and Reflecting Reconfigurable Intelligent Surfaces (STAR-RISs) offer superior geometric and functional symmetry due to their capability to simultaneously reflect and transmit signals, thereby achieving full 360° spatial coverage. This symmetry not only ensures balanced energy distribution between the Transmission (T) and Reflection (R) regions but also facilitates interference cancellation through phase alignment. Furthermore, in NOMA networks, the symmetric allocation of power coefficients and the tunable transmission and reflection coefficients of STAR-RIS elements aligns with the principle of resource fairness in multi-user systems, which is crucial for maintaining fairness under asymmetric channel conditions. In this study, key factors, such as interference sources and distance effects, are considered in order to conduct a detailed analysis of the performance of STAR-RIS-assisted NOMA wireless education networks under multiple interference devices. Specifically, a comprehensive analysis of the Signal-to-Interference-plus-Noise Ratio (SINR) for both near-end and far-end devices is conducted, considering various scenarios, such as whether or not the direct communication link exists between the base station and the near-end device, and whether or not the near-end device is affected by interference. Based on these analyses, closed-form approximate expressions for the outage probabilities of the near-end and far-end devices, as well as the closed-form approximation for the system’s Spectral Efficiency (SE), are derived. Notably, the Gamma distribution is used to approximate the square of the composite channel amplitude between the base station and the near-end device, effectively reducing computational complexity. Finally, simulation results validate the accuracy of our analytical results. Both numerical and simulation results show that adjusting the base station’s power allocation, and the transmission and reflection coefficients of the STAR-RIS, can effectively mitigate the impact of interference devices on the near-end device and enhance the communication performance of receiving devices. Additionally, increasing the number of STAR-RIS elements can effectively improve the overall performance of the near-end device, far-end device, and the entire system.
1. Introduction
Reconfigurable Intelligent Surfaces (RISs), as an emerging technology, integrate a large number of low-cost passive reflective elements on a planar surface to intelligently configure the wireless transmission environment, thereby significantly enhancing the performance of wireless networks [1,2,3,4,5]. By independently controlling the phase and amplitude, RISs enable three-dimensional beamforming to amplify desired signal power or mitigate channel interference. Moreover, their lightweight design and ease of installation allow for rapid deployment on building surfaces such as walls and ceilings without requiring modifications to existing wireless system standards or hardware [3,4,5,6]. In wireless educational device networks, RISs can optimize signal transmission efficiency and reduce power consumption. For example, by jointly designing the switching selection, phase adjustment, and power allocation of the RIS, it can reshape the electromagnetic propagation environment, thereby improving signal transmission rates and energy efficiency. In addition, Simultaneously Transmitting and Reflecting Reconfigurable Intelligent Surfaces (STAR-RISs) can be used to assist communication between multiple devices, thereby improving the overall network performance.
The concept of Simultaneously Transmitting and Reflecting Reconfigurable Intelligent Surfaces (STAR-RISs) was first introduced in [7,8]. The conventional RIS only supports signal reflection and requires that both the transmitter and the user be located on the same side, thereby imposing a half-space symmetry constraint [7]. In contrast, a STAR-RIS breaks the electromagnetic symmetry constraint by introducing magnetoelectric currents, unlike traditional RISs, which rely solely on electric field polarization [8]. This enables independent control over transmitted and reflected signals, as well as the simultaneous refraction and reflection of incident signals. Leveraging this capability, STAR-RISs overcome the limitations of full-space coverage and geographical adaptability, achieving complete 360° coverage [8]. Specifically, signals transmitted to the area behind the RIS are referred to as “transmitted signals”, while those reflected to the front of the RIS are termed “reflected signals”. These two distinct regions are correspondingly labeled as the Transmission (T) region and the Reflection (R) region [9]. Moreover, the electromagnetic properties of STAR-RIS elements can be modified using an intelligent controller, allowing for the adjustment of transmitted and reflected signals via the Transmission And Reflection Coefficients (TARCs). This mechanism provides flexibility in energy allocation between users on both sides, enabling both symmetric and asymmetric energy distribution [10].
It is worth noting that the author in [7] proposed three practical protocols—Energy Splitting (ES), Mode Selection (MS), and Time Splitting (TS). In the ES mode, each element simultaneously transmits and reflects, and by allocating transmission and reflection coefficients symmetrically or asymmetrically it can prioritize meeting the rate requirements of critical users while ensuring the energy conservation constraint. In the MS mode, each element operates at full power in either the transmission or reflection mode, forming a spatially asymmetric coverage. When most users are located on the transmission side, STAR-RISs can configure more elements in the transmission mode to enhance system capacity [11]. In the TS mode, time resources are symmetrically split into transmission and reflection periods, making it suitable for scenarios with symmetrical user distribution [10]. These three protocols effectively coordinate the T and R modes in STAR-RIS-assisted Multiple Input Single Output (MISO) networks [9]. Additionally, from a manufacturing standpoint, the suggested innovative RISs can be implemented using a variety of designs predicated on metasurfaces [7]. For instance, NTT DoCoMo from INC recently unveiled a dynamic metasurface capable of dynamically controlling both reflection and transmission within a highly transparent package [7,12]. Other effective strategies for managing transmission and reflection have also been documented, such as graphene-based dynamic metasurfaces and multilayer metasurfaces [7,13,14].
The exploration and application of Non-Orthogonal Multiple Access (NOMA) technology, an efficient multi-user service strategy, in conjunction with STAR-RIS-assisted communication, continues to expand. The study of these assisted NOMA systems spans numerous areas, such as the design of energy efficiency, improving security performance, channel allocation, and resource optimization. For instance, energy efficiency designs based on deep reinforcement learning have been shown to markedly increase the energy utilization efficiency of STAR-RIS-assisted NOMA networks [15]. Performance evaluations of these systems under Nakagami-m fading channels demonstrate their benefits across diverse channel conditions [16,17]. Additionally, extensive research has been conducted on covert communication and physical layer security within STAR-RIS-assisted NOMA systems, resulting in a variety of proposed strategies and methods to bolster security [18,19,20,21]. In the realm of STAR-RIS-assisted NOMA system research, Qureshi and Hamza Ahmed in 2024 examined the influence of Extra-Large Size Reconfigurable Intelligent Surfaces (XL-STAR-RISs) on the aggregate rate of uplink NOMA systems. Their findings indicate that XL-STAR-RISs substantially boost the aggregate rate of NOMA systems, particularly in near-field channels where its augmentation effect is notably more pronounced [22].
Furthermore, most studies indicate that STAR-RIS-assisted NOMA communication networks can significantly enhance the performance of communication systems, while effectively improving the stability and reliability of communication links [16,23,24,25,26,27,28,29]. Specifically, the authors in [16] investigated STAR-RIS-assisted Cooperative NOMA (CNOMA) networks in Nakagami-m fading channels, demonstrating that this system markedly augments both Spectral Efficiency (SE) and Energy Efficiency (EE). In a separate study, the authors modeled and validated STAR-RIS-assisted downlink NOMA communication systems. These systems leveraged energy splitting and Maximal Ratio Combining (MRC) at the user end, combined with beamforming technology at the base station, resulting in an elevated system performance [23]. Within cognitive radio frameworks, the authors in [24] examined the contribution of RISs to spectrum efficiency enhancement in cognitive NOMA networks with multi-primary constraints, suggesting that RISs can effectively elevate the overall performance of 5G and subsequent systems. In [25], the authors delved into the performance of RIS-assisted downlink NOMA wireless systems amidst D2D interference, deriving Signal-to-Interference-plus-Noise Ratio (SINR) expressions and calculating user rates, thus affirming the efficacy of RISs in intricate network scenarios.
The authors in [26] assessed the functionality of STAR-RIS in HARQ-assisted NOMA networks, highlighting that this system achieves a balance between security and reliability, which is especially advantageous for Secondary Users (SRUs). In [27], the authors analyzed the outage probability of STAR-RIS-assisted NOMA communication and derived closed-form expressions for the outage probabilities of reflection and refraction users. In [28], the authors integrated STAR-RISs into Industrial Internet of Things (IIoT) networks and proposed a STAR-RIS-assisted Cognitive Radio (CR)-NOMA network. They conducted a comprehensive performance analysis of the system from the perspectives of outage probability and Ergodic Rate (ER). In [29], the authors proposed a STAR-RIS-assisted CR-NOMA network, derived the outage probability of users under Nakagami-m fading channels, and analyzed its asymptotic behavior in the high signal-to-noise ratio regime. The above studies demonstrate that STAR-RIS-assisted NOMA communication networks offer significant advantages in terms of system performance and link stability.
Inspired by the aforementioned studies, this paper mainly investigates and analyzes the performance of STAR-RIS-assisted NOMA wireless education networks under multiple interference devices. Specifically, in the STAR-RIS-assisted wireless NOMA network based on the Nakagami-m channel, STAR-RISs are used to provide wireless communication services for both near and far-end devices, with the ES protocol based on symmetric and asymmetric transmission and reflection coefficient allocation. Considering distance factors, the SINR of both near and far-end devices are analyzed, and the exact closed-form approximate expressions for the outage probability are derived. Furthermore, to gain a more comprehensive understanding of the impact of direct communication links and interference devices on the near-end devices, a detailed analysis of the SINR in different scenarios is performed, and the exact closed-form approximate expressions for the outage probability in these different cases are derived. The main contributions of this paper are summarized as follows:
- Based on Nakagami-m fading channel, considering the effect of distance factor on the system.
- The effects of the direct communication link and interference devices on the near-end device are considered separately.
- The square of the composite channel amplitude between the base station and the near-end device is approximated using the Gamma distribution.
- A detailed analysis of the SINR for both near-end and far-end devices is provided, and closed-form approximate expressions for the outage probabilities of these devices, as well as the closed-form approximate expression for the system spectral efficiency, are derived.
- The accuracy of all analytical results is validated through simulations.
- The simulation results show that the power allocation of the base station, the allocation of the transmission and reflection coefficients of the STAR-RIS, the number of STAR-RIS elements, and the presence of interference devices all significantly impact the communication performance of the receiving devices. Furthermore, increasing the number of STAR-RIS elements can effectively enhance the overall performance of the system.
Notations: denotes the statistical expectation, denotes the statistical variance, denotes the k-th order moment, denotes the probability of an outcome or an event, denotes the Probability Density Function (PDF), denotes the Cumulative Distribution Function (CDF), denotes the Gamma function [30], eq. (8.310), denotes the lower incomplete Gamma function [30], eq. (8.350.1), denotes the upper incomplete Gamma function [30], eq. (8.350.2), denotes the modified Bessel function [30], eq. (8.432), denotes the Beta function [31], eq. (8.38), denotes the Meijer G-function [30], eq. (9.301), denotes the univariate Fox’s H-function [31], Definition 1.1, and (The bivariate Fox’s H-function can be computed by using the methods provided in [32,33,34]) denotes the bivariate Fox’s H-function [31], Definition 2.7.
2. System and Channel Models
As shown in Figure 1, considering a STAR-RIS-assisted downlink NOMA wireless educational communication system with N elements, where the Base Station (BS) serves as the transmitter and simultaneously delivers messages to two authorized devices: a near-end device () and a far-end device (). Specifically, is located on the front side of the STAR-RIS and can receive signals directly from the BS as well as reflected signals from the STAR-RIS. Meanwhile, multiple interference devices () are present near . On the other hand, is positioned on the back side of the STAR-RIS, and due to severe fading or blockage has no direct link to the BS. Consequently, can only receive transmitted signals from the STAR-RIS. Additionally, it is assumed that each device is equipped with a single antenna [35,36]. Notably, each element of the STAR-RIS is capable of simultaneously reflecting and transmitting incident signals in the desired directions.
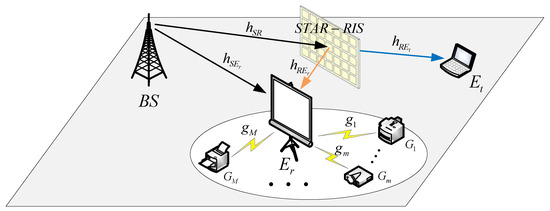
Figure 1.
System model.
It is assumed that the BS-R and R- () links are Line-Of-Sight (LOS) paths, while the BS- and - links are non-Line-Of-Sight (nLOS) paths. All LOS links are modeled as Nakagami-m fading channels, and all nLOS links are modeled as Rayleigh fading channels (a special case of the Nakagami-m distribution with ). Specifically, the direct BS- and interference - channel coefficients are denoted as ∼ and ∼, respectively, where and represent the distances of the BS- and - links, and and denote the path loss exponents for these links. The channel vectors of the S-R and R- links are represented as ∼ and ∼, respectively, where and represent the distances of the BS-R and R- links, and and denote the corresponding path loss exponents. Therefore, the magnitudes of all channel coefficients follow a Nakagami-m distribution, specifically ∼, ∼, ∼, and ∼, where the parameter (, ) and represent the shape and scale parameters of the Nakagami-m distribution. Additionally, all channels are assumed to be mutually independent.
The reflection and transmission matrices of the STAR-RIS can be represented as and , respectively, where and denote the adjustable phases introduced by the n-th element of the STAR-RIS during the reflection and transmission processes, respectively, with . In the Enhanced Sensing (ES) mode, the total incident energy is divided into reflection and transmission modes. Specifically, and represent the adjustable reflection and transmission coefficients associated with the n-th element of the STAR-RIS for devices and , respectively, with [37,38,39]. In the case of a large number of STAR-RIS elements assisting transmission, and to reduce computational complexity and facilitate simulation validation, it is assumed that the amplitude coefficients of all reflection elements are identical, and the amplitude coefficients of all transmission elements are also identical, i.e., and for [27,37,40,41], where and are constant values. Additionally, perfect Channel State Information (CSI) for all links is assumed to be available at the device nodes in order to maximize the SINR at the device end [35,36,42,43,44].
Based on the NOMA transmission scheme, the BS employs Superposition Coding (SC) to transmit the superimposed signal to and , where is the transmitted power by the BS and and represent the information intended for and , respectively. The parameters and denote the power allocation coefficients for and under the NOMA mechanism. Considering average performance, generally exhibits better channel quality than . Therefore, the BS allocates more power to the far-end device compared to the near-end device . As a result, employs Successive Interference Cancellation (SIC) to decode its signal, while directly decodes its signal without interference cancellation. The power allocation coefficients satisfy the relationship , with [45].
The received signal at device , consisting of the superimposed signals from both the BS and the STAR-RIS, can be expressed as
where represents the interference signal from the interference source and denotes the average power of the interference signal. is an Additive White Gaussian Noise (AWGN) with zero mean and variance , i.e., ∼. The device receives the combined signal from the STAR-RIS and the interference source , which is expressed as
where is also the AWGN with zero mean and variance , i.e., ∼.
In the downlink NOMA scheme, the near-end device with better channel gain performs SIC and detects the signal of the far-end device with poorer channel conditions. After performing SIC, the near-end device subtracts the signal corresponding to the data detected from the far-end device from the received signal and then decodes its own data [37,38,39]. Since is closer to the BS than , the SINR for decoding at is given by
where represents the average Signal-to-Noise Ratio (SNR) of the signal source and represents the average SNR of the interference source. After performing SIC, the near-end device, i.e., , decodes its own signal , and the corresponding SINR can be expressed as
Unlike , the far-end device directly decodes its own signal and treats the information from as interference. Therefore, the SINR at can be expressed as
For ease of analysis, define that and , which can be further expressed as
and
By adjusting the reflection or transmission phase of the STAR-RIS elements, the total phase shift of the composite S-R-Er link can be cancelled to achieve the maximum SINR, i.e., and [37]. Meanwhile, let and [38]. Considering the independence between the interference links and their identical distribution, the maximum SINR at devices and can be further written as
and
where .
For the near-end device, if the direct communication link is not considered and only the STAR-RIS reflection link is taken into account, the SINR at can be expressed as
If the impact of interference devices is neglected, the SINR at can be expressed as
3. The PDF and CDF of H1
The structure of is inherently complex. Directly employing its exact PDF and moments to derive the PDF or CDF can lead to significant computational complexity and analytical challenges. To mitigate these issues, an approximation method proposed in [5] is adopted; the Gamma distribution is leveraged to simplify the analysis, i.e.,
and the parameters and can be expressed as
and
Furthermore, if X follows a Nakagami-m distribution, i.e., X∼, its k-th moment is given by [5], i.e.,
here, , where m and represent the shape and scale parameters of the Nakagami-m distribution, respectively (note that the Rayleigh distribution is a special case of the Nakagami-m distribution when ). For convenience in the following calculations and expressions, , , . The variances are given by , , .
The expectation and variance of can be written as
and
where
and
If two random variables, X and Y,are independent, the variance of their product can be computed as . Then, we have
and the expectation of can ultimately be expressed as
For the fourth moment of , i.e., , directly solving using the integral definition is too complex. Here, we adopt the Gaussian distribution approximation method, i.e., approximate by a Gaussian distribution, i.e.,
where and . Then, based on the Gaussian distribution, the fourth moment of is calculated, i.e.,
Based on the integral equation [30], eq. 6.462.4, and the definition of the Hermite polynomials [30], eq. 8.950.1, i.e., , and the expression for given in [30], eq. 8.950.7, i.e., , we can obtain the fourth moment of , i.e., , as
Then, we can obtain the PDF and CDF of , i.e.,
and
Thus, the PDF and CDF of can be expressed as
and
Figure 2 and Figure 3 validate the accuracy of the previously derived approximate distributions. Specifically, under the conditions of , , , and , , the approximate expressions for the PDF and CDF of are compared with the estimated true distribution obtained through Monte Carlo simulations. As illustrated in the figures, the PDF and CDF curves for different values of N exhibit strong consistency with the Monte Carlo simulation results of the true distribution. This further confirms the accuracy of the derived PDF and CDF expressions for , i.e., (25) and (26).
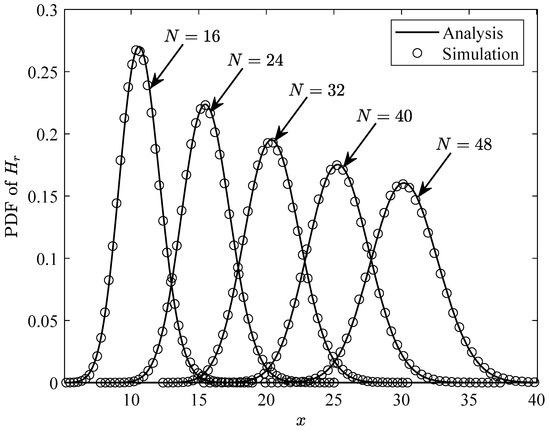
Figure 2.
Comparison of the obtained approximate distribution (27) with the Monte Carlo simulation of the estimated true distribution.
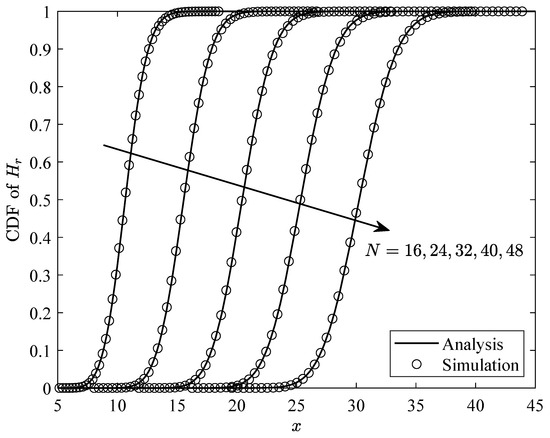
Figure 3.
Comparison of the obtained approximate distribution (28) with the Monte Carlo simulation of the estimated true distribution.
4. The PDF and CDF of H2
By employing the same analytical approach as for , the square of the composite channel amplitude between the BS and device can also be approximated using the Gamma distribution, i.e.,
here,
and
For ease of analysis, let and . The second and fourth moments of can be expressed as
and
with , .
Thus, the PDF and CDF of can be written as
and
5. Outage Probability Analysis
A lower outage probability can effectively ensure that wireless devices maintain a stable connection for a longer period, thereby guaranteeing that devices can receive the required information in a timely and reliable manner, enabling real-time information exchange [5,42]. In general, the outage probability is typically defined as , where represents the minimum required SINR threshold at the target. In this section, the closed-form approximate expressions for the outage probabilities of both near-end and far-end devices have been derived.
5.1. The Outage Probability at Device
Moreover, for any independent Random Variables (RVs) X and Y, where (with c being a constant), we have and . Thus, the PDF and CDF of can be expressed as
and
It is worth noting that the PDF and CDF of have already been provided in [42], i.e.,
and
where .
Combining the SINR at , the outage probability at can be calculated as
Next, using the relationship between the upper incomplete Gamma function and the lower incomplete Gamma function [30], eq. 8.356.3, i.e., , we have
By using the relationship between the upper incomplete Gamma function and the Meijer-G function [46], eq. 8.4.16.2, i.e., , the relationship between the power function and the Meijer-G function [46], eq. 8.4.3.1, i.e., , and the definition of the Meijer-G function [31], eq. 1.112, we can obtain
According to the integral equation [47], eq. 2.2.4.24, i.e., , and [30], eq. 3.194.3, i.e., , we can obtain
Based on the definition of the bivariate Fox’s H-function [31], eq. 2.56, eq. 2.57, the final outage probability expression at can be written as
If there is no direct communication (NDL) link at , the outage probability at can be calculated as
Note: The derivation process of is the same as that of , where and are the special values of and when and , and the proof is not repeated here.
Additionally, if there are no interference devices (NID) at , the outage probability can be calculated as
5.2. The Outage Probability at Device
Similar to the derivation process of the outage probability at , the PDF and CDF of and can be expressed as
and
and
where . By combining with the SINR at , the outage probability at can be calculated as
Following a similar approach to the calculation of , the proof is omitted for brevity. The final outage probability at device is given by
6. Spectral Efficiency Analysis
Spectral efficiency is defined as the number of bits transmitted per second per unit bandwidth, reflecting the maximum data transmission rate a communication system can support under limited spectral resources. It serves as a key metric for evaluating spectral utilization and channel capacity in wireless networks.
For the communication system considered in this paper, the ergodic rate of device is given by
Similarly, the ergodic rate of device is given by
According to the definition of ergodic rate, can be calculated as
where can be written in the form of (43), and substituting it into (55), (55) can be further expressed as
By using the integral equation [47], eq. 2.2.4.24, i.e., , and the relationship between the Beta function and the Gamma function [30], eq. 3.194.3, i.e., , it can be further written as
According to the definition of the bivariate Fox’s H-function [31], the ergodic rate at , i.e., , can ultimately be calculated as
Similarly, the ergodic rate at , i.e., , can be calculated as
Finally, the Spectral Efficiency (SE) can be expressed as
7. Numerical and Simulation Results
This chapter presents the numerical and simulation results for the outage probabilities of near-end and far-end devices, as well as the system spectral efficiency under the assistance of STAR-RISs. In order to gain a more comprehensive understanding of the performance of near-end devices, the impact of interference devices and direct communication links on the outage probability of the near-end device is discussed in detail. It is noteworthy that, unless otherwise specified in the figures, the simulation parameters are set as follows: , , , , ; , , , , , , , , , and , [16,28,29,37,38,39,48,49].
Figure 4 and Figure 5 show the relationship between the outage probability at the near-end device and the average SNR when a direct communication link and interference devices are present. Specifically, under the conditions , , , , , , and , Figure 4 and Figure 5 compare the effects of different values of N and M on the outage probability. From the figures, it can be observed that the numerical and simulation curves are in good agreement. As the average SNR increases, the outage probability gradually decreases. Furthermore, from Figure 4, it is evident that, as N increases, the outage probability decreases, suggesting that increasing the number of elements in the STAR-RIS can effectively mitigate the impact of interference devices on the receiving device. In contrast, Figure 5 shows that, as the number of interference devices around the near-end device increases, the outage probability increases, indicating that interference devices have a significant impact on the receiving device.
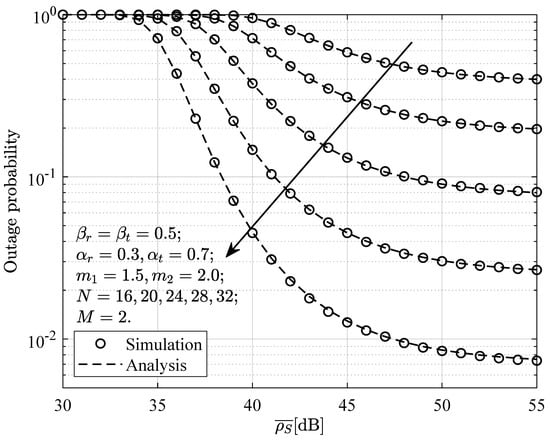
Figure 4.
Outage probability at versus the average SNR for , when and the direct link is present.
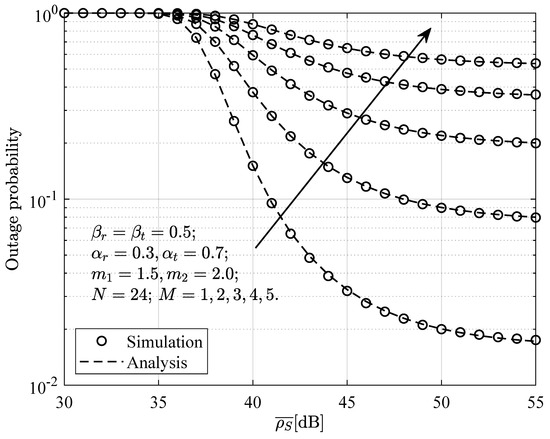
Figure 5.
Outage probability at versus the average SNR for , when and the direct link is present.
Figure 6 and Figure 7 present the relationship between the outage probability at the near-end device and the average SNR when the direct communication link is absent but interference devices are present. From the figures, it can be observed that, under certain conditions, the numerical results align well with the simulation results. Additionally, the outage probability decreases as the average SNR increases. Moreover, the outage probability also decreases as N increases, but increases as M increases. This suggests that, even in the absence of a direct communication link, increasing the number of elements in the STAR-RIS can effectively mitigate the impact of interference devices on the receiving device.
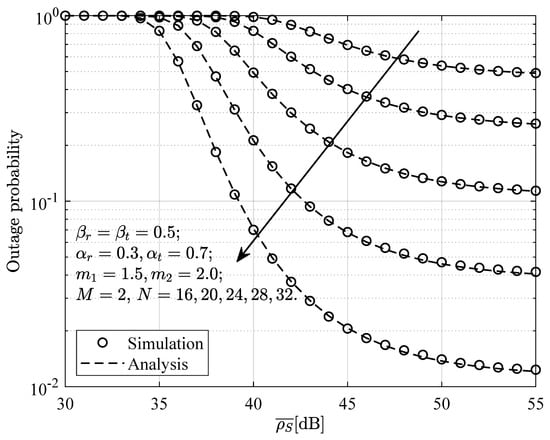
Figure 6.
Outage probability at versus the average SNR for when and no direct link is present.
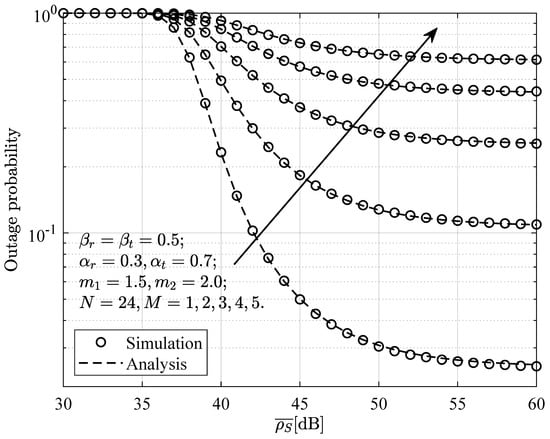
Figure 7.
Outage probability at versus the average SNR for , when and no direct link is present.
Figure 8 illustrates the relationship between the outage probability at the near-end device and the average SNR when no interference devices are present but a direct communication link exists. From the figure, it can be observed that the numerical results align well with the simulation results. As the average SNR or N value increases, the outage probability continuously decreases, which further validates the accuracy of the analytical results provided in the previous chapter.
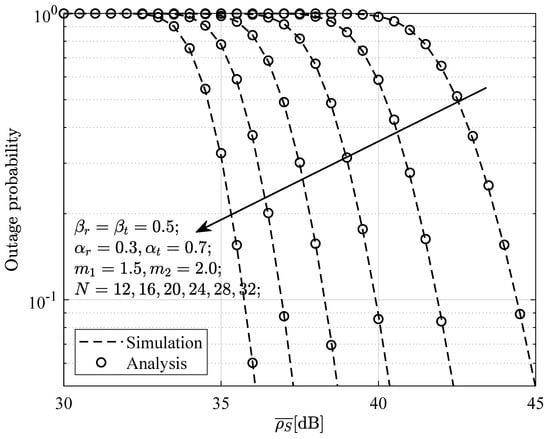
Figure 8.
Outage probability at versus the average SNR for , when no interference devices are present and the direct link is present.
Figure 9 shows the relationship between the outage probability at the far-end device and the average SNR for different values of N. From the figure, it can be observed that, as the average SNR increases, the outage probability continually decreases. Furthermore, as the N value increases, the corresponding outage probability curve becomes lower. Additionally, the numerical results align well with the simulation curves, which further confirms the accuracy of the analysis and derivation results.
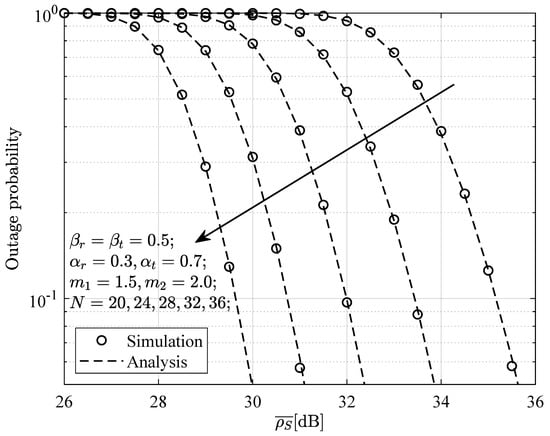
Figure 9.
Outage probability at versus the average SNR for .
Figure 10 shows the relationship between the outage probability and the average SINR for different values of and , where the two have a good fit. Specifically, under the condition , when or is fixed, the outage probability increases as or increases. In other words, as the power allocated to the far-end device or the transmission coefficient of the STAR-RIS increases, the outage probability decreases. Therefore, by controlling the power allocation at the transmitter or the transmission and reflection coefficients of the STAR-RIS, the performance of the far-end device can be significantly improved.
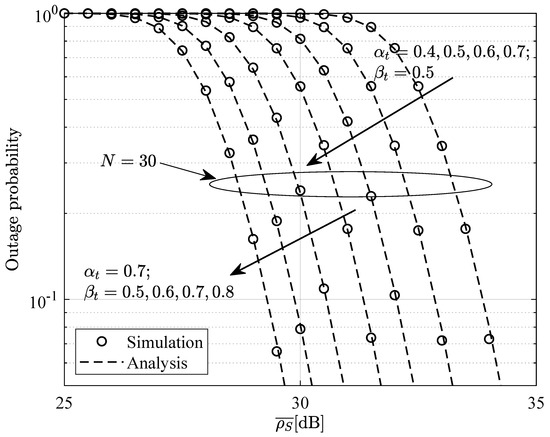
Figure 10.
Outage probability at versus the average SNR for , or , .
Figure 11 provides a comparison of the outage probability under different conditions. It is worth noting that the distance between the STAR-RIS and device is set to . From the figure, it can be observed that, under the conditions of , the outage probability is the lowest for when there are no interference devices and the direct communication link exists. The outage probability is the highest when interference devices are present and the direct communication link is absent. For , as the distance between the STAR-RIS and increases, the outage probability also increases. Furthermore, a comparison shows that, under the same conditions and with , the outage probability of device is lower than that of when interference devices are present (M = 2) and the direct communication link exists, but higher than that of when there are no interference devices and the direct communication link exists. This indicates that, under the same conditions, the direct communication link can significantly improve the communication performance of device, while the presence of interference devices can significantly degrade the communication performance.
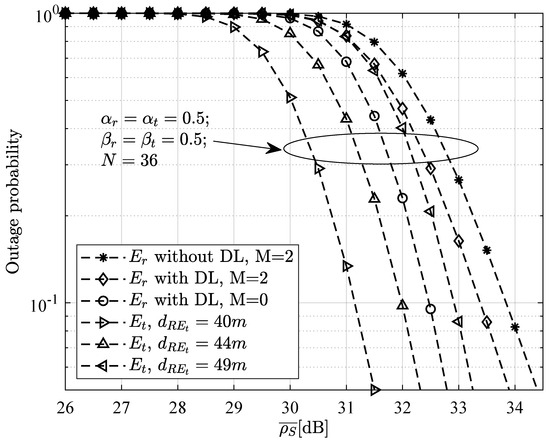
Figure 11.
Comparison of outage probabilities at and under different conditions.
Figure 12 and Figure 13 represent the relationship between the system spectral efficiency and average SNR under different values of N or M. The relevant simulation parameters are shown in the figures. From the figures, it can be observed that the spectral efficiency increases as the SNR increases. Additionally, the spectral efficiency improves with the increase in the number of elements in the STAR-RIS. However, when the number of interference devices increases, the spectral efficiency decreases. This result further demonstrates that the number of STAR-RIS elements and the interference sources at the near-end device significantly impact the system’s spectral efficiency. When the number of interference sources is fixed, increasing the number of STAR-RIS elements can effectively enhance the system’s spectral efficiency.
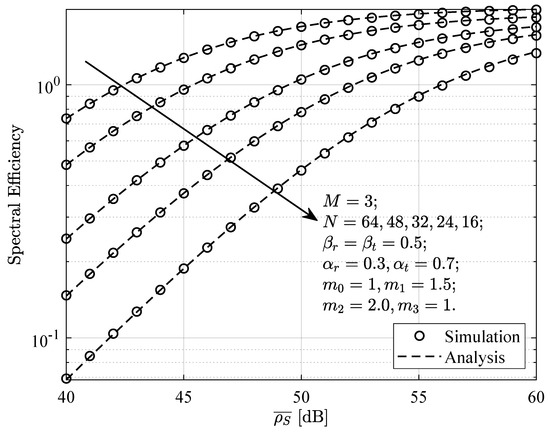
Figure 12.
The relationship between the system SE and average SNR under different values of N.
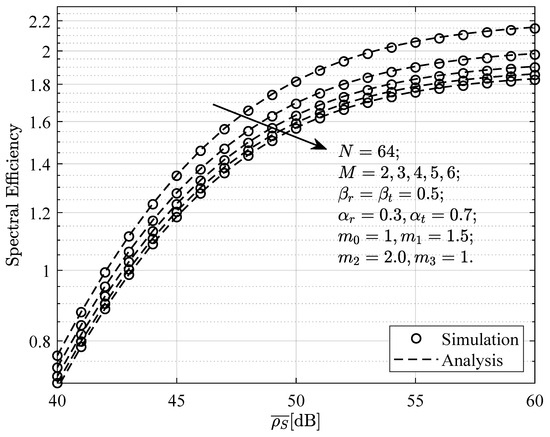
Figure 13.
The relationship between the system SE and average SNR under different values of M.
8. Conclusions
This study provides a detailed analysis of the performance of a STAR-RIS-assisted NOMA wireless education network, considering factors such as interference devices and distance. Specifically, in the STAR-RIS-assisted NOMA wireless education network the, STAR-RIS employs the ES protocol with symmetric and asymmetric transmission and reflection coefficient allocation. A detailed analysis of the SINR for both near-end and far-end devices is presented, with particular focus on the SINR conditions of the near-end device under different scenarios, such as the existence of a direct communication link between the base station and the near-end device, and the presence of interference devices near the near-end device. Based on the SINR of both near-end and far-end devices, closed-form approximate expressions for the outage probability and spectral efficiency were derived and obtained. Subsequently, all analytical results were validated through simulations. Notably, since the near-end device needs to account for the impact of the direct communication link, a Gamma distribution was used to approximate the square of the composite channel amplitude between the base station and the near-end device, and simulation results were provided. This method can also be applied to approximate the square of the channel amplitude between the base station and the far-end device. The simulation results indicate that the power allocation of the base station, the allocation of the transmission and reflection coefficients of STAR-RIS, the number of STAR-RIS elements, and the interference devices all significantly impact the communication performance of the receiving devices, and increasing the number of the STAR-RIS elements can effectively improve the overall performance of the system.
Although this study provides an in-depth analysis of the performance of a STAR-RIS-assisted NOMA wireless education network under multiple interference devices and offers valuable insights, certain limitations remain. Future research will further explore the performance of STAR-RISs in more complex environments, such as dynamically varying wireless channels, imperfect channel state information, and multi-user interference, particularly considering the effects of mobility and multi-antenna techniques. Additionally, the potential of optimization algorithms and deep-learning methods in enhancing system performance deserves further investigation. Moreover, the cooperative effects of multi-network integration based on STAR-RISs will be a significant direction for future research.
Funding
Soft Science Project of Henan Provincial Science and Technology Department (232400410369), Soft Science Project of Henan Provincial Department of Science and Technology (232400411012).
Data Availability Statement
Data is not available due to privacy or ethical constraints, and can be obtained upon request by contacting me at my personal email address.
Conflicts of Interest
The authors declare no conflicts of interest, and the funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Wu, Q.; Zhang, R. Towards Smart and Reconfigurable Environment: Intelligent Reflecting Surface Aided Wireless Network. IEEE Commun. Mag. 2020, 58, 106–112. [Google Scholar] [CrossRef]
- Tang, W.; Dai, J.Y.; Chen, M.Z.; Wong, K.K.; Li, X.; Zhao, X.; Jin, S.; Cheng, Q.; Cui, T.J. MIMO Transmission Through Reconfigurable Intelligent Surface: System Design, Analysis, and Implementation. IEEE J. Sel. Areas Commun. 2020, 38, 2683–2699. [Google Scholar] [CrossRef]
- Dai, L.; Wang, B.; Wang, M.; Yang, X.; Tan, J.; Bi, S.; Xu, S.; Yang, F.; Chen, Z.; Renzo, M.D.; et al. Reconfigurable Intelligent Surface-Based Wireless Communications: Antenna Design, Prototyping, and Experimental Results. IEEE Access 2020, 8, 45913–45923. [Google Scholar] [CrossRef]
- Cheng, Q.; Zhang, L.; Dai, J.Y.; Tang, W.; Ke, J.C.; Liu, S.; Liang, J.C.; Jin, S.; Cui, T.J. Reconfigurable Intelligent Surfaces: Simplified-Architecture Transmitters—From Theory to Implementations. Proc. IEEE 2022, 110, 1266–1289. [Google Scholar] [CrossRef]
- Ji, B.; Wang, S.; Chen, H.; Jin, X.; Zeng, S.; Song, X.; Fan, H. Vehicular Communication Based on RIS-Assisted Source: RIS-Relay Versus Energy Harvesting Relay. IEEE Trans. Intell. Transp. Syst. 2024, 1–20. [Google Scholar] [CrossRef]
- Zou, X.; Yao, J.; Chung, K.L.; Lai, G.; Zeng, W.; Gu, W. A Comparative Study Between Reconfigurable Intelligent Surface and Reflectarray Antenna. In Proceedings of the 2022 IEEE 5th International Conference on Electronic Information and Communication Technology (ICEICT), Hefei, China, 21–23 August 2022; pp. 846–848. [Google Scholar] [CrossRef]
- Xu, J.; Liu, Y.; Mu, X.; Dobre, O.A. STAR-RISs: Simultaneous Transmitting and Reflecting Reconfigurable Intelligent Surfaces. IEEE Commun. Lett. 2021, 25, 3134–3138. [Google Scholar] [CrossRef]
- Liu, Y.; Mu, X.; Xu, J.; Schober, R.; Hao, Y.; Poor, H.V.; Hanzo, L. STAR: Simultaneous Transmission and Reflection for 360° Coverage by Intelligent Surfaces. IEEE Wirel. Commun. 2021, 28, 102–109. [Google Scholar] [CrossRef]
- Niu, H.; Chu, Z.; Zhou, F.; Zhu, Z. Simultaneous Transmission and Reflection Reconfigurable Intelligent Surface Assisted Secrecy MISO Networks. IEEE Commun. Lett. 2021, 25, 3498–3502. [Google Scholar] [CrossRef]
- Mu, X.; Liu, Y.; Guo, L.; Lin, J.; Schober, R. Simultaneously Transmitting and Reflecting (STAR) RIS Aided Wireless Communications. IEEE Trans. Wirel. Commun. 2022, 21, 3083–3098. [Google Scholar] [CrossRef]
- Wu, C.; Mu, X.; Liu, Y.; Gu, X.; Wang, X. Resource Allocation in STAR-RIS-Aided Networks: OMA and NOMA. IEEE Trans. Wirel. Commun. 2022, 21, 7653–7667. [Google Scholar] [CrossRef]
- Press Releases: DOCOMO Conducts World’s First Successful Trial of Transparent Dynamic Metasurface. Available online: https://www.docomo.ne.jp/english/info/media_center/pr/2020/0117_00.html (accessed on 17 January 2020).
- Wang, X.; Ding, J.; Zheng, B.; An, S.; Zhai, G.; Zhang, H. Simultaneous Realization of Anomalous Reflection and Transmission at Two Frequencies Using Bi-Functional Metasurfaces. Sci. Rep. 2018, 8, 1876. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Li, Z.; Shao, L.; Zhu, W. Dynamical Absorption Manipulation in a Graphene-Based Optically Transparent and Flexible Metasurface. Carbon 2021, 176, 374–382. [Google Scholar] [CrossRef]
- Guo, Y.; Fang, F.; Cai, D.; Ding, Z. Energy-Efficient Design for a NOMA Assisted STAR-RIS Network with Deep Reinforcement Learning. IEEE Trans. Veh. Technol. 2023, 72, 5424–5428. [Google Scholar] [CrossRef]
- Toregozhin, T.; Shaikh, M.H.N.; Almagambetov, A.; Nauryzbayev, G. Performance of STAR-RIS-aided Cooperative NOMA Networks Under Nakagami-m Fading. Ad Hoc Netw. 2024, 156, 103399. [Google Scholar] [CrossRef]
- Li, Q.; Xu, D.; Zhang, K.; Navaie, K.; Ding, Z. Covert Communications in STAR-RIS Assisted NOMA IoT Networks Over Nakagami-m Fading Channels. IEEE Internet Things J. 2024, 11, 22456–22470. [Google Scholar] [CrossRef]
- Ukyam, U.M.R.; Gurrala, K.K. Secrecy Rate Analysis and Power Allocation Strategies for Control Jamming-Enabled STAR-RIS NOMA Wireless Network with Non Ideal Hardware. SIViP 2024, 18, 6559–6571. [Google Scholar] [CrossRef]
- Jia, H.; Ma, L.; Valaee, S. STAR-RIS Enabled Downlink Secure NOMA Network Under Imperfect CSI of Eavesdroppers. IEEE Commun. Lett. 2023, 27, 802–806. [Google Scholar] [CrossRef]
- Liu, Y.; Huang, K.; Sun, X.; Yang, J.; Zhao, J. Secure Wireless Communications for STAR-RIS-assisted Millimetre-Wave NOMA Uplink Networks. IET Commun. 2023, 17, 1127–1139. [Google Scholar] [CrossRef]
- Han, H.; Cao, Y.; Deng, N.; Xing, C.; Zhao, N.; Li, Y.; Wang, X. Secure Transmission for STAR-RIS Aided NOMA Against Internal Eavesdropping. IEEE Trans. Veh. Technol. 2023, 72, 15068–15073. [Google Scholar] [CrossRef]
- Qureshi, H.A.; Oh, S.; Khan, N.; Kim, Y.H.; Nallanathan, A. Sum Rate of Extremely Large STAR-RIS Aided Uplink NOMA. IEEE Wirel. Commun. Lett. 2024, 13, 2085–2089. [Google Scholar] [CrossRef]
- Singh, U.; Al-Tous, H.; Tirkonnen, O.; Bhatnagar, M.R. Performance Analysis of the STAR-RIS-Assisted Downlink NOMA Communication System with MRC. IEEE Commun. Lett. 2023, 27, 1739–1743. [Google Scholar] [CrossRef]
- Thien, H.T.; Le, A.T.; Minh, B.V.; Rejfek, L.; Koo, I. Performance Analysis of a Cognitive RIS-NOMA in Wireless Sensor Network. Appl. Sci. 2024, 14, 5865. [Google Scholar] [CrossRef]
- Selim, M.M.; Tomasin, S. Performance Analysis of RIS-Assisted Downlink NOMA Wireless Systems under D2D Interference. Digit. Signal Process. 2024, 144, 104269. [Google Scholar] [CrossRef]
- Sheng, X.; Li, X.; Chen, G.; Huang, G.; Han, C.; Ding, Z. Performance Analysis of STAR-RIS Assisted Secure Cognitive NOMA-HARQ Networks. IEEE Wirel. Commun. Lett. 2024, 13, 696–700. [Google Scholar] [CrossRef]
- Tang, J.; Peng, Y.; Yang, Q. Performance Analysis of STAR-RIS-assisted NOMA Communication. In Proceedings of the 2023 IEEE 7th Information Technology and Mechatronics Engineering Conference (ITOEC), Chongqing, China, 15–17 September 2023; pp. 1325–1329. [Google Scholar] [CrossRef]
- Li, X.; Gao, X.; Yang, L.; Liu, H.; Wang, J.; Rabie, K.M. Performance Analysis of STAR-RIS-CR-NOMA-Based Consumer IoT Networks for Resilient Industry 5.0. IEEE Trans. Consum. Electron. 2024, 70, 1380–1391. [Google Scholar] [CrossRef]
- Wang, S.; Lian, B.; Gao, X.; Li, X.; Zeng, M. Outage Performance Analysis of STAR-RIS Assisted CR-NOMA Networks. In Proceedings of the GLOBECOM 2023—2023 IEEE Global Communications Conference, Kuala Lumpur, Malaysia, 4–8 December 2023; pp. 4411–4417. [Google Scholar] [CrossRef]
- Gradshteĭn, I.S.; Zwillinger, D. Table of Integrals, Series, and Products, 8th ed.; Elsevier: Amsterdam, The Netherlands; Boston, MA, USA, 2015. [Google Scholar]
- Mathai, A.; Saxena, R.K.; Haubold, H.J. The H-Function; Springer: New York, NY, USA, 2010. [Google Scholar] [CrossRef]
- Illi, E.; Bouanani, F.E.; Ayoub, F. A Performance Study of a Hybrid 5G RF/FSO Transmission System. In Proceedings of the 2017 International Conference on Wireless Networks and Mobile Communications (WINCOM), Rabat, Morocco, 1–4 November 2017; pp. 1–7. [Google Scholar] [CrossRef]
- Peppas, K.P. A New Formula for the Average Bit Error Probability of Dual-Hop Amplify-and-Forward Relaying Systems over Generalized Shadowed Fading Channels. IEEE Wirel. Commun. Lett. 2012, 1, 85–88. [Google Scholar] [CrossRef]
- Soulimani, A.; Benjillali, M.; Chergui, H.; da Costa, D.B. Multihop Weibull-fading Communications: Performance Analysis Framework and Applications. J. Frankl. Inst. 2021, 358, 8012–8044. [Google Scholar] [CrossRef]
- Al-Rimawi, A.; Al-Dweik, A. On the Performance of RIS-Assisted Communications with Direct Link Over κ-μ Shadowed Fading. IEEE Open J. Commun. Soc. 2022, 3, 2314–2328. [Google Scholar] [CrossRef]
- Agrawal, N.; Bansal, A.; Singh, K.; Li, C.P. Performance Evaluation of RIS-Assisted UAV-Enabled Vehicular Communication System with Multiple Non-Identical Interferers. IEEE Trans. Intell. Transp. Syst. 2022, 23, 9883–9894. [Google Scholar] [CrossRef]
- Pandey, A.K.; Bansal, A. Coverage Analysis of STAR-RIS Empowered Downlink NOMA with Imperfect SIC. In Proceedings of the 2023 IEEE Wireless Communications and Networking Conference (WCNC), Glasgow, UK, 26–29 March 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Li, X.; Zheng, Y.; Zeng, M.; Liu, Y.; Dobre, O.A. Enhancing Secrecy Performance for STAR-RIS NOMA Networks. IEEE Trans. Veh. Technol. 2023, 72, 2684–2688. [Google Scholar] [CrossRef]
- Khales, F.A.; Abed Hodtani, G. NOMA Security Analysis with STAR-RIS: Investigating Coverage Region and Outage Probability. In Proceedings of the 2024 12th Iran Workshop on Communication and Information Theory (IWCIT), Tehran, Iran, 1–2 May 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Hu, G.; Li, Z.; Si, J.; Xu, K.; Cai, Y.; Xu, D.; Al-Dhahir, N. Analysis and Optimization of STAR-RIS-Assisted Proactive Eavesdropping with Statistical CSI. IEEE Trans. Veh. Technol. 2023, 72, 6850–6855. [Google Scholar] [CrossRef]
- Umer, M.; Mohsin, M.A.; Gidlund, M.; Jung, H.; Hassan, S.A. Analysis of STAR-RIS-Assisted Downlink CoMP-NOMA Multi-Cell Networks Under Nakagami-m Fading. IEEE Commun. Lett. 2024, 28, 1009–1013. [Google Scholar] [CrossRef]
- Ji, B.; Wang, S.; Zhang, G.; Liu, J.; Mumtaz, S. Performance Analysis of RIS-assisted V2V Communication under Multipath Interference. Veh. Commun. 2024, 45, 100696. [Google Scholar] [CrossRef]
- Salhab, A.M. Mixed RF/FSO Relay Networks: RIS-Equipped RF Source vs RIS-Aided RF Source. IEEE Wirel. Commun. Lett. 2021, 10, 1712–1716. [Google Scholar] [CrossRef]
- Shaikh, M.H.N.; Rabie, K.; Li, X.; Tsiftsis, T.; Nauryzbayev, G. On the Performance of Dual RIS-assisted V2I Communication under Nakagami-m Fading. In Proceedings of the 2022 IEEE 96th Vehicular Technology Conference (VTC2022-Fall), London, UK, 26–29 September 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Li, X.; Zhang, J.; Han, C.; Hao, W.; Zeng, M.; Zhu, Z.; Wang, H. Reliability and Security of CR-STAR-RIS-NOMA-Assisted IoT Networks. IEEE Internet Things J. 2024, 11, 27969–27980. [Google Scholar] [CrossRef]
- Prudnikov, A.; Brychkov, Y.; Marichev, O. Integrals and Series, Volume 3: More Special Functions; Gordon and Breach Science Publishers: New York, NY, USA, 1989. [Google Scholar]
- Prudnikov, A.; Brychkov, Y.; Marichev, O. Integrals and Series, Volume 1: Elementary Functions; Gordon and Breach Science Publishers: New York, NY, USA, 1986. [Google Scholar]
- Karim, F.; Singh, S.K.; Singh, K.; Prakriya, S.; Flanagan, M.F. On the Performance of STAR-RIS-Aided NOMA at Finite Blocklength. IEEE Wirel. Commun. Lett. 2023, 12, 868–872. [Google Scholar] [CrossRef]
- Xie, K.; Cai, G.; He, J.; Kaddoum, G. STAR-RIS Aided MISO SWIPT-NOMA System with Energy Buffer: Performance Analysis and Optimization. IEEE Internet Things J. 2024, 11, 37214–37230. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).