A Skill-Inspired Adaptive Fuzzy Control Framework for Symmetric Gait Tracking with Sparse Sensor Fusion in Lower-Limb Exoskeletons

Abstract

This paper presents a real-time framework for bilateral gait reconstruction and adaptive joint control using sparse inertial sensing. The system estimates full lower-limb motion from a single-side inertial measurement unit (IMU) by applying a pipeline that includes signal smoothing, temporal alignment via Dynamic Time Warping (DTW), and motion modeling using Gaussian Mixture Models with Regression (GMM-GMR). Contralateral leg trajectories are inferred using both ideal and adaptive symmetry-based models to capture inter-limb variations. The reconstructed motion serves as reference input for joint-level control. A classical Proportional–Integral–Derivative (PID) controller is first evaluated, demonstrating satisfactory results under simplified dynamics but notable performance loss when virtual stiffness and gravity compensation are introduced. To address this, an adaptive fuzzy PID controller is implemented, which dynamically adjusts control gains based on real-time tracking error through a fuzzy inference system. This approach enhances control stability and motion fidelity under varying conditions. The combined estimation and control framework enables accurate bilateral gait tracking and smooth joint control using minimal sensing, offering a practical solution for wearable robotic systems such as exoskeletons or smart prosthetics.

1. Introduction

Wearable robotic systems, especially lower-limb exoskeletons, have attracted significant attention for their ability to support human locomotion, assist rehabilitation, and improve mobility for individuals with impairments [1,2,3,4]. To be effective, these systems require not only accurate motion generation but also control strategies [5,6] that can adapt to the variability of human gait and the complexities of physical human–robot interaction [7,8,9].

Recent advances in data-driven modeling [10] have enabled the use of human movement patterns for robotic control. Among these, Dynamic Time Warping (DTW) is widely used to temporally align gait cycles of varying lengths, facilitating consistent phase matching across trials [11,12,13,14]. However, DTW alone does not create generalized models suitable for motion synthesis. To overcome this, Gaussian Mixture Models (GMM) combined with Gaussian Mixture Regression (GMR) have been employed to generate smooth, probabilistic representations of human joint trajectories [15,16,17].

After generating reference trajectories, an effective control strategy [18] is required to track them in real time. Classical Proportional–Integral–Derivative (PID) controllers remain common in exoskeleton systems due to their simplicity and low computational requirements [19,20]. However, PID controllers often perform poorly in the presence of non-linearities such as joint elasticity, friction, and gravitational disturbances [20,21]. To address these challenges, fuzzy logic controllers [22] have been proposed as adaptive alternatives capable of tuning gains in response to real-time tracking errors [7,8,9,23].

This paper presents an integrated framework that combines trajectory reconstruction, symmetry-aware motion prediction, and adaptive joint control for lower-limb exoskeletons. The proposed method reconstructs bilateral gait motion from sparse unilateral sensor input using a sequence of signal filtering, DTW alignment, and GMM-GMR modeling. A key contribution is the use of a technique that refines contralateral leg predictions using phase shifts, amplitude scaling, and offset correction, capturing real-world gait asymmetries often ignored in idealized models. Additionally, we introduce an adaptive fuzzy PID controller that dynamically adjusts control gains based on instantaneous error and error rate. This controller improves tracking fidelity under nonlinear conditions, including simulated joint stiffness and gravity effects. While many existing systems rely on dense sensor networks, our approach uses sparse sensor fusion—integrating data from IMUs, flex sensors, and pressure sensors—processed in parallel to achieve real-time gait estimation with reduced hardware complexity.

The framework is evaluated through simulation using real gait datasets. We assess trajectory accuracy and control robustness across walking, running, and stair climbing tasks, demonstrating the system’s generalization across diverse locomotion modes.

2. Materials and Methods

2.1. Sensor Setup and Dataset

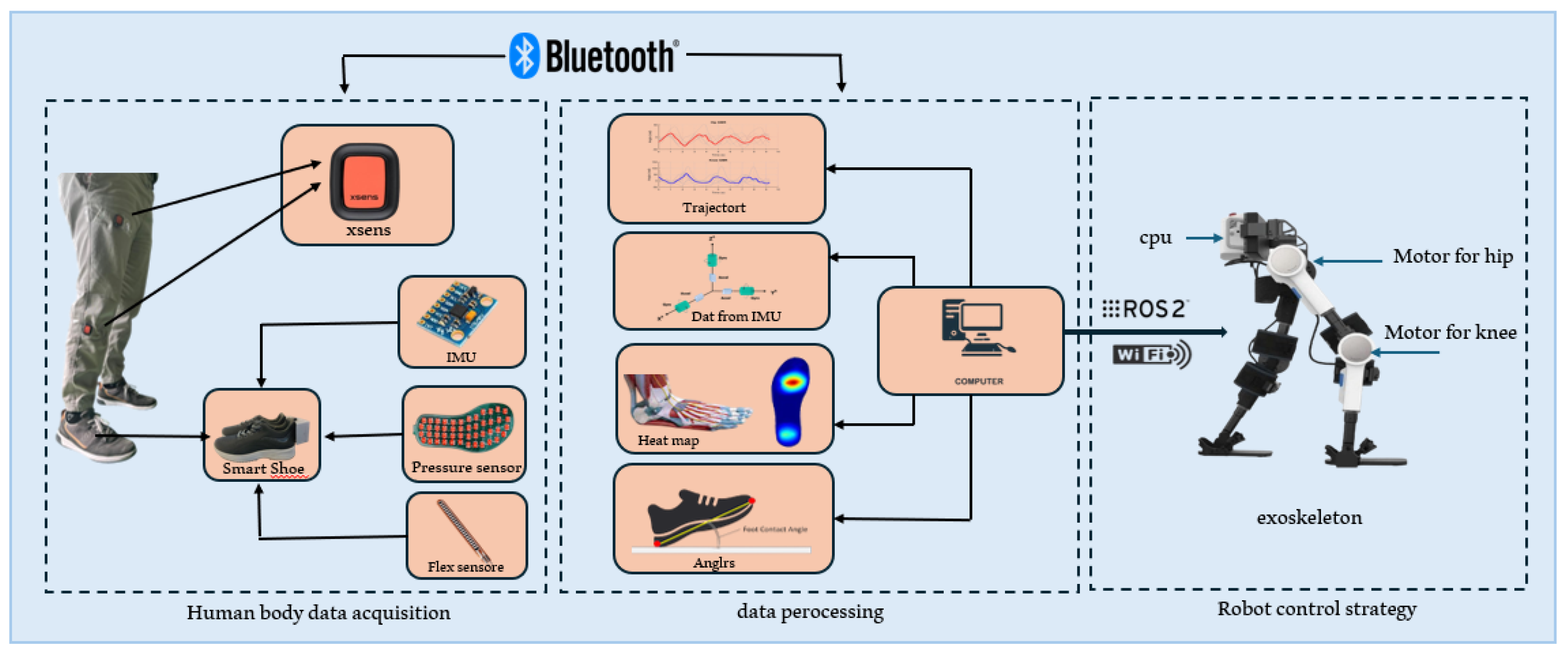
The proposed system integrates wearable sensing, trajectory reconstruction, and exoskeleton control in a modular pipeline. As shown in Figure 1, the full setup consists of three stages: human motion data acquisition, signal preprocessing, and robotic control execution. During the acquisition stage, motion data are collected from the user’s left leg using a sparse sensor configuration. Two inertial measurement units (IMUs; Xsens DOT, Movella Inc., Enschede, The Netherlands) were placed near the hip and knee joints to capture joint-level kinematics. These IMUs provide angular velocity and orientation data, which are used to reconstruct the trajectories of the hip and knee joints in the sagittal plane.

Smart shoes (Qihang Tech, Weihai, China) were equipped with embedded pressure and flex sensors to monitor foot-ground contact and foot arch deformation during dynamic locomotion. In detail, smart shoes are equipped with the following:

• One IMU positioned on the foot to reconstruct the foot’s angular motion and orientation during stance and swing phases.
• Pressure sensors embedded under the sole to monitor foot-ground contact and estimate the center of pressure (COP), which can be used to approximate the center of gravity (COG) trajectory.
• Flex (bending) sensors placed along the shoe upper to detect curvature and deformation of the foot arch during dynamic locomotion.

All sensor signals are transmitted wirelessly via Bluetooth to a central computer for real-time processing.

The system employs a parallel sensing fusion strategy, in which each sensor modality—IMU, pressure, and flex—independently contributes specific biomechanical features. IMUs provide joint kinematics and segment orientations; pressure sensors detect gait events and loading patterns; and flex sensors capture arch deformation related to foot curvature. These signals are not fused at the feature or decision level. Instead, each stream is processed in parallel and integrated only during the control and reconstruction stages. This modular design simplifies implementation, reduces latency, and enhances system interpretability, making it suitable for real-time wearable robotics applications.

Subjects performed locomotion tasks including level-ground walking, stair climbing, and running at self-selected speeds in a controlled indoor environment. IMU data were recorded at 100 Hz, capturing multiple complete gait cycles for each motion type. The data were stored in CSV format with timestamped joint angle estimates derived from the IMU signals. Only the left leg was instrumented, and its motion was used to estimate the contralateral limb motion using symmetry-based reconstruction models [4,24].

After acquisition, the raw signals were smoothed, segmented into gait cycles, and time-normalized to ensure consistency across trials. The resulting processed left-leg trajectories served as input for both motion modeling and the control strategy. All data processing and control algorithms were implemented using MATLAB R2024a (MathWorks Inc., Natick, MA, USA).

2.2. Signal Preprocessing

Raw joint angle signals captured from inertial measurement units (IMUs) often contain high-frequency noise, motion artifacts, and low-frequency drift. These disturbances result from sensor limitations, soft tissue oscillations, and mechanical impacts during locomotion. To mitigate these effects while preserving the biomechanical integrity of the signals, a locally weighted scatterplot smoothing (LOESS) filter was applied [12,24].

LOESS is a non-parametric regression technique that fits a low-order polynomial to localized segments of the data using weighted least squares. This approach enables adaptive smoothing by assigning greater weight to points near the current time t, thereby maintaining sharp motion transitions (e.g., heel strikes or peak flexion) while suppressing transient noise [12].

The smoothed value $\widehat{x}\left(t\right)$ at time t is computed as follows:

$$\widehat{x}\left(t\right)=\sum _{i=1}^N{w}_i\left(t\right)x_i$$

where $x_i$ are the original data samples, and $w_i\left(t\right)$ are weights determined by their temporal distance from t. The weights follow a tricube kernel function:

$$w_i\left(t\right)=\left\{\begin{array}{cc}{\left(1-{\left|{\displaystyle \frac{t-t_i}{h}}\right|}^3\right)}^3\hfill & \mathrm{if}|t-t_i|<h\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

Here, h defines the smoothing span or window width, and $t_i$ represents the timestamps of neighboring samples. In practice, for signals recorded at 100 Hz, a span of 20–50 samples (equivalent to 0.2–0.5 s of data) was found to provide a good balance between denoising and preserving important gait features such as joint peaks and reversals. This span was tuned empirically for each joint signal. The LOESS filter was applied independently to each joint angle across the dataset. This preprocessing step significantly reduced artifacts and jitter, enabling consistent gait cycle segmentation and supporting accurate downstream motion modeling [4,24].

2.3. Trajectory Alignment and Modeling

Human gait is inherently variable due to natural differences in timing, stride length, and joint motion. To build reliable models for gait reconstruction, this variability must be normalized. We addressed this using a two-step method: (1) Dynamic Time Warping (DTW) for temporal alignment; (2) Gaussian Mixture Modeling and Regression (GMM-GMR) for probabilistic trajectory modeling.

1. Dynamic Time Warping (DTW)

DTW is a dynamic programming technique that aligns two time-series signals with different lengths or timing. It finds the optimal non-linear mapping between two sequences by minimizing the cumulative distance between them. This is crucial for comparing gait cycles that may differ slightly in duration or phase.

Given two sequences $\mathbf{X}=\{x_1,\dots ,x_N\}$ and $\mathbf{Y}=\{y_1,\dots ,y_M\}$, the alignment cost is defined recursively as follows:

$$D(i,j)=\parallel x_i-y_j{\parallel }^2+min\left\{D(i-1,j),D(i,j-1),D(i-1,j-1)\right\}$$

The resulting cost matrix D holds the optimal alignment path from the final point $D(N,M)$ back to the start $D(1,1)$. Above all, the DTW Algorithm for gait alignment is shown in

Table 1. Pseudocode for DTW-based trajectory alignment.

Inputs:   $\mathbf{X}=\{x_1,\dots ,x_N\}$: Reference trajectory   $\mathbf{Y}=\{y_1,\dots ,y_M\}$: Target trajectory to be aligned Output: Aligned trajectory ${\mathbf{Y}}^{\prime }$, optimal warping path $P^{*}$ Procedure:   Compute local cost: $C(i,j)=\parallel x_i-y_j{\parallel }^2$   Initialize cumulative matrix: $$D(1,1)=C(1,1)$$ $$D(i,1)=D(i-1,1)+C(i,1),D(1,j)=D(1,j-1)+C(1,j)$$   For all $i=2$ to N, and $j=2$ to M: $$D(i,j)=C(i,j)+min\left\{D(i-1,j),D(i,j-1),D(i-1,j-1)\right\}$$   Backtrack from $D(N,M)$ to $D(1,1)$ to extract optimal warping path $P^{*}$   Warp $\mathbf{Y}$ along $P^{*}$ to obtain aligned ${\mathbf{Y}}^{\prime }$ Return: Warped trajectory ${\mathbf{Y}}^{\prime }$, path $P^{*}$

.

This algorithm was applied pairwise to each joint trajectory across multiple gait cycles. After DTW alignment, all cycles were normalized in time and prepared for statistical modeling. For instance, let $\mathbf{X}=[1,3,4]$ and $\mathbf{Y}=[1,2,4]$. The local cost at position $D(2,2)$ compares $x_2=3$ and $y_2=2$, giving ${\parallel 3-2\parallel }^2=1$. If the minimum of the three neighboring values is, say, $D(1,1)=0$, then $D(2,2)=1+0=1$. This process continues until the final cost at $D(3,3)$ accumulates the minimum alignment cost between sequences, which in this case is 1.

2. Trajectory Modeling with GMM-GMR

After alignment, we applied Gaussian Mixture Models (GMM) to statistically model the time-aligned joint trajectories. Each data point is represented as ${\mathit{\xi }}_n={[t_n,{\theta }_n]}^{\top }$, where $t_n$ is the normalized time and ${\theta }_n$ is the corresponding joint angle.

GMM expresses the joint distribution as a sum of Gaussian components:

$$p\left(\mathit{\xi }\right)=\sum _{k=1}^K{\pi }_k\mathcal{N}(\mathit{\xi }\mid {\mathit{\mu }}_k,{\mathbf{\Sigma }}_k)$$

To reconstruct the expected angle at time t, Gaussian Mixture Regression (GMR) is used:

$$\widehat{\theta }\left(t\right)=\sum _{k=1}^K{h}_k\left(t\right)\left[{\mu }_k^{\theta }+{\Sigma }_k^{\theta t}{\left({\Sigma }_k^{tt}\right)}^{-1}(t-{\mu }_k^t)\right]$$

where

• $h_k\left(t\right)$ is the activation weight of the k-th Gaussian at time t,
• ${\mu }_k^t$, ${\mu }_k^{\theta }$ are mean time and angle for component k,
• ${\Sigma }_k^{tt}$ and ${\Sigma }_k^{\theta t}$ are time and cross-covariance matrices.

This enables smooth and probabilistic reconstruction of the joint angle trajectory, capturing both mean behavior and variability across cycles.

The DTW + GMM-GMR pipeline allowed us to align and model hip and knee trajectories for walking, running, and stair climbing. These models were used to reconstruct full bilateral motion from unilateral input, and to generate reference trajectories for exoskeleton control. The use of DTW ensured time consistency across samples, while GMM-GMR provided a robust statistical basis for smooth trajectory generation, even from sparse sensor input.

2.4. Contralateral Trajectory Reconstruction

To reduce sensing complexity and enable lightweight deployment, the right-leg joint trajectories were reconstructed from left-leg motion using symmetry-based transformations. This leverages the approximate bilateral symmetry of human gait in the sagittal plane, particularly during steady walking and running [1,4,13,24]. By relying on sparse IMU input from only one side of the body, the system can generate full bilateral motion profiles suitable for exoskeleton control.

The reconstruction process integrates three main stages: time normalization using Dynamic Time Warping (DTW), probabilistic modeling using Gaussian Mixture Models with Regression (GMM-GMR), and contralateral estimation using both ideal and adaptive symmetry transformations. Each stage builds upon the previous to provide continuous, biologically plausible trajectories from unilateral IMU data.

Ideal Symmetry Transformation. As a baseline, the right joint angle is estimated by time-shifting and sign-inverting the left-leg signal:

$${\theta }_{\mathrm{right}}\left(t\right)=-{\theta }_{\mathrm{left}}(t+\varphi )$$

where $\varphi$ represents the phase delay between limbs, typically half the gait cycle ($\varphi =T/2$) for symmetric locomotion. This assumes idealized, mirrored motion between the left and right sides [1,11,12].

Adaptive Symmetry Refinement. To address real-world gait asymmetries caused by user variability, transitions between activities, or uneven ground, we introduce a tunable model:

$${\theta }_{\mathrm{right}}\left(t\right)=-\alpha ·{\theta }_{\mathrm{left}}(t+\varphi )+\delta$$

Here, $\alpha$ adjusts for amplitude differences, $\varphi$ allows phase misalignment, and $\delta$ corrects constant offsets. These parameters were optimized using recorded bilateral gait data by minimizing the squared prediction error:

$$L(\alpha ,\varphi ,\delta )=\sum _{t=1}^N{\left[{\theta }_{\mathrm{right},\mathrm{true}}\left(t\right)+\alpha ·{\theta }_{\mathrm{left}}(t+\varphi )-\delta \right]}^2$$

This optimization was solved using a constrained nonlinear solver with physiologically valid bounds. The learned model produced significantly more accurate right-leg reconstructions across different motion types. For example, stair climbing exhibited reduced gain values ($\alpha <1$), while running produced consistent phase shifts ($\varphi \approx T/2$) and negligible offset ($\delta \approx 0$).

This method combines time-aligned modeling and adaptive symmetry to reconstruct bilateral trajectories from unilateral IMU signals alone—without requiring dense sensing or complex hardware. The procedures are shown in Figure 2. While effective across tasks, the adaptive parameters were tuned offline and may vary by user. Future work may incorporate online learning [25,26] or subject-specific calibration for improved generalization.

2.5. Exoskeleton Modeling and Control

Accurate control of wearable robotic systems requires both a faithful dynamic model of the system and an effective control strategy that can accommodate the complexities of human–robot interaction. In this section, we describe the complete modeling of a 4-degree-of-freedom (DOF) sagittal-plane lower-limb exoskeleton [27] and the layered control architecture built upon it, which progresses from classical PID control to virtual compensation strategies and finally to adaptive fuzzy control [28].

Dynamic Modeling of the 4-DOF Exoskeleton

The modeled system consists of two legs, each with actuated hip and knee joints, yielding a total of four degrees of freedom: $\theta ={[{\theta }_{LH},{\theta }_{LK},{\theta }_{RH},{\theta }_{RK}]}^T$. The system dynamics are expressed using the Euler–Lagrange formulation:

$$\mathit{\tau }=\mathbf{M}\left(\theta \right)\ddot{\theta }+\mathbf{C}(\theta ,\dot{\theta })\dot{\theta }+\mathbf{G}\left(\theta \right)+{\mathit{\tau }}_{\mathrm{spring}}$$

where

-

$\mathbf{M}\left(\theta \right)$ is the configuration-dependent mass-inertia matrix,

-

$\mathbf{C}(\theta ,\dot{\theta })$ captures Coriolis and centrifugal forces,

-

$\mathbf{G}\left(\theta \right)$ models gravity-induced joint torques,

-

${\mathit{\tau }}_{\mathrm{spring}}$ represents the passive joint stiffness.

This structure enables simulation of realistic physical conditions, including compliance, gravitational loading, and inter-joint coupling effects [19,20,21].

2.6. Control Framework

Joint-level trajectory tracking was implemented using IMU-reconstructed reference angles for hip and knee joints, as shown in Figure 3. To assess control performance under dynamic conditions, we evaluated three strategies: classical PID control, virtual compensation for biomechanical dynamics, and adaptive fuzzy PID control.

2.6.1. PID-Based Joint Control

As a baseline, a conventional PID controller was implemented for each joint:

$${\tau }_i\left(t\right)=K_{p,i}{e}_i\left(t\right)+K_{i,i}\int e_i\left(t\right)dt+K_{d,i}{\displaystyle \frac{d{e}_i\left(t\right)}{dt}}$$

where $e_i\left(t\right)={\theta }_{i,\mathrm{ref}}\left(t\right)-{\theta }_i\left(t\right)$ is the position error between the reconstructed reference trajectory and the measured joint angle.

Initial gains were selected using the Ziegler–Nichols method [19], where the proportional gain is tuned to induce sustained oscillation, and the ultimate gain $K_u$ and oscillation period $T_u$ are used to derive:

$$K_p=0.6K_u,K_i={\displaystyle \frac{2K_p}{T_u}},K_d={\displaystyle \frac{K_p{T}_u}{8}}$$

These gains were refined manually to stabilize tracking performance during gait transitions.

While PID control performs well in linear settings, its effectiveness degrades when faced with nonlinear joint dynamics introduced by virtual spring compliance and gravitational torques, both of which depend on joint position and gait phase [20,21].

2.6.2. Virtual Spring and Gravity Compensation

To improve control under realistic joint dynamics, passive torque terms were added to model elasticity and gravitational effects. The spring-like restoring torque is computed as follows:

$${\tau }_{\mathrm{spring},i}=-k_i({\theta }_i-{\theta }_{i,\mathrm{ref}})$$

where $k_i$ is the joint stiffness constant. Gravitational torque is calculated as follows:

$${\tau }_{\mathrm{gravity},i}=m_{i}g{l}_i\sin \left({\theta }_i\right)$$

with $m_i$, $l_i$, and g representing segment mass, length to center of mass, and gravity respectively.

The total commanded torque, as shown in

Table 2. Torque computation using PID control with virtual spring and gravity compensation.

Procedure: Virtual Torque Computation   Input: ${\theta }_i,{\dot{\theta }}_i,{\theta }_{i,\mathrm{ref}},k_i,m_i,l_i,g$   1. Compute error: $e_i={\theta }_{i,\mathrm{ref}}-{\theta }_i$   2. Compute PID torque: ${\tau }_{\mathrm{PID},i}$   3. Compute spring torque: ${\tau }_{\mathrm{spring},i}=-k_i·e_i$   4. Compute gravity torque: ${\tau }_{\mathrm{gravity},i}=m_{i}g{l}_i\sin \left({\theta }_i\right)$   5. Total output: ${\tau }_i={\tau }_{\mathrm{PID},i}+{\tau }_{\mathrm{spring},i}+{\tau }_{\mathrm{gravity},i}$

, becomes:

$${\tau }_i\left(t\right)={\tau }_{\mathrm{PID},i}+{\tau }_{\mathrm{spring},i}+{\tau }_{\mathrm{gravity},i}$$

This compensation improves control fidelity, particularly during stance initiation and swing recovery phases.

2.6.3. Adaptive Fuzzy PID Controller

To overcome the limitations of fixed-gain PID control, an adaptive fuzzy PID structure [29] was implemented, based on the comparison of different controllers shown in

Table 3. Qualitative comparison of adaptive controllers for wearable robotics.

Method	Advantages	Limitations
Fuzzy PID	Real-time tuning, interpretable, low-cost [7,8]	Manual tuning, limited personalization
MPC	Optimal control with constraints [30]	Requires accurate models, high computational load
SMC	Robust to disturbances [31]	Chattering, less smooth
RL	Learns from data, adapts over time [32]	Needs large datasets, low interpretability

. The fuzzy controller adjusts PID gains online using tracking error $e\left(t\right)$ and error rate $\dot{e}\left(t\right)$ as input to a rule-based inference engine.

Fuzzy rules are of the form:

IF $e\left(t\right)$ is Large AND $\dot{e}\left(t\right)$ is Positive, THEN Decrease $K_p$, Increase $K_d$

Gain adjustments follow:

$$\begin{array}{cc}& K_p^{\mathrm{new}}=K_p+\Delta K_p(e,\dot{e})\hfill \\ & K_i^{\mathrm{new}}=K_i+\Delta K_i(e,\dot{e})\hfill \\ & K_d^{\mathrm{new}}=K_d+\Delta K_d(e,\dot{e})\hfill \end{array}$$

Triangular membership functions were defined for both inputs and outputs, as shown in Figure 4, with a 7 × 7 rule matrix designed to preserve stability. The system was executed in Simulink with a 1 ms sampling rate. This architecture improved adaptability under dynamic gait transitions and unsteady loading [7,8,9].

The fuzzy rule base was designed heuristically for average gait behavior. However, inter-subject variability or atypical motion may require retuning. Future work may incorporate learning based or self-tuning fuzzy logic systems for better generalization to diverse users or environmental contexts.

2.6.4. Validation Metrics and Evaluation Formulation

To comprehensively evaluate the performance of the proposed control strategies across the four exoskeleton joints (bilateral hip and knee), several quantitative metrics are adopted. These metrics assess tracking accuracy, smoothness of motion, and energy efficiency—critical aspects for ensuring safety and usability in wearable assistive systems [7,8,20,21].

(1)

Root Mean Square (RMS) Tracking Error.

The RMS error provides a global measure of trajectory fidelity over a gait cycle. It reflects how closely the actual joint motion follows the reference trajectory:

$$\mathrm{RMS}=\sqrt{{\displaystyle \frac{1}{N}}\sum _{i=1}^N{\left({\theta }_{\mathrm{ref},i}-{\theta }_{\mathrm{act},i}\right)}^2}$$

where ${\theta }_{\mathrm{ref},i}$ and ${\theta }_{\mathrm{act},i}$ are the reference and actual joint angles at the $i^{\mathrm{th}}$ time sample, and N is the total number of samples per cycle.

(2)

Maximum Error.

This metric captures the worst-case deviation and is critical for identifying potential instability or delay in response:

$$e_{max}=\underset{t}{max}\left|{\theta }_{\mathrm{ref}}\left(t\right)-{\theta }_{\mathrm{act}}\left(t\right)\right|$$

The maximum error defined is particularly useful in detecting overshoot or lag during rapid gait transitions [11,21].

(3)

Control Effort.

To assess actuator workload and energy usage, we compute the control effort as the time-integrated product of joint torque and angular velocity:

$$E={\int }_0^T\left|\tau \left(t\right)·\dot{\theta }\left(t\right)\right|dt$$

The control effort defined indicates system efficiency and is critical in battery-powered exoskeletons where energy optimization is essential [7,8].

(4)

Jerk Index.

Jerk, the third derivative of position with respect to time, measures motion smoothness. High jerk can cause user discomfort or biomechanical incompatibility. The jerk index is defined as follows:

$$J={\int }_0^T{\left({\displaystyle \frac{d^3\theta \left(t\right)}{d{t}^3}}\right)}^{2}dt$$

Lower values imply smoother joint motion, enhancing comfort and reducing mechanical stress [7,20].

These evaluation metrics were applied consistently to all four sagittal joints (left/right hip and knee) during simulation experiments. Performance was compared across the PID and fuzzy PID controllers, under both ideal and nonlinear conditions (e.g., elastic elements, gravity disturbances), providing a robust analysis of controller adaptability and system responsiveness.

2.7. Trajectory Reconstruction Results

The proposed reconstruction pipeline was evaluated across the locomotion modes in normal walking. For each mode, the pipeline followed two main steps: (1) Gait cycles were temporally aligned using Dynamic Time Warping (DTW); (2) Gaussian Mixture Modeling with Regression (GMM-GMR) was applied to learn a smoothed motion profile. Right-leg trajectories were then estimated using both ideal and adaptive symmetry models [7,11,12,15,17,23].

Figure 5 shows noticeable variability in raw gait cycles due to inconsistent step timing. DTW effectively normalizes this timing, revealing consistent stride structure across repetitions, essential for modeling. Similar improvements are seen in Figure 6. Temporal misalignments in raw hip signals are smoothed post-alignment, enabling accurate downstream modeling.

As seen in Figure 7, the adaptive symmetry model closely tracks the GMM-inferred motion, outperforming the ideal symmetry model, which introduces phase and amplitude offsets in the right knee prediction. The adaptive model again provides superior results (Figure 8), reducing overshoot and misalignment, demonstrating its effectiveness for estimating contralateral hip dynamics during walking.

Summary:

• DTW normalization is essential for consistent GMM modeling.
• Adaptive symmetry modeling significantly improves contralateral motion estimation.
• The method generalizes well from cyclic motions (walking, running) to asymmetric tasks (stair climbing).

Dynamic Time Warping (DTW) was chosen for its ability to temporally align gait cycles with non-uniform timing, a key challenge in human locomotion data. Unlike linear interpolation or time-normalized averaging—which assume consistent stride durations—DTW allows flexible non-linear alignment of key gait events (e.g., heel-strike, toe-off) without distorting kinematic patterns. Other alternatives, such as Principal Component Analysis (PCA)-based time normalization or Uniform Temporal Scaling, offer computational speed but lose cycle-specific variation critical for personalized modeling. DTW preserves temporal dynamics while maintaining feature correspondence across cycles, making it more suitable for accurate Gaussian Mixture Modeling in variable gait data.

2.8. PID Control Performance

The reconstructed joint trajectories—generated through DTW alignment, GMM-GMR modeling, and adaptive symmetry transformation—were used as reference inputs for joint-level control using a classical Proportional–Integral–Derivative (PID) controller. The system was evaluated under ideal linear conditions, with no additional spring compliance or gravitational loads, simulating a best-case actuation scenario.

Figure 9 presents representative tracking results for the left and right hip and knee joints. Reference trajectories are shown as dashed lines, while solid lines indicate actual joint responses. The performance of the tracking was evaluated for three types of motions: walking, running, and climbing stairs. The following observations summarize the controller’s behavior. Accurate tracking with minimal overshoot or delay. The controller handled the periodic, low-speed motion with smooth transitions and negligible steady-state error.

Overall, the results show that classical PID control performs adequately when applied to an exoskeleton model governed by approximately linear dynamics. Under these conditions, the static gain structure of PID is sufficient to achieve stable tracking with low steady-state error [8,9,19]. Its simplicity, fast response, and ease of implementation have made it a longstanding baseline in robotic control [7,13,20]. However, this performance assumes ideal actuation and neglects realistic factors such as joint elasticity, load disturbances, and unmodeled dynamics [3,21,32]. As these nonlinearities are introduced in the following sections, PID’s limitations become increasingly evident, motivating the transition to more adaptive control strategies.

2.9. Effect of Spring and Gravity Compensation on PID Performance

To simulate more realistic actuation dynamics, virtual joint stiffness and gravity effects were introduced into the exoskeleton model. Joint compliance was modeled using linear torsional springs, and segment-wise gravitational torque was incorporated based on limb orientation and mass [3,21]. The original PID controller, tuned under idealized dynamics, was retained without modification to assess its robustness under these altered conditions.

Figure 10 illustrates the impact of these added nonlinearities on joint tracking for a walking cycle. While reference trajectories remain unchanged, the simulated joint responses deviate significantly, especially in the knee joints. Amplitude attenuation, high-frequency oscillations, and phase lag are apparent, indicating deteriorated tracking performance.

The following observations highlight specific failure modes during walking:

• Left and Right Hip: Spring-induced oscillations degrade early-cycle stability. Phase lag appears post toe-off, with the system underreacting to flexion demands during swing.
• Left Knee: High overshoot and instability are observed, likely due to resonance between the spring dynamics and PID gains. The controller fails to suppress abrupt transitions near peak flexion.
• Right Knee: Motion becomes highly discontinuous, indicating loss of closed-loop stability. Gravity-induced drift and compliance mismatch lead to poor synchronization with the contralateral leg.

These results emphasize that classical PID controllers, while simple and effective under linear assumptions, are inadequate for managing the time-varying dynamics introduced by compliance and gravitational forces. Their static gain structure cannot compensate for joint-dependent variability or disturbance-induced coupling [9,19,21]. In wearable robotic systems where elastic actuators and uneven load conditions are common, more adaptive strategies such as fuzzy-PID control are required to ensure stable and reliable motion tracking [7,20,23,32].

2.10. Adaptive Fuzzy PID Controller

To overcome the limitations of classical PID under nonlinear joint dynamics, an adaptive fuzzy PID controller was developed. This controller extends a standard PID structure by integrating a Mamdani-type fuzzy inference system (FIS), enabling dynamic tuning of $K_p$, $K_i$, and $K_d$ gains based on real-time tracking behavior [7,20,23,32,33].

As shown in Figure 11, the FIS receives two inputs: the tracking error $e\left(t\right)$ and its derivative $\dot{e}\left(t\right)$, both normalized to the range $[-3,3]$. Each input is described by three triangular membership functions (MFs): Negative, Zero, and Positive. The FIS outputs three incremental adjustments: $\Delta K_p$, $\Delta K_i$, and $\Delta K_d$, each mapped over the range $[-1,1]$ using five triangular MFs (from strong decrease to strong increase).

The rule base contains nine core fuzzy rules designed to reflect intuitive control logic. For example:

• Rule 1: If Error is Negative and DeltaError is Negative, then $\Delta K_p$ is Strong Increase, $\Delta K_i$ is Neutral, and $\Delta K_d$ is Increase. This boosts responsiveness while maintaining damping.
• Rule 5: If both Error and DeltaError are Zero, then no gain changes occur—preserving current control behavior in steady state.
• Rule 9: If Error is Positive and DeltaError is Positive, then $\Delta K_p$ is Strong Decrease, $\Delta K_i$ is Slight Decrease, and $\Delta K_d$ is Increase. This reduces overshoot and improves damping.

The fuzzy system uses a min–max composition, Mamdani inference method, and centroid defuzzification. All gain updates are applied incrementally to baseline PID values, enabling adaptive behavior throughout the gait cycle [23,32].

The fuzzy PID controller was evaluated using walking trials under nonlinear joint conditions (spring compliance and gravity torque). Figure 12 and Figure 13 illustrate tracking results for ideal and non-ideal symmetry assumptions.

Observations (Ideal Symmetry):

• The controller enables precise tracking across all joints.
• Spring-induced oscillations are effectively attenuated.
• The system maintains phase alignment and amplitude fidelity.

Observations (Non-Ideal Symmetry):

• Slight increases in phase lag are observable, especially at the right knee.
• The controller compensates well for asymmetries, avoiding large deviations.
• Joint transitions remain smooth and natural despite variability.

Overall, this adaptive control strategy improves stability and tracking fidelity in the presence of real-world nonlinearities. It enables real-time adaptation to changing joint dynamics, which is particularly advantageous for wearable robotic systems [7,20,23,32,33].

While classical PID controllers are simple and widely used, they lack adaptability under time-varying dynamics. Alternative approaches such as Gain Scheduling, Model Predictive Control (MPC), and Adaptive Neural Controllers have been explored for exoskeletons. Gain scheduling requires predefined operating points and extensive tuning; MPC offers optimal control but is computationally intensive and less practical for embedded real-time systems. Neural controllers can adapt to nonlinearities but require large datasets and may lack interpretability. Fuzzy PID, by contrast, combines rule-based adaptability with low computational overhead, enabling real-time tuning of gains based on error dynamics. Its interpretability, fast response, and robustness make it a superior choice for wearable robotics where safety and transparency are essential [7,20,23,32].

2.11. Validation and Quantitative Evaluation

To rigorously assess the performance of the proposed control framework, walking experiments were conducted comparing a classical PID controller and the proposed adaptive fuzzy PID controller. The root mean square (RMS) error between actual and reference joint trajectories was used to quantify tracking performance across the left and right hip and knee joints. For comparison, the PID controller was evaluated both in an ideal (simulation-based) scenario and under real-world limitations [7,20,32].

Observations: 

Table 4. RMS Tracking Errors (in radians) for Each Joint Across Controllers.

Joint	PID (Ideal)	PID Limitations	Adaptive Fuzzy PID
Left Hip	0.019	0.149	0.014
Right Hip	0.012	0.112	0.013
Left Knee	0.127	0.727	0.141
Right Knee	0.042	0.742	0.060

highlights the joint-level tracking accuracy across controllers. In simulation (ideal conditions), the PID controller achieves low RMS errors. However, when deployed under real-world limitations, its performance degrades significantly. For instance, the right knee error rises from 0.042 to 0.742 rad—a more than 17-fold increase.

In contrast, the adaptive fuzzy PID controller maintains consistently low errors in all joints, even under uncertainty. Relative to the PID under limitations, the RMS error was reduced:

• Left hip: 90.6% (from 0.149 to 0.014 rad)
• Right hip: 88.4% (from 0.112 to 0.013 rad)
• Left knee: 80.6% (from 0.727 to 0.141 rad)
• Right knee: 91.9% (from 0.742 to 0.060 rad)

These results show that while PID may perform adequately in linear, controlled conditions, it lacks the robustness needed to handle variability. The adaptive fuzzy PID, by contrast, responds to joint-specific deviations in real time, offering reliable and accurate performance across all lower-limb joints [7,32].

Table 5. Control Effort and Motion Smoothness Comparison.

Metric	PID Controller	Adaptive Fuzzy PID Controller
Control Effort [$\int |\tau -\dot{\theta }|$]	23.7	14.5
Jerk Index [$\int {\stackrel{⃛}{\theta }}^{2}dt$]	91.6	53.8

compares the overall control effort and motion smoothness for both controllers. The adaptive fuzzy PID reduced the control effort by 38.8%, indicating less torque demand to achieve accurate tracking. This reduction directly contributes to energy efficiency, reduced actuator strain, and longer operational endurance—all critical in wearable robotic systems.

Additionally, the jerk index was reduced by 41.2%, indicating that the adaptive fuzzy controller produces smoother joint trajectories with fewer abrupt changes in acceleration. This smoother motion not only improves user comfort but also reflects better dynamic stability of the controlled limb. These improvements are also supported by the integration of a virtual spring component in the control architecture. This spring introduces passive compliance that emulates biological elasticity, allowing the system to absorb minor deviations and offload some of the control burden from the actuators. The result is more natural, energy-efficient motion with improved stability [23,33].

3. Discussion

This study presented a simulation-based framework that integrates sparse sensing and symmetry modeling for adaptive gait trajectory reconstruction and exoskeleton control. While the proposed approach demonstrated promising results in terms of tracking fidelity, robustness, and control efficiency, several ongoing developments aim to further bridge the gap between simulation and real-world deployment. A key direction is the hardware implementation and real-world validation of the proposed methods. A physical lower-limb exoskeleton system has already been constructed, integrating the same sparse IMU, flex, and pressure sensor setup described in this paper. Initial bench testing has been completed, and work is currently underway to deploy the adaptive fuzzy PID controller and energy-tank-based impedance modulation strategies on the embedded platform. These efforts will culminate in human-in-the-loop experiments that evaluate control responsiveness, trajectory accuracy, and safety under walking, stair climbing, and running conditions.

Another extension involves enhancing the sensor fusion architecture to improve estimation of the center of pressure (COP) and center of gravity (COG). Specifically, pressure and flex sensors will be leveraged to extract foot-ground contact and arch curvature information, providing richer feedback for real-time stability monitoring and energy-aware control, particularly during locomotion transitions and when traversing uneven terrain. Moreover, the current fuzzy controller operates with a predefined rule base, which, while effective, may lack adaptability for highly personalized gait dynamics. To address this limitation, future versions may adopt online learning techniques such as neuro-fuzzy adaptation or reinforcement learning [32,34]. These techniques would enable subject-specific tuning based on historical gait data and dynamic sensor patterns, thereby enhancing personalization and long-term performance.

To further improve motion planning, model predictive control (MPC) is under consideration as a complementary strategy. MPC can offer anticipatory control capabilities, particularly beneficial in scenarios involving multi-step planning or rapidly changing environments [30]. Its predictive nature could complement the adaptive fuzzy controller by providing higher-level trajectory modulation.

Finally, while the current system is limited to sagittal-plane motion, an important direction is the expansion toward 3D gait modeling and lateral control. This would involve the integration of lateral joint dynamics and quaternion-based orientation estimation for full-body motion reconstruction [35]. Such an extension would greatly enhance the system’s applicability to real-world ambulatory scenarios, including complex maneuvers such as turning, side-stepping, or adapting to inclined surfaces. In summary, while the current work establishes a strong foundation for adaptive gait tracking and control using minimal sensors, ongoing and future developments are expected to significantly advance its practical utility in wearable robotic systems.

4. Conclusions

This paper presented an integrated framework that combines gait trajectory reconstruction using unilateral IMU data with adaptive fuzzy PID control for lower-limb exoskeletons. Through a structured pipeline involving signal filtering, dynamic time warping, statistical modeling, and symmetry-based extrapolation, we reconstructed full-joint trajectories for walking, running, and stair climbing using data from a single leg. We evaluated classical PID control and found that it performs well under linear, idealized conditions. However, its effectiveness diminishes when nonlinearities such as joint stiffness and gravitational loading are introduced. To address these challenges, we incorporated a virtual spring–damper model and implemented an adaptive fuzzy PID controller capable of adjusting gains in real time based on error dynamics.

The results demonstrated that the adaptive fuzzy control strategy significantly improves tracking accuracy, motion smoothness, and energy efficiency under more realistic joint dynamics. The overall control architecture remains lightweight, modular, and scalable, making it well-suited for deployment in wearable robotic systems aimed at rehabilitation or mobility support. This work lays a foundation for future extensions involving predictive control, online adaptation, and real-world implementation in diverse locomotion environments.