Construction of Typical Scenarios for Multiple Renewable Energy Plant Outputs Considering Spatiotemporal Correlations
Abstract
1. Introduction
2. Description of Spatiotemporal Correlations Among Multiple Renewable Energy Plant Outputs
2.1. Temporal Scenario Description of Multiple Renewable Energy Plant Outputs
2.2. Description of Spatial Correlation
2.3. Description of Temporal Autocorrelation
3. Construction of A Scenario Reduction Model Considering Spatiotemporal Correlations
3.1. Difference Metric Between Typical Scenarios and Original Scenarios
- (1)
- Mean difference
- (2)
- Variance difference
- (3)
- Spatial correlation difference
- (4)
- Temporal autocorrelation difference
3.2. Modeling of Scenario Reduction
4. Solution of Typical Scenarios Based on Improved Genetic Algorithm
4.1. Improved Genetic Algorithm
- (1)
- Adaptive adjustment of parameters
- (2)
- Elitism-based evolutionary strategy
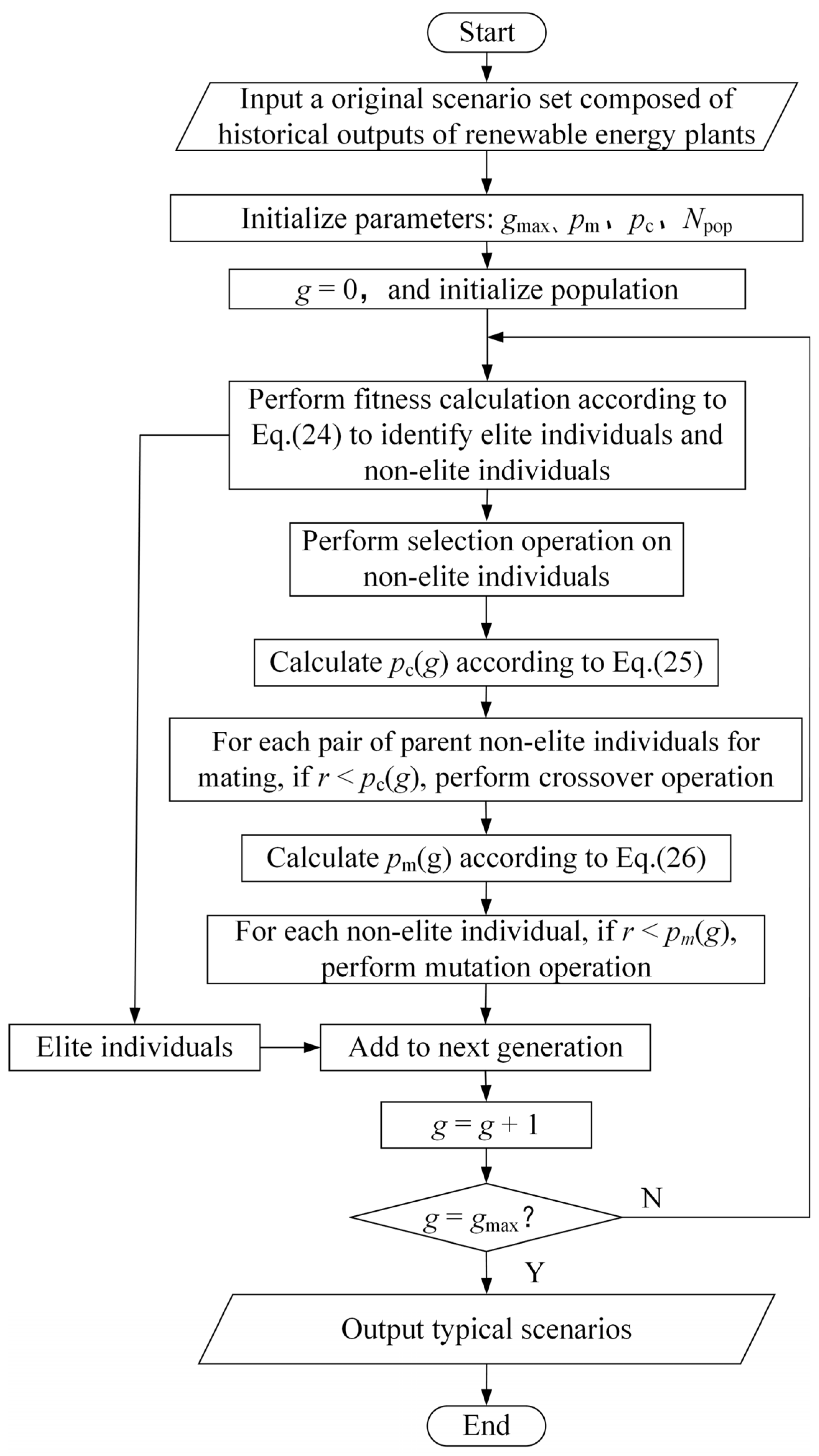
4.2. Solution Procedure of Typical Scenarios Based on Improved Genetic Algorithm
- (1)
- Population initialization
- (2)
- Calculation and ranking of fitness
- (3)
- Selection operation for non-elite individuals
- (4)
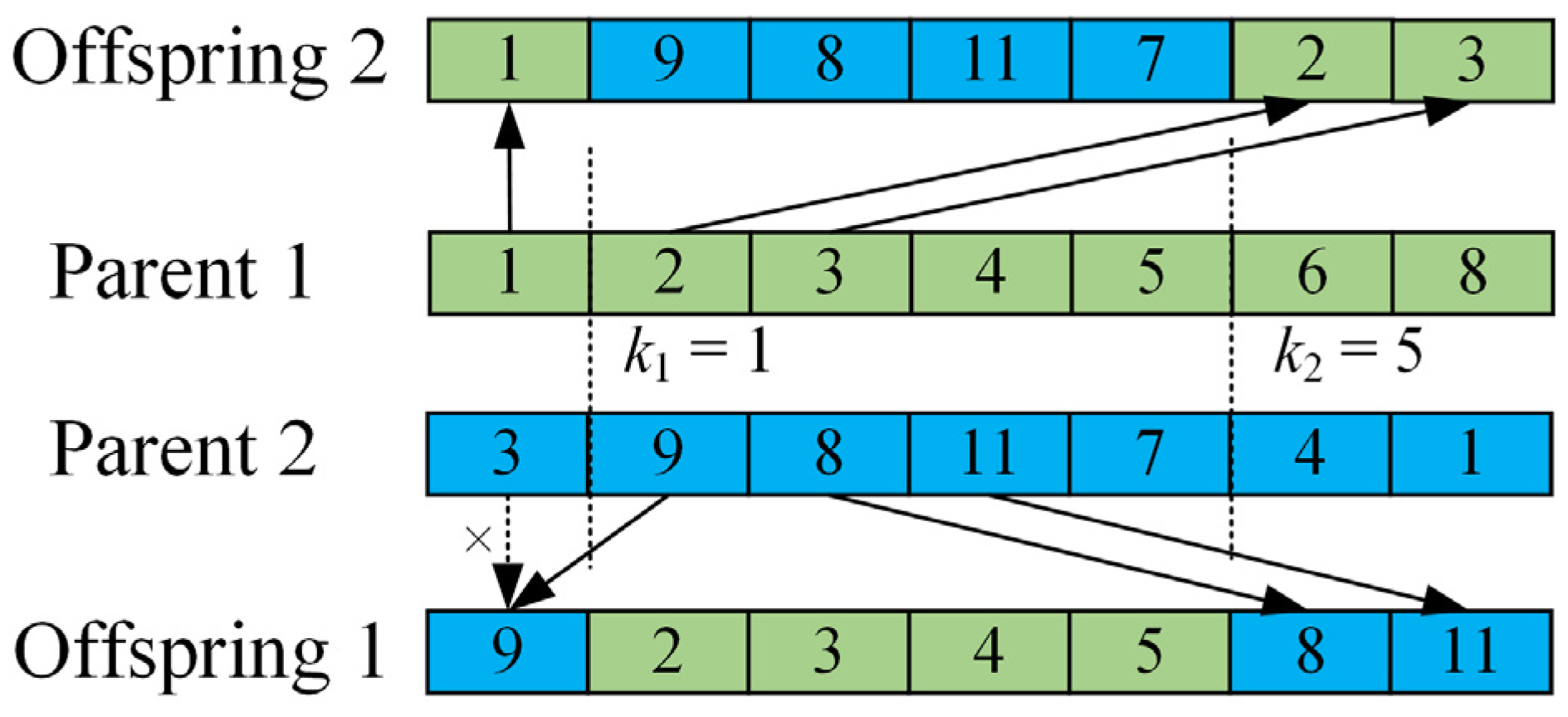
- Crossover operation for non-elite individuals
- (5)
- Mutation operation for non-elite individuals
- (6)
- Iteration termination judgment
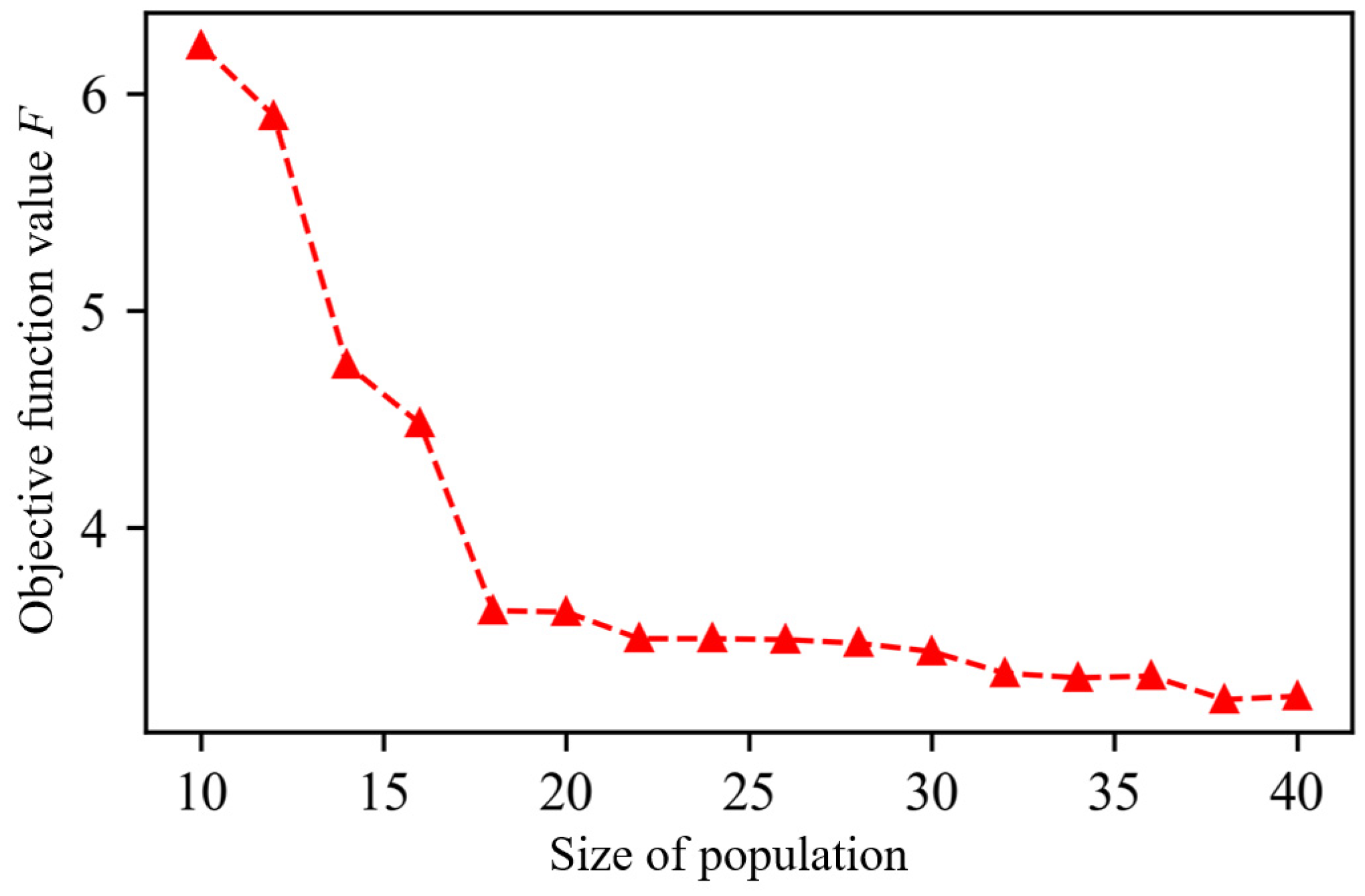
5. Case Study
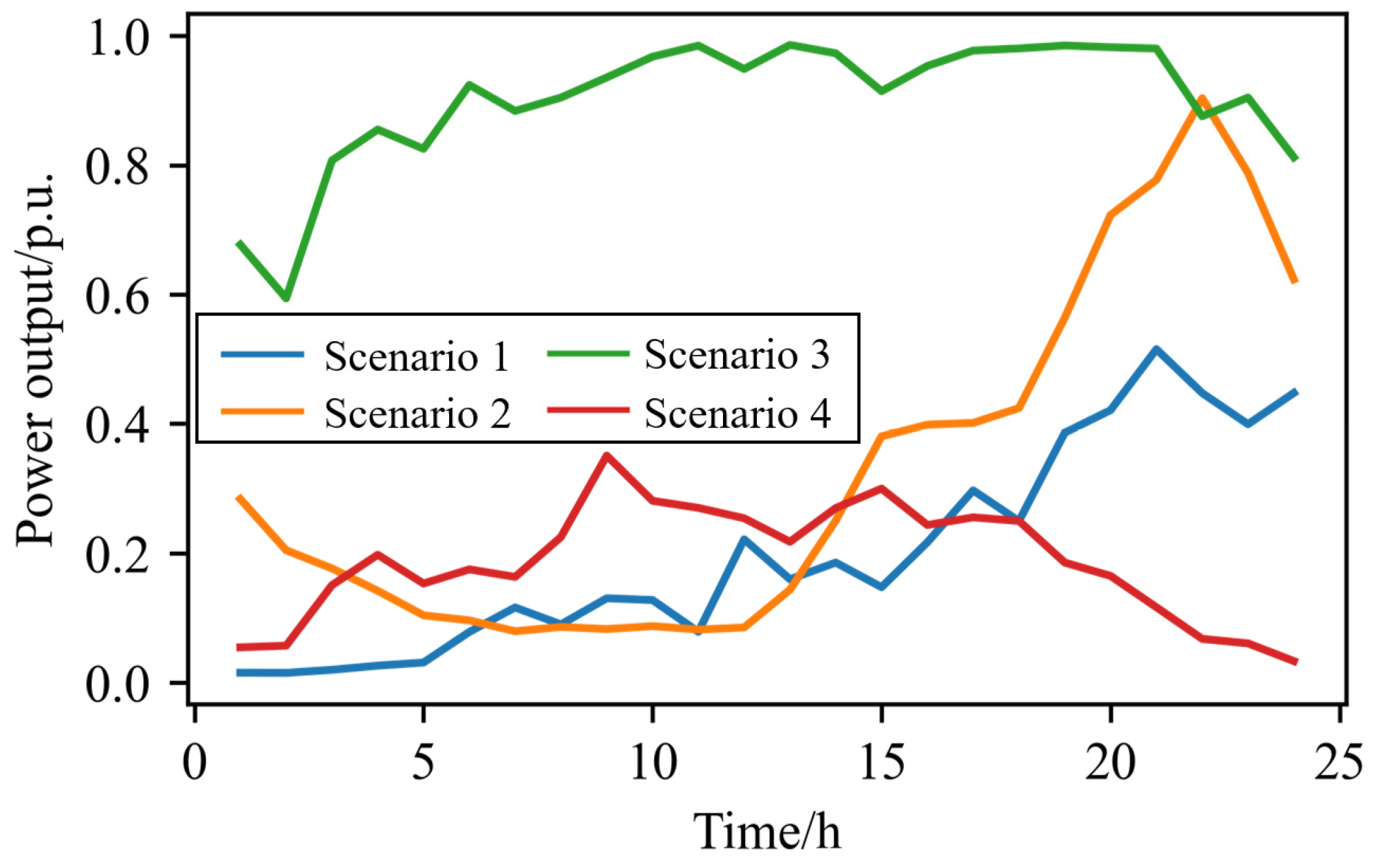
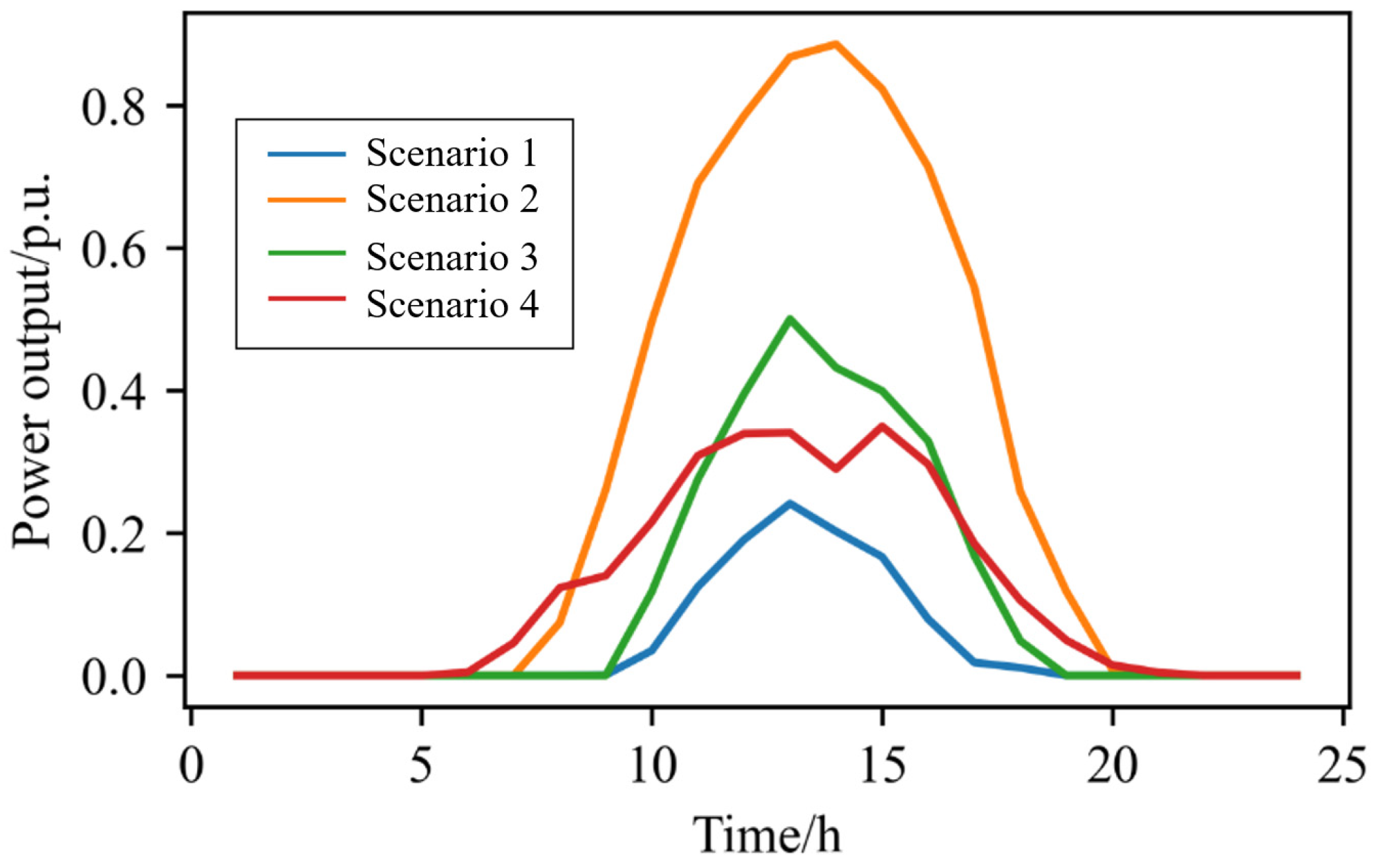
5.1. Scenario Reduction of Multiple WF Outputs
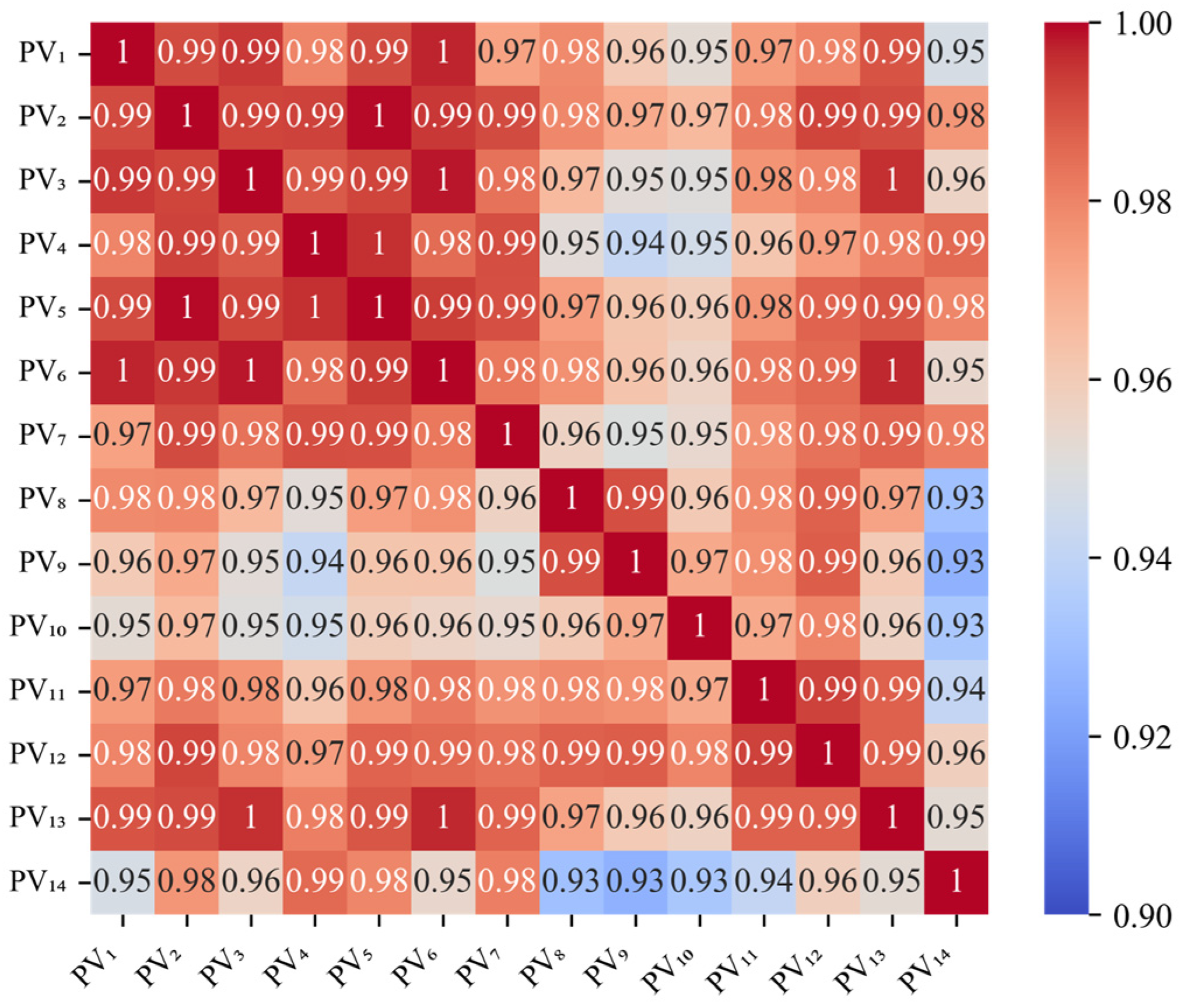
5.2. Scenario Reduction of Multiple PV Plant Outputs
6. Conclusions
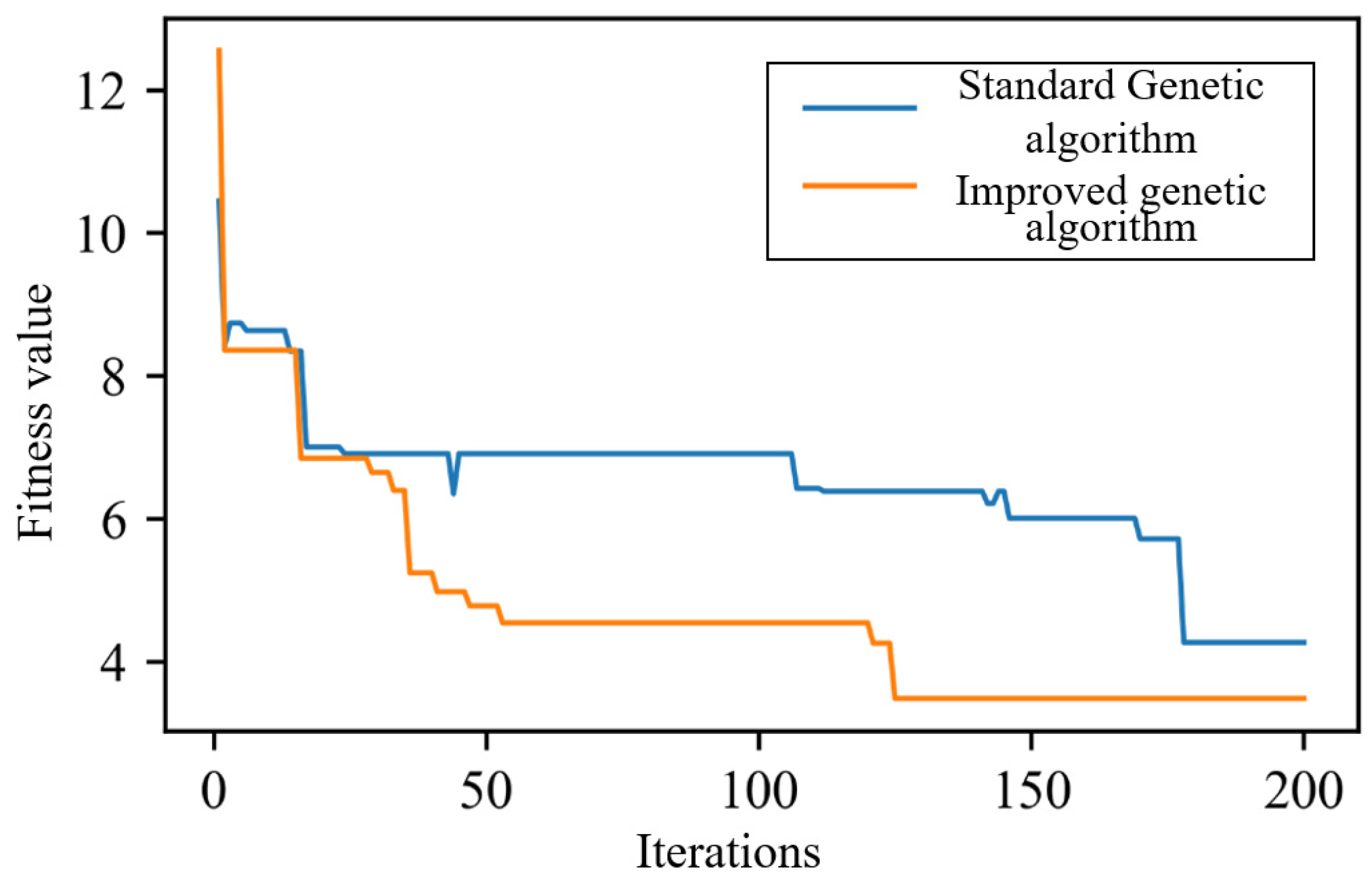
- (1)
- By incorporating adaptive parameter adjustment and an elitism strategy, the solution quality and efficiency of the improved genetic algorithm are enhanced significantly. Four high-quality typical scenarios can be obtained in 3 min.
- (2)
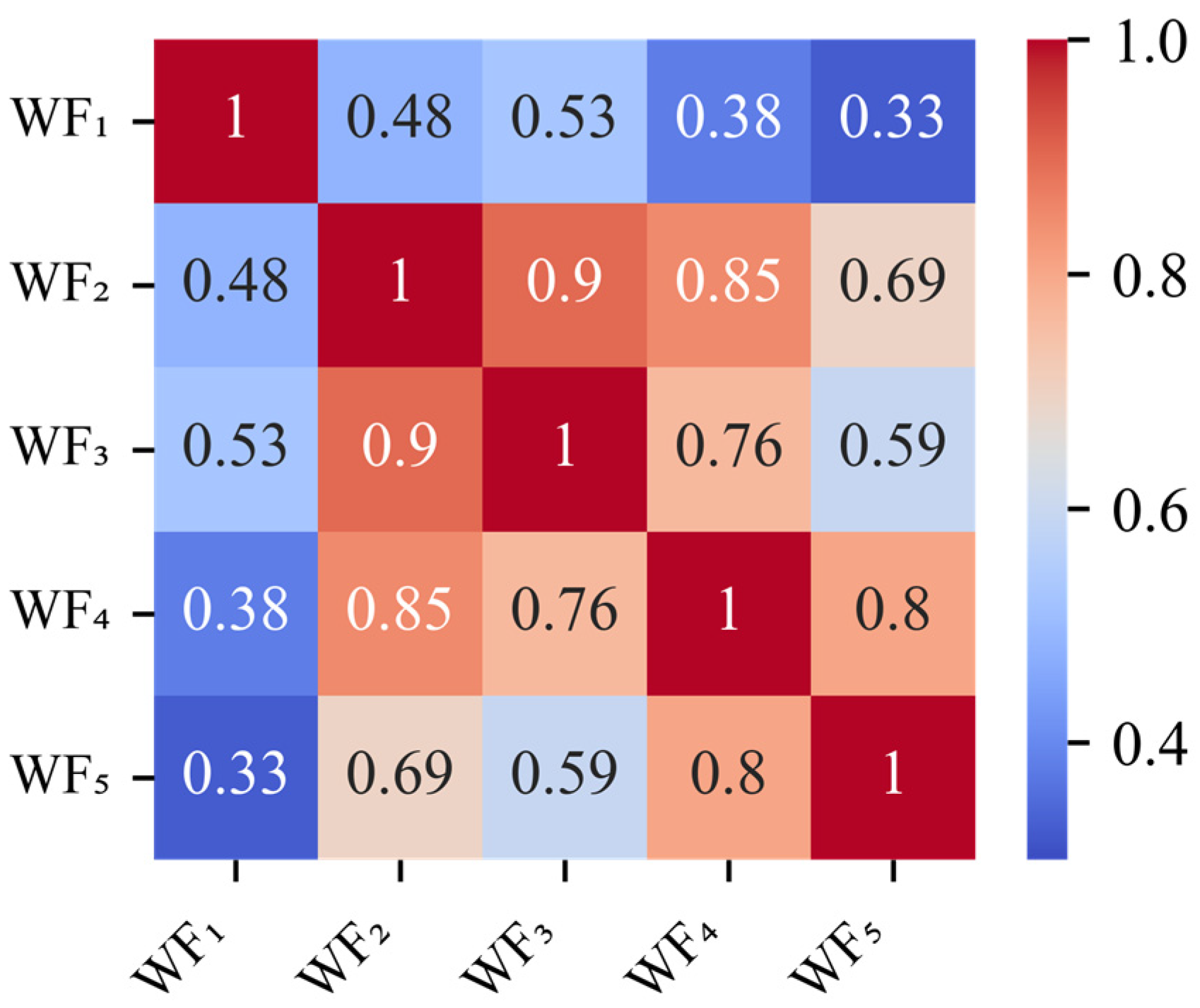
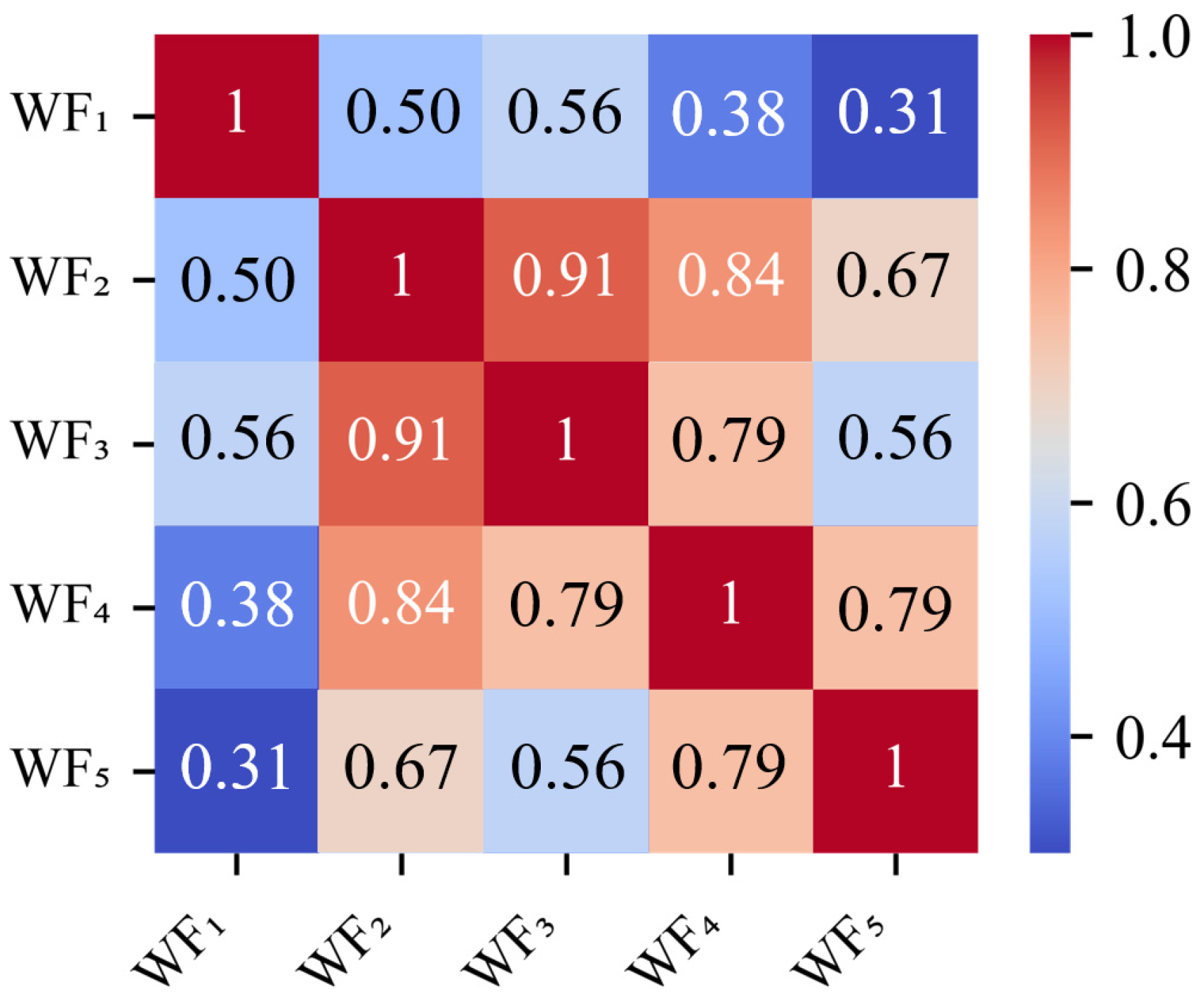
- The MAPE between spatial correlation matrices of the original and typical scenario sets for wind farms is 2.5%. The MAPE for photovoltaic plants is 0.78%. These simulation results demonstrate that the constructed typical scenarios can effectively capture the spatial correlations of the original scenarios.
- (3)
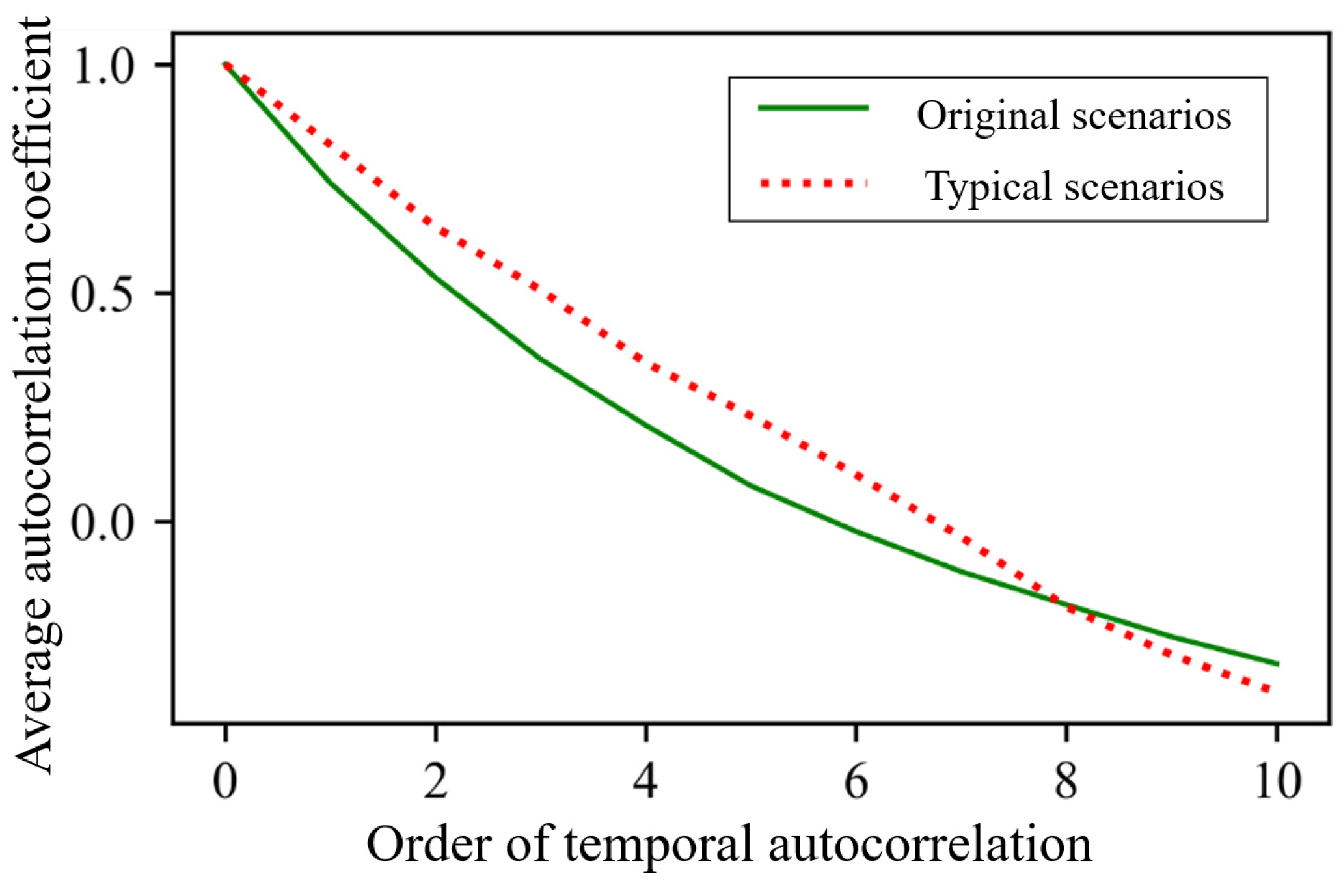
- The percentage error between first-order temporal autocorrelation coefficients of original and typical scenarios for wind farms is 2.75%. The MAPE for photovoltaic plants is 2.45%. The low errors demonstrate that typical scenarios can also capture the temporal correlations of the original scenarios.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A

References
- Khaleel, M.; Yusupov, Z.; Rekik, S. Exploring trends and predictions in renewable energy generation. Energy 360 2025, 4, 100030. [Google Scholar] [CrossRef]
- Wang, L.; Xie, L.; Yang, Y.; Zhang, Y.; Wang, K.; Cheng, S. Distributed online voltage control with fast PV power fluctuations and imperfect communication. IEEE Trans. Smart Grid 2023, 14, 3681–3695. [Google Scholar] [CrossRef]
- Zhao, L.; Huang, Y.; Dai, Q.; Yang, L.; Chen, F.; Wang, L.; Sun, K.; Huang, J.; Lin, Z. Multistage active distribution network planning with restricted operation scenario selection. IEEE Access 2019, 7, 121067–121080. [Google Scholar] [CrossRef]
- Li, H.; Ren, Z.; Fan, M.; Li, W.; Xu, Y.; Jiang, Y.; Xia, W. A review of scenario analysis methods in planning and operation of modern power systems: Methodologies, applications, and challenges. Electr. Power Syst. Res. 2022, 205, 107722. [Google Scholar] [CrossRef]
- Stappers, B.; Paterakis, N.G.; Kok, K.; Gibescu, M. A class-driven approach based on long short-term memory networks for electricity price scenario generation and reduction. IEEE Trans. Power Syst. 2020, 35, 3040–3050. [Google Scholar] [CrossRef]
- Gazijahani, F.S.; Salehi, J. Stochastic multi-objective framework for optimal dynamic planning of interconnected microgrids. IET Renew. Power Gener. 2017, 11, 1749–1759. [Google Scholar] [CrossRef]
- Safdarian, A.; Fotuhi-Firuzabad, M.; Aminifar, F. Compromising wind and solar energies from the power system adequacy viewpoint. IEEE Trans. Power Syst. 2012, 27, 2368–2376. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, Y.; Kirschen, D.; Zhang, B. Model-free renewable scenario generation using generative adversarial networks. IEEE Trans. Power Syst. 2018, 33, 3265–3275. [Google Scholar] [CrossRef]
- Yuan, R.; Wang, B.; Sun, Y.; Song, X.; Watada, J. Conditional style-based generative adversarial networks for renewable scenario generation. IEEE Trans. Power Syst. 2022, 38, 1281–1296. [Google Scholar] [CrossRef]
- Song, Z.; Huang, Y.; Xie, H.; Li, X. Generation method of multi-regional photovoltaic output scenarios-set using conditional generative adversarial networks. IEEE J. Emerg. Sel. Top. Circuits Syst. 2023, 13, 861–870. [Google Scholar] [CrossRef]
- Kang, M.; Zhu, R.; Chen, D.; Li, C.; Gu, W.; Qian, X.; Yu, W. A cross-modal generative adversarial network for scenarios generation of renewable energy. IEEE Trans. Power Syst. 2024, 39, 2630–2640. [Google Scholar] [CrossRef]
- Dong, W.; Chen, X.; Yang, Q. Data-driven scenario generation of renewable energy production based on controllable generative adversarial networks with interpretability. Appl. Energy 2022, 308, 118387. [Google Scholar] [CrossRef]
- Yao, W.; Huo, Z.; Zou, J.; Wu, C.; Wang, J.; Wang, X.; Lu, S.; Xie, Y.; Zhuo, Y.; Liang, J.; et al. Medium- and long-term power system planning method based on source-load uncertainty modeling. Energies 2024, 17, 5088. [Google Scholar] [CrossRef]
- Suo, X.; Zhao, S.; Ma, Y. Multipoint layout planning method for multi-energy sources based on time-series production simulation. Int. J. Energy Res. 2022, 46, 9323–9344. [Google Scholar] [CrossRef]
- Liu, D. An improved wind power scenario reduction method considering spatial-temporal correlation and cyber attacks. In Proceedings of the 3rd Asia Energy and Electrical Engineering Symposium (AEEES 2021), Chengdu, China, 26–29 March 2021; pp. 730–734. [Google Scholar]
- Terrén-Serrano, G.; Ludkovski, M. Extreme day-ahead renewables scenario selection in power grid operations. Appl. Energy 2025, 391, 125747. [Google Scholar] [CrossRef]
- Li, Z.; Li, Z. Linear programming-based scenario reduction using transportation distance. Comput. Chem. Eng. 2016, 88, 50–58. [Google Scholar] [CrossRef]
- Sannigrahi, S.; Ghatak, S.R.; Acharjee, P. Multi-scenario based Bi-level coordinated planning of active distribution system under uncertain environment. IEEE Trans. Ind. Appl. 2019, 56, 850–863. [Google Scholar] [CrossRef]
- Qiu, Y.; Li, Q.; Pan, Y.; Yang, H.; Chen, W. A scenario generation method based on the mixture vine copula and its application in the power system with wind/hydrogen production. Int. J. Hydrogen Energy 2019, 44, 5162–5170. [Google Scholar] [CrossRef]
- Kile, H.; Uhlen, K.; Kjølle, G. Scenario selection in composite reliability assessment of deregulated power systems. Int. J. Electr. Power Energy Syst. 2014, 63, 124–131. [Google Scholar] [CrossRef]
- Li, J.; Lan, F.; Wei, H. A scenario optimal reduction method for wind power time series. IEEE Trans. Power Syst. 2016, 31, 1657–1658. [Google Scholar] [CrossRef]
- Zhou, H.; Wu, H.; Ye, C.; Xiao, S.; Zhang, J.; He, X.; Wang, B. Integration capability evaluation of wind and photovoltaic generation in power systems based on temporal and spatial correlations. Energies 2019, 12, 171. [Google Scholar] [CrossRef]
- Tang, C.; Wang, Y.; Xu, J.; Sun, Y.; Zhang, B. Efficient scenario generation of multiple renewable power plants considering spatial and temporal correlations. Appl. Energy 2018, 221, 348–357. [Google Scholar] [CrossRef]
- Poncelet, K.; Höschle, H.; Delarue, E.; Virag, A.; D’haeseleer, W. Selecting representative days for capturing the implications of integrating intermittent renewables in generation expansion planning problems. IEEE Trans. Power Syst. 2017, 32, 1936–1948. [Google Scholar] [CrossRef]
- Zhu, N.; Wang, Y.; Yuan, K.; Yan, J.; Li, Y.; Zhang, K. GGNet: A novel graph structure for power forecasting in renewable power plants considering temporal lead-lag correlations. Appl. Energy 2024, 364, 123194. [Google Scholar] [CrossRef]
- Raik, B. Generation of time-coupled wind power infeed scenarios using pair-copula construction. IEEE Trans. Sustain. Energy 2018, 9, 1298–1306. [Google Scholar]
- Sharma, K.; Bhakar, R.; Tiwari, H.P.; Chawda, S. Scenario based uncertainty modeling of electricity market prices. In Proceedings of the 6th International Conference on Computer Applications in Electrical Engineering-Recent Advances (CERA 2017), Roorkee, India, 5–7 October 2017; pp. 164–168. [Google Scholar]
- He, Y.; Wu, H.; Ding, M.; Bi, R.; Hua, Y. Reduction method for multi-period time series scenarios of wind power. Electr. Power Syst. Res. 2023, 214, 108813. [Google Scholar] [CrossRef]
- Cheng, D.; Xing, F.; Su, R.; Qi, H.; Ma, L.; Ma, H.; Wang, T.; Zhou, N.; Li, C. Multiple wind farms power generation scenario generation and reduction based on multivariate copula function and greedy strategy. In Proceedings of the 7th International Conference on Power and Energy Engineering (ICPEE 2023), Chengdu, China, 22–24 December 2023; pp. 337–342. [Google Scholar]
- Toaza, B.; Esztergaz-Kiss, D. A review of metaheuristic algorithms for solving TSP-based scheduling optimization problems. Appl. Soft Comput. 2023, 148, 110908. [Google Scholar] [CrossRef]
- Shoaei, M.; Noorollahi, Y.; Hajinezhad, A.; Moosavian, S.F. A review of the applications of artificial intelligence in renewable energy systems: An approach-based study. Energy Convers. Manag. 2024, 306, 118207. [Google Scholar] [CrossRef]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A review on genetic algorithm: Past, present, and future. Multimed. Tools Appl. 2021, 80, 8091–8126. [Google Scholar] [CrossRef]
- Hong, Y.; Nguyen, M. Multi-objective multi-scenario under-frequency load shedding in a standalone power system. IEEE Syst. J. 2020, 14, 2759–2769. [Google Scholar] [CrossRef]
- Tang, L.; Dong, Y.; Liu, J. Differential evolution with an individual-dependent mechanism. IEEE Trans. Evol. Comput. 2015, 19, 560–574. [Google Scholar] [CrossRef]
- Pandey, A.K.; Jadoun, V.K.; Jayalakshmi, N.S. Profit maximization based optimal scheduling of a virtual power plant using red fox optimizer. In Proceedings of the IEEE 10th Power India International Conference (PIICON 2022), New Delhi, India, 25–27 November 2022; pp. 1–6. [Google Scholar]
- Pandey, A.K.; Jadoun, V.K.; Sabhahit, J.N.; Sharma, S. Interconnected operation and economic feasibility-based sustainable planning of virtual power plant in multi-area context. Smart Cities 2025, 8, 37. [Google Scholar] [CrossRef]



| Original Scenario Set | Typical Scenario Set | |||
|---|---|---|---|---|
| Mean/p.u. | Variance | Mean/p.u. | Variance | |
| WF 1 | 0.4121 | 0.0308 | 0.4723 | 0.0319 |
| WF 2 | 0.2455 | 0.0096 | 0.2765 | 0.0066 |
| WF 3 | 0.2477 | 0.0089 | 0.2975 | 0.0092 |
| WF 4 | 0.2374 | 0.0084 | 0.2532 | 0.0071 |
| WF 5 | 0.1852 | 0.0087 | 0.1609 | 0.0081 |
| Original Scenario Set | Typical Scenario Set | |||
|---|---|---|---|---|
| Mean/p.u. | Variance | Mean/p.u. | Variance | |
| PV 1 | 0.1275 | 0.0358 | 0.1361 | 0.0415 |
| PV 2 | 0.1268 | 0.0343 | 0.1347 | 0.0397 |
| PV 3 | 0.1236 | 0.0335 | 0.13167 | 0.0390 |
| PV 4 | 0.1335 | 0.0387 | 0.1410 | 0.0444 |
| PV 5 | 0.1317 | 0.0372 | 0.1394 | 0.0430 |
| PV 6 | 0.1315 | 0.0379 | 0.1420 | 0.0451 |
| PV 7 | 0.1151 | 0.0285 | 0.1185 | 0.0311 |
| PV 8 | 0.1265 | 0.0353 | 0.1376 | 0.0413 |
| PV 9 | 0.1145 | 0.0287 | 0.1272 | 0.0343 |
| PV 10 | 0.1090 | 0.0258 | 0.1235 | 0.0321 |
| PV 11 | 0.1106 | 0.0268 | 0.1126 | 0.0271 |
| PV 12 | 0.1138 | 0.0277 | 0.1221 | 0.0317 |
| PV 13 | 0.1157 | 0.0293 | 0.1216 | 0.0329 |
| PV 14 | 0.1383 | 0.0412 | 0.1413 | 0.0447 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Wen, Y.; Wang, N.; Yuan, Z.; Zhang, L.; Sun, R. Construction of Typical Scenarios for Multiple Renewable Energy Plant Outputs Considering Spatiotemporal Correlations. Symmetry 2025, 17, 1226. https://doi.org/10.3390/sym17081226
Zhang Y, Wen Y, Wang N, Yuan Z, Zhang L, Sun R. Construction of Typical Scenarios for Multiple Renewable Energy Plant Outputs Considering Spatiotemporal Correlations. Symmetry. 2025; 17(8):1226. https://doi.org/10.3390/sym17081226
Chicago/Turabian StyleZhang, Yuyue, Yan Wen, Nan Wang, Zhenhua Yuan, Lina Zhang, and Runjia Sun. 2025. "Construction of Typical Scenarios for Multiple Renewable Energy Plant Outputs Considering Spatiotemporal Correlations" Symmetry 17, no. 8: 1226. https://doi.org/10.3390/sym17081226
APA StyleZhang, Y., Wen, Y., Wang, N., Yuan, Z., Zhang, L., & Sun, R. (2025). Construction of Typical Scenarios for Multiple Renewable Energy Plant Outputs Considering Spatiotemporal Correlations. Symmetry, 17(8), 1226. https://doi.org/10.3390/sym17081226






