Abstract
In the 6G era, the proliferation of smart devices has led to explosive growth in data volume. The traditional cloud computing can no longer meet the demand for efficient processing of large amounts of data. Edge computing can solve the energy loss problems caused by transmission delay and multi-level forwarding in cloud computing by processing data close to the data source. In this paper, we propose a cloud–edge–end collaborative task offloading strategy with task response time and execution energy consumption as the optimization targets under a limited resource environment. The tasks generated by smart devices can be processed using three kinds of computing nodes, including user devices, edge servers, and cloud servers. The computing nodes are constrained by bandwidth and computing resources. For the target optimization problem, a genetic particle swarm optimization algorithm considering three layers of computing nodes is designed. The task offloading optimization is performed by introducing (1) opposition-based learning algorithm, (2) adaptive inertia weights, and (3) adjustive acceleration coefficients. All metaheuristic algorithms adopt a symmetric training method to ensure fairness and consistency in evaluation. Through experimental simulation, compared with the classic evolutionary algorithm, our algorithm reduces the objective function value by about 6–12% and has higher algorithm convergence speed, accuracy, and stability.
1. Introduction
With the rapid advancement of intelligent technology, mobile devices have become extremely popular in daily life. For example, in the Internet of Vehicles field, mobile devices equipped on vehicles are widely used for image processing, video streaming, and augmented reality/virtual reality [1]. In the smart healthcare domain, smart devices and sensors are widely used to remotely collect and monitor patient status in order to collect patient health data [2,3]. In the industrial field, Industry is the next stage of industrial development. It has become a trend to integrate modern technologies such as artificial intelligence, robotics, and the Internet of Things into manufacturing and production processes [4]. Numerous sensors and mobile devices continuously collect and generate massive amounts of data. However, mobile devices themselves have significant limitations in processing large-scale data. Their computing power and storage capacity are difficult to cope with such a huge data torrent. At the same time, the centralized processing method of traditional cloud computing is not friendly to delay-sensitive tasks [5]. Long delays will occur during data transmission, which cannot meet the immediacy requirements of scenarios such as autonomous driving and real-time industrial control. Edge computing (EC) sinks computing resources to the edge of the network. Mobile devices can offload tasks to edge servers to achieve task processing with lower transmission delays, while expanding computing resources and improving user service quality.
The continuous generation of large-scale data has led to an increasing demand for computing resources and user experience. In this context, cloud computing and mobile edge computing each play an indispensable and important role. Cloud computing provides powerful centralized computing and storage resources, which are suitable for processing tasks that require large amounts of computing and data storage [6,7]. Edge computing, due to its proximity to the data source, can provide low-latency computing services, which is particularly suitable for tasks with high real-time requirements. On the other hand, user devices themselves also have certain computing resources. For simple tasks and scenarios with high privacy protection requirements, local computing can be used for data processing. However, a single form of edge computing or cloud computing cannot meet the needs of complex scenarios and cannot balance energy consumption and time delay [8]. The cloud–edge–end collaborative computing model that integrates cloud computing, edge computing, and local computing can give full play to their respective advantages and build an efficient and flexible data processing architecture.
Task offloading is a key link in the cloud–edge–end collaborative environment, which involves the decision-making process of transferring tasks from mobile devices to edge servers or cloud servers [9]. This process requires a comprehensive consideration of the characteristics of the task itself, the performance parameters of the user device, the resource status of the edge server, and the relevant properties of the cloud server. By formulating a reasonable task offloading strategy, cloud–edge–end collaborative computing can achieve full utilization of resources and efficient processing of tasks, thereby meeting the diverse needs of users for service quality in different scenarios.
In this paper, we use the Genetic Particle Swarm Optimization (GAPSO) algorithm to solve the task offloading problem in the cloud–edge–end collaborative network environment. This algorithm helps to reduce task response time and energy consumption under the constraints of limited computing resources and edge server bandwidth. The main contributions of this paper are as follows:
- (1)
- This paper proposes a task processing framework for a cloud–edge–end collaborative environment. User devices can choose between three computing modes: local computing, edge computing, and cloud computing. Compared with the traditional mode, the cloud–edge–end collaborative environment can better utilize limited computing resources and improve data processing efficiency.
- (2)
- This paper implements a task transmission method that fully considers the bandwidth resources of edge servers. The transmission process of tasks from user devices (UDs) to edge servers (ESs) and ES to cloud servers (CSs) is more in line with the actual situation.
- (3)
- This paper designs a GAPSO algorithm, which improves the diversity of initial particles through the Opposition-Based Learning (OBL) algorithm, introduces adaptive inertia weights and adjustive acceleration coefficients, and uses a genetic algorithm (GA) to optimize the local optimal solution of particles.
- (4)
- This paper uses a symmetrical training method to conduct multiple experiments. The experimental results show that the GAPSO algorithm can achieve higher convergence accuracy, stability, and convergence speed.
In this paper, the entire experiment is constructed using a symmetric design method. All metaheuristic algorithms are applied under the same training conditions, including the same cloud–edge–end collaborative architecture and environmental parameter configuration. At the same time, the optimization target metric, number of training iterations, and experimental evaluation indicators are also kept consistent. This structured framework not only enhances the reliability of comparative analysis but also highlights the importance of symmetric experiments in the study of cloud–edge–end collaborative applications.
The rest of this paper is organized as follows. Related work is reviewed in Section 2. Section 3 presents the system model and problem formulation of this paper. The proposed GAPSO algorithm is introduced in Section 4. Section 5 provides our experimental results. Finally, in Section 6, we summarize our work.
2. Related Work
2.1. Task Offloading for Edge Computing
Edge computing task offloading refers to offloading tasks to edge servers close to data sources or user devices. Edge computing is usually deployed close to end devices, such as base stations or routers. Compared with cloud computing, edge computing can significantly reduce network latency and bandwidth usage [10,11] and is suitable for applications with high real-time requirements and large data volumes, such as intelligent transportation [12], smart healthcare [13], autonomous driving [14], unmanned aerial vehicles (UAVs) [15], and the Metaverse [16]. Zhou [17] considered the joint task offloading and resource allocation problem of multiple MEC server collaboration and proposed a two-level algorithm. The upper-level algorithm combines the advantages of algorithms such as PSO and GA to globally search for advanced offloading solutions. The lower-level algorithm is used to effectively utilize server resources and generate resource allocation plans with fairness guarantees. Sun [18] considers splitting multiple computationally intensive tasks into multiple subtasks simultaneously. A joint task segmentation and parallel scheduling scheme based on the dominant actor–critic (A2C) algorithm is proposed to minimize the total task execution delay. Chen [19] proposed a two-stage evolutionary search scheme (TESA), where the first stage optimizes computing resource selection, and the second stage jointly optimizes task offloading decisions and resource allocation based on a subset of the first stage, thereby significantly reducing latency. Zhu [20] considered the impact of user offloading decisions, uplink power allocation, and MEC computing resource allocation on system performance. An edge computing task offloading strategy based on improved genetic algorithm (IGA) is proposed.
2.2. Task Offloading for Cloud–Edge Collaboration
Cloud–edge collaborative task offloading refers to the collaborative processing between cloud computing and edge computing. Tasks can be allocated between the cloud and edge based on their characteristics and requirements. The advantage of cloud–edge collaboration is that it can take into account the powerful computing power of cloud computing and the low latency characteristics of edge computing, thereby optimizing resource utilization and service quality [21,22]. Zhang [23] proposed a task offloading strategy based on a time delay penalty mechanism and a bipartite graph matching method to optimize the task allocation between edge devices and the cloud. The aim is to minimize system energy consumption. Gao [24] established a dynamic queue model and used the drift and penalty function framework to transform the problem into a constrained optimization problem. Finally, a task offloading algorithm based on Lyapunov optimization was proposed. Lei [25] considered that the performance of geographically distributed edge servers varies over time and developed a dynamic offloading strategy based on a probabilistic evolutionary game theory model.
2.3. Task Offloading for Cloud–Edge–End Collaboration
Cloud–edge–end collaborative task offloading further extends the concept of cloud–edge collaboration by incorporating the computing capabilities of end devices (such as smartphones, sensors, and IoT devices). In this model, tasks can be flexibly allocated between end devices, edge servers, and cloud servers. This collaborative approach maximizes the use of computing resources at all levels and provides a more flexible and efficient computing solution. Liu [26] decomposed the task offloading and resource allocation problem into two sub-problems. First, the optimal solution of the task partitioning ratio was obtained using a mathematical analytical method, and then the Lagrangian dual (LD) method was used to optimize the task offloading and resource allocation strategies to minimize the task processing delay. Zhu [27] proposed a speed-aware and customized task offloading and resource allocation scheme aimed at optimizing service latency in mobile edge computing systems. By utilizing the Advantage Actor Critic (A2C) algorithm, computing nodes are dynamically selected to improve user service quality. Qu [28] takes the total task execution delay and key task execution delay as the optimization goals and proposes an emergency offloading strategy for smart factories based on cloud–edge collaboration through the Fast Chemical Reaction Optimization (Fast-CRO) algorithm. The algorithm can quickly make emergency unloading decisions for the system. Wu [29] proposed an online task scheduling algorithm based on deep reinforcement learning for mobile edge computing networks with variable task arrival intensity to achieve online task offloading and optimize overall task latency. Ji [30] performed intelligent tasks through a cloud–edge collaborative computing network. A hybrid framework that combines a model-free deep reinforcement learning algorithm and a model-based optimization algorithm was proposed to jointly optimize communication resources and computing resources, achieving near-optimal energy performance. Zhou [31] proposed an edge server placement algorithm ISC-QL to determine the optimal placement location of edge servers in the Internet of Vehicles system, which achieved optimization of load balancing, average latency, and average energy consumption.
In summary, researchers have conducted a lot of research on the task offloading problem of cloud computing and edge computing. The relevant work is shown in Table 1, but there are relatively few studies that consider the collaborative integration of cloud, edge, and end for the task offloading environment. The above research content does not clarify the impact of edge bandwidth resources on the system data transmission environment. At the same time, there is a lack of stable and efficient algorithms to solve the task offloading problem of cloud–edge–end collaboration, which is crucial for optimizing the execution of large-scale tasks in a multi-user environment.

Table 1.
Summary of related works versus our survey.
3. System Model and Problem Formulation
As shown in Figure 1, we consider a three-layer network framework for cloud–edge–end collaboration, which mainly includes the cloud computing layer, edge computing layer, and user device layer. It consists of 1 CS, S ESs, and N UDs, with a total of nodes. The coordinates of each node are composed of three-dimensional coordinates. Each node has its own CPU clock frequency f, represents the CPU clock frequency of the CS, represents the CPU clock frequency of the ES , and represents the CPU clock frequency of the UD . We assume that each UD has tasks to execute, and each task has a unique characteristic attribute to represent the computing data size of the task. Each task can be executed on its own user device, all edge servers, and cloud servers, and the offloading node is unique. Therefore, each task has execution modes. For tasks with a small computing data size, they can be executed on the user device, while for tasks with a large computing data size, they can be transferred to the edge server or cloud server for execution, that is, the processing power of the user device itself is taken into account, while the high computing resources of the cloud server are also taken into account.
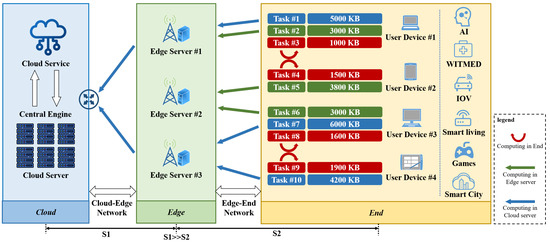
Figure 1.
Cloud–edge–end collaborative computing model.
Since users are generally concerned about task completion efficiency, while service providers focus on the energy consumption of service provision, we focus on optimizing the average response time and average energy consumption of all tasks. In the three-layer network architecture, response time must account for the influence of transmission delay factors in both edge computing and cloud computing modes. For the cloud computing mode, the edge server is selected as a transit node. Given that cloud servers feature abundant bandwidth resources, edge servers act as transit nodes for both edge computing and cloud computing modes; thus, we focus on the bandwidth resource constraints of edge servers. represents the bandwidth resource of the ES.
In order to make full use of bandwidth resources and computing resources in the three-layer computing environment, resource exclusivity will be adopted. When there is a task transmission, the remaining tasks will wait for the release of bandwidth resources. Similarly, when there is a task execution, the remaining tasks will wait for the release of computing resources. Table 2 summarizes the key symbols used in this paper. Next, we introduce the response time model and energy consumption model, respectively [32,33,34,35], and analyze the three-layer computing mode corresponding to each model.

Table 2.
Commonly used terms in cloud–edge–end model.
3.1. Response Time Model
Task response time refers to the complete time interval from task submission to the return of task processing results, and its components include task waiting time, task transmission time, and task processing time. In this subsection, we will calculate and analyze the response time of tasks in different computing modes.
- (1)
- Local computing mode: The local computing mode means that the tasks generated by the user device are directly executed on the user device. The local computing mode is not affected by the transmission delay factor. The task response time is the sum of the execution waiting time and the execution time. When UD is idle, the response time of task in UD is the local execution time of the task, and the task execution waiting time is 0. Otherwise, the response time of task needs to take into account the waiting time of the task. The task response time of the local computing mode is defined as follows:where represents the execution waiting time of task.
- (2)
- Edge computing mode: The edge computing mode refers to the transmission of tasks generated by user devices to edge servers for execution. The edge computing mode needs to consider the transmission delay of tasks between user devices and edge servers. Since the result data after the task is executed is small, the transmission delay of the result data transmitted back to the user device is ignored here. The transmission time of task is the transmission delay of task from UD to ES. The task response time is the sum of the transmission waiting time, transmission time, execution waiting time, and execution time. When the edge server bandwidth resources are not occupied, the transmission waiting time of task is 0. When ES is idle, of task is 0. The transmission rate [36] between UD and ES is defined as follows:The task response time of the edge computing model is defined as follows:where represents the transmission waiting time of task, and represents the transmission end time of task.
- (3)
- Cloud computing mode: The cloud computing model refers to the task generated by the user device being transmitted to the cloud server for execution. The task is transmitted to the cloud server, with the edge server as the transit transmission node. The selection method of the transit edge node is determined by comprehensively considering the amount of tasks to be transmitted, bandwidth resources of the edge node, and the distance between the user UD and the CS to which the task is transited using the edge node. And the occupation of the edge bandwidth resources by the task transmission is not released until it is transmitted to the cloud server. Since the result data after the task is executed is small, the transmission delay of the result data from the cloud server back to the edge server and from the edge server back to the user device is also ignored here. The transmission time of task is the sum of the transmission delays of task from UD to ES and ES to CS. The task response time is the sum of the transmission waiting time, transmission time, execution waiting time, and execution time. Similarly, when the edge server bandwidth resources are not occupied, of task is 0. When CS is idle, of task is 0. The transmission rate between ES and CS is defined as follows:The task response time of the cloud computing model is defined as follows:
3.2. Energy Consumption Model
Energy consumption refers to the total energy consumed by the system in the process of processing tasks, and its components mainly include task execution energy consumption and task transmission energy consumption. In this subsection, we will specifically calculate and analyze the energy consumption of tasks in different computing modes.
- (1)
- Local computing mode: Since the local computing mode does not perform task transmission, there is no energy consumption generated by task transmission. Therefore, the energy consumption of task is the execution energy consumption of task. The energy consumption of the local computing mode is defined as follows:where v is a positive constant.
- (2)
- Edge computing mode: Since the edge computing mode requires the transmission of tasks between user devices and edge servers, the transmission energy consumption of tasks needs to be considered. Since the result data after the task is executed is small, the transmission energy consumption of the result data transmitted from the edge server back to the user device is ignored here. The transmission energy consumption only considers the transmission energy consumption of task from UD to ES. The energy consumption of task is the sum of the transmission energy consumption and the execution energy consumption. The energy consumption of the edge computing mode is defined as follows:
- (3)
- Cloud computing mode: Since the cloud computing model requires edge servers as transit nodes, it is necessary to consider the transmission energy consumption of tasks from user devices to edge servers and from edge servers to cloud servers. Since the result data after the task is executed is small, the transmission energy consumption of the result data from the cloud server back to the edge server and from the edge server back to the user device is also ignored here. The energy consumption of the cloud computing model is defined as follows:
3.3. Problem Formulation
The purpose of this paper is to optimize the task offloading problem in the cloud–edge collaborative network environment while taking into account the full utilization of the edge server bandwidth resources and the CPU resources of the three-layer computing nodes. Formulas (1), (6), and (11) describe the task response time of the three computing modes, respectively. Since each user is mainly concerned about the efficiency of completing his or her own tasks, we use the average response time of the task as a measure of user service quality. The average response time of M tasks is defined as follows:
Formulas (12)–(14) describe the energy consumption corresponding to the three computing modes, respectively. Since service providers are mainly concerned with the energy consumption caused by providing services, we use the average energy consumption of tasks as a measure to evaluate service energy consumption. The average energy consumption of M tasks is defined as follows:
The target optimization problem is defined as follows:
where and represent the weights of average response time and average energy consumption in the target optimization problem, respectively.
4. Task Offloading Based on GAPSO
4.1. Standard Particle Swarm Optimization (SPSO) Algorithm and Coding
- (1)
- SPSO: The particle swarm optimization algorithm is a swarm intelligence optimization technology that simulates the foraging behavior of bird flocks. It finds the optimal solution by simulating information sharing between individuals in a bird flock [37]. In the algorithm, each solution is regarded as a particle flying in the solution space. The particle adjusts its flight direction and velocity according to the individual’s historical best position (individual extremum) and the group’s historical best position (global extremum). Each particle has only two attributes: speed and position. The speed indicates the particle’s moving speed, and the position indicates the particle’s moving direction [38]. Specifically, since there are M tasks in total, the spatial dimension is M, and there are L particles in the population, then the solution space can be expressed as , where the lth particle consists of two M-dimensional vectors, and . represents the position of the particle, and represents the position after h rounds of iteration. At the same time, the speed of each particle is expressed as . As the iteration proceeds, the position and speed of the particle will change according to the individual historical optimal solution and the global optimal solution , as shown in Formulas (18) and (19). The solution can be obtained by iterative execution until the end.where and are random numbers in the range .
- (2)
- Coding: The position and speed of particles in the PSO algorithm are two important properties, since each task has execution modes. The position and speed of particles are expressed by Formulas (20) and (21). Among them, means that task m is not executed at node o, and means that task m is executed at node o. The particle position is constrained by Formula (22). And is a random number between . After the calculation of Formula (18), will be calculated by Formula (23), and each value will be converted into a probability between . Formula (19) indicates that roulette is used to select execution nodes to avoid falling into local optimality. In the particle position matrix of this paper, the higher the number of rows, the lower the corresponding task transmission and execution priority. Formula (24) is used as the particle fitness.where . .
4.2. Adaptive Inertia Weight w
The inertia weight w plays a balancing role between the global search capability and local search capability of the SPSO algorithm. It determines the extent to which the current velocity of the particle is affected by the previous velocity and has a significant impact on the accuracy and convergence speed of the algorithm. In the early stage of algorithm iteration, setting a larger w can increase the movement speed of particles, thus enhancing the global search capability. As the iterative process proceeds, gradually reducing w can reduce the moving speed of particles, prompting the particle swarm to focus on local search. We adopt a linear strategy to adjust w to adaptively adjust the local and global search ability of particles. The specific adjustment method is shown in Formula (25).
where h and represent the current iteration number and the maximum iteration number, respectively, and and are the maximum and minimum values of the predefined inertia weight, respectively.
4.3. Adaptive Acceleration Coefficients ,
The acceleration coefficient determines the particle’s dependence on the local optimum, which helps to explore the local environment and maintain population diversity. The acceleration coefficient determines the particle’s dependence on the global optimum, which helps the algorithm converge quickly. We use a nonlinear strategy to dynamically adjust and . Specifically, let gradually decrease from 2.5, while gradually increases from 0.5. In the early stages of iteration, particles rely more on personal experience, increase search diversity, quickly approach the global optimal solution, and avoid falling into the local optimum. As the iteration deepens, particles gradually turn to rely on group experience, enhance local search capabilities, fine-tune the optimal solution, and accelerate convergence. The specific adjustment method is shown in Formulas (26) and (27).
where and are the maximum and minimum values of the predefined acceleration coefficients, respectively.
4.4. OBL Algorithm Initialization Population
The OBL algorithm is a search strategy for optimization problems that enhances population diversity by introducing the concept of opposition. This approach effectively improves the algorithm’s search capability and the quality of the initial population. It increases the diversity of the search by generating a corresponding opposition solution for each initial solution, which helps to explore the solution space more comprehensively. Compared with simply introducing random solutions, it is more likely to approach the global optimum, thereby accelerating the convergence of the algorithm. At the same time, it also helps to avoid falling into the local optimum and improve the global search performance of the algorithm. The detailed process of initializing the particle swarm is shown in Algorithm 1.
4.5. Crossover and Mutation
Crossover in genetic algorithms is a process that simulates biological reproduction. It allows two parent individuals to exchange some of their genetic information to produce offspring. The purpose of crossover is to combine the excellent characteristics of parent individuals to create new individuals that may have higher fitness. Mutation is a process that simulates gene mutation. It introduces new genetic diversity by randomly changing one or more gene bits in the genetic code of an individual with a certain probability. Mutation operations can sometimes guide particles out of the local optimum and find the global optimal solution.
This paper uses crossover and mutation operations in GA to update the local optimal solution of particles, that is, to update the position matrix of particles. This paper uses two-point crossover to generate new individuals. And all gene bits of new individuals are mutated probabilistically. Since each column in the position matrix represents an execution mode, the S column is edge server computing, and the two columns are local computing and cloud server computing. Therefore, when a gene bit mutates, first, the three computing methods are selected with equal probability, and then the specific execution mode is selected with equal probability, that is, the probability of mutation to local computing and cloud server computing is , and the probability of mutation to any edge server computing is . The crossover and mutation operations are shown in Figure 2 and Figure 3. Algorithm 2 details the process of GA updating the local optimal solution.
| Algorithm 1 Initialize the population-based OBL |
Input: L (population size), M (number of tasks), O (number of execution modes)
|
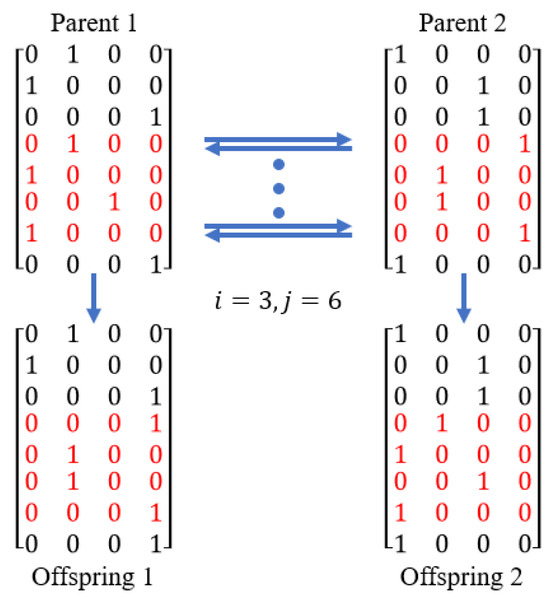
Figure 2.
Crossover operation of the position matrix.

Figure 3.
Mutation operation on the location matrix.
| Algorithm 2 Update local optimal solution based GA |
Input: p (current particle), (position matrix of the local optimal solution of the current particle), (position matrix of the global optimal solution of the population), (mutation probability)
|
4.6. GAPSO Algorithm
This paper adopts the GAPSO algorithm to solve the problem of task offloading in cloud–edge–end collaboration. Task offloading is optimized by introducing the OBL algorithm, adaptive inertia weight, and adaptive acceleration coefficient. In this algorithm, the OBL algorithm is first used to initialize the particle swarm. The OBL algorithm introduces the concept of opposition in the particle initialization process, constructs opposing particles, and avoids the initial solution being confined to a limited range, so as to improve the quality and diversity of the initial population. Then the population is updated iteratively. The inertia weight and acceleration coefficient are updated at the beginning of each iteration, responding to the evolution state of the particle swarm in real time, dynamically optimizing the balance between exploration and development, and avoiding premature convergence or slow convergence. During the iteration process, the GA algorithm is used to implement particle crossover and mutation operations, update the local optimal solutions of all particles, and guide the particles to jump out of the local optimal solution with a certain possibility. Until the end condition is met, the optimal task offloading solution is output. The detailed process is shown in Algorithm 3.
| Algorithm 3 The algorithm steps of GAPSO |
| Initialization parameters: , , , Output: The offloading solution for all tasks corresponding to the global optimal solution
|
5. Experiments and Analysis
5.1. Experimental Settings
In this section, we will consider a network topology environment covered by one CS, multiple ESs, and multiple UDs. The positions of CS, ESs, and UDs are determined by three-dimensional spatial coordinates . The position of CS is fixed. The positions of ESs and UDs are randomly distributed in the spatial area, and the distance between them is ensured to exceed a certain limit distance to avoid overcrowding. Each UD will generate a random number of tasks, each with a unique attribute, task data size, in the range of KB.
We use the Windows 11 operating system to build the experimental simulation environment on the Python 3.11.5 platform. The relevant parameters used in the simulation experiment are summarized in Table 3 [39,40]. The following algorithms are used to compare the performance with the algorithm proposed in this paper: GA, SPSO, adaptive inertia weight and chaotic learning factor particle swarm optimization (AICLPSO) [41], and chaotic adaptive particle swarm optimization algorithm (CAPSO) [42]. This experiment is based on a symmetric architecture. All algorithms are run under the same conditions, including the same cloud–edge–end topology environment, environment parameter configuration, number of iterations, and evaluation criteria. This symmetric design ensures fairness in the comparison between algorithms and helps improve the reliability of the results. At the same time, this balanced experimental structure not only helps to enhance the effectiveness of the research but also fits in with the consistency emphasized by symmetry.

Table 3.
Experimental parameter setting.
In view of the research problem in this paper, the parameter settings of each algorithm are shown in Table 4. Considering the influence of randomness, each algorithm is repeated 10 times.

Table 4.
Information on algorithm parameters settings.
5.2. Performance Evaluation
Based on actual needs, users are usually more concerned about the efficiency of task execution, while service providers regard energy consumption in the service process as a core concern. Based on this realistic scenario, in order to achieve a balanced optimization of the interests of both users and service providers, this section uses the average response time and average energy consumption with equal weights as comprehensive evaluation indicators. In this section, in order to intuitively show the significant advantages of the cloud–edge–end environment, we rely on the offloading algorithm proposed in this article. For the four environments of cloud–edge–end (CEE) collaboration, cloud–edge (CE1) collaboration, cloud–end (CE2) collaboration, and edge–end (EE) collaboration, we focus on comparing and analyzing their optimal average response time and total energy consumption performance under the task number gradient of 200, 225, 250, 275, and 300. At the same time, under the same cloud–edge–end collaboration experimental environment configuration, we will further compare the optimization performance differences between the proposed algorithm and other algorithms.
- (1)
- Parameter sensitivity analysis: Figure 4a,b are experiments conducted while keeping and unchanged. In Figure 4a, is kept unchanged. It can be seen from the figure that the curve converges earlier when is 0.2. This is because the low inertia weight in the middle and late stages of the iteration causes the particles to ignore the historical speed and completely rely on the current optimal position, resulting in too fast convergence. When is 0.6, the curve converges more slowly and the final effect is poor. This is because the particle speed is insufficiently attenuated, and a strong exploration inertia is always maintained, resulting in the inability to converge well in the over-exploration search space. In Figure 4b, is kept unchanged. It can be seen from the figure that the curve converges the worst when is 0.7. This is because when is small, the inertial component of the particle speed is weak, so the particles rely on the attraction of and earlier, which accelerates the development to the current optimal position, resulting in insufficient exploration, and the particles are easy to quickly gather in the local optimal area. When is 1.1, the effect of faster exploration of the optimal solution is shown in the early stage of the iteration. This is because the inertial component of the particle velocity is higher and more dependent on the historical velocity, which reduces the attraction of and , thereby promoting a wider exploration of the search space, so there is a greater probability of finding a better solution in the early stage, but it will not be able to converge to the optimal solution quickly in the later stage. Figure 4c,d are experiments carried out while keeping and unchanged. In Figure 4c, is kept unchanged. It can be seen from the figure that the convergence effect is the worst when is 0.2. This may be because the particles in the later stage mainly rely on inertial motion, lack traction to the optimal solution, and cannot jump out of the suboptimal solution. When is 0.8, the convergence effect is poor. This is because the and coefficients are too high in the middle and late stages, forcing the particles to develop to the current optimal position too early and fall into the local optimal solution. In Figure 4d, is kept unchanged. It can be seen from the figure that when is 2.2, the convergence is slow and the convergence effect is the worst. This is because the maximum step size is limited in the early stage, the exploration ability is insufficient, and it is impossible to jump out of the local optimum. When is set to 2.6, the initial optimization is faster, but the convergence effect is poor. This is because the higher the value, the greater the exploration advantage in the early stage. However, this will also make the particle movement step too large, which makes it easy to miss the optimal solution. Therefore, in order to achieve a balance between exploration and development and ensure robust convergence, is set to 0.9, is set to 0.4, is set to 2.5, and is set to 0.5.
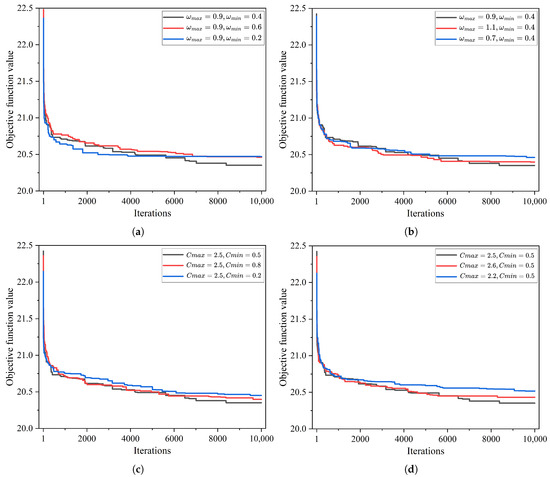 Figure 4. (a) variable. (b) variable. (c) variable. (d) variable.
Figure 4. (a) variable. (b) variable. (c) variable. (d) variable. - (2)
- Comparison of average response time, total energy consumption, and number of tasks: Figure 5 and Figure 6 show the changing trends of the average response time for completing each task and the total energy consumption for completing all tasks in different environments. In the four operating environments, as the number of tasks increases, the amount of tasks waiting to be processed in different execution modes increases due to the total amount of computing resources, resulting in an upward trend in the average response time and total energy consumption of tasks. In Figure 5, under the same number of tasks, CEE has a maximum acceleration effect of 49.64% in response time compared with CE2, a maximum acceleration effect of 27.26% compared with EE, and a maximum acceleration effect of 4.31% compared with CE1, showing a significant advantage overall. In Figure 6, under the same number of tasks, CEE has a maximum energy saving of 24.83% compared with CE2 and a maximum energy saving of 22.89% compared with CE1, showing a significant advantage. Compared with EE, CEE takes the cloud computing model into consideration. Since the distance from CS to ES is significantly increased compared to the distance from ES to UD, a large amount of transmission energy is required to offload tasks to CS for processing, resulting in more total energy consumption for CEE than EE. These two figures show that the emergence of edge computing will greatly reduce the response time and energy consumption of completing tasks. At the same time, it can also show that cloud–edge–end collaboration has significant advantages and broad development prospects.
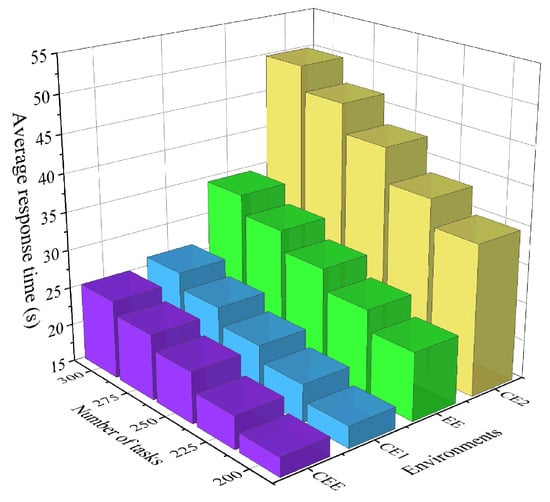 Figure 5. Average response times for different environments and number of tasks.
Figure 5. Average response times for different environments and number of tasks.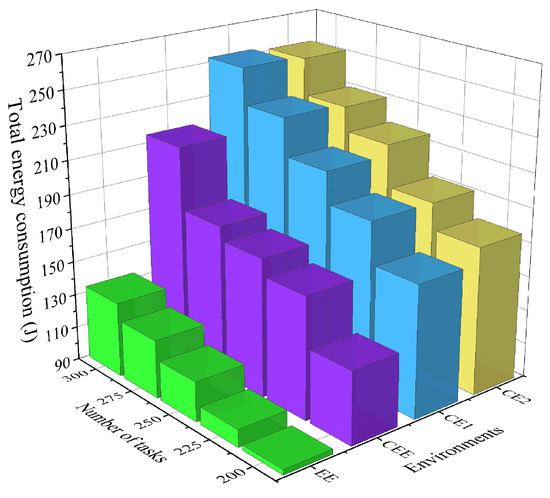 Figure 6. Total energy consumption for different environments and number of tasks.
Figure 6. Total energy consumption for different environments and number of tasks. - (3)
- Algorithm performance: Under the cloud–edge–end collaborative processing framework proposed in this paper, the time complexity of the GAPSO, GA, SPSO, AICLPSO, and CAPSO algorithms is consistent with . The average change in the objective function value obtained by repeating 10 experiments for each algorithm to process the same task data in the same cloud–edge–end collaborative environment is shown in Figure 7. From the change in the curve, the GAPSO algorithm proposed in this paper shows obvious optimization effect. In the early stage of iteration, the GAPSO algorithm can obtain better initial solutions than the GA, SPSO, and AICLPSO algorithms, which highlights that the introduction of the OBL algorithm in the GAPSO algorithm can increase the diversity of the initial population and overcome the obstacle of falling into the local optimum to a certain extent. In the later stage of iteration, the GAPSO algorithm achieves better convergence accuracy than the other four algorithms and can reduce the objective function value by about 6–12%, indicating that the algorithm can find a better task allocation solution. The objective function value does not change after 1200 consecutive iterations, which is used as the basis for judging the convergence of the algorithm. From the convergence points marked in the figure, it can be seen that the GAPSO algorithm converges faster than the GA and SPSO algorithms. As can be seen from Table 5, GAPSO has obvious advantages over other algorithms in terms of mean, variance, and standard deviation, indicating that the algorithm has high stability. In general, the GAPSO algorithm we proposed has higher convergence accuracy and stronger stability. It can effectively avoid falling into local optimal solutions and is easier to search for global optimal solutions.
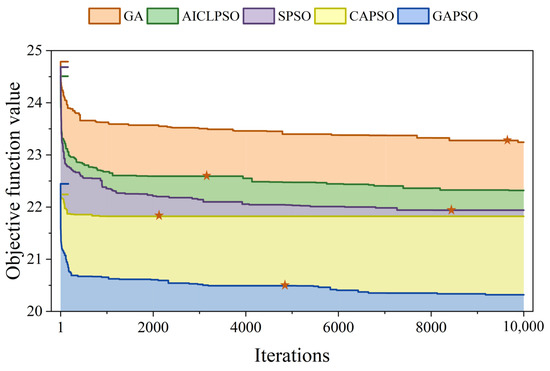 Figure 7. Change in the average objective function value of each algorithm.
Figure 7. Change in the average objective function value of each algorithm. Table 5. Test results of each algorithm.
Table 5. Test results of each algorithm.
6. Conclusions
This paper focuses on the problem of task offloading in the cloud–edge–end collaborative environment and constructs a cloud–edge–end collaborative task processing framework. The framework supports flexible allocation of tasks between user devices, edge servers, and cloud servers, can give full play to the advantages of nodes at each layer, and effectively reduce the computing pressure of user devices. At the same time, in order to reduce the average response time and execution energy consumption of task completion, this paper introduces an opposition-based learning algorithm, adaptive inertia weight, and adaptive acceleration coefficient to propose a GAPSO algorithm. The proposed algorithm is compared with other traditional algorithms and heuristic algorithms using method symmetric design. Experimental results verify that the proposed algorithm can obtain a better initialization solution set and task offloading scheme, reducing the objective function value by about 6–12%, while showing excellent convergence speed, accuracy, and stability. At the algorithm level, there are many research algorithms for the cloud–edge–device collaborative environment. However, algorithms with high adaptability to actual application scenarios are still scarce. At the practical application level, cloud–edge–end collaboration has gradually penetrated into key areas such as industrial Internet of Things, intelligent transportation, smart cities, and telemedicine. However, the heterogeneity and dynamic nature of resources in different hardware devices, as well as the privacy and security issues of user devices during collaborative task processing, have not been effectively resolved. Therefore, for cloud–edge–end collaborative applications, the development of highly adaptable algorithms, the research on resource computing power, and the privacy and security of data transmission are still issues worth studying in the future.
Author Contributions
Conceptualization, W.W., Y.H. and P.Z.; Methodology, W.W., Z.X. and L.T.; Software, W.W. and Y.H.; Investigation, Y.H., Z.X. and L.T.; Writing—original draft, W.W., Y.H. and Z.X.; Visualization: Y.H. and L.T.; Validation, W.W. and Y.H.; Formal analysis, P.Z. All authors have read and agreed to the published version of this manuscript.
Funding
This work is partially supported by the Tertiary Education Scientific research project of Guangzhou Municipal Education Bureau under Grant 2024312246, the Guangdong Province Natural Science Foundation of Major Basic Research and Cultivation Project under Grant 2024A1515011976, the Shandong Provincial Natural Science Foundation under Grant ZR2023LZH017, ZR2022LZH015, ZR2023QF025 and ZR2024MF066, the National Natural Science Foundation of China under Grant 52477138, 62471493 and 62402257, and the China University Research Innovation Fund under Grant 2023IT207.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no potential conflicts of interests.
References
- Gao, H.; Wang, X.; Wei, W.; Al-Dulaimi, A.; Xu, Y. Com-DDPG: Task offloading based on multiagent reinforcement learning for information-communication-enhanced mobile edge computing in the internet of vehicles. IEEE Trans. Veh. Technol. 2023, 73, 348–361. [Google Scholar] [CrossRef]
- Quy, V.K.; Hau, N.V.; Anh, D.V.; Ngoc, L.A. Smart healthcare IoT applications based on fog computing: Architecture, applications and challenges. Complex Intell. Syst. 2022, 8, 3805–3815. [Google Scholar] [CrossRef]
- Mahajan, H.B.; Junnarkar, A.A. Smart healthcare system using integrated and lightweight ECC with private blockchain for multimedia medical data processing. Multimed. Tools Appl. 2023, 82, 44335–44358. [Google Scholar] [CrossRef] [PubMed]
- Sharma, M.; Tomar, A.; Hazra, A. Edge computing for industry 5.0: Fundamental, applications and research challenges. IEEE Internet Things J. 2024, 11, 19070–19093. [Google Scholar] [CrossRef]
- Tang, S.; Chen, L.; He, K.; Xia, J.; Fan, L.; Nallanathan, A. Computational intelligence and deep learning for next-generation edge-enabled industrial IoT. IEEE Trans. Netw. Sci. Eng. 2022, 10, 2881–2893. [Google Scholar] [CrossRef]
- Islam, A.; Debnath, A.; Ghose, M.; Chakraborty, S. A survey on task offloading in multi-access edge computing. J. Syst. Archit. 2021, 118, 102225. [Google Scholar] [CrossRef]
- Liu, B.; Xu, X.; Qi, L.; Ni, Q.; Dou, W. Task scheduling with precedence and placement constraints for resource utilization improvement in multi-user MEC environment. J. Syst. Archit. 2021, 114, 101970. [Google Scholar] [CrossRef]
- Wang, X.; Xing, X.; Li, P.; Zhang, S. Optimization Scheme of Single-Objective Task Offloading with Multi-user Participation in Cloud-Edge-End Environment. In Proceedings of the 2022 IEEE Smartworld, Ubiquitous Intelligence & Computing, Scalable Computing & Communications, Digital Twin, Privacy Computing, Metaverse, Autonomous & Trusted Vehicles (SmartWorld/UIC/ScalCom/DigitalTwin/PriComp/Meta), Haikou, China, 15–18 December 2022; pp. 1166–1171. [Google Scholar]
- Saeik, F.; Avgeris, M.; Spatharakis, D.; Santi, N.; Dechouniotis, D.; Violos, J.; Leivadeas, A.; Athanasopoulos, N.; Mitton, N.; Papavassiliou, S. Task offloading in Edge and Cloud Computing: A survey on mathematical, artificial intelligence and control theory solutions. Comput. Netw. 2021, 195, 108177. [Google Scholar] [CrossRef]
- Zhang, Y.; Yu, H.; Zhou, W.; Man, M. Application and research of IoT architecture for End-Net-Cloud Edge computing. Electronics 2022, 12, 1. [Google Scholar] [CrossRef]
- Pan, L.; Liu, X.; Jia, Z.; Xu, J.; Li, X. A multi-objective clustering evolutionary algorithm for multi-workflow computation offloading in mobile edge computing. IEEE Trans. Cloud Comput. 2021, 11, 1334–1351. [Google Scholar] [CrossRef]
- Gong, T.; Zhu, L.; Yu, F.R.; Tang, T. Edge intelligence in intelligent transportation systems: A survey. IEEE Trans. Intell. Transp. Syst. 2023, 24, 8919–8944. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, G.; Wen, T.; Yuan, Q.; Wang, B.; Hu, B. A cloud-edge collaborative framework and its applications. In Proceedings of the 2021 IEEE International Conference on Emergency Science and Information Technology (ICESIT), Chongqing, China, 22–24 November 2021; pp. 443–447. [Google Scholar]
- McEnroe, P.; Wang, S.; Liyanage, M. A survey on the convergence of edge computing and AI for UAVs: Opportunities and challenges. IEEE Internet Things J. 2022, 9, 15435–15459. [Google Scholar] [CrossRef]
- Liu, Y.; Deng, Q.; Zeng, Z.; Liu, A.; Li, Z. A hybrid optimization framework for age of information minimization in UAV-assisted MCS. IEEE Trans. Serv. Comput. 2025, 18, 527–542. [Google Scholar] [CrossRef]
- Chen, M.; Liu, A.; Xiong, N.N.; Song, H.; Leung, V.C. SGPL: An intelligent game-based secure collaborative communication scheme for metaverse over 5G and beyond networks. IEEE J. Sel. Areas Commun. 2023, 42, 767–782. [Google Scholar] [CrossRef]
- Zhou, J.; Zhang, X. Fairness-aware task offloading and resource allocation in cooperative mobile-edge computing. IEEE Internet Things J. 2021, 9, 3812–3824. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, X. A2C learning for tasks segmentation with cooperative computing in edge computing networks. In Proceedings of the GLOBECOM 2022—2022 IEEE Global Communications Conference, Rio de Janeiro, Brazil, 4–8 December 2022; pp. 2236–2241. [Google Scholar]
- Chen, Q.; Yang, C.; Lan, S.; Zhu, L.; Zhang, Y. Two-Stage Evolutionary Search for Efficient Task Offloading in Edge Computing Power Networks. IEEE Internet Things J. 2024, 11, 30787–30799. [Google Scholar] [CrossRef]
- Zhu, A.; Wen, Y. Computing offloading strategy using improved genetic algorithm in mobile edge computing system. J. Grid Comput. 2021, 19, 38. [Google Scholar] [CrossRef]
- Chen, H.; Qin, W.; Wang, L. Task partitioning and offloading in IoT cloud-edge collaborative computing framework: A survey. J. Cloud Comput. 2022, 11, 86. [Google Scholar] [CrossRef]
- Hu, S.; Xiao, Y. Design of cloud computing task offloading algorithm based on dynamic multi-objective evolution. Future Gener. Comput. Syst. 2021, 122, 144–148. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, H.; Zhou, X.; Yuan, D. Energy minimization task offloading mechanism with edge-cloud collaboration in IoT networks. In Proceedings of the 2021 IEEE 93rd Vehicular Technology Conference (VTC2021-Spring), Helsinki, Finland, 25–28 April 2021; pp. 1–7. [Google Scholar]
- Gao, J.; Chang, R.; Yang, Z.; Huang, Q.; Zhao, Y.; Wu, Y. A task offloading algorithm for cloud-edge collaborative system based on Lyapunov optimization. Clust. Comput. 2023, 26, 337–348. [Google Scholar] [CrossRef]
- Lei, Y.; Zheng, W.; Ma, Y.; Xia, Y.; Xia, Q. A novel probabilistic-performance-aware and evolutionary game-theoretic approach to task offloading in the hybrid cloud-edge environment. In Proceedings of the Collaborative Computing: Networking, Applications and Worksharing: 16th EAI International Conference, CollaborateCom 2020, Shanghai, China, 16–18 October 2020; Proceedings, Part I 16. Springer: Berlin/Heidelberg, Germany, 2021; pp. 255–270. [Google Scholar]
- Liu, F.; Huang, J.; Wang, X. Joint task offloading and resource allocation for device-edge-cloud collaboration with subtask dependencies. IEEE Trans. Cloud Comput. 2023, 11, 3027–3039. [Google Scholar] [CrossRef]
- Zhu, D.; Li, T.; Tian, H.; Yang, Y.; Liu, Y.; Liu, H.; Geng, L.; Sun, J. Speed-aware and customized task offloading and resource allocation in mobile edge computing. IEEE Commun. Lett. 2021, 25, 2683–2687. [Google Scholar] [CrossRef]
- Qu, X.; Wang, H. Emergency task offloading strategy based on cloud-edge-end collaboration for smart factories. Comput. Netw. 2023, 234, 109915. [Google Scholar] [CrossRef]
- Wu, H.; Geng, J.; Bai, X.; Jin, S. Deep reinforcement learning-based online task offloading in mobile edge computing networks. Inf. Sci. 2024, 654, 119849. [Google Scholar] [CrossRef]
- Ji, Z.; Qin, Z. Computational offloading in semantic-aware cloud-edge-end collaborative networks. IEEE J. Sel. Top. Signal Process. 2024, 18, 1235–1248. [Google Scholar] [CrossRef]
- Zhou, Z.; Abawajy, J. Reinforcement learning-based edge server placement in the intelligent internet of vehicles environment. IEEE Trans. Intell. Transp. Syst. 2025. [Google Scholar] [CrossRef]
- Cai, J.; Liu, W.; Huang, Z.; Yu, F.R. Task decomposition and hierarchical scheduling for collaborative cloud-edge-end computing. IEEE Trans. Serv. Comput. 2024, 17, 4368–4382. [Google Scholar] [CrossRef]
- Wang, J.; Feng, D.; Zhang, S.; Liu, A.; Xia, X.G. Joint computation offloading and resource allocation for MEC-enabled IoT systems with imperfect CSI. IEEE Internet Things J. 2020, 8, 3462–3475. [Google Scholar] [CrossRef]
- An, X.; Fan, R.; Hu, H.; Zhang, N.; Atapattu, S.; Tsiftsis, T.A. Joint task offloading and resource allocation for IoT edge computing with sequential task dependency. IEEE Internet Things J. 2022, 9, 16546–16561. [Google Scholar] [CrossRef]
- Fan, W.; Liu, X.; Yuan, H.; Li, N.; Liu, Y. Time-slotted task offloading and resource allocation for cloud-edge-end cooperative computing networks. IEEE Trans. Mob. Comput. 2024, 23, 8225–8241. [Google Scholar] [CrossRef]
- Tong, Z.; Deng, X.; Mei, J.; Liu, B.; Li, K. Response time and energy consumption co-offloading with SLRTA algorithm in cloud–edge collaborative computing. Future Gener. Comput. Syst. 2022, 129, 64–76. [Google Scholar] [CrossRef]
- Alqarni, M.A.; Mousa, M.H.; Hussein, M.K. Task offloading using GPU-based particle swarm optimization for high-performance vehicular edge computing. J. King Saud Univ.-Comput. Inf. Sci. 2022, 34, 10356–10364. [Google Scholar] [CrossRef]
- Ma, S.; Song, S.; Yang, L.; Zhao, J.; Yang, F.; Zhai, L. Dependent tasks offloading based on particle swarm optimization algorithm in multi-access edge computing. Appl. Soft Comput. 2021, 112, 107790. [Google Scholar] [CrossRef]
- Wang, Y.; Ru, Z.Y.; Wang, K.; Huang, P.Q. Joint deployment and task scheduling optimization for large-scale mobile users in multi-UAV-enabled mobile edge computing. IEEE Trans. Cybern. 2019, 50, 3984–3997. [Google Scholar] [CrossRef]
- Tong, Z.; Deng, X.; Ye, F.; Basodi, S.; Xiao, X.; Pan, Y. Adaptive computation offloading and resource allocation strategy in a mobile edge computing environment. Inf. Sci. 2020, 537, 116–131. [Google Scholar] [CrossRef]
- Yuan, C.; Su, Y.; Chen, R.; Zhao, W.; Li, W.; Li, Y.; Sang, L. Multimedia task scheduling based on improved PSO in cloud environment. In Proceedings of the 2023 IEEE International Symposium on Broadband Multimedia Systems and Broadcasting (BMSB), Beijing, China, 14–16 June 2023; pp. 1–6. [Google Scholar]
- Duan, Y.; Chen, N.; Chang, L.; Ni, Y.; Kumar, S.S.; Zhang, P. CAPSO: Chaos adaptive particle swarm optimization algorithm. IEEE Access 2022, 10, 29393–29405. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).