Fingerprint-Based Secure Query Scheme for Databases over Symmetric Mirror Servers

Abstract

The Karp and Rabin (KR) fingerprint is a special hash-like function widely utilized for efficient string matching. Recently, Sharma et al.leveraged its linear and symmetric properties to facilitate private database queries. However, their approach mainly protects encrypted or secret-shared databases rather than public databases, where only the query privacy is required. In this paper, we focus explicitly on privacy-preserving queries over public read-only databases. We propose a novel fingerprint-based keyword query scheme using the distributed point function (DPF), which effectively hides users’ data access patterns across two symmetric mirror servers. Moreover, we provide a rigorous analysis of the false positive probability inherent in fingerprinting and discuss strategies for its minimization. Our scheme achieves efficiency close to plaintext methods, significantly reducing deployment complexity.

1. Introduction

A fingerprint is a type of function that maps a large data string to a value/string with relatively much shorter bit-length. Generally speaking, hash functions [1] can also be recognized as special fingerprints that are used to identify substantial blocks of data uniquely, while their cryptographic properties are believed to be safe against malicious attacks. Conversely, the Rabin–Karp (KR) fingerprint is another type of function implementing fingerprints using polynomials over a finite field. Such a function is much faster than the hash function and easy to implement.

KR Fingerprint Function. In 1987, Karp and Rabin [2] defined a fingerprint function as follows:

$${\varphi }_{r,p}\left(s\right)=\sum _{i=1}^{\ell }{s}_i{r}^{i}modp$$

for a prime modulo p, a randomly selected integer $r\in {\mathbb{F}}_p$, and a string $s=s_1{s}_2\dots s_{\ell }$ coded over the finite field ${\mathbb{F}}_p$. For the sake of brevity, throughout this paper, we also refer to such a KR fingerprint as a fingerprint.

This fingerprint is very important to string matching, as two identical strings generate the same fingerprints. Given a text string $\mathcal{T}$ and a pattern $\mathcal{P}$ of string length ℓ, one straightforward string-matching algorithm computes a fingerprint of a sliding text window of size ℓ, in $\mathcal{T}$, and compares this fingerprint to the fingerprint of $\mathcal{P}$, marking all the candidate occurrences with fingerprints equaling the pattern’s fingerprint. Clearly, compared with a letter-to-letter matching approach, a fingerprint can improve the string-matching efficiency using relatively shorter values. Based on fingerprints, many schemes have been developed to achieve better performance of string matching [3,4,5] during the last decades. In particular, a study [4] on exact online string matching has demonstrated how rolling hashes enable sublinear time search in static texts, and subsequent work [5] presents a low-latency algorithm in real-time streaming string matching. These results underscore the utility of fingerprinting not only in batch processing but also in dynamic, streaming environments, motivating our adoption of the KR fingerprint for privacy-preserving queries.

However, all these methods only work on plaintext and do not ensure any user’s privacy. That is to say, if the file is encrypted or secret shared, one cannot search the keywords over this file using previous methods. Recently, Sharma et al. proposed a secret-shared form of fingerprint, and applied it for keywords search over a secret-shared database [6]. They symmetrically distribute computational loads between servers using additive sharing, achieving highly efficient keyword queries. In fact, we note that in clouds, a database can be deployed in encryption or secret-share form, for the privacy consideration. This scheme provides protection for both datasets and users’ queries. However, the scheme by Sharma et al. is primarily tailored for privacy-preserving queries over encrypted databases. In many practical applications, the database itself may remain in plaintext while only the query privacy must be protected [7]. For example, medical records, restaurant sites, product catalogs, and positions in maps are open to everyone, but users’ queries can reveal their hobbies, locations, etc. Hiding access patterns is an important way to protect users’ privacy. Consequently, for such applications, a more efficient scheme needs to be designed.

On the other hand, note that all fingerprint functions map a long string to a short one—the collision does exist. Even in secret-share form, the collision problem still exists for the fingerprint.

For string matching, the collision problem will lead to false positive errors [8], which indicates the existence of phantom occurrence. Fortunately, differing with the hash function, the probability of a false positive error in the fingerprint function can be precisely analyzed. In order to do a precise query, we also need to reduce such probability.

Motivation: This work specifically addresses privacy-preserving keyword queries over publicly accessible datasets, where the primary privacy concern is the user’s query content rather than the data itself. Current privacy-preserving schemes such as searchable encryption, private information retrieval, or oblivious RAM often incur substantial overhead, especially when only query privacy (not database secrecy) is required. Thus, our research primarily addresses two critical challenges:

• Efficiency: achieving privacy-preserving keyword searches without heavy computational or communication burdens;
• Accuracy: reducing and precisely quantifying the false positive error inherent in fingerprint-based methods.

To overcome these challenges, we leverage KR fingerprints and distributed point functions (DPF) [9,10] to design a highly efficient and secure two-server query scheme, balancing query privacy, efficiency, and accuracy.

Related Work. Our proposed method for enabling private keyword queries on public datasets leverages a novel combination of KR fingerprint and DPF. This approach offers distinct advantages when contrasted with existing private information retrieval (PIR), particularly keyword PIR (kPIR), and oblivious RAM (ORAM) constructions.

PIR schemes, in general, aim to allow users to retrieve data from a server without revealing their query. In this domain, the kPIR scheme is a special case of PIR, and is designed to achieve exact keyword matching. However, this function often needs substantial overhead, especially within single-server PIR frameworks. For instance, Piano [11] introduced a single-server kPIR scheme, which achieves sublinear online server computation. Nonetheless, it requires clients to download the entire database during a preprocessing phase, which is often impractical for the large-scale datasets targeted in our work. Other single-server kPIR schemes, such as Spiral [12] and Vectorized Batch PIR [13], employ advanced cryptographic primitives like lattice-based homomorphic encryption to reduce the communication complexity. But these sophisticated cryptographic tools typically introduce significant computational overhead on the server side. The above kPIR schemes underscore persistent practical challenges, including substantial client-side burdens and intensive server-side computations. Broader general PIR schemes also present various trade-offs. SealPIR [14] introduces compressed queries and probabilistic batch codes to distribute computation across multiple queries, which reduces communication cost but brings a non-negligible failure probability. More recently, SimplePIR [15] attains high throughput through Pseudo-Random Function optimizations, but brings a large cost of setup and per-query communication.

ORAM schemes aim to obfuscate data access patterns. Path ORAM [16] exemplifies a widely recognized approach, employing a relatively simple tree-based construction. Although its simple design is an advantage, this method requires client-side state and multiple server interactions per query, incurring notable communication overhead. Recent works have been aiming to improve the efficiency of communication and computation. Asharov et al. [17] presented an ORAM scheme achieving a worst-case overhead of logarithmical order of block accesses for any block size, while requiring only constant client storage. Cong et al. [18] introduced an ORAM scheme based on fully homomorphic encryption (FHE) that is both non-interactive and stateless. Panacea shifts all computation to the server, greatly simplifying the client while leveraging FHE for privacy, though it incurs heavier server-side cryptographic overhead.

Additionally, beyond PIR and ORAM, some works in searchable symmetric encryption (SSE) also focus on hiding access patterns and result patterns. For example, Yuan et al. [19] propose a dynamic conjunctive SSE scheme that hides the result pattern of keyword pairs while offering forward and backward privacy. Similarly, Shang et al. [20] introduce obfuscated SSE, which obfuscates both access and search patterns at each query, achieving pattern privacy with lower communication costs than ORAM-based SSE. Although these works provide strong privacy, they often incur higher preprocessing or retrieval latency due to relying on structured encryption or oblivious data structures. In contrast, our scheme targets lightweight, public read-only databases and is based on simple symmetric primitives, which achieve lower communication and computation.

Our scheme departs from prior works by uniquely combining the KR fingerprint with DPF within a symmetric mirror-server architecture to protect query privacy over public databases. Leveraging the compressibility of DPF, we reduce the query domain to $O\left(\lambda \log p\right)$ communication complexity, where $\lambda$ is the security parameter and p is the DPF domain size. Additionally, we formally bound the false positive collision probability inherent in the KR fingerprint. Compared to traditional PIR and ORAM constructions, our scheme not only ensures query privacy but also achieves a more advantageous trade-off between client-side communication and server-side computation.

Organization. The remainder of this paper is structured as follows. Section 2 reviews preliminaries, including additive shares, distributed point function, our formal security definition, and a previous analysis of fingerprint false positive rates. Section 3 details the proposed scheme and two illustrative applications. In Section 4, we present a full security proof alongside a rigorous analysis of the false positive error probability of our scheme. Section 5 offers both theoretical complexity comparisons and experimental performance results. Finally, Section 6 concludes the paper.

2. Preliminary

This section introduces several fundamental concepts and key techniques that support the subsequent research presented in this paper. Specifically, it covers four key components: additive shares, distributed point function, security model, and fingerprint false positive error probability. Furthermore, for clarity and consistency in the following discussions, a notation table is provided in

Table 1. Notation and parameter settings used throughout the paper.

Parameter	Symbol	Value and Description
Security Parameter	$\lambda$	128/256
Fingerprint Modulo	p	A large prime number
Fingerprint Seed	r	$r\in {\mathbb{Z}}_p$
DPF Key Length	L	$\lambda ·\log p$ bits
Word Length	l	3–8
Fingerprint	$\theta$	$\theta \in {\mathbb{Z}}_p$
Number of Rows	n	Number of records

. This notation table clarifies the meaning of main parameters used throughout the paper.

2.1. Additive Shares

The additive share is the simplest form of secret share [10,21], which is defined over an Abelian group. This group is denoted by ${\mathbb{G}}_p=({\mathbb{Z}}_p,+)$, where p is a large prime and ${\mathbb{Z}}_p$ represents the finite field of integers modulo p. The additive shares of a secret S are defined as $S={\sum }_{i=1}^c{s}_i$ over ${\mathbb{G}}_p$, where all $s_i$ are shares of S and dispatched to c different servers.

2.2. Distributed Point Function (DPF)

DPF [9] is a useful cryptographic primitive that partitions a point function f into two additive function shares $f_1,f_2$, where $f=f_1+f_2$. Then, $f_1$ and $f_2$ can run in two different parties and help to evaluate f without leaking its parameters. Essentially, given a point function $f_a\left(x\right)$ where $f_a\left(x\right)=1$ if $x=a$ or $f_a\left(x\right)=0$ otherwise, its function shares can be seen as additive shares of the truth table of $f_a$. Nevertheless, for efficiency consideration, a DPF of $f_a$ actually consists of two functions:

• $Gen(\lambda ,x),(x\in {\{0,1\}}^{*})$, outputs a pair of keys $(k_1,k_2)$, each key $k_i,i\in \{1,2\}$ is much shorter than the truth table of $f_a\left(x\right)$;
• $Eval(k,x’),(x\in {\{0,1\}}^{*})$, outputs the additive shares of $f_a(x’)$.

DPF was further generalized to function secret sharing [10], which can support multiple function shares. For efficiency consideration, we use DPF to develop our query algorithm.

2.3. Security Model

This scheme assumes that the two symmetric mirror servers are semi-honest, meaning they will follow the protocol honestly but may attempt to infer private information from the data they receive or compute during execution. Additionally, we assume that the two servers do not collude [22]. Our security guarantee is formalized under the standard IND-CPA (indistinguishability under chosen plaintext attack) model, which protects against passive adversaries. In this model, an adversary can observe all query-related information and the internal view of one server during protocol execution, but cannot alter messages or inject malformed data. Under these assumptions, our security definition ensures that the adversary cannot distinguish between two different queries of its choice based solely on the observable communication. To prove the security of the proposed scheme, we formally introduce a security definition for the scheme.

Let $\lambda$ be the security parameter, and let the size of the database D be n. The user interacts with two servers, $S_1$ and $S_2$, under the scheme $\pi$. Let the public parameters be $PP=(r,p)$, and assume the adversary $A_i$ (where $i\in \{1,2\}$) controls server $S_i$. The real view for a query w on D is defined as follows:

$$RealVie{w}_i(D,w)=(D,PP,k_i,shar{e}_i),$$

where $k_i\leftarrow Gen(\lambda ,\theta )$ is the DPF key generated by the user for the fingerprint $\theta$, $shar{e}_i$ is the accumulated shared result on server $S_i$, and $D\left[j\right]$ is the keyword of the j-th record in D.

For the simulator, we define the simulated view under the leakage function $Leakage(D,w)$ as follows:

$$SimVie{w}_i\left(Leakage(D,w)\right)=(D,PP,k_i^{\prime },shar{e}_i^{\prime })$$

where $k_i^{\prime }$ is a fake key, which can be reckoned as a randomly selected string from the key space, and $shar{e}_i^{\prime }$ is a fake shared value, which can be seen as a randomly selected value from the real shared space.

Based on the parameter definitions above, we provide the following definition:

Definition 1.

The scheme π satisfies query privacy if, for every PPT adversary $A_i$, there exists a PPT simulator $Si{m}_i$ such that the real view $RealVie{w}_i(D,w)$ and the simulated view $SimVie{w}_i(D,w)$ are computationally indistinguishable.

The proof of security of the proposed scheme will be detailed in Section 4.1.

2.4. Fingerprint False Positive Error Probability

Recall that fingerprint maps a longer string to a number—the collision does exist. The false positive error probability indicates that two different strings share the same fingerprint, that can be bounded as follows:

Lemma 1.

Let u and v be two different strings of length ℓ, where $\ell \le n$ and $p\in O\left(n^{2+\alpha }\right)$, for some $\alpha \ge 0$. Then the probability that fingerprints ${\varphi }_{r,p}\left(u\right)={\varphi }_{r,p}\left(v\right)$ for a random $r\in {\mathbb{F}}_p$, is at most ${\displaystyle \frac{\ell }{p}}\le {\displaystyle \frac{1}{n^{1+\alpha }}}$.

Proof. 

See Section 2 in [5].  □

3. Fingerprint-Based Query

In this section, we provide a detailed description of the proposed scheme based on fingerprint (FP) and DPF and discuss its applicability in two typical-use case scenarios.

3.1. Concrete Construction of the Scheme

Assume that there is a table deployed over clouds, which contains several columns, e.g., name, salary, address, etc. One may want to query whether some keywords exist or not in a certain column. We note that a straightforward way is directly asking the server to return all the keywords appearing in the database and to send such a list to the user, and the user will search by himself. However, this method is a somewhat offline search, and the user should download the keywords list and search on the client side. If there are millions of different keywords, it will bring a large computational and communication overhead to users.

Thus, in this section, we develop a private online query algorithm for public datasets based on the combination of DPF and fingerprint. Our approach utilizes two servers, and each of them stores the same table. We utilize fingerprint to convert the keyword space to number domain, based on which, a DPF query can be developed. Then, this query is additively shared into two parts, which are sent to servers, separately. Servers receive such query and return the result in share form. After that, the user collects these shares and reconstructs the final result. The schematic diagram of users’ query is presented in Figure 1. The concrete construction of our scheme is Algorithm 1.

Algorithm 1: Fingerprint-Based Query Scheme

   To better understand the execution of the proposed scheme, we illustrate each step of the above algorithm through a concrete example. For simplicity, we consider a database that has only two columns, i.e., name and salary, presented in

Table 2. Simple example table.

Name	Salary
John	15
Mary	3
⋮	⋮
Johnson	4
John	11

. The explicit query is stated in the following:

• User side: If a user wants to search the keyword “john’’, firstly he chooses parameter $(r,p)$ of fingerprint, where r and p are defined in Section 1. Then, a corresponding fingerprint for the name “John’’ is generated, denoted by $F\left(John\right)=\theta ,(0\le \theta \le p-1)$. We construct a point function for the range $x\in [0,p-1]$ as follows:

  $$f_{\theta }\left(x\right)=\left\{\begin{array}{c}1,\mathrm{if}x=\theta ;\hfill \\ 0,\mathrm{otherwise};\hfill \end{array}\right.$$

  (1)

  for $x=\{0,1,\dots ,p-1\}.$ After that, based on DPF, we construct the function $Gen(\lambda ,\theta )$ and two keys are output, $k_1,k_2$. The user sent $r,p,k_1$ to server 1 and $r,p,k_2$ to server 2, respectively.
• Server side: Servers 1 (or 2) can run the DPF function $Eval(x,k_i)$ for all $x=\{0,1,\dots ,p-1\}$ to build a truth table ${\mathcal{T}}_i$, ($i=1,2$). When the servers have the truth table ${\mathcal{T}}_i$, it can provide 1) count query, the number of matching records; and 2) sum query, the sum of items in other columns corresponding to the matching records. These operations are presented in Algorithms 1 and 2. After that, they can send the results of these algorithms to the user.
• User side: Collect the results from server 1 and 2, and perform modular addition between these two results and obtain the final answer.

Comments: We firstly prove the correctness of Algorithm 1. Please notice that ${\mathcal{T}}_i$ is the additive shares of the truth table of $f_{\theta }\left(x\right)$. Only if the fingerprint of the name is “john”, servers will obtain the shares of “1”; otherwise they will obtain the shares of “0”. Therefore, when the servers add all these shares in Algorithm 1, the user finally obtains the shares of the count.

We also note that, essentially, the function $Gen(\ast )$ additively shares the truth table of $f_{\theta }$ and compress it to $k_1,k_2$. At the server side, $Eval(\ast )$ is used to decompress $k_1,k_2$. Compared with the original DPF, we prefer to use $Eval(\ast )$ to decompress $k_1,k_2$ firstly, then the matching operation will become a table lookup operation.

The algorithm compresses arbitrary string keywords into the integer domain $[0,p-1]$. It expresses point queries as key pairs via DPF without transmitting plaintext indexes with a communication cost of $O\left(\lambda \log p\right)$ bits. The construction combines the compressibility of the fingerprint function and the symmetry of the DPF for privacy queries in a symmetric mirror server architecture.

3.2. Applications of the Proposed Scheme

To demonstrate the practicality and versatility of the proposed scheme, we present two representative application examples in this subsection. The first example, privacy-preserving sum query, is designed to compute the aggregate value associated with a keyword while preserving query privacy. The second example, oblivious download, enables a secure download of a file in an ignorant way. Together, these use cases illustrate the adaptability of our scheme to aggregation and lightweight retrieval tasks.

3.2.1. Privacy-Preserving Sum Query

In many practical scenarios, users are interested not only in the existence of a keyword in the database but also in retrieving aggregate statistics associated with that keyword. For example, in a medical data platform, a researcher may wish to compute the total reported cases of a disease or the cumulative usage of a specific drug, while keeping the query intent confidential.

To support such functionality, we extend the original scheme to a privacy-preserving sum query. Similar to the count query, this approach leverages two non-colluding mirror servers and a pair of DPF keys generated for the fingerprint of the query keyword. However, unlike counting, the servers return the sum of all values associated with the matching keyword, thus enabling privacy-preserving aggregation. The core algorithm of this protocol is described in Algorithm 2. Concretely, the entire protocol consists of three main stages:

Algorithm 2: Sum Operation For Servers i ($i=1,2$).

• User: The user selects fingerprint parameters $(r,p)$ and computes the KR fingerprint of the query keyword w as $\theta ={\phi }_{r,p}\left(w\right)$. Then, the user invokes the DPF key generation algorithm $\mathsf{Gen}(\lambda ,\theta )$ to obtain the key pair $(k_1,k_2)$ and sends $(k_1,r,p)$ to server 1 and $(k_2,r,p)$ to server 2.
• Server $i=1,2$: Each server reconstructs its DPF truth table ${\mathcal{T}}_i$ over the domain $[0,p)$ using the received key $k_i$. For each row $({\mathrm{name}}_j,{\mathrm{value}}_j)$ in the dataset, the server computes ${\phi }_{r,p}\left({\mathrm{name}}_j\right)$ and checks the corresponding entry in ${\mathcal{T}}_i$. If the entry is 1, the value ${\mathrm{value}}_j$ is added to the local sum ${\mathsf{Sum}}_i$. After processing all records, the server returns ${\mathsf{Sum}}_i$ to the user.
• User: Upon receiving ${\mathsf{Sum}}_1$ and ${\mathsf{Sum}}_2$ from both servers, the user computes the final result as $\mathsf{Sum}=({\mathsf{Sum}}_1+{\mathsf{Sum}}_2)modp$. This represents the total sum of values associated with the queried keyword w in the dataset.

The communication cost remains sublinear at $O\left(\lambda \log p\right)$, and the server-side computation involves $O(n·\lambda )$ symmetric operations and modular additions. As with the count query, the only source of potential inaccuracy stems from fingerprint collisions, which are bounded and analyzed in Section 4.2. Therefore, the scheme remains secure and practical within acceptable accuracy margins.

This protocol is particularly suited for statistical data aggregation tasks in public platforms, such as opinion trend analysis in social media or cumulative sensor readings in IoT systems, offering high scalability and lightweight deployment.

3.2.2. Oblivious Download

Furthermore, our approach can be applied in another scenario where users are allowed to download files in an oblivious way. Assume that there is a list of files indexed by their filename and the filename is unique. Note that it is not necessary for all the files to have the identical size; see

Table 3. File list indexed by name.

Filename	File_Content
config	System configuration settings
report	Annual report text
⋮	⋮
research	Final draft of research paper

.

Table 3 presents a list of files indexed by their filenames and corresponding content. In the oblivious download scenario outlined in the paper, each file on this list features a unique filename and differs in both size and content. Typically stored on the server, these files can be downloaded without disclosing the specific file being requested, owing to the implementation of the DPF.

If a user wants to download one file of a certain filename, he just follows the same line as presented previously: (1) calculate the fingerprint of the desired filename; (2) construct a DPF based on such a fingerprint value, then send the shares its truth table to two servers. Then, the servers do the following operations presented in Algorithm 3.

Algorithm 3: Oblivious File Downloading from Servers i ($i=1,2$).

Finally, the user only needs to download the shares from servers 1 and 2 then recover the file. The size of the download file is equal to the maximum file size. If the desired file size is smaller, 0 will be padded at the end of the file. This padding ensures all returned files have equal length, preventing the server from inferring the actual file size and thus preserving query privacy. It introduces negligible computational and communication overhead, as padding involves only constant-time operations and a small number of additional bits. Moreover, since the client knows the true length of the desired file in advance, it can safely discard the padded zeros after retrieval without impacting the correctness or usability of the result. Clearly, during this procedure, the servers will never find which file is of interest to the user, since all the files are added together.

4. Analysis of Security and Accuracy

In this section, we will analyze the security of the schemes mentioned in the previous section and provide a theoretical analysis of the error rates of the schemes.

4.1. Security Proof of the Proposed Scheme

In this subsection, we analyze the security of the proposed scheme. Concretely, before presenting the formal security proof, we first reduce the query privacy guarantee of scheme $\pi$ to the core security of the underlying DPF scheme. Specifically, by assuming that the DPF construction is IND-CPA secure, we can conclude that scheme $\pi$ satisfies the query privacy requirement articulated in Definition 1. We capture this result in the following lemma.

Lemma 2.

If the underlying distributed point function (DPF) scheme is IND-CPA secure, then the scheme π achieves the query privacy defined in Definition 1.

Proof. 

We prove the security of the proposed scheme by adopting a standard game-hopping argument, and define two games first:

• $Gam{e}_{Real}$. In the real game, the user computes the fingerprint $\theta ={\varphi }_{r,p}\left(w\right)$ and runs $(k_1,k_2)\leftarrow Gen(\gamma ,\theta )$. Server $S_i$ ($i\in \{1,2\}$) then proceeds with the scheme $\pi$, producing the real view $RealVie{w}_i$. By definition, $Gam{e}_{Real}$ exactly captures the transcript seen by an honest execution of $\pi$.
• $Gam{e}_{Sim}$. In the simulated game, the simulator does not invoke the DPF functionality. Instead, it takes the leakage function $Leakage(D,w)=\varnothing$ and outputs a uniformly random key $k_i^{\prime }$ and a random shared value $shar{e}_i^{\prime }$. The resulting transcript is the simulated view $SimVie{w}_i\left(Leakage(D,w)\right)$.

By the IND-CPA security of the DPF scheme and the non-collusion assumption between the mirrored servers, no PPT adversary can distinguish $k_i$ from $k_i^{\prime }$ or $shar{e}_i$ from $shar{e}_i^{\prime }$. Hence, $RealVie{w}_i$ and $SimVie{w}_i$ are computationally indistinguishable, which implies that scheme $\pi$ satisfies the query privacy guarantee of Definition 1. □

4.2. Enhancing Robustness and Deployment Flexibility

While our scheme assumes two non-colluding mirror servers, which is commonly adopted in dual-server privacy-preserving frameworks, it is important to discuss strategies for enhancing robustness in case this assumption is violated.

One practical mitigation is to extend the architecture to a threshold-based multi-server model, such as a (t, n)-threshold setup. In this approach, the user splits their query into n DPF key shares and distributes them across n mirror servers. Only if t or more servers collude can the query be reconstructed, offering greater resilience to collusion at the cost of slightly increased communication. Alternatively, Trusted Execution Environments (TEEs) such as Intel SGX can be employed to protect the DPF evaluation process. Under this setting, even if the server itself is untrusted, its enclave can securely execute the fingerprint-based query without leaking sensitive information.

Both of these approaches can be flexibly integrated into our framework as optional extensions, depending on deployment scenarios and the level of trust available. They provide complementary trade-offs between deployment complexity and collusion resistance.

In addition to stronger adversary models, we also consider real-world deployment challenges. Our current scheme assumes fully replicated databases across two mirror servers. This simplifies query processing and minimizes communication. However, in large-scale or geo-distributed environments, full replication may not be practical.

To support such settings, future extensions could incorporate partial replication or erasure coding to enable fault tolerance. The database can be partitioned across multiple servers with overlap, and DPF keys can be directed to query specific partitions. It would require a lightweight scheduling protocol but would retain the core privacy guarantees of our design.

These extensions illustrate how our framework can flexibly adapt to various deployment models and how to balance trade-offs among trust assumptions, system complexity, and robustness.

4.3. False Positive Error Probability

Recall that false positives exist in fingerprint search operations, whose probability can be evaluated using Lemma 1, presented in Section 2. Note that this probability is different from that of fingerprint collision. If we assume that there are n fingerprints with each mapping a random value in the range $[0,p-1]$, we need to reassess the error rate in this case.

Based on Lemma 1, it is clear that the false positive error probability depends on the string length and magnitude of p. Considering that words in the dictionary are typically short, using a larger p can help reduce the error rate. Moreover, to illustrate the false positive probability on a real dataset composed solely of words, we conducted further evaluations on the dictionary set.

Claim 1.

Let S be a dictionary of n words, where the average length of these words is l. Assuming that the fingerprint function ϕ is uniformly distributed over ${\mathbb{F}}_p$, for any word $s\in S$, the expected number of collisions with other words in the set $S\setminus \left\{s\right\}$ satisfying $\varphi \left(s\right)=\varphi \left(t\right)$ does not exceed ${\displaystyle \frac{(n-1)l}{p}}$.

Proof. 

For each string $t\in S\setminus \left\{s\right\}$, define the indicator random variable as follows:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill X_t=\left\{\begin{array}{cc}1,\hfill & if\varphi \left(t\right)=\varphi \left(s\right),\hfill \\ 0,\hfill & otherwise.\hfill \end{array}\right.\end{array}\end{array}$$

Since $\varphi (·)$ is assumed to be uniformly distributed, according to the Lemma 1, the probability that $\varphi \left(t\right)$ equals $\varphi \left(s\right)$ is at most ${\displaystyle \frac{l}{p}}$. Thus, the expected value of $X_t$, $E\left[X_t\right]$, is less than ${\displaystyle \frac{l}{p}}$.

By the linearity of expectation, the total expected number of collisions for the word s in the dataset S is

$$E\left[{\sum }_{t\in S\setminus \left\{s\right\}}{X}_t\right]={\sum }_{t\in S\setminus \left\{s\right\}}E\left[X_t\right]<(n-1)·{\displaystyle \frac{l}{p}}.$$

This completes the proof. □

Based on Claim 1, we can accurately estimate the error rate of the proposed scheme on a commonly used dictionary dataset. Taking the Merriam-Webster dictionary (https://www.merriam-webster.com/help/faq-how-many-english-words, accessed on 26 April 2025) as an example—which contains approximately $110,000$ words with an average word length of 5 [23]—when a prime number slightly greater than 10 million is chosen for p, the error rate in this dataset is bounded above by $5\%$.

4.4. Analysis of English Word Letter-Pattern Effects on Fingerprint Collision Probability

The character sequences of English words are not random but follow specific letter-pattern structures, such as common letter combinations, prefixes, and suffixes. These linguistic patterns induce correlations among the coefficients of the fingerprint polynomial: words sharing the same morphological root tend to cluster in the hash space, whereas words from different families map more diffusely. Empirical evidence shows that even within the same word family, the actual collision rate typically lies below the worst-case bound of ${\displaystyle \frac{l}{p}}$.

Formally, let u and v be two distinct English words of length l, and consider their difference polynomial:

$$f\left(r\right)=\sum _1^l{\delta }_i{r}^{l-i},{\delta }_i=u_i-v_i.$$

Since ${\delta }_i=0$ when $u_i=v_i$, we conclude that the degree of $f\left(\right)$ is less than l. Under the uniform-random oracle model, the collision probability satisfies $Pr[f\left(r\right)=0]\le {\displaystyle \frac{l}{p}}$.

Note that English words frequently adhere to consistent spelling patterns, such as beginning with “pre-” or ending in “-ing”, which means that most character positions remain the same across different words, and only a handful of specific positions differ. Consequently, the indices i for which ${\delta }_i\ne 0$ are typically concentrated at these particular locations. Let $diff=\{i:{\delta }_i\ne 0\}$ and $d=\left|diff\right|<l$. Then $f\left(r\right)$ effectively becomes a degree-d polynomial, and its collision probability can be tightened to $Pr[f\left(r\right)=0]\le {\displaystyle \frac{d}{p}}$.

This refined bound quantitatively captures how English word letter-patterns reduce collision rates and explains why, in dictionary-like non-uniform distributions, the observed collision probability is substantially lower than the theoretical worst-case ${\displaystyle \frac{l}{p}}$.

5. Performance Analysis

In this section, we evaluate the performance of our proposed protocol from two aspects. First, in the view of theoretical analysis, we rigorously contrast the proposed scheme against representative PIR and ORAM schemes in communication and computation costs. Then, in the Experimental Evaluation subsection, we validate these theoretical predictions with experimental measurements.

5.1. Theoretical Comparison

In our scheme, the client invokes the DPF key-generation algorithm $(k_1,k_2)\leftarrow Gen(\lambda ,\theta )$ to produce two keys of length $L=O\left(\lambda \log p\right)$ bits, effectively compressing a p-entry truth table into compact key elements. For each query, the client transmits one DPF key along with the fingerprint parameters r and p, for a total communication cost of $L+O\left(\log p\right)=O\left(\lambda \log p\right)$ bits. Moreover, the client receives from each server a secret share of size $O\left(\log p\right)$ bits. On the server side, answering a query requires n calls of the function $Eval$ and n modular additions, resulting in a computational complexity of $O\left(n\right(\lambda +\log p\left)\right)$.

Although our scheme serves a different scenario than traditional PIR and ORAM schemes, we theoretically compare our scheme against representative PIR and ORAM schemes from recent work.

Table 4. Theoretical comparison of client communication and server computation.

Scheme	Client Communication	Server Computation
Proposed Scheme	$O\left(\lambda \log p\right)$ bits	$O\left(n\right(\lambda +\log p\left)\right)$ Eval & mod-add ops
[13]	$O(\lambda \log p+k)$ bits	$O(n+k)$ homomorphic encryption ops
[17]	$O\left(\log N\right)$ bits	$O\left(\log N\right)$ block accesses

summarizes the client communication and server computation complexities of the three schemes. The concrete analysis is given as follows.

In terms of communication, our scheme achieves a sublinear cost of $O\left(\lambda \log p\right)$ bits due to the transmission of DPF keys and fingerprint parameters. This makes it particularly well-suited for the large-scale database. By contrast, Vectorized Batch PIR (VB-PIR) [13] supports parallel retrieval of batch size k at a communication cost of $O(\lambda \log p+k)$ bits. Since it utilizes homomorphic encryption to amalgamate multiple queries and reduce per-query bandwidth, its communication overhead scales linearly with k, limiting its practicality for large batches. Worst-Case Logarithmic ORAM (WCL-ORAM) [17] hides arbitrary read/write patterns with a communication cost of $O\left(\log N\right)$ bits (where N is the number of blocks). This scheme adopts multiple accesses and data reshuffles to ensure privacy, but incurs the communication cost that grows logarithmically with the database size.

Regarding server computation, our scheme requires $O\left(n\right(\lambda +\log p\left)\right)$ evaluations and modular-add operations over n records. VB-PIR, in contrast, incurs $O(n+k)$ homomorphic encryption operations. The WCL-ORAM scheme performs only $O\left(\log N\right)$ block accesses, each corresponding to one symmetric encryption and one symmetric decryption. Since symmetric encryption is vastly more efficient than fully homomorphic encryption operations, WCL-ORAM achieves the best server-side efficiency, and the VB-PIR scheme needs the most computation cost.

Beyond communication and computation complexity, real-world deployment requires a comprehensive evaluation of cryptographic primitives, deployment complexity, and application suitability. To this end,

Table 5. Comprehensive comparison of PIR, ORAM, and the proposed scheme.

Property	Proposed Scheme	VB-PIR [13]	WCL-ORAM [17]
Cryptographic Primitives	SE + DPF	FHE	SE
Deployment Complexity	Stateless, lightweight	Requires FHE	Requires client-side state
Accuracy Guarantee	Approximate	Exact	Exact
Suitability for Public Databases	High	Moderate	Low

provides an extended comparison between our proposed scheme, a representative PIR scheme (VB-PIR) [13], and the WCL-ORAM scheme [17].

Our approach relies on a pair of non-colluding symmetric mirror servers, thereby avoiding the need for expensive primitives, such as fully homomorphic encryption (FHE). This lightweight design makes it particularly well-suited for large-scale, read-only public databases where the content is non-sensitive but query privacy is critical. In contrast, VB-PIR incurs significant overhead due to reliance on FHE, while WCL-ORAM requires maintaining client-side state and recursive access paths, which leads to much higher deployment complexity. Although fingerprint collisions in our scheme may introduce a small probability of false positives, this can be tightly bound through parameter tuning. Our experiments demonstrate that the accuracy consistently exceeds 99% under practical conditions.

In summary, the proposed scheme strikes a favorable balance between accuracy, efficiency, and deployment overhead. It means that our scheme is especially attractive for lightweight and publicly accessible query environments.

5.2. Experimental Evaluation

To evaluate the query performance and accuracy of our scheme, we extracted all English words of lengths 4, 5, 6, 7, and 8 from the Merriam-Webster online dictionary to form the test corpus. For approximately 11,000 seven-letter words, we randomly sampled 2000, 4000, 6000, 8000, and 10,000 entries to create query subsets of varying sizes. The fingerprint parameters were set to $r=26$ and $p\in \{$10,007, 100,003, 1,000,003, 10,000,019, 100,000,009}. Using these datasets, we quantitatively assessed the efficiency and correctness of the proposed scheme. Furthermore, to compare efficiency, we implemented the baseline Vectorized Batch PIR scheme [13] under the same hardware and input conditions, and measured its query runtime alongside our proposed method. It is worth noting that while we provide theoretical complexity comparisons with ORAM in Section 5.1, we exclude ORAM from experimental evaluation. This is because ORAM targets generic access pattern protection, often requiring trusted hardware or recursive constructions, which makes it unsuitable for our focused task of lightweight keyword count queries over public datasets. To ensure a fair and relevant comparison, we concentrate on the PIR-based scheme for experimental benchmarking. Our algorithm ran on Intel Core(TM) i5-10500 3.10 GHz processors and 8 GB of RAM. The analysis of the experiment results is given as follows.

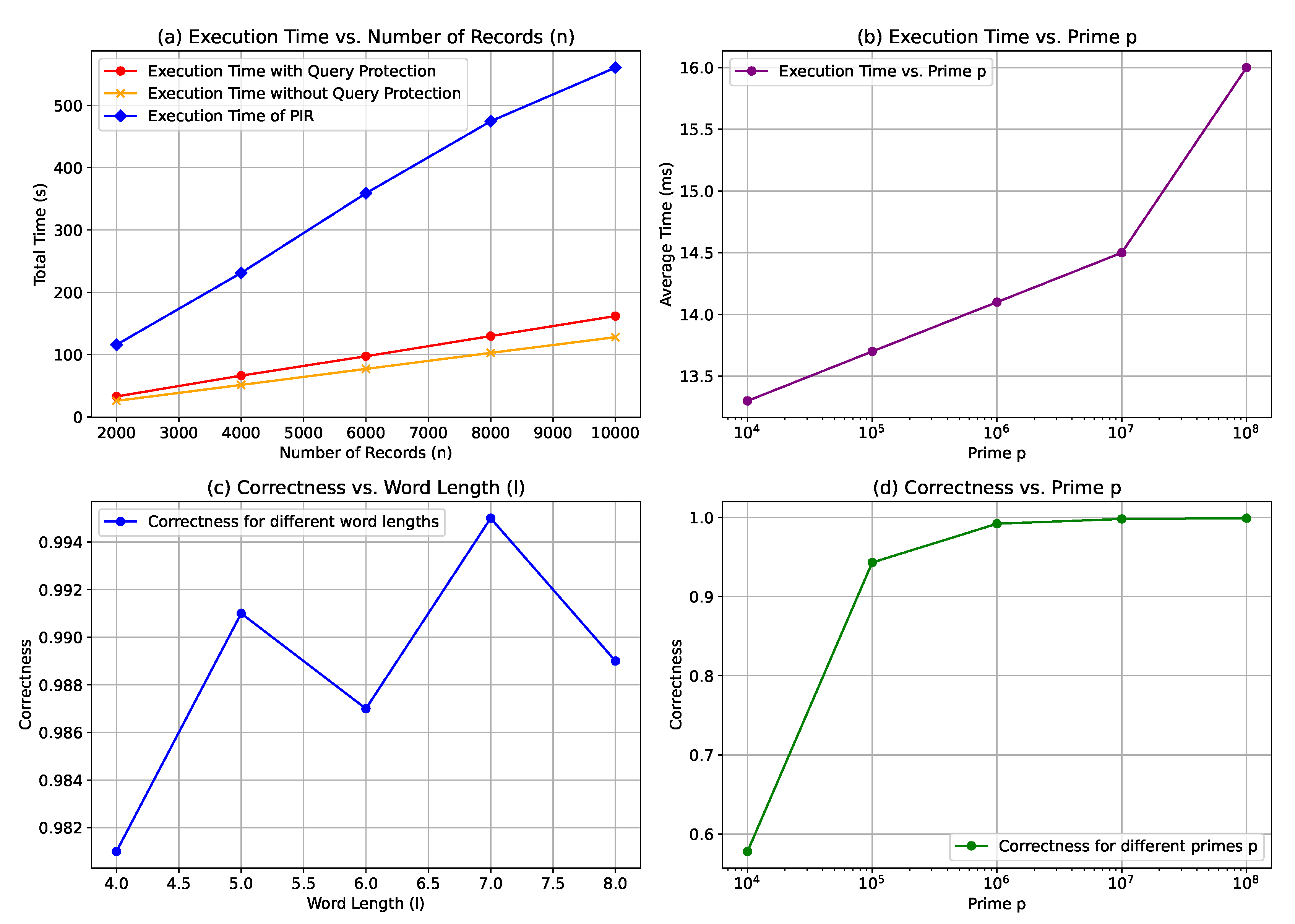
Figure 2 presents the experimental results, comparing accuracy and execution time across different word length l, modulo p, and database size n. The following part provides a detailed analysis of these results.

• Database Size n vs. Execution Time. As the number of records n increases from 2000 to 10,000, the execution time of our scheme grows linearly from 32.9 s to 161.9 s, which is consistent with the theoretical analysis. We also compare the proposed scheme to the method without query protection, finding that the unprotected version consistently runs about 20% faster at each dataset size. Furthermore, under the same hardware and input settings, the execution time of the PIR scheme increases from 115.8 s to 560.5 s, showing a clear linear trend. In contrast, our scheme completes the same queries with substantially lower runtimes, roughly one-third of the PIR overhead at each scale. Figure 2a illustrates both the linear growth and the performance gap between the three schemes.
• Modulo p vs. Execution Time. When the fingerprint modulo p increases from 10,007 to 100,000,009, the average query time rises from 13.3 ms to 16.0 ms. This moderate growth stems from the increasing bit length of p, which affects the speed of modular multiplication and addition operations. Despite the larger modulus, the overall execution time remains acceptable and does not impact scalability significantly. Figure 2b presents this trend, which aligns closely with our theoretical predictions.
• Word Length l vs. Accuracy. As shown in Figure 2c, the accuracy improves with increasing word length. This trend arises because longer words tend to have more distinctive letter patterns, which reduces the chance of fingerprint collisions. Furthermore, English vocabulary is not randomly distributed. For example, common prefixes (e.g., “pre-”, “dis-”) and suffixes (e.g., “-ing”, “-tion”) help distinguish words more effectively in the fingerprint space. This structural bias reduces collision events and thus boosts query correctness. Figure 2c clearly reflects this pattern.
• Modulo p vs. Accuracy. Figure 2d shows that, as the modulo p increases, the correctness rate increases, from 0.578 at p = 10,007 to 0.999 at p =100,000,009. Increasing the value of p significantly improves the correctness rate when the number of records n is less than p. When p is much larger than n, the correctness rate will stabilize. When p is much larger than n, its correct rate will stabilize. This phenomenon verifies the previous analysis that an increase in the modulo p leads to an increase in the fingerprint hash space and a decrease in the probability of collision. Notably, when p is only marginally larger than n, the fingerprint domain becomes densely populated, which leads to an increased chance of collisions. For example, at p = 10,007 $\approx n$, we observe significantly more false positives, which is reflected in the low accuracy. In contrast, selecting a larger p (e.g., $p\ge$ 1,000,003) ensures that the fingerprint space is much larger than the number of records, reducing collision rates and pushing the accuracy above $99\%$. Therefore, we recommend choosing p at least one order of magnitude larger than n in practice. This provides a robust trade-off between computational efficiency and accuracy. Furthermore, we also recommend two practical mitigation strategies for fingerprint collisions. First, adaptively increasing p can dynamically reduce false positives by enlarging the hash space. Second, if unexpected accuracy degradation is detected, the client can retry the query with a newly sampled random parameter r, effectively reshaping the fingerprint polynomial and reducing the probability of repeated collisions. Both techniques are lightweight and preserve the privacy guarantees of the scheme, which makes them suitable for real-world deployment.

The above experiments confirm that our scheme achieves high query accuracy while maintaining low computational and communication overhead, making it well-suited for privacy-preserving queries over large read-only databases. Overall, the experimental results are consistent with our theoretical analysis and further demonstrate the applicability and efficiency of the proposed scheme in large-scale database settings.

6. Conclusions

In this paper, we extended the cryptographic usage of Karp–Rabin (KR) fingerprints by combining them with distributed point functions (DPF) to construct a novel privacy-preserving keyword query scheme over public datasets. The scheme leverages the symmetric architecture of two non-colluding mirror servers to achieve sublinear communication overhead and query privacy. Theoretical comparisons and experimental evaluations were both conducted. The results indicate that our scheme achieves competitive performance compared to state-of-the-art PIR and ORAM-based approaches. Specifically, it outperforms VB-PIR in query efficiency and requires significantly lower deployment complexity than ORAM schemes, which makes it more practical in real-world settings. In addition, we formally analyzed the probability of false positives caused by fingerprint collisions and offered guidance on selecting parameters to minimize such errors.

This work is particularly applicable to real-world large-scale public databases, such as health records, government statistical repositories, or open bibliographic datasets. Our system enables users to perform keyword count queries without revealing their search intent, while maintaining both efficiency and scalability. While the scheme is efficient and easy to deploy, several limitations remain. First, the accuracy is inherently probabilistic due to fingerprint collisions, although the false positive rate can be tightly bounded by tuning the fingerprint parameters. Second, the scheme assumes full replication between two symmetric mirror servers, which may be less suitable for distributed or large-scale deployments. Third, it currently supports only read-only datasets. In future work, we intend to extend the scheme to fuzzy retrieval over long strings (e.g., paragraphs or full documents), as well as develop secure update mechanisms for dynamic databases. These enhancements would improve the applicability and robustness of the proposed scheme in more diverse practical scenarios.