Abstract
Large-scale integration of renewable energy introduces significant random perturbations to the power system, disrupting the symmetry and balance of active power, which complicates the stabilization of the system’s frequency. Inter-regional energy cooperation plays a crucial role in maintaining the symmetry and balance of the overall power system’s active power. However, when the power system area is expanded, automatic generation control (AGC) based on reinforcement learning faces the challenge of not being able to leverage the prior experience of the original system topology to train the new area, making it difficult to quickly develop an effective control strategy. To address these challenges, this paper proposes a novel data-driven AGC method that employs a multi-agent reinforcement learning algorithm with a learning to coordinate and teach reinforcement (LECTR) mechanism. Specifically, under the LECTR mechanism, when the power system region expands, agents in the original region will instruct the agents in the newly merged region by providing demonstration actions. This accelerates the convergence of their strategy networks and improves control accuracy. Additionally, the proposed algorithm introduces a double critic network to mitigate the issue of target critic network value overestimation in reinforcement learning, thereby obtaining higher-quality empirical data and improving algorithm stability. Finally, simulations are conducted to evaluate the method’s effectiveness in scenarios with an increasing number of IEEE interconnected grid areas.
1. Introduction
In order to solve the fossil fuel crisis and environmental pollution, a new power system primarily based on renewable energy has been rapidly developing in recent years [1,2,3]. The integration of a high proportion of large-capacity renewable energy sources into the grid leads to significant fluctuations in grid frequency, which undermines the stability of the grid system.
To ensure the safe and stable operation of the power system, researchers proposed automatic generation control (AGC) [4,5,6,7,8] as a secondary frequency regulation strategy. AGC maintains power system frequency stability by achieving “symmetry” between the amount of power generated by the system and the amount of power required on the load side, ensuring that both the two are fully matched in quantity and highly synchronized in time. The AGC controller typically takes power system frequency deviation and tie-line power deviation as inputs, and outputs power adjustment commands for each frequency-regulating unit. It maintains the frequency stability of the power system by regulating the “symmetry” between the generated power and the load demand, namely that the two are fully matched in quantity and highly synchronized in time. In [9], a new two-degree-of-freedom combined proportional–integral–derivative control scheme is applied to an interconnected power system to minimize frequency deviations. In [10], the authors present a novel sliding mode control method for load frequency control, which offers advantages such as reduced overshoot and faster response compared to traditional PID control. These aforementioned AGCs are generally designed on the basis of accurate physical system models. However, they face challenges in accurately controlling systems with inherent uncertainties [11] and in coordinating multi-area controllers [12].
As an alternative, data-driven algorithms—particularly reinforcement learning [13,14,15]—have been increasingly applied in the field of AGC due to their powerful search and learning capabilities. This data-driven AGC method constructs a decision-making agent centered around neural networks, allowing the agent to dynamically interact with the interconnected power system environment during the offline training phase. By combining a reward function to quantitatively assess the effectiveness of generation control commands, the agent’s parameters are gradually optimized, ultimately approaching the global optimal solution. After training, the agent can directly generate generation control commands upon acquiring data from the interconnected power system environment, significantly enhancing the computational efficiency of online decision-making.
In [16], the authors proposed a data-driven method for continuous-action AGC; however, this approach relies on single-agent reinforcement learning, which neglects cooperation among areas, leading to unstable training outcomes. In [17], the authors analyzed how positioning agents in each area to obtain global information can stabilize the training environment. Consequently, implementing a multi-agent control algorithm to regulate interconnected power systems has become essential. In [18], the authors proposed a multi-agent deep reinforcement learning method based on continuous action space, where multiple agents are trained to be able to independently output optimal power generation control commands so as to effectively respond to the control demands in complex power system environments. In [19], the authors introduced networks with varying exploration rates during the exploration process and employed categorical experience replay to enhance the utilization of experience. In [20], the authors proposed a centralized learning and decentralized execution automatic generation control framework based on a global action-value function multi-agent deep reinforcement learning algorithm, which can adaptively obtain the optimal coordinated control strategy for multiple LFC controllers. These studies demonstrate the successful application of multi-agent reinforcement learning in AGC, yielding significant results.
However, when a new area is integrated into the original interconnected power system, the previously mentioned algorithms become inefficient, and the training time increases as additional areas are incorporated. Meanwhile, the agents discussed in the aforementioned paper utilize only a single critic network. The AGC based on this method encounters challenges related to increased estimation errors [21] and overfitting during the training process. Consequently, the agent may mistakenly perceive certain actions as more beneficial for long-term rewards, leading to the adoption of suboptimal strategies.
To address the challenges associated with data-driven AGC, a MADRL control method based on the LECTR mechanism [22] is proposed for interconnected power systems. The approach introduces a double-target critic network delay update strategy to prevent the overestimation of target critic network value and enhance learning efficiency. Simultaneously, the newly integrated regional agents function as novice agents and interact with the expert agents of the original interconnected power system. The LeCTR mechanism introduces dynamic switching of agent roles, building upon the teach reinforcement mechanism. This enhanced interaction method further facilitates the learning of agents to collaborate and accelerates the optimization of the novice agent network. Ultimately, the trained agents are deployed within the power system environment to generate power commands in real-time.
The main contributions of this paper are as follows:
- (1)
- A novel multi-agent distributed coordinated control framework based on the LECTR mechanism is proposed. This framework improves the training speed of the newly added area agent when the regions of the power system are expanded.
- (2)
- During the training of the agents, we employed a double-target critic network architecture in place of a single critic network. This structure reduces the variance in target critic network value estimation, thereby enhancing the learning performance of the multi-agent system and facilitating superior control strategies.
- (3)
- We developed a cooperative reward function considering the control error of each region within the interconnected system, effectively guiding the training of the reinforcement learning algorithm.
The paper is structured as follows: In Section 2, we provide a detailed description of the interconnected power system model. Section 3 introduces a novel data-driven AGC framework. Section 4 describes the training process of the AGC agent utilizing the LECTR mechanism. Section 5 evaluates the effectiveness of this method in an expandable power system through simulation. Finally, in Section 6, we summarize the conclusions derived from this study.
2. Muti-Area Power System Model
Figure 1 presents a typical linearized interconnected power system model [23], expressed in transfer function form. The power system consists of various components, including generators, governors, steam turbines, renewable energy sources, and loads. The agents in each area manage the total power signal for that region, with the goal of minimizing frequency deviations and tie-line power fluctuations. They achieve this by adjusting the output of each unit within the area to optimize control performance. The dynamics of the system within the i-th area of a multi-area power system can be represented by a set of differential equations.
where are power angle and terminal voltage of equivalent machines for area i. are tie-line reactance and synchronous coefficient between area i and j. are generator mechanical output and valve position for i-th area. are governor time constant and turbine time constant for i-th area. are the machine damping coefficient, synchronous machine inertia, and speed drop for i-th area. , represent the load disturbance and the random disturbance caused by the renewable energy. The generation commands, denoted as , are typically determined based on the area control error (ACE) signal, which is denoted by . The bias factor is determined using the equation .
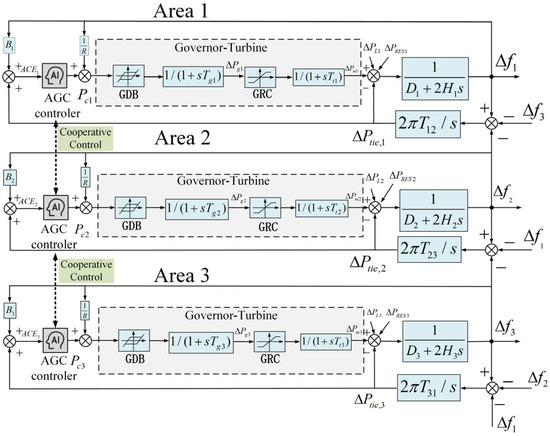
Figure 1.
Multi-area interconnected power system.
In a multi-region interconnected power system, AGC controllers in each region not only regulate locally based on the ACE information within their respective regions, but also collaborate with AGC controllers in other regions. This collaboration ensures optimal cross-region power exchange and frequency regulation through the sharing of information between interconnected regions, effectively addressing the challenges posed by fluctuating and intermittent renewable energy sources.
3. Framework for AGC Based on MADRL Algorithm with the LECTR Mechanism
3.1. Action Space
The actions of each agent determine the output of the unit in the area, and the action space is shown below:
where is the action of the i-th agent and is the regulation command of the i-th agent.
3.2. State Space
The agent generates control actions by sensing information regarding the state of the power system environment. The combination of state information constitutes the state space of the agent, which in this paper, includes the following:
where represents the ACE value for i-th region, represents the frequency deviation for i-th region, and represents the tie line deviation for i-th region.
3.3. Reward Function
To achieve optimal AGC performance in this system, minimizing the ACE is crucial. The reward function is designed to account for both system frequency deviation and tie-line power. If the ACE becomes excessively large during the training process, the reward function value is assigned a more negative value. The scaling factor determines the relative impact of ACE and power output variations on the reward and is set to 0.5. Additionally, the term is introduced as part of the reward to guide the algorithm in avoiding large fluctuations in the generation command.
3.4. Overall Training Framework
As shown in Figure 2, the proposed method is divided into two main procedures: the first procedure focuses on centralized training of the agents. The agents include an actor network and a critic network . In the centralized training procedure, the actor network observes the state and sends generation commands to the generators in their respective areas. Subsequently, the actor network receives the updated state of the system following the interaction, which is expressed as . At each time step, the reward value for the action taken in each area is calculated using a specific reward function. Finally, the data ( will be added to the experience pool. The critic network samples data from the experience pool to evaluate the effectiveness of new actions, which subsequently updates the actor network. This process facilitates the training of multi-agent systems. The second procedure involves agents that completed their training (i.e., the expert agent j) providing action suggestions for power generation commands to the agent in the newly added region (i.e., the novice agent i). This approach accelerates the the novice agent i’s learning of control strategies for cooperative control within the interconnected power system. After offline training optimization, the agents are deployed in an interconnected power system to enable efficient real-time control.
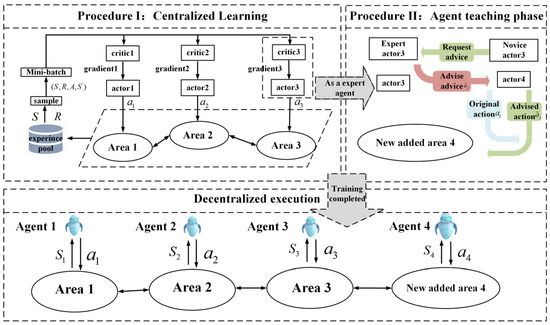
Figure 2.
Data-driven AGC based on the MADRL algorithm with the LECTR mechanism.
4. Training for Agent Based on the LECTR Mechanism
The data-driven AGC method, based on the LECTR mechanism, incorporates this mechanism to enhance the convergence speed of newly added area agents. Additionally, it introduces a double-target critic network with a delayed update strategy to address the issue of overestimation in the target critic network’s value. In the following subsections, we will present the enhanced MADRL algorithm and outline the specific steps for implementing the LECTR mechanism.
4.1. MADRL with a Double Target Critic Network Delay Update Strategy
The purpose of the improved MADRL algorithm presented in this paper is to facilitate updates to the parameters of the actor network parameters, maximizing the cumulative expected return .
where is the reward discount factor, suggesting that agents are more focused on the long-term performance of the overall reward.
In the improved MADRL algorithm, the learning process involves training a centralized critic network that has access to the policies of all agents. This centralized critic network is represented as a centralized state value function.
where o represents the overall observation value, and represents the local observations of each i-th agent. represents the action computed by the actor network for a given state .
During the update of the parameters for the i-th agent, the gradient descent methods are typically employed. The parameters of the actor network are updated by iterating in the direction opposite to the gradient. This approach allows us to gradually improve the performance of the agent.
The experience replay area D here includes of all agents.
Then, we minimize the loss function, which can be expressed as the difference between the target value and the evaluation value . The parameters of the critic network can be adjusted.
where and are the target critic and actor networks. The target critic network and actor network initially replicate the parameters of the original critic and actor networks during the offline training process. Subsequently, the parameters of the target networks are updated with a delay, which enhances the stability of the updates for both the critic and actor networks.
To address the issue of target critic network value overestimation in the traditional MADRL algorithm, a double-target critic network is employed to mitigate the overestimation of the state value function. It is essential to consider the information from all agents in MADRL. Consequently, during training, all agents should have access to comprehensive state information, allowing them to observe the entire state space.
In addition, regularization techniques are introduced to smooth the target critic network value and prevent overfitting. Normally distributed random noise, denoted as ε, is added during the update of the critic network to enhance stability against fluctuations. The improved method for calculating the target value is presented below:
Then, the parameters of the target networks are updated with a delay, which enhances the stability of the updates for both the critic network and the actor network. The updates for the actor network, critic network, target actor network, and target critic network are as follows:
where and represent the learning rates for the critic and actor networks, while τ denotes the soft update rate for the target networks.
4.2. The Application of the LECTR Mechanism in Expandable Power System
This subsection outlines the procedure for executing a cooperative multi-region load frequency control task after novice agent i received guidance from expert agent j. The entire process is further divided into two phases (see Figure 3).
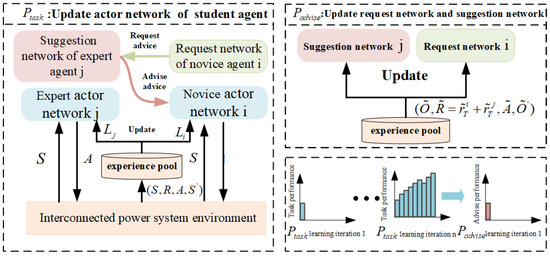
Figure 3.
LeCTR consists of two iterated phases.
Phase I: In each learning iteration, the actor networks of the expert agent and the novice agent interact with the power system environment to update their actor network parameters and based on the actions suggested by the expert agent. This process utilizes the improved MADRL algorithm and ( stands for the learning algorithm of the novice agent algorithm and for the learning algorithm of expert agent algorithm). We call this phase .
Phase II: This phase primarily focuses on updating the suggestion network of the expert agent and request network of the novice agent based on the advising-level rewards generated during the process. We refer to this phase as .
The agent in the LeCTR mechanism can assume the role of a novice agent, an expert agent, or both simultaneously. Additionally, the agent is capable of seeking advice regarding its own state while providing guidance to teammates in different states. The LeCTR mechanism uses distinct advising-level observations for the request network of the novice agent and the suggestion network of the expert agent. The request network of the novice agent for agent i decides when to request advice using observation where and are calculated by the critic network. Through , agent i observes a measure of its local task-level observation and actor network state. Similarly, the expert agent j’s suggestion network uses advising-level observation to decide when/what to advise. provides expert agent j with a measure of the task-level state/knowledge of novice agent i (via and and of its own task-level knowledge given the student’s context (via ). The novice perspective action of the agent is {request advice, do not request advice}. Meanwhile, expert agent j decides what to advise: either an action from action space of novice agent i, or a special no-advice action . Thus, the expert perspective action for agent j is . Given no advice, novice agent i executes the originally intended action . However, given advice , novice agent i executes action . Following advice execution, agents collect task-level experiences and update their actor network.
In Phase I, we set the reward function to evaluate the contribution of the actor network output actions to stabilize the power system frequency. In Phase II, we need to set up relevant advising-level reward functions to evaluate the contribution of the outputs of the suggestion network and the request network to accelerate the learning of the newly added area agents. Since request network and suggestion network must coordinate to help student i learn, they receive identical advising-level rewards = . In this paper, we set up the advising-level reward function as follows:
The above proposal-level reward function measures the strategic deviation between the action chosen by the novice agent i in state and the optimal action evaluated by the expert agent j. The proposed reward function measures the deviation between the optimal action and the optimal action evaluated by the expert agent j. By quantifying the difference in the value of the critic network, the expert agent learns to estimate the ‘cognitive error’ of its teammates in a given state and decides whether or not to intervene accordingly. This setup allows the expert agent to improve the learning collaboration between them during the teaching process, so that they not only focus on their own task benefits, but also understand and contribute to the learning process of their teammates.
When the expert agent outputs the suggested actions, and will be rewarded, otherwise the reward is zero. The parameter-updating methods of the suggestion network and the request network are referred to in the literature [22].
In order to facilitate collaborative learning among agents, the LeCTR framework employs a novel teaching mechanism that supports dynamic role switching by structurally modeling observations, actions, and strategies at the instructional level. Specifically, is ; is ; is ; is ; and is the parameter of strategy . is the experience pool of data related to the training of the request network and the suggestion network; and is the critic network for evaluating the actions of the suggestion network and the request network. With the unified modeling described above, LeCTR allows agents to simultaneously request assistance as a ‘novice agent’ and provide feedback as an ‘expert agent’ at any time step, enabling bi-directional switching of collaborative behaviors.
The training process of the LECTR mechanism and algorithmic flow of algorithm for training agents are shown in Figure 4.
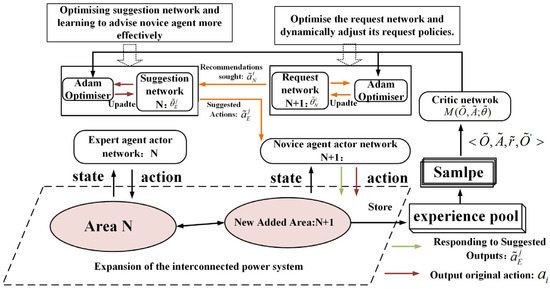
Figure 4.
The training process of the LECTR mechanism.
5. Case Study
In this section, we first establish a simulation of a three-area power system to evaluate the control performance of the improved MADRL algorithm compared to other control algorithms, including deep Q-networks (DQN) [24] and the multi-agent deep deterministic policy gradient (MADDPG) [25]. Subsequently, we demonstrate the advantages of the improved MADRL with the LECTR mechanism in accelerating the learning process of the newly added agent and improving the control performance in an expanded interconnected power system.
5.1. Experimental Environment
The simulations were carried out using the deep learning framework PaddlePaddle, with the following hardware configuration: an AMD Ryzen 7 2700 eight-core processor operating at 3.20 GHz, an NVIDIA GeForce RTX 2060 GPU, and a total of 16 GB of RAM. The sampling period of the controller during the simulation is 4 s, and the total duration of the disturbance is 1500 s. We set the baseline capacity of the system to 5000 MVA. The characteristics of the power system model presented in this paper are listed in Table 1.

Table 1.
Parameters of the interconnected power system.
For the DQN algorithm, the reward discount factor and the learning rate were set to 0.99 and 0.0005, respectively. MADDPG utilized a learning rate of 0.001 for both the actor and critic network, a reward discount factor of 0.99, and a soft update rate of 0.01. In the proposed method, the normally distributed random noise was set to 0.1, and the time interval for delayed update was set to 2. The learning rates of the actor network and critic network were set to 0.002, and a reward discount factor and soft update rate were set to 0.98 and 0.005. The number of training iterations for all algorithms was set to 30,000.
5.2. Three-Area Power System Disturbance Simulation
5.2.1. Step Load Disturbance
As shown in Figure 5, a step load disturbance is introduced to simulate the load in the power system, which experiences irregular and sudden increases and decreases. The transition process of the improved MADRL algorithm occurs in the shortest time, and the ACE of the improved MADRL algorithm remains at 0 after the step change is applied. At 300 s, 500 s, and 900 s, the absolute values of the maximum ACE changes for the three algorithms DQN, MADDPG, and the improved MADRL are (0.007 p.u., 0.0052 p.u., and 0.0032 p.u.), (0.0100 p.u., 0.0082 p.u., and 0.00526 p.u.), and (0.0066 p.u., 0.0035 p.u., and 0.0023 p.u.), respectively. The improved MADRL reduces the absolute values of the maximum ACE changes compared to the other algorithms by (21.28–53.46%), (23.28–56.85%), and (26.53–54.32%).
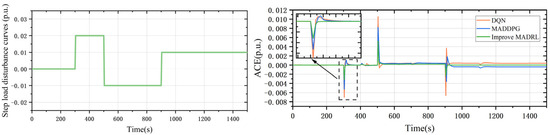
Figure 5.
Step load disturbance curves and the ACE variations step load disturbance in a three-area power system.
5.2.2. Random Renewable Energy Disturbance
Renewable energy sources exhibit considerable randomness and fluctuations. To examine the impact of these stochastic variations in renewable energy on the interconnected power system, we treat renewable energy as a random disturbance without accounting for its secondary frequency regulation capabilities. Figure 6 presents the data for renewable energy sources in a three-area system.
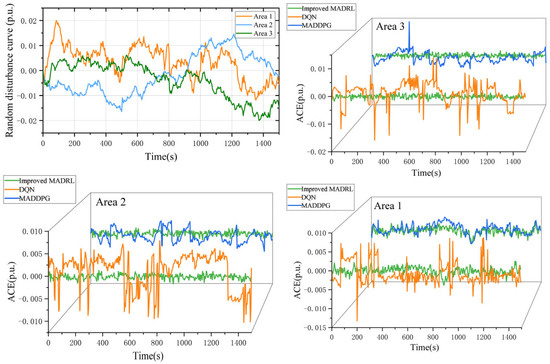
Figure 6.
Random disturbance curve and the ACE variations under random disturbance in a three-area power system.
Figure 6 shows that the mean absolute ACE of the improved MADRL algorithm is significantly lower than that of other algorithms, while maintaining ACE within a reasonable range across multiple power system areas. The MADDPG algorithm can reduce the ACE to within 0.005 p.u. However, there are still regions exhibiting unsatisfactory performance. This is because the improved MADRL algorithm introduces a double-target critic network, which enhances the stability of the algorithm’s convergence and prevents over-rewarding. Consequently, the improved MADRL algorithm demonstrates greater adaptability to power system environments characterized by a high proportion of renewable energy sources, resulting in superior control performance. In contrast, DQN is a single-agent algorithm that employs discrete generation control commands. As the interconnected power system expands, the dimensionality of the action space increases exponentially, leading to challenges in both exploration and convergence for the DQN algorithm. As a result, the DQN algorithm exhibits the poorest control performance, resulting in the highest average fluctuations in ACE.
Figure 7 shows the power output of the generator with different algorithms in Area 1. It can be seen that the improved MADRL algorithm has the best stability in the face of renewable energy disturbances, followed by MADDPG. Due to the strong stochastic variation of the output power of the renewable energy sources, the DQN has difficulties keeping up with the load for a short period of time.

Figure 7.
Output curve of the Area 1 unit under random disturbance.
The comparison of specific data is presented in Table 2. The power system data indicate that the mean absolute ACE of other algorithms was 2.5 to 6.10 times higher than that of the improved MADRL algorithm. Furthermore, the improved MADRL algorithm reduces the maximum variation in absolute ACE by 66.08% to 80.83% and achieves a reward value that is 72.61% to 132.14% higher than that of the other algorithms. Therefore, the improved MADRL algorithm demonstrates the best control performance.

Table 2.
Numerical results of regional system performance comparisons.
5.3. Extension of Power System Disturbance Simulation
This section of the simulation extends the power system to a fourth area to evaluate the control and learning performance of the enhanced MADRL with the LECTR mechanism in a highly stochastic power system environment.
5.3.1. Comparison of Offline Training Speed
Figure 8 shows the reward convergence curves of the newly added regional agents trained offline under the guidance of four different algorithms. The proposed method achieves convergence within 6833 rounds, demonstrating improvements in convergence speed of 58.73%, 67.95%, and 75.01% compared to the other three algorithms (improved MADRL, MADDPG, and DQN), respectively.
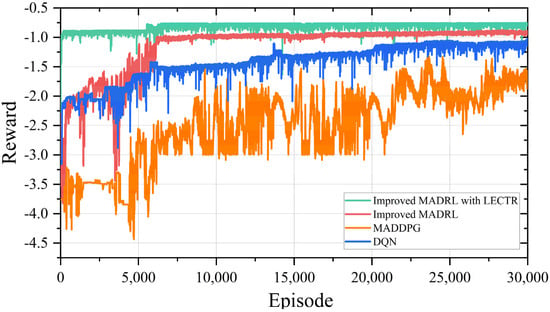
Figure 8.
Reward convergence curves of different algorithms.
This is because we use a trained expert agent from the original power system region to provide action suggestions, which the novice agent in the newly joined area selectively accepts during the training process. This method ensures that the novice agent explores the power system environment through stochastic actions while assimilating the suggested actions from the expert agent’s perspective and effectively translating them into local empirical knowledge. Consequently, this enables the novice agent to learn how to make improved control decisions in a scalable power system environment, thereby reducing the time required for independent learning.
For the other algorithms, there are serious challenges in dealing with the expanding interconnected power system. Each agent in the newly joined area must be retrained individually, which increases the training complexity of the multi-agent algorithms. As a result, the convergence of rewards under these algorithms becomes slower.
5.3.2. Step Load Disturbance
Figure 9 illustrates the change in ACE of the four algorithms following a step disturbance in the extended power system. It is evident that the improved MADRL with the LECTR mechanism recovers to 0 p.u. more rapidly after the disturbance. At 200 s, 600 s, and 900 s, the improved MADRL with the LECTR mechanism reduces the absolute values of the maximum ACE change compared to the other algorithms by 21.28% to 53.46%, 23.28% to 56.85%, and 26.53% to 54.32%, respectively.
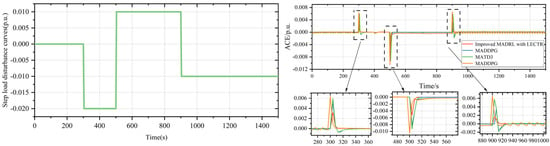
Figure 9.
Step load disturbance curves and the ACE variations under step load disturbance in an expanded power system.
5.3.3. Random Renewable Energy Disturbance
Figure 10 shows the disturbance data of renewable energy sources, such as wind power, in the newly extended area. It also compares the control strategies developed by the agent in the fourth area using four different algorithms: the improved MADRL with the LECTR mechanism, improved MADRL, MADDPG, and DQN, based on ACE metrics. The results indicate that the control performance of the improved MADRL with the LECTR mechanism is superior not only to that of DQN and MADDPG, but also shows further enhancement compared to the improved MADRL.
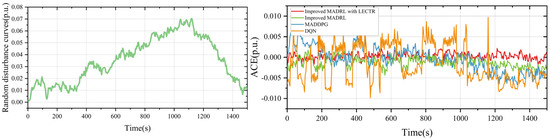
Figure 10.
ACE variations under random disturbance in an expanded power system.
The comparative data for each algorithm are presented in Table 3. The improved MADRL with the LECTR mechanism reduces the mean absolute ACE by 54.93% to 84.80%, decreases the largest variation in absolute ACE by 50.03% to 78%, and achieves a reward value that is 25.33% to 150.66% higher than that of other algorithms.

Table 3.
Numerical results of four-area system performance comparisons.
During the expansion of power system regions, it is essential to integrate new agents into the existing multi-agent framework to develop innovative coordination control strategies for the expanded power system area. Simulations demonstrate that our proposed improved MADRL with LECTR algorithm does not require re-centralized training of all regional agents, while maintaining excellent convergence and control performance. The improved MADRL with the LECTR mechanism offers a valuable reference for data-driven AGC in more flexibly interconnected power systems.
6. Conclusions
To achieve real-time frequency response control in extended power systems, we propose a MADRL framework based on the LECTR mechanism for the dynamic optimization of AGC.
- (1)
- The LECTR mechanism is introduced to facilitate the joint development of control strategies when interconnected power system regions are expanded. The LECTR mechanism enhances the learning speed of agents in the newly integrated region by 58.73% to 75.01% and reduces the average ACE by 54.93% to 84.80% by enabling peer-to-peer action suggestions from agents in the original region to those in the new region.
- (2)
- In a fixed-area power system environment, the proposed method effectively reduces ACE fluctuations and demonstrates superior control performance.
Author Contributions
Methodology, Y.S. (Yuexing Shi); software, F.Y., B.Z. and Y.S. (Yunwei Shen); formal analysis, X.S.; investigation, Y.S. (Yunwei Shen); data curation, D.L.; writing—review and editing, B.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by “National Natural Science Foundation of China”, grant number “52377111” and “National Natural Science Foundation of China”, grant number “52407122”.
Data Availability Statement
The data presented in this study are available on request from the corresponding author due to privacy reasons.
Conflicts of Interest
Xinyi Shao was employed by the Shanghai Electric Power Company. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest. The authors declare that this study received funding from “National Natural Science Foundation of China”, grant number “52377111” and “National Natural Science Foundation of China”, grant number “52407122”. The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article, or the decision to submit it for publication. The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as potential conflicts of interest.
References
- Wang, H.; Zhang, Z.; Wang, Q. Generating adversarial deep reinforcement learning -based frequency control of island city microgrid considering generalization of scenarios. Front Energy Res. 2024, 12, 1377465. [Google Scholar] [CrossRef]
- Basit, M.; Dilshad, S.; Badar, R.; Rehman, S.M.S. Limitations, challenges, and solution approaches in grid-connected renewable energy systems. Int. J. Energy Res. 2020, 44, 4132–4162. [Google Scholar] [CrossRef]
- Xu, D.; Zhou, B.; Wu, Q.; Chung, C.; Li, C.; Huang, S.; Chen, S. Integrated modelling and enhanced utilization of power-to-ammonia for high renewable penetrated multi-energy systems. IEEE Trans Power Syst. 2020, 35, 4769–4780. [Google Scholar] [CrossRef]
- Liu, Z.; Li, J.; Zhang, P.; Ding, Z.; Zhao, Y. An AGC dynamic optimization method based on proximal policy optimization. Front. Energy Res. 2022, 10, 947532. [Google Scholar] [CrossRef]
- Kazemi, M.V.; Sadati, S.J.; Gholamian, S.A. Adaptive frequency control of microgrid based on fractional order control and a data-driven control with stability analysis. IEEE Trans. Smart Grid. 2022, 13, 381–392. [Google Scholar] [CrossRef]
- Barakat, M. Novel chaos game optimization tuned-fractional-order PID fractional-order Pi Controller for load–frequency control of interconnected power systems. Prot. Control. Mod. Power Syst. 2022, 7, 16. [Google Scholar] [CrossRef]
- El-Bahay, M.H.; Lotfy, M.E.; El-Hameed, M.A. Effective participation of wind turbines in frequency control of a two-area power system using Coot Optimization. Prot. Control. Mod. Power Syst. 2023, 8, 14. [Google Scholar] [CrossRef]
- Karanam, A. and Shaw. B. A new two-degree of Freedom Combined PID controller for automatic generation control of a wind integrated interconnected power system. Prot. Control. Mod. Power Syst. 2022, 7, 20. [Google Scholar] [CrossRef]
- Guo, J. A novel proportional-derivative sliding mode for load frequency control. IEEE Access. 2024, 12, 127417–127425. [Google Scholar] [CrossRef]
- Saha, D.; Saikia, L.C.; Rahman, A. Cascade Controller based modeling of a four area thermal: Gas AGC system with dependency of wind turbine generator and pevs under restructured environment. Prot. Control. Mod. Power Syst. 2022, 7, 47. [Google Scholar] [CrossRef]
- Singh, V.P.; Kishor, N.; Samuel, P. Distributed multi-agent system-based load frequency control for multi-area power system in smart grid. IEEE Trans. Ind. Electron. 2017, 64, 5151–5160. [Google Scholar] [CrossRef]
- Yu, T.; Wang, H.Z.; Zhou, B.; Chan, K.W.; Tang, J. Multi-agent correlated equilibrium Q(λ) learning for coordinated smart generation control of interconnected power grids. IEEE Trans Power Syst. 2015, 30, 1669–1679. [Google Scholar] [CrossRef]
- Zhang, Q.; Dehghanpour, K.; Wang, Z.; Qiu, F.; Zhao, D. Multi-agent safe policy learning for power management of networked microgrids. IEEE Trans. Smart Grid. 2021, 12, 1048–1062. [Google Scholar] [CrossRef]
- Xi, L.; Wu, J.; Xu, Y.; Sun, H. Automatic Generation Control Based on Multiple Neural Networks with Actor-Critic Strategy. IEEE Trans. Neural Networks Learn. Syst. 2021, 32, 2483–2493. [Google Scholar] [CrossRef] [PubMed]
- Yu, T.; Zhou, B.; Chan, K.W.; Chen, L.; Yang, B. Stochastic Optimal Relaxed Automatic Generation Control in Non-Markov Environment Based on Multi-Step Q(λ). IEEE Trans. Power Syst. 2011, 26, 1272–1282. [Google Scholar] [CrossRef]
- Xi, L.; Chen, J.; Huang, Y.; Xu, Y.; Liu, L.; Zhou, Y.; Li, Y. Smart generation control based on multi-agent reinforcement learning with the idea of the Time Tunnel. Energy 2018, 153, 977–987. [Google Scholar] [CrossRef]
- Daneshfar, F.; Bevrani, H. Load–frequency control: A GA-based multi-agent reinforcement learning. IET Gener. Transm. Distrib. 2010, 4, 13. [Google Scholar] [CrossRef]
- Kamruzzaman, M.d.; Duan, J.; Shi, D.; Benidris, M. A Deep Reinforcement Learning-Based Multi-Agent Framework to Enhance Power System Resilience Using Shunt Resources. IEEE Trans. Power Syst. 2021, 36, 5525–5536. [Google Scholar] [CrossRef]
- Li, J.; Yu, T. Deep Reinforcement Learning Based Multi-Objective Integrated Automatic Generation Control for Multiple Continuous Power Disturbances. IEEE Access 2020, 8, 156839–156850. [Google Scholar] [CrossRef]
- Yang, F.; Huang, D.; Li, D.; Lin, S.; Muyeen, S.M.; Zhai, H. Data-driven load frequency control based on multi-agent reinforcement learning with attention mechanism. IEEE Trans. Power Syst. 2023, 38, 5560–5569. [Google Scholar] [CrossRef]
- Xi, L.; Yu, L.; Xu, Y.; Wang, S.; Chen, X. A novel multi-agent DDQN-AD method-based distributed strategy for automatic generation control of Integrated Energy Systems. IEEE Trans. Sustain. Energy 2020, 11, 2417–2426. [Google Scholar] [CrossRef]
- Omidshafiei, S.; Kim, D.-K.; Liu, M.; Tesauro, G.; Riemer, M.; Amato, C. Learning to teach in cooperative multiagent reinforcement learning. Proc. AAAI Conf. Artif. Intell. 2019, 33, 6128–6136. [Google Scholar] [CrossRef][Green Version]
- Li, J.; Zhou, T.; Cui, H. Brain-inspired deep meta-reinforcement learning for active coordinated fault-tolerant load frequency control of multi-area grids. IEEE Trans. Autom Sci Eng. 2024, 21, 2518–2530. [Google Scholar] [CrossRef]
- Yin, L.; Yu, T.; Zhou, L. Design of a novel smart generation controller based on deep Q learning for large-scale interconnected power system. J. Energy Chem. 2018, 144, 04018033. [Google Scholar] [CrossRef]
- Yan, Z.; Xu, Y. Data-driven load frequency control for stochastic power systems: A deep reinforcement learning method with Continuous Action Search. IEEE Trans. Power Syst. 2019, 34, 1653–1656. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).