Scalable Graph Coloring Optimization Based on Spark GraphX Leveraging Partition Asymmetry
Abstract
1. Introduction
- (1)
- Symmetry-aware EdgePartition1D initialization: The input graph is loaded into GraphX and partitioned using the EdgePartition1D strategy. Within each partition, vertices are pre-colored according to local degree ranking. This produces a high-quality initial configuration that accounts for inherent structural symmetries and effectively manages regions of high structural density arising from asymmetry.
- (2)
- Partitioned repaint stage: Each partition independently reassigns its vertices to the smallest available colors in parallel, obviating costly global iterations and substantially curtailing inter-partition messaging.
- (3)
- Minimum-based merge for boundary resolution: Vertices spanning multiple partitions exchange only the minimal valid color in localized merge operations, thereby avoiding full-graph synchronization.
- (4)
- Two-stage MapReduce conflict detection and correction pipeline: A concluding Spark MapReduce job enumerates residual conflicts and applies targeted corrections in a single pass over the conflict set, ensuring convergence without traversing the entire graph.
2. Motivation

3. Algorithm Design
3.1. Design Philosophy
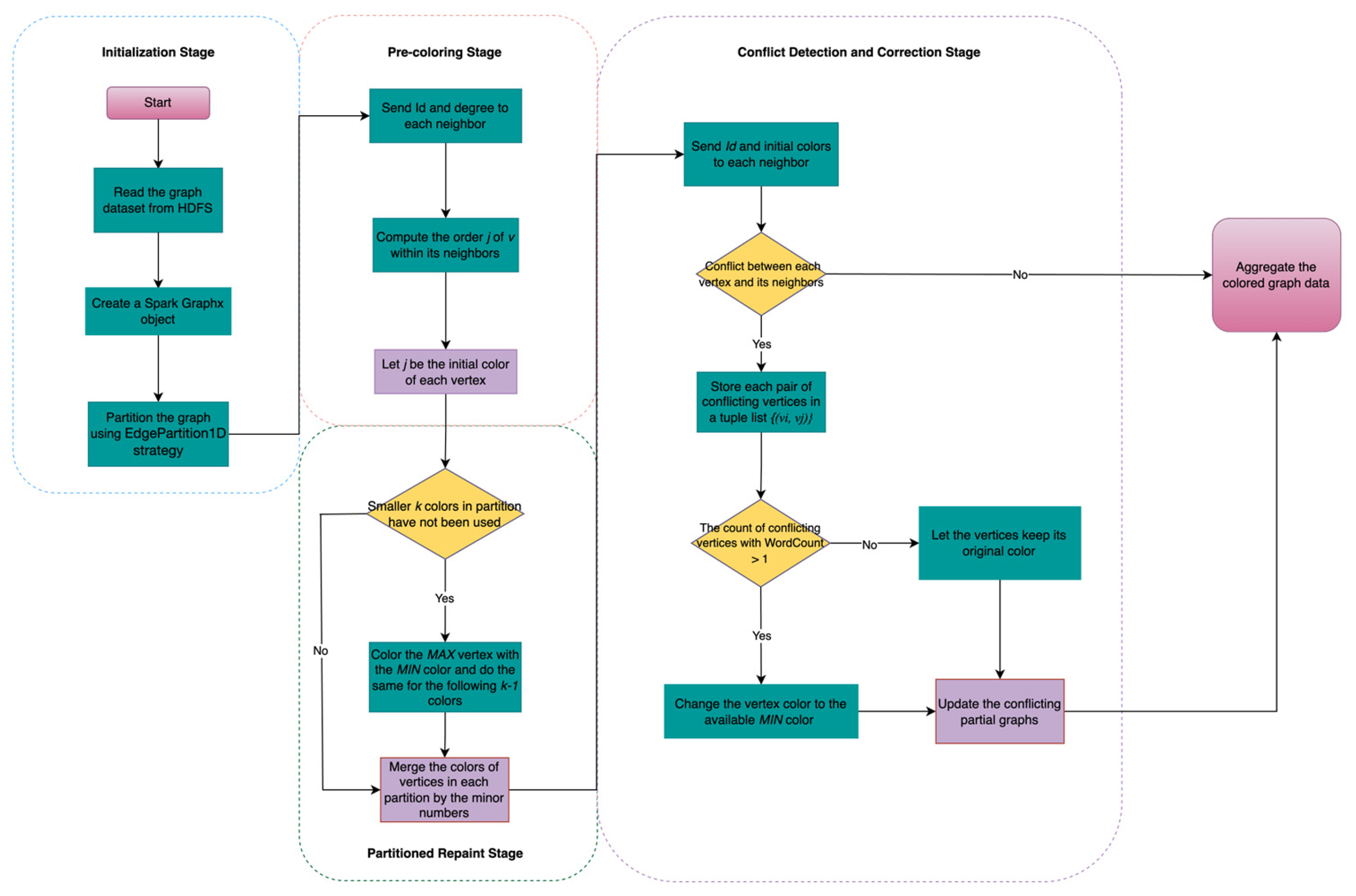
3.2. Spark-Based Graph Coloring Algorithm
| Algorithm 1. Spardex: a high-parallelism graph coloring algorithm |
| Require: Graph, ; Ensure: Graph coloring plan, ; and the colors used for coloring graph ; 1: function (Vertex, ; message, ) 2: ← the_biggest_vertexId() 3: for ( = 1; < ; ++) 4: for (message: ) do 5: ← 1; 6: if ( < ) (( = ) ( < )) ++; 7: end function 8: function (, ) 9: k ← 0; ← ; 10: for (partition = 0; partition < ; partition++) 11: for ( = ; > 0; - -) 12: if ( ) 13: stack ← ; 14: ++; 15: if ( == ) return 0; 16: else for ( = ; > ; - -) 17: pull (); 18: ← ; 19: for ( = 1; < ; ++) 20: while () ← ; 21: end function 22: function (Tuple, ) 23: for ( = 1; < ; ++) 24: if ( == ) 25: ← Tuple (, ); 26: (); 27: ← (); ← .filter (. _ > 1) 28: while () do in parallel: () 29: end function |
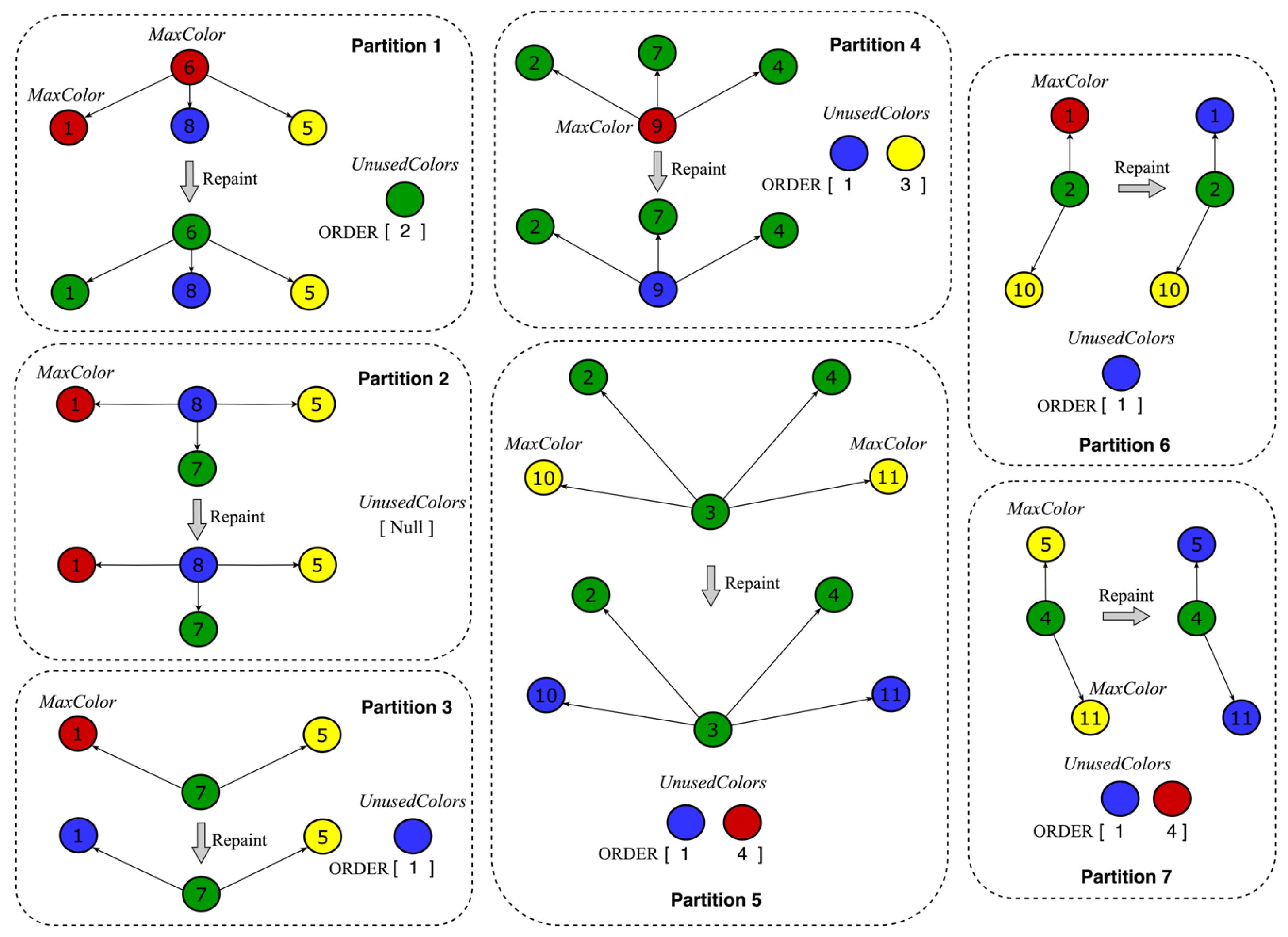
- Initial Conditions and Repainting Strategy
- 2.
- Definition of Conflict Vertices
- 3.
- Critical Conflict Vertices
- 4.
- Assumption of No Critical Conflict Vertices
- 5.
- Analysis After Repainting Within the Partition
- 6.
- Conflicts After Merging
- 7.
- Emergence of Contradictions
- Map Phase: Each executor processes its assigned vertices and flags repeated colors in local partitions.
- Reduce Phase: The results from each executor are combined to generate a final list of conflict vertices across all partitions.
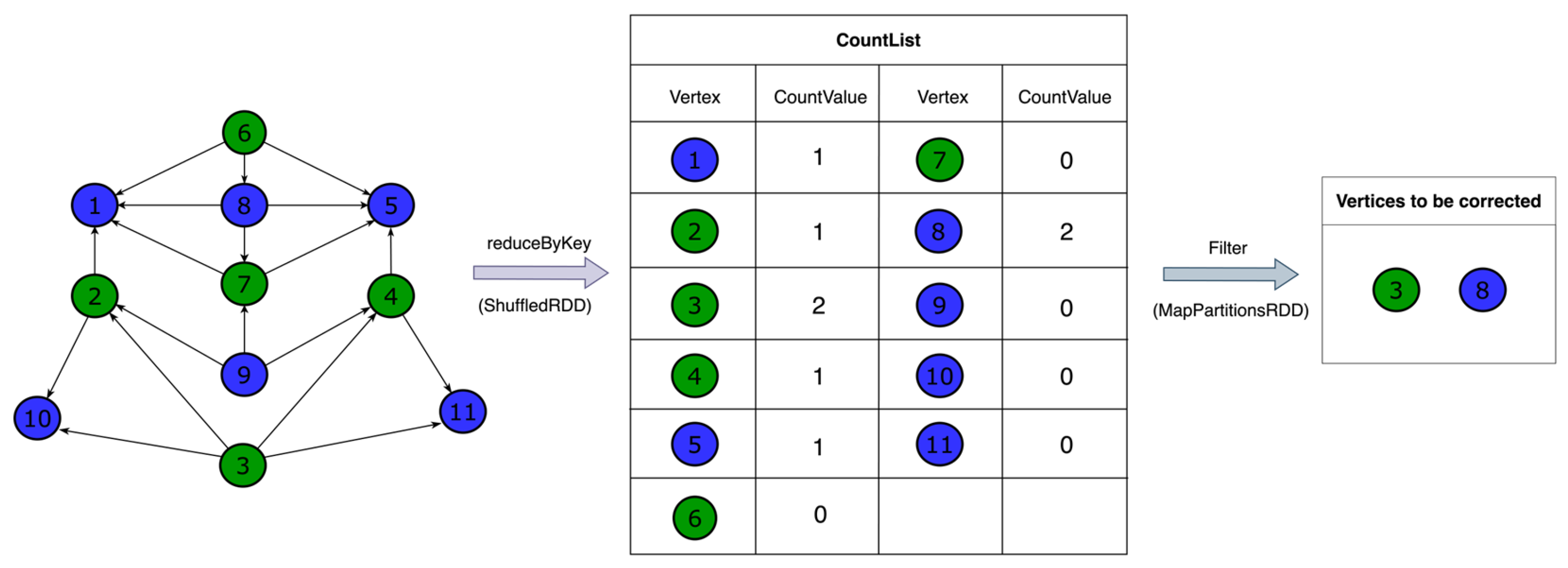
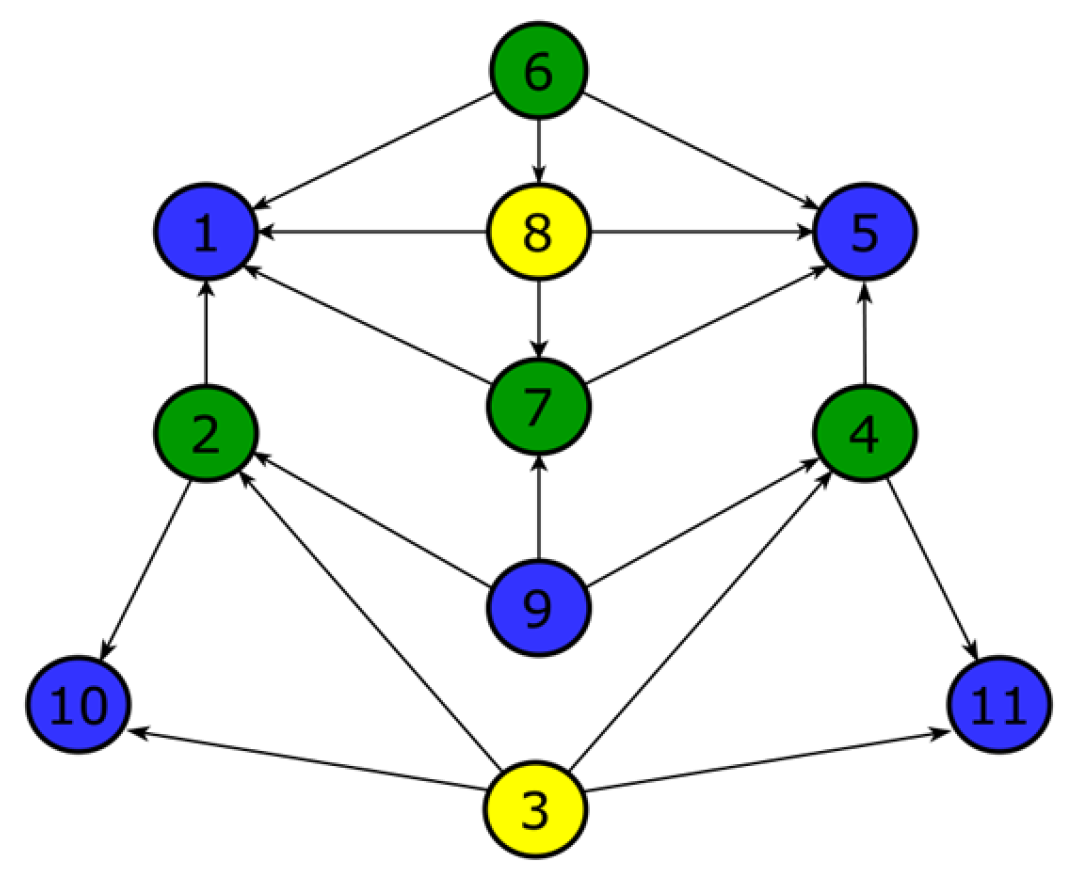
3.3. Illustrated Example
4. Optimization Technique
4.1. Data Locality Optimization in Spardex
4.2. Memory Management in Spardex
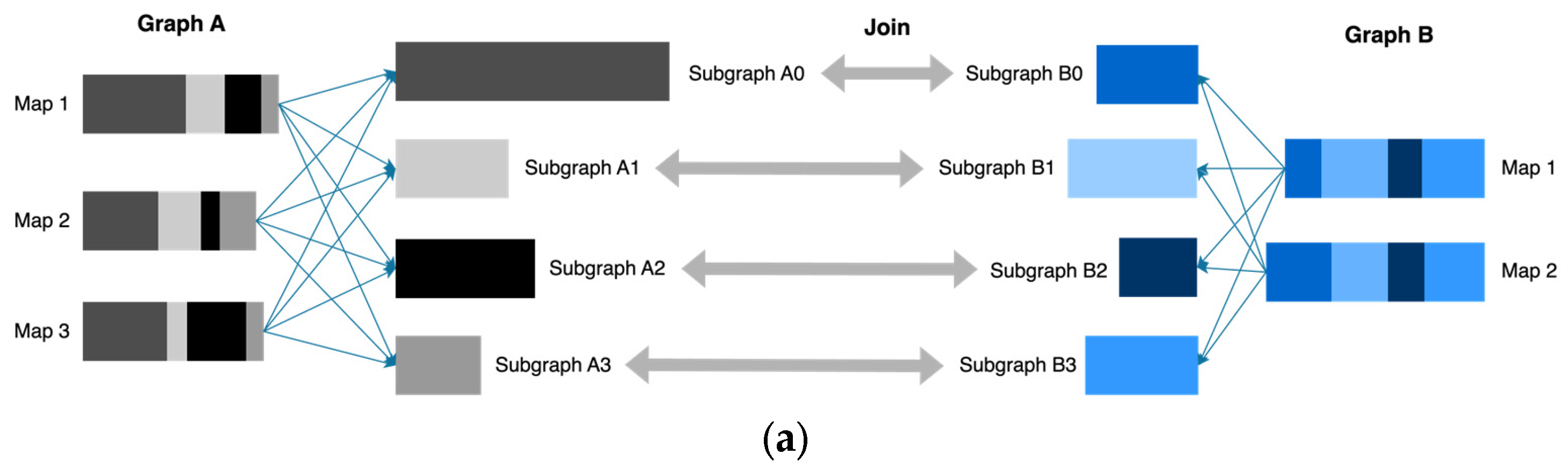
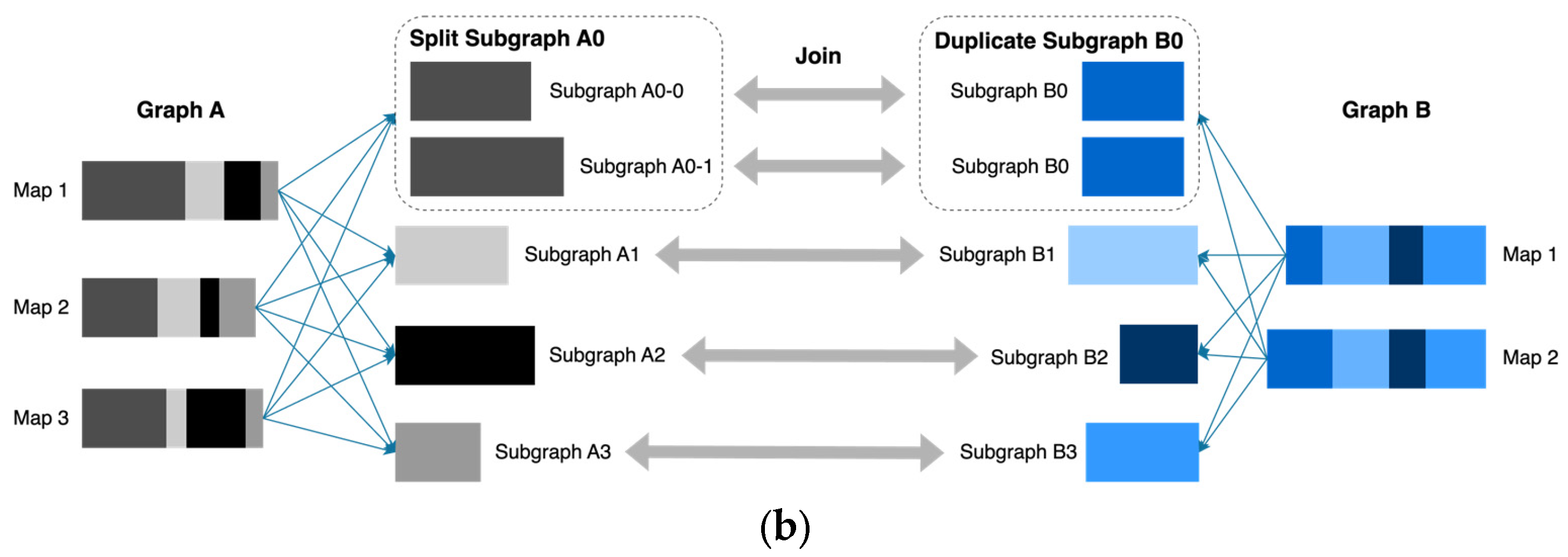
4.3. Dynamical Optimization for the Data Skew Caused by Join in Spardex
5. Evaluation
5.1. Experimental Setup
5.2. The Algorithms for Comparison
5.3. Experimental Results and Discussion
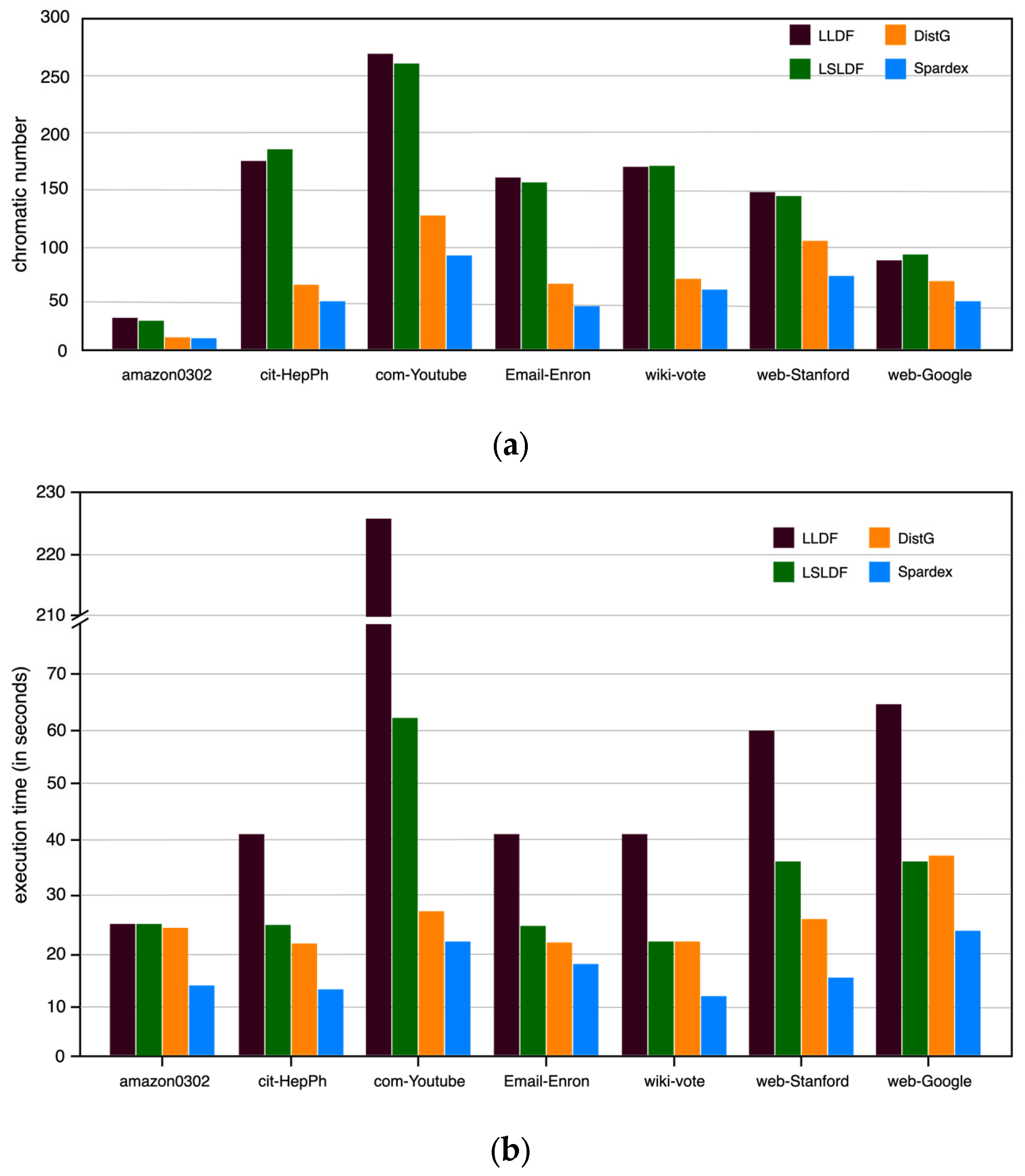
5.3.1. Performance Comparison
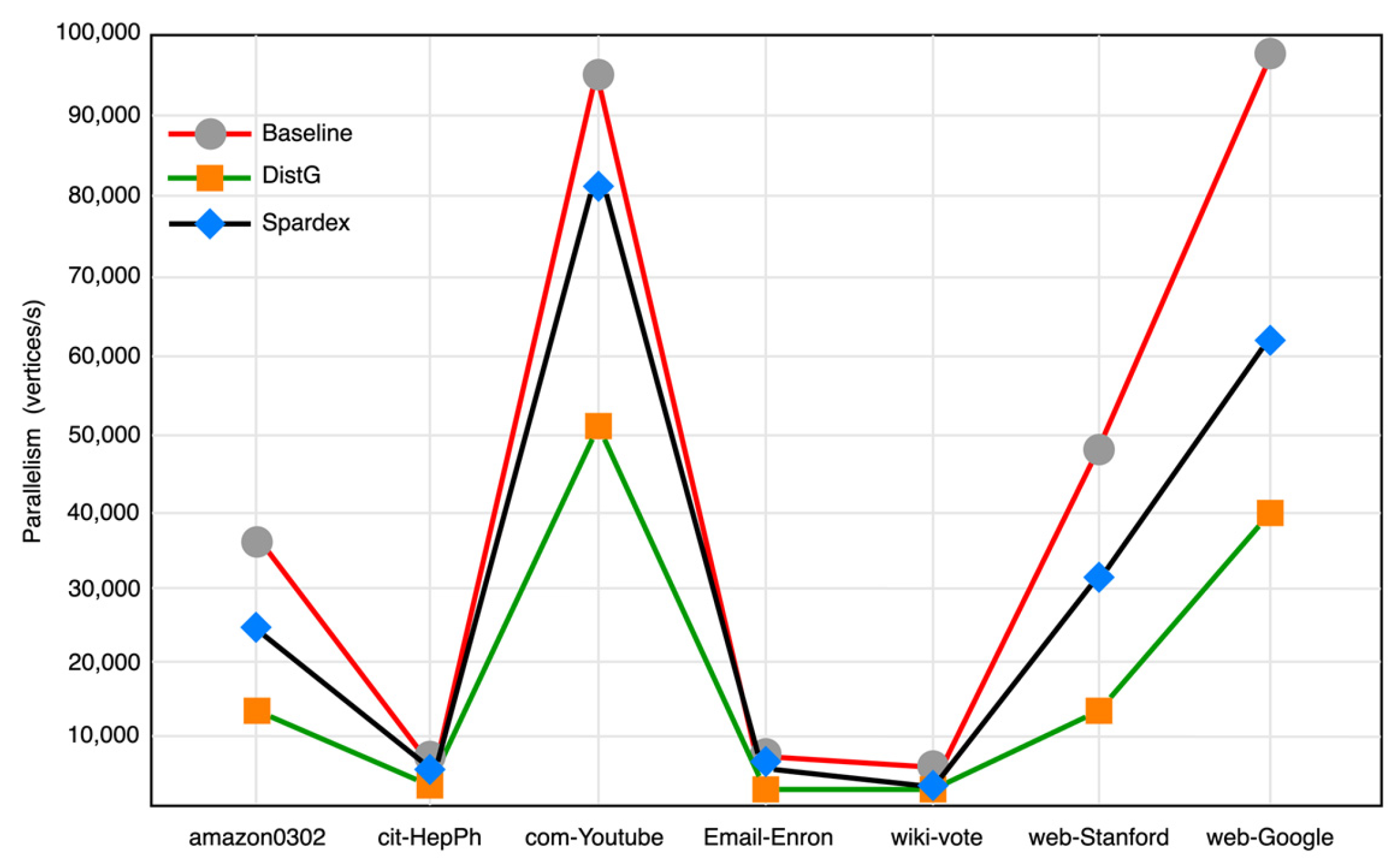
5.3.2. Parallelism Evaluation
5.3.3. Complexity Analysis and Resource Usage
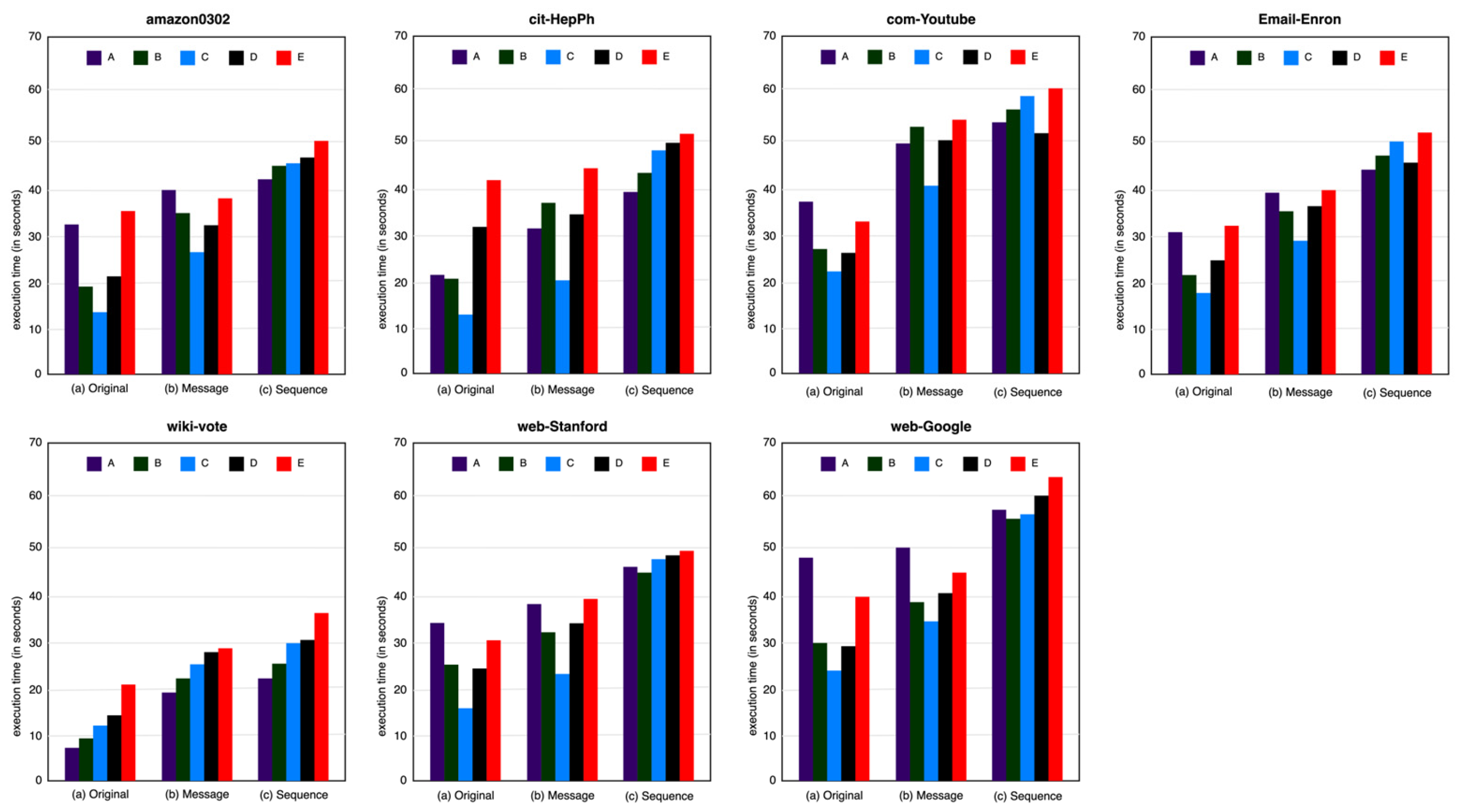
5.4. Running Spardex on Different Cluster Configurations
6. Conclusions and Future Opportunities
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| VGCP | Vertex Graph Coloring Problem |
| HDFS | Hadoop Distributed File System |
| AQE | Adaptive Query Execution |
| LLDF | Local Largest Degree First |
| LSLDF | Local Smallest Largest Degree First |
References
- Jones, M.T.; Plassmann, P.E. A parallel graph coloring heuristic. SIAM J. Sci. Comput. 1993, 14, 654–669. [Google Scholar] [CrossRef]
- Luby, M. A simple parallel algorithm for the maximal independent set problem. SIAM J. Comput. 1986, 15, 1036–1053. [Google Scholar] [CrossRef]
- Bui, T.N.; Jones, C. Finding good approximate vertex and edge partitions is NP-hard. Inf. Process. Lett. 1993, 42, 153–159. [Google Scholar] [CrossRef]
- Berman, P.; Karpinski, M. On some tighter inapproximability results. In Proceedings of the Twenty-Sixth Annual ACM Symposium on Theory of Computing, Prague, Czech Republic, 11–15 July 1999; Springer: Berlin/Heidelberg, Germany, 1999; pp. 301–309. [Google Scholar]
- Naumov, M.; Castonguay, P.; Cohen, J. Parallel Graph Coloring with Applications to the Incomplete-LU Factorization on the GPU; Nvidia White Paper; May 2015. Available online: https://research.nvidia.com/sites/default/files/pubs/2015-05_Parallel-Graph-Coloring/nvr-2015-001.pdf (accessed on 26 May 2024).
- Misra, J.; Gries, D. A constructive proof of Vizing’s theorem. Inf. Process. Lett. 1992, 41, 131–133. [Google Scholar] [CrossRef]
- Brighen, A.; Slimani, H.; Rezgui, A.; Kheddouci, H. A new distributed graph coloring algorithm for large graphs. Clust. Comput. 2024, 27, 875–891. [Google Scholar] [CrossRef]
- Schuetz, M.J.A.; Brubaker, J.K.; Zhu, Z.; Katzgraber, H.G. Graph coloring with physics-inspired graph neural networks. Phys. Rev. Res. 2022, 4, 043131. [Google Scholar] [CrossRef]
- Grosset, A.V.P.; Zhuand, P.; Venkatasubramanian, S.; Hall, M. Evaluating graph coloring on GPUs. In Proceedings of the PPoPP’11 Proceedings of the 16th ACM Symposium on Principles and Practice of Parallel Programming, San Antonio, TX, USA, 12–16 February 2011; ACM SIGPLAN Notices-PPoPP’11. Volume 46, pp. 297–298. [Google Scholar] [CrossRef]
- Zheng, Z.; Shi, X.; He, L.; Jin, H.; Wei, S.; Dai, H.; Peng, X. Feluca: A two-stage graph coloring algorithm with color-centric paradigm on GPU. IEEE Trans. Parallel Distrib. Syst. 2020, 32, 160–173. [Google Scholar] [CrossRef]
- Che, S.; Rodgers, G.; Beckmann, B.; Reinhardt, S. Graph coloring on the GPU and some techniques to improve load imbalance. In Proceedings of the 2015 IEEE International Parallel and Distributed Processing Symposium Workshop, Hyderabad, India, 25–29 May 2015; pp. 610–617. [Google Scholar]
- Boman, E.G.; Devine, K.D.; Rajamanickam, S. Scalable matrix computations on large scale-free graphs using 2D graph partitioning. In Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, Denver, CO, USA, 17–22 November 2013; pp. 1–12. [Google Scholar] [CrossRef]
- Gandhi, N.M.; Misra, R. Performance comparison of parallel graph coloring algorithms on bsp model using hadoop. In Proceedings of the 2015 International Conference on Computing, Networking and Communications (ICNC), Garden Grove, CA, USA, 25–29 May 2015; pp. 110–116. [Google Scholar] [CrossRef]
- Sharafeldeen, A.; Alrahmawy, M.; Elmougy, S. Graph partitioning MapReduce-based algorithms for counting triangles in large-scale graphs. Sci. Rep. 2023, 13, 166. [Google Scholar] [CrossRef]
- Leighton, F.T. Introduction to Parallel Algorithms and Architectures: Arrays, Trees, Hypercubes; Elsevier: Amsterdam, The Netherlands, 1985. [Google Scholar]
- Gebremedhin, A.H.; Manne, F.; Pothen, A. What color is your Jacobian? Graph coloring for computing derivatives. SIAM Rev. 2002, 44, 347–355. [Google Scholar] [CrossRef]
- Alon, N.; Kahale, N. A spectral technique for coloring random 3-colorable graphs. SIAM J. Comput. 1997, 26, 1733–1748. [Google Scholar] [CrossRef]
- Gavril, F. Algorithms for a maximum clique and a maximum independent set of a circle graph. Networks 1972, 2, 211–221. [Google Scholar] [CrossRef]
- Galinier, P.; Hao, J.K. Hybrid Evolutionary Algorithms for Graph Coloring. J. Comb. Optim. 1999, 3, 379–397. [Google Scholar] [CrossRef]
- Eiben, A.E.; Van Der Hauw, J.K.; van Hemert, J.I. Graph coloring with adaptive evolutionary algorithms. J. Heuristics 1998, 4, 25–46. [Google Scholar] [CrossRef]
- Vizing, V.G. On an estimate of the chromatic class of a p-graph. Diskret. Analiz 1964, 3, 25–30. [Google Scholar]
- Chung, F.R.K.; Lu, L. The average distances in random graphs with given expected degrees. Proc. Natl. Acad. Sci. USA 2002, 99, 15879–15882. [Google Scholar] [CrossRef]
- Edmonds, J. Paths, Trees, and Flowers. Can. J. Math. 1965, 17, 449–467. [Google Scholar] [CrossRef]
- Karypis, G.; Kumar, V. A fast and high quality multilevel scheme for partitioning irregular graphs. SIAM J. Sci. Comput. 1998, 20, 359–392. [Google Scholar] [CrossRef]
- Gibbons, P.B. A more practical PRAM model. In Proceedings of the First Annual ACM Symposium on Parallel Algorithms and Architectures, Santa Fe, NM, USA, 18–21 June 1989; pp. 158–168. [Google Scholar]
- Kawarabayashi, K.; Khoury, S.; Schild, A.; Schwartzman, G. Improved distributed approximations for maximum independent set. arXiv 2019, arXiv:1906.11524. [Google Scholar] [CrossRef]
- Tarjan, R.E. Depth-first search and linear graph algorithms. SIAM J. Comput. 1972, 1, 146–160. [Google Scholar] [CrossRef]
- Hopcroft, J.E.; Tarjan, R.E. Algorithm 447: Efficient algorithms for graph manipulation. Commun. ACM 1973, 16, 372–378. [Google Scholar] [CrossRef]
- Karger, D.R.; Stein, C. A new approach to the minimum cut problem. J. ACM 1996, 43, 601–640. [Google Scholar] [CrossRef]
- Tarjan, R.E. Efficiency of a good but not linear set union algorithm. J. ACM 1975, 22, 215–225. [Google Scholar] [CrossRef]
- Geng, Y.; Shi, X.; Pei, C.; Jin, H.; Jiang, W. LCS: An Efficient Data Eviction Strategy for Spark. Int. J. Parallel Prog. 2017, 45, 1285–1297. [Google Scholar] [CrossRef]
- Yao, Y. A Partition Model of Granular Computing. In Transactions on Rough Sets I. Lecture Notes in Computer Science; Peters, J.F., Skowron, A., Grzymała-Busse, J.W., Kostek, B., Świniarski, R.W., Szczuka, M.S., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; Volume 3100. [Google Scholar] [CrossRef]
- Adinew, D.M.; Zhou, S.; Liao, Y. Spark performance optimization analysis in memory management with deploy mode in standalone cluster computing. In Proceedings of the 2020 IEEE 36th International Conference on Data Engineering (ICDE), Dallas, TX, USA, 20–24 April 2020; pp. 2049–2053. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, Y.; Zhang, L.; Cao, N.; Pang, C. An Improved Memory Cache Management Study Based on Spark. Comput. Mater. Contin. 2018, 56, 415–431. [Google Scholar]
- Gannon, D.; Jalby, W.; Gallivan, K. Strategies for cache and local memory management by global program transformation. In International Conference on Supercomputing; Springer: Berlin/Heidelberg, Germany, 1987; pp. 229–254. [Google Scholar]
- Tang, Z.; Zeng, A.; Zhang, X.; Yang, L.; Li, K. Dynamic memory-aware scheduling in spark computing environment. J. Parallel Distrib. Comput. 2020, 141, 10–22. [Google Scholar] [CrossRef]
- Perez, T.B.; Zhou, X.; Cheng, D. Reference-distance eviction and prefetching for cache management in spark. In Proceedings of the 47th International Conference on Parallel Processing, Eugene, OR, USA, 13–16 August 2018; pp. 1–10. [Google Scholar] [CrossRef]
- Zhou, P.; Ruan, Z.; Fang, Z.; Shand, M.; Roazen, D.; Cong, J. Doppio: I/o-aware performance analysis, modeling and optimization for in-memory computing framework. In Proceedings of the 2018 IEEE International Symposium on Performance Analysis of Systems and Software (ISPASS), Belfast, UK, 2–4 April 2018; pp. 22–32. [Google Scholar] [CrossRef]
- Yang, Z.; Jia, D.; Ioannidis, S.; Mi, N.; Sheng, B. Intermediate data caching optimization for multi-stage and parallel big data frameworks. In Proceedings of the 2018 IEEE 11th International Conference on Cloud Computing (CLOUD), San Francisco, CA, USA, 2–7 July 2018; pp. 277–284. [Google Scholar] [CrossRef]
- Huang, S.; Huang, J.; Dai, J.; Xie, T.; Huang, B. The HiBench benchmark suite: Characterization of the MapReduce-based data analysis. In Proceedings of the 2010 IEEE 26th International Conference on Data Engineering Workshops (ICDEW 2010), Long Beach, CA, USA, 1–6 March 2010; pp. 41–51. [Google Scholar] [CrossRef]
- Bhattacharjee, A. Large-reach memory management unit caches. In Proceedings of the 46th Annual IEEE/ACM International Symposium on Microarchitecture (MICRO-46), Davis, CA, USA, 7–11 December 2013; Association for Computing Machinery: New York, NY, USA, 2013; pp. 383–394. [Google Scholar] [CrossRef]
- Leskovec, J.; Krevl, A. Snap Datasets: Stanford Large Network Dataset Collection. 2014. Available online: http://snap.stanford.edu/data (accessed on 26 May 2024).
- Blelloch, G.E.; Maggs, B.M. Parallel algorithms. Commun. ACM 1996, 39, 85–97. [Google Scholar] [CrossRef]
- Alon, N.; Spencer, J.H. The Probabilistic Method; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Papadimitriou, C.H. Computational complexity. In Encyclopedia of Computer Science; John Wiley and Sons Ltd.: Hoboken, NJ, USA, 2003; pp. 260–265. [Google Scholar]
- Matula, D.W.; Beck, L.L. Smallest-last ordering and clustering and graph coloring algorithms. J. ACM 1983, 30, 417–427. [Google Scholar] [CrossRef]
- Arora, S.; Safra, S. Probabilistic checking of proofs: A new characterization of NP. J. ACM 1998, 45, 70–122. [Google Scholar] [CrossRef]
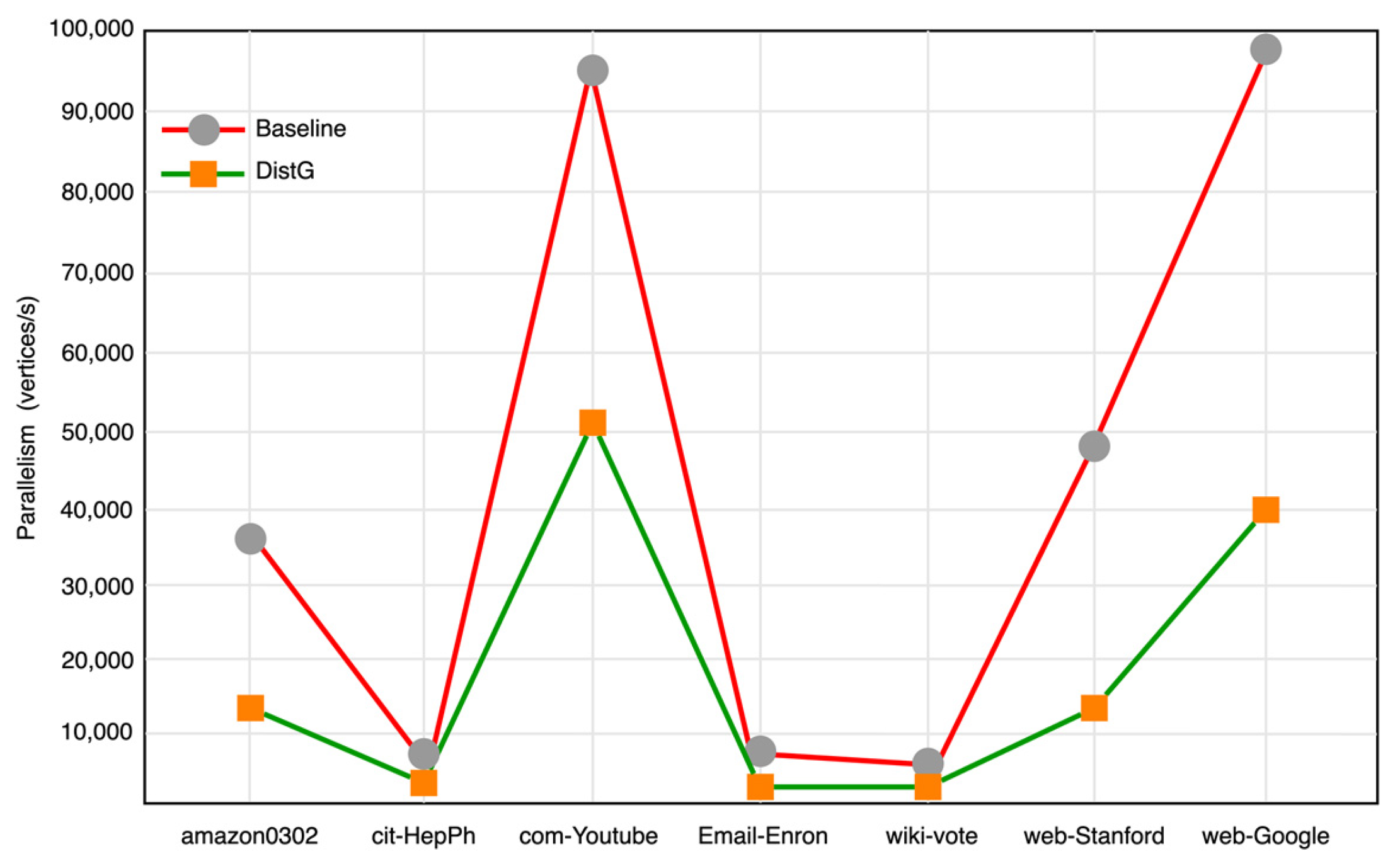


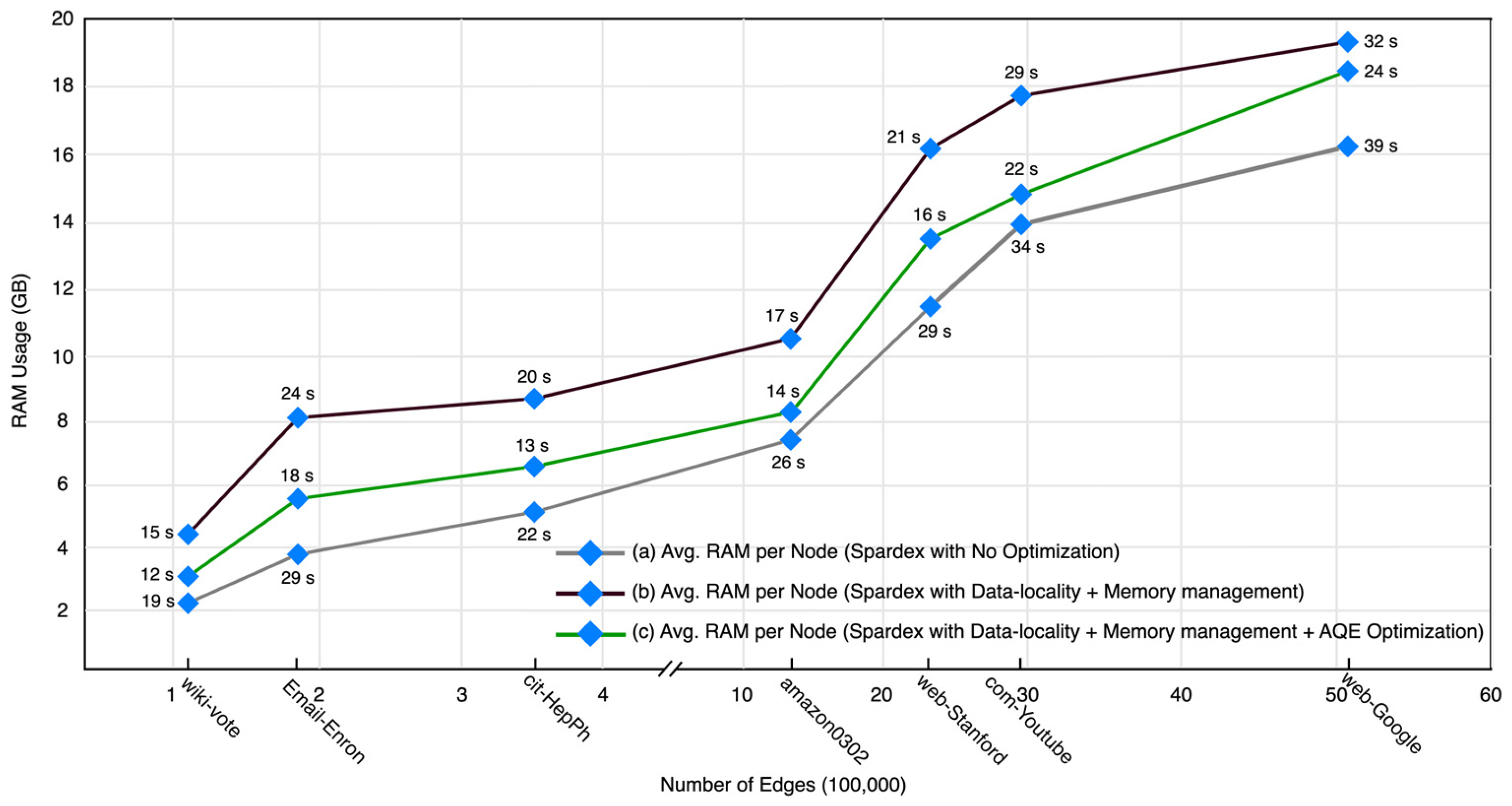
| Dataset | Vertices | Edges | Max_degree | Partitions | Direction |
|---|---|---|---|---|---|
| amazon0302 | 262,111 | 1,234,877 | 420 | 257,570 | Directed |
| Cit-HepPh | 27,770 | 352,807 | 2468 | 25,059 | Directed |
| com-Youtube | 1,134,890 | 2,987,624 | 28,754 | 374,785 | Undirected |
| email-Enron | 36,692 | 183,831 | 1383 | 36,692 | Undirected |
| wiki-Vote | 7115 | 103,689 | 1065 | 6110 | Directed |
| web-Stanford | 281,903 | 2,312,497 | 38,625 | 281,731 | Directed |
| web-Google | 875,713 | 5,105,039 | 6332 | 739,454 | Directed |
| System Parameter | Description | Value |
|---|---|---|
| Spark.master | The cluster manager to connect to: “yarn” indicates that Spark runs on the Hadoop YARN resource scheduler. | yarn |
| Spark.executor.cores | The number of cores used on each executor to run tasks. | 3 |
| Spark.driver.cores | Number of cores used for the driver process. | 3 |
| Spark.executor.memory | Total amount of memory used per executor process. | 7 g |
| Spark.driver.memory | Amount of memory used for the driver process. | 2 g |
| Spark.dynamicAllocation.enabled | Whether Spark automatically adjusts the number of executors and the number of resources allocated to each executor based on the workload of the application. | true |
| Spark.shuffle.service.enabled | Whether the external shuffle service is set as a standalone component that manages shuffle data (intermediate data exchanged between tasks) for each node in a Spark cluster | true |
| Spark.serializer | “Spark.serializer” specifies the serialization mechanism Spark uses when transmitting data over the network or when storing it in memory. | org.apache.spark.serializer.KryoSerializer |
| Algorithm | amazon0302 | cit-HepPh | com-Youtube | email-Enron | wiki-Vote | web-Stanford | web-Google | Speedup/Decrease | |
|---|---|---|---|---|---|---|---|---|---|
| Spardex | time(s) | 14 | 13 | 22 | 18 | 12 | 16 | 24 | \ |
| colors | 11 | 51 | 88 | 49 | 64 | 77 | 54 | ||
| LLDF [6] | time(s) | 26 | 41 | 226 | 41 | 41 | 60 | 65 | 1.86–10.27 |
| colors | 32 | 177 | 267 | 160 | 172 | 149 | 84 | 36–71% | |
| LSLDF [6] | time(s) | 26 | 25 | 62 | 25 | 22 | 36 | 36 | 1.39–2.82 |
| colors | 29 | 183 | 262 | 157 | 173 | 145 | 87 | 38–72% | |
| DistG [7] | time(s) | 25 | 22 | 27 | 22 | 22 | 26 | 27 | 1.13–1.83 |
| colors | 12 | 65 | 128 | 69 | 74 | 104 | 74 | 8–31% | |
| System Parameter | Spark.executor.cores | Spark.executor.memory | Spark.driver.cores | Spark.driver.memory | Executors in Each Node | |
|---|---|---|---|---|---|---|
| Configuration Types | ||||||
| A | 6 | 14 GB | 3 | 2 GB | 2 | |
| B | 4 | 9 GB | 3 | 2 GB | 3 | |
| C | 3 | 7 GB | 3 | 2 GB | 4 | |
| D | 2 | 4.5 GB | 3 | 2 GB | 6 | |
| E | 1 | 2.5 GB | 3 | 2 GB | 12 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, Y.; Li, X.; Yuan, T.; Chen, S. Scalable Graph Coloring Optimization Based on Spark GraphX Leveraging Partition Asymmetry. Symmetry 2025, 17, 1177. https://doi.org/10.3390/sym17081177
Shen Y, Li X, Yuan T, Chen S. Scalable Graph Coloring Optimization Based on Spark GraphX Leveraging Partition Asymmetry. Symmetry. 2025; 17(8):1177. https://doi.org/10.3390/sym17081177
Chicago/Turabian StyleShen, Yihang, Xiang Li, Tao Yuan, and Shanshan Chen. 2025. "Scalable Graph Coloring Optimization Based on Spark GraphX Leveraging Partition Asymmetry" Symmetry 17, no. 8: 1177. https://doi.org/10.3390/sym17081177
APA StyleShen, Y., Li, X., Yuan, T., & Chen, S. (2025). Scalable Graph Coloring Optimization Based on Spark GraphX Leveraging Partition Asymmetry. Symmetry, 17(8), 1177. https://doi.org/10.3390/sym17081177







